Predicting reaction conditions from limited data through active transfer learning

Abstract

Transfer and active learning have the potential to accelerate the development of new chemical reactions, using prior data and new experiments to inform models that adapt to the target area of interest. This article shows how specifically tuned machine learning models, based on random forest classifiers, can expand the applicability of Pd-catalyzed cross-coupling reactions to types of nucleophiles unknown to the model. First, model transfer is shown to be effective when reaction mechanisms and substrates are closely related, even when models are trained on relatively small numbers of data points. Then, a model simplification scheme is tested and found to provide comparative predictivity on reactions of new nucleophiles that include unseen reagent combinations. Lastly, for a challenging target where model transfer only provides a modest benefit over random selection, an active transfer learning strategy is introduced to improve model predictions. Simple models, composed of a small number of decision trees with limited depths, are crucial for securing generalizability, interpretability, and performance of active transfer learning.

---

Introduction

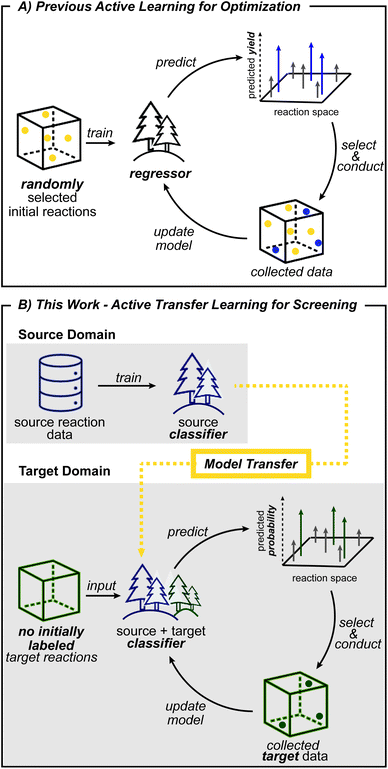
Computers are becoming increasingly capable of performing high-level chemical tasks.^1–4 Machine learning approaches have demonstrated viable retrosynthetic analyses,^5–7 product prediction,^8–11 reaction condition suggestion,^12–16 prediction of stereoselectivity,^17–20 regioselectivity,^19,21–24 and reaction yield^25,26 and optimization of reaction conditions.^27–30 These advances allow computers to assist synthesis planning for functional molecules using well-established chemistry. For machine learning to aid the development of new reactions, a model based on established chemical knowledge must be able to generalize its predictions to reactivity that lies outside of the dataset. However, because most supervised learning algorithms learn how features (e.g. reaction conditions) within a particular domain relate to an outcome (e.g. yield), the model is not expected to be accurate outside its domain. This situation requires chemists to consider other machine learning methods for navigating new reactivity.

Expert knowledge based on known reactions plays a central role in the design of new reactions. The assumption that substrates with chemically similar reaction centers have transferable performance provides a plausible starting point for experimental exploration. This concept of chemical similarity, together with literature data, guides expert chemists in the development of new reactions. Transfer learning, which assumes that data from a nearby domain, called the source domain, can be leveraged to model the problem of interest in a new domain, called the target domain,³¹ emulates a tactic commonly employed by human chemists.

Transfer learning is a promising strategy when limited data is available in the domain of interest, but a sizeable dataset is available in a related domain.^31,32 Models are first created using the source data, then transferred to the target domain using various algorithms.^19,33–35 For new chemical targets where no labeled data is available, the head start in predictivity a source model can provide becomes important. However, when a shift in distribution of descriptor values occurs (e.g., descriptors outside of the original model ranges) in the target data, making predictions becomes challenging. For such a situation, the objective of transfer learning becomes training a model that is as predictive in the target domain as possible.^31,36 Toward this end, cross-validation is known to improve generalizability by providing a procedure to avoid overfitting on the training data.³⁷ The reduction of generalization error, however, may not be sufficient outside the source domain. Accordingly, new methods that enhance the applicability of a transferred model to new targets would be beneficial for reaction condition prediction.

Another machine learning method that can help tackle data scarcity is active learning. By making iterative queries of labeling a small number of datapoints, active learning updates models with knowledge from newly labeled data. As a result, exploration is guided into the most informative areas and avoids collection of unnecessary data.^38,39 Active learning is therefore well-suited for reaction development, which greatly benefits from efficient exploration and where chemists conduct the next batch of reactions based on previous experimental results. Based on this analogy, reaction optimization^27,28 and reaction condition identification⁴⁰ have been demonstrated to benefit from active learning. However, these prior works initiate exploration with randomly selected data points (Fig. 1A) which does not leverage prior knowledge, and therefore does not reflect how expert chemists initiate exploration. Initial search directed by transfer learning could identify productive regions early on, which in turn will help build more useful models for subsequent active learning steps.

Fig. 1 Workflow of (A) previous active learning studies and (B) this work. Distinctions that arise from the different problem setting and incorporation of transfer learning are highlighted bold in (B).

To align transfer and active learning closer to how expert chemists develop new reactions, appropriate chemical reaction data is necessary.⁴¹ Available datasets⁴² that are often used for machine learning are overrepresented by positive reactions, failing to reflect reactions with negative outcomes. On the other hand, reaction condition screening data of methodology reports—which chemists often refer to—only constitute a sparse subset of possible reagent combinations, making it hard for machine learning algorithms to extract meaningful knowledge.⁴³

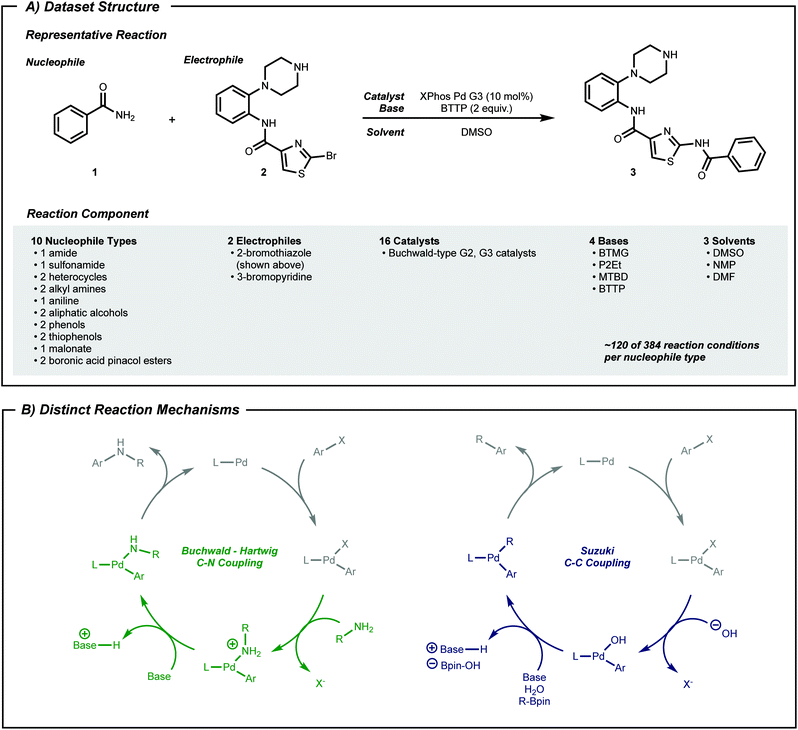
High-throughput experimentation^44–46 (HTE) data can fill this gap. HTE provides reaction data^{16,25,27,47,48} with reduced variations in outcome due to systematic experimentation. Pd-catalyzed coupling data was therefore collected from reported work using nanomole scale HTE in 1536 well plates.^49–51 In the current work, subsets of this data, classified by nucleophile type as shown in Fig. 2A, were selected to a dataset size of approximately 100 datapoints, which captured both positive and negative reaction performance.

Fig. 2 (A) Structure of reactions in the dataset. A total of 1220 reactions across 10 types of nucleophiles are in the dataset. (B) Two distinct mechanisms included in the dataset. Nucleophilic aromatic substitution is another mechanism that is involved in the dataset, but it is not shown here.

Reaction condition exploration could be made more efficient if algorithmic strategies could leverage prior knowledge. Toward this goal, model transfer and its combination with active learning were evaluated. Taking advantage of diverse campaigns, this study will show that transferred models can be effective in applying prior reaction conditions to a new substrate type under certain conditions. Next, the source model's ability to predict reaction conditions with new combinations of reagents will also be evaluated. Lastly, challenging scenarios are considered where productive reaction conditions for one class of substrate are not useful for the substrate of interest. Active transfer learning, which uses a transferred source model as a starting point for active learning in the target domain, however, overcomes the limited predictability of the transferred model and efficiently identifies desired reaction conditions.

Results

Predicting reaction conditions for a new nucleophile in Pd-catalyzed cross-coupling reactions

To expand the applicability of a transformation, chemists often start by applying known reaction conditions to a substrate with a new reactive group. For machine learning guided exploration, this is analogous to a model—built from prior data—making suggestions for the target substrate. Therefore, the first procedure herein tests whether a model can predict the applicability of known above-the-arrow reaction conditions to a new substrate, before any new data is collected. Pd-catalyzed cross-coupling reactions will serve as the testing grounds.

Phosphine-ligated palladium can catalyze reactions between aryl halides and various nucleophiles to form C–X (X = C,⁵² N,⁵³ O,⁵⁴ S⁵⁵) bonds. Despite similar reaction components across these classes of reactions (Fig. 2A), the mechanism may be qualitatively different depending on the nucleophile (Fig. 2B). Moreover, different substrate pairs in a single class of reacting nucleophiles, such as anilines or secondary alkyl amines, may require different combinations of phosphine ligand and base for optimal performance.

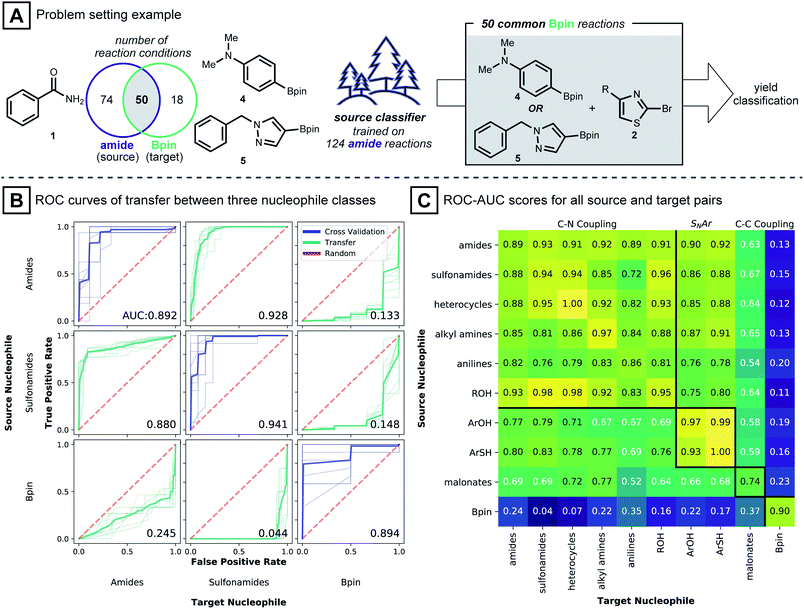
To study the situation of using a model to transfer information between distinct nucleophile types, amide, sulfonamide and pinacol boronate esters were selected as nucleophile types. For each nucleophile type, random forest classifier models were trained under cross-validation (see Computational Details). These models were used to predict the outcome of reactions in the other nucleophile sets. To transfer known reaction conditions to the new nucleophile types, we focused on combinations of electrophile, catalyst, base and solvent that were common between source and target datasets (Fig. 3A). A binary yield system was used to classify success of the reaction (0% yield vs. >0% yield). Classification performances were evaluated with the receiver operating characteristic area under the curve (ROC-AUC). For the ROC-AUC, perfect predictions have a value of 1.0 and random guessing leads to a value of 0.5.

Fig. 3 (A) Scheme of a model transfer experiment between amide source and boronic acid pinacol ester target. (B) Trellis plot of ROC-AUC curves. Diagonals correspond to cross-validation scores when source models were trained. Off-diagonals show the performance of source models predicting target reactions with reaction conditions used in the training set. (C) Heatmap of average ROC-AUC scores of model transfer between all nucleophile types within the dataset. Diagonal elements correspond to cross-validation scores. Square blocks, divided by bold black lines, show pairs of nucleophiles that fall under the same reaction type.

Fig. 3B shows that models trained on reactions using benzamide (1) as nucleophile made excellent predictions on reactions using phenyl sulfonamide (ROC-AUC = 0.928), where the two nucleophiles presumably follow a closely related C–N coupling mechanism.⁵⁶ On the other hand, predictions for reactions using pinacol boronate esters (4 and 5) as the coupling partner, made by the same benzamide-trained model, were inferior to random selection (ROC-AUC = 0.133). This observation is repeated for models trained on the sulfonamide dataset: sulfonamide models classified reactions of 1 well (ROC-AUC = 0.880), while for pinacol boronate esters, the performance was again worse than random (ROC-AUC = 0.148). Models trained on reactions using pinacol boronate esters did not show meaningful performance on either amide or sulfonamide-based reactions (ROC-AUC values of 0.245, 0.044, respectively). The near-perfect misclassification on sulfonamide reactions is further analyzed in the ESI,† where it is shown that nearly opposite yield labels guide the models to predict the inverse outcome (Table S2†).

Intrigued by these observations, the reaction condition prediction experiment was expanded to include all 90 pairs of source and target nucleophile types available in the dataset (Fig. 3C). Following the expectation that a model would be more predictive for mechanistically similar reactions, models trained on nitrogen-based nucleophiles are effective in classifying yields of other nitrogen nucleophiles. ROC-AUC scores for models of phenols and thiophenols transferred to nitrogen-based nucleophiles, however, were somewhat lower. This may be because the reaction mechanism involved with the former is more likely via S_NAr than Pd-catalyzed coupling.⁴⁹ For malonate nucleophile models, predictions on nitrogen-based nucleophiles are not particularly accurate (ROC-AUC between 0.52 and 0.77), and vice versa.

The model transfer results can be explained by considering the coupling mechanisms and molecular structures that differentiate the source and target nucleophile types. First, for a source model to make effective predictions in a target domain, the reaction mechanism of the source-target pair should be closely related. For many pairs of source and target nucleophiles that fall under the same reaction type (Fig. 3C, presumed mechanistically similar reactions are grouped by bold black lines) the transfer ROC-AUC is high, mostly above 0.8. However, despite the mechanistic similarity of diethyl malonate and the nitrogen nucleophiles,⁵⁷ the transfer ROC-AUC was only ∼0.7 with malonate as target. This might be attributed to the difference of the reacting atom's identity (C vs. N) and its adjacency to two electron withdrawing groups.

Generalizing to new reaction conditions

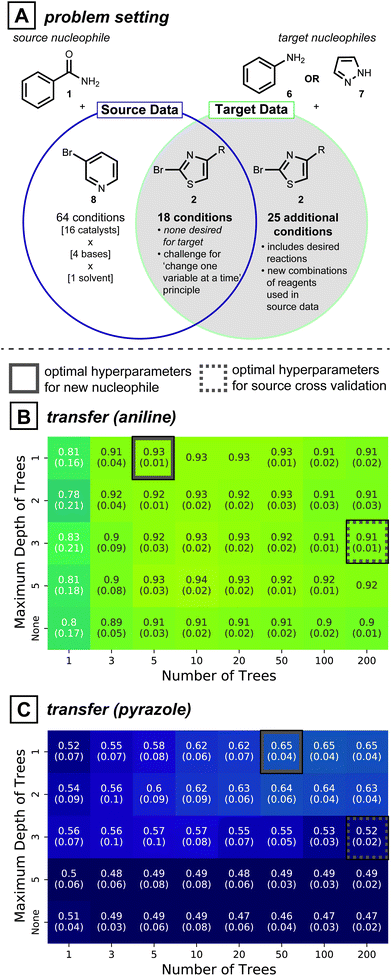
Directly adopting previous reaction conditions, as considered in the section above, may not ultimately be viable for the target of interest. Therefore, new reagent combinations usually need to be considered when developing reaction conditions for a new substrate. In this case, model generalizability is vital to making accurate predictions. Cross-validation is a standard procedure in model training because it avoids overfitting: a model that is too tightly tuned to the training data is unlikely to generalize well to dissimilar data points. Inspired by the model simplification effect of cross-validation, we hypothesized that simplifying the model form⁵⁸—beyond what is determined by cross-validation—may further improve predictivity for unseen reaction conditions. Like the section above, predictions are made without target reaction data.

To test whether model simplification will lead to improved predictions, the reaction development case study shown in Fig. 4A was analyzed. The source data for this realistic situation consists of 64 distinct reaction conditions involving 1 (nucleophile) and 3-bromopyridine (8, electrophile), and 18 reaction conditions involving 1 and 2-bromothiazole (2, electrophile). The first 64 can be seen as the original attempt at discovering reaction conditions, and the next 18 were created to expand the scope to a second electrophile, while keeping the nucleophile constant. With this source data in hand, the overall goal is to expand the reaction conditions to handle two new nucleophiles, aniline (6) and pyrazole (7). For coupling of either of these new nucleophiles to electrophile 2, however, none of the original 18 reaction conditions showed positive yields. Therefore, 25 additional reaction conditions available in our dataset but previously unseen by the model were considered, giving 43 possible conditions for the two new nucleophiles.

Fig. 4 (A) Summary of dataset considered for the rest of the study. The 18 reactions common across the source and target reflects a realistic situation of changing only one variable (nucleophile). However, there being no desired outcomes for the target nucleophiles presents a challenge, therefore 25 more reaction conditions were considered. (B) and (C) Average performance of 25 benzamide models with various hyperparameter values, transferred to aniline and pyrazole data, respectively. Values in parentheses correspond to standard deviations. Dashed grey boxes show the optimal combination determined by cross-validation. Solid grey boxes show the simplest hyperparameter combination with optimal transfer performance.

In this context of reaction scope expansion, a random forest classifier can be tailored to different degrees of complexity. Since decision trees in a random forest are a series of nodes that evaluate feature values to make a prediction, model complexity can be regulated by limiting the number of trees and the maximum number of evaluations. Accordingly, models varying these two hyperparameters were compared.

Cross-validated source models show random forests with 200 decision trees trained with depths constrained to 3 is the most effective model (Fig. S5A†). While these cross validated models applied to reactions of 6 and 7 (grey dotted squares in Fig. 4B and C, respectively) show some predictivity, slightly higher ROC-AUC scores (0.93 vs. 0.91 for 6, 0.65 vs. 0.52 for 7) can be achieved with simpler models (Fig. 4B and C, solid grey boxes). Analogous analyses conducted on all 30 possible pairs of source-target nucleophiles show simpler models give comparable transfer performances to cross-validated source models in 14 cases and better performances in 9 cases (See ESI Fig. S6, S7 and Table S3† for further details). An added benefit of model simplification is that it can make models easier to interpret and can assist in active learning protocols, as will be described below and in the Discussion Section.

A strategy for choosing optimal hyperparameters in a prospective transfer setting is not obvious. Moreover, with a subsequent collection of target reaction data, different hyperparameter choices may be favorable for the source model. Accordingly, an alternative strategy to improve transfer performance is required. The following section describes an active-transfer learning approach to do just that.

Adapting the source model to a new substrate space for efficient iterative experimentation

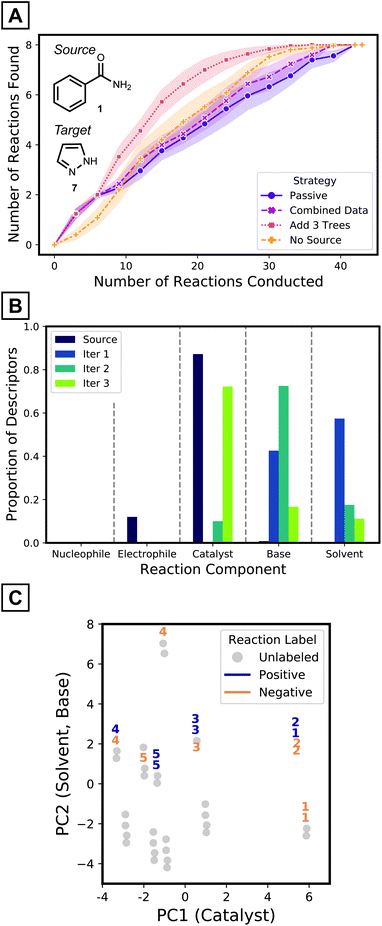
Iterative batch experimentation is a traditional way to evaluate reaction conditions, where the best proposals are tested in the laboratory and the results are used to decide the next experiments to try. This expert process is mimicked by active-transfer learning (ATL),^59,60 where specific decisions – how to select the reactions to label and how to update the model – also need to be made as experiments are conducted. The utility of ATL for predicting desired reaction conditions for a new nucleophile is therefore explored by revisiting the problem described in Fig. 4A, assuming a starting point where no target data has been acquired. Performance is measured by the cumulative number of reaction conditions identified that achieve desired outcomes. Based on the hypothesis that simple models will more easily adapt to target data, source models with five decision trees of depth one are considered.

The pyrazole target is a challenging test case. First, the reaction conditions that gave positive results for the coupling of source nucleophile 1 and electrophile 2 are not effective for coupling target nucleophile 7 and electrophile 2. Also, transferred models, without additional training with target data, do not show good predictivity (Fig. 4C). The ROC-AUC of 0.58 for the same amide source models applied to the target 7 (Fig. 4C, five trees of maximum depth of one) suggest the source model is only slightly better than random selection of target reaction conditions (Fig. 5A, purple curve). Therefore, this challenging scenario requires a different strategy to enhance the predictivity of the transferred model. The pyrazole target 7 is also interesting because Pd-catalyzed N-arylation of diazoles are much less studied than couplings involving other N-nucleophiles.⁵⁶

Fig. 5 (A) Cumulative number of reactions of desired outcomes found per iteration for different modeling strategies. Points are an average of 25 model instances and shades depict 95% confidence interval. (B) Average portion of descriptor components added in each iteration across 25 experiments. (C) Reactions selected in the first five batches of one tree growth instance, visualized on a PCA plot. PCA was conducted on standardized descriptor vectors. Clusters of reactions are separated along PC1 and PC2 following catalyst and solvent descriptors, respectively. Within the clusters, base descriptors differentiate PC2 value of each reaction. PC2 values were jittered to prevent overlap between points. The numbers on the markers indicate the iteration the corresponding reaction was sampled in.

To improve the prediction of coupling conditions of 7, ATL was employed. Similar to what might be done in laboratory experimentation, three reactions from our available dataset were collected and labeled in each active learning step. To choose the three reactions at each iteration, the entries with highest predicted probability values from the current generation model were selected (greedy selection; other reaction selection strategies and their results are presented in the Computational Methods and the ESI,† respectively). Models were updated after each batch according to various strategies that are detailed below.

As a simple tactic for ATL, newly collected target data was combined with the source dataset after each round of experimentation and a random forest model was retrained on the combined dataset. When retraining, errors were more heavily weighted for the target data, since the size of the source dataset is much larger. As shown in Fig. 5A's magenta curve, however, this procedure was not much more effective than the passive source model (where no retraining was performed as target data is collected; Fig. 5A, purple curve). This indicates that the data combination strategy failed to adapt to the target reaction space (Fig. S13†).

One way to adapt the iterative model to the new results—in particular when using random forest models—is to add new trees to the (fixed) source model, where the new trees are trained using only labeled target data. To test this strategy, three trees of depth one—trained on the three target reactions collected in that batch—were added to the model at each iteration. This strategy (Fig. 5A, red curve) outperforms models with the same number of trees trained on the combined dataset (Fig. 5A, magenta curve) from the third iteration and onwards. The target tree growth method identifies about 50% more desired reactions at this point. The target tree growth model (with source data) outperforms the same strategy without the source model (Fig. 5A, orange curve). By the third batch, the source-bolstered tree growth model predicts >3 desired reaction conditions on average, compared to 2 for the source-less model. The ATL tree growth model therefore outperforms the other possibilities, especially once it gathers sufficient labeled data to adapt to the target space. ATL studies on all source-target pairs (ESI† pages S22–S25) show that the target tree growth strategy is particularly effective for challenging cases with a low proportion of positive yields.

To gain insight on how ATL adapts models to the target domain, the simplified source models and the first three batches of added trees were analyzed. The source model mostly utilizes descriptors of catalysts (Fig. 5B purple bars). In contrast, descriptors of bases and solvents are added after the first iteration (Fig. 5B blue bars), and the next iteration introduces even more base features (Fig. 5B green bars). The third iteration prefers to add catalyst descriptors (Fig. 5B olive bars). This analysis implies models become aware of aspects that were unspecified in the source model, but still need to be considered for effective classification of target reactions. This complies to the accelerated pace of discoveries being made only after the first two iterations (Fig. 5A, red curve).

To further understand the model's decision-making process, the reactions that were selected for labeling at each iteration were investigated. Reactions were visualized on the first two principal components of the input descriptor vectors of the pyrazole dataset (Fig. 5C). Along the x-axis, different clusters have different catalysts while clusters that are separated vertically differ by solvent identity. Within a cluster, a reaction's position is determined by base. In the early iterations, reactions are selected within a single cluster, explained by the source model's exclusive use of catalyst descriptors. At later iterations, the selection may spread out to different clusters as other components start to be considered. This behavior, as opposed to selecting reactions from numerous clusters, is expected from greedy selection and has been observed in previous active learning studies.^27,28,39 Comparisons with the behaviors of baseline strategies are discussed in the ESI (Fig. S12†).

Discussion

Decisions made during reaction development are often supported by generalized chemical knowledge, which can be simple and qualitative. The present investigation supports this approach. Models were trained on physical descriptors assumed to best represent the reaction mechanism,²⁵ which could help transfer to mechanistically relevant reactions. Adversarial controls^61,62 against models trained on concatenated Morgan fingerprints⁶³ and one-hot labels show that unlike cross-validation where fingerprint models perform best, transfer performance favors descriptor-based models in most cases (Fig. S9 and S10†). On the other hand, models that are simpler than those tuned for the source domain by cross-validation were also considered for transfer. As a result, these models include only the most dominant factors that influence the outcomes of reactions of the source nucleophile, in this case the catalysts for C–N couplings (Fig. 5C). Ultimately, these models have the potential to generalize better⁶⁴ to reactions with new nucleophiles and reagent combinations (Fig. 4B and C). A similar idea to secure generalizability was also demonstrated in our previous work,¹⁴ where catalyst identity played a central role in a simple model that predicts solvents for several named reactions.

The improvement to generalization, however, could not be achieved between C–N coupling and Suzuki reactions (Fig. 3C), probably due to significant mechanistic differences between the source and target reactions (Fig. 2B). Negative transfer⁶⁵ describes the situation where the utilization of source information results in reduced performance for classifying target data compared to no transfer. Negative transfer can occur when the difference between the source and target domains is large (e.g. between pinacol boronate esters and nitrogen-based nucleophiles, Fig. 3C). Unfortunately, foresight of negative transfer is currently an unsolved problem^32,65 for machine learning. Domain expertise, however, can help overcome such limitations in scientific applications of machine learning.⁶⁶ In the current context of reaction condition identification, reaction type classification based on chemical knowledge appears to be a useful working concept for determining whether a transfer will be viable. Since there are no known data-driven predictors for transferability between a given source and target,³² incorporation of expert knowledge into machine learning workflows appears to be a welcome near-term remedy.

The transfer of benzamide source models to pyrazole target reactions showed a relatively weak benefit, though it did not fall into the realm of negative transfer. Pyrazole is significantly different in structure—compared to species like benzamide and aniline—since it is the only nucleophile where the reacting center is part of an aromatic ring. The relative acidity and low nucleophilicity of pyrazole also differentiate it from other nucleophiles.⁶⁷ As a result, use of the benzamide source model (without updates) is only slightly better than random selection (Fig. 5A, purple curve) for determining good reaction conditions for pyrazole. Fortunately, the ATL strategy was able to sufficiently boost the source model to quickly locate working reaction conditions.

The use of a small number of the simplest decision trees—depth one⁵⁷—as source model plays an important role in the performance of the target tree growth ATL. The impacts of the maximum depth of each tree (when the number of trees in the source model is fixed to five) and the number of trees (when the maximum depth is limited to one) of the source model were evaluated (Fig. 6). Although the transfer ROC-AUC of source models of five trees of maximum depth one is on the lower side among the models considered here (Fig. 4C), ATL had the highest performance using this simple source model (Fig. 6, purple curve vs. others). In contrast, increasing the number of decision trees⁶⁸ in the source model did not impact ATL performance as much as increasing the depth⁶⁹ of the trees. Collectively, for iterative updates with new target data, source model simplification beyond cross-validation seems to be beneficial.

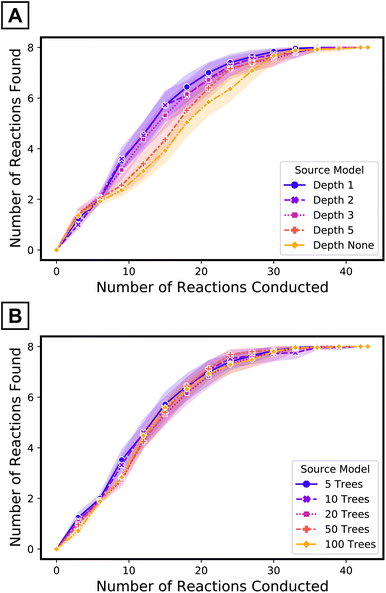Fig. 6 Performance of target tree growth ATL with source models of (A) five trees of varying maximum depths and (B) varying number of trees with maximum depth limited to one.

The target tree growth ATL strategy was effective for a wide range of transfer scenarios (Fig. S19 and S20†) and appears to be even more effective when the portion of positive yields in the target are low (Fig. S21 and Table S4†). For those target datasets with less than 20% positives, tree growth identified a significantly larger number of productive reactions compared to either active learning without model transfer (from the first iteration) and ATL on combined source and target data (from the third iteration). This benefit of ATL over its separate components is a result of adaptation of the model to the target data (Fig. S13†), which was achieved through adding simple target decision trees to a simple source model.

The goal of finding desired reaction conditions is qualitatively different from the goals of other active learning studies for classification, which usually aim to minimize error in the domain of interest.^40,47 A similar formulation was used in the context of drug discovery (up to ∼17 500 molecules), where data points were selectively labeled based on the farthest distance from the support vector machine's classification hyperplane.⁷⁰ Another study⁷¹ under a similar setting (with ∼100 million molecules) showed greedy selection to be effective at identifying molecules with the best docking scores. The present results, at the lower extreme of dataset size (<100 reactions), also support that the greedy approach works well for reaction condition finding (see Computational Details and ESI† for other reaction selection criteria and their results). For active learning, selecting the initial data labeling choices to be as close to the productive area as possible is beneficial. Fortunately, this low-data, effective transfer learning can be performed in a chemical setting where experts usually aim for new reactions based on analogy to prior ones.

Challenges in learning when few data points are available

The target tree growth strategy is expected to be implemented at the earliest stage of substrate scope expansion, when there is some source data but no target data in hand. Under this situation, a realistic set of candidate reaction conditions needs to be considered for the transferred source model to show meaningful predictivity (note how Fig. 4C shows ROC-AUC values below 0.5 in some cases). Here, the electrophile was common across the source and target datasets (species 2) and only the reagents from the source data are used in the target space (Fig. S4B†). This resembles the common experimental chemical practice of using familiar reagents in the early stage of exploration. Once sufficient target reaction data is collected, other modeling strategies should be applied to steer exploration directions to involve new substrates or reagents.

The proposed ATL strategy, while promising for quickly finding reaction conditions, will need to be further tested to better understand its scope and limitations. For instance, while mechanistic similarity may be a criterion for model transfer, knowledge of reaction mechanism may be limited especially for new reaction methods. Therefore, it is clear that being able to estimate model transferability—in general—will enhance the applicability of ATL approaches toward reaction condition discovery. In addition, the ATL approach should be considered as a means to prioritize experiments and help identify working reaction conditions in the early stages of reaction development, but subsequent reaction condition optimization is to be expected.

Despite the success of the target tree growth ATL across numerous types of nucleophiles that undergo C–N coupling (Fig. S19 and S20†), further studies on different stages of ATL would facilitate its adaptation. First, establishment of design principles that guide the construction of datasets to be effective toward both reaction discovery and transfer learning could make ATL easier to incorporate in practical workflows. Most importantly, as discussed above, the premise for effective model transfer, deeper than ‘mechanistic or chemical similarity’ would be immensely valuable. Lastly, new active sampling methods, along with different approaches to combine with transfer learning are expected to emerge and further streamline chemical exploration.

Conclusions

Transfer and active learning are useful concepts for finding conditions for a new substrate type in cross-coupling reactions. To maximize the transferability of source models to new substrates not represented in the source dataset, random forests were constructed as models where only the most impactful features on reactivity are present. This modeling procedure relies on mechanistic and chemical relevance, which appear necessary for predictive accuracy. In the most challenging reaction development scenarios, an adaptive ATL strategy is needed, using the concepts of transfer and active learning in concert with one another. Put together, transfer learning and active learning are envisioned to facilitate automated chemical synthesis, opening opportunities for expert chemists to focus on the discovery of novel reactions.

Computational details

Dataset

The dataset used in this study is a compilation of subsets of data from previous HTE studies.^49–51 These HTE experiments were conducted during the development of the HTE and analysis platform but were not specifically intended to be used in machine learning applications. Accordingly, a subset of 1220 available reactions were chosen to narrow the set of reaction conditions to those that were common to many nucleophiles. Catalysts were in the form of Buchwald-type 2^nd (ref. 72) or 3^rd (ref. 67) generation pre-catalysts. Non-volatile solvents (e.g. dimethyl sulfoxide) and soluble organic bases (e.g. P2Et) were used. There are ten types of nucleophiles, and each type includes one or two specific molecules (e.g. amide only has benzamide, where aliphatic alcohol has two molecules). Two electrophiles, 3-bromopyridine and 2-bromothiazole, are considered as the coupling partner. For classes where there are two nucleophile molecules, one nucleophile reacts only with one electrophile. The stoichiometry between nucleophile and electrophile differs across the dataset. For yield arrays, if no product was detected, a reaction's yield was labeled 0. For all other values, it was labeled 1. Since we conduct binary classification of yield (rather than regression) stoichiometry was ignored, assuming minimal impact on label noise. See Fig. S1† for a distribution of yield labels for each nucleophile type. The full reaction dataset is available online as a structured query language database.⁷³

For C–N coupling reactions, while outcomes of reactions with 3-bromopyridine are relatively well balanced, yield labels involving 2-bromothiazole heavily favor positive reactions. This distribution is reasonable given that the dataset was built to showcase the HTE platform, and negative reactions were of less interest at that time. Therefore, we framed desired reactions as negative reactions to understand factors that hinders reactivity of these well-known reactions in this platform. This amounts to a label switch when applied to real-life situations where the probability of positive hits is significantly smaller than negative outcomes. See Fig. S3† for the distribution of yield labels for the active learning setting.

Physical descriptors

All compounds that constitute the reaction dataset were represented with a series of physical descriptors calculated with density functional theory (B3LYP/6-31G*). MOPAC^74,75 was used to compute area and volume descriptors. Q-Chem⁷⁶ was used to compute other physical descriptors. For pre-catalysts, the buried volume⁷⁷ was computed by using the web application SambVca and sterimol parameters⁷⁸ with python.⁷⁹ For bases, proton affinity was approximated as the energy difference between bases and their protonated forms. Hansen parameter values of solvents were used from ref. 80 and 81. The procedure for extraction of vibration frequencies and intensities of electrophiles and ligands is explained in the ESI.† The extracted values are organized within the structured query language database file. To represent a reaction, all descriptors of the five compounds in the reactions were concatenated using numpy⁸² arrays in the order of nucleophile, electrophile, catalyst, base followed by solvent, which results in vectors of length 73.

Adversarial controls

For y-shuffling experiments,⁶¹ 25 randomly shuffled yield labels were prepared for each source nucleophile. These shuffled labels, along with unmodified input array of physical descriptors, were used to train models through 5-fold cross-validation. The predictions of these models on target reactions were then evaluated with unmodified target yield labels. These transfer ROC-AUC scores were compared with scores of models that were prepared from original yield labels.

In addition to physical descriptors, models trained on reactions represented with concatenated one-hot labels^61,62 and Morgan fingerprints⁶³ were also evaluated. One-hot label arrays of source reactions were prepared by transforming reactions represented with ids of each component through scikit-learn's OneHotEncoder^83,84 with the handle_unknown parameter set to ‘ignore’. Target one-hot label arrays were transformed from the array of reaction component id, using the one-hot encoder that was fit on the source dataset. Morgan fingerprints of each reaction component were prepared as bit vectors of length 1024 and radius of 2 with rdkit,⁸⁵ resulting in a concatenated vector of length 5120 for each reaction. Highest cross-validation and transfer ROC-AUC scores from each representation were compared.

Random forest classifiers

All random forest classifiers⁸⁶ were instantiated with scikit-learn.⁸⁴ Descriptor arrays were used as is, without any feature transformation, to train and evaluate models. For training a source model in Fig. 3, we conducted five-fold cross-validation on data with randomized orders. Default values were used for all hyperparameters except for the number of trees (n_estimators) and the number of nodes in a tree (max_depth). Throughout the study, multiple models were instantiated (25 for result sections 2 and 3) using different random state values in which average results and the corresponding standard deviation or confidence interval of 95% were provided either in the main text or ESI.† Models were evaluated with ROC-AUC scores,⁸⁷ which describe how well the model ranks positive datapoints above negative data.

Active transfer learning

To select reactions to query labels of, ATL first uses the model to make predictions on the target reaction data. Random forest classifiers provide probability values for each reaction by computing the average of output probabilities from each tree. The exploitation (greedy) approach, which was used in most of the experiments, selects reactions that result in the highest probability values ([small mu, Greek, circumflex](x)). The highest variance (exploration) approach selects reactions that have highest variance across all trees in the forest ([small sigma, Greek, circumflex]²(x)). Lastly, upper confidence bound selects reactions that show the highest values of [small mu, Greek, circumflex](x) + β[small sigma, Greek, circumflex](x), where β is a hyperparameter, in which 0.5 and 2 were considered in this study. Only results from the greedy approach are shown in the main text, while the other two approaches are examined in the ESI.†

When updating models based on the combined source and target dataset, a list of importance weights that correspond to each datapoint of the combined dataset can be passed into the function fit() of the random forest classifier. For source reactions, the weight was fixed to one, while the weights of target reactions were varied. New random forest classifiers were trained every iteration, with the number of trees increasing by three compared to the previous model. Maximum depth was fixed to one throughout the exploration.

For models that add target trees every iteration onto the (fixed) source random forest, a separate random forest instance of three trees of depth one was trained on only the target data collected at each iteration. Then, the list of decision trees was appended to the list of decision trees of the previous model. All implementations are provided as Jupyter notebooks on Github.⁷³

Data availability

Code for this study is available at https://github.com/zimmermangroup/ActiveTransfer.

Author contributions

E. S., J. A. K. and Z. X. designed the experiments; E. S. conducted the experiments; A. T., T. C. and P. M. Z. supervised the work. All authors contributed to writing the paper.

Conflicts of interest

T. C. is a co-founder and equity holder of Entos, Inc. and equity holder of Scorpion therapeutics. The Cernak Lab receives research funding from MilliporeSigma, Janssen Therapeutics and Relay Therapeutics, and Entos, Inc. as well as gifts from Merck Sharp & Dohme and SPT Labtech. Other authors declare no competing financial interest.

Acknowledgements

This work was supported by NIH-R35GM128830 (PMZ), NSF IIS-2007055 (AT) and start-up funds from the University of Michigan College of Pharmacy (TC).

Notes and references

1. L. Wilbraham, S. H. M. Mehr and L. Cronin, Digitizing Chemistry Using the Chemical Processing Unit: From Synthesis to Discovery, Acc. Chem. Res., 2021, 54(2), 253–262,  DOI:10.1021/acs.accounts.0c00674.
2. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, A Mobile Robotic Chemist, Nature, 2020, 583(7815), 237–241,  DOI:10.1038/s41586-020-2442-2.
3. C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous Discovery in the Chemical Sciences Part I: Progress, Angew. Chem., Int. Ed., 2020, 59(51), 22858–22893,  DOI:10.1002/anie.201909987.
4. S. Yuning, E. B. Julia, A. H. Melissa, S. Richmond, G. D. Abigail and C. Tim, Automation and Computer-Assisted Planning for Chemical Synthesis, Nat. Rev. Methods Primers, 2021, 1(1), 23,  DOI:10.1038/s43586-021-00022-5.
5. M. H. S. Segler, M. Preuss and M. P. Waller, Planning Chemical Syntheses with Deep Neural Networks and Symbolic AI, Nature, 2018, 555(7698), 604–610,  DOI:10.1038/nature25978.
6. B. Mikulak-Klucznik, P. Gołębiowska, A. A. Bayly, O. Popik, T. Klucznik, S. Szymkuć, E. P. Gajewska, P. Dittwald, O. Staszewska-Krajewska, W. Beker, T. Badowski, K. A. Scheidt, K. Molga, J. Mlynarski, M. Mrksich and B. A. Grzybowski, Computational Planning of the Synthesis of Complex Natural Products, Nature, 2020, 588(7836), 83–88,  DOI:10.1038/s41586-020-2855-y.
7. C. W. Coley, D. A. Thomas, J. A. M. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao, R. W. Hicklin, P. P. Plehiers, J. Byington, J. S. Piotti, W. H. Green, A. J. Hart, T. F. Jamison and K. F. Jensen, A Robotic Platform for Flow Synthesis of Organic Compounds Informed by AI Planning, Science, 2019, 365(6453), eaax1566,  DOI:10.1126/science.aax1566.
8. C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A Graph-Convolutional Neural Network Model for the Prediction of Chemical Reactivity, Chem. Sci., 2018, 10(2), 370–377,  10.1039/c8sc04228d.
9. P. Schwaller, T. Gaudin, D. Lányi, C. Bekas and T. Laino, “Found in Translation”: Predicting Outcomes of Complex Organic Chemistry Reactions Using Neural Sequence-to-Sequence Models, Chem. Sci., 2018, 9(28), 6091–6098,  10.1039/c8sc02339e.
10. P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, Molecular Transformer: A Model for Uncertainty-Calibrated Chemical Reaction Prediction, ACS Cent. Sci., 2019, 5(9), 1572–1583,  DOI:10.1021/acscentsci.9b00576.
11. C. W. Coley, R. Barzilay, T. S. Jaakkola, W. H. Green and K. F. Jensen, Prediction of Organic Reaction Outcomes Using Machine Learning, ACS Cent. Sci., 2017, 3(5), 434–443,  DOI:10.1021/acscentsci.7b00064.
12. M. R. Maser, A. Y. Cui, S. Ryou, T. J. DeLano, Y. Yue and S. E. Reisman, Multilabel Classification Models for the Prediction of Cross-Coupling Reaction Conditions, J. Chem. Inf. Model., 2021, 61(1), 156–166,  DOI:10.1021/acs.jcim.0c01234.
13. G. Marcou, J. A. de Sousa, D. A. R. S. Latino, A. de Luca, D. Horvath, V. Rietsch and A. Varnek, Expert System for Predicting Reaction Conditions: The Michael Reaction Case, J. Chem. Inf. Model., 2015, 55(2), 239–250,  DOI:10.1021/ci500698a.
14. E. Walker, J. Kammeraad, J. Goetz, M. T. Robo, A. Tewari and P. M. Zimmerman, Learning To Predict Reaction Conditions: Relationships between Solvent, Molecular Structure, and Catalyst, J. Chem. Inf. Model., 2019, 59(9), 3645–3654,  DOI:10.1021/acs.jcim.9b00313.
15. H. Gao, T. J. Struble, C. W. Coley, Y. Wang, W. H. Green and K. F. Jensen, Using Machine Learning To Predict Suitable Conditions for Organic Reactions, ACS Cent. Sci., 2018, 4(11), 1465–1476,  DOI:10.1021/acscentsci.8b00357.
16. M. K. Nielsen, D. T. Ahneman, O. Riera and A. G. Doyle, Deoxyfluorination with Sulfonyl Fluorides: Navigating Reaction Space with Machine Learning, J. Am. Chem. Soc., 2018, 140(15), 5004–5008,  DOI:10.1021/jacs.8b01523.
17. J. P. Reid and M. S. Sigman, Holistic Prediction of Enantioselectivity in Asymmetric Catalysis, Nature, 2019, 571(7765), 343–348,  DOI:10.1038/s41586-019-1384-z.
18. A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Prediction of Higher-Selectivity Catalysts by Computer-Driven Workflow and Machine Learning, Science, 2019, 363(6424), eaau5631,  DOI:10.1126/science.aau5631.
19. G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Transfer Learning Enables the Molecular Transformer to Predict Regio- and Stereoselective Reactions on Carbohydrates, Nat. Commun., 2020, 11(1), 4874,  DOI:10.1038/s41467-020-18671-7.
20. S.-Y. Moon, S. Chatterjee, P. Seeberger and K. Gilmore, Predicting Glycosylation Stereoselectivity Using Machine Learning, Chem. Sci., 2021, 12(8), 2931–2939,  10.1039/d0sc06222g.
21. T. J. Struble, C. W. Coley and K. F. Jensen, Multitask Prediction of Site Selectivity in Aromatic C–H Functionalization Reactions, React. Chem. Eng., 2020, 5(5), 896–902,  10.1039/d0re00071j.
22. Y. Guan, C. W. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green and K. F. Jensen, Regio-Selectivity Prediction with a Machine-Learned Reaction Representation and on-the-Fly Quantum Mechanical Descriptors, Chem. Sci., 2021, 12(6), 2198–2208,  10.1039/d0sc04823b.
23. X. Li, S. Zhang, L. Xu and X. Hong, Predicting Regioselectivity in Radical C−H Functionalization of Heterocycles through Machine Learning, Angew. Chem., Int. Ed., 2020, 59(32), 13253–13259,  DOI:10.1002/anie.202000959.
24. W. Beker, E. P. Gajewska, T. Badowski and B. A. Grzybowski, Prediction of Major Regio-, Site-, and Diastereoisomers in Diels–Alder Reactions by Using Machine-Learning: The Importance of Physically Meaningful Descriptors, Angew. Chem., Int. Ed., 2019, 58(14), 4515–4519,  DOI:10.1002/anie.201806920.
25. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Predicting Reaction Performance in C–N Cross-Coupling Using Machine Learning, Science, 2018, 360(6385), 186–190,  DOI:10.1126/science.aar5169.
26. P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Prediction of Chemical Reaction Yields Using Deep Learning, Mach. Learn.: Sci. Technol., 2021, 2(1), 015016,  DOI:10.1088/2632-2153/abc81d.
27. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Bayesian Reaction Optimization as a Tool for Chemical Synthesis, Nature, 2021, 590(7844), 89–96,  DOI:10.1038/s41586-021-03213-y.
28. D. Reker, E. A. Hoyt, G. J. L. Bernardes and T. Rodrigues, Adaptive Optimization of Chemical Reactions with Minimal Experimental Information, Cell Rep. Phys. Sci., 2020, 1(11), 100247,  DOI:10.1016/j.xcrp.2020.100247.
29. Z. Fu, X. Li, Z. Wang, Z. Li, X. Liu, X. Wu, J. Zhao, X. Ding, X. Wan, F. Zhong, D. Wang, X. Luo, K. Chen, H. Liu, J. Wang, H. Jiang and M. Zheng, Optimizing Chemical Reaction Conditions Using Deep Learning: A Case Study for the Suzuki–Miyaura Cross-Coupling Reaction, Org. Chem. Front., 2020, 7(16), 2269–2277,  10.1039/d0qo00544d.
30. Z. Zhou, X. Li and R. N. Zare, Optimizing Chemical Reactions with Deep Reinforcement Learning, ACS Cent. Sci., 2017, 3(12), 1337–1344,  DOI:10.1021/acscentsci.7b00492.
31. S. J. Pan and Q. Yang, A Survey on Transfer Learning, IEEE Trans. Knowl. Data Eng., 2009, 22(10), 1345–1359,  DOI:10.1109/tkde.2009.191.
32. C. Cai, S. Wang, Y. Xu, W. Zhang, K. Tang, Q. Ouyang, L. Lai and J. Pei, Transfer Learning for Drug Discovery, J. Med. Chem., 2020, 63(16), 8683–8694,  DOI:10.1021/acs.jmedchem.9b02147.
33. D. Kreutter, P. Schwaller and J.-L. Reymond, Predicting Enzymatic Reactions with a Molecular Transformer, Chem. Sci., 2021, 12(25), 8648–8659,  10.1039/d1sc02362d.
34. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Approaching Coupled Cluster Accuracy with a General-Purpose Neural Network Potential through Transfer Learning, Nat. Commun., 2019, 10(1), 2903,  DOI:10.1038/s41467-019-10827-4.
35. H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, Predicting Materials Properties with Little Data Using Shotgun Transfer Learning, ACS Cent. Sci., 2019, 5(10), 1717–1730,  DOI:10.1021/acscentsci.9b00804.
36. A. Arnold, R. Nallapati and W. W. Cohen, A Comparative Study of Methods for Transductive Transfer Learning, IEEE Int. Conf. Data Min. Workshops ICDMW, 2007 2007, 77–82,  DOI:10.1109/icdmw.2007.109.
37. M. Stone, Cross-Validatory Choice and Assessment of Statistical Predictions, J. R. Stat. Soc., B: Stat. Methodol., 1974, 36(2), 111–133,  DOI:10.1111/j.2517-6161.1974.tb00994.x.
38. B. Settles, Active Learning, Synth. lectures Artif. Intell. Mach. Learn., 2012, 6, 1–114,  DOI:10.2200/S00429ED1V01Y201207AIM018.
39. D. Reker and G. Schneider, Active-Learning Strategies in Computer-Assisted Drug Discovery, Drug Discovery Today, 2015, 20(4), 458–465,  DOI:10.1016/j.drudis.2014.12.004.
40. S. V. Johansson, H. G. Svensson, E. Bjerrum, A. Schliep, M. H. Chehreghani, C. Tyrchan and O. A. Z. Engkvist, Using Active Learning to Develop Machine Learning Models for Reaction Yield Prediction, ChemRxiv, 2021 DOI:10.33774/chemrxiv-2021-bpv0c.
41. J. A. Kammeraad, J. Goetz, E. A. Walker, A. Tewari and P. M. Zimmerman, What Does the Machine Learn? Knowledge Representations of Chemical Reactivity, J. Chem. Inf. Model., 2020, 60(3), 1290–1301,  DOI:10.1021/acs.jcim.9b00721.
42. D. M. Lowe, Extraction of Chemical Structures and Reactions from the Literature, 2012.
43. M. Saebi, B. Nan, J. E. Herr, J. Wahlers, Z. Guo, A. M. Zurański, T. Kogej, P.-O. Norrby, A. G. Doyle, O. Wiest and N. V. Chawla, On the Use of Real-World Datasets for Reaction Yield Prediction, ChemRxiv, 2021 DOI:10.33774/chemrxiv-2021-2x06r-v3.
44. M. Babak, S. Yuning and C. Tim, Ultrahigh-Throughput Experimentation for Information-Rich Chemical Synthesis, Acc. Chem. Res., 2021, 54(10), 2337–2346,  DOI:10.1021/acs.accounts.1c00119.
45. W. Hazel and C. Tim, Reaction Miniaturization in Eco-Friendly Solvents, Curr. Opin. Green Sustainable Chem., 2018, 11, 91–98,  DOI:10.1016/j.cogsc.2018.06.001.
46. S. Michael, Practical High-Throughput Experimentation for Chemists, ACS Med. Chem. Lett., 2017, 8(6), 601–607,  DOI:10.1021/acsmedchemlett.7b00165.
47. N. S. Eyke, W. H. Green and K. F. Jensen, Iterative Experimental Design Based on Active Machine Learning Reduces the Experimental Burden Associated with Reaction Screening, React. Chem. Eng., 2020, 5(10), 1963–1972,  10.1039/d0re00232a.
48. F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, A Structure-Based Platform for Predicting Chemical Reactivity, Chem, 2020, 6(6), 1379–1390,  DOI:10.1016/j.chempr.2020.02.017.
49. N. J. Gesmundo, B. Sauvagnat, P. J. Curran, M. P. Richards, C. L. Andrews, P. J. Dandliker and T. Cernak, Nanoscale Synthesis and Affinity Ranking, Nature, 2018, 557(7704), 228–232,  DOI:10.1038/s41586-018-0056-8.
50. S. Lin, S. Dikler, W. D. Blincoe, R. D. Ferguson, R. P. Sheridan, Z. Peng, D. V. Conway, K. Zawatzky, H. Wang, T. Cernak, I. W. Davies, D. A. DiRocco, H. Sheng, C. J. Welch and S. D. Dreher, Mapping the Dark Space of Chemical Reactions with Extended Nanomole Synthesis and MALDI-TOF MS, Science, 2018, 361(6402), eaar6236,  DOI:10.1126/science.aar6236.
51. A. B. Santanilla, E. L. Regalado, T. Pereira, M. Shevlin, K. Bateman, L.-C. Campeau, J. Schneeweis, S. Berritt, Z.-C. Shi, P. Nantermet, Y. Liu, R. Helmy, C. J. Welch, P. Vachal, I. W. Davies, T. Cernak and S. D. Dreher, Organic Chemistry. Nanomole-Scale High-Throughput Chemistry for the Synthesis of Complex Molecules, Science, 2014, 347(6217), 49–53,  DOI:10.1126/science.1259203.
52. R. Martin and S. L. Buchwald, Palladium-Catalyzed Suzuki−Miyaura Cross-Coupling Reactions Employing Dialkylbiaryl Phosphine Ligands, Acc. Chem. Res., 2008, 41(11), 1461–1473,  DOI:10.1021/ar800036s.
53. B. T. Ingoglia, C. C. Wagen and S. L. Buchwald, Biaryl Monophosphine Ligands in Palladium-Catalyzed C–N Coupling: An Updated User's Guide, Tetrahedron, 2019, 75(32), 4199–4211,  DOI:10.1016/j.tet.2019.05.003.
54. H. Zhang, P. Ruiz-Castillo and S. L. Buchwald, Palladium-Catalyzed C–O Cross-Coupling of Primary Alcohols, Org. Lett., 2018, 20(6), 1580–1583,  DOI:10.1021/acs.orglett.8b00325.
55. C.-F. Lee, Y.-C. Liu and S. S. Badsara, Transition-Metal Catalyzed C-S Bond Coupling Reaction, Chem. - Asian J., 2014, 9, 706–722,  DOI:10.1002/asia.201301500.
56. P. Ruiz-Castillo and S. L. Buchwald, Applications of Palladium-Catalyzed C–N Cross-Coupling Reactions, Chem. Rev., 2016, 116(19), 12564–12649,  DOI:10.1021/acs.chemrev.6b00512.
57. D. A. Culkin and J. F. Hartwig, Palladium-Catalyzed α-Arylation of Carbonyl Compounds and Nitriles, Acc. Chem. Res., 2003, 36(4), 234–245,  DOI:10.1021/ar0201106.
58. N. C. Iovanac and B. M. Savoie, Simpler Is Better: How Linear Prediction Tasks Improve Transfer Learning in Chemical Autoencoders, J. Phys. Chem., 2020, 124(18), 3679–3685,  DOI:10.1021/acs.jpca.0c00042.
59. P. Rai; A. Saha; H. Daumé and S. Venkatasubramanian, Domain Adaptation Meets Active Learning, in Proceedings of the NAACL HLT 2010 Workshop on Active Learning for Natural Language Processing; ALNLP ’10, Association for Computational Linguistics, USA, 2010, pp. 27–32.
60. X. Shi; W. Fan and J. Ren, Actively Transfer Domain Knowledge, Lecture Notes in Computer Science, Springer Berlin Heidelberg, 2008, pp. 342–357,  DOI:10.1007/978-3-540-87481-2_23.
61. K. V. Chuang and M. J. Keiser, Adversarial Controls for Scientific Machine Learning, ACS Chem. Biol., 2018, 13(10), 2819–2821,  DOI:10.1021/acschembio.8b00881.
62. K. V. Chuang and M. J. Keiser, Comment on “Predicting Reaction Performance in C–N Cross-Coupling Using Machine Learning, Science, 2018, 362(6416), eaat8603,  DOI:10.1126/science.aat8603.
63. D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 50(5), 742–754,  DOI:10.1021/ci100050t.
64. A. B. Leonard and W. A. David, Simplifying Decision Trees: A Survey, Knowl. Eng. Rev., 1997, 12(01), 1–40,  DOI:10.1017/S0269888997000015.
65. W. Zhang; L. Deng; L. Zhang and D. Wu, A Survey on Negative Transfer, Arxiv, 2020, DOI:  DOI:10.48550/arXiv.2009.00909.
66. C. Deng, X. Ji, C. Rainey, J. Zhang and W. Lu, Integrating Machine Learning with Human Knowledge, Iscience, 2020, 23(11), 101656,  DOI:10.1016/j.isci.2020.101656.
67. S. , S. David and L. , B. Stephen, Dialkylbiaryl Phosphines in Pd-Catalyzed Amination: A User's Guide, Chem. Sci., 2010, 2(1), 27–50,  10.1039/c0sc00331j.
68. P. Probst and A.-L. Boulesteix, To Tune or Not to Tune the Number of Trees in Random Forest, J. Mach. Learn. Res., 2017, 18(1), 6673–6690.
69. Y. Lin and Y. Jeon, Random Forests and Adaptive Nearest Neighbors, J. Am. Stat. Assoc., 2006, 101(474), 578–590.
70. M. K. Warmuth, J. Liao, G. Rätsch, M. Mathieson, S. Putta and C. Lemmen, Active Learning with Support Vector Machines in the Drug Discovery Process, J. Chem. Inf. Comput. Sci., 2003, 43(2), 667–673,  DOI:10.1021/ci025620t.
71. D. E. Graff, E. I. Shakhnovich and C. W. Coley, Accelerating High-Throughput Virtual Screening through Molecular Pool-Based Active Learning, Chem. Sci., 2021, 12(22), 7866–7881,  10.1039/d0sc06805e.
72. T. Kinzel, Y. Zhang and S. L. Buchwald, A New Palladium Precatalyst Allows for the Fast Suzuki−Miyaura Coupling Reactions of Unstable Polyfluorophenyl and 2-Heteroaryl Boronic Acids, J. Am. Chem. Soc., 2010, 132(40), 14073–14075,  DOI:10.1021/ja1073799.
73. ATL code, https://github.com/ZimmermanGroup/ActiveTransfer.
74. J. J. P. Stewart, MOPAC2016, http://OpenMOPAC.net.
75. J. J. P. Stewart, Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-Optimization of Parameters, J. Mol. Model., 2013, 19(1), 1–32,  DOI:10.1007/s00894-012-1667-x.
76. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. H. Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. V. Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, Software for the Frontiers of Quantum Chemistry: An Overview of Developments in the Q-Chem 5 Package, J. Chem. Phys., 2021, 155(8), 084801,  DOI:10.1063/5.0055522.
77. A. Poater, B. Cosenza, A. Correa, S. Giudice, F. Ragone, V. Scarano and L. Cavallo, SambVca: A Web Application for the Calculation of the Buried Volume of N-Heterocyclic Carbene Ligands, Eur. J. Inorg. Chem., 2009, 2009(13), 1759–1766,  DOI:10.1002/ejic.200801160.
78. A. V. Brethomé, S. P. Fletcher and R. S. Paton, Conformational Effects on Physical-Organic Descriptors: The Case of Sterimol Steric Parameters, ACS Catal., 2019, 9(3), 2313–2323,  DOI:10.1021/acscatal.8b04043.
79. Sterimol, https://github.com/bobbypaton/Sterimol.
80. Hansen Parameters, https://hansen-solubility.com/downloads.php.
81. M. D. de los Ríos and E. H. Ramos, Determination of the Hansen Solubility Parameters and the Hansen Sphere Radius with the Aid of the Solver Add-in of Microsoft Excel, SN Appl. Sci., 2020, 2(4), 676,  DOI:10.1007/s42452-020-2512-y.
82. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Array Programming with NumPy, Nature, 2020, 585(7825), 357–362,  DOI:10.1038/s41586-020-2649-2.
83. OneHotEncoder, https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html(accessed 2022-02-27).
84. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-Learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12(85), 2825–2830.
85. G. A. Landrum, RDKit, http://www.rdkit.org (accessed 2022-02-27).
86. B. Leo, Random Forests, Mach. Learn., 2001, 45(1), 5–32,  DOI:10.1023/a:1010933404324.
87. T. Fawcett, An Introduction to ROC Analysis, Pattern Recognit. Lett., 2006, 27(8), 861–874,  DOI:10.1016/j.patrec.2005.10.010.

---

Footnote

† Electronic supplementary information (ESI) available: Additional results. See https://doi.org/10.1039/d1sc06932b.

---