Open Access Article
Open Access ArticleCharge transport through single-molecule bilayer-graphene junctions with atomic thickness†
Shiqiang
Zhao‡
a,
Ze-Ying
Deng‡
a,
Shadiah
Albalawi‡
b,
Qingqing
Wu‡
b,
Lijue
Chen
a,
Hewei
Zhang
a,
Xin-Jing
Zhao
a,
Hao
Hou
a,
Songjun
Hou
b,
Gang
Dong
a,
Yang
Yang
a,
Jia
Shi
a,
Colin J.
Lambert
 *b,
Yuan-Zhi
Tan
*b,
Yuan-Zhi
Tan
 *a and
Wenjing
Hong
*a and
Wenjing
Hong
 *a
*a
aState Key Laboratory of Physical Chemistry of Solid Surfaces, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China. E-mail: whong@xmu.edu.cn; yuanzhi_tan@xmu.edu.cn
bDepartment of Physics, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: c.lambert@lancaster.ac.uk
First published on 30th March 2022
Abstract
The van der Waals interactions (vdW) between π-conjugated molecules offer new opportunities for fabricating heterojunction-based devices and investigating charge transport in heterojunctions with atomic thickness. In this work, we fabricate sandwiched single-molecule bilayer-graphene junctions via vdW interactions and characterize their electrical transport properties by employing the cross-plane break junction (XPBJ) technique. The experimental results show that the cross-plane charge transport through single-molecule junctions is determined by the size and layer number of molecular graphene in these junctions. Density functional theory (DFT) calculations reveal that the charge transport through molecular graphene in these molecular junctions is sensitive to the angles between the graphene flake and peripheral mesityl groups, and those rotated groups can be used to tune the electrical conductance. This study provides new insight into cross-plane charge transport in atomically thin junctions and highlights the role of through-space interactions in vdW heterojunctions at the molecular scale.
Introduction
Two-dimensional (2D) materials such as graphene and related heterojunctions have aroused great interest due to their unique electrical properties and potential applications as quantum devices.1–3 Multilayer heterojunctions formed from 2D van der Waals (vdW) materials are promising platforms for investigating strongly correlated phenomena, such as superconductivity,4,5 insulativity,6,7 and Moiré excitons,8–10 which are absent in monolayer materials. Interlayer tunneling11 and Coulomb interactions12 offer an additional degree of freedom for modulating the electrical properties of multilayers.13 However, the experimental investigation of cross-plane charge transport through well-defined multilayer 2D materials remains challenging due to the difficulties in achieving atomically precise control. Here we demonstrate that molecular bilayer graphene (MBLG), composed of well-defined π–π stacked graphene nanoflakes, is a solution to this problem and provide unique insights into the cross-plane charge transport through multilayer structures.Single-molecule electrical characterization techniques can be used to investigate charge transport through molecular junctions by trapping molecules with different lengths inside a nanogap.14–21 However, when the nanogap is located between metallic electrodes, it is essential to modify the molecule by attaching anchor groups at each end, which binds to the electrodes. Such anchor groups can significantly affect transport through the parent molecular core. In contrast, by utilizing non-covalent interactions to bridge between two graphene electrodes, the cross-plane break junction technique (XPBJ) can access the intrinsic properties of molecules without adding anchor groups.22,23 This technique takes advantage of the π–π orbital overlap between graphene electrodes and planar molecules, which can form a cross-plane transport channel for electrons passing between the graphene electrodes.
Herein, we investigate charge transport through molecular bilayer-graphene (MBLG) junctions using the XPBJ technique with graphene electrodes at room temperature. We find that a single MBLG can couple to the two graphene electrodes via vdW interactions, and that the resulting electrical conductances increase with the atomic number of MBLG. It is also found that the tunneling distance of monolayer and bilayer molecular graphene junctions correlates with the thickness of the molecules, which is an indicator of cross-plane charge transport, in which current flows perpendicular to the plane of the molecule. DFT calculations reveal that the conductance variation originates from the size dependence of the bandgap of the molecules, combined with a fine tuning of the coupling to the graphene electrodes associated with the rotation angles of the peripheral mesityl groups. Our study demonstrates the direct measurement of through-space charge transport in π-stacked assemblies and using a new type of sub-nano device based on molecular vdW stacks.
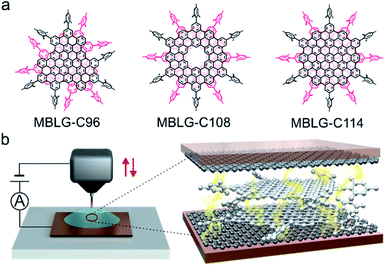
Three well-defined MBLGs, denoted as MBLG-C96, MBLG-C108, and MBLG-C114 [(C96H24R6)2, (C108H24R6)2, and (C114H24R6)2, R = mesityl], were synthesized,24,25 whose molecular structures are shown in Fig. 1a. Compared with MBLG-C114, MBLG-C108 contains a cavity defect at its centre, and the stable bilayer structure is obtained by two vertically stacked graphene nanoflakes via π–π stacking interaction. Their peripheral mesityl groups were introduced to tune the aggregation behavior.24,25 The graphene-based single-molecule junctions based on MBLGs are constructed with our home-built XPBJ setup (Fig. 1b), which is modified from the scanning tunneling microscopy break junction (STM-BJ) setup for the gold electrode. The gold tip and gold substrate are replaced by O-ring shaped copper wire and copper foil coated with single-layer graphene respectively. The liquid cell alleviates solvent volatilization, and helps to retain copper foil flatness. Nanogaps with different sizes between the two graphene electrodes are formed by moving the tip up and down repeatedly. The target molecule without anchoring groups can be trapped at the appropriate nanogap size and couple weakly to the two graphene electrodes via vdW interactions. The microscopic structure of the single-molecule bilayer-graphene junction is shown in Fig. 1b, in which electrons are transported through the molecular junctions in a cross-plane direction.
Results and discussion
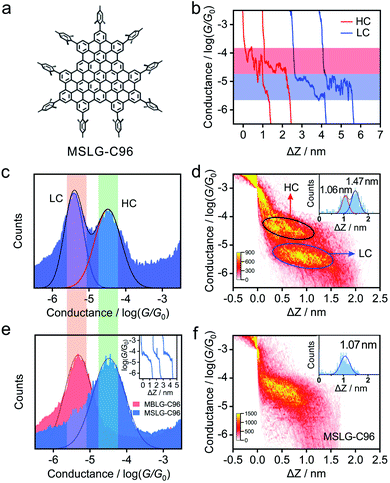
To investigate the charge transport through molecular graphene, the conductance measurement of graphene-based single-molecule junctions was performed at 100 mV bias voltage via soft contact as in our previous work,22 in which the conductance feedback ranged from the lower limit of 10−6.5G0 (∼24.6 pS, where G0 is quantum conductance) to the upper limit of 10−2.5G0 (∼245.4 nS). As shown in Fig. 2a, the 1D conductance histograms of the three MBLGs show obvious peaks, indicating the successful fabrication of single-MBLG junctions in the mixed solvent of tetrahydrofuran (THF)/decane (1/4, v/v). The most probable conductances of single-molecule junctions formed from MBLG-C96, MBLG-C108, and MBLG-C114 are 10−5.32G0 (∼0.37 nS), 10−5.02G0 (∼0.74 nS), and 10−4.65G0 (∼1.74 nS), respectively. Among the three MBLGs, the measured conductance of molecular junctions for MBLG-C96 is the lowest, because MBLG-C96 with the smallest size bridges the two graphene electrodes, which is consistent with our previous research.22MBLG-C114 with the largest number of benzene rings shows the highest π electron overlap, the measured conductance of which is about 370% higher than that of MBLG-C96. In contrast with MBLG-C114, the structure of MBLG-C108 possesses a cavity defect at the centre, leading to the decrease of interlayer π-electron coupling. As a result, the conductance of MBLG-C108 is 50% lower than that of single-molecule junctions of MBLG-C114. The one-dimensional (1D) conductance histogram and 2D conductance–distance histogram of mixed solvent (THF/decane) show no distinct peak and plateau (Fig. S15†). Therefore, we can conclude from the above that the conductance of molecules with similar structures increases with increasing intermolecular π-electron coupling. As in our previous study, we found that the conductance of single-fullerene junctions decreases when the intramolecular π conjugation of the fullerene molecule is interrupted.26The inset of Fig. 2a shows typical individual traces of three MBLGs with a notable plateau. To further demonstrate the conductance differences, 2D conductance–distance histograms of MBLG-C96, MBLG-C108, and MBLG-C114 are shown in Fig. 2b–d, respectively. It can be seen that all the 2D conductance–distance histograms possess highly distinct intensity clouds, indicating the formation of well-defined single-molecule junctions of MBLGs. The plateau lengths of molecular junctions for MBLG-C96, MBLG-C108, and MBLG-C114 are statistically analyzed to be 1.47 nm, 1.37 nm, and 1.48 nm, which are obviously shorter than the diameter of the carbon skeleton of these MBLGs, suggesting that charge transport takes place in a cross-plane direction. The plateau length of single-MBLG junctions is longer than that of molecular junctions based on PAHs, which only have a single-atom thickness.22 This is consistent with a junction structure composed of a stacked bilayer graphene nanoflake and two graphene electrodes.
To further investigate the influence of the layer number of molecular graphene on charge transport through molecular junctions, C96H24R9 (MSLG-C96, R = mesityl) shown in Fig. 3a was synthesized, in which mesityl groups are grafted to the periphery of the graphene nanoflake to hinder the interlayer stacking. Mass and NMR spectroscopy clearly demonstrated that C96H24R9 adopts a single-layer structure without interlayer stacking in C2D2Cl4 (see Fig. S12 and S13 in the ESI†), and therefore C96H24R9 can be regarded as molecular single-layer graphene (MSLG). The conductance of single-molecule junctions for MSLG-C96 is measured in the mixed solvent of THF/decane, in which two kinds of typical individual conductance–distance traces with high conductance (HC) and low conductance (LC) appear (Fig. 3b). The most probable conductances of HC and LC are determined to be 10−4.48G0 (∼2.56 nS) and 10−5.41G0 (∼0.32 nS) from the corresponding 1D histogram (Fig. 3c). In the corresponding 2D histogram of MSLG-C96 in THF/decane (Fig. 3d), it can be found that the plateau length of molecular junctions for MSLG-C96 with HC (∼1.06 nm) is shorter than that of LC (∼1.44 nm). The conductance value and plateau length of LC are consistent with those of MBLG-C96 in THF/decane, indicating that the dimer of MSLG-C96 may be formed in THF/decane. The conductance curves of HC and LC show uncorrelated relation verified in the 2D cross-correlation histogram shown in Fig. S25,† which indicated that the appearance of each conductance state is independent during the XPBJ process. To validate the formation of the dimer, C2H2Cl4 is mixed with the nonpolar solvent CCl4 (1/9, v/v) as the solvent to avoid MSLG-C96 aggregation. As shown in Fig. 3e, the conductance of molecular junctions for MSLG-C96 is 10−4.49G0 (∼2.51 nS), which is very close to its HC in THF/decane as shown in the green frame in Fig. 3c and e, suggesting that the measured LC of MBLGs could be attributed to their stacked structures in the experiment. In our previous work, it was shown that increasing the number of benzene rings in planar PAHs, enhances the coupling strength between the graphene electrode and molecules and increases the conductance of their molecular junctions.22 However, the conductance of MSLG-C96 with 34 benzene rings is much lower than that of anthanthrene with 6 benzene rings. Our DFT calculations (below) suggest that this is due to the steric hindrance of the peripheral mesityl groups that enlarges the distance between the plane of MSLG-C96 and the graphene electrodes. The 2D conductance–distance histogram also presents a clear molecular plateau (Fig. 3f), with a plateau length of 1.07 nm. The consistent conductance value and plateau length of MSLG-C96 in C2H2Cl4/CCl4 and its HC in THF/decane suggest that the HC in THF/decane is the intrinsic conductance of MSLG-C96. The plateau length difference between MSLG-C96 and MBLG-C96 is 0.40 nm, which matches well with the interlayer distance (∼0.35 nm) of MBLGs revealed by single-crystal X-ray diffraction,24 suggesting the cross-plane charge transport through the MSLG-C96 and the dimers. Besides, to gain a deep understanding of evolution during the pulling process, the averaged conductance values and standard derivations from Gaussian fitting from the 2D histograms for the four nanographene molecules during stretching are calculated and shown in Fig. S24.† The distribution of conductance variations of MSLG-C96 is much wider than that of the other three bilayer graphene molecules, indicating that the interfacial change between molecules and electrodes dominates during the pulling process.
To elucidate the charge transport properties of molecular junctions for MBLG and MSLG observed in the experiment, we calculated the transport properties of MBLG-C96, MBLG-C108, MBLG-C114, and MSLG-C96 using the ab initio density functional theory package SIESTA27 and the quantum transport code GOLLUM.28Fig. 4a and b show the graphene sheets, which form the electrodes in the calculations. The electrons are injected from leads 1 and 2, and collected by leads 3 and 4. Each graphene sheet is extended to ± infinity in the z-direction, while in the y-direction, periodic boundary conditions are used. The MBLGs and MSLG-C96 are placed between the two graphene sheets and their electrical properties are calculated (for details see the ESI†). Fig. 4c shows the average transmission of MBLG-C96, MBLG-C108, MBLG-C96, and MSLG-C96 (see Fig. S28–S32†). Among the three MBLGs, MBLG-C114 has the highest transmission coefficient, originating from the smallest HOMO–LUMO gap and the largest molecular area. MBLG-C108 possesses a higher transmission compared to MBLG-C96, due to a stronger coupling with electrodes (indicated by wider HOMO and LUMO transmission resonances) even though the former has a larger HOMO–LUMO gap than the latter (Table S3†). To understand how the molecules are sandwiched and interact with graphene sheets in the experiment, we calculated the transmission functions for geometries in which the angles between the graphene flake and the side groups are around 90° for those MBLGs. The molecular geometries of MBLG-C108 and MBLG-C96 are obtained from the crystal data. The results show low conductance (10−10 to 10−9G0) between the two graphene sheets (Fig. S28†) compared to the experimental values (10−5 to 10−4G0) (Fig. 2a and 3e). Consequently, it is estimated that the angles between the side mesityl groups and the graphene flake of MBLGs would be smaller than those from the crystal configurations. To demonstrate this feature, we manually rotate the angle of the side groups to 30° and 10°. It is found (Fig. S29–S32†) that the transmission probabilities increase when the angles between the core and the mesityl groups decrease. In other words, the rotation angles of the mesityl groups tune the charge transport between the two graphene sheets. In detail, a higher transmission probability of 10−6 to 10−4G0 was obtained at an angle of 10° while the junctions of 30° show relatively lower transmission functions, which appear in the range of 10−7 to 10−6G0 (Fig. S29†). Considering the dynamic configuration evolution in the pulling process, the average transmission functions are obtained over the 18 molecular junctions with the side groups rotated to 30° and 10° which are represented by the thicker black solid lines (Fig. S29†) and all the colored lines shown in Fig. 4. The higher transmission functions of 10° geometries make the majority contributions to the average ones where the distance between the bottom graphene sheet and the lower flake of MBLGs is 4.3 Å (see Fig. S28 of the ESI† for details).
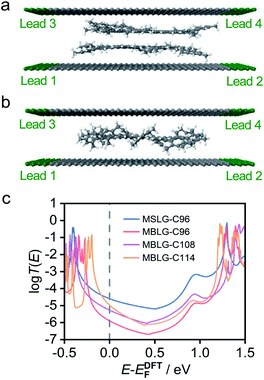 | ||
| Fig. 4 Theoretical simulations for molecular graphene. Sandwiched structures of the molecular junction based on MBLG-C114 (a) and MSLG-C96 (b). (c) The average transmission function of MBLG-C96 (salmon curve), MBLG-C108 (purple curve), MBLG-C114 (orange curve), and MSLG-C96 (blue curve) as a function of the Fermi energy EF, estimated by density functional theory (DFT). The average transmission function is obtained from those of different contact geometries (see Fig. S26–S32† for details). Fermi energy EF is shown by the gray vertical dashed line, which is predicted by DFT. | ||
To demonstrate the effect of the side mesityl groups, the side groups of the monomer were artificially rotated to 20°, 30°, 35°, and 40°. It is found that a side group angle of 40° relative to the plane of MSLG-C96 gives the closest agreement with the experimental conductance. This corresponds to a distance between the bottom graphene sheet and MSLG of 4.7 Å (see Fig. S30†). The distance between the two graphene sheets calculated from 4.7 Å × 2 matches with the separation in the experiment 1.07 Å. To further illustrate our results, many different configurations (Fig. S26†) between the graphene sheets and MSLG-C96 are also considered (see Fig. S30 and S31† for further details). These results demonstrate that the rotation angle of the peripheral mesityl groups could be dramatically different from those in the crystal structure and that charge transport through the molecular junctions of MBLGs and MSLG-C96 is sensitive to the angles between the graphene flake and peripheral mesityl groups. It is also interesting to note that the mesityl groups can also mediate electron transport. This is demonstrated in Fig S32,† where it is shown that by artificially removing the mesityl groups, whilst maintaining the spacing between the graphene electrodes, the electrical conductance is reduced. Finally, it is demonstrated that the large area of the molecule and a smaller HOMO–LUMO gap improve the cross-plane conductance of the molecular junctions, which is consistent with the conclusion of our previous studies on PAHs.22
Conclusions
To conclude, single-molecule vdW heterojunctions based on molecular graphene were fabricated by employing the XPBJ technique. The electrical conductance of molecular junctions based on MBLG-C114 is larger than those of the smaller molecules MBLG-C96 and MBLG-C108, suggesting that the size of MBLG could be used to tune charge transport through vdW heterojunctions. It was found that the molecular junctions based on single-layer molecular graphene are more conductive than double-layer molecular graphene junctions and furthermore, the tunneling distances between MBLG-C96 and MSLG-C96 match the interlayer distance, which is consistent with cross-plane charge transport. DFT calculations demonstrate that the angle between the core of molecular graphene and peripheral mesityl groups has a significant effect on the charge transport through single-molecule graphene junctions, and the flattening of the mesityl groups leads to higher electrical conductance. This work provides new insight into cross-plane transport and interactions in vdW heterojunctions, and highlights new strategies for designing and fabricating electronic devices based on molecular vdW assemblies.Methods
Synthesis of MBLG-C96, MBLG-C108, MBLG-C114, and MSLG-C96
MBLG-C96, MBLG-C108, and MBLG-C114 were synthesized according to previously reported literature.24,25MSLG-C96 was synthesized and the synthetic routes are described in Section S1 of the ESI.†Single-molecule conductance measurements
The single-molecule conductance measurements were performed using the XPBJ technique with a home-built setup at room temperature. For more details, see Section S2 in the ESI.† As reported in previous research,29 the conductance of the graphene–graphene point contact is approximately 10−3G0. Therefore, the conductance traces in 2D histograms are aligned on the x axis (ΔZ) as the zero point when the conductance value is 10−3G0.Theoretical methods
Geometrical optimization was performed using the standard Kohn–Sham self-consistent density functional code SIESTA, with a vdW-DF functional of Dion et al.30 with exchange modified by Berland and Hyldgaard,31 and a double ζ-polarized atomic-orbital basis set for carbon and hydrogen. The cutoff energy was 200 Rydberg, and the force tolerance was 0.02 eV Å−1. To compute their electrical conductance, the MBLGs and MSLG were placed between two graphene electrodes. For each structure, the transmission coefficients T(E) were calculated using the Gollum quantum transport code,28 which uses the DFT mean-field Hamiltonian and overlap matrices from SIESTA27 and T(E) is computed using the following formula| T(E) = Tr[Γ1(E)g(E)Γj(E)g†(E)] | (1) |
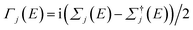 is the anti-Hermitian part of the self-energies Σj, which encode the electronic structure of the semi-infinite electrodes and molecule and the electrode–molecule interface. Γj determines the broadening of transmission resonances due to the contact between the molecule and the electrode j. g0 is Green's function of an isolated molecule. Lastly, the transmission coefficient between lead 1 and lead j, T1j(E) was obtained for electrons of energy E traveling separately from lead 1 to any other leads (j = 2, 3, 4).
is the anti-Hermitian part of the self-energies Σj, which encode the electronic structure of the semi-infinite electrodes and molecule and the electrode–molecule interface. Γj determines the broadening of transmission resonances due to the contact between the molecule and the electrode j. g0 is Green's function of an isolated molecule. Lastly, the transmission coefficient between lead 1 and lead j, T1j(E) was obtained for electrons of energy E traveling separately from lead 1 to any other leads (j = 2, 3, 4).
Data availability
All data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
W. H., Y. Z. T. and C. L. co-supervised the project. S. Z., S. A., and Q. W. wrote the manuscript with input from all authors. S. Z., L. C., H. Z. and G. D. carried out the break junction experiments and analyzed the data. S. Z., W. H., Y. Y. and J. S. built the electrical measurement instrument and wrote the software to control the break junction setup. Z. Y. D., X. J. Z., H. H. and Y. Z. T. synthesized and provided the characterization of the molecules. S. A., Q. W., S. H. and C. L. developed theoretical concepts and conducted modeling and analysis. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21771155 21721001, and 92061103), the National Key R&D Program of China (2017YFA0204902), the Fundamental Research Funds for the Central Universities (Xiamen University: No. 20720190002), and the UK EPSRC grants EP/N017188/1 and EP/M014452/1 in Lancaster.Notes and references
- K. S. Novoselov, V. I. Fal'ko, L. Colombo, P. R. Gellert, M. G. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- C. Tan, X. Cao, X.-J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G.-H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6331 CrossRef CAS PubMed.
- F. R. Fan, R. Wang, H. Zhang and W. Wu, Chem. Soc. Rev., 2021, 50, 10983–11031 RSC.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS PubMed.
- M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young and C. R. Dean, Science, 2019, 363, 1059–1064 CrossRef CAS PubMed.
- J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151–157 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80–84 CrossRef CAS PubMed.
- C. Jin, E. C. Regan, A. Yan, M. Iqbal Bakti Utama, D. Wang, S. Zhao, Y. Qin, S. Yang, Z. Zheng, S. Shi, K. Watanabe, T. Taniguchi, S. Tongay, A. Zettl and F. Wang, Nature, 2019, 567, 76–80 CrossRef CAS PubMed.
- J. Li, X. Yang, Y. Liu, B. Huang, R. Wu, Z. Zhang, B. Zhao, H. Ma, W. Dang, Z. Wei, K. Wang, Z. Lin, X. Yan, M. Sun, B. Li, X. Pan, J. Luo, G. Zhang, Y. Liu, Y. Huang, X. Duan and X. Duan, Nature, 2020, 579, 368–374 CrossRef CAS PubMed.
- K. Tran, G. Moody, F. Wu, X. Lu, J. Choi, K. Kim, A. Rai, D. A. Sanchez, J. Quan, A. Singh, J. Embley, A. Zepeda, M. Campbell, T. Autry, T. Taniguchi, K. Watanabe, N. Lu, S. K. Banerjee, K. L. Silverman, S. Kim, E. Tutuc, L. Yang, A. H. MacDonald and X. Li, Nature, 2019, 567, 71–75 CrossRef CAS PubMed.
- Z. Wang, D. A. Rhodes, K. Watanabe, T. Taniguchi, J. C. Hone, J. Shan and K. F. Mak, Nature, 2019, 574, 76–80 CrossRef CAS PubMed.
- Y. Zhou, J. Sung, E. Brutschea, I. Esterlis, Y. Wang, G. Scuri, R. J. Gelly, H. Heo, T. Taniguchi, K. Watanabe, G. Zaránd, M. D. Lukin, P. Kim, E. Demler and H. Park, Nature, 2021, 595, 48–52 CrossRef CAS PubMed.
- X. Zhu, S. Lei, S.-H. Tsai, X. Zhang, J. Liu, G. Yin, M. Tang, C. M. Torres, A. Navabi, Z. Jin, S.-P. Tsai, H. Qasem, Y. Wang, R. Vajtai, R. K. Lake, P. M. Ajayan and K. L. Wang, Nano Lett., 2018, 18, 682–688 CrossRef CAS PubMed.
- F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga-Alcalde, L. M. K. Vandersypen and H. S. J. van der Zant, Nano Lett., 2011, 11, 4607–4611 CrossRef CAS PubMed.
- A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef CAS PubMed.
- D. Xiang, H. Jeong, T. Lee and D. Mayer, Adv. Mater., 2013, 25, 4845–4867 CrossRef CAS PubMed.
- S. Kaneko, E. Montes, S. Suzuki, S. Fujii, T. Nishino, K. Tsukagoshi, K. Ikeda, H. Kano, H. Nakamura, H. Vázquez and M. Kiguchi, Chem. Sci., 2019, 10, 6261–6269 RSC.
- H. X. Li, M. H. Garner, Z. C. Shangguan, Q. W. Zheng, T. A. Su, M. Neupane, P. P. Li, A. Velian, M. L. Steigerwald, S. X. Xiao, C. Nuckolls, G. C. Solomon and L. Venkataraman, Chem. Sci., 2016, 7, 5657–5662 RSC.
- M. Naher, D. C. Milan, O. A. Al-Owaedi, I. J. Planje, S. Bock, J. Hurtado-Gallego, P. Bastante, Z. M. Abd Dawood, L. Rincón-García, G. Rubio-Bollinger, S. J. Higgins, N. Agraït, C. J. Lambert, R. J. Nichols and P. J. Low, J. Am. Chem. Soc., 2021, 143, 3817–3829 CrossRef CAS PubMed.
- J. Zhou, K. Wang, B. Xu and Y. Dubi, J. Am. Chem. Soc., 2018, 140, 70–73 CrossRef CAS PubMed.
- J. Zheng, J. Liu, Y. Zhuo, R. Li, X. Jin, Y. Yang, Z.-B. Chen, J. Shi, Z. Xiao, W. Hong and Z.-q. Tian, Chem. Sci., 2018, 9, 5033–5038 RSC.
- S. Zhao, Q. Wu, J. Pi, J. Liu, J. Zheng, S. Hou, J. Wei, R. Li, H. Sadeghi, Y. Yang, J. Shi, Z. Chen, Z. Xiao, C. Lambert and W. Hong, Sci. Adv., 2020, 6, eaba6714 CrossRef CAS PubMed.
- S. Zhao, H. Chen, Q. Qian, H. Zhang, Y. Yang and W. Hong, Nano Res., 2021 DOI:10.1007/s12274-021-3687-2.
- X.-J. Zhao, H. Hou, X.-T. Fan, Y. Wang, Y.-M. Liu, C. Tang, S.-H. Liu, P.-P. Ding, J. Cheng, D.-H. Lin, C. Wang, Y. Yang and Y.-Z. Tan, Nat. Commun., 2019, 10, 3057 CrossRef PubMed.
- X.-J. Zhao, H. Hou, P.-P. Ding, Z.-Y. Deng, Y.-Y. Ju, S.-H. Liu, Y.-M. Liu, C. Tang, L.-B. Feng and Y.-Z. Tan, Sci. Adv., 2020, 6, eaay8541 CrossRef CAS PubMed.
- Z. Tan, D. Zhang, H.-R. Tian, Q. Wu, S. Hou, J. Pi, H. Sadeghi, Z. Tang, Y. Yang, J. Liu, Y.-Z. Tan, Z.-B. Chen, J. Shi, Z. Xiao, C. Lambert, S.-Y. Xie and W. Hong, Nat. Commun., 2019, 10, 1748 CrossRef PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029 CrossRef.
- S. Caneva, P. Gehring, V. M. García-Suárez, A. García-Fuente, D. Stefani, I. J. Olavarria-Contreras, J. Ferrer, C. Dekker and H. S. J. van der Zant, Nat. Nanotechnol., 2018, 13, 1126–1131 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- K. Berland and P. Hyldgaard, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc07024j |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |

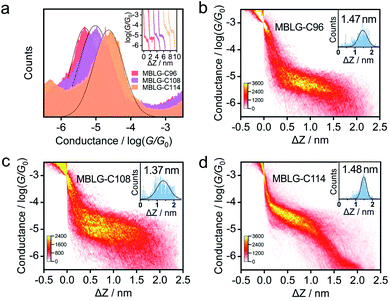
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 traces according to the plateau length. The peaks with Gaussian fitting are the conductance signals. The inset shows the corresponding typical individual conductance–distance traces. (b–d) 2D conductance–distance histograms of MBLG-C96, MBLG-C108, and MBLG-C114 with the corresponding plateau distributions by Gaussian fitting shown in the insets.
000 traces according to the plateau length. The peaks with Gaussian fitting are the conductance signals. The inset shows the corresponding typical individual conductance–distance traces. (b–d) 2D conductance–distance histograms of MBLG-C96, MBLG-C108, and MBLG-C114 with the corresponding plateau distributions by Gaussian fitting shown in the insets.