Open Access Article
Open Access ArticleUnparalleled selectivity and electronic structure of heterometallic [LnLn′Ln] molecules as 3-qubit quantum gates†
Diamantoula
Maniaki
 ab,
Diego
Garay-Ruiz
ab,
Diego
Garay-Ruiz
 cd,
Leoní A.
Barrios
cd,
Leoní A.
Barrios
 ab,
Daniel O. T. A.
Martins
ab,
Daniel O. T. A.
Martins
 ef,
David
Aguilà
ef,
David
Aguilà
 ab,
Floriana
Tuna
ab,
Floriana
Tuna
 ef,
Daniel
Reta
ef,
Daniel
Reta
 ag,
Olivier
Roubeau
ag,
Olivier
Roubeau
 hi,
Carles
Bo
hi,
Carles
Bo
 *cd and
Guillem
Aromí
*cd and
Guillem
Aromí
 *ab
*ab
aDepartament de Química Inorgànica i Orgànica, Secció Química Inorgànica, Universitat de Barcelona, Barcelona, Spain. E-mail: aromi@ub.edu; cbo@iciq.cat
bInstitute of Nanoscience and Nanotechnology of the University of Barcelona (IN2UB), Barcelona, Spain
cInstitute of Chemical Research of Catalonia (ICIQ), The Barcelona Institute of Science and Technology, Av. Països Catalans 16, 43007 Tarragona, Spain
dDepartament de Química Física i Inorgànica, Universitat Rovira i Virgili, Marcel·lí Domingo s/n, 43007 Tarragona, Spain
eDepartment of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
fPhoton Science Institute, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
gKimika Fakultatea, Euskal Herriko Unibertsitatea, UPV/EHU, Donostia International Physics Center (DIPC), IKERBASQUE, Basque Foundation for Science, Donostia, Euskadi, Bilbao, Spain
hInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC-Universidad de Zaragoza, Zaragoza, Spain
iDepartamento de Física de la Material Condensada, Universidad de Zaragoza, Zaragoza, Spain
First published on 14th April 2022
Abstract
Heterometallic lanthanide [LnLn′] coordination complexes that are accessible thermodynamically are very scarce because the metals of this series have very similar chemical behaviour. Trinuclear systems of this category have not been reported. A coordination chemistry scaffold has been shown to produce molecules of type [LnLn′Ln] of high purity, i.e. exhibiting high metal distribution ability, based on their differences in ionic radius. Through a detailed analysis of density functional theory (DFT) based calculations, we discern the energy contributions that lead to the unparalleled chemical selectivity of this molecular system. Some of the previously reported examples are compared here with the newly prepared member of this exotic list, [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) (1) (H2LA and H2LB are two β-diketone ligands). A magnetic analysis extracted from magnetization and calorimetry determinations identifies the necessary attributes for it to act as an addressable, conditional multiqubit spin-based quantum gate. Complementary ab initio calculations confirm the feasibility of these complexes as composite quantum gates, since they present well-isolated ground states with highly anisotropic and distinct g-tensors. The electronic structure of 1 has also been analyzed by EPR. Pulsed experiments have allowed the establishment of the quantum coherence of the transitions within the relevant spin states, as well as the feasibility of a coherent control of these states via nutation experiments.
Introduction
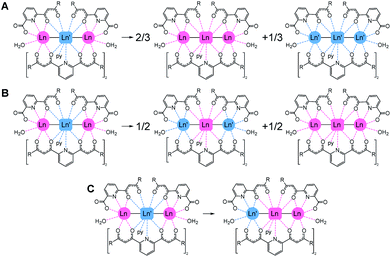
The importance of molecular heterometallic lanthanide species has been recognized in various fields of great current interest. Indeed, the combination of different lanthanides in one material enhances their potential applications in medical imaging (e.g. by enabling multiplex analysis or exploiting up-conversion),1,2 in data transmission and telecommunications3 or within exotic light-emitting diodes.4 The ability to incorporate lanthanides of different atomic numbers selectively at distinct locations of a molecule would offer tremendous advantages to these areas,5–11 with a special bearing on nanotechnology applications.12–14 Recently, lanthanide ions have become promising candidates as quantum bits (qubits) for quantum computing (QC) based on the coherent manipulation of the molecular spin.15–19 In this context, a major step forward is the engineering of heterometallic lanthanide complexes to implement multiqubit quantum gates (qugates).20Most reported heterometallic lanthanide molecules have been obtained following multistep procedures where the different metals are incorporated sequentially.8,9,21–25 On the other hand, methods enabling the selective distribution of metals thermodynamically, despite being more desirable, are very scarce. The reason is that their 4f electrons are highly shielded by occupied 5s and 5p shells, thus hampering the segregation of lanthanides based on chemical reactivity. Interestingly, lanthanide contraction causes a quadratic decrease of their bond distances to donor atoms.26 This property can be used to selectively direct the location of different lanthanide ions to distinct molecular positions. For this, the latter must feature coordination sites that favour different bond lengths, thus leading to heterometallic non-statistical distributions.27,28 In this context, we discovered a coordination scaffold hosting two Ln(III) ions within two distinct coordination environments, following the reaction of Ln(NO3)3 salts with the ligand [3-oxo-3-(2-hydroxyphenyl)propionyl]pyridine-2-carboxylic acid (H3L), which exhibits two different chelating pockets. This reaction yields non-symmetric dinuclear molecules with formula (Hpy)[Ln2(HL)3(NO3)(py)(H2O)2] for all the elements of the 4f series.29–31 Structural analysis of these complexes unveiled that the average Ln–O bond distances to HL2− donors are approximately 0.04 Å longer in one site with respect to the other. The preference of these sites for two metals of different sizes, respectively, was exploited to prepare a large series of dinuclear heterometallic lanthanide complexes of outstanding purity.20,32,33 The remarkable selectivity of this system was corroborated by means of DFT calculations, confirming that larger separations in ionic radii favour the enthalpy of the segregation further.32,34 In view of such properties, these molecules were studied as an excellent platform for the realization of 2-qubit quantum processors, furnishing good quantum coherence features, Rabi oscillations and fulfilling the basic requirements to act as CNOT or SWAP qugates.19,20,35 We expanded the above methodology with the simultaneous use of two ligands, H2LA and H2LB (Fig. 1), both containing the same two types of chelating pockets as H3L: a tridentate O,N,O and a bidentate O,O one. Mixing both donors with combinations of two Ln(NO3)3 salts gives access to a unique family of trinuclear heterometallic complexes with formula [Ln2Ln′(LA)2(LB)2(py)(H2O)2](NO3).36,37 This molecular architecture disposes three lanthanide ions in a linear LnLn′Ln sequence, linked by monoatomic bridges that ensure a weak magnetic interaction between them. These features render the trinuclear clusters as very interesting candidates to implement 3-qubit quantum gates. The [ErCeEr] analogue was shown recently to embody a molecular device incorporating a quantum bit provided with a quantum error correction mechanism.37
 | ||
| Fig. 1 Representation of ligands 6-(3-(naphthalene-2-yl)-3-oxopropanoyl)-picolinic acid (H2LA)36 and 2,6-bis[(3-oxo-3-naphth-2-yl)propionyl]pyridine (H2LB)38 in their fully diketone forms. | ||
We show in this paper a theoretical analysis concluding that for this molecular architecture, the thermodynamically controlled selectivity in distributing different Ln metals at predetermined positions is unparalleled. For this study, we have performed density functional theory (DFT) based calculations on a novel member of the series with metal composition [ErPrEr] (1), presented here, as well as on the reported analogues36,37 [HoCeHo] (2), [ErCeEr] (3), [YbCeYb] (4), [LuCeLu] (5) and [ErLaEr] (6). The suitability as multiqubit quantum gates of these molecules is assessed through a combination of appropriate techniques. Specifically, we need to prove that the following requirements are fulfilled.
(A) Qubit addressability. Addressing qubits specifically requires magnetically unique metals in the molecule. The unambiguous existence of two different qubits at selective positions (here a central one, next to the two peripheral ones) is proven by single-crystal X-ray diffraction (SCXRD), mass spectrometry (MS), metal microanalysis and DFT calculations.
(B) Good qubit definition. This necessitates proof that the metals display two well defined magnetic states to encode the binary information, well separated from any other excited state. This is probed with the magnetic measurements and the results of ab initio complete active space self-consistent spin–orbit (CASSCF-SO) calculations on each individual lanthanide ion in 1, 5 and 6.
(C) Interqubit interaction. The implementation of conditional qugates requires a weak interaction between qubits that does not remove their ability to be factorized. The weak interaction is estimated through specific heat measurements.
(D) Quantum coherence. The magnetic states involved during the quantum processing of information need to exhibit quantum coherence. This property has been evaluated through a complete pulsed EPR analysis of 1.
This investigation illustrates the potential of this unique family of heterometallic [LnLn′Ln] molecules, especially for the design of three-qubit quantum gates.
Results and discussion
Synthesis and structure of [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) (1)
Ligands H2LA and H2LB in equal molar amounts were made to react in pyridine solution with stoichiometric quantities of Er(NO3)3 and Pr(NO3)3 to obtain [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) (1). Addition of one equivalent of CuCl2 was necessary for the crystallization of 1, as found previously serendipitously,36 presumably for its role of modulator of the self-assembly and/or crystallization process (see below).39 Diffusing hexane into the reaction mixture led to the formation of large yellow crystals of 1 suitable for SCXRD, together with green crystals of [Cu(py)4(NO3)2]. Both products were very easy to separate manually. The balanced equation below helps to interpret the role of CuCl2 as a modulator in the crystallization of 1.| 2Er(NO3)3 + Pr(NO3)3 + 2H2LA +2H2LB + 4CuCl2 + 25py + 2H2O → [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) + 4[Cu(py)4(NO3)2] + 8HpyCl |
The crystal lattice of 1 is found in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , with an asymmetric unit composed of one main complex cation, its NO3− counter ion, and ten molecules of pyridine (some disordered), the unit cell including two such ensembles. The complex cation [Er2Pr(LA)2(LB)2(py)(H2O)2]+ (Fig. 2 and S1†) consists of a heterometallic cluster with the metals disposed in a linear [Er⋯Pr⋯Er] fashion (forming an angle of 174.18°, with an Er⋯Er separation of 7.910 Å, and Pr⋯Er distances of 3.961 and 3.959 Å, respectively). The refinement of the structure provides strong initial evidence of the proposed distribution of the metals in this molecule since the agreement parameters obtained for any other distribution were significantly worse. The Er(III) ions are linked to the central Pr(III) metal, each by three monoatomic O-bridges from the alkoxide-like moieties of two LB2− and one LA2− ligand. Each Er centre is in turn chelated by these three ligands through one O,N,O dipicolinate-like (LA2−) and two O,O β-diketonate (LB2−) pockets. In this manner, the four ligands of the cluster converge on the central Pr ion chelating it with two O,O (LA2−) and two O,N,O (LB2−) pockets respectively.
, with an asymmetric unit composed of one main complex cation, its NO3− counter ion, and ten molecules of pyridine (some disordered), the unit cell including two such ensembles. The complex cation [Er2Pr(LA)2(LB)2(py)(H2O)2]+ (Fig. 2 and S1†) consists of a heterometallic cluster with the metals disposed in a linear [Er⋯Pr⋯Er] fashion (forming an angle of 174.18°, with an Er⋯Er separation of 7.910 Å, and Pr⋯Er distances of 3.961 and 3.959 Å, respectively). The refinement of the structure provides strong initial evidence of the proposed distribution of the metals in this molecule since the agreement parameters obtained for any other distribution were significantly worse. The Er(III) ions are linked to the central Pr(III) metal, each by three monoatomic O-bridges from the alkoxide-like moieties of two LB2− and one LA2− ligand. Each Er centre is in turn chelated by these three ligands through one O,N,O dipicolinate-like (LA2−) and two O,O β-diketonate (LB2−) pockets. In this manner, the four ligands of the cluster converge on the central Pr ion chelating it with two O,O (LA2−) and two O,N,O (LB2−) pockets respectively.
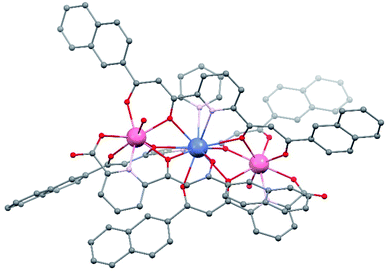 | ||
| Fig. 2 Representation of the molecular structure of the complex cation of [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) (1). Colors: pink, Er; blue, Pr; red, O; grey, C; purple, N. Hydrogen atoms not shown. | ||
The selectivity for the metal allocation within the molecule of 1 was ascertained in solution by mass spectrometry (MS). Electrospray ionization (ESI) MS diagrams (Fig. S3 to S6†) exhibit pristine signals of the [Er2Pr(LA)2(LB)2]+ and ([Er2Pr(LA)2(LB)2] + H+)2+ fragments with no trace of any other metal composition for these moieties. These results were consistent with the very satisfactory outcome of inductively coupled plasma (ICP) metal analysis (ESI†), which is especially informative, given the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of the metals within this molecule; any random scrambling would be extremely unlikely to furnish only species with a Pr
2 molar ratio of the metals within this molecule; any random scrambling would be extremely unlikely to furnish only species with a Pr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Er ratio of 1
Er ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, exactly as in the structure [ErPrEr] suggested by the crystal data.
2, exactly as in the structure [ErPrEr] suggested by the crystal data.
Analysis of metal selectivity through DFT studies
DFT based calculations on 1–6 were performed in order to investigate their relative stability and metal selectivity. For this, three scrambling pathways have been explored for each [LnLn′Ln] complex (Fig. 3), where Ln′ and Ln refer to ions with larger and smaller ionic radii, respectively. The energy associated with these processes has been adjusted to the evolution of one mole of the starting compound.For each reaction path, molecular geometries were optimised using the BP86 functional within the ADF2019 program, resulting in 25 individual structures. Table 1 lists the energies calculated for each scrambling process.
| Complex | Δr | ΔE(A) | ΔE(B) | ΔE(C) |
|---|---|---|---|---|
| a Complexes with Yb as the central ion ([YbYbYb], [CeYbYb] and [CeYbCe]) are handled without a bonded pyridine molecule in this position, in analogy with the dimeric [LaYb] complex reported previously.34 | ||||
| [HoCeHo] | 0.258 | 7.5 | 12.7 | 14.0 |
| [ErPrEr] | 0.262 | 11.7 | 17.9 | 17.7 |
| [ErCeEr] | 0.269 | 10.0 | 16.3 | 17.0 |
| [YbCeYb]a | 0.288 | 17.3 | 26.2 | 26.3 |
| [ErLaEr] | 0.295 | 13.8 | 22.8 | 22.0 |
| [LuCeLu] | 0.296 | 14.1 | 21.7 | 22.4 |
The calculated energies show that the predicted [LnLn′Ln] distribution (i.e. the large metal in the middle and the small ones on the sides) is always the preferred one. The ionic radii of the Ln(III) species are remarkably dependent on the coordination number (CN) of the ion (CN = 11 at the central position and CN = 8 at the sides). Thus, in order to compute Δr (difference in ionic radius between central Ln and side Ln′ cations), we considered a recent extension of Shannon's ionic radii, covering a wide variety of coordination numbers and oxidation states.40 A plot of the computed scrambling energies versus Δr (Fig. 4, top) indicates a few interesting trends: (i) the energies for processes ‘B’ and ‘C’ are very comparable and systematically larger than those for pathway ‘A’, with gaps ranging 5.2 to 9.0 kcal mol−1. This suggests that transformations leading to homometallic analogues are favoured compared to paths swapping the metals from their preferred positions, which indicates that not only contributions from the first coordination sphere are important but also the overall structure of the molecule. (ii) While the observed correlation between Δr and ΔE is not very regular, the pattern is maintained with high fidelity by the three pathways. This adds confidence to the calculations and corroborates that besides Δr, the accommodation within the ensemble of the molecular structure of a given combination of metals plays a role.
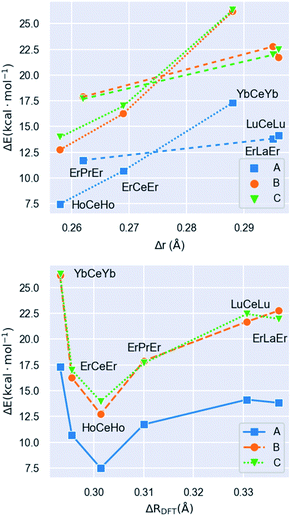 | ||
| Fig. 4 Molar energies (ΔE) associated with processes ‘A’, ‘B’ and ‘C’ represented in Fig. 3versus (top) Δr and versus (bottom) ΔRDFT (this parameter is the difference between the median Ln–O distances at the central and the side ions, see text), for complexes 1 to 6. In the upper plot, dotted and dashed lines are used to distinguish the two identifiable patterns of the data. | ||
The lack of an overall energy vs. Δr correlation (Fig. 4, top) can be justified by the presence of two distinct trends: a steep one (dotted line, [HoCeHo] – [ErCeEr] – [YbCeYb]) and a flatter one (dashed line, [ErPrEr] – [ErLaEr] – [LuCeLu]). This is due to the molecular structure having to accommodate different combinations of metals. To assess this accommodation effect, we computed the median Ln–O distances at the central and the side ions in complexes 1–6 from the DFT-optimized geometries, furnishing a distance difference adapted to the structure of each complex (ΔRDFT; Fig. 4, bottom). Under this new descriptor, selectivity appears large for low ΔRDFT values, sharply drops with increasing ΔRDFT (until [HoCeHo]), and then rises smoothly to reach a plateau for [LuCeLu] and [ErLaEr]. Interestingly, the ordering of the complexes with respect to Δr (computed a priori for a given ion arrangement) is very different from how they range according to ΔRDFT (computed a posteriori after full DFT geometry optimization). However, two different trends are again observed for the two groups of complexes identified on the previous analysis, a steep one (with negative slope) and a flatter one (with positive slope). The presence of two trends with the same two groups is a source of consistency between both approaches.
The above results confirm that the selectivity in the [LnLn′Ln] series is indeed superior to that of the related family of dinuclear [LnLn′] complexes previously published. For example, the lowest calculated value of the energy cost for swapping two metals in the trinuclear family (14.0 kcal mol−1 in [HoCeHo]) is larger than the highest value seen for the analogous process in the dinuclear series (11.7 kcal mol−1 for [LaYb]).34 In addition, the least favourable value of formation energy from homometallic precursors (pathway opposite to ‘A’) obtained here (−7.5 kcal mol−1 for [HoCeHo]) overcomes the analogous energy of formation for all the analysed [LnLn′] complexes, with only one exception (that of [LaEr], with molar energy of formation of −14.2 kcal mol−1).
Magnetothermal properties of [ErPrEr] (1)
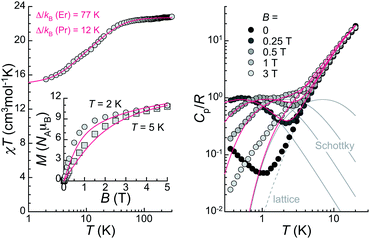
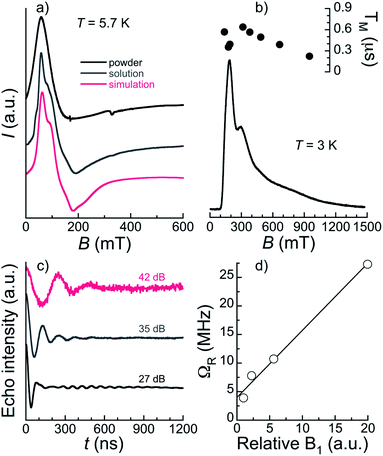
The bulk magnetic properties of 1 were studied through variable temperature bulk magnetic susceptibility and isothermal, variable field magnetization measurements. The χT vs. T plot (Fig. 5, left) shows a value of χT at 300 K of 22.82 cm3 K mol−1, very close to the value of 22.74 cm3 K mol−1 expected for two Er(III) (4I15/2; L = 6, S = 3/2, J = 15/2) and one Pr(III) ion (3H4; L = 5, S = 1, J = 4) with no interactions among them. The decline observed with decreasing the temperature, down to 15.51 at 2 K, is tentatively attributed to depopulation of the Kramers and non-Kramers doublets embedded within the J = 15/2 and J = 4 states, respectively; a weak antiferromagnetic interaction may also have an effect at the lowest temperatures (see below). In fact, the χT vs. T plot can be simulated by the sum of a simplified van Vleck susceptibility model for two Er(III) and one Pr(III) ions,41 indicating that the interaction is likely very weak (Fig. 5, left). The model considers two spin doublets with an energy gap Δ/kB of 77 K for [ErLaEr],37 and fitted to 12 K for Pr. These results show that both Pr(III) and Er(III) ions in 1 behave as two-level spin systems at sufficiently low temperatures. M vs. H data (inset in Fig. 5, left) at 2 and 5 K exhibit abrupt increases with increasing field levelling off at 10.96 and 10.79 μB, respectively, in the unsaturated region. The latter is likely the result of the population of excited states.Continuous-wave (CW) EPR spectra collected at the X-band and T = 5.7 K for 1 both in the solid-state and as a frozen solution (5 mM in a mixture of deuterated methanol/ethanol/dmso in a ratio 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v/v) are shown in Fig. 6a. The spectra are very similar confirming that the [ErPrEr] molecule is stable in solution and that solvation does not significantly alter its magnetic properties. The frozen solution spectrum is better resolved, as a result of the narrowing of EPR lines due to the reduction of intermolecular dipolar interactions. The spectra can be simulated satisfactorily using the gEr tensor determined previously for [ErLaEr] and gPr = 3.4. The latter may not be determined with high accuracy because the spectrum is largely dominated by the contributions of Er ions. Indeed, the spectra are relatively similar to those of [ErCeEr] studied previously.37
1 v/v/v) are shown in Fig. 6a. The spectra are very similar confirming that the [ErPrEr] molecule is stable in solution and that solvation does not significantly alter its magnetic properties. The frozen solution spectrum is better resolved, as a result of the narrowing of EPR lines due to the reduction of intermolecular dipolar interactions. The spectra can be simulated satisfactorily using the gEr tensor determined previously for [ErLaEr] and gPr = 3.4. The latter may not be determined with high accuracy because the spectrum is largely dominated by the contributions of Er ions. Indeed, the spectra are relatively similar to those of [ErCeEr] studied previously.37
Specific heat, Cp, measurements as a function of the temperature under various applied magnetic fields were performed in the range 0.35–20 K (Fig. 5, right). The data are reminiscent of those of [ErCeEr], with Schottky-type anomalies under applied fields, and a contribution in zero-field at the lowest temperatures not present in the case of [ErLaEr]. The Schottky anomalies are the expected outcome of the presence of few accessible energy levels, thus confirming the assumption that the lanthanide centres in 1 behave as two-level systems at these low temperatures. Meanwhile, the zero-field feature suggests the existence of an additional energy splitting between the spin levels arising from a non-zero magnetic exchange coupling between the central Pr(III) spin and the two Er(III) spins. The in-field data are well reproduced by the sum of a lattice contribution and Schottky-type anomalies calculated for fields B + Bint, where Bint stands as an interaction field arising from dipolar interactions. The intramolecular exchange interaction is in turn very weak (probably <0.1 cm−1), considering the similarity of the zero-field data with those of [ErCeEr].37 This explains why no magnetic exchange is detected in DC magnetization experiments.
Electronic structure calculations
The above results demonstrate a very small magnetic interaction between Ln ions in 1. We take advantage of this and calculate the electronic structure of the independent spin-bearing centres using a simplified model where only one Ln ion is explicitly considered, the other two being substituted by their diamagnetic analogues, i.e. systems [ErLaLu], [LuPrLu] and [LuLaEr]. We employ the atomic coordinates from the SCXRD experimental structure of [ErPrEr] (1), without performing any geometry optimisation. The electronic structures of Er and Pr were determined by means of CASSCF-SO-RASSI calculations (details in the ESI, Table S6†) using OpenMolcas. This methodology has consistently succeeded at describing the electronic structure of lanthanides42–44 and so it is well suited to address the basic aspects that make a spin-bearing center a good qubit, namely the character of the electronic ground state (wavefunction composition and g-values) and its energy separation from excited states.To assess the validity of our approach, we compare calculated g-values of the ground state to available experimental data on [ErLaEr] (6), obtained by CW X-band EPR,37 finding a very good agreement (CASSCF-SO: [1.5, 4.2, 10.8] for [ErLaLu], [2.2, 4.6, 10.5] for [LuLaEr], EPR: [1, 5 ± 0.3, 11.5 ± 0.3]). The g-value of 3.55 calculated for the ground state of [LuPrLu] is also in good agreement with the gPr value of 3.4 determined here through CW-EPR on [ErPrEr]. Additionally, the experimental bulk magnetization data of compounds [ErPrEr] (1), [LuCeLu] (5) and [ErLaEr] (6)37 can be reproduced as the sum of the contributions from independent Ln ions. For [ErLaEr] (6), we observe a very good agreement at low temperatures (in the susceptibility, Fig. S10†) and low fields (<1 T, in the magnetisation curves), which deteriorates only as the latter variables increase (inset in Fig. S10†). This indicates that the description of the ground doublet is accurate, as suggested by the good agreement with the g-values. However, the disagreement at higher fields and temperatures indicates that CASSCF-SO underestimates the energy separation with the excited states (the approximate fit of the experimental data estimated a first separation from the ground state of 77 K, versus the calculated 20 K). For [ErPrEr] (1), the discrepancies in the magnetization do not follow the same correlation as for 6 while the overall agreement is better (inset in Fig. 5, left). For [LuCeLu] (5), included to validate the approach against available experimental data on a monomeric paramagnetic compound, the agreement is very good, with only a slight overestimation at higher fields, again probably due to CASSCF underestimating the energy gap to the first excited state (Fig. S11†). Some of the CASSCF shortcomings could be addressed by expanding the considered active space and/or including dynamical correlation, however, the size of these molecules makes this practically impossible. Another unavoidable source of error is the exact structure used for the calculation – for 6, both Er sites studied are chemically equivalent but not crystallographically identical, and we observed that small structural differences cause significant disparities in the electronic parameters (Tables S7 and S9†). Furthermore, the results from microanalysis on the [LnLn′Ln] molecules consistently show replacement of pyridine molecules of crystallization by molecules of atmospheric water. The associated changes to the structural parameter of these molecular exchanges cannot be determined, while a geometry optimization would not solve this uncertainty. Therefore, we conclude that despite the various shortcomings, the applied methodology (i) correctly describes the investigated macroscopic magnetic properties and (ii) can assess whether a Ln ion in a given pocket offers a qubit that can be integrated into an addressable quantum gate.
Quantum coherence and coherent control
The magnetothermal characterization of 1 described above indicates that [ErPrEr] has very similar Zeeman energy levels as previously determined for [ErCeEr], so that it should also allow implementing a three qubit repetition code.37 A further requirement is that all the involved transitions can be induced coherently, which depends on the spin-lattice and spin–spin quantum coherence times. The spin dynamics of 1 were thus studied on diluted frozen deuterated solutions through time-domain X-band EPR. Using a 2-pulse Hahn echo sequence, an electron spin echo (ESE) signal was detected over a very wide field range spanning 100 mT to 1.5 T. A characteristic echo-detected field-swept (EDFS) EPR spectrum is shown in Fig. 6b. We note that the shape of the EDFS spectrum depends on the interpulse delay, τ, most likely due to strong modulation in the ESE decay. This was already observed in a [Gd2] complex proposed to host 6 qubits,19 and is the reason why the EDFS spectra do not strictly coincide with the CW spectrum. We note that this was also the case for [ErCeEr].37 The observation of an echo-induced spectrum covering all accessible transitions suggests that coherent manipulation of all the relevant spin states should be possible.Phase memory times TM and spin-lattice relaxation times T1 were measured at several field positions through Hahn-echo and inversion recovery pulse sequences, respectively (Fig. S13–S16†). T1 was found to be in the range 70–300 μs (see ESI† for details) for 2.5 and 5 mM concentrations at 3 and 5 K and for fields from 145 to 700 mT (Table S11†). These spin-lattice relaxation times are relatively long compared to most other Ln systems studied as qubits16,19,45 and ensure that the different spin states can be initialized while TM should not be limited by T1 in these temperature and field conditions. Indeed, TM at 3 K on a 2.5 mM frozen solution is found below the μs, in the 0.35–0.64 μs range over the main part of the EDFS spectrum and only decreasing to 0.22 μs at 1 T (see Table S11† and Fig. 6b). The maximum TM of 0.64 μs is obtained at 330 mT and compares favourably with the value of 0.5 μs reported for the [ErCeEr] molecule. While still modest, this quantum coherence surpasses the estimated value of 0.5 μs for which an advantage is obtained by using the error correction code.37
Spin nutation experiments were performed at 330 mT and 3 K to evaluate the ability to coherently manipulate the spin states in [ErPrEr]. These involve the measurement of the ESE generated by a variable duration pulse (0.1 ≤ tp ≤ 1.2 μs) refocused by a π pulse (see ESI† for details). Representative results are shown in Fig. 6c for various attenuation values of microwave power, evidencing the observation of Rabi oscillations. These coherent oscillations decay relatively fast, which is likely a consequence of working with frozen solutions, in addition to the modest TM measured in the system. Indeed, the excitation of randomly oriented molecules by the microwave pulse produces Rabi oscillations between different states, as well as different Rabi frequencies, resulting in a faster decay than for a single coherent transition. Here, this is particularly true for lower attenuations, while at the strongest attenuation of 42 dB the oscillation remains detectable up to values of tp in the range of TM. Rabi frequencies were determined by Fourier transformation of the nutation signal (Fig. S17†) and are shown in Fig. 6d. A linear variation of the Rabi frequency with the relative microwave magnetic field intensity B1 is observed, as expected for a quantum system. At low attenuations, an additional narrow component is detected whose frequency does not vary with the field and coincides with that of the Larmor frequency of 1H (see Fig. S17†). It can thus be ascribed to Hartmann–Hahn cross polarization with protons,46 indicating that at least one source of quantum decoherence of the [ErPrEr] spin states arises from the coupling with surrounding protons nuclear spins. Ligand deuteration could thus be an efficient means to improve TM.
Overall, [ErPrEr] presents significant quantum coherence over the whole field span of its transitions, which together with the ability to coherently manipulate its spin states demonstrates it is a viable multi-qubit system to implement quantum error correction protocols.
Conclusions
The β-diketones H2LA and H2LB in combination with binary mixtures of Ln(NO3)3 salts in solution form a coordination architecture capable of distributing two different lanthanides in a [LnLn′Ln] disposition with great selectivity, based on their different atomic radius. DFT calculations have confirmed quantitatively this unparalleled discriminating ability, unveiling scrambling energies of up to 26 kcal mol−1. The analysis of the electronic structure of the new complex [Er2Pr(LA)2(LB)2(py)(H2O)2](NO3) (1) by magnetization and calorimetric measurements confirms that the Ln ions exhibit the requirements to embody spin-based qubits within a potential molecular quantum gate, where they are addressable. Ab initio calculations support these results and afford a satisfactory simulation of the experimental magnetic data by assuming magnetically independent Ln ions. The quantum coherence of complex 1 has been investigated in depth through pulsed EPR experiments, yielding phase memory times TM up to 0.64 μs and allowing coherent control through nutation experiments. Highly selective heterometallic lanthanide complexes are very rare, especially if made in one step reactions. This is absolutely unprecedented for trinuclear systems. This architecture is especially relevant in its capacity to provide platforms of possible three-qubit quantum gates and molecular quantum devices capable of performing complex operations and protocols.Data availability
The structures of the optimized complexes used in this paper are available as a dataset collection in the ioChem-BD repository and can be accessed through the following link https://doi.org/10.19061/iochem-bd-1-227.Author contributions
DM synthesized and crystallized the [ErPrEr] complex. DGR prepared and performed the DFT calculations. LAB made the organic ligand and obtained and solved the SCXRD data. DA originally devised the synthesis of the coordination complexes and contributed to the analysis of crystallographic and mass spectrometry data. He supervised the inorganic synthesis. DOTAM collected and prepared the EPR data. FT interpreted the EPR data and wrote the corresponding discussion. DR performed the ab initio calculations and wrote the corresponding discussion. OR performed the magnetocaloric experiements, fitted the data and wrote the corresponding discussion. CB interpreted the DFT data and wrote the corresponding discussion. GA organized the whole paper, wrote a large part of it and oversaw the full discussion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the European Union's Horizon 2020 research and innovation programmes QUANTERA project SUMO and FET-OPEN grant 862893 FATMOLS (GA and OR) the Spanish AEI for grants PGC2018-098630-B-I00 (GA and DA), PID2020-118329RB-I00 (OR), PID2020-112806RB-I00 (DGR and CB) and the Severo Ochoa Excellence Accreditation 2020–2023 CEX2019-000925-S (DGR and CB), the ICIQ foundation (DGR and CB) and the Generalitat de Catalunya for a Beatriu de Pinós fellowship (2019-BP-00015, DR), an FI grant (also financed by AGAUR and the European Social Fund, DGR) an FI-SDUR Grant (2020-FISDU-00492, DM), the CERCA program and the ICREA Academia 2018 Prize (GA), as well as the National EPR Facility at the University of Manchester for support with the EPR measurements. This work used resources of the ALBA synchrotron through access to beamline 13-XALOC.Notes and references
- H. H. Gorris and O. S. Wolfbeis, Angew. Chem., Int. Ed., 2013, 52, 3584–3600 CrossRef CAS PubMed.
- J. T. Xu, J. J. Zhou, Y. H. Chen, P. P. Yang and J. Lin, Coord. Chem. Rev., 2020, 415, 19 CrossRef.
- T. Soukka, T. Rantanen and K. Kuningas, Ann. N. Y. Acad. Sci., 2008, 1130, 188–200 CrossRef CAS PubMed.
- N. Thejo Kalyani and S. J. Dhoble, Renewable Sustainable Energy Rev., 2012, 16, 2696–2723 CrossRef CAS.
- S. Lis, M. Elbanowski, B. Mąkowska and Z. Hnatejko, J. Photochem. Photobiol., A, 2002, 150, 233–247 CrossRef CAS.
- F. Artizzu, A. Serpe, L. Marchiò, M. Saba, A. Mura, M. L. Mercuri, G. Bongiovanni, P. Deplano and F. Quochi, J. Mater. Chem. C, 2015, 3, 11524–11530 RSC.
- L. Abad Galán, A. N. Sobolev, B. W. Skelton, E. Zysman-Colman, M. I. Ogden and M. Massi, Dalton Trans., 2018, 47, 12345–12352 RSC.
- S. Faulkner and S. J. A. Pope, J. Am. Chem. Soc., 2003, 125, 10526–10527 CrossRef CAS PubMed.
- A. Nonat, S. Bahamyirou, A. Lecointre, F. Przybilla, Y. Mély, C. Platas-Iglesias, F. Camerel, O. Jeannin and L. J. Charbonnière, J. Am. Chem. Soc., 2019, 141, 1568–1576 CrossRef CAS PubMed.
- H. Yao, G. Calvez, C. Daiguebonne, K. Bernot, Y. Suffren and O. Guillou, Inorg. Chem., 2019, 58, 16180–16193 CrossRef CAS PubMed.
- L. S. Natrajan, Curr. Inorg. Chem., 2011, 1, 61–75 CrossRef CAS.
- Y. H. Lan, S. Klyatskaya, M. Ruben, O. Fuhr, W. Wernsdorfer, A. Candini, V. Corradini, A. L. Rizzini, U. del Pennino, F. Troiani, L. Joly, D. Klar, H. Wende and M. Affronte, J. Mater. Chem. C, 2015, 3, 9794–9801 RSC.
- J. J. Le Roy, J. Cremers, I. A. Thomlinson, M. Slota, W. K. Myers, P. H. Horton, S. J. Coles, H. L. Anderson and L. Bogani, Chem. Sci., 2018, 9, 8474–8481 RSC.
- R. Sato, K. Suzuki, M. Sugawa and N. Mizuno, Chem.–Eur. J., 2013, 19, 12982–12990 CrossRef CAS PubMed.
- E. Moreno-Pineda, D. O. T. A. Martins and F. Tuna, in Electron Paramagnetic Resonance, The Royal Society of Chemistry, 2021, vol. 27, pp. 146–187 Search PubMed.
- G. Aromí and O. Roubeau, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2019, vol. 56, pp. 1–54 Search PubMed.
- G. Aromí, F. Luis and O. Roubeau, in Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-WCH, 2015, pp. 185–221, DOI: DOI:10.1002/9783527673476.ch7.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- F. Luis, P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, D. Aguilà, J. I. Martínez, L. A. Barrios and G. Aromí, Commun. Chem., 2020, 3, 176 CrossRef CAS.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- L. S. Natrajan, A. J. L. Villaraza, A. M. Kenwright and S. Faulkner, Chem. Commun., 2009, 6020–6022 RSC.
- I. Mamedov, T. N. Parac-Vogt, N. K. Logothetis and G. Angelovski, Dalton Trans., 2010, 39, 5721–5727 RSC.
- M. P. Placidi, A. J. L. Villaraza, L. S. Natrajan, D. Sykes, A. M. Kenwright and S. Faulkner, J. Am. Chem. Soc., 2009, 131, 9916–9917 CrossRef CAS.
- C. D. Buch, S. H. Hansen, D. Mitcov, C. M. Tram, G. S. Nichol, E. K. Brechin and S. Piligkos, Chem. Sci., 2021, 12, 6983–6991 RSC.
- J.-P. Costes and F. Nicodème, Chem.–Eur. J., 2002, 8, 3442–3447 CrossRef CAS.
- M. Seitz, A. G. Oliver and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 11153–11160 CrossRef CAS PubMed.
- F. Artizzu, F. Quochi, L. Marchiò, E. Sessini, M. Saba, A. Serpe, A. Mura, M. L. Mercuri, G. Bongiovanni and P. Deplano, J. Phys. Chem. Lett., 2013, 4, 3062–3066 CrossRef CAS.
- N. Dalla-Favera, J. Hamacek, M. Borkovec, D. Jeannerat, G. Ercolani and C. Piguet, Inorg. Chem., 2007, 46, 9312–9322 CrossRef CAS PubMed.
- D. Aguilà, L. A. Barrios, V. Velasco, L. Arnedo, N. Aliaga-Alcalde, M. Menelaou, S. J. Teat, O. Roubeau, F. Luis and G. Aromí, Chem.–Eur. J., 2013, 19, 5881–5891 CrossRef PubMed.
- D. Aguilà, L. A. Barrios, F. Luis, A. Repollés, O. Roubeau, S. J. Teat and G. Aromí, Inorg. Chem., 2010, 49, 6784–6786 CrossRef PubMed.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed.
- D. Aguilà, V. Velasco, L. A. Barrios, J. Gonzalez-Fabra, C. Bo, S. J. Teat, O. Roubeau and G. Aromí, Inorg. Chem., 2018, 57, 8429–8439 CrossRef PubMed.
- L. Abad Galán, D. Aguilà, Y. Guyot, V. Velasco, O. Roubeau, S. J. Teat, M. Massi and G. Aromí, Chem.–Eur. J., 2021, 27, 7288–7299 CrossRef PubMed.
- J. González-Fabra, N. A. G. Bandeira, V. Velasco, L. A. Barrios, D. Aguilà, S. J. Teat, O. Roubeau, C. Bo and G. Aromí, Chem.–Eur. J., 2017, 23, 5117–5125 CrossRef PubMed.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682–16693 RSC.
- V. Velasco, L. A. Barrios, M. Schütze, O. Roubeau, F. Luis, S. J. Teat, D. Aguilà and G. Aromí, Chem.–Eur. J., 2019, 25, 15228–15232 CrossRef CAS.
- E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, L. A. Barrios, J. I. Martínez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337–10343 RSC.
- L. A. Barrios, E. Peyrecave-Lleixa, G. A. Craig, O. Roubeau, S. J. Teat and G. Aromí, Eur. J. Inorg. Chem., 2014, 6013–6021 CrossRef CAS.
- R. S. Forgan, Chem. Sci., 2020, 11, 4546–4562 RSC.
- A. A. B. Baloch, S. M. Alqahtani, F. Mumtaz, A. H. Muqaibel, S. N. Rashkeev and F. H. Alharbi, Phys. Rev. Mater., 2021, 5, 043804 CrossRef CAS.
- E. Bartolomé, P. J. Alonso, A. Arauzo, J. Luzón, J. Bartolomé, C. Racles and C. Turta, Dalton Trans., 2012, 41, 10382–10389 RSC.
- C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724 CrossRef CAS PubMed.
- J. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem.–Eur. J., 2019, 25, 7749–7758 CrossRef CAS PubMed.
- O. Stetsiuk, L. La Droitte, V. Goudy, B. Le Guennic, O. Cador and G. Nocton, Organometallics, 2022, 41, 133–140 CrossRef CAS.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- S. R. Hartmann and E. L. Hahn, Phys. Rev., 1962, 128, 2042–2053 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis, crystallographic tables and figures, DFT methods, physical measurements, and simulation details. CCDC 2142740. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc00436d |
| This journal is © The Royal Society of Chemistry 2022 |