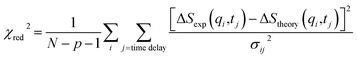Open Access Article
Open Access ArticleReaction dynamics studied via femtosecond X-ray liquidography at X-ray free-electron lasers
Eun Hyuk
Choi
 abc,
Yunbeom
Lee
abc,
Yunbeom
Lee
 abc,
Jun
Heo
abc,
Jun
Heo
 abc and
Hyotcherl
Ihee
abc and
Hyotcherl
Ihee
 *abc
*abc
aDepartment of Chemistry, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, 34141, Republic of Korea. E-mail: hyotcherl.ihee@kaist.ac.kr
bKI for the BioCentury, Korea Advanced Institute of Science and Technology (KAIST), Daejeon, 34141, Republic of Korea
cCenter for Advanced Reaction Dynamics, Institute for Basic Science (IBS), Daejeon, 34141, Republic of Korea
First published on 6th June 2022
Abstract
X-ray free-electron lasers (XFELs) provide femtosecond X-ray pulses suitable for pump–probe time-resolved studies with a femtosecond time resolution. Since the advent of the first XFEL in 2009, recent years have witnessed a great number of applications with various pump–probe techniques at XFELs. Among these, time-resolved X-ray liquidography (TRXL) is a powerful method for visualizing structural dynamics in the liquid solution phase. Here, we classify various chemical and biological molecular systems studied via femtosecond TRXL (fs-TRXL) at XFELs, depending on the focus of the studied process, into (i) bond cleavage and formation, (ii) charge distribution and electron transfer, (iii) orientational dynamics, (iv) solvation dynamics, (v) coherent nuclear wavepacket dynamics, and (vi) protein structural dynamics, and provide a brief review on each category. We also lay out a plausible roadmap for future fs-TRXL studies for areas that have not been explored yet.
1. Introduction
Studying chemical reaction dynamics generally means exploring the elementary physical and chemical processes involved in the transformation of reactants into products at the molecular level.1,2 Understanding chemical reactions in terms of reaction dynamics has been key to designing a chemical reaction beyond simple-mindedly optimizing macroscale factors such as concentrations of substances and the external temperature to obtain a desired product and reaction rate. Probing chemical reactions at the molecular level is a challenging task because ultrafast motions of atoms and molecules on the angstrom scale need to be monitored. To this end, various experimental methods to study reaction dynamics have been devised.3 Among them, femtosecond pump–probe spectroscopies using ultrashort laser pulses birthed the field of femtochemistry and made it possible to capture fundamental processes in chemical reactions on the femtosecond timescale.3,4 Here, the development of femtosecond lasers has played a critical role as one of the major technological innovations in the field of physical chemistry. Various pump–probe techniques utilizing femtosecond lasers have been key tools for chemists to study the fundamentals of ultrafast physicochemical phenomena. Nonlinear spectroscopic methods such as transient absorption, time-resolved photoluminescence, time-resolved Raman, and multi-dimensional spectroscopies are well-known examples of such pump–probe techniques. Time-resolved experiments with femtosecond temporal resolutions have deepened our understanding of important aspects of physical/chemical processes, such as time scales of fundamental processes. These achievements were also recognized by the Nobel Prize awarded to the late Prof. Ahmed Zewail in 1999.5In a typical pump–probe spectroscopic method, a pump pulse is used to trigger a photoreaction of a molecule of interest, and a probe pulse sent to the sample after a well-defined time delay with respect to the pump pulse is used to probe the progress of the reaction. One of the most common choices of pump and probe pulses is femtosecond ‘optical’ pulses, as in femtosecond transient absorption (TA) spectroscopy. In general, pump–probe spectroscopic data have high sensitivities to time-dependent energy flow across the ground and excited states or local structural perturbations influencing the spectroscopic signals. Nevertheless, they generally cannot provide direct structural information since they capture the molecular dynamics based on the spectral signals originating from transitions between the energy levels (the electronic states in the case of UV-visible spectra) of molecules. With spectroscopic methods, chemical species with high oscillator strengths for the used spectral region can be sensitively and selectively detected even at very low concentrations. For example, in the case of time-resolved IR spectroscopy, a species with IR-active vibrational modes can be detected sensitively. On the other hand, species-specific sensitivities mean that the detected species may not be the major species in the studied reaction, and the detected kinetics may not represent the global kinetics with actual quantitative populations and branching ratios of multiple reaction pathways. In addition, simulation to reproduce the observed transient spectral signals is generally difficult, especially for molecules with a complex excited-state energy landscape. Furthermore, the calculated spectra are often not accurate enough unless one knows the exact potential energy surface (PES) and related parameters for the excited states involved in the observed signals. Typically, the theoretical calculation for the excited state of many-electron systems requires approximations for the electronic state, which intrinsically limits the accuracy of the calculated spectra.
To overcome the shortcomings of pump–probe spectroscopic methods, time-resolved X-ray/electron diffraction (or scattering) techniques have been developed by using short X-ray or electron pulses as direct structural probes instead of optical pulses.5–12 Since the diffraction signal is the Fourier transform of the pair distribution function of electron density, it can provide direct structural information of a target molecular system via a well-established mathematical relation.13,14 In this regard, the diffraction signals obtained in a time-resolved manner contain information on the real-time structural change of the molecules participating in reactions. In other words, the time-resolved diffraction signal can be expressed with a formula as a function of the structural change of target molecules undergoing a reaction. Such a well-defined mathematical relationship makes it possible to accurately calculate theoretical time-resolved diffraction signals from hypothesized molecular structures of the species involved in the reaction. Fitting the theoretical signals to the experimental time-resolved diffraction signals by using the structural parameters as fitting parameters allows determining molecular structures of reaction intermediates, which is generally not obtained directly from pump–probe spectroscopic data. X-ray diffraction intensity is quantitatively proportional to a term containing the number of electrons in an atom, which in turn means that the diffraction signal is proportional to the number of atoms and molecules in the irradiated volume. This scalability of the diffraction intensity means that time-resolved diffraction signals can have low sensitivity to minor species but contain information on global population kinetics of all species involved in the reaction. It is not trivial to obtain such global population kinetics from pump–probe spectroscopic data. These characteristics of time-resolved diffraction with respect to time-resolved spectroscopies make the time-resolved diffraction a highly complementary tool for pump–probe spectroscopic techniques. In short, time-resolved spectroscopy mainly observes the electronic dynamics while the time-resolved diffraction captures the nuclear dynamics. In terms of structural dynamics, spectroscopic methods require an additional layer of computing electronic properties of the system to render the spectroscopic signals from structural models. For time-resolved diffraction, even though the interpretation of the signals often requires quantum or DFT calculations for initial guesses for the structures of solute molecules and MD simulations for cage structures, translation of a model structure into experimental diffraction/scattering signals is more straightforward.
Time-resolved diffraction can be applied to molecules in diverse phases, including gas, liquid, and solid. Among them, the application of time-resolved diffraction to the systems in the liquid phase has great importance for the following reasons. First, numerous chemical and biological reactions occur in the liquid phase. Second, the liquid phase offers a microscopic environment for a molecule to interact with other molecules such as solvent molecules. In this regard, the liquid phase allows investigating the interaction between molecules, which can influence the reaction dynamics. For a system in the liquid phase, X-rays can be a better structural probe than electrons considering the higher transmittance of X-rays compared to electrons. Indeed, it has been demonstrated that time-resolved X-ray solution scattering (TRXSS), also known as time-resolved X-ray liquidography (TRXL), can unveil structural dynamics of various chemical reactions in the liquid solution phase.15 TRXL experiments at third-generation synchrotrons have contributed to revealing the kinetics and structures of reactants and intermediates participating in photoreactions of various molecular systems, covering from small molecules to macromolecules such as proteins with a time resolution of ∼100 ps. From those studies, the photodissociation of haloalkanes (C2H4I2,16–18 C2F4I2,19,20 CHI3,21,22 CH2I2,23–25 CBr4 (ref. 26)), halogen compounds (Br2,27 I2,28,29 and I3− (ref. 30 and 31)), and metal halides (HgI2,32,33 HgBr2,32,33 BiI3 (ref. 34)), and photo-induced structural rearrangement of metal complexes ([Ir2(dimen)4]2+ (dimen = 1,8-diisocyano-p-menthane),35 [Fe(btbip)2]2+ (btbip = 2,6-bis(3-tert-butyl-imidazol-1-ylidene)pyridine),36 and [Pt2(P2O5H2)4]4−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37). For macromolecular systems such as proteins, information about the overall structure such as size and shape can be obtained through the small-angle X-ray scattering (SAXS) region of TRXL signals, and more detailed structures such as the movement of alpha helices or beta sheets can be obtained through the signal from the wide-angle X-ray scattering (WAXS) region of TRXL signals. Examples of representative proteins studied using TRXL are hemoglobin (Hb),38 myoglobin (Mb),38–40 homodimeric hemoglobin (HbI),41–43 photoactive yellow protein (PYP),44,45 cytochrome c (cyt-c),38,46–48 bacteriorhodopsin (bR),49 phytochrome,50,51 cyclophilin A (CypA),52 and light-oxygen-voltage (LOV) domain.53,54
37). For macromolecular systems such as proteins, information about the overall structure such as size and shape can be obtained through the small-angle X-ray scattering (SAXS) region of TRXL signals, and more detailed structures such as the movement of alpha helices or beta sheets can be obtained through the signal from the wide-angle X-ray scattering (WAXS) region of TRXL signals. Examples of representative proteins studied using TRXL are hemoglobin (Hb),38 myoglobin (Mb),38–40 homodimeric hemoglobin (HbI),41–43 photoactive yellow protein (PYP),44,45 cytochrome c (cyt-c),38,46–48 bacteriorhodopsin (bR),49 phytochrome,50,51 cyclophilin A (CypA),52 and light-oxygen-voltage (LOV) domain.53,54
One of the weak points of synchrotron-based TRXL studies is the insufficient time resolution, which is typically limited to ∼100 ps set by the temporal width of the X-ray pulse generated by synchrotrons. Hence, investigating the ultrafast structural dynamics that occur in the femtosecond time scale was not possible with synchrotron-based TRXL. The advent of XFELs changed the situation and allowed overcoming such a limitation with femtosecond TRXL (fs-TRXL). Due to the different X-ray generation mechanisms in a synchrotron and an XFEL, the generated X-ray pulses have vastly different characteristics. In a synchrotron, the electron bunches travel following a series of magnets aligned along a closed-loop path, and the X-ray radiation occurs in an insertion device such as an undulator. In contrast, in an XFEL, X-ray pulses are generated via self-amplified spontaneous emission (SASE) from micro-bunched electrons produced inside a long series of linearly arranged undulators.55 During the SASE process, X-ray pulses are produced with much higher intensity, brilliance, and coherence, as well as a shorter temporal width compared to those generated in a synchrotron. XFELs provide hard X-ray pulses with ∼1012 photons per pulse and a temporal width of <∼50 fs, compared with ∼109 and ∼100 ps at a typical synchrotron. Along with the temporal width shortened to the level of several tens of femtoseconds, these improvements offer an opportunity to observe much finer molecular behaviors that could not be investigated with synchrotron sources. In addition, the improved photon flux of the X-ray pulse in an XFEL renders a substantial reduction in the acquisition time for collecting signals with an appropriate level of signal-to-noise ratios. XFEL facilities providing hard X-rays include LCLS,56 SACLA,57 PAL-XFEL,58 European XFEL,59 and SwissFEL.60
In addition to fs-TRXL, there are many other time-resolved techniques, such as time-resolved gas-phase X-ray scattering, time-resolved serial femtosecond crystallography (TR-SFX), time-resolved X-ray emission spectroscopy (TR-XES), and X-ray transient absorption spectroscopy (XTA), which is also known as time-resolved X-ray absorption spectroscopy (TR-XAS), that attained the femtosecond time resolution with the advent of XFELs. Using these experimental techniques, numerous systems of physicochemical and biological importance have been studied in the gas and solid phases as well as the liquid solution phase. Thus, the scope of all time-resolved studies using XFELs is too wide to cover. In this review, instead, we focus on solution-phase photochemical reactions and discuss various molecular systems studied using fs-TRXL. Even with this narrowed focus, the number of molecular systems studied via fs-TRXL is not small. So far, fs-TRXL studies on 15 molecular systems, including [Co(terpy)2]2+,61 [Au(CN)2−]3,62–64 BiI3,65 I3−,93 CH2I2,66,67 Ru3(CO)12,68 [(bpy)21RuII(tpphz)1CoIII(bpy)2]5+,69 [Fe(bmip)2]2+,70 [Fe(bpy)3]2+,71,72 [Ir2(dimen)4]2+,73 [NCFe(CN)5(NH3)5Ru]−,74 [Pt2(P2O5H2)4]4−,75 photosynthetic reaction center of B. viridis,76 myoglobin,77,78 cyt-c,79 and HbI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 have been reported. We divide our discussion into the major categories of bond cleavage/formation (Section 3), charge distribution and electron transfer (Section 4), orientational dynamics (Section 5), solvation dynamics (Section 6), coherent nuclear wavepacket dynamics (Section 7), and protein structural dynamics (Section 8). Before introducing the various studies using fs-TRXL, we briefly describe the experimental setup and analysis scheme in Section 2. Since the chemical dynamics in the femtosecond timescale normally involve multiple electronic states, it is often difficult to fully elucidate the dynamics by relying solely on the structural information from fs-TRXL. In such cases, molecular dynamics simulations or spectroscopic methods providing complementary information on the energetics and structural dynamics were used in several studies.69,70,72,74 Depending on the reaction dynamics of interest, such information plays a pivotal role and, therefore, will also be discussed with the results of fs-TRXL experiments.
80 have been reported. We divide our discussion into the major categories of bond cleavage/formation (Section 3), charge distribution and electron transfer (Section 4), orientational dynamics (Section 5), solvation dynamics (Section 6), coherent nuclear wavepacket dynamics (Section 7), and protein structural dynamics (Section 8). Before introducing the various studies using fs-TRXL, we briefly describe the experimental setup and analysis scheme in Section 2. Since the chemical dynamics in the femtosecond timescale normally involve multiple electronic states, it is often difficult to fully elucidate the dynamics by relying solely on the structural information from fs-TRXL. In such cases, molecular dynamics simulations or spectroscopic methods providing complementary information on the energetics and structural dynamics were used in several studies.69,70,72,74 Depending on the reaction dynamics of interest, such information plays a pivotal role and, therefore, will also be discussed with the results of fs-TRXL experiments.
2. Experiments and data analysis
2.1. Data collection
The TRXL experiment is conducted during the assigned beam time in a large facility providing X-ray pulses and with the general pump–probe experimental geometry.81–83 The sample is typically provided in the form of a liquid jet so that a fresh sample is delivered at every pump–probe event. In the fs-TRXL experiment at an XFEL, a 50 μm–100 μm thick liquid jet is used to reduce the velocity mismatch in the liquid sample between the optical pump laser pulse and the X-ray probe pulse and to increase the temporal resolution. The scattering signal is obtained in the form of an image measured by an area detector located at a certain distance from the liquid jet. By subtracting the scattering images at a negative time delay (pump-off signal) from those at positive time delays (pump-on signal), the difference scattering images in which the large background by the unexcited sample is removed are obtained at various time delays between the optical pump pulse and the X-ray pulse. X-ray pulses generated at an XFEL have different characteristics compared with those at a third-generation synchrotron. With a much shorter pulse width, which is advantageous in terms of time resolution, X-ray pulses at an XFEL have larger fluctuations in intensity, arrival time, and energy due to the stochastic characteristics of SASE radiation.84 For this reason, in fs-TRXL experiments performed at a beamline of an XFEL, the timing-jitter between the X-ray pulse and the optical laser pulse needs to be corrected to improve the temporal resolution. As one method, by using a timing tool that measures the arrival time of the X-ray pulse compared to the optical laser pulse, the actual timing-jitter is stamped for every scattering image, and the timing-jitter can be corrected through post-processing.85 Additionally, random and systematic noises are contained in the fs-TRXL data due to larger fluctuations in intensity and energy of X-rays, in addition to the instability of thin liquid jets and inherent noises in detectors. Therefore, it is necessary to properly remove such noise before actual data analysis. For this reason, several methods have been devised for noise processing.84,86,87In contrast to well-ordered samples such as crystals, the molecules in a liquid sample generally have random orientations, yielding isotropic diffuse scattering images. Such isotropic scattering images are generally analyzed by reducing their dimension from two-dimensional images to one-dimensional curves through an azimuthal average, in which the average scattering intensities are obtained as a function of the modulus of the momentum transfer vector, q.88–90 The obtained one-dimensional difference scattering curve contains transient structural information in the form of an atomic pair distribution, in which the orientation of molecules is averaged. The data obtained at a synchrotron are usually processed in this manner, where the molecular orientation is assumed to be random. In contrast, the scattering image obtained using XFEL is, in general, largely anisotropic immediately after excitation and gradually turns isotropic. The main contributions to this anisotropic signal are the transient alignment effect of solvent molecules by the electric field of the pump laser (Kerr effect), the preferential excitation of the solute molecules with a transition dipole moment parallel to the polarization direction of the optical pump laser (photoselective alignment), and the subsequent structural change of the solute and cage. Since the anisotropic signal decays by randomizing orientation within several hundred femtoseconds to several tens of picoseconds depending on the origin, such an anisotropic signal is not observed in typical TRXL data from a synchrotron with a temporal resolution of 100 ps. The anisotropic scattering signal can be mathematically separated into the isotropic component and the anisotropic component in the form of a one-dimensional curve as a function of q.91,92 The anisotropic signal provides another degree of freedom for the structural analysis and therefore has the potential to be usefully exploited to study structural dynamics. In the fs-TRXL studies so far, the azimuthally average signal or isotropic component of signals has been mainly analyzed. Even though there are some cases in which anisotropic components originating from solute molecules are analyzed,64,75 examples where the anisotropy for the cage term is fully analyzed are still rare.74,93
2.2. Data analysis
The TRXL signal is obtained as a difference scattering signal by subtracting the pump-off scattering signal from the pump-on scattering signal, as shown in the following equation: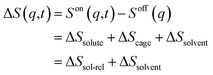 | (1) |
Each term can be expressed as follows:
 | (2) |
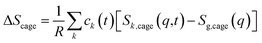 | (3) |
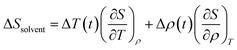 | (4) |
For ΔSsolute in eqn (2), Sk,solute(q,t) can be expressed as follows:91,92
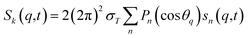 | (5) |
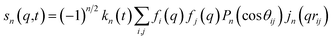 | (6) |
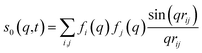 | (7) |
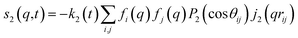 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(x)/x2, and s0(q,t) is the well-known Debye formula. The s0 and s2 signal components represent the isotropic and anisotropic contributions to the signal, respectively.
cos(x)/x2, and s0(q,t) is the well-known Debye formula. The s0 and s2 signal components represent the isotropic and anisotropic contributions to the signal, respectively.
For ΔSk,cage in eqn (3) where the interatomic pair distances should be considered, a more general expression involving the atomic pair-distribution function (gij), which can be obtained through molecular dynamics (MD) simulations, is exploited to calculate Sk,cage(q,t).94 The gij for the cage structure around a solute molecule is obtained through the molecular snapshots from MD simulations. Key parameters for an accurate MD simulation include the atomic charge and the structure of the solute molecule. These parameters are initially obtained via density functional theory (DFT) calculations. In this way, the cage structure of transient species at their equilibrium state can be obtained. In the case of non-equilibrium cage structures, non-equilibrium MD simulations should be performed to get the snapshots of relaxing cage structures as well as the corresponding scattering signals. The isotropic and anisotropic components of Sk,cage(q,t) can be described as follows:
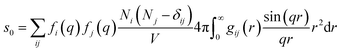 | (9) |
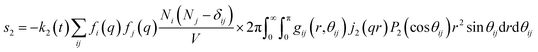 | (10) |
When the time dependence of rij is considered, a so-called molecular movie can be created by obtaining a signal of a real-time change in molecular structure. Such analysis has recently been frequently utilized to analyze fs-TRXL signals obtained at XFELs, as will be discussed throughout this review.
The solvent term (eqn (4)) contains (∂S/∂T)ρ and (∂S/∂ρ)T, which are the dependence of scattering intensity on temperature and density changes, respectively. The atomic pair-distribution function between solvent molecules can be obtained through MD simulation performed at various temperatures and densities to calculate (∂S/∂T)ρ and (∂S/∂ρ)T. However, in general, (∂S/∂T)ρ and (∂S/∂ρ)T are obtained from a separate experiment in which the solvent heating signals from a dye solution are measured to obtain those two derivative terms. Detailed experimental methods and examples for this are described elsewhere.95 The experimental heating signals corresponding to (∂S/∂T)ρ and (∂S/∂ρ)T can be obtained relatively simply and accurately through the experiment. Often, the difference scattering signals of (∂S/∂T)ρ and (∂S/∂ρ)T obtained from MD simulations do not describe the experimental data as satisfactorily as the experimentally obtained heating signals do. For these reasons, the experimental method is typically preferred over MD simulations.96
The experimental scattering intensity is scaled to the absolute electronic intensity based on the unperturbed scattering intensity of one solvent molecule and can be directly compared with the theoretical signal obtained using eqn (1)–(10). The structural and kinetic information of chemical reactions is obtained by fitting the experimental data, ΔSexp, using the theoretical signals, ΔStheory. In the fitting process, the fitting parameters such as rij(t) used to construct ΔStheory are optimized. For the signal in the time scale comparable to an instrumental response function (IRF) in the vicinity of time-zero, the theoretical curve obtained through eqn (1)–(10) is convolved with the IRF prior to comparison with the experimental curves. In this case, the structural movement occurring near time-zero is modeled by assuming a time-dependent function, and often, a polynomial is used. Finally, fitting the experimental curves to the theoretical curves results in the quantitative structural, kinetic, and thermodynamic information, including the transient molecular structures, the concentration profile of each species, and the temperature or density changes of solvent. During the fitting process, the value of χred2 expressed by the following equation is minimized to fit the experimental curves with theoretical curves.
2.3. Sensitivity toward molecular structure
The fitting of the TRXL signal is performed by using various structural parameters such as the internuclear distances as fitting parameters, and it is important to select appropriate structural parameters for the fitting. In this sense, it is useful to estimate how sensitively the TRXL signal is affected by various factors such as the internuclear distances and atomic positions.100 One way to quantify the sensitivity of the TRXL signal is to use qΔZ(q), which is the standard deviation of qΔS(q) upon various structural changes. The more sensitive the TRXL signal is to the structural changes, the larger qΔZ(q) is, since qΔS(q) would change more. If qΔZ(q) is summed over a q range, the summed qΔZ(q) can be used to estimate the relative sensitivities. The relative sensitivities of the TRXL signal can be visualized via a sensitivity plot. An example of sensitivity plots is shown in Fig. 1. The larger the relative sensitivity of an atomic position, the larger the radius of a sphere. Similarly, the color of an internuclear distance becomes darker as the relative sensitivity of an internuclear distance increases. The sensitivity plot offers an intuitive way to compare the sensitivities of various factors contributing to the TRXL signal, which can help select the structural parameters for the fitting of the TRXL signal. For example, the structural parameters with high relative sensitivities can be selected for fitting parameters.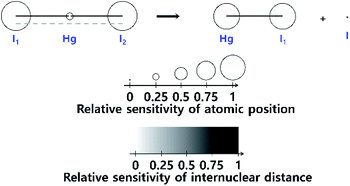 | ||
| Fig. 1 A sensitivity plot for the dissociation reaction of HgI2, in which HgI2 dissociates into HgI and I radicals. A sensitivity plot visualizes the relative sensitivities of the atomic positions and internuclear distances to a TRXL signal. The relative sensitivity of the atomic position is indicated by the radius of the sphere, and the relative sensitivity of each internuclear distance is indicated by the color of the line. As the relative sensitivity increases, the radius of a sphere increases, or the color of a line becomes darker. Reproduced from ref. 100 with the permission of John Wiley & Sons, copyright 2022. | ||
3. Bond cleavage and formation
Chemical reactions often involve processes where chemical bonds of reactants are broken, and subsequently new bonds are formed to yield products having molecular structures different from those of reactants. Reaction intermediates, which are transiently formed and eventually transform to the reaction products or regenerate the reactants, can play crucial roles in determining the reaction mechanism. Thus, identifying the structures of reaction intermediates in the course of chemical reactions is an important step toward understanding the chemical reactions and finally controlling those reactions. In this respect, TRXL has been successfully applied in many photochemical reactions to unravel the structures of transiently formed intermediates and their kinetics.15,101,102 XFELs have allowed for improving the temporal resolution of the TRXL experiment down to the femtosecond regime and enabled the visualization of the moment of bond formation as well as cleavage. In the following, the molecular systems relevant to the topic of bond cleavage and formation are reviewed.3.1. [Au(CN)2−]3 in water
Photoinduced bond dissociation, isomerization, and subsequent chemical dynamics have been intensely studied by various time-resolved methods, including the studies introduced in the following sections. On the other hand, photochemical reactions initiated by a bond formation have rarely been studied, in terms of ultrafast chemical dynamics, because of the bimolecular nature of the bond formation process; it is difficult to initiate the bimolecular bond formation, which is generally limited by slow diffusion of reactants, by the laser excitation of the reactants in a synchronized manner.In this regard, the oligomers of Au(CN)2− afford a unique opportunity to investigate the structural dynamics initiated by an ultrafast bond formation process. The Au(CN)2− complexes are weakly bound to each other, forming oligomers with bent structures, [Au(CN)2−]n, by a non-covalent interatomic interaction between Au atoms. This interaction originates from the relativistic effect called aurophilicity, which refers to a tendency of Au(I) species to form clusters or oligomers via non-covalent interaction between Au(I) atoms.103,104 Whereas the aurophilic interaction is as weak as hydrogen bonds, the photoexcitation of the electron from the antibonding σ* dz2 orbital to the bonding σ pz orbital leads to the formation of tight covalent bonds between the Au atoms. Because the Au atoms in the ground state of [Au(CN)2−]n are already located in close proximity, the photoinduced Au–Au bond formation occurs without being limited by slow diffusion through the solvent.
The bond formation process and subsequent structural dynamics of Au(CN)2− complexes were initially investigated using femtosecond transient absorption (TA) spectroscopy.105 As the model system, the trimer, [Au(CN)2−]3, in aqueous solution was selected, as it is the most simple and prototypical system. Through the TA study, three representative time constants of 500 fs, 2 ps, and 2 ns were observed during the relaxation dynamics of the excited-state [Au(CN)2−]3. In particular, the 500 fs, 2 ps, and 2 ns dynamics were attributed to the singlet excited state (S1) to the triplet excited state (T1) intersystem crossing (ISC), bent-to-linear structural change in the T1 state after the Au–Au bond formation, and the tetramer formation via the reaction between the T1 trimer and a monomer by diffusion process, respectively. Because the TA signal is not directly related to the molecular structure, the assignments had to rely on the complementary quantum chemical calculation. Since the lack of direct structural information can sometimes lead to missing or misinterpretation of important information, the bond-formation dynamics of [Au(CN)2−]3 had to be further investigated. Indeed, later molecular dynamics simulations on the [Au(CN)2−]3 suggested a different mechanism in which the bent-to-linear structural relaxation with the formation of the Au–Au bond occurs on the sub ps time scale while the S1 to T1 ISC takes place at the linear structure after the fast relaxation process.106
The discrepancy between the suggested mechanism from the TA signal and quantum calculation has been resolved by the fs-TRXL study on [Au(CN)2−]3 in an aqueous solution by Kim et al.62 Three kinetic components with time constants of 1.6 ps, 3 ns, and 100 ns were obtained from the analysis of fs-TRXL signals. The kinetic component of 500 fs, identified and assigned to the ISC in the previous TA study, was not observed in the fs-TRXL signals. Because the TRXL signal is sensitive only to processes accompanying structural changes, the lack of the 500 fs component in the fs-TRXL signal suggests that the ISC does not involve any significant structural change. In fact, a later femtosecond time-resolved luminescence study on [Au(CN)2−]3 revealed that the ISC proceeds in an even much faster time scale (<20 fs).107 Meanwhile, the two earlier time constants (1.6 ps and 3 ns) are similar to those obtained from the TA signals. While the 3 ns component is consistent with the assignment of the tetramer formation, the 1.6 ps component was assigned to a different process. In the TA study, these picosecond dynamics were assigned to the conformational change from bent to linear geometry. According to the fs-TRXL study, however, the bent-to-linear structural transition is found to occur in a much faster timescale than a few picoseconds. The structural information obtained from the fs-TRXL signal unambiguously indicates that the Au–Au bond formation and bent-to-linear structural transition of the trimer occur within 200 fs rather than the timescale of 2 ps determined in the TA study (Fig. 2a). A more recent fs-TRXL study on the same molecular system with an improved temporal resolution has succeeded in observing the atomic trajectories during the ultrafast Au–Au bond formation and bent-to-linear transformation.63 Specifically, the photoexcited [Au(CN)2−]3 follows an asynchronous bond-formation mechanism in which one Au–Au bond is formed within 35 fs first, and the other bond is formed later in a much slower timescale (∼360 fs) through the delayed movement of the remaining Au atom around the pre-formed Au–Au moiety, eventually constructing a linear structure. Some representative structures during the bond-formation and bent-to-linear structural transition are shown in Fig. 2b. Then, the linear [Au(CN)2−]3 complex undergoes further structural relaxation of Au–Au bond contraction with the time constant of 1.6 ps. Finally, a tetramer, [Au(CN)2−]4, is formed with the time constant of 3 ns and decays to the ground-state trimer of bent structure with the apparent time constant of 100 ns.
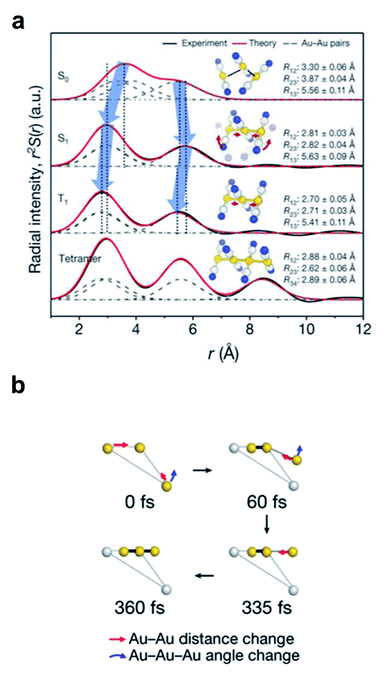 | ||
| Fig. 2 (a) Radial distribution functions of the four states of [Au(CN)2−]3 determined from a fs-TRXL study. Reproduced from ref. 62 with the permission of Springer Nature, copyright 2015. (b) The transient structures associated with the bond-formation dynamics at representative time delays. Reproduced from ref. 63 with the permission of Springer Nature, copyright 2020. | ||
This work presents the first example to visualize the process of ultrafast bimolecular bond formation. Furthermore, a series of studies on [Au(CN)2−]3 complex using both fs-TRXL and time-resolved spectroscopies provide a prime example that structural information plays an important role in accurately understanding chemical reaction mechanisms.
3.2. BiI3 in acetonitrile
Bismuth triiodide (BiI3) with a trigonal pyramidal structure incorporating Bi as the center atom serves as a model system to investigate the chemical dynamics of bismuth halides. A TRXL study at a synchrotron with 100 ps temporal resolution investigated the photochemical reaction dynamics of BiI3 in acetonitrile solution and found that BiI3 undergoes complex photoreactions involving two parallel reaction pathways.34 Specifically, upon 400 nm excitation, a BiI3 molecule (i) dissociates to yield radical fragments,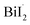 and I˙, or (ii) isomerizes to form iso-BiI2–I. The photodynamics of BiI3 is schematically depicted in Fig. 3a.
and I˙, or (ii) isomerizes to form iso-BiI2–I. The photodynamics of BiI3 is schematically depicted in Fig. 3a.
 | ||
| Fig. 3 (a) Schematic representation of the photodynamics of BiI3 in acetonitrile. (b) Changes of the Bi–Ib–Ic angle and Ia–Bi–Ib–Ic dihedral angle during the roaming-mediated isomerization determined from structural analysis on the fs-TRXL data for BiI3 in acetonitrile. (c) Changes of the Bi⋯Ic distance and the root-mean-squared displacement (σ) associated with the pair distances containing Ic. Insets in (b) and (c) show transient structures at representative time delays. (d–f) Comparison of the structural motions for the dissociation and roaming-mediated isomerization channels through (d) Bi⋯Ic distance, (e) Bi–Ib–Ic angle, and (f) Ib⋯Ic distance. Reproduced from ref. 65 with the permission of Springer Nature, copyright 2021. | ||
The isomer of BiI3 is analogous to the isomers of geminal tri-bromides (XBr3 where X = CH, B, or P) or isomers of halocarbons such as CHI3, CH2I2, CH2BrI, or CF2I2. Generally, those isomers are formed by radical recombination via collision with the solvent cage in several hundreds of femtoseconds to tens of picoseconds. However, in a spectroscopic study on the photodissociation of several geminal tri-bromides, it was found that an isomer, iso-XBr2–Br is formed, regardless of the coordination center, via roaming-mediated isomerization within 100 fs, which is too fast to be assigned as radical recombination through collision with solvent cage.108 The roaming reaction was initially proposed to explain the formation of vibrationally excited molecular hydrogen from the decomposition reaction of formaldehyde (H2CO) in the gas phase,109 and is now regarded as a ubiquitous mechanism for the photoinduced dissociation and isomerization reactions in gas as well as solution phase. In a roaming reaction, the molecular product is generated through the wandering motion of the incipient fragments in the van der Waals region of typically 3–8 Å, which is the origin of the term ‘roaming’. So far, however, the nuclear trajectories of the reacting molecules during a roaming reaction have been demonstrated only through theoretical simulations. In this regard, fs-TRXL can offer an opportunity to directly observe the ultrafast structural motions during the roaming reactions.
To uncover the underlying mechanism for the formation of the isomer species as well as the structural movement involved in the early stage of the two reaction pathways, BiI3 in acetonitrile solution was investigated from 0 fs to 100 ps using fs-TRXL by Choi et al.65 Analysis of the fs-TRXL data for the BiI3 solution revealed that an early isomer with a slightly different structure than the previously found late isomer, iso-BiI2–I, is formed at the early stage of the photoreaction. In particular, the obtained snapshots of the molecular structures during the isomerization unveiled that the early isomer is mainly formed via the movement of the partially dissociated iodine atom within 100 fs, as shown in Fig. 3b, which is much faster than the time scale of the geminate recombination via collisions with the solvent cage.110 Thus, the observed ultrafast isomerization via intramolecular rearrangement in the long-range distance was attributed to the roaming-mediated isomerization. On the other hand, for the BiI3 molecules undergoing complete dissociation, the structural motion for dissociation is captured in the form of the continually increasing distance between the bismuth atom and one of the three iodine atoms, as shown in Fig. 3c. Specifically, the Bi⋯I distance is elongated with a mean velocity of ∼11 Å ps−1 followed by a relatively slow mean velocity of ∼3 Å ps−1. Additionally, the broadening of the wavepacket of the dissociating molecule is reflected through the increasing root-mean-squared displacement (σ) of the Debye–Waller factor (DWF) applied to the atomic pairs containing the departing iodine atom.
The BiI3 molecules in the two reaction pathways show distinctly different structural movements, as shown in Fig. 3d–f. With respect to the Bi⋯I distance, BiI3 molecules in both pathways similarly increase up to ∼100 fs, showing the frustrated bond fission of the Bi–I bond, but the Bi⋯I distance for the isomerization pathway stops increasing thereafter while that of dissociation pathway keeps increasing further away (Fig. 3d). The Bi–I–I angle and I⋯I distance also show distinct contrast. For the isomer formation, a significant increase in the Bi–I–I angle and decrease in I⋯I distance are observed, whereas only a marginal increase in Bi–I–I angle with continuously increasing I⋯I distance are observed for the dissociation of BiI3 (Fig. 3e and f). These structural contrasts vividly visualize the characteristic features of both roaming-mediated isomerization and dissociation. Moreover, through this work, the time-resolved structural motions related to the roaming reaction have been experimentally captured for the first time.
3.3. I3− in methanol
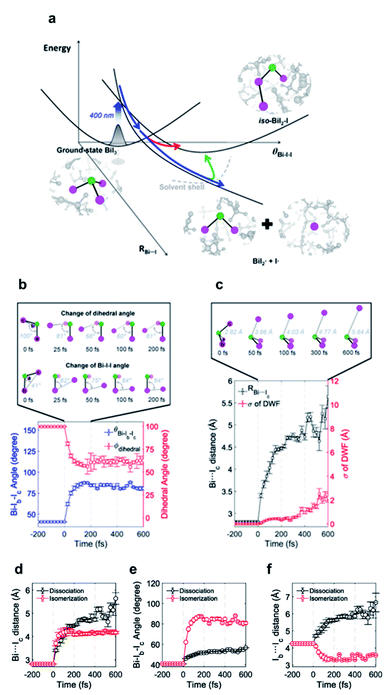
I3− is widely known as a model system for photodissociation dynamics studies. Upon photo excitation, I3−, dissociates into I2− + I radical.111,112 According to the results of spectroscopic studies and TRXL results from a synchrotron, I3− has an asymmetric bent structure in solvents such as water and methanol, which have a strong dipole interaction with I3−.31,113–115 These results raised questions about the interpretations on the photodissociation dynamics of I3−. In a non-polar solvent in which I3− has a symmetric linear structure, the terminal I atoms are in a chemically ‘equivalent’ environment, and two directions of bond dissociation are also equivalent. On the other hand, the two terminal I atoms of I3− in water or methanol are in chemically different environments due to the asymmetric bent structure of I3− in those solvents.116–118 Thus, it is worth discussing which of the asymmetric I–I bonds (one is a longer I–I bond, and the other is a shorter I–I bond) dissociates upon photoexcitation. Many studies had attempted to provide evidence of the direction of bond dissociation using computational tools and ultrafast electron diffraction119–121 However, direct evidence for the shorter-bond dissociation from the experimental observation without theoretical support had not been provided. This question was recently addressed via fs-TRXL experiments at XFELs by Heo et al.,93 which allowed a significantly improved signal-to-noise ratio thanks to the high photon flux. In addition, if the relationship between the charge distribution and the direction of the bond dissociation can be obtained, such results can provide invaluable insights into how the atomic charge distribution is linked to which bond dissociates. This issue related to charge distribution is discussed in a later section (Section 4.1).Based on the analysis of the fs-TRXL data, the structure of I3− in methanol was determined to be asymmetric and bent (Fig. 4a, RAB = 3.09 ± 0.01 Å, RBC = 2.96 ± 0.01 Å and θ = 152 ± 0.4°). Such an asymmetric and bent structure had also been suggested by spectroscopic studies.89,90 To determine the direction of the bond dissociation of the molecule, the anisotropic information of the molecular orientation and the corresponding anisotropic scattering signals were considered (Fig. 4). Because the anisotropic scattering signal arises from the anisotropic orientational distribution of the excited I3− induced by the polarization direction of the linearly polarized pump laser, analyzing anisotropic scattering signal should provide critical information on the anisotropy of the molecules: (1) anisotropic orientation of the molecules indicating which transition dipole would be excited during the excitation, (2) the overall information on the orientation and diffusive motion of reactant and product molecules. Among these two issues, the latter is covered in a later section (in Section 5.2). For the former issue, analysis of the anisotropic fs-TRXL data for the I3− solution revealed that transition dipole along with the shorter bond of I3− is excited upon photoexcitation, indicating that the shorter bond of I3− dissociates upon excitation. This direction of bond dissociation revealed in this work is consistent with the previously reported result using ab initio MD simulations.113,114 It should be noted that the direction of bond cleavage could be determined solely based on the TRXL signal without the aid of ab initio calculations or MD simulations.
 | ||
| Fig. 4 (a) The optimized structure of I3− in methanol determined from a fs-TRXL study. (b) Schematic of two models for bond dissociation of I3−: the shorter-bond dissociation and the longer-bond dissociation. (c) The wRs obtained when the shorter-bond dissociation (black) or the longer-bond dissociation (red) model is used to fit the isotropic and anisotropic data simultaneously. (d) The wRs for the isotropic data. (e) The wRs for the anisotropic data. Reproduced from ref. 93 with the permission of Springer Nature, copyright 2022. | ||
In addition to the orientational information of excited molecules, the ultrafast structural dynamics of I3− are also of importance and were thoroughly investigated in the fs-TRXL work.30,31 Although the impulsive dynamics and vibrational relaxation of I2− had been studied using spectroscopic tools,122,123 the dynamics of the dissociated I radical, including diffusion dynamics, had rarely been studied. In the fs-TRXL study, the dissociation dynamics of I3− and the subsequent diffusion dynamics of the photofragments were analyzed in terms of the inter-fragment distance and the DWF, respectively. The structural analysis using TRXL data in the early time domain revealed that the dissociated I radical initially has a fast speed of 5.6 Å ps−1, moving away from I2−, and then gradually decelerating. The deceleration of the speed is interpreted as slowing down due to the diffusive motion and existence of the inter-fragment potential.124 This study is the first example in which the anisotropic information of fs-TRXL was used to determine the direction of bond dissociation of a molecule with asymmetric structure.
3.4. CH2I2 in methanol and cyclohexane
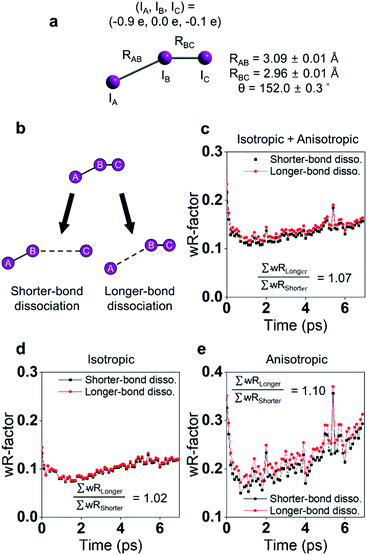
The photodissociation reaction of diiodomethane (CH2I2) in solution has been widely studied as a model system for understanding chemical bond fission and subsequent photochemical reaction. Ultraviolet (UV) light (200–300 nm) absorption induces C–I bond cleavage and generates CH2I˙ + I˙ radical fragments. Some portion of the radical fragments recombines to yield an isomer species within the picoseconds timescale, which has rarely been observed in the gas phase. Early spectroscopic studies investigated the photodissociation timescales and confirmed the formation of the isomer in solution.125,126 Those studies suggested that the isomer formation occurs via the in-cage recombination between the radical fragments that fail to escape the solvent cage shell. It was not trivial to specify the exact timescales for this mechanism due to the overlap of the spectral features between the vibrationally hot photofragments and the photoisomer. Moreover, the atomic trajectories at the onset of the photodissociation, which is the initial step for the isomer formation, as well as the structure of the isomer, remained to be determined. In this regard, TRXL is advantageous in distinguishing the dynamics of the photofragments and that of the photoisomer because TRXL signals are sensitive to the molecular structure. Indeed, the structures and kinetics of the photofragments and the photoisomer from 100 ps to the microseconds time scale were determined using TRXL.23–25 Those TRXL studies, however, failed to uncover the detailed mechanism of the isomer formation at the onset of the photoreaction due to the limited temporal resolution. Subsequent studies using fs-TRXL by Panman et al.66 and Kim et al.67 revisited the photochemistry of CH2I2 in cyclohexane and methanol, respectively. These studies succeeded in tracking the atomic trajectories during the photodissociation and identified the structural and physical nature of the photoisomer species of CH2I2.In particular, in the fs-TRXL study of CH2I2 in cyclohexane,66 geminal radical pairs in the first solvent shell were observed, and two dominating I⋯I distances of 4.35 ± 0.03 Å and 5.40 ± 0.02 Å, which originate from the rotating CH2I˙ fragment, were determined for the radical pairs. The radical pairs subsequently form the final isomer species biphasically with the time constants of 8 ps and 2.8 ns. A notable fraction of the radical pairs stably remains in the solvent cage for more than several hundreds of picoseconds to nanoseconds. Quantum chemical calculation supported this observation by suggesting the existence of the strong dispersion forces confining the radical pairs within the solvent cage. In addition, the increasing I⋯I distance upon the impulsive photodissociation of the chemical bond was observed, and the relative velocity of the fragments was determined to be 2.1 ± 0.4 Å ps−1. Angular velocity for the CH2I˙ fragment was estimated to be 4.1 rad ps−1via the rotational transition between the radical pairs having the two dominating I⋯I distances. The overall reaction dynamics are summarized in Fig. 5a.
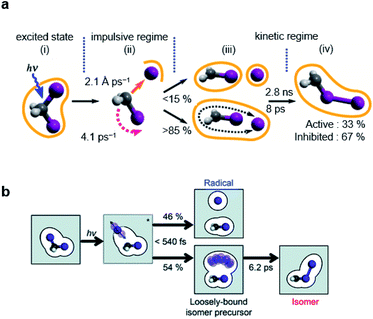 | ||
| Fig. 5 Photochemical dynamics of CH2I2 in (a) cyclohexane and (b) methanol, from fs-TRXL studies. The scheme in (a) is reproduced from ref. 66 with the permission of the American Physical Society, copyright 2020, and the scheme in (b) is reproduced from ref. 67. with the permission of the Royal Society of Chemistry, copyright 2021. | ||
Similarly, a geminal radical pair of CH2I2 has also been identified in the fs-TRXL study of CH2I2 in methanol.67 The geminal radical pair stems from the non-covalent interaction between CH2I˙ and I˙ in a solvent cage and, therefore, does not have a well-defined structure, as has been the case for the study of the radical pair of CH2I2 in cyclohexane. This structural feature has been further confirmed by the unusually large σ2 value of the DWF for the I⋯I distances of the radical pair of CH2I2, which is contrary to the final photoisomer, CH2I–I, whose σ2 for the I–I bond length was a typical small value of a well-defined atomic pair distance. The I⋯I distance and σ2 of the radical pair of CH2I2 in methanol were determined to be 4.17 Å and 0.45 Å2, respectively, which are much longer and larger than the values of the I–I bond length (3.15 Å) and σ2 (<1.2 × 10−3 Å2) of the final photoisomer. Kinetic analysis has shown that the radical pair of CH2I2, which is the loosely-bound isomer precursor, transforms into the rigid late isomer (the final photoisomer), CH2I–I, with a time constant of 6.2 ± 0.2 ps, while the fully dissociated CH2I˙ and I˙ radicals remain unreacted up to a time scale of 100 ps (see Fig. 5b).
In short, using fs-TRXL, the chemical dynamics of the radical fragments and isomers of CH2I2 in two different solvents were unambiguously identified thanks to their distinctively different structures, which was not trivial using time-resolved UV-visible spectroscopic methods because of the superimposed spectral features of the radical fragments and isomer of CH2I2. Importantly, it was consistently observed in both studies that a loosely-bound geminal radical pair is involved in the isomer formation process. Although the newly observed intermediate does not have a definite structure by its nature, a key structural parameter, the I–I distance, was successfully determined.
3.5. Ru3(CO)12 in cyclohexane
Ru3(CO)12, whose molecular structure is shown in Fig. 6a, is a thermally stable metal carbonyl cluster having an equilateral triangle metal core with each Ru atom coordinated by four carbon monoxides, and it has been used as a photocatalyst in photo-activated synthesis. In particular, the metal–metal or metal–ligand bonds in the complex can be selectively broken upon photoexcitation at a specific wavelength, resulting in different photofragmentation pathways so that Ru3(CO)12 can serve as a wavelength-dependent catalyst in the photocatalytic cycle, enabling the control of photocatalytic reactions. To understand the photochemistry of Ru3(CO)12, ultrafast infrared (IR) spectroscopy, in which the reaction intermediates were monitored via the absorption bands of the carbonyl ligands, was employed in several studies.127,128 Several transients in the photoreaction of Ru3(CO)12 were identified in those studies, and the two representative intermediates are shown in Fig. 6b. For example, under ∼267 nm excitation, the CO-loss channel is dominant due to the metal to ligand charge transfer (MLCT) character of the absorption, generating transient species such as Ru3(CO)11 and a CO-bridged complex, Ru3(CO)10(μ-CO). Meanwhile, upon ∼400 nm excitation, which is attributed to the bonding to antibonding (4dσ → 4dσ*) transition, a comparable portion of the reactants to those losing CO ligand undergoes heterolytic cleavage of a metal–metal bond, yielding a CO-bridged complex, Ru3(CO)11(μ-CO). The dynamics of these reaction intermediates are found to be strongly dependent on the properties of the solvent as well.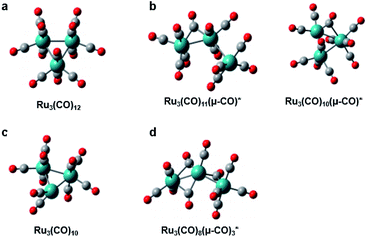 | ||
| Fig. 6 Molecular structures of Ru3(CO)12 and intermediates in its photoreaction. (a) Ru3(CO)12. (b) Intermediates identified by ultrafast IR spectroscopy. (c) Intermediate identified by synchrotron-based TRXL. (d) Intermediate identified by fs-TRXL. Reproduced from ref. 68 with the permission of the Royal Society of Chemistry, copyright 2019. | ||
Following the spectroscopic investigations, synchrotron-based TRXL studies provided fruitful complementary information. Those studies focused on the photochemistry of Ru3(CO)12 in the noncoordinating solvent (cyclohexane) under both 266 nm and 400 nm excitation conditions and revealed an additional intermediate, shown in Fig. 6c, as well as the wavelength-dependent reaction kinetics.129,130 Briefly, in both wavelength conditions, three reaction intermediates, (i) Ru3(CO)11(μ-CO), (ii) Ru3(CO)10(μ-CO), and (iii) Ru3(CO)10, were identified. For both wavelengths, intermediate (iii) was the dominating species, while intermediate (ii) was only formed only after 50 ns with a small portion in a 266 nm excitation condition. Though the intermediate (iii) contributes as a major species, which has also been confirmed in transient X-ray absorption signals,131 this intermediate has not been detected in the IR spectra because it only contains terminal CO ligands without any bridging CO ligands. Thus it is plausible that its IR bands were hidden under the terminal CO-stretching bands of other species.
A recent fs-TRXL study by Kong et al. has disclosed the formation mechanism of the newly found transient, Ru3(CO)10, and a new earlier intermediate in cyclohexane (Fig. 6d).68 Upon 400 nm excitation, a single Ru–Ru bond is broken to form Ru3(CO)11(μ-CO). Subsequently, Ru3(CO)11(μ-CO) loses one CO ligand, generating a new intermediate, Ru3(CO)8(μ-CO)3, with a reaction rate constant of 6.6 ± 0.5 × 1011 s−1. Ru3(CO)8(μ-CO)3 finally forms Ru3(CO)10 by losing another CO ligand and reconstituting the Ru–Ru bond with a reaction rate constant of 1.0 ± 0.2 × 1011 s−1. The newly found intermediate, Ru3(CO)8(μ-CO)3, during the formation of Ru3(CO)10, has a triple-bridge structure with a broken Ru–Ru bond. Although it contains bridging CO ligands, it has not been captured in previous transient IR signals. According to DFT calculations, the triple-bridge Ru3(CO)8(μ-CO)3 has three IR absorption bands originating from the stretching mode of bridging CO ligands. The IR absorption bands of Ru3(CO)8(μ-CO)3, however, either overlap with those of bridging CO or terminal CO ligands of other transients. This case is a good example showing how the structural sensitivity and the ultrafast resolution of fs-TRXL can be exploited to provide complementary information to that provided by spectroscopic observations, especially when some optically silent or hidden species are involved in the photoreaction.
4. Charge distribution and electron transfer
Photoinduced electron transfer (ET) is a fundamental process throughout chemical and biological systems associated with essential processes such as photosynthesis,132 photoredox reactions,133,134 and energy transduction.135 Many efforts have been made to rationalize the physical and chemical nature of ET reactions, including how the molecular structure and the surroundings respond to the change of electronic configuration and how they affect the rate of ET.136,137 Because the photon energy is transferred via donating the electrons or partial charges from a donor group to an acceptor group during a photoinduced ET reaction, various spectroscopic techniques that can monitor the flow of the energy or change of the oxidation states have been exploited as effective tools for understanding ET processes. Beyond understanding the mechanism of ET reactions in many molecular systems, researchers also have taken a step forward to ultimately controlling the ET reactions. In this regard, it has been found that structural aspects such as the intramolecular vibration and solute–solvent interactions can play a governing role in ET reactions.99,138 Therefore, ET reactions need to be investigated in terms of the structures of reactants and surrounding solvent cages as well as energetics. In this sense, an experiment in which fs-TRXL is combined with spectroscopic methods can be one of the powerful approaches used to accomplish the goal of controlling ET reactions.4.1. [(bpy)21RuII(tpphz)1CoIII(bpy)2]5+ in acetonitrile
[(bpy)21RuII(tpphz)1CoIII(bpy)2]5+ is a bimetallic RuCo complex where bpy is bipyridine and tpphz is tetrapyrido(3,2-a:2′,3′-c:3′′,2′′-h:2′′′,3′′′-j)phenazine, and it is known as a ‘molecular wire’. The light-harvesting 1RuII-based chromophore is linked to an optically dark 1CoIII electron acceptor at a fixed distance of ∼13 Å by a bridge of tpphz. Upon photoexcitation, ultrafast ET reaction from 1RuII to the 1CoIII center occurs. The 1RuII and 1CoIII atoms are in the low-spin (LS) state of (t2g).6 The 400 nm excitation of the 1RuII side induces a metal-to-ligand charge transfer (MLCT) transition from the 1RuII center to the tpphz bridge, whose charge is, in turn, transferred to the 1CoIII center. This ET process involves not only the change of oxidation state of the metal centers but also their spin-state transition and the structural change around the metal center. To disentangle the complicated features of the ET reaction of the RuCO complex, Canton et al. used three different time-resolved techniques, which are optical TA, TR-XES, and fs-TRXL.69 The results from each method provided complementary information, giving a more definite picture of the mechanism of the ET reaction of the RuCO complex. Shortly, the ET reaction itself was not monitored with fs-TRXL, but through the optical TA and TR-XES signals. The structural dynamics associated with the ET reaction were then interpreted via fs-TRXL signals.Dynamics taking place at the Ru center were investigated by an optical TA measurement probing a visible spectral range from 450 nm to 750 nm following a 400 nm photoexcitation. The spectral analysis of TA signals showed that the bridge-localized CT state is instantaneously populated (<50 fs), and the reduced pyrazine state decays with a lifetime of ∼490 ± 17 fs to a hot 3MLCT state while the hot excited state cools down with an 8 ± 3 ps time constant. The residence time, the duration that the electron donated from the Ru center resides on the bridge, was determined by the optical TA experiment, while the dynamics occurring at the Co side, including the arrival of the electron and the spin-state relaxation of the Co center, remained elusive. The electronic dynamics for the Co center were uncovered by a Co Kα1 TR-XES based on 2p to 1s transition. The TR-XES signal indicated that the localization of the electron on the Co center forming the 4CoII(HS) occurs with the time constant of 1.9 ± 0.6 ps, which shows a mismatch with the time taken by the electron to leave the bridge (∼490 fs), implying that the electron could localize on the distal portion of tpphz as a reduced ligand state or on the Co center as a metal-centered state. Based on these observations, a mechanism involving the 2CoII(LS) electronically excited state was proposed, that is [1RuII = 1CoIII(LS)] + hν (<50 fs) → [2RuIII(=·)1CoIII(LS)] (490 fs by optical TA) → [2RuIII = 2CoII(LS)] (1.9 ps by XES) → [2RuIII = 4CoII(HS)]. Finally, the structural relaxation around the Co center and heat-dissipation dynamics were elucidated by fs-TRXL. The Co–N bond elongation by ∼0.2 Å in the 4CoII(HS) was captured, and temperature rise by 1.0 ± 0.1 K of the bulk solvent with the time constant of 12 ± 3 ps was determined. Those results indicated that the charge localization involves very large structural rearrangements occurring almost an order of magnitude faster than the thermalization of the hot molecule. Combining all the observations by optical TA, TR-XES, and fs-TRXL, the mechanism of the ET reaction of the RuCo complex is illustrated in Fig. 7. This work highlights that a combined approach using both X-ray and an optical probe is a powerful method to decipher the energetical and structural dynamics of the intramolecular ET process, especially when optically dark donors or acceptors (the Co center in this study) are involved.
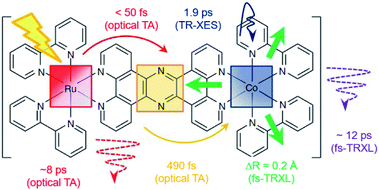 | ||
| Fig. 7 Schematic representation for the various dynamics associated with the photoinduced intramolecular electron transfer revealed by optical TA, TR-XES, and fs-TRXL. Reproduced from ref. 69 with the permission of Springer Nature, copyright 2015. | ||
4.2. [Fe(bmip)2]2+ in acetonitrile
Iron–carbene complexes have attracted much attention due to their unusually long 3MLCT lifetime compared with other iron complexes. The long lifetime of the 3MLCT state of iron–carbene complexes has offered the prospect of utilizing iron metal instead of rare elements for solar-energy-converting materials. In general, the MLCT states of Fe(II) complexes are deactivated to the low-lying metal-centered (MC) excited states within hundreds of femtoseconds, which inhibits efficient electron injection. In the iron–carbene complexes, however, the strongly σ-donating carbene ligand destabilizes the MC state, prolonging the lifetime of the MLCT state.139,140 Motivated by the interesting features of iron–carbene complexes, Kunnus et al. investigated an iron–carbene complex [Fe(bmip)2]2+, where bmip denotes 2,6-bis(3-methyl-imidazole-1-ylidine)-pyridine, to understand the excited-state dynamics of Fe–carbene complexes.70 The chemical structure and UV-visible absorption spectrum of [Fe(bmip)2]2+ are shown in Fig. 8a. In their study, the ET dynamics of [Fe(bmip)2]2+ were observed through TR-XES signals, and the simultaneously measured fs-TRXL signals provided information on the structural change during the ET reaction.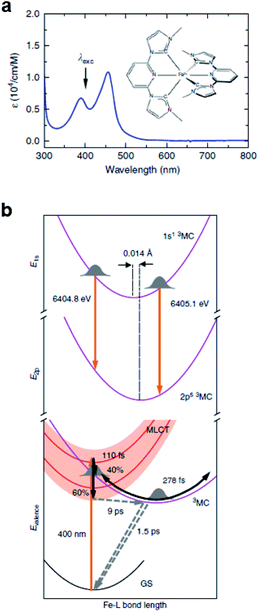 | ||
| Fig. 8 (a) UV-visible absorption spectrum of [Fe(bmip)2]2+ in acetonitrile with its chemical structure (inset). (b) Schematic representation of the excited-state dynamics of [Fe(bmip)2]2+ determined from a combined study of TR-XES and fs-TRXL. Reproduced from ref. 70 with the permission of Springer Nature, copyright 2020. | ||
According to the kinetic model proposed based on the excited-state population dynamics probed via Kα/Kβ TR-XES signals, the initially populated MLCT* state by the 400 nm photoexcitation branches into a 3MC state (40%) and a long-lived 3MLCT state (60%) with a time constant of 110 ± 10 fs. The 3MC state relaxes back to the ground state via ultrafast non-adiabatic back-electron transfer to Fe with a time constant of 1.5 ± 0.5 ps. Meanwhile, the 3MLCT state decays, possibly mediated by the 3MC state, to the ground state with a time constant of 9 ± 1 ps. The structural dynamics during the excited state population dynamics were captured by fs-TRXL. Based on the pre-determined kinetic model of the excited states and the SVD of the fs-TRXL data, a PCA analysis, instead of fitting the data using a specific structural model, was carried out to obtain the scattering signal corresponding to each excited state. The scattering curve of the 3MC state obtained in this analysis showed much more negative signals in the low-q region (<1 Å−1) than that of the 3MLCT state. It was suggested that the negative feature in the low-q region of the difference scattering curve implies an expansion of the structure, which is consistent with the previous theoretical prediction that the 3MC state has a significantly elongated metal–ligand bond compared to that of the 3MLCT state. In particular, the detailed structural analysis showed that the average Fe–ligand bond length of the 3MC state is elongated by 0.123 Å. Moreover, in both TR-XES and fs-TRXL signals, coherent oscillations with a period of 278 ± 2 fs were observed. Those oscillations originated from the vibrational wavepacket dynamics, and a more detailed discussion for the wavepacket dynamics of [Fe(bmip)2]2+ is given in Section 7.2. Briefly, the structural analysis on the fs-TRXL signals showed that the oscillating signal component arises from the periodic modulation of the Fe–ligand bond length on the 3MC excited state. According to the ab initio calculation results, the XES spectrum shifts linearly as a function of the Fe–ligand bond length, indicating that the periodic modulation of the Fe–ligand bond length leads to the oscillation in the Kα TR-XES signals. A schematic illustration summarizing the population and structural dynamics of [Fe(bmip)2]2+ is shown in Fig. 8b. This work is one of the most successful examples showing how the combined implementation of time-resolved X-ray emission and TRXL experiments can be applied to disentangle the non-equilibrium dynamics of both electrons and nuclei during photoinduced electronic excited state dynamics.
4.3. I3− in methanol
Energy, structure, and charge are fundamental characteristics of a molecule. While the energy flow and structural change of a molecule during chemical reactions have been measured experimentally,141,142 determining the charge distribution in a molecule in the solution phase, even for a simple triatomic molecule like triiodide ion, I3−, was challenging. Moreover, the relationship between the charge distribution and the molecular structure remained vague. TRXL has the potential to observe the molecular charge distribution, which affects the cage-scattering signal. Indeed, the charge distribution of I3− in methanol was recently unraveled using fs-TRXL by Heo et al.93 Although TRXL on I3− had been performed at synchrotrons, the charge distribution of I3− could not be determined in those studies due to the limited signal-to-noise ratio. The signal-to-noise ratio of fs-TRXL data acquired at an XFEL is much higher than that of the previous TRXL data collected at synchrotrons. The improved signal-to-noise ratio turned out to be critical for refining the atomic charge distribution.30,31To extract the charge distribution of I3−, the TRXL data were analyzed, considering all possible charge distributions of the molecule (Fig. 9a). Specifically, the cage terms of I3− with various charge distributions were calculated using MD simulations. Then, the optimal charge distribution yielding the cage term, which has the best description to the TRXL signal at 100 ps, was determined by minimizing the discrepancy between the theoretical and experimental data (Fig. 9b and c). The fitting was performed at each charge distribution, and the fitting parameters included the structural parameters of I3−. As a result, the model with most of the excess charge localized on the terminal iodine atom participating in the longer I–I bond gave the best agreement with the experimental data. This optimized result implies that the I3− has a highly localized charge distribution ((IA, IB, IC) = (−0.9e, 0.0e, −0.1e)). This atomic charge distribution extracted from the TRXL data is in excellent agreement with the previous theoretical expectations,113,114 and the hydrogen bond between the hydroxy group of methanol and I3− can account for the symmetry breaking and charge localization. Rotational correlation functions (RCFs) of I3− calculated using MD simulations provided additional support to this charge distribution determined from the structural analysis. RCFs of I3− were calculated using MD simulations assuming three different atomic charge distributions: (i) (IA, IB, IC) = (−0.9e, 0.0e, −0.1e), (ii) (IA, IB, IC) = (−0.5e, 0.0e, −0.5e), and (iii) (IA, IB, IC) = (0.0e, −1.0e, 0.0e) (Fig. 9d). Then, the RCFs were fitted using an exponential function to obtain the rotational dephasing time constants of I3−. Among the three atomic charge distributions, the rotational diffusion time constants of the first case, which was determined from fitting the fs-TRXL data, showed the best agreement to those obtained from the experiment.
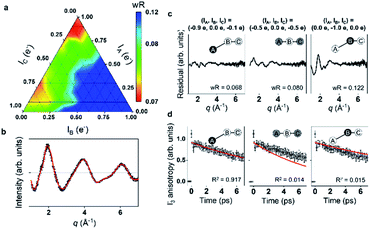 | ||
| Fig. 9 (a) The weighted R-factors (wRs) presented as a function of the charges of three I atoms of I3− in methanol determined from a fs-TRXL study. The best fit, which gives the smallest wR, is obtained with IA = −0.9e, IB = 0.0e, and IC = −0.1e. (b) The difference curve at 100 ps (black) and the best fit curve (red) with (IA, IB, IC) = (−0.9e, 0.0e, −0.1e). (c) Residuals for the differences between the experimental curve and the fit curves obtained for three representative cases of the atomic charge distributions. (d) Comparison of the experimental anisotropy change (black dots with error bars) and the calculated rotational correlation functions (RCFs) for the three representative cases of the atomic charge distributions shown in (c). The coefficient of determination (R2) for each case is also shown. The best agreement, which gives the lowest wR in (c) and the R2 value closest to 1 in (d), is found with the first case, providing strong evidence for the localized charge on the terminal iodine atom participating in the longer I–I bond. Reproduced from ref. 93 with the permission of Springer Nature, copyright 2022. | ||
When the determined charge distribution is linked to which I–I bond of I3− dissociates to yield I2− and I upon photoexcitation, it can provide insights into how the charge distribution of I3− is related to the direction of the bond dissociation. As discussed in Section 3.3, the shorter I–I bond of I3− dissociates. Since most of the negative charge of I3− is localized in the terminal iodine atom participating in the longer I–I bond, the dissociation of the shorter I–I bond indicates that the movement of charge is not substantial in the bond dissociation process, compared with the other case where the longer I–I bond dissociates. Meanwhile, in the ground state, the formation of I2 and I− is favoured upon the dissociation of the longer I–I bond, according to the ab initio calculation for the ground state. In the ground state, where the formation of I2 and I− is operational in the equilibrium, the longer, weaker I–I bond is likely to be broken unlike in the excited state. It should be noted that the movement of the charge is small in this case as well, compared with the other case where the shorter I–I bond dissociates. One can see that the bond dissociation and the charge distribution are coupled in such a way that the dissociation occurs in the direction where the redistribution of the atomic charge among atoms is minimized.
This work is the first case where the atomic charge distribution of a molecule in the solution phase was unveiled via TRXL and shows the potential of TRXL as a tool to investigate the atomic charge distribution. Additionally, the different bond dissociations in the excited and ground states and the determined atomic charge distribution provide insight into how the direction of bond dissociation is linked to the atomic charge distribution.
5. Orientational dynamics
Photochemical reactions induced by an ultrashort laser pulse can accompany various changes; not only changes in the intramolecular structures or cage structures, but also changes in the molecular orientations. For example, a photoexcitation of solute molecules by a linearly polarized pump laser pulse generates a transient anisotropic distribution of molecular orientation via the preferential excitation of molecules with transition dipoles oriented along the direction of polarization of the pump laser pulse. Such an anisotropic orientational distribution gradually recovers the random orientation through rotational motions of the molecules. Another example includes the optical Kerr effect (OKE), in which birefringence is created in the liquid material due to the partial alignment of molecules caused by the interaction between the molecules and the instantaneous electric field of the linearly polarized ultrashort laser pulse.143,144 Measuring the molecular responses to preferential excitation or the light-induced alignment by laser pulses provides useful information regarding the orientational dynamics of the molecules. The molecular orientational dynamics are inherently ultrafast, ranging from several tens of femtoseconds to tens of picoseconds, and for this reason, it was not trivial to investigate such ultrafast dynamics using a synchrotron-based TRXL experiment, and so far, it has mostly been investigated through time-resolved spectroscopic methods.145,146 With the advent of XFEL, fs-TRXL has become a powerful tool to elucidate the ultrafast orientational dynamics at the molecular level. In a fs-TRXL experiment incorporating a linearly polarized ultrashort pump laser pulse, scattering images obtained at early time delays are often anisotropic and contain direct structural information related to the molecular orientations as well as kinetic information complementary to that obtained from spectroscopy. In the following sections, we introduce three relevant studies in which the orientational dynamics have been investigated using fs-TRXL.5.1. [Au(CN)2−]3 in water
A transient anisotropic orientational distribution generated by a preferential excitation of molecules using a linearly polarized pump laser results in anisotropic difference scattering images, and the rotational dephasing through which the random orientation of the excited molecules is recovered can be monitored through the decay of anisotropy in the measured time-resolved scattering signals. Kim et al. applied this approach to investigate the kinetics of rotational dephasing of the gold trimer complex, [Au(CN)2−]3, using fs-TRXL.64To extract the information of orientational dynamics, the difference scattering images were dissected into vertical and horizontal regions with respect to the polarization direction of the pump laser in a laboratory-fixed reference frame. Each region was azimuthally averaged, yielding two distinct difference scattering curves, ΔSV(q,t) and ΔSH(q,t). Fig. 10a and b show the obtained ΔSV(q,t) and ΔSH(q,t) from the fs-TRXL signals of aqueous [Au(CN)2−]3 and water heating, respectively. As shown in Fig. 10a and c, ΔSV(q,t) and ΔSH(q,t) exhibited discrepancies, which gradually decayed over time with the time constant of 13 ± 4 ps. Based on the known population kinetics of [Au(CN)2−]3, which has been introduced in Section 3.1, the major species within the measured time range is identified as the T1 state of [Au(CN)2−]3. Therefore, the observed time constant corresponds to the rotational dephasing time of the T1 state of [Au(CN)2−]3. In contrast to the signals of [Au(CN)2−]3 solution, the difference scattering signals of FeCl3 in water, which provide the solvent heating signal induced by solute-to-solvent heat transfer, does not show any significant discrepancy between ΔSV(q,t) and ΔSH(q,t) (Fig. 10b). Based on this observation, it was concluded that the solute-to-solvent heat transfer does not contain anisotropic dynamics within the measured time range (Fig. 10c). This work presents the first example where the orientational dynamics of a small molecule, such as rotational dephasing, were unveiled using fs-TRXL.
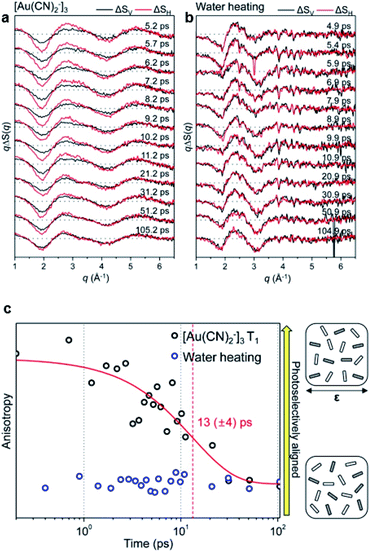 | ||
| Fig. 10 (a) Fs-TRXL data of [Au(CN)2−]3 in an aqueous solution. (b) Fs-TRXL data of solvent heating induced by the excitation of FeCl3 in an aqueous solution. ΔSV (shown in black curves) and ΔSH (shown in red curves) were obtained by the azimuthal integration of the vertical and horizontal region of the 2D difference scattering images, respectively. (c) Transient anisotropy of [Au(CN)2−]3 (black circles) and solvent heating (blue circles) extracted from the fs-TRXL measurement. The red curve represents the fit result with a single exponential function. Reproduced from ref. 64 with the permission of IOP Publishing, copyright 2015. | ||
5.2. I3− in methanol
In general, molecules in the solution phase have an isotropic orientational distribution in space through continuous rotational motion. The anisotropic orientational distribution can be generated by external stimuli such as photoexcitation.147 Afterward, the orientational distribution of the molecules returns to isotropic via rotational diffusion dynamics. As difference scattering signals contain information on both excited species and the depleted ground state, anisotropic scattering signal also contains anisotropic information of both ground state and excited state intermediates. For the ground-state hole, TRXL signal provides the information on how the hole generated by photoexcitation recovers its initial isotropic distribution, which directly shows the diffusive motion of the ground-state molecule.To reveal the rotational diffusion dynamics upon photoexcitation using fs-TRXL, Heo et al.93 analyzed the anisotropic scattering signal in terms of the rotational diffusion dynamics of molecules in the ground state and excited state. For the analysis, the TRXL data were divided into isotropic and anisotropic signals, which contain information on the radial distribution and the orientation distribution, respectively. Then, the anisotropic signal was fitted using anisotropic solute and cage scattering curves. As a result, rotational diffusion time constants of 13.5 ps and 6.3 ps were obtained for I3− and its dissociation product I2−, respectively. The rotational diffusion time constants are consistent with those obtained from the RCF analysis, as discussed in Section 4.1, and (Fig. 9d) those reported by spectroscopic studies as well.148,149 This work is the first example where the rotational dephasing dynamics of the depleted ground-state molecule as well as the newly generated photoproducts were observed via fs-TRXL.
5.3. Optical Kerr effect
OKE describes the optically induced birefringence, the polarization-dependent refractive index in a material. The molecular origin of OKE stems from the partial alignment of the molecules that make up the material. Much effort has been devoted to understanding this intriguing phenomenon, and it has been proposed that the molecular motions contributing to the ultrafast OKE response of molecular liquids can be understood through three different types of motion, which are libration, interaction-induced motion, and orientational diffusion. These molecular motions associated with the OKE have been assigned and investigated mostly via optical spectroscopy combined with theoretical simulations. However, due to the lack of direct structural probes capable of tracking such ultrafast dynamics in solution, the microscopic structural details during the OKE had rarely been investigated experimentally. To tackle this issue, recently, Ki et al. investigated OKE response in liquid acetonitrile using fs-TRXL.150The measured fs-TRXL signals showed anisotropic scattering patterns, as depicted in Fig. 11a. The anisotropic component is particularly sensitive to the change of the molecular orientations, whereas the isotropic component is more sensitive to the change of intermolecular distance, which can provide two different aspects of microscopic structural dynamics involved in the OKE. Each scattering component was separated and analyzed by modeling the molecular configurations using MD simulations and reproducing the experimentally obtained scattering signals. In particular, two distinct state-associated scattering curves (SACs) were observed from the anisotropic component, and one SAC was obtained from the isotropic component. Kinetic analysis revealed that the two anisotropic SACs corresponded to (i) a photoaligned state and (ii) the first intermediate state, while the isotropic SAC was attributed to (iii) the second intermediate. The photoaligned state is impulsively prepared from the equilibrium state and converted to the first intermediated with a time constant of 60 ± 35 fs followed by the transition to the second intermediate with a time constant of 350 ± 210 fs. Finally, the second intermediate relaxes back to the equilibrium state with a time constant of 1.5 ± 0.5 ps. It is noteworthy that the first intermediate state was captured in the anisotropic component of the signal, whereas the second intermediate state was detected in the isotropic component. Such a result implies that molecular motions of different characters and timescales are involved in OKE.
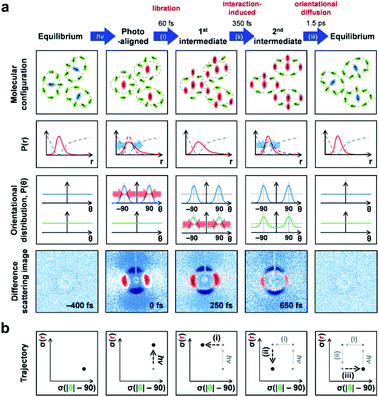 | ||
| Fig. 11 (a) A schematic for the molecular motion during the OKE determined in a fs-TRXL study. (Top row) schematic representation of the molecular configurations of various states involved in the OKE response of liquid acetonitrile shown in the chronological order of appearance (from left to right). (Second row) the population distribution (solid red curve) in terms of the intermolecular distance. The dashed red curves indicate the distribution of the intermolecular distance in a previous state and the dashed gray curves indicate the potential energy curve of the ground electronic state of the molecule. (Third row) the population distributions in terms of the angular orientation of the photoaligned molecules (blue line) and their cage molecules (green line). The directions of laser polarization were set to be θ = 90° and θ = −90°, and the molecular alignment was made accordingly along those directions. (Bottom row) the representative experimental 2D difference scattering images corresponding to the states shown in the first row. (b) Trajectory of the OKE response in terms of the width of the orientational distribution of cage molecules (x-axis) and the width of the distribution of intermolecular distance (y-axis). Reproduced from ref. 150 with the permission of the American Chemical Society, copyright 2021. | ||
The obtained SACs were reproduced using theoretical difference scattering curves based on MD snapshots, and detailed structural information was extracted by describing the molecular configurations of the MD snapshots using the population distribution in terms of intermolecular distance and angular orientation, P(r) and P(θ), as summarized in Fig. 11a. Specifically, the photoexcitation with a linearly polarized laser pulse impulsively aligns some portion of the molecules along the direction of laser polarization and, as a result, the P(r) becomes broader compared to that in the equilibrium state while P(θ) for the photoaligned molecules show clear peaks at the angular values of the laser polarization. At this stage, the molecules surrounding the photoaligned molecules, which are the cage molecules, still maintain the random orientation, and therefore the P(θ) of the cage molecules is flat. Then, the cage molecules rearrange, which is libration, in 60 fs, without significant change in the intermolecular distances, leading to the first intermediate state observed in the anisotropic SACs. The intermolecular distance changes during the transition to the second intermediate in 350 fs via interaction-induced motion, which results in the narrowing of P(r) and the amplitude change of the isotropic scattering signal. Finally, the anisotropic orientations of the photoaligned molecules and their cage molecules become randomized through orientational diffusion, leading to a flat P(θ), and consequently recovers the initial equilibrium configuration in 1.5 ps. With respect to the width of the orientational distribution of cage molecules and the width of the distribution of intermolecular distance, the trajectory of the OKE response is plotted in Fig. 11b. Via fs-TRXL, this work, for the first time, directly visualized the real-space molecular motions, which had only been indirectly investigated using spectroscopic and theoretical means.
6. Solvation dynamics
Solvation dynamics is an essential process of chemical reactions in the liquid solution phase. Change of the electronic and nuclear configurations of the reacting solute molecules perturb the surrounding solvent molecules, leading them to rearrange their orientations or alter the caging structures. How quickly the solvent adapts mechanically and dielectrically to the new configuration of the solute and how the excess energy is released through this process are critical in determining the reaction rate and even the outcome of the reaction.151–153 Due to this significance, solvation dynamics has been one of the most studied subjects in the field of physical chemistry. In particular, various nonlinear spectroscopic techniques with the aid of molecular dynamics simulations have provided profound knowledge of the solute–solvent interaction, including the energetics, predicted motions, and their timescales.154–156 With respect to the structural dynamics, however, such experimental methods only provide indirect information averaged over all length scales, for example, based on a continuum solvation model157 in which the solvent is approximated as a dielectric medium rather than explicitly represented. Therefore, atomistic structural dynamics of the solvation process remained elusive. A more detailed structural nature of the solvation process can be obtained using fs-TRXL. In particular, as already introduced in the previous technical section, the fs-TRXL signal contains the cage term originating from the change of the atomic pair distribution between the solute and solvent molecules, which provides the real-space information during the ultrafast solvation motions. The following sections summarize three examples of fs-TRXL studies that provide independent but progressively more detailed structural pictures of the solvation dynamics.6.1. [Fe(bpy)3]2+ in water
Aqueous [Fe(bpy)3]2+, whose chemical structure is shown in Fig. 12a, is a well-known spin transition compound, with which the first attempt to observe the solvation dynamics using fs-TRXL combined with TR-XES at LCLS was made.71 In this work by Haldrup et al., the temporal resolution of the experiment was limited to 0.5 ps, which was not enough to capture the detailed ultrafast spin-crossover (SCO) dynamics of [Fe(bpy)3]2+, whose brief introduction is given in Section 7.4. Nevertheless, it was possible to observe the subsequent solute–solvent interaction in the sub-ps regime. Through the TR-XES signals, the transition to the high-spin (HS) state was identified (Fig. 12b), and the simultaneously measured fs-TRXL signals captured the ∼0.2 Å Fe–ligand bond elongation as well as the increase in solvent density and temperature (Fig. 12c and d). Those signals from fs-TRXL showed an exponential rise delayed with respect to the TR-XES signals, which were a purely electronic response of the photoexcited solute molecules. In particular, the solvent density changed by 2.0 ± 0.2 kg m−3 through an exponential rise with a time constant of 1.1 ± 0.2 ps. This rather unusual ultrafast increase of solvent density was interpreted as the release of approximately two caging water molecules into the bulk solvent following the Fe–ligand bond expansion of each photoexcited solute molecule. This work suggested the possibility that simultaneous measurement of time-resolved X-ray scattering and emission signals could reveal the complex interplay between the excited solute and surrounding local environment, which was realized in subsequent studies.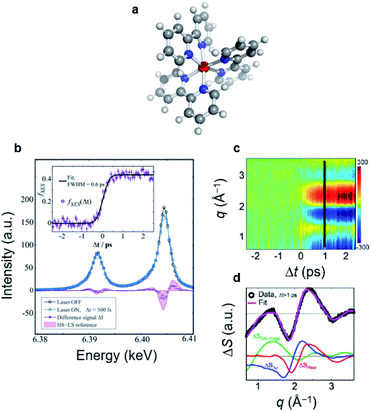 | ||
| Fig. 12 (a) Chemical structure of [Fe(bpy)3]2+. (b) Measured Kα TR-XES spectrum of the ground-state (laser OFF) and photoexcited (laser ON) [Fe(bpy)3]2+ with the difference spectrum at 500 fs time delay. The static difference spectrum obtained from the spectra of the HS and LS states of a reference sample is shown in the light-purple area. (c) Fs-TRXL data of [Fe(bpy)3]2+. (d) The fs-TRXL data at 1 ps together with a corresponding fit. The different components contributing to the fitted curve are shown in the bottom part of (d). Reproduced from ref. 71 with the permission of the American Chemical Society, copyright 2016. | ||
6.2. [Ir2(dimen)4]2+ in acetonitrile
The [Ir2(dimen)4]2+ is one of the d8–d8 binuclear ligand-bridged complexes known to show high redox activity in their electronic excited state, facilitating various photoinduced redox reactions and electrocatalysis. The lowest energy transition of those d8–d8 dimeric complexes induces a metal localized electronic transition from an antibonding dzσ* to a bonding pzσ orbital, resulting in the shortening of the metal–metal distance. In addition, due to the partially occupied dzσ* and pzσ orbitals along the metal–metal axis, the metal atoms become available for an additional ligand binding, allowing efficient photoredox and photocatalytic activities. Based on these excited-state structural dynamics, van Driel et al. studied [Ir2(dimen)4]2+ in acetonitrile using fs-TRXL to investigate how the solvent, which might be either a substrate or competitor, interacts with the active site of a photoexcited solute (Fig. 13a and b).73 The measured fs-TRXL signals and the fitted curves are shown in Fig. 13c.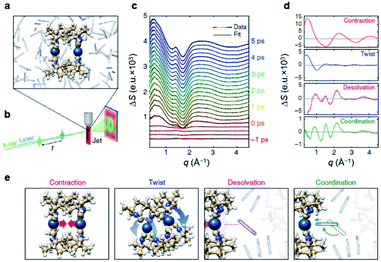 | ||
| Fig. 13 (a) Chemical structure of [Ir2(dimen)4]2+ in acetonitrile obtained from MD simulations. (b) Experimental setup for a fs-TRXL experiment. (c) Measured fs-TRXL data at various time delays and the corresponding fit curves. (d) Four signal components related to the intramolecular structural changes and solvation processes. (e) Schematic representation of the dynamics giving rise to the four signal components shown in (d). Reproduced from ref. 73 with the permission of Springer Nature, copyright 2016. | ||
The expected Ir–Ir contraction, as well as dihedral twisting, was observed from the quantitative structural analysis on the solute term of the fs-TRXL signals. Specifically, a significant Ir–Ir bond contraction was observed within 300 fs, followed by an additional shortening on a 2 ps time scale, eventually reaching a bond length of 2.92 ± 0.05 Å. The dihedral twisting begins about one picosecond after the initial Ir–Ir contraction, reaching a dihedral angle change of 15 ± 3° within 3.5 ps. The corresponding scattering signals and schematic representations for the structural motions are shown in Fig. 13d and e, respectively.
The solvation dynamics were captured in the cage term of the fs-TRXL signals. Comparing the cage terms from the experimental data with those from MD simulations, two distinctive cage terms representing the solvation process were obtained. One of the cage terms, contributing from the sub-ps time range, showed strongly negative features at the low-q (<0.5 Å) region, implying the increase in the average distance between the acetonitrile and Ir atom. Based on the results from MD simulations, the early component of the cage signal was attributed to the desolvation process due to the inward movement of Ir atoms upon photoexcitation (Fig. 13d and e). On the other hand, the other cage term grew with a delayed exponential function starting from roughly 1.3 ps and showed a significantly decreased negative feature at the low-q region. The cage signals from the MD simulations reproducing this slower component indicated a structural movement corresponding to the coordination process where the acetonitrile molecules rotate and translate to preferentially coordinate to the Ir atom with the cyano group (Fig. 13d and e). Overall, these results successfully visualized the solvation process in terms of atomic-site-specific structural dynamics but did not provide frame-by-frame movement during the solvation process, which has been achieved through the work given in the following section.
6.3. [NCFe(CN)5(NH3)5Ru]− in water
[NCFe(CN)5(NH3)5Ru]−, abbreviated to FeRu, is a bimetallic complex where the metal atoms are connected by a cyanide bridge, and the chemical structure is shown in Fig. 14a. The 800 nm photoexcitation initiates the metal-to-metal charge transfer (MMCT) excitation in which an electron is transferred from Fe to Ru, and subsequently, the MMCT excited state relaxes back to the ground state via ultrafast back electron transfer (BET) within ∼100 fs. The sudden changes in the charge distribution will affect the surrounding solvent configuration and vice versa. Focusing on the solvation dynamics, Biasin et al. have investigated the FeRu complex in water by using a combined experiment of fs-TRXL and TR-XES to visualize how the solvent responds to the series of ET processes.74 They took advantage of the kinetic parameter obtained from the TR-XES to carry out non-equilibrium MD simulations, through which the fs-TRXL signals were reproduced without relying on any structural fitting process (Fig. 14b and c).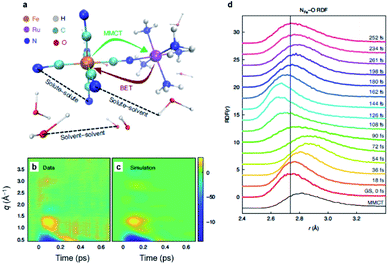 | ||
| Fig. 14 (a) Chemical structure of [NCFe(CN)5(NH3)5Ru]− (FeRu) in water. The 800 nm photoexcitation leads to MMCT from Fe to the Ru center followed by ultrafast BET. The structural dynamics are captured by fs-TRXL. (b) Fs-TRXL data of FeRu in water upon 800 nm excitation. Here, the contribution from the solvent–solvent atomic pair distances are subtracted. (c) The calculated fs-TRXL signal arising from changes in solute–solvent atomic pair distances obtained from non-equilibrium MD simulations. (d) Time-dependent radial distribution function of NFe–O atom pair obtained from non-equilibrium MD simulations. Reproduced from ref. 74 with the permission of Springer Nature, copyright 2021. | ||
Through the Kβ TR-XES, the local oxidation state of Fe was monitored. The temporal profile of the Kβ TR-XES signal revealed that the initial excitation fraction is 25 ± 4% and the lifetime of the MMCT state is 62 ± 10 fs. For the fs-TRXL signals, firstly, the bulk solvent heating contribution was removed. Furthermore, through the equilibrium MD simulations, it was verified that the cage signal originating from the solvation process due to the structural changes in solute was negligible for the FeRu complex. Therefore, this contribution, as well as the intramolecular structural changes of FeRu to the fs-TRXL signals, were ruled out, and only the response of the solvent to the changes in the charge distribution of the solute, that is, the dielectric solvation, was considered as the dominant process. To analyze the fs-TRXL signals based on these assumptions, multiple non-equilibrium MD simulations were performed by modifying the timing of BET upon MMCT excitation at the frozen solute structure, and the subsequent response of solvent molecules was captured. Following the MMCT population kinetics obtained from the exponential decay of the temporal profile of Kβ TR-XES signal, the simulated fs-TRXL signals derived from each MD simulation were weighted and linearly combined to reproduce the experimental fs-TRXL signals.
The radial distribution functions (RDFs) generated by the MD simulations were used to visualize the ultrafast solvation process in the real space (Fig. 14d). As the solvation process implies the reorganization of the solvent cage, the peak positions of RDFs corresponding to solute–solvent atom pairs of the first solvent shell were traced. Specifically, the motions of the first solvent shell were illustrated via the changes in the hydrogen-bonded atom-pair distances, such as NFe–O and NRu–O. The peak position of RDF showed dynamic shifts in which the original peak position at the ground state moves to a longer distance upon MMCT. Upon BET, the peak position shifted to a shorter distance, even shorter than the original position. After a damped oscillation around the original position, the solvent structure finally settled down in its original configuration. The initial translation of water molecules away from FeRu could be rationalized considering the weakened but not broken hydrogen bond upon MMCT transition. Besides, it was found that the additional rotational or diffusional motions make little contribution to the structural reorganization of the first solvent shell on the MMCT and BET timescales. Thus, it was argued that the collective translational motions of water molecules predominantly contribute to the reorganization energy of the ET process in the FeRu complex. This work has demonstrated how specific solute–solvent interactions can be accessed at the atomistic level using fs-TRXL, deepening our understanding of solvent reorganization processes.
7. Coherent nuclear wavepacket dynamics
Photoexcitation with a spectrally broad and temporally ultrashort laser pulse can create coherent nuclear wavepackets, which is the coherent superposition of multiple vibrational wavefunctions, on both ground- and excited-state potential energy surfaces. The coherent nuclear wavepacket dynamics have been observed in numerous systems using various time-resolved spectroscopic techniques.158–161 Typically, in those these experiments, the nuclear wavepacket dynamics are manifested in the oscillating spectral signals along the time axes, and the Fourier transform of the signals provides the vibrational frequencies. Such information about molecular vibrations during a chemical reaction sheds light on how the molecular structure changes at the initial stage of various chemical reactions, including all the categories covered in previous sections. The time-dependent positions of the nuclear wavepacket, however, had to be retrieved only through theoretical simulations because the oscillating spectroscopic signal does not represent direct structural parameters. In this respect, enabling real-space visualization of the nuclear wavepackets is one of the most remarkable breakthroughs achieved by fs-TRXL studies. We describe the examples of such studies in the following sections, and some of the molecular systems already introduced in previous sections are revisited, focusing on the nuclear wavepacket dynamics.7.1. [Co(terpy)2]2+ in water
The first example of observing wavepacket dynamics using fs-TRXL was reported on [Co(terpy)2]2+ in water, where terpy denotes 2,2′:6′, 2′′-terpyridine by Biasin et al.61 [Co(terpy)2]2+ is a complex with an axially distorted pseudo-octahedral structure (Fig. 15a). In the solution phase, Co(II) at room temperature predominantly has an LS state with a d7 configuration. It is also known that photoexcitation of [Co(terpy)2]2+ by a visible light induces the spin-state transition from the LS to HS. The studies of this Co complex in the solid and gas phases proposed that the axial and equatorial Co–N bonds elongate anisotropically upon spin-state transition.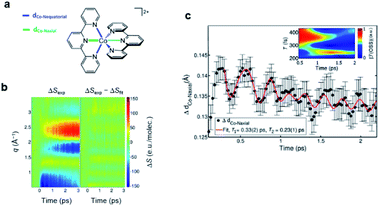 | ||
| Fig. 15 (a) Chemical structure of [Co(terpy)2]2+. The axial and equatorial Co–N bonds, which show anisotropic expansion upon spin state transition from LS to HS induced by 530 nm photoexcitation, are indicated by green and blue lines. (b) Fs-TRXL data (ΔSexp, left) and corresponding fit (ΔSfit, right). (c) Time evolution of the Co–N bond lengths showing coherent wavepacket motions of [Co(terpy)2]2+. The inset shows a time-resolved Fourier transform of the oscillatory component of the fs-TRXL signal in (b), which shows a sequential activation of two vibrational modes. A heuristic fit is shown in solid red line incorporating sequential activation of two vibrational modes: one showing a breathing motion (period of ∼0.33 ps) and the other showing a pincerlike movements (period of ∼0.23 ps). Reproduced from ref. 61 with the permission of the American Physical Society, copyright 2016. | ||
The fs-TRXL signals of the aqueous [Co(terpy)2]2+ showed strong negative features at the low-q region (<1 Å−1), consistent with the predicted structural expansion of the complex (Fig. 15b).61 To obtain the time-dependent structural evolution, structural fitting was performed on the measured TRXL signals. Based on the symmetry condition, the ratio between the lengths of axial and equatorial Co–N bonds was fixed with a constant parameter. Thus, a single structural parameter, dCo–N(t), was used for modeling both the axial and equatorial Co–N bonds of the solute molecule. The temporal profile of dCo–N(t) of axial bonds is shown in Fig. 15c. The Co–N bonds show damped oscillations after the initial bond elongation upon photoexcitation, representing the nuclear wavepacket dynamics in real space. The Fourier transform of the oscillating signal indicates two sequential vibrational modes. The time-resolved Fourier spectra of the oscillating signal indicate the appearance of the earlier mode with a relatively low frequency followed by the high frequency mode. To obtain more quantitative values, the oscillatory structural signal was fitted using a model function derived based on the observation in the Fourier spectra. Through the analysis, it was determined that under the exponential decay of the overall signal with the time constant of 0.7 ± 0.1 ps, the first oscillation with the period of 0.33 ± 0.03 ps appeared and decayed with the damping time constant of 0.4 ± 0.1 ps. Sequentially, the second oscillation, whose period was 0.23 ± 0.01 ps, grew as the first component was damped down. The two sequential vibrational modes were interpreted with the aid of DFT-calculated vibrational modes of the HS state. The early vibrational mode was assigned to the symmetric breathing-like mode, whereas the second one was assigned to a pincer-like mode of the tridentate ligands. Coherent vibrational motions had only been indirectly observed through spectroscopic signals prior to this study, and this study captured the coherent vibration motion directly in real space for the first time. Therefore, this work is one of the representative achievements showing that the fs-TRXL is very effective in studying coherent molecular vibrations, which are further demonstrated via the examples in the following sections.
7.2. [Fe(bmip)2]2+ in acetonitrile
In addition to the charge transfer dynamics of [Fe(bmip)2]2+ introduced in Section 4.2, coherent vibrational wavepacket dynamics of the complex were also observed through the temporally oscillating signals in both fs-TRXL and TR-XES (Fig. 16a).70 Through the analysis based on the SVD of fs-TRXL signals and the kinetic model obtained from TR-XES, it was found that the difference scattering signal corresponding to the oscillatory signal closely resembled the signal shape of the 3MC state. Furthermore, the difference scattering signal of the 3MLCT state was too weak due to the relatively small structural change compared with that of the 3MC state to result in the marked amplitude of oscillation observed in the fs-TRXL signals. Therefore, the coherent oscillation in the fs-TRXL signal was attributed to the Fe–ligand vibration on the potential energy surface (PES) of the 3MC state.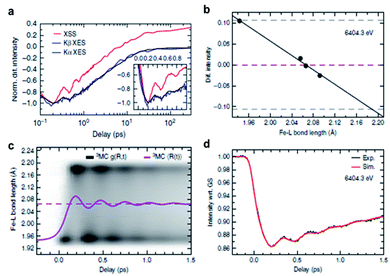 | ||
| Fig. 16 (a) Time profiles for the normalized X-ray emission spectra (Kα for black, Kβ for blue) and normalized TRXL signal between 0.7 and 1.0 Å−1 (red). (b) Change of the difference X-ray emission intensity of 3MC state with respect to the Fe–L bond length. (c) Distribution of the simulated Fe–L bond length (white-black gradient color scale), the ensemble averaged Fe–L bond length (solid magenta line), and the equilibrium Fe–L bond length (dashed magenta line). (d) Time profiles for the experimental (black) and simulated (red) X-ray emission intensities at 6404.3 eV. Reproduced from ref. 70 with the permission of Springer Nature, copyright 2020. | ||
A quantitative structural simulation assuming a Gaussian distribution of the Fe–ligand bond length, g(R,t), on the 3MC PES showed that the structural origin for the oscillating fs-TRXL data is a harmonic stretching of the ensemble average Fe–ligand bond length, 〈R〉, around the equilibrium 3MC geometry of 〈R〉 = 2.066 Å (Fig. 16b). The vibrational period and the damping constant were found to be 278 fs and 500 fs, respectively. For the oscillating signals in the TR-XES signals, ab initio calculation showed that the modification of the Fe–ligand bond length could linearly shift the Kα XES spectrum due to the first-order vibronic coupling between the core-levels (Fig. 16c). The estimated displacement between the 1s and 2p state is 0.014 Å, where the 2p state has a longer Fe–ligand bond length. Thus, based on the g(R,t) obtained from the analysis of fs-TRXL signals, the oscillating XES could be simulated to fit the experimental time-dependent intensity of Kα XES signals (Fig. 16d). From the fitting results, a structural sensitivity of ΔI/ΔR = 16%/0.123 Å was obtained, where the ΔI is the Kα XES signal intensity at the measured energy of 6404.3 eV, and ΔR is the change of Fe–ligand bond length. This work showed how the coherent vibrational wavepacket dynamics could be manifested in two different signals, the fs-TRXL and TR-XES signals, and explained the relation between them.
7.3. [Pt2(P2O5H2)4]4− in water
Tuning the condition of the excitation pulse can manipulate the formation and properties of a coherent vibrational wavepacket.162,163 For example, excitation with an off-resonance pump pulse can selectively generate a coherent wavepacket on the ground electronic state via a Raman transition. In the fs-TRXL study by Haldrup et al.,75 such a method was applied to probe the ground-state wavepacket dynamics of an aqueous diplatinum complex [Pt2(P2O5H2)4]4−.The [Pt2(P2O5H2)4]4−, also known as the PtPOP complex, has been intensely studied as a model binuclear d8 complex. The lowest energy transition promoting an electron from 5dσ* to 6pσ orbital leads to a significant contraction (∼0.2 Å) of the Pt–Pt distance. To investigate the ground state wavepacket, the wavelength of the optical pump pulse was tuned to the red side of the lowest visible absorption band, which prepared the vibrationally cold excited-state population by selectively exciting a molecule with the Pt–Pt distance around the equilibrium geometry of the excited state (Fig. 17a). Furthermore, since the transition dipole moment of visible excitation of PtPOP is aligned along the Pt–Pt axis, the scattering pattern is highly anisotropic due to the preferential excitation of the molecules parallel with the polarization of the optical pump pulse. The anisotropic signal component originates only from structural changes that have a well-defined orientational dependency with respect to the polarization axis of the optical pump laser. Among the candidate structural changes which satisfy this condition, it was found that the change of the Pt–Pt distance of the solute molecule dominantly contributes to the anisotropic component of a fs-TRXL signal. Thus, a single structural parameter modulating the Pt–Pt distance was selected for constructing the theoretical anisotropic fs-TRXL signals.
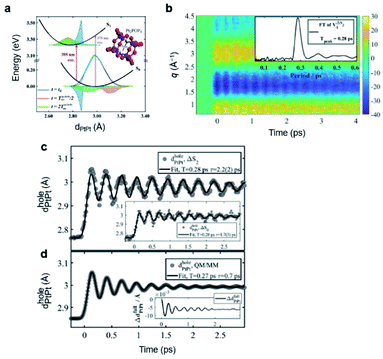 | ||
| Fig. 17 (a) PESs of PtPOP and the coherent wavepacket motions obtained from QM/MM simulations. The distribution of Pt–Pt distances at t = 0, t = Tgs,holesim/2, and t = 2Tgs,holesim are represented by blue, red, and green areas, respectively, where Tgs,holesim is the vibrational period of the hole created upon 395 nm photoexcitation. The inset shows the molecular structure of PtPOP. (b) Anisotropic component of the fs-TRXL data from PtPOP. The inset shows the Fourier transform of the first right singular vector obtained from SVD of the fs-TRXL data. (c) Time-dependent Pt–Pt internuclear distances of the hole (dholePtPt) obtained from the analysis of the anisotropic component of the TRXL data (gray circles) and the fit with a damped sine function convoluted by an IRF and a step function (black line). The inset shows time-dependent Pt–Pt internuclear distances obtained from the analysis of the isotropic component of the TRXL data and the fit. (d) Time-dependent Pt–Pt internuclear distance of the hole obtained from the QM/MM simulation and the fit. The fit was generated in the same way used for fit of the experimental results. Reproduced from ref. 75 with the permission of the American Physical Society, copyright 2019. | ||
The measured fs-TRXL signals of PtPOP showed marked oscillatory signals along the time axis (Fig. 17b). The oscillatory signal was modeled well through the structural fit solely by assuming the ground-state wavepacket (Fig. 17c). The obtained time-dependent profile of Pt–Pt distance showed a vibration near the equilibrium Pt–Pt distance of the ground state PtPOP with an amplitude of 0.06 ± 0.01 Å. The vibrational period was 0.283 ± 0.001 ps with a damping constant of 2.2 ± 0.2 ps. This experimental observation was supported by quantum mechanics/molecular mechanics (QM/MM) simulations in which the movement of the hole created in the ground state distribution of Pt–Pt distances was traced, and the results reproduced the experimental findings well with a discrepancy of within 5% (Fig. 17d). This work is a good example showing that the off-resonance excitation condition, which enables the exclusion of the contribution of excited-state wavepackets, can be used to selectively investigate the hole dynamics.
7.4. [Fe(bpy)3]2+ in water
For the photochemical reactions occurring on the PESs of electronically excited states, the intersection regions between the PESs play an important role because those regions are effective channels enabling extremely fast population transfer through a non-adiabatic process. From an experimental point of view, spectroscopic signals of coherent nuclear wavepacket have been a tool to explore the dynamics near the crossing points between the excited-state PESs. Locating the intersection positions between electronic excited-state PESs, however, is not trivial, and there are only a few examples that have succeeded in explicitly detecting such positions. In an effort to find the intersection points, Kjær et al.72 applied fs-TRXL and TR-XES on a model spin-crossover compound, aqueous [Fe(bpy)3]2+. Such a combination of a direct structural probe with spectroscopy provides a good example of detecting the intersection points between PESs by mapping parts of PES in the energy-structure axes.Before discussing this work, we note that the excited-state charge and SCO dynamics of [Fe(bpy)3]2+ had long been in debate. The main issue was the mechanism of SCO upon the excitation into the MLCT state; one side argued for a direct SCO from the 3MLCT to 5MC state,164–166 while the other proposed a sequential transition,72,167 in which the 3MC state is involved as a transient intermediate between the 5MC and 3MLCT states. In the TRXL work, the experimental data confirmed the involvement of the 3MC state, supporting the sequential mechanism.
The population dynamics of the excited states were observed through TR-XES. The kinetic model used to fit the TR-XES data shows that, upon 400 nm photoexcitation, the initially prepared excited-state population in the MLCT state is transferred to the 3MC state followed by the transition into the 5MC state (Fig. 18a). In particular, the observed transition from the 3MC state to the 5MC state is governed by non-exponential dynamics in which a forward population transfer followed by a backward one between those two electronic states occurs. Therefore, the location of intersection positions between the 3MC and 5MC states could be specified if the structural parameters at the turning points of the population transfer were obtained. This was achieved through the structural analysis of the fs-TRXL data. A single structural parameter quantifying the symmetric modification of the Fe–N bond length, R(Fe–N), was employed for simulating the fs-TRXL data. The resultant temporal profile of R(Fe–N) showed a coherent wavepacket motion with a period of 235 ± 14 fs and a dephasing time of 350 ± 80 fs. Through theoretical modeling for the excited-state cascade, which reproduced the experimentally determined temporal evolution of the R(Fe–N) and the excited-state population dynamics, it was revealed that the initial 3MC to 5MC intersection is located at R(Fe–N) = 2.05 ± 0.01 Å, while the subsequent back transfer from 5MC to 3MC occurs at R(Fe–N) = 1.98 ± 0.02 Å (Fig. 18b). Because the equilibrium R(Fe–N) is longer in the 5MC state than that in the 3MC state, the fact that the back transfer occurs at a shorter R(Fe–N) than the forward transfer cannot be easily understood under the one-dimensional PES relying only on the R(Fe–N), strongly implying the involvement of another reaction coordinate. Considering the pseudo-Jahn–Teller distortion originating from the occupation of a single electron in a 3d-dominated eg orbital for the 3MC state, it was proposed that the tetragonal Fe–N bond distortion might be involved in the evolution of the excited-state population. The representation of excited-state PESs related to this proposal is shown in Fig. 18c. It was not possible, however, to directly observe the involvement of such a reaction coordinate in this study. This shortcoming was caused by the following reason. The fs-TRXL signals of [Fe(bpy)3]2+ were sensitive mostly to the Fe–N distance as the interatomic pairs with other structural coordinates did not contribute to the signals. Consequently, it was not trivial to visualize the structural dynamics on the multi-dimensional PES. Thus, the involvement of other structural coordinates had to be inferred indirectly. Nevertheless, this work provides a good example of specifying the explicit locations, at least through a single structural coordinate, of the intersection points between the excited-state PESs using fs-TRXL and, at the same time, the results of this study imply the necessity of expansion of our experimental observation into the multi-dimensional PES. We expect that the future XFEL facilities providing much brighter X-ray pulses will break through this limit. With the currently available XFELs, nevertheless, a recent work, which is discussed in the following section, succeeded in visualizing wavepacket trajectories on the multi-dimensional PES via a gold trimer system using fs-TRXL.
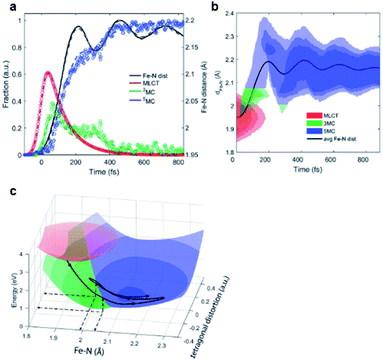 | ||
| Fig. 18 (a) Time profiles for the Fe–N distance obtained from fs-TRXL and the excited-state populations obtained from TR-XES. The solid lines and circles indicate the experimentally determined values and the dashed line indicates the fit results for the experimentally determined values. (b) The result of theoretical excited-state modeling that best describes the experimental dynamics shown in (a). Both electronic and structural dynamics are shown as a function of time and Fe–N distance. (c) A schematic for the structural dynamics and the PES of [Fe(bpy)3]2+ upon photoexcitation. Reproduced from ref. 72 with the permission of the Royal Society of Chemistry, copyright 2019. | ||
7.5. [Au(CN)2−]3 in water
The nuclear wavepacket dynamics introduced in the previous sections were observed through a single structural parameter that approximated multiple reaction coordinates. For the chemical reactions of polyatomic molecules, however, several reaction coordinates are generally involved, and, therefore, tracing the nuclear wavepacket in the explicitly defined multi-dimensional reaction coordinates is crucial to fully understanding the ultrafast structural dynamics of polyatomic molecules. This challenging but important task was accomplished in a recent work by Kim et al. in which the nuclear wavepacket trajectories were observed during and after the bond formation reaction of aqueous trimer complex of Au(CN)2−,63 whose overall reaction dynamics is given in Section 3.1.The photoexcitation of aqueous [Au(CN)2−]3 complex launches nuclear wavepackets on both excited- and ground-state PESs. The excited-state wavepacket, for example, travels along the slope of the PES, starting from the initially located Franck–Condon region, to find a new equilibrium geometry (Fig. 19a). Therefore, the ultrafast bent-to-linear structural change, as well as the Au–Au bond formation in [Au(CN)2−]3, can be visualized by tracing the trajectory of the excited-state wavepacket. Using fs-TRXL, the wavepacket trajectories on the multi-dimensional nuclear coordinates consisting of two Au–Au distances, RAB and RBC, and the Au–Au–Au angle, θ, were mapped. The experimental fs-TRXL signals and corresponding fits related to the coherent wavepacket motion are shown in Fig. 19b.
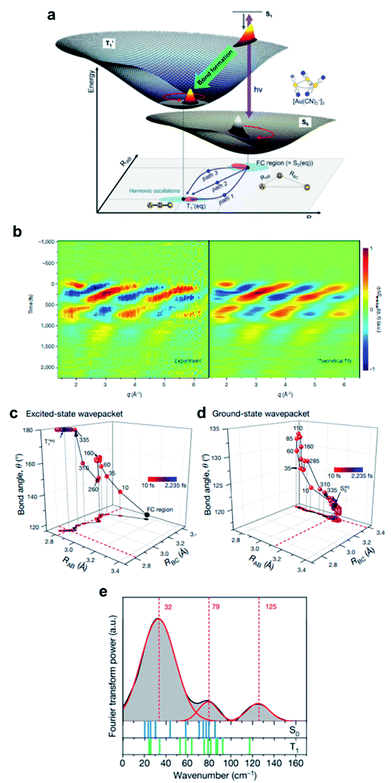 | ||
Fig. 19 (a) A schematic for the bond formation of [Au(CN)2−]3 upon photoexcitation. In the ground state, the trimer forms a loosely bound state. Upon photoexcitation, molecular vibration emerges along with the chemical bond formation. (b) Fs-TRXL data (left) for the molecular vibrations and the theoretical fits obtained using the ground-state (S0) and excited-state  vibrations (right). (c and d) Wavepacket trajectories in real space for (c) the excited state and (d) the ground state. (e) Averaged experimental Fourier power spectrum (black) and the fits with three Gaussian functions (red). The blue and green lines indicate the vibrational frequencies of the ground and excited states obtained from the DFT calculation. Reproduced from ref. 63 with the permission of Springer Nature, copyright 2020. vibrations (right). (c and d) Wavepacket trajectories in real space for (c) the excited state and (d) the ground state. (e) Averaged experimental Fourier power spectrum (black) and the fits with three Gaussian functions (red). The blue and green lines indicate the vibrational frequencies of the ground and excited states obtained from the DFT calculation. Reproduced from ref. 63 with the permission of Springer Nature, copyright 2020. | ||
For the excited-state wavepacket (Fig. 19c), the time evolution of the three structural parameters obtained from the structural fit for the fs-TRXL data revealed that the RAB quickly decreases within ∼60 fs, representing the formation of a covalent Au–Au bond, while the RBC remains in a much longer distance than the covalent bond length at this stage. The formation of the other Au–Au covalent bond accompanied with the bent-to-linear transition is completed at a much longer time delay of ∼360 fs through the decrease in RBC and increase in θ. Finally, the equilibrium geometry of the excited state is reached after dephasing of the harmonic oscillation of the wavepacket around the minimum of excited-state PES. Therefore, the observed wavepacket trajectory reveals that the covalent bonds of the excited state of [Au(CN)2−]3 are formed asynchronously. For the ground-state wavepacket (Fig. 19d), initially, a decrease in RAB and increase in θ were observed within ∼85 fs, which reflects the trajectory of the excited-state wavepacket undergoing ultrafast bond formation and bent-to-linear structural change. Afterward, the wavepacket bounces back to the minimum of the ground-state PES. Subsequently, the harmonic oscillation of the ground-state wavepacket was observed around the equilibrium geometry of the ground-state [Au(CN)2−]3. The observed structural movements during the harmonic oscillations of wavepackets on both excited- and ground-state PESs were simulated by various combinations of vibrational normal modes to find which normal modes had been activated for each wavepacket dynamics. Two symmetric stretching modes with frequencies of 79 cm−1 and 125 cm−1 were identified for the excited-state wavepacket, while a symmetric stretching mode and an asymmetric stretching mode with frequencies of 32 cm−1 and 44 cm−1, respectively, were observed for the ground-state wavepacket (Fig. 19e).
This study also underscores the importance of direct structural information in interpreting the observed frequencies of nuclear wavepacket motions. DFT calculations for the vibrational normal modes provide 11 and 13 normal modes in the frequency range of 20 cm−1 to 170 cm−1 for the ground- and excited-state [Au(CN)2−]3, respectively (Fig. 19e). Had it not been for the structural information but only the frequency values, one would have had to compare those values with the frequencies of normal modes obtained from DFT calculations, which has been the typical situation for spectroscopic studies for nuclear wavepacket dynamics. For polyatomic molecules containing many normal modes, simply comparing the experimentally obtained vibrational frequencies with those of DFT calculations, however, is vulnerable to the possibility of incorrectly interpreting the observed wavepacket dynamics. In the case of [Au(CN)2−]3, for example, among the 11 normal modes identified from DFT calculations, assigning the observed frequency of 32 cm−1 to a bending mode with a frequency of 33 cm−1 that is numerically most closest to the observed value leads to misinterpretation.
Briefly, this work is the first example of visualizing the wavepacket trajectories in a multi-dimensional space of reaction coordinates. This work emphasizes that direct structural information is critical for correctly assigning the temporal oscillation of the signal to vibrational motions, particularly for a polyatomic molecule, for which theoretical calculations predict multiple vibrational modes with similar frequencies close to the observed frequencies.
7.6. [NCFe(CN)5(NH3)5Ru]− in water
Not only the nuclear wavepacket dynamics of solute molecules but also the coherent oscillations of the solvent molecules caused by their collective motion during the solvation process can be observed through the cage term of fs-TRXL signals. A good example is the damped oscillation of water molecules observed in the solvation processes of the FeRu complex introduced in Section 5.3.74The fs-TRXL signals of the aqueous FeRu complex show oscillatory features in the low-q region (<1 Å−1), where the cage term is dominant, as a function of pump–probe time-delay as shown in Fig. 20a and b. The observed signals were reproduced via non-equilibrium MD simulations, and the resultant RDFs showed damped oscillations of the peak position corresponding to the first solvent shell around Fe and Ru ligands, as shown in Fig. 20c and d, respectively. Therefore, those oscillations represent the coherent motion during the solvent reorganization induced by the ET reaction. Specifically, at the onset of ET from Fe to Ru, ultrafast (<60 fs) expansion of the first shell was observed through the RDFs of NFe–O and NRu–O, whose average expansion velocities were 2.5 Å ps−1 and 1.8 Å ps−1, respectively. Subsequently, both RDFs showed a damped oscillation with a relaxation time of ∼100 fs. The oscillation frequency was approximately 200 cm−1, which is in good agreement with the frequency of ∼180 cm−1 present in the vibrational spectrum of water and is assigned to translational motions of the intermolecular hydrogen bonding coordinate.
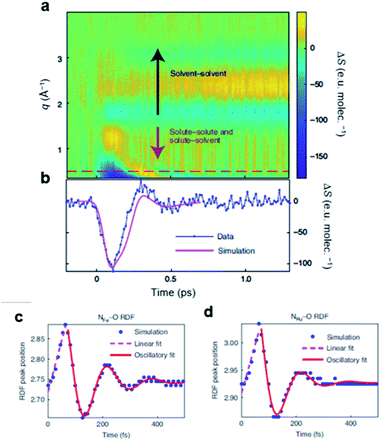 | ||
| Fig. 20 (a) Isotropic TRXL signal of FeRu upon photoexcitation. (b) Time profiles of experimental (blue) and calculated (magenta) TRXL signals between 0.4 and 0.6 Å −1. (c and d) Time profiles of the peak positions of the first solvation shell obtained from the radial distribution functions of (c) NFe–O and (d) NRu–O. The simulation results, linear fit results, and oscillatory fit results are plotted in blue, magenta, and red. Reproduced from ref. 74 with the permission of Springer Nature, copyright 2021. | ||
This work demonstrates the power of fs-TRXL combined with TR-XES and MD simulations in investigating the coherent response of solute–solvent interaction upon intramolecular electron transfer. It is expected that the methodology exploited in this study can be applied in a variety of chemical reactions to study the influence of specific solute–solvent interactions on reactions. Additionally, the method of this study can be further improved by analyzing the data using a full quantum-mechanical treatment for the solute–solvent interactions. For example, the energetic contribution of the observed translational motion of water molecules to the overall solvent reorganization energy during the ET process in FeRu is one of important questions, but it cannot be reliably answered with classical MD simulations based on non-polarizable force fields. Also, it may be possible to describe the ET process itself more accurately with quantum mechanical treatment, which may give a more precise picture of the solvent reorganization process than simply transferring an electron from a donor to an acceptor as in this study.
8. Protein structural dynamics
It is well known that the function of a protein is correlated to the structure of the protein. The structural dynamics of proteins have been investigated for decades to elucidate the fundamentals of the protein function using various experimental methods, including various time-resolved spectroscopic methods and time-resolved X-ray crystallography.168,169,183 However, time-resolved spectroscopic methods have rarely clarified the global structural changes of proteins since the typical spectroscopic methods are typically only sensitive to the energy state of the protein or local structural changes of proteins. Time-resolved X-ray crystallography, which was widely used to study the structural change of proteins, can only be applied to proteins in the crystalline phase. In this regard, the global structural change of proteins in the solution phase had been investigated scarcely until TRXL was used to explore the global structural dynamics of various proteins in solution.38,170,171 The emergence of fs-TRXL opened a new door for protein structural dynamics research, as it can directly visualize the global structural change of proteins in the ultrafast time regime. The ultrafast structural dynamics of proteins exhibit not only key structural changes that are related to the subsequent dynamics but also structural changes associated with a coherent motion. Here, we review the studies on protein structural dynamics using fs-TRXL.8.1. Photosynthetic reaction center
The photosynthetic reaction center (RC) is a protein that mediates photosynthesis upon light absorption. One of the key features of RC is how it reacts when it is exposed to light, particularly to intense light. To protect the integrity of the protein, the excessive energy generated by light absorption should dissipate before the excessive energy deforms the protein. Using fs-TRXL, the structural dynamics of RC under the experimental condition where it absorbed ∼800 photons due to the intensive light were investigated by Arnlund et al.76From the TRXL data, four components were extracted based on a kinetic model: the ultrafast component (C1), the protein component (C2), and the non-equilibrated (C3) and equilibrated (C4) heating components (Fig. 21a). In terms of the kinetics, the temporal behaviors of C3 and C4 exhibited good agreement with the temporal behaviors of the heat flow in the protein and from the protein to the surrounding, which were obtained from MD simulations, respectively. For instance, the time for the excess heat energy in the protein to reach the maximum, which was obtained from the MD simulation, agreed well with the time for C3 to become the maximum. Hence, C3 and C4 were assigned to the heat flow in the protein and the heat flow to the surrounding environment, respectively. The protein component (C2) emerges within several picoseconds, and it precedes the non-equilibrium heating component. Such a phenomenon indicates that the protein quake in which the protein dissipates its energy via ultrafast quake-like structural deformation occurs upon photoexcitation of RC.
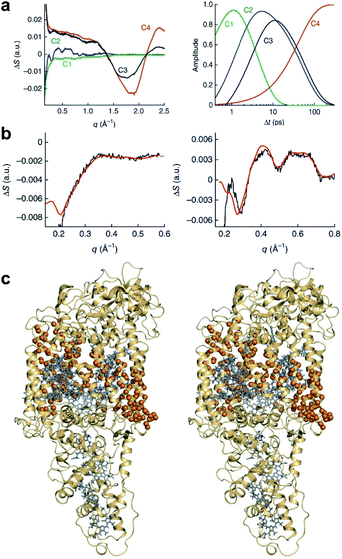 | ||
| Fig. 21 (a) (Left) species-associated difference scattering curves of four components involved in the ultrafast structural dynamics of photosynthetic reaction center and (right) the time profiles of the four components determined from a fs-TRXL study. C1, C2, C3, and C4 were assigned as the ultrafast component, the protein component, the non-equilibrated heating component, and the equilibrated heating components, respectively. (b) Species-associated difference scattering curves of C1 and C2 (black) and theoretical scattering curves obtained from the structure refinement (red). The results for C1 and C2 are plotted in left and right panels, respectively. C1 and C2 were fitted using the motions of the cofactors and the whole protein, respectively. (c) Stereo-view representation of the movements corresponding to C2 obtained from the structure refinement. The orange spheres indicate the Cα atoms that exhibit movements away from other Cα atoms. Reproduced from ref. 76 with the permission of Springer Nature, copyright 2014. | ||
In addition, since the X-ray scattering signal is sensitive to the structures of protein, the initial structural changes of RC upon photoexcitation were visualized using C1 and C2. The SADS of C1 could be described by the motion of the cofactors obtained from the MD simulations with the other atoms frozen. On the other hand, the SADS of C2 was retrieved using the structural change of the whole protein obtained from MD simulations which allowed the motion in the whole protein (Fig. 21b). For the structural change that corresponds to C2, the internal distance between the Cα atoms of the residues in the transmembrane domain increases, which indicates the expansion of the transmembrane domain occurs (Fig. 21c). As the first fs-TRXL study on a protein, this work demonstrated the feasibility of the application of fs-TRXL to protein systems. In addition, the results of this work showed that a protein can exhibit an appreciable structural change even in the ultrafast time domain, confirming that the ultrafast structural dynamics of proteins are worth investigating.
8.2. Myoglobin
For decades, myoglobin (Mb) has served as a model system to study the structural dynamics of proteins due to its simple structure and capability to induce structural change due to the ligand dissociation upon photoexcitation. Although the structural dynamics of Mb have been extensively investigated, the ultrafast structural dynamics studies using an experimental technique with the sensitivity to the global structure change in solution had been scarce until the ultrafast global structural dynamics of Mb were successfully elucidated using fs-TRXL by Levantino et al.77The TRXL signal both in the small-angle X-ray scattering (SAXS) and wide-angle X-ray scattering (WAXS) regions emerges within ∼1 ps after the photolysis, and the changes of the signal shape and intensity are mostly completed within 10 ps. By analyzing the signal in the SAXS region using the Guinier analysis, the ultrafast increase in the radius of gyration (Rg) within a picosecond, which was followed by the protein volume expansion, was observed. Similar ultrafast change of Rg and volume and delayed volume change compared to the Rg change were observed in another study on Mb by Shelby et al., which combined XTA and TRXL and used the SAXS region of TRXL signal for the analysis.78 Such an ultrafast structural response of Mb, which has a similar time scale with the speed of sound in proteins, indicated that the protein quake was observed under the condition without severe multiphoton absorption. In addition to the ultrafast increase in Rg and volume, their analysis showed that Rg and volume of Mb undergo an underdamped oscillation,77 although this conclusion was challenged later by a theoretical study.172 For example, Rg of Mb exhibits an oscillation with a time period of 3.6 ps and a decay time of 6 ps. Such an underdamped oscillation contrasts the well-known idea that the protein dynamics typically exhibit exponential behavior due to the ensemble average effect of the experimental observables. In addition, the observation of underdamped oscillation is in opposition to the conventional concept that the global structural change of proteins is overdamped. It was suggested that the oscillatory behavior obtained by analyzing the SAXS region implied the ballistic-like motion of the protein upon the photoexcitation rather than the thermally activated process.
Later, this work sparked the discussion on how to analyze the fs-TRXL data of proteins. A theoretical study by Brinkmann et al.172 challenged the interpretation suggested by this work and proposed that the fs-TRXL data in the SAXS region could be dominantly affected by the change of the hydration shell instead of the structural change of the protein. In addition, it was argued that the underdamped oscillation of Mb originated from the change of the hydration shell instead of the structural change of the protein, and this proposal was confirmed by a fs-TRXL study that used the WAXS region rather than the SAXS region for the structural analysis.80
8.3. Cytochrome c
The cytochrome c (cyt-c) protein is well-known for its various responses upon photoexcitation, such as protein folding and change of the protein function. For example, upon photoexcitation, one of the axial ligands (Met80) coordinated to the heme group dissociates, which may be linked to the change of the function from an electron transfer protein to a peroxidase. Reinhard et al. investigated the electronic state and structural changes of cyt-c, which are responsible for such axial ligand dissociation by combining TR-XES and fs-TRXL.79By using TR-XES, a short-lived electronic state with a lifetime of 87 fs, which precedes the 5MC state observed in a previous TR-XES study,173 was observed (Fig. 22a). The electronic state was assigned to a 3MC state with 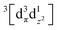 configuration, although the mechanism of how such a state is formed is not clear. The d2z orbital has an antibonding σ* character, which enables the Fe–S bond dissociation. The detailed structural change of cyt-c was investigated using fs-TRXL. Even in the ultrafast time domain (<600 fs), a difference scattering signal was observed in the q region between 0.4 and 1.1 Å−1, which indicates that the structural change of cyt-c occurs in the ultrafast time domain. For the first 300 fs, the structural change of cyt-c was analyzed in terms of the distance between the axial ligands and the heme group, with the assumption that the global structural change would be less important compared to the local structural change such as the heme–ligand bond dissociation during this time domain. The analysis results indicate that the distance between two axial ligands (Met80 and His18) and the heme group should be elongated to retrieve the fs-TRXL signal (Fig. 22b). Such observation is in accordance with the assignment from the TR-XES analysis that the 3MC state is responsible for the axial ligand dissociation. The structural analysis on the later time domain (300–600 fs) using the same structural change model, however, could not reproduce the large Fe–S distance elongation obtained from a previous TR-XES study. These results indicate that the signal in the later time domain originates from multiple structural changes rather than the simple ligand–heme group distance change. In summary, by combining the results of TR-XES and fs-TRXL, this work offers a comprehensive description of the ultrafast reaction dynamics of cyt-c, which is one of the well-known model systems for the reaction dynamics study of proteins upon photoexcitation.
configuration, although the mechanism of how such a state is formed is not clear. The d2z orbital has an antibonding σ* character, which enables the Fe–S bond dissociation. The detailed structural change of cyt-c was investigated using fs-TRXL. Even in the ultrafast time domain (<600 fs), a difference scattering signal was observed in the q region between 0.4 and 1.1 Å−1, which indicates that the structural change of cyt-c occurs in the ultrafast time domain. For the first 300 fs, the structural change of cyt-c was analyzed in terms of the distance between the axial ligands and the heme group, with the assumption that the global structural change would be less important compared to the local structural change such as the heme–ligand bond dissociation during this time domain. The analysis results indicate that the distance between two axial ligands (Met80 and His18) and the heme group should be elongated to retrieve the fs-TRXL signal (Fig. 22b). Such observation is in accordance with the assignment from the TR-XES analysis that the 3MC state is responsible for the axial ligand dissociation. The structural analysis on the later time domain (300–600 fs) using the same structural change model, however, could not reproduce the large Fe–S distance elongation obtained from a previous TR-XES study. These results indicate that the signal in the later time domain originates from multiple structural changes rather than the simple ligand–heme group distance change. In summary, by combining the results of TR-XES and fs-TRXL, this work offers a comprehensive description of the ultrafast reaction dynamics of cyt-c, which is one of the well-known model systems for the reaction dynamics study of proteins upon photoexcitation.
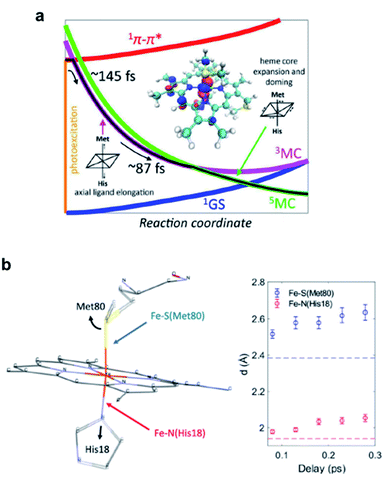 | ||
| Fig. 22 (a) A schematic for the excited-state dynamics of cyt-c upon photoexcitation revealed by TR-XES. (b) (Left) a schematic for the structural parameters used for the structure refinement of the fs-TRXL data from cyt-c and (right) the time profile of Fe–S and Fe–N distances obtained from the structure refinement. Reproduced from ref. 79 with the permission of Springer Nature, copyright 2021. | ||
8.4. Homodimeric hemoglobin
Homodimeric hemoglobin (HbI) is a heme protein with a homodimeric structure. Due to the relatively simple structure of HbI compared to hemoglobin with a tetrameric structure, HbI has been investigated using synchrotron-based TRXL as a model system for the allosteric regulation of proteins. Still, due to the limitation in the time resolution of the previous TRXL study on HbI, the ultrafast structural dynamics of HbI had remained elusive.41 Lee et al. investigated the ultrafast structural dynamics of HbI, as well as the change of the hydration shell, using fs-TRXL and an advanced structural analysis scheme.80 As mentioned in Section 7.2, it was proposed that the signal in the SAXS region of the fs-TRXL data can be dominantly affected by the change of the hydration shell. In the advanced analysis scheme, based on such an argument, the WAXS region of the fs-TRXL data was used to retrieve the structural change of the protein, and the SAXS region of the data was used to elucidate the change of the electron density of the hydration shell. In addition, the structural change of the protein obtained by analyzing the SAXS region was compared to that obtained by analyzing the WAXS region to experimentally confirm the effect of the change of the hydration shell to the SAXS region of the fs-TRXL data.With the improved time resolution of an fs-TRXL experiment (∼800 fs) compared to that of a TRXL experiment performed at a synchrotron, various phenomena that had not been resolved in the previous TRXL study on HbI were revealed (Fig. 23a).41 In addition, detailed structural changes during these processes were elucidated via the structure refinement using rigid-body modeling and Monte Carlo simulations. In this refinement method, the protein structure was divided into rigid bodies according to the helices and heme groups, and the rigid bodies were moved to give the calculated curves that showed satisfactory agreement with the experimental difference scattering curves. As a result of the analysis, the fs-TRXL study identified the formation of a reaction intermediate (I0), which had not been observed in the previous TRXL study. Although the formation of I0 occurs within the time resolution of the experiment, it accompanies the structural change all over the protein. It was suggested that the protein quake, in which the structural deformation of the protein propagates from a focus to the entire protein in a quake-like manner, is responsible for such a rapid global structural change. Then, I0 transforms into the second intermediate (I1) with a time constant of 8.7 ps accompanying the structural change, such as the movement of the C helix and CD loop region. In addition to the transition to I1, the amplitude of the fs-TRXL data in the ultrafast time domain (<3 ps) exhibits an oscillatory feature over time, indicating that I0 undergoes a coherent motion. According to the results of kinetic and structural analyses, the coherent motion had a frequency of ∼13 cm−1 and a damping time constant of ∼800 fs, and the overall expansion and contraction of protein occurred during the coherent motion.
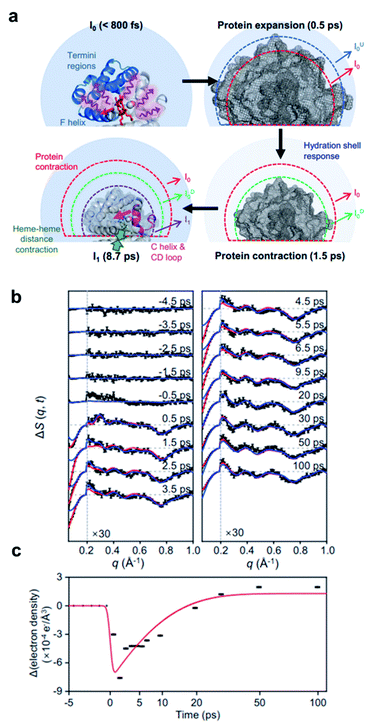 | ||
| Fig. 23 (a) A schematic for the ultrafast structural dynamics of HbI determined from a fs-TRXL study. (b) Experimental difference scattering curves (black), the theoretical difference scattering curves obtained by protein structure refinement using the signal in the WAXS regions (blue), and the theoretical difference scattering curves after the electron density of the hydration shell was modulated using the signal in the SAXS region (red). (c) Time profile of the electron density of the hydration shell obtained from structure refinement (black) and comparison with an exponential function with 8.7 ps time constant (red). Reproduced from ref. 80 with the permission of Springer Nature, copyright 2021. | ||
The structural change of HbI exhibited different temporal behavior when the WAXS and SAXS regions were used for the analysis. For example, the changes of the Rg show overdamped-like and underdamped-like behavior when the WAXS and SAXS regions were used for the analysis, respectively. Such a difference indicates that the signal in the SAXS region is largely affected by the change of the hydration shell. Indeed, the SAXS region of the theoretical signal calculated by assuming a constant electron density of the hydration shell during the structural change disagreed with the experimental data. By modulating the electron density of the hydration shell, the SAXS region of the experimental data could be described well without impairing the agreement between the theoretical and experimental signals in the WAXS region (Fig. 23b). In this way, the electron density of the hydration shell was tracked using the fs-TRXL signal in the SAXS region. The electron density of the hydration shell decreases by ∼0.2% up to ∼1.5 ps after photoexcitation. Then, the electron density of the hydration shell changes along with the formation of I1 (Fig. 23c). Using fs-TRXL, this work successfully revealed the ultrafast structural dynamics of HbI occurring in the timescale earlier than 100 ps after photoexcitation, which had been not accessible via synchrotron-based TRXL. In addition, this work provided experimental evidence for the proposal that the fs-TRXL signal in the SAXS region is largely affected by the change of the hydration shell and provided an advanced analysis method in which the WAXS and SAXS regions were analyzed separately. With this method, this work unveiled the change of the electron density of the hydration shell using the fs-TRXL data in the SAXS region.
9. Summary and outlook
Since the arrival of XFELs, fs-TRXL has been applied to study multiple categories of solution-phase structural dynamics in the femtosecond domain. In this review, we classify the studies with fs-TRXL applied to chemical and biological reactions into the topics of bond cleavage/formation, charge distribution and electron transfer, orientational dynamics, solvation dynamics, wavepacket dynamics, and protein structural dynamics. The reviewed examples demonstrate that fs-TRXL allows observing the dynamic changes of the structures of solute molecules and the interatomic distances between the solute and solvent molecules, in the non-equilibrium state, beyond revealing the equilibrium structures and the kinetics of the reacting species, such as the concentration or reaction rate. The sub-angstrom structural sensitivity and femtosecond time resolution of fs-TRXL provides complementary information that cannot be easily obtained with other experimental techniques, giving invaluable insights into reaction dynamics.Nevertheless, the full scope of information available from fs-TRXL has not been exploited yet. One notable example is the anisotropic dynamics of the solvent cage. When the structural change of the solute appears anisotropic, the change in the cage structure can also be anisotropic. Therefore, such anisotropic structural change of the cage needs to be analyzed properly to extract detailed cage dynamics, as performed in a recent work.93 In addition, information on changes in nuclear positions was mainly obtained based on the independent atom model from the TRXL signal. In principle, fs-TRXL data contain information on changes in electronic charge distribution, which cannot be retrieved solely by data analysis based on the independent atom model. Such fine information may be obtained through quantum mechanical treatment of X-ray scattering signals. Although such attempts have been made to analyze gas-phase time-resolved X-ray scattering data,174,175 extracting information on changes in electronic charge distribution in solution through fs-TRXL signals has not yet been achieved and remains a future task.
Another aspect that can be explored in the future is extending the research area to wider target systems. In particular, for many biochemical or catalytic reactions, the chemical reactions are initiated by substrate-binding or heat rather than light. Taking this into consideration, it is expected that a wider range of reactions can be studied if photo-uncaging or T-jump is introduced to TRXL experiments. Such an approach can broaden the scope of the target systems for TRXL. Another challenging but important avenue of extending fs-TRXL is in situ/operando experiments. Recently, in situ/operando experiments using X-ray diffraction/scattering have been performed to investigate the application of various materials.176–181 These experiments mostly deal with chemical reactions that are irreversible in heterogeneous phases (gas/solid or liquid/solid interfaces, for example). One of the obstacles in in situ/operando study using TRXL, especially using fs-TRXL, is that the sample can be damaged by intense X-ray pulses. Because of these characteristics, it is not trivial to perform a TRXL experiment for a long time (for example, several days) using a single sample, and accordingly, a large amount of sample is required to continuously provide a fresh sample. A method to overcome such a limitation is using a thinner liquid jet to reduce the amount of sample required for the experiment. Another approach is using a pulsed droplet or fixed-target system rather than a continuously flowing liquid jet. Typically, the time for which the sample is exposed to X-ray pulses is much shorter than the total experimental time. Using a pulsed droplet or fixed-target system can greatly increase the fraction of the experimental time used for the actual pump–probe measurement, thereby reducing the amount of sample required for the experiment. In addition, in order to realize in situ/operando characterization of such reactions using fs-TRXL, a specialized sample cell need to be devised.177,179,182
So far, most of the molecules studied using TRXL contain heavy atoms, partly because in the absence of a heavy atom, the TRXL signal is relatively small and difficult to analyze. In this respect, the scope of research using TRXL has been somewhat limited. For a reaction of a molecule with no heavy atom, one strategy to increase the contrast in difference scattering signals is to attach heavy atoms to the molecule, with the possibility of the target reaction being altered by heavy-atom labeling. In fact, through a TRXL experiment at the upcoming LCLS-II HE, it is expected that even structural changes of hydrocarbons can be sufficiently observed, without attaching a heavy atom, since the signal-to-noise ratio can be significantly improved using LCLS-II HE, which is expected to offer ∼1000 times higher photon flux compared to typical XFEL facilities. In addition, the upcoming LCLS-II HE offers higher energy (∼25 keV) of X-ray pulses than the typical ones currently available. This expands the measurable q-range possibly over 10 Å−1, which contains additional structural information for the solute. Therefore, the extended q range should increase the accuracy of the structure refinement. If the time-resolved positions of a wider class of atoms including hydrogen and carbon can be resolved using enhanced signal quality, TRXL is expected to provide invaluable insights into chemical reactions of organic molecules, catalysts, and substrates, as well as more detailed interaction between solute and solvent molecules.
Author contributions
H. I. proposed and designed the review. E. H. C., Y. L., J. H., and H. I. collected the literature and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Institute for Basic Science (IBS-R033).Notes and references
- R. D. Levine, Molecular reaction dynamics, Cambridge University Press, 2009 Search PubMed.
- P. L. Houston, Chemical kinetics and reaction dynamics, Courier Corporation, 2012 Search PubMed.
- L. R. Khundkar and A. H. Zewail, Ultrafast Molecular Reaction Dynamics in Real-Time: Progress Over a Decade, Annu. Rev. Phys. Chem., 1990, 41, 15–60 CrossRef CAS.
- A. H. Zewail, Laser Femtochemistry, Science, 1988, 242, 1645–1653 CrossRef CAS.
- A. H. Zewail, Femtochemistry: Atomic-Scale Dynamics of the Chemical Bond Using Ultrafast Lasers (Nobel Lecture), Angew. Chem., Int. Ed., 2000, 39, 2586–2631 CrossRef CAS.
- A. A. Ischenko, V. V. Golubkov, V. P. Spiridonov, A. V. Zgurskii, A. S. Akhmanov, M. G. Vabischevich and V. N. Bagratashvili, A stroboscopical gas-electron diffraction method for the investigation of short-lived molecular species, Appl. Phys. B: Lasers Opt., 1983, 32, 161–163 CrossRef.
- S. Williamson, G. Mourou and J. C. M. Li, Time-Resolved Laser-Induced Phase Transformation in Aluminum, Phys. Rev. Lett., 1984, 52, 2364–2367 CrossRef CAS.
- J. C. Williamson and A. H. Zewail, Structural femtochemistry: experimental methodology, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 5021–5025 CrossRef CAS.
- C. W. Siders, et al., Detection of Nonthermal Melting by Ultrafast X-ray Diffraction, Science, 1999, 286, 1340–1342 CrossRef CAS.
- J. C. Williamson, J. Cao, H. Ihee, H. Frey and A. H. Zewail, Clocking transient chemical changes by ultrafast electron diffraction, Nature, 1997, 386, 159–162 CrossRef CAS.
- C. Rischel, et al., Femtosecond time-resolved X-ray diffraction from laser-heated organic films, Nature, 1997, 390, 490–492 CrossRef CAS.
- C. Rose-Petruck, et al., Picosecond–milliångström lattice dynamics measured by ultrafast X-ray diffraction, Nature, 1999, 398, 310–312 CrossRef CAS.
- M. H. Pirenne, The Diffraction of X-rays and Electrons by Free Molecules, Cambridge University Press, 1946 Search PubMed.
- J. Als-Nielsen and D. McMorrow, X-rays and their interaction with matter, Elements of Modern X-ray Physics, 2011, pp. 1–28, DOI:10.1002/9781119998365.ch1.
- H. Ihee, Visualizing Solution-Phase Reaction Dynamics with Time-Resolved X-ray Liquidography, Acc. Chem. Res., 2009, 42, 356–366 CrossRef CAS PubMed.
- H. Ihee, M. Lorenc, T. K. Kim, Q. Y. Kong, M. Cammarata, J. H. Lee, S. Bratos and M. Wulff, Ultrafast X-ray Diffraction of Transient Molecular Structures in Solution, Science, 2005, 309, 1223–1227 CrossRef CAS PubMed.
- Q. Kong, J. Kim, M. Lorenc, T. K. Kim, H. Ihee and M. Wulff, Photodissociation Reaction of 1,2-Diiodoethane in Solution: A Theoretical and X-ray Diffraction Study, J. Phys. Chem. A, 2005, 109, 10451–10458 CrossRef CAS PubMed.
- J. Kim, J. H. Lee, J. Kim, S. Jun, K. H. Kim, T. W. Kim, M. Wulff and H. Ihee, Structural Dynamics of 1,2-Diiodoethane in Cyclohexane Probed by Picosecond X-ray Liquidography, J. Phys. Chem. A, 2012, 116, 2713–2722 CrossRef CAS PubMed.
- J. H. Lee, T. K. Kim, J. Kim, Q. Kong, M. Cammarata, M. Lorenc, M. Wulff and H. Ihee, Capturing Transient Structures in the Elimination Reaction of Haloalkane in Solution by Transient X-ray Diffraction, J. Am. Chem. Soc., 2008, 130, 5834–5835 CrossRef CAS PubMed.
- J. Gu, et al., Structural Dynamics of C2F4I2 in Cyclohexane Studied via Time-Resolved X-ray Liquidography, Int. J. Mol. Sci., 2021, 22, 9793 CrossRef CAS.
- J. H. Lee, J. Kim, M. Cammarata, Q. Kong, K. H. Kim, J. Choi, T. K. Kim, M. Wulff and H. Ihee, Transient X-ray diffraction reveals global and major reaction pathways for the photolysis of iodoform in solution, Angew. Chem., Int. Ed., 2008, 47, 1047–1050 CrossRef CAS.
- C. W. Ahn, et al., Direct Observation of a Transiently Formed Isomer During Iodoform Photolysis in Solution by Time-Resolved X-ray Liquidography, J. Phys. Chem. Lett., 2018, 9, 647–653 CrossRef CAS.
- J. Davidsson, et al., Structural Determination of a Transient Isomer of CH2I2 by Picosecond X-Ray Diffraction, Phys. Rev. Lett., 2005, 94, 245503 CrossRef.
- J. Vincent, et al., Solvent dependent structural perturbations of chemical reaction intermediates visualized by time-resolved x-ray diffraction, J. Chem. Phys., 2009, 130, 154502 CrossRef PubMed.
- S. Park, et al., Fate of transient isomer of CH2I2: mechanism and origin of ionic photoproducts formation unveiled by time-resolved x-ray liquidography, J. Chem. Phys., 2019, 150, 224201 CrossRef.
- Q. Kong, M. Wulff, J. H. Lee, S. Bratos and H. Ihee, Photochemical Reaction Pathways of Carbon Tetrabromide in Solution Probed by Picosecond X-ray Diffraction, J. Am. Chem. Soc., 2007, 129, 13584–13591 CrossRef CAS PubMed.
- Q. Kong, et al., Photolysis of Br2 in CCl4 studied by time-resolved X-ray scattering, Acta Crystallogr., 2010, A66, 252–260 CrossRef PubMed.
- M. Wulff, S. Bratos, A. Plech, R. Vuilleumier, F. Mirloup, M. Lorenc, Q. Kong and H. Ihee, Recombination of photodissociated iodine: a time-resolved x-ray-diffraction study, J. Chem. Phys., 2006, 124, 034501 CrossRef CAS PubMed.
- K. H. Kim, H. Ki, J. H. Lee, S. Park, Q. Kong, J. Kim, J. Kim, M. Wulff and H. Ihee, Solvent-dependent structure of molecular iodine probed by picosecond X-ray solution scattering, Phys. Chem. Chem. Phys., 2015, 17, 8633–8637 RSC.
- K. H. Kim, et al., Solvent-Dependent Molecular Structure of Ionic Species Directly Measured by Ultrafast X-Ray Solution Scattering, Phys. Rev. Lett., 2013, 110, 165505 CrossRef PubMed.
- K. H. Kim, et al., Global reaction pathways in the photodissociation of I3− ions in solution at 267 and 400 nm studied by picosecond X-ray liquidography, ChemPhysChem, 2013, 14, 3687–3697 CrossRef CAS PubMed.
- T. K. Kim, et al., Spatiotemporal reaction kinetics of an ultrafast photoreaction pathway visualized by time-resolved liquid x-ray diffraction, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9410–9415 CrossRef CAS PubMed.
- D. Leshchev, D. Khakhulin, G. Newby, H. Ki, H. Ihee and M. Wulff, Sub-nanosecond secondary geminate recombination in mercury halides HgX2 (X = I, Br) investigated by time-resolved x-ray scattering, J. Chem. Phys., 2019, 151, 054310 CrossRef.
- E. H. Choi, et al., Structural Dynamics of Bismuth Triiodide in Solution Triggered by Photoinduced Ligand-to-Metal Charge Transfer, J. Phys. Chem. Lett., 2019, 10, 1279–1285 CrossRef CAS.
- K. Haldrup, et al., Bond Shortening (1.4 Å) in the Singlet and Triplet Excited States of [Ir2(dimen)4]2+ in Solution Determined by Time-Resolved X-ray Scattering, Inorg. Chem., 2011, 50, 9329–9336 CrossRef CAS PubMed.
- D. Leshchev, et al., Tracking the picosecond deactivation dynamics of a photoexcited iron carbene complex by time-resolved X-ray scattering, Chem. Sci., 2018, 9, 405–414 RSC.
- M. Christensen, et al., Time-Resolved X-ray Scattering of an Electronically Excited State in Solution. Structure of the 3A2u State of Tetrakis-μ-pyrophosphitodiplatinate(II), J. Am. Chem. Soc., 2009, 131, 502–508 CrossRef CAS PubMed.
- M. Cammarata, M. Levantino, F. Schotte, P. A. Anfinrud, F. Ewald, J. Choi, A. Cupane, M. Wulff and H. Ihee, Tracking the structural dynamics of proteins in solution using time-resolved wide-angle X-ray scattering, Nat. Methods, 2008, 5, 881–886 CrossRef CAS PubMed.
- K. Y. Oang, J. G. Kim, C. Yang, T. W. Kim, Y. Kim, K. H. Kim, J. Kim and H. Ihee, Conformational Substates of Myoglobin Intermediate Resolved by Picosecond X-ray Solution Scattering, J. Phys. Chem. Lett., 2014, 5, 804–808 CrossRef CAS PubMed.
- K. Y. Oang, K. H. Kim, J. Jo, Y. M. Kim, J. G. Kim, T. W. Kim, S. Jun, J. Kim and H. Ihee, Sub-100-ps structural dynamics of horse heart myoglobin probed by time-resolved X-ray solution scattering, Chem. Phys., 2014, 442, 137–142 CrossRef CAS PubMed.
- K. H. Kim, et al., Direct Observation of Cooperative Protein Structural Dynamics of Homodimeric Hemoglobin from 100 ps to 10 ms with Pump-Probe X-ray Solution Scattering, J. Am. Chem. Soc., 2012, 134, 7001–7008 CrossRef CAS PubMed.
- H. Kim, J. G. Kim, S. Muniyappan, T. W. Kim, S. J. Lee and H. Ihee, Effect of Occluded Ligand Migration on the Kinetics and Structural Dynamics of Homodimeric Hemoglobin, J. Phys. Chem. B, 2020, 124, 1550–1556 CrossRef CAS PubMed.
- M. Choi, J. G. Kim, S. Muniyappan, H. Kim, T. W. Kim, Y. Lee, S. J. Lee, S. O. Kim and H. Ihee, Effect of the abolition of intersubunit salt bridges on allosteric protein structural dynamics, Chem. Sci., 2021, 12, 8207–8217 RSC.
- P. L. Ramachandran, J. E. Lovett, P. J. Carl, M. Cammarata, J. H. Lee, Y. O. Jung, H. Ihee, C. R. Timmel and J. J. van Thor, The Short-Lived Signaling State of the Photoactive Yellow Protein Photoreceptor Revealed by Combined Structural Probes, J. Am. Chem. Soc., 2011, 133, 9395–9404 CrossRef CAS.
- T. W. Kim, et al., Protein Structural Dynamics of Photoactive Yellow Protein in Solution Revealed by Pump-Probe X-ray Solution Scattering, J. Am. Chem. Soc., 2012, 134, 3145–3153 CrossRef CAS PubMed.
- D. J. Hsu, D. Leshchev, D. Rimmerman, J. Hong, M. S. Kelley, I. Kosheleva, X. Y. Zhang and L. X. Chen, X-ray snapshots reveal conformational influence on active site ligation during metalloprotein folding, Chem. Sci., 2019, 10, 9788–9800 RSC.
- T. W. Kim, et al., Protein folding from heterogeneous unfolded state revealed by time-resolved X-ray solution scattering, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14996–15005 CrossRef PubMed.
- T. W. Kim, J. G. Kim, C. Yang, H. Ki, J. Jo and H. Ihee, Pump-Probe X-ray Solution Scattering Reveals Accelerated Folding of Cytochrome c Upon Suppression of Misligation, Bull. Korean Chem. Soc., 2014, 35, 697–698 CrossRef CAS PubMed.
- M. Andersson, et al., Structural Dynamics of Light-Driven Proton Pumps, Structure, 2009, 17, 1265–1275 CrossRef CAS.
- H. Takala, et al., Signal amplification and transduction in phytochrome photosensors, Nature, 2014, 509, 245–248 CrossRef CAS PubMed.
- A. Bjorling, et al., Structural photoactivation of a full-length bacterial phytochrome, Sci. Adv., 2016, 2, e1600920 CrossRef.
- M. C. Thompson, B. A. Barad, A. M. Wolff, H. S. Cho, F. Schotte, D. M. C. Schwarz, P. Anfinrud and J. S. Fraser, Temperature-jump solution X-ray scattering reveals distinct motions in a dynamic enzyme, Nat. Chem., 2019, 11, 1058–1066 CrossRef CAS PubMed.
- O. Berntsson, et al., Time-Resolved X-Ray Solution Scattering Reveals the Structural Photoactivation of a Light-Oxygen-Voltage Photoreceptor, Structure, 2017, 25, 933–938 CrossRef CAS PubMed.
- O. Berntsson, et al., Sequential conformational transitions and α-helical supercoiling regulate a sensor histidine kinase, Nat. Commun., 2017, 8, 284 CrossRef.
- S. V. Milton, et al., Exponential gain and saturation of a self-amplified spontaneous emission free-electron laser, Science, 2001, 292, 2037–2041 CrossRef CAS PubMed.
- P. Emma, et al., First lasing and operation of an ångstrom-wavelength free-electron laser, Nat. Photonics, 2010, 4, 641–647 CrossRef CAS.
- T. Ishikawa, et al., A compact X-ray free-electron laser emitting in the sub-ångström region, Nat. Photonics, 2012, 6, 540–544 CrossRef CAS.
- H.-S. Kang, et al., Hard X-ray free-electron laser with femtosecond-scale timing jitter, Nat. Photonics, 2017, 11, 708–713 CrossRef CAS.
- W. Decking, et al., A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator, Nat. Photonics, 2020, 14, 391–397 CrossRef CAS.
- E. Prat, et al., A compact and cost-effective hard X-ray free-electron laser driven by a high-brightness and low-energy electron beam, Nat. Photonics, 2020, 14, 748–754 CrossRef CAS.
- E. Biasin, et al., Femtosecond X-Ray Scattering Study of Ultrafast Photoinduced Structural Dynamics in Solvated [Co(terpy)2]2+, Phys. Rev. Lett., 2016, 117, 013002 CrossRef PubMed.
- K. H. Kim, et al., Direct observation of bond formation in solution with femtosecond X-ray scattering, Nature, 2015, 518, 385–389 CrossRef CAS PubMed.
- J. G. Kim, et al., Mapping the emergence of molecular vibrations mediating bond formation, Nature, 2020, 582, 520–524 CrossRef CAS PubMed.
- J. G. Kim, et al., Rotational dephasing of a gold complex probed by anisotropic femtosecond x-ray solution scattering using an x-ray free-electron laser, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 244005 CrossRef.
- E. H. Choi, et al., Filming ultrafast roaming-mediated isomerization of bismuth triiodide in solution, Nat. Commun., 2021, 12, 4732 CrossRef CAS PubMed.
- M. R. Panman, et al., Observing the Structural Evolution in the Photodissociation of Diiodomethane with Femtosecond Solution X-Ray Scattering, Phys. Rev. Lett., 2020, 125, 226001 CrossRef CAS.
- H. Kim, J. G. Kim, T. W. Kim, S. J. Lee, S. Nozawa, S. I. Adachi, K. Yoon, J. Kim and H. Ihee, Ultrafast structural dynamics of in-cage isomerization of diiodomethane in solution, Chem. Sci., 2021, 12, 2114–2120 RSC.
- Q. Y. Kong, et al., Initial metal-metal bond breakage detected by fs X-ray scattering in the photolysis of Ru3(CO)12 in cyclohexane at 400 nm, Photochem. Photobiol. Sci., 2019, 18, 319–327 CrossRef CAS PubMed.
- S. E. Canton, et al., Visualizing the non-equilibrium dynamics of photoinduced intramolecular electron transfer with femtosecond X-ray pulses, Nat. Commun., 2015, 6, 6359 CrossRef CAS PubMed.
- K. Kunnus, et al., Vibrational wavepacket dynamics in Fe carbene photosensitizer determined with femtosecond X-ray emission and scattering, Nat. Commun., 2020, 11, 634 CrossRef CAS PubMed.
- K. Haldrup, et al., Observing Solvation Dynamics with Simultaneous Femtosecond X-ray Emission Spectroscopy and X-ray Scattering, J. Phys. Chem. B, 2016, 120, 1158–1168 CrossRef CAS PubMed.
- K. S. Kjær, et al., Finding intersections between electronic excited state potential energy surfaces with simultaneous ultrafast X-ray scattering and spectroscopy, Chem. Sci., 2019, 10, 5749–5760 RSC.
- T. B. van Driel, et al., Atomistic characterization of the active-site solvation dynamics of a model photocatalyst, Nat. Commun., 2016, 7, 13678 CrossRef CAS PubMed.
- E. Biasin, et al., Direct observation of coherent femtosecond solvent reorganization coupled to intramolecular electron transfer, Nat. Chem., 2021, 13, 343–349 CrossRef CAS PubMed.
- K. Haldrup, et al., Ultrafast X-Ray Scattering Measurements of Coherent Structural Dynamics on the Ground-State Potential Energy Surface of a Diplatinum Molecule, Phys. Rev. Lett., 2019, 122, 063001 CrossRef CAS PubMed.
- D. Arnlund, et al., Visualizing a protein quake with time-resolved X-ray scattering at a free-electron laser, Nat. Methods, 2014, 11, 923–926 CrossRef CAS PubMed.
- M. Levantino, et al., Ultrafast myoglobin structural dynamics observed with an X-ray free-electron laser, Nat. Commun., 2015, 6, 6772 CrossRef CAS PubMed.
- M. L. Shelby, et al., Interplays of electron and nuclear motions along CO dissociation trajectory in myoglobin revealed by ultrafast X-rays and quantum dynamics calculations, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018966118 CrossRef CAS PubMed.
- M. E. Reinhard, et al., Short-lived metal-centered excited state initiates iron-methionine photodissociation in ferrous cytochrome c, Nat. Commun., 2021, 12, 1086 CrossRef CAS PubMed.
- Y. Lee, et al., Ultrafast coherent motion and helix rearrangement of homodimeric hemoglobin visualized with femtosecond X-ray solution scattering, Nat. Commun., 2021, 12, 3677 CrossRef CAS PubMed.
- J. Park, et al., Design of a hard X-ray beamline and end-station for pump and probe experiments at Pohang Accelerator Laboratory X-ray Free Electron Laser facility, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 810, 74–79 CrossRef CAS.
- M. Chollet, et al., The X-ray Pump-Probe instrument at the Linac Coherent Light Source, J. Synchrotron Radiat., 2015, 22, 503–507 CrossRef CAS PubMed.
- M. Yabashi, H. Tanaka and T. Ishikawa, Overview of the SACLA facility, J. Synchrotron Radiat., 2015, 22, 477–484 CrossRef CAS PubMed.
- T. B. van Driel, K. S. Kjaer, E. Biasin, K. Haldrup, H. T. Lemke and M. M. Nielsen, Disentangling detector data in XFEL studies of temporally resolved solution state chemistry, Faraday Discuss., 2015, 177, 443–465 RSC.
- M. Harmand, et al., Achieving few-femtosecond time-sorting at hard X-ray free-electron lasers, Nat. Photonics, 2013, 7, 215–218 CrossRef CAS.
- K. Haldrup, Singular value decomposition as a tool for background corrections in time-resolved XFEL scattering data, Philos. Trans. R. Soc., B, 2014, 369, 20130336 CrossRef PubMed.
- H. Ki, Y. Lee, E. H. Choi, S. Lee and H. Ihee, SVD-aided non-orthogonal decomposition (SANOD) method to exploit prior knowledge of spectral components in the analysis of time-resolved data, Struct. Dyn., 2019, 6, 024303 CrossRef CAS PubMed.
- G. Ashiotis, A. Deschildre, Z. Nawaz, J. P. Wright, D. Karkoulis, F. E. Picca and J. Kieffer, The fast azimuthal integration Python library: pyFAI, J. Appl. Crystallogr., 2015, 48, 510–519 CrossRef CAS PubMed.
- A. P. Hammersley, FIT2D: a multi-purpose data reduction, analysis and visualization program, J. Appl. Crystallogr., 2016, 49, 646–652 CrossRef CAS.
- R. Kahn, R. Fourme, A. Gadet, J. Janin, C. Dumas and D. Andre, Macromolecular crystallography with synchrotron radiation: photographic data collection and polarization correction, J. Appl. Crystallogr., 1982, 15, 330–337 CrossRef CAS.
- U. Lorenz, K. B. Moller and N. E. Henriksen, On the interpretation of time-resolved anisotropic diffraction patterns, New J. Phys., 2010, 12, 113022 CrossRef.
- E. Biasin, et al., Anisotropy enhanced X-ray scattering from solvated transition metal complexes, J. Synchrotron Radiat., 2018, 25, 306–315 CrossRef CAS PubMed.
- J. Heo, J. G. Kim, E. H. Choi, H. Ki, D.-S. Ahn, J. Kim, S. Lee and H. Ihee, Determining the charge distribution and the direction of the bond cleavage with femtosecond anisotropic x-ray liquidography, Nat. Commun., 2022, 13, 522 CrossRef CAS PubMed.
- A. O. Dohn, E. Biasin, K. Haldrup, M. M. Nielsen, N. E. Henriksen and K. B. Moller, On the calculation of x-ray scattering signals from pairwise radial distribution functions, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 244010 CrossRef.
- M. Cammarata, et al., Impulsive solvent heating probed by picosecond x-ray diffraction, J. Chem. Phys., 2006, 124, 124504 CrossRef CAS PubMed.
- K. S. Kjær, et al., Introducing a standard method for experimental determination of the solvent response in laser pump, X-ray probe time-resolved wide-angle X-ray scattering experiments on systems in solution, Phys. Chem. Chem. Phys., 2013, 15, 15003–15016 RSC.
- T. K. Kim, J. H. Lee, M. Wulff, Q. Kong and H. Ihee, Spatiotemporal Kinetics in Solution Studied by Time-Resolved X-Ray Liquidography (Solution Scattering), ChemPhysChem, 2009, 10, 1958–1980 CrossRef CAS PubMed.
- I. H. M. van Stokkum, D. S. Larsen and R. van Grondelle, Global and target analysis of time-resolved spectra, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Interplay of vibrational wavepackets during an ultrafast electron transfer reaction, Nat. Chem., 2021, 13, 70–76 CrossRef CAS PubMed.
- H. Jung, H. Ki, J. G. Kim, J. Kim, Y. Lee and H. Ihee, Sensitivity of Time-Resolved Diffraction Data to Changes in Internuclear Distances and Atomic Positions, Bull. Korean Chem. Soc., 2022, 43, 376–390 CrossRef.
- H. Ihee, M. Wulff, J. Kim and S.-i. Adachi, Ultrafast X-ray scattering: structural dynamics from diatomic to protein molecules, Int. Rev. Phys. Chem., 2010, 29, 453–520 Search PubMed.
- K. Møller and N. Henriksen, Time-Resolved X-Ray Diffraction: The Dynamics of the Chemical Bond, Struct. Bonding, 2011, 142, 185–212 CrossRef.
- S.-G. Wang and W. H. E. Schwarz, Quasi-Relativistic Density Functional Study of Aurophilic Interactions, J. Am. Chem. Soc., 2004, 126, 1266–1276 CrossRef CAS PubMed.
- H. Schmidbaur and A. Schier, A briefing on aurophilicity, Chem. Soc. Rev., 2008, 37, 1931–1951 RSC.
- M. Iwamura, K. Nozaki, S. Takeuchi and T. Tahara, Real-Time Observation of Tight Au-Au Bond Formation and Relevant Coherent Motion upon Photoexcitation of [Au(CN)2−] Oligomers, J. Am. Chem. Soc., 2013, 135, 538–541 CrossRef CAS PubMed.
- G. L. Cui, X. Y. Cao, W. H. Fang, M. Dolg and W. Thiel, Photoinduced Gold(I)-Gold(I) Chemical Bonding in Dicyanoaurate Oligomers, Angew. Chem., Int. Ed., 2013, 52, 10281–10285 CrossRef CAS PubMed.
- S. H. Sohn, W. Heo, C. Lee, J. Kim and T. Joo, Electronic and Structural Dynamics of Dicyanoaurate Trimer in Excited State, J. Phys. Chem. A, 2019, 123, 6904–6910 CrossRef CAS PubMed.
- A. S. Mereshchenko, E. V. Butaeva, V. A. Borin, A. Eyzips and A. N. Tarnovsky, Roaming-mediated ultrafast isomerization of geminal tri-bromides in the gas and liquid phases, Nat. Chem., 2015, 7, 562–568 CrossRef CAS PubMed.
- D. Townsend, S. A. Lahankar, S. K. Lee, S. D. Chambreau, A. G. Suits, X. Zhang, J. Rheinecker, L. B. Harding and J. M. Bowman, The roaming atom: Straying from the reaction path in formaldehyde decomposition, Science, 2004, 306, 1158–1161 CrossRef CAS PubMed.
- B. J. Schwartz, J. C. King, J. Z. Zhang and C. B. Harris, Direct femtosecond measurements of single collision dominated geminate recombination times of small molecules in liquids, Chem. Phys. Lett., 1993, 203, 503–508 CrossRef CAS.
- U. Banin, R. Kosloff and S. Ruhman, Vibrational relaxation of nascent diiodide ions studied by femtosecond transient resonance impulsive stimulated Raman scattering (TRISRS); experiment and simulation, Chem. Phys., 1994, 183, 289–307 CrossRef CAS.
- A. Baratz and S. Ruhman, UV photolysis of I3− in solution – multiple product channels detected by transient hyperspectral probing, Chem. Phys. Lett., 2008, 461, 211–217 CrossRef CAS.
- N. K. Jena, I. Josefsson, S. K. Eriksson, A. Hagfeldt, H. Siegbahn, O. Bjorneholm, H. Rensmo and M. Odelius, Solvent-Dependent Structure of the I3− Ion Derived from Photoelectron Spectroscopy and Ab Initio Molecular Dynamics Simulations, Chem.–Eur. J., 2015, 21, 4049–4055 CrossRef CAS PubMed.
- I. Josefsson, S. K. Eriksson, N. Ottosson, G. Ohrwall, H. Siegbahn, A. Hagfeldt, H. Rensmo, O. Bjorneholm and M. Odelius, Collective hydrogen-bond dynamics dictates the electronic structure of aqueous I3−, Phys. Chem. Chem. Phys., 2013, 15, 20189–20196 RSC.
- E. Gershgoren, E. Gordon and S. Ruhman, Effect of symmetry breaking on vibrational coherence transfer in impulsive photolysis of trihalide ions, J. Chem. Phys., 1997, 106, 4806–4809 CrossRef CAS.
- F. S. Zhang and R. M. Lynden-Bell, Solvent-induced symmetry breaking, Phys. Rev. Lett., 2003, 90, 185505 CrossRef CAS PubMed.
- A. E. Johnson and A. B. Myers, Solvent effects in the Raman spectra of the triiodide ion: Observation of dynamic symmetry breaking and solvent degrees of freedom, J. Phys. Chem., 1996, 100, 7778–7788 CrossRef CAS.
- E. Gershgoren, E. J. Gordon and S. Ruhman, Effect of symmetry breaking on vibrational coherence transfer in impulsive photolysis of trihalide ions, J. Chem. Phys., 1997, 106, 4806–4809 CrossRef CAS.
- R. M. Lynden-Bell, R. Kosloff, S. Ruhman, D. Danovich and J. Vala, Does solvation cause symmetry breaking in the I3− ion in aqueous solution?, J. Chem. Phys., 1998, 109, 9928–9937 CrossRef CAS.
- K. Ledbetter, et al., Photodissociation of aqueous I3− observed with liquid-phase ultrafast mega-electron-volt electron diffraction, Struct. Dyn., 2020, 7, 064901 CrossRef CAS PubMed.
- J. Vala, R. Kosloff and J. N. Harvey, Ab initio and diatomics in molecule potentials for I2−, I2, I3−, and I3, J. Chem. Phys., 2001, 114, 7413–7423 CrossRef CAS.
- P. Gilch, I. Hartl, Q. R. An and W. Zinth, Photolysis of triiodide studied by femtosecond pump-probe spectroscopy with emission detection, J. Phys. Chem. A, 2002, 106, 1647–1653 CrossRef CAS.
- U. Banin and S. Ruhman, Ultrafast Photodissociation of I3−. Coherent Photochemistry in Solution, J. Chem. Phys., 1993, 98, 4391–4403 CrossRef CAS.
- S. Hess, H. Bursing and P. Vohringer, Dynamics of fragment recoil in the femtosecond photodissociation of triiodide ions in liquid solution, J. Chem. Phys., 1999, 111, 5461–5473 CrossRef CAS.
- A. N. Tarnovsky, J.-L. Alvarez, A. P. Yartsev, V. Sundström and E. Åkesson, Photodissociation dynamics of diiodomethane in solution, Chem. Phys. Lett., 1999, 312, 121–130 CrossRef CAS.
- A. N. Tarnovsky, V. Sundström, E. Åkesson and T. Pascher, Photochemistry of Diiodomethane in Solution Studied by Femtosecond and Nanosecond Laser Photolysis. Formation and Dark Reactions of the CH2I–I Isomer Photoproduct and Its Role in Cyclopropanation of Olefins, J. Phys. Chem. A, 2004, 108, 237–249 CrossRef CAS.
- E. A. Glascoe, M. F. Kling, J. E. Shanoski and C. B. Harris, Nature and role of bridged carbonyl intermediates in the ultrafast photoinduced rearrangement of Ru3(CO)12, Organometallics, 2006, 25, 775–784 CrossRef CAS.
- J. P. Lomont and C. B. Harris, Primary photochemical dynamics of metal carbonyl dimers and clusters in solution: Insights into the results of metal-metal bond cleavage from ultrafast spectroscopic studies, Inorg. Chim. Acta, 2015, 424, 38–50 CrossRef CAS.
- Q. Kong, J. H. Lee, A. Plech, M. Wulff, H. Ihee and M. H. Koch, Ultrafast X-ray solution scattering reveals an unknown reaction intermediate in the photolysis of [Ru3(CO)12], Angew. Chem., Int. Ed., 2008, 47, 5550–5553 CrossRef CAS PubMed.
- Q. Kong, J. H. Lee, K. H. Kim, J. Kim, M. Wulff, H. Ihee and M. H. Koch, Ultrafast X-ray solution scattering reveals different reaction pathways in the photolysis of triruthenium dodecacarbonyl (Ru3(CO)12) after ultraviolet and visible excitation, J. Am. Chem. Soc., 2010, 132, 2600–2607 CrossRef CAS PubMed.
- M. R. Harpham, A. B. Stickrath, X. Zhang, J. Huang, M. W. Mara, L. X. Chen and D.-J. Liu, Photodissociation Structural Dynamics of TrirutheniumDodecacarbonyl Investigated by X-ray Transient Absorption Spectroscopy, J. Phys. Chem. A, 2013, 117, 9807–9813 CrossRef CAS PubMed.
- R. C. Leegood, Handbook of photosynthesis, ed. M. Pessarakli, CRC Press, Boca raton, 2nd edn, 2005, p. 952 Search PubMed.
- A. Nicewicz David and W. C. MacMillan David, Merging Photoredox Catalysis with Organocatalysis: The Direct Asymmetric Alkylation of Aldehydes, Science, 2008, 322, 77–80 CrossRef CAS PubMed.
- M. A. Ischay, M. E. Anzovino, J. Du and T. P. Yoon, Efficient Visible Light Photocatalysis of [2+2] Enone Cycloadditions, J. Am. Chem. Soc., 2008, 130, 12886–12887 CrossRef CAS PubMed.
- M. Gilbert and B. Albinsson, Photoinduced charge and energy transfer in molecular wires, Chem. Soc. Rev., 2015, 44, 845–862 RSC.
- C. S. Ponseca, P. Chábera, J. Uhlig, P. Persson and V. Sundström, Ultrafast Electron Dynamics in Solar Energy Conversion, Chem. Rev., 2017, 117, 10940–11024 CrossRef CAS PubMed.
- F. Scandola, M. T. Indelli, C. Chiorboli and C. A. Bignozzi, Photoinduced electron and energy transfer in polynuclear complexes, in: Photoinduced Electron Transfer II. Topics in Current Chemistry, ed. J. Mattay, Springer, Berlin, Heidelberg, 1990, vol. 158 Search PubMed.
- Y. Yoneda, B. Kudisch, S. Rafiq, M. Maiuri, Y. Nagasawa, G. D. Scholes and H. Miyasaka, Vibrational Dephasing along the Reaction Coordinate of an Electron Transfer Reaction, J. Am. Chem. Soc., 2021, 143, 14511–14522 CrossRef CAS PubMed.
- Y. Z. Liu, et al., Towards longer-lived metal-to-ligand charge transfer states of iron(II) complexes: an N-heterocyclic carbene approach, Chem. Commun., 2013, 49, 6412–6414 RSC.
- T. C. B. Harlang, et al., Iron sensitizer converts light to electrons with 92% yield, Nat. Chem., 2015, 7, 883–889 CrossRef CAS PubMed.
- V. Coropceanu, X. K. Chen, T. H. Wang, Z. L. Zheng and J. L. Bredas, Charge-transfer electronic states in organic solar cells, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- M. Cammarata, et al., Charge transfer driven by ultrafast spin transition in a CoFe Prussian blue analogue, Nat. Chem., 2021, 13, 10–14 CrossRef CAS PubMed.
- P. P. Ho and R. R. Alfano, Optical Kerr effect in liquids, Phys. Rev. A, 1979, 20, 2170–2187 CrossRef CAS.
- R. Righini, Ultrafast Optical Kerr Effect in Liquids and Solids, Science, 1993, 262, 1386–1390 CrossRef CAS PubMed.
- C. Thaler, P. Blank, S. Koushik and S. Vogel, in Flim Microscopy in Biology and Medicine, 2009, vol. 1, pp. 245–320 Search PubMed.
- A. Tokmakoff, Orientational correlation functions and polarization selectivity for nonlinear spectroscopy of isotropic media. I. Third order, J. Chem. Phys., 1996, 105, 1–12 CrossRef CAS.
- J. S. Baskin and A. H. Zewail, Oriented ensembles in ultrafast electron diffraction, ChemPhysChem, 2006, 7, 1562–1574 CrossRef CAS PubMed.
- M. Volk, S. Gnanakaran, E. Gooding, Y. Kholodenko, N. Pugliano and R. M. Hochstrasser, Anisotropy measurements of solvated HgI2 dissociation: Transition state and fragment rotational dynamics, J. Phys. Chem. A, 1997, 101, 638–643 CrossRef CAS.
- T. Kühne and P. Vöhringer, Transient Anisotropy and Fragment Rotational Excitation in the Femtosecond Photodissociation of Triiodide in Solution, J. Phys. Chem. A, 1998, 102, 4177–4185 CrossRef.
- H. Ki, et al., Optical Kerr Effect of Liquid Acetonitrile Probed by Femtosecond Time-Resolved X-ray Liquidography, J. Am. Chem. Soc., 2021, 143, 14261–14273 CrossRef CAS PubMed.
- B. Bagchi and R. Biswas, in Advances in Chemical Physics, ed. S. A. R. I. Prigogine, 1999, vol. 109, pp. 207–433 Search PubMed.
- F. Barbara Paul, C. Walker Gilbert and P. Smith Terrance, Vibrational Modes and the Dynamic Solvent Effect in Electron and Proton Transfer, Science, 1992, 256, 975–981 CrossRef PubMed.
- V. A. Roytman and D. A. Singleton, Solvation Dynamics and the Nature of Reaction Barriers and Ion-Pair Intermediates in Carbocation Reactions, J. Am. Chem. Soc., 2020, 142, 12865–12877 CrossRef CAS PubMed.
- G. R. Fleming and M. Cho, CHROMOPHORE-SOLVENT DYNAMICS, Annu. Rev. Phys. Chem., 1996, 47, 109–134 CrossRef CAS.
- O. Dopfer and M. Fujii, Probing Solvation Dynamics around Aromatic and Biological Molecules at the Single-Molecular Level, Chem. Rev., 2016, 116, 5432–5463 CrossRef CAS PubMed.
- W. P. de Boeij, M. S. Pshenichnikov and D. A. Wiersma, Ultrafast Solvation Dynamics Explored by Femtosecond Photon Echo Spectroscopies, Annu. Rev. Phys. Chem., 1998, 49, 99–123 CrossRef CAS PubMed.
- M. Persico and G. Granucci, Continuum Solvation Models in Chemical Physics: From Theory to Application, 2007 Search PubMed.
- H. L. Fragnito, J. Y. Bigot, P. C. Becker and C. V. Shank, Evolution of the Vibronic Absorption Spectrum in a Molecule Following Impulsive Excitation with a 6 Femtosecond Optical Pulse, Quantum Electronics and Laser Science Conference, 1989, vol. 12 Search PubMed.
- U. Banin, A. Bartana, S. Ruhman and R. Kosloff, Impulsive excitation of coherent vibrational motion ground surface dynamics induced by intense short pulses, J. Chem. Phys., 1994, 101, 8461–8481 CrossRef CAS.
- C. Chudoba, E. Riedle, M. Pfeiffer and T. Elsaesser, Vibrational coherence in ultrafast excited state proton transfer, Chem. Phys. Lett., 1996, 263, 622–628 CrossRef CAS.
- M. Iwamura, H. Watanabe, K. Ishii, S. Takeuchi and T. Tahara, Coherent Nuclear Dynamics in Ultrafast Photoinduced Structural Change of Bis(diimine)copper(I) Complex, J. Am. Chem. Soc., 2011, 133, 7728–7736 CrossRef CAS PubMed.
- B. Kohler, V. V. Yakovlev, J. W. Che, J. L. Krause, M. Messina, K. R. Wilson, N. Schwentner, R. M. Whitnell and Y. J. Yan, Quantum Control of Wave-Packet Evolution with Tailored Femtosecond Pulses, Phys. Rev. Lett., 1995, 74, 3360–3363 CrossRef CAS PubMed.
- M. C. Yoon, D. H. Jeong, S. Cho, D. Kim, H. Rhee and T. Joo, Ultrafast transient dynamics of Zn(II) porphyrins: Observation of vibrational coherence by controlling chirp of femtosecond pulses, J. Chem. Phys., 2003, 118, 164–171 CrossRef CAS.
- H. T. Lemke, et al., Coherent structural trapping through wave packet dispersion during photoinduced spin state switching, Nat. Commun., 2017, 8, 15342 CrossRef CAS PubMed.
- C. Bressler, et al., Femtosecond XANES Study of the Light-Induced Spin Crossover Dynamics in an Iron(II) Complex, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- G. Aubock and M. Chergui, Sub-50-fs photoinduced spin crossover in [Fe(bpy)3]2+, Nat. Chem., 2015, 7, 629–633 CrossRef CAS PubMed.
- W. K. Zhang, et al., Tracking excited-state charge and spin dynamics in iron coordination complexes, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- D. Buhrke and P. Hildebrandt, Probing Structure and Reaction Dynamics of Proteins Using Time-Resolved Resonance Raman Spectroscopy, Chem. Rev., 2020, 120, 3577–3630 CrossRef CAS PubMed.
- M. C. Thielges and M. D. Fayer, Protein Dynamics Studied with Ultrafast Two-Dimensional Infrared Vibrational Echo Spectroscopy, Acc. Chem. Res., 2012, 45, 1866–1874 CrossRef CAS PubMed.
- J. G. Kim, T. W. Kim, J. Kim and H. Ihee, Protein Structural Dynamics Revealed by Time-Resolved X-ray Solution Scattering, Acc. Chem. Res., 2015, 48, 2200–2208 CrossRef CAS PubMed.
- M. Andersson, et al., Structural Dynamics of Light-Driven Proton Pumps, Structure, 2009, 17, 1265–1275 CrossRef CAS PubMed.
- L. U. L. Brinkmann and J. S. Hub, Ultrafast anisotropic protein quake propagation after CO photodissociation in myoglobin, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10565–10570 CrossRef CAS PubMed.
- W. Mara Michael, et al., Metalloprotein entatic control of ligand-metal bonds quantified by ultrafast x-ray spectroscopy, Science, 2017, 356, 1276–1280 CrossRef CAS PubMed.
- B. Stankus, et al., Ultrafast X-ray scattering reveals vibrational coherence following Rydberg excitation, Nat. Chem., 2019, 11, 716–721 CrossRef CAS PubMed.
- H. Yong, et al., Ultrafast X-ray scattering offers a structural view of excited-state charge transfer, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2021714118 CrossRef CAS PubMed.
- S.-M. Bak, Z. Shadike, R. Lin, X. Yu and X.-Q. Yang, In situ/operando synchrotron-based X-ray techniques for lithium-ion battery research, NPG Asia Mater., 2018, 10, 563–580 CrossRef.
- F. Lin, et al., Synchrotron X-ray Analytical Techniques for Studying Materials Electrochemistry in Rechargeable Batteries, Chem. Rev., 2017, 117, 13123–13186 CrossRef CAS PubMed.
- V. K. Peterson and C. M. Papadakis, Functional materials analysis using in situ and in operando X-ray and neutron scattering, IUCrJ, 2015, 2, 292–304 CrossRef CAS PubMed.
- O. Gustafsson, A. Schökel and W. R. Brant, Design and Operation of an Operando Synchrotron Diffraction Cell Enabling Fast Cycling of Battery Materials, Batteries Supercaps, 2021, 4, 1599–1604 CrossRef CAS.
- G. Esteves, C. M. Fancher and J. L. Jones, In situ characterization of polycrystalline ferroelectrics using x-ray and neutron diffraction, J. Mater. Res., 2015, 30, 340–356 CrossRef CAS.
- C.-J. Pan, et al., An operando X-ray diffraction study of chloroaluminate anion-graphite intercalation in aluminum batteries, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5670–5675 CrossRef CAS PubMed.
- L. Vitoux, M. Reichardt, S. Sallard, P. Novák, D. Sheptyakov and C. Villevieille, A Cylindrical Cell for Operando Neutron Diffraction of Li-Ion Battery Electrode Materials, Front. Energy Res., 2018, 6, 76 CrossRef.
- G. Brändén and R. Neutze, Advances and challenges in time-resolved macromolecular crystallography, Science, 2021, 373(6558) CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2022 |