An electric field-based approach for quantifying effective volumes and radii of chemically affected space

Abstract

Chemical shape and size play a critical role in chemistry. The van der Waals (vdW) radius, a familiar manifold used to quantify size by assuming overlapping spheres, provides rapid estimates of size in atoms, molecules, and materials. However, the vdW method may be too rigid to describe highly polarized systems and chemical species that stray from spherical atomistic environments. To deal with these exotic chemistries, numerous alternate methods based on electron density have been presented. While each boasts inherent generality, all define the size of a chemical system, in one way or another, by its electron density. Herein, we revisit the longstanding problem of assessing sizes of atoms and molecules, instead through examination of the local electric field produced by them. While conceptually different than nuclei-centered methods like that of van der Waals, the field assesses chemically affected volumes. This approach implicitly accounts for long-range fields in highly polar systems and predicts that cations should affect more space than neutral counterparts.

---

Introduction

Chemical shape, size, and accompanying surface area and volume are fundamental properties that govern a wealth of intermolecular phenomena in atoms, molecules, and materials.^1–7 Determination of chemical volumes and surface area is, however, obscured by the definition of the atomic “surface”.^8,9 Today, there are numerous approaches to quantify chemical size and while the van der Waals method is certainly the most prevalent, alternatives have been developed through a synergy of experiment and theory.⁹ Understanding the limitations and applicability of these alternatives is important because numerous advanced measurements implicitly rely on size in some form (e.g., specific surface area of gas molecules used in surface area and volumetric measurements of porous materials within the Brunauer–Emmett–Teller (BET) formalism,¹⁰ quantifying void-space docking sites in enzymes,^11,12 and so forth). Hence, there remains intrinsic value in revisiting this age-old problem: how big are molecules?

Initial experimental measurements of atomic size were performed by Meyer in 1870,¹³ where he identified a relationship between material density and atomic size, and obtained a periodic trend in atomic volumes. These values were later refined by Bragg¹⁴ and Pauling,¹⁵ who developed methods for assessing atomic radii through X-ray scattering. In two separate works, Bondi and Batsanov revisited the radii presented by Pauling and Bragg, and it is these works that are synonymous with the “van der Waals (vdW) radii” of atoms and ions in the solid state.^16–18 An alternate approach was taken by Alvarez,^19,20 Biswas, and Ghosh,²¹ who extracted atomic radii using statistical analyses of online databases. The generality of this approach is limited however because of the uncertainty for chemical environments not represented in the those data,⁹ for systems featuring regions of high polarity,^22–24 molecules with elongated bonds,^25–27 atoms under high pressure,^28,29 and other exotic chemistries. Further, it is not immediately evident that crystal-derived atomic size³⁰ is necessarily applicable to gas and solution phase atoms and ions.³¹

First principle simulations have provided another alternative, boasting inherent generality to recover volumetric data of both known and undiscovered molecules from their computed electronic structures while also in principle providing some insight into gas phase radii.³² Early examples of these calculations were presented by Slater who employed the maximum radial density of outermost single particle wavefunctions to define atomic radii,^33–35 and several other related methods have also been reported.^36–41 Among these advances, Bader computed elemental size at the Hartree–Fock level of theory.⁴² There, the surface of a chemical system was defined by the deduced electron density at a cutoff = 0.002 e bohr⁻³. This cutoff was refined by Boyd⁴³ to be 0.001 e bohr⁻³ within the Density Function Theory (DFT) construct,^44,45 with the justification that any smaller value of electron density would result in a negligible change in calculated radii. Later, Rahm and Hoffmann furthered Boyd's work, applying the method to atomic ions using electron densities obtained from hybrid-GGA DFT⁹ (PBE0,^46–48 with a large basis set).

Yet the use of electron density alone poses problems for modeling cations, which certainly interact with their surroundings beyond their electron cloud; they create a large electric field.⁴⁹ With this in mind, we thought to revisit the size quantification problem through examination of the electric field, a value computed from the derivative of the electrostatic potential. While other approaches concern the space that a chemical system occupies, an electric field description captures the volume that a chemical system affects. In this regard, both cations and anions should be larger than their charge neutral counterparts (i.e. they affect more space) because their coulombic charge increases, polar bonds should produce larger fields than non-polar analogues, and size/shape should be affected by external fields. Additionally, the effective size of the atom should still depend on quantum chemical properties, such as orbital filling and effective core charge (i.e. the charge experienced by valence electrons as described by Slater's rule), and so forth. Thus, an electric field metric should provide a conceptually different description of chemical size, and a unique approach for defining the edge of a chemical system. Herein, we explore the generality and implications of quantifying chemical size through examination of atomic and polyatomic electric fields, and provide some examples of the utility of this approach.

Results and discussion

Method description

To sample the electric field, we have developed a post-electronic structure processing software called STREUSEL (Structure Topology REcovery Using Sampling of the ELectric field),⁵⁰ which computes chemically “affected” volumes and surface areas of atoms, molecules, and materials. Since the electric field is defined as the negative gradient of the electrostatic potential it is highly sensitive to subtle changes in polarization. Here, the edge of the chemical system is defined as the point in space where there is near-zero variance in the electric field magnitude (variance is computed by considering magnitude of the field in neighboring volumetric pixels, voxels). Conventional and ab initio calculations return reliable electrostatic potential values on the order of 10⁻⁶ eV per electron (i.e. ∼2.3 × 10⁻⁵ kcal mol⁻¹), thus we consider a change of less than 10⁻⁵ eV per electron (∼2.3 × 10⁻⁴ kcal mol⁻¹) to be conservative. Conceptually, as cutoff decreases more vacuum space becomes included in the regions associated with the molecule, and while it is undoubtedly a variable, we justify our 10⁻⁵ eV potential cutoff thermodynamically; the energy cutoff is on the order of k_B, around 10⁻⁵ eV K⁻¹. For reference, a typical van der Waals interaction is on the order of 0.956–1.912 kcal mol⁻¹.^51,52 Our cutoff accounts for fluctuations in the third decimal place, in principle providing sensitive, but still experimentally measurable information.

To employ this cutoff, one must first sample the electrostatic potential generated from a DFT or ab initio calculation, with the density computed at a discrete number of voxels. Like the field cutoff, there is a dependence of the voxel size on the computed molecular size coming at a trade-off between time-to-solution and voxel resolution, see Fig. S1.† From these data, a voxel of volume 0.008 ų yields a desirable balance between computation time and volumetric resolution, while being sufficiently high fidelity to describe rapid changes in field across conventional chemical bonds.

To illustrate the conceptual difference between our approach and other size metrics, we present the Mg⁰ and Mg²⁺ vdW radii alongside the electric field radii computed using CCSD-full^53–55/aug-cc-pVTZ,⁵⁶Fig. 1. Conventional chemical tenets suggested by Batsanov would indicate that Mg²⁺, and cations in general, are smaller than their neutral counterparts (see Table S1, and Fig. S3† for a Mg-specific example). Yet, from an electrical field perspective, Mg²⁺ should be significantly larger than Mg⁰, because the electric field ultimately depends on the ratio of the number of protons-to-electrons. In other words, the area affected by a cation should be large, while the density of electrons should be small. Hence, the Mg²⁺ example serves as an illustration that the field-defined size is not “atomic size” in the conventional sense and provides different insights than other existing atomic size models.

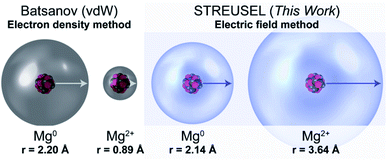Fig. 1 Comparison of atomic radii of Mg and Mg²⁺ between the Batsanov metal compressibility method and the electric field-based method presented in this work (isosurface drawn from our cutoff using data from CCSD-full/aug-cc-pVTZ data). A coordination number of 8 is used for the Mg²⁺ from Batsanov. See Fig. S3 and Table S1† for a comparison of other size comparisons of Mg⁰ and Mg²⁺.

The computed volume, however, should heavily depend on familiar quantum chemical variables such as functional, basis set, density grid size, etc. Size should also depend on quantum chemical aspects of orbital filling. For cations, we expect that the radius should be inversely proportional to the electronic screening of the nuclear charge,⁵⁷ whereas for anions we hypothesize that the radius will be governed by both the magnitude of charge as well as some consideration for which orbitals are occupied (e.g. one might expect that anions with 4s valence to be larger than an isoelectronic 3d valence, see Fig. S9†). We will explore these and other parameters throughout this paper.

Atoms

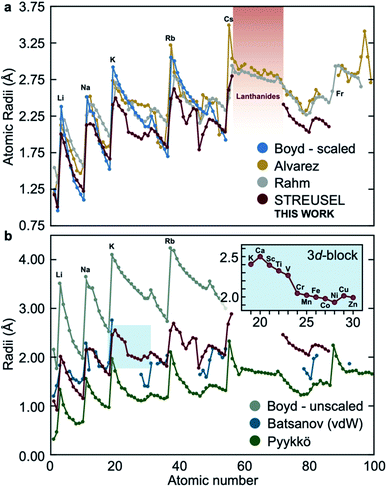
Most sizing methods delineate between charged and charge neutral chemical systems, and free atoms and those in bonded environments. For example, the Pyykkö family of atomic radii⁵⁸ should only be used for covalently bonded systems, the Shannon and Prewitt^59,60 formalism is reserved for oxidized metals, and the vdW radii presented by Bondi are useful for charge neutral atoms. To contrast our method to these and other reported approaches, we compute the periodic table of elements using CCSD-full/def2-TZVP as implemented in Gaussian09 (ref. 61) (see Fig. S4† for a periodic table of elements) alongside some comparable and widely used methods, Fig. 2. Although other calculations throughout this paper invoke the aug-cc-pVTZ basis, the def2-TZVP afforded up to Rn. Fortunately, differences in these triple zeta bases yielded negligible difference in computed size (see Table S2†).

Fig. 2 A comparison of atomic radii recovered using various size metrics. (a) Sizes computed from STREUSEL are like other electronic structure-based methods, and (b) comparable to the vdW (Batsanov) sizes. Alternative size metrics (singly-bound data are presented for Pyykkö, and Boyd's unscaled approach) define the upper and lower limits. Inset: the first row transition metals show a contraction between V and Cr, attributed to the transition from 4s² to 4s¹ orbital filling.

Generally, the atomic radius computed from the electric field is comparable with other electronic structure-based approaches (those presented by Alvarez,^19,20 Boyd⁴³ and Rahm,⁹Fig. 2a). For the most part, our approach seems to predict similar size trends for free neutral atoms. Fig. 2b reveals larger deviations between compared methods; Boyd's unscaled DFT-derived sizes and Pyykkö radii for singly-bonded atoms bracket the radii of neutral elements. Pyykkö's singly-bound radii serves as an important reminder that the local environment plays a significant role in determining the interatomic radii. We would expect that the electric field produced by atoms in interacting environments would also deviate from the neutral sizes, Fig. 2. The other striking conclusion is that the vdW radii seem to align well with electric field-derived sizing for the first 20 atoms, with subtle deviations in heavier main group elements. Indeed, the general shape of the predicted atomic sizes using STREUSEL seems to obey a trend common to other electronic structure-based methods (per Fig. 2a).

Ions

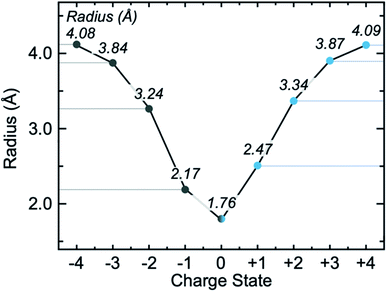
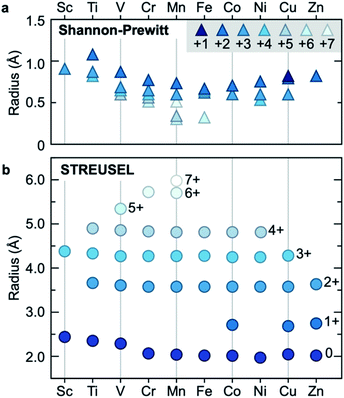
Most atoms exist in some formal, non-zero oxidation state. Previous work by Sen and Politzer studied the radii of anions by examination of their electrostatic potential.⁶² In that study, the authors highlighted that anions have a minimum radius in which the nuclear potential is cancelled by the radial electron charge. Moving beyond this minimum, the potential progresses towards zero. In contrast, cationic potential decays steadily towards zero and governs the potential produced by both neutral and cationic species. By examining the magnitude of the field, however, we can make comparisons between anions and cations directly. To complement Sen and Politzer's study, feedback provided on the preprint of this paper noted that if classical electrostatics (i.e. Coulombs law) were to dominate the field magnitude, then one could expect the radius of C²⁺ to be half that of C⁴⁺. To assess this, we computed the radius of the range of carbon-based anions, C^4−⋯4+, Fig. 3. These data point to two outcomes; (i) the radius of C²⁺ is much greater than half that of C⁴⁺ indicating that the effect is not purely classical, and (ii) anionic and cationic C of equal charge magnitude have roughly the same radii. However, the anions are consistently smaller than the cations, with the most striking difference being the singly charged systems C⁻ and C⁺. We interpret this result to be determined by the extent of 2s–2p electron mixing: C⁻ should maximize mixing between 2s and 2p states (as each p orbital is singly occupied), resulting in field contraction. Since both C⁻ and C⁺ carry the same magnitude of charge, but the valence electron in C⁺ has reduced s–p mixing, the valence electron should have elevated energy hence creating a marginally larger field.

Fig. 3 The radius of carbon as a function of oxidation state. Cations and anions of equal charge magnitude have approximately similar radii, but differences can be attributed to the mixing of s–p orbitals. Radii are presented in italics, effective core charge is shown for C⁻ and C⁺.

Additionally, we computed ionic radii for some transition metals in the periodic table, Fig. 4, and compared our computed size to yet another conventional volumetric approach presented by Shannon and Prewitt.^59,60 The Shannon–Prewitt method shows a clear dependence on the oxidation state of the ion, but convolutes a direct comparison through the inclusion of a number of inner-sphere ligands (with a general relationship between increasing number of inner-sphere ligands and reducing ionic radii). Given our approach computes size in the absence of ligands, we expected that STREUSEL radii should be larger than those from Shannon–Prewitt, Fig. 4b. From our method, the key observation is that radii are proportional to atomic charge (e.g. the extent of polarization), not necessarily identity of the atom. As an example, this contrasts with the Shannon–Prewitt finding that both Ti²⁺ and Zn²⁺ are larger than Fe³⁺. There is also a dependence on orbital filling, with larger radii predicted for Sc, Ti, V, and Cr when computed in non-ground state electronic configurations (see Table S4 and Fig. S9†). Another conclusion from these data is that the oxidation states appear in bands. For example, Fe²⁺/Fe³⁺ and Co²⁺/Co³⁺ have similar differences in radii. These values will of course dramatically reduce in the presence of external fields, highlighting the Shannon–Prewitt-type dependence on local coordination.

Fig. 4 A comparison of ionic radii in the d-block. (a) The Shannon–Prewitt sizes depend on oxidation state and show a reduced size for mid-block elements (computed for 8-inner sphere ligands). (b) The electric field sizes are computed using the free ion and show a general relationship in radius to oxidation state.

Bonded atoms

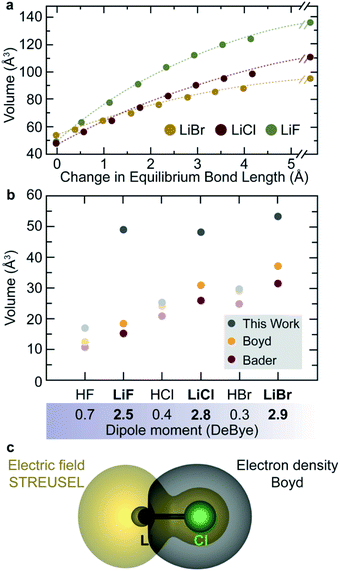
Like the Shannon–Prewitt method, an electric field-derived approach should show a change in chemical size depending on proximity to other electric fields (e.g. those produced by ligands, atoms, molecules, surfaces of materials etc.). For example, the field produced by a free Li⁺ should be larger than Li⁺ in proximity of Cl⁻ simply because they interact with one another. We can demonstrate that the size of ions depends on atomic proximity through progressive increase in bond lengths of some simple diatomics (LiF, LiCl, LiBr), Fig. 5a.

Fig. 5 (a) STREUSEL volumes for lithium halides at arbitrarily expanded bond lengths. At infinite separation the volumes are equivalent to Li⁺ and the corresponding halide anion. Even at 4 Å, separation the ions are affected by one another, as evidenced by reduced field size, and atomic volume. (b) Comparison of molecular volumes for a series of geometrically equilibrated diatomic molecules with varying dipole moments. Divergence between electron density-based size metrics and STREUSEL depends on the system polarity and atomic electronegativity. (c) The difference in size between Boyd and STREUSEL for LiCl.

Here, the volumes of LiF, LiCl, and LiBr increase with increasing bond length. They inevitably converge to the size of the sum of Li⁺ and X⁻, computed either separately or very far apart within the same calculation (>10 Å, to exceed the long-range cation interactions^63,64). While the trend of increasing size with increasing interatomic separation is common to both the vdW and STREUSEL approaches, Fig. S5,† the volumetric trend of the dissociated lithium halides reveals an opposing trend in atomic sizes based on electron density. STREUSEL predicts that the radius of F⁻ > Cl⁻ > Br⁻. This can be readily understood from Slater's rules by examination of the effective screening of core charge. The valence electrons experience an effective nuclear charge (Z_eff) of 4.85, 5.75, and 7.25 for F⁻, Cl⁻ and Br⁻ respectively. Hence, a significantly lighter ion of similar charge should create a larger field. Noting that this is at odds with the generally accepted metric that Br⁻ is the largest of the three, this serves as a prime example of the unique perspective provided by the electric field. It is an inherent measure of affected size, and seemingly follows the general trend offered by Lewis' hard/soft acid/base theory (i.e. soft ions are indicative of small fields).

We can further highlight this relationship by examining the predicted volumes of HF, HCl, HBr, Fig. 4b. These data reveal two key observations; (i) the acidic halides have near-zero dipole moment, resulting in volumes predicted by STREUSEL to align more closely with electron density-based methods (like data shown in Fig. 2a for charge neutral atoms), and (ii) large dipole moment results in significant increase in volume. The latter also results in a significant shift in the regions of the molecule producing this volume, Fig. 5c and S6.† In summary, ions of comparable mass with identical oxidation state will have similar electric fields, and hence similar radii. As the atom becomes heavy, the effective core charge increases, resulting in smaller fields for identically charged ions. Finally, as two chemical system approach, the fields polarize one another. To investigate the latter we now turn more complex molecular systems.

DFT and applications to complex systems

The utility of the presented approach is somewhat limited by the dependence on using CCSD-full and a triple zeta basis. The following section seeks to identify alternate, less computationally intensive DFT-based methods that provide reliable size comparisons which can be used for large molecules and materials. Such an approach would boast the benefit of increased time-to-solution, and the ability to be applied to more diverse chemical systems.

As with all electronic structure methods, the size and shape of molecules depends on both the functional and basis set used for geometric equilibration. For this purpose, our basis remains constant (aug-cc-pVTZ), and the electronic structure method is explored. In a recent assessment of 128 DFT functionals, the authors canvassed the method performance for recovery of total energy and, separately, electron density.⁶⁵ That paper highlighted that approximations in the DFT formalism⁶⁶ leads to significant energetic dependency on functional (having an indirect effect on the shape of the molecule).⁶⁷ The latter is true because atomic position is determined by electron density, and electron density is determined by atomic position (i.e. the self-consistent field and geometry optimization routine). In this context we are interested in molecular volumes, surface areas, and shape, with energetics playing a secondary role (although there are certainly obvious future studies that may harness the energetics of interactions from electric field overlap).

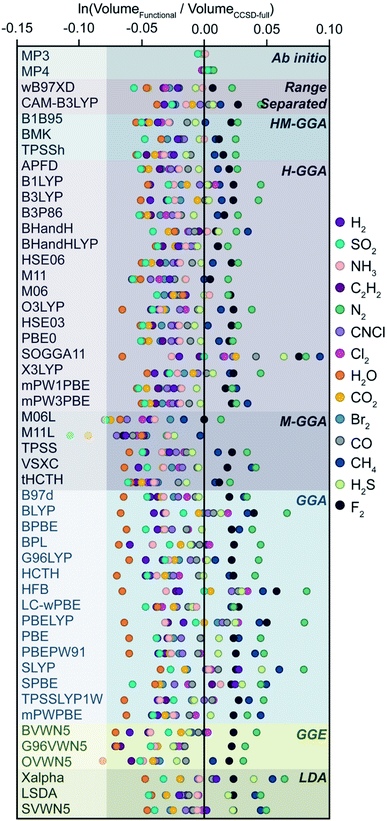
To arrive at an ideal method to recover size using STREUSEL, we examined 15 neutral molecules (Ne, H₂, N₂, F₂, Cl₂, Br₂, H₂O, H₂S, NH₃, CO, CO₂, CH₄, C₂H₂, CNCl, and SO₂) using 49 DFT and ab initio methods (Table S3†). The selection of small molecules spans a range of polarizations and oxidation states. While the methods in Fig. 6 only canvas the upper rungs of Jacob's ladder,⁶⁷ eight electronic structure classes are included (ab initio, generalized gradient approximation (GGA), generalized gradient exchange (GGE), hybrid-GGA (H-GGA), hybrid-meta-GGA (HM-GGA), local-density approximation (LDA), meta-GGA (M-GGA), and range separated functionals). Like before, CCSD-full is used as our geometric and electronic reference for the exact solution, and each molecule was geometrically equilibrated using the stated functional. Its volume, radius, surface area, and other topological properties were then computed from the electrostatic potential.

Fig. 6 The calculated sizes for the small molecule systems shown, compared to the volumes computed using the structure and volume from CCSD-full. The x-axis presents the natural logarithm of the volume fraction, y-axis groups functionals based on their electronic structure method.

As we ascend Jacob's ladder, higher level DFT functionals do not immediately appear to outperform lower-level ones, excluding ab initio methods which are highly accurate. Generally, GGE, HM-GGA, and M-GGA functionals appear to systematically underestimate molecular volumes (revealed in the mean volume deviations, Fig. S7†), and F₂ and Ne are anomalously overestimated independent of DFT method. It should be noted that the axis in Fig. 6 is deliberately presented as logarithmic to show differences between functionals, and perhaps a better comparison is achieved by examining average mean deviations between functional classes, Fig. S7.† It becomes apparent that there is no clear preferred functional, at least not predictably so. It also highlights one plausible reason why the vdW approach has been widely adopted—there is very little dependence on minor fluctuations in bond length in predicted molecule volume (see Table S4†). In addition the mean absolute error for molecules optimized with B3LYP, a widely used functional for small organic molecules, appears to reliably approximate that of CCSD-full.

Instead of naming a clear champion, we acknowledge that it is difficult to compare sizes of molecular systems computed using different levels of theory. This, however, is no surprise—one would not compare the energies of a chemical system computed with two different functionals, nor should one compare their size. The utility of our approach is rather self-contained; the user should simply select a functional from a tractable rung of the ladder. One could select a functional using game theory,⁶⁸ or perhaps the old-fashioned way of simply balancing both accuracy and time-to-solution. With respect to Fig. 6, we are guided to favor functionals and ab initio methods displaying lowest mean absolute deviation within their functional class: MP3 and MP4 (ab initio); CAM-B3LYP (range separated); BMK (HM-GGA): BHandH, BHandHLYP, X3LYP, B1LYP, and B3LYP (H-GGA); TPSS and VSXC (M-GGA), BPL, G96LYP, and TPSSLYP1W (GGA); BVWN5 (GGE); Xalpha (LDA). However, one can use any functional within a given study. By way of example, the following case study invokes M06L, one of the worst performing functionals to obtain sizes comparable to that produced from CCSD-full.

Case study

In the case of ionic liquids, molar volume is a critical parameter which is thought to govern the physical properties of the bulk, including density, viscosity, and so forth.⁶⁹ The density and molar volume should depend on the size of the ions, which itself may depend on whether they are computed together or separately. It may be useful to predict the packing volumes from small molecule calculations, ideally of the free ions themselves, to overcome sampling of the various geometric configurations. By way of example, we consider two simple chemical systems, [BMIM][VCl₄] and [BMIM]₂[CoCl₄] (BMIM = 1-butyl-3-methylimidazolium, Table 1).⁷⁰ Using the geometries computed using M06L, several volume metrics are presented. Both STREUSEL and vdW appear to predict similar sizes of the free ions, while electron density methods significantly under-estimate the sizes of the molecular ions.

Table 1 Boyd, Bader, Batsanov and STREUSEL-derived molecular volumes (ų) for the [BMIM]₂[CoCl₄] ionic liquid, BMIM = 1-butyl-3-methylimidazolium. The sum of single molecule volumes for the individual constituents ([BMIM]⁺, [CoCl₄]²⁻) are presented, as well an equilibrium ion pair. The percent difference (%) is presented for each ionic liquid model

		Boyd		Bader		STREUSEL		Batsanov		Dipole
Single molecules	[BMIM]^+	73.98		66.62		158.8		161.3		5.32
	[VCl4]^−	64.37		58.24		87.94		107.3		0.055
	[BMIM]^+ + [VCl4]^−	138.3	19%	124.9	17%	246.7	0.16%	268.6	21%
Ion pair	[BMIM][VCl4]	114.8		105.1		247.1		217.6
Single molecules	[BMIM]^+	73.98		66.62		158.8		161.3		5.32
	[CoCl4]^2−	68.35		61.95		86.63		107.6		0.403
	2[BMIM]^+ + [CoCl4]^2−	216.3	22%	195.2	20%	404.2	3.6%	430.2	38%
Ion pair	[BMIM]2[CoCl4]	173.1		159.6		390.1		293.6

---

From Fig. 5, one may initially assume that the free molecular ions would always be larger than their paired analogues. Yet, within polynuclear systems there are three competing phenomena determining the size of the ions;

(i) Anionic and cationic electric fields interfering with one another. As electric fields of opposing magnitude interact, they should screen one another leading to a decrease in net volume.

(ii) A change in molecular shape due to intermolecular interactions. As molecules (charged or neutral) interact, they progress towards new equilibrium geometries. As a result, intermolecular interactions lead to an unpredictable change in shape.

(iii) The possibility of the external field polarizing the neighboring molecule. Depending on the polarity of the field some bond may increase in length, other decrease. Some may become more polarized than others. Together, increasing polarity should lead to an increase in volume.

To explore these nuances, we further computed the same ionic liquid components as ion pairs in an equilibrium geometry, Table 1 (entry 2). There, the vdW, Boyd, and Bader methods show a dramatic decrease in volume due to intermolecular overlap between the species. However, STREUSEL appears to recover similar volumes for the molecules computed separately or together (<4% change). Unlike those data presented in Fig. 5, the lack of change is likely because the atoms carrying the formal charge are heavily buried within the molecule, thereby being shielded from external fields. We can imagine a multitude of follow-up studies that isolate the screening effects of bound substituents in diverse chemical systems.

Undoubtedly, the utility of this approach may prove to be more general than a single example we imagined for this paper. This finding may prove to be a useful design principle for assessing volumes, densities, and other 3D chemical properties a priori. These data may feed into computer accelerated materials discovery^71–73 by rapidly screening molecular libraries for ideal multimolecular aggregates, forgoing arduous sampling of intermolecular interacting geometries.

Conclusions

The calculation of atomic, molecular, and material size has always been defined by an arbitrary cutoff where one chemical system ends and another begins. In prior approaches, the determination of atomic radii, volume, and associated surface area, has depended on electron density (either experimental or from simulation). Yet the limitations of these models have been highlighted by comparison of highly polarized systems, with the most striking being a difference in affected volume of free cations. Indeed, the contrast between the work presented herein, and the van der Waals metric is the description of the atomic surface being defined by a field smaller than the thermal energy provided at near absolute 0 K. The value of the latter is multifold: it allows for an assessment of how large an area is affected by the presence of the ion (an effect that may prove to be significant in applied electrochemistry,⁷⁴ and other complex systems^75,76). It also allows for direct estimates of dispersion interactions (by redefining the cutoff to account for temperature effects such that materials can interact via their fields more strongly than k_BT).

Beyond atomic cations, there are clear pathways to future fundamental studies examining how electric fields interact with, and are shielded by, chemical moieties (e.g. examining the field dissipation in a series of related cations, (CH₃)₄N⁺, (C₂H₅)₄N⁺etc.). We can imagine studies that broaden our understanding of how fields permeate both through space and through bond, elucidating limitations of electric field-based descriptions of atomic, molecular, and material effective size. While our method undoubtedly does not replace the vdW radius or other size definitions, it does provide an alternative framework to contemplate the boundaries of chemistry.

Data availability

STREUSEL is available on github (see ESI†). Example input and output files are also hosted on the same site.

Author contributions

The computations were performed by AMM, AMD, JS and JD. The project was conceived by AMM and CHH. All authors partook in the drafting of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is based upon work supported by the National Science Foundation through the Division of Materials Research under grant no. DMR-1956403. CHH also acknowledges the Research Corporation for Science Advancement (Cottrell Award). We are grateful for the continued access to the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation [ACI-1548562] and the PICS Coeus High Performance Computer, which is supported by the National Science Foundation [1624776]. The authors would also like to thank Prof. Roald Hoffmann, Prof. Martin Rahm, Prof. Aron Walsh, and Prof. Carl K. Brozek for their thoughtful comments on the manuscript, as well as Dr Andrew Tarzia for their valuable suggestions and discussion.

References

1. X. Yue, M. B. Taraban, L. L. Hyland and Y. B. Yu, Avoiding Steric Congestion in Dendrimer Growth through Proportionate Branching: A Twist on Da Vinci's Rule of Tree Branching, J. Org. Chem., 2012, 77, 8879–8887.
2. P. Luo, J. P. Dinnocenzo, P. B. Merkel, R. H. Young and S. Farid, Bimolecular Electron Transfers That Deviate from the Sandros–Boltzmann Dependence on Free Energy: Steric Effect, J. Org. Chem., 2012, 77, 1632–1639.
3. D. J. Durand and N. Fey, Computational Ligand Descriptors for Catalyst Design, Chem. Rev., 2019, 119, 6561–6594.
4. R. K. Mohamed, P. W. Peterson and I. V. Alabugin, Concerted Reactions That Produce Diradicals and Zwitterions: Electronic, Steric, Conformational, and Kinetic Control of Cycloaromatization Processes, Chem. Rev., 2013, 113, 7089–7129.
5. D. Ravelli, M. Fagnoni, T. Fukuyama, T. Nishikawa and I. Ryu, Site-Selective C–H Functionalization by Decatungstate Anion Photocatalysis: Synergistic Control by Polar and Steric Effects Expands the Reaction Scope, ACS Catal., 2018, 8, 701–713.
6. J. P. Wagner and P. R. Schreiner, London Dispersion in Molecular Chemistry: Reconsidering Steric Effects, Angew. Chem., Int. Ed., 2015, 54, 12274–12296.
7. G. Poli, A. Martinelli and T. Tuccinardi, Reliability Analysis and Optimization of the Consensus Docking Approach for the Development of Virtual Screening Studies, J. Enzyme Inhib. Med. Chem., 2016, 31, 167–173.
8. M. Ue, A. Murakami and S. Nakamura, A Convenient Method to Estimate Ion Size for Electrolyte Materials Design, J. Electrochem. Soc., 2002, 149, A1385–A1388.
9. M. Rahm, R. Hoffmann and N. Ashcroft, Atomic and Ionic Radii of Elements 1-96, Chem.–Eur. J., 2016, 22, 14625–14632.
10. S. Brunauer, P. H. Emmett and E. Teller, Adsorption of Gases in Multimolecular Layers, J. Am. Chem. Soc., 1938, 60, 309–319.
11. R. Thomsen and M. H. Christensen, MolDock: A New Technique for High-Accuracy Molecular Docking, J. Med. Chem., 2006, 49, 3315–3321.
12. X.-Y. Meng, H.-X. Zhang, M. Mezei and M. Cui, Molecular Docking: A Powerful Approach for Structure-Based Drug Discovery, Curr. Comput.-Aided Drug Des., 2011, 7, 146–157.
13. L. Meyer, Die Natur Der Chemischen Elemente Als Function Ihrer Atomgewichte, Ann. Chem. Pharm., 1870, 354–364.
14. W. L. Bragg, The Arrangement of Atoms in Crystals, Philos. Mag., 1920, 40, 169–189.
15. L. C. Pauling, The Nature of the Chemical Bond and the Structure of Molecules and Crystals, in An Introduction to Modern Structural Chemistry, Cornell University Press, Ithaca, NY, 1960, p. 644.
16. A. Bondi, Van Der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
17. A. Bondi, Van Der Waals Volumes and Radii of Metals in Covalent Compounds, J. Phys. Chem., 1966, 70, 3006–3007.
18. S. Batsanov, Van Der Waals Radii of Elements, Inorg. Mater., 2001, 37, 1031–1046.
19. B. Cordero, V. Gomez, A. E. Platero-Prats, M. Reves, J. Echeverria, E. Cremades, F. Barragan and S. Alvarez, Covalent Radii Revisited, Dalton Trans., 2008, 2832–2838.
20. S. Alvarez, A Cartography of the van Der Waals Territories, Dalton Trans., 2013, 42, 8627–8636.
21. D. C. Ghosh and R. Biswas, Theoretical Calculation of Absolute Radii of Atoms and Ions. Part 1. The Atomic Radii, Int. J. Mol. Sci., 2002, 3, 87–113.
22. C. Delgado-Andrade and F. J. Morales, Unraveling the Contribution of Melanoidins to the Antioxidant Activity of Coffee Brews, J. Agric. Food Chem., 2005, 53, 1403–1407.
23. J. Vincze, M. Valiskó and D. Boda, The Nonmonotonic Concentration Dependence of the Mean Activity Coefficient of Electrolytes is a Result of a Balance between Solvation and Ion-Ion Correlations, J. Chem. Phys., 2010, 133, 154507.
24. D. Fraenkel, Computing Excess Functions of Ionic Solutions: The Smaller-Ion Shell Model versus the Primitive Model. 1. Activity Coefficients, J. Chem. Theory Comput., 2015, 11, 178–192.
25. P. R. Schreiner, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, S. Schlecht, J. E. P. Dahl, R. M. K. Carlson and A. A. Fokin, Overcoming Lability of Extremely Long Alkane Carbon–Carbon Bonds through Dispersion Forces, Nature, 2011, 477, 308–311.
26. Y. Ishigaki, T. Shimajiri, T. Takeda, R. Katoono and T. Suzuki, Longest C-C Single Bond among Neutral Hydrocarbons with a Bond Length beyond 1.8 Å, Chem, 2018, 4, 795–806.
27. J. Li, R. Pang, Z. Li, G. Lai, X.-Q. Xiao and T. Muller, Exceptionally Long C-C Single Bonds in Diamino-o-Carborane as Induced by Negative Hyperconjugation, Angew. Chem., Int. Ed., 2019, 58, 1397–1401.
28. M. Rahm, M. Ångqvist, J. M. Rahm, P. Erhart and R. Cammi, Non-Bonded Radii of Atoms Under Compression, ChemPhysChem, 2020, 21, 2441–2453.
29. S. S. Batsanov, Determination of Ionic Radii from Metal Compressibilities, J. Struct. Chem., 2004, 45, 896–899.
30. J. C. Slater, Atomic Radii in Crystals, J. Chem. Phys., 1964, 41, 3199–3204.
31. Y. Marcus, Ionic Radii in Aqueous Solutions, Chem. Rev., 1988, 88, 1475–1498.
32. K. L. Bak, J. Gauss, P. Jørgensen, J. Olsen, T. Helgaker and J. F. Stanton, The Accurate Determination of Molecular Equilibrium Structures, J. Chem. Phys., 2001, 114, 6548–6556.
33. E. Clementi and D. L. Raimondi, Atomic Screening Constants from SCF Functions, J. Chem. Phys., 1963, 38, 2686.
34. E. Clementi, D. L. Raimondi and W. P. Reinhardt, Atomic Screening Constants from SCF Functions. II. Atoms with 37-86 Electrons, J. Chem. Phys., 1967, 47, 1300–1307.
35. J. C. Slater, Atomic Shielding Constants, Phys. Rev., 1930, 36, 57.
36. A. Zunger and M. L. Cohen, First-Principles Nonlocal-Pseudopotential Approach in the Density-Functional Formalism: Development and Application to Atoms, Phys. Rev. B: Solid State, 1978, 18, 5449–5472.
37. A. Zunger and M. L. Cohen, First-Principles Nonlocal-Pseudopotential Approach in the Density-Functional Formalism. II. Application to Electronic and Structural Properties of Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4082–4108.
38. S. B. Zhang, M. L. Cohen and J. C. Phillips, Relativistic Screened Orbital Radii, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 5861–5867.
39. S. Nath, S. Chattaqcharya and P. K. Chattaraj, Density Functional Calculation of a Characteristic Atomic Radius, Theochem, 1995, 331, 267–279.
40. M. V. Putz, N. Russo and E. Sicilia, Atomic Radii Scale and Related Size Properties from Density Functional Electronegativity Formulation, J. Phys. Chem. A, 2003, 107, 5461–5465.
41. J. W. Hollett, A. Kelly and R. A. Poirier, Quantum Mechanical Size and Steric Hindrance, J. Phys. Chem. A, 2006, 110, 13884–13888.
42. R. F. W. Bader, W. H. Henneker and P. E. Cade, Molecular Charge Distributions and Chemical Binding, J. Chem. Phys., 1967, 46, 3341–3363.
43. R. Boyd, The Relative Sizes of Atoms, J. Phys. B: At. Mol. Phys., 1977, 10, 2283.
44. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138.
45. W. Kohn, A. D. Becke and R. G. Parr, Density Functional Theory of Electronic Structure, J. Phys. Chem., 1996, 100, 12974–12980.
46. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
47. J. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. J. Perdew, K. Burke and M. Ernzerhof, Errata: Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396.
49. P. Politzer and J. S. Murray, The Fundamental Nature and Role of the Electrostatic Potential in Atoms and Molecules, Theor. Chem. Accounts Theor. Comput. Model., 2002, 108, 134–142.
50. STREUSEL release, v2022, 2022, DOI:  DOI:10.5281/zenodo.6459535.
51. F. O. Kannemann and A. D. Becke, Van Der Waals Interactions in Density-Functional Theory: Intermolecular Complexes, J. Chem. Theory Comput., 2010, 6, 1081–1088.
52. A. B. Rubin, Different Types of Interactions in Macromolecules, in Compendium of Biophysics, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2017, pp. 109–116.
53. G. D. Purvis and R. J. Bartlett, A Full Coupled-cluster Singles and Doubles Model: The Inclusion of Disconnected Triples, J. Chem. Phys., 1982, 76, 1910–1918.
54. G. E. Scuseria, C. L. Janssen and H. F. Schaefer, An Efficient Reformulation of the Closed-shell Coupled Cluster Single and Double Excitation (CCSD) Equations, J. Chem. Phys., 1988, 89, 7382–7387.
55. G. E. Scuseria and H. F. Schaefer, Is Coupled Cluster Singles and Doubles (CCSD) More Computationally Intensive than Quadratic Configuration Interaction (QCISD)?, J. Chem. Phys., 1989, 90, 3700–3703.
56. T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
57. N. Agmon, Isoelectronic Theory for Cationic Radii, J. Am. Chem. Soc., 2017, 139, 15068–15073.
58. P. Pyykkö, Additive Covalent Radii for Single-, Double-, and Triple-Bonded Molecules and Tetrahedrally Bonded Crystals: A Summary, J. Phys. Chem. A, 2015, 119, 2326–2337.
59. R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
60. R. D. Shannon and C. T. Prewitt, Effective Ionic Radii in Oxides and Fluorides, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925–946.
61. M. Frisch, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Li, et al., Gaussian09, Gaussian Inc., Wallingford CT, 2009.
62. K. D. Sen and P. Politzer, Characteristic features of the electrostatic potentials of singly negative monoatomic ions, J. Chem. Phys., 1989, 90, 4370.
63. K. C. Park and T. Tsukahara, Quantitative Evaluation of Long-Range and Cooperative Ion Effect on Water in Polyamide Network, J. Phys. Chem. B, 2019, 123, 2948–2955.
64. M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Long Range Electrostatic Forces in Ionic Liquids, Chem. Commun., 2017, 53, 1214–1224.
65. M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Density Functional Theory Is Straying from the Path toward the Exact Functional, Science, 2017, 355, 49–52.
66. A. E. Mattsson, In Pursuit of the “Divine” Functional, Science, 2002, 298, 759–760.
67. J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Electronic Structure Modeling of Metal–Organic Frameworks, Chem. Rev., 2020, 120, 8641–8715.
68. S. McAnanama-Brereton and M. P. Waller, Rational Density Functional Selection Using Game Theory, J. Chem. Inf. Model., 2018, 58, 61–67.
69. V. V. Chaban, N. A. Andreeva and E. E. Fileti, Graphene/Ionic Liquid Ultracapacitors: Does Ionic Size Correlate with Energy Storage Performance?, New J. Chem., 2018, 42, 18409–18417.
70. M. A. LeRoy, A. M. Mroz, J. L. Mancuso, A. Miller, A. Van Cleve, C. Check, H. Heinz, C. H. Hendon and C. K. Brozek, Post-Synthetic Modification of Ionic Liquids Using Ligand-Exchange and Redox Coordination Chemistry, J. Mater. Chem. A, 2020, 8, 22674–22685.
71. A. Chandrasekaran, D. Kamal, R. Batra, C. Kim, L. Chen and R. Ramprasad, Solving the Electronic Structure Problem with Machine Learning, npj Comput. Mater., 2019, 5, 22.
72. A. Grisafi, A. Fabrizio, B. Meyer, D. M. Wilkins, C. Corminboeuf and M. Ceriotti, Transferable Machine-Learning Model of the Electron Density, ACS Cent. Sci., 2019, 5, 57–64.
73. M. Tsubaki and T. Mizoguchi, Quantum Deep Field: Data-Driven Wave Function, Electron Density Generation, and Atomization Energy Prediction and Extrapolation with Machine Learning, Phys. Rev. Lett., 2020, 125, 206401.
74. M. Liu, Y. Pang, B. Zhang, P. De Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. de Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Enhanced Electrocatalytic CO₂ Reduction via Field-Induced Reagent Concentration, Nature, 2016, 537, 382–386.
75. E. C. Sutton, C. E. McDevitt, J. Y. Prochnau, M. V. Yglesias, A. M. Mroz, M. C. Yang, R. M. Cunningham, C. H. Hendon and V. J. DeRose, Nucleolar Stress Induction by Oxaliplatin and Derivatives, J. Am. Chem. Soc., 2019, 141, 18411–18415.
76. C. E. McDevitt, M. V. Yglesias, A. M. Mroz, E. C. Sutton, M. C. Yang, C. H. Hendon and V. J. DeRose, Monofunctional Platinum(II) Compounds and Nucleolar Stress: Is Phenanthriplatin Unique?, JBIC, J. Biol. Inorg. Chem., 2019, 24, 899–908.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc00780k

---