Open Access Article
Open Access ArticleRevealing hydrogen spillover pathways in reducible metal oxides†
Kazuki
Shun
a,
Kohsuke
Mori
 *abc,
Shinya
Masuda
a,
Naoki
Hashimoto
a,
Yoyo
Hinuma
*abc,
Shinya
Masuda
a,
Naoki
Hashimoto
a,
Yoyo
Hinuma
 d,
Hisayoshi
Kobayashi
d,
Hisayoshi
Kobayashi
 e and
Hiromi
Yamashita
e and
Hiromi
Yamashita
 *abc
*abc
aDivision of Materials and Manufacturing Science, Graduate School of Engineering, Osaka University, 2-1 Yamadaoka, Suita, Osaka 565-0871, Japan. E-mail: mori@mat.eng.osaka-u.ac.jp; yamashita@mat.eng.osaka-u.ac.jp
bUnit of Elements Strategy Initiative for Catalysts Batteries (ESICB), Kyoto University, Katsura, Kyoto 615-8520, Japan
cInnovative Catalysis Science Division, Institute for Open and Transdisciplinary Research Initiatives (ICS-OTRI), Osaka University, Suita, Osaka 565-0871, Japan
dDepartment of Energy and Environment, National Institute of Advanced Industrial Science and Technology (AIST), 1-8-31, Midorigaoka, Ikeda, Osaka 563-8577, Japan
eKyoto Institute of Technology, Matsugasaki, Sakyo-ku, Kyoto, 606-8585, Japan
First published on 24th June 2022
Abstract
Hydrogen spillover, the migration of dissociated hydrogen atoms from noble metals to their support materials, is a ubiquitous phenomenon and is widely utilized in heterogeneous catalysis and hydrogen storage materials. However, in-depth understanding of the migration of spilled hydrogen over different types of supports is still lacking. Herein, hydrogen spillover in typical reducible metal oxides, such as TiO2, CeO2, and WO3, was elucidated by combining systematic characterization methods involving various in situ techniques, kinetic analysis, and density functional theory calculations. TiO2 and CeO2 were proven to be promising platforms for the synthesis of non-equilibrium RuNi binary solid solution alloy nanoparticles displaying a synergistic promotional effect in the hydrolysis of ammonia borane. Such behaviour was driven by the simultaneous reduction of both metal cations under a H2 atmosphere over TiO2 and CeO2, in which hydrogen spillover favorably occurred over their surfaces rather than within their bulk phases. Conversely, hydrogen atoms were found to preferentially migrate within the bulk prior to the surface over WO3. Thus, the reductions of both metal cations occurred individually on WO3, which resulted in the formation of segregated NPs with no activity enhancement.
Introduction
Hydrogen spillover is an interfacial dynamic behaviour, which is initiated by the dissociation of gaseous hydrogen molecules at noble metal sites (e.g., Pt, Pd, and Ru). Spontaneously, the activated hydrogen atoms migrate to the adjacent hydrogen-poor surface driven by a concentration gradient.1–5 At the metal–support interface, the protons (H+) diffuse to O2− anions to form O–H bonds, whereas the concurrently generated electrons (e−) reduce metal cations adjacent to O–H bonds.1,6 Principally, this process is governed by the following reaction: Mn+ + O2− + H → M(n−1)+ + OH−. Because of the facile reduction of metal cations, hydrogen spillover is specific for reducible metal oxides, such as TiO2,7–10 CeO2 (ref. 11–13) and WO3,14–16 while it is energetically difficult over non-reducible metal oxides.17The detailed mechanism and the utilization of the hydrogen spillover effect have been continually studied since the first report by Khoobiar in 1964.18 It is undergoing a revival of interest, because unprecedented functions that seem to involve hydrogen spillover have been observed not only in the field of catalysts,19–24 but also in the fields of hydrogen fuel cells,25 hydrogen storage materials,26–28 and hydrogen sensors.29,30 In order to extend the opportunities for utilizing the spillover effect and developing advanced hydrogen energy devices, comprehensive understanding is indispensable.
Recently, several studies have been performed to further deepen the knowledge of the unique behaviour of hydrogen spillover. Bokhoven and coworkers quantified the spatial extent of hydrogen migration on Al2O3 and TiO2 by observing the reduction of supported iron oxides located at precisely varied distances from co-supported Pt by X-ray absorption fine structure (XAFS) analysis.6 The results demonstrated that hydrogen spillover over reducible metal oxide TiO2 is ten orders of magnitude faster than over non-reducible metal oxide Al2O3, and enables the reduction of iron oxide located more than 1 μm away from Pt. Zheng et al. reported the effect of the support structure on the spillover hydrogenation by utilizing two different exposed facets of Cu (111) and Cu (100) involving dispersed Pd atoms.31 It was found that hydrogen atoms spilled from Pd atoms only on Cu (100) were active for the semi-hydrogenation of alkynes, although hydrogen spillover from Pd to Cu was facet independent. Furthermore, novel low-temperature catalytic reactions using surface protonics, which is regarded as hydrogen migration activated by an electric field, have been achieved, in which the migrated H+ atoms play a crucial role in activating the robust C–H and N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bonds.32,33
N triple bonds.32,33
In addition to the above experiments, in situ characterization techniques, including low-temperature scanning tunneling microscopy (LT-STM),34 near-ambient pressure X-ray photoelectron spectroscopy (NAP-XPS),35,36 and tip-enhanced Raman spectroscopy combined with scanning tunneling microscopy (STM-TERS), have been used for real-time monitoring of the hydrogen spillover effect.37 Despite accumulated reports concerning hydrogen spillover, its dynamic behaviour, such as at what temperature it can take place, what pathway it follows, and the region to where hydrogen migrates, is still poorly understood even for typical reducible metal oxides, because the detailed spillover mechanism is influenced by the difference in reducibility of the metal cations, number of oxygen vacancies and/or surface hydroxyl groups, and the crystal structure.5,38
Our group has succeeded in the synthesis of binary solid solution alloy NPs catalysts with essentially immiscible metal combinations (Ru–Ni and Rh–Cu) by utilizing spilled hydrogen atoms as a strong reductant.39–41 On the other hand, non-reducible γ-Al2O3 and MgO supports, whose hydrogen spillover abilities are inferior to that of TiO2, afforded segregated NPs under the identical synthetic conditions. This means that the formation of non-equilibrium solid solution alloys strongly reflects the hydrogen spillover ability of the support surface. In this study, we first used the above phenomena to identify hydrogen spillover in typical reducible metal oxides, such as TiO2, CeO2, and WO3. The obtained results were further discussed based on systematic in situ characterization techniques, kinetic analysis, and density functional theory (DFT) calculations. The combined experiments revealed that TiO2 and CeO2 allowed the preferential migration of dissociated hydrogen atoms over their surfaces, whereas hydrogen atoms preferably migrated within the bulk over WO3. This study provides not only fundamental insights into the spillover pathways but also new strategies for utilizing hydrogen spillover for the design of advanced materials for the up-coming hydrogen society.
Results & discussion
Formation of RuNi solid solution alloy nanoparticles assisted by hydrogen spillover
Ru exists as a hexagonal close-packed (hcp) structure, while Ni exists as a face-centered cubic (fcc) structure in a bulk state, which makes it difficult to form the RuNi solid solution alloy NPs due to their positive enthalpy of mixing. Actually, Ru and Ni are thermodynamically stable in segregation even at 773 K under most of equilibrium composition. Recently, Chen et al. succeeded in the synthesis of RuNi solid solution alloy NPs by a hot-injection method with co-reduction of Ni(acac)2 and Ru(acac)3 (acac = acetylacetonate) in oleylamine with super hydride (LiBEt3H) as the reducing agent at 300 °C.42 Note that if a weaker reducing agent (such as NaBH4) is used, separate growth of Ni and Ru NPs was confirmed. Thus a strong reducing agent, high temperature, and a high-boiling solvent were indispensable for achieving the formation of RuNi solid solution alloy NPs.We have previously demonstrated that spilled H atoms enabled the simultaneous reduction of deposited Ru3+ and Ni2+ ions with distinctly different redox potentials to form non-equilibrium RuNi solid solution alloy NPs. TiO2, one of the typical reducible metal oxides, was shown to be a promising platform for the formation of RuNi NPs due to its prominent hydrogen spillover ability associated with the concurrent proton–electron transfer.39,40 On the other hand, non-reducible metal oxides, such as Al2O3, and MgO, were demonstrated not to be suitable owing to the lack of hydrogen spillover on their surfaces. The formation of RuNi solid solution alloy NPs was confirmed by HR-TEM and EDX analysis, in which Ru and Ni were randomly distributed over RuNi/TiO2 without segregation (Fig. S1†). Moreover, RuNi/TiO2 showed drastically improved activity during the hydrolysis of ammonia borane (AB) compared to monometallic Ru/TiO2, even though Ni exhibited only negligible activity at the same condition. This synergistic promotional effect is attributed to neighboring Ru–Ni pairs with an electronic imbalance, as proven by DFT calculations (Fig. S2†).40
Thus, the catalytic performance of each catalyst during the hydrolysis of AB is strongly reflected by whether the RuNi solid solution alloy NPs are formed or not, which may be conventionally utilized as a method for evaluating the surface hydrogen spillover ability of a series of reducible metal oxides, such as TiO2, Ga2O3, CeO2, Nb2O5, and WO3. Ru and Ni were deposited on each support by an impregnation method and subsequently reduced under H2 atmosphere at 300 °C. The mean particle diameters of RuNi catalysts over TiO2 and WO3 were comparable with those obtained for the monometallic Ru catalysts (Fig. S2 and S3†). The particles sizes of RuNi and Ru over the CeO2 catalysts cannot be defined because of its heavy characteristic, but the elemental mapping indicates the high dispersion of Ru and Ni species without agglomeration (Fig. S4†). These results clearly exclude the effect of particle size on catalytic activity.
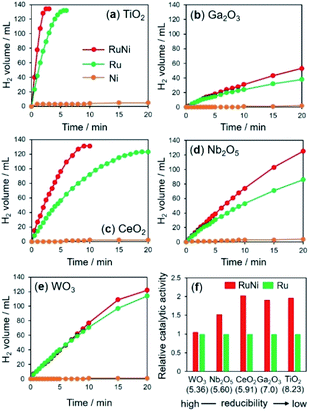
The time courses of hydrogen evolution during the hydrolysis of AB (NH3BH3 + 2H2O → NH4+ + BO2− + 3H2) are shown in Fig. 1a–e. Fig. 1f summarizes the normalized turnover frequency (TOF) values for RuNi catalysts based on Ru. Notably, the reactions using pure Ni catalysts were extremely sluggish, regardless of the supports. The activity enhancement ratio was strongly dependent on the reducibility of the catalyst supports, which was determined by Helali and coworkers based on the formation energy of oxygen vacancies.43
RuNi supported on TiO2, Ga2O3, and CeO2 catalysts, with relatively low reducibility, showed enhanced activity over those of the corresponding monometallic Ru catalysts by a factor of approximately 2, suggesting the formation of RuNi solid solution alloy NPs by the assistance of hydrogen spillover on their surfaces. Similarly, the activity of RuNi/Nb2O5 was 1.5 times higher than that of Ru/Nb2O5. By contrast, RuNi/WO3 did not show any improvement in the activity by the addition of Ni, which indicates that no RuNi solid solution alloy was formed on the surface of WO3 despite its high reducibility, as will be discussed later. For subsequent detailed characterizations, we used TiO2, CeO2, and WO3 as typical supports in an effort to investigate the hydrogen spillover ability.
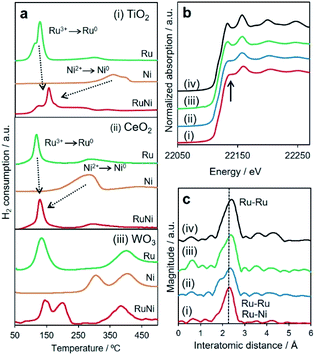
H2-TPR measurements were performed to evaluate the reduction behaviour of each sample (Fig. 2a). The reduction peaks for Ni2+ ions of as-deposited Ni samples appeared at much higher temperature than those for Ru3+ in Ru deposited samples for all supports (Table 1). These results are reasonable because Ru3+ ions are easier to reduce than Ni2+ ions due to their higher reduction potential (E0(Ni2+/Ni) = −0.26 V vs. NHE, E0(Ru3+/Ru) = 0.80 V vs. NHE). Interestingly, both Ru3+- and Ni2+-deposited TiO2 and CeO2 showed only one peak with a maximum at around 158 °C and 126 °C, respectively. These results suggest that hydrogen spillover occurs at low temperature on TiO2 and CeO2, which promotes the reduction of Ni2+ ions, and then both Ru3+ and Ni2+ions were simultaneously reduced to form a RuNi solid-solution alloy despite the difference in redox potentials. On the other hand, RuNi/WO3 showed several peaks attributed to the reduction of Ru3+ and Ni2+ species. Such reduction profiles indicate that hydrogen spillover on WO3 occurs at much higher temperature than the reduction temperature of only Ru3+, which cause sequential reduction of Ru3+ and Ni2+ ions, resulting in segregated NPs rather than solid solution alloy ones.
| Sample | H2-TPR | In situ XANES spectra | |
|---|---|---|---|
| Ru K-edge | Ni K-edge | ||
| Ru/TiO2 | 130 °C | 125 °C | — |
| Ni/TiO2 | 370 °C | — | 325 °C |
| RuNi/TiO2 | 160 °C | 200 °C | 200 °C |
| Ru/CeO2 | 125 °C | 150 °C | — |
| Ni/CeO2 | 300 °C | — | 330 °C |
| RuNi/CeO2 | 125 °C | 190 °C | 200 °C |
| Ru/WO3 | 130, 405 °C | 140 °C | — |
| Ni/WO3 | 310, 405 °C | — | 320 °C |
| RuNi/WO3 | 145, 200, 390 °C | 170 °C | 240 °C |
In the separate experiments, Ni2+-deposited samples including pre-reduced Ru NPs was employed. The details were summarized in Fig. S5.† The CO pulsed measurement and TEM analysis indicated that no significant differences were found in the dispersion and particle sizes of Ru NPs on each support. The reduction temperature of the Ni2+ ions on TiO2 and CeO2 were substantially decreased in the presence of pre-reduced Ru NPs. On the other hand, the reduction temperature of Ni2+ ions on WO3 was not promoted even in the presence of pre-reduced Ru NPs. These results exclude the effect of particle size on the reduction of metals due to the hydrogen spillover.
In order to distinctly assess the reduction sequences, in situ XAFS measurements were performed under H2 atmosphere at elevated temperature. The reduction temperatures for the deposited Ru3+ and Ni2+ were determined from the change in the X-ray absorption near edge structure (XANES) spectra during a reduction sequence (Table 1 and Fig. S6–S8†). In preliminary results, as deposited Ni and Ru species were found to be single-atom in 2+ and 3+ oxidation states for all samples, respectively (Fig. S9†). Additionally, the reduction temperatures of Ni2+ and Ru3+ ions for monometallic samples were not dependent on the support materials. These results indicate that the effect of interaction between metal precursors and supports on spillover effect can be excluded. It should be noted that the reduction temperatures for Ru3+ slightly increased in the presence of Ni2+, while the reduction temperature of Ni2+ drastically decreased in the presence of Ru3+ for all samples. More importantly, the reduction temperatures for Ni2+ and Ru3+ ions were nearly consistent for RuNi/TiO2 and RuNi/CeO2. In contrast, the reduction temperatures for Ru3+ and Ni2+ species on the surface of WO3 were determined to be 170 °C and 240 °C, respectively, suggesting the subsequent reduction of Ru3+ followed by Ni2+. These results are all consistent with the H2-TPR results and clearly indicate that TiO2 and CeO2 allow a more rapid and homogeneous reduction at lower temperatures driven by the pronounced hydrogen spillover effect in comparison to WO3. The retarded reducibility of the Ru3+ species in the presence of Ni2+ in comparison with that for the monometallic samples over the TiO2 and CeO2 supports may be ascribed to the interaction between Ru3+ and Ni2+ and the decrease of the coverage of the Ru3+.
A comparison of the X-ray absorption results after reduction at 300 °C provides additional local structural information. The shapes of the normalized XANES spectra at the Ru K-edge and the edge positions for three RuNi samples resembled those of Ru foil (Fig. 2b). More detailed inspection revealed that the intensity of two distinct peaks at approximately 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 and 22
136 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 eV for RuNi/TiO2 and RuNi/CeO2 were different from those for RuNi/WO3 and Ru foil, indicating that the symmetry of the Ru metal hcp structure was slightly disordered by integration with the Ni.44 The Ru K-edge Fourier transform-extended X-ray absorption fine structure (FT-EXAFS) spectra contained a single sharp peak associated with Ru–Ru bonds at approximately 2.4 Å (Fig. 2c). For RuNi/TiO2 and RuNi/CeO2, the position of this peak was slightly shifted to shorter interatomic distances in comparison with Ru foil, which suggests the formation of heteroatomic Ru–Ni bonding. Moreover, the inverse FT was well fitted by using Ru–Ru and Ru–Ni shells, respectively (Table 2 and Fig. S10†). On the other hand, no shift of the main peak was observed for RuNi/WO3, in which curve fitting was completed with only Ru–Ru bonds without the contribution of Ru–Ni bonds. EDX analysis of RuNi/WO3 showed the random distribution of Ru and Ni, and the formation of definite RuNi solid solution alloy was not observed (Fig. S12†). Conclusively, the RuNi alloy NPs were evidently formed not only on TiO2, but also on CeO2, while Ru3+ and Ni2+ species were reduced separately on the surface of WO3, which results in the formation of segregated NPs rather than the solid solution alloy.
159 eV for RuNi/TiO2 and RuNi/CeO2 were different from those for RuNi/WO3 and Ru foil, indicating that the symmetry of the Ru metal hcp structure was slightly disordered by integration with the Ni.44 The Ru K-edge Fourier transform-extended X-ray absorption fine structure (FT-EXAFS) spectra contained a single sharp peak associated with Ru–Ru bonds at approximately 2.4 Å (Fig. 2c). For RuNi/TiO2 and RuNi/CeO2, the position of this peak was slightly shifted to shorter interatomic distances in comparison with Ru foil, which suggests the formation of heteroatomic Ru–Ni bonding. Moreover, the inverse FT was well fitted by using Ru–Ru and Ru–Ni shells, respectively (Table 2 and Fig. S10†). On the other hand, no shift of the main peak was observed for RuNi/WO3, in which curve fitting was completed with only Ru–Ru bonds without the contribution of Ru–Ni bonds. EDX analysis of RuNi/WO3 showed the random distribution of Ru and Ni, and the formation of definite RuNi solid solution alloy was not observed (Fig. S12†). Conclusively, the RuNi alloy NPs were evidently formed not only on TiO2, but also on CeO2, while Ru3+ and Ni2+ species were reduced separately on the surface of WO3, which results in the formation of segregated NPs rather than the solid solution alloy.
| Shell | CN | R/Å | σ 2 | |
|---|---|---|---|---|
| RuNi/TiO2 | Ru–Ru | 5.4 | 2.64 | 0.0064 |
| Ru–Ni | 4.2 | 2.54 | 0.0056 | |
| RuNi/CeO2 | Ru–Ru | 3.7 | 2.63 | 0.0077 |
| Ru–Ni | 2.0 | 2.59 | 0.0022 | |
| RuNi/WO3 | Ru–Ru | 6.4 | 2.65 | 0.0056 |
Mechanistic investigation by DFT calculations
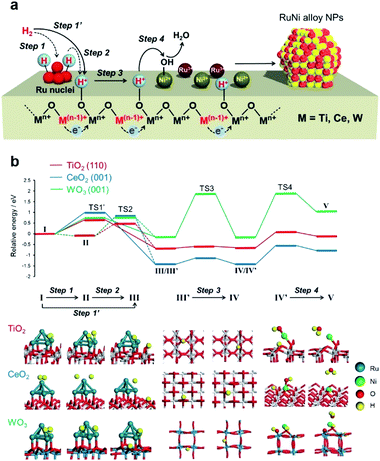
Considering the H2-TPR and in situ XAFS results, a mechanism for the formation of the RuNi solid solution alloy NPs in conjunction with hydrogen spillover is proposed in Fig. 3a. The Ru3+ precursors are first partially reduced to generate nuclei, which then act as uptake sites to dissociate H2 to form Ru–H species (step 1). The reduction of Mn+ to M(n−1)+, together with the transfer of H atoms from Ru nuclei at the metal–support interfaces (step 2), is accompanied by the migration of electrons from M(n−1)+ ions to neighboring Mn+ ions. This promotes the subsequent simultaneous transfer of protons to O2− anions attached to these adjacent Mn+ ions (step 3). In this manner, hydrogen atoms rapidly reduce all metal ions by moving over the support surface (step 4).DFT calculations were performed to simulate the activation energies for each step. Rutile TiO2 (110), CeO2 (001), and WO3 (001) were employed as the models of supports due to their superior stability. Ru5 clusters with a square pyramidal arrangement were chosen as Ru nuclei because 5 is the magic number for Run clusters.45,46 The energy diagram and the obtained activation energy (Ea) are displayed in Fig. 3b and Table 3, in which step 1 (I → II), step 2 (II → III), step 3 (III′ → IV), and step 4 (IV′ → V) were considered as the representative elementary steps in the hydrogen spillover process. Energy profiles and calculated models were shown in Fig. S11–S23.†
| Step 1 (I → II) | Step 2 (II → III) | Step 3 (III → IV) | Step 4 (IV → V) | Step 1′ (I → III) | Step 4′ | |
|---|---|---|---|---|---|---|
| H2 cleavage on Ru5 (homolytic) | H atom transfer from Ru5 to oxide | H atom migration on oxide | Reduction of Nin+ by spilled H (Langmuir–Hinshelwood mechanism) | H2 cleavage on Ru5 and oxide (heterolytic) | Reduction of Nin+ by H2 vapor (Eley–Rideal mechanisms) | |
| a The H2 molecule was dissociated spontaneously upon adsorption on a Ru atom away from the Ru5/support interfaces. | ||||||
| TiO2 (110) | ∼0.0a | 0.92 | 0.08 | 0.72 | 0.66 | 3.69 |
| CeO2 (001) | ∼0.0a | 1.31 | 0.28 | 0.87 | 1.00 | 2.54 |
| WO3 (001) | ∼0.0a | 1.26 | 2.04 | 2.01 | 0.73 | 5.16 |
The activation energies (Ea) in the dissociation of H2 at Ru5 (step 1) are barrier-less for all models. The H2 molecule was dissociated spontaneously upon adsorption on a Ru atom away from the Ru5/support interfaces.47 In the case of TiO2 (110), the Ea of step 2 was calculated to be 0.92 eV. Alternatively, the heterolytic H2 splitting at the metal–support interface (denoted as step 1′ (I → III) in Table 3) was calculated to be 0.66 eV, indicating that this is the energetically more reasonable pathway than the homolytic H2 splitting at the Ru followed by the migration from Ru to supports.47 The migration of a H atom (step 3) over the TiO2 (110) is energetically favourable between 3-coordinated oxygen atom and 2-coordinated one (Fig. S13†). The Ea of 0.72 eV for step 4 was the largest among the four steps, suggesting that reduction of Nin+ by the spilled H atom is rate-determining. A relatively low Ea for all steps indicates the easy occurrence of hydrogen spillover over TiO2 without a large external energy input. In the case of CeO2, step 1 was barrier-less and the Ea values for step 3 was small, whereas that of step 2 was 1.31 eV. The heterolytic H2 splitting pathway (step 1′) was determined to be 1.00 eV, indicating the involvement of the energetically reasonable alternative pathway. The H atom migration on this substrate (step 3) preferentially occurs at the nearest oxygen sites, and there is a relatively high activation energy for migration to the secondary-adjacent oxygen site (Fig. S17†). In contrast, step 3 was found to be the rate-determining step for WO3 and the Ea was as large as 2.04 eV for possible two pathways (Fig. S19†).
Adsorption of neutral H on the surface could, in some cases, be more appropriately described as adsorption of H+ and e−, and the excess electron may be localized on a metal nanoparticle at the surface.48 A related phenomenon where excess electrons appear at the surface is surface O removal as a neutral species. The surface O vacancy formation energy can be reduced when a nearby metal nanoparticle can absorb excess electrons (electron scavenger effect).49 Hinuma et al. showed that manifestation of the electron scavenger effect is determined by the order of the oxide defect level after O removal and the metal work function.50 Compared to late transition metals typically adsorbed as nanoparticles, fully oxidized group 3, 4, 5 oxides as well as CeO2 have very large ionization potentials (IPs), or in other words, the valence band maximum is very deep with respect to the vacuum level. However, the IPs become smaller when the cation is reduced. In particular, reduced titanium oxides have very small IPs and the electron scavenger effect could happen, which could explain the surface reactivity of reduced oxides. That being said, diffusion of H over long distances of the TiO2 surface requires diffusion over regions where nanoparticles are far away and are less reduced. We focused on calculating the activation barrier in such regions because this would become the bottleneck.
The reduction of deposited Nin+ ions by the spilled H atoms (step 4) was qualitatively evaluated by calculating Ea for the attack of a neighbouring H atom on a Nin+–OH species on the support, together with the loss of H2O. The Mulliken atomic charges of Ni atom decreased after the reduction for all models (Fig. S23–S25†), suggesting the reduction of Ni atoms. The electron density in the vicinity of the Fermi level (E = 0) clearly increased after the reduction of Ni species, suggesting the change of oxidation state of Ni atoms from oxide to metallic nature (Fig. S24†). These Ea values according to Langmuir–Hinshelwood mechanism were estimated to be 0.72, 0.87, and 2.01 eV for TiO2 (110), CeO2 (001), and WO3 (001), respectively, which are substantially lower than those for the same process by the direct reduction with a gaseous H2 molecule (step 4′ in Table 3; 3.69 eV for TiO2 (110), 2.54 eV for CeO2 (001), and 5.16 eV for WO3 (001), which follows Eley–Rideal mechanisms, as shown in Fig. S25†). Consequently, the order of Ea in the rate-determining steps is TiO2 (110) < CeO2 (001) < WO3 (001) and the TiO2 and CeO2 surfaces do not require a higher energy input than that on WO3 for the formation of RuNi alloy NPs by the assist of hydrogen spillover, despite the stronger binding energy of metals over TiO2 and CeO2 rather than WO3 (Table S1 and Fig. S26†). Moreover, the Ea for the removal of lattice oxygen by the spilled H atoms to form H2O and oxygen vacancy were 3.60 eV for TiO2 (110), 3.09 eV for CeO2 (001), and 2.40 eV for WO3 (001) (Fig. S27†), which were substantially larger than those in step 4. This verified that spilled H atoms promoted the rapid and simultaneous reduction of the metal precursors at low temperatures, and the reduction of metal cations of support themselves is negligible on a thermodynamic basis.
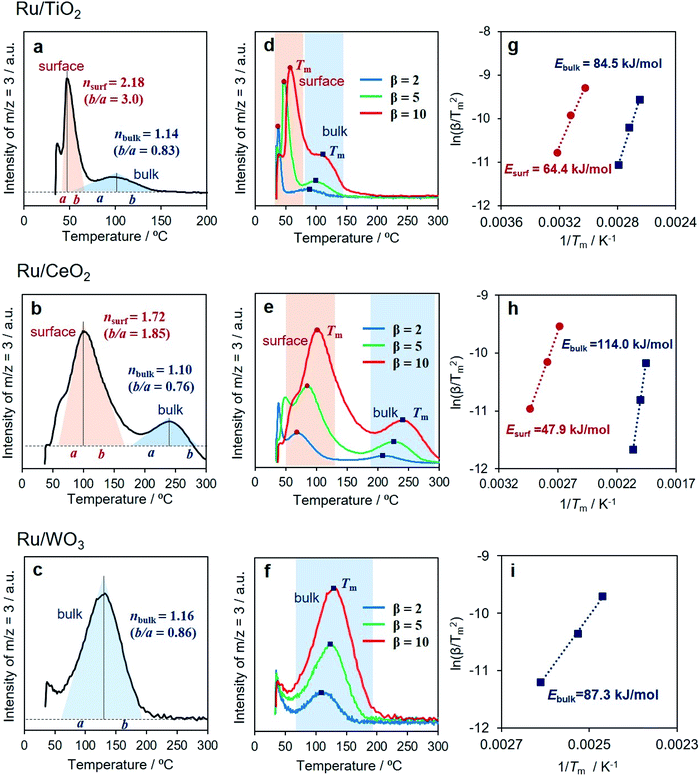
Identification of surface and internal hydrogen spillover
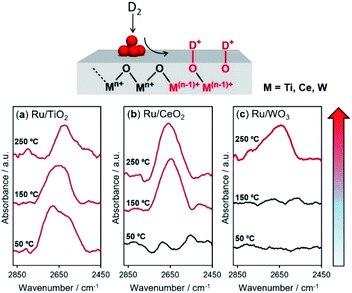
In the hydrogen spillover process, the dissociated hydrogen atoms generate O–H bonds via a concurrent proton–electron transfer pathway. We evaluated the hydrogen spillover characteristics on the surface of Ru-supported TiO2, CeO2 and WO3 by in situ DRIFT experiments after D2 introduction at 50, 150, and 250 °C. Ru/TiO2 generated a distinct peak assignable to δO–D stretching vibrations ranging from 2550–2750 cm−1 at 50 °C, as displayed in Fig. 4.51,52 No peaks were detected for Ru/CeO2 or Ru/WO3 at 50 °C, suggesting the absence of hydrogen spillover, while peaks appeared at 150 °C for Ru/CeO2 and 250 °C for Ru/WO3. It should be noted that this characteristic peak cannot be observed in the intrinsic metal oxides without Ru, indicating that formation of δO–D definitely originated from hydrogen spillover via the supporting Ru, not the direct insertion of gaseous H2. These results prove that hydrogen spillover occurred at different temperatures depending on the metal oxides, i.e., TiO2 (below 50 °C), CeO2 (50–150 °C), and WO3 (150–250 °C), which supports the above experimental results for the formation of RuNi solid solution alloy NPs and theoretical calculations. Moreover, the BET surface areas (SBET) determined by N2 adsorption–desorption were TiO2 (60.1 m2 g−1), CeO2 (135.3 m2 g−1), and WO3 (5.5 m2 g−1), respectively. This means that the hydrogen spillover on WO3 is slow albeit the coverage of Ru is quite high, which further verify that the hydrogen spillover on TiO2 and CeO2 favourably occur than that on WO3.The reducibility (formation energy for oxygen vacancies) of WO3 (5.36 eV) is higher than those of TiO2 (8.23 eV) and CeO2 (5.91 eV). However, the results described above demonstrated that H atom transfer on WO3 is energetically more difficult than that on TiO2 and CeO2. In order to understand this contradiction, we must consider the hydrogen spillover pathway not only from the surface but also from the bulk point of view, because the obtained results for the formation of RuNi alloy NPs and DFT calculations are essentially reflected by the hydrogen spillover pathway on the surface of metal oxides.
By employing Ru/TiO2, Ru/CeO2 and Ru/WO3 as specimens, H/D exchange via the spillover process was monitored at elevated temperature, and the reaction can be simply described as
| 2Had + Olattice–D → HD (g) + Olattice–H | (1) |
All samples showed an immediate HD production peak at low temperature after switching to H2, which originated from H/D exchange at the Ru NPs, not on the metal oxides related to hydrogen spillover. Ru/TiO2 showed strong peaks at around 50 °C accompanied by a small peak at around 100 °C (Fig. 5a). Our DRIFT experiment revealed that Ru/TiO2 produced O–D bonds via hydrogen spillover at lower than 50 °C. Moreover, it has been reported that hydrogen atoms can quickly migrate more than 1 μm over a TiO2 surface.6 Thus, the peak observed at lower temperature can be assigned to the HD formed on the surface, while the peak at higher temperature is assignable to the HD formed in the bulk (internal phase). Notably, the contribution from the bulk is small, indicating that migration of hydrogen atoms is limited to the subsurface of TiO2 (the second O–Ti–O tri-layer) at less than 300 °C. Similarly, Ru/CeO2 displayed a bimodal peak involving a prominent peak at 90 °C and a minor peak at 230 °C (Fig. 5b). The slight shift of both peaks toward higher temperatures indicates slower H/D exchange compared to TiO2, which is in agreement with the DRIFT experiment.
Interestingly, Ru/WO3 showed only one peak at 130 °C (Fig. 5c). This temperature was substantially lower than that observed by in situ DRIFT, where the δO–D bond appeared at 250 °C. From the XRD pattern after H2 reduction at 150 °C, the crystal structure of Ru/WO3 was completely changed from monoclinic WO3 (JCPDS No. 43-1035) to W19O55 (JCPDS No. 45-0167) by the introduction of oxygen vacancies (Fig. S28†).53 Moreover, a significant colour change from white to bronze, which is due to the appearance of mixed valence transfer bands between W6+ and W5+,14,15 can be observed in the in situ UV-vis measurements under H2 flow at temperatures between 70 °C and 180 °C (Fig. S29†). This temperature range matches well with that of the HD production peaks via H–D exchange (Fig. 5c). These supplementary results clearly confirmed that the peak observed at around 130 °C can be assigned to the HD formed via internal hydrogen spillover within the bulk, and hydrogen spillover over WO3 preferentially occurs within the bulk phase accompanied by partial reduction of W6+ to W5+ rather than on the surface.
It should be noted that there is an obvious difference in the shape of both peaks for Ru/TiO2 and Ru/CeO2 (Fig. 5d and e). Kissinger reported that the symmetry of the peaks obtained by differential thermal analysis gave the reaction order (n) according to the following equation:54
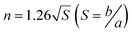 | (2) |
Furthermore, the H/D exchange via spillover process was analyzed by applying the Kissinger equation given by
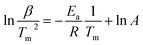 | (3) |
Upon consideration of the above results, a possible reaction pathway for hydrogen spillover over each reducible metal oxide is proposed in Fig. 6. Ru/TiO2 allows preferential hydrogen spillover on its surface at less than 50 °C, which extends to its subsurface from 50 °C to 150 °C (Fig. 6a). The spillover within the bulk does not occur even at higher temperature, because almost no peak due to the formation of HD was observed at higher temperature than even 150 °C (Fig. 5a). Ru/CeO2 also favours hydrogen spillover on its surface in the temperature range from 50 °C to 150 °C, which migrates to its subsurface at higher than 150 °C (Fig. 6b). It can be said that the spillover within the bulk is suppressed at around 250 °C, since the activation energy within the bulk is substantially higher (Ea,bulk = 114.0 kJ mol−1) (Fig. 5h). In the case of Ru/WO3, hydrogen spillover hardly occurs at less than 50 °C. In the temperature range from 50 °C to 150 °C, H atoms predominantly migrate to within the bulk phase rather than the surface. It can be deduced that a further increase in temperature allows migration to the surface, because the reduction temperature of the deposited Ni2+ ions, which is accelerated by surface hydrogen spillover, dropped from 320 to 240 °C in the presence of Ru3+ (Table 1).
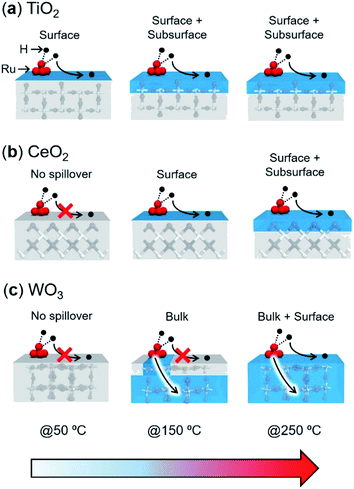 | ||
| Fig. 6 Proposed spillover pathways for (a) TiO2, (b) CeO2, and (c) WO3 at various temperatures. The blue highlighted shows the H-migrated area. | ||
In order to support the experimental results for the hydrogen spillover pathway, H diffusion energy from the surface to the subsurface was calculated for TiO2 (110), CeO2 (001), and WO3 (001). The results were shown in Fig. S32.† The energy of the H atom migration over TiO2 (110) from the top surface to the first and second inside oxide layers were 0.90 and 1.17 eV, respectively, which were larger than that of the surface H atom migration (0.08 eV, see Table 3). A similar tendency was observed over CeO2 (001). On the contrary, H diffusion from surface to first and second inside oxide layers over WO3 (001) occurs with a barrier of 0.75 and 0.52 eV, respectively, which were substantially lower than that of the surface H atom migration (2.04 eV, see Table 3). These results agree with the experimental data obtained from the DRIFT and HD formation reaction.
With respect to the differences in the hydrogen spillover pathway, we point out the importance of the redox properties of metal oxides, because hydrogen spillover proceeds with concurrent proton–electron transfer associated with reversible reduction and oxidation of metal oxides (Mn+ + e− ↔ M(n−1)+). Since TiO2 and CeO2 have moderate reducing properties (the formation energies of oxygen vacancies), the redox of metal oxides is likely to proceed reversibly on their surfaces. Accordingly, hydrogen spillover preferentially occurs on their surfaces, since metal oxides are less likely to be reduced within the bulk due to the increase in the number of coordinated oxygen atoms, resulting in limited hydrogen spillover into the bulk.
The high reducibility of WO3 tends to accelerate the reduction of W6+ ions, thus retarding the oxidation of W5+ ions. Consequently, hydrogen spillover on the surface of Ru/WO3 is limited because the reversible redox reaction is unlikely to proceed. As the number of adjacent oxygen atoms increases, such a trade-off relationship would be improved. Thus, WO3 allows the reversible reduction and oxidation of W ions within the bulk and preferentially transfers H atoms. It can be concluded that the reducibility of the metal oxides is responsible for not only the improvement of hydrogen spillover but also its pathway.
Conclusions
We explored the inherent hydrogen spillover properties of three representative reducible metal oxides. Reduction profiles for the deposited ions obtained using H2-TPR and in situ XAFS data suggest the simultaneous reduction of Ru3+ and Ni2+ species on the TiO2 and CeO2 supports, which generates RuNi binary solid solution alloy NPs exhibiting a synergistic effect in AB hydrolysis. These two cations were reduced individually on WO3, resulting in the formation of segregated NPs without activity enhancement. These results indicated that the hydrogen spillover on the surface of TiO2 and CeO2 is more likely proceed than on WO3. DFT calculations revealed that the rate-determining steps were different, and the activation energy increased in the order of TiO2 (110) < CeO2 (001) < WO3 (001). In situ DRIFT and kinetic analysis of HD formation based on the Kissinger method verified that hydrogen spillover on TiO2 and CeO2 favorably occurred on their surfaces rather than within their bulk phases. Conversely, hydrogen spillover on WO3 preferentially proceeded within the bulk prior to the surface. These insights into the occurrence temperature of hydrogen spillover as well as its migration pathway will provide an opportunity to select an optimized metal oxide and maximize its properties according to the desired application fields, such as hydrogen storage, catalysts/photocatalyst design, and enhancement of catalytic functions. Meanwhile, a more in-depth study combined with an experimental approach, theoretical calculation, and advanced characterization should be performed for the construction of key technology in the upcoming hydrogen society.Experimental
Materials
TiO2 (JRC-TIO-4, anatase![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rutile = 7
rutile = 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), CeO2 (JRC-CEO-2), and Nb2O5 (JRC-NBO-2) were supplied by the Catalysis Society of Japan. WO3 and Ga2O3 were obtained from Wako Pure Chemical Industries, Ltd. RuCl3·nH2O and NiCl2·6H2O were obtained from Nacalai Tesque. Ammonia borane (AB, NH3BH3) was purchased from Aldrich Chemical Co. All commercially available chemicals were used as received. Distilled water was employed as the reaction solvent.
3), CeO2 (JRC-CEO-2), and Nb2O5 (JRC-NBO-2) were supplied by the Catalysis Society of Japan. WO3 and Ga2O3 were obtained from Wako Pure Chemical Industries, Ltd. RuCl3·nH2O and NiCl2·6H2O were obtained from Nacalai Tesque. Ammonia borane (AB, NH3BH3) was purchased from Aldrich Chemical Co. All commercially available chemicals were used as received. Distilled water was employed as the reaction solvent.
Preparation of catalysts
RuCl3·3H2O (0.0324 g, 0.124 mmol) and NiCl2·6H2O (0.038 mmol, Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 1
Ni = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3) were added to a mixture of TiO2 (0.6 g) and distilled water (100 mL). This suspension was stirred at room temperature for 1 h, after which the solvents were evaporated under vacuum. Finally, the sample was reduced under H2 dosage at a heating rate of 5 °C min−1 (20 mL min−1, 300 °C) for 2 h to yield RuNi/TiO2 (Ru 2.0 wt%; Ru
0.3) were added to a mixture of TiO2 (0.6 g) and distilled water (100 mL). This suspension was stirred at room temperature for 1 h, after which the solvents were evaporated under vacuum. Finally, the sample was reduced under H2 dosage at a heating rate of 5 °C min−1 (20 mL min−1, 300 °C) for 2 h to yield RuNi/TiO2 (Ru 2.0 wt%; Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 1
Ni = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3). RuNi/CeO2, RuNi/WO3, RuNi/Ga2O3, and RuNi/Nb2O5 with the same Ru and Ni loadings were also prepared by the same procedure.
0.3). RuNi/CeO2, RuNi/WO3, RuNi/Ga2O3, and RuNi/Nb2O5 with the same Ru and Ni loadings were also prepared by the same procedure.
Characterization
Transmission electron microscopy (TEM) images were obtained with a field emission (FE) TEM instrument (Hf-2000, Hitachi). Scanning transmission electron microscopy (STEM) images, elemental mapping and line analysis were obtained using a JEOL-ARM 200F instrument equipped with a Kevex EDX detector (JED 2300T) operated at 200 kV. Powder X-ray diffraction (XRD) patterns were recorded using a Rigaku Ultima IV diffractometer with Cu Kα radiation (λ = 1.54056 Å). Temperature-programmed reduction with H2 (H2-TPR) was conducted on a BEL-CAT (BEL Japan, Inc.) instrument by heating 50 mg specimens at 5 °C min−1 from 50 to 600 °C under a 5.0% H2/Ar flow. Ru K-edge and Ni K-edge in situ X-ray absorption fine structure (XAFS) spectra were acquired in transmission mode at the 01B1 beamline station in conjunction with a Si (111) monochromator at SPring-8, JASRI, Harima, Japan (Proposal No. 2020A1062 and 2020A0523). In a typical experiment, spectra were acquired while a pellet sample was held in a batch-type in situ XAFS cell. XAFS data were examined using the REX2000 and ATHENA programs (Demeter).56In situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) measurements were conducted using an IR Spirit (Shimadzu) instrument equipped with a heating chamber connected to a gas-exchange system. HD (m/z 3) production via the hydrogen spillover process at heating rates of 2, 5 and 10 °C min−1 was measured by mass spectrometry (MS) using a BELMass (BEL Japan, Inc.) connected to a BEL-CAT instrument. In situ ultraviolet-visible adsorption spectroscopy (UV-vis) measurements were conducted using a V-750 (JACSO International Co., Ltd).Hydrolysis of AB
In a typical experiment, the RuNi/TiO2 catalyst (10 mg) and distilled water (8 mL) were mixed in a Schlenk-type reaction vessel (30 mL) connected to a gas burette. After the system was purged three times with Ar, 2 mL of a 2 mmol aqueous solution of AB was added into the vessel to react at 30 °C. The reaction progress was evaluated by the amount of evolved H2. TOF values were calculated as (H2 mol)/((total Ru mol) min).DFT calculations
All calculations were performed using the DMol3 program in the Materials Studio 17.2 software package.57,58 The generalized gradient approximation (GGA) exchange-correlation functional proposed by Perdew, Burke, and Ernzerhof (PBE) was used. This function was combined with the double-numerical basis set plus polarization functions (DNP) in conjunction with a cutoff value of 4.0 Å. We adopted the medium level in the DMol3 program for the integration grid.The simulations of hydrogen spillover on reducible metal oxides were conducted using 3 × 3 rutile TiO2 (110) supercell with a cell dimension of 5.918 × 12.994 × 20.785 Å, 3 × 3 CeO2 (001) supercell with a cell dimension of 11.479 × 11.479 × 19.058 Å and 3 × 3 WO3 (001) supercell with a cell dimension of 10.662 × 10.662 × 21.070 Å, respectively. Herein, rutile TiO2 was used as the TiO2 model because the hydrogen spillover mechanism over anatase TiO2 was thoroughly investigated in other reports.6,52,59,60 The number of oxide layers was 4, 4, and 3 for TiO2 (110), CeO2 (001) and WO3 (001) planes, respectively. The slab was separated by a vacuum space with a height of 15 Å and tetrahedral Ru5 clusters were loaded on the surface of each oxide. The reactant atoms, Ru cluster and top oxide layer were relaxed during geometry optimizations and the other layers were fixed at the corresponding bulk positions. Transition states (TSs) were determined by the nudged elastic band method and the activation energy was defined by the energy difference between the TS and the reactant.
Data availability
All data generated and analyzed during this study are included in this article and its ESI,† or are available from the corresponding authors upon reasonable request.Author contributions
K. S. performed the catalyst preparation, calculation, and characterization. K. M. supervised the project, performed a part of calculation, and wrote the manuscript. S. M. and N. H. helped the catalyst preparation and characterization. Y. H. provided advice on analysing calculations. H. K. helped calculations. H. Y. helped supervise the project. The manuscript was written through the discussion with all authors. All authors have given approval to the final version of manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work was supported by the Kakenhi Grant-in-Aid for Transformative Research Areas (B) (No. 21B206) from the Japan Society for the Promotion of Science (JSPS), Element Strategy Initiative of MEXT, Japan (No. JPMXP0112101003), and “Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials” from MEXT. A part of the present experiments was carried out by using a facility in the Research Center for Ultra-High Voltage Electron Microscopy, Osaka University.Notes and references
- R. Prins, Chem. Rev., 2012, 112, 2714–2738 CrossRef CAS PubMed
.
- M. Choi, S. Yook and H. Kim, ChemCatChem, 2015, 7, 1048–1057 CrossRef CAS
.
- K. Murakami and Y. Sekine, Phys. Chem. Chem. Phys., 2020, 22, 22852–22863 RSC
.
- M. Xiong, Z. Gao and Y. Qin, ACS Catal., 2021, 11, 3159–3172 CrossRef CAS
.
- P. A. Sermon and G. C. Bond, Catal. Rev., 1974, 8, 211–239 CrossRef
.
- W. Karim, C. Spreafico, A. Kleibert, J. Gobrecht, J. VandeVondele, Y. Ekinci and J. A. van Bokhoven, Nature, 2017, 541, 68–71 CrossRef CAS PubMed
.
- K. Liu, P. Yan, H. Jiang, Z. Xia, Z. Xu, S. Bai and Z. C. Zhang, J. Catal., 2019, 369, 396–404 CrossRef CAS
.
- T. M. David, K. I. Gnanasekar, P. Wilson, P. Sagayaraj and T. Mathews, ACS Omega, 2020, 5, 11352–11360 CrossRef CAS PubMed
.
- C. Mao, J. Wang, Y. Zou, G. Qi, J. Y. Yang Loh, T. Zhang, M. Xia, J. Xu, F. Deng, M. Ghoussoub, N. P. Kherani, L. Wang, H. Shang, M. Li, J. Li, X. Liu, Z. Ai, G. A. Ozin, J. Zhao and L. Zhang, J. Am. Chem. Soc., 2020, 142, 17403–17412 CrossRef CAS PubMed
.
- K. Mori, N. Hashimoto, N. Kamiuchi, H. Yoshida, H. Kobayashi and H. Yamashita, Nat. Commun., 2021, 12, 3884 CrossRef CAS PubMed
.
- M. Pudukudy, Z. Yaakob, Q. Jia and M. Sobri Takriff, New J. Chem., 2018, 42, 14843–14856 RSC
.
- Y. Nakagawa, S. Tazawa, T. Wang, M. Tamura, N. Hiyoshi, K. Okumura and K. Tomishige, ACS Catal., 2017, 8, 584–595 CrossRef
.
- Z. Peng, Z. Li, Y.-Q. Liu, S. Yan, J. Tong, D. Wang, Y. Ye and S. Li, Chem. Commun., 2017, 53, 5958–5961 RSC
.
- H. Cheng, M. Wen, X. Ma, Y. Kuwahara, K. Mori, Y. Dai, B. Huang and H. Yamashita, J. Am. Chem. Soc., 2016, 138, 9316–9324 CrossRef CAS PubMed
.
- Y. F. Li, N. Soheilnia, M. Greiner, U. Ulmer, T. Wood, A. A. Jelle, Y. Dong, A. P. Yin Wong, J. Jia and G. A. Ozin, ACS Appl. Mater. Interfaces, 2019, 11, 5610–5615 CrossRef CAS PubMed
.
- J. Park, S. Lee, H.-E. Kim, A. Cho, S. Kim, Y. Ye, J. W. Han, H. Lee, J. H. Jang and J. Lee, Angew. Chem., Int. Ed., 2019, 58, 16038–16042 CrossRef CAS PubMed
.
- R. Prins, V. K. Palfi and M. Reiher, J. Phys. Chem. C, 2012, 116, 14274–14283 CrossRef CAS
.
- S. Khoobiar, J. Phys. Chem., 1964, 68, 411–412 CrossRef CAS
.
- N. M. Briggs, L. Barrett, E. C. Wegener, L. V. Herrera, L. A. Gomez, J. T. Miller and S. P. Crossley, Nat. Commun., 2018, 9, 3827 CrossRef PubMed
.
- J. Im, H. Shin, H. Jang, H. Kim and M. Choi, Nat. Commun., 2014, 5, 3370 CrossRef PubMed
.
- J. Zhang, Z. Gao, S. Wang, G. Wang, X. Gao, B. Zhang, S. Xing, S. Zhao and Y. Qin, Nat. Commun., 2019, 10, 4166 CrossRef PubMed
.
- M. Xiong, Z. Gao, P. Zhao, G. Wang, W. Yan, S. Xing, P. Wang, J. Ma, Z. Jiang, X. Liu, J. Ma, J. Xu and Y. Qin, Nat. Commun., 2020, 11, 4773 CrossRef CAS PubMed
.
- S. K. Beaumont, S. Alayoglu, C. Specht, N. Kruse and G. A. Somorjai, Nano Lett., 2014, 14, 4792–4796 CrossRef CAS PubMed
.
- M. Takabatake, A. Hashimoto, W.-J. Chun, M. Nambo, Y. Manaka and K. Motokura, JACS Au, 2021, 1, 124–129 CrossRef CAS PubMed
.
- R. C. Maher, P. R. Shearing, E. Brightman, D. J. L. Brett, N. P. Brandon and L. F. Cohen, Adv. Sci., 2016, 3, 1500146 CrossRef PubMed
.
- S. K. Konda and A. Chen, Mater. Today, 2016, 19, 100–108 CrossRef CAS
.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef CAS PubMed
.
- G. Dutta, U. V. Waghmare, T. Baidya and M. S. Hegde, Chem. Mater., 2007, 19, 6430–6436 CrossRef CAS
.
- S. S. E. Collins, M. Cittadini, C. Pecharromán, A. Martucci and P. Mulvaney, ACS Nano, 2015, 9, 7846–7856 CrossRef CAS PubMed
.
- M. Horprathum, T. Srichaiyaperk, B. Samransuksamer, A. Wisitsoraat, P. Eiamchai, S. Limwichean, C. Chananonnawathorn, K. Aiempanakit, N. Nuntawong, V. Patthanasettakul, C. Oros, S. Porntheeraphat, P. Songsiriritthigul, H. Nakajima, A. Tuantranont and P. Chindaudom, ACS Appl. Mater. Interfaces, 2014, 6, 22051–22060 CrossRef CAS PubMed
.
- L. Jiang, K. Liu, S.-F. Hung, L. Zhou, R. Qin, Q. Zhang, P. Liu, L. Gu, H. M. Chen, G. Fu and N. Zheng, Nat. Nanotechnol., 2020, 15, 848–853 CrossRef CAS PubMed
.
- M. Torimoto, K. Murakami and Y. Sekine, Bull. Chem. Soc. Jpn., 2019, 92, 1785–1792 CrossRef CAS
.
- M. Torimoto, S. Ogo, D. Harjowinoto, T. Higo, J. G. Seo, S. Furukawa and Y. Sekine, Chem. Commun., 2019, 55, 6693–6695 RSC
.
- G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212 CrossRef CAS PubMed
.
- S. Kato, M. Ammann, T. Huthwelker, C. Paun, M. Lampimäki, M.-T. Lee, M. Rothensteiner and J. A. van Bokhoven, Phys.
Chem. Chem. Phys., 2015, 17, 5078–5083 RSC
.
- S. Alayoglu, K. An, G. Melaet, S. Chen, F. Bernardi, L. W. Wang, A. E. Lindeman, N. Musselwhite, J. Guo, Z. Liu, M. A. Marcus and G. A. Somorjai, J. Phys. Chem. C, 2013, 117, 26608–26616 CrossRef CAS
.
- H. Yin, L.-Q. Zheng, W. Fang, Y.-H. Lai, N. Porenta, G. Goubert, H. Zhang, H.-S. Su, B. Ren, J. O. Richardson, J.-F. Li and R. Zenobi, Nat. Catal., 2020, 3, 834–842 CrossRef CAS
.
- H. Yoon, Y. Kim, E. J. Crumlin, D. Lee, K. Ihm and J. Son, J. Phys. Chem. Lett., 2019, 10, 7285–7292 CrossRef CAS PubMed
.
- K. Mori, K. Miyawaki and H. Yamashita, ACS Catal., 2016, 6, 3128–3135 CrossRef CAS
.
- S. Masuda, K. Mori, T. Sano, K. Miyawaki, W.-H. Chiang and H. Yamashita, ChemCatChem, 2018, 10, 3526–3531 CrossRef CAS
.
- S. Masuda, K. Shun, K. Mori, Y. Kuwahara and H. Yamashita, Chem. Sci., 2020, 11, 4194–4203 RSC
.
- G. Chen, S. Desinan, R. Rosei, F. Rosei and D. Ma, Chem.–Eur. J., 2012, 18, 7925–7930 CrossRef CAS PubMed
.
- Z. Helali, A. Jedidi, O. A. Syzgantseva, M. Calatayud and C. Minot, Theor. Chem. Acc., 2017, 136, 100 Search PubMed
.
- V. Vorotnikov, T. R. Eaton, A. E. Settle, K. Orton, E. C. Wegener, C. Yang, J. T. Miller, G. T. Beckham and D. R. Vardon, ACS Catal., 2019, 9, 11350–11359 Search PubMed
.
- S. Ghoshal, A. Pramanik and P. Sarkar, Phys. Chem. Chem. Phys., 2021, 23, 1527–1538 RSC
.
- G.-X. Ge, H.-X. Yan, Q. Jing and Y.-H. Luo, J. Cluster Sci., 2011, 22, 473 CrossRef CAS
.
- R. C. Nelson, B. Baek, P. Ruiz, B. Goundie, A. Brooks, M. C. Wheeler, B. G. Frederick, L. C. Grabow and R. N. Austin, ACS Catal., 2015, 5, 6509–6523 CrossRef CAS
.
- G.-J. Xia, M.-S. Lee, V.-A. Glezakou, R. Rousseau and Y.-G. Wang, ACS Catal., 2022, 12, 4455–4464 CrossRef CAS
.
- A. R. Puigdollers and G. Pacchioni, ChemCatChem, 2017, 9, 1119–1127 CrossRef CAS
.
- Y. Hinuma, T. Toyao, N. Hamamoto, M. Takao, K.-i. Shimizu and T. Kamachi, J. Phys. Chem. C, 2020, 124, 27621–27630 CrossRef CAS
.
- T. Whittaker, K. B. S. Kumar, C. Peterson, M. N. Pollock, L. C. Grabow and B. D. Chandler, J. Am. Chem. Soc., 2018, 140, 16469–16487 CrossRef CAS PubMed
.
- S. Wang, Z. J. Zhao, X. Chang, J. Zhao, H. Tian, C. Yang, M. Li, Q. Fu, R. Mu and J. Gong, Angew. Chem., Int. Ed., 2019, 58, 7668–7672 CrossRef CAS PubMed
.
- F. Peng, W. Yu, Y. Lu, Y. Sun, X. Fu, J. m. Hao, X. Chen, R. Cong and N. Dai, ACS Appl. Mater. Interfaces, 2020, 12, 41230–41238 CrossRef CAS PubMed
.
- H. E. Kissinger, Anal. Chem., 1957, 29, 1702–1706 CrossRef CAS
.
- Y. Tang, Y. Kobayashi, K. Shitara, A. Konishi, A. Kuwabara, T. Nakashima, C. Tassel, T. Yamamoto and H. Kageyama, Chem. Mater., 2017, 29, 8187–8194 CrossRef CAS
.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed
.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS
.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS
.
- A. Sihag, Z.-L. Xie, H. V. Thang, C.-L. Kuo, F.-G. Tseng, M. S. Dyer and H.-Y. T. Chen, J. Phys. Chem. C, 2019, 123, 25618–25627 CrossRef CAS
.
- H.-Y. T. Chen, S. Tosoni and G. Pacchioni, ACS Catal., 2015, 5, 5486–5495 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc00871h |
| This journal is © The Royal Society of Chemistry 2022 |