Open Access Article
Open Access ArticleForecasting molecular dynamics energetics of polymers in solution from supervised machine learning†
James
Andrews
ab,
Olga
Gkountouna
b and
Estela
Blaisten-Barojas
 *ab
*ab
aCenter for Simulation and Modeling, George Mason University, Fairfax, Virginia 22030, USA. E-mail: blaisten@gmu.edu
bDepartment of Computational and Data Sciences, George Mason University, Fairfax, Virginia 22030, USA
First published on 24th May 2022
Abstract
Machine learning techniques including neural networks are popular tools for chemical, physical and materials applications searching for viable alternative methods in the analysis of structure and energetics of systems ranging from crystals to biomolecules. Efforts are less abundant for prediction of kinetics and dynamics. Here we explore the ability of three well established recurrent neural network architectures for reproducing and forecasting the energetics of a liquid solution of ethyl acetate containing a macromolecular polymer–lipid aggregate at ambient conditions. Data models from three recurrent neural networks, ERNN, LSTM and GRU, are trained and tested on half million points time series of the macromolecular aggregate potential energy and its interaction energy with the solvent obtained from molecular dynamics simulations. Our exhaustive analyses convey that the recurrent neural network architectures investigated generate data models that reproduce excellently the time series although their capability of yielding short or long term energetics forecasts with expected statistical distributions of the time points is limited. We propose an in silico protocol by extracting time patterns of the original series and utilizing these patterns to create an ensemble of artificial network models trained on an ensemble of time series seeded by the additional time patters. The energetics forecast improve, predicting a band of forecasted time series with a spread of values consistent with the molecular dynamics energy fluctuations span. Although the distribution of points from the band of energy forecasts is not optimal, the proposed in silico protocol provides useful estimates of the solvated macromolecular aggregate fate. Given the growing application of artificial networks in materials design, the data-based protocol presented here expands the realm of science areas where supervised machine learning serves as a decision making tool aiding the simulation practitioner to assess when long simulations are worth to be continued.
1 Introduction
The popularity of machine learning (ML) techniques in chemistry, physics and materials science has seen an impressive growth over the past decade1 for a multitude of applications covering a vast spectrum of ML methodologies.2,3 Our focus is on recurrent neural networks (RNN)s, developed for sequence prediction that, nowadays, constitute a viable forecasting model.4 RNNs differ from other neural networks (NN) in that they contain a hidden layer that operates on an ordered sequence where each step includes a hidden state that is updated as a function of it's respective input features and the hidden state of the previous step.5,6 The process entails use of a window of data from a sequence and predicting the following sequence data points moving forward one data point at a time. Under this perspective, RNNs are self-supervised learning approaches.7 Most popular RNN architectures comprise the Elman RNN (ERNN),8 the long-short term memory (LSTM),9 and the gated recurrent unit (GRU).10 The ERNN is among the simplest RNNs containing one hyperbolic tangent function as the activation function. LSTM is a newer architecture explicitly designed to eliminate the long-term dependency problem where temporally distant data have a vanishing gradient, or are “forgotten” by the network. The GRUs are modifications of LSTM containing fewer parameters while improving performance on certain tasks.11 Being RNNs contemporary forecasting models, global software libraries12 have added them since 2018.Among others, LSTM has been used for calibrating Brownian particles force fields,13 for learning the constitutive laws of viscosity in history-dependent materials,14 for enhancing drug discovery through learning to write the SMILES of drug analogs,15 for improving the conformation of proteins,16 or improve the materials infrastructure.17 Supervised NN learning with LSTM and GRU has addressed complex systems such as biomolecular function recognition,18 multiscale approaches linking molecular dynamics trajectories with continuum dynamics,19 to categorize the hydrogen bond mobility in water,20 for following the geometric changes of the SARS-CoV-2 spike protein in aqueous solutions,21 predicting signal peptides and their cleavage sites from protein sequences.22 There is evidence that LSTM and GRU have potential to be considered as alternative models to ab initio molecular dynamics23,24 by predicting short time series forecasts given a fair amount of time series data on the atomic positions and velocities.
Empirical use of block copolymers with amphiphilic behavior as building blocks of complex assemblies25 that endow stimuli-responsive functions has, for example, enabled the accessibility of drug delivery in nano-therapeutics.26–28 Lipids, surfactants, and copolymers have the ability of self-aggregating into diverse assemblies in aqueous solutions and are capable of morphing into other structures when the solvating condition changes.29 The self-assembling characteristic entails both, the interaction between the macromolecules composing the aggregates and the extent the solution affects the macromolecular aggregate. The aggregated structures are fluid-like, soft, with the macromolecules coiling, twisting, rotating, or diffusing within each aggregate due to thermal motions.30 Thus, these soft structures do not exhibit a definite shape or size and are characterized by size distributions in a solution. Time is also important since properties of the assembly require a sufficiently long time evolution for avoiding biases from conformational local minima. From the perspective of computational simulations, to follow the fate of these solvated macromolecular assemblies is a challenge because emulation of actual wet lab conditions require large systems at the nano-to-micro scale and very lengthy computer simulations at the nanosecond scale and beyond. Specifically for polymers, LSTM has been used in the development of polymeric materials for solar cell applications,31 benchmarking NN predictions on enumeration of polymer sequence space,32 engineering dielectric parameters based on the nonlinear structure of polymers,33 among others.
In this paper we investigate the prospect of employing the RNN forecasting model as a prognosis tool that aids the molecular dynamics (MD) practitioner in deciding if large and long MD simulations are worthy of continuation or not. Necessarily, this type of MD simulations entail complex systems at the nano-to-micro spatial and temporal scales, thus requiring access to high performance computing facilities. Our selected forecasting application is the estimation of the future energetics behavior of a liquid solution containing as solute a pre-self-assembled aggregate of four polymer–lipid macromolecules in methyl acetate (EA), a non-polar, organic solvent at ambient conditions. This is a large system from the perspective of MD simulations. The rule of like attracts like is applicable in solvation processes, i.e., polar solutes are solvated by polar solvents and are not solvated by non-polar solvents. Our system, however, entails a non-polar solvent with a solute made of lipid macromolecules that have a polar polymer bound at their head and are terminated by a pair of non-polar acyl chains. There is an intriguing compromise between the acyl chains desire to solvate in the EA and the polymer cohesion propensity to keep the aggregate together. Because of the nanoscale size of the aggregate and the low relative concentration of the solution, the polymer–lipid aggregate will dissolve given enough time.
Therein, we have elucidated the aggregate solvation fate by conducting large MD simulations based on a reliable force field for the modeling of interactions. This is the first time such liquid solution has been modeled and simulated. Meanwhile, we aim at building a ML tool able of producing periodic prognosis of the aggregate status along the MD simulations. Our goal is to assess via an automatable experimental protocol how effective the RNN forecasting model is in the context of monitoring the polymer–lipid aggregate lifespan in solution. We envision that MD simulations of a few nanoseconds are good candidates for training artificial energetics forecasts as decision making tools providing estimates that indicate if the MD simulation is worth continuing and consequently avoiding unnecessarily long simulations. Automated energetics estimates will also be instrumental in taking decisions for concatenating independently run MD simulations34 or ML generated stochastic trajectories with static, underlying, Boltzmann's distribution.35,36 Our recent MD predictions37 have confirmed that aggregates of four DSPE–PEG(2000) (lipid–polymer) macromolecules, self-assemble in water giving rise to pre-micellar formations. While investigating a substance solubility, researchers have been able to formulate intelligently based on the key insight that solvents, polymers, or solid matter are well characterized by solubility parameters derived from their cohesive energy density.38 Indeed, based on the Hildebrand solubility parameter of the EA liquid39 and of the bulk polymer PEG(2000),40 we have determined that the polymer dissolves in EA at ambient conditions. Most likely, the EA also solvates the DSPE–PEG(2000) bulk solid. In search for the solubility of the macromolecular aggregate under study in EA, the unraveling fingerprints are the intra-DSPE–PEG(2000) potential energy, the polymer–lipid aggregate interaction energy with EA and the cohesive energy of the polymer–lipid macromolecules within the self-assembled aggregate.
Hence, we present the in silico prototype based on applying RNNs to forecast the time evolution of two system energies without predicting the temporal behavior of the atomic positions and velocities that serve to calculate them. The prototype protocol requires MD simulations of a few nanoseconds and, yet, permits access to forecasted system energies without extending the simulation time. The forecasting process can be applied multiple times for a given process, each time requiring only a few more nanoseconds of MD evolution. Additionally, the protocol eliminates the need of storing the atomic positions required for calculating the forecasted energetics, thus saving on terabytes of archival storage and substantial electric power. The energy time series are used for the RNN learning tasks of training and testing of ERNN, LSTM, and GRU. The dynamics of polymers is slow requiring tens to hundreds of nanoseconds to observe the evolution of processes such as the life span of a macromolecular solute in a solvent. In fact, it is not excluded that the macromolecular DSPE–PEG(2000) aggregate will dissociate over time if ethyl acetate proves to be a good solvent. However, the solvation process may require long and costly MD simulations. Hence, diagnosing with the forecast estimate if the MD simulation needs to be continued or not is the main motivation of this paper. We explore RNN forecasts of the polymer–lipid aggregate energy properties over a time period of 20% the time length of the series entering in the RNN training/testing tasks using the cyber implementation of PyTorch.12 The generated RNN data models not only yield an excellent reproduction of the input energy series but additionally serve for predicting short (0.5 to 5 ps) and long time forecasts (1 ns). We found that the three RNN models tend to forecast smooth time series around the mean value of the series used for training/testing. The outcome is short of capturing the distribution of points underlying the forecasted energetics. Based on this evidence, we augment our prototype protocol by building an ensemble of training time series that yield an ensemble of data models that generate and ensemble of energetics forecasts. When inspected as a whole, the ensemble of forecasts is perceived as a band of energy values that span the range of the MD energy fluctuations. However, the distribution of the ensemble of forecasted energy values differ from the distributions of the original time series.
This paper is organized as follows. Section Models and methods describes the molecular system followed by a compendium of methods and computer implementations of: (a) the MD simulations of the polymer–lipid in EA solution that generated the time series on which this study is based, (b) the data organization into time series with equal length but different granularity, and (c) the ML model for clustering time patterns in the series and the chosen parameters and learning strategies employed for the three RNNs selected. The Results section enumerates the outcomes describing the ML clustering results, the training and testing evaluation errors of the generated RNN data models as function of the time interval granularity of the inspected series, the building of RNN data models ensembles and their effect on the forecasted energetics of the system along short and long term forecasts. The Discussion section conveys perspectives of the work while a summary in the Conclusion section concludes this work.
2 Models and methods
2.1 Molecular description
The macromolecule DSPE–PEG(2000), 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[amino(polyethylene glycol)-2000], is a block copolymer–lipid with chemical formula (C2H4O)45C44H86N2O10P containing 452 atoms. Multiple applications of this macromolecule include thermo-sensitive liposomal nanoparticles and in the formation of micelles, disks, vesicles, and bilayers that are commonly assembled for therapeutic drug delivery.41–45 We term this macromolecule DSPE–PEG and point out that PEG(2000) is a water soluble linear polymer40 and DSPE is a water insoluble lipid derivative of phosphatidylethanolamine with two long saturated fatty acid chains of stearic acid. Ethyl acetate (EA), C4H8O2, is a non-polar organic solvent commonly used for the fabrication of nanoparticles.26,46,47 Both EA and DSPE–PEG were modeled using the all-atom generalized Amber force field (GAFF)48,49 with our custom-calculated restrained electrostatic potential(RESP) atomic charges,37,39,40 which was combined with the compatible Amber-Lipid17 (ref. 50) force field for the DSPE portion of the polymer–lipid macromolecule. Section S1 of the ESI† has a description of the force field, while our topology files of EA, DSPE–PEG, and initial geometry coordinates prepared for the GROMACS input are open access available in the Zenodo archive.51The system under study was a liquid solution composed of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 EA molecules (224
000 EA molecules (224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms) and one self-assembled aggregate formed by four DSPE–PEG macromolecules (1808 atoms) yielding an EA solution with a 0.787% by mass solute relative concentration.
000 atoms) and one self-assembled aggregate formed by four DSPE–PEG macromolecules (1808 atoms) yielding an EA solution with a 0.787% by mass solute relative concentration.
2.2 Molecular dynamics approach
There is a literature scarcity on describing the temporal fate of self-assembled aggregates of a few macromolecules in non-aqueous solutions while the full system is in equilibrium.52 Our MD simulations are the first for the liquid solution of a DSPE–PEG aggregate in EA. In that context, three samples of the same system were prepared for evaluating our prototype protocol, as is a general practice in wet labs and in silico experiments. Hence, three different geometries of the four DSPE–PEG self-assembled aggregates were generated from 1 ns NVT-MD simulations in vacuum at 300 K along which the macromolecules yielded flexible, prolate spheroidal aggregates. The four DSPE–PEG also self-assembled in implicit solvent with the EA dielectric constant of 6.02. Each self-assembled aggregate was set in the central region of a 13.75 nm edge length cubic box while the EA molecules were placed randomly inside the box. Each system was first minimized, followed by a sequence of short NVT-MD runs to bring the temperature up to 300 K, and brought to thermodynamics equilibrium through 10 ns NPT-MD runs using the Parrinello–Rahman53,54 and Berendsen55 pressure couplings, 1 fs time step, periodic boundary conditions, 1.4 nm cutoff, and particle-mesh Ewald (PME) with an optimized Fourier spacing of 0.145 and cubic spline interpolation. All methods employed followed the implementations in the GROMACS 2018-2020 package.56–58 The three systems equilibrated at a density of 906.3 ± 0.1 kg m−3 at 300 K, comparable to the density of pure EA.39 These three simulations are herein termed sets 1, 2, and 3. At the conclusion of the three equilibrations, the structure of the solvated macromolecular aggregate in each set differed significantly between them with positional root mean squared atomic deviation (RMSD) of 1.74 nm between set 1 and set 2, 1.74 nm between set 2 and set 3, and 1.58 nm between set 1 and set 3. The RMSDs were calculated with the VMD59 corresponding plugin60 that aligns the compared structures by optimizing consecutive rotations between specified groups of atoms. Visual renderings of these aggregates macromolecular structure are depicted in Fig. 1.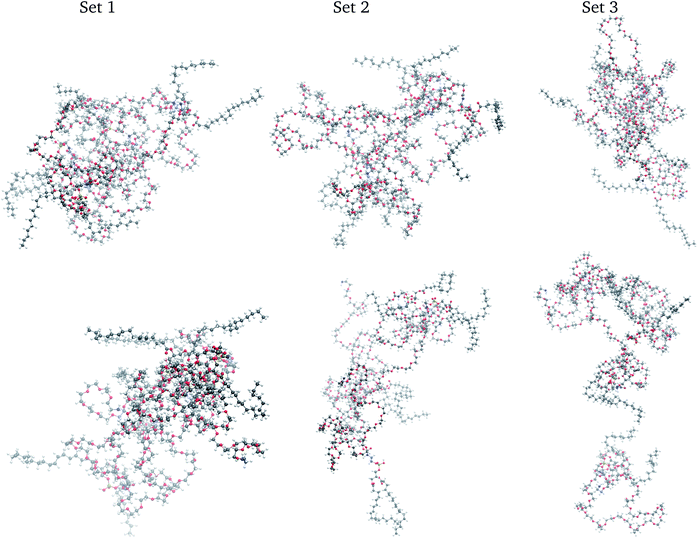 | ||
| Fig. 1 Snapshots of the DSPE–PEG macromolecular aggregate at the beginning (top) and end (bottom) of the NVT MD simulations. Color scheme; C (grey), O (red), H (white), N (blue), and P (yellow). | ||
Following the equilibration process, the three sets underwent 10 ns NVT-MD runs at a temperature of 300 K using the velocity rescale approach.61 Instantaneous geometry of the DSPE–PEG aggregates at the end of these runs are illustrated in Fig. 1. A buffer of the first 5 ns simulation time was not used in the forthcoming ML analyses, while the subsequent 5 ns of trajectories were retained for a total of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations to be analyzed for each set under study. With the saved trajectories, the desired energetics was calculated including the total system potential energy Etotal, the potential energy of the full solvent Esolvent, the four macromolecules intra-potential energy sum PE, the four macromolecule–solvent interaction energies IE, and the macromolecular aggregate cohesive energy Ecoh. Both, IE and Ecoh were sums of the Coulomb and Lennard-Jones terms between solvent atoms and DSPE–PEG atoms for the former and between atoms in different DSPE–PEG macromolecules for the latter. Calculation of the energetics entailed repeated use of the GROMACS rerun utility,56 which involved preparation of separate files with the atomic coordinates of each system subcomponent for which the potential energy required calculation. The Esolvent had fluctuations on the order of 0.03% and its contribution to the Etotal was greater than 99.99%. The system total energy, the solvent energy, and their difference, ΔE = Etotal − Esolvent were considered basically constant for the purpose of the forthcoming RNN learning analysis that focused on the three points energy components entering in ΔE:
000 configurations to be analyzed for each set under study. With the saved trajectories, the desired energetics was calculated including the total system potential energy Etotal, the potential energy of the full solvent Esolvent, the four macromolecules intra-potential energy sum PE, the four macromolecule–solvent interaction energies IE, and the macromolecular aggregate cohesive energy Ecoh. Both, IE and Ecoh were sums of the Coulomb and Lennard-Jones terms between solvent atoms and DSPE–PEG atoms for the former and between atoms in different DSPE–PEG macromolecules for the latter. Calculation of the energetics entailed repeated use of the GROMACS rerun utility,56 which involved preparation of separate files with the atomic coordinates of each system subcomponent for which the potential energy required calculation. The Esolvent had fluctuations on the order of 0.03% and its contribution to the Etotal was greater than 99.99%. The system total energy, the solvent energy, and their difference, ΔE = Etotal − Esolvent were considered basically constant for the purpose of the forthcoming RNN learning analysis that focused on the three points energy components entering in ΔE:
| ΔE = PE + IE + Ecoh | (1) |
The MD simulations provided energy time series with 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points for each energy and set considered. Table 1 lists the series means and standard deviation, evidencing that the PE and IE magnitudes were more than one order of magnitude larger than Ecoh and displayed smaller standard deviations. Hence, the analyses focused primarily on PE and IE.
000 points for each energy and set considered. Table 1 lists the series means and standard deviation, evidencing that the PE and IE magnitudes were more than one order of magnitude larger than Ecoh and displayed smaller standard deviations. Hence, the analyses focused primarily on PE and IE.
| Time (ns) | ΔE (MJ mol−1) | E coh (MJ mol−1) | PE (MJ mol−1) | IE (MJ mol−1) | |
|---|---|---|---|---|---|
| Set 1 | 0–5 | 2.22 ± 0.17 | −0.52 ± 0.08 | 8.97 ± 0.15 | −6.23 ± 0.15 |
| 4–5 | 2.29 ± 0.17 | −0.54 ± 0.06 | 8.98 ± 0.16 | −6.15 ± 0.16 | |
| Set 2 | 0–5 | 2.20 ± 0.17 | −0.47 ± 0.05 | 8.77 ± 0.17 | −6.11 ± 0.16 |
| 4–5 | 2.13 ± 0.18 | −0.46 ± 0.03 | 8.76 ± 0.15 | −6.16 ± 0.14 | |
| Set 3 | 0–5 | 2.28 ± 0.18 | −0.71 ± 0.08 | 9.09 ± 0.16 | −6.10 ± 0.20 |
| 4–5 | 2.31 ± 0.19 | −0.76 ± 0.04 | 9.05 ± 0.15 | −5.98 ± 0.18 |
Two ensembles of time series were created. In ensemble100 each 5 ns time series having 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time points was sampled 10 times with systematic sampling, with the initial ten consecutive time points of the series as starting points and populating the sampled series with points selected after a fixed 100 fs sampling interval. This probability sampling method yielded a manifold of 10 time series, each of them spanning the full 5 ns time series and containing 50
000 time points was sampled 10 times with systematic sampling, with the initial ten consecutive time points of the series as starting points and populating the sampled series with points selected after a fixed 100 fs sampling interval. This probability sampling method yielded a manifold of 10 time series, each of them spanning the full 5 ns time series and containing 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time points separated by 100 fs. In ensemble10, the original series of 500
000 time points separated by 100 fs. In ensemble10, the original series of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time points were segmented into 10 consecutive series, each one of them with a span of 0.5 ns with time intervals of 10 fs.
000 time points were segmented into 10 consecutive series, each one of them with a span of 0.5 ns with time intervals of 10 fs.
In all forthcoming analyses, the data points in each series of the two ensembles were regularized by subtracting the series average to each time point and dividing by the standard deviation.
2.3 Machine learning approach
The purpose of a first machine learning (ML) analysis consisted in identifying groups of time points in the PE and IE energy time series. These patterns served to characterize the data from a machine learning perspective. Clustering is a ML unsupervised learning technique. We employed the expectation maximization (EM)62 clustering algorithm as implemented in scikit-learn,63,64 a Python-based library of machine learning methods. The EM features (or descriptors) used were the ten PE and ten IE time series of ensemble100 for a total of twenty features and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 instances. The clustering process was performed on each of the sets 1–3, independently. The number of retained clusters was based on the inter-cluster variance
000 instances. The clustering process was performed on each of the sets 1–3, independently. The number of retained clusters was based on the inter-cluster variance 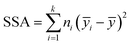 , with ȳi being the mean of clusters with ni points and ȳ the mean of all of the points to be clustered. When SSA reached a plateau value with less than 2% change, we identified six relevant clusters, cluster 0–5. The task yielded six time patters embedded in each time series to be used later within the neural network (NN) analyses. These clusters were considered as distinct themes that could modulate the NN models. Thus, when employing them for the NN training, the task was referred as cluster seeding of the pristine energy series.
, with ȳi being the mean of clusters with ni points and ȳ the mean of all of the points to be clustered. When SSA reached a plateau value with less than 2% change, we identified six relevant clusters, cluster 0–5. The task yielded six time patters embedded in each time series to be used later within the neural network (NN) analyses. These clusters were considered as distinct themes that could modulate the NN models. Thus, when employing them for the NN training, the task was referred as cluster seeding of the pristine energy series.
The purpose of a second ML analysis was based on evaluating the possibility of employing the PE and IE time series for forecasting estimated future values as a diagnostic ML tool. A subfield of ML is deep learning and its foundational methodology of artificial NNs. In particular, RNNs are recognized as a forecasting model for predicting how sequenced data may be cyber-continued without using the technique employed for generating the original sequence. We based our ML in silico experiment on ERNN, LSTM and GRU, three very well established and extensively used RNNs available in a variety of cyber libraries and software frameworks. The RNN functions were implemented as included in the PyTorch 1.7.0 package.12,65 Our computing implementation required multiple scripts that were written in Python 3.6 and are open access available.51
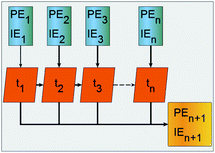
RNNs are a class of NNs that enable previous processed output to be used as input to the next step while keeping hidden states. Fig. 2 is a schematic representation of how a basic recurrent neuron operates. The blue cells are the one step at a time feeds from the PE and IE series points to the network orange cells where an activation process combines the current with previous processed input, gives an approximated output depicted yellow, and simultaneously passes the previously processed feed to the next orange activation cell and to a hidden layer. The process is done one step at a time across the input time window. The neuron activation cells are functions that modulate a weighted mixing of the previously processed step with the pristine input at the next step and are different for the ERNN, LSTM and GRU. The recurrent neurons are organized as belonging to a layer. At each time step a neuron activates an input that is sent to all other neurons in the layer and the compounded activation is propagated one step at a time, simultaneously, by all neurons in the layer.
The RNN hyperparameters were determined after testing a multitude of different alternatives. Taking together the PE and IE time series as input yielded the best results. The time window size was set to 50 consecutive time points for each series. The quality assessment metrics of a NN data model was based on training on a fold containing the input series first 80% points and testing on a second fold containing the remaining 20% points. Hence, each generated NN data model had its own errors. The loss and validation error are the errors incurred on the training and testing regions of the series, respectively. The loss was calculated as the mean squared error MSE between each of the N targeted series points yi and the N corresponding xi NN-approximated points:
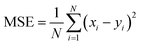 | (2) |
The MSE is minimized with respect to the NN parameters in an iterative manner, each iteration is termed epoch. The root mean squared error is termed RMSE.
Concerning the RNN user-adjustable hyperparameters, neurons (or nodes) and layers refer to the width and depth of the network, respectively. Each layer contains a number of neurons that pass their output to the following layer. Dropout refers to an additional layer where each element has a probability of being set to zero, which improves regularization and prevents co-adaptation of neurons.66 Meanwhile, the regularization factor is a constant applied to weights during training that helps preventing overfitting and the learning rate is the optimizer rate of approaching the minimum. Our optimal RNN hyperparameters for series in ensemble100 were: 300 neurons, one layer, zero% dropout, zero regularization factor, and 10−4 learning rate, visually summarized in Fig. S1 of the ESI.† Learning from the data decreased with more than one layer and with high regularization factor. The number of neurons affected the rate by which the data model approached the minimum error, hence, neurons primarily affected the number of epochs needed for training rather than the ability for the network to learn. The NN data model ability to produce a small loss was more affected by the size and granularity of the training data than by the selection of the hyperparameters. As visually evidenced in Fig. S1,† variation of the hyperparameters yielded averages within the standard deviation of each other, suggesting that the choice of these hyperparameters are relatively inconsequential.
Concerning the forecasting ability of the RNNs,4 we adopted the evaluation on a rolling forecasting origin67 as measure of the short term forecast accuracy. For this process the cross-validation were folds containing the full series minus one point out of the last m points for testing, with m = 1–50 limited by the size of one time window. In fact, the origin at which the forecast was based rolled forward in time when started after the mth point. We considered data models predicting a single time step forward. Hence, for predicting more than one time step the output is appended to the input time window and the oldest time point is dropped. The outcome was a sliding time window that feeds into the next prediction. Consequently, errors in previous predicted values propagated to the subsequent predictions and compounded. In the context of the RNN forecast model terminology, short term forecasts refer to estimates containing the number of points in the time window while long term forecasts relate to any number of points beyond the short term. Short and long term forecasts were done for the two energies, PE and IE. When considering the full series with 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time points, the short term predictions covered only 0.5 ps, while considering series members of the ensemble100 allowed for 5 ps short term forecasting. Challenging the validity of these forecasts, we generated long term forecasts extending from the last time window up to 1 ns forecast by appending the predicted time points to the end of the series as to propagate the sliding input window forward in time, one step at a time. Our goal was to forecast a time lapse of a fifth of the original time series's length. Hence long term forecasts were 1 ns in length. The best model was expected to maintain the lowest error for the longest time, however, along the long term forecasts there were no known data to determine the MSE.
000 time points, the short term predictions covered only 0.5 ps, while considering series members of the ensemble100 allowed for 5 ps short term forecasting. Challenging the validity of these forecasts, we generated long term forecasts extending from the last time window up to 1 ns forecast by appending the predicted time points to the end of the series as to propagate the sliding input window forward in time, one step at a time. Our goal was to forecast a time lapse of a fifth of the original time series's length. Hence long term forecasts were 1 ns in length. The best model was expected to maintain the lowest error for the longest time, however, along the long term forecasts there were no known data to determine the MSE.
3 Results
The 5 ns MD runs generated trajectories along which the energy times series of interest are PE, total intra-macromolecule potential energy, IE, total interaction of the DSPE–PEG aggregate with the solvent, and Ecoh, cohesive energy that keeps together the DSPE–PEG macromolecular aggregate. These series are visualized in Fig. 3 for sets 1, 2, and 3 and open access available.51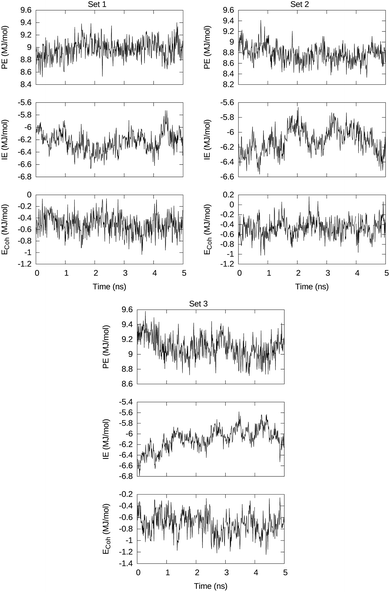 | ||
| Fig. 3 Visualization of the total intra-macromolecule potential energy PE, the total interaction energy between macromolecules and solvent molecules, and the DSPE–PEG cluster cohesive energy Ecoh. | ||
The distribution of the 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points comprising the PE and IE energy series is depicted in Fig. 4. The PE distribution corroborated the expected Gaussian distribution of MD potential energies in equilibrium. Meanwhile, the IE distribution was indicative that there was energy exchange between the solvent and the macromolecular aggregate. Indeed, lower IE corresponded to higher Ecoh and vice versa. Eventually, with enough time, we expected that the aggregate would dissociate into its four macromolecules with Ecoh tending to zero. As is apparent for set 3 in Fig. 1, the snapshot at the end of the time series considered was indicative that the aggregate dissociation might had started.
000 points comprising the PE and IE energy series is depicted in Fig. 4. The PE distribution corroborated the expected Gaussian distribution of MD potential energies in equilibrium. Meanwhile, the IE distribution was indicative that there was energy exchange between the solvent and the macromolecular aggregate. Indeed, lower IE corresponded to higher Ecoh and vice versa. Eventually, with enough time, we expected that the aggregate would dissociate into its four macromolecules with Ecoh tending to zero. As is apparent for set 3 in Fig. 1, the snapshot at the end of the time series considered was indicative that the aggregate dissociation might had started.
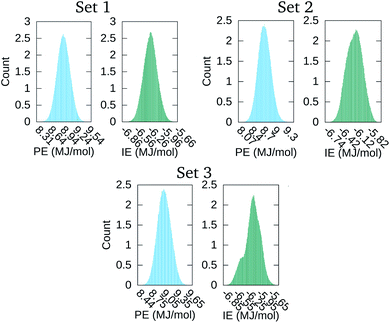 | ||
| Fig. 4 Distribution of the time values in the PE and IE series of Fig. 3. | ||
The split of the two energy properties PE and IE into six EM data clusters for the ensemble100 evidenced that the ten series members of the ensemble of each energy type behave very similar to one another. In addition, the clustering outlook of the three studied sets was comparable. The data distribution associated to each of the ten member series of the ensemble was even and unimodal as shown in Fig. 5 for set 1. It is evident that the IE data were most influential in producing the clustering since the PE datasets displayed only a gentle increase in value over the six data clusters. In addition, the violin plots feature a very similar density estimation of the underlying distribution for the ten participating time series in ensemble100. Table S1 of the ESI† provides the percentage of time points in each cluster, the energetics average values and standard deviations. The macromolecular aggregate radius of gyration Rg in set 2 was slightly larger than in the other two sets, peculiarity that persisted in the split datasets generated by the EM clustering process.
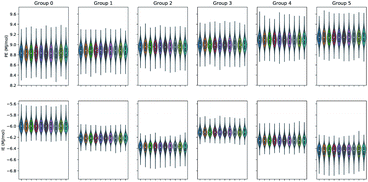 | ||
| Fig. 5 PE and IE violin plots of the ensemble100 series clustered with EM into six data clusters for set 1. | ||
Concerning the generation of data models from the three RNN architectures, Fig. 6 illustrates the training loss and testing validation error resulting for time series in ensemble10 (left) and ensemble100 (right). The time series in both ensembles have equal number of points. However, the training loss is significantly higher when the interval between time points is larger, as occurs in ensemble100. The figure also evidenced that for the two ensembles the GRU architecture achieved the lowest loss at the end of training in all cases. The ERNN was the most sensitive to the training process in the early epochs, containing the widest range of error. The speed at which the networks converge to a minimum error relates to the complexity of the neuron. ERNN neurons containing a single activation function reach the minimum relatively quickly, although this RNN is the least descriptive of the data as evidenced by its comparatively poor validation performance. The most complex neuron, LSTM, displays the slowest training process from among the three architectures, outperforming ERNN, and achieving comparable results than GRU. We concluded that for our system the GRU model outperformed the other two NNs, evidenced by the lowest validation error shown in Fig. 6. The statistical distribution of the time points in the PE and IE series composing the ensemble10 is shown in the ESI Fig. S2 (top)† and compared with the corresponding distributions obtained from the GRU models shown in Fig S3 (top).† Comparison between original series and GRU approximated series for ensemble100 is given in Fig S4 (top) and S5 (top).† Consistent with the smaller loss and validation error, the agreement between the underlying distribution of time points in the original series and in the GRU approximated values is better for ensemble10 than for ensemble100 since the time interval between points is ten times smaller in the former. Building an ensemble with 100 series of 1 ps granularity, increased the loss by a factor of six when compared to ensemble10, which was too high for the application under study.
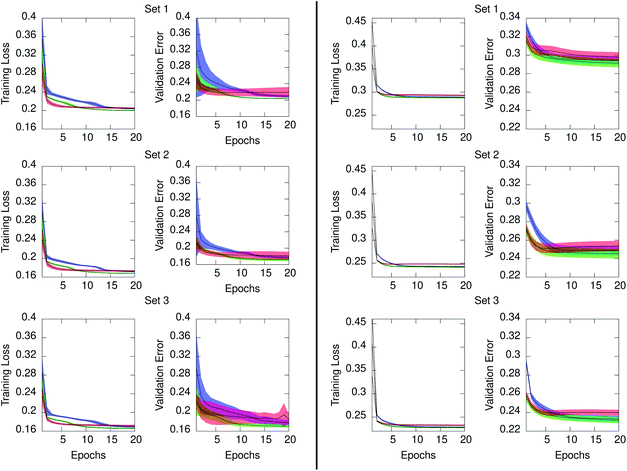 | ||
| Fig. 6 Mean training loss and testing validation error for the approximated series generated from the ERNN (red), LSTM (blue), and GRU (green) data models. Series in ensemble10 (left) and ensemble100 (right). Shaded regions denote ±one standard deviation from the mean. Loss and validation errors are the MSE of eqn (2) pertaining to the training and testing regions of each series in the ensemble, respectively. Values are provided for the regularized data as described in Section 2.2. | ||
Additionally we analyzed the distribution of first neighbor intervals between points in the series, ΔPE = PEtn+1 − PEtn and ΔIE = IEtn+1 − IEtn, using the generated GRU models. Fig. S2 (bottom) and S3 (bottom) in the ESI† show the statistical distribution of these time differences for ensemble10 while the bottom part of ESI Fig. S4 and S5† show the corresponding distributions for ensemble100. The GRU-based distributions are consistently on the order of 50–70% more compressed that the original distributions. The trend was similar for the two ensembles, although in ensemble100 the ΔPE distribution from the GRU models is almost 80% narrower. This effect will impact the type of forecasts that the GRU models give rise to.
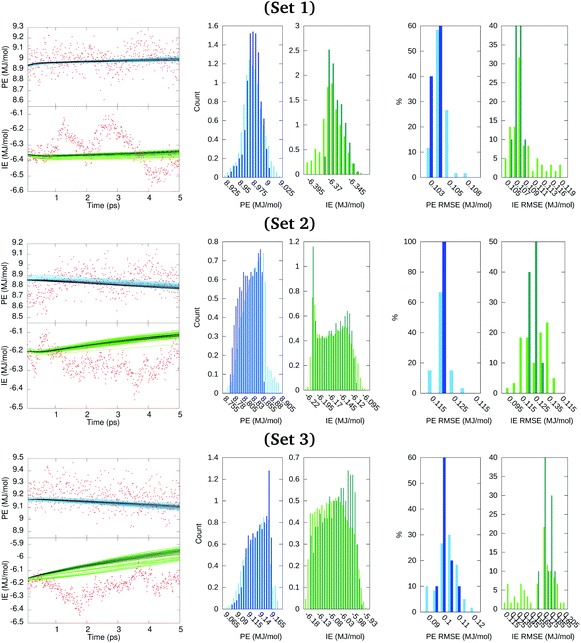
Results described in the forthcoming paragraphs on the GRU forecasts constituted our best output scenario. Other scenarios considered are listed in Section S5 of the ESI.† We generated ten GRU models for the ensemble100 series considering 4.995 ns of the PE and IE time series as the training data and using the last 0.005 ns for starting short terms forecasts and yet having time points to evaluate the error incurred. Then, each model propagated its prediction along 50 iterations that spanned 0.005 ns. Moreover, for each member of ensemble100, six additional GRU models were generated in which the clustered PE and IE series obtained before were added to the model training for a total of 4 participating series. This task produced a set of sixty additional cluster-seeded models for which a forecast over 0.005 ns was also obtained. This process was repeated for data in sets 1, 2, and 3. Results from these short term forecasts are illustrated in Fig. 7, where dark and light colored points identify the GRU model forecasts without and with cluster-seeded input, respectively. The RMSE of each of the 70 model predictions spanned from about 0.1 MJ mol−1 for the cluster-unseeded model predictions to almost 0.2 MJ mol−1 for the cluster-seeded models, as seen from the histograms of RMSE in Fig. 7. This figure also depicts the distribution of predicted points from the 70 inspected models clearly indicating that the GRU-predicted time series distributions from the cluster-seeded models approximated fairly the PE distribution shape of the original series of Fig. 4 with a maximum–minimum spread of about half the standard deviation reported in Table 1. Meanwhile, resemblance between original and GRU-forecasted IE distributions fades dramatically in shape and spread.
We had set a 1 ns period as a desirable time span for the long term energetics forecast. Thus, the long term forecasting ability of the GRU data models created from the 70 series in ensemble100 was also explored. The GRU data models trained on 4.995 ns for the short time forecasting obtained previously, without and with cluster-seeding, were reutilized as initial models for the forecast of predicting the 1 ns future behavior of PE and IE time series. The last time window of each series in the ensemble was used to define different initial times for the long term forecasts.
Fig. 8 depicts the forecast of PE in blue and IE in green along the targeted time span of 1 ns into the future. Dark-colored and light-colored dots in the figure identify predictions without and with cluster-seeded models and the shaded area illustrates the maximum–minimum dispersion of predictions coming from the 70 models and the 50 initial steps for the forecast. In a nutshell, the future predicted values tend to gather around specific energy regions maintaining a fairly constant spread around them.
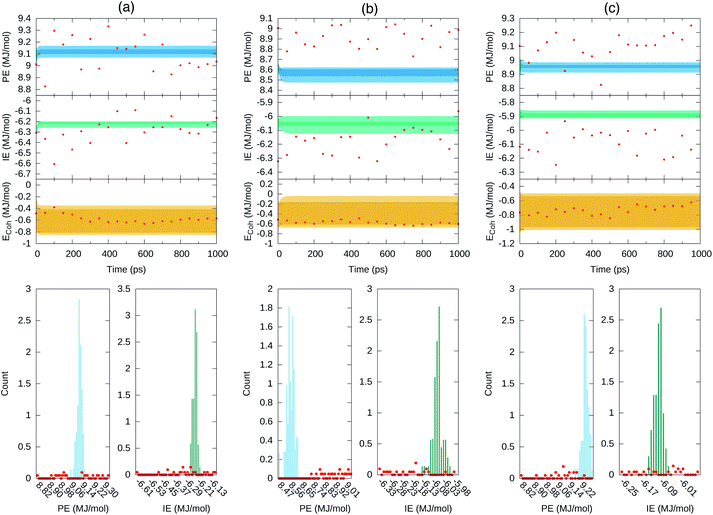 | ||
Fig. 8 Forecast prediction of PE and IE for a time span of 1 ns for series in ensemble100 (top) and the distribution of predicted PE and IE values (bottom). The Ecoh is estimated from the forecasted energetics, eqn (1), and ΔE mean during the 4–5 ns MD trajectory time reported in Table 1. (a) Set 1, (b) set 2 and (c) set 3. The dark shaded region denotes forecasted energies from GRU models without cluster-seeding. Light shaded area denotes forecast energies from GRU models with cluster-seeding. Normalization of the histograms is with respect to 70 × 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 evaluated time points. Red dots are true energies from a posterior MD simulation for each set. 000 evaluated time points. Red dots are true energies from a posterior MD simulation for each set. | ||
At this point we went back and continued the three simulations for 1 ns saving configurations every 0.05 ns, which are depicted as red points in Fig. 8. We assess that the GRU forecast models predict the energetics behavior on average and do not generate temporal fluctuations typical of MD simulations. Averages of the 70 predicted forecasts along 1 ns were 9.13, 8.57, 8.95 MJ mol−1 for PE and −6.23, −6.05, −5.88 MJ mol−1 for IE of set 1, 2, 3, respectively. These averages are 0.1–0.2 MJ mol−1 either larger or smaller than the actual mean over the last 1 ns of Table 1. One forecast from the RNN data model trained on the full series of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 points yielded similar energetics, a converged value steered by the last portion of the series and sustaining a needle-like distribution of energy values. Summarizing, the GRU data models yielded energetics forecasts with series displaying a distribution of points that agglomerated close to the mean with an overall spread smaller than the standard deviations reported in Table 1. The short and long term energetics forecasts of Fig. 7 and 8 are confined to narrow bands, markedly different from the expected potential energies fluctuations. The forecast model does not maintain the underlying distribution of series points. Indeed, the studied energies are Gaussian-distributed or superposition of Gaussian functions as expected for systems in thermodynamic equilibrium and evidenced in Fig. 4; this statistical property appears to be lost even by building the ensemble of forecasts as visualized in the middle panels of Fig. 8.
000 points yielded similar energetics, a converged value steered by the last portion of the series and sustaining a needle-like distribution of energy values. Summarizing, the GRU data models yielded energetics forecasts with series displaying a distribution of points that agglomerated close to the mean with an overall spread smaller than the standard deviations reported in Table 1. The short and long term energetics forecasts of Fig. 7 and 8 are confined to narrow bands, markedly different from the expected potential energies fluctuations. The forecast model does not maintain the underlying distribution of series points. Indeed, the studied energies are Gaussian-distributed or superposition of Gaussian functions as expected for systems in thermodynamic equilibrium and evidenced in Fig. 4; this statistical property appears to be lost even by building the ensemble of forecasts as visualized in the middle panels of Fig. 8.
4 Discussion
Our results showed that the ensemble10 and ensemble100 RNN data models reproduced very well the original energy series and the statistical distributions of their points with a small loss as shown in Fig. 6 and S2 through S5 of the ESI.† Regarding the ten GRU forecast models obtained from ensemble100, the outcome was instrumental in providing a band of forecasted energetics encompassing the mean and spread of the fed energy series. However, in the very early forecasted times each series forecast had the distinct peculiarity of converging toward a particular value that depended on the time points close to the end of the series employed during training/testing. Thereafter, the forecast model kept the converged value as constant along the remaining forecasting time with a needle-like distribution of energy values. Hence, a compendium of the ten forecast needle-like distributions resulted in an atypical underlying distribution if compared to the thermodynamics fluctuations characteristic of the MD energetics. Relatively, the short term forecast RMSEs were very similar between PE and IE as shown in Fig. 7. We have proven that the time series granularity was crucial for decreasing the loss on the RNN data models, yielding a 30% loss decrease by reducing the granularity by a factor of ten, as seen in Fig. 6. However, reducing the series granularity did not affect the GRU forecasts with underlying needle-like distribution of points.Given that forecasted energetics retained strongly the character acquired in their corresponding short term forecasts, we devised the PE and IE seeding mechanism by including the ML selected time patters obtained from the EM clustering shown in Fig. 5. Thus, the seeded RNN data models were trained/tested on four time series, PE, IE, plus the duo of their patterns corresponding to each of the six EM clusters. In turn, the ensemble100 population did increase to contain 70 series. Based on the enhanced ensemble the energetics forecast added complexity, enabling a band of predicted energy values with a maximum–minimum spread of about the standard deviation of the actual MD calculated energies as evidenced in Figs. 7 and 8. Using the finalized ML protocol, we demonstrated that the temporal behavior of the Ecoh energy derived from the PE and IE forecast values constituted a reasonable estimate of the DSPE–PEG aggregate solvation fate along 1 ns within a 95% confidence interval from the MD values, as evidenced in Fig. 8. The macromolecular aggregate Ecoh kept weak, displaying a band spread of the same order than the MD standard deviation for the three sets investigated.
Polymers have a slow dynamics as evidenced by the PE and IE time autocorrelation functions depicted in Fig. S6 of the ESI.† These time autocorrelation functions manifested that the correlation time of the IE is on the order of 1 ns, indicative that the system memory persist over the time span of the attempted forecasts in what concerns how the solvent affected the macromolecular aggregate. On the other hand, the relatively short correlation time of a few picoseconds of the PE was typical of the molecular internal vibrational modes. It is disappointing that GRU model forecast predicted narrowly confined fluctuations for the PE and IE time series, whereas these energies possess distinct and different correlation times and, when considered together, these energy series have proven optimal in building the GRU data model with the lowest error. A measure of the RNN forecast model uncertainty is volatile when the truth is unknown. Pertaining to the macromolecular aggregate solvation fate, we performed several predictions based on forecasts from RNN data models with different random activation weights and asserted that the forecasts were very similar. Such uncertainty measure became rapidly computationally expensive and demanded human participation. Furthermore, uncertainties are particular to the system under study. There is no expectation that by changing a few parameters the RNN forecast model for this liquid solution will be transferable to other molecular systems undergoing solvation. What prevails is the in silico experiment protocol, the roadmap, to build it, and the milestones to overcome. Our work showed that one RNNs forecast alone did not handle effectively the fluctuations associated with thermodynamic energy properties in equilibrium. Nonetheless, an ensemble of RNN forecasts render a useful estimate of future energetics.
There are challenges unique to polymers related to the structure of self-assembled aggregates in solution. For example, two order parameters popular for polymers are Z, orientational, and S, vector alignment, order parameters.68 For DSPE–PEG along the MD simulation, either when self-assembled into an aggregate or solvated, Z fluctuates around zero characterizing the random coil polymer conformation where the distribution of angles formed between consecutive bonds along the polymer backbone is random. The S order parameter along the simulation was instrumental in determining that the aggregate rotated, but the alignment between the macromolecules remained null along the simulation. The structural characteristics of the aggregate are not good candidate functions for solvation. Solvation of a polymer aggregate occurs when the four polymer chains dissociate away from the aggregate and each independent polymer remains a random coil signifying maximum interaction with the solvent and maximum exposure to the solvent. Within the DSPE–PEG aggregate each polymer was a random coil as depicted in Fig. 1. A polymer random coil does not have a fixed geometry or state prone to be catalogued as native state as occurs in proteins. The solvent is the culprit in solvation of a solute. In addition, in the liquid solution investigated here there is no formation of hydrogen bonds between solvent and polymer–lipid macromolecules, which in other solutions may steer a preferred conformation.
5 Conclusions
This work focused on developing an automatable protocol to implement the forecast model of RNNs to a nanoscale system. The prototype forecasting protocol was applied to the solution of ethyl acetate containing a self-assembled aggregate of four DSPE–PEG macromolecules. Data models from ERNN, LSTM, and GRU were trained and tested on the energetics time series obtained from molecular dynamics in the nanosecond regime. This complex system had 225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 atoms, and the analyzed energetics were series with half a million time points. The main goal was to obtain forecasts that would estimate energetics that otherwise required 106 MD time steps. The targeted energetics of the DSPE–PEG aggregate in solution included the sum of intra-macromolecules potential energy and the macromolecules–solvent interaction energy. The resulting RNN data models were extensively trained and tested evidencing 1% errors, hence, ensuring that the original time series and the underlying distribution of time points were reproduced satisfactorily. We demonstrated that for the system studied here, an isolated energetics forecast predicted well the mean energies in the short term. Nonetheless, the forecast model maintained the converged energy value from the short term into the long term forecast. Indeed, a single forecast consisted of points with a very narrow spread, resembling a delta function.
808 atoms, and the analyzed energetics were series with half a million time points. The main goal was to obtain forecasts that would estimate energetics that otherwise required 106 MD time steps. The targeted energetics of the DSPE–PEG aggregate in solution included the sum of intra-macromolecules potential energy and the macromolecules–solvent interaction energy. The resulting RNN data models were extensively trained and tested evidencing 1% errors, hence, ensuring that the original time series and the underlying distribution of time points were reproduced satisfactorily. We demonstrated that for the system studied here, an isolated energetics forecast predicted well the mean energies in the short term. Nonetheless, the forecast model maintained the converged energy value from the short term into the long term forecast. Indeed, a single forecast consisted of points with a very narrow spread, resembling a delta function.
To alleviate the RNN forecast model difficulty of developing a distribution of time points with a broader spread, a machine learning protocol was set forth encompassing two strategies. The first strategy consisted in sampling an ensemble of time series with larger granularity than the original ones that covered the original series time span. An ensemble of RNN data models was generated from the sampled series. The second strategy consisted in identifying a group of time patterns from the original time series based on machine learning clustering and enhancing each RNN data model in the ensemble series with one of these patterns, which augmented the ensemble size. The combination these strategies yielded an ensemble of 70 time series of each of the two desired energies with which independent RNN data models were generated, all of them yielding a small loss. These RNN data models produced an ensemble of forecasts spanning a band of predicted energetics with a spread of half the standard deviation of the original series. For example, the estimate of the macromolecular aggregate fate during the forecasted time span was correct when compared to actual molecular dynamics extra runs, even if the actual fluctuations were not capture in detail. We demonstrated that the aggregate cohesive energy calculated from the two forecasted energies yielded an excellent estimate, predicting that the macromolecular aggregate persisted associated during the time span of the forecast. By using time series of system energies, rather than the time series of atomic positions, we demonstrated the feasibility of generating RNN forecasts of the temporal energetics of a nanoscale polymer–lipid aggregate in solution with a molecular non-polar solvent.
Our RNN forecast protocol is scalable and automatable. In building the protocol, we demonstrate with an in silico solvation experiment that for systems at the nano temporal and spatial scales the RNN forecast model requires consideration of ensembles of forecasts to become a proficient tool that provides estimates of future events as diagnoses helpful for decision making along the analysis of complex systems. The protocol will find application for cyber monitoring solute solvation or self-assembly formations in solution such as micelles and liposomes and other mechanisms of polymers and solution dynamics such as determination of the solvation boundaries LCST and UCST, since miscibility enters in multiple industrial and academic applications.
Data availability
The DSPE–PEG and EA topology files, the .gro file with a geometry of DSPE–PEG, files of the time series depicted in Fig. 3, and multiple scripts for the MD and ML are available open access at the Zenodo archive.51 Software packages used in this study12,49,56,59,63 are open source.Author contributions
Conceptualization, methodology, investigation, validation, JA, OG and EBB.; software, analysis, data curation, writing original draft, JA and EBB; writing review & editing, EBB; supervision, project administration, funding acquisition, OG and EBB. All authors have agreed to the published version of the manuscript.Conflicts of interest
Authors have no conflicts to declare.Acknowledgements
Acknowledgment of partial support by the Commonwealth of Virginia, USA, is extended for the 4-VA 2018-2021 grants. Computations were done in the supercomputer facility of the Office for Research Computing, George Mason University, USA.References
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger and K.-R. Müller, et al. , Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS PubMed.
- L. Zdeborová, Nat. Phys., 2017, 13, 420–421 Search PubMed.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld and N. Tishby, et al. , Rev. Mod. Phys., 2019, 91, 045002 CrossRef CAS.
- K. Greff, R. K. Srivastava, J. Koutník, B. R. Steunebrink and J. Schmidhuber, IEEE Trans. Neural Netw. Learn. Syst., 2017, 28, 2222–2232 Search PubMed.
- S. Weidman, Deep Learning from Scratch, O'Reilly, 2019 Search PubMed.
- Z. Lipton, J. Berkowitz and C. Elkan, 2015, ArXiv preprint, arXiv:1506.00019v4.
- A. Sherstinsky, Phys. D, 2020, 404, 132306 CrossRef.
- J. L. Elman, Cognit. Sci., 1990, 14, 179–211 CrossRef.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS PubMed.
- K. Cho, B. van Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, et al., 2014, ArXiv preprint, arXiv:1406.1078.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, 2014, ArXiv preprint, arXiv:1412.3555.
- PyTorch from research to production, 2019–2021, https://pytorch.org/, accessed February 22, 2021 Search PubMed.
- A. Argun, T. Thalheim, S. Bo, F. Cichos and G. Volpe, Appl. Phys. Rev., 2020, 7, 041404 CAS.
- G. Chen, Comput. Mech., 2021, 67, 1009–1019 CrossRef.
- M. Awale, F. Sirockin, N. Stiefl and J.-L. Reymond, J. Chem. Inf. Model., 2019, 59, 1347–1356 CrossRef CAS PubMed.
- E. Pfeiffenberger and P. A. Bates, PLoS One, 2018, 13, e0202652 CrossRef PubMed.
- K. Yang, Y. Cao, Y. Zhang, S. Fan, M. Tang and D. Aberg, et al. , Patterns, 2021, 2, 100243 CrossRef PubMed.
- T. Grear, C. Avery, J. Patterson and D. J. Jacobs, Sci. Rep., 2021, 11, 4247 CrossRef CAS PubMed.
- C. Han, P. Zhang, D. Bluestein, G. Cong and Y. Deng, J. Comput. Phys., 2021, 427, 110053 CrossRef.
- J. Huang, G. Huang and S. Li, ChemPhysChem, 2022, 23, 42–49 Search PubMed.
- D. Liang, M. Song, Z. Niu, P. Zhang, M. Rafailovich and Y. Deng, MRS Adv., 2021, 6, 362–367 CrossRef CAS PubMed.
- W.-X. Zhang, X. Pan and H.-B. Shen, J. Chem. Inf. Model., 2020, 60, 3679–3686 CrossRef CAS PubMed.
- J. Wang, C. Li, S. Shin and H. Qi, J. Phys. Chem. C, 2020, 124, 14838–14846 CrossRef CAS.
- M. J. Eslamibidgoli, M. Mokhtari and M. H. Eikerling, 2019, ArXiv preprint, arXiv:1909.10124.
- C. Wang, Z. Wang and X. Zhang, Acc. Chem. Res., 2012, 45, 608–618 CrossRef CAS PubMed.
- C. Salvador-Morales, B. Brahmbhatt, V. Márquez-Miranda, I. Araya-Duran, J. Canan and F. Gonzalez-Nilo, et al. , Langmuir, 2016, 32, 7929–7942 CrossRef CAS PubMed.
- A. A. D'souza and R. Shegokar, Expert Opin. Drug Delivery, 2016, 13, 1257–1275 CrossRef PubMed.
- R. Takayama, Y. Inoue, I. Murata and I. Kanamoto, Colloids Interfaces, 2020, 4, 28 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 3rd edn, 2011, ch. 20 Search PubMed.
- M. Johnsson, P. Hansson and K. Edwards, J. Phys. Chem. B, 2001, 105, 8420–8430 CrossRef CAS.
- J. Munshi, W. Chen, T. Chien and G. Balasubramanian, J. Chem. Inf. Model., 2021, 61, 134–142 CrossRef CAS PubMed.
- M. Werner, Y. Guo and V. A. Baulin, npj Comput. Mater., 2020, 72, 1–8 Search PubMed.
- A. L. Nazarova, L. Yang, K. Liu, A. Mishra, R. K. Kalia and K.-i. Nomura, et al. , J. Chem. Inf. Model., 2021, 61, 2175–2186 CrossRef CAS PubMed.
- D. Perez, R. Huang and A. F. Voter, J. Mater. Res., 2018, 33, 813–822 CrossRef CAS.
- H. Sidky, W. Chen and A. L. Ferguson, Chem. Sci., 2020, 11, 9459 RSC.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365, eaaw1147 CrossRef PubMed.
- J. Andrews and E. Blaisten-Barojas, J. Phys. Chem. B, 2022, 126, 1598–1608 CrossRef CAS PubMed.
- A. Barton, Handbook of Solubility Parameters end Other Cohesion Parameters, CRC Press, Inc., Boca Raton, Florida, 1983 Search PubMed.
- J. Andrews and E. Blaisten-Barojas, J. Phys. Chem. B, 2019, 123, 10233–10244 CrossRef CAS PubMed.
- D. Sponseller and E. Blaisten-Barojas, J. Phys. Chem. B, 2021, 125, 12892–12901 CrossRef CAS PubMed.
- L. Zhang, J. M. Chan, F. X. Gu, J.-W. Rhee, A. Z. Wang and A. F. Radovic-Moreno, et al. , ACS Nano, 2008, 2, 1696–1702 CrossRef CAS PubMed.
- L. Vukovic, F. A. Khatib, S. P. Drake, A. Madriaga, K. S. Brandenburg and P. Král, et al. , J. Am. Chem. Soc., 2011, 133, 13481–13488 CrossRef CAS PubMed.
- R. J. Bose, S.-H. Lee and H. Park, Biomater. Res., 2016, 20, 34 CrossRef PubMed.
- J. Ghitman, E. I. Biru, R. Stan and H. Iovu, Mater. Des., 2020, 108805 CrossRef CAS.
- S. Bochicchio, G. Lamberti and A. A. Barba, Pharmaceutics, 2021, 13, 198 CrossRef CAS PubMed.
- C. E. Astete and C. M. Sabliov, J. Biomater. Sci., Polym. Ed., 2006, 17, 247–289 CrossRef CAS PubMed.
- A. Kumari, S. K. Yadav and S. C. Yadav, Colloids Surf., B, 2010, 75, 1–18 CrossRef CAS PubMed.
- J. Wang, R. Wolf, J. Caldwell, P. Kollman and D. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- Amber18 and AmberTools18 reference manual, 2018, https://ambermd.org/doc12/Amber18.pdf, accessed February 22, 2021 Search PubMed.
- C. J. Dickson, B. D. Madej, Å. A. Skjevik, R. M. Betz, K. Teigen and I. R. Gould, et al. , J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef CAS PubMed.
- J. Andrews, O. Gkountouna and E. Blaisten-Barojas, Forecasting molecular dynamics simulation of polymer-Lipids in solution with RNNs, 2022, DOI:10.5281/zenodo.6503359, accessed May 1, 2022.
- M. Gilbert, in States of aggregation in polymers, ed. M. Gilbert, Elsevier, 8th edn, 2017, ch. 3, pp. 39–57 Search PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nosé and M. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- H. Berendsen, J. Postma, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- Welcome to the GROMACS documentation, 2018–2020, https://manual.gromacs.org/documentation/2020/index.html, accessed February 22, 2021 Search PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Eargle, D. Wright and Z. Luthey-Schulten, Bioinformatics, 2006, 22, 504–506 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- A. P. Dempster, N. M. Laird and D. B. Rubin, J. Roy. Stat. Soc. B Stat. Methodol., 1977, 39, 1–38 Search PubMed.
- sckit-learn: Machine Learning in Python, 2021, https://scikit-learn.org/stable/, accessed February 22, 2021 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, et al., in PyTorch: An imperative style, high-performance deep learning library, ed. H. Wallach, et al., Curran Associates, Inc., 2019, vol. 32, pp. 8024–8035 Search PubMed.
- G. E. Hinton, N. Srivastava, A. Krizhevsky, I. Sutskever and R. R. Salakhutdinov, 2012, ArXiv preprint, arXiv:1207.0580.
- L. J. Tashman, Int. J. Forecast., 2000, 16, 437–450 CrossRef.
- Y. Dai and E. Blaisten-Barojas, J. Chem. Phys., 2010, 133, 034905 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting figures and tables on the machine learning parameters and statistics of energy time series. See https://doi.org/10.1039/d2sc01216b |
| This journal is © The Royal Society of Chemistry 2022 |