Open Access Article
Open Access ArticleThe (not so) simple prediction of enantioselectivity – a pipeline for high-fidelity computations†
Rubén
Laplaza‡
ab,
Jan-Grimo
Sobez‡
cd,
Matthew D.
Wodrich
 ab,
Markus
Reiher
ab,
Markus
Reiher
 *cd and
Clémence
Corminboeuf
*cd and
Clémence
Corminboeuf
 *ab
*ab
aLaboratory for Computational Molecular Design (LCMD), Institute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch
bNational Center for Competence in Research-Catalysis (NCCR-Catalysis), École Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
cLaboratorium für Physikalische Chemie, ETH Zürich, Vladimir-Prelog-Weg 2, 8093 Zürich, Switzerland. E-mail: markus.reiher@phys.chem.ethz.ch
dNational Center for Competence in Research-Catalysis (NCCR-Catalysis), ETH Zürich, Vladimir-Prelog-Weg 1-5/10, 8093 Zürich, Switzerland
First published on 18th May 2022
Abstract
The computation of reaction selectivity represents an appealing complementary route to experimental studies and a powerful means to refine catalyst design strategies. Accurately establishing the selectivity of reactions facilitated by molecular catalysts, however, remains a challenging task for computational chemistry. The small free energy differences that lead to large variations in the enantiomeric ratio (er) represent particularly tricky quantities to predict with sufficient accuracy to be helpful for prioritizing experiments. Further complicating this problem is the fact that standard approaches typically consider only one or a handful of conformers identified through human intuition as pars pro toto of the conformational space. Obviously, this assumption can potentially lead to dramatic failures should key energetic low-lying structures be missed. Here, we introduce a multi-level computational pipeline leveraging the graph-based Molassembler library to construct an ensemble of molecular catalysts. The manipulation and interpretation of molecules as graphs provides a powerful and direct route to tailored functionalization and conformer generation that facilitates high-throughput mechanistic investigations of chemical reactions. The capabilities of this approach are validated by examining a Rh(III) catalyzed asymmetric C–H activation reaction and assessing the limitations associated with the underlying ligand design model. Specifically, the presence of remarkably flexible chiral Cp ligands, which induce the experimentally observed high level of selectivity, present a rich configurational landscape where multiple unexpected conformations contribute to the reported enantiomeric ratios (er). Using Molassembler, we show that considering about 20 transition state conformations per catalysts, which are generated with little human intervention and are not tied to “back-of-the-envelope” models, accurately reproduces experimental er values with limited computational expense.
1 Introduction
Computational modeling of catalytic processes, often achieved through the creation of free energy profiles based on density functional theory computations, can provide key information about viable mechanistic pathways.1–5 First-principles calculations are not only used to rationalize experimental results, but also to optimize the activity/selectivity of a desired chemical transformation through catalyst design.6–10 In this regard, experimental strategies involve the judicious placement of functional groups possessing tuned stereoelectronic and steric elements with the aim of inducing high enantioselectivity. Generally, the ideal location of functionalization, as well as the steric/electronic nature of newly appended functional groups, is discerned through a combinatorial-like optimization process where those elements resulting in higher enantioselectivity are retained until a desired enantiomeric ratio (er) is achieved. Obviously, the laboratory-based testing and optimization of potential catalysts is resource and time intensive and even the most conceptually elegant “back-of-the-envelope” catalyst design strategies may fail in practice. On the other hand, the computational validation of design strategies represents an appealing complementary route to experimental testing, where the selectivity of novel conceptual designs can rapidly be assessed in silico.Because the design of enantioselective catalysts often involves blocking access of a substrate to a reaction center from a non-desired orientation, large ligands are employed. Computationally, this represents a challenging situation, as these systems possess vast and complex conformational landscapes. Since er values vary dramatically based on very small free energy differences, it is critically important that any computational analysis systematically identifies the most stable of these structures, such that reliable er values can be obtained and the overarching catalyst design model validated or rejected. Generally, this “conformational problem” is treated using one of two diametrically opposed approaches, either by ignoring conformational flexibility altogether and applying chemical intuition to select the presumed “most reasonable” conformation pars pro toto or by comprehensive explorations of the conformational landscape using (ab initio) molecular dynamics coupled with enhanced sampling techniques (e.g., metadynamics with suitable collective variables).11 The latter fully accounts for the conformational flexibility of the catalyst but comes with a great computational cost, while the former can lead to completely erroneous results if human intuition fails to reliably identify the most important conformations.
While rotamer libraries12,13 and inexpensive potentials13–18 combined with sampling techniques (e.g., molecular dynamics or Monte Carlo simulations) facilitate the generation of conformational ensembles of ligands,19 substrates,13,20 or organocatalysts,15 the important functionalization process of catalyst design represents an additional computational hurdle. As such, numerous research groups have created computer programs that modifying catalyst structures through functionalization,21,22 including molSimplify23 and AARON,24,25 as well as evolutionary algorithms.26–30 Some of these also include additional functionalities that allow for basic conformational searching, but they continue to rely on sets of predefined conformers and are therefore subject to the same caveats previously mentioned. Because functionalization can open or close different regions of conformational space, using predefined conformations taken from parent catalysts may cause structurally distinct yet energetically meaningful conformers to be missed.
Given the conceptual and technical limitations discussed above, a clear need exists for an alternative approach that simultaneously merges comprehensive conformational searching with functionalization, such that chemical structures possessing enhanced flexibility can be easily manipulated without relying upon either molecular dynamic simulations or fixed rigid fragments. Such a tailored approach to automatically construct functionalized conformers would benefit from a graph-based treatment of chemical structure, which would allow even complex structural modifications to be undertaken easily. Here, we introduce a computational pipeline utilizing the graph-based (i.e., where molecular structures are interpreted as mathematical graphs where atoms are represented by nodes and bonds by edges) Molassembler library,31 a recently developed molecular construction and manipulation tool that couples automated functionalization with conformer generation on the fly to predict reaction enantioselectivity. We then demonstrate how the results of this pipeline can be used to further refine “back-of-the-envelope” catalyst design models.§
In the following sections, we describe our “design-and-sample” approach and its application to the asymmetric C–H functionalization of benzohydroxamates by chiral cyclopentadienyl Rh(III) catalysts.
2 Methodology
Before describing the computational methodology that forms the basis of our design-and-sample pipeline, we first introduce our selected catalyst target space that is used to demonstrate the capabilities of our method.2.1 The catalyst target space
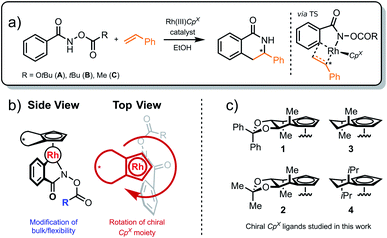
Chiral Cp ligands32 form highly stable η5 haptic complexes with metal centers and have been used as a route to achieve highly enantioselective reactions.33–39 Cramer and co-workers have invoked a “back-of-the-envelope” design model (Fig. 1) to explain these enantioselective transformations, where the achiral ligand components form back- and side-walls that direct an incoming substrate to react at a specific face of the catalyst.33,39 Broadly speaking, this class of ligands is amenable to a myriad of chemical modifications, which potentially affect reactivity and selectivity across a broad range of chemical reactions. Indeed, the developers of the model have even called for “computationally-derived design principles” in order to identify the most selective ligands for a desired chemical transformation. Clearly, computational ligand design of this type will require structural modifications to the catalyst by functionalization as well as the associated exploration and identification of the low-energy conformers that dictate the reaction enantioselectivity. Specifically, the nearly free rotation of the Cp-M haptic bond in solution,40 in addition to the flexible nature of other ligand components, implies that no single predefined conformation can be considered as dominant. As such, these systems represent an ideal computational playground to test our new theoretical procedure while retaining important experimental relevance.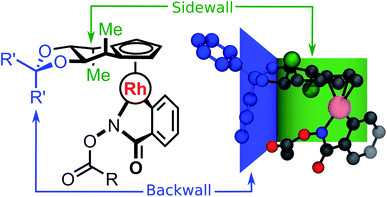 | ||
| Fig. 1 Schematic (left) and ball and stick (right) representation of the stereochemical model for catalyst 1C (R = Me, R′ = Ph), with the backwall and sidewall components highlighted. | ||
As a demonstration of the potential of our approach, we investigate the asymmetric C–H functionalization of benzohydroxamates to form dihydroisoquinolones catalyzed by chiral cyclopentadienyl (Cp) Rh(III) catalysts (Scheme 1a). Notably, the aforementioned high degree of rotational flexibility of the Cp moiety (as illustrated in red, Scheme 1b) along with the different size and flexibility of the hydroxamate substrate (blue, Scheme 1b) is known to strongly influence the experimentally observed enantiomeric ratio (er).33 Our results demonstrate the ability of our methodology to reproduce experimental er values by the automated location of mechanistic and conformational information that likely would be missed in a manual mechanism elucidation and design study relying on human input.
2.2 The Molassembler library
Molassembler31 is a graph-based software that provides algorithms for the construction of molecules containing any element of the periodic table. Most importantly, Molassembler can handle mono- and poly-nuclear transition metal complexes. In its molecular model, structural information is encoded as a graph. Conformers are generated with full stereoisomer control by four spatial dimensional Distance Geometry. Stereocenter configurations are extracted from Cartesian coordinates; they are then represented as an abstract index of permutation for an arbitrary and freely extensible set of polyhedral shapes. The arrangements represented by these stereoconfiguration indices are screened for three-dimensional feasibility.For a detailed description of the algorithms implemented in Molassembler we refer the reader to ref. 31.
2.3 Automated workflow
The employed two-step workflow begins with an illustrative template for the transition state (TS) under consideration. For the example investigated here, this template corresponds to a simplified complex where Rh is coordinated to the bare carbon skeleton of a Cp ligand (dark blue, Fig. 2). In the first step, Molassembler31,41 is used to interpret the coordinates of the reference TS into a graph, upon which chemical modifications are performed. Fifty conformers are then generated and projected back to three-dimensional coordinates using the non-Cp coordination sphere of the Rh atom as a constraint in order to ensure good guesses for TS optimization. For the studied systems, this first step generally takes less than a minute (detailed information regarding the code available to perform the aforementioned steps using Molassembler is available in the ESI†). In the second step, the resulting ensembles of geometries are refined with the semiempirical GFN2-xTB Hamiltonian42 using an implicit ethanol solvent through the ALPB formalism,43 and Gaussian16 (ref. 44) to drive the TS optimization. Successfully converged TS optimizations are further refined with the B3PW91 (ref. 45–47)-D3BJ48,49/def2-SVP50 combination of density functional, semiclassical dispersion correction, and basis set, which lead to a total of 248 distinct transition state structures (characterized by the relevant vibrational mode) across the 12 catalytic systems studied here. Single-point energies were then determined with B3PW91-D3BJ/def2-TZVP SMD(ethanol),51i.e., considering also a model for the surrounding solvent. The resulting solvation-corrected free energies of the TS with respect to the separated catalyst and substrate (ΔGTS) were determined, grouped by selectivity (R/S), and Boltzmann weighted at 296.15 K (the experimental temperature) leading to effective values ΔGTSeff,R and ΔGTSeff,S. Enantiomeric ratios (er) were computed from the theoretical kinetic constants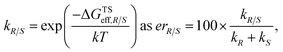 assuming identical concentrations and pre-exponential factors throughout. Note that our choice of functional was motivated by previous literature reports,52 however, the use of alternative density functionals did not lead to significant degradation of the results (see ESI Fig. S4 and S5†).
assuming identical concentrations and pre-exponential factors throughout. Note that our choice of functional was motivated by previous literature reports,52 however, the use of alternative density functionals did not lead to significant degradation of the results (see ESI Fig. S4 and S5†).
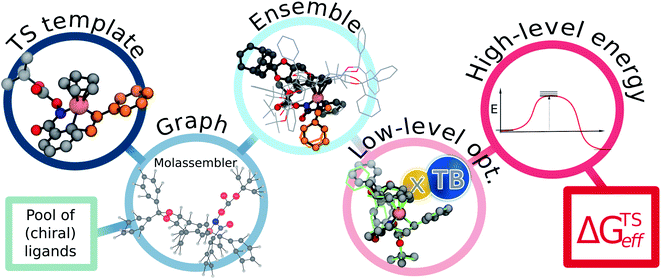 | ||
| Fig. 2 Flowchart of the proposed pipeline used to compute the effective relative free energies of the relevant pathways (ΔGTSeff). As a first step, the non-functionalized TS-template is interpreted as a graph by Molassembler, which tracks the spatial arrangement of all atoms and performs the required substitutions on the graph (i.e., adding the chiral Cp ligand). From the edited graph, a conformational ensemble respecting the first coordination shell of the Rh atom is generated. Execution of the first step takes less than a minute on average (see ESI† for timing details). As a second step, structures are optimized with the semiempirical GFN2-xTB approach, refined using DFT, and relative energies determined. See ESI† for exemplary code. | ||
3 Results and discussion
Our work specifically focuses on the chiral Cp ligands shown in Scheme 1c. Experimentally, the Mannitol-Cp derivative 1 afforded the R-product with an enantiomeric ratio of 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
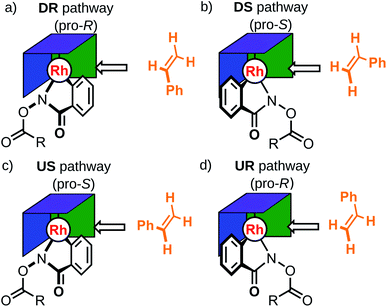
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. Related chiral catalysts 2, 3 and 4 were also tested in combination with various protecting groups (i.e., R = OtBu, tBu, Me), as depicted in Scheme 1. Despite their obvious structural similarities, reaction selectivity varied significantly as a function of the chiral Cp ligand constituents. Specifically, three functional moieties were identified as key structural elements: two pro-chiral sidewalls (green, Fig. 1) and a back wall (blue, Fig. 1). Cramer et al.33 proposed a specific function for each of these structural units, where the sidewalls direct the hydroxamate substrate into a particular conformation while the backwall provides steric bulk that hinders the coordination of the incoming olefin on the back face of the hydroxamate. In this model, two possible relative orientations of the catalyst and the substrate were postulated to exist, with one, DR (where D denotes the Ph group points downward), leading to the (R)-product and the other, DS, to the (S)-product (Fig. 3). Here, the sidewall should disfavor the DS pathway, which leads to a more favorable DR conformation and a resulting high R
4. Related chiral catalysts 2, 3 and 4 were also tested in combination with various protecting groups (i.e., R = OtBu, tBu, Me), as depicted in Scheme 1. Despite their obvious structural similarities, reaction selectivity varied significantly as a function of the chiral Cp ligand constituents. Specifically, three functional moieties were identified as key structural elements: two pro-chiral sidewalls (green, Fig. 1) and a back wall (blue, Fig. 1). Cramer et al.33 proposed a specific function for each of these structural units, where the sidewalls direct the hydroxamate substrate into a particular conformation while the backwall provides steric bulk that hinders the coordination of the incoming olefin on the back face of the hydroxamate. In this model, two possible relative orientations of the catalyst and the substrate were postulated to exist, with one, DR (where D denotes the Ph group points downward), leading to the (R)-product and the other, DS, to the (S)-product (Fig. 3). Here, the sidewall should disfavor the DS pathway, which leads to a more favorable DR conformation and a resulting high R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S enantiomeric ratio. Two additional pathways UR and US, which also lead to the (R)- and (S) products, presumably have a negligible contribution due to the assumed higher energy associated with a steric clash between the Ph group of styrene and the Cp ring (purple, Fig. 3) that occurs when coordinating the olefin with an upward pointing phenyl group; they were not considered in the original “back-of-the-envelope” model. Nonetheless, including these conformations in the analysis of reaction selectivity represents a prudent choice, particularly given that unforeseen low-energy conformations featuring the “up” configuration may play a key role in defining the er (Fig. 4).
S enantiomeric ratio. Two additional pathways UR and US, which also lead to the (R)- and (S) products, presumably have a negligible contribution due to the assumed higher energy associated with a steric clash between the Ph group of styrene and the Cp ring (purple, Fig. 3) that occurs when coordinating the olefin with an upward pointing phenyl group; they were not considered in the original “back-of-the-envelope” model. Nonetheless, including these conformations in the analysis of reaction selectivity represents a prudent choice, particularly given that unforeseen low-energy conformations featuring the “up” configuration may play a key role in defining the er (Fig. 4).
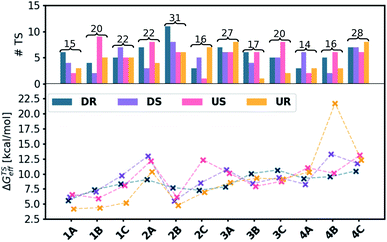
As an initial demonstration of the Molassembler pipeline and its ability to reproduce accurately experimental results, we examined catalyst 1A (R = OtBu) in detail. Initially, a pool of transition state (TS) structures associated with the stereocontrolling olefin insertion step leading to C–C bond formation between the styrene and hydroxamate moiety for each of the four possible pathways (DR, DS, US and UR) was generated. Generation of this TS pool (which took only 46.8 seconds) only requires a representative template (in this case, an optimized TS with a bare Cp ligand) as an input. Following the generation, optimization, refinement, and removal of redundant conformers produced in the pipeline, a total of 15 TS conformations (6 DR, 4 DS, 2 UR, 3 US) were found for catalyst 1A (see Fig. 5a). Clearly evident from the superposition of these structures (Fig. 4) is that the rotational freedom of the Cp ring cannot be ignored if a holistic picture of the energetics and the resulting enantioselectivity is desired. Further analysis of the various TS structures also shows key contributions from the US and UR pathways. In fact, the lowest energy transition state (Fig. 4b, c and 5), which leads to formation of the (R)-product, actually originates from the UR pathway where the phenyl group of the styrene conceivably would “clash” with the Cp ring of the catalyst. This indicates a fundamental breakdown of the original model and illustrates the truly dynamic ability of the catalyst to adopt energetically favorable, yet non-intuitive conformations.
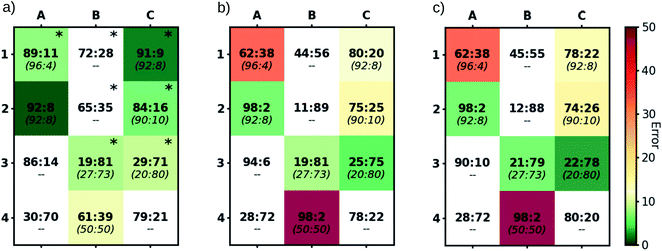
To determine the er of this catalyst, the computationally determined relative free energies (see Computational details for methods) of each of the conformations were Boltzmann weighted and the effective relative energy of each of the four pathways with respect to the separated catalyst and substrate determined (Fig. 5). Transition states were then separated as either pro-R or pro-S and the computationally derived er values computed.¶ As shown in Fig. 6a, the er estimations from our protocol (89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11, upper left square) closely parallels those determined by experiment (96
11, upper left square) closely parallels those determined by experiment (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) with catalyst 1A being very selective for the (R)-product.
4) with catalyst 1A being very selective for the (R)-product.
In order to probe the ability of our workflow to reproduce experimental results as well as to predict the er values of unreported systems, we examined 11 other systems where the protecting group of the hydroxamate substrate (A = OtBu, B = tBu, C = Me) and the chiral Cp ligands (1–4, Scheme 1c) were changed. In this regard, the design of our computational protocol mirrors the experimental optimization efforts aimed at producing high R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S product ratios by invoking catalyst design techniques involving functionalization.
S product ratios by invoking catalyst design techniques involving functionalization.
Comparing our computationally derived results with those obtained from experiment (colored boxes, Fig. 6), it is clear that the test case presented above is not a singular success, but rather that our computational workflow broadly reproduces experimental er values (darker green colors indicate closer matching with experimental values, Fig. 6a). This includes correct identification of species both that preferentially form the (R)- (e.g., 1A) and (S)-products (e.g., 3B). In addition to those species having experimental er values, we also computed the selectivity of five catalysts not tested in the laboratory. Notable amongst these is 3A, which is predicted to form the (R)-product, unlike 3B and 3C, which favor the (S)-product.
Given the importance of models in the development of ligand design, we reevaluated our results within the context of Cramer's “back-of-the-envelope” model by examining the er values of catalysts if only the lowest energy DR and DS conformers (Fig. 6b) or a Boltzmann weighting of all DR and DS conformers (Fig. 6c) are considered. In contrast to the er values obtained when all conformers (i.e., DR, DS, UR, US) are Boltzmann weighted (Fig. 6a), considering only conformers featuring downward pointing phenyl groups can lead to significant errors (red and orange colored boxes). Even in cases with seemingly good quantitative er agreement when only the DR and DS conformers are considered, the UR and US conformers were often found to be energetically lower-lying (indicated by asterisks, Fig. 6a). Thus, some of the predictions seen in Fig. 6b and c “accidently” arrive at the correct er because the (Boltzmann weighted) energy difference between the DR and DS conformers closely matches the difference between the UR and US conformers (i.e., the right answer for the wrong reason). Overall, these results demonstrate the utility of our pipeline not only as a screening tool for identifying selective catalysts prior to experimental testing, but also as a tool for developing better tailored design models.
4 Conclusions
In this work we demonstrated an efficient, automated pipeline that facilitates the exploration of multiple reaction pathways characteristic of asymmetric reactions. Powered by the Molassembler software, which simultaneously handles functionalization and conformational sampling through the construction of molecular graphs, this computational workflow successfully reproduced experimentally reported er values for several chiral-Cp Rh(III)-catalyzed C–H activation reactions. By sampling around 20 transition states per catalyst through unbiased conformational exploration with minimal human intervention, we illustrate how simple, yet elegant, “back-of-the-envelope” design models can be quickly confirmed or refuted based on computation. Given the encouraging results obtained here, we envision this approach to be beneficial both in the screening for new highly selective catalysts across a broad range of reactions as well as for refining and developing conceptual catalyst design models.Data availability
All data used to reach the results presented in this manuscript can be found in the ESI.†Author contributions
JGS developed the software components with contribution by RL. RL performed DFT computations and analyzed the results with help from MDW. RL, MDW and CC jointly wrote the first draft. All the authors edited the manuscript. MDW, CC, and MR conceived the project, provided supervision, and wrote the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the EPFL for financial support and computational resources. This publication was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation. The authors thank Simone Gallarati and Nicolai Cramer for fruitful discussions. Terry Blaskovits is acknowledged for his help with graphics.Notes and references
- Y.-h. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750–762 CrossRef CAS PubMed.
- W. Thiel, Angew. Chem., Int. Ed., 2014, 53, 8605–8613 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2018, 119, 2453–2523 CrossRef PubMed.
- J. N. Harvey, F. Himo, F. Maseras and L. Perrin, ACS Catal., 2019, 9, 6803–6813 CrossRef CAS.
- M. Steiner and M. Reiher, Top. Catal., 2022, 65, 6–39 CrossRef CAS PubMed.
- C. Poree and F. Schoenebeck, Acc. Chem. Res., 2017, 50, 605–608 CrossRef CAS PubMed.
- S. Ahn, M. Hong, M. Sundararajan, D. H. Ess and M.-H. Baik, Chem. Rev., 2019, 119, 6509–6560 CrossRef CAS PubMed.
- I. Funes-Ardoiz and F. Schoenebeck, Chem, 2020, 6, 1904–1913 CAS.
- M. Burai Patrascu, J. Pottel, S. Pinus, M. Bezanson, P.-O. Norrby and N. Moitessier, Nat. Catal., 2020, 3, 574–584 CrossRef CAS.
- N. Fey and J. M. Lynam, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021 DOI:10.1002/wcms.1590.
- K. L. Fleming, P. Tiwary and J. Pfaendtner, J. Phys. Chem. A, 2016, 120, 299–305 CrossRef CAS PubMed.
- P. C. D. Hawkins, A. G. Skillman, G. L. Warren, B. A. Ellingson and M. T. Stahl, J. Chem. Inf. Model., 2010, 50, 572–584 CrossRef CAS PubMed.
- A. R. Rosales, J. Wahlers, E. Limé, R. E. Meadows, K. W. Leslie, R. Savin, F. Bell, E. Hansen, P. Helquist, R. H. Munday, O. Wiest and P.-O. Norrby, Nat. Catal., 2018, 2, 41–45 CrossRef.
- A. R. Rosales, T. R. Quinn, J. Wahlers, A. Tomberg, X. Zhang, P. Helquist, O. Wiest and P.-O. Norrby, Chem. Commun., 2018, 54, 8294–8311 RSC.
- R. Petraglia, A. Nicolaï, M. D. Wodrich, M. Ceriotti and C. Corminboeuf, J. Comput. Chem., 2016, 37, 83–92 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- P. Pracht and S. Grimme, Chem. Sci., 2021, 12, 6551–6568 RSC.
- T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D’Addario, M. S. Sigman and A. Aspuru-Guzik, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- E. Hansen, A. R. Rosales, B. Tutkowski, P.-O. Norrby and O. Wiest, Acc. Chem. Res., 2016, 49, 996–1005 CrossRef CAS PubMed.
- T. A. Young, J. J. Silcock, A. J. Sterling and F. Duarte, Angew. Chem., Int. Ed., 2020, 60, 4266–4274 CrossRef PubMed.
- S. Chen, T. Nielson, E. Zalit, B. B. Skjelstad, B. Borough, W. J. Hirschi, S. Yu, D. Balcells and D. H. Ess, Top. Catal., 2021, 65, 312–324 CrossRef.
- E. I. Ioannidis, T. Z. H. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261 CrossRef CAS PubMed.
- V. M. Ingman, A. J. Schaefer, L. R. Andreola and S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e1510 Search PubMed.
- Y. Chu, W. Heyndrickx, G. Occhipinti, V. R. Jensen and B. K. Alsberg, J. Am. Chem. Soc., 2012, 134, 8885–8895 CrossRef CAS PubMed.
- M. Foscato, V. Venkatraman, G. Occhipinti, B. K. Alsberg and V. R. Jensen, J. Chem. Inf. Model., 2014, 54, 1919–1931 CrossRef CAS PubMed.
- M. Foscato, G. Occhipinti, V. Venkatraman, B. K. Alsberg and V. R. Jensen, J. Chem. Inf. Model., 2014, 54, 767–780 CrossRef CAS PubMed.
- M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- R. Laplaza, S. Gallarati and C. Corminboeuf, Chem.–Methods,, 2022 DOI:10.1002/cmtd.202100107.
- J.-G. Sobez and M. Reiher, J. Chem. Inf. Model., 2020, 60, 3884–3900 CrossRef CAS PubMed.
- R. L. Halterman, Chem. Rev., 1992, 92, 965–994 CrossRef CAS.
- B. Ye and N. Cramer, Science, 2012, 338, 504–506 CrossRef CAS PubMed.
- T. K. Hyster, L. Knörr, T. R. Ward and T. Rovis, Science, 2012, 338, 500–503 CrossRef CAS PubMed.
- B. Ye and N. Cramer, J. Am. Chem. Soc., 2013, 135, 636–639 CrossRef CAS PubMed.
- J. Zheng, W.-J. Cui, C. Zheng and S.-L. You, J. Am. Chem. Soc., 2016, 138, 5242–5245 CrossRef CAS PubMed.
- Z.-J. Jia, C. Merten, R. Gontla, C. G. Daniliuc, A. P. Antonchick and H. Waldmann, Angew. Chem., Int. Ed., 2017, 56, 2429–2434 CrossRef CAS PubMed.
- S.-G. Wang, S. H. Park and N. Cramer, Angew. Chem., Int. Ed., 2018, 57, 5459–5462 CrossRef CAS PubMed.
- J. Mas-Roselló, A. G. Herraiz, B. Audic, A. Laverny and N. Cramer, Angew. Chem., Int. Ed., 2020, 60, 13198–13224 CrossRef PubMed.
- Y. Okada, S. Yamamoto, Y. Namba, T. Masuda and K. Sakamoto, Spectr. Anal. Rev., 2016, 04, 41–48 CrossRef CAS.
- J.-G. Sobez and M. Reiher, qcscine/molassembler: Release 1.1.0, 2021, https://zenodo.org/record/5782843.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. P. Perdew, Electronic structure of solids, Akademie Verlag, Berlin, 1991, p. 11 Search PubMed.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- M. P. Waller, H. Braun, N. Hojdis and M. Bühl, J. Chem. Theory Comput., 2007, 3, 2234–2242 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01714h |
| ‡ These authors contributed equally to this work. |
| § In this work we examine rhodium-catalyzed asymmetric C–H functionalization, however the proposed pipeline is far more general. For selected examples involving other catalytic systems (including information on timing) the interested reader is encouraged to examine the ESI.† |
| ¶ In order to better track selectivities, we treated each pathway separately and constrained the relative orientation of styrene accordingly. This allowed us to easily track the pro-R or pro-S configurations, which was convenient but not necessary. As an alternative, all configurations could have been examined in parallel and classified a posteriori by examining the relative disposition of the olefin. |
| This journal is © The Royal Society of Chemistry 2022 |