Open Access Article
Open Access ArticleProbing longitudinal carrier transport in perovskite thin films via modified transient reflection spectroscopy†
Shengli
Zhao
ab,
Jing
Leng
 *b,
Shiping
Wang
bc,
Xianchang
Yan
b,
Zixi
Yin
b,
Yanfeng
Yin
b,
Jun
Zhang
*b,
Shiping
Wang
bc,
Xianchang
Yan
b,
Zixi
Yin
b,
Yanfeng
Yin
b,
Jun
Zhang
 *ad and
Shengye
Jin
*ad and
Shengye
Jin
 *b
*b
aState Key Laboratory of Heavy Oil Processing, College of Chemical Engineering, China University of Petroleum (East China), Qingdao 266580, China. E-mail: zhangj@upc.edu.cn
bState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian 116023, China. E-mail: sjin@dicp.ac.cn; ljjx@dicp.ac.cn
cDepartment of Chemistry, School of Science, Tianjin University, Tianjin 300354, China
dCollege of Materials Science and Engineering, China University of Petroleum (East China), Qingdao 266580, China
First published on 21st June 2022
Abstract
Accurate characterization of the longitudinal (along the thickness direction) carrier transport property is of significant importance for evaluating the quality and performance of perovskite thin films. Herein, we report the development of a modified transient reflection (TR) spectroscopy method to realize the direct observation and determination of the longitudinal carrier transport process in MAPbI3 polycrystalline thin films. Unlike the traditional TR spectroscopy, the carrier transport dynamics along the film thickness is resolved by making the pump (excitation) and probe beams spatially separated on each side of the film, so that the carrier transport from the excitation side to the probe side is directly captured. Utilizing this method, the longitudinal carrier diffusion coefficients (D) in various perovskite films with different thicknesses and grain sizes (extracted from SEM images) are determined, showing D values of ∼1.5 to 1.8 cm2 s−1 (∼0.5 to 0.8 cm2 s−1) for films with grain size larger (smaller) than the thickness. This empirical correlation between the longitudinal D and film thickness/grain size provides a reference for quick quality screening and evaluation of perovskite polycrystalline thin films.
Introduction
Organolead halide perovskites MAPbX3 (MA = CH3NH3+; X = Cl−, Br−, and I−) have attracted extensive interest owing to their excellent photophysical properties, such as strong light absorption, long carrier lifetime and long carrier diffusion distance.1–6 Owing to these extraordinary properties and numerous engineering studies, the power conversion efficiency (PCE) of planar perovskite solar cells (PSCs) rose quickly in the past decade and has reached a current champion value of 25.5%.7,8 In evaluating the quality of perovskite films, the characterization of carrier transport property is essential as it directly relates to the charge collection efficiency in a solar cell. The carrier transport distance (LD) can be theoretically estimated using the carrier lifetime (τ) and diffusion coefficient (D) via LD = (Dτ)1/2. However, the quantification of LD or D can become complicated in a PSC using a polycrystalline film, where the carrier transport is significantly impacted by the heterogeneous microstructure (e.g. grain size, grain boundary and thickness). Furthermore, due to the microstructural difference in the film's lateral and thickness (longitudinal) dimensions, the carrier transport behaviour can differ prominently between the planar and vertical directions, whereas the latter directly reflects the carrier transport between the two charge collection electrodes in a PSC and thus is considered to be a key efficiency-limiting factor. Therefore, a reliable evaluation of carrier transport property, particularly in the longitudinal dimension, as well as finding its microstructural impact, is very necessary for the further optimization of PSCs.The carrier transport in various perovskite materials is usually examined through the measurement of charge mobility (μ) by using traditional electrical methods, such as time-of-flight (TOF),9,10 Hall effect9,11 and dark current–voltage.12 The charge mobility directly correlates to D through μ = D·e/kBT (kB is Boltzmann's constant, T is the temperature and e is the electronic charge). These electrical techniques all rely on the construction of a device structure and in principle need a perfect ohmic contact between the perovskite and electrode to reduce the contact resistance.13 However, the deposition of electrode materials inevitably alters the perovskite surface and/or introduces defective interfacial structures, obscuring an accurate determination of charge mobility inside the perovskite layer. Complementary to the electrical methods, THz spectroscopy (steady state or time-resolved) is also a widely used technique to probe the charge mobility in perovskite materials.14,15 However, in perovskite polycrystalline films, THz spectroscopy actually measures the inner-grain (or intrinsic) charge mobility, and is thus inappropriate to be directly applied for the estimation of LD, as the transport of carriers is also limited by the inter-grain structure.16
In parallel with the traditional techniques, various time-resolved microscopic and spectroscopic methodologies are also developed to probe the carrier transport dynamics in perovskite materials.17–19 Recently, ultrafast transient absorption (TA) and photoluminescence (PL) imaging microscopy techniques were successfully applied to directly visualize the micrometer-scale carrier transport process along the lateral dimension in both perovskite single crystals and polycrystalline films.20–22 Besides, two-photon-excitation PL microscopy can probe lateral carrier transport in perovskite samples at different detection depths.23 However, due to the limited spatial resolution, these methods are incapable of probing the longitudinal carrier transport in a thin film of sub-micrometer thickness.
Time-resolved spectroscopy (e.g. time-resolved PL, TA or transient reflection (TR)) is also able to probe the carrier diffusion coefficient by analyzing the carrier kinetics.24–27 For example, in a perovskite thin film deposited with carrier quenchers, the carrier dynamics usually involves carrier diffusion to the interface and the subsequent interfacial charge transfer, and therefore the diffusion coefficient can be deduced from appropriate kinetics modeling.24,25 Similarly, TR spectroscopy, which particularly probes the carrier dynamics at the sample surface, was also applied to estimate the longitudinal carrier diffusion coefficient by observing the accelerated TR kinetics once the carriers diffuse away from the surface.26,27 Nevertheless, these time-resolved spectroscopy methods resolve the carrier transport process in an indirect way, and their accuracy largely depends on the kinetic model.
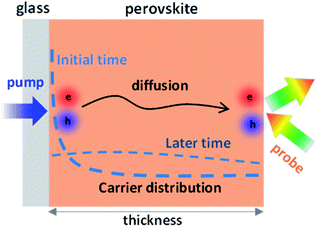
Herein, to realize a direct probe of longitudinal carrier transport kinetics in perovskite polycrystalline thin films, we developed a modified pump–probe TR spectroscopy method by spatially separating the pump (excitation) and probe (detection) beams on each side of the perovskite thin film (named back-exc. TR). The detection configuration is shown in Fig. 1. Upon excitation at a specific wavelength, most of the photoinduced carriers initially locate close to the excitation surface, following the distribution N(x) = N0 exp(−αx), and driven by the concentration gradient, the carriers at a later time can diffuse toward the opposite side of the film, where the reflection of probe light is changed by carriers arriving to the surface. Therefore, the back-exc. TR can directly reflect the longitudinal carrier diffusion process by recording the time evolution of diffusing carriers at the probe surface.
In the past years, great efforts were devoted to controlling the growth of large perovskite grains to maximize the carrier transport property in a perovskite polycrystalline film. A common belief is that a polycrystalline film with grain size larger than its thickness should exhibit efficient longitudinal carrier transport and thus higher device performance. However, how the longitudinal carrier diffusion coefficient differs quantitatively between thin films of different grain sizes and thicknesses remains undefined. In this work, by utilizing the back-exc. TR spectroscopy, we successfully studied the longitudinal carrier transport dynamics in perovskite polycrystalline thin films of various film thicknesses and grain sizes. The result enables us to develop an empirical correlation between the longitudinal D and the thickness-to-grain-size ratio (R), which shows dramatically varied D values of ∼1.5 to 1.8 cm2 s−1 for R < 1 (thickness is smaller than grain size) to ∼0.5 cm2 s−1 for R > 2 (thickness is much larger than grain size).
Results and discussion
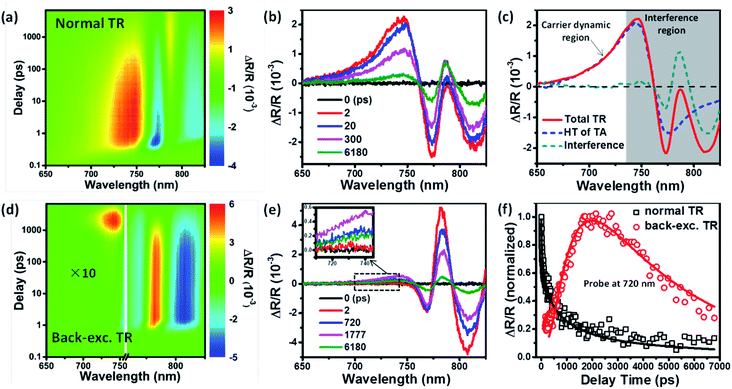
We prepared MAPbI3 perovskite polycrystalline films by using a modified non-stoichiometric precursor.28 The details of the film preparation are provided in the ESI.† By controlling spin-coating conditions and the amount of MACl additive, we realized the synthesis of MAPbI3 films with different thicknesses and grain sizes. Fig. S1 and S2† show the top-view and cross-sectional SEM images of a set of thin films, and based on these images we determined the statistically averaged grain size (Fig. S3†) and thickness of each film. Fig. S4a† shows the UV-vis absorption and PL spectra of a typical MAPbI3 film with an average grain size of >1 μm and a thickness of 1200 nm. According to the Elliott's model, we fitted the absorption spectrum to isolate the contributions from exciton absorption and continuum absorption (Fig. S4b†) and determined the bandgap (Eg) and exciton binding energy (Rex) to be Eg = 1.652 ± 0.001 eV and Rex = 11.4 ± 0.7 meV, which are in good agreement with recent reports.29,30Ultrafast TR spectroscopy is a unique technique for probing the photoinduced carrier dynamics particularly at the surface or interface of materials.31,32 The reflection of probe light at the surface is sensitive to the photoinduced change of refractive indices caused by the carriers residing within about tens of nm depth from the surface. It has been successfully applied to determine the surface recombination velocity of carriers in perovskite thin films and single crystals.26,27 For comparison, we first conducted normal TR measurement on this perovskite film under excitation at 635 nm with a low flux of 3.5 μJ cm−2. Fig. 2a shows the pseudocolor image of the TR spectra under normal excitation and the corresponding TR spectra at indicated delays are shown in Fig. 2b, exhibiting a very complicated spectral shape. According to the previous report by Beard et al., the TR spectrum from a perovskite film usually comprises two different components: a pair of antisymmetric peaks and a series of sharp oscillations.26 The antisymmetric peaks are completely due to the bleach of the exciton transition, which meanwhile induces the opposite changes of sample reflectivity between shorter and longer wavelength regions relative to the exciton absorption peak because of the presence of abnormal dispersion near the absorption peak position, and thus the intensity of TR signal can reflect the carrier density at the probing surface. The sharp oscillations can be attributed to the photomodulation of an interference fringe due to changes in the refractive index.26,33 Since the interference fringe originates from the reflection of the probe light from the front and back surfaces of the film, the oscillations occur only at relatively long wavelengths as higher-energy photons are significantly attenuated by absorption.26 In order to separate the contribution of the antisymmetric TR signal arising solely from the surface carriers, we compare in Fig. 2c a typical TR spectrum at 5 ps delay and the Hilbert transform (HT) of the TA (transient absorption) spectrum (see Fig. S5†) from the sample. According to the Kramers–Kronig relationship, the Hilbert transform of a TA spectrum can represent the TR spectrum but without the interference fringe.34,35 It is shown that the central position of the antisymmetric peak in the TR spectrum at ∼760 nm well matches the bleach peak position of the TA spectrum (Fig. S5a†) and is also consistent with the above bandgap data obtained from the absorption spectrum. The comparison in Fig. 2c shows that the TR spectrum consists of the HT of TA (HT-TA) only in the region of <735 nm, indicating that this TR spectrum region is dominated by the carriers without the disturbance of the interference fringe. Subtraction of the HT-TA from the TR spectra provides the pure interference signal, which shows a similar character to that in a previous report.26
We then performed the back-exc. (635 nm and 3.5 μJ cm−2) TR measurement on the same film. The pseudocolor image of the back-exc. TR spectra and the corresponding TR spectra at indicated delays are, respectively, shown in Fig. 2d and e. Similar to normal TR, the back-exc. TR spectra also contain sharp oscillation signals at the >750 nm region due to the interference fringe. The spectrum at <735 nm is also consistent with the HT of the TA spectrum and is dominated by the carriers (see Fig. S6†); however, its time evolution is significantly different from that of normal TR. Fig. 2f shows the comparison of the normal TR and back-exc. TR kinetics probed at 720 nm. The normal TR signal exhibits a decay process with the increase of delay time and is faster than TA kinetics (Fig. S7†), suggesting a faster depopulation of surface carriers than bulk carriers due to both surface recombination and carrier diffusion out of the probe surface.26 In contrast, under back excitation, the antisymmetric TR signal exhibits a prominent rising kinetics during the initial 2000 ps (Fig. 2f), which represents the carrier diffusion process from the excitation side to the probe side in the film. Compared to normal TR measurement, the back-exc. TR kinetics directly reflects the longitudinal carrier transport in the perovskite thin film.
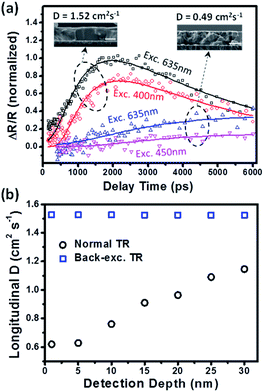
The carrier transport along the longitudinal direction in the thin film is driven by the gradient of carrier density between the excitation side and probe side. Therefore, the back-exc. TR kinetics is correlated with the initial carrier distribution, which is determined by the excitation wavelength and absorption coefficient of the perovskites. Furthermore, the longitudinal carrier transport process is also related to the grain structure in the perovskite polycrystalline film. Therefore, in order to validate the back-exc. TR method, we carried out the measurements on two films with different grain structures by using different excitation wavelengths. Note that the excitation power used here is low enough to avoid the influence of higher-order recombination (see Fig. S8 and S9†). Fig. 3a shows the normalized back-exc. TR kinetics probed at 720 nm under excitation at the indicated wavelengths. Based on the absorption coefficient of perovskites, the initial carrier distributions along the film thickness at different excitation wavelengths are simulated in Fig. S10.† A shorter excitation wavelength has a larger absorption coefficient and thus leads to a carrier density distribution closer to the excitation side (meaning an averagely longer carrier transport distance to the probe side). Therefore, as shown in Fig. 3a a slower back-exc. TR rising kinetics at a shorter excitation wavelength is observed due to the longer diffusion distance.
Furthermore, we also compared the back-exc. TR kinetics between two films with similar thickness but with clearly different grain sizes as shown in the cross-sectional SEM images in the insets of Fig. 3a (see their clearer SEM images in Fig. S1a and S2c†). The perovskite film with larger grains (showing single grains in the thickness dimension) exhibits much faster rising kinetics than the film with smaller grains (showing multiple grains in the thickness dimension) (see Fig. 3a), indicating that the carrier transport speed in the film with smaller grains is significantly reduced. This result, together with the wavelength-dependent one, confirms the capability of the back-exc. TR method in examining the longitudinal carrier transport property of a perovskite polycrystalline thin film.
Considering that the pump/probe spot size used in our TR experiments is on the order of hundreds of micrometers, much larger than the carrier diffusion distance in the lateral dimension within a few nanoseconds, we thus believe that the carrier diffusion out of the laser spot should not occur in TR measurement to disturb our results. To quantitatively determine the longitudinal carrier diffusion coefficient, we developed a 1D carrier diffusion model to simulate the back-exc. TR kinetics. The evolution of carrier density in the whole film can be described using26,33,36
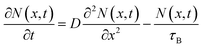 | (1) |
| N(x, 0) = N0 exp(−αx) | (2) |
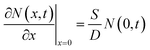 | (3) |
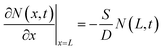 | (4) |
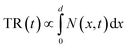 | (5) |
Under the back-exc. mode, the TR signal is described using
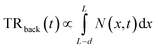 | (6) |
Note that the S values for the front and back surfaces are approximately equal in our as-prepared perovskite films, which is also confirmed by the similar TR kinetics collected at the front and back surfaces under normal excitation (see Fig. S12†). To constrain the fitting, the bulk carrier lifetime is experimentally measured from their TA kinetics (see Fig. S5b†) and only S and D are set as free fitting parameters. By using this 1D diffusion model, D and S can be extracted through the global fitting of the back-exc. TR kinetics at different excitation wavelengths. As shown in Fig. 3a, the back-exc. TR kinetics are well described by the diffusion model, yielding a D value of 1.52 cm2 s−1 for the film with larger grains and 0.49 cm2 s−1 for the film with smaller grains (using d = 25 nm for the detection depth of 720 nm; the detailed fitting results are summarized in Table S1†). We noted that the measured D by back-exc. TR should be an ambipolar diffusion coefficient because electron and hole contributions are indistinguishable in the TR signal. This ambipolar diffusion model is also consistent with the reported balanced transport properties of electrons and holes,24,38,39 which means that the electron and hole diffusion coefficients are indeed similar.
We also compared the determination of the D value using our back-exc. TR method and the normal TR method. Fig. S13† shows the normal TR kinetics at different excitation wavelengths for the same film shown in Fig. 3a (the one with larger grains), and the D value is found to be 1.1 cm2 s−1, smaller than that in back-exc. TR. We attribute this difference to the initial set of the detection depth (d) parameter during the kinetics fitting. Fig. S14† shows the simulation of longitudinal carrier distribution in a film at different delay times after excitation (assuming D = 1.5 cm2 s−1), where the change of carrier distribution is due to the diffusion of carriers away from the excitation side driven by the density gradient. It is found that the kinetics of carrier density probed at the excitation side (as in the normal TR case) is significantly varied when using different detection depth (d) parameters (Fig. S15a†). However, the kinetics probed at the opposite side to excitation (as in the back-exc. TR case) is almost unchanged with d (Fig. S15b†). This is because the carrier distribution more sharply changes along the thickness direction at the excitation side (Fig. S14†). Fig. 3b shows the D values determined by using back-exc. TR and normal TR with the setup of different detection depths (d) in kinetics fitting. The resolved D value in the normal excitation mode is found to decrease from 1.1 to 0.6 cm2 s−1 when using d = 30 to 1 nm, while those determined by back-exc. TR are almost unchanged. Indeed, a precise determination of the detection depth in a TR measurement is very difficult particularly for a heterogeneous polycrystalline thin film. We believe that our back-exc. TR method can provide a more reliable measurement of the longitudinal carrier diffusion coefficients in perovskite films. Beard et al. previously reported a D value of 0.17 cm2 s−1 in a similar perovskite film by using normal TR and assuming d = 0 nm;26 we speculate that their D value is likely underestimated according to our result in Fig. 3b.
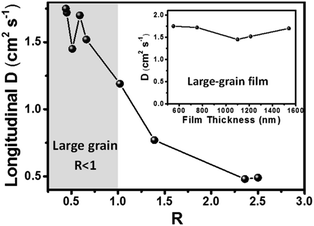
It is also interesting to note that the D value (∼1.5 cm2 s−1) obtained via the back-exc. TR method in a larger-grain film is very close to those reported in perovskite single crystals (1.5–2.5 cm2 s−1)9,10,17,40–42 and much larger than those reported previously in perovskite films (0.01–0.5 cm2 s−1).24,33,38,40,43–45 This difference might be attributed to the large grain size and the absence of the grain boundary in the longitudinal direction in our perovskite film (SEM image in Fig. S1a†), which is also reflected in the XRD patterns (Fig. S16†). For large-grain films, their XRD patterns only exhibit two very strong diffraction peaks, corresponding to the (200) and (400) planes of the orthorhombic structure,46 which suggests that each grain within the film is highly oriented and has high crystallinity. This confirms that the longitudinal carrier transport in a perovskite film with large grains is not limited by the grain boundary, showing an apparent diffusion coefficient similar to that in perovskite single crystals.
To study the effect of the grain boundary on the longitudinal transport of carriers, we also measured the longitudinal carrier diffusion coefficients (D) in a series of perovskite films with different thicknesses and grain sizes by using the back-exc. TR method. The top-view and cross-sectional SEM images of these films are presented in Fig. S1 and S2,† where the film thicknesses and the averaged grain sizes (in the lateral dimension) are determined. The TR kinetics probed at 720 nm under different excitation wavelengths in these perovskite films and their corresponding kinetics fitting are shown in Fig. S17,† from which a set of D values with different film thickness-to-grain-size ratios (R) are obtained (Fig. 4). The D is found to be 1.45 to 1.75 cm2 s−1 for films with R < 1 (averagely a single grain in the thickness dimension) and drop greatly to ∼0.5 cm2 s−1 for films with R > 2 (averagely two grains in the thickness dimension). This result indicates that the apparent carrier diffusion coefficient can decrease by 2 to 3 times even when the carriers transport across the grain boundary. This finding is also consistent with our previous measurement of the change of D (in the lateral dimension) when the carriers transport between adjacent grains.47
Conclusions
In summary, we have demonstrated a purely optical (non-contact) and direct measurement of the longitudinal carrier diffusion coefficient in perovskite films via back-exc. TR spectroscopy. Since the excitation and probe beams separately impinge on each side of the film, the carrier kinetics probed by this method exhibits a clear increase trend, which directly reflects the longitudinal carrier transport process in perovskite films and provides a more accurate determination of the longitudinal carrier diffusion coefficient in thin films than the normal TR spectroscopy. We believe that our result provides an empirical correlation between the longitudinal diffusion coefficient and grain size/thickness, which might be very useful for quick quality screening and evaluation of polycrystalline thin films.Author contributions
S. J., J. L. and J. Z. conceived and designed this research. S. Z. synthesized the samples and conducted all characterization studies. S. Z. conducted TA and TR experiments with the help of S. W. and Z. Y., and X. Y. and Y. Y. performed TRPL measurements. S. J., J. L., J. Z. and S. Z. wrote the paper with comments from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. J. acknowledges the financial support from the MOST (2018YFA0208704, 2016YFA0200602), the National Natural Science Foundation of China (21725305) and the Strategic Priority Research Program of CAS (No. XDB17000000). J. L. acknowledges the financial support from the National Natural Science Foundation of China (22073098). J. Z. acknowledges the financial support from the Fundamental Research Funds for the Central Universities (19CX05001A) and Taishan Scholar Program of Shandong Province.Notes and references
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- Y. Chen, H. T. Yi, X. Wu, R. Haroldson, Y. N. Gartstein, Y. I. Rodionov, K. S. Tikhonov, A. Zakhidov, X.-Y. Zhu and V. Podzorov, Nat. Commun., 2016, 7, 12253 CrossRef CAS PubMed.
- D. W. deQuilettes, S. M. Vorpahl, S. D. Stranks, H. Nagaoka, G. E. Eperon, M. E. Ziffer, H. J. Snaith and D. S. Ginger, Science, 2015, 348, 683–686 CrossRef CAS PubMed.
- S.-T. Ha, R. Su, J. Xing, Q. Zhang and Q. Xiong, Chem. Sci., 2017, 8, 2522–2536 RSC.
- N. Li, S. Tao, Y. Chen, X. Niu, C. K. Onwudinanti, C. Hu, Z. Qiu, Z. Xu, G. Zheng, L. Wang, Y. Zhang, L. Li, H. Liu, Y. Lun, J. Hong, X. Wang, Y. Liu, H. Xie, Y. Gao, Y. Bai, S. Yang, G. Brocks, Q. Chen and H. Zhou, Nat. Energy, 2019, 4, 408–415 CrossRef CAS.
- Y. Miao, Y. Chen, H. Chen, X. Wang and Y. Zhao, Chem. Sci., 2021, 12, 7231–7247 RSC.
- M. Kim, J. Jeong, H. Lu, T. K. Lee, F. T. Eickemeyer, Y. Liu, I. W. Choi, S. J. Choi, Y. Jo, H. B. Kim, S. I. Mo, Y. K. Kim, H. Lee, N. G. An, S. Cho, W. R. Tress, S. M. Zakeeruddin, A. Hagfeldt, J. Y. Kim, M. Grätzel and D. S. Kim, Science, 2022, 375, 302–306 CrossRef CAS PubMed.
- H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2021, 598, 444–450 CrossRef CAS PubMed.
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- Z. Xiao, Q. Dong, C. Bi, Y. Shao, Y. Yuan and J. Huang, Adv. Mater., 2014, 26, 6503–6509 CrossRef CAS PubMed.
- M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He, G. Maculan, A. Goriely, T. Wu, O. F. Mohammed and O. M. Bakr, Nat. Commun., 2015, 6, 7586 CrossRef PubMed.
- Y. Wang, Z. Wan, Q. Qian, Y. Liu, Z. Kang, Z. Fan, P. Wang, Y. Wang, C. Li, C. Jia, Z. Lin, J. Guo, I. Shakir, M. Goorsky, X. Duan, Y. Zhang, Y. Huang and X. Duan, Nat. Nanotechnol., 2020, 15, 768–775 CrossRef CAS PubMed.
- S. G. Motti, J. B. Patel, R. D. J. Oliver, H. J. Snaith, M. B. Johnston and L. M. Herz, Nat. Commun., 2021, 12, 6955 CrossRef CAS PubMed.
- H. Zhang, E. Debroye, J. A. Steele, M. B. J. Roeffaers, J. Hofkens, H. I. Wang and M. Bonn, ACS Energy Lett., 2021, 6, 568–573 CrossRef CAS.
- H. Hempel, A. Redinger, I. Repins, C. Moisan, G. Larramona, G. Dennler, M. Handwerg, S. F. Fischer, R. Eichberger and T. Unold, J. Appl. Phys., 2016, 120, 175302 CrossRef.
- W. Tian, C. Zhao, J. Leng, R. Cui and S. Jin, J. Am. Chem. Soc., 2015, 137, 12458–12461 CrossRef CAS PubMed.
- Z. Guo, Y. Wan, M. Yang, J. Snaider, K. Zhu and L. Huang, Science, 2017, 356, 59–62 CrossRef CAS PubMed.
- Z. Guo, J. S. Manser, Y. Wan, P. V. Kamat and L. Huang, Nat. Commun., 2015, 6, 7471 CrossRef CAS PubMed.
- T. Wang, Y. Fu, L. Jin, S. Deng, D. Pan, L. Dong, S. Jin and L. Huang, J. Am. Chem. Soc., 2020, 142, 16254–16264 CrossRef CAS PubMed.
- G. Delport, S. Macpherson and S. D. Stranks, Adv. Energy Mater., 2020, 10, 1903814 CrossRef CAS.
- C. Zhao, W. Tian, Q. Sun, Z. Yin, J. Leng, S. Wang, J. Liu, K. Wu and S. Jin, J. Am. Chem. Soc., 2020, 142, 15091–15097 CrossRef CAS PubMed.
- C. Stavrakas, G. Delport, A. A. Zhumekenov, M. Anaya, R. Chahbazian, O. M. Bakr, E. S. Barnard and S. D. Stranks, ACS Energy Lett., 2020, 5, 117–123 CrossRef CAS PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS PubMed.
- J. Leng, J. Liu, J. Zhang and S. Jin, J. Phys. Chem. Lett., 2016, 7, 5056–5061 CrossRef CAS PubMed.
- Y. Yang, M. Yang, D. T. Moore, Y. Yan, E. M. Miller, K. Zhu and M. C. Beard, Nat. Energy, 2017, 2, 16207 CrossRef CAS.
- Y. Yang, Y. Yan, M. Yang, S. Choi, K. Zhu, J. M. Luther and M. C. Beard, Nat. Commun., 2015, 6, 7961 CrossRef CAS PubMed.
- M. Yang, Z. Li, M. O. Reese, O. G. Reid, D. H. Kim, S. Siol, T. R. Klein, Y. Yan, J. J. Berry, M. F. A. M. van Hest and K. Zhu, Nat. Energy, 2017, 2, 17038 CrossRef CAS.
- Y. Yang, D. P. Ostrowski, R. M. France, K. Zhu, J. van de Lagemaat, J. M. Luther and M. C. Beard, Nat. Photonics, 2016, 10, 53–59 CrossRef CAS.
- Y. Yang, M. Yang, Z. Li, R. Crisp, K. Zhu and M. C. Beard, J. Phys. Chem. Lett., 2015, 6, 4688–4692 CrossRef CAS PubMed.
- Y. Yang, J. Gu, J. L. Young, E. M. Miller, J. A. Turner, N. R. Neale and M. C. Beard, Science, 2015, 350, 1061–1065 CrossRef CAS PubMed.
- J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. Al-Jassim, M. F. A. M. van Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475–479 CrossRef CAS PubMed.
- Y. Zhai, K. Wang, F. Zhang, C. Xiao, A. H. Rose, K. Zhu and M. C. Beard, ACS Energy Lett., 2020, 5, 47–55 CrossRef CAS.
- D. S. Chemla, D. A. B. Miller, P. W. Smith, A. C. Gossard and W. Wiegmann, IEEE J. Quantum Electron., 1984, 20, 265–275 CrossRef.
- H. Zhu, M. T. Trinh, J. Wang, Y. Fu, P. P. Joshi, K. Miyata, S. Jin and X.-Y. Zhu, Adv. Mater., 2017, 29, 1603072 CrossRef PubMed.
- B. Wu, Y. Zhou, G. Xing, Q. Xu, H. F. Garces, A. Solanki, T. W. Goh, N. P. Padture and T. C. Sum, Adv. Funct. Mater., 2017, 27, 1604818 CrossRef.
- M. M. Waegele, X. Chen, D. M. Herlihy and T. Cuk, J. Am. Chem. Soc., 2014, 136, 10632–10639 CrossRef CAS PubMed.
- C. S. Ponseca Jr, T. J. Savenije, M. Abdellah, K. Zheng, A. Yartsev, T. Pascher, T. Harlang, P. Chabera, T. Pullerits, A. Stepanov, J.-P. Wolf and V. Sundström, J. Am. Chem. Soc., 2014, 136, 5189–5192 CrossRef PubMed.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Gratzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347 CrossRef CAS PubMed.
- A. A. Zhumekenov, M. I. Saidaminov, M. A. Haque, E. Alarousu, S. P. Sarmah, B. Murali, I. Dursun, X.-H. Miao, A. L. Abdelhady, T. Wu, O. F. Mohammed and O. M. Bakr, ACS Energy Lett., 2016, 1, 32–37 CrossRef CAS.
- V. Adinolfi, M. Yuan, R. Comin, E. S. Thibau, D. Shi, M. I. Saidaminov, P. Kanjanaboos, D. Kopilovic, S. Hoogland, Z.-H. Lu, O. M. Bakr and E. H. Sargent, Adv. Mater., 2016, 28, 3406–3410 CrossRef CAS PubMed.
- O. E. Semonin, G. A. Elbaz, D. B. Straus, T. D. Hull, D. W. Paley, A. M. Van der Zande, J. C. Hone, I. Kymissis, C. R. Kagan, X. Roy and J. S. Owen, J. Phys. Chem. Lett., 2016, 7, 3510–3518 CrossRef CAS PubMed.
- J. Lim, M. T. Hörantner, N. Sakai, J. M. Ball, S. Mahesh, N. K. Noel, Y.-H. Lin, J. B. Patel, D. P. McMeekin, M. B. Johnston, B. Wenger and H. J. Snaith, Energy Environ. Sci., 2019, 12, 169–176 RSC.
- T. W. Crothers, R. L. Milot, J. B. Patel, E. S. Parrott, J. Schlipf, P. Müller-Buschbaum, M. B. Johnston and L. M. Herz, Nano Lett., 2017, 17, 5782–5789 CrossRef CAS PubMed.
- R. Ihly, A.-M. Dowgiallo, M. Yang, P. Schulz, N. J. Stanton, O. G. Reid, A. J. Ferguson, K. Zhu, J. J. Berry and J. L. Blackburn, Energy Environ. Sci., 2016, 9, 1439–1449 RSC.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss, W. L. Mao and H. I. Karunadasa, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS PubMed.
- W. Tian, R. Cui, J. Leng, J. Liu, Y. Li, C. Zhao, J. Zhang, W. Deng, T. Lian and S. Jin, Angew. Chem., Int. Ed., 2016, 55, 13067–13071 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details about sample preparation and TA and TR measurements, and additional TA and TR data. See https://doi.org/10.1039/d2sc01826h |
| This journal is © The Royal Society of Chemistry 2022 |