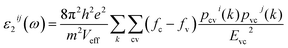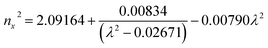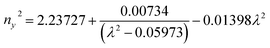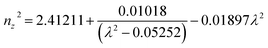A flexible functional module to regulate ultraviolet optical nonlinearity for achieving a balance between a second-harmonic generation response and birefringence

Abstract

Rigid planar π-conjugated groups are adopted for designing ultraviolet (UV) nonlinear optical (NLO) materials extensively. However, for these UV NLO crystals, the realization of a strong second harmonic generation (SHG) response is commonly accompanied by undesired overlarge birefringence. Herein, we propose a new functional gene, the flexible π-conjugated (C₃H₂O₄)²⁻ group, for designing a UV NLO crystal with a balance between the SHG response and birefringence. Furthermore, the combination of low-coordinated and high-coordinated alkali cations with the flexible (C₃H₂O₄)²⁻ group results in finding a new mixed alkali malonate, KLi(C₃H₂O₄)·H₂O (KLMW). As expected, KLMW exhibits a strong SHG efficiency (3 × KDP) and moderate birefringence (0.103 @ 1064 nm). In addition, it has a short UV cut-off edge of 231 nm and can be conveniently grown from solution. More importantly, it realized fourth harmonic generation with type-I phase-matching. Therefore, these excellent properties make KLMW a potential practical UV NLO material.

---

1. Introduction

Ultraviolet (UV) all-solid-state lasers are widely used in optical communication and laser processing, in which UV nonlinear optical (NLO) crystals as an essential component play an indispensable role in extending the wavelength.^1–3 In the past several decades, the continuous pursuit of high-performance UV NLO crystals has promoted the development of many explorative systems, such as borates (fluorooxoborates),^4–9 carbonates,^10,11 phosphates (monofluorophosphates),^12–15 sulfates,^16,17 and so on. To date, however, although a lot of UV NLO crystals have been reported, the progress of their commercialization has been retarded, mainly due to either the difficulty of crystal growth or some performance pitfalls. Thus, the development of new UV NLO crystals with excellent comprehensive performance and easy growth is significant and challenging.

Currently, fundamental building blocks (FBBs) for constructing UV NLO crystals can be classified into two main categories, π-conjugated planar groups and non-π-conjugated tetrahedral groups. Among them, π-conjugated planar groups are widely recognized as ideal FBBs for UV NLO crystals because they possess large microscopic second-order susceptibility and strong optical anisotropy, which are beneficial for achieving remarkable SHG efficiency and large birefringence (Δn). Particularly, π-conjugated planar B–O groups, such as (BO₃)³⁻ units in KBe₂BO₃F₂ (KBBF) and Sr₂Be₂B₂O₇ (SBBO),¹⁸ and (B₃O₆)³⁻ units in β-BaB₂O₄ (BBO),⁴ play dominant roles in building superior UV NLO materials. In recent years, inspired by these classical functional modules, some organic π-conjugated planar groups have been successfully developed, such as [C(NH₂)]₃⁺ units in C(NH₂)₃SO₃F¹⁹ similar to (BO₃)³⁻ units, and (C₃N₃O₃)³⁻ units in KLi(HC₃N₃O₃)·2H₂O (KLHCY)²⁰ similar to (B₃O₆)³⁻ units. However, when these rigid π-conjugated planar triangle or planar six-membered ring groups are employed in constructing UV NLO crystals with strong SHG responses, there will be a generally ignored issue, namely, accompanying overlarge birefringence (Δn > 0.11 at 1064 nm) due to the alignment of π-conjugated planar groups. For UV NLO crystals, overlarge birefringence tends to cause the spatial walk-off effect that affects the frequency doubling efficiency, which limits the practical application of crystals. The famous example is the commercial BBO crystal, which has a strong SHG efficiency of more than 5 times that of KH₂PO₄ (KDP) but suffers from an overlarge birefringence (0.113 @ 1064 nm) hindering its high-power output. To our knowledge, thus far, there has been no study on designing UV NLO crystals with a balance between a strong SHG response and moderate birefringence (0.07 < Δn < 0.11).

In 2019, Pan et al. employed a flexible π-conjugated (B₂O₅)⁻ functional module for designing birefringent crystals. They adopted reasonable cation collocation to make the flexible (B₂O₅)⁻ functional module completely coplanar, which results in a large birefringence of 0.095 @ 532 nm in Li₂Na₂B₂O₅.²¹ Inspired by this work, we proposed that flexible π-conjugated groups should be employed for the performance modulation in NLO crystals because the delocalized π electrons within the group are favourable for the enhancement of the SHG response on one hand, and on the other hand the flexible rotation of the groups is beneficial for modulating the birefringence, consequently which may achieve a balance between a strong SHG response and moderate birefringence of UV NLO materials. Guided by this idea, we screened out malonic acid as a functional module because it has a similar geometric configuration to flexible (B₂O₅)⁻ groups. In addition to malonic acid, alkali-metal cations were considered as counter ions to crystals for the following reasons. Firstly, the introduction of alkali-metals with strong ionicity is conducive to expanding the band gap. Secondly, the reasonable combination of low coordinated and highly coordinated alkali-metal cations can adjust the arrangement of flexible π-conjugated groups, thus modulating the birefringence, which has been confirmed by Pan et al.^21–24

Based on the above considerations, a systematic exploration of mixed alkali-metal (including both low-coordinated Li⁺ cations and highly coordinated cations (Na⁺, K⁺, Rb⁺, and Cs⁺)) malonates results in finding a non-centrosymmetrical (NCS) compound KLi(C₃H₂O₄)·H₂O (KLMW). As expected, benefiting from the modulation of flexible π-conjugated (C₃H₂O₄)²⁻ groups, KLMW achieves a balance between a large SHG response (3 × KDP) and suitable birefringence (0.103 @ 1064 nm). Notably, such a birefringence is very suitable and the smallest among those of recently reported organic–inorganic hybrid UV NLO crystals. In addition, centimeter-level KLMW single crystals can be grown conveniently by an aqueous solution method (Fig. S1†). More importantly, the fourth harmonic generation of Nd:YAG laser radiation (1064 nm) with type-I phase-matching was realized in KLMW.

2. Experimental section

2.1. Reagents

LiOH·H₂O (98%, Sinopharm), KOH (85.0%, Sinopharm) and C₃H₄O₄ (99%, Adamas) were of analytical grade from commercial sources and used without further purification.

2.2. Synthesis and crystal growth

A reaction mixture of LiOH·H₂O (0.21 g, 5 mmol), KOH (0.28 g, 5 mmol), and C₃H₄O₄ (0.52 g, 5 mmol) in H₂O (2.5 mL) was placed in a 25 mL glass beaker. The beaker was placed on a magnetic stirrer and the reaction mixture was stirred until it became a clear solution. Then, the beaker was heated to 40 °C in an oven, and held at this temperature for 2 days. Colorless and transparent single crystals were gradually precipitated with the evaporation of the solution. Crystals of KLMW were grown via an aqueous solution evaporation method. The reaction mixture of LiOH·H₂O (294 g, 7 mol), KOH (392.7 g, 7 mol), and C₃H₄O₄ (728.42 g, 7 mol) was dissolved in H₂O (1400 mL) using a water bath (40 °C). Then the solution was poured into a glass crucible (Φ 200 mm × 300 mm) that was placed in a constant temperature (40 °C) water bath with a rotating speed of 466 rpm. The solution was evaporated for 30 days. High-quality, colorless bulk crystals of KLMW with the largest size up to 17 × 14 × 10 mm³ were obtained (Fig. S1†).

2.3. Single crystal structure determination

Single crystal X-ray diffraction data of the title compounds were collected at room temperature on a Rigaku Mercury CCD diffractometer with graphite-monochromatic Mo Kα radiation (λ = 0.71073 Å). A transparent block of crystal was mounted on a glass fiber with epoxy for structure determination. The intensity datasets were corrected with the ω-scan technique. The data were integrated with the CrystalClear program. The intensities were corrected for Lorentz polarization, air absorption, and absorption attributable to the variation in the path length through the detector faceplate. Absorption corrections were also applied based on the Multiscan technique. The structures were solved with direct methods, refined with difference Fourier maps and full-matrix least-squares fitting on F² with SHELXL-97.²⁵ In addition, the PLATON²⁶ program was used for checking the structures, and no higher symmetry was found. The crystallographic data are listed in Table S1.† The related atomic coordinates, isotropic displacement coefficients, and bond lengths and angles are listed in Tables S2–S4.†

2.4. Powder X-ray diffraction (XRD)

The powder X-ray diffraction (PXRD) data were collected with a Mini-flex 600 Powder X-ray diffractometer (Cu Kα radiation with λ = 1.540598 Å, 2θ = 5–85°, scan step width = 0.02°) at room temperature. No impurity is found in KLMW (Fig. S2†).

2.5. EDS analysis

Microprobe elemental analyses were performed using a field emission scanning electron microscope (FESEM, SU-8010) equipped with an energy dispersive X-ray spectrometer (EDS). EDS measurements confirm the presence of relevant elements including K, C, and O, in the title crystal (Fig. S3†).

2.6. Thermal analysis

Thermogravimetric analysis (TGA) was performed using a NETZSCH STA449F3 simultaneous analyser with an Al₂O₃ crucible as a reference. Crystal samples (5–10 mg) were enclosed in Al₂O₃ crucibles and heated from 30 to 1000 °C at a rate of 10 °C min⁻¹ under a constant flow of nitrogen gas (Fig. S4†).

2.7. Optical properties

UV-Vis-NIR transmittance spectroscopy data in the wavelength range of 190–2500 nm were recorded at room temperature using a polished wafer of KLMW on a PerkinElmer Lambda-950 UV/vis/NIR spectrophotometer.

2.8. Refractive index dispersion measurements

The refractive index measurements were carried out using three ((100), (010), (001)) crystal plates (polished, size: 6 × 6 × 2 mm³) on a Metricon model 2010/M prism coupler (Metricon Co.) at five wavelengths (407, 514, 636, 965, and 1547 nm), and the accuracy of the measurements was estimated to be 2 × 10⁻⁴. By changing the polarization state of the laser, index anisotropy, i.e., birefringence can be measured along the X, Y and Z directions, respectively.

2.9. SHG response

Powder second-harmonic generation (SHG) signal tests were performed by the Kurtz–Perry²⁷ powder method with a Q-switched Nd:YAG solid-state laser of fundamental wavelength 1064 nm with frequency doubling at 532 nm. Polycrystalline samples of KLMW were ground and sieved into the following particle size ranges: 25–45, 45–62, 62–75, 75–109, 109–150, and 150–212 μm. The sieved KDP samples were used as standard samples. The samples were pressed between two glass slides and secured in 1 mm thick aluminum holders with an 8 mm diameter hole. Then the samples were irradiated with a pulsed laser, and the second harmonic output was separated by a narrowband pass filter (530 ± 10 nm) and detected by a photomultiplier tube attached to a RIGOL DS1052E 50 MHz oscilloscope. The above procedures were repeated for the reference samples of KDP. No index-matching fluid was used in any of the experiments.

2.10. Computational methods

The first principles calculations were performed by the plane-wave pseudopotential method implemented in the CASTEP²⁸ code. The exchange–correlation interaction was calculated by using the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE).²⁹ The energy cutoff for the plane wave was chosen as 750 eV, and the self-consistent convergence of the total energy was set to 0.1 × 10⁻⁵ eV per atom. The Monkhorst–Pack³⁰k-point in the Brillouin zone was set as 2 × 2 × 2 for KLMW. The norm-conserving pseudopotentials were applied to express the interactions between the valence electrons and ionic core, and the following valence configurations were regarded: Li, 2s¹; K, 3s²3p⁶4s¹; C, 2s²2p²; O, 2s²2p⁴. The SHG coefficients were calculated by the classical anharmonic oscillator (AHO)³¹ model. The formula of calculated second-order susceptibilities can be expressed as follows:

x⁽²⁾_ijk(−ω₃;ω₁,ω₂) = F⁽²⁾x⁽¹⁾_ii(ω₃)x⁽¹⁾_jj(ω₁)x⁽¹⁾_kk(ω₂)

where x⁽¹⁾_ii denotes the first-order susceptibility, and it is given by x⁽¹⁾(ω)_ii = [ε(ω)_ii − 1]/4π in the low-frequency region, and the dielectric function

δ[E_c(k) − E_v(k) − hω]

where f_c and f_v represent the Fermi distribution functions of the conduction and valence bands, respectively. δ[E_c(k) − E_v(k) − hω] denotes the energy difference between the conduction and valence bands at the k point with absorption of a quantum hω. It is generally acknowledged that the GGA calculations commonly underestimate the energy band gap of the crystal. Therefore, to match with the experimental band gap, the scissors operation should be employed to shift up the conduction band energy.

3. Results and discussion

3.1. Crystal structure

KLMW crystallizes in an orthorhombic polar space group Pna2₁ (no. 33). The asymmetric unit of KLMW contains one unique K atom, one Li atom, three C atoms and five O atoms. As shown in Fig. 1, the anionic structural motif of KLMW is the (C₃H₂O₄)²⁻ group, showing typical bond lengths (C–C: 1.524(4)–1.536(4) Å; C–O: 1.250(4)–1.260(4) Å) and bond angles (C–C–C: 110.5(2)°; O–C–C: 116.7(3)–118.4(3)°; O–C–O: 123.5(3)–124.9(3)°). (C₃H₂O₄)²⁻ groups exhibit interesting flexibility, and the rotation angle of (C₃H₂O₄)²⁻ groups (the bond angle of C–C–C) and the dihedral angle between two C₂O₂ planes in one (C₃H₂O₄)²⁻ group are defined as α and β, with values of 110.5° and 73.74°, respectively. Because of the symmetrical operation of the space group, the unique (C₃H₂O₄)²⁻ groups crystallographically express four directions in the unit cell, but the polarization directions of all anionic groups are along the c axis. Moreover, the Li atom is surrounded by four O atoms, forming distorted tetrahedron LiO₄ with Li–O bond lengths of 1.899(6)–1.951(6) Å. It is noteworthy that the (C₃H₂O₄)²⁻ groups are bridged by LiO₄ polyhedra to form an intricate three dimensional (3D) [Li(C₃H₂O₄)O₃]_∞ network structure (Fig. 1c). The K⁺ cations are tidily located in framework gaps to keep the structural stability and electrovalence balance (Fig. 1d). Therefore, the structure of KLMW can be described as an intricate 3D [Li(C₃H₂O₄)O₃]_∞ framework embedded with K atoms and H₂O molecules.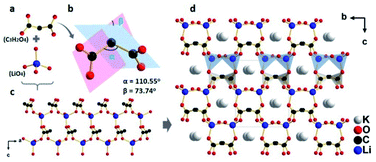

Fig. 1 (a) (C₃H₂O₄)²⁻ group and LiO₄ tetrahedron, (b) rotation and dihedral angles of the (C₃H₂O₄)²⁻ group, (c) [Li(C₃H₂O₄)O₃] network structure, and (d) crystal structure of KLMW.

3.2. Structural comparison and evolution

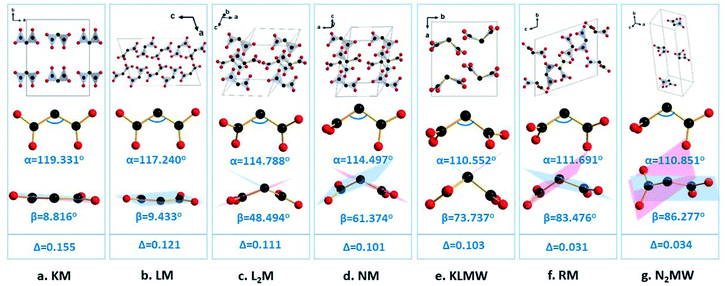
Previous studies showed that alkali metal cations with different radii can be employed to modulate the arrangement of anionic groups, and thus control optical properties.^32–34 In order to show the effects of alkali metal cations on the structural modulation in KLMW, three alkali malonates, Li(C₃H₃O₄)(C₃H₄O₄) (LM), Li₂(C₃H₂O₄) (L₂M),³⁵ and K(C₃H₃O₄) (KM),³⁶ are selected for comparison. For these four compounds, alkali metal Li atoms have two different coordination numbers (CNs) of 4 and 5, and alkali metal K atoms have the same CN of 7. Notably, for LM, L₂M and KM, it can be seen that the lower the CN of Li is, the more positive the rotation of the dihedral angle β of (C₃H₂O₄)²⁻ is (β(LM) = 9.433, β(L₂M) = 48.494 and β(KLMW) = 73.737°) (Fig. 4). This suggests that the four-coordinated Li atoms may have the potential to regulate the flexibility of (C₃H₂O₄)²⁻ groups. In addition, for the selected three compounds, there is only a single alkali metal Li or K atom, which further combined with malonate groups forming the centrosymmetric structures. Compared with them, the combination of the four-coordinated Li atoms and seven-coordinated K atoms in KLMW drives the formation of the NCS structure. According to previous studies, the combination of low-coordinated and high-coordinated cations is beneficial to optimizing the arrangement of anionic groups and producing excellent NLO properties, such as the KBBF family,^7,37–39 AB₂O₅ (A = Li₄, Na₄, Li₂Na₂),²¹ LiBa₃Bi₆(SeO₃)₇F₁₁ and Ba₃Bi_6.5(SeO₃)₇F_10.5O_0.5.⁴⁰ Therefore, it can be expected that KLMW will have superior linear and nonlinear optical properties.

3.3. Thermal analysis

The thermodynamic analysis of KLMW exhibited three steps of weight loss (Fig. S4†). The first weight loss was at about 120 °C with the weightlessness ratios 10.73% (10.85%), corresponding to the release of 1 mol of H₂O per formula. The second and third weight losses were in the range of 300–920 °C with the weightlessness ratios 53.98% (51.78%), corresponding to the release of 1 mol of C₃H₂O₄ per formula. Several endothermic peaks in DTA are expressed in this temperature range, showing that the decomposition of KLMW is a complex reaction.

3.4. Linear optical properties

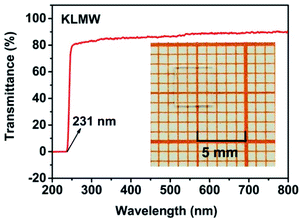
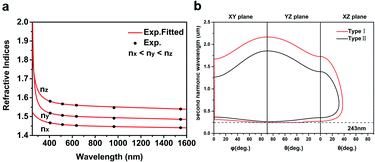
Ultraviolet-visible-near infrared (UV-Vis-NIR) transmittance spectroscopy was performed by using a polished wafer of KLMW (Fig. 2), revealing that KLMW has no obvious absorption peak in the range of 250–800 nm. Also, the UV cut-off edge of KLMW is 231 nm, which is shorter than those of the most reported organic–inorganic hybrid UV crystals including KLi(HC₃N₃O₃)·2H₂O (237 nm),²⁰ RbNa(HC₃N₃O₃)·H₂O (241 nm),⁴¹ (C₅H₆ON)⁺(H₂PO₄)⁻ (264 nm),⁴² (H₇C₃N₆)(H₆C₃N₆)ZnCl₃ (236 nm)⁴³ and Ba₃(C₃N₃O₃)₂ (241 nm).⁴⁴

Fig. 2 Ultraviolet-visible-near-infrared transmittance spectrum of the KLMW crystal wafer.

In addition to the short UV cut-off edge, to achieve a UV coherent light output, the key is to realize phase-matching conditions, which depend on the appropriate birefringence and chromatic dispersion. Therefore, refractive index dispersion was measured by the prism coupling method at five different wavelengths (407, 514, 636, 965 and 1547 nm). Then, the Sellmeier equation was employed to fit the function between the refractive index and wavelength based on the least-squares method, i.e.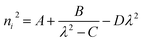, where n_i is the refractive index, A–D are the parameters, and λ is the wavelength (Fig. 3a).

Fig. 3 (a) Refractive indices of the KLMW single crystal. (b) Phase-matching conditions of KLMW.

The birefringence of KLMW calculated from the above equations is 0.103 @ 1064 nm. Such a birefringence is not only smaller than that of BBO (0.113 @ 1064 nm), but also the smallest among those of recently reported organic–inorganic hybrid UV NLO crystals (Table 1), which is befitting for the UV NLO crystal.

Table 1 The SHG response and birefringence of some recently reported organic–inorganic hybrid UV NLO crystals

Crystal	SHG response (× KDP)	Δn	Ref
a This work.
Ca(H3C4N2O3)2·H2O	1.15	0.49 @ 546 nm^Exp	48
Cs3Na(H2C3N3O3)4·3H2O	2.3	0.29 @ 514 nm	49
(H7C3N6)(H6C3N6)ZnCl3	2.8	0.255 @ 1064 nm	36
RbNa(HC3N3O3)·2H2O	5.3	0.194 @ 546 nm^Exp	50
RbLi(HC3N3O3)·2H2O	2.1	0.18 @ 546 nm^Exp	51
KLiHC3N3O3·2H2O	5.3	0.166 @ 1064 nm	20
KCs2[Pb2Br5(HCOO)2]	6.5	0.16 @ 1064 nm	52
(NH4)3[B(OH)3]2(COOH)3	0.6	0.156 @ 546 nm^Exp	53
Y[N(CN)2]4[NH(C2H5)3]∙3H2O	2.8	0.137 @ 546 nm	54
NH4Sb2(C2O4)F5	1.1	0.111 @ 546 nm	55
KLi(C3H2O4)·H2O	3	0.103 @ 1064 nm

---

Furthermore, based on the Sellmeier equations, the phase matching ability of KLMW was evaluated. According to the calculated phase matching curves (Fig. 3b), KLMW could achieve type I phase matching SHG wavelengths down to 243 nm which can be comparable to those of many excellent UV NLO crystals, including KLi(HC₃N₃O₃)·2H₂O (246 nm), CsLiB₆O₁₀ (CLBO) (237 nm),⁴⁵ KH₂PO₄ (KDP) (258 nm),⁴⁶ LiB₃O₅ (LBO) (277 nm)⁴⁵ and K₃B₆O₁₀Cl (255 nm).⁴⁷ Such a short UV phase matching SHG wavelength suggests that KLMW has potential application in the UV region.

According to the anionic group theory, the birefringence of the NLO crystal depends on the contribution of the valence electron orbitals of anionic groups and the influence of the direction cosines (between the macroscopic coordinate axis of the unit cell and the microscopic coordinate axis of anionic groups).

Therefore, the flexible (C₃H₂O₄)²⁻ groups should be responsible for the moderate birefringence of KLMW. In order to demonstrate the modulation of birefringence by flexible π-conjugated malonate groups, a series of alkali metal malonates containing different geometrical configurations of malonate groups is investigated. Furthermore, their birefringence was calculated by the first-principles theory (Fig. S6†). It is well known that, for an isolated group, the closer the geometrical configuration is to being planar, the larger the optical anisotropy is. Therefore, the rigid planar π-conjugated groups, such as (BO₃)³⁻ and (B₃O₆)³⁻ groups, have considerable optical anisotropies. If these rigid π-conjugated groups further have a coplanar arrangement in the crystal, overlarge birefringence is inevitable, such as in BBO. With regard to the malonate groups, since they are flexible, their geometrical configurations are determined by the rotation angle α and dihedral angle β, by which their optical anisotropies can be modulated. The rotation angles (α) of the malonate groups are in-plane and similar (110.552–119.331°) in these examples, and will not cause great effects on their optical anisotropies. Therefore, it can be deduced that the optical anisotropy of the malonate group should be determined by its dihedral angle β. In principle, the larger the dihedral angle β (<90°) is, the smaller the optical anisotropy of the malonate group is. It is noteworthy that, in addition to the intrinsic optical anisotropies of malonate groups, their arrangement will affect the birefringence. Herein, for the convenience of discussion, the arrangement of malonate groups is not being considered in these cases, which results in slightly irregular variation trends of birefringence from Na(C₃H₃O₄) to KLMW and from Rb₂(CH₃O₄)₂(C₃H₄O₄) to Na₂(C₃H₂O₄)·3H₂O. Even so, as shown in Fig. 4, with the increase of β from 8.816° to 86.277°, the birefringence of the crystals gradually decreased as a whole from 0.155 to 0.034 @ 1064 nm, which is basically consistent with the above deduction. In addition, it can be seen that the overlarge angle β leads to small birefringence in Rb₂(CH₃O₄)₂(C₃H₄O₄) and Na₂(C₃H₂O₄)·3H₂O, which indicates that the suitable angle β is key to obtaining moderate birefringence. Therefore, rationally regulating the flexible π-conjugated groups will be an effective approach to obtain NLO crystals with suitable birefringence.

Fig. 4 Comparisons of rotation angles, dihedral angles, and birefringence for (C₃H_xO₄) groups in (a) K(C₃H₃O₄) (KM), (b) Li(C₃H₃O₄)(C₃H₄O₄) (LM), (c) Li₂(C₃H₂O₄) (L₂M), (d) Na(C₃H₃O₄) (NM), (e) KLi(C₃H₂O₄)·H₂O (KLMW), (f) Rb₂(C₃H₃O₄)₂(C₃H₄O4) (RM), and (g) Na₂(C₃H₂O₄)·3H₂O (N₂MW).

3.5. NLO properties

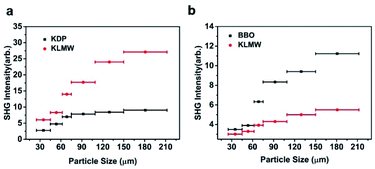
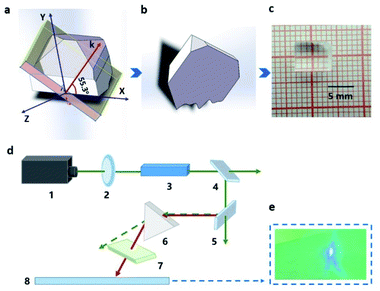
The powder SHG measurement of KLMW was performed at 1064 nm and 532 nm laser wavelengths based on the Kurtz and Perry method, respectively. The results reveal that KLMW can realize phase-matching in the visible and UV regions, which supports the above-mentioned phase matching calculations of KLMW. Meanwhile, the SHG efficiency of KLMW is about 3.0 times that of KDP at 1064 nm and 0.5 times that of BBO at 532 nm (Fig. 5). Such a strong SHG response is larger than those of most of the recently reported organic–inorganic hybrid UV NLO crystals (Table 1) and can be comparable with those of some well-known UV NLO materials, including NH₄B₄O₆F (∼3 × KDP),⁸ M₂B₁₀O₁₄F₆ (M = Ca, Sr) (2.5, 2.3 × KDP),⁹ ABCO₃F (A = K, Rb; B = Mg, Ca, Sr) (3–3.6 × KDP),^10,56 LBO (2.2 × KDP)⁵ and CLBO (2.4 × KDP).⁵² According to the anionic group theory, the SHG response of KLMW is dominated by the flexible π-groups. Although the (C₃H₂O₄)²⁻ groups are non-coplanar in order to achieve moderate birefringence, the microscopic second order polarizabilities produced by the (C₃H₂O₄)²⁻ groups are superimposed along the c-axis (Fig. S7†), which makes a major contribution to the SHG response. Therefore, owing to the rational arrangement of (C₃H₂O₄)²⁻ groups, KLMW achieves a balance between a strong SHG response and suitable birefringence.

Fig. 5 Powder SHG measurements of KLMW at (a) 1064 nm and (b) 532 nm.

The fourth-harmonic generation of 266 nm light was carried out using a Nd:YAG laser. According to the phase condition (angle between the wave vector and optical axis (θ): 90°, and azimuth angle of wave vector (φ): 55.3°), a crystal plate of KLMW with a size of 7 × 6 × 4 mm³ after polishing was prepared as a sample (Fig. 6a–c). In the experiment (Fig. 6d), a blue laser spot on the UV-sensitive paper was observed (Fig. 6e), indicating that the 266 nm SHG process was successfully realized. This result further supports the phase-matching ability of KLMW.

Fig. 6 Scheme of the 266 nm SHG experiment. (a) The principle of crystal plate processing. (b) Crystal plate model. (c) The single crystal plate has a size of 7 × 6 × 4 mm³. (d) The SHG experimental setup: (1) Nd:YAG solid-state laser; (2) convex lens; (3) KLMW crystal plate; (4) and (5) high reflective lens; (6) equilateral dispersive prism; (7) narrowband pass filter (at 266 nm); (8) UV-sensitive paper. (e) The blue laser spot on the UV-sensitive paper indicates the generation of a 266 nm laser.

3.6. Theoretical calculation description

To gain further insight into the mechanism behind the optical properties of KLMW, its electronic structures were calculated by DFT methods. The band structure of KLMW based on the GGA method is shown in Fig. S8,† where the calculated band gap (5.08 eV) is slightly underestimated compared with the experimental one (5.32 eV). The total and partial densities of states (PDOSs) are shown in Fig. 7a. It is clear that the uppermost part of the valence band (VB; −7.5 to 0 eV) is essentially occupied by O 2p orbitals with an appreciable contribution of the C 2p orbital, while the bottom of the conduction band (CB) is also occupied by O 2p and C 2p orbitals. It is well known that the optical properties are essentially influenced by electronic transitions in the states around the Fermi level. Thus, it can be seen that (C₃H₂O₄)²⁻ groups should make a major contribution to the linear and nonlinear optical properties of the title compound.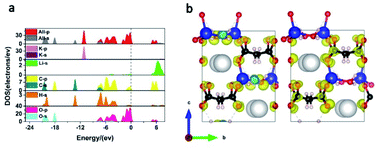

Fig. 7 (a) Total and partial densities of states. (b) SHG-weighted density for the occupied (left) and the unoccupied (right) electronic states of KLMW.

The calculated refractive index curves of the title compound are plotted in Fig. S9,† which shows that the birefringence of KLMW is 0.108 @ 1064 nm, which is in accordance with the experimental value. In addition, the theoretical values of NLO coefficients were investigated. Under the consideration of the point group of mm2, KLMW has three nonzero independent NLO coefficients d₃₁, d₃₂ and d₃₃. The calculated results showed that they are −0.441, −1.597 and 1.914 pm V⁻¹ at 1064 nm, respectively (Fig. S10†). Among them, the largest NLO coefficient d₃₃ is 4.9 times that of KDP, which is slightly larger than the experimental one. Furthermore, in order to reveal the SHG origin of KLMW, the SHG-weighted density of the largest tensor d₃₃ was calculated (Fig. 7b). Obviously, the nonbonding 2p orbitals of O atoms in (C₃H₂O₄)²⁻ groups make major contributions to the SHG response of KLMW.

Conclusions

In summary, a new inorganic–organic compound KLi(C₃H₂O₄)·H₂O was successfully designed and synthesized. KLi(C₃H₂O₄)·H₂O has excellent optical nonlinearity including a short UV cut-off edge (231 nm), strong SHG response (3 × KDP) and moderate birefringence (0.103 @ 1064 nm). In addition, its bulk crystals can be easily grown via simple solution evaporation. Preliminary laser experiments indicated that KLi(C₃H₂O₄)·H₂O is suitable for fourth harmonic generation of the Nd:YAG laser output. Importantly, our study showed that it is a feasible way to employ flexible functional modules to design UV NLO materials with a balance between a strong SHG response and moderate birefringence, which will guide the design of new UV NLO materials.

Data availability

Crystal data, structure refinement, atomic coordinates, isotropic displacement coefficients, bond lengths and angles, and additional tables/figures can be found in the ESI.†

Author contributions

L. L. Cao: conceptualization, methodology, investigation, writing – original draft, and writing – review & editing. H. T. Tian and B. X. Li: data curation. D. H. Lin: conceptualization, investigation. C. S. Lin, F. Xu and Y. L. Han: software. T. Yan and J. D. Chen: investigation. N. Ye: resources, supervision. M. Luo: formal analysis, project administration, resources, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant no. 21975255 and 21921001), the Foundation of Fujian Science & Technology Innovation Laboratory (2021ZR202), and Youth Innovation Promotion Association CAS (2019303). We thank Professor Shilie Pan and Doctor Miriding Mutailipu at CAS Key Laboratory of Functional Materials and Devices for Special Environments, Xinjiang Technical Institute of Physics & Chemistry, CAS, and Xinjiang Key Laboratory of Electronic Information Materials and Devices for their help with refractive index measurements.

Notes and references

1. D. F. Eaton, Science, 1991, 253, 281–287.
2. T. Kiss, T. Shimojima, F. Kanetaka, K. Kanai, T. Yokoya, S. Shin, Y. Onuki, T. Togashi, C. Q. Zhang and C. T. Chen, J. Electron. Spectrosc., 2005, 144, 953–956.
3. N. Savage, Nat. Photonics, 2007, 1, 83–85.
4. C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. Sin. Ser. B (Chem. Biol. Agric. Med. Earth Sci.), 1985, 28, 235–243.
5. C. T. Chen, Y. C. Wu, A. D. Jiang, B. C. Wu, G. M. You, R. K. Li and S. J. Lin, J. Opt. Soc. Am. B, 1989, 6, 616–621.
6. Y. C. Wu, T. Sasaki, S. Nakai, A. Yokotani, H. G. Tang and C. T. Chen, Appl. Phys. Lett., 1993, 62, 2614–2615.
7. C. T. Chen, G. L. Wang, X. Y. Wang and Z. Y. Xu, Appl. Phys., 2009, 97, 9–25.
8. G. Q. Shi, Y. Wang, F. F. Zhang, B. B. Zhang, Z. H. Yang, X. L. Hou, S. L. Pan and K. R. Poeppelmeier, J. Am. Chem. Soc., 2017, 139, 10645–10648.
9. M. Luo, L. Fei, Y. X. Song, D. Zhao and F. Xu, J. Am. Chem. Soc., 2018, 140, 3884–3887.
10. T. T. Tran, J. G. He, J. M. Rondinelli and P. S. Halasyamani, J. Am. Chem. Soc., 2015, 137, 10504–10507.
11. L. L. Cao, Y. X. Song, G. Peng, M. Luo, Y. Yang, C. S. Lin, D. Zhao, F. Xu, Z. S. Lin and N. Ye, Chem. Mater., 2019, 31, 2130–2137.
12. W. G. Zhang, J. M. Rondinelli, J. Young and P. S. Halasyamani, Chem. Mater., 2017, 29, 1845–1855.
13. Z. Y. Bai, C. L. Hu, L. H. Liu, L. Z. Zhang, Y. S. Huang, F. F. Yuan and Z. B. Lin, Chem. Mater., 2019, 31, 9540–9545.
14. L. Lu, J. L. Yue, L. Xiong, W. K. Zhang and C. Chen, J. Am. Chem. Soc., 2019, 141, 8093–8097.
15. F. Xu, G. Peng, C. S. Lin, D. Zhao, B. X. Li, G. Zhang, S. D. Yang and N. Ye, J. Mater. Chem. C, 2020, 8, 4965–4972.
16. F. F. He, Q. Wang, C. F. Hu, W. He, X. Y. Luo, L. Huang, D. J. Gao, J. Bi, X. Wang and G. H. Zou, Cryst. Growth Des., 2018, 18, 6239.
17. F. F. He, Y. L. Deng, X. Y. Zhao, L. Huang, D. J. Gao, J. Bi, X. Wang and G. H. Zou, J. Mater. Chem. C, 2019, 7, 5748–5754.
18. C. T. Chen, B. C. Wu, K. C. Wu, W. L. Zeng, L. H. Yu and Y. B. Wang, Nature, 1995, 373, 322–324.
19. M. Luo, C. S. Lin, D. H. Lin and N. Ye, Angew. Chem., Int. Ed., 2020, 59, 15978–15981.
20. D. H. Lin, M. Luo, C. S. Lin, F. Xu and N. Ye, J. Am. Chem. Soc., 2019, 141, 3390–3394.
21. M. Zhang, D. H. An, C. Hu, X. L. Chen, Z. H. Yang and S. L. Pan, J. Am. Chem. Soc., 2019, 141, 3258–3264.
22. X. H. Meng, F. Liang, M. J. Xia and Z. S. Lin, Inorg. Chem., 2018, 57, 5669–5676.
23. H. P. Wu, H. W. Yu, S. L. Pan and P. S. Halasyamani, Inorg. Chem., 2017, 56, 8755–8758.
24. S. G. Zhao, L. Kang, Y. G. Shen, X. D. Wang, M. A. Asghar, Z. S. Lin, Y. Y. Xu, S. Y. Zeng, M. C. Hong and J. H. Luo, J. Am. Chem. Soc., 2016, 138, 2961–2964.
25. G. M. Sheldrick, Acta Crystallogr., 2008, 64, 112–122.
26. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
27. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
28. S. J. Clark, M. Segallii, C. J. Pickardii, P. J. Hasnip, M. I. J. Probertiv, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 77, 3865–3868.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
31. R. W. Boyd, Nonlinear Opt., 1992, 21.
32. K. M. Ok, Acc. Chem. Res., 2016, 49, 2774–2785.
33. G. S. Yang, P. F. Gong, Z. S. Lin and N. Ye, Chem. Mater., 2016, 28, 9122–9131.
34. G. H. Zou, N. Ye, L. Huang and X. S. Lin, J. Am. Chem. Soc., 2011, 133, 20001–20007.
35. M. Soriano-Garcia and S. N. Rao, Acta Crystallogr. C, 1983, 39, 850–852.
36. M. Barnes, Can. J. Chem., 1956, 34, 563–566.
37. C. T. Chen, Opt. Mater., 2004, 26, 425–429.
38. D. Cyranoski, Nature, 2009, 457, 953–955.
39. G. Peng, N. Ye, Z. S. Lin, L. Kang, S. L. Pan, M. Zhang, C. S. Lin, X. F. Long, M. Luo, Y. Chen, Y. H. Tang, F. Xu and T. Yan, Angew. Chem., Int. Ed., 2018, 57, 8968–8972.
40. S. S. Shi, C. S. Lin, D. Zhao, M. Luo, L. L. Cao, G. Peng and N. Ye, Chem. Commun., 2021, 57, 2982–2985.
41. Y. X. Song, D. H. Lin, M. Luo, C. S. Lin, Q. T. Chen and N. Ye, Inorg. Chem. Front., 2020, 7, 150–156.
42. J. Lu, X. Liu, M. Zhao, X. B. Deng, K. X. Shi, Q. R. Wu, L. Chen and L. M. Wu, J. Am. Chem. Soc., 2021, 143, 3647–3654.
43. L. H. Liu, Z. Y. Bai, L. Hu, D. S. Wei, Z. B. Lin and L. Z. Zhang, J. Mater. Chem. C, 2021, 9, 7452–7457.
44. J. Tang, F. Liang, X. H. Meng, K. J. Kang, T. X. Zeng, W. L. Yin, M. J. Xia, Z. S. Lin and B. Kang, Dalton Trans., 2019, 48, 14246–14250.
45. C. T. Chen, T. Sasaki, R. K. Li, Y. C. Wu, Z. S. Lin, Y. Mori, Z. G. Hu, J. Y. Wang, A. Gerard, Y. Masashi and K. Yushi, Nonlinear Optical Borate Crystals: Principles and Applications, Wiley, 2012, pp. 153–171.
46. D. Eimerl, Ferroelectrics, 1987, 72, 95–139.
47. H. P. Wu, S. L. Pan, H. W. Yu, D. Z. Jia, A. M. Chang, H. Y. Li, F. F. Zhang and X. Huang, CrystEngComm, 2012, 14, 799–803.
48. Y. Y. Xu, C. S. Lin, D. H. Lin, M. Luo, D. Zhao, L. L. Cao and N. Ye, Inorg. Chem., 2020, 59, 15962–15968.
49. X. H. Meng, F. Liang, J. Tang, K. J. Kang, Q. Huang, W. L. Yin, Z. S. Lin and M. J. Xia, Eur.–J. Inorg. Chem., 2019, 23, 2791–2795.
50. Y. X. Song, D. H. Lin, M. Luo, C. S. Lin, Q. T. Chen and N. Ye, Inorg. Chem. Front., 2020, 7, 150–156.
51. X. H. Meng, F. Liang, K. J. Kang, J. Tang, T. X. Zeng, Z. S. Lin and M. J. Xia, Inorg. Chem., 2019, 58, 11289–11293.
52. Z. Q. Zhou, Q. R. Shui, R. B. Fu, Y. B. Fang, Z. J. Ma and X. T. Wu, Chem.–Eur. J., 2021, 27, 12976–12980.
53. Y. L. Deng, L. Wang, Y. W. Ge, L. Huang, D. J. Gao, J. Bi and G. H. Zou, Chem. Commun., 2020, 56, 9982–9985.
54. X. Chen, H. Wang, Y. C. Liu, Y. Zhou, W. Q. Huang, M. J. Li, Y. Q. Li, Y. X. Chen, S. G. Zhao and J. H. Luo, Chem.–Eur. J., 2021, 27, 1–5.
55. D. Zhang, Q. Wang, T. Zheng, L. Huang, L. L. Cao, D. J. Gao, J. Bi and G. H. Zou, J. Alloys Compd., 2021, 896, 162921.
56. T. T. Tran, J. S. Young, J. M. Rondinelli and P. S. Halasyamani, J. Am. Chem. Soc., 2017, 139, 1285–1295.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2130636. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc01910h

---