Open Access Article
Open Access ArticleTantalum, easy as Pi: understanding differences in metal–imido bonding towards improving Ta/Nb separations†
Alexander B.
Weberg‡
 a,
Subhajyoti
Chaudhuri‡
a,
Subhajyoti
Chaudhuri‡
 b,
Thibault
Cheisson§
b,
Thibault
Cheisson§
 a,
Christian
Uruburo
a,
Christian
Uruburo
 a,
Ekaterina
Lapsheva
a,
Pragati
Pandey
a,
Ekaterina
Lapsheva
a,
Pragati
Pandey
 a,
Michael R.
Gau
a,
Michael R.
Gau
 a,
Patrick J.
Carroll
a,
Patrick J.
Carroll
 a,
George C.
Schatz
a,
George C.
Schatz
 *b and
Eric J.
Schelter
*b and
Eric J.
Schelter
 *a
*a
aP. Roy and Diana T. Vagelos Laboratories, Department of Chemistry, University of Pennsylvania, 231 S. 34th St., Philadelphia, PA 19104, USA. E-mail: schelter@sas.upenn.edu
bDepartment of Chemistry, Northwestern University, 2145 Sheridan Rd., Evanston, IL 60208, USA. E-mail: g-schatz@northwestern.edu
First published on 12th May 2022
Abstract
The separation and purification of niobium and tantalum, which co-occur in natural sources, is difficult due to their similar physical and chemical properties. The current industrial method for separating Ta/Nb mixtures uses an energy-intensive process with caustic and toxic conditions. It is of interest to develop alternative, fundamental methodologies for the purification of these technologically important metals that improve upon their environmental impact. Herein, we introduce new Ta/Nb imido compounds: M(tBuN)(TriNOx) (1-M) bound by the TriNOx3− ligand and demonstrate a fundamental, proof-of-concept Ta/Nb separation based on differences in the imido reactivities. Despite the nearly identical structures of 1-M, density functional theory (DFT)-computed electronic structures of 1-M indicate enhanced basic character of the imido group in 1-Ta as compared to 1-Nb. Accordingly, the rate of CO2 insertion into the M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Nimido bond of 1-Ta to form a carbamate complex (2-Ta) was selective compared to the analogous, unobserved reaction with 1-Nb. Differences in solubility between the imido and carbamate complexes allowed for separation of the carbamate complex, and led to an efficient Ta/Nb separation (STa/Nb = 404 ± 150) dependent on the kinetic differences in nucleophilicities between the imido moieties in 1-Ta and 1-Nb.
Nimido bond of 1-Ta to form a carbamate complex (2-Ta) was selective compared to the analogous, unobserved reaction with 1-Nb. Differences in solubility between the imido and carbamate complexes allowed for separation of the carbamate complex, and led to an efficient Ta/Nb separation (STa/Nb = 404 ± 150) dependent on the kinetic differences in nucleophilicities between the imido moieties in 1-Ta and 1-Nb.
Introduction
Tantalum (Ta) and niobium (Nb) are two metals that are essential to various modern technologies and have been deemed “critical” due to their risk of supply. Ta metal is the optimal material for use in electrolytic capacitors and high-power resistors and cannot be replaced by alternatives without a corresponding loss of performance or increase in device size.1,2 Nb is most commonly applied as an additive for high-strength steels (ca. 80%) and in superalloys (ca. 19%) with superior heat and corrosion resistance.1 Ta and Nb have been classified as “critical” by the National Research Council of the United States and Ta has been classified as a conflict metal.3 Both metals were included on the European Union's 2017 list of the 27 most critical raw materials.4Ta and Nb are often referred to as “chemical twins” owing to their virtually identical physical and chemical properties.2 While Ta is most commonly obtained from the mineral tantalite [Fe, Mn][(Ta, Nb)O6], which is composed of 40–86% Ta2O5, and Nb is most commonly obtained from the mineral columbite [Fe, Mn][(Nb, Ta)O6], which is composed of 38–80% Nb2O5, each of these minerals always contains mixtures of Ta/Nb in different ratios.2,5 As such, generating suitably pure samples of either metal involves a Ta/Nb separation step, which is challenging due to their similar properties.
Historically, Ta/Nb separation was achieved through a tedious fractional crystallization, first proposed by Jean-Charles de Marignac in the 19th century, that took advantage of differing Ta/Nb speciation in dilute hydrofluoric acid (HF): K2TaF7versus K2NbOF5·2H2O (Fig. 1).8 This process was replaced in the 1960s with the Ames Laboratory process whereby TaF6− is extracted from dilute HF solutions of Nb(O)F52− using organic solvents such as methyl isobutyl ketone (MIBK), octanol, or cyclohexanone.9,10 Today, the primary methods for Ta/Nb separation are derived from this process.9–12 A drawback of these methods is the need for large quantities of HF. While the use of HF allows for good separation efficiencies and high concentrations of metal ions, the use of this toxic and corrosive reagent is nonideal, and ultimately leads to caustic and environmentally damaging waste streams. Developing new methods towards more sustainable, fluoride-free Ta/Nb separations is therefore an important fundamental chemical challenge and highly desirable from an industrial standpoint.5 Early research into fluoride-free Ta/Nb separations did not lead to economically competitive separations procedures.13–20 More recent work in this area has led to valuable insight into Ta/Nb digestion and separation,21–25 but are less efficient than currently adopted practices. Notably, Nete and coworkers recently published a fluoride-free Ta/Nb separation study wherein HF was substituted for a NaH2PO4/Na2HPO4 flux (800 °C), and achieved an ion-exchange chromatographic separation, with separation factors (STa/Nb)¶ ranging 9.5–11.5.25 Although not strictly fluoride-free, Nete and coworkers also reported on the selective precipitation of Nb over Ta from a mixture of the metal pentafluorides using 1,4-phenylenediamine, which led to a STa/Nb value of 100 ± 9.26 Hydrometallurgical methods for imparting fluoride-free Ta/Nb separations have been developed, which have resulted in more efficient separations (STa/Nb = 200–250).21 However, the majority of studies in this area of fluoride-free Ta/Nb separations have tended to be empirically driven, with less emphasis being placed on understanding the fundamental bonding interactions that lead to the metal–metal separations.
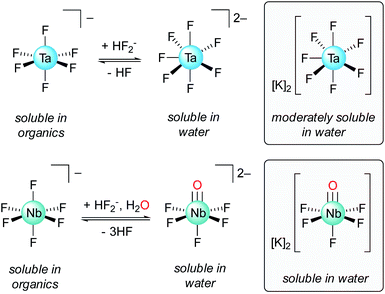 | ||
| Fig. 1 Ta/Nb equilibria in solutions of HF relevant to the industrial Ta/Nb separation procedure, and structures of the potassium heptafluoro-tantalate and pentafluoro-oxy-niobate complexes.6,7 | ||
While there exists a rich foundation of coordination chemistry for both Ta and Nb, comparatively few reports27–33 in this field directly compare fundamental differences in bonding and electronic structure between complexes of these two elements, with even fewer exploring these differences through the lens of Ta/Nb separations. As such, the task of designing alternative Ta/Nb separations procedures is made more difficult and is therefore studied almost exclusively through empirical approaches. Towards addressing this gap, our groups recently published a set of isostructural Ta/Nb tris(binolate) complexes in which differences in the metal–ligand π-bonding contributed to MV/IV redox couples that differed by ca. 0.75 V, allowing for the selective reduction and leaching of the Nb complex, resulting in a STa/Nb value of 6 ± 2.34 This study demonstrated a proof-of-concept Ta/Nb separation procedure based on fundamental differences in bonding interactions in Ta versus Nb complexes.
Herein we provide a fundamental study into new isostructural Ta/Nb-imido complexes and detailed analysis of their electronic structures and differences in bonding. In turn, this information is used to demonstrate predictable differences in their reactivity and ultimate proof-of-concept separation of their mixtures. The imido substituent critically provides a reactive site in the complexes that localizes π-bonding interactions with the metal centers and affords unique Ta/Nb reactivity differences with CO2, providing important new insights for the efficient reactive separations of these critical elements.
Results and discussion
Syntheses of Ta/Nb imido complexes
The tripodal TriNOx3− ligand (Scheme 1) was selected as a supporting ligand due to its demonstrated success in stabilizing high-oxidation state imido complexes.35–39 We reasoned that the strongly donating character of TriNOx3− would enhance the basicity of the imido groups, while its bulky tert-butyl groups would sterically shield the metal center, directing reactivity to the imido fragments.40 Treatment of H3TriNOx with an excess of triethylamine (15 equiv.) under an inert (N2) atmosphere, followed by the addition of one equiv. of tBuN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) MCl3(py)2 (M = Nb, Ta; py = pyridine) resulted in the formation of well-defined Ta/Nb imido complexes tBuN
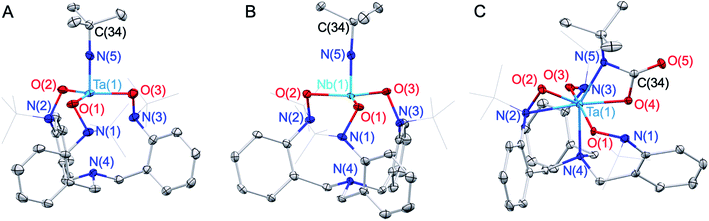
MCl3(py)2 (M = Nb, Ta; py = pyridine) resulted in the formation of well-defined Ta/Nb imido complexes tBuN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) M(TriNOx) (1-M, M = Ta, Nb) (Scheme 1) in low to moderate yields (ca. 20–50%). Elucidation of the solid-state structures by X-ray crystallography revealed 1-M to have C3-symmetric geometries due to the propeller-like orientations of the TriNOx3− aryl groups (Fig. 2A and B). The metal–N(5) bond distances are 1.748(4) and 1.749(4) Å for 1-Ta and 1-Nb respectively, consistent with metal–imido distances from previously-reported Ta/Nb imido complexes.41 The imido binding angles in 1-M are nearly linear, however the Ta(1)–N(5)–C(34) bond angle in 1-Ta (174.9(4)°) deviates slightly more from 180° than the analogous bond angle in 1-Nb (176.8(4)°). The primary coordination spheres of 1-M are best described as trigonal pyramidal, wherein the three TriNOx3− ligand oxygen atoms occupy the equatorial positions of the trigonal pyramid. The TriNOx3− tertiary amino nitrogen atoms are not bound to the metal centers of 1-M in the solid state, with M(1)–N(4) distances = 3.708(4) and 3.673(4) Å for 1-Ta and 1-Nb respectively, while the nitrogen atoms of the hydroxylamido moieties, N(1) to N(3), are positioned ca. 2.6 Å from the metal centers, indicating no appreciable bonding interactions.
M(TriNOx) (1-M, M = Ta, Nb) (Scheme 1) in low to moderate yields (ca. 20–50%). Elucidation of the solid-state structures by X-ray crystallography revealed 1-M to have C3-symmetric geometries due to the propeller-like orientations of the TriNOx3− aryl groups (Fig. 2A and B). The metal–N(5) bond distances are 1.748(4) and 1.749(4) Å for 1-Ta and 1-Nb respectively, consistent with metal–imido distances from previously-reported Ta/Nb imido complexes.41 The imido binding angles in 1-M are nearly linear, however the Ta(1)–N(5)–C(34) bond angle in 1-Ta (174.9(4)°) deviates slightly more from 180° than the analogous bond angle in 1-Nb (176.8(4)°). The primary coordination spheres of 1-M are best described as trigonal pyramidal, wherein the three TriNOx3− ligand oxygen atoms occupy the equatorial positions of the trigonal pyramid. The TriNOx3− tertiary amino nitrogen atoms are not bound to the metal centers of 1-M in the solid state, with M(1)–N(4) distances = 3.708(4) and 3.673(4) Å for 1-Ta and 1-Nb respectively, while the nitrogen atoms of the hydroxylamido moieties, N(1) to N(3), are positioned ca. 2.6 Å from the metal centers, indicating no appreciable bonding interactions.
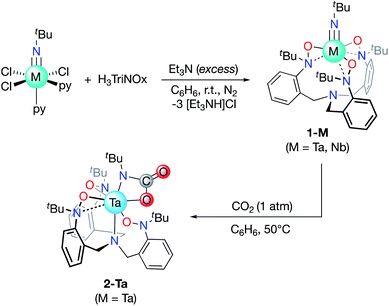 | ||
| Scheme 1 Formation of the Ta/Nb imido complexes (1-M) and the reaction of 1-Ta with CO2 to form 2-Ta. | ||
Two sets of doublets are observed in the 1H NMR spectra (C6D6) of 1-M between 2.25–4.50 ppm associated with the diastereotopic methylene protons of the TriNOx-ligand and indicating that the C3-symmetric geometries observed in the solid-state are preserved in solution on the NMR timescale. 1H NMR spectral resonances associated with 1-Ta and 1-Nb are similar (Δδ ≤ 0.05 ppm) but distinct, indicating the presence of differing electronic environments imparted by the identity of the metal (Fig. S7–S10†). The infrared (IR) spectra of 1-M are virtually identical throughout the fingerprint region, except for two strong features at 1305 cm−1 and 1286 cm−1 in the spectrum of 1-Ta that are absent in the spectrum of 1-Nb, and a single feature at 1269 cm−1 in the spectrum of 1-Nb that is absent in the spectrum of 1-Ta (Fig. S16†). These bands are within the range of previously reported group V metal–imido stretching frequencies.42–45
Density functional theory (DFT) calculations on 1-M
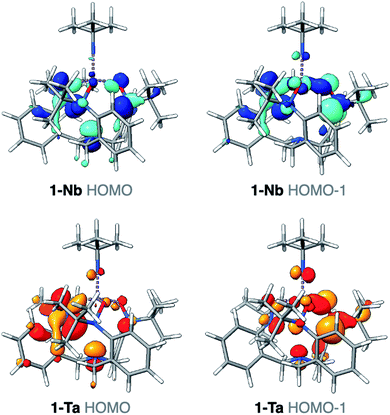
The differences identified in the NMR and IR spectra of 1-M imply slightly different electronic environments between the two complexes. To gain insight into these differences in the electronic structure, ground-state density functional theory (DFT) calculations were performed on 1-M. Geometry optimizations using B3LYP46/def2-SVP47 closely reproduced the bond metrics observed in the solid-state structures of 1-M. Frequency calculations at the same level of theory were performed on 1-M, and the simulated spectra are in qualitative agreement with experiment. Of note, consistent with the experimental spectra, two asymmetric Ta-imido stretching vibrational modes are predicted for 1-Ta (1314, 1315 cm−1), while only one Nb-imido stretching vibrational mode is predicted for 1-Nb (1292 cm−1) (see ESI for details, Fig. S18–S20†). The Nb-imido stretching frequency in 1-Nb is calculated to be lower in energy than the two Ta-imido stretching frequencies in 1-Ta (ΔνTa/Nb = 22 and 23 cm−1), which is similar what is observed in the experimental spectra of 1-M (ΔνTa/Nb = 17 and 36 cm−1). These energy differences are also consistent with previous reports of isostructural Ta/Nb complexes, wherein the M-imido stretching modes are observed at lower energies for Nb.43,44 Examination of the computed valence manifold of 1-Ta revealed that the highest occupied molecular orbital (HOMO) contains p-orbital-like lobes on the imido nitrogen atom, as does the next lowest energy orbital (HOMO−1) in an orthogonal orientation (Fig. 3). In contrast, the HOMO of 1-Nb is primarily TriNOx3−-ligand based and does not exhibit appreciable imido character. Similarly, the HOMO−1 was calculated to contain far less imido character as compared with the HOMO−1 of 1-Ta (Fig. 3). This predicted difference in the valence electronic structures in 1-Taversus1-Nb suggests potential for reactivity differences between the two complexes.Differing reactivities of 1-Taversus1-Nb: hydrolysis and CO2 insertion
Consistent with the DFT-predicted differences in the HOMOs/HOMO−1s of 1-M, we noted that 1-Ta hydrolyzes at a faster rate than 1-Nb. Upon treatment of a benzene solution of 1-Ta/1-Nb (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) with 5 equiv. of water, NMR spectroscopy indicated the decay of 1-Ta, while 1-Nb remained intact. A white precipitate, likely metal oxide and/or hydroxide, was observed to form within seconds. This white solid was removed by filtration and the filtrate from this experiment was analyzed using inductively coupled plasma-optical emission spectroscopy (ICP-OES). The filtrate was determined to be enriched in Nb (EFNb = 25),¶ corroborating observations from the NMR experiment. Assuming a proton-gated mechanism of hydrolysis of 1-M, the larger water sensitivity observed for 1-Ta could result from the presence of the destabilized imido-based lone pairs in this complex, which are absent in 1-Nb, providing anecdotal support for the DFT predictions outlined above. It should be noted that this difference in reactivity of the imido lone pair is consistent with the industrial process for Ta/Nb separation wherein NbOF52− is observed at milder pH while the analogous Ta complex is not observed (Fig. 1), thus implying a less reactive Nb-oxo interaction under these conditions.48 Similarly, Muetterties and Wright have shown related metal-oxo reactivity differences between isostructural Ta/Nb tetrakis-tropolonate complexes (T4M+, M = Ta, Nb). In this system, pH-dependent equilibria between T4M+ and the hydrolysis oxo products, T3MO, were observed. The conversion of T3NbO to T4Nb+ was found to require highly acidic conditions (pH < 3), while T4Ta+ was found to be resistant to hydrolysis under less acidic conditions (up to pH = 7), implying a more basic oxo moiety in the putative T3TaO as compared with T3NbO.49
1 ratio) with 5 equiv. of water, NMR spectroscopy indicated the decay of 1-Ta, while 1-Nb remained intact. A white precipitate, likely metal oxide and/or hydroxide, was observed to form within seconds. This white solid was removed by filtration and the filtrate from this experiment was analyzed using inductively coupled plasma-optical emission spectroscopy (ICP-OES). The filtrate was determined to be enriched in Nb (EFNb = 25),¶ corroborating observations from the NMR experiment. Assuming a proton-gated mechanism of hydrolysis of 1-M, the larger water sensitivity observed for 1-Ta could result from the presence of the destabilized imido-based lone pairs in this complex, which are absent in 1-Nb, providing anecdotal support for the DFT predictions outlined above. It should be noted that this difference in reactivity of the imido lone pair is consistent with the industrial process for Ta/Nb separation wherein NbOF52− is observed at milder pH while the analogous Ta complex is not observed (Fig. 1), thus implying a less reactive Nb-oxo interaction under these conditions.48 Similarly, Muetterties and Wright have shown related metal-oxo reactivity differences between isostructural Ta/Nb tetrakis-tropolonate complexes (T4M+, M = Ta, Nb). In this system, pH-dependent equilibria between T4M+ and the hydrolysis oxo products, T3MO, were observed. The conversion of T3NbO to T4Nb+ was found to require highly acidic conditions (pH < 3), while T4Ta+ was found to be resistant to hydrolysis under less acidic conditions (up to pH = 7), implying a more basic oxo moiety in the putative T3TaO as compared with T3NbO.49
Based on the compositional differences in the HOMO/HOMO−1 for 1-Taversus1-Nb, combined with the observed difference in the rates of hydrolysis of 1-Taversus1-Nb, we reasoned that the 1-Ta imido-substituent should similarly be more nucleophilic than that of 1-Nb. Diverse early metal–imido complexes have shown reactivity with carbon dioxide (CO2) to form carbamate,50–58 carboxylate,59 iminodicarboxylate,50,58–60 ureate,61 and oxo/hydroxo55,61–65 complexes, resulting from nucleophilic attack on the carbon atom of CO2. Accordingly, benzene solutions of 1-M were individually treated with CO2 (1 atm) to test for differences in reactivity (Scheme 1). 1-Ta was found to fully react with CO2 at 50 °C over the course of several hours to form a pale-yellow precipitate. Single crystals of the product were obtained from the slow evaporation of a dichloromethane (DCM) solution, and elucidation of the solid-state structure by X-ray crystallography revealed the formation of a TaV carbamate complex (2-Ta, 64%, Fig. 2C). Interestingly, to the best of our knowledge, 2-Ta represents the first isolated Ta carbamate complex (vide infra). The carbamate moiety in 2-Ta is bound κ2 to Ta at the nitrogen atom N(5) and one oxygen atom O(4) to form a 4-membered metallacycle. The primary coordination sphere geometry of 2-Ta is best described as pentagonal bipyramidal, owing to one of the three TriNOx3− hydroxylamide donors rearranging to bind η2, as evidenced by the short Ta(1)–N(2) distance of 2.221(5) Å and more acute Ta(1)–O(2)–N(2) bond angle of 79.0(3)°. The propeller-like arrangement of the TriNOx3− aryl groups observed in 1-M is also apparent in 2-Ta, thus giving the overall complex a C1-symmetric geometry. This symmetry is maintained in the solution phase on the NMR timescale; the 1H NMR spectrum of 2-Ta displays six distinct doublet resonances associated with the TriNOx3− ligand methylene protons and three distinct singlet resonances associated with the tert-butyl group protons (Fig. S11†).
Unlike 1-Ta, 1-Nb was found to be unreactive with CO2 under identical conditions (benzene, 1 atm CO2, 50 °C). Heating a sample of 1-Nb to 80 °C in C6D6 under 1 atm of CO2 likewise did not result in any appreciable reactivity, with only minor decomposition observed over the course of 18 h. No new resonances consistent with a Nb-carbamate complex were observed in the 1H NMR spectra (Fig. S3†) over this 18 h time span. It is also notable that the starting materials tBuN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) MCl3(py)2 (M = Nb, Ta) showed no reactivity with CO2 (50 °C, 18 h), indicating the importance of the supporting ligand to achieve selective metal reactivity.
MCl3(py)2 (M = Nb, Ta) showed no reactivity with CO2 (50 °C, 18 h), indicating the importance of the supporting ligand to achieve selective metal reactivity.
Demonstration of Ta/Nb separation
The CO2 reactivity difference between 1-Ta and 1-Nb, combined with the observed differences in solubility properties between 1-M and 2-Ta, provide a direct route for Ta/Nb separation. As such, a proof-of-concept Ta/Nb separation was undertaken to demonstrate the relevance of this system to the field of fundamental separations science. A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
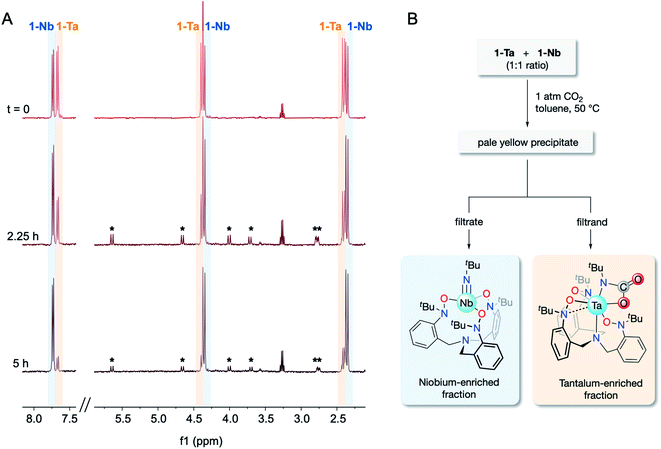
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 1-Ta/1-Nb was treated with 1 atm of CO2 in a sealed J-Young tube (C6D6) and heated to 60 °C for 5 h. Over the course of the reaction, spectral resonances associated with 1-Ta were observed to diminish, while spectral resonances associated with 1-Nb were found to be largely unchanged (Fig. 4A). Additionally, weak resonances associated with 2-Ta were observed to form, although the intensity of these features remained low due to its partial precipitation. Having confirmed that (a) the differences in CO2 reactivity is maintained when 1-Ta and 1-Nb are co-dissolved in the same solution, and (b) imido–carbamate ligand exchange between 1-Nb and 2-Ta does not occur under the reaction conditions, lab-scale (ca. 20 mg of each metal complex) separation procedures were undertaken on equimolar mixtures of 1-Ta and 1-Nb in toluene (Fig. 4B). An approximate 1
1 mixture of 1-Ta/1-Nb was treated with 1 atm of CO2 in a sealed J-Young tube (C6D6) and heated to 60 °C for 5 h. Over the course of the reaction, spectral resonances associated with 1-Ta were observed to diminish, while spectral resonances associated with 1-Nb were found to be largely unchanged (Fig. 4A). Additionally, weak resonances associated with 2-Ta were observed to form, although the intensity of these features remained low due to its partial precipitation. Having confirmed that (a) the differences in CO2 reactivity is maintained when 1-Ta and 1-Nb are co-dissolved in the same solution, and (b) imido–carbamate ligand exchange between 1-Nb and 2-Ta does not occur under the reaction conditions, lab-scale (ca. 20 mg of each metal complex) separation procedures were undertaken on equimolar mixtures of 1-Ta and 1-Nb in toluene (Fig. 4B). An approximate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of the two metals were tested to demonstrate versatility across the wide range of Ta/Nb ratios found in various mineral ores.2,5 Across three trials, between 70–75% (based on the theoretical yield of 2-Ta) of highly pure Ta material precipitated (EFTa = 103 ± 31 by ICP-OES), while virtually all of the Nb, and the remaining 25–30% of Ta remained in solution (EFNb = 3.85 ± 0.56 by ICP-OES). Averaging across the three trials gave a notable separations factor (STa/Nb) of 404 ± 150 (n = 3). To the best of our knowledge, this value of STa/Nb represents an improvement over other fluoride-free Ta/Nb separations systems, which demonstrate separation factors between ca. 4–250.19–25,34 However, it should be understood that this system is not yet industrially viable due to the air/moisture sensitivity of the compounds, the moderate to low yields of 1-M, and the high cost of the starting materials. Instead, this result should be viewed as a fundamental proof-of-concept separation demonstrating the viability of this novel separation strategy.
1 ratio of the two metals were tested to demonstrate versatility across the wide range of Ta/Nb ratios found in various mineral ores.2,5 Across three trials, between 70–75% (based on the theoretical yield of 2-Ta) of highly pure Ta material precipitated (EFTa = 103 ± 31 by ICP-OES), while virtually all of the Nb, and the remaining 25–30% of Ta remained in solution (EFNb = 3.85 ± 0.56 by ICP-OES). Averaging across the three trials gave a notable separations factor (STa/Nb) of 404 ± 150 (n = 3). To the best of our knowledge, this value of STa/Nb represents an improvement over other fluoride-free Ta/Nb separations systems, which demonstrate separation factors between ca. 4–250.19–25,34 However, it should be understood that this system is not yet industrially viable due to the air/moisture sensitivity of the compounds, the moderate to low yields of 1-M, and the high cost of the starting materials. Instead, this result should be viewed as a fundamental proof-of-concept separation demonstrating the viability of this novel separation strategy.
Kinetics of CO2 insertion (1-Ta → 2-Ta)
The stark difference in the reactivity observed for 1-Taversus1-Nb is fundamentally interesting; however, an understanding for why these metals show such different reactivity was not immediately apparent. In effort to address this question, a mechanistic proposal for the reaction between 1-M and CO2 was explored both experimentally and computationally. To provide an experimental benchmark for the computational study (vide infra), the kinetics of the reaction between 1-Ta and CO2 were monitored under pseudo-first-order conditions with [CO2] ≥ 20 × [1-Ta] using 1H NMR spectroscopy (C6D6) at 303 K. The reaction was followed by monitoring the decrease in the intensity of the characteristic NMR resonance at 4.38 ppm, associated with the methylene protons in 1-Ta, and the increase in the intensity of the resonance at 4.01 ppm, associated with a methylene proton in 2-Ta. The concentrations of 1-Ta/2-Ta were determined by comparing the integrals of these resonances with respect to an internal standard, toluene. The resulting kinetic traces were fit to single exponentials (Fig. S1†). Plotting the natural logarithm of concentration versus time produced linear fits (Fig. S2†), consistent with the reaction being first order in 1-Ta. Pseudo-first-order rate constants were obtained for the reaction at four different concentrations of CO2, each of which was performed in triplicate (see ESI for details†). Plotting the observed rate constants kobsversus [CO2] revealed a linear relationship with a negligible y-intercept (Fig. 5A), indicating that the reaction is first order in CO2. Taken together, these results indicate the following bimolecular rate law (eqn (1)):| Rate = kobs [1-Ta] = ks [1-Ta] [CO2] | (1) |
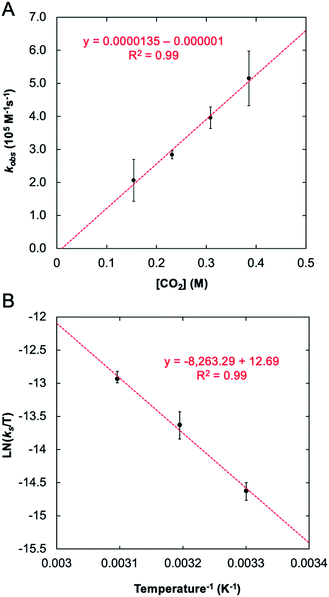 | ||
| Fig. 5 Observed rate constant for reaction between 1-Ta and CO2 as a function of CO2 concentration: T = 303 K, [1-Ta] = 7 mM (A) and the Eyring plot associated with this transformation (B). | ||
| Ta (exp.) | Ta (comp.) | Nb (comp.) | |
|---|---|---|---|
| ΔH‡ (kcal mol−1) | 16(1) | 14.3 | 17.7 |
| ΔS‡ (cal K−1 mol−1) | −22(3) | −44.8 | −44.5 |
| ΔG‡ (kcal mol−1) | 23(2) | 27.6 | 31.0 |
DFT-generated potential energy surfaces for 1-M → 2-M
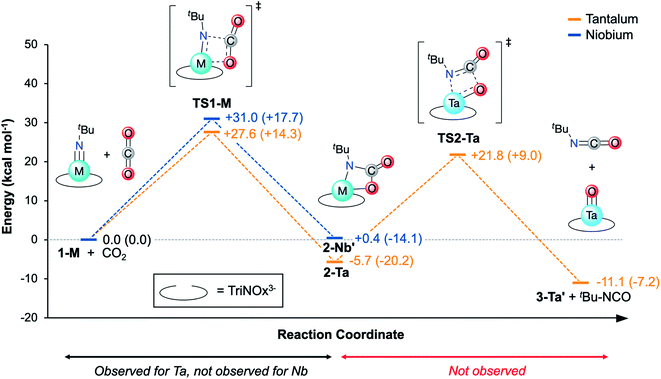
With experimental activation parameters in hand for the reaction of 1-Ta with CO2, the potential energy surfaces for this reaction with both 1-Ta and 1-Nb were evaluated computationally (Fig. 6). Accordingly, ground state geometry optimizations using B3LYP/def2-SVP were performed on 2-Ta and the hypothetical 2-Nb′. The reaction was calculated to be exergonic for 1-Ta (ΔG = −5.7 kcal mol−1) and slightly endergonic for 1-Nb (ΔG = +0.4 kcal mol−1). Transition states for these reactions (TS1-M) were approximated through identification of local maxima in relaxed surface scans wherein the N(5)–C(34) distances in 2-M were constrained to larger distances in steps of 0.025 Å. The transition state structures were confirmed as being saddle points on the potential energy surfaces through frequency calculations in which a single imaginary vibration frequency was obtained for each structure. The activation enthalpy, ΔH‡ = 14.3 kcal mol−1, calculated for the reaction of 1-Ta is in excellent agreement with the experimentally-determined value of 16.7 kcal mol−1, while the calculated activation entropy, ΔS‡ = −44.8 cal K−1 mol−1, is roughly twice as negative as the experimentally obtained value of −22.0 cal K−1 mol−1, leading to a slight overestimation of the activation Gibbs free energy: ΔG‡ = 27.6 kcal mol−1 (computed) as compared with 23.0 kcal mol−1 (experiment) (Table 1). Notably TS1-Nb is predicted to be ca. 3.4 kcal mol−1 higher in energy than TS1-Ta, suggesting that the reaction is kinetically more facile for 1-Ta as compared to 1-Nb. Remarkably consistent 1-Ta/Nb differences in the kinetics and thermodynamics for this reaction profile were determined using various alternate functionals/level of theory combinations (see ESI for details, Fig. S17†).Based on the computed potential energy surfaces, both the kinetics and thermodynamics determine the observed selectivity of this reaction for 1-Ta over 1-Nb. The reaction with 1-Ta is sluggish near room temperature, indicating that elevated temperatures are required to make the reaction possible for 1-Nb. However, given the large negative entropy of ΔS = −48.8 cal K−1mol−1 calculated for the hypothetical reaction of 1-Nb with CO2, increasing the reaction temperature would be expected to make the transformation more endergonic, which could explain why it is not observed experimentally.
Insights into the stability of 2-Ta
Reported Ta-imido complexes have been shown to react with CO2 to form isocyanates and Ta-oxo/hydroxo products;63,66 the reaction to form 2-Ta is unprecedented in tantalum chemistry. Additionally, despite Nb-carbamate complexes being reported,59,672-Ta represents the first isolated Ta-carbamate complex. The TriNOx3−tert-butyl groups in 2-Ta may be essential for stabilizing the Ta-carbamate moiety; steric demands between the carbamate tert-butyl group and the TriNOx-ligand tert-butyl groups are proposed to kinetically prevent an intramolecular rearrangement to extrude tert-butyl isocyanate product. Alternatively, the TriNOx3−tert-butyl groups may be important in preventing oxide cluster formation, which has been shown to be a thermodynamic sink in a previous example of Ta-imido reactivity with CO2.63 To shed light on these possible contributors to the stability of 2-Ta, a hypothetical reaction pathway for isocyanate extrusion from 2-Ta was explored using DFT.A relaxed surface scan was performed in which the C(34)–O(4) bond distance was increased in sequential steps of 0.1 Å (B3LYP/def2-SVP). From this scan, a local maximum in electronic energy at ca. 2.2 Å and a local minimum in electronic energy at ca. 3.0 Å were identified. The local maximum was resolved into TS2-Ta, and the local minimum was resolved into a putative C3-symmetric Ta-oxo compound, O=Ta(TriNOx) (3-Ta′) in combination with a free equivalent of tert-butyl isocyanate (tBuNCO). Frequency calculations were performed on TS2-Ta, 3-Ta′, and tBuNCO and the thermodynamics and kinetics of this hypothetical process were assessed (Fig. 6). The Gibbs Free Energy barrier associated with the formation of 3-Ta′ and tBuNCO from 2-Ta was calculated to be 27.5 kcal mol−1, which should be kinetically feasible since this represents a smaller global maximum than TS1-Ta (Fig. 6). Additionally, the overall reaction (2-Ta → 3-Ta′ + tBuNCO) was calculated to be exergonic by 5.4 kcal mol−1. However, since the activation entropy for TS1-Ta was found to be notably overestimated by DFT (vide supra), it is reasonable to expect that the large positive entropy calculated for this reaction (+61.6 cal K−1 mol−1 for 2-Ta → 3-Ta′ + tBuNCO) is similarly overestimated. Decreasing the calculated entropic contribution would result in global Gibbs Free Energy increases for 3-Ta′/tBuNCO, which could explain why 2-Ta is unreactive toward formation of oxo complex 3-Ta′ and tBuNCO. Heating a sample of 2-Ta in pyridine-d5 (80 °C) led to slow decomposition, but neither 1-Ta, the putative 3-Ta′, nor tBuNCO were observed to form as determined by 1H NMR spectroscopy (Fig. S4†).
Broader context: analogy to the industrial Ta/Nb separation
This new Ta/Nb separations procedure, although squarely in the fundamental scientific space,5,9–12 represents a notable model system from which valuable chemical insights can be gained. The observed differences in metal–imido reactivity/stability between 1-Ta and 1-Nb is reminiscent of the industrial process wherein Nb(O)F52− is a stable entity in solution, while the analogous Ta complex is not observed under identical conditions. In this case, Nb(O)F52− undergoes a formal protonation reaction with 3 equiv. of HF to form NbF6−, H2O, and HF2− (eqn (2), Fig. 1):| Nb(O)F52− + 3HF ⇌ NbF6− + H2O + HF2− | (2) |
This process is a pH-dependent and reversible equilibrium.5 Since the analogous Ta(O)F52− complex is not observed to form, the hypothetical Ta(O)F52− complex can be thought of as undergoing the analogous (hypothetical) reaction irreversibly (eqn (3)):
| Ta(O)F52− + 3HF → TaF6− + H2O + HF2− | (3) |
The reactivity of Ta(O)F52− toward electrophiles would therefore be expected to be far greater than that of Nb(O)F52−, which mirrors the trend observed in the reactivities of 1-M reported herein. Terminal metal–imido complexes are routinely studied as analogs for terminal metal oxo complexes since the metal–ligand multiple bonding is isoelectronic between these classes of molecules.41,68–72 As such, 1-M can be viewed as model complexes for the industrially relevant M(O)F52− complexes; the greater reactivity of the imido group in 1-Ta, as compared to 1-Nb, directly parallels the strategy used in the industrial Ta/Nb separations procedure, and similarly results in differing Ta/Nb speciation under identical conditions.
Conclusions
Isostructural Ta/Nb-imido complexes bound by the TriNOx3− ligand (1-M) were synthesized and fully characterized. Although the structures of 1-Ta/1-Nb are nearly identical, DFT analysis indicated that the HOMO/HOMO−1 of 1-Ta contain imido lone pair character, while the HOMO/HOMO−1 of 1-Nb do not. This difference in electronic structure results in reactivity differences between the two complexes; 1-Ta reacts with both water and CO2 at much faster rates than 1-Nb. Heating 1-Ta in the presence of CO2 resulted in the complete conversion to the first isolated example of a TaV carbamate complex (2-Ta), while 1-Nb was found to be unreactive, even at higher temperatures. Differences in solubility between 1-Nb and 2-Ta allowed for a facile proof-of-concept separations procedure that led to an efficient fluoride-free Ta/Nb separation (STa/Nb = 404 ± 150). A combined experimental and theoretical mechanistic study suggests that the formation of 2-Ta is both kinetically and thermodynamically advantaged over the formation of the hypothetical 2-Nb′. Although this system, as reported here, is not yet applicable to an industrial setting due to the air sensitivity of the complexes and the need for specialized starting materials, this study provides valuable information on fundamental differences in bonding for Ta versus Nb – insights that are essential for developing sustainable, fluoride-free Ta/Nb separations procedures. Specifically, understanding and controlling differences in π-bonding in Ta/Nb complexes is expected to be a key strategy for developing new and sustainable procedures to separate these critical elements.Author contributions
Alexander B. Weberg developed and optimized the syntheses of the Ta/Nb imido complexes (1-M), discovered the selective reaction between CO2 and the Ta-imido complex, characterized the novel Ta-carbamate complex (2-Ta), designed/implemented the kinetic study between the Ta-imido complex and CO2, developed the Ta/Nb separation procedure between the isostructural Ta/Nb-imido complexes, and wrote/edited the manuscript and ESI. Subhajyoti Chaudhuri performed predictive DFT geometry optimizations on the Ta/Nb-imido complexes that suggested differences in Ta/Nb-imido basicities/nucleophilicities, generated potential energy surfaces for the reactions between the Ta/Nb-imido complexes and CO2, and contributed to the writing of the ESI. Thibault Cheisson synthesized the Nb-imido complex (1-Nb) that provided a starting point for the study. Christian Uruburo aided in the experimental kinetic study for the reaction between the Ta-imido complex (1-Ta) and CO2. Ekaterina Lapsheva and Pragati Pandey performed elemental analyses that demonstrated bulk purity of the complexes. Michael R. Gau and Patrick J. Carroll solved and refined the X-ray structures of the Ta/Nb-imido complexes (1-M) and the Ta-carbamate complex (2-Ta). George C. Schatz provided guidance, support, and funding for the DFT calculations, and contributed to the editing of the manuscript and ESI. Eric J. Schelter provided guidance, support and funding for the experimental studies described within, contributed to the writing/editing of the manuscript and ESI, and managed all aspects of the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Drs Jun Gu and Chad Lawrence for their help in designing the high-temperature NMR experiments. We also thank Prof. Karen Goldberg's group (University of Pennsylvania) for their help in setting up the CO2 pressurization system and for lending us the necessary hardware. We thank and acknowledge Fatmata J. Fahnbulleh for support in the synthesis of 1-Nb. E. J. S. and G. C. S. thank the Center for Sustainable Separations of Metals, an NSF Center for Chemical Innovation (CHE-1925708) for support of this work. E. J. S. also thanks the University of Pennsylvania.Notes and references
- USGS, Niobium (Columbium) and Tantalum Statistics and Information, 2022 Search PubMed.
- R. Linnen, D. L. Trueman and R. Burt, Crit. Met. Handb., 2014, 361–384 CAS.
- N. A. Mancheri, B. Sprecher, S. Deetman, S. B. Young, R. Bleischwitz, L. Dong, R. Kleijn and A. Tukker, Resour., Conserv. Recycl., 2018, 129, 56–69 CrossRef.
- E. Commission, I. Directorate-General for Internal Market Entrepreneurship and SMEs, S. Bobba, P. Claudiu, D. Huygens, P. Alves Dias, B. Gawlik, E. Tzimas, D. Wittmer, P. Nuss, M. Grohol, H. Saveyn, F. Buraoui, G. Orveillon, T. Hámor, S. Slavko, F. Mathieux, M. Gislev, C. Torres De Matos, G. Blengini, F. Ardente, D. Blagoeva and E. Garbarino, Report on critical raw materials and the circular economy, Publications Office, 2018 Search PubMed.
- Z. Zhu and C. Y. Cheng, Hydrometallurgy, 2011, 107, 1–12 CrossRef CAS.
- C. C. Torardi, L. H. Brixner and G. Blasse, J. Solid State Chem., 1987, 67, 21–25 CrossRef CAS.
- (a) PAULING FILE in: Inorganic Solid Phases, SpringerMaterials (online database), ed. P. Villars, Springer, Heidelberg, SpringerMaterials https://materials.springer.com/isp/crystallographic/docs/sd_1102038 Search PubMed; (b) reproduced from: Z. G. Pinsker, Electron-diffraction analysis of the structure of K2NbOF5 crystals, Soviet Physics – Crystallography, 1967, 11, 634–639 Search PubMed.
- A. Tressaud, Fluorine: A Paradoxical Element, ed. A. Tressaud, Candice Janco, Amsterdam, 2019, pp. 43–44 Search PubMed.
- E. L. J. Koerner, Separation of Niobium and Tantalum by Liquid Extraction, Iowa State College, 1956 Search PubMed.
- E. L. J. Koerner, M. Smutz and H. A. Wilhelm, Separation of Niobium and Tantalum by Liquid Extraction, 1956 Search PubMed.
- J. R. Werning, K. B. Higbie, J. T. Grace, B. F. Speece and H. L. Gilbert, Ind. Eng. Chem., 1954, 46, 644–652 CrossRef CAS.
- A. Agulyansky, ed. A. Agulyansky, Elsevier Science, Amsterdam, 2004, pp. 253–338.
- F. Cuvelliez, Treatment of Materials Containing Tantalum and Niobium, US Pat., 2429671, 1947 Search PubMed.
- C. F. Hiskey, L. Newman and R. H. Atkinson, Anal. Chem., 1952, 24, 1988–1991 CrossRef CAS.
- W. J. Kroll and F. E. Bacon, Method of Treating Material Containing Columbium and Tantalum, US Pat., 2427360, 1945 Search PubMed.
- W. J. Kroll and F. E. Bacon, Separation of Columbium and Tantalum Oxides, US Pat., 2443254, 1945 Search PubMed.
- S. L. May, A. W. Henderson and H. A. Johansen, Ind. Eng. Chem., 1954, 46, 2495–2499 CrossRef CAS.
- O. Ruff and F. Thomas, Z. Anorg. Allg. Chem., 1926, 156, 213–225 CrossRef CAS.
- K. B. Higbie and J. R. Werning, Separation of Tantalum-Columbium by Solvent Extraction, 1956 Search PubMed.
- C. Djordjević, H. Goričan and S. L. Tan, J. Less-Common Met., 1966, 11, 342–350 CrossRef.
- A. Agulyansky, L. Agulyansky and V. F. Travkin, Chem. Eng. Process., 2004, 43, 1231–1237 CrossRef CAS.
- S. N. Bhattacharyya and B. (Nandi) Ganguly, Solvent Extr. Ion Exch., 1984, 2, 699–740 CrossRef CAS.
- G. J.-P. Deblonde, D. Bengio, D. Beltrami, S. Bélair, G. Cote and A. Chagnes, Sep. Purif. Technol., 2019, 215, 634–643 CrossRef CAS.
- L. M. M. Kinsman, R. A. M. Crevecoeur, A. Singh-Morgan, B. T. Ngwenya, C. A. Morrison and J. B. Love, Met., 2020, 10, 346 CAS.
- M. Nete, W. Purcell and J. T. Nel, Hydrometallurgy, 2017, 173, 192–198 CrossRef CAS.
- M. Nete, W. Purcell and J. T. Nel, J. Met., 2016, 68, 2817–2823 CAS.
- K. J. Covert, D. R. Neithamer, M. C. Zonnevylle, R. E. LaPointe, C. P. Schaller and P. T. Wolczanski, Inorg. Chem., 1991, 30, 2494–2508 CrossRef CAS.
- K. F. Hirsekorn, A. S. Veige, M. P. Marshak, Y. Koldobskaya, P. T. Wolczanski, T. R. Cundari and E. B. Lobkovsky, J. Am. Chem. Soc., 2005, 127, 4809–4830 CrossRef CAS PubMed.
- R. Wei, J. Hu, X. Chen and Y. Gong, Dalton Trans., 2021, 50, 11300–11306 RSC.
- J. J. Sorensen, E. Tieu, C. Nielson, A. Sevy, K. H. Tomchak and M. D. Morse, J. Chem. Phys., 2020, 152, 194307 CrossRef CAS PubMed.
- J. Zhao, B. Xu, W. Yu and X. Wang, Chin. J. Chem. Phys., 2016, 29, 10–20 CrossRef CAS.
- R. E. Wilson, S. De Sio and V. Vallet, Eur. J. Inorg. Chem., 2016, 5467–5476 CrossRef CAS.
- M. J. Ungerer, C. G. C. E. van Sittert, D. J. van der Westhuizen and H. M. Krieg, J. Phys. Chem. Solids, 2019, 135, 109121 CrossRef CAS.
- M. H. Furigay, S. Chaudhuri, S. M. Deresh, A. B. Weberg, P. Pandey, P. J. Carroll, G. C. Schatz and E. J. Schelter, Inorg. Chem., 2022, 61, 23–27 CrossRef CAS PubMed.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2016, 138, 6928–6931 CrossRef CAS PubMed.
- L. A. Solola, A. V. Zabula, W. L. Dorfner, B. C. Manor, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2017, 139, 2435–2442 CrossRef CAS PubMed.
- E. N. Lapsheva, T. Cheisson, C. Álvarez Lamsfus, P. J. Carroll, M. R. Gau, L. Maron and E. J. Schelter, Chem. Commun., 2020, 56, 4781–4784 RSC.
- T. Cheisson, L. A. Solola, M. R. Gau, P. J. Carroll and E. J. Schelter, Organometallics, 2018, 37, 4332–4335 CrossRef CAS.
- T. Cheisson, K. D. Kersey, N. Mahieu, A. McSkimming, M. R. Gau, P. J. Carroll and E. J. Schelter, J. Am. Chem. Soc., 2019, 141, 9185–9190 CrossRef PubMed.
- J. A. Bogart, C. A. Lippincott, P. J. Carroll and E. J. Schelter, Angew. Chem., Int. Ed., 2015, 54, 8222–8225 CrossRef CAS PubMed.
- T. R. Cundari, J. Am. Chem. Soc., 1992, 114, 7879–7888 CrossRef CAS.
- J. H. Osborne and W. C. Trogler, Inorg. Chem., 1985, 24, 3098–3099 CrossRef CAS.
- K. S. Heinselman, V. M. Miskowski, S. J. Geib, L. C. Wang and M. D. Hopkins, Inorg. Chem., 1997, 36, 5530–5538 CrossRef CAS.
- A. V Korolev, A. L. Rheingold and D. S. Williams, Inorg. Chem., 1997, 36, 2647–2655 CrossRef.
- S. M. Rocklage and R. R. Schrock, J. Am. Chem. Soc., 1982, 104, 3077–3081 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Nete, W. Purcell and J. T. Nel, Hydrometallurgy, 2014, 149, 31–40 CrossRef CAS.
- E. L. Muetterties and C. M. Wright, J. Am. Chem. Soc., 1965, 87, 4706–4717 CrossRef CAS.
- L. R. Groom, A. F. Russell, A. D. Schwarz and P. Mountford, Organometallics, 2014, 33, 1002–1019 CrossRef CAS.
- Z. J. Tonzetich, R. R. Schrock and P. Müller, Organometallics, 2006, 25, 4301–4306 CrossRef CAS.
- S. C. Dunn, N. Hazari, A. R. Cowley, J. C. Green and P. Mountford, Organometallics, 2006, 25, 1755–1770 CrossRef CAS.
- C. L. Boyd, E. Clot, A. E. Guiducci and P. Mountford, Organometallics, 2005, 24, 2347–2367 CrossRef CAS.
- B. D. Ward, E. Clot, S. R. Dubberley, L. H. Gade and P. Mountford, Chem. Commun., 2002, 2618–2619 RSC.
- A. J. Blake, J. M. McInnes, P. Mountford, G. I. Nikonov, D. Swallow and D. J. Watkin, J. Chem. Soc., Dalton Trans., 1999, 379–392 RSC.
- A. E. Guiducci, A. R. Cowley, M. E. G. Skinner and P. Mountford, J. Chem. Soc., Dalton Trans., 2001, 1392–1394 RSC.
- A. E. Guiducci, C. L. Boyd, E. Clot and P. Mountford, Dalton Trans., 2009, 5960–5979 RSC.
- P. J. Tiong, A. Nova, L. R. Groom, A. D. Schwarz, J. D. Selby, A. D. Schofield, E. Clot and P. Mountford, Organometallics, 2011, 30, 1182–1201 CrossRef CAS.
- J. I. Fostvedt, L. N. Grant, B. M. Kriegel, A. H. Obenhuber, T. D. Lohrey, R. G. Bergman and J. Arnold, Chem. Sci., 2020, 11, 11613–11632 RSC.
- J. Chu, E. Lu, Z. Liu, Y. Chen, X. Leng and H. Song, Angew. Chem., Int. Ed., 2011, 50, 7677–7680 CrossRef CAS PubMed.
- F. Akagi, S. Suzuki, Y. Ishida, T. Hatanaka, T. Matsuo and H. Kawaguchi, Eur. J. Inorg. Chem., 2013, 3930–3936 CrossRef CAS.
- L. Suresh, J. Finnstad, K. W. Törnroos and E. Le Roux, Inorg. Chim. Acta, 2021, 521, 120301 CrossRef CAS.
- P. Royo and J. Sánchez-Nieves, J. Organomet. Chem., 2000, 597, 61–68 CrossRef CAS.
- C. L. Boyd, T. Toupance, B. R. Tyrrell, B. D. Ward, C. R. Wilson, A. R. Cowley and P. Mountford, Organometallics, 2005, 24, 309–330 CrossRef CAS.
- S.-H. Hsu, J.-C. Chang, C.-L. Lai, C.-H. Hu, H. M. Lee, G.-H. Lee, S.-M. Peng and J.-H. Huang, Inorg. Chem., 2004, 43, 6786–6792 CrossRef CAS PubMed.
- E. Blake Robert, D. M. Antonelli, L. M. Henling, W. P. Schaefer, K. I. Hardcastle and J. E. Bercaw, Organometallics, 1998, 17, 718–725 CrossRef.
- O. Blacque, H. Brunner, M. M. Kubicki, J.-C. Leblanc, W. Meier, C. Moise, Y. Mugnier, A. Sadorge, J. Wachter and M. Zabel, J. Organomet. Chem., 2001, 634, 47–54 CrossRef CAS.
- N. H. Anderson, S. O. Odoh, Y. Yao, U. J. Williams, B. A. Schaefer, J. J. Kiernicki, A. J. Lewis, M. D. Goshert, P. E. Fanwick, E. J. Schelter, J. R. Walensky, L. Gagliardi and S. C. Bart, Nat. Chem., 2014, 6, 919–926 CrossRef CAS PubMed.
- J. J. Kiernicki, M. G. Ferrier, J. S. Lezama Pacheco, H. S. La Pierre, B. W. Stein, M. Zeller, S. A. Kozimor and S. C. Bart, J. Am. Chem. Soc., 2016, 138, 13941–13951 CrossRef CAS PubMed.
- D. S. J. Arney and C. J. Burns, J. Am. Chem. Soc., 1995, 117, 9448–9460 CrossRef CAS.
- N. H. Anderson, J. Xie, D. Ray, M. Zeller, L. Gagliardi and S. C. Bart, Nat. Chem., 2017, 9, 850–855 CrossRef CAS PubMed.
- J. J. Kiernicki, C. J. Tatebe, M. Zeller and S. C. Bart, Inorg. Chem., 2018, 57, 1870–1879 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2154007–2154009. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2sc01926d |
| ‡ These authors contributed equally to this work (ABW experimental, SC theoretical). |
| § Current address: Eramet Ideas, 1 Albert Einstein Ave, 78190 Trappes, France. |
| ¶ The separation factor, STa/Nb, is an indication of the ratios of Ta/Nb in each phase. It is calculated as the ratio of distribution coefficients, DM, of each metal (STa/Nb = DTa/DNb), where DM is the ratio of metal concentration in the two reaction phases (DM = [M]phase1/[M]phase2). Alternatively, STa/Nb can be expressed in terms of the product of enrichment factors, EFM, of metals in each phase, where EFM1 = molesM1/molesM2 for a given phase (STa/Nb = EFTa,phase1 × EFNb,phase2). It should be noted that higher separation factors can be achieved via multiple passes of a material through a separation procedure (Stotal = Spass1 × Spass2), which is more easily accomplished for liquid–liquid extraction separations, as compared with precipitation-based separations. |
| This journal is © The Royal Society of Chemistry 2022 |