Open Access Article
Open Access ArticleTheoretical prediction of a graphene-like 2D uranyl material with p-orbital antiferromagnetism†‡
Xiao-Kun
Zhao
 a,
Chang-Su
Cao
a,
Chang-Su
Cao
 a,
Jin-Cheng
Liu
a,
Jun-Bo
Lu
b,
Jun
Li
a,
Jin-Cheng
Liu
a,
Jun-Bo
Lu
b,
Jun
Li
 ab and
Han-Shi
Hu
ab and
Han-Shi
Hu
 *a
*a
aDepartment of Chemistry and Key Laboratory of Organic Optoelectronics & Molecular Engineering of Ministry of Education, Tsinghua University, Beijing 100084, China. E-mail: hshu@mail.tsinghua.edu.cn
bDepartment of Chemistry, Southern University of Science and Technology, Shenzhen 518055, China
First published on 26th May 2022
Abstract
Versatile graphene-like two-dimensional materials with s-, p- and d-block elements have aroused significant interest because of their extensive applications while there is a lack of such materials with f-block elements. Herein we report a unique one composed of the f-block element moiety of uranyl (UO22+) through a global-minimum structure search. Its geometry is found to be similar to that of graphene with a honeycomb-like hexagonal unit composed of six uranyl ligands, where each uranyl is bridged by two superoxido groups and a pair of hydroxyl ligands. All the uranium and bridging oxygen atoms form an extended planar 2D structure, which shows thermodynamic, kinetic and thermal stabilities due to σ/π bonding as well as electrostatic interactions between ligands. Each superoxido ligand has one unpaired (2pπ*)1 electron and is antiferromagnetically coupled through uranyl bridges with 2pπ*–5fδ–2pπ* superexchange interactions, forming a rare type of one-dimensional Heisenberg chain with p-orbital antiferromagnetism, which might become valuable for application in antiferromagnetic spintronics.
Introduction
Two-dimensional (2D) materials have versatile applications in physics, chemistry, and materials science.1–12 There has been an exponential increase in 2D material research since the isolation of single-layer graphene by Novoselov and Geim in 2004 due to its promising mechanical, superconducting, optical, and chemical properties.13–16 Currently, a number of graphene-like materials from various types of elements are known, such as 2D ionic boron, transition-metal-doped borophene, monolayer monoxides and monochlorides of MgO and NaCl, MX2 (M = Mo, W; X = S, Se), MXene and so on.17–23The computational design of novel 2D materials has covered a wide range of s-, p- and d-block elements in the periodic table mainly through the bottom-up and/or global-minimum (GM) structure search approaches.24–29 For example, the prediction of B2C/Al2C monolayers is inspired by the planar geometry and delocalized electronic structures in CB4/C2Al62− molecular building blocks through a bottom-up design process.30–32 Luo et al. predicted graphene-like monolayer monoxides and monochlorides (e.g., MgO and NaCl) based on their rock-salt-like bulks with space point group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.19 Besides, a GM structure search is another approach based on the development of relevant packages such as USPEX, CALYPSO, LASP, and TGMin.33–36 By using the GM approach, a series of 2D materials, such as boron–carbon and Cu2Si monolayer, are predicted to be stable both dynamically and thermodynamically.37,38 Apart from that, Wang et al. predicted the Be5C2 monolayer by combining these two strategies.39 All these computationally predicted 2D materials are composed of s- and p-block main-group elements as well as d-block transition metal elements,17–19,40,41 whereas those composed of f-block elements (lanthanides and actinides) are relatively rare, with only a few examples such as the low-dimensional f-block element borides.42,43
m.19 Besides, a GM structure search is another approach based on the development of relevant packages such as USPEX, CALYPSO, LASP, and TGMin.33–36 By using the GM approach, a series of 2D materials, such as boron–carbon and Cu2Si monolayer, are predicted to be stable both dynamically and thermodynamically.37,38 Apart from that, Wang et al. predicted the Be5C2 monolayer by combining these two strategies.39 All these computationally predicted 2D materials are composed of s- and p-block main-group elements as well as d-block transition metal elements,17–19,40,41 whereas those composed of f-block elements (lanthanides and actinides) are relatively rare, with only a few examples such as the low-dimensional f-block element borides.42,43
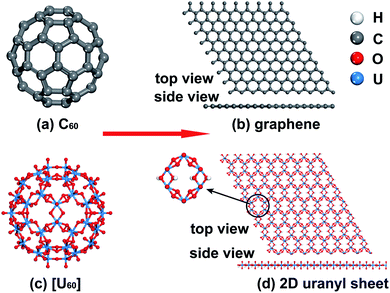
Uranium is the heaviest abundant f-block actinide element available in natural environments and its most stable form is uranyl, which is the linear divalent cation UO22+ with significant stability.44,45 Uranyl-based compounds, clusters, and 2D/3D materials46–51 have sparked tremendous interest due to their fascinating topological structures and potential applications in the field of underground water, nuclear waste, and fuel reprocessing.52–56 Among them, a variety of uranyl clusters experimentally synthesized by Burns and colleagues show similar topologies to carbon fullerene clusters such as C20 and C60. For example, [UO2(O2)(OH)]6060− (denoted as [U60] hereafter) is experimentally found to adopt the same topology as C60 buckyballs consisting of 12 pentagons and 20 hexagons shown in Scheme 1(a) and (c).54,57–60 The topological similarity between the fullerene-like uranyl cluster [U60] and C60 prompts us to wonder whether the graphene-like 2D uranyl sheet as presented in Scheme 1(d) is stable or not. In this regard, it is worth noting that low-dimensional mineral materials of uranyl indeed exist, as exemplified by rutherfordine (UO2CO3) and studtite (UO2(O2)(H2O)2) discovered in the early 20th century.61,62
In this work, by combining both bottom-up and GM structure search strategies, a novel graphene-like 2D uranyl material is computationally predicted to be highly stable, thus extending the design of graphene-like 2D materials to the domain of f-block actinides that are stable kinetically and thermodynamically. Furthermore, the 2D uranyl sheet features a rare type of 1D spin-1/2 Heisenberg chain with a long-range antiferromagnetic (AFM) spin order on the superoxido groups,63–66 where there exists a new type of 2pπ*–5fδ–2pπ* superexchange interaction. Most often, the AFM order in crystals is caused by the superexchange interaction among the d-type AOs of transition metals via the p-type AOs of the ligands.67,68 Therefore, this antiferromagnetically coupled 1D spin-1/2 Heisenberg chain of p-orbital based superoxido centers with surrounding uranyl ions forms a new pillar in the field of f-block element low-dimensional spin systems.69,70
Results and discussion
The graphene-like 2D uranyl monolayer sheet is designed through the bottom-up approach inspired by the analogy of the uranyl nanocluster of [U60] with C60, and thus the atomic composition is set as (UO2)2(μ2-O2)2(μ2-OH)2 for further GM structure search. This selection of composition aims at circumventing formation of discrete small clusters in the presence of counterions. The evolutionary algorithm code USPEX for the GM search, which has been successfully used to predict a number of experimentally confirmed new materials, is applied to search for thermodynamically stable structures of a given fixed-composition system.71–74 Based on the optimal structures found from USPEX, we performed relativistic quantum chemical calculations and ab initio molecular dynamics simulations using density functional theory. The recently developed Goedecker–Teter–Hutter (GTH) pseudopotential by Lu et al. was used to model the core electrons with 14 valence electrons for U.75 Various chemical bonding analyses are applied to provide understanding of the stability and electronic structures. The computational details are given in the ESI.‡Geometric structures of the 2D uranyl monolayer sheet
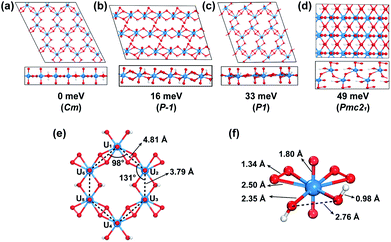
Through an extensive GM structure search with evolutionary algorithm USPEX, a planar hexagonal graphene-like 2D uranyl sheet has been located, as shown in Fig. 1(a), where the uranyl groups are connected by two superoxido groups and a pair of hydroxyl bridges. This structure is found to be 16 meV per atom lower in energy than the second-most stable one with a uranyl ribbon structure (Fig. 1(b)). The third-most stable one seen in Fig. 1(c) is a distorted hexagonal quasi-2D structure lying 33 meV per atom higher, in which the superoxido groups are slightly off the plane due to the steric effect. Comparatively, the fourth one in Fig. 1(d), 49 meV per atom higher in energy, tends to form a bulk 3D structure with hydrogen bonds rather than the 2D pattern. To verify the reliability of the DFT functional, we did further calculations by employing the HSE06 functional to determine the single point energies of these four most stable isomers and the calculated order is consistent with the results obtained from the PBE functional (Table S1‡). More isomers within the range of 320 meV per atom higher in energy are shown in Fig. S1.‡ In addition, this optimal structure has been further confirmed to be stable by phonon spectrum calculations along the high-symmetry lines in the Brillouin zone. As shown in Fig. S2,‡ there is no imaginary phonon mode in the phonon spectrum, suggesting the kinetic stability of this uranyl sheet.The GM structure search and phonon spectrum suggest that the graphene-like 2D uranyl sheet is stable in terms of energy and kinetics. Our calculation shows that the computationally optimized 2D uranyl structure has maintained the planar graphene-like 2D topology, which is in line with the previous quantum chemical calculations and experimental results of the molecular compound K6[(UO2)(O2)2(OH)]2(H2O)7, where the U–(OH)2–U structure is planar with a dihedral angle of 180°.76–78 As shown in Fig. 1, our 2D sheet is composed of a honeycomb-like hexagonal unit with six uranyl ligands (Fig. 1(e)). The six U atoms in each unit form a hexagon with D2h local symmetry, where the four neighboring U–U distances bridged by superoxido are 4.81 Å and the remaining two bridged by a pair of hydroxyl groups are 3.79 Å. Consequently, there are two kinds of interior angles of 98° and 131°, respectively. This distortion from ideal D6h to D2h local symmetry of the hexagonal ring is attributed to the two types of bridging ligands of superoxido and hydroxyl connecting the six uranyl groups altogether. All the U and O atoms from the bridging ligands form one planar 2D structure while the remaining Oyl atoms are perpendicularly connected with U with a rather short U–O bond length of 1.80 Å, which is almost the same as that in the naked uranyl complex. The H atoms are off the plane and the O–H bond length is 0.98 Å, close to that in water (0.97 Å). The U–Osuperoxido bond length is 2.50 Å, which is longer than that of U–Ohydroxyl (2.35 Å). The O–O bond length of the superoxido ligand in the 2D uranyl sheet is 1.34 Å, close to that of the naked one (1.33 Å) as well as that of a recently reported uranyl superoxide compound (1.39 Å).79
The similarities between [U60] and C60 clusters as well as between graphene and the 2D uranyl sheet underscore the analogy between the sp2-hybridized carbon atom and uranyl. Firstly, both of them prefer forming ligand connections on the equatorial plane since the axial direction is occupied by the perpendicular pz AO of the sp2-hybridized carbon atom or two rigid linear Oyl ligands in the linear uranyl cation of [O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) U
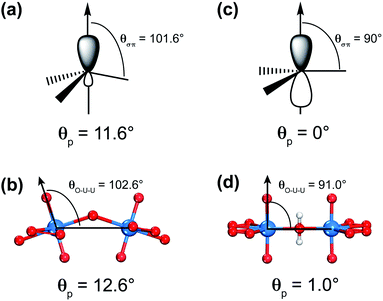
U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O]2+. Secondly, this analogy of the sp2-hybridized carbon atom and uranyl has been further confirmed by using the π-orbital axis vector (POAV) method with pyramidalization angle as shown in Scheme 2.80–82 For carbon atoms in the C60 cluster, the pyramidalization angle defined as θp = (θσπ − 90°) = 11.6°, where θσπ is the angle between the σ- and π-bonding orbitals (Scheme 2(a)), is almost equal to the angle of θp = (θO–U–U − 90°) = 12.6° in the [U60] cluster, where θO–U–U is the angle between one Oyl atom and its connected U atom as well as the neighboring U atom bridged by the superoxido group (Scheme 2(b)). Comparatively, the θp = 0° in graphene (Scheme 2(c)) is very close to the θp = 1.0° based on an optimized 2D uranyl sheet (Scheme 2(d)), further showing the similarity between the sp2-hybridized carbon atom and uranyl.
O]2+. Secondly, this analogy of the sp2-hybridized carbon atom and uranyl has been further confirmed by using the π-orbital axis vector (POAV) method with pyramidalization angle as shown in Scheme 2.80–82 For carbon atoms in the C60 cluster, the pyramidalization angle defined as θp = (θσπ − 90°) = 11.6°, where θσπ is the angle between the σ- and π-bonding orbitals (Scheme 2(a)), is almost equal to the angle of θp = (θO–U–U − 90°) = 12.6° in the [U60] cluster, where θO–U–U is the angle between one Oyl atom and its connected U atom as well as the neighboring U atom bridged by the superoxido group (Scheme 2(b)). Comparatively, the θp = 0° in graphene (Scheme 2(c)) is very close to the θp = 1.0° based on an optimized 2D uranyl sheet (Scheme 2(d)), further showing the similarity between the sp2-hybridized carbon atom and uranyl.
In order to better understand the geometric structure of this novel 2D uranyl sheet, we have also made a detailed geometry comparison between the experimentally synthesized [U60] cluster and this computationally predicted graphene-like 2D uranyl sheet. As shown in Table S2,‡ the U–Oyl bond length (1.80 Å) of uranyl in this 2D sheet is comparable to that in the [U60] cluster (1.76–1.84 Å). Besides, both the U–O2–U and U–(OH)2–U dihedral angles are planar (180.0°) in the 2D uranyl sheet, while the corresponding ones are within the range of 143.2–159.7° and 174.0–175.0° in the cluster, respectively. In contrast to the aforementioned 1.34 Å bond length of the O2 moiety in the 2D uranyl sheet, the shortest O–O bond length of the peroxide in the [U60] cluster is 1.46 Å, which is in agreement with the bond length in the naked peroxide group (1.49 Å). The O–O bond length difference between the 2D uranyl sheet and [U60] cluster likely arises from the fact that the O2 moiety in the 2D uranyl sheet is indeed a superoxide (O2−), rather than the typical peroxide group (O22−) in the uranyl clusters.
Thermodynamic and thermal stabilities of the 2D uranyl sheet
To investigate the thermodynamics of the 2D uranyl sheet, we have computed the formation energies from the reactants available in nature (H2O, O2 and solid UO2) and the proposed reaction is shown in eqn (1). The formation free energy (ΔG300K) at a temperature of 300 K was calculated using the formula ΔG300K = G((UO2)4(μ2-O2)4(μ2-OH)4) − 4G(UO2) − 2G(H2O) − 5G(O2), where G(UO2) is the energy of the uranium dioxide crystal with the entropy and zero-point energies corrected. The calculated ΔG300K is negative, with a value of −41.3 kcal mol−1, indicating that the formation of the 2D uranyl sheet is energetically favorable under these conditions.| 2H2O + 5O2 + 4UO2 → (UO2)4(μ2-O2)4(μ2-OH)4, ΔG300K = −41.3 kcal mol−1 | (1) |
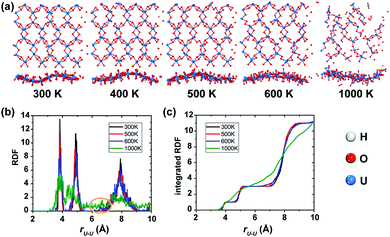
In order to examine the thermal stability of the predicted uranyl sheet, a series of spin-polarized AIMD simulations were carried out at various temperatures of 300 K, 400 K, 500 K, and 600 K for durations of 10 ps, respectively, and 5 ps for the simulations at 1000 K because the structure starts to collapse. Snapshots with top and side views taken at the end of each simulation are shown in Fig. 2(a). The hexagonal framework of the uranyl sheet is well-maintained at the temperature of 300 K after 10 ps simulations, indicating that it is stable at room temperature. As expected, at the relatively high temperature of 500 K, it shows a little more disordering while there is much more disordering at 600 K. At the temperature of 1000 K, the monolayer structure breaks down rapidly even in 5 ps. Since uranyl is the backbone of the material, the radial distribution function (RDF) of the neighboring U–U distances is a good parameter for quantitatively evaluating the structure deformation of the sheet during the AIMD simulations at different temperatures. As shown in Fig. 2(b), the RDF in the range of 6–7 Å starts to have noise at 600 K which becomes larger at 1000 K, while it remains at zero at 300 K and 500 K. It follows that the uranyl sheet begins to reconstruct at the temperature of 600 K and collapses at 1000 K. Furthermore, there are no obvious steps in the integrated RDF at 1000 K (shown in Fig. 2(c)), indicating the it has become completely disordered within 5 ps. Fluctuations of the total potential energy for the sheet at different temperatures during AIMD simulations (see Fig. S3‡) also confirm that it is relatively thermally stable up to 500 K. When the temperature goes higher such as between 600 K and 1000 K, the sheet has enough kinetic energy to cross the barrier and tends to decompose. Meanwhile, similar non-spin-polarized AIMD simulations were also carried out at temperatures of 100 K, 300 K, 400 K, 500 K, and 1000 K for durations of 10 ps, 10 ps, 10 ps, 10 ps, and 4 ps, respectively for comparison. Both the corresponding snapshots (Fig. S4‡) and RDF (Fig. S5‡) analysis show that the reconstruction of the non-spin-polarized 2D uranyl sheet happens at merely 400 K compared to the aforementioned distortion temperature of 600 K for the spin-polarized calculation. The relatively more stable structure in the spin-polarized state indicates that the AFM coupling interactions may contribute to the stability of the uranyl sheet when compared with the non-magnetic sheet.
Electronic structures and stabilization mechanism in the graphene-like 2D uranyl sheet
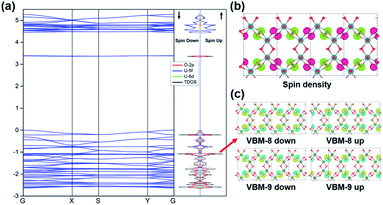
The stability of the 2D graphene-like uranyl sheet is dependent on the electronic structures as well as the thermodynamic conditions. The electronic structure and related properties of the uranyl sheet are revealed by the calculated band structure, density-of-states (DOS), spin densities, and real space wavefunctions at the gamma point, as displayed in Fig. 3. The 2D uranyl sheet turns out to be a semiconductor with an approximate 3.4 eV energy gap at the HSE06 hybrid functional level. The flat band above the Fermi level in Fig. 3(a) can be attributed to the out-of-plane 2pπ* orbitals of the superoxido groups and the corresponding charge density of the conduction band minimum (CBM) (see in Fig. S7‡). Meanwhile, the valence band maximum (VBM) shows some π-type bonding interaction between the in-plane 2pπ* orbitals in the superoxido groups and 5f/6d orbitals of the uranium atoms.Additionally, more bonding interactions in this 2D uranyl sheet are revealed by the inner nine real space wavefunctions shown in Fig. S8,‡ among which there are the π-type (i.e., VBM-2, VBM-3, and VBM-14) and σ-type (i.e., VBM-4, VBM-5, VBM-10, VBM-12, VBM-13, and VMB-17) bonding interactions contributing to stabilizing this uranyl sheet. The above-mentioned σ/π bonding interactions are mainly contributed by O-2p and U-5f/6d AOs which can be revealed by the partial DOS analysis in Fig. 3(a). As U 5f orbitals are energetically close to O 2p ones while 6d orbitals are radially more extended, they both interact with the O2− species significantly. From the DFT optimized results, the 2D uranyl sheet has an AFM singlet ground state which is more stable than the ferromagnetic (FM) state by 4.3 meV per atom. Moreover, the AFM ground state is also confirmed by the spin densities located on the superoxido groups as shown in Fig. 3(b), where each group has a spin density of 0.81 with spin up (green) or spin down (pink), respectively. Meanwhile, Fig. 3(c) shows the real space wavefunction VBM-8 and VBM-9 corresponding to singly occupied 2pπ* electrons of the superoxido groups, indicating the AFM order in the 2D uranyl sheet as well.
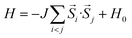 | (2) |
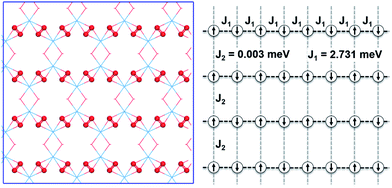
To further study the novel magnetic behavior in the 2D uranyl sheet, the Heisenberg model (see eqn (2)) and three different magnetic states with ferromagnetic (FM), antiferromagnetic (AFM), and antiferromagnetic/ferromagnetic (AF/FM) coupling (see in Fig. S9‡) were applied to calculate the intra-chain (J1) and inter-chain (J2) exchange coupling constants of this 2D material. In eqn (2), J is the exchange coupling constant, H0 is the nonmagnetic Hamiltonian, and ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) i and
i and ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) j are the spin momenta at sites i and j, respectively. As shown in Fig. 4, the simulated exchange coupling constant J1 is 2.731 meV (22.03 cm−1) and J2 is 0.003 meV (0.024 cm−1). Due to the relatively small interchain exchange coupling (J2 ≪ J1), the 2D uranyl sheet shows a novel type of long-range 1D spin-1/2 Heisenberg chains with the superexchange interaction between the AFM p-type spin on each superoxido group, owing to unpaired 2pπ* electrons on the superoxido groups via the empty 5fδ orbitals of the uranyl ligands. As shown in Scheme 3, the 5fδ orbital of the uranyl center and adjacent superoxido 2pπ* orbitals are symmetry matching, thus providing a possible pathway for the superexchange interaction. For the case of the AFM state, the unpaired 2pπ* electrons on the neighboring superoxido groups have opposite spins. One 2pπ* electrons can hop directly to the nearby site via an intermediate 5fδ orbital of the uranyl due to the adaptable symmetry. This hopping reduces the kinetic energy of the electrons and stabilizes the 2D uranyl sheet. In contrast, for the case of the FM state, the neighboring unpaired 2pπ* electrons have parallel spins. Thus, direct hopping is forbidden in the FM state, as the intermediate state with two electrons on the same orbital of same spin would violate the Pauli exclusion principle. The possible 2pπ*–5fδ–2pπ* superexchange interactions help explain the AFM ground state of the 2D uranyl sheet. As quantum antiferromagnets like the one-dimensional Heisenberg antiferromagnetic chain of S = 1/2 spins (1D-HAF) are the ground for finding new states of matter and testing magnetic theoretical models, our system achieves the first inorganic p-orbital 1D-HAF with f-block elements. In all known 1D-HAFs, the spin states arise from the electrons in the d orbitals of transition-metal ions, except in the recently found CsO2;83 our system thus provides a new p-orbital 1D-HAF with f-block elements. Furthermore, the p-orbital antiferromagnetism with weak spin–orbit interaction can also be characterized by the small magnetic anisotropy energy (MAE) value of 0.06 meV per superoxido group obtained via the calculated energies with seven types of different spin orientations shown in Table S5‡.84
j are the spin momenta at sites i and j, respectively. As shown in Fig. 4, the simulated exchange coupling constant J1 is 2.731 meV (22.03 cm−1) and J2 is 0.003 meV (0.024 cm−1). Due to the relatively small interchain exchange coupling (J2 ≪ J1), the 2D uranyl sheet shows a novel type of long-range 1D spin-1/2 Heisenberg chains with the superexchange interaction between the AFM p-type spin on each superoxido group, owing to unpaired 2pπ* electrons on the superoxido groups via the empty 5fδ orbitals of the uranyl ligands. As shown in Scheme 3, the 5fδ orbital of the uranyl center and adjacent superoxido 2pπ* orbitals are symmetry matching, thus providing a possible pathway for the superexchange interaction. For the case of the AFM state, the unpaired 2pπ* electrons on the neighboring superoxido groups have opposite spins. One 2pπ* electrons can hop directly to the nearby site via an intermediate 5fδ orbital of the uranyl due to the adaptable symmetry. This hopping reduces the kinetic energy of the electrons and stabilizes the 2D uranyl sheet. In contrast, for the case of the FM state, the neighboring unpaired 2pπ* electrons have parallel spins. Thus, direct hopping is forbidden in the FM state, as the intermediate state with two electrons on the same orbital of same spin would violate the Pauli exclusion principle. The possible 2pπ*–5fδ–2pπ* superexchange interactions help explain the AFM ground state of the 2D uranyl sheet. As quantum antiferromagnets like the one-dimensional Heisenberg antiferromagnetic chain of S = 1/2 spins (1D-HAF) are the ground for finding new states of matter and testing magnetic theoretical models, our system achieves the first inorganic p-orbital 1D-HAF with f-block elements. In all known 1D-HAFs, the spin states arise from the electrons in the d orbitals of transition-metal ions, except in the recently found CsO2;83 our system thus provides a new p-orbital 1D-HAF with f-block elements. Furthermore, the p-orbital antiferromagnetism with weak spin–orbit interaction can also be characterized by the small magnetic anisotropy energy (MAE) value of 0.06 meV per superoxido group obtained via the calculated energies with seven types of different spin orientations shown in Table S5‡.84
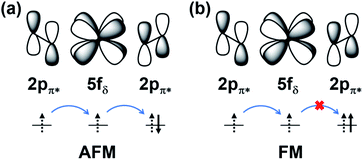 | ||
| Scheme 3 The schematic illustration of 2pπ*–5fδ–2pπ* superexchange interactions of AFM (a) and FM (b) states. | ||
The stabilizing mechanism of this novel 2D uranyl sheet can be further analyzed on the basis of cluster models containing two/six uranyl ligands from the 2D sheet through the principal interacting orbital (PIO) and energy decomposition analysis with natural orbitals for chemical valence (EDA-NOCV) approaches.85–88 Herein, we adopt the dimer molecular models of (UO2)2(μ2-O2)(O2)2(OH)43− and (UO2)2(O2)4(μ2-OH)22− anions for the PIO analysis and the hexagonal ring model of the (UO2)6(μ2-O2)4(μ2-OH)44+ cluster for the EDA-NOCV analysis. The corresponding EDA-NOCV results for the interactions between the superoxido groups (μ2-O2)44− and uranyl fragment (UO2)6(μ2-OH)48+ are listed in Table S6.‡ The calculated electrostatic interaction reaches up to −2734.64 kcal mol−1. The orbital interaction (ΔEorb) is divided into two major terms, ΔEorb(π) and ΔEorb(σ), with energies of −218.35 and −67.76 kcal mol−1, respectively. The σ- & π-types of interactions are revealed by the π-type (PIMO 1) and σ-type (PIMO 4) bonding interactions from PIO analysis (Fig. S11‡). As for the bonding interactions between the fragments of (μ2-OH)44− and (UO2)6(μ2-O2)48+, Table S7‡ shows that the orbital interaction energies of ΔEorb(π) and ΔEorb(σ) are −252.55 and −143.30 kcal mol−1, respectively. Overall, the results show that the σ/π bonding interactions and the electrostatic attraction between the superoxido/hydroxyl ligands and the uranyl cations play an important role in stabilizing the 2D hexagonal structure, which account for the special stability of the 2D uranyl sheet. Besides, based on the O–O bond length (1.34 Å) mentioned above, the O2 moiety in the 2D uranyl sheet is a superoxide group with a singly occupied electron on each moiety. This assignment has further been supported by the electronic structure analysis of a hexagonal uranyl model cluster. As shown in Fig. S14,‡ there are twelve electrons occupied on the 2pπ* orbitals of the four superoxido moieties in the cluster, where each superoxido has three occupied 2pπ* electrons with the spin density close to 1, similar to other superoxides.
Conclusions
In summary, an unexpected graphene-like 2D uranyl material has been designed and predicted by the combination of both bottom-up and GM structure search strategies. This planar sheet has a geometry similar to that of graphene with a honeycomb-like hexagonal unit of six uranyl ligands and each of the uranyl groups are bridged by superoxido/hydroxyl moieties. The superoxido bridges are calculated to possess one unpaired 2pπ* electron each and are antiferromagnetically coupled with each other through the uranyl center. The rather small inter-chain exchange coupling constant (J2 = 0.003 meV) and much larger intra-chain exchange coupling constant (J1 = 2.731 meV) lead to a 1D spin-1/2 Heisenberg chain on superoxido groups. It forms a unique type of 2pπ*–5fδ–2pπ* superexchange pathway across the two neighboring superoxido groups via the uranyl. Especially noteworthy is the novel occurrence of p-orbital antiferromagnetism with this new material. A computational investigation shows that this 2D f-block actinide material has thermodynamic, kinetic and thermal stabilities, suggesting it is likely to be synthesized experimentally under a suitable environment. Our study extends the design of graphene-like 2D materials to f-block actinide elements, and helps to enrich the diversity and potential applications of 2D materials in p-orbital antiferromagnetic spintronics.Data availability
The data that supports the findings of this study is available from the corresponding author upon reasonable request.Author contributions
H. S. H. designed the project. X. K. Z. performed GM structure search, relativistic quantum chemical calculations and ab initio molecular dynamics simulations. C. S. C. and J. C. L. help to analyse the details and results of density functional theory calculations. J. B. L. provided the GTH pseudopotential basis of uranium. X. K. Z., H. S. H., and J. L. wrote and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Professors Xiaojun Wu from the University of Science and Technology of China and Yong Xu and Hai Xiao from Tsinghua University for helpful discussions. This work was financially supported by the National Natural Science Foundation of China (Grant No. 21906094, 22076095, and 22033005) and Guangdong Provincial Key Laboratory of Catalysis (No. 2020B121201002). The calculations were performed using supercomputers at SUSTech Supercomputer Center and Tsinghua National Laboratory for Information Science and Technology. The Tsinghua Xuetang Talents Program is acknowledged for providing computational resources.References
- D. Basko, Science, 2011, 334, 610–611 CrossRef CAS PubMed
.
- A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed
.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. M. Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137–1140 CrossRef CAS PubMed
.
- Z. Du, S. Yang, S. Li, J. Lou, S. Zhang, S. Wang, B. Li, Y. Gong, L. Song and X. Zou, Nature, 2020, 577, 492–496 CrossRef CAS PubMed
.
- M. Zeng, Y. Chen, E. Zhang, J. Li, R. G. Mendes, X. Sang, S. Luo, W. Ming, Y. Fu, M.-H. Du, L. Zhang, D. S. Parker, R. R. Unocic, K. Xiao, C. Wang, T. Zhang, Y. Xiao, M. H. Rümmeli, F. Xiu and L. Fu, CCS Chem., 2019, 1, 117–127 CAS
.
- Q.-Q. Huang, Y.-Z. Li, Z. Zheng, X.-M. Jiang, S.-S. Sun, H.-J. Jiang, W.-H. Deng, G.-E. Wang, T.-Y. Zhai, M.-D. Li and G. Xu, CCS Chem., 2020, 2, 655–662 CrossRef CAS
.
- W. Zeng and J. Wu, Chem, 2021, 7, 358–386 CAS
.
- X. Liu, Z. Yang, C. Ge, H. Li, M. Hao, C. Wan, Y. Song, B. Li and Q. Dong, CCS Chem., 2021, 3, 2576–2583 CrossRef CAS
.
- S. Tao and D. Jiang, CCS Chem., 2021, 3, 2003–2024 CrossRef CAS
.
- J. Wang, P. Yang, L. Liu, B. Zheng, J. Jiang, J.-p. Ma, Y. Yan, S. Yang, L. Yang, Q.-K. Liu, Y. Han and Y. Chen, CCS Chem., 2021, 3, 2372–2381 Search PubMed
.
- Q. Pan, S. Chen, C. Wu, F. Shao, J. Sun, L. Sun, Z. Zhang, Y. Man, Z. Li, L. He and Y. Zhao, CCS Chem., 2021, 3, 1368–1375 CrossRef CAS
.
- C. Liu, Y. Wang, H. Li, Y. Wu, Y. Li, J. Li, K. He, Y. Xu, J. Zhang and Y. Wang, Nat. Mater., 2020, 19, 522–527 CrossRef CAS PubMed
.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed
.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed
.
- R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. Peres and A. K. Geim, Science, 2008, 320, 1308 CrossRef CAS PubMed
.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS PubMed
.
- F. Ma, Y. Jiao, G. Gao, Y. Gu, A. Bilic, Z. Chen and A. Du, Nano Lett., 2016, 16, 3022–3028 CrossRef CAS PubMed
.
- H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651 CrossRef CAS PubMed
.
- B. Luo, Y. Yao, E. Tian, H. Song, X. Wang, G. Li, K. Xi, B. Li, H. Song and L. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17213–17218 CrossRef CAS PubMed
.
- H. S. S. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. N. R. Rao, Angew. Chem., Int. Ed., 2010, 49, 4059–4062 CrossRef PubMed
.
- M. Barsoum, J. Golczewski, H. Seifert and F. Aldinger, J. Alloys Compd., 2002, 340, 173–179 CrossRef CAS
.
- L. Ding, Y. Wei, Y. Wang, H. Chen, J. Caro and H. Wang, Angew. Chem., Int. Ed., 2017, 56, 1825–1829 CrossRef CAS
.
- S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115 CrossRef CAS PubMed
.
- P. D. Pancharatna, M. A. Méndez-Rojas, G. Merino, A. Vela and R. Hoffmann, J. Am. Chem. Soc., 2004, 126, 15309–15315 CrossRef CAS PubMed
.
- Y. Wang, Y. Li and Z. Chen, J. Mater. Chem. C, 2015, 3, 9603–9608 RSC
.
- L.-M. Yang, E. Ganz, Z. Chen, Z.-X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS PubMed
.
- W.-L. Li, X. Chen, T. Jian, T.-T. Chen, J. Li and L.-S. Wang, Nat. Rev. Chem., 2017, 1, 0071 CrossRef CAS
.
- Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895 CrossRef CAS PubMed
.
- D. Wu, H. Lv, Z. Zhuo, X. Li, X. Wu and J. Yang, J. Phys. Chem. Lett., 2021, 12, 3528–3534 CrossRef CAS PubMed
.
- Y. Li, Y. Liao, P. von Ragué Schleyer and Z. Chen, Nanoscale, 2014, 6, 10784–10791 RSC
.
- J. Dai, X. Wu, J. Yang and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 2058–2065 CrossRef CAS PubMed
.
- X. Wu, Y. Pei and X. C. Zeng, Nano Lett., 2009, 9, 1577–1582 CrossRef CAS
.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS
.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS
.
- S. D. Huang, C. Shang, P. L. Kang, X. J. Zhang and Z. P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415 CAS
.
- X. Chen, Y. F. Zhao, Y. Y. Zhang and J. Li, J. Comput. Chem., 2019, 40, 1105–1112 CAS
.
- X. Luo, J. Yang, H. Liu, X. Wu, Y. Wang, Y. Ma, S.-H. Wei, X. Gong and H. Xiang, J. Am. Chem. Soc., 2011, 133, 16285–16290 CrossRef CAS PubMed
.
- L.-M. Yang, V. Bacic, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed
.
- Y. Wang, F. Li, Y. Li and Z. Chen, Nat. Commun., 2016, 7, 11488 CrossRef CAS PubMed
.
- H. Zhang, Y. Li, J. Hou, A. Du and Z. Chen, Nano Lett., 2016, 16, 6124–6129 CrossRef CAS PubMed
.
- Y. Jiao, F. Ma, J. Bell, A. Bilic and A. Du, Angew. Chem., Int. Ed., 2016, 55, 10292–10295 CrossRef CAS PubMed
.
- A. Lopez-Bezanilla, J. Phys.: Mater., 2020, 3, 024002 CAS
.
- A. Lopez-Bezanilla, Phys. Rev. Mater., 2021, 5, 034007 CrossRef CAS
.
- J. Qiu and P. C. Burns, Chem. Rev., 2013, 113, 1097–1120 CrossRef CAS PubMed
.
- B. E. Cowie, J. M. Purkis, J. Austin, J. B. Love and P. L. Arnold, Chem. Rev., 2019, 119, 10595–10637 CrossRef CAS PubMed
.
- P. Wei, N. Pu, X. Dong, J. Yuan, Y. Li, L. Xu, J. Chen and C. Xu, Inorg. Chem., 2019, 58, 11664–11671 CrossRef CAS PubMed
.
- Y. Hao, P. Kegler, T. E. Albrecht-Schmitt, S. Wang, Q. Dong and E. V. Alekseev, Eur. J. Inorg. Chem., 2020, 4, 407–416 CrossRef
.
- L. Mei, P. Ren, Q. Y. Wu, Y. B. Ke, J. S. Geng, K. Liu, X. Q. Xing, Z. W. Huang, K. Q. Hu, Y. L. Liu, L. Y. Yuan, G. Mo, Z. H. Wu, J. K. Gibson, Z. F. Chai and W. Q. Shi, J. Am. Chem. Soc., 2020, 142, 16538–16545 CrossRef CAS PubMed
.
- L. Wang, Z. Li, Q. Wu, Z. Huang, L. Yuan, Z. Chai and W. Shi, Environ. Sci.: Nano, 2020, 7, 724–752 RSC
.
- J. Xie, Y. Wang, W. Liu, C. Liang, Y. Zhang, L. Chen, D. Sheng, Z. Chai and S. Wang, Sci. China: Chem., 2020, 63, 1608–1612 CrossRef CAS
.
- H. Hu, X. Xu, C. Xu and J. Li, Chin. J. Struct. Chem., 2020, 39, 1201–1212 Search PubMed
.
- K.-A. Hughes Kubatko, K. B. Helean, A. Navrotsky and P. C. Burns, Science, 2003, 302, 1191–1193 CrossRef CAS PubMed
.
- P. C. Burns, K. A. Kubatko, G. Sigmon, B. J. Fryer, J. E. Gagnon, M. R. Antonio and L. Soderholm, Angew. Chem., Int. Ed., 2005, 44, 2135–2139 CrossRef CAS PubMed
.
- P. Miro and C. Bo, Inorg. Chem., 2012, 51, 3840–3845 CrossRef CAS PubMed
.
- L. Zhang, M. Dembowski, A. Arteaga, S. Hickam, N. P. Martin, L. N. Zakharov, M. Nyman and P. C. Burns, Inorg. Chem., 2019, 58, 439–445 CrossRef CAS PubMed
.
- C. R. Armstrong, M. Nyman, T. Shvareva, G. E. Sigmon, P. C. Burns and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1874–1877 CrossRef CAS PubMed
.
- T. Z. Forbes, J. G. McAlpin, R. Murphy and P. C. Burns, Angew. Chem., Int. Ed., 2008, 47, 2824–2827 CrossRef CAS PubMed
.
- G. E. Sigmon, D. K. Unruh, J. Ling, B. Weaver, M. Ward, L. Pressprich, A. Simonetti and P. C. Burns, Angew. Chem., Int. Ed., 2009, 48, 2737–2740 CrossRef CAS PubMed
.
- G. E. Sigmon, J. Ling, D. K. Unruh, L. Moore-Shay, M. Ward, B. Weaver and P. C. Burns, J. Am. Chem. Soc., 2009, 131, 16648–16649 CrossRef CAS PubMed
.
- V. Parasuk and J. Almlöf, Chem. Phys. Lett., 1991, 184, 187–190 CrossRef CAS
.
- C. L. Christ, J. R. Clark and H. T. Evans, Science, 1955, 121, 472–473 CrossRef CAS PubMed
.
- P. C. Burns and K.-A. Hughes, Am. Mineral., 2003, 88, 1165–1168 CrossRef CAS
.
- J. Kohler, Angew. Chem., Int. Ed., 2010, 49, 3114–3115 CrossRef PubMed
.
- D. Hirobe, M. Sato, T. Kawamata, Y. Shiomi, K.-i. Uchida, R. Iguchi, Y. Koike, S. Maekawa and E. Saitoh, Nat. Phys., 2016, 13, 30–34 Search PubMed
.
- O. Breunig, M. Garst, A. Klümper, J. Rohrkamp, M. M. Turnbull and T. Lorenz, Sci. Adv., 2017, 3, eaao3773 Search PubMed
.
- C. Wang, R. Sun, Y. Chen, B.-W. Wang, Z.-M. Wang and S. Gao, CCS Chem., 2020, 2, 362–368 Search PubMed
.
- O. Domanov, E. Weschke, T. Saito, H. Peterlik, T. Pichler, M. Eisterer and H. Shiozawa, Nanoscale, 2019, 11, 10615–10621 RSC
.
- A. Bonanni and T. Dietl, Chem. Soc. Rev., 2010, 39, 528–539 RSC
.
- J. L. Manson, K. H. Stone, H. I. Southerland, T. Lancaster, A. J. Steele, S. J. Blundell, F. L. Pratt, P. J. Baker, R. D. McDonald, P. Sengupta, J. Singleton, P. A. Goddard, C. Lee, M.-H. Whangbo, M. M. Warter, C. H. Mielke and P. W. Stephens, J. Am. Chem. Soc., 2009, 131, 4590–4591 CrossRef CAS PubMed
.
- J. Zhang, L. Duan, Z. Wang, X. Wang, J. Zhao, M. Jin, W. Li, C. Zhang, L. Cao, Z. Deng, Z. Hu, S. Agrestini, M. Valvidares, H. J. Lin, C. T. Chen, J. Zhu and C. Jin, Inorg. Chem., 2020, 59, 5377–5385 CrossRef CAS PubMed
.
- N. P. Salke, M. M. Davari Esfahani, Y. Zhang, I. A. Kruglov, J. Zhou, Y. Wang, E. Greenberg, V. B. Prakapenka, J. Liu, A. R. Oganov and J.-F. Lin, Nat. Commun., 2019, 10, 4453 CrossRef PubMed
.
- D. Zhou, D. V. Semenok, H. Xie, X. Huang, D. Duan, A. Aperis, P. M. Oppeneer, M. Galasso, A. I. Kartsev, A. G. Kvashnin, A. R. Oganov and T. Cui, J. Am. Chem. Soc., 2020, 142, 2803–2811 CrossRef CAS
.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed
.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS
.
- J.-B. Lu, D. C. Cantu, C.-Q. Xu, M.-T. Nguyen, H.-S. Hu, V.-A. Glezakou, R. Rousseau and J. Li, J. Chem. Theory Comput., 2021, 17, 3360–3371 CrossRef CAS PubMed
.
- B. Vlaisavljevich, L. Gagliardi and P. C. Burns, J. Am. Chem. Soc., 2010, 132, 14503–14508 CrossRef CAS PubMed
.
- A. Arteaga, D. Ray, E. Glass, N. P. Martin, L. N. Zakharov, L. Gagliardi and M. Nyman, Inorg. Chem., 2020, 59, 1633–1641 CrossRef CAS PubMed
.
- K.-A. Kubatko, T. Z. Forbes, A. L. Klingensmith and P. C. Burns, Inorg. Chem., 2007, 46, 3657–3662 CrossRef CAS PubMed
.
- D. V. Kravchuk, N. N. Dahlen, S. J. Kruse, C. D. Malliakas, P. M. Shand and T. Z. Forbes, Angew. Chem., Int. Ed., 2021, 60, 15041–15048 CrossRef CAS PubMed
.
- R. C. Haddon, J. Am. Chem. Soc., 1987, 109, 1676–1685 CrossRef CAS
.
- R. C. Haddon, Science, 1993, 261, 1545–1550 CrossRef CAS
.
- X. Lu and Z. Chen, Chem. Rev., 2005, 105, 3643–3696 CrossRef CAS PubMed
.
- T. Knaflič, M. Klanjšek, A. Sans, P. Adler, M. Jansen, C. Felser and D. Arčon, Phys. Rev. B, 2015, 91, 174419 CrossRef
.
- A. Lehnert, S. Dennler, P. Błoński, S. Rusponi, M. Etzkorn, G. Moulas, P. Bencok, P. Gambardella, H. Brune and J. Hafner, Phys. Rev. B, 2010, 82, 094409 CrossRef
.
- J.-X. Zhang, F. K. Sheong and Z. Lin, Chem.–Eur. J., 2018, 24, 9639–9650 CrossRef CAS PubMed
.
- J.-X. Zhang, F. K. Sheong and Z. Lin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1469 CAS
.
- F. K. Sheong, J.-X. Zhang and Z. Lin, Phys. Chem. Chem. Phys., 2020, 22, 10076–10086 RSC
.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed
.
Footnotes |
| † Dedicated to Professor Zhifang Chai on the occasion of his 80th birthday. |
| ‡ Electronic supplementary information (ESI) available: Theoretical and computational details. See https://doi.org/10.1039/d2sc02017c |
| This journal is © The Royal Society of Chemistry 2022 |