Open Access Article
Open Access ArticleLearning size-adaptive molecular substructures for explainable drug–drug interaction prediction by substructure-aware graph neural network†
Ziduo
Yang‡
a,
Weihe
Zhong‡
a,
Qiujie
Lv
a and
Calvin
Yu-Chian Chen
 *abc
*abc
aArtificial Intelligence Medical Center, School of Intelligent Systems Engineering, Sun Yat-sen University, Shenzhen, 510275, China. E-mail: chenyuchian@mail.sysu.edu.cn; Tel: +86 02039332153
bDepartment of Medical Research, China Medical University Hospital, Taichung 40447, Taiwan
cDepartment of Bioinformatics and Medical Engineering, Asia University, Taichung, 41354, Taiwan
First published on 13th July 2022
Abstract
Drug–drug interactions (DDIs) can trigger unexpected pharmacological effects on the body, and the causal mechanisms are often unknown. Graph neural networks (GNNs) have been developed to better understand DDIs. However, identifying key substructures that contribute most to the DDI prediction is a challenge for GNNs. In this study, we presented a substructure-aware graph neural network, a message passing neural network equipped with a novel substructure attention mechanism and a substructure–substructure interaction module (SSIM) for DDI prediction (SA-DDI). Specifically, the substructure attention was designed to capture size- and shape-adaptive substructures based on the chemical intuition that the sizes and shapes are often irregular for functional groups in molecules. DDIs are fundamentally caused by chemical substructure interactions. Thus, the SSIM was used to model the substructure–substructure interactions by highlighting important substructures while de-emphasizing the minor ones for DDI prediction. We evaluated our approach in two real-world datasets and compared the proposed method with the state-of-the-art DDI prediction models. The SA-DDI surpassed other approaches on the two datasets. Moreover, the visual interpretation results showed that the SA-DDI was sensitive to the structure information of drugs and was able to detect the key substructures for DDIs. These advantages demonstrated that the proposed method improved the generalization and interpretation capability of DDI prediction modeling.
1 Introduction
Complex or co-existing diseases are commonly treated using drug combinations by taking advantage of the synergistic effects caused by drug–drug interactions (DDIs).1 However, unexpected DDIs also increase the risk of triggering adverse side effects or even serious toxicity.2 With the increasing need for multi-drug treatments, the identification of unexpected DDIs becomes increasingly crucial. Traditionally, the detection of DDIs is performed through extensive biological or pharmacological assays. However, this process is time-consuming and labor-intensive, because a great number of combinations of drugs should be considered for experiments. As a result, computational methods can be used as a low-cost, yet effective alternative to predict potential DDIs by identifying patterns from known DDIs.Existing computational methods can be divided into two categories, namely, text mining-based and machine learning-based methods.2 Text mining-based methods extract drug–drug relations between various entities from scientific literature,3–7 insurance claim databases, electronic medical records,8 and the FDA Adverse Event Reporting System;9 these methods are efficient in building DDI-related datasets. However, they cannot detect unannotated DDIs or potential DDIs before a combinational treatment is made.10 Conversely, machine learning-based methods have the potential to identify unseen DDIs for downstream experimental validations by generalizing the learned knowledge to unannotated DDIs.
Machine learning-based methods can be further classified into three categories, namely, deep neural network (DNN)-based methods, knowledge graph-based, and molecular structure-based methods. DNN-based methods11–15 first represent drugs as handcrafted feature vectors according to drug properties, such as structural similarity profiles,12,13 chemical substructures, targets, and pathways.11,14 Then, they use them to train a DNN to predict DDIs.
Knowledge graph-based methods16–23 represent biomedical data as graphs and use different graph-specific methods, such as label propagation,20 matrix factorization,21,23 and graph auto-encoders,18 to analyze them. The advantage of knowledge graph-based methods is that the model performance can be boosted by external biomedical knowledge. However, these approaches cannot be generalized to drugs in the early development phase, because the only available information at that time is chemical structure.18,20,24,25
In contrast, molecular structure-based methods25–30 regard drugs as independent entities, and predict DDIs only by relying on drug pairs. This is no need for external biomedical knowledge. DDIs depend on chemical reactions among local chemical structures (i.e., substructures) rather than their whole structure.25,31 Molecular structure-based methods assume that the learned chemical substructure information can be generalized to different drugs with similar substructures.25,30 For instance, MR-GNN29 leveraged the powerful structure extraction ability of graph neural networks (GNNs) to extract multi-scale chemical substructure representations of a molecular graph. CASTER25 designed a chemical sequential pattern mining algorithm to generate recurring chemical substructures molecular representations of drugs, followed by an auto-encoding module and dictionary learning to improve model generalizability and interpretability. SSI-DDI,28 MHCADDI,27 and CMPNN-CS30 leveraged the co-attention mechanism between the learned substructures of a drug pair so that each drug can communicate with the other. CMPNN-CS considered bonds as gates that control the flow of message passing of GNN, thereby delimiting the substructures in a learnable way. However, the gates are computed before the message passing, which means that they do not fully exploit the molecular structure information.
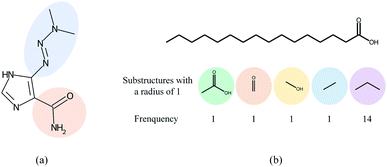
Overall, many computational models for DDI prediction have been developed, and these methods show promising performance on various datasets. However, at least three problems have not been well addressed for structure-based methods in DDI prediction. First, most of the works consider molecular substructures as fixed size and therefore use GNNs with a predetermined number of layers/iterations to capture substructures with the fixed radii. However, the sizes and shapes of chemical substructures are often irregular as shown in Fig. 1(a). Second, we argue that the most common readout functions (i.e., global mean/sum pooling) for GNNs are inappropriate for DDI prediction. For example, the essential substructures (e.g., ethanoic acid) may be overwhelmed by the minor ones (e.g., propyl) by directly calculating the sum/mean of the substructure representations, as shown in Fig. 1(b). Third, most of the works only conducted experiments under a warm start scenario (i.e., training and test sets share common drugs). However, practical applications usually require cold start scenarios for DDI prediction to deduce interactions between new drugs and known drugs or interactions among new drugs.
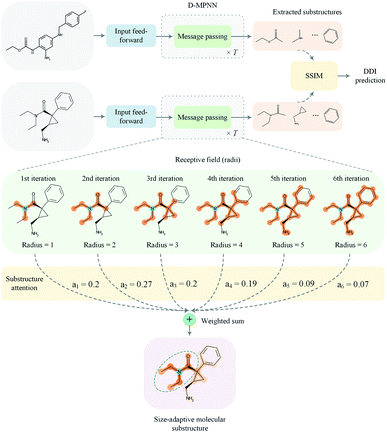
In this paper, we proposed a substructure-aware GNN based on medicinal chemistry knowledge for DDI prediction (SA-DDI). An overview of the proposed SA-DDI is shown in Fig. 2. SA-DDI mitigates the aforementioned limitations via the following technical contributions:
(a) A directed message passing neural network (D-MPNN)32 equipped with a novel substructure attention mechanism was presented to extract flexible-sized and irregular-shaped substructures. In SA-DDI, different scores determined by the substructure attention mechanism were assigned to substructures with different radii (i.e., different receptive fields). The weighted sum of substructures centering at an atom with different radii results in a size-adaptive molecular substructure, as shown in Fig. 2. The substructure attention was also expected to assign a lower score to a substructure from a higher level to prevent over-smoothing.33
(b) A novel substructure–substructure interaction module (SSIM) was introduced to model the chemical reactions among functional substructures of a drug pair. SSIM leverages the structure information of a drug to identify the important substructures of another drug for a drug pair. This overcomes the limitation of global mean/sum pooling, which regards each substructure as equally important.
(c) The experiments were conducted under both warm and cold start scenarios, where the latter provides a more realistic and challenging evaluation scheme for the models.
2 Methods
This section presents the technical details of the SA-DDI. The overall framework is shown in Fig. 2. In general, the DDI prediction task was to develop a computational model that takes two drugs dx and dy with an interaction type r as inputs and generates an output prediction that indicates whether an interaction (i.e., side effect) exists between them. First, an input feed-forward module (i.e., a multi-layer perceptron) was utilized to nonlinearly transform the nodes for better feature representation. Then, the two molecular graphs are fed into a GNN (D-MPNN in our case) equipped with substructure attention to extract the size- and shape-adaptive substructures. Finally, the extracted substructures are fed into the SSIM to learn the substructure–substructure interactions from which the model makes a DDI prediction.2.1 Graph neural network for substructures extraction
GNNs have received attention for their natural fit in chemical problems to describe the atoms and bonds of a molecule. In the current application, the atoms of a molecule serve as nodes of a graph, and edges/bonds are formed by the chemical bonds. Formally, a drug d is represented as a molecular graph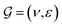 , where ν is the set of nodes/atoms, and ε is the set of edges/bonds. In a molecule, vi ∈ ν is the i-th atom and eij ∈ ε is the chemical bond between i-th and j-th atoms. Each node vi has a corresponding feature vector
, where ν is the set of nodes/atoms, and ε is the set of edges/bonds. In a molecule, vi ∈ ν is the i-th atom and eij ∈ ε is the chemical bond between i-th and j-th atoms. Each node vi has a corresponding feature vector 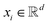 , and each bond eij has a feature vector
, and each bond eij has a feature vector 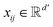 . The features used for atoms and bonds can be found in Tables S1 and S2 of ESI.†
. The features used for atoms and bonds can be found in Tables S1 and S2 of ESI.†
A typical workflow of GNNs is depicted in Fig. 3(a). In general, GNNs are composed of three stages, as follows: (1) updating node-level features by aggregating messages from their neighbor nodes (i.e., message passing), as shown in Fig. 3(b); (2) generating a graph-level feature vector by aggregating all the node-level features from a molecule graph using a readout function, as shown in Fig. 3(c); and (3) predicting a label of the graph based on the graph-level feature vector, as shown in Fig. 3(a). In the first stage, the node-level hidden feature h(t)i, which represents the attribute of the i-th node at the time step t (or t-th iteration) and h(0)i = xi, is updated T times (i.e., T iterations) by passing the message between its neighboring nodes. At each iteration, the receptive field, which represents the radius of a node, can be enlarged by accessing information from its neighbor nodes, as shown in Fig. 3(a) and (b). A node can be viewed as a substructure centered on itself with a radius of T after T-th iteration, as shown in Fig. 3(a). Then, the updated node-level hidden features h(T)i at the last time step T are aggregated across all nodes to produce a graph-level feature vector 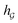 for a given graph
for a given graph 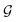 , as shown in Fig. 3(c). Finally, the graph-level feature vector is used to predict a label of the entire graph, e.g., molecular properties. In this study, we used the D-MPNN,32 a variant of the generic message passing neural network (MPNN)34 architecture, for molecule substructures extraction. The precise definition of MPNN and D-MPNN as well as their difference can be found in Section S1 of ESI.†
, as shown in Fig. 3(c). Finally, the graph-level feature vector is used to predict a label of the entire graph, e.g., molecular properties. In this study, we used the D-MPNN,32 a variant of the generic message passing neural network (MPNN)34 architecture, for molecule substructures extraction. The precise definition of MPNN and D-MPNN as well as their difference can be found in Section S1 of ESI.†
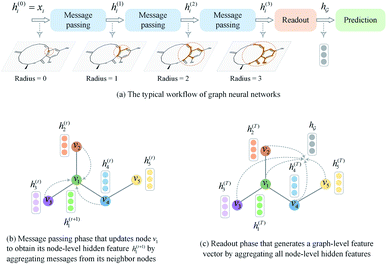 | ||
| Fig. 3 A brief introduction to graph neural networks. (a) The typical workflow of graph neural networks. (b) Message passing phase. (c) Readout phase. | ||
So far the GNN is learned in a standard manner, which has two shortcomings for DDI prediction. First, the GNN extracts fixed-size substructures after the T-th iteration, as shown in Fig. 3(a), which has a drawback as described in Fig. 1(a). Second, a typical readout function (i.e., global mean/sum pooling) computes the mean/sum of all node-level features from a graph (i.e., 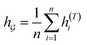 or
or 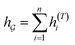 ) to obtain the graph-level representation
) to obtain the graph-level representation 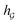 for a given graph
for a given graph 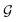 , but it has a disadvantage for DDI prediction as described in Fig. 1(b). Therefore, we introduced the novel substructure attention mechanism and SSIM in Sections 2.2 and 2.3 to solve these two limitations.
, but it has a disadvantage for DDI prediction as described in Fig. 1(b). Therefore, we introduced the novel substructure attention mechanism and SSIM in Sections 2.2 and 2.3 to solve these two limitations.
2.2 Substructure attention mechanism
The substructure attention was designed to extract substructures with arbitrary sizes and shapes. During the k-th iteration, the D-MPNN extracts substructures with a radius of k. The weighted sum of substructures centering on an atom with different radii leads to size-adaptive molecular substructures, as shown in Fig. 2.Unlike standard GNN which operates on nodes, the messages are propagated through bonds in D-MPNN, as shown in Fig. S1(b) of ESI.† Similar to standard GNN, in which there is a node-level hidden feature h(t)i with each node vi, we use h(t)ij to represent a bond-level hidden feature with each bond ei→j. The D-MPNN first operates on bonds in a way similar to standard GNN that operates on nodes. Then, it transforms the bond-level hidden feature h(T)ij back to node-level hidden feature h(T)i after the last iteration.
The idea of substructure attention is to assign different scores to substructures with different radii. Concretely, for a bond-level hidden feature h(t)ij at t step, we first obtained its graph-level representation 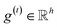 by utilizing a topology-aware bond global pooling:
by utilizing a topology-aware bond global pooling:
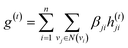 | (1) |
| βji = softmax(GNN(Ae,Xe)) | (2) |
| e(t) = a(t)⊙σ(Wg(t) + b) | (3) |
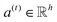 is a weight vector for step t, and σ is an activation function. We chose the tanh function as the activation function, because it works fairly well in practice. To make coefficients easily comparable across different steps, we normalize e(t) across all steps using the softmax function
is a weight vector for step t, and σ is an activation function. We chose the tanh function as the activation function, because it works fairly well in practice. To make coefficients easily comparable across different steps, we normalize e(t) across all steps using the softmax function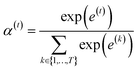 | (4) |
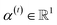 indicates the importance of the substructures with a radius of t. The final representation of a bond ei→j, which captures the substructure information with different radii, is given by the weighted sum of bond-level hidden features across all steps according to the following:
indicates the importance of the substructures with a radius of t. The final representation of a bond ei→j, which captures the substructure information with different radii, is given by the weighted sum of bond-level hidden features across all steps according to the following: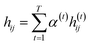 | (5) |
Finally, we returned to the node-level features by aggregating the incoming bond-level features as follows:
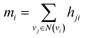 | (6) |
| hi = f(xi + mi) | (7) |
2.3 Substructure–substructure interaction module
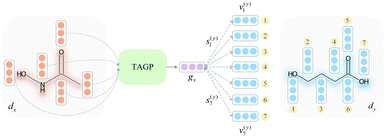
To overcome the limitation of the most common readout functions for GNN (i.e., global mean/sum pooling), as shown in Fig. 1(b), we proposed an SSIM to identify the crucial substructures for DDIs. By using substructure attention, the SA-DDI extracted several size-adaptive substructures, each centering at an atom, as shown in Fig. 2. The SSIM was used to assign each substructure of the drug a score, where the score is determined by its interaction probability with another drug, as shown in Fig. 4.Given a drug pair (dx, dy), we assumed that the substructure information of dx can be used to detect the essential substructures of dy. Specifically, we first used a topology-aware global pooling (TAGP) to obtain the graph-level representation of dx as follows:
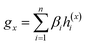 | (8) |
| βi = softmax(GNN(Av,Xv)) | (9) |
| s(y)i = softmax((Wxgx)⊙(Wyh(y)i)) | (10) |
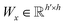 and
and 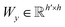 are two weight matrices. s(y)i can be viewed as the importance for substructure centering at i-th atom of dy. The overall computational steps for s(y)i are depicted in Fig. 4. Finally, the graph-level representation of dy can be computed by the following:
are two weight matrices. s(y)i can be viewed as the importance for substructure centering at i-th atom of dy. The overall computational steps for s(y)i are depicted in Fig. 4. Finally, the graph-level representation of dy can be computed by the following: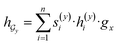 | (11) |
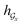 ) can be calculated by using computational steps similar to those described in eqn (8)–(11).
) can be calculated by using computational steps similar to those described in eqn (8)–(11).
2.4 Drug–drug interaction prediction
Given a DDI tuple (dx, dy, r), the DDI prediction can be expressed as the joint probability as follows: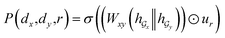 | (12) |
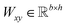 ,
, 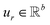 is a learnable representation of interaction type r, σ is the sigmoid function, and ∥ represents concatenation. The learning process of the model can be achieved by minimizing the cross-entropy loss function,36 which is given as follows:
is a learnable representation of interaction type r, σ is the sigmoid function, and ∥ represents concatenation. The learning process of the model can be achieved by minimizing the cross-entropy loss function,36 which is given as follows: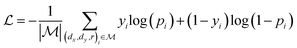 | (13) |
3 Results and discussion
3.1 Dataset
We evaluated the model performance in two real-world datasets—DrugBank and TWOSIDES.• DrugBank is a unique bioinformatics and cheminformatics resource that combines detailed drug data with comprehensive drug target information.37 It contains 1706 drugs with 191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 DDI tuples. Eighty-six interaction types describe how one drug affects the metabolism of another one. Each drug is represented as the simplified molecular-input line-entry system (SMILES) and we converted it into a molecular graph using RDKit. Each DDI tuple from DrugBank is a positive sample from which a negative sample is generated using the strategy described by Wang et al.38 In the DrugBank dataset, each drug pair is only associated with a single type of interaction.
808 DDI tuples. Eighty-six interaction types describe how one drug affects the metabolism of another one. Each drug is represented as the simplified molecular-input line-entry system (SMILES) and we converted it into a molecular graph using RDKit. Each DDI tuple from DrugBank is a positive sample from which a negative sample is generated using the strategy described by Wang et al.38 In the DrugBank dataset, each drug pair is only associated with a single type of interaction.
• TWOSIDES is constructed by Zitnik et al.39 after filtering and preprocessing the original TWOSIDES dataset.40 It includes 645 drugs with 963 interaction types and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 576
576![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 DDI tuples. As against the DrugBank dataset, these interactions are at the phenotypic level (i.e., headache, pain in the throat, and others) rather than metabolic. The negative samples are generated by a procedure the same as the DrugBank dataset.
287 DDI tuples. As against the DrugBank dataset, these interactions are at the phenotypic level (i.e., headache, pain in the throat, and others) rather than metabolic. The negative samples are generated by a procedure the same as the DrugBank dataset.
3.2 Experimental setup
We compared the proposed SA-DDI with state-of-the-art methods, namely, DeepCCI,26 MR-GNN,29 SSI-DDI,28 GAT-DDI,30 and GMPNN-CS.30 These baselines only consider chemical structure information as input and can work in both warm and cold start scenarios. The parameter settings for MR-GNN, SSI-DDI, and GMPNN-CS are consistent with their published source codes. As the source codes for DeepCCI and GAT-DDI are not provided, we implemented them with parameters recommended by the papers.26,30 To investigate how the D-MPNN, substructure attention and substructure–substructure interaction module improve the model performance, we also consider the following variants of SA-DDI:• SA-DDI_MPNN replaces the D-MPNN with MPNN.
• SA-DDI_noSA is a variant of the SA-DDI that removes substruction attention.
• SA-DDI_GMP replaces the SSIM with global mean pooling (i.e., 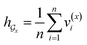 and
and 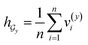 ).
).
Experiments were conducted using an NVIDIA GeForce RTX A4000 with 16 GB memory. Adam optimizer41 with a 0.001 learning rate was used to update model parameters. The batch size was set to 256 for all baselines. We optimized the hyper-parameters of the model in the validation set. Table S3 of ESI† lists the detailed hyper-parameters setting. The accuracy (ACC), area under the curve (AUC), F1-score (F1), precision (Prec), recall (Rec), and average precision (AP) were the performance indicators.
3.3 Performance evaluation under warm start scenario
The warm start scenario was the most common dataset split scheme where the whole dataset was split randomly and each drug in the test set can be found in the training set. In this scenario, we split the datasets randomly into training (60%), validation (20%), and test (20%) sets. All experiments were repeated thrice, each with a different random seed. Note that all methods share the same training, validation, and test sets each time. We finally reported the mean and standard deviation of results in the test set. We applied a weight decay of 5 × 10−4 for all methods to prevent overfitting.Tables 1 to 2 summarize the predictive performance of SA-DDI and previous models on the DrugBank and TWOSIDES datasets. The SA-DDI surpasses other baselines in the two datasets, which demonstrates the effectiveness of the proposed SA-DDI for DDI prediction. The SA-DDI exceeds SA-DDI_GMP by a notable margin in two datasets, which reveals the validity of the proposed SSIM. We analyzed why the SSIM improves model performance in Section 3.6. Moreover, we found that the SA-DDI gains less improvement from the substruction attention. However, the substruction attention can reduce the over-smooth problem and improve the model's generalization ability, as discussed in Section 3.5.
| ACC | AUC | F1 | Prec | Rec | AP | |
|---|---|---|---|---|---|---|
| DeepCCI | 93.21 ± 0.27 | 97.03 ± 0.14 | 93.37 ± 0.27 | 91.26 ± 0.25 | 95.58 ± 0.47 | 95.95 ± 0.20 |
| MRGNN | 93.23 ± 0.19 | 97.31 ± 0.08 | 93.39 ± 0.17 | 91.14 ± 0.39 | 95.76 ± 0.09 | 96.45 ± 0.09 |
| SSI-DDI | 92.48 ± 0.21 | 97.01 ± 0.09 | 92.65 ± 0.20 | 90.59 ± 0.27 | 94.80 ± 0.19 | 96.11 ± 0.14 |
| GAT-DDI | 92.03 ± 0.18 | 96.28 ± 0.09 | 92.29 ± 0.16 | 89.47 ± 0.34 | 95.29 ± 0.21 | 94.64 ± 0.12 |
| GMPNN-CS | 95.31 ± 0.07 | 98.45 ± 0.01 | 95.40 ± 0.07 | 93.58 ± 0.14 | 97.29 ± 0.01 | 97.91 ± 0.02 |
| SA-DDI_MPNN | 94.27 ± 0.09 | 97.91 ± 0.03 | 94.37 ± 0.09 | 92.74 ± 0.14 | 96.06 ± 0.06 | 97.22 ± 0.04 |
| SA-DDI_noSA | 96.00 ± 0.07 | 98.72 ± 0.07 | 96.06 ± 0.07 | 94.63 ± 0.05 | 97.53 ± 0.09 | 98.25 ± 0.12 |
| SA-DDI_GMP | 93.54 ± 0.16 | 97.22 ± 0.06 | 93.62 ± 0.15 | 92.49 ± 0.43 | 94.79 ± 0.42 | 95.80 ± 0.07 |
| SA-DDI | 96.23 ± 0.10 | 98.80 ± 0.02 | 96.29 ± 0.09 | 95.02 ± 0.12 | 97.59 ± 0.07 | 98.36 ± 0.04 |
| ACC | AUC | F1 | Prec | Rec | AP | |
|---|---|---|---|---|---|---|
| DeepCCI | 75.16 ± 0.30 | 82.42 ± 0.31 | 77.03 ± 0.05 | 71.65 ± 0.68 | 83.31 ± 0.84 | 79.47 ± 0.35 |
| MRGNN | 85.39 ± 0.31 | 91.93 ± 0.20 | 86.46 ± 0.27 | 80.57 ± 0.37 | 93.28 ± 0.21 | 89.32 ± 0.22 |
| SSI-DDI | 82.21 ± 0.41 | 89.27 ± 0.38 | 83.11 ± 0.44 | 79.10 ± 0.31 | 87.56 ± 0.81 | 86.19 ± 0.41 |
| GAT-DDI | 67.32 ± 2.04 | 75.16 ± 2.47 | 63.70 ± 3.28 | 71.54 ± 2.31 | 57.62 ± 5.09 | 72.50 ± 2.45 |
| GMPNN-CS | 86.96 ± 0.03 | 92.94 ± 0.02 | 87.85 ± 0.04 | 82.20 ± 0.03 | 94.35 ± 0.10 | 90.38 ± 0.04 |
| SA-DDI_MPNN | 87.23 ± 0.02 | 93.02 ± 0.03 | 88.17 ± 0.01 | 82.09 ± 0.05 | 95.23 ± 0.06 | 90.32 ± 0.03 |
| SA-DDI_noSA | 87.21 ± 0.09 | 93.03 ± 0.05 | 88.12 ± 0.10 | 82.23 ± 0.05 | 94.92 ± 0.17 | 90.33 ± 0.07 |
| SA-DDI_GMP | 75.32 ± 0.43 | 82.59 ± 0.66 | 78.14 ± 0.80 | 70.11 ± 0.70 | 88.35 ± 2.90 | 78.22 ± 0.74 |
| SA-DDI | 87.45 ± 0.03 | 93.17 ± 0.04 | 88.35 ± 0.04 | 82.43 ± 0.02 | 95.18 ± 0.10 | 90.51 ± 0.08 |
Fig. 5 shows the performance of each DDI type for each method on the two datasets. In general, the results for the DrugBank dataset have a much larger standard deviation than those for the TWOSIDES data. This phenomenon stems from the fact that the DrugBank dataset has a very unbalanced distribution of DDI types as shown in Fig. S2(a) of ESI.† The SA-DDI still leads to competitive results on each DDI type on the two datasets.
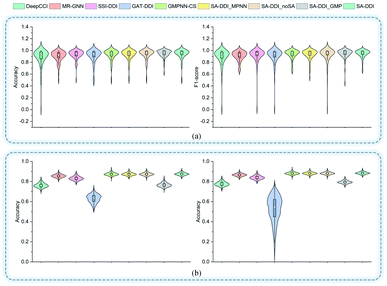 | ||
| Fig. 5 The accuracy and F1-score of different methods for each interaction type in the (a) DrugBank dataset and (b) TWOSIDES dataset. | ||
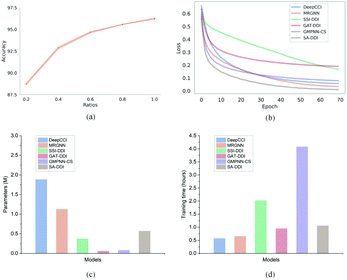
Furthermore, to evaluate how the size of the training set affects the model performance, we randomly sampled 20%, 40%, 60%, 80%, and 100% of the original training set from the DrugBank dataset and considered them as the new training sets to retrain the SA-DDI. Increasing the training data always adds information and improves the model performance in the test set, as shown in Fig. 6(a). A significant jump can be observed by increasing the ratios of training data from 20% to 40%. However, the performance increment shows the trend of slowing down with increasing ratios from 40% to 100%. Having more data certainly increases the accuracy of the model, but there comes a stage where even adding infinite amounts of data can no longer improve accuracy, which is caused by the natural noise of the data. When 60% of data are used, the model achieves an accuracy of 94.67%, which is only about 1.5% lower than the best (i.e., 100% of data are used).
Moreover, we analyze the training efficiency of the proposed SA-DDI in the DrugBank dataset. The SA-DDI achieves the fastest training speed (i.e., convergence rate), as shown in Fig. 6(b), with a moderate number of parameters and training time, as shown in Fig. 6(c) and (d). A larger number of parameters do not mean better performance. The number of parameters for DeepCCI is about thrice those of SA-DDI, whereas its test accuracy is approximately 3% lower than the SA-DDI. Although GMPNN-CS has a lower number of parameters compared with SA-DDI, it requires a much larger training time. GMPNN-CS uses a co-attention to compute the interaction between substructures of a drug pair, which leads to a much lower computation efficiency. Overall, the SA-DDI achieves the best performance with a moderate training efficiency.
3.4 Performance evaluation under cold start scenarios
The warm start scenario can lead to over-optimistic results, because it causes information leakage (i.e., drug structure information) to the test set. To further demonstrate the efficacy of the proposed SA-DDI, we assessed all the baselines in two additional splitting schemes:• Cold start for a single drug (new ↔ old) is a cold start scenario in which one drug in a drug pair in the test set is inaccessible in the training set. We further considered two settings in this scenario, as follows: (1) the drugs are split randomly; and (2) the drugs are split according to their structures. Drugs in the training and test sets are structurally different (i.e., the two sets have guaranteed minimum distances in terms of structure similarity). We used Jaccard distance on binarized ECFP4 features to measure the distance between any two drugs in accordance with the method described in a previous study.42
• Cold start for a pair of drugs (new ↔ new) is also a cold start scenario where both drugs in a drug pair in the test set are inaccessible in the training set.
The cold start scenarios provide a realistic and more challenging evaluation scheme for the models. In the cold start scenarios, we randomly held 20% DDI tuples as the test set following the criterion described above. Other experimental settings are the same as those in the warm start scenario. We only considered the cold start scenarios in the DrugBank dataset, because the TWOSIDES dataset contains some false positives (i.e., drug pairs included in the TWOSIDES do not interact) that would cause unreliable assessments for the models in the cold start scenarios.20 We applied a weight decay of 5 × 10−3 for all methods, because the models are easy to overfit to the drugs on which the model is trained in the cold start scenarios.28
Tables 3 to 4 summarize the experimental results in the cold start scenarios. A significant degradation in performance was found in the cold start scenarios. Moreover, the structure-based split is more challenging to the DDI prediction models compared to the random split, which is consistent with the fact that the structure-based split can prevent the structural information of drugs from leaking to the test set.33 Improving the generalization ability of the DDI model is still a challenge. Another possible reason for this phenomenon is that most of the drugs in the DrugBank dataset are significantly different in terms of scaffolds (core chemical structure). Therefore, drugs in the test and training sets are not only different but also share a few common structures in the cold start scenarios.28 However, the SA-DDI still outperforms the other methods. By comparing SA-DDI with SA-DDI_MPNN, SA-DDI_noSA, and SA-DDI_GMP, we found that the model can benefit from the proposed strategies for DDI prediction. Although the performance of DDI prediction models in the cold start scenarios is significantly lower than in the warm start scenario, the results are still much better than random guesses, which suggests that the learned chemical substructure information can be generalized to different drugs with similar substructures.
| Setting | Models | ACC | AUC | F1 | Prec | Rec | AP |
|---|---|---|---|---|---|---|---|
| Random split | DeepCCI | 79.53 ± 0.44 | 87.28 ± 1.47 | 77.17 ± 0.10 | 87.39 ± 2.47 | 69.18 ± 1.69 | 87.57 ± 1.19 |
| MRGNN | 75.99 ± 0.53 | 84.85 ± 1.53 | 72.30 ± 0.32 | 85.52 ± 2.19 | 62.68 ± 1.22 | 84.89 ± 1.55 | |
| SSI-DDI | 75.13 ± 0.32 | 83.26 ± 0.52 | 72.36 ± 0.34 | 81.52 ± 2.24 | 65.15 ± 1.94 | 83.48 ± 0.86 | |
| GAT-DDI | 77.94 ± 0.25 | 86.58 ± 0.21 | 75.28 ± 0.27 | 85.63 ± 0.32 | 67.16 ± 0.24 | 85.81 ± 0.01 | |
| GMPNN-CS | 79.95 ± 0.57 | 89.34 ± 0.43 | 77.22 ± 0.79 | 89.33 ± 0.45 | 68.02 ± 1.16 | 89.25 ± 0.39 | |
| SA-DDI_MPNN | 79.09 ± 1.19 | 87.85 ± 1.91 | 76.45 ± 1.17 | 87.62 ± 2.74 | 67.86 ± 1.41 | 88.14 ± 1.97 | |
| SA-DDI_noSA | 83.66 ± 0.41 | 91.56 ± 0.80 | 81.90 ± 0.21 | 91.83 ± 1.77 | 73.95 ± 0.82 | 92.31 ± 0.88 | |
| SA-DDI_GMP | 79.39 ± 0.22 | 88.12 ± 0.11 | 76.46 ± 0.36 | 89.13 ± 0.25 | 66.94 ± 0.66 | 87.73 ± 0.13 | |
| SA-DDI | 84.18 ± 0.11 | 92.22 ± 0.55 | 82.45 ± 0.37 | 92.56 ± 1.34 | 74.38 ± 1.47 | 92.99 ± 0.50 | |
| Structure-based split | DeepCCI | 73.32 ± 1.20 | 81.56 ± 2.67 | 69.07 ± 0.83 | 83.05 ± 6.26 | 59.72 ± 4.76 | 81.98 ± 3.39 |
| MRGNN | 67.33 ± 1.38 | 76.52 ± 2.65 | 59.71 ± 2.16 | 78.41 ± 5.04 | 48.59 ± 4.10 | 75.25 ± 3.25 | |
| SSI-DDI | 68.52 ± 1.75 | 77.41 ± 2.45 | 62.06 ± 0.71 | 78.63 ± 5.30 | 51.43 ± 1.32 | 77.14 ± 3.70 | |
| GAT-DDI | 71.55 ± 0.39 | 80.71 ± 1.18 | 65.91 ± 0.29 | 82.23 ± 1.60 | 55.02 ± 0.87 | 80.44 ± 1.20 | |
| GMPNN-CS | 71.57 ± 0.72 | 81.90 ± 1.30 | 63.83 ± 1.29 | 87.68 ± 1.11 | 50.21 ± 1.62 | 82.90 ± 1.17 | |
| SA-DDI_MPNN | 72.33 ± 0.53 | 81.42 ± 1.17 | 64.93 ± 1.03 | 88.58 ± 0.42 | 51.26 ± 1.35 | 83.39 ± 0.72 | |
| SA-DDI_noSA | 75.94 ± 0.15 | 84.58 ± 0.94 | 70.83 ± 0.36 | 90.04 ± 2.10 | 58.42 ± 1.38 | 86.39 ± 0.94 | |
| SA-DDI_GMP | 74.14 ± 0.31 | 84.64 ± 0.16 | 68.04 ± 0.89 | 89.08 ± 1.15 | 55.08 ± 1.61 | 84.98 ± 0.45 | |
| SA-DDI | 76.49 ± 0.16 | 85.75 ± 0.37 | 71.15 ± 0.34 | 92.07 ± 0.79 | 57.98 ± 0.70 | 87.71 ± 0.26 |
| ACC | AUC | F1 | Prec | Rec | AP | |
|---|---|---|---|---|---|---|
| DeepCCI | 66.21 ± 2.37 | 73.79 ± 3.66 | 61.57 ± 1.55 | 72.00 ± 5.63 | 54.13 ± 2.96 | 71.65 ± 4.22 |
| MRGNN | 61.92 ± 1.07 | 66.89 ± 1.45 | 60.71 ± 1.11 | 62.71 ± 1.15 | 58.83 ± 1.07 | 64.31 ± 2.70 |
| SSI-DDI | 63.42 ± 0.94 | 68.33 ± 1.08 | 63.21 ± 1.16 | 63.80 ± 2.43 | 63.03 ± 4.70 | 66.01 ± 0.92 |
| GAT-DDI | 66.36 ± 0.23 | 72.95 ± 0.29 | 64.09 ± 0.46 | 68.75 ± 1.02 | 60.07 ± 1.58 | 71.42 ± 0.27 |
| GMPNN-CS | 69.30 ± 0.53 | 77.48 ± 0.97 | 66.36 ± 0.52 | 73.41 ± 0.77 | 60.54 ± 0.45 | 75.57 ± 0.72 |
| SA-DDI_MPNN | 67.79 ± 1.81 | 76.12 ± 2.83 | 65.03 ± 0.74 | 71.84 ± 4.98 | 60.00 ± 4.87 | 75.27 ± 3.03 |
| SA-DDI_noSA | 68.37 ± 0.97 | 75.34 ± 1.94 | 67.37 ± 0.82 | 69.87 ± 3.06 | 65.44 ± 4.46 | 73.19 ± 2.45 |
| SA-DDI_GMP | 63.55 ± 2.59 | 68.88 ± 4.13 | 64.60 ± 0.36 | 63.38 ± 4.54 | 66.47 ± 4.15 | 66.09 ± 3.73 |
| SA-DDI | 70.52 ± 0.85 | 79.14 ± 1.07 | 67.12 ± 1.98 | 75.81 ± 1.18 | 60.38 ± 3.88 | 78.06 ± 0.93 |
3.5 How does substruction attention solve over-smoothing problems?
Theoretically, a GNN with more layers/iterations would be more aware of the graph structure.33 However, increasing the depth of the GNN may cause an over-smoothing representation of vertices. Our demand for a model that is more expressive and aware of the graph structure (by adding more layers/iterations so that vertices can have a large receptive field) could be transformed into a demand for a model that treats vertices all the same (i.e., features at vertices within each connected component converging to the same value).33In our design, the substruction attention is used to extract substructures with arbitrary size and shape. Therefore, the substruction attention is expected to identify which size of the substructures (i.e., receptive field) is the most important. Moreover, as over-smoothing is caused by the substructures from higher levels, the substruction attention is also expected to assign less weight to the substructures from higher levels.
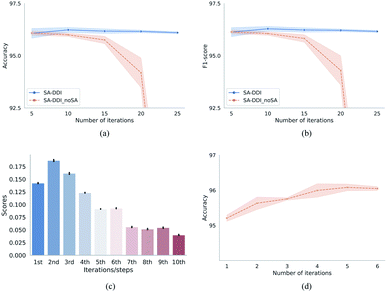
Fig. 7 provides the quantitative analysis of the substructure attention mechanism. As shown in Fig. 7(a) and (b), the performance of SA-DDI_noSA decreases greatly with increasing network depth (by adding more iterations). On the other hand, the SA-DDI can be extended to 25 iterations without significant degradation in performance. This is because the substructure attention decreases the weight of substructures from higher levels as shown in Fig. 7(c), which is consistent with our original design. The distribution of attention scores is plotted from all of the data in the DrugBank dataset. Moreover, Fig. 7(c) shows that the substructures with a radius of 2 are the most important for the model, which is consistent with the result of a previous study.43 This result is reasonable, because extracting the substructures with a radius of 2 leads to more substructure types than that with a radius of 1.44 The finding is also consistent with the result shown in Fig. 7(d), in which the model gains the most significant improvement from increasing the number of iterations from 1 to 2.
One of the advantages of substructure attention is that it increases the robustness of the model. A previous study has found that the number of iterations would affect the generalizability of the message passing model, and using a pre-specified number of iterations might not work well for different kinds of datasets.45 This problem can be alleviated by the substructure attention mechanism, as it makes the model insensitive to the number of iterations, as shown in Fig. 7(a) and (b).
Besides, as shown in Tables 1, 3, and 4, the SA-DDI achieves improvements of 0.23%, 0.52%, 0.55%, and 2.15% in terms of accuracy by using substructure attention for the warm start, cold start for a single drug (random split), cold start for a single drug (structure-based split), and cold start for a pair of drugs, respectively. A correlation was found between improvements and task difficulties. The more difficult the task was, the more improvement can be obtained by using substructure attention, suggesting that substructure attention can improve the generalization capability of DDI prediction by detecting size-adaptive substructures.
3.6 Why does SSIM improve model performance?
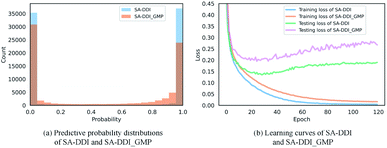
The key substructures may be overwhelmed by the minor ones by using a global mean/max pooling as the readout function, as shown in Fig. 1(b). In fact, treating each substructure equally important (i.e., equal probability) has the largest entropy/uncertainty.46 Conversely, the SSIM reduces the entropy by increasing the weight of central substructures while scaling it down for unimportant ones. To analyze SSIM from the perspective of entropy, we plotted the distribution of predictive probability across the DrugBank dataset for the SA-DDI and SA-DDI_GMP. The results are shown in Fig. 8(a). The SA-DDI_GMP has a relatively broad probability distribution compared with the SA-DDI, which means that it has a larger entropy. The idea of selecting important features by reducing entropy is similar to feature selection using decision trees.47 Moreover, reducing the entropy by the SSIM can accelerate training as well as improve the generalization ability, as shown in Fig. 8(b).3.7 Visual explanations for SA-DDI
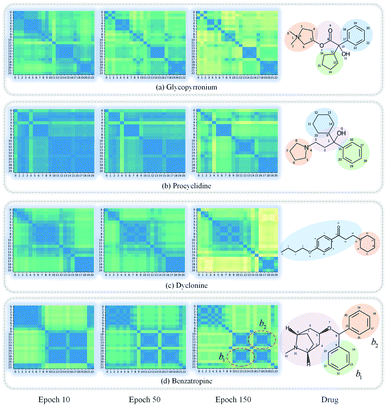
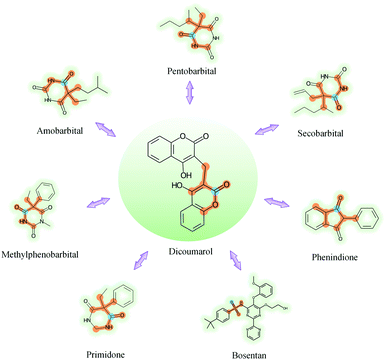
GNNs cannot be fully trusted without understanding and verifying their inner working mechanisms, which limits their application in drug discovery scenarios.48,49 In this study, we conducted two visual explanation-related experiments to rationalize the SA-DDI. First, to investigate how the atom hidden vectors evolved during the learning process, we obtained the similarity coefficient between atom pairs by measuring the Pearson correlation coefficient for those hidden vectors. We chose the hidden vectors after the last iteration (i.e., vi in eqn (7)), because they have the best compromise between high-level semantics and detailed spatial information.33Fig. 9 gives four drugs with their atom similarity matrices during the learning process. The heat maps show some degree of chaos at the beginning and then clearly group into clusters during the learning process. Taking Fig. 9(b) as an example, we found that the atoms in procyclidine at epoch 150 approximately separate into four clusters, as follows: isopropanol (atoms 0–3), tetrahydropyrrole (atoms 4–8), phenylcyclohexane (atoms 9–14), and benzene (atoms 15–20). This finding is in accordance with our intuition regarding the procyclidine structure. These results suggest that the SA-DDI can capture the structure information of a molecule. Besides, the SA-DDI is able to recognize the same functional groups in a molecule such as the benzenes b1 and b2, as shown in Fig. 9(d). It can also distinguish the functional groups with subtle structural differences, such as phenylcyclohexane and benzene, as shown in Fig. 9(b).To further explore which substructures provide the most significant contribution to DDI prediction, we visualized the most essential substructures for drug–drug interactions between dicoumarol and the other seven drugs in the warm start scenario, as shown in Fig. 10. Specifically, we chose two atoms with the largest interaction probability s(x)i and s(y)j, which are described by eqn (10), as the center of the most vital substructures. Their size and shape can be determined by the largest attention score as described by eqn (4) (e.g., a substructure with a radius of 2 is determined if the second iteration has the largest attention score). The SA-DDI identifies the common substructures (i.e., barbituric acid) for secobarbital, pentobarbital, amobarbital, methylphenobarbital, and primidone, which agrees with the fact that drugs with a barbituric acid substructure can decrease the curative effect of dicoumarol by accelerating its metabolism, because barbituric acid can enhance the activity of human liver microsomes.50 The SA-DDI also detects sulfonamide and indanedione substructures for drugs bosentan and phenindione, which is consistent with the fact that drugs with these two functional groups may increase the anticoagulant activities of dicoumarol, because they can bind to plasma proteins competitively.51 More examples are found in Fig. S3 of ESI.†
In addition, to explore why cold start scenarios lead to poor performance from the perspective of the substructure, we also visualized the most central substructures for these eight drugs under cold start scenarios. We first removed drug pairs containing dicoumarol and the other seven drugs from the training set and retrained the SA-DDI. We then visualized the key substructures of these eight drugs, as shown in Fig. S4 of ESI.† In general, the substructures that the model highlights in the cold start scenarios had a larger size than those in the warm start scenario. This result was in accordance with our intuition that a model would try to include more information (larger substructures in this case) when it shows higher uncertainty for its predictions in unseen drugs. The mean uncertainty of the predictions made by the SA-DDI trained in cold start scenarios is 0.62, whereas that in the warm start scenario is 0.05, which is consistent with our analysis above. However, DDIs are mainly caused by essential chemical substructure interactions. Thus, the large-sized substructures may introduce noise and cause a degradation of performance.
4 Conclusion
This work presented a graph-based model called SA-DDI for DDI prediction. Based on the fact that DDIs are fundamentally caused by chemical substructure interactions, two novel strategies, including the substructure attention and SSIM, were proposed specifically to detect substructures with irregular size and shape and model the substructure–substructure interactions. Extensive experiments verified the superiority of the proposed method, exceeding the state-of-the-art methods on two datasets under different scenarios. Moreover, we visualized the atom similarity and key substructures for DDI prediction of certain molecules from the DrugBank dataset. The visual interpretation results showed that SA-DDI can capture the structure information of a drug and detect the essential substructures for DDIs, making the learning process of the model more transparent and operable. SA-DDI is a powerful tool to improve the generalization and interpretation capability of DDI prediction modeling.Data availability
Demo, instructions, and code for SA-DDI are available at https://github.com/guaguabujianle/SA-DDI.Author contributions
Calvin Yu-Chian Chen designed research. Ziduo Yang, Weihe Zhong worked together to complete the experiment and analyze the data. Calvin Yu-Chian Chen contributed to analytic tools. Ziduo Yang, Weihe Zhong, Qiujie Lv, and Calvin Yu-Chian Chen wrote the manuscript together.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 62176272), Guangzhou Science and Technology Fund (Grant No. 201803010072), Science, Technology & Innovation Commission of Shenzhen Municipality (JCYL 20170818165305521), and China Medical University Hospital (DMR-111-102, DMR-111-143, DMR-111-123). We also acknowledge the start-up funding from SYSU's “Hundred Talent Program”.References
- K. Han, E. E. Jeng, G. T. Hess, D. W. Morgens, A. Li and M. C. Bassik, Nat. Biotechnol., 2017, 35, 463–474 CrossRef CAS PubMed.
- Y.-H. Feng, S.-W. Zhang and J.-Y. Shi, BMC Bioinf., 2020, 21, 1–15 CrossRef PubMed.
- C. Park, J. Park and S. Park, Expert Syst. Appl., 2020, 159, 113538 CrossRef.
- H. Wu, Y. Xing, W. Ge, X. Liu, J. Zou, C. Zhou and J. Liao, J. Biomed. Inf., 2020, 106, 103432 CrossRef PubMed.
- Z. Zhao, Z. Yang, L. Luo, H. Lin and J. Wang, Bioinformatics, 2016, 32, 3444–3453 CAS.
- Y. Zhang, W. Zheng, H. Lin, J. Wang, Z. Yang and M. Dumontier, Bioinformatics, 2018, 34, 828–835 CrossRef CAS PubMed.
- H. He, G. Chen and C. Yu-Chian Chen, Briefings Bioinf., 2022, 23, bbac134 CrossRef PubMed.
- J. D. Duke, X. Han, Z. Wang, A. Subhadarshini, S. D. Karnik, X. Li, S. D. Hall, Y. Jin, J. T. Callaghan and M. J. Overhage, et al. , PLoS Comput. Biol., 2012, 8, 1–13 CrossRef PubMed.
- S. Vilar, C. Friedman and G. Hripcsak, Briefings Bioinf., 2018, 19, 863–877 CrossRef CAS PubMed.
- T. Takeda, M. Hao, T. Cheng, S. H. Bryant and Y. Wang, J. Cheminf., 2017, 9, 1–9 Search PubMed.
- N. Rohani and C. Eslahchi, Sci. Rep., 2019, 9, 1–11 CrossRef CAS PubMed.
- G. Lee, C. Park and J. Ahn, BMC Bioinf., 2019, 20, 1–8 CrossRef PubMed.
- J. Y. Ryu, H. U. Kim and S. Y. Lee, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4304–E4311 CrossRef CAS PubMed.
- Y. Deng, X. Xu, Y. Qiu, J. Xia, W. Zhang and S. Liu, Bioinformatics, 2020, 36, 4316–4322 CrossRef CAS PubMed.
- S. Lin, Y. Wang, L. Zhang, Y. Chu, Y. Liu, Y. Fang, M. Jiang, Q. Wang, B. Zhao and Y. Xiong, et al. , Briefings Bioinf., 2022, 23, bbab421 CrossRef PubMed.
- Y. Chen, T. Ma, X. Yang, J. Wang, B. Song and X. Zeng, Bioinformatics, 2021, 37, 2651–2658 CrossRef CAS PubMed.
- F. Wang, X. Lei, B. Liao and F.-X. Wu, Briefings Bioinf., 2022, 23, bbab511 CrossRef PubMed.
- T. Ma, C. Xiao, J. Zhou and F. Wang, 2018, arXiv preprint arXiv:1804.10850.
- H. Wang, D. Lian, Y. Zhang, L. Qin and X. Lin, 2020, arXiv preprint arXiv:2005.05537.
- P. Zhang, F. Wang, J. Hu and R. Sorrentino, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- H. Yu, K.-T. Mao, J.-Y. Shi, H. Huang, Z. Chen, K. Dong and S.-M. Yiu, BMC Syst. Biol., 2018, 12, 101–110 CrossRef PubMed.
- W. Zhang, Y. Chen, F. Liu, F. Luo, G. Tian and X. Li, BMC Bioinf., 2017, 18, 1–12 Search PubMed.
- W. Zhang, Y. Chen, D. Li and X. Yue, J. Biomed. Inf., 2018, 88, 90–97 CrossRef PubMed.
- R. Ferdousi, R. Safdari and Y. Omidi, J. Biomed. Inf., 2017, 70, 54–64 CrossRef PubMed.
- K. Huang, C. Xiao, T. Hoang, L. Glass and J. Sun, Proceedings of the AAAI Conference on Artificial Intelligence, 2020, pp. 702–709 Search PubMed.
- S. Kwon and S. Yoon, Proceedings of the 8th ACM international conference on bioinformatics, computational biology, and health informatics, 2017, pp. 203–212 Search PubMed.
- A. Deac, Y.-H. Huang, P. Veličković, P. Liò and J. Tang, 2019, arXiv preprint arXiv:1905.00534.
- A. K. Nyamabo, H. Yu and J.-Y. Shi, Briefings Bioinf., 2021, 22, bbab133 CrossRef PubMed.
- N. Xu, P. Wang, L. Chen, J. Tao and J. Zhao, 2019, arXiv preprint arXiv:1905.09558.
- A. K. Nyamabo, H. Yu, Z. Liu and J.-Y. Shi, Briefings Bioinf., 2022, 23, bbab441 CrossRef PubMed.
- R. B. Silverman and M. W. Holladay, The organic chemistry of drug design and drug action, Academic press, 2014 Search PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS PubMed.
- Z. Yang, W. Zhong, L. Zhao and C. Y.-C. Chen, Chem. Sci., 2022, 13(3), 816–833 RSC.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed.
- J. Lee, I. Lee and J. Kang, International conference on machine learning, 2019, pp. 3734–3743 Search PubMed.
- Z. Yang, L. Zhao, S. Wu and C. Y.-C. Chen, IEEE J. Biomed. Health Inform., 2021, 25, 1864–1872 Search PubMed.
- D. S. Wishart, Y. D. Feunang, A. C. Guo, E. J. Lo, A. Marcu, J. R. Grant, T. Sajed, D. Johnson, C. Li and Z. Sayeeda, et al. , Nucleic Acids Res., 2018, 46, D1074–D1082 CrossRef CAS PubMed.
- Z. Wang, J. Zhang, J. Feng and Z. Chen, Proceedings of the AAAI Conference on Artificial Intelligence, 2014 Search PubMed.
- M. Zitnik, M. Agrawal and J. Leskovec, Bioinformatics, 2018, 34, i457–i466 CrossRef CAS PubMed.
- N. P. Tatonetti, P. P. Ye, R. Daneshjou and R. B. Altman, Sci. Transl. Med., 2012, 4 CrossRef PubMed , 125ra31.
- D. P. Kingma and J. L. Ba, 3rd International Conference on Learning Representations, ICLR 2015 – Conference Track Proceedings, 2015 Search PubMed.
- A. Mayr, G. Klambauer, T. Unterthiner, M. Steijaert, J. K. Wegner, H. Ceulemans, D.-A. Clevert and S. Hochreiter, Chem. Sci., 2018, 9, 5441–5451 RSC.
- M. Tsubaki, K. Tomii and J. Sese, Bioinformatics, 2019, 35, 309–318 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- Y. Rong, Y. Bian, T. Xu, W. Xie, Y. Wei, W. Huang and J. Huang, Adv. Neural. Inf. Process. Syst., 2020, 33, 12559–12571 Search PubMed.
- C. Adami, Philos. Trans. R. Soc., A, 2016, 374, 20150230 CrossRef PubMed.
- M. Dash and H. Liu, Intell. Data Anal., 1997, 1, 131–156 Search PubMed.
- Z. Yang, W. Zhong, L. Zhao and C. Y.-C. Chen, J. Phys. Chem. Lett., 2021, 12, 4247–4261 CrossRef CAS PubMed.
- Z. Yang, W. Zhong, Q. Lv and C. Y.-C. Chen, Phys. Chem. Chem. Phys., 2022, 24, 5383–5393 RSC.
- C. Ioannides and D. V. Parke, J. Pharm. Pharmacol., 1975, 27, 739–746 CrossRef CAS PubMed.
- M. D. Freedman and A. G. Olatidoye, Drug Saf., 1994, 10, 381–394 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02023h |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2022 |