An exsolution constructed FeNi/NiFe₂O₄ composite: preferential breaking of octahedral metal–oxygen bonds in a spinel oxide

Abstract

Exsolution is an ingenious strategy for the in situ construction of metal- or alloy-decorated oxides and, due to its promising energy related catalysis applications, has advanced from use in perovskites to use in spinels. Despite its great importance for designing target composites, the ability to identify whether active metal ions at octahedral or tetrahedral sites will preferentially exsolve in a spinel remains unexplored. Here, an inverse spinel NiFe₂O₄ (NFO) was employed as a prototype and FeNi/NFO composites were successfully constructed via exsolution. The preferential breaking of octahedral metal–oxygen bonds in the spinel oxide was directly observed using Mössbauer and X-ray absorption spectroscopy. This was further verified from the negative segregation energies calculated based on density-functional theory. One exsolved FeNi/NFO composite exhibits enhanced electrochemical activity with an overpotential of 283 mV at 10 mA cm⁻² and a long stability time for the oxygen evolution reaction. This work offers a unique insight into spinel exsolution based on the preferential breaking of chemical bonds and may be an effective guide for the design of new composite catalysts where the desired metal ions are deliberately introduced to octahedral and/or tetrahedral sites.

---

Introduction

Decorating the surface of an oxide support with active metal nanoparticles is an effective strategy to design functional materials that utilizes exceptional synergistic effects and has been widely applied in energy conversion and catalysis applications.^1,2 Exogenous loading methods such as physical mixing, wet chemical impregnation, physical or chemical vapor deposition techniques, etc. are commonly used to prepare such functional composites.^3–6 However, the irregular growth, agglomeration, and weak adhesion of the nanoparticles, all of which seriously affect the stability of catalysts, are inevitable problems that these methods suffer from. Over the past decade, the in situ growth of metal or alloy nanoparticles from prefabricated oxides under a reducing atmosphere, known as “exsolution”, has proved to be an ingenious scheme that addresses the above mentioned shortcomings.^7–9 Spontaneously exsolved nanoparticles distribute uniformly on the surface of parent oxides, resulting in a great lifetime enhancement during the catalytic process.⁷ Furthermore, a strong interaction between the deeply anchored nanoparticles and supported oxides also has the benefit of access to higher catalytic reactivity.^9,10

Exsolved nanoparticles of transition metals/alloys, noble metals and simple oxides that cooperate with the parent oxides, such as perovskites, spinels etc., have been extensively constructed to exploit their higher electrocatalytic performance.^11–13 In our previous work, the second phase of Ru,¹⁴ Co,¹⁵ and a CoFe alloy¹⁶ were exsolved from perovskite-type oxides and presented excellent activity and stability in the oxygen evolution reaction/oxygen reduction reaction (OER/ORR). This activity originates from the embedded configuration of the materials and from optimized charge transfer. Until now, compared with research on the structure–activity relationships of exsolved composites, there has been relatively little work focused on the exsolution process. Generally, the key to exsolution is to re-establish the thermodynamic equilibrium of the reducible species from the ionic state of the parent oxide lattice to the metallic state on the surface. The exsolution process can be described as four consecutive chemically driven steps, including diffusion, reduction, nucleation, and growth.^17–19 A variety of standpoints have been proposed for exploring the fundamentals of exsolution, which is extremely important for achieving the desired composite architecture. The Gibbs free energy change (ΔG < 0) from the ionic state to the metallic state has been known as the main driving force for the exsolution, for example, Fe is non-reducible due to its positive Gibbs free energy change at low temperature.¹⁷ Kwon et al. investigated the reducibility of several transition metals in perovskites, and revealed that the co-segregation energy of B-site dopants and oxygen vacancies can be used as a central descriptor of the exsolution reaction. However, the co-segregation energy of Fe is too positive for it to exsolve favorably towards the surface.²⁰ Even so, Fe ion can also be exsolved into forms of alloy by introducing Co and Ni into the perovskite, which can be largely attributed to the decrease of the stability of the lattice and the corresponding segregation energy.^15,21,22 Moreover, exsolution has always been found to occur preferentially at rough surfaces, grain boundaries, and corner/edge sites due to their higher free energies and geometrical suitability for nucleation.^23,24 Recently, the exsolution of CoFe alloy nanoparticles has also been pursued in spinel oxides due to their promising catalytic properties. Wang et al. reported that exsolved CoFe nanoparticles can be prepared by annealing the parent oxide CoFe₂O₄ in H₂.²⁵ Xiao et al. found that an active phase CoFe alloy could be embedded on the spinel support CoFeAlO_x by controlling the exsolution atmosphere.²⁶ In contrast to the structures of perovskite-type oxides, transition metal ions can be located at the centers of octahedra and tetrahedra simultaneously in spinel oxides. In other words, octahedral and tetrahedral Fe–O coordinate bonds are both present in the two abovementioned spinels.²⁷ However, it is hard to identify from which site the exsolved Fe comes. Thus, having a fundamental understanding of whether octahedral or tetrahedral transition ions preferentially exsolve is of great importance for constructing functional composites based on spinel oxides.

Herein, NiFe₂O₄ (NFO) with an inverse spinel structure was employed as a prototype, in which each half of the Fe³⁺ is distributed equally to tetrahedral and octahedral sites, and all the Ni²⁺ fills octahedral sites.²⁸ NiFe alloy nanoparticles were successfully exsolved from NFO by varying the reduction temperature. We observed, using Mössbauer spectroscopy and synchrotron radiation measurements, that metal–oxygen (M–O) bonds located at the octahedral coordination environment of the spinel structure were preferentially broken during the in situ exsolution process. This finding is also consistent with the results of the segregation energy calculations. The obtained FeNi/NFO composite exhibits an enhanced electrochemical activity with an overpotential of 283 mV at 10 mA cm⁻² and remains stable for a long time during the oxygen evolution reaction (OER). Our work offers a unique insight into spinel exsolution based on the preferential breaking of chemical bonds and may be an effective guide for the targeted design of composite catalysts via exsolution.

Experimental

Preparation of catalysts

NFO was prepared by a hydrothermal method. First, nickel chloride and ferric nitrate were dissolved in a certain amount of water in a stoichiometric ratio of 1 to 2 under magnetic stirring. Then, 18 mL of 2 mol L⁻¹ of KOH (mineralizing agent) was added. After stirring for 0.5 h, the homogeneous solution was transferred into a sealed Teflon-lined autoclave (80 mL) and kept at 160 °C for 10 h. The precipitate was washed with distilled water and centrifuged several times. Eventually, the sample was freeze-dried for 5 h. The obtained powder was heated at different temperatures (400 °C, 500 °C, 600 °C) for 3 h under 5% H₂/Ar with a heating rate of 2 °C min⁻¹ (denoted as NFO-400H, NFO-500H, and NFO-600H, respectively). The sample named as NFO + NF was prepared by mechanically grinding NFO and FeNi with a sample at a ratio of 2 : 1.

Materials and methods

X-ray diffraction (XRD) characterization was recorded on a D/Max 2550 V/PC diffractometer from Rigaku. The crystal structure of the material was scanned over a range from 10° to 80° at a 4°/min scan rate. Scanning electron microscopy (SEM) measurements were used to observe the morphology of the samples, utilizing a Helios NanoLab 600i DualBeam System of FEI Corporation. The morphologies of the materials were also observed using transmission electron microscopy (TEM) using a Tecnai G2 F20. X-ray photoelectron spectroscopy (XPS) is an effective tool and was used to characterize the surface element states and chemical compositions of the materials. XPS was conducted on an ESCALAB 250Xi electron energy spectrometer from the Thermo corporation using Al Kα (1486.6 eV) radiation. Raman spectroscopy was conducted using an inVia (Renishaw Company) instrument with irradiation at 532 nm. Fourier-transform infrared spectroscopy (FT-IR) was carried out on a VERTEX 80V (Brucker Company) instrument. X-ray absorption near-edge spectroscopy (XANES) of the Fe L-edge, Ni L-edge, and O K-edge was undertaken at the BL12B-a beamline of the National Synchrotron Radiation Laboratory (NSRL) at the University of Science and Technology using the total electron yield mode under a vacuum better than 5 × 10⁻⁸ Pa. X-ray absorption spectroscopy (XAS) of the Fe K-edge and Ni K-edge was conducted at beamline BL11b of Shanghai Synchrotron Radiation Facility (SSRF). The spectra were collected under transmission mode and a Si(111) channel-cut monochromator was utilized for monochromatizating.

Electrochemical measurements of OER activities

Electrochemical measurements were investigated using a CHI 660E analyzer (Shanghai Chenhua Apparatus, China) with a three-electrode system, including a rotating disk working electrode, counter electrode, and reference electrode. The working electrode was made of glassy carbon. The counter electrode and the reference electrode were a Pt ring and Hg/HgO electrode, respectively. Prior to the electrochemical measurements, the glassy carbon electrode was polished using a 50 nm Al₂O₃ slurries. All the potentials measured were calibrated to the reversible hydrogen electrode (RHE) using the equation: E_RHE = E vs. Hg/HgO + 0.059 × pH + 0.098. The as-prepared catalysts (4.5 mg) and vulcan carbon black (1.5 mg) were dispersed in 1 mL of 1 : 1 (isopropanol : water) with 15 μL of binder to form a homogeneous ink, which was then sonicated for 0.5 h. 10 μL of the catalyst ink was dropped onto the glassy carbon disk with a diameter of 5 mm and was naturally dried. The electrolyte was a 1 M KOH solution. The electrode was activated via running cyclic voltammetry (CV). The OER polarization curve was scanned from 0.2 to 0.9 V at a scan rate of 5 mV s⁻¹ at 1600 rpm. Tafel plots were fitted to the potentiostatic response: the steady-state polarization curves were constructed by sampling the OER current density at the 150th second of the chronoamperometry responses acquired at various overpotentials in the catalytic turnover region with a regular interval of 0.01 V. The time to reach steady state at different potentials was 5 min. The electrochemically active surface area (ECSA) was evaluated based on the double layer capacitance (C_dl) in nonaqueous media. Specifically, double layer capacitive measurements were performed by recording CV cycles over a narrow range (±50 mV) centered on the open circuit potential in 0.15 M LiClO₄ and a CH₃CN electrolyte. CV cycling was repeated at scan rates from 20 to 100 mV s⁻¹. The ECSA was calculated using the formula: ECSA = S_c × C_dl/C_s, where S_c is the geometric area of the GC electrode and C_s denotes the specific electrochemical double-layer capacitance of the smooth surface substrate. Electrochemical linear sweep voltammetry (LSV) curves were normalized according to the ECSA. The stability of NFO-500H was evaluated via a chronoamperometric curve at 1.54 V (vs. RHE).

Results and discussion

Crystal structure and microscopy

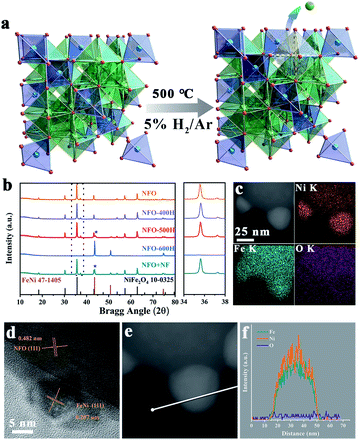
The FeNi/NFO composites were constructed by in situ exsolution of NiFe₂O₄ at 500 °C under a reducing atmosphere. M–O bonds located at the octahedral coordination environment of the spinel structure were preferentially broken during this process, and a schematic illustration is shown in Fig. 1a. The crystal structure of all the samples were examined using XRD (Fig. 1b). The diffraction pattern of the parent NFO can be well indexed to cubic spinel NiFe₂O₄ (JCPDS card no. 10-0325). The NFO-400H sample shows no change with respect to NFO except that the (311) peak of the spinel phase is shifted to a higher angle, as shown in an enlargement of the region of 34°–38°. The shift signifies the shrinkage of the lattice caused by thermal reduction. For the sample treated at a temperature of 500 °C, a diffraction peak arises at 43.6°, corresponding to the FeNi alloy exsolved from the host spinel oxide (JCPDS card no. 47-1405). When the temperature increases to 600 °C, only the peaks of the FeNi alloy can be found in the resulting composite, which reveals that the structure of spinel collapsed completely. For comparison, we prepared a composite by physically mixing NFO and FeNi alloy, named as NFO + NF, which possesses a similar elemental composition and XRD pattern to NFO-500H. The metallic stoichiometry in NFO and the NFO samples annealed at different temperatures was determined by inductively coupled plasma-optical emission spectrometry, revealing that the Fe : Ni ratio in all samples is close to the original proportions of NFO (Table S1†). The SEM images of NFO, NFO-400H, NFO-500H, and NFO-600H are shown in Fig. S1a–c and S2.† The NFO particles crystallized with a well-defined octahedral morphology with an average size of about 100 nm and showed more agglomeration with increasing synthesis temperature (Fig. S1a–c†). The morphologies of NFO and the reduced NFO samples with different annealing temperatures were further studied using TEM. As shown in Fig. S1e,† pristine NFO is very smooth and angular. When NFO is reduced at 400 °C, the edges and corners of the octahedron seem to be obviously passivated (Fig. S1f†). For the sample treated at 500 °C, the exsolved nanoparticles, approximately 20–30 nm in size, that were decorated in situ on the surface of the octahedra can be observed in Fig. S2.† The HRTEM of NFO-500H shows two interplanar spacings of 0.482 nm and 0.207 nm, which could be indexed to the (111) plane of the NiFe₂O₄ and the (111) plane of the FeNi alloy, respectively (Fig. 1d). The embedded configuration guarantees a strong interfacial interaction between the FeNi alloy and the parent NFO, which will be beneficial for charge transfer during the electrochemical reaction.¹⁶ To further confirm the composition of the exsolved nanoparticles, high-angle annular dark-field imaging scanning transmission electron microscopy (HAADF-STEM) images of NFO-500H, with energy-dispersive X-ray spectrometry (EDX) elemental mapping, were recorded. As shown in Fig. 1c, the EDX mapping images show enrichment of the Fe and Ni signals in the exsolved nanoparticles and a homogeneous distribution of the Fe, Ni, O elements in octahedral region, indicating that the nanoparticles consist of Fe and Ni. Moreover, the line-scanning results show two intense peaks for Fe and Ni located at the center of the profile (Fig. 1e and f). Similarly, the line-scanning results were supported by the spot-scanning data (Fig. S3†). NFO-600H shows an aggregated morphology of accumulated irregular nanoparticles (Fig. S1c and g†), where the interplane distance of 0.207 nm corresponds with the (111) plane of the FeNi alloy (Fig. S1k†). The clear interface between the FeNi alloy and NFO in NFO-500H indicates that the FeNi alloy nanoparticles were anchored in situ at the surface of the NFO parent phase. In contrast, there is a weak connection between the FeNi alloy and NFO in NFO + NF (Fig. S1h and l†).

Fig. 1 (a) Schematic showing the breaking of octahedral M–O bonds in NFO-500H. (b) XRD patterns of NFO, NFO-400H, NFO-500H, NFO-600H, and NFO + NF. (c) HAADF-STEM image of NFO-500H and the corresponding EDX elemental mapping. (d) HRTEM image of NFO-500H. (e and f) HAADF-STEM image of NFO-500H and the corresponding compositional line profiles.

Surface electronic structure

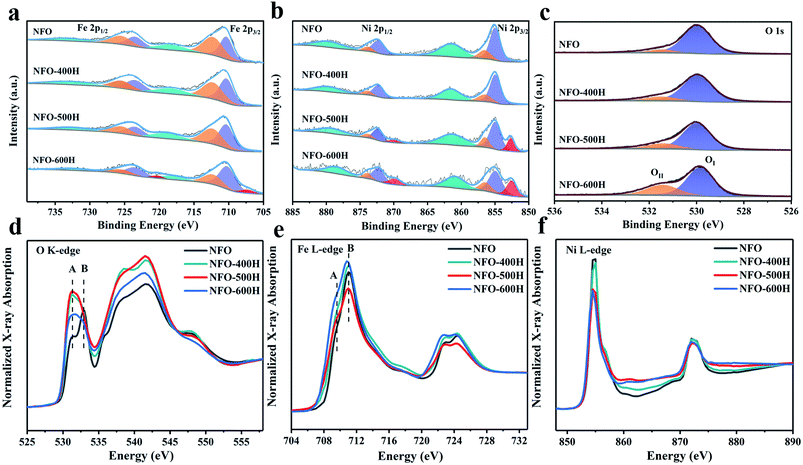
XPS measurements were performed to determine the nature of the NFO exsolution. Peaks at 711 eV and 724 eV can be assigned to Fe 2p_3/2 and Fe 2p_1/2 (Fig. 2a). The binding energies at ∼707.3, ∼710.3, ∼712.3, and ∼718.3 eV can be attributed to Fe⁰, Fe²⁺, Fe³⁺, and the satellite peaks, respectively. Table S2† shows that increasing the reduction temperature induces an increase in the peak area ratio of Fe²⁺/Fe³⁺. Compared to NFO, the peak position of NFO-600H moves 0.1 eV towards a lower binding energy, which means that a lower valence state is present due to the exsolution of Fe⁰ metal. Typical Ni³⁺ 2p_3/2 and Ni²⁺ 2p_3/2 peaks and a satellite are obtained at 856.5, 854.9, and 861.5 eV, respectively (Fig. 2b). A weak peak at 852.5 eV is assigned to metallic Ni 2p_3/2.^29,30 On the contrary, most nickel takes the form of Ni²⁺ and only a small fraction in NFO-500H is reduced to Ni⁰ metal. The Ni⁰ peak area ratio in NFO-600H was visibly higher than that of NFO-500H, as shown in Table S2.† In the Ni 2p and Fe 2p XPS spectra of NFO + NF (Fig. S4†), the typical peaks are very similar to those of NFO, the Ni⁰ peak appears at a lower binding energy and this can be attributed to the NiFe alloy. The trends for Fe and Ni are consistent with the reduction process, and some slight differences can be ascribed to the inevitable surface oxidation in the air and the limited depth with which the XPS method probes. The O 1s spectra of all samples are shown in Fig. 2c and can be deconvoluted into two peaks, the lattice oxygen (O_I, ∼529.9 eV) and defect oxygen (O_II, ∼531.5 eV) peaks, respectively.^25,31,32 The O_II/(O_I + O_II) ratio follows the trend NFO-600H (32.43%) > NFO-500H (20.63%) > NFO-400H (16.66%) > NFO (11.50%). Obviously, the peak area ratio gradually increases as the reduction temperature increases and this will have a strong influence on the performance of the material in the OER.²⁵ XAS is an effective spectroscopic tool and was performed to further characterize the atomic electronic structure. The O K-edge X-ray absorption near-edge spectra (Fig. 2d) probe unoccupied states with O 2p symmetry, due to dipole selection rules, which are mainly generated by hybridizing the 3d state in the transition metal and the 2p state in oxygen.^33,34 Specifically, peak A and peak B correspond to the t_2g states and e_g states. The intensity ratios of peaks B/A for all the reduced NFO samples are obviously smaller than that of pristine NFO, which reveals that the electron transition probability from the O 1s to the t_2g orbitals is increased after annealing (Table S3†).³⁵ Peak A and peak B are blurred in the all annealed NFO samples, which is mainly due to the mismatch in the origin crystal symmetry caused by thermal exsolution.³⁵Fig. 2e shows the Fe L-edge XANES spectra and was normalized from 704 to 734 eV. Peak A is assigned to the Fe t_2g orbitals and peak B is regarded as the 3d e_g orbitals.³⁶ The peak gap between A and B was calibrated to study the electronic structure. As shown in Table S3,† we observe the smallest peak gap (1.19 eV) in NFO-500H, which can be attributed to the distortion of the structure between the FeNi alloy and host NFO oxide.³⁷ Peak A and peak B of NFO-600H shift to lower energies compared to other samples, which means that the lower valence state of Fe is caused by the reducing atmosphere. Ni L-edge XANES spectra normalized from 850 to 890 eV show trends similar to those of Fe (Fig. 2f), where the Ni L-edge of NFO-600H shifts to a lower energy, indicating that its valence state is lower than in other samples.

Fig. 2 XPS spectra of (a) Fe 2p, (b) Ni 2p, and (c) O 1s for NFO, NFO-400H, NFO-500H, and NFO-600H. XAS spectra for (d) O K-edge XANES, (e) Fe L-edge XANES, and (f) Ni L-edge XANES for NFO, NFO-400H, NFO-500H, and NFO-600H.

Spinel exsolution mechanism

The Fe chemical environment was characterized using ⁵⁷Fe Mössbauer spectroscopy at room temperature.³⁸ The Mössbauer spectra of NFO and the annealed NFO samples show asymmetric six-line spectra with broad lines where the outmost lines are obviously discernable as double sextets for NFO, NFO-400H, and NFO-600H, while the outmost lines in NFO-500H fit well into four sextets (Figure 3a). The hyperfine parameters of all samples are listed in Table S4.† The isomer shift (IS) is related to the difference in s-electron density between the studied sample and the source and gives information such as oxidation state. An IS value relative to α-Fe larger than 0.15 mm s⁻¹ is consistent with those reported for high spin Fe³⁺.³⁹ Usually, an IS value can reach above 0.65 mm s⁻¹ and can be attributed to Fe²⁺.⁴⁰ IS in the range of very small or negative values can be attributed to Fe⁰.⁴¹ As shown in Table S4,† the presence of double sextets in NFO illustrates that Fe has two different coordination environments. We assigned component I (red line) and component II (blue line) to the Fe ions in the octahedral and tetrahedral sites, respectively. In addition, the area ratios of the sextets give information about the occupancy of the Fe ions in different positions, because the integral area of each sextet is in proportion to the number of Fe ions at different sites. From Table S4† it can be seen that there is nearly equal Fe ion occupancy at the octahedral sites and tetrahedral sites in both NFO and NFO-400H, consistent with the structure of the inverse spinel. The Mössbauer spectrum of NFO-500H exhibits four sextets, corresponding to four different Fe ion coordination environments, including Fe³⁺ in the octahedral sites, Fe³⁺ in the tetrahedral sites and Fe²⁺ (component III) and Fe⁰ (component IV), respectively. Obviously, Fe ion occupancy ratio at the octahedral sites in NFO-500H is much lower than in NFO. Reduced Fe²⁺ and Fe⁰ species were also observed in NFO-500 (Fig. 3b). More importantly, the Fe ion occupancy ratio at octahedral sites evidently decreased (from 49.87% to 17.59%) when compared with the tetrahedral sites (from 50.13% to 43.17%). This implies that the Fe atoms in the FeNi alloy originate preferentially from the Fe ions located at the octahedral sites and further indicates that the octahedrally coordinated iron–oxygen bonds were preferentially broken during the spinel exsolution process. Notably, all Fe ions in NFO were reduced to Fe⁰ when annealed at 600 °C, which is in agreement with the XRD results for NFO-600H. In addition, the NFO + NF sample was characterized using Mössbauer spectroscopy, and iron in three different environments could be fitted from the spectrum. It was observed that Fe³⁺ occupies an almost equal area ratio between the octahedral and tetrahedral sites (Table S4†). Fe⁰ species are also observed in the NFO + NF Mössbauer spectrum (Fig. S5†). It is worth noting that the Fe²⁺ in the NFO-500H composite reveals a more complicated electronic structure or interaction between the two phases than in the physical NFO + NF mixture where Fe²⁺ is absent.⁴²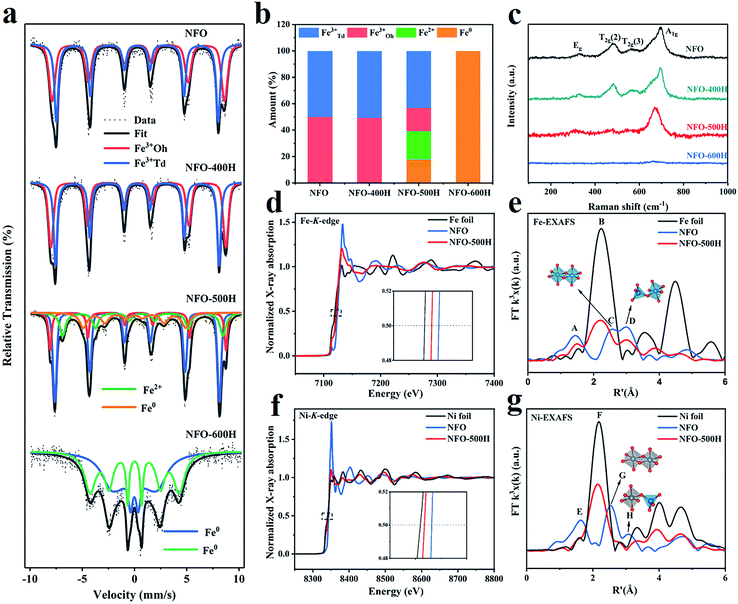

Fig. 3 Chemical state and coordination state, electronic states and bonding structures of the samples. (a) Mössbauer spectra of NFO, NFO-400H, NFO-500H, and NFO-600H. (b) Histogram showing the proportions of tetrahedral Fe³⁺ (blue), octahedral Fe³⁺ (red), Fe²⁺ (light blue), and Fe⁰ (orange) based on the values given in Table S1.† (c) Raman spectra of NFO, NFO-400H, NFO-500H, and NFO-600H. (d) Fe K-edge XANES spectrum and (e) R-space Fourier-transformed FT (k³χ(k)) of Fe K-edge EXAFS for NFO and NFO-500H. (f) Ni K-edge XANES spectrum and (g) R-space Fourier-transformed FT (k³χ(k)) of Ni K-edge EXAFS for NFO and NFO-500H.

The exsolution phenomenon was resolved using Raman spectra. Modes at 326, 480, 565, and 693 cm⁻¹ could be ascribed to the E_g, T_2g (2), T_2g (3), and A_1g modes, respectively, which could be assigned to the vibrations of the symmetric, asymmetric bending, and asymmetric stretching of the oxygen atom in the Fe–O bond at the octahedral void, respectively (Fig. 3c).^43,44 The Raman band at 693 cm⁻¹ corresponds to symmetric stretching of the oxygen atom along the Fe–O bond at the tetrahedral void. As for the other three Raman bands of the NFO-500H octahedral voids, the relative intensity was decreased, which implies that the metal–oxygen bond of the octahedra broke first. The Raman band belonging to the tetrahedral voids exhibited a redshift caused by structure symmetry after annealing. Comparatively, all modes for NFO-600H disappeared, indicating that the spinel structure was completely destroyed. A similar change is also observed in the IR spectra, as shown in Fig. S6.† The broad bands centered at 3430 cm⁻¹ and 1630 cm⁻¹ were assigned to the stretching modes and H–O–H bending vibration of free or absorbed water. The characteristic absorptions for NFO were located at 613 cm⁻¹ and 417 cm⁻¹.^45,46 The broad high-intensity band at 613 cm⁻¹ was due to the stretching of the Fe–O bond of the tetrahedra, while the band at 417 cm⁻¹ was assigned to the stretching of the Fe–O bond of the octahedra. These peaks show a redshift when annealed at 500 °C, which is consistent with the Raman results.

To further prove the conclusion that the octahedral bond was broken preferentially, the Fe K-edge and Ni K-edge absorption spectra of NFO and NFO-500H were measured to study the fine electronic structure and bulk valences of the samples. As shown in Fig. 3d, compared to NFO, the Fe K-edge absorption peak position of NFO-500H was shifted to a lower energy, indicating that the valence of Fe in NFO-500H was lower than in NFO.⁴⁷ In addition, the Fe valence follows the order NFO > NFO-500H > Fe foil. The phenomenon can be attributed to the exsolution of the FeNi alloy which influences the valence state of Fe. To clarify the local bonding structure of the Fe atom in the spinel oxides, the Fe K-edge extended X-ray absorption fine spectra (EXAFS) of two samples were transformed via R-space Fourier-transformed FT (k³χ(k)), as shown in Fig. 3e. Peak A at R′ ∼ 1.5 Å and corresponds to the Fe–O coordination peak. In the radial structure functions of the Fe K-edge spectrum, the spinel has two main peaks caused by Fe cations occupying octahedral (Oh) and tetrahedral (Td) positions. Peak C at R′ ∼ 2.5 Å and relates to Fe_Oh–Fe_Oh/Ni_Oh bond bridging Fe_Oh. Peak D at R′ ∼ 3.0 Å can be assigned to Fe_Td–Ni_Oh/Fe_Oh bond bridging Fe_Td.^48,49 NFO-500H shows some significant changes in the R-space function. Firstly, compared to NFO, NFO-500H exhibits a new peak B at ∼2.2 Å, which is a typical scattering feature of Fe–Fe bonds, further indicating the presence of metallic Fe.⁵⁰ Secondly, the intensity of peak A, associated with Fe–O coordination, becomes less intense, which is indicative of part of the Fe–O bond being broken and the Fe–O coordination number decreasing. Thirdly, peak C disappeared, however, the intensity of peak D was obviously decreased, which demonstrates that the disorder of the NiFe₂O₄ and Fe_Oh–Fe_Oh/Ni_Oh bond bridging Fe_Oh was broken preferentially in the process of exsolution. As shown in Fig. 3f, the Ni K-edge spectrum shows a similar edge shift toward lower energy, indicating that the valence of Ni was reduced in NFO-500H. Obvious changes can also be observed in the Ni FT-EXAFS spectra (Fig. 3g). Peak E at ∼1.6 Å corresponds to the Ni–O coordination peak.⁵¹ Peak F at R′ = ∼2.2 Å is related to the Ni–Ni bond of metallic Ni, Ni foil was also used for comparison. Peaks G and H at R′ ∼ 2.5 and ∼3.0 Å originate from the Ni_Oh–Ni_Oh/Fe_Td bonds and Ni_Oh–Fe_Td bridging Ni_Oh in the NiO₆ octahedra, respectively. Compared to NFO, peaks E, G, and H in NFO-500H almost disappear and this can be attributed to the breaking of the NiO₆ octahedral bonds. Meanwhile, NFO-500H showed a strong Ni–Ni coordination peak at ∼2.2 Å, indicating the formation of metallic Ni. Combined with the Mössbauer spectra and the analysis of the Raman spectra, we can conclude that the octahedral Fe–O and Ni–O bonds were broken preferentially and that Fe³⁺ was reduced to Fe²⁺ or Fe⁰, subsequently forming a FeNi alloy anchored on the surface of the host spinel oxide.

Theoretical calculations

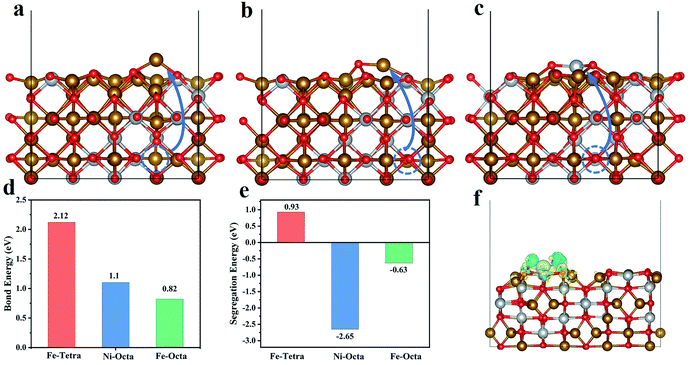
To explore the reason for the preferential breaking of the octahedral coordinated metal–oxygen bonds, density-functional theory (DFT) calculations were performed. Firstly, the unit cell of NiFe₂O₄ was employed as a model and the bond energies of three typical structures, the Fe–O bond of tetrahedral FeO₄, the Ni–O bond of octahedral NiO₆, and the Fe–O bond of octahedral FeO₆, were calculated. From Fig. 4d, we can clearly see that the bond energies of the M–O bonds at the octahedral positions are less than that at the tetrahedral position, indicating that M–O bonds at the octahedral sites will break preferentially. Secondly, we constructed a (110) slab model of NiFe₂O₄ to calculate the segregation energy of the transition metal (Fig. S7†). The initial positions of the metal atoms are indicated with blue circles. The atomic structure model after exsolution is shown in Fig. 4a–c and demonstrate the exsolution of Fe in Fe–O tetrahedra (Fe-Tetra), the exsolution of Fe in Fe–O octahedra (Fe-Octa), and the exsolution of Ni in Ni–O octahedra (Ni-Octa), respectively. As we can see, the exsolved metal from the octahedral structures has negative segregation energies (−2.65 eV, −0.63 eV), indicating that the system energy is lower and more stable than in pristine NFO. However, the segregation of tetrahedral Fe will lead to an increase in the energy of the system, indicating that tetrahedral Fe is not easily exsolved (Fig. 4e). Moreover, we constructed a model of the FeNi/NFO composite to investigate the electronic structure and the charge differences (Fig. 4f). It was found that there is a charge transfer at the interface between the FeNi alloy and the parent spinel, indicating that the composite material has strong interactions which are mainly responsible for the improvement in electrochemical performance.

Fig. 4 Schematic illustrations of (a) the exsolution of Fe in Fe–O tetrahedra, (b) the exsolution of Fe in Fe–O octahedra, and (c) the exsolution of Ni in Ni–O octahedra. (d) Comparison of the bond energies of the metal–oxygen bonds. (e) Comparison of the segregation energies of the exsolved metal. (f) The charge density difference plot of NFO-500H. The charge accumulation and depletion are shown in yellow and green.

Electrocatalytic oxygen evolution reaction

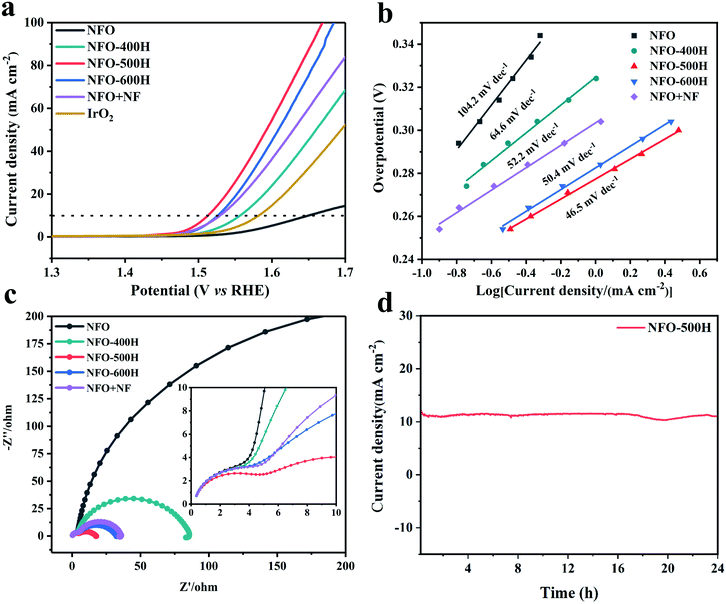
The OER activities of NiFe₂O₄ and the NFO samples reduced at different annealing temperatures were examined using a rotating disk electrochemical (RDE) testing device in 1.0 M KOH electrolyte. For comparison, commercial IrO₂ was also examined under the same conditions. The overpotential at a current density of 10 mA cm⁻² is considered a primary indicator to evaluate the OER activity.⁵² As shown in Fig. 5a, linear sweep voltammetry (LSV) curves reveal that the optimized NFO-500H catalyst has excellent catalytic activity with an onset potential (∼1.46 V) and an overpotential of 283 mV at 10 mA cm⁻². Remarkably, of all the samples, NFO-500H shows the lowest overpotential, 137 mV lower than that of NFO and 57 mV lower than that of IrO₂. Compared to NFO, a lower overpotential (335 mV) was observed for NFO-400H at 10 mA cm⁻², which can probably be ascribed to the formation of defect oxygen in the reducing environment. Control experiments for NFO + NF were conducted to evaluate the catalytic activity of the chemical and physical composites in the OER. NFO + NF exhibited a poorer performance, which is mainly attributed to the interaction between the NFO and FeNi alloy, which is not as strong as that obtained from NFO-500H via exsolution.⁵³ It is worth mentioning that the overpotential of NFO-500H is also lower than that of many previously reported spinel-based materials (Table S5†). Moreover, a steady-state polarization curve was constructed to obtain the corresponding Tafel plots, which could be used to evaluate the kinetics of the OER⁵⁴ (Fig. 5b and S8†). The Tafel slope for NFO-500H was fitted to 46.5 mV dec⁻¹, and is superior to those of NFO (104.2 mV dec⁻¹), NFO-400H (64.6 mV dec⁻¹), NFO-600H (50.4 mV dec⁻¹), and NFO + NF (52.2 mV dec⁻¹). This suggests that the NFO-500H sample possesses fast reaction kinetics for the OER. We evaluated the charge-transfer resistances of the prepared samples using electrochemical impedance spectroscopy (EIS) measurements (Fig. 5c). NFO-500H has the smallest charge-transfer resistance, demonstrating its faster reaction kinetics during the OER. In fact, each curve in the Nyquist diagram includes two semicircles, as shown in the enlarged view. The diameter of the smaller arc in the high frequency region is almost unchanged and mainly corresponds to the resistance of the catalyst itself and related factors.⁵⁵ The electrochemically active surface area of the samples was calculated using double layer capacitive measurements in nonaqueous media (Fig. S9†).⁵⁶ The ECSA-normalized electrochemical LSV curves, shown in Fig. S10,† show similar trends to those normalized to the geometric area for the OER, indicating the intrinsically high electrocatalytic activity of the NFO-500H. The OER stability of NFO-500H was investigated via its chronoamperometric curve and a 1000 CV cycles. As displayed in Fig. 5d, NFO-500H exhibits excellent stability and maintains its activity for about 24 h. In addition, the OER activities of NFO-500H, NFO-600H, and NFO + NF after 1000 cycles were tested and it was found that NFO-500H has the least decrease in activity compared with NFO-600H and NFO + NF, indicating NFO-500H has good stability (Fig. S11†). The structure of NFO-500H before and after the 24 h stability test was characterized using XRD and HRTEM. The XRD results showed that after the electrochemical stability test, the phase of NFO-500H remained (Fig. S12†). An HRTEM image revealed that the morphology of NFO-500H was well preserved after the LSV measurements (Fig. S13†). These results clearly and consistently indicate that exsolution remarkably enhances the OER activity and stability in our system.

Fig. 5 Electrochemical performance of NFO and the samples reduced at different temperatures. (a) LSV curves for the OER on an RDE testing device for NFO, NFO-400H, NFO-500H, NFO-600H, NFO + NF, and IrO₂ catalysts. (b) Tafel plots of the corresponding catalysts. (c) Nyquist diagrams for all samples. (d) Chronoamperometric curve at 1.54 V (vs. RHE) for NFO-500H.

A look to the future of spinel exsolution

Composites of oxide-supported nanoparticles are extensively applied in a wide range of chemical and energy applications due to their excellent catalytic performance.⁵⁷ Exsolution provides an efficient pathway to produce a second phase by separating active ions from the lattice and then uniformly anchoring them on the surface of a matrix oxides.¹⁸ In typical spinel oxides, the octahedral and tetrahedral interstices can be filled with different catalytically active ions. However, it was previously not possible to explain from which site an ion would be more easily exsolved. Combined with existing knowledge on spinel synthesis and structural regulation,^58,59 we propose that these findings may be an effective guide for the design of new composite catalysts via exsolution. For example, cations with high reactivity could be pre-set in octahedral sites in the spinel for constructing high performance composite catalyst via exsolution. The radii of the ions, their ratios, valence states, and tolerance factors,⁶⁰ even after treatment, should be taken into consideration to ensure their desired distributions before the chemical synthesis of parent compounds. Of course, the exsolution procedure must also be followed taking into account other existing factors such as the Gibbs free energy,¹⁷ co-segregation energy,²⁰ and so on.

Conclusions

In summary, we exploited a range of analytical tools to understand the entire procedure of spinel exsolution from the perspective of the breaking of chemical bonds. Mössbauer spectra reveal that the occupancy percentage of Fe³⁺ at octahedral sites decreases preferentially as the annealing temperature increases. They also reveal direct evidence that Fe_Oh and Ni_Oh collapse much more easily than Fe_Td, which is also reflected in the X-ray absorption and Raman spectra. Those results are further corroborated by density-functional theory calculations. We conclude that the octahedral metal–oxygen bonds in the spinel oxide preferentially break over those bonds in the tetrahedral coordination environment. The FeNi/NiFe₂O₄ composite prepared by in situ exsolution shows a great enhancement in the electrochemical water oxidation reaction as it has better charge transfer between its two phases. Our result not only enriches the fundamental knowledge of exsolution, but also provides new guidance for the design and preparation of desired functional composites whereby pre-exsolved metal ions can be deliberately introduced at octahedral sites.

Data availability

All related data are provided in ESI.†

Author contributions

X. G., K. H. and X. W. conceived the idea. X. G. and S. L. performed the electrocatalytic performance tests. Z. G., X. H., L. Y., Y. J. and S. F. analysed some characterization. Q. Z. performed and analysed theoretical calculations. Y. Z. performed synchrotron radiation measurement. X. G. and X. W. wrote the paper with the input of all authors. All the authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC; 22090044, 21831003, 21801090, 21621001, 22171102), the Jilin Province Science and Technology Development Plan (20200802003GH, 20200801005 GH, and 20210509035RQ) and the Scientific Research Project in the Education Department of Jilin Province (JJKH20211044KJ). This work was supported by Users with Excellence Program of Hefei Science Center CAS (2020HSC-UE002). The authors thank Beamline BL11b (Shanghai Synchrotron Radiation Facility) and NSRL beamlines MCD-A and MCD-B (Soochow Beamline for Energy Materials) in National Synchrotron Radiation Laboratory for providing beam time. We acknowledge the Center for Advanced Mössbauer Spectroscopy, Dalian Institute of Chemical Physics, CAS, for providing the Mössbauer measurement and analysis.

Notes and references

1. S. Schauermann and H. J. Freund, Acc. Chem. Res., 2015, 48, 2775–2782.
2. P. Vernoux, L. Lizarraga, M. N. Tsampas, F. M. Sapountzi, A. De Lucas-Consuegra, J. L. Valverde, S. Souentie, C. G. Vayenas, D. Tsiplakides, S. Balomenou and E. A. Baranova, Chem. Rev., 2013, 113, 8192–8260.
3. J. Lu, B. Fu, M. C. Kung, G. Xiao, J. W. Elam, H. H. Kung and P. C. Stair, Science, 2012, 335, 1205–1208.
4. C. Ruocco, V. Palma and A. Ricca, Chem. Eng. J., 2019, 377, 119778.
5. N. Byamba-Ochir, W. G. Shim, M. S. Balathanigaimani and H. Moon, Appl. Surf. Sci., 2016, 379, 331–337.
6. M. Haruta, Cattech, 2002, 6, 102–115.
7. C. Y. Liu and A. J. Bard, Nature, 2002, 418, 162–164.
8. H. Tanaka, M. Taniguchi, M. Uenishi, N. Kajita, I. Tan, Y. Nishihata, J. Mizuki, K. Narita, M. Kimura and K. Kaneko, Angew. Chem., Int. Ed., 2006, 45, 5998–6002.
9. D. Neagu, T. S. Oh, D. N. Miller, H. Menard, S. M. Bukhari, S. R. Gamble, R. J. Gorte, J. M. Vohs and J. T. S. Irvine, Nat. Commun., 2015, 6, 8120.
10. J. T. S. Irvine, D. Neagu, M. C. Verbraeken, C. Chatzichristodoulou, C. Graves and M. B. Mogensen, Nat. Energy, 2016, 1, 1–13.
11. Z. Du, H. Zhao, S. Yi, Q. Xia, Y. Gong, Y. Zhang, X. Cheng, Y. Li, L. Gu and K. Swierczek, ACS Nano, 2016, 10, 8660–8669.
12. M. L. Weber, M. Wilhelm, L. Jin, U. Breuer, R. Dittmann, R. Waser, O. Guillon, C. Lenser and F. Gunkel, ACS Nano, 2021, 15, 4546–4560.
13. Y. Jeon, Y. Ji, Y. I. Cho, C. Lee, D. H. Park and Y. G. Shul, ACS Nano, 2018, 12, 6819–6829.
14. Y. Jiang, Z. Geng, L. Yuan, Y. Sun, Y. Cong, K. Huang, L. Wang and W. Zhang, ACS Sustainable Chem. Eng., 2018, 6, 11999–12005.
15. Y. Cong, Z. Geng, Q. Zhu, H. Hou, X. Wu, X. Wang, K. Huang and S. Feng, Angew. Chem., Int. Ed., 2021, 60, 23380–23387.
16. Y. Jiang, Z. Geng, Y. Sun, X. Wang, K. Huang, Y. Cong, F. Shi, Y. Wang, W. Zhang and S. Feng, ACS Sustainable Chem. Eng., 2019, 8, 302–310.
17. Y. Gao, D. Chen, M. Saccoccio, Z. Lu and F. Ciucci, Nano Energy, 2016, 27, 499–508.
18. J. Zhang, M.-R. Gao and J.-L. Luo, Chem. Mater., 2020, 32, 5424–5441.
19. D. Neagu, V. Kyriakou, I. L. Roiban, M. Aouine, C. Tang, A. Caravaca, K. Kousi, I. Schreur-Piet, I. S. Metcalfe, P. Vernoux, M. C. M. van de Sanden and M. N. Tsampas, ACS Nano, 2019, 13, 12996–13005.
20. O. Kwon, S. Sengodan, K. Kim, G. Kim, H. Y. Jeong, J. Shin, Y. W. Ju, J. W. Han and G. Kim, Nat. Commun., 2017, 8, 15967.
21. H. Lv, L. Lin, X. Zhang, Y. Song, H. Matsumoto, C. Zeng, N. Ta, W. Liu, D. Gao, G. Wang and X. Bao, Adv. Mater., 2020, 32, 1906193.
22. S. Ding, M. Li, W. Pang, B. Hua, N. Duan, Y.-Q. Zhang, S.-N. Zhang, Z. Jin and J.-L. Luo, Electrochim. Acta, 2020, 335.
23. Y. R. Jo, B. Koo, M. J. Seo, J. K. Kim, S. Lee, K. Kim, J. W. Han, W. Jung and B. J. Kim, J. Am. Chem. Soc., 2019, 141, 6690–6697.
24. J. Zhang, Q. Kuang, Y. Jiang and Z. Xie, Nano Today, 2016, 11, 661–677.
25. Y.-R. Hao, H. Xue, L. Lv, J. Sun, N. Guo, T. Song, H. Dong, J. Zhang and Q. Wang, Appl. Catal., B, 2021, 295, 120314.
26. D. Zeng, Y. Qiu, S. Peng, C. Chen, J. Zeng, S. Zhang and R. Xiao, J. Mater. Chem. A, 2018, 6, 11306–11316.
27. Q. Zhao, Z. Yan, C. Chen and J. Chen, Chem. Rev., 2017, 117, 10121–10211.
28. C. T. Cherian, J. Sundaramurthy, M. V. Reddy, P. S. Kumar, K. Mani, D. Pliszka, C. H. Sow, S. Ramakrishna and B. V. R. Chowdari, ACS Appl. Mater. Interfaces, 2013, 5, 9957–9963.
29. A. Fan, C. Qin, X. Zhang, X. Dai, Z. Dong, C. Luan, L. Yu, J. Ge and F. Gao, ACS Sustainable Chem. Eng., 2019, 7, 2285–2295.
30. W. Zhang, J. Qi, K. Liu and R. Cao, Adv. Energy Mater., 2016, 6, 1502489.
31. X. T. Wang, T. Ouyang, L. Wang, J. H. Zhong, T. Ma and Z. Q. Liu, Angew. Chem., Int. Ed., 2019, 58, 13291–13296.
32. Y. Tian, Y. Liu, A. Naden, L. Jia, M. Xu, W. Cui, B. Chi, J. Pu, J. T. S. Irvine and J. Li, J. Mater. Chem. A, 2020, 8, 14895–14899.
33. D. N. Mueller, M. L. Machala, H. Bluhm and W. C. Chueh, Nat. Commun., 2015, 6, 6097–6105.
34. S. Lafuerza, G. Subias, J. Garcia, S. Di Matteo, J. Blasco, V. Cuartero and C. R. Natoli, J. Phys.: Condens. Matter, 2011, 23, 325601.
35. X. Gao, J. Wang, D. Zhang, K. Nie, Y. Ma, J. Zhong and X. Sun, J. Mater. Chem. A, 2017, 5, 5007–5012.
36. J. Leveneur, G. I. N. Waterhouse, J. Kennedy, J. B. Metson and D. R. G. Mitchell, J. Phys. Chem. C, 2011, 115, 20978–20985.
37. L. X. Zhang, J. Chen, L. L. Fan, O. Dieguez, J. L. Cao, Z. Pan, Y. L. Wang, J. G. Wang, M. Kim, S. Q. Deng, J. O. Wang, H. H. Wang, J. X. Deng, R. B. Yu, J. F. Scott and X. R. Xing, Science, 2018, 361, 494–497.
38. A. de Kergommeaux, J. Faure-Vincent, A. Pron, R. de Bettignies, B. Malaman and P. Reiss, J. Am. Chem. Soc., 2012, 134, 11659–11666.
39. L. P. Li, G. S. Li, R. L. Smith and H. Inomata, Chem. Mater., 2000, 12, 3705–3714.
40. Y. Wang, L. Li, Y. Zhang, X. Chen, S. Fang and G. Li, J. Phys. Chem. C, 2017, 121, 19467–19477.
41. A. L. Tiano, G. C. Papaefthymiou, C. S. Lewis, J. Han, C. Zhang, Q. Li, C. Shi, A. M. M. Abeykoon, S. J. L. Billinge, E. Stach, J. Thomas, K. Guerrero, P. Munayco, J. Munayco, R. B. Scorzelli, P. Burnham, A. J. Viescas and S. S. Wong, Chem. Mater., 2015, 27, 3572–3592.
42. X. Wang, Z. Pan, X. Chu, K. Huang, Y. Cong, R. Cao, R. Sarangi, L. Li, G. Li and S. Feng, Angew. Chem., Int. Ed., 2019, 58, 11720–11725.
43. S.-Q. Liu, B. Xiao, L.-R. Feng, S.-S. Zhou, Z.-G. Chen, C.-B. Liu, F. Chen, Z.-Y. Wu, N. Xu, W.-C. Oh and Z.-D. Meng, Carbon, 2013, 64, 197–206.
44. A. Ahlawat and V. G. Sathe, J. Raman Spectrosc., 2011, 42, 1087–1094.
45. P. Sivakumar, R. Ramesh, A. Ramanand, S. Ponnusamy and C. Muthamizhchelvan, Mater. Res. Bull., 2011, 46, 2204–2207.
46. M. A. Gabal, D. F. Katowah, M. A. Hussein, A. A. Al-Juaid, A. Awad, A. M. Abdel-Daiem, A. Saeed, M. M. Hessien and A. M. Asiri, ACS Omega, 2021, 6, 22180–22187.
47. L. Yao, Z. Geng, W. Zhang, X. Wu, J. Liu, L. Li, X. Wang, X. Hou, K. Xu, K. Huang and S. Feng, ACS Sustainable Chem. Eng., 2020, 8, 17194–17200.
48. J. Landon, E. Demeter, N. Inoglu, C. Keturakis, I. E. Wachs, R. Vasic, A. I. Frenkel and J. R. Kitchin, ACS Catal., 2012, 2, 1793–1801.
49. D. Carta, M. F. Casula, A. Falqui, D. Loche, G. Mountjoy, C. Sangregorio and A. Corrias, J. Phys. Chem. C, 2009, 113, 8606–8615.
50. X. Wang, Y. Jia, X. Mao, D. Liu, W. He, J. Li, J. Liu, X. Yan, J. Chen, L. Song, A. Du and X. Yao, Adv. Mater., 2020, 32.
51. M. Islam, G. Ali, M.-G. Jeong, W. Choi, K. Y. Chung and H.-G. Jung, ACS Appl. Mater. Interfaces, 2017, 9, 14833–14843.
52. Y. Liu, H. Dai, J. Deng, L. Zhang, Z. Zhao, X. Li, Y. Wang, S. Xie, H. Yang and G. Guo, Inorg. Chem., 2013, 52, 8665–8676.
53. J. W. Li, B. Wei, Z. Q. Cao, X. Yue, Y. X. Zhang and Z. Lu, ChemSusChem, 2018, 11, 254–263.
54. S. Anantharaj, S. Noda, M. Driess and P. W. Menezes, ACS Energy Lett., 2021, 6, 1607–1611.
55. Q. Zhang, Z. D. Wei, C. Liu, X. Liu, X. Q. Qi, S. G. Chen, W. Ding, Y. Ma, F. Shi and Y. M. Zhou, Int. J. Hydrogen Energy, 2012, 37, 822–830.
56. Y. Yoon, B. Yan and Y. Surendranath, J. Am. Chem. Soc., 2018, 140, 2397–2400.
57. G. Zhan, P. Li and H. C. Zeng, Adv. Mater., 2018, 30, 1802094.
58. B. Rivas-Murias, M. Testa-Anta, P. Torruella, S. Estradé, F. Peiró, B. Rodríguez-González, M. Comesaña-Hermo and V. Salgueiriño, Chem. Mater., 2020, 32, 10435–10446.
59. G. Wu, J. Wang, W. Ding, Y. Nie, L. Li, X. Qi, S. Chen and Z. Wei, Angew. Chem., Int. Ed., 2016, 55, 1340–1344.
60. Z. Song and Q. Liu, Cryst. Growth Des., 2020, 20, 2014–2018.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02149h

---