Open Access Article
Open Access ArticleSpinterface chirality-induced spin selectivity effect in bio-molecules†
Yonatan
Dubi
 *ab
*ab
aDepartment of Chemistry, Ben Gurion University of the Negev, Be'er Sheva, Israel 8410501. E-mail: jdubi@bgu.ac.il
bIlse Katz Center for Nanoscale Science and Technology, Ben Gurion University of the Negev, Be'er Sheva, Israel 8410501
First published on 16th August 2022
Abstract
The chirality-induced spin selectivity (CISS) effect, namely the dependence of current through a chiral molecule on spin of the electron, was discovered over two decades ago, and has been suggested for various spin- and chirality-related applications. Yet, quite surprisingly, its physical origin remains elusive, and no theoretical description can quantitatively describe it. Here, we propose a theory for the CISS effect in bio-molecular junctions, based on the interplay between spin–orbit coupling in the electrodes, molecular chirality and spin-transfer torque across the electrode-molecule interface. This theory leads to the first ever quantitative analysis of experimental data, and provides insights into the origin of the CISS effect. The theory presented here can be used to analyze past experiments and to design new experiments, which may lead to deeper understanding of what is considered one of the outstanding problems in molecular electronics and nano-scale transport.
When electrons are forced to pass through chiral molecules, the resulting current (either generated optically or electrically) can become spin-polarized.1–5 This implies that one spin-species (majority spins) has preferable transport over the other (minority) spin-species, the identity of the majority and minority spins determined by the chirality of the molecular moiety. This chirality-induced spin-selectivity (CISS) has been observed in numerous experimental platforms and settings, and was suggested to be used for various chemical and spintronic applications.6–13
Surprisingly, despite the fact that over a decade has passed since its discovery, the origin of the CISS effect remains an outstanding open question.4,14 Many theoretical studies have pushed forward the idea that the CISS effect originates from spin–orbit coupling (SOC) inside the molecular moiety, which is enhanced by chirality.15–19 However (as was recently pointed out explicitly3,14,20), these explanations require a huge (several orders of magnitude) renormalization of the molecular SOC, and while electron correlations21,22 or vibrations23–28 may reduce this normalization to some extent, realistic values for the SOC seem to predict a much smaller CISS effect than experimentally observed. Attempts for using density functional theory to address the CISS effect (e.g. (ref. 29–33)) met only partial success; while they indeed predict the presence of the CISS effect under certain conditions, they cannot address its magnitude nor its apparent non-equilibrium nature. Importantly, to date, none of the suggested theories (either theoretical or ab initio) were able to quantitatively reproduce experimental data.
Recently, inspired by the interface mechanism suggested some time ago,34 we have suggested an alternative theoretical explanation to the CISS effect.35 We argued that the CISS effect is a result of interplay between the (spin–orbit induced) surface magnetization in the metal electrode and spin-imbalance in the molecule, which interact via a spin-torque interaction. Due to spin-transfer torque, the surface magnetization obtains a preferred direction (parallel or anti-parallel to the molecular axis), thus forming a spin-dependent barrier for electrons entering the molecule. The preferred direction is determined by the molecular chirality, which generates a (solenoid) magnetic field depending on the handedness of the molecule, thus breaking the spin symmetry.35 For the sake of having this manuscript self-contained, the so-called the “spinterface” mechanism is described in the ESI Sec. 1.† While this model requires spin–orbit coupling in the electrode to be finite, it still reproduces the CISS effect even for relatively small SOC, see discussion and examples in ESI Sec. S2.† It is thus in line with various experiments showing the CISS effect even for electrodes with small SOC, e.g.(ref. 36 and 37).
The model presented in ref. 35 was limited to small molecules with coherent transport. Here, we extend the theory to bio-molecules, which are characterized by electron–phonon (e–ph) interactions which lead to finite dephasing and diffusive transport.38–41 Using a self-consistent Green's function approach42 we evaluate how e–ph coupling and molecular length affect spin-selectivity. With insights gained from the theoretical calculation, we use the spinterface theory to reproduce the experimental data presented in one of the pioneering papers on the CISS effect, ref. 43, with remarkable quantitative agreement between theory and experiment.
Model and method
Let us first briefly outline the methodology and model (full details can be found in the ESI Sec. S3†). The general setting for the calculation is a molecular junction (MJ) in a CISS measurement setting, composed of a single bio-molecule in contact with a metallic (typically Au) and magnetic (typically Ni) electrodes; the latter electrode can be magnetized parallel (anti-parallel) to the molecular axis, thus blocking the passage of minority (majority) spins; the identity of majority and minority spins is reversed when the molecular chirality is flipped.As a generic example for a bio-molecule of varying length we consider a poly-CG double-strand DNA, described by a tight-binding single-particle Hamiltonian, ![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) DNA, with standard numerical parametrization.44–48 To account for dephasing due to e–ph interactions, we follow a self-consistent self-energy approximation,42,49 valid for “soft” phonons, i.e. acoustic phonons with a broad spectrum. Here, the important parameter is the strength of e–ph coupling, denoted by γ (in units of eV). This approximation allows us to calculate the Green's functions of the system in the presence of electrodes and dephasing.
DNA, with standard numerical parametrization.44–48 To account for dephasing due to e–ph interactions, we follow a self-consistent self-energy approximation,42,49 valid for “soft” phonons, i.e. acoustic phonons with a broad spectrum. Here, the important parameter is the strength of e–ph coupling, denoted by γ (in units of eV). This approximation allows us to calculate the Green's functions of the system in the presence of electrodes and dephasing.
Once the Green's functions are evaluated, we follow the procedure outlined in ref. 35 to evaluate the current–voltage (J–V) characteristics of the molecular junction, specifically the magnetization dependent currents, Jσ(V), where σ = ↑, ↓ (or ± 1) represents the magnetization of the Ni electrodes, parallel or anti-parallel to the molecular axis. From these currents we evaluate the CISS polarization, namely 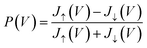 . The important parameters for the evaluation of the CISS effect are the SOC constant in the metal electrode, αA, and the spin-torque coupling α1 (both in eV).
. The important parameters for the evaluation of the CISS effect are the SOC constant in the metal electrode, αA, and the spin-torque coupling α1 (both in eV).
Results I – theoretical model
Polarization: dependence on dephasing and molecular length
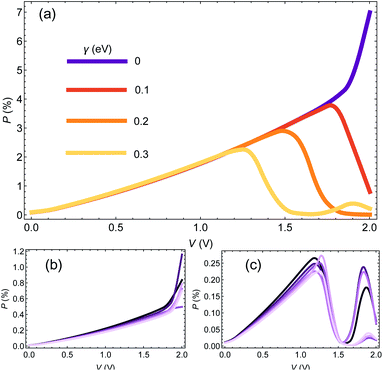
We start the Results section with an analysis of the dependence of CISS-induced polarization on dephasing (encoded in the e–ph coupling) and molecular length. In Fig. 1(a) we plot the polarization P(V) as a function of voltage for a chain of 25 base pairs (BPs) for different e–ph coupling strengths γ = 0, 0.1, 0.2, 0.3 eV (we consider only room temperature hereafter). We set αA = 1 eV and α1 = 50 meV. At low biases, the polarization does not depend on γ, but as a certain (resonant) bias voltage is reached, the polarization reduces substantially, essentially vanishing at high biases.In Fig. 1(b and c) we plot the polarization as a function of voltage for different molecular length (i.e. the number of BPs), with n = 15, 17, …, 25 (dark to bright curves) for γ = 0 (Fig. 1(b)) and γ = 0.3 eV (Fig. 1(c)). We select only odd number of BPs to avoid an odd-even effect.42,50 As can be readily seen, the molecular length has a minor influence on the polarization. The reason is that within the spinterface model, the CISS is an interface effect, and is thus determined predominantly by the interface properties of the molecule, and therefore one indeed expects insignificant length dependence.
It would seem that this result, i.e. the weak dependence of the CISS effect on length, is inconsistent with recent studies of the length dependence of CISS effect,51 which seem to show an increase in polarization with length (specifically, with the number of base pare sequence repeats in DNA molecules). However, this is not the case, and there is no real inconsistency. To understand this, we point out that while the mechanism of the CISS effect indeed does not depend on length per se, it does depend on the transport properties of the molecule, i.e. on its transmission and spin-imbalance (or equivalently its magnetic polarizability). Since these properties are length-dependent, the CISS polarization will appear to be length-dependent. In the example we provide in Fig. 1, the transport properties are weakly length-dependent, hence the CISS effect is also length-weakly length-dependent. As we show in the following sections, the data from 51 can be reconstructed by a length-independent CISS mechanism, by allowing the transport properties to be length-dependent.
Connection between polarization and current
In order to understand the nontrivial dependence of the polarization on e–ph coupling and the relative indifference to molecular length, we turn back to the spinterface model for the CISS effect.35 A central feature of the model is that the current–voltage curves Jσ(V) for different electrode polarizations σ = ±1 are given by| Jσ(V) = J(V + σΞ), | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θM〉 is the spin-dependent shift of the chemical potential (αA is the metal SOC and θM is the average surface-magnetization tilt angle, determined self-consistently as described above and in the ESI Sec. S3†).
θM〉 is the spin-dependent shift of the chemical potential (αA is the metal SOC and θM is the average surface-magnetization tilt angle, determined self-consistently as described above and in the ESI Sec. S3†).
The difference between the currents for the two electrode magnetization directions is J↑ − J↓ ∼ J(V + Ξ) − J(V − Ξ). If Ξ is small compared to voltage, it follows directly that the polarization is proportional to the differential conductance, 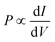 . Thus, in order to understand the origin of the results seen in Fig. 1, it is useful to look at the dependence of the current and differential conductance on the e–ph couplings and molecular length.
. Thus, in order to understand the origin of the results seen in Fig. 1, it is useful to look at the dependence of the current and differential conductance on the e–ph couplings and molecular length.
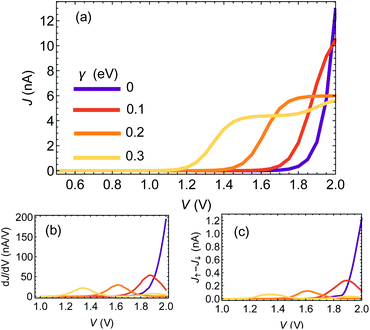
Fig. 2(a) shows the J–V curves for a chain of 25 base pairs (BPs) for different e–ph coupling strengths γ = 0, 0.1, 0.2, 0.3 eV. Two apparent features can be seen: first, the resonance (marked by the rise of current) shifts towards lower biases. Second, at high biases the current is reduced with increasing γ. This is because dephasing effectively mixes the molecular orbitals, opens additional channels for transport and redistributes the weight of the different resonances.42
In Fig. 2(b) and (c) we plot the differential conductance dJ/dV and the differences between the currents for different electrode magnetization in the CISS calculation, J↑ − J↓ (the numerator of the polarization P(V)). The clear resemblance between Fig. 2(b) and (c) is evident. This explains the decay in the polarization in Fig. 1(a) for biases larger than the resonance; the numerator J↑ − J↓ vanishes, because the differential conductance 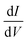 vanishes.
vanishes.
To understand the indifference of polarization to dephasing for biases lower than the resonance, we note that the polarization also has a denominator – the total current. At low biases, the denominator completely dominates the polarization, because the off-resonance (low bias) currents are essentially independent of dephasing rate (see ESI Sec. S4†). A similar argument holds for explaining the length-independence of polarization, Fig. 1(b and c); the differential conductance is essentially length-independent (see ESI Fig. S1;† this can also be inferred from the apparent length-independence of the transmission function in the coherent regime35), resulting in a length-independent CISS effect.
The observation that the polarization P(V) exhibits different behavior at different regimes raises an intriguing question in the context of the CISS effect – is P(V) indeed the best quantity to describe it? Natively, the polarization was suggested because it is a unitless quantity, which encodes the CISS effect and is indifferent to global changes in the total current magnitude. However, as apparent from the arguments above, the fact that it is composed of a ratio between J↑ − J↓ and the total current may add features to the polarization which are not directly relevant to the CISS effect itself. Furthermore, from an experimental point of view, the low bias regime is characterized by very low currents, thus increasing the sensitivity of polarization to noise. It is thus useful, when considering experimental data, to consider both the polarization and J↑ − J↓.
Results II – comparison between theory and experiment
One of the pioneering papers in the field of the CISS effect is the paper by Xie et al.,43 where three sets of DNA chains with different sequences (and different lengths) were shown to exhibit the CISS effect, with polarization reaching a few percent. Armed with the insights from the previous section, we now move to compare between the theory presented above and the data of ref. 43.The first step is to establish, using the experimental data, the connection between polarization and differential conductance, namely J↑ − J↓ ∝ dJ/dV, which arises naturally from the spinterface model. In Fig. 3(a) we plot J↑ − J↓ as a function of bias voltage V for the 26, 40 and 50BPs chains, extracted from the data of ref. 43. In Fig. 3(b) we plot the differential conductance dJ/dV, extracted numerically from the average currents  measured in ref. 43. The similarity between the two plots (and hence between J↑ − J↓ and dJ/dV, as predicted by the theory) is evident, and can clearly be seen through, e.g. the merge of the data for all three samples at low biases, and the increase in J↑ − J↓ for the 26BP sample above 1 V.
measured in ref. 43. The similarity between the two plots (and hence between J↑ − J↓ and dJ/dV, as predicted by the theory) is evident, and can clearly be seen through, e.g. the merge of the data for all three samples at low biases, and the increase in J↑ − J↓ for the 26BP sample above 1 V.
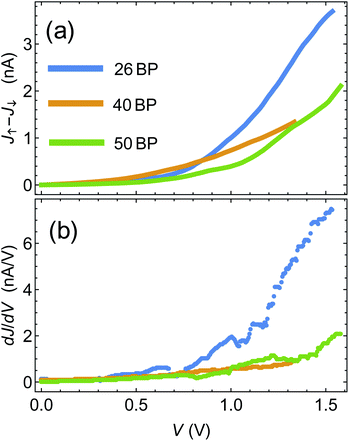 | ||
| Fig. 3 (a) Difference between magnetization-dependent currents, J↑ − J↓ as a function of voltage. Data extracted from ref. 43. (b) Differential conductance dJ/dV extracted from ref. 43. | ||
The next step is to reproduce the data of Xie et al. from the theory, using the spinterface mechanism formulation. For this to be achieved, the first requirement is a theoretical model for the current through the molecular junction, which can be fitted to the bare experimental J–V curves (i.e. without electrode magnetization) of the different junctions. In principle, the model presented in the previous sections can be used for that aim. However, this will require a large number of fit parameters and alterations of the model. The reason is that the realistic bio-molecules are much more complicated than the simple model presented here; knowing the exact sequence of the DNA chain is not enough, and knowledge on the detailed phonon distribution is required (and even then, it is not guaranteed to give reasonable fits).
Fortunately, the situation can be resolved and a simple model for the experimental data can be devised, based on the observation that the J–V curves of the full microscopic model described in the previous sections can be fitted, to great accuracy, with a simple model of transport through a set of single levels, each with its own resonance orbital energy εi and electrode-molecule electron transfer rate γi (see ESI Sec. S5†). We thus proceed by first fitting the bare J–V curves of Xie et al. with an expression of the form J(V) = ∑iγi(fL(εi) − fR(εi)), where are the left and right electrodes' Fermi distributions in the presence of voltage bias.35 We use the average currents for the different samples of ref. 43 to obtain the set of parameters {εi, γi} for each sample (see ESI Sec. S5†).
Once expressions for current (and hence density35) are obtained, we proceed with evaluating the CISS effect. Here, two comments are in order: (i) we assume that the interface and CISS parameters (i.e. the Au SOC parameter αA and the spin–torque coupling α1) are the same for all samples in Xie et el., because these parameters only depend on the molecule–electrode interface and the electrode themselves, and (ii) noting that the CISS polarization is sensitive to the total current magnitude (which appears in its denominator), especially at low biases, we reproduce directly the currents for different electrode magnetizations Jσ(V), rather than the polarization. This is also reasonable because the currents are the measured quantity, and polarization is a quantity derived from them. Put simply, a reliable theoretical description of the CISS effect should reproduce not only the polarization P(V), but also the currents Jσ(V) themselves.
In Fig. 4 we plot the currents for different electrode magnetizations for molecular junctions with 26, 40 and 50BPs. The open markers are the data of ref. 43, blue and orange mark the current for parallel and anti-parallel magnetizations. The fit parameters were set to be αA = 0.95 eV and α1 = 5.5 meV (the same for all three calculations). The excellent agreement between the experimental data and the theory is apparent, and provides further confidence in the validity of the spinterface mechanism as the origin of the CISS effect. A direct conclusion that comes out of this fit is that the experimental data of ref. 43 does not reflect any dependence of the CISS on length. This is because although the chains in ref. 43 have different lengths, they also have different sequences, which alter the transport properties and hence the CISS effect. However, we note that in increase in the CISS effect with length was indeed observed,52 but not in a transport setup, but in photo-excitation experiments. Thus, the effect of molecular length on the CISS effect should be further examined experimentally. A useful (and relatively simple) experiment in this context would be a repeat of the experiments of ref. 43 with a uniform sequence (e.g., poly-CG) with repeating units, which can indeed probe the length-dependence of the CISS effect.
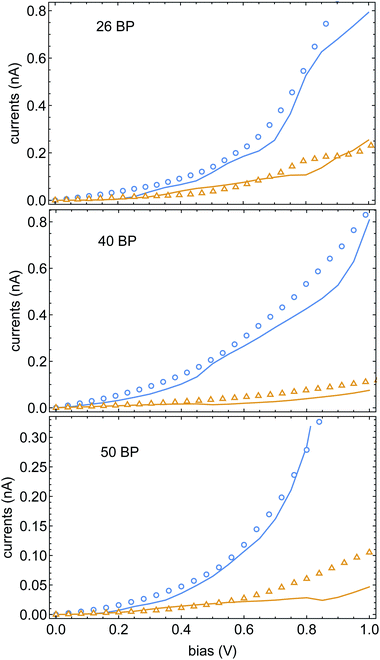 | ||
| Fig. 4 Currents Jσ(V) as a function of voltage, blue and orange encode the Ni electrode magnetization parallel and anti-parallel to the molecular axis. The open markers are the data of ref. 43, solid lines are theoretical fits. All three samples share the same CISS parameters, namely αA and α1 (see text). | ||
The methodology presented here, namely fitting the I–V curves for different (e.g. length-dependent) data sets first, and then plugging them into the spinterface model with length-independent SOC and spin–torque parameters, can be applied to other experiments as well. In the ESI, Sec. S6,† we show the fits to the data of Mishra et al.,51 again showing remarkable agreement between data and theory with a length-independent CISS mechanism.
Summary and discussion
To summarize, here we presented a theoretical model for the CISS effect in long bio-molecules, including the role of dephasing. We find that while dephasing tends to reduce the CISS, the polarization is rather insensitive to the molecular length. In order to explain this, a surprising and simple connection between the magnitude of the CISS effect and the differential conductance was established. This connection allowed us to clarify the behavior of the polarization as a function of dephasing and molecular length.We again stress that the length-independence of the spinterface mechanism does not mean that the CISS polarization measurements will be length-independent, because the polarization depends on the transport properties and the molecular spin polarizability, which indeed may show length-dependence. Disentangling the length-dependence of the transport properties from the CISS effect can be done by finding a molecular system with length-independent transport properties; our results predict that in such a system the CISS effect will also be length-independent.
Using the theoretical model, we then proceeded to analyze the data from the paper of Xie et al.. First, the connection between the CISS magnitude and the differential conductance was demonstrated with the experimental data. Then, using a simplified model for the current through bio-molecules (motivated by the microscopic theory), we were able to reproduce the experimental data of the CISS effect with remarkable agreement, keeping the parameters of the CISS effect (namely the metal electrode SOC and the spin-torque coupling) molecule-independent, as expected.
To our knowledge, this is the first theoretical formulation of the CISS effect which can quantitatively fit experimental raw data (i.e. the magnetization-dependent currents). Indeed, recent studies aiming to fit data with theory53 show a factor of two difference in polarization between theory and data, and show a qualitative experiment-theory difference in the I–V curves (which are the real experimental signal, and the polarization is only a quantity extracted from the currents); while in experiments currents increase as a function of temperature, the calculated currents decrease with temperature (compare Fig. 1(c) with Fig. S1 in ref. 53).
The methodology presented here opens a route for a deeper understanding of the CISS effect in bio-molecules, as past and future experiments (some suggested in ref. 35) can now be analyzed using a microscopic theory and fitted quantitatively. Future studies will be aimed at extracting the dependence of the CISS effect on other experimental parameters, especially temperature (which is not accounted in the model presented here directly).
Author contributions
The author confirms sole responsibility for the following: study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.Conflicts of interest
There are no conflicts to declare.Notes and references
- R. Naaman and D. H. Waldeck, J. Phys. Chem. Lett., 2012, 3, 2178–2187 CrossRef CAS PubMed.
- R. Naaman and D. H. Waldeck, Annu. Rev. Phys. Chem., 2015, 66, 263–281 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- R. Naaman, Y. Paltiel and D. Waldeck, J. Phys. Chem. Lett., 2020, 11, 3660–3666 CrossRef CAS PubMed.
- K. Michaeli, N. Kantor-Uriel, R. Naaman and D. H. Waldeck, Chem. Soc. Rev., 2016, 45, 6478–6487 RSC.
- K. Banerjee-Ghosh, O. Ben Dor, F. Tassinari, E. Capua, S. Yochelis, A. Capua, S.-H. Yang, S. S. P. Parkin, S. Sarkar, L. Kronik, L. T. Baczewski, R. Naaman and Y. Paltiel, Science, 2018, 360, 1331–1334 CrossRef CAS PubMed.
- K. B. Ghosh, W. Zhang, F. Tassinari, Y. Mastai, O. Lidor-Shalev, R. Naaman, P. Möllers, D. Nürenberg, H. Zacharias, J. Wei, E. a Wierzbinski and D. H. Waldeck, J. Phys. Chem. C, 2019, 123, 3024–3031 CrossRef CAS.
- A. Kumar, E. Capua, K. Vankayala, C. Fontanesi and R. Naaman, Angew. Chem., Int. Ed., 2017, 56, 14587–14590 CrossRef CAS PubMed.
- O. B. Dor, S. Yochelis, A. Radko, K. Vankayala, E. Capua, A. Capua, S.-H. Yang, L. T. Baczewski, S. S. P. Parkin and R. Naaman, et al. , Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- H. Al-Bustami, G. Koplovitz, D. Primc, S. Yochelis, E. Capua, D. Porath, R. Naaman and Y. Paltiel, Small, 2018, 14, 1801249 CrossRef PubMed.
- R. Torres-Cavanillas, G. Escorcia-Ariza, I. Brotons-Alcázar, R. Sanchis-Gual, P. C. Mondal, L. E. Rosaleny, S. Giménez-Santamarina, M. Sessolo, M. Galbiati and S. Tatay, et al. , J. Am. Chem. Soc., 2020, 142, 17572–17580 CrossRef CAS PubMed.
- J. M. Abendroth, K. M. Cheung, D. M. Stemer, M. S. El Hadri, C. Zhao, E. E. Fullerton and P. S. Weiss, J. Am. Chem. Soc., 2019, 141, 3863–3874 CrossRef CAS PubMed.
- C.-H. Ko, Q. Zhu, F. Tassinari, G. Bullard, P. Zhang, D. N. Beratan, R. Naaman and M. J. Therien, Proc. Natl. Acad. Sci., 2022, 119, e2116180119 CrossRef CAS PubMed.
- F. Evers, R. Korytár, S. Tewari and J. M. van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 035001 CrossRef CAS.
- A.-M. Guo and Q.-f. Sun, Phys. Rev. Lett., 2012, 108, 218102 CrossRef PubMed.
- R. Gutierrez, E. Díaz, R. Naaman and G. Cuniberti, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 081404 CrossRef.
- A.-M. Guo and Q.-f. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035424 CrossRef.
- R. Gutierrez, E. Díaz, C. Gaul, T. Brumme, F. Domínguez-Adame and G. Cuniberti, J. Phys. Chem. C, 2013, 117, 22276–22284 CrossRef CAS.
- A.-M. Guo and Q.-F. Sun, Proc. Natl. Acad. Sci., 2014, 111, 11658–11662 CrossRef CAS PubMed.
- A. Ghazaryan, Y. Paltiel and M. Lemeshko, J. Phys. Chem. C, 2020, 124, 11716–11721 CrossRef CAS PubMed.
- J. Fransson, J. Phys. Chem. Lett., 2019, 10, 7126–7132 CrossRef CAS PubMed.
- X. Li, J. Nan and X. Pan, Phys. Rev. Lett., 2020, 125, 263002 CrossRef CAS PubMed.
- S. Dalum and P. Hedegård, Nano Lett., 2019, 19, 5253–5259 CrossRef CAS PubMed.
- J. Fransson, Phys. Rev. B, 2020, 102, 235416 CrossRef CAS.
- J. Fransson, Nano Lett., 2021, 21, 3026–3032 CrossRef CAS PubMed.
- X. Li, J. Nan and X. Pan, Phys. Rev. Lett., 2020, 125, 263002 CrossRef CAS PubMed.
- G.-F. Du, H.-H. Fu and R. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 035431 CrossRef CAS.
- L. Zhang, Y. Hao, W. Qin, S. Xie and F. Qu, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 102, 214303 CrossRef CAS.
- M. S. Zollner, S. Varela, E. Medina, V. Mujica and C. Herrmann, J. Chem. Theory Comput., 2020, 16, 2914–2929 CrossRef PubMed.
- J. M. Matxain, J. M. Ugalde, V. Mujica, S. I. Allec, B. M. Wong and D. Casanova, ChemPhotoChem, 2019, 3, 770–777 CrossRef CAS.
- M. S. Zollner, A. Saghatchi, V. Mujica and C. Herrmann, J. Chem. Theory Comput., 2020, 16, 7357–7371 CrossRef PubMed.
- V. Kiran, S. P. Mathew, S. R. Cohen, I. Hernández Delgado, J. Lacour and R. Naaman, Adv. Mater., 2016, 28, 1957–1962 CrossRef CAS PubMed.
- V. V. Maslyuk, R. Gutierrez, A. Dianat, V. Mujica and G. Cuniberti, J. Phys. Chem. Lett., 2018, 9, 5453–5459 CrossRef CAS PubMed.
- J. Gersten, K. Kaasbjerg and A. Nitzan, J. Chem. Phys., 2013, 139, 114111 CrossRef PubMed.
- S. Alwan and Y. Dubi, J. Am. Chem. Soc., 2021, 143, 14235–14241 CrossRef CAS PubMed.
- M. Kettner, V. V. Maslyuk, D. Nurenberg, J. Seibel, R. Gutierrez, G. Cuniberti, K.-H. Ernst and H. Zacharias, J. Phys. Chem. Lett., 2018, 9, 2025–2030 CrossRef CAS PubMed.
- D. Mishra, T. Z. Markus, R. Naaman, M. Kettner, B. Göhler, H. Zacharias, N. Friedman, M. Sheves and C. Fontanesi, Proc. Natl. Acad. Sci., 2013, 110, 14872–14876 CrossRef CAS PubMed.
- S. H. Choi, C. Risko, M. C. R. Delgado, B. Kim, J.-L. Brédas and C. D. Frisbie, J. Am. Chem. Soc., 2010, 132, 4358–4368 CrossRef CAS PubMed.
- L. Xiang, J. L. Palma, C. Bruot, V. Mujica, M. A. Ratner and N. Tao, Nat. Chem., 2015, 7, 221–226 CrossRef CAS PubMed.
- Y. Li, L. Xiang, J. L. Palma, Y. Asai and N. Tao, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- R. Korol, M. Kilgour and D. Segal, J. Chem. Phys., 2016, 145, 224702 CrossRef PubMed.
- Y. Dubi, J. Phys. Chem. C, 2014, 118, 21119–21127 CrossRef CAS.
- Z. Xie, T. Z. Markus, S. R. Cohen, Z. Vager, R. Gutierrez and R. Naaman, Nano Lett., 2011, 11, 4652–4655 CrossRef CAS PubMed.
- D. Brisker-Klaiman and U. Peskin, J. Phys. Chem. C, 2010, 114, 19077–19082 CrossRef CAS.
- K. Siriwong, A. A. Voityuk, M. D. Newton and N. Rösch, J. Phys. Chem. B, 2003, 107, 2595–2601 CrossRef CAS.
- A. A. Voityuk, N. Rösch, M. Bixon and J. Jortner, J. Phys. Chem. B, 2000, 104, 9740–9745 CrossRef CAS.
- A. A. Voityuk, J. Jortner, M. Bixon and N. Rösch, J. Chem. Phys., 2001, 114, 5614–5620 CrossRef CAS.
- C. Guo, K. Wang, E. Zerah-Harush, J. Hamill, B. Wang, Y. Dubi and B. Xu, Nat. Chem., 2016, 8, 484–490 CrossRef CAS PubMed.
- G. Penazzi, A. Pecchia, V. Gupta and T. Frauenheim, J. Phys. Chem. C, 2016, 120, 16383–16392 CrossRef CAS.
- H. Kim, M. Kilgour and D. Segal, J. Phys. Chem. C, 2016, 120, 23951–23962 CrossRef CAS.
- S. Mishra, A. K. Mondal, S. Pal, T. K. Das, E. Z. Smolinsky, G. Siligardi and R. Naaman, J. Phys. Chem. C, 2020, 124, 10776–10782 CrossRef CAS.
- B. Göhler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef PubMed.
- T. K. Das, F. Tassinari, R. Naaman and J. Fransson, arXiv preprint arXiv:2108.08037, 2021.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02565e |
| This journal is © The Royal Society of Chemistry 2022 |