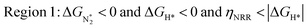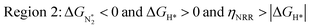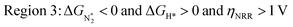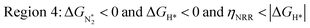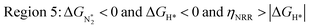Descriptors and graphical construction for in silico design of efficient and selective single atom catalysts for the eNRR

Abstract

The electrochemical nitrogen reduction reaction (eNRR) offers the possibility of ammonia synthesis under mild conditions; however, it suffers from low yields, a competing hydrogen evolution reaction pathway, and hydrogen poisoning. We present a systematic approach toward screening single atom catalysts (SACs) for the eNRR, by focusing on key parameters computed from density functional theory and relationships between them. We illustrate this by application to 66 model catalysts of the types, TM-Pc, TM-N_XC_Y, and TM-N₃, where TM is a 3d transition metal or molybdenum. We identified the best SACs as Sc-Pc, Cr-N₄, Mn-Pc, and Fe-N₂C₂; these show eNRR selectivity over the HER and no hydrogen poisoning. The catalysts are identified through multi-parameter optimization which includes the condition of hydrogen poisoning. We propose a new electronic descriptor O_val, the valence electron occupancy of the metal center that exhibits a volcano-type relationship with eNRR overpotential. Our multi-parameter optimization approach can be mapped onto a simple graphical construction to find the best catalyst for the eNRR over the HER and hydrogen poisoning.

---

1 Introduction

The Haber–Bosch process for ammonia synthesis has been described as possibly the most important scientific discovery of the twentieth century.¹ However, it requires high temperatures and pressures, and results in high energy consumption and the emission of greenhouse gases.² Alternative synthetic routes are therefore urgently needed. An environmentally friendly possibility is the electrochemical nitrogen reduction reaction (eNRR), which synthesizes ammonia from nitrogen and water under mild conditions (N₂ + 6H⁺ + 6e⁻ → 2NH₃).^3–5 However, currently available eNRR catalysts need improvement in three respects: (i) the efficiency of nitrogen fixation needs to be increased,^6,7 (ii) the competing hydrogen evolution reaction (HER) needs to be suppressed,^8,9 and (iii) hydrogen poisoning of active sites has to be avoided.^10,11 Transition metals are popular eNRR catalysts; however they tend to favor hydrogen adsorption due to the formation of strong metal d – hydrogen σ bonds, and also tend to have low affinity for N₂ adsorption.^12,13 We aim to mitigate these problems by appropriately tuning the electronic structure by altering the environment surrounding metal atoms at the active site of single atom catalysts (SACs).^14–20

In contrast to many previously studied SACs where the metal atom was adsorbed over a suitably modified two-dimensional (2D) support,^21–25 in our systems the metal atom is embedded within the 2D layer.^26–29 Moreover, in previous work, typically only one criterion (usually the competing HER) was used to optimize catalyst function,^30–38 whereas we will simultaneously optimize with respect to multiple criteria. Among embedded SACs, the Fe–N–C system was reported to be an efficient SAC, with a high eNRR faradaic efficiency (FE) of 56.55%, but its efficacy is limited due to the competitive HER.³⁹ Recently, we studied Co and Fe centers in phthalocyanines,⁴⁰ and concluded that Co-phthalocyanine should be the better catalyst, with a low eNRR overpotential.

We have performed density functional theory (DFT) based calculations on 66 different SACs to investigate the efficiency and selectivity of the eNRR over the HER, as well as the likelihood of H-poisoning. We show that the binding energy of the NNH intermediate and the valence electron occupancy of the metal center are descriptors for the catalytic activity toward the eNRR.

2 Results and discussion

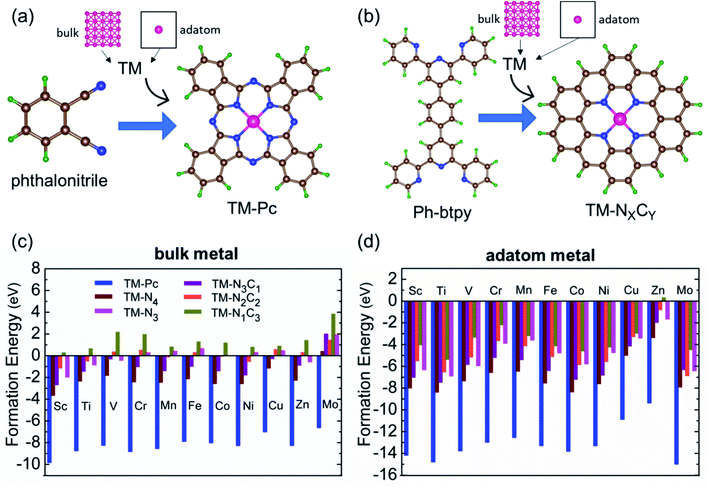
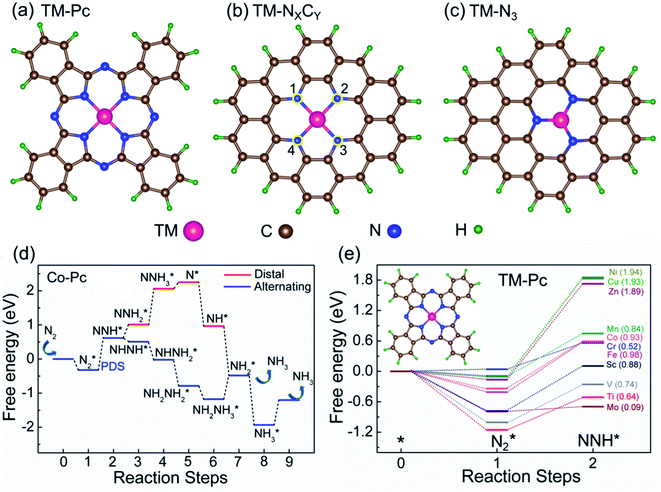
We consider six kinds of systems as model catalysts: transition metal doped phthalocyanines (TM-Pcs), four types of TM-N_XC_Y embedded graphene systems (TM-N₄, TM-N₂C₂, TM-N₃C_1, and TM-N₁C₃) and TM-N₃ embedded graphene systems^41–45 [see Fig. S1 in the ESI].† For the metal centers, we consider the ten 3d transition metals as well as molybdenum (TM- Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, and Mo).^46–50 We thus construct 66 SAC systems.

We first calculate the formation energies (E_f) of all the proposed SACs, see Table S1 in the ESI.† In experiments, the phthalonitrile and Ph-btpy compounds are used as sources to synthesize TM-phthalocyanine (TM-Pc) and TM-N_XC_Y SACs respectively.^51–57 Therefore, these structures are taken as reference systems when computing the E_f of the respective SACs (Fig. 1a and b). E_f is computed using the formula: E_f = E_SAC + xμ_H + yμ_N − (E_ref + zμ_C + E_TM), where E_SAC, E_ref, and E_TM are the total energies of the SAC, the phthalonitrile or Ph-btpy system, and a single transition metal (TM) atom, respectively (see SI-1 in the ESI for details).† Here, μ_C is the chemical potential of a single C atom in the phthalonitrile or Ph-btpy system. μ_H and μ_N are the chemical potentials of hydrogen and nitrogen, respectively, taken as the total energy of 1/2H₂ and 1/2N₂ in the gas phase. x is the number of hydrogen atoms that remain, y is the number of nitrogen atoms that remain, and z is the number of carbon atoms replaced in the SAC. For E_TM, we have considered two possibilities: the total energy of a single metal atom in the bulk system or the energy of a metal adatom. The computed values of formation energies E_f are displayed in Fig. 1c (bulk metal as reference) and Fig. 1d (adatom as reference). The values of E_f computed using metal adatoms as the reference energy, and the trends in the values of E_f with changes in the coordination configuration, are in agreement with previous reports.⁵⁸ Also, the dissolution potential (U_diss) is calculated to examine the electrochemical stability of these SACs considering both bulk and adatoms as sources of metal atoms. By employing the values of E_f in the equation, U_diss = U_diss0 − E_f/ne, we calculated the U_diss for all 66 SACs (Fig. S2 in the ESI†), where U⁰_diss and n are the standard dissolution potential of the bulk metal and number of electrons involved in the dissolution respectively⁵⁹ (SI-1 in the ESI†). We see that in most cases the value of E_f is negative, indicating thermodynamic stability and U_diss is positive, indicating electrochemical stability that shows easy formation of the systems from their sources. Also, we have performed molecular dynamics calculations to investigate the dynamic stability of one of our catalysts as an illustrative example. For this, we considered Mn-Pc as an example to find its dynamic stability at different temperatures (300 K, 500 K, 700 K, and 900 K) (Fig. S3 in the ESI†). Here, we found small fluctuations in the planarity of the Mn-Pc molecule, but a distortion or breaking of the bond is not observed, which shows the high dynamic stability of these SACs.⁶⁰

Fig. 1 Examples of structures of (a) phthalonitrile and (b) Ph-btpy. The schemes show the source of metals and molecules used when computing the formation energy (E_f) of SACs. The computed results for E_f for all 66 single atom catalysts, upon considering source of metal atoms as (c) bulk and (d) adatom.

To study the performance of these systems (Fig. 2a–c) as eNRR catalysts, we will plot the free energy profile of all the steps in the reaction, and then focus on three aspects (Fig. S4 in the ESI†): (a) binding of nitrogen to the catalyst, quantified by the change in the free energy of N₂ adsorption 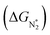, (b) overpotential of the eNRR (η_NRR), quantified by the free energy change in the highest uphill step (potential determining step or PDS) in the free energy profile,⁶¹ and (c) the competing HER, quantified by the change in the free energy of H adsorption (ΔG_H*): a low value of |ΔG_H*| indicates the possibility of hydrogen evolution, and if ΔG_H* < 0, one will have hydrogen poisoning.

Fig. 2 Schematic structures of (a) TM-Pc, (b) TM-N_XC_Y and (c) TM-N₃ systems. Atoms in positions 1, 2, 3, and 4 in figure (b) are replaced with either N or C to make TM-N_XC_Y systems (d) free energy profile of the eNRR via alternating and distal pathways, for Co-Pc. (e) Free energy profile of N₂ and NNH adsorption for various TM-Pcs. The numbers in parentheses indicate the corresponding values of η_NRR.

We first plot the free energy profile, as obtained from DFT calculations (see SI-2 of the ESI for computational details),† at electrode potential U = 0 V. Fig. 2d shows these results for the Co-Pc system and further examples are shown in Fig. S5 in the ESI.† Two possible pathways have previously been identified for the eNRR: alternating and distal (see Fig. S6 of the ESI†).^62,63 We find that for the systems considered here, the alternating pathway is favored over the distal one, due to the lower free energy of the NHNH* intermediate, as compared to the 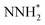intermediate. We also observe that both pathways have the same PDS: the step from 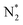to NNH*.^64,65 Furthermore, we performed the N₂ adsorption calculations with a side-on configuration on all 66 SACs to investigate the presence of the enzymatic or mixing mechanism. The values of 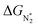with end-on and side-on configurations are listed in Table S2 of the ESI† for a comparison. We observed that the nine TM-N₃ and Mo metal center based SACs (Mo-N₄, Mo-N₃C₁, Mo-N₁C_3, Mo-N₃, Sc-N₃, Ti-N₃, V-N₃, Mn-N₃, and Fe-N₃) show a lower free energy value of side-on N₂ adsorption as compared to the end-on configuration. So, we computed the intermediate energies for these nine SACs to plot a full free energy profile of the eNRR (as shown in Fig. S7†) and compared them with the end-on pathway. It is seen that the both end-on and side-on N₂ adsorption pathways have the same PDS step ( 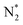to NNH*) but a small change is observed in the value of overpotential. In the case of the other 57 SACs, the adsorption of N₂ in an end-on form is more favourable than that in a side-on configuration. So, the enzymatic or mixed mechanism is not feasible in these systems.⁶²

We will now screen these 66 SACs, imposing the three conditions mentioned above. As the first screening step, we demand that be negative, indicating a favorable exothermic reaction. As an example, in Fig. 2e, we compare the results for the free energy profile of N₂ and NNH adsorption for the 11 TM-Pc systems; the values of η_NRR and the corresponding overpotentials toward the eNRR are given in parentheses in the figure. The results for the remaining systems are given in Table S1 and Fig. S8 in the ESI.† We find that for 65 of the 66 SACs (the single exception is Cr-Pc). We also note that our values of (−0.41 eV) and η_NRR (0.98 V) for the Fe-Pc system are in fairly good agreement with previously reported values of −0.39 eV and 0.85 V respectively.⁶² The metal centers of TM-Pc, TM-N₄ and TM-N₃ may influence the nearby carbon (C) and nitrogen (N) sites due to their electronic environments. We therefore also investigated N₂ and NNH adsorption on the other possible sites (C and N) of Sc-Pc, Sc-N₄, Sc-N₃ and of pristine phthalocyanine (without metal center) systems (see Fig. S9 and S10 of the ESI†). Importantly, very high values of eNRR overpotentials are obtained on all the carbon and nitrogen sites.⁶⁶ Therefore, the nitrogen and carbon sites of these SACs are unable to promote the eNRR, due to the weaker binding of the NNH intermediate. However, we see that changing the metal center in the SAC also does not succeed in enhancing the adsorption of NNH on nitrogen and carbon sites (Fig. S11 of the ESI†). Furthermore, we have considered the counter anion “Cl” for Sc-Pc and V-Pc SACs to mimic their +3 oxidation state and estimate the free energy profile of N₂ and NNH adsorption (see the comparison in Fig. S12 of the ESI†). We find that the presence of the Cl anion can improve the selectivity of the catalyst for the eNRR over the HER by increasing the value of +ΔG_H*.

Earlier authors have proposed various descriptors to capture the behavior of catalysts.^67–80 We demonstrate two such descriptors: an energetic one and an electronic one, to correlate with η_NRR for the SACs considered here. On plotting the data for all 66 systems, we see (Fig. 3a) that η_NRR correlates linearly with ΔG_NNH*, the change in the adsorption free energy of NNH (R² = 0.88). This underlines the key role played by the NNH* step in the eNRR and confirms that ΔG_NNH* is an energy descriptor for the performance of SACs toward the eNRR. We note that there are previous reports where ΔG_NNH* has been used as a descriptor to screen the eNRR performance of various catalysts.^{12,46,59,64,73,76} We find that O_val, the valence electron occupancy of the metal center, is an electronic descriptor which exhibits a volcano-type relationship with η_NRR for all 66 SACs (see Fig. 3b). It is clearly observed that the value of O_val on the metal center should be less than 8e to obtain η_NRR < 1 V. In the case of Ni-, Cu- and Zn- based SACs, the O_val value is more than 8e and η_NRR > 1 V. So, the descriptor O_val is an origin, which is more effective to define the eNRR activity for various SACs. In addition, we have plotted the eNRR activity as a function of other frequently considered parameters, such as the “d-band center” and “Bader charge” but find that these quantities do not show any correlation with η_NRR and they are not appropriate descriptors to define the eNRR activity of SACs with different metal centres, as has also been reported in the previous studies^81,82 (Fig. S13 in the ESI†). Furthermore, we have obtained charge density difference plots to gain insight into the effect of different environments and metal centers on adsorption properties (see SI-3, Fig. S14 and S15 in the ESI†). Our results show that it is possible to modify the performance of SACs by changing the surrounding environment and O_val of the metal centers. Considering the optimum value of η_NRR as a second screening criterion, we demand that η_NRR < 1 V.⁵⁹ We find that 42 of the 65 SAC systems (left after screening step 1) satisfy this criterion. Furthermore, we computed the N–N bond length after adsorption to analyse the activation of N₂ by each SAC⁸³ (see Table S3 in the ESI†). It is seen that the weak activation of N₂ (N–N bond length close to 1.11 Å) obtained mostly on Ni-, Cu- and Zn- based SACs leads to a higher eNRR overpotential (>1 V).^17,84 Also, we observed that the mainly TM-N₃ and Mo-center based SACs show a large expansion in N–N bond length. So, we correlated the values of N–N bond length with the energy descriptor, ΔG_NNH* and the linear relationship is observed with an R² of 0.85 (Fig. S16 in the ESI†). Through charge density differences, the N₂ activation can be visualized on different metal centers in the TM-Pc system (Fig. S17 in the ESI†).

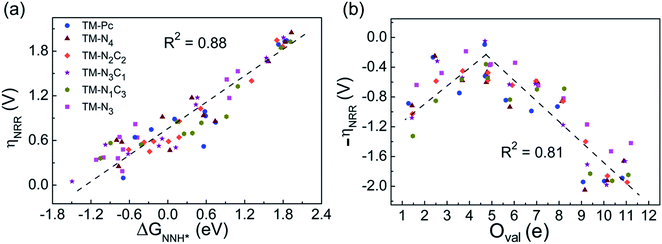Fig. 3 (a) Correlation between eNRR overpotential η_NRR and ΔG_NNH* and (b) correlation between η_NRR and valence electron occupancy (O_val) of the metal center.

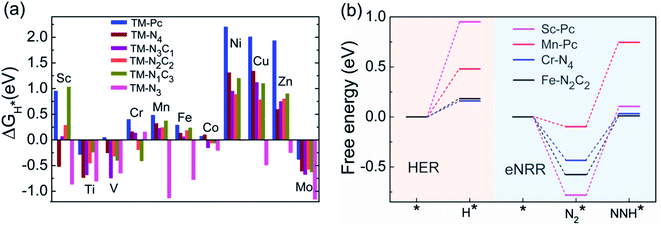
We now come to the third screening step. As mentioned above, both the FE and the NH₃ yield of the eNRR are highly impacted by the competing pathway of the HER. In Fi. S18 of the ESI,† we present our results for the free energy profile of the HER for all 66 SAC systems. We will now demand that the free energy of adsorbed H, ΔG_H* > 0, since this will lead to low H poisoning. To enable comparison, we plot the values of ΔG_H* of all 66 SACs in Fig. 4a. We see that changing the environment of the metal centers has an impact on ΔG_H*.⁸¹ Moreover, for each metal center, the trends in changes in 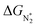and ΔG_NNH* are similar (Fig. S19 in the ESI†). We find that 36 of the 66 SACs have ΔG_H* > 0, and therefore should show no H poisoning. However, of the 42 SACs left after screening step 2 (η_NRR < 1 V), only 16 SACs have ΔG_H* > 0 (see Table S1†). Of these, we consider, for four different metal centers, the best SACs (Sc-Pc, Mn-Pc, Cr-N₄ and Fe-N₂C₂) to display the computed free energy profile of H, N₂ and NNH adsorption (see Fig. 4b). We emphasize again that for these four SACs, ΔG_H* > 0 and 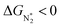and they have high selectivity for the eNRR over the HER, as well as low η_NRR (<1 V).

Fig. 4 (a) Bar chart showing the values of ΔG_H* for different metal centers, data for all 66 SACs and (b) comparison of the values of ΔG_H*, and η_NRRof the eNRR for the 4 ‘best’ SACs, viz., Sc-Pc, Mn-Pc, Cr-N₄ and Fe-N₂C₂.

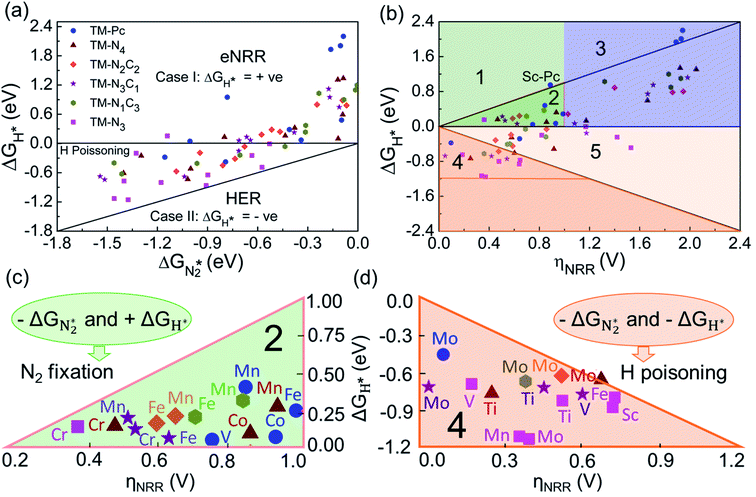
Thus, the optimal SAC for the eNRR should satisfy multiple criteria; we now show that this screening procedure can be visualized in a simple way that should prove very useful. We define five equations corresponding to these criteria and represent them graphically, as shown in Fig. 5. First, in Fig. 5a, for the 65 SACs that satisfy the first criterion 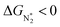(i.e., all except Cr-Pc), we plot ΔG_H*vs.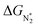. In general, as 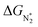becomes more negative, so does 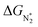. However, 35 SACs have 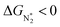and ΔG_H* > 0, making them suitable catalysts for the eNRR. For the remaining 30 SACs (mostly Mo-, Ti-, and V- based SACs and TM-N₃), 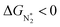and ΔG_H* < 0, favoring hydrogen poisoning as well as the possibility of the HER.

Fig. 5 (a) Free energy of adsorption of H vs. free energy of adsorption for N₂, for 65 model SACs (all except Cr-Pc). (b) Free energy of adsorption of H vs. overpotential of the eNRR for 65 SACs, with the plot being divided into 5 regions; panels (c) and (d) show zoomed in views of Regions 2 and 4, respectively.

In Fig. 5b, we plot ΔG_H*vs. η_NRR for the remaining 65 SACs. We separate the data in the plot into five different regions, as follows:

We predict that SACs that fall in Region 1 will have optimal performance, with very high eNRR selectivity over the HER. We can see from Fig. 5b that only Sc-Pc falls in Region 1, and the corresponding values of ΔG_H*, 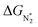, and η_NRR are (+0.95 eV, −0.78 eV, 0.88 V). 15 SACs are found to lie in Region 2, mostly Mn, Cr, Fe and Co-based SACs (see Fig. 5c). These have high N₂ adsorption and low H poisoning, making them selective toward the eNRR; however, as |ΔG_H*| < η_NRR, they have a possibility, though low, of the HER. The SACs in Region 3, which mostly have Ni, Cu and Zn centers, should have the lowest H poisoning, but they have a large η_NRR > 1 V, leading to a low NH₃ yield. In Region 4 (see Fig. 5d) there are 14 SACs (Mo, Ti, V centers and TM-N₃), which have η_NRR < ΔG_H*, so the HER should be suppressed; however, they have a high likelihood of H poisoning (ΔG_H* < 0). In Table S4,† we show that, indeed, lower yield and FE are obtained for Region 4 SACs as compared to Region 2 SACs, upon extracting data from previously reported experimental studies. Finally, in Region 5, we have the 16 most undesirable SACs, where the eNRR is disfavored and the HER is likely favored. For easy understanding, a flowchart is given in Fig. S20 of the ESI† to visualize the screening process and criteria of catalysts for the eNRR.

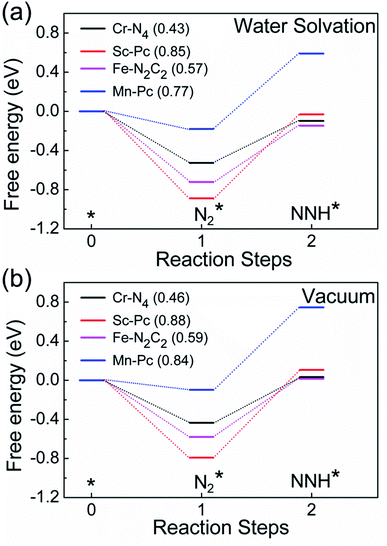
Finally, motivated by the fact that experiments are usually carried out in an aqueous environment, we have performed DFT calculations using an implicit solvation model, to understand the effect of the solvent water.^85,86 First, as a benchmark, we computed the solvation energy of a water molecule using this model, obtaining a result of 0.31 eV, which is close to the reported experimental value of 0.27 eV.⁸⁵ Next, we calculate the free energy profile of N₂ and NNH adsorption of Cr-N₄, Sc-Pc, Mn-Pc and Fe-N₂C₂ SACs using the implicit water solvation effect (Fig. 6a). The free energy profile of N₂ and NNH adsorption without solvation is shown in Fig. 6b. On comparing the two figures, we observe that there is only a very small change in the free energy steps due to the presence of the solvent. The presence of the solvent leads to essentially negligible changes in the overpotential values, for these four SACs. In Fig. S21 of the ESI,† we have plotted a full free energy profile for the eNRR, with and without the implicit solvent, for Cr-N₄ SAC. The changes in the free energy steps are very small in the whole free energy profile. Therefore, we can infer that the effect of solvent is not sufficient to change the reaction mechanism, as has also been reported in previous studies.^87–89

Fig. 6 Computed free energy profiles of N₂ and NNH adsorption on Cr-N₄, Sc-Pc, Fe-N₂C₂, and Mn-Pc in (a) the presence of an aqueous solvent and (b) vacuum. The corresponding values of overpotential are given in parentheses in the figure legends.

3 Conclusions

In summary, we have screened 66 different transition metal-based SACs for possible use in the eNRR. To determine the best possible catalyst, we have considered three factors: N₂ adsorption, hydrogen poisoning and the overpotential of the eNRR. Here, the valence electron occupancy (O_val) is identified as a new electronic descriptor that can predict the overpotential value. We emphasize that having a low η_NRR alone does not suffice to indicate a suitable eNRR catalyst, since if the adsorption free energy is higher for H than for N₂, active sites will be poisoned, hindering the eNRR. We present a simple graphical procedure for identifying the most promising catalysts. To carry out this procedure, one has to compute only ΔG_H* and ΔG_NNH*, the changes in the free energies of H and NNH adsorption, respectively (note that η_NRR can be deduced if ΔG_NNH* is known). The most promising candidate is identified as Sc-Pc, which we predict will have no H poisoning and will be highly selective for the eNRR over the HER. Moreover, we predict that Mn-Pc, Cr-N₄, and Fe-N₂C₂ should also be highly efficient, with low overpotential (η_NRR < 1 V) toward the eNRR and no H poisoning.

Data availability

All the data is provided in the supporting information file. Any specific data can be requested to corresponding author.

Author contributions

R. T. conceived and designed the work. S. K. has performed all the DFT based calculations. R. T. & S. N. analyzed the results. S. K. and R. T. wrote the first draft. All the authors took part in writing the manuscript and commented on the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

RT thanks the Science and Engineering Research Board (SERB), India, for financial support (Grant No. CRG/2021/000620) and National Supercomputer Mission (NSM), India for financial support (Ref No: DST/NSM/R&D_HPC_Applications/2021/19). SN acknowledges the Sheikh Saqr Laboratory of ICMS, JNCASR and TUE-CMS, JNCASR. The authors thank the High-Performance Computing Center, SRM Institute of Science and Technology for providing computational facilities.

References

1. V. Smil, Nature, 1999, 400, 415.
2. J. Nørskov, J. Chen, R. Miranda, T. Fitzsimmons and R. Stack, United States, 2016 DOI:10.2172/1283146.
3. C. J. M. van der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Chem. Soc. Rev., 2014, 43, 5183–5191.
4. Y. Yang, L. Zhang, Z. Hu, Y. Zheng, C. Tang, P. Chen, R. Wang, K. Qiu, J. Mao, T. Ling and S.-Z. Qiao, Angew. Chem., Int. Ed., 2020, 59, 4525–4531.
5. A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, ACS Catal., 2017, 7, 706–709.
6. C.-X. Huang, G. Li, L.-M. Yang and E. Ganz, ACS Appl. Mater. Interfaces, 2021, 13, 608–621.
7. W. Qiu, N. Yang, D. Luo, J. Wang, L. Zheng, Y. Zhu, E. M. Akinoglu, Q. Huang, L. Shui, R. Wang, G. Zhou, X. Wang and Z. Chen, Appl. Catal., B, 2021, 293, 120216.
8. C. Choi, S. Back, N.-Y. Kim, J. Lim, Y.-H. Kim and Y. Jung, ACS Catal., 2018, 8, 7517–7525.
9. B. H. R. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Nat. Catal., 2019, 2, 290–296.
10. H. Li, B. Yu, Z. Zhuang, W. Sun, B. Jia and T. Ma, J. Mater. Chem. A, 2021, 9, 4184–4192.
11. S. Wu, Y.-K. Peng, T.-Y. Chen, J. Mo, A. Large, I. McPherson, H.-L. Chou, I. Wilkinson, F. Venturini, D. Grinter, P. Ferrer Escorihuela, G. Held and S. C. E. Tsang, ACS Catal., 2020, 10, 5614–5622.
12. J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186.
13. S. B. Patil and D.-Y. Wang, Small, 2020, 16, 2002885.
14. Y. Qiu, X. Peng, F. Lü, Y. Mi, L. Zhuo, J. Ren, X. Liu and J. Luo, Chem.–Asian J., 2019, 14, 2770–2779.
15. Y. Zhai, Z. Zhu, C. Zhu, K. Chen, X. Zhang, J. Tang and J. Chen, Mater. Today, 2020, 38, 99–113.
16. X. Li, Q. Zhou, S. Wang, Y. Li, Y. Liu, Q. Gao and Q. Wu, J. Phys. Chem. C, 2021, 125, 11963–11974.
17. W. Zang, T. Yang, H. Zou, S. Xi, H. Zhang, X. Liu, Z. Kou, Y. Du, Y. P. Feng, L. Shen, L. Duan, J. Wang and S. J. Pennycook, ACS Catal., 2019, 9, 10166–10173.
18. B. Singh, V. Sharma, R. P. Gaikwad, P. Fornasiero, R. Zbořil and M. B. Gawande, Small, 2021, 17, 2006473.
19. G. Chen, H. Zhong and X. Feng, Chem. Sci., 2021, 12, 15802–15820.
20. X. Chen, W.-J. Ong, X. Zhao, P. Zhang and N. Li, J. Energy Chem., 2021, 58, 577–585.
21. S. Tang, Q. Dang, T. Liu, S. Zhang, Z. Zhou, X. Li, X. Wang, E. Sharman, Y. Luo and J. Jiang, J. Am. Chem. Soc., 2020, 142, 19308–19315.
22. Z. Chen, J. Zhao, C. R. Cabrera and Z. Chen, Small Methods, 2019, 3, 1800368.
23. Z. Wang, Z. Yu and J. Zhao, Phys. Chem. Chem. Phys., 2018, 20, 12835–12844.
24. H. Zou, W. Rong, S. Wei, Y. Ji and L. Duan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 29462–29468.
25. B. Huang, N. Li, W.-J. Ong and N. Zhou, J. Mater. Chem. A, 2019, 7, 27620–27631.
26. Q. Wu, R. Peng, B. Huang, L. Kou, Y. Dai and Y. Ma, J. Mater. Chem. A, 2020, 8, 26075–26084.
27. C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2019, 3, 1800376.
28. J. Xie, H. Dong, X. Cao and Y. Li, Mater. Chem. Phys., 2020, 243, 122622.
29. Q. Qu, S. Ji, Y. Chen, D. Wang and Y. Li, Chem. Sci., 2021, 12, 4201–4215.
30. C. Liu, Q. Li, C. Wu, J. Zhang, Y. Jin, D. R. MacFarlane and C. Sun, J. Am. Chem. Soc., 2019, 141, 2884–2888.
31. S. Agarwal, R. Kumar, R. Arya and A. K. Singh, J. Phys. Chem. C, 2021, 125, 12585–12593.
32. Y. Guo, G. Wang, S. Shen, G. Wei, G. Xia and J. Zhang, Appl. Surf. Sci., 2021, 550, 149283.
33. J. Wang, L. Yu, L. Hu, G. Chen, H. Xin and X. Feng, Nat. Commun., 2018, 9, 1795.
34. H. Tao, C. Choi, L.-X. Ding, Z. Jiang, Z. Han, M. Jia, Q. Fan, Y. Gao, H. Wang, A. W. Robertson, S. Hong, Y. Jung, S. Liu and Z. Sun, Chem, 2019, 5, 204–214.
35. X. Peng, H.-X. Liu, Y. Zhang, Z.-Q. Huang, L. Yang, Y. Jiang, X. Wang, L. Zheng, C. Chang, C. Au, L. Jiang and J. Li, Chem. Sci., 2021, 12, 7125–7137.
36. B. Huang, Y. Wu, B. Chen, Y. Qian, N. Zhou and N. Li, Chin. J. Catal., 2021, 42, 1160–1167.
37. M. Yao, Z. Shi, P. Zhang, W.-J. Ong, J. Jiang, W.-Y. Ching and N. Li, ACS Appl. Nano Mater., 2020, 3, 9870–9879.
38. X. Chen, X. Zhao, Z. Kong, W.-J. Ong and N. Li, J. Mater. Chem. A, 2018, 6, 21941–21948.
39. M. Wang, S. Liu, T. Qian, J. Liu, J. Zhou, H. Ji, J. Xiong, J. Zhong and C. Yan, Nat. Commun., 2019, 10, 341.
40. U. K. Ghorai, S. Paul, B. Ghorai, A. Adalder, S. Kapse, R. Thapa, A. Nagendra and A. Gain, ACS Nano, 2021, 15, 5230–5239.
41. P. Song, M. Luo, X. Liu, W. Xing, W. Xu, Z. Jiang and L. Gu, Adv. Funct. Mater., 2017, 27, 1700802.
42. F. Yang, P. Song, X. Liu, B. Mei, W. Xing, Z. Jiang, L. Gu and W. Xu, Angew. Chem., Int. Ed., 2018, 57, 12303–12307.
43. W. Song, K. Xie, Y. Guo, L. Fu and C. He, ChemPhysChem, 2021, 22, 1712–1721.
44. W. Zhao, L. Zhang, Q. Luo, Z. Hu, W. Zhang, S. Smith and J. Yang, ACS Catal., 2019, 9, 3419–3425.
45. J. Li, S. Zhao, L. Zhang, S. P. Jiang, S.-Z. Yang, S. Wang, H. Sun, B. Johannessen and S. Liu, Small, 2021, 17, 2004579.
46. J. Zhao and Z. Chen, J. Am. Chem. Soc., 2017, 139, 12480–12487.
47. Z.-Y. Wu, M. Karamad, X. Yong, Q. Huang, D. A. Cullen, P. Zhu, C. Xia, Q. Xiao, M. Shakouri, F.-Y. Chen, J. Y. T. Kim, Y. Xia, K. Heck, Y. Hu, M. S. Wong, Q. Li, I. Gates, S. Siahrostami and H. Wang, Nat. Commun., 2021, 12, 2870.
48. L. Han, X. Liu, J. Chen, R. Lin, H. Liu, F. Lü, S. Bak, Z. Liang, S. Zhao, E. Stavitski, J. Luo, R. R. Adzic and H. L. Xin, Angew. Chem., Int. Ed., 2019, 58, 2321–2325.
49. C. Ling, X. Bai, Y. Ouyang, A. Du and J. Wang, J. Phys. Chem. C, 2018, 122, 16842–16847.
50. C. Zhang, Z. Wang, J. Lei, L. Ma, B. I. Yakobson and J. M. Tour, Small, 2022, 18, 2106327.
51. S. Sarkar, A. Biswas, N. Kamboj and R. S. Dey, Inorg. Chem., 2020, 59, 13453–13464.
52. H. Yang, L. Shang, Q. Zhang, R. Shi, G. I. N. Waterhouse, L. Gu and T. Zhang, Nat. Commun., 2019, 10, 4585.
53. Y. Pan, Y. Chen, K. Wu, Z. Chen, S. Liu, X. Cao, W.-C. Cheong, T. Meng, J. Luo, L. Zheng, C. Liu, D. Wang, Q. Peng, J. Li and C. Chen, Nat. Commun., 2019, 10, 4290.
54. X. Wang, Z. Chen, X. Zhao, T. Yao, W. Chen, R. You, C. Zhao, G. Wu, J. Wang, W. Huang, J. Yang, X. Hong, S. Wei, Y. Wu and Y. Li, Angew. Chem., Int. Ed., 2018, 57, 1944–1948.
55. R. H. Platel, T. Teixeira Tasso, W. Zhou, T. Furuyama, N. Kobayashi and D. B. Leznoff, Chem. Commun., 2015, 51, 5986–5989.
56. L. Meng, K. Wang, Y. Han, Y. Yao, P. Gao, C. Huang, W. Zhang and F. Xu, Prog. Nat. Sci.: Mater. Int., 2017, 27, 329–332.
57. M. Mukherjee, M. Samanta, P. Banerjee, K. K. Chattopadhyay and G. P. Das, Electrochim. Acta, 2019, 296, 528–534.
58. X. Guo, J. Gu, X. Hu, S. Zhang, Z. Chen and S. Huang, Catal. Today, 2020, 350, 91–99.
59. X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721.
60. Z. Lu, G. Xu, C. He, T. Wang, L. Yang, Z. Yang and D. Ma, Carbon, 2015, 84, 500–508.
61. W. Qiu, X.-Y. Xie, J. Qiu, W.-H. Fang, R. Liang, X. Ren, X. Ji, G. Cui, A. M. Asiri, G. Cui, B. Tang and X. Sun, Nat. Commun., 2018, 9, 3485.
62. C. He, Z.-Y. Wu, L. Zhao, M. Ming, Y. Zhang, Y. Yi and J.-S. Hu, ACS Catal., 2019, 9, 7311–7317.
63. H. Li, S. Wei, H. Wang, Q. Cai and J. Zhao, J. Colloid Interface Sci., 2021, 588, 1–8.
64. Y.-X. Lin, S.-N. Zhang, Z.-H. Xue, J.-J. Zhang, H. Su, T.-J. Zhao, G.-Y. Zhai, X.-H. Li, M. Antonietti and J.-S. Chen, Nat. Commun., 2019, 10, 4380.
65. S. Murmu, S. Paul, S. Kapse, R. Thapa, S. Chattopadhyay, N. Abharana, S. N. Jha, D. Bhattacharyya and U. K. Ghorai, J. Mater. Chem. A, 2021, 9, 14477–14484.
66. F. Wang and J. Mao, Diamond Relat. Mater., 2021, 118, 108494.
67. B. Hammer and J. K. Nørskov, in Impact of Surface Science on Catalysis, Academic Press, 2000, vol. 45, pp. 71–129.
68. H. Niu, X. Wang, C. Shao, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2020, 8, 13749–13758.
69. M. Lokanathan, I. M. Patil, M. Navaneethan, V. Parey, R. Thapa and B. Kakade, Nano Energy, 2018, 43, 219–227.
70. C. Choi, S. Yoon and Y. Jung, Chem. Sci., 2021, 12, 3551–3557.
71. L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Phys. Rev. Lett., 2015, 114, 105503.
72. B. Huang, B. Chen, G. Zhu, J. Peng, P. Zhang, Y. Qian and N. Li, ChemPhysChem, 2022, 23, e202100785.
73. X. Liu, Y. Jiao, Y. Zheng, M. Jaroniec and S.-Z. Qiao, J. Am. Chem. Soc., 2019, 141, 9664–9672.
74. S. Kapse, S. Janwari, U. V. Waghmare and R. Thapa, Appl. Catal., B, 2021, 286, 119866.
75. J. Long, X. Fu and J. Xiao, J. Mater. Chem. A, 2020, 8, 17078–17088.
76. W. Nong, S. Qin, F. Huang, H. Liang, Z. Yang, C. Qi, Y. Li and C. Wang, Carbon, 2021, 182, 297–306.
77. T. Wang and F. Abild-Pedersen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2106527118.
78. S. Sinthika and R. Thapa, RSC Adv., 2015, 5, 93215–93225.
79. S. Sinthika, U. V. Waghmare and R. Thapa, Small, 2018, 14, 1703609.
80. E. S. Erakulan and R. Thapa, Appl. Surf. Sci., 2022, 574, 151613.
81. V. Fung, G. Hu, Z. Wu and D. Jiang, J. Phys. Chem. C, 2020, 124, 19571–19578.
82. G. Di Liberto, L. A. Cipriano and G. Pacchioni, ACS Catal., 2022, 12, 5846–5856.
83. B. Qin, Y. Li, Q. Zhang, G. Yang, H. Liang and F. Peng, Nano Energy, 2020, 68, 104374.
84. J. Mukherjee, S. Paul, A. Adalder, S. Kapse, R. Thapa, S. Mandal, B. Ghorai, S. Sarkar and U. K. Ghorai, Adv. Funct. Mater., 2022, 2200882.
85. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 84106.
86. M. Garcia-Ratés and N. López, J. Chem. Theory Comput., 2016, 12, 1331–1341.
87. Q. Zhang and A. Asthagiri, Catal. Today, 2019, 323, 35–43.
88. V. Sinha, D. Sun, E. J. Meijer, T. J. H. Vlugt and A. Bieberle-Hütter, Faraday Discuss., 2021, 229, 89–107.
89. Q. Yuan, Y. Li, P. Yu, B. Ma, L. Xu, Q. Sun, H. Yang, M. Xie and T. Cheng, J. Exp. Nanosci., 2021, 16, 255–264.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02625b

---