Open Access Article
Open Access ArticleActivating charge-transfer state formation in strongly-coupled dimers using DNA scaffolds†
Stephanie M.
Hart‡
 a,
James L.
Banal‡
a,
James L.
Banal‡
 b,
Maria A.
Castellanos‡
b,
Maria A.
Castellanos‡
 a,
Larysa
Markova
c,
Yuliia
Vyborna
a,
Larysa
Markova
c,
Yuliia
Vyborna
 c,
Jeffrey
Gorman
c,
Jeffrey
Gorman
 b,
Robert
Häner
b,
Robert
Häner
 c,
Adam P.
Willard
c,
Adam P.
Willard
 *a,
Mark
Bathe
*a,
Mark
Bathe
 *b and
Gabriela S.
Schlau-Cohen
*b and
Gabriela S.
Schlau-Cohen
 *a
*a
aDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: awillard@mit.edu; gssc@mit.edu
bDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: mark.bathe@mit.edu
cDepartment of Chemistry, Biochemistry and Pharmaceutical Sciences, University of Bern, Freiestrasse 3, CH-3012, Bern, Switzerland
First published on 6th October 2022
Abstract
Strongly-coupled multichromophoric assemblies orchestrate the absorption, transport, and conversion of photonic energy in natural and synthetic systems. Programming these functionalities involves the production of materials in which chromophore placement is precisely controlled. DNA nanomaterials have emerged as a programmable scaffold that introduces the control necessary to select desired excitonic properties. While the ability to control photophysical processes, such as energy transport, has been established, similar control over photochemical processes, such as interchromophore charge transfer, has not been demonstrated in DNA. In particular, charge transfer requires the presence of close-range interchromophoric interactions, which have a particularly steep distance dependence, but are required for eventual energy conversion. Here, we report a DNA-chromophore platform in which long-range excitonic couplings and short-range charge-transfer couplings can be tailored. Using combinatorial screening, we discovered chromophore geometries that enhance or suppress photochemistry. We combined spectroscopic and computational results to establish the presence of symmetry-breaking charge transfer in DNA-scaffolded squaraines, which had not been previously achieved in these chromophores. Our results demonstrate that the geometric control introduced through the DNA can access otherwise inaccessible processes and program the evolution of excitonic states of molecular chromophores, opening up opportunities for designer photoactive materials for light harvesting and computation.
1 Introduction
Molecular chromophores mediate the absorption and evolution of photonic energy for a wide range of phenomena including photovoltaics, chemical conversion, and communication.1–3 In photoactive materials, coupling between chromophores enables delocalized electronic excitations, i.e. excitons,4,5 and drives the transport of energy and charge carriers within nanoscale systems. Long-range excitonic coupling can be systematically varied in multiple synthetic systems.6–8 However, short-range effects, including charge-transfer coupling and electrostatic interactions, are non-negligible, particularly at distances approaching the π–π interaction distances for conjugated chromophores in both dimer and higher-order aggregate assemblies.9–13 The balance between long-range and short-range couplings has been examined in covalent chromophore dimers as a strategy to control singlet fission, and excimer and charge-transfer state formation.11,14–25 However, the geometries of these small molecules have been limited by synthetic constraints, which, in turn, limited the ability to select for desired functionality.9,10 Here, we introduce DNA as a scaffold for flexible and programmable dimer geometries. The DNA scaffold also affords easy integration of the coupled chromophores into higher-order assemblies for functional materials, which has not been possible with small-molecule systems.The fidelity of base pairing in DNA can be exploited for the design and production of highly specific nanoscale structures.26–29 Covalent incorporation of molecular chromophores into synthetic DNA sequences allows for the precise selection of the orientation, position, and number of chromophores upon assembly.26,30–34 DNA-based multichromophore systems have been used to control the excited state evolution, including energy transfer pathways and non-radiative decay timescales.35–40 Functional charge separation, a key target for photocatalysis and photovoltaic conversion, has also been achieved through hole transfer to the DNA itself.41–43 In previous work, the inherent coupling between the properties of the DNA bases and charge-carrier generation and direction limits full spatiotemporal control over charge transport throughout the DNA scaffold. Directed charge transport through incorporated chromophores has the potential to deliver charge carriers to desired sites for functional applications through decoupling of the DNA scaffold from the charge transfer process. However, charge transfer has not yet been demonstrated exclusively within the synthetic chromophores on DNA, limiting the ability to introduce controlled photochemistry into these programmable materials.
In this work, we report DNA scaffolded squaraines as a platform for controllable symmetry-breaking charge transfer. We incorporated zwitterionic squaraine chromophores into DNA strands and synthesized distinct geometries of strongly-coupled dimers that were screened using high-throughput spectroscopic approaches. Using a combined experimental and theoretical approach, we established that the DNA scaffold can affect the strength of long-range (excitonic) and short-range (charge-transfer and electrostatic) interactions, and the subsequent picosecond timescale charge-transfer process. Sequence dependence and corresponding simulations revealed significant electrostatic interaction energy between neighboring chromophores, on the order of the base pair hydrogen bond strength, which can be overcome through selection of the DNA scaffold. The level of control over coupling established here provides designer strategies towards combining light harvesting and charge separation machinery that can be integrated into higher-order functional assemblies.
2 Results
2.1 Construction and characterization of squaraine DNA constructs
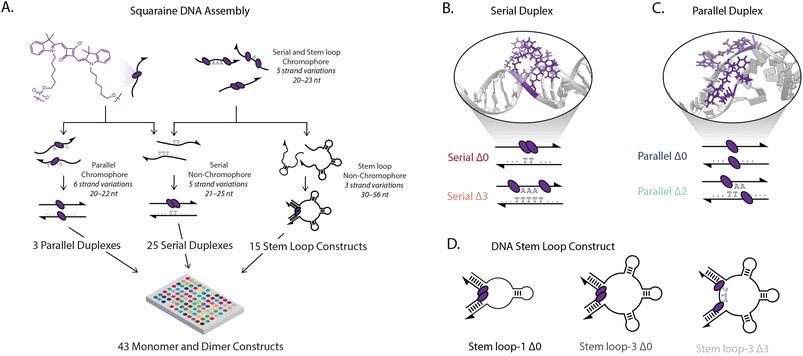
We controlled the spatial position and relative orientation of zwitterionic squaraine chromophores (Fig. 1A), known for their susceptibility to electron donating and accepting groups.44 We attached the chromophores onto a DNA scaffold using phosphoramidite chemistry, which tethers the indolenine squaraine molecule through the two hexyl linkers (Fig. 1A).45–47 The double tether confines both the position and relative orientation of the squaraine within the scaffold, contrasting the amine-reactive conjugation strategies used previously to introduce a single floppy tether.39,48,49 We observed a small hypsochromic shift in the steady-state absorbance and fluorescence spectra of the squaraine-DNA construct relative to the free squaraine dye in solution. The quantum yield of the squaraine monomer on DNA in 1× phosphate-buffered saline (PBS) was 0.25 and was retained relative to the free-dye squaraine in ethanol, which is 0.26 (ESI Fig. S32†).Strongly-coupled molecular assemblies of squaraine dimers, subject to both long-range and short-range interactions, were built in various geometries and scaffolds to introduce a range of excitonic properties. To investigate the large configurational space of dimer organizations, we synthesized and characterized the DNA constructs using high-throughput spectroscopic methods. Single-stranded DNA (ssDNA) was synthesized (ESI Table 1†) and hybridized with complementary strands in three strategies, as shown in Fig. 1A (ESI Table 2†). In the first strategy, two squaraines were incorporated into ssDNA with 0 to 3 bases inserted between the chromophores (chromophore serial Δ0–Δ3 ssDNA) and hybridized with their non-chromophore containing complementary pairs (complementary serial Δ0–Δ3 ssDNA) to form serial Δ0–Δ3 duplexes. In the second strategy, chromophore-containing serial strands (chromophore serial Δ0–Δ3 ssDNA) were hybridized with complementary strands that contained one to three 10-base stem-loops (complementary stem loop-1 through stem loop-3 ssDNA). This enabled formation of stem loop constructs according to the number of stem loops (e.g., 3) and the number of bases separating the squaraine dimers (e.g., Δ0), such as the stem loop-3 Δ0 construct shown in the center of Fig. 1D. In total, the five chromophore-containing strands (monomer and Δ0–Δ3 dimers) hybridized with the eight complementary strands allowed for the generation of 40 distinct architectures. For the third strategy one squaraine was incorporated into ssDNA (chromophore parallel Δ0–Δ2 ssDNA A) and hybridized with a second squaraine-containing strand (chromophore parallel Δ0–Δ2 ssDNA B) generating parallel duplexes with a zero to two nucleotide offset between the chromophores (parallel Δ0–Δ2 duplexes), giving rise to three additional constructs. For the varying duplexes and stem-loop constructs examined, the same local sequences were used for both monomers and dimers to ensure that the resulting photophysics originated from interchromophore coupling, and not from interactions with the DNA scaffold.
The absorption spectra of all constructs exhibited a 0–0 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) and a 0–1 (17
300 cm−1) and a 0–1 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) vibronic band, also present in the monomer spectrum (Fig. 2A). A redistribution in oscillator strength from the 0–0 to the 0–1 vibronic band and a hypsochromic shift in the transition energy relative to the monomer are characteristic signatures for strongly coupled dimers stacked cofacially, which is known as an H-type aggregate.7 In particular, the redistribution in oscillator strength, quantified as the 0–0 to 0–1 band ratio, provides a relative measure for electronic coupling and was calculated for all dimeric constructs (Fig. 1B–D). While a range of band ratios was observed, most dimers exhibited values of ∼0.3–0.7, consistent with strong coupling. In strongly-coupled assemblies, changes in emissive properties reflect the presence of distinct photophysical pathways that emerge from interchromophore interactions. To evaluate these interactions, the quantum yield was measured for all samples, and exhibited trends similar to the vibronic band ratio. The redistribution of oscillator strength observed in the strongly-coupled configurations reported here is 1.8-fold greater than that previously reported for squaraine dimers scaffolded by a Holliday junction.39,48,50 This observation indicates significantly stronger coupling was achieved, and highlights the sensitivity of these coupled chromophores to their local scaffold configuration.
000 cm−1) vibronic band, also present in the monomer spectrum (Fig. 2A). A redistribution in oscillator strength from the 0–0 to the 0–1 vibronic band and a hypsochromic shift in the transition energy relative to the monomer are characteristic signatures for strongly coupled dimers stacked cofacially, which is known as an H-type aggregate.7 In particular, the redistribution in oscillator strength, quantified as the 0–0 to 0–1 band ratio, provides a relative measure for electronic coupling and was calculated for all dimeric constructs (Fig. 1B–D). While a range of band ratios was observed, most dimers exhibited values of ∼0.3–0.7, consistent with strong coupling. In strongly-coupled assemblies, changes in emissive properties reflect the presence of distinct photophysical pathways that emerge from interchromophore interactions. To evaluate these interactions, the quantum yield was measured for all samples, and exhibited trends similar to the vibronic band ratio. The redistribution of oscillator strength observed in the strongly-coupled configurations reported here is 1.8-fold greater than that previously reported for squaraine dimers scaffolded by a Holliday junction.39,48,50 This observation indicates significantly stronger coupling was achieved, and highlights the sensitivity of these coupled chromophores to their local scaffold configuration.
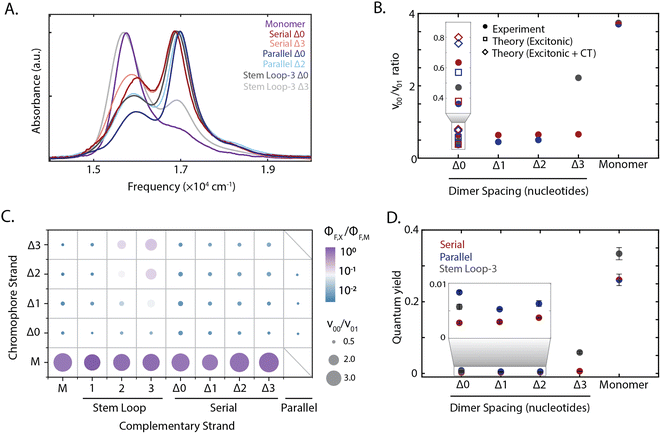 | ||
| Fig. 2 Tuning squaraine dimer photophysics. (A) Absorption spectra of squaraine monomers and dimer duplexes and stem loop constructs shown in Fig. 1. (B) Extraction of vibronic peak ratio between the 0–0 and 0–1 bands (ν00/ν01) shown as a function of DNA construct on the x-axis. Serial and parallel duplexes and stem loop-3 constructs are shown in maroon, blue, and gray, respectively. (C) High throughput characterization of squaraine monomer and dimer modified DNA scaffolds. Y-axis corresponds to chromophore containing strand and x-axis corresponds to complementary strand (non-chromophore containing strand for serial and stem loop, chromophore containing for parallel). Hybridized duplexes and stem loop constructs were screened through measurement of the quantum yield relative to the monomer (color) and absorption spectrum derived vibronic band ratio (circle size). (D) Quantum yield for DNA scaffolded monomers and dimers within serial and parallel duplexes and stem loop-3 constructs. | ||
To disentangle the nature of the intradimer interactions, three of the strongly coupled dimers were compared in more detail: the stem loop-3 Δ0 construct, the chromophore serial Δ0 strand hybridized with the complementary stem loop-3 strand; serial Δ0 duplex, the chromophore serial Δ0 strand hybridized with the complementary serial Δ0 strand; and parallel Δ0 duplex, comprised of two complementary strands each containing a single squaraine. Of the hybridized structures, the redistribution of oscillator strength and spectral shift was the largest for the parallel dimers and smallest for the serial dimers, suggesting that the coupling was the strongest and weakest, respectively. The difference in response among these three dimers demonstrates the variety of interactions that can be accessed within the strong-coupling limit. The fluorescence was almost completely quenched with a near-zero quantum yield (0.003–0.008) for all three strongly coupled dimers. While H-aggregates are expected to have moderately reduced quantum yields,6,7,10 the measured quantum yields were nearly two orders-of-magnitude lower than the monomer. Furthermore, the excitation spectra of the dsDNA squaraine dimers were similar to the dsDNA monomer absorption, indicating that the remaining emission originated from the monomer subpopulation (ESI Fig. S34†). Both of these observations indicate a deviation from the radiative yield of typical H-aggregates,10 in contrast to previous work on DNA-scaffolded cyanine chromophores.37 The unexpectedly strong quenching suggests additional photophysics occurring within squaraines, such as the formation of an optically dark state, e.g., a charge-transfer state, or the activation of an additional non-radiative pathway.
2.2 Balance between intradimer charge-transfer and excitonic coupling
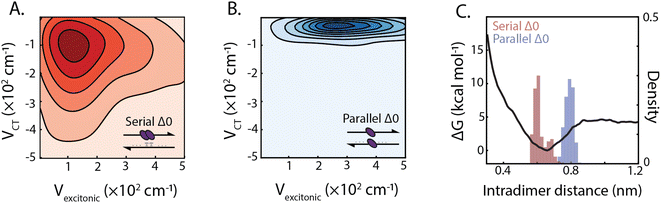
The design of the serial and parallel Δ0 duplexes—with the chromophores localized on the same or opposing strands, respectively—allows for the study of the interplay between excitonic and charge-transfer interactions present across distinct package geometries. We characterized these interactions in greater detail by employing molecular dynamics (MD) and quantum chemical calculations. All-atom models of both DNA-squaraine structures in explicit solvent were constructed and simulated using classical MD (ESI Section S5 and Fig. S18†). Snapshots of the simulated trajectories can be seen in Fig. 1B and C for the serial and parallel Δ0 duplexes, respectively. Quantum chemical calculations were performed on isolated squaraine dimer configurations extracted from the MD simulations. These calculations were analyzed to quantify the long-range excitonic coupling and short-range charge-transfer coupling (shown in Fig. 3A and B). The excitonic coupling was determined by explicitly calculating two-electron integrals between monomer transition dipoles obtained using time-dependent density functional theory (TDDFT) with the Tamn–Dancoff approximation (eqn (1)). Charge-transfer coupling was calculated from electron and hole transfer integrals via DFT calculations13 (eqn (2)).The simulation results yielded average long-range excitonic couplings, Vexcitonic = 207 and 319 cm−1, and short-range charge-transfer couplings, VCT = −199 and −45 cm−1, for the serial and parallel Δ0 duplexes, respectively. The larger excitonic coupling for the parallel dimer compared to the serial dimer is consistent with their relative 0–0/0–1 vibronic band ratios (Fig. 2). Owing to the sub-50 cm−1 charge-transfer coupling in comparison to the excitonic coupling, the parallel Δ0 dimer excitonic coupling can be adequately described using Kasha's theory, which treats excitonic interactions only. In contrast, a description for the serial Δ0 dimer must include both excitonic and charge-transfer contributions.10 The observed charge-transfer coupling could explain why the 0–0/0–1 band ratio of the serial dimer is closer to that of the monomer (Fig. 2B). Based on the relative phase of the molecular orbitals for each monomer, we determined the charge-transfer coupling was negative, while the excitonic coupling is positive as expected for an H-type dimer. The opposite signs of the excitonic and charge-transfer couplings result in destructive interference between the two contributions, similar to previously examined null aggregates.11,22
Serial and parallel duplex dimers exhibited significantly different charge-transfer couplings. One possible explanation for this difference is the apparent π-stacked structure that forms more frequently on the serial dimer. While the intramolecular distance for the parallel dimer is only slightly longer than that for the serial (Fig. 3C and ESI Fig. S19†), we observed the monomers in this configuration were twisted relative to each other, resulting in weaker orbital overlap. Horizontal displacement on serial π-stacked aggregates was, on the other hand, observed to decrease the long-range interaction while maintaining strong orbital overlap. The parallel configuration resulted in an orientation with less probability of dark state formation, while also generating stronger excitonic coupling. Thus the parallel configuration selects for more excitonic and less charge-transfer character, whereas the serial configuration has near-equal couplings for both processes.
2.3 Intradimer attraction
In addition to the short-range charge-transfer coupling, closely spaced chromophores are subject to attractive molecular forces. In particular, the electron polarizability of zwitterionic chromophores contributes to their propensity for charge separation yet can lead to intermolecular electrostatic interactions. To estimate the effective strength of interchromophore forces, we performed umbrella sampling calculations on the isolated dimer in liquid water (Fig. 3C). We compared these interaction energies with the DNA hydrogen bonding free energy, which is typically more dominant than base π-stacking energy.51 The potential energy surface for the dimer revealed an intermolecular interaction energy of ΔG = −4.6 kcal mol−1 which is lower than the guanine-cytosine hydrogen bond strength (ΔG = −5.5 kcal mol−1) and slightly higher than the adenine–thymine hydrogen bond strength (ΔG = −4.3 kcal mol−1) under similar conditions.52,53 This suggests that the free-energy of intradimer interactions is sufficient to potentially disrupt the stability of canonical base–pair interactions of DNA. While the energetics of the DNA duplex interactions involve contributions beyond simple base-pairing hydrogen bond strengths, this analysis points to the critical role intradimer forces play driving the spatial configuration of strongly-coupled dimers. These results, in conjunction with analysis of the charge-transfer coupling effects, point to the complex interplay between long and short-range intradimer interaction in the strong coupling limit.2.4 Dependence of dimer interactions on DNA architectures
To disentangle this complex interplay, we examined additional configurations from the high-throughput synthesis in which nucleotide separations were inserted between the chromophores, which is expected to introduce geometric changes that alter the magnitude of both short-range and long-range couplings.37 The stem loop-3 Δ3 construct (with three 10-base stem-loops) was identified as having the weakest coupling among the configurations generated. The stem loop-3 Δ3 construct exhibited a recovery of the 0–0 oscillator strength towards a monomer-like species and a 18-fold enhancement in quantum yield relative to the stem loop-3 Δ0 construct. The 0–0/0–1 ratio and quantum yields of the stem loop-3 Δ3 construct were still below those of the stem loop-3 monomer construct (Fig. 2C and D and ESI Tables S2, S9 and S10†), suggesting that residual coupling persisted. In contrast to the stem loop-3 motif, significantly smaller changes in spectral features were observed for the duplex configurations. To examine the changes in coupling, we plotted the 0–0/0–1 band ratio upon insertion of nucleotide spacers (Fig. 2B). In the serial duplex dimers, the progression from Δ0 to Δ3 resulted in a 0–0/0–1 band ratio increase of only 4%, whereas, in the parallel duplex dimers, the progression from Δ0 to Δ2 led to a 38% increase. The quantum yield for all duplex scaffolded dimers was less than 0.01, suggesting significant dark state character across all constructs (Fig. 2D).The stem loop-3 Δ3 construct differed from the serial Δ3 duplex in complementary strand only, yet showed a significantly higher 0–0/0–1 band ratio and quantum yield. Simple structural models of DNA predict increased intradimer distances, and thus weaker coupling, upon nucleotide insertion. For the serial dimers, the similar vibronic band ratios suggest similar coupling strengths for all constructs, inconsistent with model predictions. These results point to a distinct structural organization, such as the intervening bases separating from the canonical duplex, for example, by looping out from the backbone. The similar spectra also contrast with duplex-scaffolded cationic cyanine chromophores, where a progression from 0 to 3 base separation led to a 133% enhancement of the 0–1/0–1 band ratio and recovery of the monomer spectrum.37 The minimal changes observed for the squaraine dimer duplexes is likely due to the presence of electrostatic attractions between the zwitterionic squaraines that were overcome by mechanical force imposed by the stem loop-3 construct. Similarly, in previous work the DNA scaffold exerted mechanical force to tune the interactions, and thereby photophysics, of incorporated chromophores.38 Therefore, the intradimer attractions can play an important role in controlling the dimer configuration.
2.5 Observation of symmetry-breaking charge transfer
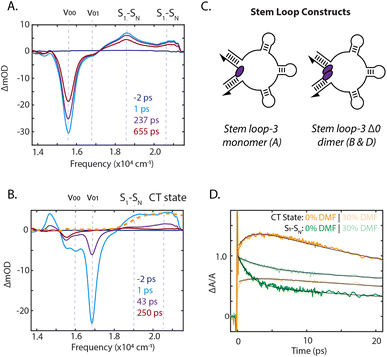
To identify the photoinduced excited-state pathways that emerge in the coupled chromophores, we performed femtosecond time-resolved transient absorption spectroscopy on the DNA-scaffolded squaraine assemblies. The evolution of the transient spectra was quantified by fitting the kinetics at the peak maxima. Transient absorption spectra of the stem loop-3 monomer construct are shown in Fig. 4A and ESI Section 7.2.† A significant ground state bleach (GSB) feature dominated the spectra at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 cm−1, the 0–0 energy in the absorption spectrum, with two excited-state absorption (ESA) features at 18
570 cm−1, the 0–0 energy in the absorption spectrum, with two excited-state absorption (ESA) features at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 and 20
600 cm−1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, likely corresponding to a manifold of S1 to SN transitions. All features decayed on a timescale similar to the fluorescence lifetime (ESI Section 3†), and thus are ascribed to the S1 state.
500 cm−1, likely corresponding to a manifold of S1 to SN transitions. All features decayed on a timescale similar to the fluorescence lifetime (ESI Section 3†), and thus are ascribed to the S1 state.
Significant differences in the spectra and dynamics were observed for the stem loop-3 Δ0 construct, where strong coupling is present. The transient spectra were also dominated by GSB features, but at 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 16
000 cm−1 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1, which match the transition energies of the absorption spectrum for this sample (Fig. 4B). The lower energy 0–0 band exhibited a biexponential decay with timescales of 12 ps and 1.1 ns, likely corresponding to photoisomerization and decay of a weakly coupled sub-population. The higher energy 0–1 band decayed largely monoexponentially on a 35 ps timescale. The 19
800 cm−1, which match the transition energies of the absorption spectrum for this sample (Fig. 4B). The lower energy 0–0 band exhibited a biexponential decay with timescales of 12 ps and 1.1 ns, likely corresponding to photoisomerization and decay of a weakly coupled sub-population. The higher energy 0–1 band decayed largely monoexponentially on a 35 ps timescale. The 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 ESA, corresponding to the S1 to SN transitions, decayed on multiple timescales, including a 1.8 ps component and components similar to the GSB decay (ESI Section 7.3†).
000 cm−1 ESA, corresponding to the S1 to SN transitions, decayed on multiple timescales, including a 1.8 ps component and components similar to the GSB decay (ESI Section 7.3†).
The higher energy ESA band at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 grew in on a 2.2 ps timescale, similar to the fast component of the lower energy ESA decay and then decayed biexponentially on picosecond timescales with the GSB decay. The electrochemically generated cation and anion absorbs between 20
500 cm−1 grew in on a 2.2 ps timescale, similar to the fast component of the lower energy ESA decay and then decayed biexponentially on picosecond timescales with the GSB decay. The electrochemically generated cation and anion absorbs between 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 22
000 cm−1 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.54 The higher energy ESA band in this spectral region was therefore assigned to direct observation of symmetry-breaking charge transfer. This was further confirmed through oxidation of the squaraine dye, generating cation signatures shown in Fig. 4B. The concomitant rise of this band and decay of the S1 to SN ESA indicated charge transfer occurs from the S1 state. No similar signatures were observed in the monomer spectra, indicating a bimolecular process. The presence of charge transfer suggested that the rapid decay of the 0–1 GSB band is likely due to recombination, consistent with the dark state character identified through the quantum yield of the dimers. In previous work on more weakly-coupled DNA-scaffolded squaraine dimers, an optically-dark excited state was also observed, but with no cationic features.39,55 While charge-transfer interactions in self-assembled squaraine films were suggested to play a role in intermolecular coupling,56,57 here, we report the first direct observation of photoinduced charge-transfer signatures in squaraine dimer assemblies.
000 cm−1.54 The higher energy ESA band in this spectral region was therefore assigned to direct observation of symmetry-breaking charge transfer. This was further confirmed through oxidation of the squaraine dye, generating cation signatures shown in Fig. 4B. The concomitant rise of this band and decay of the S1 to SN ESA indicated charge transfer occurs from the S1 state. No similar signatures were observed in the monomer spectra, indicating a bimolecular process. The presence of charge transfer suggested that the rapid decay of the 0–1 GSB band is likely due to recombination, consistent with the dark state character identified through the quantum yield of the dimers. In previous work on more weakly-coupled DNA-scaffolded squaraine dimers, an optically-dark excited state was also observed, but with no cationic features.39,55 While charge-transfer interactions in self-assembled squaraine films were suggested to play a role in intermolecular coupling,56,57 here, we report the first direct observation of photoinduced charge-transfer signatures in squaraine dimer assemblies.
Reducing the solvent polarity generally increases the energy of the charge-transfer state with respect to neutral decay pathways, thus disfavoring symmetry-breaking charge transfer. The presence of charge transfer was further established by comparing the photophysical properties of the stem loop-3 scaffolded monomer and Δ0 dimer in a 1× PBS solution with those in 30% dimethylformamide (DMF). The stem loop-3 monomer construct absorption bathochromically shifted by 50 cm−1 in DMF, but the vibronic 0–0/0–1 band ratio and excited-state lifetime did not change (ESI Fig. S24 and S36, Table S10†), suggesting the monomer photophysics were not affected by DMF. For the stem loop-3 Δ0 construct, the addition of DMF led to an increase in 0–0/0–1 band ratio, indicating a decrease in the magnitude of electronic coupling. The cation peak also exhibited minimal growth and, correspondingly, a 1.6-fold slower S1 to SN ESA decay was observed (Fig. 4D). The decrease in charge-transfer state formation typically results from reduced charge-transfer coupling owing to the solvent polarity. However, the decreased electronic coupling could also give rise to the observed effects. Increased intersystem crossing or photoisomerization could decrease the level of cation formation, but these two pathways were experimentally excluded (ESI Section 8†).
2.6 Steering charge-transfer formation using DNA scaffolds
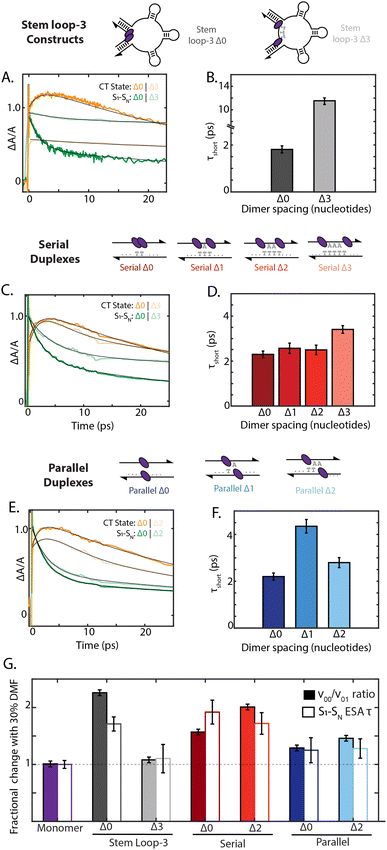
To examine how chromophore configuration dictates symmetry-breaking charge transfer, we compared the dynamics of all nine dimer geometries shown in Fig. 5. Due to overlapping S1 to SN and cation ESA features at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1, the charge-transfer timescale is best compared through the short timescale component of the decay of the 19
500 cm−1, the charge-transfer timescale is best compared through the short timescale component of the decay of the 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 ESA band (Fig. 5). Whereas the stem loop-3 Δ0 construct exhibited rapid charge-transfer on the 2 ps timescale, the stem loop-3 Δ3 construct exhibited a charge-transfer timescale of only 12 ps (Fig. 5A and B). Minimal growth of the cation peak was also observed. Commensurate with these ultrafast results, the quantum yield of the stem loop-3 Δ3 construct is 18-fold higher than the stem loop-3 Δ0 construct. These spectroscopic signatures indicate limited charge-transfer character in the stem loop-3 Δ3 constructs, likely due to the ability of the three stem loop motifs to introduce physical separation between the chromophores. These differences between the stem loop-3 Δ0 and stem loop-3 Δ3 constructs establish the ability of DNA scaffolds to suppress charge-transfer coupling and its effects while retaining a network of excitonically coupled chromophores.
000 cm−1 ESA band (Fig. 5). Whereas the stem loop-3 Δ0 construct exhibited rapid charge-transfer on the 2 ps timescale, the stem loop-3 Δ3 construct exhibited a charge-transfer timescale of only 12 ps (Fig. 5A and B). Minimal growth of the cation peak was also observed. Commensurate with these ultrafast results, the quantum yield of the stem loop-3 Δ3 construct is 18-fold higher than the stem loop-3 Δ0 construct. These spectroscopic signatures indicate limited charge-transfer character in the stem loop-3 Δ3 constructs, likely due to the ability of the three stem loop motifs to introduce physical separation between the chromophores. These differences between the stem loop-3 Δ0 and stem loop-3 Δ3 constructs establish the ability of DNA scaffolds to suppress charge-transfer coupling and its effects while retaining a network of excitonically coupled chromophores.
In contrast to the stem loop-3 constructs, the serial and parallel duplexes exhibited minimal changes in charge-transfer state formation according to DNA sequence. Despite variations in calculated charge-transfer coupling, both the serial and parallel Δ0 duplexes exhibited charge-transfer timescale of ∼2 ps. Their similar timescales suggest their rates may be dominated by additional parameters affecting charge transfer, including reorganization energy and the timescale of fluctuations in the coupling (Fig. 5C and E). The duplex motifs showed minimal scaling with increased nucleotide separation for charge-transfer state formation, consistent with the trends in the absorption spectra. Given the typical exponential distance scaling of 0.2–0.3 nm for intermolecular charge transfer, one would expect the charge-transfer timescale to increase by over an order of magnitude across the series from Δ0 to Δ3 configurations.58,59 However, the charge-transfer timescale only minimally increased from 2.2 ps to 3.4 ps from the Δ0 to Δ3 serial duplexes and exhibited non-monotonic scaling in the 2–4 ps range for the Δ0 to Δ2 parallel duplexes (ESI Section 7.4†). These minimal changes and anomalous scaling of the duplex motifs are indicative of the intra-dimer electrostatic attraction that is overcome in the case of the stem loop-3 construct, consistent with the large interaction energy calculated in Fig. 3C.
Finally, we examined how the local solvent environment influences the charge transfer properties of the dimer and the sensitivity of this effect to geometry. We quantified the solvent dependence of the coupling and charge-transfer state formation by extracting the vibronic band ratio and charge transfer timescale (Fig. 5G and ESI Tables S11 and S12†). In all cases, these two trends were consistent, and so we focus our discussion on the charge-transfer timescale. While the stem loop-3 Δ0 construct showed ∼1.6-fold slower charge transfer upon the addition of 30% DMF, the stem loop-3 Δ3 construct did not show a significant decrease. Likely, the Δ3 configuration overcomes the hydrophobic π stacking of the squaraines present in the Δ0 configuration, and thus exhibits minimal changes according to solvent polarity. The serial Δ0 duplex exhibited 1.8-fold slower charge-transfer state formation in DMF, whereas the parallel Δ0 duplex exhibited only a ∼25% slower charge-transfer timescale. Much like the steady state optical properties and charge-transfer timescales, the solvent-dependent behavior scales minimally with nucleotide separation distance for both types of dimers. The differences between the serial and parallel duplex constructs further highlight the ability of the scaffold to tune local interactions and in turn mediate exciton dynamics in strongly-coupled assemblies.
3 Discussion
Strongly-coupled chromophores can be subject to effects beyond a Kasha-type picture of excitonic coupling, particularly through short-range interactions. Similar to excitonic coupling, charge-transfer coupling is sensitive to the spatial relationships of chromophores within an aggregate but with a steeper distance dependence owing to its reliance on molecular orbital overlap.9,10 Charge-transfer coupling is often implicated in photoinduced charge carrier generation, thus suggesting control over short-range interactions is necessary for functional photochemical conversion.11,60 While squaraines have long been a promising candidate for photoinduced charge carrier generation due to their zwitterionic nature, previous studies were only able to identify charge-transfer character rather than charge separation for carrier generation. Here, we used the nanoscale positioning of chromophores uniquely accessible via DNA scaffolds to demonstrate symmetry-breaking charge transfer in squaraine dimers, which was not accessible for covalently bound dimers (Fig. 4B and D).25,61,62DNA-based materials offer the nanoscale structural precision required to tune short-range interactions. Using this tunability, we designed and screened 35 dimer geometries (Fig. 2C) in a high-throughput manner. Through this study, configurations of dimers with maximal and minimal charge transfer character were identified. Therefore, the functionality for charge transfer can easily be tuned exclusively through changes to the non-chromophore containing elements of the DNA scaffold. For example, the serial Δ3 duplex and stem loop-3 Δ3 construct exhibited 3.4 ps and 12 ps timescales of charge separation, respectively, yet differed only in the complementary strand, thereby establishing the role of DNA hybridization structure in controlling photoproduct formation. Furthermore, these complementary strands can easily be exchanged on a ∼seconds timescale to switch between photochemical modalities. Emulating ideas from an optical transistor, this also builds a framework for use as a molecular switch for photoinduced charge carriers. While DNA-scaffolded cyanines have been developed and optimized for energy transfer,35,37,55,63,64 this work establishes that the DNA scaffold can also incorporate photoactive elements for charge separation, thus laying the groundwork for dual light harvesting and charge separation nanoscale machinery similar to photosynthetic proteins.
Remarkably, symmetry-breaking charge transfer was observed on similar timescales for the serial and parallel dimers (Fig. 5D and F), despite charge-transfer coupling that varied by 4-fold (Fig. 3A and B). The high polarizability of the zwitterionic squaraine chromophores leads to a propensity for charge separation, yet, in this close packed geometry, also induces electrostatic attractions between the chromophores. Indeed, the large ∼5 kcal mol−1 interaction energy (Fig. 3C) overcomes traditional base–pair interactions for many scaffold architectures. Thus, the electrostatics involving the chromophores themselves are an important design consideration in generating construct geometries for charge separation and transport. Despite the complex mixture of excitonic coupling, charge-transfer coupling, and electrostatic attraction in the dimers, the flexibility and programmability of the DNA scaffold allowed for the synthesis of optically active materials with desired excitonic properties.
4 Conclusion
We demonstrated the use of DNA scaffolds as a strategy to control the photochemistry of strongly-coupled squaraine chromophores. In this study, the spatial organization imposed by varying DNA motifs examined in a high-throughput manner provided a synthetic knob to control the interplay between excitonic coupling, charge-transfer coupling, and electrostatic attractions in squaraine dimers. Computational results established the presence of a complex mixture of intradimer interactions, while femtosecond transient absorption spectroscopy revealed signatures of symmetry-breaking charge transfer, which had not been previously observed in squaraines. The ability to control photochemistry using DNA scaffolds enables their attachment in higher-order nanostructures formed by DNA origami.65,66 The combination of chemical modification and structural control easily implemented on DNA provides a diverse molecular toolbox for the fabrication of higher-order circuits with desired excitonic properties. We anticipate that the advances we have shown here will provide new opportunities to discretely program the electronic structure of individual aggregates, paving the way for the application of DNA-scaffolded materials in devices.5 Methods
5.1 Synthesis of squaraine-modified DNA strands
The oligonucleotides were prepared via automated oligonucleotide synthesis on an Applied Biosystems 394-DNA/RNA synthesizer. UltraMild phosphoramidites and supports from Glen Research were used for the synthesis. Squaraine phosphoramidites and similar DNA sequences with flanking A and C deoxynucleotides were used as previously described, ensuring that nucleotide identity did not modulate the resulting photophysics.45 Cleavage from the solid support and final deprotection were done by treatment with tert-butylamine:methanol:water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by volume) at 55 °C overnight. All squaraine-modified oligonucleotides were purified by ion-pair reversed-phase high-performance liquid chromatography: Column: Supelco apHera™ column C4 polymer, 250 mm × 4.6 mm, 5 μm particle size; aqueous mobile phase: 0.1 M triethylammonium acetate (pH 7.1); organic mobile phase: acetonitrile; temperature: elution at 40 °C; method: linear gradient 0–100% acetonitrile over 20 minutes.
2 by volume) at 55 °C overnight. All squaraine-modified oligonucleotides were purified by ion-pair reversed-phase high-performance liquid chromatography: Column: Supelco apHera™ column C4 polymer, 250 mm × 4.6 mm, 5 μm particle size; aqueous mobile phase: 0.1 M triethylammonium acetate (pH 7.1); organic mobile phase: acetonitrile; temperature: elution at 40 °C; method: linear gradient 0–100% acetonitrile over 20 minutes.
Canonical ssDNA sequences were purchased from Integrated DNA Technologies (Coralville, IA) as desalted and received as dried pellets. The concentrations of all strands were normalized to 500 μM using 100 mM phosphate buffer (pH 7.4) and stored at −20 °C until further use.
5.2 Quantum yield measurements
Quantum yield (ΦF) measurements were performed using cresyl violet perchlorate (Millipore Sigma, catalog number: 255246) in HPLC-grade ethanol as standard (ΦF = 58% determined using the integrating sphere method). Samples and cresyl violet standards were excited at λexc = 590 nm and the resulting fluorescence was collected at λems = 600–800 nm. Concentrations of samples were kept at 0.5 μM in 1× PBS.5.3 Theoretical model
The squaraine dimers were modeled with a Frenkel–Holstein type model, which includes an electronic Hamiltonian and coupling to a phonon bath. Here the coupling between chromophores is captured by the sum of excitonic (long-range) and charge-transfer (short-range) terms. Further details are given in Section 3 of the ESI.† Briefly, using time-dependent density functional theory (TDDFT) with the Tamn–Dancoff approximation, the excitonic coupling can be described through two-electron transfer integrals,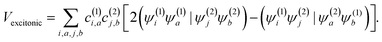 | (1) |
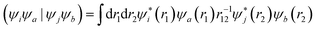 , while (ΨiΨj|ΨaΨb) is an exchange integral.
, while (ΨiΨj|ΨaΨb) is an exchange integral.
The charge-transfer coupling was calculated through the electron and hole integrals, te and th,
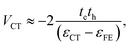 | (2) |
| εCT = εunbCT − UCT. | (3) |
U = ε unb CT − ε FE corresponds to the binding energy of the local excitation and was taken to be constant at 0.7 eV.13 The total coupling is then given as the sum of excitonic and charge-transfer terms,
| Vtotal = Vexcitonic + VCT. | (4) |
5.4 Molecular dynamics simulations
A force field for the squaraine molecule and hexyl linkers was generated through optimization with the restricted Hartree-Fock method and 6-31G(d) basis set, as included in the Q-chem software.67 Simulations of the DNA-scaffolded dimer constructs were prepared using the PyMol software68 from the DNA duplex and squaraine optimized structures. The B-form DNA duplex was modeled with the nucleic acid builder (NAB) from AmberTools.69 All-atom molecular dynamics (MD) simulations were performed on the DNA-squaraine constructs using the software Amber18 (ref. 69) with the GAFF2 force field. The structures were solvated in TIP3P water molecules, and a distance of 12 Å with respect to the solvent box. Explicit Na+ ions were added to neutralize the DNA, and Cl− ions were added to set a concentration of 100 mM NaCl, according to experimental conditions. Periodic boundary conditions were applied on all MD simulations, and the SHAKE algorithm was used to constrain the H atoms to their equilibrium bond length. A 12 Å cutoff was used to calculate the van der Waals energies, while the Particle Mesh Ewald (PME) method was employed to calculate full electrostatics. The simulations were carried out in a NPT ensemble using the Langevin thermostat for temperature control with a collision frequency of 5 ps−1, and the Berendsen barostat for pressure control, with a reference pressure of 1 bar.Minimization of the constrained system was carried before the production simulation for 5000 steps. Then, the constrained system was slowly heated to 300 K for a total time of 20 ps and time-step 2 fs, and then left to equilibrate at constant temperature for 2 ns. The production dynamics were then generated at 300 K for a total time of 5 ns with 2 fs time step, which is within the timescale where CT effects were detected in the experiment. The serial dimer simulations were done on duplicate, while the parallel dimer coordinates were averaged over 3 trajectories for 5 ns each. Additional details including a description of the umbrella sampling calculations is given in Sections 4 and 5 of the ESI.†
5.5 Ultrafast transient absorption spectroscopy
The broadband transient absorption set-up is described elsewhere.70,71 Briefly, the output of a Ti:sapphire regenerative amplifier (Coherent Libra, 5 kHz) was used to generate a white light supercontinuum by passing the 800 nm light through a pressurized argon gas chamber (20 psi). Chirped mirrors (ultrafast innovations GmbH, −40 fs2 mm−1 GVD compensation per double bounce) were used to compress the pump to a duration of 14 fs. The pump was spectrally filtered to 560 nm using a Schott glass filter (7.5 nJ pulse−1). The broadband probe pulse spanned 480–780 nm (18 pJ pulse−1). Spectra were collected on a line CCD (e2v AViiVA) coupled to a 2.5 kHz chopper to collect spectra with the “pump on” and “pump off”. Samples were contained in a 2 mm cuvette with a continuous stirring solution.Data availability
All the data files used to generate the plots in this manuscript are available from the authors upon request.Author contributions
S. M. H. perfomed ultrafast spectroscopy and analysis of all the constructs. J. L. B. designed and assembled the constructs, perfomed high-throughput screening, and steady-state measurements, and analyzed the data. M. A. C. performed MD and subsequent quantum chemical calculations of the MD snapshots and analyzed the data. L. M. and Y. V. synthesized and characterized all squaraine-modified oligonucleotides. J. G. synthesized and characterized the free-dye squaraine and performed the chemical doping experiments and analyzed the data. R. H. supervised the synthesis of squaraine-modified oligonucleotide strands. A. P. W. supervised the MD and quantum chemical calculations and analysis. M. B. supervised the design and fabrication of constructs. G. S. S. C. supervised the entire study. All authors contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work by S. M. H., M. A. C., A. P. W., M. B., and G. S. S.-C. were supported by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES) under award DE-SC0019998. Work by J. L. B. was supported by the DOE, Office of Science, BES under award DE-SC0019998 (DNA construct assembly and characterization steady-state photophysics characterization), by the National Science Foundation (NSF) RAISE TAQS under award number 1839155 (high-throughput screening of DNA constructs), and by the US Army Research Office accomplished under cooperative agreement W911NF-19-2-0026 for the Institute for Collaborative Biotechnologies (DNA denaturation and high-throughput additive screening experiments). Work by L. M., Y. V., and R. H. were supported by the Swiss Nation Foundation grant number 200020_188468. S. M. H. acknowledges an NSF Graduate Research Fellowship. M. B. acknowledges funding from the preceding sources to support research design and direction according to the attributions of J. L. B. Part of the computational simulations in this manuscript was performed using resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.References
- E. Romero, V. Novoderezhkin and R. van Grondelle, Nature, 2017, 543, 355–365 CrossRef CAS PubMed.
- J.-L. Brédas, E. Sargent and G. Scholes, Nat. Mater., 2017, 16, 35–44 CrossRef PubMed.
- A. H. Proppe, Y. C. Li, A. Aspuru-Guzik, C. P. Berlinguette, C. J. Chang, R. Cogdell, A. G. Doyle, J. Flick, N. M. Gabor, R. van Grondelle, S. Hammes-Schiffer, S. A. Jaffer, S. O. Kelley, M. Leclerc, K. Leo, T. E. Mallouk, P. Narang, G. S. Schlau-Cohen, G. D. Scholes, A. Vojvodic, V. W.-W. Yam, J. Y. Yang and E. H. Sargent, Nat. Rev. Mater., 2020, 5, 828–846 CrossRef CAS.
- S. J. Jang and B. Mennucci, Rev. Mod. Phys., 2018, 90, 035003 CrossRef CAS.
- G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- G. D. Scholes, X. J. Jordanides and G. R. Fleming, J. Phys. Chem. B, 2001, 105, 1640–1651 CrossRef CAS.
- N. J. Hestand and F. C. Spano, J. Chem. Phys., 2015, 143, 244707 CrossRef PubMed.
- N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163 CrossRef CAS PubMed.
- E. Sebastian and M. Hariharan, J. Am. Chem. Soc., 2021, 143, 13769–13781 CrossRef CAS PubMed.
- Y. J. Bae, D. Shimizu, J. D. Schultz, G. Kang, J. Zhou, G. C. Schatz, A. Osuka and M. R. Wasielewski, J. Phys. Chem. A, 2020, 124, 8478–8487 CrossRef CAS PubMed.
- H. Yamagata, D. S. Maxwell, J. Fan, K. R. Kittilstved, A. L. Briseno, M. D. Barnes and F. C. Spano, J. Phys. Chem. C, 2014, 118, 28842–28854 CrossRef CAS.
- A. Aster, F. Zinna, C. Rumble, J. Lacour and E. Vauthey, J. Am. Chem. Soc., 2021, 143, 2361–2371 CrossRef CAS PubMed.
- P. Roy, G. Bressan, J. Gretton, A. N. Cammidge and S. R. Meech, Angew. Chem., Int. Ed., 2021, 60, 10568–10572 CrossRef CAS PubMed.
- T. N. Lewis, C. Tonnelé, W. G. Shuler, Z. A. Kasun, H. Sato, A. J. Berges, J. R. Rodriguez, M. J. Krische, D. Casanova and C. J. Bardeen, J. Am. Chem. Soc., 2021, 143, 18548–18558 CrossRef CAS PubMed.
- S. J. Bradley, M. Chi, J. M. White, C. R. Hall, L. Goerigk, T. A. Smith and K. P. Ghiggino, Phys. Chem. Chem. Phys., 2021, 23, 9357–9364 RSC.
- R. M. Young and M. R. Wasielewski, Acc. Chem. Res., 2020, 53, 1957–1968 CrossRef CAS PubMed.
- Y. Hong, J. Kim, W. Kim, C. Kaufmann, H. Kim, F. Würthner and D. Kim, J. Am. Chem. Soc., 2020, 142, 7845–7857 CrossRef CAS PubMed.
- A. Aster, G. Licari, F. Zinna, E. Brun, T. Kumpulainen, E. Tajkhorshid, J. Lacour and E. Vauthey, Chem. Sci., 2019, 10, 10629–10639 RSC.
- W. Kim, A. Nowak-Król, Y. Hong, F. Schlosser, F. Würthner and D. Kim, J. Phys. Chem. Lett., 2019, 10, 1919–1927 CrossRef CAS PubMed.
- C. Kaufmann, D. Bialas, M. Stolte and F. Würthner, J. Am. Chem. Soc., 2018, 140, 9986–9995 CrossRef CAS PubMed.
- C. Kaufmann, W. Kim, A. Nowak-Król, Y. Hong, D. Kim and F. Würthner, J. Am. Chem. Soc., 2018, 140, 4253–4258 CrossRef CAS PubMed.
- R. E. Cook, B. T. Phelan, R. J. Kamire, M. B. Majewski, R. M. Young and M. R. Wasielewski, J. Phys. Chem. A, 2017, 121, 1607–1615 CrossRef CAS PubMed.
- P. Malỳ, J. Lüttig, S. Mueller, M. H. Schreck, C. Lambert and T. Brixner, Phys. Chem. Chem. Phys., 2020, 22, 21222–21237 RSC.
- E.-C. Wamhoff, J. L. Banal, W. P. Bricker, T. R. Shepherd, M. F. Parsons, R. Veneziano, M. B. Stone, H. Jun, X. Wang and M. Bathe, Annu. Rev. Biophys., 2019, 48, 395–419 CrossRef CAS PubMed.
- H. Jun, T. R. Shepherd, K. Zhang, W. P. Bricker, S. Li, W. Chiu and M. Bathe, ACS Nano, 2019, 13, 2083–2093 CAS.
- C. E. Castro, F. Kilchherr, D.-N. Kim, E. L. Shiao, T. Wauer, P. Wortmann, M. Bathe and H. Dietz, Nat. Mater., 2011, 8, 221 CAS.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- F. Garo and R. Häner, Angew. Chem., Int. Ed., 2012, 51, 916–919 CrossRef CAS PubMed.
- P. K. Dutta, R. Varghese, J. Nangreave, S. Lin, H. Yan and Y. Liu, J. Am. Chem. Soc., 2011, 133, 11985–11993 CrossRef CAS PubMed.
- P. Ensslen and H.-A. Wagenknecht, Acc. Chem. Res., 2015, 48, 2724–2733 CrossRef CAS PubMed.
- J. S. Melinger, R. Sha, C. Mao, N. C. Seeman and M. G. Ancona, J. Phys. Chem. B, 2016, 120, 12287–12292 CrossRef CAS PubMed.
- E. Boulais, N. P. D. Sawaya, R. Veneziano, A. Andreoni, J. L. Banal, T. Kondo, S. Mandal, S. Lin, G. S. Schlau-Cohen, N. W. Woodbury, H. Yan, A. Aspuru-Guzik and M. Bathe, Nat. Mater., 2018, 17, 159–166 CrossRef CAS PubMed.
- P. D. Cunningham, A. Khachatrian, S. Buckhout-White, J. R. Deschamps, E. R. Goldman, I. L. Medintz and J. S. Melinger, J. Phys. Chem. B, 2014, 118, 14555–14565 CrossRef CAS PubMed.
- B. L. Cannon, D. L. Kellis, L. K. Patten, P. H. Davis, J. Lee, E. Graugnard, B. Yurke and W. B. Knowlton, J. Phys. Chem. A, 2017, 121, 6905–6916 CrossRef CAS PubMed.
- S. M. Hart, W. J. Chen, J. L. Banal, W. P. Bricker, A. Dodin, L. Markova, Y. Vyborna, A. P. Willard, R. Häner, M. Bathe and G. S. Schlau-Cohen, Chem, 2021, 7, 752–773 CAS.
- S. M. Hart, X. Wang, J. Guo, M. Bathe and G. S. Schlau-Cohen, J. Phys. Chem. Lett., 2022, 13, 1863–1871 CrossRef CAS PubMed.
- M. S. Barclay, S. K. Roy, J. S. Huff, O. A. Mass, D. B. Turner, C. K. Wilson, D. L. Kellis, E. A. Terpetschnig, J. Lee and P. H. Davis, et al. , Commun. Chem., 2021, 4, 1–11 CrossRef.
- J. Gorman, S. R. Orsborne, A. Sridhar, R. Pandya, P. Budden, A. Ohmann, N. A. Panjwani, Y. Liu, J. L. Greenfield and S. Dowland, et al. , J. Am. Chem. Soc., 2022, 144, 368–376 CrossRef CAS PubMed.
- F. D. Lewis, R. M. Young and M. R. Wasielewski, Acc. Chem. Res., 2018, 51, 1746–1754 CrossRef CAS PubMed.
- A. K. Thazhathveetil, M. A. Harris, R. M. Young, M. R. Wasielewski and F. D. Lewis, J. Am. Chem. Soc., 2017, 139, 1730–1733 CrossRef CAS PubMed.
- T. Takada, M. Fujitsuka and T. Majima, Proc. Natl. Acad. Sci., 2007, 104, 11179–11183 CrossRef CAS PubMed.
- G. Barcenas, A. Biaggne, O. A. Mass, C. K. Wilson, O. M. Obukhova, O. S. Kolosova, A. L. Tatarets, E. Terpetschnig, R. D. Pensack and J. Lee, et al. , RSC Adv., 2021, 11, 19029–19040 RSC.
- L. I. Markova, V. L. Malinovskii, L. D. Patsenker and R. Häner, Org. Biomol. Chem., 2012, 10, 8944–8947 RSC.
- L. I. Markova, V. L. Malinovskii, L. D. Patsenker and R. Häner, Chem. Commun., 2013, 49, 5298–5300 RSC.
- L. Markova, M. Probst and R. Häner, RSC Adv., 2020, 10, 44841–44845 RSC.
- O. A. Mass, C. K. Wilson, S. K. Roy, M. S. Barclay, L. K. Patten, E. A. Terpetschnig, J. Lee, R. D. Pensack, B. Yurke and W. B. Knowlton, J. Phys. Chem. B, 2020, 124, 9636–9647 CrossRef CAS PubMed.
- O. A. Mass, C. K. Wilson, G. Barcenas, E. A. Terpetschnig, O. M. Obukhova, O. S. Kolosova, A. L. Tatarets, L. Li, B. Yurke, W. B. Knowlton, R. D. Pensack and J. Lee, J. Phys. Chem. C, 2022, 126, 3475–3488 CrossRef CAS PubMed.
- M. S. Barclay, C. K. Wilson, S. K. Roy, O. A. Mass, O. M. Obukhova, R. P. Svoiakov, A. L. Tatarets, A. U. Chowdhury, J. S. Huff and D. B. Turner, et al. , ChemPhotoChem, 2022, 6, e202200039 CrossRef CAS.
- J. Poater, M. Swart, F. M. Bickelhaupt and C. F. Guerra, Org. Biomol. Chem., 2014, 12, 4691–4700 RSC.
- F. A. Vendeix, A. M. Munoz and P. F. Agris, RNA, 2009, 15, 2278–2287 CrossRef CAS PubMed.
- E. Stofer, C. Chipot and R. Lavery, J. Am. Chem. Soc., 1999, 121, 9503–9508 CrossRef CAS.
- J. Chen and R. F. Winter, Chem.–Eur. J., 2012, 18, 10733–10741 CrossRef CAS PubMed.
- A. U. Chowdhury, S. A. Díaz, J. S. Huff, M. S. Barclay, M. Chiriboga, G. A. Ellis, D. Mathur, L. K. Patten, A. Sup and N. Hallstrom, et al. , J. Phys. Chem. Lett., 2022, 13, 2782–2791 CrossRef CAS PubMed.
- Z. S. Walbrun, L. C. Leibfried, A. R. Roban, B. C. Rasmussen, T. J. Wiegand, C. J. Collison and C. Y. Wong, MRS Adv., 2022, 7, 239–244 CrossRef CAS.
- C. Zheng, A. R. Penmetcha, B. Cona, S. D. Spencer, B. Zhu, P. Heaphy, J. A. Cody and C. J. Collison, Langmuir, 2015, 31, 7717–7726 CrossRef CAS PubMed.
- S. Arnott, R. Chandrasekaran, I. Hall, L. Puigjaner, J. Walker and M. Wang, Cold Spring Harbor Symp. Quant. Biol., 1983, 53–65 CrossRef CAS PubMed.
- S. A. Serron, W. S. Aldridge, C. N. Fleming, R. M. Danell, M.-H. Baik, M. Sykora, D. M. Dattelbaum and T. J. Meyer, J. Am. Chem. Soc., 2004, 126, 14506–14514 CrossRef CAS PubMed.
- M. Kellogg, A. Akil, D. S. M. Ravinson, L. Estergreen, S. E. Bradforth and M. E. Thompson, Faraday Discuss., 2019, 216, 379–394 RSC.
- M. I. Röhr, H. Marciniak, J. Hoche, M. H. Schreck, H. Ceymann, R. Mitric and C. Lambert, J. Phys. Chem. C, 2018, 122, 8082–8093 CrossRef.
- H. Marciniak, N. Auerhammer, S. Ricker, A. Schmiedel, M. Holzapfel and C. Lambert, J. Phys. Chem. C, 2019, 123, 3426–3432 CrossRef CAS.
- J. L. Banal, T. Kondo, R. Veneziano, M. Bathe and G. S. Schlau-Cohen, J. Phys. Chem. Lett., 2017, 8, 5827–5833 CrossRef CAS PubMed.
- P. D. Cunningham, C. M. Spillmann, J. S. Melinger, M. G. Ancona, Y. C. Kim, D. Mathur, S. Buckhout-White, E. R. Goldman and I. L. Medintz, Adv. Opt. Mater., 2021, 9, 2170084 CrossRef.
- H. Jun, X. Wang, M. F. Parsons, W. P. Bricker, T. John, S. Li, S. Jackson, W. Chiu and M. Bathe, Nucleic Acids Res., 2021, 49, 10265–10274 CrossRef CAS PubMed.
- S. Dey, C. Fan, K. V. Gothelf, J. Li, C. Lin, L. Liu, N. Liu, M. A. Nijenhuis, B. Saccà and F. C. Simmel, et al. , Nat. Rev. Methods Primers, 2021, 1, 1–24 CrossRef.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- The PyMOL Molecular Graphics System, Version 2.5, Schrödinger, LLC Search PubMed.
- D. Case, I. Ben-Shalom, S. Brozell, D. Cerutti, T. Cheatham III, V. Cruzeiro, T. Darden, R. Duke, D. Ghoreishi, M. Gilson, H. Gohlke, A. Goetz, D. Greene, R. Harris, N. Homeyer, Y. Huang, S. Izadi, A. Kovalenko, T. Kurtzman, T. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. Mermelstein, K. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. Simmerling, J. Smith, R. SalomonFerrer, J. Swails, R. Walker, J. Wang, H. Wei, R. Wolf, X. Wu, L. Xiao, D. York and P. Kollman, AMBER 2018, University of California, San Francisco, 2018 Search PubMed.
- M. Son, S. Mosquera-Vázquez and G. S. Schlau-Cohen, Opt. Express, 2017, 25, 18950–18962 CrossRef CAS PubMed.
- P. T. Cesana, B. X. Li, S. G. Shepard, S. I. Ting, S. M. Hart, C. M. Olson, J. I. Martinez Alvarado, M. Son, T. J. Steiman, F. N. Castellano, A. G. Doyle, D. W. MacMillan and G. S. Schlau-Cohen, Chem, 2022, 8, 174–185 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Sample characterization, spectroscopic and theoretical methods, and supplementary tables and figures. See DOI: https://doi.org/10.1039/d2sc02759c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |