Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pseudo-mono-axial ligand fields that support high energy barriers in triangular dodecahedral Dy(III) single-ion magnets†
Ben
Zhang‡
a,
Zhijie
Cheng‡
a,
Yingying
Wu
b,
Lei
Chen
 *a,
Rong
Jing
a,
Xingwei
Cai
a,
Chunhui
Jiang
*a,
Rong
Jing
a,
Xingwei
Cai
a,
Chunhui
Jiang
 a,
Yi-Quan
Zhang
a,
Yi-Quan
Zhang
 *c,
Aihua
Yuan
*c,
Aihua
Yuan
 *a,
Hui-Hui
Cui
d and
Zhao-Yang
Li
*a,
Hui-Hui
Cui
d and
Zhao-Yang
Li
 *b
*b
aSchool of Environmental and Chemical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212100, PR China. E-mail: chenlei@just.edu.cn; aihua.yuan@just.edu.cn
bSchool of Materials Science and Engineering, Nankai University, 38 Tongyan Road, Haihe Educational Park, Tianjin 300350, PR China. E-mail: zhaoyang@nankai.edu.cn
cJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, PR China. E-mail: zhangyiquan@njnu.edu.cn
dSchool of Chemistry and Chemical Engineering, Nantong University, Jiangsu 226019, PR China
First published on 31st October 2022
Abstract
The synthesis of air-stable, high-performance single-molecule magnets (SMMs) is of great significance for their practical applications. Indeed, Ln complexes with high coordination numbers are satisfactorily air stable. However, such geometries easily produce spherical ligand fields that minimize magnetic anisotropy. Herein, we report the preparation of three air-stable eight-coordinate mononuclear Dy(III) complexes with triangular dodecahedral geometries, namely, [Dy(BPA-TPA)Cl](BPh4)2 (1) and [Dy(BPA-TPA)(X)](BPh4)2·nCH2Cl2 (X = CH3O− and n = 1 for 2; L = PhO− and n = 2 for 3), using a novel design concept in which the bulky heptadentate [2,6-bis[bis(2-pyridylmethyl)amino]methyl]-pyridine (BPA-TPA) ligand enwraps the Dy(III) ion through weak coordinate bonds leaving only a small vacancy for a negatively charged (Cl−), methoxy (CH3O−) or phenoxy (PhO−) moiety to occupy. Magnetic measurements reveal that the single-molecule magnet (SMM) property of complex 1 is actually poor, as there is almost no energy barrier. However, complexes 2 and 3 exhibit fascinating SMM behavior with high energy barriers (Ueff = 686 K for 2; 469 K for 3) and magnetic hysteresis temperatures up to 8 K, which is attributed to the pseudolinear ligand field generated by one strong, highly electrostatic Dy–O bond. Ab initio calculations were used to show the apparent difference in the magnetic dynamics of the three complexes, confirming that the pseudo-mono-axial ligand field has an important effect on high-performance SMMs compared with the local symmetry. This study not only presents the highest energy barrier for a triangular dodecahedral SMM but also highlights the enormous potential of the pseudolinear Dy–L ligand field for constructing promising SMMs.
Introduction
A single-molecule magnet (SMM) exhibits blocked magnetization below a critical temperature (TB) due to an anisotropy barrier (Ueff). Such magnets have attracted unprecedented interest because they represent the ultimate size limit for future spin-based devices.1–5 Furthermore, obtaining SMMs with high Ueff and TB values, ambient stabilities, and coercivities for technological applications is important.6 Mononuclear lanthanide single-molecule magnets (SMMs), also referred to as “single-ion magnets” (SIMs), are particularly preferred for realizing the goals of high-performance SMMs because the coordination environment of a single lanthanide ion can be manipulated to constantly refresh the records of Ueff and TB.7–20A linear Ln(III) complex (either one- or two-coordinated) is well known to provide an ideal coordination environment with a pure axial ligand field, which maximizes crystal field (CF) splitting and significantly improves axial doublets and magnetic properties.21–26 However, constructing such linear L–Ln–L or Ln–L complexes is synthetically challenging. Fortunately, this synthetically challenging geometry has been approached by constructing pseudolinear L–Ln–L complexes that possess two very short chemical bonds with an approximate angle of 180°, such as in octahedral (Oh),27–30 pentagonal bipyramidal (D5h),31–43 hexagonal bipyramidal (D6h)44–49 and sandwich Dy(III) complexes,50–54 resulting in impressive relaxation barriers and high blocking temperatures. Significantly, a dysprosium metallocene complex bearing cyclopentadienyl (CpR) derivative ligands, as an example of the latter sandwich structure, has the most linear CpR–Dy–CpR angle and short Dy–CpR distance, leading to a record hysteresis temperature of 80 K.50 Therefore, systems with pseudolinear L–Dy–L units have been shown to effectively produce high-performance SMMs. The other pseudolinear type of Dy–L complex, with only one very short coordinate bond, has rarely been explored, although computational studies suggest that such structures should possess significant energy barriers.21 Notable examples include [DyF(Tppy)(sol)x][PF6] (Tppy = tris(3-(2-pyridyl)pyrazolyl)hydroborate; x = 1, 2) and [DyF(Lpy)](CF3SO3) (Lpy = 1,4,7,10-tetrakis(2-pyridylmethyl)-1,4,7,10-tetraazacyclododecane), which are air-stable Dy–F complexes with two configurations, as reported by Norel and Canaj et al.55–57 Bulky polydentate ligands with six to eight donor atoms can chelate most of the Dy(III) ion coordination sites in these complexes with weak coordinate bonds, leaving only small vacancies for fluoride to occupy.58 This system, with its dominant short dysprosium–fluoride bond, induces strong axial anisotropy and exhibits remarkable Ueff values (>600 K). In addition, these complexes generally exhibit high coordination numbers and are air stable as a consequence.
In this respect, our attention was drawn to the bulky heptadentate [2,6-bis[bis(2-pyridylmethyl)amino]methyl]pyridine (BPA-TPA) ligand15 that can enwrap metal centers, as demonstrated in the reported [Co(BPA-TPA)](A)2 (A = BF4, PF6 and BPh4) and [Co(BPA-TPA)](ClO4)2·H2O Co(II) complexes.59–63 Monoanionic O-donor ligands, such as alkoxide, siloxide, and aryloxide, are distributed at axial sites and are particularly effective in high-performance Dy-based SMM complexes. Because most of the coordination sites of the Dy(III) ion are occupied by a single bulky BPA-TPA ligand, we selected a sterically small methoxy (CH3O−) or phenoxy (PhO−) moiety as a candidate for forming a short, strong Dy–O bond. Herein, we report the synthesis, structural and magnetic characterization, and ab initio calculations of three novel air-stable complexes, [Dy(BPA-TPA)Cl](BPh4)2 (1) and [Dy(BPA-TPA)(X)](BPh4)2·nCH2Cl2 (X = CH3O− and n = 1 for 2; L = PhO− and n = 2 for 3), which possess a triangular dodecahedral coordinate geometry with D2d symmetry. Dynamic magnetic susceptibility studies reveal that complex 1 only exhibits frequency-dependent out-of-phase (χM′′) signals below 2.4 K under an 800 Oe dc field, whereas 2 and 3 are zero-field single-ion magnets with large energy barriers (Ueff = 686 K for 2; 469 K for 3); such magnets are unprecedented for the triangular dodecahedral geometry. Furthermore, complete-active-space self-consistent field (CASSCF) ab initio computational methods were used to provide detailed insight into the magnetic dynamics for these complexes and to understand the role of the axial Dy–O crystal field in realizing the observed excellent properties. This study provides a unique design approach toward a new class of complexes with the desired pseudolinear Dy–L ligand field.
Results and discussion
Crystal structures
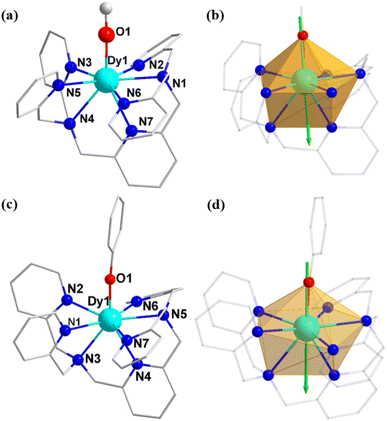
The crystallographic structures of the three above mentioned complexes reveal that complex 1 crystallizes in the monoclinic P21/c space group, while complexes 2 and 3 crystallize in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group (Table S1 in the ESI†). The coordinate structures of the cations of the three complexes are depicted in Fig. 1 and S4, with selected bond lengths given in Tables 1 and S2.†
space group (Table S1 in the ESI†). The coordinate structures of the cations of the three complexes are depicted in Fig. 1 and S4, with selected bond lengths given in Tables 1 and S2.†
| 2 | 3 | ||
|---|---|---|---|
| Dy(1)–O(1) | 2.108(5) | Dy(1)–O(1) | 2.087(3) |
| Dy(1)–N(1) | 2.523(5) | Dy(1)–N(1) | 2.514(3) |
| Dy(1)–N(2) | 2.616(6) | Dy(1)–N(2) | 2.567(3) |
| Dy(1)–N(3) | 2.495(5) | Dy(1)–N(3) | 2.638(3) |
| Dy(1)–N(4) | 2.616(5) | Dy(1)–N(4) | 2.508(3) |
| Dy(1)–N(5) | 2.555(5) | Dy(1)–N(5) | 2.548(3) |
| Dy(1)–N(6) | 2.602(5) | Dy(1)–N(6) | 2.496(3) |
| Dy(1)–N(7) | 2.507(5) | Dy(1)–N(7) | 2.540(3) |
The Dy(III) site in complexes 1–3 is eight-coordinated by one BPA-TPA ligand and one Cl−, CH3O− or PhO− anion. The seven-nitrogen “pocket” of the BPA-TPA ligand three-dimensionally surrounds the central Dy(III) ion with long Dy–N distances of 2.458(5)–2.619(5) Å for 1, 2.495(5)–2.616(6) Å for 2 and 2.496(3)–2.638(3) Å for 3, indicative of a fully weak crystal field in each case. The one remaining site is occupied by a CH3O− or PhO− anion with a very short Dy–O distance of 2.108(5) Å (for 2) or 2.087(3) Å (for 3), which induces an axially strong ligand field, whereas a long Dy–Cl axial bond of 2.5835(16) Å is observed for 1, suggesting a nearly spherical and weak ligand field. This allows us to unambiguously reveal that complexes 2 and 3 bear a pseudolinear Dy–O ligand field. Continuous shape measures (CShMs) were used to evaluate each configuration,64–66 the results of which are given in Table S3.† The triangular dodecahedral geometry (D2d) provided the lowest CShM value in each case: 2.166 for 1, 2.130 for 2 and 1.820 for 3. In addition, the shortest Dy(III)⋯Dy(III) distances were determined to be 10.770, 10.095 and 11.798 Å for 1–3, respectively, suggesting negligible direct and superexchange magnetic interactions (Fig. S8–S10†).
Magnetic properties
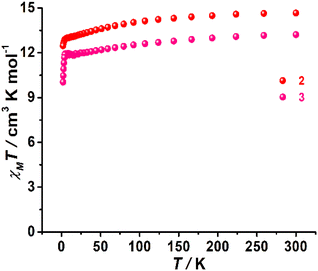
Complexes 1–3 exhibited χMT values of 13.65, 14.66 and 13.21 cm3 K mol−1, respectively, at room temperature, which are close to the theoretical value of 14.17 cm3 K mol−1 for an isolated Dy(III) ion (g = 4/3, 6H15/2, S = 5/2, L = 5). These χMT values decreased slightly upon cooling and then suddenly dropped at low temperature to final values of 6.98 cm3 K mol−1 for 1, 12.47 cm3 K mol−1 for 2, and 10.04 cm3 K mol−1 for 3 (Fig. 2 and S11†), which were likely attributed to thermal depopulation of MJ sublevels or the presence of large crystal field (CF) splitting. Field-dependent magnetization (M) curves were also acquired for three complexes at 2 K in the 0–7 T dc field range, which revealed respective magnetizations of 6.27 Nβ for 1, 6.11 Nβ for 2 and 5.06 Nβ for 3 at 7 T and 2.0 K (Fig. S12–S14†).Dynamic magnetic relaxation was investigated by measuring the alternating current (ac) magnetic susceptibilities of 1–3 in the 1–999 Hz range under a zero external dc field. In the case of 1, no maximum of out-of-phase (χM′′) susceptibilities was observed in the absence of a dc field (Fig. S15†). Further ac measurements were carried out under various dc fields. When applying the dc field, the χM′′ signals only exhibit frequency dependence without the maximum. The temperature and frequency dependence of the ac susceptibilities under an 800 Oe dc field show the poor performance that is not χM′′ signals above 2.4 K for 1 (Fig. S16†).
In the case of complexes 2 and 3, the in-phase (χM′) and out-of-phase (χM′′) ac susceptibility components show typical SMM behavior under zero dc field (Fig. 3, S17 and S18†). Well-defined χM′′ maxima were observed for 2 and 3 at temperatures above 45 and 34 K, respectively, indicative of high barriers for magnetization reversal. Invariable χM′′ (ν) peak maxima and χM′′ (T) “tails” were observed below 10 K, consistent with the quantum tunneling of magnetization (QTM) that is commonly observed in lanthanide-based SMMs.31–43 The relaxation time (τ) extracted using the generalized Debye model67–69 obeys the Arrhenius law at high temperatures (Fig. S19 and S20, Tables S4 and S5†); linear regression provided the following best-fitted results: Ueff = 686 K and τ0 = 3.1 × 10−11 s for 2 and Ueff = 469 K and τ0 = 9.3 × 10−11 s for 3 (Fig. 4). To the best of our knowledge, these are the highest energy barriers for SIMs with triangular dodecahedrons and highlight the potential of the unique pseudolinear Dy–L ligand field.
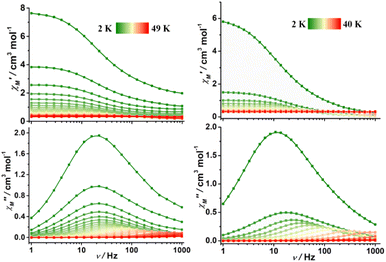 | ||
| Fig. 3 Frequency dependence of in-phase (top) and out-of-phase (bottom) ac susceptibility for 2 (left) and 3 (right) in zero dc field; the solid lines are guides for the eye. | ||
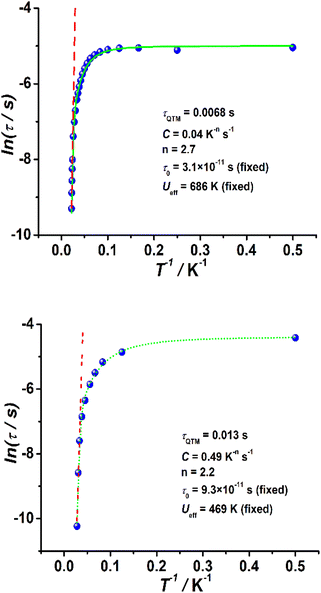 | ||
| Fig. 4 Plots of ln(τ) as functions of T−1 in a zero dc field for 2 (top) and 3 (bottom). The green solid lines are best fits to eqn (1), while the red dotted lines correspond to the Arrhenius law at high temperatures. | ||
Prominent QTM was observed below 10 K in each case. Indeed, Raman processes make significant contributions in most reported SIMs. In addition, direct processes can be neglected for relaxation time products in a zero dc field. Therefore, the magnetization dynamics of 2 and 3 can be fitted using eqn (1), which considers the QTM, Raman, and Orbach mechanisms:
τ−1 = τQTM−1 + CTn + τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) exp(−Ueff/kBT) | (1) |
To avoid overparameterization, the fixed values of Ueff and τ0 obtained from the Arrhenius law were applied in the fit processes, yielding τQTM = 0.0068 s, C = 0.04 s−1 K−n, n = 2.7, Ueff = 686 K (fixed) and τ0 = 3.1 × 10−11 s (fixed) for 2, and τQTM = 0.013 s, C = 0.49 s−1 K−n, n = 2.2, Ueff = 469 K (fixed) and τ0 = 9.3 × 10−11 s (fixed) for 3, as shown in Fig. 4. The values of the Raman parameters C and n are within the ranges observed for Dy-based SMMs.
Upon applying the optimized field of 1500 Oe, the ac susceptibility data for both complexes show temperature dependence in the whole temperature region (Fig. S21–S24†) due to the suppression of the QTM at low temperature. The χM′′ peak is located at 45 K for 2 and 34 K for 3, revealing almost unchanged relaxation at high temperature with respect to the zero-field data. These frequency-dependent data were also analyzed by the generalized Debye model (Fig. S25–S26 and Tables S6 and S7†). The Arrhenius fit at high temperatures generates Ueff = 688 K and τ0 = 3.8 × 10−11 s for 2 and Ueff = 492 K and τ0 = 6.7 × 10−11 s for 3 (Fig. S27 and S28†). These values of the Orbach parameters were employed for the fit based on the combination of the Raman and Orbach processes, as shown in Fig. S29 and S30.† The energy barrier values for 2 and 3 under 1500 Oe are in keeping with those for zero dc field, suggesting the Raman and Orbach processes at the high temperature region are unacted on the application of dc field.
To investigate the blocking of magnetization, polycrystalline samples of complexes 1–3 were subjected to magnetic hysteresis at a slow average sweep rate of 200 Oe s−1. It can be expected that no hysteresis loop was found at 2 K for complex 1 (Fig. S31†). In contrast, clear butterfly shaped hysteresis loops that open below 8 K were observed for complexes 2 and 3 (Fig. 5). Magnetization is observed to suddenly drop at low fields that approach H = 0, which reveals the strong contribution from a faster QTM effect, in good agreement with the temperature independence observed below 10 K in the χM′′ (ν) curves and the rapid increase in χM′′ (T) at low temperatures observed for 2 and 3.
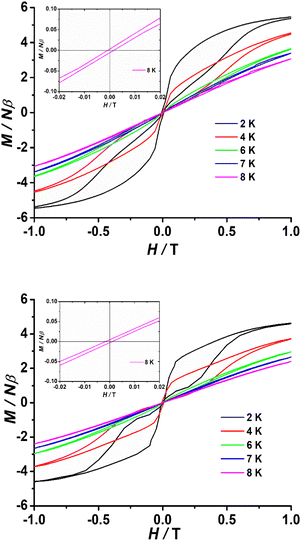 | ||
| Fig. 5 Powder magnetic hysteresis data for 2 (top) and 3 (bottom) at an average sweep rate of 0.02 T s−1. Inset: M(H) loops in the zero field region open up to 8 K. | ||
Theoretical analysis
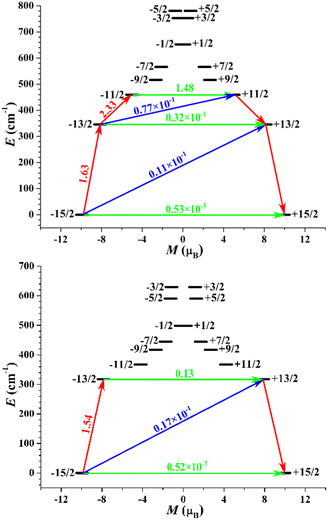
To gain further insight into the magnetic anisotropies and relaxation mechanisms of complexes 1–3, CASSCF calculations on the basis of their X-ray determined geometries were carried out with the OpenMolcas and SINGLE_ANISO programs.70–73 For complex 1, a very small energy gap between the ground state and first excited states of 18.5 cm−1 was predicted. Relatively large gx,y values of 0.428 and 3.426 with the impure ground state of mJ = 63%|±15/2 were observed, yielding a large magnetic moment matrix element of 0.64 μB between the ground Kramers doublets (KDs), which indicates that probable magnetic relaxation occurs via the ground state. These computed results explain the weak ac magnetic property even under the applied dc field for 1.In contrast to complex 1, a highly anisotropic ground Kramers doublet (KD) with gz ≈ 19.86 was obtained for complexes 2 and 3 together with the first excited KD assigned to a rather pure mJ = ±13/2 state, whereas other KDs show substantial magnetic state mixing (Tables S5 and S6†). The main magnetic axes on the DyIII ions of 2 and 3 in their ground KDs are shown in Fig. 1b and d; each lies exactly along the Dy–O direction and reveals the strong crystal field resulting from the short, strong Dy–O bond. The magnetization-blocking barriers of complexes 2 and 3 are shown in Fig. 6, where both ground KD transversal magnetic moments are smaller than 10−3μB; hence, the QTM in their ground KDs is suppressed at low temperature. Complex 2 exhibits a transversal magnetic moment in the first excited KD of 0.32 × 10−1μB; therefore, relaxation probably proceeds through the second excited KD. On the other hand, complex 3 shows a transversal magnetic moment in the first excited KD of 0.13 μB; consequently, fast QTM is likely to occur in its first excited KD. The transversal magnetic moment in the second excited KD of 2 was found to be 1.48 μB; therefore, fast QTM is expected to occur in its second excited KD. Accordingly, the energy barriers for 2 and 3 calculated according to the schemes in Fig. 6 are 459.6 and 317.5 cm−1, respectively, which agree well with the experimental values of 476.8 cm−1 (686 K) and 326 cm−1 (469 K).
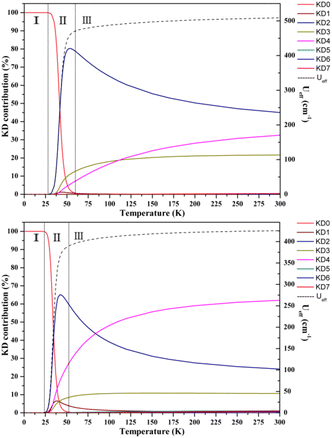
Aravena et al. reported a new method for predicting effective demagnetization barriers (Ueff) that considers all state energies and their contributions to the tunneling rate.74–76 The entire temperature range for complexes 1–3 can be divided into three regions (Fig. 7 and S33†). Ueff is always nearly zero in region I, since the contribution from the ground state dominates, while the ground state contribution drops in region II and KD1 becomes the first state to function; however, the dominating state changes to other higher excited KDs as the temperature continues to rise. Ueff grows to a constant value as the Orbach regime is approached as the temperature increases further in region III. KD2–4 are the three most important KD contributions to the Ueff values of complexes 1–3. We determined the Ueff values of complexes 1–3 using eqn (1)–(3); the saturated Ueff values for complexes 1–3 were calculated to be 159.3, 508.8 and 425.6 cm−1, respectively. Only when the relaxation temperatures exceed ca. 55 K for 1, ca. 60 K for 2 and ca. 50 K for 3, these saturations may be achieved. However, in reality, the highest experimental temperatures of the ac susceptibility signals for all complexes are below 50 K, thus leading to the calculated saturation Ueff being higher than the experimental values.
CF parameters B (k, q) with high percentages were calculated to further elucidate the mechanism of relaxation, the results of which are shown in Table S7.† The weight of the axial parameters B (2, 0) for 1 is very low, suggesting poor axial CF. However, for 2 and 3, the weights of absolute axial parameters B (2, 0) and B (4, 0) exceed 20% and 10%, respectively, and their values are both negative and larger than transverse B (k, q) (k = 2, 4; q ≠ 0), suggesting strong uniaxial anisotropy. Moreover, the value of the axial parameter B (2, 0) for complex 2 is larger than that of 3, which shows that 2 exhibits a larger CF than 3.
Taken together, the computational results are in complete accordance with the experimental observations. The high performance of SMM for 2 and 3 can be directly related to the strong axial nature of the ligand field arising from the short axial Dy–O bonds (2.108(5) Å for 2 and 2.087(3) Å for 3). Conversely, the SMM property of 1 is very poor, although the local symmetry of 1 is similar to that of 2 and 3. It is understandable that the long Dy–Cl bond generates the weak and spherical CF for 1, which may not be able to induce the strong magnetic anisotropy and afford a large mJ splitting. It is well known that the magnetic anisotropy and the local symmetry around the spin center seriously affect the properties of SMMs. The magnetic anisotropy determines the upper limit of the total CF splitting energy, while the high symmetry can suppress the QTM, resulting in the relaxation process in which the relaxation process passes through the higher excited KD. Therefore, a strong magnetic anisotropy is an essential precondition for high-performance SMMs. Despite the relatively low local symmetry around the Dy site, fascinating SMM behavior was observed for 2 and 3, which is ascribed to their strong, highly electrostatic Dy–O bond.
In addition, the apparent difference in the energy barrier for 2 and 3 is attributable to differences in the axial ligand. At first glance, complex 3 has a shorter axial Dy–O bond compared to 2; this should lead to a stronger axial ligand field acting on Dy(III) for 3. However, this expectation contrasts with the fact that 2 possesses a better SMM property. Actually, the Dy(III) electron density is oblate in shape, which requires the charge to be in the axial direction as much as possible. As reported previously,35,41,42 the introduction of electron-donating groups in the axial ligand improves the energy barrier. The LoProp charges in the ground KDs of 2 and 3 were calculated using the CASSCF wavefunction (Table S11†), with the axial oxygen atom in 2 found to be more charged than that in 3, which is ascribable to the superior electron-donating ability of the –CH3 group compared to the phenyl group. Therefore, the axial CH3O− ligand improves SMM properties. Moreover, the charges on the axial oxygen atoms of both complexes are nearly three times larger than those on the neutral nitrogen atoms, which also indicates the axial nature of the total ligand field felt by the Dy(III) ion in each case.
Conclusion
The bulky heptadentate BPA-TPA ligand was successfully used to synthesize triangular dodecahedral dysprosium(III)-based complexes with mono-axially ligated Cl− (1), CH3O− (2) or PhO− (3) moieties. The large axial CF splitting of the J = 15/2 ground state induced by the short axial Dy–O bond results in slow magnetization relaxation through large anisotropic energy barriers (686 K for 2 and 469 K for 3). However, although the local coordination geometry of 1 was similar, only weak frequency-dependent ac signals without the χM′′ maximum were observed for complex 1, which is caused by the weak and spherical CF generated by the long Dy–Cl bond. Ab initio calculations reveal that 2 and 3 exhibit dominant magnetization reversal barriers that expand to the second and first Kramers doublets, respectively.According to theoretical predictions,21 the blocking barrier limit for a SIM is defined by a one-coordinate diatomic complex, such as [DyO]+, to be above 3000 K.6 However, the synthesis of a model compound with perfect axial symmetry is highly unrealistic and almost impossible to achieve. In the present case, the bulky pentapyridyldiamine ligand prevents additional coordination, and the methoxy or phenoxy oxygen atom provides strong CF splitting and forms a pseudo [DyO]2+ ligand field. This finding not only provides a promising blueprint for accessing linear mono-coordinate [DyO]+ complexes but also extends the kinds of high-performance SMMs available.
Experimental section
General procedures
All chemicals were commercially available and used without further purification. The [2,6-bis[bis(2-pyridylmethyl)amino]methyl]-pyridine (BPA-TPA) ligand was prepared as described previously.59–61 C, H and N elemental analyses were performed on an Elementar Vario EL III elemental analyzer. Powder XRD (PXRD) patterns were recorded at room temperature on a Bruker D8 Advance X-ray diffractometer (Fig. S1–S3†). Experimental PXRD patterns for bulk polycrystalline samples are consistent with those simulated from the single-crystal X-ray data, confirming the phase purity of complexes 1–3 and their stability in air. Single-crystal XRD data for 1–3 were collected at 296 K on a Bruker APEX II diffractometer equipped with a CCD area detector (Mo Kα radiation, λ = 0.71073 Å).77,78 All structures were solved using the SHELXTL-2016 program. Further crystallographic details are provided in Table S1 and Fig. S5–S7.† Complexes 1–3 were subjected to direct-current (dc) magnetic measurements between 2 and 300 K on a Quantum Design SQUID VSM magnetometer at fields up to 7 T. Alternating-current (ac) susceptibility measurements were carried out at ac frequencies in the 1–1000 Hz range in various applied static fields with an oscillating ac field of 2 Oe. Magnetic susceptibility data were corrected for diamagnetism associated with the constituent atoms, and the sample holder was estimated using Pascal constants.Synthesis of [Dy(BPA-TPA)Cl](BPh4)2 (1)
DyCl3·6H2O (0.188 g, 0.5 mmol), BPA-TPA (0.250 g, 0.5 mmol) and NaBPh4 (0.513 g, 1.5 mmol) were dissolved in methanol (20 mL), stirred for 30 min and then filtered, affording a white precipitate. White crystals suitable for single-crystal XRD were grown by the slow diffusion of diethyl ether into a CH3CN solution of the white precipitate over 2 d. Yield: 68% based on Dy(III); elemental analysis (%) found (calcd) for C79H71B2ClDyN7: C, 70.86 (70.91); H, 5.34 (5.35); N, 7.30 (7.33).Synthesis of [Dy(BPA-TPA)(CH3O)](BPh4)2·CH2Cl2 (2)
DyCl3·6H2O (0.188 g, 0.5 mmol), BPA-TPA (0.250 g, 0.5 mmol) and sodium trimethylsilanolate (0.113 g, 1 mmol) were dissolved in methanol (15 mL) and refluxed for 4 h to give a yellow solution. NaBPh4 (0.343 g, 1 mmol) was then added to the yellow solution, and the reaction mixture was stirred for 30 min, at which time the product formed a light yellow precipitate. Yellow crystals suitable for single-crystal XRD were grown by the slow diffusion of hexane into a CH2Cl2 solution of the light yellow product over 2 d. Yield: 63% based on Dy(III); elemental analysis (%) found (calcd) for C81H76B2Cl2DyN7O: C, 68.52 (68.58); H, 5.37 (5.40); N, 6.96 (6.91).Synthesis of [Dy(BPA-TPA)(OPh)](BPh4)2·2CH2Cl2 (3)
DyCl3·6H2O (0.188 g, 0.5 mmol) and BPA-TPA (0.250 g, 0.5 mmol) were dissolved in methanol (15 mL) and refluxed for 2 h. The solvent was removed under reduced pressure, and acetonitrile (10 mL) was added to the light yellow residue, after which phenol (0.0471 g, 0.5 mmol) and sodium trimethylsilanolate (0.0566 g, 0.5 mmol) were added to the resulting solution. The mixture was refluxed for 2 h and then filtered, and a solution of NaBPh4 (0.343 g, 1 mmol) in acetonitrile (10 mL) was added to the filtrate. After stirring for 30 min, the mixture was filtered, and the solvent was removed under vacuum to give the product as a yellow powder. Yellow crystals suitable for single-crystal XRD were grown by the slow diffusion of hexane into a CH2Cl2 solution of the light yellow product over 2 d. Yield: 59% based on Dy(III); elemental analysis found (%) (calcd) for C86H78B2Cl2DyN7O: C, 69.74 (69.77); H, 5.28 (5.31); N, 6.66 (6.62).Computational details
CASSCF calculations on mononuclear complexes 1–3 (see Fig. 1 and S3† for the calculated complete structures of 1–3) based on single-crystal X-ray-determined geometries were performed using the OpenMolcas70 program package.Atomic natural orbital basis sets from the MOLCAS ANO-RCC library were used: ANO-RCC-VTZP for DyIII; VTZ for close N and O; VDZ for distant atoms. The calculations used the second order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set, and spin–orbit couplings were handled separately in the restricted active space state interaction (RASSI-SO) procedure. For complexes 1–3, active electrons in seven active orbitals include all f electrons (CAS (9 in 7 for DyIII)) in the CASSCF calculation. To exclude all doubt, we calculated all roots in the active space. We mixed the maximum number of spin-free states that are possible using our hardware (all from 21 sextets, 128 from 224 quadruplets, 130 from 490 doublets for DyIII). The SINGLE_ANISO71–73 program was used to obtain energy levels, g tensors, magnetic axes (etc.), based on the above CASSCF/RASSI-SO calculations.
The theoretically predicted effective barrier has the following form as a function of temperature:74,75
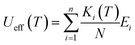 | (2) |
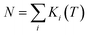 | (3) |
Each Kramers doublet (KD) has a particular demagnetization rate, namely:
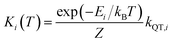 | (4) |
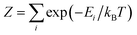 | (5) |
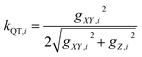 | (6) |
Data availability
The datasets supporting this article have been uploaded as part of the ESI material.†Author contributions
L. C. supervised and conceived the project. B. Z. and Z. C. designed and performed the experiments. X. C. and R. J. performed the structural characterization and the data analysis. C. J. synthesized the ligands. Y.-Q. Z. developed the theoretical model. Y. W. performed the magnetic measurements. L. C. and Y.-Q. Z. wrote the paper. Z.-Y. L., A. Y., and H. K. reviewed and edited the manuscript. All coauthors discussed and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation (21601070, 21971124, 21973046) and the Six Talent Peaks Project in Jiangsu Province, China (XCL-026).Notes and references
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Electronic read-out of a single nuclear spin using a molecular spin transistor, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- E. M. Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Molecular spin qudits for quantum algorithms, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Operating Quantum States in Single Magnetic Molecules: Implementation of Grover's Quantum Algorithm, Phys. Rev. Lett., 2017, 119, 187702–187705 CrossRef CAS PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing coherence in molecular spin qubits via atomic clock transitions, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Supramolecular spin valves, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- R. Sessoli and A. K. Powell, Strategies towards single molecule magnets based on lanthanide ions, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS.
- A. Zabala-Lekuona, J. M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS.
- V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Mononuclear Dysprosium Alkoxide and Aryloxide Single-Molecule Magnets, Chem. Eur. J., 2021, 27, 7625–7645 CrossRef CAS PubMed.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Molecular magnetism of lanthanide: Advances and perspectives, Coord. Chem. Rev., 2019, 378, 350–364 CrossRef CAS.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- B. M. Day, F.-S. Guo and R. A. Layfield, Cyclopentadienyl Ligands in Lanthanide Single-Molecule Magnets: One Ring To Rule Them All?, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- M. Feng and M.-L. Tong, Single Ion Magnets from 3d to 5f: Developments and Strategies, Chem. Eur. J., 2018, 24, 7574–7594 CrossRef CAS PubMed.
- A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets, Coord. Chem. Rev., 2018, 367, 163–216 CrossRef CAS.
- S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. S. Walsh and F. Tuna, Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies, Coord. Chem. Rev., 2017, 346, 216–239 CrossRef CAS.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Radical ligand-containing single-molecule magnets, Coord. Chem. Rev., 2015, 289, 149–176 CrossRef.
- F.-S. Guo, A. K. Bar and R. A. Layfield, Main Group Chemistry at the Interface with Molecular Magnetism, Chem. Rev., 2019, 119, 8479–8505 CrossRef CAS PubMed.
- F. Lu, M. M. Ding, J. X. Li, B. L. Wang and Y. Q. Zhang, Why lanthanide ErIII SIMs cannot possess huge energy barriers: a theoretical investigation, Dalton Trans., 2020, 49, 14576–14583 RSC.
- L. Ungur and L. F. Chibotaru, Magnetic anisotropy in the excited states of low symmetry lanthanide complexes, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090 RSC.
- S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078–2085 RSC.
- N. F. Chilton, Design Criteria for High-Temperature Single-Molecule Magnets, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, The first near-linear bis(amide) f-block complex: a blueprint for a high temperature single molecule magnet, Chem. Commun., 2015, 51, 101–103 RSC.
- L. Ungur and L. F. Chibotaru, Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets, Inorg. Chem., 2016, 55, 10043–10056 CrossRef CAS PubMed.
- B. Na, X.-J. Zhang, W. Shi, Y.-Q. Zhang, B.-W. Wang, C. Gao, S. Gao and P. Cheng, Six-Coordinate Lanthanide Complexes: Slow Relaxation of Magnetization in the Dysprosium(III) Complex, Chem. Eur. J., 2014, 20, 15975–15980 CrossRef CAS PubMed.
- M. Li, H. Wu, Z. Xia, L. Ungur, D. Liu, L. F. Chibotaru, H. Ke, S. Chen and S. Gao, An Inconspicuous Six-Coordinate Neutral DyIII Single-Ion Magnet with Remarkable Magnetic Anisotropy and Stability, Inorg. Chem., 2020, 59, 7158–7166 CrossRef CAS PubMed.
- J.-J. Lai, Z.-Y. Ruan, G.-Z. Huang, J.-L. Liu and M.-L. Tong, A high-performance dysprosium(III) single-ion magnet with quasi-Oh symmetry, Inorg. Chem. Commun., 2021, 132, 108807 CrossRef CAS.
- J. Long, A. O. Tolpygin, E. Mamontova, K. A. Lyssenko, M. D. Albaqami, D. Liu, L. F. Chibotaru, Y. Guari, J. Larionova and A. A. Trifonov, An unusual mechanism of building up of a high magnetization blocking barrier in an octahedral alkoxide Dy3+-based single-molecule magnet, Inorg. Chem. Front., 2021, 8, 1166–1174 RSC.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- Y. Ma, Y.-Q. Zhai, Y.-S. Ding, T. Han and Y.-Z. Zheng, Understanding a pentagonal-bipyramidal holmium(iii) complex with a record energy barrier for magnetisation reversal, Chem. Commun., 2020, 56, 3979–3982 RSC.
- Y.-S. Ding, T. Han, Y.-Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, A Study of Magnetic Relaxation in Dysprosium(III) Single-Molecule Magnets, Chem. Eur. J., 2020, 26, 5893–5902 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(iii) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181–5191 RSC.
- Y.-S. Ding, K.-X. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y.-Z. Zheng and N. F. Chilton, Field- and temperature-dependent quantum tunnelling of the magnetisation in a large barrier single-molecule magnet, Nat. Commun., 2018, 9, 3134 CrossRef PubMed.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Switching the anisotropy barrier of a single-ion magnet by symmetry change from quasi-D5h to quasi-Oh, Chem. Sci., 2013, 4, 3310–3316 RSC.
- A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Engineering macrocyclic high performance pentagonal bipyramidal Dy(III) single-ion magnets, Chem. Commun., 2020, 56, 12037–12040 RSC.
- M. Li, H. Wu, Q. Yang, H. Ke, B. Yin, Q. Shi, W. Wang, Q. Wei, G. Xie and S. Chen, Experimental and Theoretical Interpretation on the Magnetic Behavior in a Series of Pentagonal-Bipyramidal DyIII Single-Ion Magnets, Chem. Eur. J., 2017, 23, 17775–17787 CrossRef CAS PubMed.
- Z. Jiang, L. San, Q. Yang, B. Yin, H. Ke, J. Han, Q. Wei, G. Xie and S. Chen, Excess axial electrostatic repulsion as a criterion for pentagonal bipyramidal DyIII single-ion magnets with high Ueff and TB, J. Mater. Chem. C, 2018, 6, 4273–4280 RSC.
- H. Wu, M. Li, B. Yin, Z. Xia, H. Ke, Q. Wei, G. Xie, S. Chen and S. Gao, Fine-tuning the type of equatorial donor atom in pentagonal bipyramidal Dy(III) complexes to enhance single-molecule magnet properties, Dalton Trans., 2019, 48, 16384–16394 RSC.
- L. Zhu, Y. Dong, B. Yin, P. Ma and D. Li, Improving the single-molecule magnet properties of two pentagonal bipyramidal Dy3+ compounds by the introduction of both electron-withdrawing and-donating groups, Dalton Trans., 2021, 50, 12607–12618 RSC.
- M. Murrie, A. Canaj, S. Dey, E. R. Marti, C. Wilson and G. Rajaraman, Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets, Angew. Chem., Int. Ed., 2019, 58, 14146–14151 CrossRef PubMed.
- Z.-H. Li, Y.-Q. Zhai, W.-P. Chen, Y.-S. Ding and Y.-Z. Zheng, Air-Stable Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets with Nearly Perfect D6h Local Symmetry, Chem. Eur. J., 2019, 25, 16219–16224 CrossRef CAS PubMed.
- Z. Zhu, Z. Zhao, T. Feng, X. Liu, X. Ying, X.-L. Li, Y.-Q. Zhang and J. Tang, Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K, J. Am. Chem. Soc., 2021, 143, 10077–10082 CrossRef CAS PubMed.
- J. Li, S. Gómez-Coca, B. S. Dolinar, L. Yang, F. Yu, M. Kong, Y.-Q. Zhang, Y. Song and K. R. Dunbar, Hexagonal Bipyramidal Dy(III) Complexes as a Structural Archetype for Single-Molecule Magnets, Inorg. Chem., 2019, 58, 2610–2617 CrossRef CAS PubMed.
- W. Zhao, H. Cui, X.-Y. Chen, G. Yi, L. Chen, A. Yuan and C.-L. Luo, An eight-coordinate ytterbium complex with a hexagonal bipyramid geometry exhibiting field-induced single-ion magnet behaviour, Dalton Trans., 2019, 48, 5621–5626 RSC.
- X. Cai, Z. Cheng, Y. Wu, R. Jing, S.-Q. Tian, L. Chen, Z.-Y. Li, Y.-Q. Zhang, H.-H. Cui and A. Yuan, Tuning the Equatorial Negative Charge in Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets to Improve the Magnetic Behavior, Inorg. Chem., 2022, 61, 3664–3673 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. Layfield, A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, High-temperature magnetic blocking and magneto-structural correlations in a series of dysprosium(III) metallocenium single-molecule magnets, Chem. Sci., 2018, 9, 8492–8503 RSC.
- C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, Synthesis and Magnetism of Neutral, Linear Metallocene Complexes of Terbium(II) and Dysprosium(II), J. Am. Chem. Soc., 2019, 141, 12967–12973 CrossRef CAS PubMed.
- L. Norel, L. E. Darago, B. L. Guennic, K. Chakarawet, M. I. Gonzalez, J. H. Olshansky, S. Rigaut and J. R. Long, A Terminal Fluoride Ligand Generates Axial Magnetic Anisotropy in Dysprosium Complexes, Angew. Chem., Int. Ed., 2018, 57, 1933–1938 CrossRef CAS PubMed.
- A. B. Canaj, M. K. Singh, E. R. Marti, M. Damjanović, C. Wilson, O. Céspedes, W. Wernsdorfer, G. Rajaraman and M. Murrie, Boosting axiality in stable high-coordinate Dy(III) single-molecule magnets, Chem. Commun., 2019, 55, 5950–5953 RSC.
- M. Hojorat, H. A. Sabea, L. Norel, K. Bernot, T. Roisnel, F. Gendron, B. L. Guennic, E. Trzop, E. Collet, J. R. Long and S. Rigaut, Hysteresis Photomodulation via Single-Crystal-to-Single-Crystal Isomerization of a Photochromic Chain of Dysprosium Single-Molecule Magnets, J. Am. Chem. Soc., 2020, 142, 931–936 CrossRef CAS PubMed.
- B.-K. Ling, Y.-Q. Zhai, J. Han, T. Han and Y.-Z. Zheng, A stable dysprosium(III) complex with a terminal fluoride ligand showing high resolution luminescence and slow magnetic relaxation, Dalton Trans., 2020, 49, 6969–6973 RSC.
- F. A. Mautner, M. Koikawa, M. Mikuriya, E. V. Harrelson and S. S. Massoud, Copper(II)–azido complexes constructed from polypyridyl amine ligands, Polyhedron, 2013, 59, 17–22 CrossRef CAS.
- D. G. Lonnon, D. C. Craig, S. B. Colbran and P. V. Bernhardt, Novel one-dimensional structures and solution behaviour of copper(II) bromide and chloride complexes of a new pentapyridyldiamine ligand, Dalton Trans., 2004, 778–787 RSC.
- D. G. Lonnon, D. C. Craig and S. B. Colbran, Monomeric and dimeric metal complexes of a simply prepared and versatile pentapyridyldiamine, Inorg. Chem. Commun., 2002, 5, 958–962 CrossRef CAS.
- G. Yi, H.-H. Cui, C. Zhang, W. Zhao, L. Chen, Y.-Q. Zhang, X.-T. Chen, Y. Song and A. Yuan, A capped trigonal prismatic cobalt(II) complex as a structural archetype for single-ion magnets, Dalton Trans., 2020, 49, 2063–2067 RSC.
- G. Yi, C. Zhang, W. Zhao, H. Cui, L. Chen, Z. Wang, X.-T. Chen, A. Yuan, Y.-Z. Liu and Z.-W. Ouyang, Structure, magnetic anisotropy and relaxation behavior of seven-coordinate Co(II) single-ion magnets perturbed by counter-anions, Dalton Trans., 2020, 49, 7620–7627 RSC.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, Shape Program, Version 2.1, 2013 Search PubMed.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- D. Casanova, M. Llunell, P. Alemany and S. Alvarez, The Rich Stereochemistry of Eight-Vertex Polyhedra: A Continuous Shape Measures Study, Chem. Eur. J., 2005, 11, 1479–1494 CrossRef CAS PubMed.
- K. S. Cole and R. H. Cole, Dispersion and absorption in dielectrics I. Alternating current characteristics, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Relaxation dynamics of dysprosium(III) single molecule magnets, Dalton Trans., 2011, 40, 9953–9963 RSC.
- D. Reta and N. F. Chilton, Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575 RSC.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur and A. Soncini, The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- L. Ungur, W. V. Heuvel and L. F. Chibotaru, Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles, New J. Chem., 2009, 33, 1224–1230 RSC.
- L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, Structure, Magnetism, and Theoretical Study of a Mixed-Valence CoII3CoIII4 Heptanuclear Wheel: Lack of SMM Behavior despite Negative Magnetic Anisotropy, J. Am. Chem. Soc., 2008, 130, 12445–12455 CrossRef CAS PubMed.
- D. Aravena, Ab Initio Prediction of Tunneling Relaxation Times and Effective Demagnetization Barriers in Kramers Lanthanide Single-Molecule Magnets, J. Phys. Chem. Lett., 2018, 9, 5327–5333 CrossRef CAS PubMed.
- B. Yin and C. C. Li, A method to predict both the relaxation time of quantum tunneling of magnetization and the effective barrier of magnetic reversal for a Kramers single-ion magnet, Phys. Chem. Chem. Phys., 2020, 22, 9923–9933 RSC.
- A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, High performance single-molecule magnets, Orbach or Raman relaxation suppression, Inorg. Chem. Front., 2020, 7, 2478–2486 RSC.
- G. M. Sheldrick, A short history of SHELX, Acta Cryst, 2008, 64, 112–122 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELX-97, Program for Crystal Structure Refinement, University of Göttingen, Germany, 1997 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The powder XRD pattern, detailed crystallographic data, additional magnetic data, ab initio studies. CCDC 2212617, 2166032 and 2166033. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc03182e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |