Open Access Article
Open Access ArticleState-resolved infrared spectrum of the protonated water dimer: revisiting the characteristic proton transfer doublet peak†
Henrik R. Larsson *ab,
Markus Schröder
*ab,
Markus Schröder c,
Richard Beckmannd,
Fabien Brieuc‡
d,
Christoph Schran§
c,
Richard Beckmannd,
Fabien Brieuc‡
d,
Christoph Schran§
 d,
Dominik Marxd and
Oriol Vendrell
d,
Dominik Marxd and
Oriol Vendrell c
c
aDepartment of Chemistry and Biochemistry, University of California, Merced, CA 95343, USA
bDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125, USA
cTheoretische Chemie, Physikalisch-Chemisches Institut, Universität Heidelberg, Im Neuenheimer Feld 229, D – 69120 Heidelberg, Germany
dLehrstuhl für Theoretische Chemie, Ruhr-Universität Bochum, 44780 Bochum, Germany
First published on 30th August 2022
Abstract
The infrared (IR) spectra of protonated water clusters encode precise information on the dynamics and structure of the hydrated proton. However, the strong anharmonic coupling and quantum effects of these elusive species remain puzzling up to the present day. Here, we report unequivocal evidence that the interplay between the proton transfer and the water wagging motions in the protonated water dimer (Zundel ion) giving rise to the characteristic doublet peak is both more complex and more sensitive to subtle energetic changes than previously thought. In particular, hitherto overlooked low-intensity satellite peaks in the experimental spectrum are now unveiled and mechanistically assigned. Our findings rely on the comparison of IR spectra obtained using two highly accurate potential energy surfaces in conjunction with highly accurate state-resolved quantum simulations. We demonstrate that these high-accuracy simulations are important for providing definite assignments of the complex IR signals of fluxional molecules.
1 Introduction
Protonated water clusters play a key role in chemistry and biology, yet their quantum nature continues to puzzle scientists.1–5 One of the smallest clusters, the protonated water dimer or Zundel ion, H(H2O)2+, is particularly important and interesting as it can be understood as one of the building blocks of acidic water,6,7 where its infrared (IR) spectral signatures appear.8–10 Its structure of a proton being “sandwiched” by two water units leads to an unconventional bonding,7,11 serving as a limiting case of a characteristic pattern6,12 that is observed in a variety of protonated clusters.7 Its IR spectrum is of particular importance, as it reveals information about chemical bonding and the quantum nature of molecular vibrations. However, the IR spectrum of the Zundel ion is complicated – as such and due to tagging effects.3,13–16 Unexpectedly, its complexity even increases upon deuteration.17,18 Most dominant in the spectrum is the famous doublet near 1000 cm−1, whose vibrational character had not been understood initially.13 Quantum dynamics simulations of the Zundel ion allow us to understand the spectrum in full detail. However, they are difficult to perform for the following three reasons: (i) its dimensionality with 15 vibrational degrees of freedom, (ii) the non-obvious quantum entanglement of the vibrational zero-order states, and (iii) the fluxional nature of the protons in the Zundel ion with several equivalent minima, connected by only shallow potential barriers. When combined as in case of the Zundel ion, these difficulties severely challenge quantum dynamics simulations even today.To date, the multiconfiguration time-dependent Hartree (MCTDH) method has been the only one that could fully reproduce the experimental IR spectrum (save for tagging effects) and it revealed for the first time the characteristics of the doublet.14,15,19 According to MCTDH analysis, it consists of a Fermi resonance, where low-frequency, low-intensity wagging (pyramidalization) motions of the water units entangle with the proton transfer motion. The analysis has later been confirmed by other simulations.16,20,21
While MCTDH wavefunction propagation enables the understanding of the Zundel IR spectrum, the analysis of the vibrational transitions is cumbersome because information on the vibrational structure is only indirectly accessible through observables and low-dimensional probability densities. Further, the spectral resolution of wavefunction propagations is limited by the propagation time and the longer the propagation time, the more complicated the propagated wavefunction becomes. It is desirable to being able to obtain the actual vibrational excited wavefunction that is responsible for a particular peak in the IR spectrum, but this is difficult due to the sheer number of excited eigenstates that are present in such a system of high anharmonicity and dimensionality.
Here, we present new simulations that not only give more accurate vibrational spectra via wavefunction propagations but also reveal the full eigenstate spectrum with up to 900 eigenstates to high accuracy for a vibrational energy up to ∼1900 cm−1. Two highly accurate potential energy surfaces (PESs) and dipole moment surfaces (DMSs) are used, namely the pioneering permutationally-invariant-polynomial-based HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) surfaces22 and the more recent BBSM
surfaces22 and the more recent BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) neural-network-based surfaces,23,24 which so far has not been used for fully, rigorous quantum simulations. In the following, by referring to one of the used PESs we imply the usage of the corresponding DMS as well.
neural-network-based surfaces,23,24 which so far has not been used for fully, rigorous quantum simulations. In the following, by referring to one of the used PESs we imply the usage of the corresponding DMS as well.
Our full-dimensional quantum dynamics simulations consist of recently introduced vibrational tree tensor network states (TTNS) methodology,25 as well as new, more accurate and more compact representations of the PES.26,27 The TTNS method is based on the density matrix renormalization group (DMRG),28,29 shares the same wavefunction ansatz as the multilayer (ML) MCTDH method, enables both time-independent and time-dependent simulations25,30,31 (denoted as ti-TTNS and td-TTNS), and, most importantly here, the time-independent simulations are computationally much less demanding than in ML-MCTDH.25 This allows us to fully identify the nature of each peak in the spectrum by systematically characterising the eigenstates.
The key finding of this study is that the interplay between the wagging and the proton motions is more complex than previously thought in a critical way. In particular, we disclose that astonishingly subtle changes in the energetics of the Zundel ion can lead to very different features in the IR spectrum. This not only has important implications to PES development and the quantum dynamics of fluxional molecules in general, but it will also open the door toward understanding the chemistry of (micro-)solvated species.
Previous MCTDH simulations on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES revealed that the characteristic doublet contains contributions of two states, one with one quantum in the proton transfer motion, and another one with one quantum in the water–water stretch motion and two quanta in the wagging motions. Here, in contrast, our simulations on the same PES reveal that there are not two but three dominant eigenstates that are responsible for the “doublet” in the IR spectrum. Besides the known contributions from a state with two quanta in the wagging motions, there is an additional dominant contribution from a state having four quanta – only discovered with our novel TTNS-based quantum dynamics method – giving overall three dominant peaks in the IR spectrum. In contrast, and in accord with the established knowledge from the MCTDH simulations, the newer BBSM
PES revealed that the characteristic doublet contains contributions of two states, one with one quantum in the proton transfer motion, and another one with one quantum in the water–water stretch motion and two quanta in the wagging motions. Here, in contrast, our simulations on the same PES reveal that there are not two but three dominant eigenstates that are responsible for the “doublet” in the IR spectrum. Besides the known contributions from a state with two quanta in the wagging motions, there is an additional dominant contribution from a state having four quanta – only discovered with our novel TTNS-based quantum dynamics method – giving overall three dominant peaks in the IR spectrum. In contrast, and in accord with the established knowledge from the MCTDH simulations, the newer BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES displays again only two peaks for the doublet whereas the state with four quanta in the wagging motion is blueshifted and can indeed be identified as satellite peak of the doublet in the experimental spectrum, in support of our assignment.
PES displays again only two peaks for the doublet whereas the state with four quanta in the wagging motion is blueshifted and can indeed be identified as satellite peak of the doublet in the experimental spectrum, in support of our assignment.
2 Setup
Our benchmark-quality simulations are based on the Hamiltonian in polyspherical coordinates set up by Vendrell et al.15,19,32 We fitted both the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and the BBSM
and the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PESs into a form more suitable for (ML-)MCTDH and TTNS simulations. We use the recently developed Monte Carlo canonical polyadic decomposition (MCCPD) approach for refitting the PESs.26,27 The refitting introduced a mean/root-mean-square error of ∼0.2 cm−1/∼11 cm−1. For comparison, the mean/root-mean-square error of the original cluster expansion of the HBB
PESs into a form more suitable for (ML-)MCTDH and TTNS simulations. We use the recently developed Monte Carlo canonical polyadic decomposition (MCCPD) approach for refitting the PESs.26,27 The refitting introduced a mean/root-mean-square error of ∼0.2 cm−1/∼11 cm−1. For comparison, the mean/root-mean-square error of the original cluster expansion of the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES used in ref. 14, 15, 19 and 32 is about ∼24 cm−1/∼4 × 103 cm−1.27 To validate the accuracy of both the two PESs and, as additional validation, of the two MCCPDs of the respective PESs, we compare the energies of the PESs from samples of ∼2000 configurations with direct, “gold standard” basis-set-extrapolated coupled cluster singles and doubles with perturbative triples (CCSD(T)) electronic structure energies, see ESI† for details. With these ∼2000 configurations, for the HBB
PES used in ref. 14, 15, 19 and 32 is about ∼24 cm−1/∼4 × 103 cm−1.27 To validate the accuracy of both the two PESs and, as additional validation, of the two MCCPDs of the respective PESs, we compare the energies of the PESs from samples of ∼2000 configurations with direct, “gold standard” basis-set-extrapolated coupled cluster singles and doubles with perturbative triples (CCSD(T)) electronic structure energies, see ESI† for details. With these ∼2000 configurations, for the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES we obtain a mean absolute error (MAE) of 203 cm−1, whereas for the BBSM
PES we obtain a mean absolute error (MAE) of 203 cm−1, whereas for the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES we obtain an improved accuracy with an MAE of 75 cm−1. The MCCPDs have essentially the same accuracy.
PES we obtain an improved accuracy with an MAE of 75 cm−1. The MCCPDs have essentially the same accuracy.
We represent the wavefunction as TTNS, which has the same mathematical structure as the wavefunction used in the ML-MCTDH method.25,33 It differs, however, by the use of more efficient algorithms that are based on a generalization of the density matrix renormalization group (DMRG).25,28,29 For the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) /BBSM
/BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES we computed up to ∼900/550 of the lowest eigenstates, despite the large density of states that is evident in this fluxional cluster. We verify the eigenstate “stick” spectrum by comparing with the spectrum obtained from wavefunction propagation using the time-dependent DMRG for TTNSs.30,31 The Fourier-transformed propagation-based spectrum allows us to obtain the full spectrum with broadened peaks, while the stick spectrum reveals every single detail. Details of the employed methodology, the numerical parameters, convergence tests, as well as additional results are presented in the ESI.†
PES we computed up to ∼900/550 of the lowest eigenstates, despite the large density of states that is evident in this fluxional cluster. We verify the eigenstate “stick” spectrum by comparing with the spectrum obtained from wavefunction propagation using the time-dependent DMRG for TTNSs.30,31 The Fourier-transformed propagation-based spectrum allows us to obtain the full spectrum with broadened peaks, while the stick spectrum reveals every single detail. Details of the employed methodology, the numerical parameters, convergence tests, as well as additional results are presented in the ESI.†
3 Results and discussion
Fig. 1 displays the experimental spectrum13,17 and the spectra simulated using either of the two used PESs. For the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) /BBSM
/BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES we show in Fig. 1 up to ∼900/550 states up to ∼1900 cm−1/∼1700 cm−1; note that most of these states are not IR-active so that much fewer lines are visible in the spectra. The total spectrum, including IR inactive states, is shown as small lines on the abscissa. The higher the energy, the higher the density of states, thus indicating the large spectral complexity of the Zundel ion. The energies of the IR inactive states differ substantially between the two PESs, which will be discussed in more detail elsewhere. Compared to the propagation-based spectrum (td-TTNS), the stick spectrum (ti-TTNS) has slightly different intensities and the transitions are centered at slightly lower wavenumbers. This is because the stick spectrum is not convoluted to account for finite resolution, and because we computed the eigenstate spectrum with higher accuracy than the wavefunction propagation. Convergence tests show that the eigenstates for levels up to ∼1030 cm−1 are converged to less than 1.5 cm−1, much less than the errors of the PES representation (see ESI† for further details). This is the first time that so many states have been computed to such a high accuracy for such a high-dimensional, fluxional cluster.
PES we show in Fig. 1 up to ∼900/550 states up to ∼1900 cm−1/∼1700 cm−1; note that most of these states are not IR-active so that much fewer lines are visible in the spectra. The total spectrum, including IR inactive states, is shown as small lines on the abscissa. The higher the energy, the higher the density of states, thus indicating the large spectral complexity of the Zundel ion. The energies of the IR inactive states differ substantially between the two PESs, which will be discussed in more detail elsewhere. Compared to the propagation-based spectrum (td-TTNS), the stick spectrum (ti-TTNS) has slightly different intensities and the transitions are centered at slightly lower wavenumbers. This is because the stick spectrum is not convoluted to account for finite resolution, and because we computed the eigenstate spectrum with higher accuracy than the wavefunction propagation. Convergence tests show that the eigenstates for levels up to ∼1030 cm−1 are converged to less than 1.5 cm−1, much less than the errors of the PES representation (see ESI† for further details). This is the first time that so many states have been computed to such a high accuracy for such a high-dimensional, fluxional cluster.
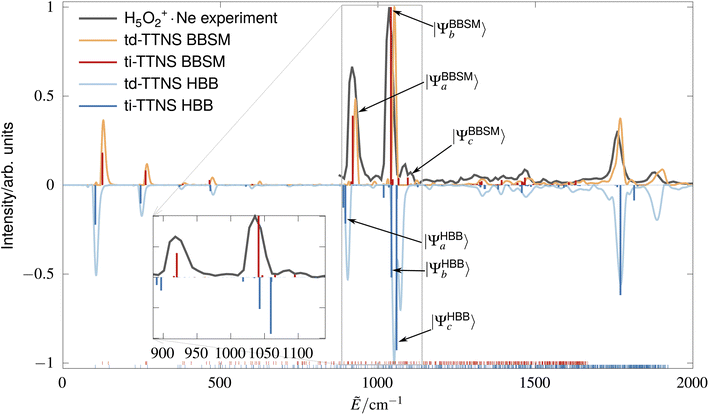 | ||
Fig. 1 Infrared spectrum of the Zundel ion: the experimental predissociation spectrum using neon tagging (gray)13,17 and computed spectra using either the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (red) or the HBB (red) or the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (blue, negative intensities) potential energy surfaces; the inset magnified the spectral region in the gray box. The computed spectra are either based on time-dependent wavefunction propagations (td-TTNS: lines) or based on eigenstate optimizations (ti-TTNS: sticks). The wavefunction labels mark the states as analyzed in the text. All eigenstates computed, regardless of intensities, are shown as small lines on the abscissa. (blue, negative intensities) potential energy surfaces; the inset magnified the spectral region in the gray box. The computed spectra are either based on time-dependent wavefunction propagations (td-TTNS: lines) or based on eigenstate optimizations (ti-TTNS: sticks). The wavefunction labels mark the states as analyzed in the text. All eigenstates computed, regardless of intensities, are shown as small lines on the abscissa. | ||
While both PESs, in particular the newer BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) one, yield spectra that overall are in very good agreement with the experimental spectrum, a closer look reveals a striking difference between the simulated spectra: the most characteristic signal of the IR spectrum, the doublet around 1000 cm−1, consists of two dominant peaks on the BBSM
one, yield spectra that overall are in very good agreement with the experimental spectrum, a closer look reveals a striking difference between the simulated spectra: the most characteristic signal of the IR spectrum, the doublet around 1000 cm−1, consists of two dominant peaks on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES whereas on the HBB
PES whereas on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES it consists of three peaks! This is in contrast to the pioneering MCTDH simulations on the HBB
PES it consists of three peaks! This is in contrast to the pioneering MCTDH simulations on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES.14,15,18,32 These early MCTDH simulations of such a complicated system were less accurate and thus had simply missed the additional peak on the HBB
PES.14,15,18,32 These early MCTDH simulations of such a complicated system were less accurate and thus had simply missed the additional peak on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. Indeed, our modern ML-MCTDH simulations with improved convergence parameters also yield three peaks on the HBB
PES. Indeed, our modern ML-MCTDH simulations with improved convergence parameters also yield three peaks on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES and overall are in full agreement with our TTNS simulations. Comparing the overlaps between the states on each PES reveals that the third peak observed for the HBB
PES and overall are in full agreement with our TTNS simulations. Comparing the overlaps between the states on each PES reveals that the third peak observed for the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES is not missing in the BBSM
PES is not missing in the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES, but it is blueshifted and has a much smaller intensity.
PES, but it is blueshifted and has a much smaller intensity.
We focus now on the nature of the three dominating vibrational transitions and pinpoint the differences resulting from the quality of the PESs. According to Fig. 1, we label these states as Ψa, Ψb, and Ψc, respectively, see also Fig. 1. When needed, we will use superscripts to display which PES has been used for their optimization. There are two additional, satellite peaks between ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b and ΨBBSM
b and ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c that have a similar intensity than ΨBBSM
c that have a similar intensity than ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c and contain a combination of various excitations. More details on these and other eigenstates that do not dominate the doublet will be presented elsewhere.
c and contain a combination of various excitations. More details on these and other eigenstates that do not dominate the doublet will be presented elsewhere.
Our main findings, namely (i) the nature of the signals dominant in the doublet, (ii) the decomposition of the corresponding wavefunctions into coupling zero-order states, and (iii) their critical dependence on subtle energetic shifts, are summarised in Fig. 2. Panel (a) displays the coupling – a Fermi resonance – identified in the previous MCTDH studies on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES.14,19 There, the doublet consists of two states that can be described as linear combination (entanglement) of two zero-order states: one zero-order state with one quantum in the water–water stretch motion (R) and two quanta in the two wagging modes (|02〉–|20〉), and another zero-order state with one quantum in the proton transfer motion (z). These two zero-order states are labeled |1R, 02–20〉 and |1z〉 respectively. Panel (b) displays our revised coupling scheme on the HBB
PES.14,19 There, the doublet consists of two states that can be described as linear combination (entanglement) of two zero-order states: one zero-order state with one quantum in the water–water stretch motion (R) and two quanta in the two wagging modes (|02〉–|20〉), and another zero-order state with one quantum in the proton transfer motion (z). These two zero-order states are labeled |1R, 02–20〉 and |1z〉 respectively. Panel (b) displays our revised coupling scheme on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. There, an additional zero-order state |04–40〉, consisting of four quanta in the wagging motion, has a low enough energy that it couples with the two other zero-order states, leading to a more complex quantum resonance and a significant intensity sharing of the |ΨHBB
PES. There, an additional zero-order state |04–40〉, consisting of four quanta in the wagging motion, has a low enough energy that it couples with the two other zero-order states, leading to a more complex quantum resonance and a significant intensity sharing of the |ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b〉 and |ΨHBB
b〉 and |ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c〉. Panel (c) displays the coupling scheme on the BBSM
c〉. Panel (c) displays the coupling scheme on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES, which, ironically, is much more similar to that of panel (a) than to (b). Here, the |04–40〉 state is blueshifted and, therefore, does not contribute anymore to the doublet. There is no intensity-sharing and |ΨBBSM
PES, which, ironically, is much more similar to that of panel (a) than to (b). Here, the |04–40〉 state is blueshifted and, therefore, does not contribute anymore to the doublet. There is no intensity-sharing and |ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c〉 only appears in the spectrum as one of two satellite peaks on the blue wing of |ΨBBSM
c〉 only appears in the spectrum as one of two satellite peaks on the blue wing of |ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b〉 – in good agreement with the experimental IR spectrum as depicted in the upper panel of Fig. 1. (The other satellite peak is more complicated and will be discussed elsewhere.)
b〉 – in good agreement with the experimental IR spectrum as depicted in the upper panel of Fig. 1. (The other satellite peak is more complicated and will be discussed elsewhere.)
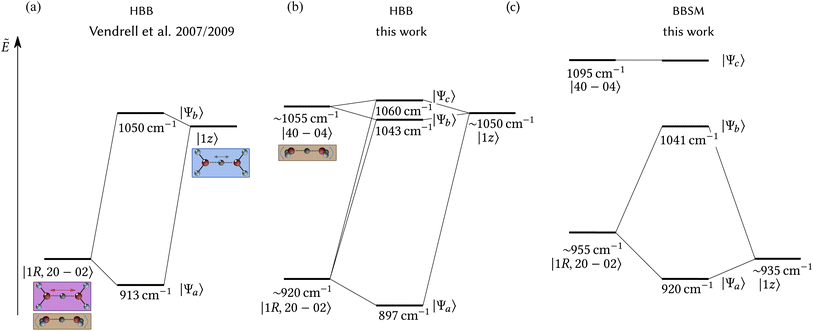 | ||
Fig. 2 Schematics of the coupling scheme of the zero-order states around the doublet in the Zundel infrared spectrum. Panel (a) displays the previously identified coupling on the pioneering HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES.14,19 Panel (b) displays our revised coupling on the same PES. Panel (c) displays the coupling on the recent BBSM PES.14,19 Panel (b) displays our revised coupling on the same PES. Panel (c) displays the coupling on the recent BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. The insets visualize schematically the vibrational excitations of the zero-order states. The energies of the zero-order states are estimated either from the exact |1R〉 and |02–20〉/|04–40〉 states, or from the |1z, 1α〉 combination state, where α represents the torsion motion. PES. The insets visualize schematically the vibrational excitations of the zero-order states. The energies of the zero-order states are estimated either from the exact |1R〉 and |02–20〉/|04–40〉 states, or from the |1z, 1α〉 combination state, where α represents the torsion motion. | ||
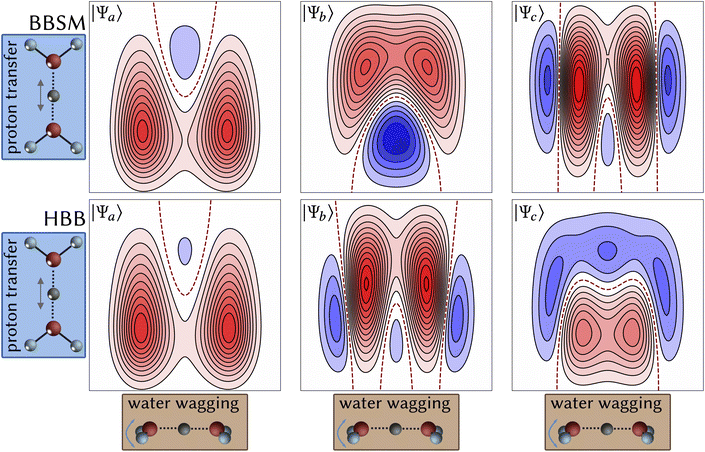
Let us now explain our findings in more detail. Our analysis is based on the time-independent eigenstate simulations, which enable us to directly analyze the wavefunctions responsible for each peak, thus providing rigorous assignment of IR peaks to the structural dynamics at the level of vibrational motion. Moreover, we confirm this analysis by computing overlaps of the wavefunctions with constructed zero-order states (see ESI†). Fig. 3 shows cuts of the three most relevant eigenstates Ψa, Ψb, and Ψc on the two PESs along one of the wagging motions and the proton transfer motion. Each node (zero-crossing) corresponds to one quantum in a particular coordinate. The plots of Ψa clearly indicate two quanta (nodes) for the wagging motion (|02–20〉) and one quantum for the proton transfer motion (|1z〉). Further inspections reveal an additional quantum for the water–water stretch motion (|1R〉). This confirms the assignment shown in Fig. 2: |Ψa〉 consists of two entangled zero-order states, namely |02–20; 1R〉 and |1z〉. There is no significant difference between ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a and ΨHBB
a and ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a.
a.
In stark contrast to Ψa, for Ψb and Ψc we find significant differences between the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES and the HBB
PES and the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. At first sight, ΨBBSM
PES. At first sight, ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b looks much more similar to ΨHBB
b looks much more similar to ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c than to ΨHBB
c than to ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b. We first analyze the states on the BBSM
b. We first analyze the states on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES and then compare them with the states on the HBB
PES and then compare them with the states on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. ΨBBSM
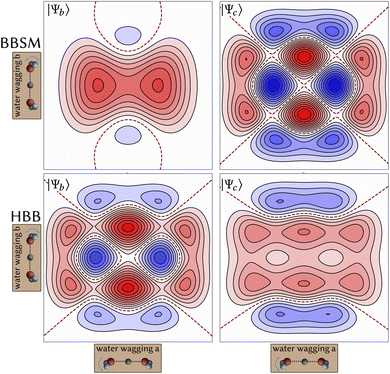
PES. ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b has a similar nodal pattern as Ψa, as it also displays two quanta along the wagging motion and one quantum along the proton transfer motion. These similarities are the characteristics of a Fermi resonance. ΨBBSMc, however, shows a dominant contribution of not two, but four quanta in the wagging motion. The rich vibrational structure along the two wagging coordinates is displayed in Fig. 4. This enables us to clearly assign ΨBBSM
b has a similar nodal pattern as Ψa, as it also displays two quanta along the wagging motion and one quantum along the proton transfer motion. These similarities are the characteristics of a Fermi resonance. ΨBBSMc, however, shows a dominant contribution of not two, but four quanta in the wagging motion. The rich vibrational structure along the two wagging coordinates is displayed in Fig. 4. This enables us to clearly assign ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c as |04–40〉 wagging state.
c as |04–40〉 wagging state.
We now turn to the states on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES. For ΨHBB
PES. For ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b and unlike ΨBBSMb, in addition to one quantum in the proton transfer motion, there are not two but four quanta along the wagging motion. Fig. 4 clearly shows the similarities to ΨBBSM
b and unlike ΨBBSMb, in addition to one quantum in the proton transfer motion, there are not two but four quanta along the wagging motion. Fig. 4 clearly shows the similarities to ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c. Here, however, Fig. 3 and additional analysis reveals a more dominant excitation along the proton transfer motion, and we assign ΨHBB
c. Here, however, Fig. 3 and additional analysis reveals a more dominant excitation along the proton transfer motion, and we assign ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b as linear combination of the |04–40〉 wagging and the |1z〉 proton transfer zero-order states. Finally, similar to Ψa, we identify in ΨHBB
b as linear combination of the |04–40〉 wagging and the |1z〉 proton transfer zero-order states. Finally, similar to Ψa, we identify in ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c not only dominating contributions of the |02–20; 1R〉 and the |1z〉 states, but also contributions of the |04–40〉 wagging state. Thus, on the HBB
c not only dominating contributions of the |02–20; 1R〉 and the |1z〉 states, but also contributions of the |04–40〉 wagging state. Thus, on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES next to the resonance of the |02–20; 1R〉 and the |1z〉 state, which alone would lead to two dominant peaks, the |1z〉 state also resonates with the |04–40〉 wagging state. This coupling creates an additional splitting, leading to overall three peaks in the spectrum, a clear example of intensity sharing.
PES next to the resonance of the |02–20; 1R〉 and the |1z〉 state, which alone would lead to two dominant peaks, the |1z〉 state also resonates with the |04–40〉 wagging state. This coupling creates an additional splitting, leading to overall three peaks in the spectrum, a clear example of intensity sharing.
Why do the three particular zero-order states, |1R, 02–20〉, |04–40〉, and |1z〉, couple on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES and why is the |04–40〉 not involved in the coupling on the BBSM
PES and why is the |04–40〉 not involved in the coupling on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES? Estimating the energetics of the zero-order states as shown in Fig. 2 is the clue. The |02–20〉 and the |1R〉 states alone do not have enough energy (374 and 546 cm−1, respectively) to couple with |1z〉. Only a combination of these vibrational excitations leads to a state with similar energy than the |1z〉 state, which is required for efficient coupling. Next to the |02–20; 1R〉 state, on the HBB
PES? Estimating the energetics of the zero-order states as shown in Fig. 2 is the clue. The |02–20〉 and the |1R〉 states alone do not have enough energy (374 and 546 cm−1, respectively) to couple with |1z〉. Only a combination of these vibrational excitations leads to a state with similar energy than the |1z〉 state, which is required for efficient coupling. Next to the |02–20; 1R〉 state, on the HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES the |04–40〉 state has an energy that is very close to that of |1z〉. This leads to additional coupling, resulting in ΨHBB
PES the |04–40〉 state has an energy that is very close to that of |1z〉. This leads to additional coupling, resulting in ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b and ΨHBB
b and ΨHBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c. While |04–40〉 and |02–20; 1R〉 alone are barely IR active, large components of the |1z〉 lead to intensity sharing and thus large IR intensities in the spectrum for all three entangled states.
c. While |04–40〉 and |02–20; 1R〉 alone are barely IR active, large components of the |1z〉 lead to intensity sharing and thus large IR intensities in the spectrum for all three entangled states.
In contrast, on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES the |04–40〉 state is blueshifted by 40 cm−1 and the |1z〉 state is redshifted by 115 cm−1. This disfavors additional coupling between these states. Hence, only the |02–20; 1R〉 couples with |1z〉, leading to the pair of states, ΨBBSM
PES the |04–40〉 state is blueshifted by 40 cm−1 and the |1z〉 state is redshifted by 115 cm−1. This disfavors additional coupling between these states. Hence, only the |02–20; 1R〉 couples with |1z〉, leading to the pair of states, ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a and ΨBBSMb, which form a classical Fermi resonance. ΨBBSM
a and ΨBBSMb, which form a classical Fermi resonance. ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c is almost a pure |04–40〉 state with only minor contributions from |1z〉 and thus a weak IR intensity.
c is almost a pure |04–40〉 state with only minor contributions from |1z〉 and thus a weak IR intensity.
Which of these two scenarios reflects now the actual situation in experiment? While the experimental resolution is not high enough to fully reject the possibility of two states lying under one of the peaks of the doublet, there are two indications that the scenario on the BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES is more realistic: (1) the peak positions obtained from the newer BBSM
PES is more realistic: (1) the peak positions obtained from the newer BBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES are closer to the experimental spectrum and the PES is much closer to basis-set-extrapolated CCSD(T) energies as shown in the left panels of Fig. S3.† (2) ΨBBSM
PES are closer to the experimental spectrum and the PES is much closer to basis-set-extrapolated CCSD(T) energies as shown in the left panels of Fig. S3.† (2) ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c can be attributed to one of two satellite peaks in the experimental spectrum, and (3) another state between ΨBBSM
c can be attributed to one of two satellite peaks in the experimental spectrum, and (3) another state between ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b and ΨBBSM
b and ΨBBSM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c likely corresponds to the second satellite peak. We thus conclude that the additional coupling seen in the older HBB
c likely corresponds to the second satellite peak. We thus conclude that the additional coupling seen in the older HBB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PES is most likely an artifact that has previously been missed due to less accurate computation of the IR spectrum, which is only now disclosed in view of much improved methodologies.
PES is most likely an artifact that has previously been missed due to less accurate computation of the IR spectrum, which is only now disclosed in view of much improved methodologies.
Based on these findings, it is striking to demonstrate that such relatively small changes in the energetics lead to such drastic differences in the entanglement of the eigenstates and in the IR intensities, which serve as the experimental observables for these intricate phenomena. Moreover, we infer that minute changes in the environment can lead to even larger energy differences and we anticipate effects similar to those shown here for microsolvated clusters and larger clusters with additional solvation shells. To give three examples: (1) deuteration of the Zundel ion significantly alters the energetics of the zero-order states and vastly complicates the IR spectrum.18 (2) The experimental spectrum of H5O2+·Ar (and that of H5O2+·H2) is strikingly different to that of H5O2+·Ne, as it displays four and not two peaks around 1000 cm−1,17 indicating a similar complex coupling situation (the Ar atom attaches to one of the OH units and thus lifts degeneracy; in contrast, the spectra of H5O2+·Ne and H5O2+·He do not show significant differences and their spectra should be very close to that of the bare H5O2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34). (3) Recent ML-MCTDH simulations on the solvated hydronium or Eigen ion (H9O4+) reveal the contribution of dozens of eigenstates that dominate the IR activation of the hydronium O–H stretch motion and show that the proton vibrations of the Eigen ion can be understood in terms of an embedded Zundel subunit.35 Likewise, recent experimental studies indicate that the dynamics of protonated water clusters can be related to fluctuations of local electrical fields,36 which also appear for solvated H5O2+.9,37,38
34). (3) Recent ML-MCTDH simulations on the solvated hydronium or Eigen ion (H9O4+) reveal the contribution of dozens of eigenstates that dominate the IR activation of the hydronium O–H stretch motion and show that the proton vibrations of the Eigen ion can be understood in terms of an embedded Zundel subunit.35 Likewise, recent experimental studies indicate that the dynamics of protonated water clusters can be related to fluctuations of local electrical fields,36 which also appear for solvated H5O2+.9,37,38
4 Conclusions
In conclusion, we report high-accuracy, state-resolved simulations of the Zundel ion on two PESs with unprecedented accuracy. Using variational DMRG-like algorithms adapted to tree tensor network states and polyspherical coordinates, we are able to compute up to 900 eigenstates up to 1900 cm−1 with hitherto unreached accuracy for such a complex. Obtaining this large number of eigenstates has so far never been accomplished for a 15-dimensional, fluxional system using curvilinear coordinates, and this will serve as a benchmark for future quantum dynamics method developments. Only applying this advanced methodology allows us to draw definite conclusions on the quantum dynamics of the Zundel ion, in particular for the most dominant feature of the IR spectrum, namely the doublet around 1000 cm−1. Previous assignments are shown to be incomplete due to several limitations of the methods available close to two decades ago. The novel assignment of the doublet around 1000 cm−1 not only confirms the Fermi resonance nature of this proton transfer mode, but also explains so-far unassigned low-intensity satellite peaks in the experimental spectrum. In broader terms, our findings not only highlight the striking mechanistic consequences of the strong anharmonicity and fluxional character of this challenging but important molecular cluster, but also reveal how subtle effects of the energetics of the zero-order states can lead to qualitative changes of the IR spectrum, revealing fundamental quantum effects such as resonances, entanglement and intensity sharing. We are therefore convinced that the same computational approach as unleashed here for the first time will unveil similar spectral complexity upon assigning high-resolution IR spectra in a multitude of molecular complexes, notably when it comes to proton transfer in (micro-)solvation environments.Data availability
Further data is available from the authors upon reasonable request.Author contributions
H. R. L. and O. V. conceived the study; H. R. L. designed the study, developed the TTNS methodology and performed and analyzed the TTNS simulations; M. S. and O. V. performed the MCCPD fits and additional ML-MCTDH simulations; R. B., F. B., C. S., and D. M. created the interface for the BBSM PES, provided samples for the MCCPD procedure, and performed benchmarks for DMC configurations provided by M. S.; H. R. L. drafted the manuscript; all authors contributed to discussing the results and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Professor Joel Bowman for having made their potential energy surface available. HRL acknowledges support from the University of California Merced start-up funding during the last part of this work. HRL acknowledges support from a postdoctoral fellowship from the German Research Foundation (DFG) via grant LA 4442/1-1 during the first part of this work. HRL acknowledges computational time both on the Pinnacles cluster at UC Merced (supported by NSF OAC-2019144) and at the Resnick High Performance Computing Center, a facility supported by the Resnick Sustainability Institute at the California Institute of Technology. The Bochum work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – 390677874 – RESOLV as well as by the individual DFG grant MA 1547/19 to DM and supported by the “Center for Solvation Science ZEMOS” funded by the German Federal Ministry of Education and Research and by the Ministry of Culture and Research of North Rhine-Westphalia. RB acknowledges funding from the Studienstiftung des deutschen Volkes and CS acknowledges partial financial support from the Alexander von Humboldt-Stiftung. MS and OV thank the High Performance Computing Center in Stuttgart (HLRS) under the grant number HDQM_MCT as well as the bwHPC project of the state of Baden-Württemberg under grant number bw18K011 for providing computational resources.Notes and references
- K. R. Asmis, N. L. Pivonka, G. Santambrogio, M. Brümmer, C. Kaposta, D. M. Neumark and L. Wöste, Science, 2003, 299, 1375–1377 CrossRef CAS.
- J.-W. Shin, N. I. Hammer, E. G. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. A. Duncan, R. A. Christie and K. D. Jordan, Science, 2004, 304, 1137–1140 CrossRef CAS PubMed.
- J. M. Headrick, E. G. Diken, R. S. Walters, N. I. Hammer, R. A. Christie, J. Cui, E. M. Myshakin, M. A. Duncan, M. A. Johnson and K. D. Jordan, Science, 2005, 308, 1765–1769 CrossRef CAS.
- J. A. Fournier, C. J. Johnson, C. T. Wolke, G. H. Weddle, A. B. Wolk and M. A. Johnson, Science, 2014, 344, 1009–1012 CrossRef CAS PubMed.
- C. T. Wolke, J. A. Fournier, L. C. Dzugan, M. R. Fagiani, T. T. Odbadrakh, H. Knorke, K. D. Jordan, A. B. McCoy, K. R. Asmis and M. A. Johnson, Science, 2016, 354, 1131–1135 CrossRef CAS PubMed.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS.
- H. J. Zeng and M. A. Johnson, Annu. Rev. Phys. Chem., 2021, 72, 667–691 CrossRef CAS PubMed.
- M. Thämer, L. De Marco, K. Ramasesha, A. Mandal and A. Tokmakoff, Science, 2015, 350, 78–82 CrossRef.
- F. Dahms, B. P. Fingerhut, E. T. J. Nibbering, E. Pines and T. Elsaesser, Science, 2017, 357, 491–495 CrossRef CAS PubMed.
- J. A. Fournier, W. B. Carpenter, N. H. C. Lewis and A. Tokmakoff, Nat. Chem., 2018, 10, 932–937 CrossRef CAS PubMed.
- B. Dereka, Q. Yu, N. H. C. Lewis, W. B. Carpenter, J. M. Bowman and A. Tokmakoff, Science, 2021, 371, 160–164 CrossRef CAS PubMed.
- M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, Science, 1997, 275, 817–820 CrossRef CAS.
- N. I. Hammer, E. G. Diken, J. R. Roscioli, M. A. Johnson, E. M. Myshakin, K. D. Jordan, A. B. McCoy, X. Huang, J. M. Bowman and S. Carter, J. Chem. Phys., 2005, 122, 244301 CrossRef PubMed.
- O. Vendrell, F. Gatti and H.-D. Meyer, Angew. Chem., Int. Ed., 2007, 46, 6918–6921 CrossRef CAS PubMed.
- O. Vendrell, F. Gatti and H.-D. Meyer, J. Chem. Phys., 2007, 127, 184303 CrossRef.
- M. Baer, D. Marx and G. Mathias, Angew. Chem., Int. Ed., 2010, 49, 7346–7349 CrossRef CAS PubMed.
- L. R. McCunn, J. R. Roscioli, M. A. Johnson and A. B. McCoy, J. Phys. Chem. B, 2008, 112, 321–327 CrossRef CAS PubMed.
- O. Vendrell, F. Gatti and H.-D. Meyer, Angew. Chem., Int. Ed., 2009, 48, 352–355 CrossRef CAS.
- O. Vendrell, F. Gatti and H.-D. Meyer, J. Chem. Phys., 2009, 131, 034308 CrossRef.
- S. M. Dietrick and S. S. Iyengar, J. Chem. Theory Comput., 2012, 8, 4876–4890 CrossRef CAS PubMed.
- G. Bertaina, G. Di Liberto and M. Ceotto, J. Chem. Phys., 2019, 151, 114307 CrossRef CAS PubMed.
- X. Huang, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2005, 122, 044308 CrossRef.
- C. Schran, J. Behler and D. Marx, J. Chem. Theory Comput., 2020, 16, 88–99 CrossRef PubMed.
- R. Beckmann, F. Brieuc, C. Schran and D. Marx, J. Chem. Theory Comput., 2022 DOI:10.1021/acs.jctc.2c00511.
- H. R. Larsson, J. Chem. Phys., 2019, 151, 204102 CrossRef PubMed.
- M. Schröder and H.-D. Meyer, J. Chem. Phys., 2017, 147, 064105 CrossRef.
- M. Schröder, J. Chem. Phys., 2020, 152, 024108 CrossRef PubMed.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef PubMed.
- S. R. White, Phys. Rev. B, 1993, 48, 10345–10356 CrossRef CAS PubMed.
- J. Haegeman, C. Lubich, I. Oseledets, B. Vandereycken and F. Verstraete, Phys. Rev. B, 2016, 94, 165116 CrossRef.
- F. A. Y. N. Schröder, D. H. P. Turban, A. J. Musser, N. D. M. Hine and A. W. Chin, Nat. Commun., 2019, 10, 1062 CrossRef PubMed.
- O. Vendrell, M. Brill, F. Gatti, D. Lauvergnat and H.-D. Meyer, J. Chem. Phys., 2009, 130, 234305 CrossRef.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- C. J. Johnson, A. B. Wolk, J. A. Fournier, E. N. Sullivan, G. H. Weddle and M. A. Johnson, J. Chem. Phys., 2014, 140, 221101 CrossRef PubMed.
- M. Schröder, F. Gatti, D. Lauvergnat, H.-D. Meyer and O. Vendrell, arXiv:2204.03744, 2022.
- N. Yang, C. H. Duong, P. J. Kelleher and M. A. Johnson, Nat. Chem., 2020, 12, 159–164 CrossRef CAS PubMed.
- F. Dahms, R. Costard, E. Pines, B. P. Fingerhut, E. T. J. Nibbering and T. Elsaesser, Angew. Chem., Int. Ed., 2016, 55, 10600–10605 CrossRef CAS PubMed.
- W. B. Carpenter, Q. Yu, J. H. Hack, B. Dereka, J. M. Bowman and A. Tokmakoff, J. Chem. Phys., 2020, 153, 124506 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03189b |
| ‡ Current address: Laboratoire Matière en Conditions Extrêmes, Université Paris-Saclay, CEA, DAM, DIF, 91297 Arpajon, France. |
| § Current address: Yusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK. |
| This journal is © The Royal Society of Chemistry 2022 |