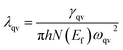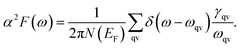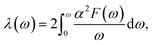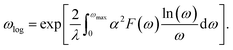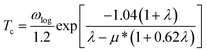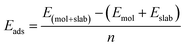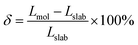Open Access Article
Open Access ArticleA two-dimensional Be2Au monolayer with planar hexacoordinate s-block metal atoms: a superconducting global minimum Dirac material with two perfect Dirac node-loops†
Meng-hui
Wang
a,
Zhong-hua
Cui
 *ae,
Sheng
Wang
c,
Quan
Li
*ae,
Sheng
Wang
c,
Quan
Li
 c,
Jijun
Zhao
d and
Zhongfang
Chen
c,
Jijun
Zhao
d and
Zhongfang
Chen
 *b
*b
aInstitute of Atomic and Molecular Physic, Jilin University, Changchun 130012, China. E-mail: zcui@jlu.edu.cn
bDepartment of Chemistry, University of Puerto Rico, San Juan, PR 00931, USA. E-mail: zhongfangchen@gmail.com
cState Key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun 130023, People's Republic of China
dKey Laboratory of Materials Modification by Laser, Ion and Electron Beams (Dalian University of Technology), Ministry of Education, Dalian, 116024, China
eKey Laboratory of Physics and Technology for Advanced Batteries (Ministry of Education), Jilin University, Changchun 130012, China
First published on 29th August 2022
Abstract
Using a starlike Be6Au7− cluster as a building block and following the bottom-up strategy, an intriguing two-dimensional (2D) binary s-block metal Be2Au monolayer with a P6/mmm space group was theoretically designed. Both the Be6Au7− cluster and the 2D monolayer are global minima featuring rule-breaking planar hexacoordinate motifs (anti-van't Hoff/Le Bel arrangement), and their high stabilities are attributed to good electron delocalization and electronic-stabilization-induced steric force. Strikingly, the Be2Au monolayer is a rare Dirac material with two perfect Dirac node-loops in the band structure and is a phonon-mediated superconductor with a critical temperature of 4.0 K. The critical temperature can be enhanced up to 11.0 K by applying compressive strain at only 1.6%. This study not only identifies a new binary s-block metal 2D material, namely Be2Au, which features planar hexacoordination, and a candidate superconducting material for further explorations, but also provides a new strategy to construct 2D materials with novel chemical bonding.
1. Introduction
Planar hypercoordinate motifs represent a class of exotic geometries and rule-breaking bonding, and have been constantly pushing the limits of our understanding and knowledge. This area was triggered by the planar tetracoordinate carbon (ptC) imagination, vividly going beyond two well-established rules in organic chemistry, i.e., tetracoordinate (Kekulé, 1857)1 and tetrahedral geometries (van't Hoff and Le Bel, 1874).2,3 In 1968, Monkhorst raised the question of the possibility of atypical ptC molecules.4 In 1970, Hoffmann et al. proposed strategies to stabilize ptC motifs by using electronic and/or mechanical approaches,5 following which in 1976 Schleyer and coworkers theoretically designed the first ptC-containing molecule (1,1-dilithiocyclopropane).6 In 1991, Schleyer and Boldyrev further suggested considering both geometrical and electronic factors for the effective design of viable ptC species.7 Since then, many ptC and ptX (non-carbon atoms)-containing molecules, well-known as anti-van't Hoff and Le Bel's molecules, have been explored.8,9 Among others, various such unique molecules were confirmed to be global minima,10–12 and even detected by gas-phase photoelectron spectroscopy,13–17 and several compounds were realized in the wet lab.18–21Inspired by ptC/ptX, explorations have been extended to planar hypercoordinate motifs with even higher coordinations.22,23 Only a few global-minimum examples,24 however, have been found so far because many more critical geometric and electronic prerequisites are needed along with increasing the coordination number.24 In particular, planar hexacoordinate motifs are almost unimaginable. Though the first planar hexacoordinate carbon (CB62− with D6h symmetry) was predicted in 2000,23 it was confirmed to be only a local minimum, not a global minimum.25 To date, to achieve the global-minimum planar hexacoordinate species, mixed ligands and non-uniform bonding of planar center-ligands have to be used,26,27 and the D6h-symmetry planar hexacoordination as a global minimum is still rare.
The concept of atypical planar hypercoordination has also been extended to two-dimensional (2D) and 3D materials.8,24,28 In 2004, Hoffmann and coworkers first demonstrated that a ptC C52− system can serve as a building block to construct a variety of 3D extended networks.29 Since then, this idea has been extensively used to extend CB4,30 CAl42−,31 C2Al4,32 starbenzene,33 and hydrometal complexes34 into 1D (nanotubes) and 2D systems. These studies have strongly promoted the connection between anti-van't Hoff/Le Bel molecules and bulk materials, making the first step towards unique geometric structures and promising physical properties, albeit a detailed potential energy surface (PES) was hardly explored.
The effective structure search algorithm of 2D and 3D systems opens a new avenue for designing global-minimum extended materials containing rule-breaking planar hypercoordinate motifs, especially making it possible to uncover experimentally more feasible candidates and their potential applications. In this respect, a series of 2D nanosheets, such as Cu2Si,35 Cu2Ge,36 Ni2Ge,37 Ni2Si,37 Be2C,38 CoC,39 Be2C5,40 Fe2Si,41 and M2Si (M = Mg, Ca, Sr, Ba42 and CaSi43) containing planar or quasi-planar hypercoordinate motifs, have been verified as global minima in the 2D space. Amazingly, the Cu2Si monolayer with planar hexacoordinate Cu/Si was predicted as a global minimum in 2015.35 Only two years later, this unique monolayer was experimentally realized,44 and shortly after it was revealed as a superconductor with a Dirac nodal-line in the band structure.45 In 2016, the global-minimum Be5C2 monolayer containing quasi-planar ppC was predicted to be a gapless semiconductor with a Dirac-like point in the band structure and a negative Poisson's ratio.40 Recently, it was predicted that multiple-layer 2D AlB6 with ptAl has rare triple Dirac cones and node-loop features and is superconducting with a critical temperature (Tc) of 4.7 K.46
The striking connection between rule-breaking isolated clusters and promising 2D materials as mentioned above strongly inspired us to explore extended materials using stable or global-minimum clusters by following the “bottom-up” approach. Note that many stable or global-minimum planar hypercoordinate clusters are available, and searching for PESs of clusters is much easier as compared to those of 2D systems, and thus designing 2D systems based on stable clusters is expected to be more efficient than searching for 2D materials from scratch.
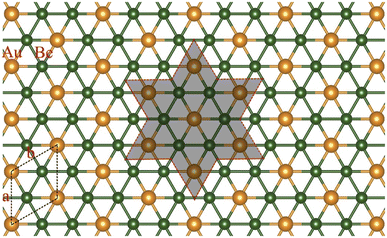
The polygonal core surrounded by bridging atoms, namely star-like molecules,47 can effectively embrace planar hypercoordinate centers, in which the star-like framework plays a crucial role for electronic and steric supports.48,49 Hence, global minimum star-like molecules could possess a great possibility to extend to global-minimum 2D networks, making an unprecedented bottom-up case. However, the significant differences in the design strategy and stabilization mechanism of planar hypercoordinate motifs between isolated clusters and 2D space (no electronic-stabilization-induced steric force for isolated clusters) make exploring stable 2D systems from stable clusters a rather difficult task.
Herein, by thorough examinations of the possibility of star-like BenAun frameworks, the isoelectronic analogues of monocyclic boron rings,50–52 to form planar hypercoordinate motifs, we found that the Be6Au7−cluster, which has a planar hexacoordinate gold atom embedded in a Be6Au6 ring and features a 20-electron starlike structure, is a global minimum (see Scheme 1), and its high stability is mainly due to high electron delocalization (6σ + 2π double aromaticity). Using this planar hexacoordinate motif as a building block, we constructed a binary s-block metal Be2Au monolayer with a P6/mmm space group (see Scheme 1), and confirmed that this monolayer is a global minimum where the electronic-stabilization-induced steric force and electron delocalization both help stabilize the unique structure. Hence, an unprecedented bottom-up case is vividly presented. Strikingly, the Be2Au monolayer is predicted to be a rare Dirac material with two perfect Dirac node-loops in the band structure. This 2D nanosheet displays phonon-mediated superconductivity with a critical temperature (Tc) of 4.0 K, and by applying compressive strain at only 1.6%, the Tc value can be enhanced up to 11.0 K, higher than the boiling point of liquid helium (4.2 K). The intriguing two-dimensional (2D) binary s-block metal Be2Au monolayer represents the first non-p-orbital element 2D networks with superconductivity, ultimately connecting the “anti-van't Hoff/Le Bel” structure with promising physical properties.
2. Computational details
The geometric structures of Be6Au7− isomers with singlet and triplet spin states were fully optimized first at the PBE0 (ref. 53)/def2-SVP level of theory, for the low-lying energy isomers (<40 kcal mol−1 above the global minimum), and a bigger def2-TZVP basis set was employed to obtain more accurate structural parameters and frequency data. The relative energies of these Be6Au7− isomers were further refined at the level of CCSD(T)54/def2-TZVP//PBE0/def2-TZVP with zero-point energy (ZPE) corrections.For the freestanding Be2Au monolayer and Be2Au with the Si(111) substrate, the geometric structure was fully optimized with the Perdew–Burke–Ernzerhof (PBE)55 functional and the projector augmented wave (PAW)56,57 approach, where a 500 eV energy cutoff for the plane-wave basis set was adopted. To well describe van der Waals interactions, Grimme's DFT-D2 corrections were included.58 The convergence criteria were set as 10−5 eV in energy and 10−3 eV Å−1 in force. The Brillouin zone was sampled with a 12 × 12 × 1 Γ-centered Monkhorst–Pack (MP) K-point grid. The Be2Au monolayer was placed in the xy plane with the z direction perpendicular to the layer plane, and a vacuum space of 15 Å in the z direction was used. The Heyd–Scuseria–Ernzerhof (HSE06) functional59 was employed to obtain accurate electronic properties (band structure, density of states, and projected density of states).
The chemical bonding analysis of the Be6Au7− cluster was performed by the natural bonding orbital (NBO)60,61 and adaptive natural density partitioning (AdNDP) methods.62 The nucleus-independent chemical shift (NICS) and the quantum theory atoms in molecules (QTAIM) analysis were visualized using Multiwfn.63–66
The molecular dynamics simulations of Be6Au7− were performed at 300 and 600 K, respectively, for 10 ps at the PBE0/def2-SVP level, where a canonical NVT ensemble (i.e. constant temperature and volume) with a time step of 0.5 fs was used. For the Be2Au monolayer, the molecular dynamics simulations in the NVT ensemble were carried out at different temperatures of 300, 600, 900, 1200, 1500, and 2000 K using a 4 × 4 supercell (32 Be and 16 Au atoms), where the Nosé–Hoover thermostat was applied to control the temperature.67,68 The whole simulation lasts for 10 ps with a time step of 1.0 fs.
The structure search of the isolated Be6Au7− cluster and the Be2Au monolayer was performed using the PSO algorithm within the revolutionary scheme, as implemented in the CALYPSO (crystal structure analysis by particle swarm optimization) code.69,70 In our PSO simulation, the population size was set to be 30, and the number of generations was maintained at 30. For the Be2Au monolayer, the number of formula units per simulation cell was set as 2, 4 and 6, that is, unit cells containing a total number of 6, 12 and 18 atoms were considered. The calculations for the isolated Be6Au7− cluster and the Be2Au monolayer were carried out using the Gaussian 09 code and the Vienna ab initio simulation package (VASP), respectively.71,72
The computations to examine the electron–phonon coupling (EPC) and superconducting properties of the Be2Au monolayer were performed utilizing the density functional perturbation theory (DFPT)73 through the Quantum ESPRESSO (QE) code.74,75 The VASP optimized structure was reoptimized within QE. For the QE calculations, the PBEsol form of GGA from the standard solid-state pseudopotentials (SSSP) library was employed.76 The plane wave kinetic-energy cutoff and charge-density cutoff were set as 80 and 800 Ry, respectively. The charge densities were calculated on a 32 × 32 × 1 k-point grid in combination with a Gaussian smearing of 0.02 Ry. Both dynamical matrices and EPC were calculated by using a 4 × 4 × 1 q-point grid.
3. Results and discussion
3.1 Stability of the Be6Au7− cluster containing the planar hexacoordinate motifs
We carried out a global minimum search of the Be6Au7− cluster, and Supplementary Fig. S1† presents the low-lying isomers (within 20 kcal mol−1 at the CCSD(T)/def2-TZVP//PBE0/def2-TZVP level of theory). The singlet state with a perfectly planar hexacoordinate gold (phAu) structure (Fig. 1a) is found to be not only a local minimum (with the lowest vibrational frequency of 15.7 cm−1), but also a global minimum (a) of Be6Au7−, and it is 3.1–12.0 kcal mol−1 lower in energy than all the other 3D alternatives (b–g). The lowest-energy triplet isomer of Be6Au7− also features a phAu (h) atom, but is 16.0 kcal mol−1 higher in energy than the singlet state.The Born–Oppenheimer molecular dynamics (BOMD) simulations were carried out at 300 and 600 K, respectively, to examine the thermal stability of the cluster and the robustness of the phAu structure. The BOMD trajectories with rather small RMSD (root mean square deviation) values suggest that phAu maintains its integrity without any isomerization or dissociation for at least 10 ps (see Fig. S2†). Thus, the global minimum nature and its considerable thermodynamic, kinetic, and thermal stabilities strongly indicate that the phAu-containing Be6Au7− is a promising candidate for experimental detection. To facilitate future experimental characterization, photoelectron spectroscopy of Be6Au7− was simulated according to generalized Koopmans' theorem77 as shown in Fig. S3.†
3.2 Structural and electronic properties of the Be6Au7− cluster
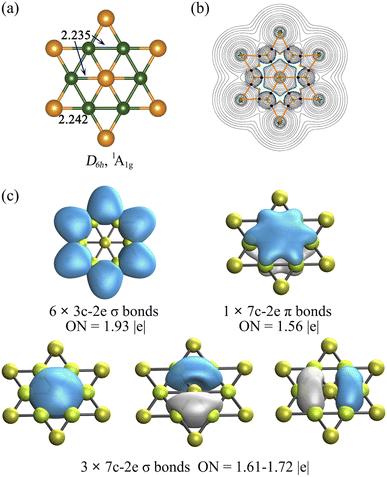
The geometric match between the planar center and ligand ring is a key factor for designing planar hexacoordinate species, and it is even more crucial for the binary D6h-symmetry starlike planar molecules since identical ligand–ligand and planar center-ligand distances are required. To the best of our knowledge, no stable binary D6h starlike molecule has been reported so far.Our computations showed that the D6h starlike Be6Au7− structure (Fig. 1a) featuring a perfect planar hexacoordinate gold atom is a global minimum. In the inner hexagon core, the Be–Be and Be–Au (central one) bonds have an identical bond distance of 2.235 Å, similar to but slightly longer than their single bonds according to the self-consistent covalent radii proposed by Pyykkö78 (2.04 and 2.26 Å for Be–Be and Be–Au), respectively. The slightly longer Be–Be bonds in Be6Au7− can be indicative of its electron delocalization discussed below. Thus, the peripheral Be6Au6 ring creates a perfect cavity to fit the gold atom, making it possible for this gold atom to form optimal bonding with the surrounding Be atoms. According to the natural population analysis (NPA), a significant charge transfer from Be to Au atoms occurs (the NPA charges are +0.48 |e| at Be, and −0.49 |e| and −0.99 |e| at peripheral and central Au, respectively). Meanwhile, a clear pz occupation of Be (2s0.962px0.092py0.092pz0.23) and Au (6s1.386px0.036py0.036pz0.54) vividly manifests the back-donation from phAu to Be ligands.
The electronic properties of the Be6Au7− cluster were further considered by QTAIM analysis and the out-of-plane tensor component of nucleus-independent chemical shift (NICSzz). The QTAIM results clearly show that all the Au–Be bonds have the corresponding bond paths and bond critical points (BCPs), suggesting that six Be ligands are coordinated to a phAu atom (see Fig. 1b). The NICSzz grid and its canonical molecular orbital (CMO) dissection into delocalized π and σ orbitals, and localized σ orbitals (Fig. S4b–d†)79 reveal that the Be6Au7− cluster is aromatic, and the delocalized σ orbitals possess larger contributions to the aromaticity of the Be6Au7− cluster than the delocalized π orbitals.
We also analyzed the chemical bonding of the Be6Au7− (D6h) cluster using the AdNDP method (Fig. 1c). The six 3c–2e (three center-two electrons) σ bonds of the Be–Au–Be peripheral ring with occupation numbers (ONs) of 1.93 |e| are responsible for stabilizing the peripheral ring. The remaining delocalized orbitals, including three 7c–2e σ bonds with ONs of 1.61–1.72 |e| and one 7c–2e π bond with an ON of 1.56 |e|, are associated with the central phAu atom. The existence of a delocalized π bond is consistent with the clear pz occupations of the phAu center and Be ligands. The valence shell of the central phAu atom has eight electrons, fulfilling the octet rule (3σ + 1π bonds) and meeting the Hückel (4n + 2) rule for 6σ + 2π double aromaticity.80 Note that the d-type lone pairs on Au atoms are found to have rather large occupation numbers (1.96–2.00 |e|), suggesting the relatively high localization of d-type lone pairs (see Fig. S5†). Thus, the high electron delocalization and the electrostatic interaction between Be and Au atoms give rise to the extraordinary stability of the planar Be6Au7− structure.
3.3 Structure and stability of the Be2Au monolayer containing planar hexacoordinate Be/Au
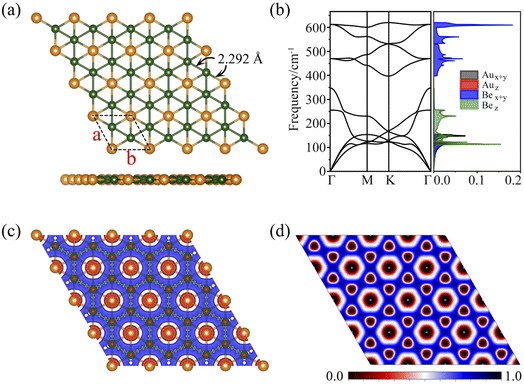
As discussed above, the phAu-containing Be6Au7− cluster is a highly stable structure. Its hexagonal symmetry indicates that this starlike structure may serve as a building block to form a 2D nanosheet. As illustrated in Fig. S6,† the 2D extended system can be designed by placing six Be6Au7 units around one Be6Au7 unit. By maintaining the main structural feature and integrity of phAu Be6Au7−, the 2D network is vividly constructed by sharing the bridging Au atoms (circled in Fig. S6†) of the Be6Au7 unit among three neighboring Be6Au7 units. Following this bottom-up strategy, we constructed a 2D s-block metal Be2Au monolayer with a P6/mmm symmetric group (Group 191) as shown in Fig. 2a. For this monolayer, each unit cell contains two Be atoms and one Au atom, and the lattice parameters are a = b = 3.970 Å. In this 2D extended system, both beryllium and gold are planar hexacoordinate centers, and the distances of Au–Be and Be–Be bonds are only slightly longer (by ca. 0.05 Å) than those in the isolated Be6Au7− cluster.Most excitingly, the global minimum searches revealed that this P6/mmm symmetrical 2D Be2Au monolayer is of the lowest energy in the 2D space, and its energy is at least ca. 120 meV per atom lower than that of other low-lying isomers (see Fig. S7†). Note that the Be2Au monolayer has a nonmagnetic ground state as verified by our spin-polarized calculations.
To evaluate the thermodynamic stability of the Be2Au monolayer, we computed its cohesive energy using Ecoh = (2nEBe + nEAu − nEBe2Au)/3n, where EBe, EAu, and EBe2Au are the total energies of a single Be and Au atom and a unit cell of the Be2Au monolayer, respectively. According to this definition, a more positive Ecoh value indicates a higher thermodynamic stability. The calculated cohesive energy of the Be2Au monolayer is 3.37 eV per atom. For comparison, the Ecoh values of graphene, 2D Cu2Si, and stanene at the same theoretical level are 7.90,81 3.44,35 and 2.73 (ref. 82) eV per atom, respectively. Though the atomic polymerization of these materials cannot be directly compared due to their different compositions, the rather positive Ecoh value (3.37 eV per atom) verifies that the Be2Au monolayer is a strongly bonded network.
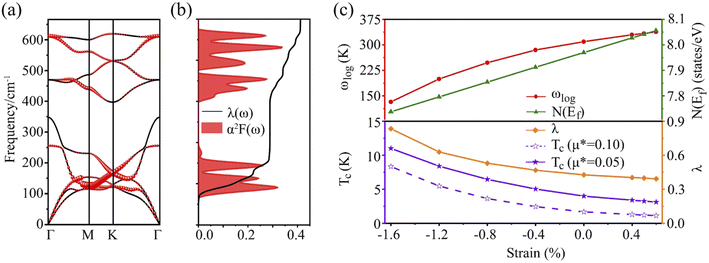
Fig. 2b displays the phonon dispersions and phonon density of states (PhDOS), respectively. No appreciable imaginary phonon modes were found, and thus the Be2Au monolayer is kinetically stable. The main contributions below 200 cm−1 are from out-of-plane vibrations of Be atoms and in-plane vibrations of Au atoms. The highest frequencies (from in-plane modes of Be atoms) can reach up to ∼630 cm−1, suggesting strong bonding interactions between Be atoms.
Ab initio molecular dynamics (AIMD) simulations were performed to evaluate its thermal stability. Six independent AIMD simulations at 300, 600, 900, 1200, 1500, and 2000 K were carried out using a 4 × 4 × 1 supercell. The Be2Au monolayer can retain its structural integrity with slight out-of-plane distortions throughout a 10 ps AIMD simulation up to 1500 K (see Fig. S8†).
We also calculated the mechanical properties of the Be2Au monolayer by examining its elastic constants (Cij). In accordance with the Born criteria,83 a mechanically stable 2D structure should satisfy C11C22–C122 > 0 and C66 > 0. The computed elastic constants are C11 = C22 = 94 N m−1, C12 = C21 = 41 N m−1, and C66 = 27 N m−1, which meet the Born criteria, indicating that the Be2Au monolayer is mechanically stable. The in-plane Young modulus, or in-plane stiffness, is a reasonable descriptor for the mechanical stability of 2D materials. The in-plane Young modulus of the Be2Au monolayer was predicted to be 76 N m−1, which is lower than that of graphene81 and 2D Cu2Si35 (295 and 96 N m−1, respectively), but higher than that of silicone (57 N m−1) and84 germanene (33 N m−1)85 obtained at the same level, suggesting that the Be2Au monolayer has considerable mechanical stability.
3.4 Electronic properties of the Be2Au monolayer
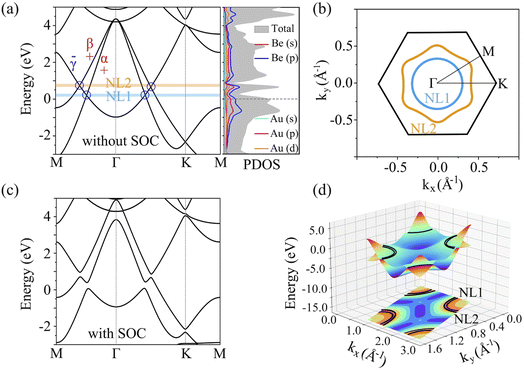
To evaluate the stabilization mechanism of the Be2Au monolayer, the deformation electronic density and electron local function (ELF) were examined (Fig. 2c and d). The deformation electronic density is defined as the total electron density of the Be2Au monolayer minus the electron density of isolated Au and Be atoms at their respective positions. Obviously, electron transfer occurs from the 6s orbitals of the Au atoms to Be atoms, which are delocalized over the Be–Be and Be–Au bonds (see Fig. 2c), contributing to the stabilization of the Be2Au monolayer. Note that σ rather than π delocalization is dominant in the 2D Be2Au monolayer indicated by the 3D representation of the ELF in Fig. S9,† which is quite different from the bonding nature of the Be6Au7− cluster (3σ + 1π bonds). The ELF is an important tool to study electronic structure. Generally, the values of 1.0 and 0.5 denote the fully localized and fully delocalized electrons, respectively, while the value near 0.0 refers to very low charge density. As shown in Fig. 2d, the electron delocalization across the whole Be2Au sheet suggests that the delocalized multicenter bonding gives rise to strong Be–Be and Be–Au bonds, which are crucial to electronically stabilize the Be2Au monolayer. According to the Hirshfeld charge analysis, each Au atom transfers 0.12 |e| to two Be atoms in the Be2Au monolayer.To get insights into the electronic properties of the Be2Au monolayer, we have computed the band structure and projected density of states (PDOS) without considering the spin orbit coupling (SOC) effect (Fig. 3). The band structure of Be2Au clearly reveals the metallic characteristics. The calculated band structures for the Be2Au monolayer without SOC using both PBE and HSE06 functionals (Fig. 3a and S10†) show that there are two hole-like bands (marked as α and β bands) and one electron-like band (denoted as γ band) near the Fermi level. The γ band goes across α and β bands linearly at approximately 0.21 and 0.76 eV without opening gaps. Note that all these bands are double degenerated; hence, the gapless nodes correspond to the 4-fold Dirac fermions. According to the PDOS (Fig. 3b), the momentum distributions of 4-fold Dirac fermions are two Dirac nodal lines (NL1 and NL2). To get a clearer observation of the band dispersion and Dirac structure, we plotted the 3D band structure of the Be2Au monolayer (Fig. 3d). Clearly the Be2Au monolayer is not only a Dirac material, but has two Dirac node-loops in the entire Brillouin zone.
Similar to previously reported 2D materials (Cu2Si,44 CuSe,86 and AgSe87), as shown in Fig. S11,† the α/β bands of Be2Au are dominated by in-plane orbitals (Be px/py and Au px/py/dxy/dx2−y2), and the γ band is contributed by out-of-plane orbitals (Be pz and Au pz). The symmetry-protected properties of two Dirac nodal lines in the Be2Au monolayer are similar to the above mentioned monolayers, where the mirror parities for the α/β and γ are even and odd, respectively, thus termed “+” and “−” in Fig. 3a. The opposite mirror parities verify the existence of these two gapless Dirac nodal lines in Fig. 3b. However, as shown in Fig. 3c, when the spin–orbit coupling (SOC) effect is considered, the nodal lines in the calculated band structure are fully gapped. The opened gaps along the M–Γ–K direction are 0.24, 0.32, 0.35 and 0.23 eV, respectively, vividly suggesting that the mirror reflection symmetry only protects the Dirac nodal loops in the absence of SOC. The SOC effect on the Be2Au monolayer is similar to that on the Cu2Si monolayer, which was predicted theoretically and realized experimentally as the 2D Dirac nodal line fermions.35,44
The Fermi velocity (vf) is the most important feature in Dirac cone materials. Therefore, we calculated the Fermi velocity by using the expression 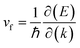 , where
, where 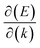 is the slope of the linear band and ℏ is the reduced Planck's constant. The corresponding vf values are 6.60 × 105 m s−1 (DC1), 8.95 × 105 m s−1 (DC2), 9.57 × 105 m s−1 (DC3), and 8.70 × 105 m s−1 (DC4), which are higher than those in Na3Bi (2.43 × 105 m s−1),88 α-Cu2C (2.45 × 105 m s−1)89 and Bi2Se3 (3.43 × 105 m s−1),90 but smaller than that in 2D AlB6 (1.10 × 106).46
is the slope of the linear band and ℏ is the reduced Planck's constant. The corresponding vf values are 6.60 × 105 m s−1 (DC1), 8.95 × 105 m s−1 (DC2), 9.57 × 105 m s−1 (DC3), and 8.70 × 105 m s−1 (DC4), which are higher than those in Na3Bi (2.43 × 105 m s−1),88 α-Cu2C (2.45 × 105 m s−1)89 and Bi2Se3 (3.43 × 105 m s−1),90 but smaller than that in 2D AlB6 (1.10 × 106).46
According to the PDOS of the Be2Au monolayer (Fig. 3a), the states below the Fermi energy are mainly contributed by the Au (5d) states, while the states at the Fermi level are mainly dominated by the Be (2p), Au (6p), and Au (5d) states, in which Be (2p) and Au (6p) are more pronounced than Au (5d). The empty Au (6p) orbitals split in the Be2Au monolayer, which makes it possible for the B atoms to back donate some of their received electrons to the low-lying 6p orbitals of Au, leading to a partial occupancy of 6p orbitals and strong p–d hybridization. The electron donation/back-donation mechanism essentially helps stabilize the Be2Au monolayer despite the lack of p electrons in this 2D material.
To explain the stability of the Be2Au monolayer, we also examined the nature of its electronic bonding. As shown in Fig. S12,† in-plane bonds formed from px and py orbitals (delocalization σ-bonds) are stronger than out-of-plane π-bonds derived from pz orbitals. Note that different from the stabilization mechanism of planar clusters (electronic and mechanical), the Be2Au monolayer is stabilized with the help of electronic-stabilization-induced steric forces.28
3.5 Electron–phonon coupling and superconductivity of the Be2Au monolayer
Our above analyses revealed that the rule-breaking Be2Au monolayer containing planar hexacoordinate s-block metal atoms has high stability and unique electronic properties. Then, will this “anti-van't Hoff/Le Bel” 2D structure also have certain promising physical properties? Given that the main electronic properties of the Be2Au monolayer are similar to those of graphene81 (see Fig. S13†), but the Be2Au monolayer has a higher density of states at the Fermi level, we further considered the electron–phonon coupling (EPC) of the Be2Au monolayer to test the possibility of its potential superconductivity.We calculated the phonon linewidth (λqv) according to the Bardeen–Cooper–Schrieffer (BCS) theory:91
The total EPC constant is calculated using the frequency-space integration:
It is found that the main contribution of the total EPC (λ = 0.43) of the Be2Au monolayer is derived from the low-frequency region ranging from 90–200 cm−1 (68.3%) and the high-frequency region ranging from 400–630 cm−1 (31.2%). In the low-frequency region, the λqv values along the M → K → Γ directions are rather large (Fig. 4a), leading to three sharp peaks of the α2F(ω) (Fig. 4b). As a result, λ(ω) increases rapidly in the low-frequency region and generates a step of λ(ω) around 150 cm−1, where the main contributions are from out-of-plane vibrations of Be atoms and in-plane vibrations of Au atoms as shown in Fig. 2b.
According to the BCS theory, the superconducting transition temperature (Tc) can be calculated by using the McMillan–Allen–Dynes formula:93
The carrier doping or external strains have been proved to be powerful tools for tuning superconducting properties of 2D materials.46,96 We first checked the carrier doping effect. The insignificant changes of Tc (less than 0.4 K as shown in Fig. S14–S17†) suggest that carrier doping has almost no impact on the superconductivity of the 2D Be2Au monolayer. Then, we examined the effect of external strains. The Be2Au monolayer is kinetically stable under strains of −1.6 to +0.6% (a compressive/tensile strain is denoted by a negative/positive value), as indicated by the phonon spectrum (Fig. S18†) where no appreciable imaginary phonon modes are available. Fig. 4c presents the changes of superconductor parameters, λ, ωlog, N(Ef), and Tc, as a function of external strains. Note that the density of states at the Fermi level N(Ef) and the logarithmic average frequency ωlog are gradually reduced along with increasing applied compressive strain, provided that these were the only parameters used to determine the Tc value and a descending Tc trend could be expected. However, the involvement of λ overturns this trend: both λ and Tc increase significantly along with increasing applied compressive strain. Specifically, the Tc reaches the maximum value of 11.0 K with μ* = 0.05 at a strain of −1.6%. Under this external strain (−1.6%), a softened acoustic frequency along Γ → M in the range of 0–100 cm−1 (Fig. S19†) contributes 59.0% to the total EPC (λ = 0.84), and there is a new step of λ(ω) at around 100 cm−1 (Fig. S19c†). In comparison, the total EPC in the intrinsic phase is much smaller (λ = 0.43). The softened frequency in the strained monolayer is mainly contributed by the out-of-plane vibrations of Be atoms, which could increase electron–phonon pairing potential at the Fermi level, and is a key factor in enhancing the EPC of the Be2Au monolayer. Note that enhanced superconductivity has been found in several other strained 2D materials, such as graphene, h-MnB3, and YS monolayers.97–99
Given the highly stable Be2Au monolayer discussed above, we further considered whether the Be2Au monolayer can be chemically bonded to another layer or be fabricated on some potential substrates. For two-layer systems, two stacking configurations, including eclipsed and staggered models, were obtained with considerable binding energies of 0.42 and 0.51 eV per atom, respectively, suggesting that in the two-layer systems the monolayers are strongly chemically bonded instead of van der Waals interaction. It is well known that 2D materials can be synthesized on a suitable substrate,100,101 among which silicon substrates are widely used for growing nanomaterials.102,103 Herein, we found that the lattice parameters of Si(111) are similar to that of the Be2Au monolayer, suggesting that Si(111) is a promising substrate. To assess the effects of substrates, we evaluated two parameters, namely the adsorption energy (Eads) and lattice mismatch (δ).
The adsorption energy is calculated according to the following equation:
where Lmol and Lslab are the corresponding lattice parameters of the Be2Au monolayer and the slab, respectively.
As shown in Fig. S20,† the Be2Au monolayer is slightly distorted as compared to the freestanding monolayer. Compared with Be atoms, Au atoms are closer to the Si(111) substrate. The short interlayer distance between the Be2Au monolayer and the Si(111) substrate reflected by Au–Si contacts is about 2.49 Å, which is comparable to the single covalent Au–Si (2.40 Å) bond length according to the self-consistent covalent radii proposed by Pyykkö.78 The negative Eads of −0.52 eV per atom indicates that the Be2Au monolayer is energetically favorable to be prepared on the Si(111) substrate. Relative to the free-standing layer, on the Si(111) substrate, the Be–Be and Be–Au bond lengths in the adsorbed Be2Au monolayer are shortened only by 0.03 Å. The small lattice mismatch (1.34%) suggests that the Be2Au monolayer could be epitaxially grown on the Si(111) substrate. However, the relatively large negative Eads reveals that once grown epitaxially on the Si(111) substrate, the fabricated Be2Au monolayer may not be easily peeled off from the substrate. Thus, further efforts are needed to find an even better substrate, which not only enables the growth of the Be2Au monolayer, but also has a relatively weak interaction to ensure the exfoliation of the Be2Au monolayer.
4. Conclusion
In summary, based on the global minimum of an isolated Be6Au7− cluster featuring a unique hexagonal starlike structure, we theoretically designed a Be2Au monolayer, a global minimum in the 2D space. Specifically, both the isolated Be6Au7− cluster and 2D Be2Au monolayer possess the rule-breaking planar hexacoordinate motifs, well-known as anti-van't Hoff/Le Bel arrangements. The extraordinary stability of both the Be2Au monolayer and its building block (Be6Au7−) benefits from the good electron delocalization, and the Be2Au monolayer also benefits from the electronic-stabilization-induced steric force. Strikingly, this Be2Au monolayer is a rare Dirac material with two perfect Dirac node-loops in the band structure. The newly designed Be2Au monolayer is predicted to be a 2D phonon-mediated superconductor with Tc = 4.0 K, and the critical temperature can be significantly increased to 11.0 K by applying a small compressive stain of 1.6%. This work not only identified a new 2D material containing anti-van't Hoff/Le Bel motifs, namely the Be2Au monolayer with planar hexacoordinate s-block metal atoms, which is a global minimum Dirac material and superconducting, but also provides a new approach to design 2D materials by rationally assembling stable clusters.Data availability
The extra data for all compounds are provided in the ESI† accompanying this paper.Author contributions
Z.-h. C. and Z.-f. C. conceived the project, wrote the draft, and finalized it. M.-h. W. performed the calculations. S. W., J.-j. Z. and Q. L. analyzed the data. All authors took part in the discussions and approved the final version.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was funded in China by the National Natural Science Foundation of China (No. 11922405, 11874178, and 91961204), and in the USA by the NSF Center for the Advancement of Wearable Technologies (Grant 1849243). The partial calculations in this work were supported by the High Performance Computing Center of Jilin University, China.References
- A. Kekulé, Ann. Chem. Pharm., 1857, 104, 129–150 CrossRef.
- J. H. v. t. Hoff, Arch. Neerl. Sci. Exactes Nat., 1874, 9, 445–454 Search PubMed.
- J. A. L. Bel, Bull. Soc. Chim. Fr., 1874, 22, 337–347 Search PubMed.
- H. J. Monkhorst, Chem. Commun., 1968, 1111–1112 RSC.
- R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4492–4493 CrossRef.
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427 CrossRef CAS.
- P. v. R. Schleyer and A. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 21, 1536–1538 RSC.
- L. M. Yang, E. Ganz, Z. F. Chen, Z. X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS.
- G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS.
- A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972 CrossRef CAS.
- G. Merino, M. A. Mendez-Rojas and A. Vela, J. Am. Chem. Soc., 2003, 125, 6026–6027 CrossRef CAS PubMed.
- G. Castillo-Toraya, M. Orozco-Ic, E. Dzib, X. Zarate, F. Ortiz-Chi, Z. H. Cui, J. Barroso and G. Merino, Chem. Sci., 2021, 12, 6699–6704 RSC.
- J. Xu, X. Zhang, S. Yu, Y. H. Ding and K. H. Bowen, J. Phys. Chem. Lett., 2017, 8, 2263–2267 CrossRef CAS PubMed.
- X. Li, H. J. Zhai and L. S. Wang, Chem. Phys. Lett., 2002, 357, 415–419 CrossRef CAS.
- X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3633 CrossRef CAS.
- A. I. Boldyrev, X. Li and L. S. Wang, Angew. Chem., Int. Ed., 2000, 39, 3445–3448 CrossRef.
- X. Li, L. S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038 CrossRef CAS.
- F. Ebner, H. Wadepohl and L. Greb, J. Am. Chem. Soc., 2019, 141, 18009–18012 CrossRef CAS PubMed.
- P. Ghana, J. Rump, G. Schnakenburg, M. I. Arz and A. C. Filippou, J. Am. Chem. Soc., 2021, 143, 420–432 CrossRef CAS PubMed.
- F. Ebner and L. Greb, Chem, 2021, 7, 2151–2159 CAS.
- F. Ebner and L. Greb, J. Am. Chem. Soc., 2018, 140, 17409–17412 CrossRef CAS PubMed.
- Z. X. Wang and P. v. R. Schleyer, Science, 2001, 292, 2465–2469 CrossRef CAS PubMed.
- K. Exner and P. v. R. Schleyer, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114 CrossRef CAS.
- B. B. Averkiev, D. Y. Zubarev, L. M. Wang, W. Huang, L. S. Wang and A. I. Boldyrev, J. Am. Chem. Soc., 2008, 130, 9248–9250 CrossRef CAS PubMed.
- L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2020, 133, 8782–8786 CrossRef.
- Y. B. Wu, Y. Duan, G. Lu, H. G. Lu, P. Yang, P. V. Schleyer, G. Merino, R. Islas and Z. X. Wang, Phys. Chem. Chem. Phys., 2012, 14, 14760–14763 RSC.
- Y. Wang, Y. Li and Z. Chen, Acc. Chem. Res., 2020, 53, 887–895 CrossRef CAS PubMed.
- P. D. Pancharatna, M. A. Mendez-Rojas, G. Merino, A. Vela and R. Hoffmann, J. Am. Chem. Soc., 2004, 126, 15309–15315 CrossRef CAS PubMed.
- X. J. Wu, Y. Pei and X. C. Zeng, Nano Lett., 2009, 9, 1577–1582 CrossRef CAS.
- L. M. Yang, Y. H. Ding and C. C. Sun, J. Am. Chem. Soc., 2007, 129, 658–665 CrossRef CAS PubMed.
- Y. B. Wu, Z. X. Li, X. H. Pu and Z. X. Wang, Comput. Theor. Chem., 2012, 992, 78–83 CrossRef CAS.
- Y. B. Wu, J. L. Jiang, R. W. Zhang and Z. X. Wang, Chem.–Eur. J., 2010, 16, 1271–1280 CrossRef CAS PubMed.
- Y. B. Wu, C. X. Yuan, F. Gao, H. G. Lu, J. C. Guo, S. D. Li, Y. K. Wang and P. Yang, Organometallics, 2007, 26, 4395–4401 CrossRef CAS.
- L. M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed.
- L.-M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551 RSC.
- L.-M. Yang, I. A. Popov, T. Frauenheim, A. I. Boldyrev, T. Heine, V. Bačić and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 26043–26048 RSC.
- Y. Li, Y. Liao and Z. Chen, Angew. Chem., Int. Ed., 2014, 53, 7248–7252 CrossRef CAS PubMed.
- C. Zhu, H. Lv, X. Qu, M. Zhang, J. Wang, S. Wen, Q. Li, Y. Geng, Z. Su, X. Wu, Y. Li and Y. Ma, J. Mater. Chem. C, 2019, 7, 6406–6413 RSC.
- Y. Wang, F. Li, Y. Li and Z. Chen, Nat. Commun., 2016, 7, 1–7 CAS.
- Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777 CrossRef CAS.
- D. B. Migas, V. O. Bogorodz, A. B. Filonov, V. E. Borisenko and N. V. Skorodumova, Surf. Sci., 2018, 670, 51–57 CrossRef CAS.
- Y. Wang, M. Qiao, Y. Li and Z. Chen, Nanoscale Horiz., 2018, 3, 327–334 RSC.
- B. J. Feng, B. T. Fu, S. Kasamatsu, S. Ito, P. Cheng, C. C. Liu, Y. Feng, S. L. Wu, S. K. Mahatha, P. Sheverdyaeva, P. Moras, M. Arita, O. Sugino, T. C. Chiang, K. Shimada, K. Miyamoto, T. Okuda, K. H. Wu, L. Chen, Y. G. Yao and I. Matsuda, Nat. Commun., 2017, 8, 1–6 CrossRef CAS.
- L. Yan, P. F. Liu, T. Bo, J. R. Zhang, M. H. Tang, Y. G. Xiao and B. T. Wang, J. Mater. Chem. C, 2019, 7, 10926–10932 RSC.
- B. Y. Song, Y. Zhou, H. M. Yang, J. H. Liao, L. M. Yang, X. B. Yang and E. Ganz, J. Am. Chem. Soc., 2019, 141, 3630–3640 CrossRef CAS PubMed.
- Y. Xie and H. F. Schaefer, Chem. Phys. Lett., 1991, 179, 563–567 CrossRef CAS.
- M. H. Wang, C. Chen, S. Pan and Z. H. Cui, Chem. Sci., 2021, 12, 15067–15076 RSC.
- J. C. Guo, W. J. Tian, Y. J. Wang, X. F. Zhao, Y. B. Wu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2016, 144, 244303 CrossRef PubMed.
- R. Islas, T. Heine, K. Ito, P. v. R. Schleyer and G. Merino, J. Am. Chem. Soc., 2007, 129, 14767–14774 CrossRef CAS PubMed.
- Y. L. Liao, C. L. Cruz, P. v. R. Schleyer and Z. F. Chen, Phys. Chem. Chem. Phys., 2012, 14, 14898–14904 RSC.
- C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 78, 3865–3868 CrossRef PubMed.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- J. Poater, M. Duran, M. Solà and B. Silvi, Chem. Rev., 2005, 105, 3911–3947 CrossRef CAS PubMed.
- F. Corts-Guzman and R. F. W. Bader, Coord. Chem. Rev., 2005, 249, 633–662 CrossRef.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef.
- Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kucukbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Ponce, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- K. Lejaeghere, G. Bihlmayer, T. Bjorkman, P. Blaha, S. Blugel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dulak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Granas, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iusan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Kucukbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordstrom, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunstrom, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351, add3000 CrossRef PubMed.
- J. C. Phillips, Phys. Rev., 1961, 123, 420–424 CrossRef CAS.
- P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337 CrossRef PubMed.
- Z. F. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- J. Chandrasekhar, E. D. Jemmis and P. v. R. Schleyer, Tetrahedron Lett., 1979, 20, 3707–3710 CrossRef.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- F. F. Zhu, W. J. Chen, Y. Xu, C. L. Gao, D. D. Guan, C. H. Liu, D. Qian, S. C. Zhang and J. F. Jia, Nat. Mater., 2015, 14, 1020–1025 CrossRef CAS PubMed.
- M. Born and H. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1954 Search PubMed.
- A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Phys. Rev. Lett., 2012, 108, 245501 CrossRef.
- L. F. Li, S. Z. Lu, J. B. Pan, Z. H. Qin, Y. Q. Wang, Y. L. Wang, G. Y. Cao, S. X. Du and H. J. Gao, Adv. Mater., 2014, 26, 4820–4824 CrossRef CAS.
- L. Gao, J. T. Sun, J. C. Lu, H. Li, K. Qian, S. Zhang, Y. Y. Zhang, T. Qian, H. Ding, X. Lin, S. Du and H. J. Gao, Adv. Mater., 2018, 30, 1707055 CrossRef.
- J. C. Lu, L. Gao, S. R. Song, H. Li, G. F. Niu, H. Chen, T. Qian, H. Ding, X. Lin, S. X. Du and H. J. Gao, ACS Appl. Nano Mater., 2021, 4, 8845–8850 CrossRef CAS.
- Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S. K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain and Y. L. Chen, Science, 2014, 343, 864–867 CrossRef CAS PubMed.
- B. S. Wang and G. Frapper, Phys. Rev. Mater., 2021, 5, 034003 CrossRef CAS.
- Y. Xia, D. Qian, D. Hsieh, L. Wray, A. Pal, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava and M. Z. Hasan, Nat. Phys., 2009, 5, 398–402 Search PubMed.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175–1204 CrossRef CAS.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 905–922 CrossRef CAS.
- E. S. Penev, A. Kutana and B. I. Yakobson, Nano Lett., 2016, 16, 2522–2526 CrossRef CAS.
- L. Yan, B. T. Wang, X. Y. Huang, Q. Q. Li, K. Xue, J. Zhang, W. C. Ren and L. J. Zhou, Nanoscale, 2021, 13, 18947–18954 RSC.
- C. Cheng, J. T. Sun, H. Liu, H. X. Fu, J. Zhang, X. R. Chen and S. Meng, 2D Mater., 2017, 4, 025032 CrossRef.
- Z. Y. Qu, F. J. J. Han, T. Yu, M. L. Xu, Y. W. Li and G. C. Yang, Phys. Rev. B, 2020, 102, 075431 CrossRef CAS.
- Z. Y. Qu, S. Y. Lin, M. L. Xu, J. Hao, J. M. Shi, W. W. Cui and Y. W. Li, J. Mater. Chem. C, 2019, 7, 11184–11190 RSC.
- C. Si, Z. Liu, W. H. Duan and F. Liu, Phys. Rev. Lett., 2013, 111, 196802 CrossRef PubMed.
- B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. L. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 CrossRef CAS.
- W. Heywang and K. H. Zaininger, in Silicon, Springer, 2004, pp. 25–42 Search PubMed.
- T. Martensson, C. P. T. Svensson, B. A. Wacaser, M. W. Larsson, W. Seifert, K. Deppert, A. Gustafsson, L. R. Wallenberg and L. Samuelson, Nano Lett., 2004, 4, 1987–1990 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03614b |
| This journal is © The Royal Society of Chemistry 2022 |