Open Access Article
Open Access ArticleDirect detection of spin polarization in photoinduced charge transfer through a chiral bridge†
Alberto
Privitera
 ab,
Emilio
Macaluso
ab,
Emilio
Macaluso
 cd,
Alessandro
Chiesa
cd,
Alessandro
Chiesa
 cd,
Alessio
Gabbani
cd,
Alessio
Gabbani
 e,
Davide
Faccio
e,
Davide
Faccio
 f,
Demetra
Giuri
f,
Demetra
Giuri
 f,
Matteo
Briganti
f,
Matteo
Briganti
 b,
Niccolò
Giaconi
b,
Niccolò
Giaconi
 bg,
Fabio
Santanni
bg,
Fabio
Santanni
 b,
Nabila
Jarmouni
e,
Lorenzo
Poggini
b,
Nabila
Jarmouni
e,
Lorenzo
Poggini
 h,
Matteo
Mannini
h,
Matteo
Mannini
 b,
Mario
Chiesa
b,
Mario
Chiesa
 a,
Claudia
Tomasini
a,
Claudia
Tomasini
 f,
Francesco
Pineider
f,
Francesco
Pineider
 e,
Enrico
Salvadori
e,
Enrico
Salvadori
 *a,
Stefano
Carretta
*a,
Stefano
Carretta
 *cd and
Roberta
Sessoli
*cd and
Roberta
Sessoli
 *b
*b
aDepartment of Chemistry and NIS Centre, University of Torino, Via Giuria 7, Torino, I-10125, Italy. E-mail: enrico.salvadori@unito.it
bDepartment of Chemistry “U. Schiff” (DICUS), University of Florence & UdR INSTM Firenze, Via della Lastruccia 3-13, Sesto Fiorentino, I-50019, Italy. E-mail: roberta.sessoli@unifi.it
cDepartment of Mathematical, Physical and Computer Sciences, University of Parma & UdR INSTM, I-43124, Parma, Italy. E-mail: stefano.carretta@unipr.it
dINFN–Sezione di Milano-Bicocca, gruppo collegato di Parma, I-43124 Parma, Italy
eDepartment of Chemistry and Industrial Chemistry, University of Pisa & UdR INSTM Pisa, Via Moruzzi 13, Pisa, I-56124, Italy
fDepartment of Chemistry “Giacomo Ciamician”, University of Bologna, Via Selmi 2, Bologna, I-40126, Italy
gDepartment of Industrial Engineering (DIEF), University of Florence & UdR INSTM Firenze, Via Santa Marta 3, Firenze, I-50139, Italy
hCNR-ICCOM, Via Madonna del Piano 10, Sesto Fiorentino, I-50019, Italy
First published on 4th October 2022
Abstract
It is well assessed that the charge transport through a chiral potential barrier can result in spin-polarized charges. The possibility of driving this process through visible photons holds tremendous potential for several aspects of quantum information science, e.g., the optical control and readout of qubits. In this context, the direct observation of this phenomenon via spin-sensitive spectroscopies is of utmost importance to establish future guidelines to control photo-driven spin selectivity in chiral structures. Here, we provide direct proof that time-resolved electron paramagnetic resonance (EPR) can be used to detect long-lived spin polarization generated by photoinduced charge transfer through a chiral bridge. We propose a system comprising CdSe quantum dots (QDs), as a donor, and C60, as an acceptor, covalently linked through a saturated oligopeptide helical bridge (χ) with a rigid structure of ∼10 Å. Time-resolved EPR spectroscopy shows that the charge transfer in our system results in a C60 radical anion, whose spin polarization maximum is observed at longer times with respect to that of the photogenerated C60 triplet state. Notably, the theoretical modelling of the EPR spectra reveals that the observed features may be compatible with chirality-induced spin selectivity, but the electronic features of the QD do not allow the unambiguous identification of the CISS effect. Nevertheless, we identify which parameters need optimization for unambiguous detection and quantification of the phenomenon. This work lays the basis for the optical generation and direct manipulation of spin polarization induced by chirality.
Introduction
The second quantum revolution is unfolding now, exploiting the enormous advancements in our ability to detect and coherently manipulate single quantum objects.1 In this context, the possibility of controlling the electron spin of molecular qubits2–4 – or reading out the information encoded in their spin states – through the use of visible photons represents an attractive approach toward the realization of smaller, faster, and more energy-efficient Quantum Information (QI) and spintronic technologies.5–7 An emerging possibility to address this challenge is the use of chirality.8–10 Chiral structures have recently received significant attention thanks to their spin filtering behaviour in the phenomenon described as Chirality-Induced Spin Selectivity (CISS).11,12 This mechanism has been adopted to interpret a wide range of experimental results in which chiral systems impart significant spin selectivity in electron transport through chiral molecules, oligomers, and polymers.8–15 Notably, the spin selectivity of the CISS effect is exceptionally high, even at room temperature.16,17 In contrast to alternative methods previously used to achieve spin-to-light (or vice versa) interconversion, the CISS effect – which operates at the molecular scale – has the potential to reach the sensitivity for the readout of individual spins.18 The latter appears even more interesting considering that the molecular flexibility achievable through chemical tunability allows controlling key features like the qubit–qubit interactions, crucial for implementing quantum gates.19Despite the recent experimental and theoretical efforts to rationalize the origin and potentialities of the CISS effect, the phenomenon is not fully understood yet. Most scientific results come from experiments performed on hybrid materials comprising chiral molecules supported on metallic substrates.8,11,12 Conversely, the implementation of the CISS effect in molecular charge transfer (CT) through the use of light has tentatively been tested only recently via indirect methods, e.g. probing competitive nonradiative and radiative relaxation processes as a function of an external magnetic field, light polarization, and molecular or helical handedness.5 The challenge of directly detecting at the molecular level the non-Boltzmann spin populations that arise from photoinduced CISS originates from the lack of suitable donor–chiral bridge–acceptor (D–χ–A) systems. The latter must simultaneously show good photoinduced CT efficiencies and an efficient spin-filtering effect through the chiral bridge.20 In this regard, semiconductor quantum dots (QD) have demonstrated to be robust platforms for investigating the CISS effect.21–23 In addition, systems comprising QD as a donor and an organic molecule as an acceptor have recently been demonstrated to transfer long-lived spin polarization from the photoexcited QD to the organic molecule.24 The resulting non-Boltzmann spin populations can be investigated in detail through the use of time-resolved electron paramagnetic resonance (trEPR) spectroscopy.24,25 The development of a sound theoretical framework to rationalize the trEPR spectra of these systems is mandatory for investigating spin selectivity in the CT process through an effective chiral potential. A deeper understanding of spin selectivity would dramatically advance our capabilities to control and harness CISS at a fundamental scale.10
Here, we directly probe the spin-polarized CT process through a chiral bridge via time-resolved EPR (trEPR) spectroscopy in a model system comprising CdSe QD-chiral bridge-fullerene (hereafter QD–χ–C60). The studied chiral system is favourable for several reasons: (i) QDs are an effective reservoir of electrons that can be donated via CT towards C60,25–27 (ii) C60 is a good electron acceptor,26,28 and (iii) the used chiral bridge is a two-unit polypeptide belonging to the most investigated class of chiral linkers in CISS-based spintronic devices.5,10,12,29 The QD–χ–C60 system is synthesized via a ligand exchange approach and characterized through optical spectroscopies and X-ray photoemission spectroscopy (XPS), the latter allowing a quantitative analysis that confirms the chemisorption of the C60 chiral derivative. trEPR spectroscopy shows that the photoinduced CT from the QD to the fullerene generates a spin-polarized state assigned to the fullerene radical anion. Detailed modelling of the EPR features indicates that they are compatible with the presence of CISS, albeit the unambiguous detection of CISS is hampered by the equilibration of spin population on the photo-excited QD. Though not yet conclusive, our investigation represents the first attempt to probe the spin selectivity of the CISS effect by directly detecting the spin populations of the CT state generated following the photoinduced electron transfer through chiral bridges. This provides a fundamental step to formulate clear and handy guidelines for designing future materials based on CISS and ultimately championing the burgeoning field of QI science.
Results and discussion
Chiral system engineering and synthesis
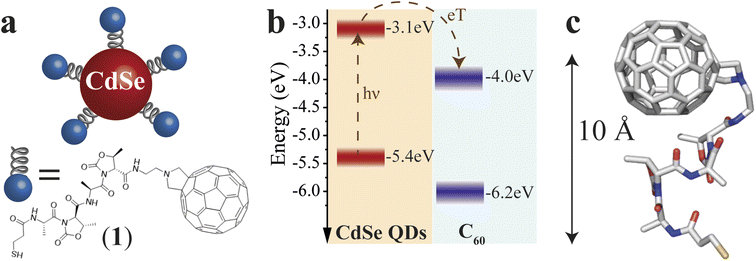
The QD–χ–C60 system investigated in this paper is shown in Fig. 1a. We engineered our system to optimize the CT process, which is the main focus of our analysis. CdSe QDs represent a sound model system thanks to their tailorable light absorption (through their size) and excellent electron-donating properties.30 Prior studies, based on different experimental methods, e.g. photoelectron spectroscopy in air (PESA) and theoretical calculations, have shown that the approximate valence and conduction band energies of CdSe QDs with a diameter of 5 nm are −3.1 and −5.4 eV, respectively.31 However, it should be noted that different techniques give different band energies, which are also strongly affected by the environment and the ligand nature. Thus, we represent these states as a distribution. The C60 molecule is one of the best performing electron acceptors,32 whose frontier energy levels, also distributed in energy, are approximately found at −4.0 and −6.2 eV.33 The diagram in Fig. 1b also reports approximate energetics and a possible path for the CT in our system. Specifically, after the photoexcitation of the QD, an electron transfer to the C60 can occur due to the favourable energy levels alignment. If C60 is photoexcited, a hole transfer will occur, resulting in the same final CT state (hole in the QD and electron in the C60).The selected linker, reported in Fig. 1a, is composed of two units comprising L-Alanine and the pseudo amino acid (4S,5R)-4-methyl-5-carboxyl-oxazolidin-2-one (D-Oxd). The grafting thiolate group is on the N termination of the peptide chain, while NH2(CH2)2-fulleropyrrolidine is bound to the C-termination of the polypeptide to give SH–(CH2)2–(CO)–(L-Ala-D-Oxd)2–NH–(CH2)2–fulleropyrrolidine, 1. This choice aims to find an acceptable compromise between CT efficiency and effective chiral potential for the CT process. CISS can still be observed in a system where CT occurs in all directions, as suggested by our previous work,18 though it is independent of the chosen enantiomer. Thus, we focused our analysis only on one of the two possible ligand enantiomers. Since the X-ray structure of the C60 functionalized foldamer 1 is not accessible, to clarify the geometrical conformation of the chiral bridge after C60 grafting, we performed density functional theory (DFT) geometry optimization of the isolated structure of 1 (see Computational Details in ESI†). In Fig. 1c, the final optimized structure is reported. Minor deviations from the available X-ray structure of the S-protected oligopeptide lacking the fullerene unit [Tri-S–(CH2)2–(CO)–(L-Ala-D-Oxd)2–OBn]34 have been computed (see Fig. S1†). The small root mean square deviation (RMSD) of 0.516 Å between the optimized structure of the oligopeptide moiety in 1 and the crystal structure of the free oligopeptide suggests that the geometry of the pristine chiral bridge is preserved even after the bonding to the fulleropyrrolidine. This can be rationalized considering that the chiral bridge is relatively rigid despite its shortness and the absence of intermolecular interactions in the crystal.
For this reason, we can conclude that the intramolecular hydrogen bonds between the two peptide units of the linker are enough to stabilize the structure of 1 and that the structure of 1 is reasonably preserved also upon grafting on the QD. In addition, the insertion process of individual 1 ligands into a dense layer of capping molecules should prevent the folding of C60 on the QD.35–37 This is further corroborated by the observation of a trEPR signal (vide infra), suggesting slow charge recombination and, therefore, a significant distance between the QD and C60.24
After thoughtfully selecting the chiral linker, we turn to the synthesis and experimental characterization of the proposed QD–χ–C60 system. CdSe QDs were prepared via the hot injection method reported by Dai et al. with minor modifications.38 The average diameter of the QDs is ∼5 nm, as shown by TEM analysis. Further details on the synthesis and morphological characterization are reported in ESI.†
The fullerene-functionalized polypeptide 1 was prepared through liquid phase synthesis. The D-Oxd-OBn group was prepared from threonine and coupled with Boc-L-Ala.39 Fullerene-C60 was derivatized according to the Prato reaction to afford N-2-aminoethyl-fulleropyrrolidine.40 Then, Boc-(L-Ala-D-Oxd)2-OBn was derivatized by replacing the OBn protecting group with the previously obtained N-2-aminoethyl-fulleropyrrolidine and the N-Boc protecting group with 3-(tritylthio)propanoic acid by standard coupling reactions. Finally, the S-protecting trityl group was removed,41 and compound 1 was obtained. For further details, see ESI.†
The ligand-exchange reaction of the as-synthesized CdSe QDs capped with trioctylphosphine oxide (TOPO) was favoured by the strong affinity of thiols to the CdSe surface, according to HSAB theory for an X-type ligand.42 We performed ligand exchange by adding an excess of 1 (10 times higher than the estimated quantity for maximum coverage of the QD surface) to a solution of QDs in chloroform and keeping the mixture overnight under mechanical stirring. After the exchange reaction, the newly-formed QDs (QD–χ–C60 system) precipitate, as the presence of C60 in the ligand drastically reduces their colloidal stability. The change in solubility is the first evidence of the successful exchange of the native ligands with 1. The QD–χ–C60 system was subsequently re-dispersed in a solution of 1,2,4-trichlorobenzene and purified (details in ESI†). For comparative studies, two other molecular systems were synthesized: (i) SH–(CH2)2–(CO)-(L-Ala-D-Oxd)2-L-Val-OMe (2) to obtain a similar functionalization of the QDs without the C60 acceptor; (ii) fulleropyrrolidine–(CH2)2–NH–COOtBu lacking the thiol grafting group (3). For the molecular structures, see Schemes S1 and S2† in the ESI.†
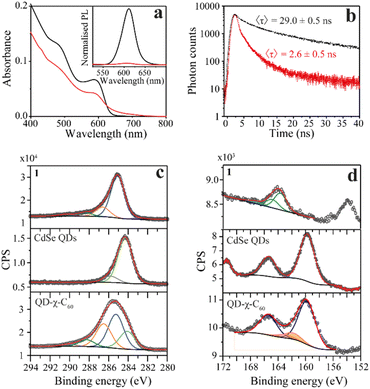
To confirm the success of the ligand-exchange reaction, we started by carrying out optical measurements. In particular, we used UV-vis absorption, steady-state PL, and transient PL to investigate the photophysics of our model system as an initial platform on which to build the study of the spin dynamics mediated by light. In Fig. 2a, we compare the UV-vis and PL spectra of the pristine CdSe QDs and the CdSe QD–χ–C60 system. The UV-vis absorption spectrum of the CdSe QD–χ–C60 system can be rationalized as the sum of two main contributions. The first originates from the CdSe QDs and shows a clear excitonic peak at around 600 nm, in analogy with the pristine CdSe QDs. The second is a broad absorption tail extending up to 700 nm typical of C60 derivatives43 and strongly resembles the UV-vis absorption spectrum of the free 1 ligand shown in Fig. S16.† The PL spectra provide a first fingerprint of the success of the ligand exchange reaction. Specifically, the inset of Fig. 2a shows that the PL intensity is strongly quenched in the CdSe QD–χ–C60 system compared to the pristine CdSe QDs. This quenching is mainly ascribed to the thiol-mediated hole trapping process becoming dominant over radiative recombination.44 A comparable PL quenching was obtained for CdSe QDs functionalized with 2, where the C60 molecule is absent, thus confirming the predominant role of thiols in the PL quenching mechanism (see Fig. S17†).
We further probed the role of 1 ligand on the QD exciton decay by performing time-resolved photoluminescence (trPL) decay measurements on the QDs before and after the ligand exchange. The luminescence decay curves recorded at the emission maximum (Fig. 2b) show a multiexponential decay that we modelled using triexponential decay kinetics, as shown in eqn (1):
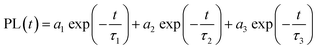 | (1) |
The fitting results are reported in Table S1† in the ESI.† The explanation for the origin of the multiexponential PL decay has been thoroughly discussed in the literature.45 The main reason is the presence of QD surface defects that give rise to trap states within the bandgap and affect the emission dynamics.46–48 As a result, the photogenerated hole–electron pair exciton can follow different decay paths.46 The most direct one consists of a rapid relaxation of the hole and the electron to the bottom of the valence and conduction bands, respectively, followed by the radiative relaxation to the ground state. This process contributes to the fastest lifetime decay. However, the hole (or the electron) can be localized in shallow trap states. These trapped charges can either repopulate the valence (or conduction) band or thermalize into deeper trap states. The former case contributes to the longer PL lifetimes, while the latter contributes to nonradiative mechanisms. The combination of all these processes and differences between the individual QDs give rise to multiexponential emission dynamics that occur over a nanosecond time scale, in agreement with literature values for similar systems.45 In addition, the possibility of charge transfer from the CdSe QD to the C60 fullerene in the QD–χ–C60 system can also occur, as reported in the next section. To compare the PL lifetimes of the QDs before and after the ligand exchange, we calculated their average PL lifetime τ using eqn (2):45
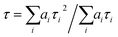 | (2) |
The results are τ = 29.0 ± 0.5 ns to 2.6 ± 0.5 ns for the pristine CdSe QDs and the CdSe QD–χ–C60 system, respectively. As expected from steady-state PL, the significant decrease in the PL lifetimes after ligand exchange confirms the fast nonradiative decay process induced by the thiol capping molecules, thereby confirming the success of the exchange interaction.44
We gathered further information on the surface of the functionalized QDs with XPS experiments. We analysed the C 1s and S 2p/Se 3p regions of the pristine CdSe QD and the QD–χ–C60 system since they are the most relevant regions to investigate the chemical functionalization of the CdSe QDs. The analysis of Se 3d and Cd 3d regions is reported in ESI (Fig. S19–S23†), together with the C 1s and S 2p XPS of the bulk phase of the individual building blocks (1, 2, and C60). The spectra of the C 1s region are reported in Fig. 3c and S19.† In the spectrum of pristine CdSe QDs, the main component at 284.3 eV is attributed to aliphatic carbon atoms of the TOPO ligand, plus a minor component at 285.8 eV attributable to adventitious carbon.49 Conversely, the C 1s region acquired on the QD–χ–C60 system features the components of both 1 and TOPO ligands (reported in Fig. S19†), thereby demonstrating the coexistence of both ligands on the surface of CdSe QDs after the exchange reaction. However, the components belonging to TOPO decrease after the ligand exchange. Further confirmation of the presence of both ligands on the QDs surface is given by the P 2p XPS signal (132.4 eV) detectable on samples before and after the exchange reaction (see Fig. S21†).50
Crucial insight regarding the assembly of molecules on the surface of the CdSe QDs can be deduced by analysing the S 2p/Se 3p region (Fig. 2d and S20†). In the pristine CdSe QDs sample, the Se 3p signal (159.7 eV) and its relative spin–orbit contribution (+5.7 eV) are clearly visible.51 In the QD–χ–C60 system, we observe a change in the lineshape of the Se 3p signal due to the overlap with additional components at 161.8 eV (highlighted in orange) attributable to sulfur atoms bound to the surface of the QDs.52 Furthermore, the spectra do not feature signals at 163.5 eV and ca. 167 eV, which are characteristic of S–H and S–On groups, thus excluding the presence of both physisorbed and oxidized species of 1.
Spin-polarized photoinduced charge transfer
With the synthesis of the CdSe QD–χ–C60 system confirmed, we turned to trEPR spectroscopy to investigate the photoinduced CT and its spin dynamics.53,54 trEPR is sensitive to the presence of spin-polarized states, which show signals in enhanced absorption (A) and/or emission (E),55 and, under favourable circumstances, can reach a time resolution as low as tens of nanoseconds. In trEPR spectroscopy, the detected signals result from non-Boltzmann population of the spin sublevels following the CT process.20 The generation and time evolution of spin polarization is very informative about the spin dynamics of paramagnetic states.56,57 We performed trEPR measurements at 40 K on our model system CdSe QD–χ–C60 (7.8 μM in 1,2,4-trichlorobenzene, red line, Fig. 3a). For comparison, we also investigated a solution containing both CdSe QD functionalized with 2 (CdSe QD–χ) (7.8 μM) and 1 mM of 3 (black line, Fig. 3a). The concentration of QDs was chosen to have an optical density below 1 at the excitation wavelength used in the EPR experiment (450 nm) in the 0.3 cm EPR quartz tube (UV-vis spectrum shown in Fig. S18†). In Fig. 3a, we show the trEPR spectra taken at 1 μs after excitation at 450 nm. In both spectra, we observe a broad signal between 335–358 mT that we assign to the C60 triplet state formed via intersystem crossing (ISC) promoted by spin–orbit coupling (SOC).25,58 This signal results from photogenerated singlet states in C60 that do not undergo electron transfer. The C60 triplet spectra in the two samples show some differences, specifically the shoulders in the QD–χ–C60 sample are more pronounced. This small difference is most likely due to a different environment of the C60 molecule: linked to the CdSe QDs in the target system or dispersed in the frozen solution in the control experiment. The different environment may affect the SOC-promoted ISC in the two C60 triplets.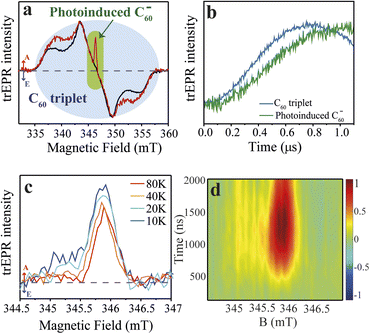 | ||
| Fig. 3 Time-resolved EPR spectra of the QD–χ–C60 (model) and QD–χ + C60 (test) systems. (1) Experimental trEPR spectra of QD–χ–C60 (red line) and QD–χ + C60 (black line) taken at 1 μs after 450 nm laser pulse (7 ns, 2 mJ) acquired at 40 K. Both spectra show a broad signal between ∼335–358 mT, which is assigned to the C60 triplet, but only the spectrum of QD–χ–C60 displays a narrow signal in enhanced absorption centred at ∼346 mT, which is attributed to the photogenerated C60 radical anion. Arrows legend: A = enhanced absorption, E = emission. The dashed line represents the zero. (b) Normalized trEPR transients of QD–χ–C60 excited at 450 nm (40 K). The transients are integrated on a magnetic field window of 0.5 mT and are centred at 343 and 346 mT for the C60 triplet and the photoinduced C60 radical anion, respectively. The transients show a slower generation of the photoinduced C60 radical anion compared with the formation of the C60 triplet. (c) Temperature-dependent trEPR spectra of QD–χ–C60 taken at 1 μs after 450 nm laser pulse (7 ns, 2 mJ). The spectra show a mostly enhanced absorptive signal associated with the C60 radical anion. The dashed line represents the zero. The transients are available in Fig. S24.† (d) 2D experimental trEPR contour plot of QD–χ–C60 of the charge transfer signal acquired after 450 nm laser pulse (7 ns, 2 mJ) at T = 10 K. Colour legend: red = enhanced absorption, blue = emission, green = baseline. | ||
More interestingly, only in the spectrum of QD–χ–C60 we observe an additional intense and spectrally narrow feature in enhanced absorption centred at ∼346 mT (g-value ≈ 2.00), which we attribute to the C60 radical anion.25,59 We propose that this absorptive signal results from the photoinduced electron transfer from the QDs to C60. Specifically, after the absorption of 450 nm light by the CdSe QDs, an exciton is generated, which undergoes a CT process thanks to the favourable energy alignment (see Fig. 1b).25 As a result, a hole localized on the CdSe QD and a radical anion localized on the C60 are formed. In agreement with literature reports,24 the signal of the counterpart hole on the CdSe QDs is not visible in our spectra due to the fast spin relaxation induced by the large spin–orbit coupling of heavy Cd atoms. The lack of the trEPR signature of the hole was similarly reported by Olshansky et al.24 As for the radical anion, the enhanced absorption polarization reminds of that recently observed in similar systems.24,60 However, a significant difference between our results and previous literature is the time evolution of spin polarization in the first μs after the laser pulse, reported in Fig. 3b. In our case, the spin polarization of the C60 signal rises even more slowly than the polarization of the C60 ISC triplet and shows a maximum at ∼1 μs, as further discussed in the theoretical modelling. In addition, most trEPR investigations of the CT process in similar QD/organic molecule systems involve D and A species that are nearby or connected by conjugated bonds,24,25 while, in our case, the CdSe QD and the C60 are covalently attached through a ∼10 Å long saturated bridge which in principle hinders the electron transfer process. Notably, our trEPR observation appears even more interesting considering the presence of a chiral bridge which has been suggested to favor the efficiency of the CT process.5,12
To achieve better insight into the CT process, we investigated the signal of the spin-polarized C60 anion by performing experiments at different temperatures (10–80 K), as reported in Fig. 3c. The absorptive signal of the C60 radical anion is observed at all temperatures. Notably, the data show a reduction in the absorptive feature at low fields as the temperature increases. Polarization patterns of similar systems were tentatively rationalized in literature by considering two main contributions: (i) a main absorptive feature that originates from the triplet excited state of the photoexcited QD from which the CT process starts, and (ii) a minor absorption/emission (AE) contribution showing up at lower temperatures (<10 K) which originates from the spin-correlated radical pair (SCRP) mechanism.24 However, the origin of spin polarization in our and similar systems is still little understood, and it is of paramount importance to theoretically understand the time evolution of the spin polarization of photoinduced CT states. This study appears even more fundamental in view of a rationalization of the role of the chiral linker in the spin-selectivity of the photoinduced CT process.
Simulation of trEPR spectra
In order to gain a deeper understanding of the CT process, we simulated trEPR spectra as a function of both time and static magnetic field.61–65 Theoretical modelling focuses solely on the magnetic field region relevant for the charge transfer signal since the signal associated with the C60 triplet (see Fig. 3b) is due to a spin-polarized triplet state originating from SOC-promoted ISC independent of CISS. In our simulation, the initial state of the radical pair is described by the density matrix ρ(0), written in the four-level basis composed by singlet and triplet spin states for the hole–electron pair. The time evolution of ρ(0) is computed using the stochastic Liouville equation (see ESI† and ref. 61–65 and 81), considering both coherent and incoherent contributions.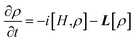 | (3) |
Coherent evolution is determined by the Hamiltonian H, which in the high-field approximation can be written in the rotating frame as follows:
| H = μBB0⋅(gDSD + gASA) + SD⋅D(Ω)⋅SA − ℏω0(gDSDz + gASAz) + μBB1(gDSDx + gASAx) | (4) |
Incoherent evolution is accounted for by the super-operator L, which includes the effects of charge recombination from the singlet spin state (with rate kCR), spin relaxation, and dephasing. Since the two g-factors are very different (see below), the eigenstates of the system are practically factorized. In addition, we expect a much shorter relaxation time for the electron spin on the QD. Hence, it is reasonable to assume two different relaxation times (TD1 and TA1) for the two electrons of the radical pair. Finally, the dephasing time T2 (assumed to be the same for all transitions) induces a Lorentzian broadening of the EPR peaks.
By using the ρ(Ω, t) obtained for each time and magnetic field value, we compute the spherical average to obtain the trEPR spectrum:
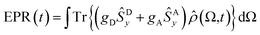 | (5) |
The result of eqn (5) is then convoluted with the exponential response function of the spectrometer, determined by its Q-factor of 6800, giving rise to a response time tR = 2Q/ω0 = 225 ns.66 Simulated spectra are plotted as a function of both time and magnetic field in Fig. 4. For a better comparison, in Fig. 3d, we report the 2D experimental trEPR acquired at 10 K as a contour plot similar to the computed ones.
 | ||
| Fig. 4 Simulated time-resolved EPR spectra as a function of both time and field. Panels (a, b, c): spectra calculated for the S, T, and ST initial states. Panels (d, e, f): corresponding spectra calculated for the S, T, and ST initial states, filtered by the CISS effect. Simulations are performed by considering a temperature of T = 10 K and using the parameters found in Table 1. | ||
This procedure allows us to investigate the initial state ρ(0), the Hamiltonian parameters, and relaxation/recombination rates. In Fig. 4, we consider three initial states:
• A pure singlet state (S), as shown in Fig. 4, panel (a);
• A pure triplet state, with the three states equally populated (T), Fig. 4, panel (b);
• A mixture of singlet and triplet (ST case), with all four levels equally populated, Fig. 4, panel (c).
Note that these three cases all share spherical symmetry. In Fig. 4, panels (a, b, c) show that only the ST case is in qualitative agreement with the measured time dependence, showing a negligible short-time signal rising slowly until reaching its maximum at ≈1.2 μs. We also explored more asymmetric states, where the singlet and triplet sublevels are not equally populated (see ESI† for further details). In this case, additional averaging over the spherical distribution of the chiral ligands with respect to the QD initial state is required. The calculations further corroborate the results of the symmetrical model and suggest that when the S population approaches ≈1/4 (and in turn T+ + T0 + T− ≈ 3/4), the simulations do not substantially differ from the ST “symmetric” case, independently of the three triplet sublevels populations (see Fig. S26†).
To better rationalise this result, it is worth revising the relevant spin relaxation times involved in the ET process. Equilibration between the S and T states in the QD occurs in a few picoseconds, well before the ET occurs, as reported for similar systems in the literature up to 5 K.24 This suggests that the precursor state in the QD consists of thermally equilibrated S and T exciton states.24 As a result, to have S population ≈1/4, S and T energy levels must be close in energy. Our QDs have an average diameter of 5 nm which should result in a ST energy difference of ≈1 meV,59,60 thereby corroborating our assumption.67,68
Table 1 reports the Hamiltonian parameters manually optimized to obtain our best simulation reported in Fig. 5 in the spherical symmetry assumption (ST state) at different times and temperatures. For simplicity, we neglected the isotropic exchange coupling and considered only an axial dipolar coupling D = −26 MHz, which we determined from the separation between different peaks (Fig. 5, panels a, c). In turn, by using the point-dipole approximation for calculating D and a distance of 10 Å between QD and C60 and neglecting any distribution of conformations for simplicity, we obtain the g-value of the QD gD ≈ 1. The extracted g-value is consistent with what we expected for these nanoparticles21 and justifies the relatively weak dipolar coupling we determined from peak separation. At this distance, one could also expect an isotropic exchange contribution of the same order of magnitude. However, we prefer to limit the number of parameters and only assume a dipolar contribution. This simplified model leads to a higher g-value of the C60 radical anion (gA = 2.0037) than literature reports.69,70
| g D | g A | D | T D1 | T A1 | T 2 | k CR |
|---|---|---|---|---|---|---|
| 1 | 2.0037 | −26 MHz | 200 ns | 10 μs | 33.4 ns | 1 μs−1 |
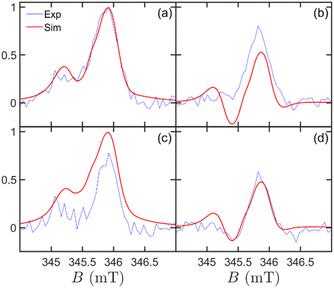 | ||
| Fig. 5 Simulated time-resolved EPR spectra as a function of magnetic field, temperature, and delay from the laser pulse. Experimental (blue line) and simulated (red line) spectra obtained at (a) t = 1 μs, T = 10 K, (b) t = 1 μs, T = 40 K, (c) t = 2 μs, T = 10 K, and (d) t = 2 μs, T = 40 K. All simulations were performed using the parameters in Table 1 and with the ST initial state. | ||
As a matter of clarity, it is worth stressing that in Fig. 4c, the absence of a signal at short times is due to the equally populated initial CT state. With time, the population of the four levels evolves because of incoherent processes, namely relaxation and recombination. A thorough study of the time dependence of the spectra allows us to fit the relaxation parameters (Table 1). The rate of charge recombination is estimated considering the time at which the maximum signal occurs (Fig. 4, panels c, f) and its value of kCR = 1 μs−1 is aligned to what we expected for this system.24 Spin relaxation is described by the two different characteristic times TD1 = 200 ns for the QD and TA1 = 10 μs for C60. As for the former, we are able to provide an estimate thanks to its effect on the relative height of the two peaks, which is more evident at low temperature (Fig. 5, panels a, c). As for the latter, we can only infer a lower bound of about 2 μs, consistently to what expected for the C60 anion, since the simulation does not significantly change for larger values of TA1. An overall dephasing time T2 = 33 ns was obtained by fitting the Lorentzian peak width. From the analysis of Fig. 5, we note that the main experimental spectral features, their time evolution and temperature dependence are in good agreement with our theoretical simulations, with only minor differences, e.g. an emissive calculated spin polarisation at 1 μs for 40 K.
We now consider the possibility of having a CT process that is spin filtered by the CISS effect. To this aim, we simulate the effect of CISS on the trEPR spectra for all three previously considered ρ(0). We model CISS as a “filter” which ideally keeps only the component of the transferred electron spin parallel (or anti-parallel, depending on the enantiomer) to the chiral bridge axis (see ESI†).18,71,72 Hence, all the initial states are modified by CISS and produce different features in the resulting trEPR spectrum at short times on a randomly oriented solution. Notably, we considered only one of the two possible spin orientations because the isotropic QD generates identical EPR spectra for the two enantiomers. As shown in Fig. 4d and e, in the presence of an anisotropic dipole–dipole coupling, CISS filter strongly affects trEPR spectra for both the singlet and triplet cases, giving rise to opposite AE vs. EA features at short times. Conversely, CISS does not significantly affect the spectrum with ST initial state (Fig. 4f). Note that the presence of an anisotropic spin–spin interaction is crucial to detect the occurrence of CISS in an isotropic solution.18,73
Our current combined experimental and theoretical results do not allow distinguishing between a standard CT vs. a CISS-mediated CT yet, due to the initial CT state composed of a mixture of singlet and triplet states. However, our results provide an essential step towards this ambitious goal since they allow drawing new guidelines for developing model systems for CISS detection. Specifically, our calculations demonstrate that a “pure” precursor (or a precursor with different weights of S and T) would allow unravelling the occurrence of CISS even in a randomly oriented sample. This could occur in systems characterized by a larger singlet-triplet splitting than the CdSe QD employed here. For example, a larger splitting may be achieved by introducing a shell to increase the electron confinement, as done in literature for similar QD-organic molecule dyads.24 However, introducing a shell might further reduce the CT efficiency through the long and non-conjugated chiral bridge.
Conclusions
In conclusion, we have engineered and developed a model system comprising a CdSe QD as a donor and a C60 derivative as an acceptor linked by a rigid and saturated bi-peptidic chiral bridge (χ). This chiral system has shown spin polarization as a result of the photoinduced CT between the CdSe QD and the C60 through χ. The CdSe QD–χ–C60 system was fabricated through the ligand exchange approach and characterized through the combination of optical spectroscopies and XPS analysis. We then used time-resolved EPR to demonstrate that the photoinduced CT process generates an organic radical localized on the C60, which shows a peculiar spin-polarization evolution in the first few μs after the laser pulse. We modelled the trEPR signal of our system in two different cases: (i) a standard spin-polarized photoinduced CT, and (ii) a CISS-mediated photoinduced CT. Our calculations demonstrated that the observed EPR features might be compatible with the photoinduced CISS effect.Though not conclusive yet, our combined experimental and theoretical work represents a first promising attempt toward the direct spectroscopic observation of photodriven CISS effect. Although the search for the perfect model system simultaneously showing good CT efficiencies, efficient spin-filtering, and a well-defined precursor state is still in its infancy, our results suggest that QD–χ–organic molecule dyads are very promising. In addition, our work builds up a sound theoretical framework that will allow a better understanding of spin-polarization arising from photoinduced CT processes in chiral hybrid systems comprising QD and organic molecules.
Ultimately, the possibility of observing a CISS-mediated charge transfer at the molecular level would provide a new tool for molecule-based quantum information processing. Indeed, the QD–χ–C60 could form an important building block of a quantum computing architecture, in which polarization resulting from CISS could be harnessed to initialize/readout qubits or implement quantum gates. Thanks to the remarkable efficiency displayed by CISS at high temperatures, this could pave the way toward room-temperature operation of a molecular quantum processor.
Experimental section
Synthesis
Details on the synthesis and characterisation of organic ligands 1, 2 and 3 are presented in ESI.†DFT calculations
All DFT calculations were performed with ORCA 4.2.1 quantum chemistry package.74 For the geometry optimizations, PBE0 functional75 and D3 empirical dispersion correction76,77 were used, while def2-TZVP basis set78 was employed for all the atoms. The thresholds on the maximum force gradient and the energy change were set to 3 × 10−4 Hartree/Bohr and 5 × 10−6 Hartrees, respectively. The root mean square deviation was computed on the heavy atoms C, N, O, and S of the polypeptide chain within the formula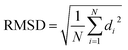 where di is the distance between a pair of equivalent atoms in the two structures and N is the total number of equivalent atoms.
where di is the distance between a pair of equivalent atoms in the two structures and N is the total number of equivalent atoms.
CdSe quantum dots (QDs) fabrication
Details on the fabrication of pristine CdSe QDs, their morphological characterisation, and ligand exchange process are presented as ESI.†Optical spectroscopy
UV-Vis spectra were recorded at room temperature by using a Cary 5000 spectrophotometer (Agilent) in the range 400–800. The PL spectra were measured at room temperature using an excitation wavelength (λex) of 400 nm on a FluoroMax P (Horiba). The measurements were performed using quartz cuvettes with a path length of 1 cm. PL spectra were normalized for the optical density of the same solution at the maximum of the excitonic peak.Time-resolved photoluminescence (TRPL) measurements were carried out using the time-correlated single-photon counting (TCSPC) technique. The experimental apparatus is based on the FluoroMax P spectrofluorometer detection unit (grating monochromator and photomultiplier tube), powered by the FluoroHub Single Photon Counting unit. The excitation source was a blue pulsed Horiba NanoLED, generating picosecond pulses in the UV (375 nm). The instrument response function (IRF) for the whole apparatus was determined by means of scattered light detection using a reference sample of LUDOX® colloidal silica. LED radiation was focused by means of a spherical lens on a sample holder, and sample emission was collected with a 90° geometry to minimize scattering interferences. The measurements were carried out on dilute solutions of TOPO-capped and 1-capped QDs solutions in 1,2,4 trichlorobenzene. Solutions were prepared to keep optical absorbance at 400 nm below 0.2 in 1 cm path quartz cuvettes.
X-ray photoelectron spectroscopy (XPS)
X-ray photoelectron spectroscopic (XPS) analyses were carried out in an UHV chamber with a base pressure lower than 10−9 mbar. The chamber was equipped with non-monochromatized Mg Kα radiation (hν = 1253.6 eV) and a hemispherical electron/ion energy analyser (VSW mounting a 16-channel detector). The operating parameters of the X-ray source were 12 kV and 12 mA, and photoelectrons were collected normal to the sample surface, maintaining the analyser angle between analyser axis and X-ray source fixed at 54.5°. All the samples were drop cast on In foil and on a slab of Au on mica and XPS spectra acquired in a fixed analyser transmission mode with pass energy of 44.0 eV. The spectra were analysed by using the CasaXPS software. Linear or Shirley functions were used to subtract the background. The deconvolution of the XPS spectra was performed by applying a combination of Gaussian and Lorentzian functions (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30). The binding energy scale was calibrated using the Au 4f7/2 peak or the In 3d5/2 peak respectively at 84 eV,79 and 443.9 eV.80
30). The binding energy scale was calibrated using the Au 4f7/2 peak or the In 3d5/2 peak respectively at 84 eV,79 and 443.9 eV.80
Time-resolved electron paramagnetic resonance (trEPR)
All trEPR spectra were recorded on a Bruker Elexsys E580 X-band spectrometer equipped with a dielectric ring resonator (ER 4118X-MD5). The sample temperature was maintained using a helium gas-flow cryostat Oxford Instruments CF9350 and controlled with an Oxford Instruments ITC503. Laser excitation at different wavelengths was provided by a Litron AURORA II opto-parametric oscillator (OPO) tuneable laser (model number: A23-39-21, 21 Hz repetition rate, E/pulse ≈ 2 mJ, λ = 410–700 nm, pulse duration = 7 ns). The laser beam was coupled into the resonator through an optical window. No effects of laser beam polarisation are detected, which suggests the laser beam is non-polarised at the sample position. trEPR experiments were performed by direct detection with the transient recorder without lock-in amplification. The instrument response time was about 200 ns. The spectra were acquired with 2 mW microwave power and averaging 100 transient signals at each field position. The magnetic field was measured with a Bruker ER035M NMR Gaussmeter.The trEPR measurements were performed on the model system CdSe QD–χ–C60 and the control sample, as a comparison, consisting of CdSe QD–χ to which 1 mM of PCBM was added. The concentration of CdSe QD was 7.8 μM in 1,2,4-trichlorobenzene. The solutions were poured inside EPR quartz tubes that were sealed with Teflon under N2 atmosphere.
After data acquisition, baseline correction in both time and field dimensions was performed. First, we subtracted the pre-trigger offset for each field point; second, we filtered out the laser induced background signal by subtracting the off-resonance signal intensity from the spectra at each time point. For the narrow sweep spectra, the C60 anion signal is superimposed to the C60 triplet signal. We applied first-order background subtraction for each time point to remove the drifting baseline. The transient EPR spectrum at different time delays after the laser pulse was extracted from the corrected dataset. The reported trEPR spectra were averaged over a time window of 0.2 μs.
Theoretical modelling
Details on theoretical modelling are presented in ESI.†Data availability
All experimental and computed data are available from the authors upon request.Author contributions
The manuscript was written through the contributions of all authors.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work has received funding from the Italian Ministry of Education and Research (MUR) through PRIN Project 2017CR5WCH Q-chiSS ``Quantum detection of chiral-induced spin selectivity at the molecular level'' and “Progetto Dipartimenti di Eccellenza 2018-2022 (ref. no. B96C1700020008), and from the European Union's Horizon 2020 research and innovation programme (FET-OPEN project FATMOLS) under grant agreement no. 862893. The authors acknowledge MatchLab Interdepartmental Research Unit (Università degli Studi di Firenze) for the XPS facilities. We acknowledge also financial support from “Fondazione Cariparma”. We acknowledge Michael R. Wasielewski and Robert Bittl for their critical manuscript reading.Notes and references
- A. J. Heinrich, W. D. Oliver, L. M. K. Vandersypen, A. Ardavan, R. Sessoli, D. Loss, A. B. Jayich, J. Fernandez-Rossier, A. Laucht and A. Morello, Nat. Nanotechnol., 2021, 16, 1318–1329 CrossRef CAS PubMed.
- M. Atzori and R. Sessoli, JACS, 2019, 141, 11339–11352 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS.
- J. M. Abendroth, D. M. Stemer, B. P. Bloom, P. Roy, R. Naaman, D. H. Waldeck, P. S. Weiss and P. C. Mondal, ACS Nano, 2019, 13, 4928–4946 CrossRef CAS PubMed.
- A. Privitera, M. Righetto, F. Cacialli and M. K. Riede, Adv. Opt. Mater., 2021, 9, 2100215 CrossRef CAS.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed.
- S.-H. Yang, R. Naaman, Y. Paltiel and S. S. P. Parkin, Nat. Rev. Phys., 2021, 3, 328–343 Search PubMed.
- K. Michaeli, N. Kantor-Uriel, R. Naaman and D. H. Waldeck, Chem. Soc. Rev., 2016, 45, 6478–6487 RSC.
- C. D. Aiello, J. M. Abendroth, M. Abbas, A. Afanasev, S. Agarwal, A. S. Banerjee, D. N. Beratan, J. N. Belling, B. Berche, A. Botana, J. R. Caram, G. L. Celardo, G. Cuniberti, A. Garcia-Etxarri, A. Dianat, I. Diez-Perez, Y. Guo, R. Gutierrez, C. Herrmann, J. Hihath, S. Kale, P. Kurian, Y.-C. Lai, T. Liu, A. Lopez, E. Medina, V. Mujica, R. Naaman, M. Noormandipour, J. L. Palma, Y. Paltiel, W. Petuskey, J. C. Ribeiro-Silva, J. J. Saenz, E. J. G. Santos, M. Solyanik-Gorgone, V. J. Sorger, D. M. Stemer, J. M. Ugalde, A. Valdes-Curiel, S. Varela, D. H. Waldeck, M. R. Wasielewski, P. S. Weiss, H. Zacharias and Q. H. Wang, ACS Nano, 2022, 16, 4989–5035 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Acc. Chem. Res., 2020, 53, 2659–2667 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- F. Evers, A. Aharony, N. Bar-Gill, O. Entin-Wohlman, P. Hedegård, O. Hod, P. Jelinek, G. Kamieniarz, M. Lemeshko, K. Michaeli, V. Mujica, R. Naaman, Y. Paltiel, S. Refaely-Abramson, O. Tal, J. Thijssen, M. Thoss, J. M. van Ruitenbeek, L. Venkataraman, D. H. Waldeck, B. Yan and L. Kronik, Adv. Mater., 2022, 34, 2106629 CrossRef CAS PubMed.
- T. S. Metzger, S. Mishra, B. P. Bloom, N. Goren, A. Neubauer, G. Shmul, J. Wei, S. Yochelis, F. Tassinari, C. Fontanesi, D. H. Waldeck, Y. Paltiel and R. Naaman, Angew. Chem., Int. Ed., 2020, 59, 1653–1658 CrossRef CAS PubMed.
- T. P. Fay, J. Phys. Chem. Lett., 2021, 12, 1407–1412 CrossRef CAS PubMed.
- Y.-H. Kim, Y. Zhai, H. Lu, X. Pan, C. Xiao, E. A. Gaulding, S. P. Harvey, J. J. Berry, Z. V. Vardeny, J. M. Luther and M. C. Beard, Science, 2021, 371, 1129–1133 CrossRef CAS PubMed.
- D. H. Waldeck, R. Naaman and Y. Paltiel, APL Mater., 2021, 9, 040902 CrossRef CAS.
- A. Chiesa, M. Chizzini, E. Garlatti, E. Salvadori, F. Tacchino, P. Santini, I. Tavernelli, R. Bittl, M. Chiesa, R. Sessoli and S. Carretta, J. Phys. Chem. Lett., 2021, 12, 6341–6347 CrossRef CAS PubMed.
- J. Ferrando-Soria, E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- S. M. Harvey and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 143, 15508–15529 CrossRef CAS PubMed.
- O. Ben Dor, N. Morali, S. Yochelis, L. T. Baczewski and Y. Paltiel, Nano Lett., 2014, 14, 6042–6049 CrossRef CAS PubMed.
- B. P. Bloom, B. M. Graff, S. Ghosh, D. N. Beratan and D. H. Waldeck, JACS, 2017, 139, 9038–9043 CrossRef CAS PubMed.
- H. Al-Bustami, B. P. Bloom, A. Ziv, S. Goldring, S. Yochelis, R. Naaman, D. H. Waldeck and Y. Paltiel, Nano Lett., 2020, 20, 8675–8681 CrossRef CAS PubMed.
- J. H. Olshansky, S. M. Harvey, M. L. Pennel, M. D. Krzyaniak, R. D. Schaller and M. R. Wasielewski, J. Am. Chem. Soc., 2020, 142, 13590–13597 CrossRef CAS PubMed.
- M. Righetto, A. Privitera, F. Carraro, L. Bolzonello, C. Ferrante, L. Franco and R. Bozio, Nanoscale, 2018, 10, 11913–11922 RSC.
- D. Wróbel and A. Graja, Coord. Chem. Rev., 2011, 255, 2555–2577 CrossRef.
- X.-B. Li, C.-H. Tung and L.-Z. Wu, Nat. Rev. Chem., 2018, 2, 160–173 CrossRef CAS.
- M. Prato, Fullerene Materials, In Fullerenes and Related Structures, Springer Berlin Heidelberg, Berlin, 1999, pp. 173–187 Search PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, J. Phys. Chem. Lett., 2020, 11, 3660–3666 CrossRef CAS PubMed.
- R. D. Harris, S. Bettis Homan, M. Kodaimati, C. He, A. B. Nepomnyashchii, N. K. Swenson, S. Lian, R. Calzada and E. A. Weiss, Chem. Rev., 2016, 116, 12865–12919 CrossRef CAS PubMed.
- J. Jasieniak, M. Califano and S. E. Watkins, ACS Nano, 2011, 5, 5888–5902 CrossRef CAS PubMed.
- I. Ramirez, A. Privitera, S. Karuthedath, A. Jungbluth, J. Benduhn, A. Sperlich, D. Spoltore, K. Vandewal, F. Laquai and M. Riede, Nat. Commun., 2021, 12, 471 CrossRef CAS PubMed.
- S. Engmann, A. J. Barito, E. G. Bittle, N. C. Giebink, L. J. Richter and D. J. Gundlach, Nat. Commun., 2019, 10, 227 CrossRef PubMed.
- R. Fanelli, L. Milli, A. Cornia, A. Moretto, N. Castellucci, N. Zanna, G. Malachin, R. Tavano and C. Tomasini, Eur. J. Org. Chem., 2015, 2015, 6243–6248 CrossRef CAS.
- A. Friggeri, H. Schönherr, H.-J. van Manen, B.-H. Huisman, G. J. Vancso, J. Huskens, F. C. J. M. van Veggel and D. N. Reinhoudt, Langmuir, 2000, 16, 7757–7763 CrossRef CAS.
- E. Colangelo, J. Comenge, D. Paramelle, M. Volk, Q. Chen and R. Lévy, Bioconj. Chem., 2017, 28, 11–22 CrossRef CAS PubMed.
- E. Colangelo, Q. Chen, A. M. Davidson, D. Paramelle, M. B. Sullivan, M. Volk and R. Lévy, Langmuir, 2017, 33, 438–449 CrossRef CAS PubMed.
- Q. Dai, D. Li, J. Chang, Y. Song, S. Kan, H. Chen, B. Zou, W. Xu, S. Xu, B. Liu and G. Zou, Nanotechnology, 2007, 18, 405603 CrossRef.
- C. Tomasini, G. Luppi and M. Monari, J. Am. Chem. Soc., 2006, 128, 2410–2420 CrossRef CAS PubMed.
- K. Kordatos, T. Da Ros, S. Bosi, E. Vázquez, M. Bergamin, C. Cusan, F. Pellarini, V. Tomberli, B. Baiti, D. Pantarotto, V. Georgakilas, G. Spalluto and M. Prato, J. Org. Chem., 2001, 66, 4915–4920 CrossRef CAS PubMed.
- M. Kicsák, M. Bege, I. Bereczki, M. Csávás, M. Herczeg, Z. Kupihár, L. Kovács, A. Borbás and P. Herczegh, Org. Biomol. Chem., 2016, 14, 3190–3192 RSC.
- M. A. Boles, D. Ling, T. Hyeon and D. V. Talapin, Nat. Mater., 2016, 15, 141–153 CrossRef CAS PubMed.
- M. Karakawa, T. Nagai, K. Adachi, Y. Ie and Y. Aso, RSC Adv., 2017, 7, 7122–7129 RSC.
- S. F. Wuister, C. de Mello Donegá and A. Meijerink, J. Phys. Chem. B, 2004, 108, 17393–17397 CrossRef CAS.
- I. S. Liu, H.-H. Lo, C.-T. Chien, Y.-Y. Lin, C.-W. Chen, Y.-F. Chen, W.-F. Su and S.-C. Liou, J. Mater. Chem., 2008, 18, 675–682 RSC.
- P. Kambhampati, J. Phys. Chem. C, 2011, 115, 22089–22109 CrossRef CAS.
- P. Tyagi and P. Kambhampati, J. Chem. Phys., 2011, 134, 094706 CrossRef PubMed.
- M. Righetto, A. Minotto and R. Bozio, J. Phys. Chem. C, 2017, 121, 896–902 CrossRef CAS.
- A. Keller, M. Fritzsche, R. Ogaki, I. Bald, S. Facsko, M. Dong, P. Kingshott and F. Besenbacher, J. Chem. Phys., 2011, 134, 104705 CrossRef PubMed.
- A. J. Morris-Cohen, M. D. Donakowski, K. E. Knowles and E. A. Weiss, J. Phys. Chem. C, 2010, 114, 897–906 CrossRef CAS.
- R. Ospina, S. A. Rincón-Ortiz and J. Rodriguez-Pereira, Surf. Sci. Spectra, 2020, 27, 014021 CrossRef CAS.
- S. Liu, X. Zhang, Y. Yu and G. Zou, Biosens. Bioelectron., 2014, 55, 203–208 CrossRef CAS PubMed.
- J. Niklas, S. Beaupré, M. Leclerc, T. Xu, L. Yu, A. Sperlich, V. Dyakonov and O. G. Poluektov, J. Phys. Chem. B, 2015, 119, 7407–7416 CrossRef CAS PubMed.
- J. Niklas and O. G. Poluektov, Adv. Energy Mater., 2017, 7, 1602226 CrossRef.
- T. Biskup, Front. Chem., 2019, 7, 10 CrossRef CAS PubMed.
- A. Privitera, J. Grüne, A. Karki, W. K. Myers, V. Dyakonov, T.-Q. Nguyen, M. K. Riede, R. H. Friend, A. Sperlich and A. J. Gillett, Adv. Energy Mater., 2022, 12, 2103944 CrossRef CAS.
- A. J. Gillett, A. Privitera, R. Dilmurat, A. Karki, D. Qian, A. Pershin, G. Londi, W. K. Myers, J. Lee, J. Yuan, S.-J. Ko, M. K. Riede, F. Gao, G. C. Bazan, A. Rao, T.-Q. Nguyen, D. Beljonne and R. H. Friend, Nature, 2021, 597, 666–671 CrossRef CAS PubMed.
- L. Franco, A. Toffoletti, M. Ruzzi, L. Montanari, C. Carati, L. Bonoldi and R. Po’, J. Phys. Chem. C, 2013, 117, 1554–1560 CrossRef CAS.
- J. Niklas, K. L. Mardis and O. G. Poluektov, J. Phys. Chem. Lett., 2018, 9, 3915–3921 CrossRef CAS PubMed.
- P. J. Hore, Chem. Phys. Lett., 1980, 69, 563–566 CrossRef CAS.
- Y. Kobori, R. Noji and S. Tsuganezawa, J. Phys. Chem. C, 2013, 117, 1589–1599 CrossRef CAS.
- G. Kothe, S. Weber, R. Bittl, E. Ohmes, M. C. Thurnauer and J. R. Norris, Chem. Phys. Lett., 1991, 186, 474–480 CrossRef CAS.
- R. Bittl and G. Kothe, Chem. Phys. Lett., 1991, 177, 547–553 CAS.
- S. Weber, T. Biskup, A. Okafuji, A. R. Marino, T. Berthold, G. Link, K. Hitomi, E. D. Getzoff, E. Schleicher and J. R. Norris, J. Phys. Chem. B, 2010, 114, 14745–14754 CrossRef CAS PubMed.
- F. Kraffert and J. Behrends, Mol. Phys., 2017, 115, 2373–2386 CrossRef CAS.
- K. Möbius and A. Savitsky, High-field EPR Spectroscopy on Proteins and Their Model Systems: Characterization of Transient Paramagnetic States, Royal Society of Chemistry, 2008 Search PubMed.
- M. Nirmal, D. J. Norris, M. Kuno, M. G. Bawendi, A. L. Efros and M. Rosen, Phys. Rev. Lett., 1995, 75, 3728–3731 CrossRef CAS PubMed.
- A. L. Efros, M. Rosen, M. Kuno, M. Nirmal, D. J. Norris and M. Bawendi, Phys. Rev. B, 1996, 54, 4843–4856 CrossRef CAS PubMed.
- M. Brustolon, A. Zoleo, G. Agostini and M. Maggini, J. Phys. Chem. A, 1998, 102, 6331–6339 CrossRef CAS.
- D. Carbonera, M. Di Valentin, C. Corvaja, G. Agostini, G. Giacometti, P. A. Liddell, D. Kuciauskas, A. L. Moore, T. A. Moore and D. Gust, JACS, 1998, 120, 4398–4405 CrossRef CAS.
- X. Yang, C. H. van der Wal and B. J. van Wees, Phys. Rev. B, 2019, 99, 024418 CrossRef CAS.
- Y. E. Kandrashkin and K. M. Salikhov, Appl. Magn. Reson., 2009, 37, 549 CrossRef.
- J. Luo and P. J. Hore, New J. Phys., 2021, 23, 043032 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. P. Seah, G. C. Smith and M. T. Anthony, Surf. Interface Anal., 1990, 15, 293–308 CrossRef CAS.
- R. Nyholm and N. Mårtensson, Solid State Commun., 1981, 40, 311–314 CrossRef CAS.
- Y. Kobori, N. Ponomarenko and J. R. Norris Jr, J. Phys. Chem. C, 2015, 119, 8078–8088 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis of organic ligands 1, 2, and 3. CdSe Quantum Dots (QDs) fabrication and morphological characterization. Ligand exchange methods. Optical measurements. X-ray photoelectron spectroscopy (XPS) analysis. DFT calculations. Time-resolved Electron Paramagnetic Resonance (trEPR) measurements and best-fit simulations. Theoretical modeling. See DOI: https://doi.org/10.1039/d2sc03712b |
| This journal is © The Royal Society of Chemistry 2022 |