Unraveling hydridic-to-protonic dihydrogen bond predominance in monohydrated dodecaborate clusters

Abstract

Hydridic-to-protonic dihydrogen bonds (DHBs) are involved in comprehensive structural and energetic evolution, and significantly affect reactivity and selectivity in solution and solid states. Grand challenges exist in understanding DHBs’ bonding nature and strength, and how to harness DHBs. Herein we launched a combined photoelectron spectroscopy and multiscale theoretical investigation using monohydrated closo-dodecaborate clusters B₁₂X₁₂²⁻·H₂O (X = H, F, I) to address such challenges. For the first time, a consistent and unambiguous picture is unraveled demonstrating that B–H⋯H–O DHBs are superior to the conventional B–X⋯H–O HBs, being 1.15 and 4.61 kcal mol⁻¹ stronger than those with X = F and I, respectively. Energy decomposition analyses reveal that induction and dispersion terms make pronounced contributions resulting in a stronger B–H⋯H–O DHB. These findings call out more attention to the prominent roles of DHBs in water environments and pave the way for efficient and eco-friendly catalytic dihydrogen production based on optimized hydridic-to-protonic interactions.

---

Introduction

The hydrogen bond (HB), first discussed in 1912, represents one of the most important research topics in modern chemistry.^1–4 In a typical HB, a protonic hydrogen (HB donor) of an X–H^δ+ bond (X is a highly electronegative atom, e.g., N, O, halogen) interacts with an adjacent lone pair of an electronegative atom (HB acceptor) in the X–H^δ+⋯A^δ− form.⁵ The HB acceptor A^δ− could be a H atom when it is bonded to an electropositive atom such as boron or transition metal Y, and this can result in a specific HB pattern, X–H^δ+⋯H^δ−–Y, known as hydridic-to-protonic interactions.⁶ This interaction was first recognized as a real intermolecular N–H⋯H–B attraction in borane–ammonia complexes in 1968,⁷ and the term “dihydrogen bond” (DHB) was coined in 1995 to describe such chemical bonding patterns,^8,9 eighty-three years after the original HB concept was formulated. So far, the DHB has attracted considerable attention due to its involvement in comprehensive structural and energetic evolution, as well as its major impact on reactivity and selectivity in both the solution and solid state.^6,10–16 For example, the DHB has manifested its crucial roles in broad and diverse fields such as molecular recognition,¹⁷ hydrogen storage materials,¹⁸ catalytic dehydrogenation,^19,20 synthetic chemistry,²¹ supramolecular self-assembly,^12,22 and drug design.^13,23

Despite the aforementioned importance and previous experiments (i.e. solution NMR spectroscopy,^24–26 neutron diffraction/inelastic neutron scattering technique,^27,28 and IR vibrational spectroscopy^29–32) and theoretical calculations,^6,11,33,34 the nature and strength of DHBs have not been well understood. Particularly, only in rare cases³⁵ has the strength of DHBs been well defined and comparisons made to conventional HBs, but the generality of these observations remains unclear.⁶ This deficiency of understanding is largely due to the lack of proper models^31,32 and precise spectroscopic measurements, in which well-defined DHBs exist without interferences from other conventional HBs and bulk environments. Until now, a direct quantitative measurement of the strength of DHBs and their comparison to typical HBs has not been reported, leading to two important open questions: (1) how strong is a DHB compared to conventional strong HBs? and (2) what is the chemical bonding nature and dynamics in DHB formation?

To address these questions, in this work, a series of size-selected monohydrated closo-dodecaborate clusters B₁₂X₁₂²⁻·H₂O (X = H, F, I) were generated and characterized in the gas phase. B₁₂X₁₂²⁻ clusters are the most well-known boron-based molecules with icosahedral (I_h) symmetry and exceptionally high electronic and structural stability that are tunable with different ligands X.^36–38 In addition, B₁₂X₁₂²⁻ molecules also have important medical applications, including boron-based neutron capture therapy of cancer.³⁹ The nucleophilic H atoms in B₁₂H₁₂²⁻ allow the formation of sole B–H⋯H–O DHBs in monohydrates, making B₁₂H₁₂²⁻·H₂O an ideal model, in which DHBs can be precisely spectroscopically characterized. This model can then be compared to conventional HBs ranging from strong B–F⋯H–O in B₁₂F₁₂²⁻·H₂O to weak B–I⋯H–O in B₁₂I₁₂²⁻·H₂O. Note that the electronegative fluorine as a HB acceptor always represents a strong HB system, with the bifluoride ion [F–H–F]⁻ as an outstanding example whose HB strength exists at an intersection between a classical electrostatic interaction and a covalent chemical bond.^40,41 We combined size-selective cryogenic negative ion photoelectron (NIPE) spectroscopy^42,43 and high-level quantum-chemical calculations to directly investigate these solvated anion clusters. The results unraveled herein consistently imply that the B–H⋯H–O DHB is surprisingly strong, even prevailing over the traditionally strong B–F⋯H–O HB. Dynamic simulations further confirm the superior strength and thermodynamic stability of DHBs in B₁₂H₁₂²⁻·H₂O.

Results and discussion

NIPE spectra of B₁₂X₁₂²⁻·nH₂O (X = H, F, I; n = 0, 1)

Fig. 1 shows the 20 K NIPE spectra of B₁₂X₁₂²⁻·nH₂O (X = H, F, I; n = 0, 1). The spectral shapes of hydrated B₁₂X₁₂²⁻·H₂O show similar patterns to those of each corresponding isolated B₁₂X₁₂²⁻, with their electron binding energies (EBEs) blue shifted. The B₁₂H₁₂²⁻ with the smallest vertical detachment energy (VDE) among the three B₁₂X₁₂²⁻ anions exhibits the largest VDE shift with a ΔVDE of 0.31 eV when one H₂O molecule is attached, in comparison to the 0.26 and 0.11 eV for X = F and I, respectively (Fig. 1 and Table 1). The measured NIPE spectra provide crucial information for determining the structures of these clusters when combining with theoretical calculations. More importantly, ΔVDE—the VDE difference between a hydrated anion cluster and the corresponding isolated anion, can be regarded as a direct measurement of intrinsic water binding energy (wBE) in anionic hydrated systems.^38,44 Therefore, these obtained ΔVDE values unequivocally indicate that the DHB-driven wBE in B₁₂H₁₂²⁻·H₂O is superior to those based on traditional HBs in B₁₂X₁₂²⁻·H₂O.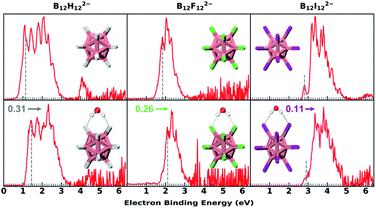

Fig. 1 The 20 K NIPE spectra of B₁₂X₁₂²⁻·nH₂O (X = H, F, I; n = 0, 1) measured with 193 nm photons. The dashed gray lines denote the spectral vertical detachment energy (VDE) positions. Due to the existence of the repulsive Coulomb barrier (RCB) in photodetaching dianions, spectral bands at higher binding energy are suppressed (see Fig. S1† for comparing 193 and 157 nm spectra). The noisy spikes in the spectrum of the hydrated F beyond 4 eV are due to the imperfect background subtraction originating from weak signals and scaled down by a factor of 0.2 to enhance the presentation clarity. VDE blue shifts upon hydration are noted with the color-coded numbers and arrows. The insets show the lowest-lying structures. Boron, hydrogen, oxygen, fluorine, and iodine atoms are, respectively, coloured in pink, grey, red, green, and magenta.

Table 1 Experimental VDEs (eV) and ΔVDEs (kcal mol⁻¹ and eV in parentheses) in comparison to calculated VDEs (eV) at the DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) level, and water binding energies (wBEs, in kcal mol⁻¹) at the SAPT2+/aug-cc-pVDZ(-pp) level as well as from direct energy difference (direct ΔE) calculations for B₁₂X₁₂²⁻·nH₂O (X = H, F, I; n = 0, 1)

	VDE (Exp.)	VDE (Cal.)	ΔVDE^a (Exp.)	wBE (SAPT)	wBE^b (direct ΔE)
a Experimentally determined as VDE difference between B12X12^2−·H2O and isolated B12X12^2−, which equals the water binding energy (wBE) difference in hydrated dianionic and anionic clusters, i.e., [E(B12X12^2−·H2O) − E(B12X12^2−)] − [E(B12X12˙^−·H2O) − E(B12X12˙^−)]. b Direct ΔE = E(B12H12^2−·H2O) − E(H2O) − E(B12H12^2−) at the DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) level with the zero-point energy and entropy corrections.
B12H12^2−	1.15	1.36	—	—
B12H12^2−·H2O	1.46	1.70	7.15 (0.31)	14.31	12.26
B12F12^2−	1.85	2.07	—	—
B12F12^2−·H2O	2.11	2.34	6.00 (0.26)	13.16	11.45
B12I12^2−	2.80	2.86	—	—
B12I12^2−·H2O	2.91	3.05	2.54 (0.11)	8.74	9.76

---

B–H⋯H–O DHB versus B–X⋯H–O HB (X = F and I)

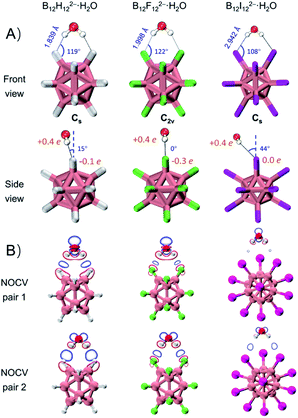
DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) calculations⁴⁵ predict that these monohydrates share very similar geometric structures with a H₂O molecule attaching simultaneously to two adjacent B–X bonds (Fig. 2A) and their calculated VDEs are in good agreement with the experimental results (Tables 1 and S1†). The major geometric difference lies in the dihedral angle between B–X–X–B and H–X–X–H planes, which is 15° for B₁₂H₁₂²⁻·H₂O (C_s), 0° for B₁₂F₁₂²⁻·H₂O (C_2v), and 44° for B₁₂I₁₂²⁻·H₂O (C_s). It is worth noting that unlike the X = H or F clusters, B₁₂I₁₂²⁻·H₂O tends to have hydrogens of water pointing to the middle valley of two B–I bonds. This is possibly due to the large atomic radius of iodine and its relatively “positive” charge distribution (Fig. 2A and Table S2†). As such, all three B₁₂X₁₂²⁻·H₂O clusters feature optimal structures with the formation of two identical B–X⋯H–O bonds, making them an ideal model enabling direct comparison of B–H⋯H–O DHBs with classical B–F(I)⋯H–O HBs in a similar chemical environment.

Fig. 2 (A) Lowest-lying structures of B₁₂X₁₂²⁻·H₂O (X = H, F, I) with the corresponding bond lengths, bond angles of B–X⋯H, dihedral angles between X–B–B–X and H–X–X–H planes, and restrained electrostatic potential charge (RESP charge) of X atoms and H atoms in H₂O. (B) Plot of electron density changes of two dominant ETS-NOCV pairs arising from orbital interactions between B₁₂X₁₂²⁻ (X = H, F, I) and H₂O with an isovalue of 0.0007 a.u.

As shown in Table 1, ΔVDEs for B₁₂X₁₂²⁻·H₂O, with X = H, F and I, are measured to be 7.15 (0.31), 6.00 (0.26), and 2.54 (0.11) kcal mol⁻¹ (eV), respectively. The results suggest an advantageous binding strength of B₁₂H₁₂²⁻·H₂O that is 1.15 and 4.61 kcal mol⁻¹ stronger than those of B₁₂X₁₂²⁻·H₂O, X = F and I. The superiority of binding strength of the former over the latter two is in accordance with the trend in their calculated X–H bond lengths/B–X–H angles (1.839 Å/119°, 1.998 Å/122°, and 2.942 Å/108° in B₁₂X₁₂²⁻·H₂O, X = H, F, and I, respectively). To compare with the experimental ΔVDEs, theoretical wBEs were calculated using both the symmetry-adapted perturbation theory (SAPT) at the SAPT2+/aug-cc-pVDZ(-pp) level and the direct energy difference (direct ΔE) method at the DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) level with the zero-point energy (ZPE) and entropy corrections. The calculated wBEs are larger than the corresponding ΔVDE values (Table 1) due to the existence of appreciable interactions between the singly charged post-detached B₁₂X₁₂˙⁻ species and water molecule.^38,44 However, the differences in the SAPT-calculated wBEs for the three monohydrates indicate that the intermolecular interaction strength in B₁₂H₁₂²⁻·H₂O is 1.14 and 5.57 kcal mol⁻¹ larger than that in B₁₂F₁₂²⁻·H₂O and B₁₂I₁₂²⁻·H₂O, respectively, in excellent agreement with the corresponding measured values of 1.15 and 4.61 kcal mol⁻¹ (vide supra). The wBEs calculated using the direct ΔE-method suggested that the DHB strength in B₁₂H₁₂²⁻·H₂O is 0.82 and 2.50 kcal mol⁻¹ larger than that in B₁₂F₁₂²⁻·H₂O and B₁₂I₁₂²⁻·H₂O, respectively, consistent with the SAPT results. And the contributions of ZPE and entropy corrections to the total wBEs are within 3% for all the clusters, suggesting their negligible effects (Table S3†). The stronger B–H⋯H–O interaction is also evidenced via the extended transition state-natural orbitals for chemical valence (ETS-NOCV)⁴⁶ analysis (Fig. 2B). The orbital interaction between B₁₂X₁₂²⁻ and H₂O leads to various degrees of charge transfer (occupied orbitals of B₁₂X₁₂²⁻ mixed with unoccupied orbitals of H₂O) and electron polarization (occupied orbitals of B₁₂X₁₂²⁻ mixed with its own empty orbitals). Based on the first two dominant NOCV pairs, there exists a region of increased electron density marked in blue, and such a density change is more significant in B₁₂H₁₂²⁻·H₂O than in B₁₂X₁₂²⁻·H₂O (X = F, I). This analysis therefore suggests that the B–H⋯H–O bond is more covalent-like binding and contributes more to the total interaction energy than the other two conventional HBs. To further compare DHBs vs. traditional HBs, quantum theory of atoms-in-molecules (QTAIM) descriptors⁴⁷ and core–valence bifurcation (CVB)⁴⁸ indices were calculated based on high-quality wave functions at the bond critical point (BCP) of the intermolecular interaction of interest as listed in Table S4.† Interestingly, the QTAIM descriptors well-defined for traditional HBs show different predictive abilities for the studied DHB. Only the |V(r)|/G(r) descriptor within the QTAIM and the ELF(C–V) index can confirm the binding strength advantage of DHBs, suggesting the robustness and versatility of the two indexes. The |V(r)|/G(r) denotes the ratio of absolute potential energy density |V(r)| to Lagrangian kinetic energy density G(r) at the BCP, and the ELF(C–V) index represents the electron localization function (ELF) bifurcation value between the ELF core domain and valence domain. Notably, most of the QTAIM descriptors based on electron density fail to describe the strength advantage of DHBs herein, highlighting the urgency of collecting more spectroscopic DHB data to benchmark the theoretical descriptors that can be universally operative.

Energy decomposition analysis

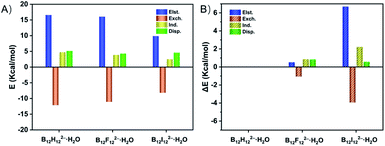
To quantitatively reveal the bonding nature of the B–H⋯H–O DHB, the wBEs are decomposed into four physically meaningful components (Fig. 3 and Table S5A†). It is shown that the larger wBE of B₁₂H₁₂²⁻·H₂O arises from its greater electrostatic, induction and dispersion terms than those of B₁₂F₁₂²⁻·H₂O and B₁₂I₁₂²⁻·H₂O. Specifically, the electrostatic, and induction plus dispersion terms contribute 0.521, and 1.691 kcal mol⁻¹ to the total wBE difference between B₁₂H₁₂²⁻·H₂O and B₁₂F₁₂²⁻·H₂O (Table S5B†), respectively, suggesting the key role of induction and dispersion terms. The larger contribution of induction plus dispersion terms in B₁₂H₁₂²⁻·H₂O can be attributed to its bigger polarizability, i.e., isolated B₁₂H₁₂²⁻ (168 a.u.) versus B₁₂F₁₂²⁻ (141 a.u.). In contrast, the induction plus dispersion terms only contribute 2.806 kcal mol⁻¹ to the ΔwBE between B₁₂H₁₂²⁻·H₂O and B₁₂I₁₂²⁻·H₂O, significantly smaller than the 6.701 kcal mol⁻¹ of the electrostatic term, suggesting the essential advantage of the B–H⋯H–O DHB over B–I⋯H–O HB is driven by the well-established electrostatic interaction.

Fig. 3 (A) Electrostatic (Elst.), exchange (Exch.), induction (Ind.), and dispersion (Disp.) terms (kcal mol⁻¹) derived from the energy decomposition analysis at the SAPT2+/aug-cc-pVDZ(-pp) level for B₁₂X₁₂²⁻·H₂O (X = H, F, I). (B) Energy difference (ΔE, in kcal mol⁻¹) of each term that contributes to the total binding energy difference (ΔBE) between B₁₂H₁₂²⁻·H₂O and B₁₂X₁₂²⁻·H₂O (X = F, I).

Ab initio molecular dynamics simulation

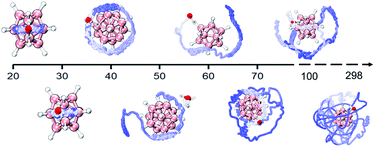
In addition, the DHB predominance is also seen from the analyses of bonding dynamics and molecular vibrations. An extensive ab initio molecular dynamics (AIMD) simulation on B₁₂H₁₂²⁻·H₂O (Fig. S2A,† left panel) shows an orderly oscillating pattern of the B–H⋯H–O DHB length with a 263 fs period, in which the lengths of two B–H⋯H–O DHBs are found to increase or decrease simultaneously. However, for the strong B–F⋯H–O HBs in B₁₂F₁₂²⁻·H₂O, a clear periodicity in the bond length change is not observed (Fig. S2A,† right panel). The two HBs are anti-correlated, i.e., an increase in one bond length accompanies a decrease in the other one. For a water molecule bound onto a borate cage, there are six vibrational modes to describe the bond length, angle, torsional and wagging motions (Fig. S3†). Based on the simulated vibrational spectra (Fig. S2B and Table S6†), the single water stretching vibrations (symmetric ν₇₄ and asymmetric ν₇₅, around 3700 cm⁻¹) shift to lower frequencies with enhanced intensities upon forming HBs. Such red-shifts of −97 cm⁻¹ for ν₇₅ and −50 cm⁻¹ for ν₇₄ are predicted in B₁₂H₁₂²⁻·H₂O, which are more significant than those in B₁₂F₁₂²⁻·H₂O (−38 cm⁻¹ and −12 cm⁻¹) and B₁₂I₁₂²⁻·H₂O (−22 cm⁻¹ and −8 cm⁻¹). But the bending vibration mode of water around 1600 cm⁻¹ seems to be insensitive to the complexation with B₁₂X₁₂²⁻. Interestingly, in the low frequency region, two new mixed modes labelled ν₄ (233 cm⁻¹) and ν₅ (253 cm⁻¹) are also predicted in B₁₂H₁₂²⁻·H₂O, showing unusual vibrations involving combinations of planar swing and nonplanar torsion (Fig. S4†). The corresponding modes, however, do not exist in B₁₂F₁₂²⁻·H₂O or B₁₂I₁₂²⁻·H₂O, indicating that these modes are possibly related to the nuclear quantum effect^49,50 involving two coupled light H atoms in B₁₂H₁₂²⁻·H₂O.

In order to further reveal the water binding stability in B₁₂H₁₂²⁻·H₂O, temperature-dependent dynamics simulations are conducted (Fig. 4). At 20 K, the water molecule moves back and forth within a limited range restricted by two DHBs. As the temperature increases to 40 K, the water molecule seems to move freely on the spherical surface of B₁₂H₁₂²⁻. As the temperature further increases, the water molecule possesses more freedom. Interestingly, even at temperatures up to 298.15 K, the water molecule can still make irregular movements around the B₁₂H₁₂²⁻ cage without completely detaching, in accord with the remaining strong DHB strength.

Fig. 4 Water molecule trajectories in B₁₂H₁₂²⁻·H₂O at different temperatures revealed by AIMD simulations and the trajectory tracking is extracted every 10 fs and varies from blue (start) to white (end).

Conclusions

In summary, a series of hydrated closo-dodecaborate dianions B₁₂X₁₂²⁻·H₂O (X = H, F, I) have been investigated by combining experimental NIPE spectroscopy (NIPES) and multiscale theoretical simulation. A consistent conclusion can be drawn that the B–H⋯H–O DHB shows its strength superiority over conventional B–F(I)⋯H–O HBs. The differences of water binding energy determined by NIPES measurements agree well with the theoretical predictions. The strength advantage of B–H⋯H–O DHBs over strong B–F⋯H–O HBs mainly arises from the greater contribution of dispersion and induction terms, although the electrostatic interaction still plays a dominant role when compared with relatively weak B–I⋯H–O HBs. This work, for the first time, quantifies the strength of DHBs, and unequivocally proves the superiority of DHBs over the traditional strong HBs. It is conceivable that DHBs in hydrated metal-hydrides may become even stronger due to more prominent negative charges located on hydrogen ligands, a fact that certainly deserves to be explored more in the future for catalytic reactions and dihydrogen production. Perspectives on implications derived from the superiority of DHBs and how the predominance of DHBs governs the water cluster growth are warranted to better explore aqueous borate chemistry, as anion solvation often plays a key role in understanding the related chemical reactivity and solvation dynamics.⁵¹ Therefore, these outstanding molecular properties of DHBs, unravelled in this work, can promote more applications in catalysis, chemical transformations, and selectivity, and have potential to promise new synthetic routes towards rational assembly of novel extended covalent materials and structural coding of water clusters based on the unique dihydrogen interaction.

Data availability

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Author contributions

H. S., Z. R. S., and X. B. W. designed the research; Y. J., Q. Y., W. C., Z. H., Y. Y., C. Z., T. Y. and H. S. conducted the research; Y. J., H. S., Z. R. S. and X. B. W. analyzed the data; Y. J., H. S., Z. R. S., and X. B. W. wrote the paper. All the authors contributed to the discussions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by the National Natural Science Foundation of China (No. 11727810, 12034008 and 51873160), the Shanghai Rising-Star Program (No. 21QA1402600) and the Program of Introducing Talents of Discipline to Universities 111 Project (B12024). The NIPES work was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, and performed using EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is operated by Battelle Memorial Institute for the DOE. We acknowledge the ECNU Multifunctional Platform for Innovation (001) and HPC Research Computing Team for providing computational and storage resources and the support of the NYU-ECNU Center for Computational Chemistry at NYU Shanghai.

References

1. K. Liu, J. D. Cruzan and R. J. Saykally, Science, 1996, 271, 929–933.
2. N. Yang, C. H. Duong and P. J. Kelleher, et al. , Nat. Chem., 2020, 12, 159–164.
3. N. Yang, H. Duong Chinh and J. Kelleher Patrick, et al. , Science, 2019, 364, 275–278.
4. A. Shokri, J. Schmidt and X.-B. Wang, et al. , J. Am. Chem. Soc., 2012, 134, 2094–2099.
5. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1960.
6. R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980.
7. M. P. Brown and R. W. Heseltine, Chem. Commun., 1968, 1551–1552.
8. T. Richardson, S. de Gala and R. H. Crabtree, et al. , J. Am. Chem. Soc., 1995, 117, 12875–12876.
9. R. H. Crabtree, Science, 1998, 282, 2000–2001.
10. J. Echeverría, G. Aullón and D. Danovich, et al. , Nat. Chem., 2011, 3, 323–330.
11. R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769.
12. J. G. Planas, C. Viñas and F. Teixidor, et al. , J. Am. Chem. Soc., 2005, 127, 15976–15982.
13. J. Fanfrlík, M. Lepšík and D. Horinek, et al. , ChemPhysChem, 2006, 7, 1100–1105.
14. X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675.
15. K. Verma and K. S. Viswanathan, Phys. Chem. Chem. Phys., 2017, 19, 19067–19074.
16. Y. Xiao, J. T. Mague and R. A. Pascal Jr, Angew. Chem., Int. Ed., 2018, 57, 2244–2247.
17. P.-F. Cui, Y.-J. Lin and Z.-H. Li, et al. , J. Am. Chem. Soc., 2020, 142, 8532–8538.
18. T. K. A. Hoang and D. M. Antonelli, Adv. Mater., 2009, 21, 1787–1800.
19. M. Pang, J.-Y. Chen and S. Zhang, et al. , Nat. Commun., 2020, 11, 1249–1257.
20. A. Rossin, A. Rossi and M. Peruzzini, et al. , ChemPlusChem, 2014, 79, 1316–1325.
21. Q. Zhao, R. D. Dewhurst and H. Braunschweig, et al. , Angew. Chem., Int. Ed., 2019, 58, 3268–3278.
22. K. I. Assaf, M. S. Ural and F. Pan, et al. , Angew. Chem., Int. Ed., 2015, 54, 6852–6856.
23. M. Kožíšek, P. Cígler and M. Lepšík, et al. , J. Med. Chem., 2008, 51, 4839–4843.
24. F. A. Jalon, A. Otero and B. R. Manzano, et al. , J. Am. Chem. Soc., 1995, 117, 10123–10124.
25. P. A. Maltby, M. Schlaf and M. Steinbeck, et al. , J. Am. Chem. Soc., 1996, 118, 5396–5407.
26. R. H. Morris, Coord. Chem. Rev., 2008, 252, 2381–2394.
27. R. Bau and M. H. Drabnis, Inorg. Chim. Acta, 1997, 259, 27–50.
28. C. Gunanathan, S. C. Capelli and U. Englert, et al. , Eur. J. Inorg. Chem., 2013, 2013, 5075–5080.
29. C. Prestipino, L. Regli and J. G. Vitillo, et al. , Chem. Mater., 2006, 18, 1337–1346.
30. V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954–14965.
31. G. Naresh Patwari, T. Ebata and N. Mikami, J. Chem. Phys., 2000, 113, 9885–9888.
32. G. N. Patwari, A. Fujii and N. Mikami, J. Chem. Phys., 2006, 124, 241103–241106.
33. F. Maseras, A. Lledós and E. Clot, et al. , Chem. Rev., 2000, 100, 601–636.
34. T. Kar and S. Scheiner, J. Chem. Phys., 2003, 119, 1473–1482.
35. R. H. Crabtree, P. E. M. Siegbahn and O. Eisenstein, et al. , Acc. Chem. Res., 1996, 29, 348–354.
36. J. Warneke, G.-L. Hou and E. Aprà, et al. , J. Am. Chem. Soc., 2017, 139, 14749–14756.
37. R. T. Boeré, J. Derendorf and C. Jenne, et al. , Chem.–Eur. J., 2014, 20, 4447–4459.
38. Y. Jiang, Q. Yuan and W. Cao, et al. , Phys. Chem. Chem. Phys., 2021, 23, 13447–13457.
39. A. H. Soloway, W. Tjarks and B. A. Barnum, et al. , Chem. Rev., 1998, 98, 1515–1562.
40. B. Dereka, Q. Yu and H. C. Lewis Nicholas, et al. , Science, 2021, 371, 160–164.
41. R. H. Crabtree, Hydrogen Bonding & Dihydrogen Bonding, John Wiley & Sons, New York, 2005.
42. X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108–073115.
43. X.-B. Wang, J. Phys. Chem. A, 2017, 121, 1389–1401.
44. Z. Li, Y. Jiang and Q. Yuan, et al. , Phys. Chem. Chem. Phys., 2020, 22, 7193–7200.
45. L. M. J. Huntington, A. Hansen and F. Neese, et al. , J. Chem. Phys., 2012, 136, 064101–064117.
46. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
47. S. Emamian, T. Lu and H. Kruse, et al. , J. Comput. Chem., 2019, 40, 2868–2881.
48. F. Fuster and B. Silvi, Theor. Chem. Acc., 2000, 104, 13–21.
49. M. Ceriotti, J. Cuny and M. Parrinello, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596.
50. X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373.
51. A. Lietard, G. Mensa-Bonsu and J. R. R. Verlet, Nat. Chem., 2021, 13, 737–742.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental and computational details, and additional experimental data. See https://doi.org/10.1039/d2sc03986a

‡ These authors contributed equally to this work.

---