Defect-engineered surfaces to investigate the formation of self-assembled molecular networks

Abstract

Herein we report the impact of covalent modification (grafting), inducing lateral nanoconfinement conditions, on the self-assembly of a quinonoid zwitterion derivative into self-assembled molecular networks at the liquid/solid interface. At low concentrations where the compound does not show self-assembly behaviour on bare highly oriented pyrolytic graphite (HOPG), close-packed self-assembled structures are visualized by scanning tunneling microscopy on covalently modified HOPG. The size of the self-assembled domains decreases with increasing the density of grafted molecules, i.e. the molecules covalently bound to the surface. The dynamics of domains are captured with molecular resolution, revealing not only time-dependent growth and shrinkage processes but also the orientation conversion of assembled domains. Grafted pins play a key role in initiating the formation of on-surface molecular self-assembly and their stabilization, providing an elegant route to study various aspects of nucleation and growth processes of self-assembled molecular networks.

---

Introduction

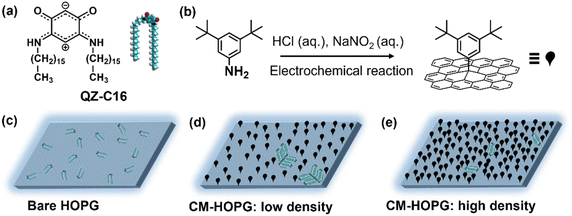
Supramolecular self-assembly on surfaces is a fascinating research topic, which can lead to the formation of functional two-dimensional (2D) architectures with potential nanotechnology applications.^1,2 Achieving mechanistic understanding and precise control over the formation of self-assembled molecular networks (SAMNs) allows the modulation of interfacial properties in a predictable manner. This is often a prerequisite for technological applications.³ Scanning tunneling microscopy (STM) has been demonstrated as a powerful tool for visualizing the structural details and dynamic processes of organic molecular assembly on solid conductive surfaces at the molecular level.⁴ However, because of the often fast kinetics of the self-assembly process, most studies only focused on the morphology and properties of the as-obtained structures, not on the actual mechanism of their formation.^5–8

Nevertheless, there are several strategies to impact the growth kinetics of self-assembly. For instance, it is known that solute concentration directly affects the rates of nucleation and growth of 2D crystals, defining the outcome of self-assembly processes.^9–12 The underlying substrate is also an important factor in achieving control of and stabilizing the monolayer structure.^13–16 Several groups have revealed the role of defects or foreign bodies in the nucleation and growth processes of 2D molecular assemblies.^17,18 Different stabilization mechanisms may come into play when molecules self-assemble on surfaces with such topological defects at the initial stage.¹⁹ For instance, Beebe and co-workers used flat-bottomed pits, with controllable depth, diameter, and artificial step edges, to isolate and study the assembly of liquid crystals. They were able to determine the nucleation rate constant, as molecules nucleated independently inside each pit or on the surrounding terraces.^20–23 Apart from high-temperature etched pits that were introduced intentionally on the HOPG surface, solid surfaces can also be artificially modified with covalently grafted molecules with desired density by using electrochemical, photochemical, or chemical activation approaches.^24–26 A strategy developed in our group is the use of intentionally introduced grafted molecules that serve as defects on the substrate. It was shown that the nucleation rate on such rough surfaces is increased.^27–32 On the other hand, these grafts have an impact on the subsequent growth processes as well.^33–36 Given that both solute concentration and the presence of defects have an impact on self-assembly, thus, it is possible to create experimental conditions that facilitate the investigation of the early stages of self-assembly on solid surfaces by combining both effects.

The present work is an exploratory study into the application of covalently modified substrates for the advanced physicochemical characterization of interfacial processes at the liquid–solid interface, showcasing the estimation of thermodynamic (e.g. Langmuir adsorption equilibrium constant) and kinetic characteristics (e.g. estimation of critical nuclei size, nucleation and growth rates ratio) as well as enhanced in situ dynamics of supramolecular self-assembly. Here, continuing our interest in the unusual class of quinoid zwitterions,^37,38 we studied the self-assembly of QZ-C16 (Scheme 1a) from its 1-phenyloctane solutions on pristine as well as chemically modified HOPG (CM-HOPG) surfaces. CM-HOPG surfaces are prepared via an electrochemical method, by which 3,5-bis-tert-butylaniline (3,5-TBA) molecules are converted to aryl radicals which then attack and bind to the HOPG surface (Scheme 1b). For a straightforward analysis, it is helpful to find experimental conditions (i.e. nature of the solvent, concentration, temperature, etc.) when self-assembly on pristine and chemically modified substrates differs qualitatively.^39–41 No QZ-C16 self-assembly was observed on bare HOPG at or below 10⁻⁶ M (Scheme 1c), while close-packed domains of QZ-C16 could be visualized on CM-HOPG even at 5 × 10⁻⁷ M (Scheme 1d and e). Fully controlling the surface density of such covalently bound aryl pins empowers advanced investigation and control of various interfacial processes.

Scheme 1 (a) Molecular structure and model of QZ-C16. (b) Schematic illustration of the electrochemical grafting procedure. (c–e) Schematic representation of the self-assembly of QZ-C16 at concentration 10⁻⁶ M on bare HOPG, CM-HOPG with low and high grafting density, respectively.

Materials and methods

Covalent modification of HOPG

2.00 mg 3,5-bis-tert-butylaniline (3,5-TBA, >98%, TCI-Tokyo Chemical Industry Co., Ltd.) was dissolved in 5 mL aqueous hydrochloric acid (50 mM), and then 100 μL of aqueous NaNO₂ (0.1 M, 99.999%, purchased from Sigma-Aldrich and dissolve in water without further purification) was added to initiate the diazotization reaction. The solution was shaken gently for 90 s before injecting into a lab-built single-compartment three-electrode cell (HOPG as working electrode, Pt wire as counter electrode, Ag/AgCl/3.0 M NaCl as reference electrode). Chronoamperometry (CA) was conducted using an Autolab PGSTAT101 potentiostat (Metrohm_Autolab BV, The Netherlands). After modification, the CM-HOPG surface was sequentially rinsed with high purity water (Milli-Q, Millipore, 18.2 MΩ cm, TOC < 3 ppb) and acetone (with purity 99%) to remove any physisorbed material. Milli-Q water was also used for the preparation of the aqueous solutions. All the HOPG (ZYB grade, Advanced Ceramics Inc., Cleveland, USA) used during the experiments were freshly cleaved using Scotch™ tape.

The grafting density of the surface could be well controlled by carefully adjusting the parameters involved in the CA experiments, including the amount of 3,5-TBA (the weight varies from 0.04 to 2.00 mg), the applied fixed potential on the sample (varies from +0.02 to +0.10 V) and the reaction period (varies from 5 to 15 s). In general, the more reactant, the higher the applied voltage or the longer the reaction period, the higher the density of the grafted monolayer. The number of grafted pins (or clusters of grafted molecules) varies from 250 to more than 2050 per 0.01 μm². These were calculated by Scanning Probe Imaging Processor (SPIP) software, where the features with high contrast are recognized automatically (Fig. S3†).

STM experiments

A saturated solution of QZ-C16 (synthesized as reported in ref. 37) was prepared by adding 0.35 mg of solid to 300 μL 1-phenyloctane (1-PO, 99%, purchased in Sigma-Aldrich then rotary evaporated to further purification), followed by repeated heating at 70 °C and sonication cycles before diluting. Subsequently, the saturated solution was diluted to 1 × 10⁻³ M, 1 × 10⁻⁴ M, 1 × 10⁻⁵ M, 1 × 10⁻⁶ M and 5 × 10⁻⁷ M. STM experiments were performed by drop-casting the solution on bare HOPG or CM-HOPG at room temperature (20–22 °C), followed by imaging using a PicoLE (Agilent) STM system operating in constant current mode. STM tips were cut manually from a Pt/Ir wire (80%/20%, Advent Research Materials, diameter 0.25 mm). Imaging parameters V_s (for sample bias) and I_t (for tunneling current) are indicated in the figure captions. All images were processed using the SPIP software. The unit cell parameters of QZ-C16 on bare HOPG are averaged values deduced from high-resolution STM images that have been corrected for drift using a reference image of the underlying graphite lattice, with imaging parameters: V_s = −0.001 V, I_t = 0.6 nA.

Results and discussion

Self-assembly of QZ-C16 at the 1-PO/HOPG interface

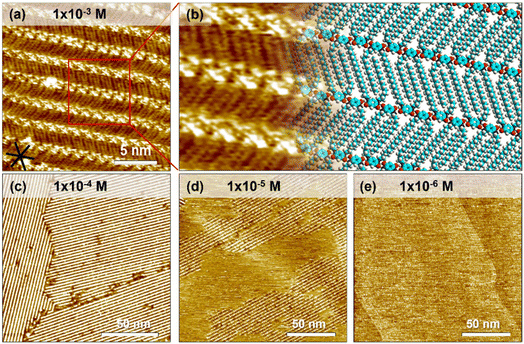
A droplet of 1-PO solution containing QZ-C16 was added onto the freshly cleaved HOPG surface. Subsequent STM imaging at the liquid/solid interface yielded a lamellar self-assembly of QZ-C16 (Fig. 1a, a tentative model is proposed in Fig. 1b). The bright spots of the lamellae are attributed to the charge-assisted hydrogen bonded quinonoid zwitterion units and the relatively low-contrast stripes are attributed to the alkyl chains packed into a unique double-decker fashion.^37,38 More specifically, the charge-assisted hydrogen bonding is so strong that it locked the distance between quinonoid zwitterion head units (1.48 ± 0.02 nm). This distance is so small that not all alkyl chains can adsorb on the surface, thus periodically some alkyl chains are popped out and adsorbed on the second layer (e.g. Fig. S1 and Table S1†). A detailed investigation of this subtle polymorphism, its mechanism and rational control over the kinetic/thermodynamic factors governing the formation and stability of different phases on bare and modified HOPG will be reported elsewhere. In the scope of the present work, all analyses and interpretations concern the adsorption, desorption and self-assembly process of QZ-C16 disregarding all fine differences between the closely-related polymorphs. On HOPG, large domains (>10⁴ nm²) of QZ-C16 are routinely observed for room temperature depositions (Fig. 1c). At 10⁻⁵ M, the surface coverage becomes incomplete (sub-monolayer, Fig. 1d), while at and below 10⁻⁶ M, QZ-C16 self-assembly was never observed (Fig. 1e and S2†). Thus, 10⁻⁶ M is referred to as the threshold concentration at and below which no stable SAMNs can be detected by room temperature STM imaging on pristine HOPG.

Fig. 1 (a) High-resolution STM image of QZ-C16 monolayer formation at the 1-PO/HOPG interface, three black lines indicated three main symmetry axes of HOPG. (b) A zoom-in STM image of QZ-C16 SAMNs with the proposed structural model. (c–e) Large-scale STM images showing the concentration dependence of QZ-C16 assembly/non-assembly. Concentration: (a) 1 × 10⁻³ M; (c) 1 × 10⁻⁴ M; (d) 1 × 10⁻⁵ M; (e) 1 × 10⁻⁶ M. Imaging conditions: V_s = −0.8 V, I_t = 0.08 nA.

Similar to other molecular systems, the observed self-assembly behavior of QZ-C16 is a cooperative process where the final outcome is the result of a complex interplay between molecular adsorption, diffusion, intermolecular interactions, and desorption during nucleation, growth and ripening of 2D assemblies.^42,43 Not only are such experiments hard to model and analyze, but even the proper design of experiments (DOE) allowing reliable, statistically sound acquisition of the required data (e.g. domain size, domain orientation, surface coverage) is currently underdeveloped.^44–46 For example, large scale STM images (e.g.Fig. 1c and d) are simultaneously too large to determine the supramolecular structure of self-assembly (simply not enough data points for (sub)molecular resolution), yet too small to be used for any kind of statistical domain size analysis. Indeed, we cannot use Fig. 1c and d in the estimation of fundamental physicochemical characteristics such as the molecular surface coverage, the average size or surface density of domains since all of the imaged domains are incomplete (i.e. parts are outside of the image frame). On the other hand, a proper DOE defining requirements for image resolution, image size, maximum observed drift, etc. is always labor intensive and potentially can become impractical or even impossible due to technical limitations of the selected technique and instrument. Instead, we promote the use of modified substrates (e.g. CM-HOPG) on which the compartmentalization of individual self-assembly events allows advanced, reliable and convenient investigation of complex interfacial phenomena.

Self-assembly of QZ-C16 on CM-HOPG surface

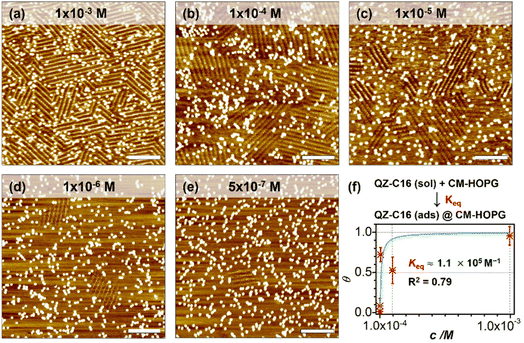
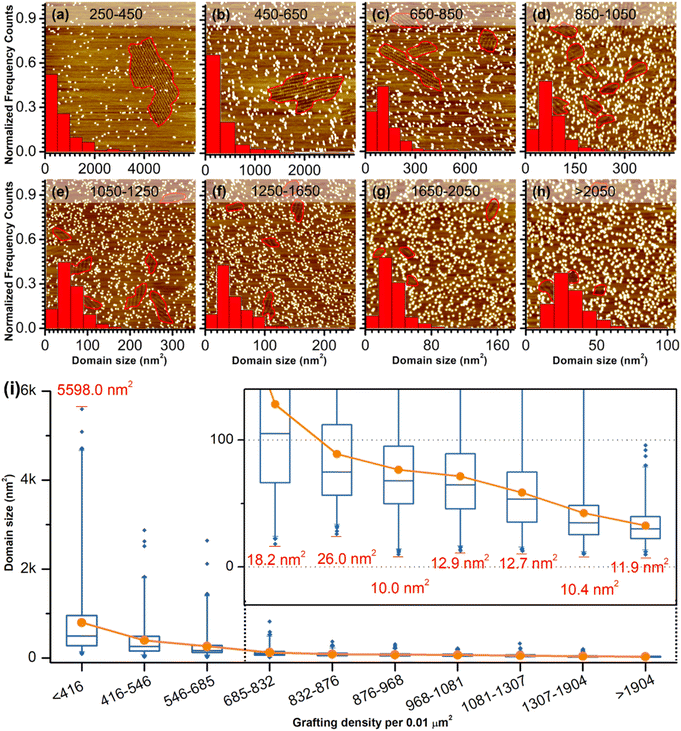
As a comparison, the investigation of concentration-dependent QZ-C16 self-assembly was also carried out on CM-HOPG substrates. CM-HOPG surface with a moderate density of grafted molecules (450–650 pins/0.01 μm²) was prepared via chronoamperometry (see Materials and methods section). When a concentrated QZ-C16 solution (10⁻³ M) was applied to the CM-HOPG surface, smaller domains are formed compared to the large domains obtained on bare HOPG (Fig. 2a). We attribute this to the barriers created by these randomly distributed grafted molecules, which appear as bright pins (dots) in the image. These pins serve as defects and play a key role in limiting the free growth of domains, as discussed previously by our group.^27–29 When the concentration was diluted to 10⁻⁴ or 10⁻⁵ M, both SAMN domains and empty regions co-exist on the surface (Fig. 2b and c). When the solution was further diluted to the threshold concentration for the self-assembly of QZ-C16 on bare HOPG (10⁻⁶ M and below, ca. 5 × 10⁻⁷ M), domains of QZ-C16 self-assembly were still routinely detected, thus demonstrating a stabilizing effect of covalent grafts for on-surface localization of supramolecular agglomerates (Fig. 2d and e). Furthermore, the variation of surface coverage over a wide range of concentrations (>3 orders of magnitude) follows a simple Langmuir isotherm model (equilibrium constant reaching 1.1 × 10⁵ M⁻¹, Fig. 2f and Table S2†), implying that spontaneous corrals dotted with randomly grafted molecules can be regarded as independent adsorption sites for individual 2D crystals. Effectively, the self-assembly compartmentalization on CM-HOPG substrates allows for a significant reduction in the minimum image size sufficient to represent the global surface composition. We believe this is an important starting point for the improved DOE of interfacial studies that should be applicable to other supramolecular assemblies at the liquid–solid interfaces.

Fig. 2 Typical STM images showing the self-assembly of QZ-C16 on CM-HOPG (with a grafting density of 450–650 pins/0.01 μm²) at various concentrations (a) 1 × 10⁻³ M, (b) 1 × 10⁻⁴ M, (c) 1 × 10⁻⁵ M, (d) 1 × 10⁻⁶ M, (e) 5 × 10⁻⁷ M. Scale bars: 20 nm. Imaging conditions: V_s = −0.8 V, I_t = 0.08 nA. (f) Langmuir isotherm fitting curve of QZ-C16 assembly on the CM-HOPG surface. K_eq represents the equilibrium constant for adsorption, which is estimated to be 1.1 × 10⁵ M⁻¹.

The previous section illustrates the use of CM-HOPG in the investigation and thermodynamic analysis of adsorption–desorption equilibrium at the liquid–solid interface. It is also possible to get insight into the nucleation and growth processes by designing self-assembly experiments at fixed solute concentration but with varied grafting densities. Thus, 688 STM images (containing 3295 domains) were collected for the systematic analysis of the self-assembly behavior of QZ-C16 (at concentration 10⁻⁶ M) on CM-HOPG with controlled grafting densities (from 250 to >2050 pins/0.01 μm², Fig. 3a–h and S4† and discussion of manually determining the QZ-C16 domains in ESI, Table S3†). The histograms inserted in the respective STM images show the domain size distribution. When the grafting density ranges from 250–450 pins/0.01 μm², the domain size varies from 38.5 nm² to ∼5598 nm², showing a broad size distribution in the histogram. The existence of such large domains (2.8% of domains are larger than 3000 nm²) is attributed to the relatively large distance between grafted pins, which offers enough space for QZ-C16 to grow around them. When the grafting density increases to between 450–650 pins/0.01 μm², the size distribution of domains shifts to smaller values, i.e. 83% of domains are smaller than 500 nm². A further increase in grafting density scales down the observed domain size to a point that, when the grafting density is over 2050 pins/0.01 μm², all domains are smaller than 100 nm², with 72% of domains sized around 40.0 ± 10.0 nm².

Fig. 3 STM images showing the self-assembly of QZ-C16 (at concentration 10⁻⁶ M) on CM-HOPG surface with various grafting densities. The grafting density (the number of pins per 0.01 μm²) is shown on top of each image (a) 250–450, (b) 450–650, (c) 650–850, (d) 850–1050, (e) 1050–1250, (f) 1250–1650, (g) 1650–2050, (h) >2050. The histograms of the domain size distribution are shown at the bottom of the STM images. Red lines inside STM images mark out well-ordered QZ-C16 domains. Image size: (a) 150 × 150 nm, (b–f) 100 × 100 nm, (g and h) 70 × 70 nm. Imaging conditions: V_s = −0.8 V, I_t = 0.08 nA. (i) Box plot shows the distribution of domain size in 10 groups of various grafting densities. The upper-right insert shows the zoom-in box plot. The x-axis of box plot shows the grafting density range, the y-axis shows the domain size distribution. The first quartile and third quartile of the domain size are indicated as the upper border and lower border of the box. The maximum and minimum domain sizes are indicated by the red horizontal lines at the end of the whiskers and indicated partially with exact values. The outliers indicated by blue diamonds are observations that represent 1% of the data. The orange line plot shows the average domain size at each grafting density.

Complementary to the histograms, the box plot in Fig. 3i shows intuitively the locality, spread and skewness of QZ-C16 domain size collected on a modified substrate with various grafting densities. The sample size of each group is around 320 domains, but the box shapes vary. First, the box gets shorter as the grafting density increases, indicating a decrease in domain size dispersion. The median size of the domain, indicated by the blue crossbar, is not in the middle of the box, but is positively skewed. The average domain size, indicated by the orange line plot, decreases and gets close to the median size as the grafting density increases. Clearly, the increase of grafting density reduces the effective size of corrals formed by the randomly grafted pins and, in turn, limits the growth of the QZ-C16 domains. Also, the decrease in domain size gets compensated by the increase in the surface density of domains (Fig. S5†), thus maintaining the QZ-C16 molecular surface coverage constant.

The smallest QZ-C16 domain we have ever observed in this set of experiments is ∼10.4 nm² (Fig. 3i, S6, S8 and Tables S3–S5†) which can be taken as an experimental estimate of the critical nucleus size for the QZ-C16 self-assembly at room temperature (at concentration 10⁻⁶ M). A conservative upper estimate of the critical nucleus size under these conditions is around 93 nm², since this is the smallest domain size experimentally observed at the lowest grafting density (<416 pins/0.01 μm², Table S5†). Two factors should be considered when deciding between these two estimates: (1) the possibility of strong intermolecular interactions between grafted molecules and QZ-C16 that results in the stabilization of nuclei smaller than the critical nucleus size in the absence of the grafted molecules and (2) the growth of the domains beyond the critical nuclei size inside larger corrals. Considering the chemical structures of grafted molecule and QZ-C16, there are no specific or directional interactions expected between them, only weak CH⋯HC and CH⋯π van der Waals interactions. As such, the examination of the smallest recorded domains, the corrals in which they have nucleated and interacting pins (Fig. S6 and Table S5†), allows lowering the upper estimate of the critical nucleus from ∼93 nm² down to ∼10.4 nm² (row #4 in Table S5 and corresponding discussion in ESI†). Of course, one should remember that critical nucleus size is just a useful oversimplification developed within the framework of classical nucleation theory. In practice, the size of the smallest observed “stable” nucleus should also depend on the specific molecular arrangement due to the strong asymmetry in the type, energy and directionality of the QZ-C16 intermolecular interactions. Another important aspect of nucleation that should be considered is its intrinsic stochastic nature: the observation of molecular assembly inside specific corrals is not guaranteed. Among other dependencies, the probability of nucleation depends on the corral size and can be increased by external stimuli. For example, we have recorded QZ-C16 self-assembly when the already existing empty corrals were in situ enlarged by STM lithography (Fig. S7,† see also the dynamics section below).

Once a nucleus reaches the critical size, within the classical nucleation theory the probability for such a nucleus growing is higher than the probability of its dissolution. This is considered the beginning of the growth step, which can end when the further growth of one domain is only possible at the expense of the dissolution of another domain (i.e. ripening step). In our experiments at the concentration of 10⁻⁶ M, the QZ-C16 surface coverage is incomplete (≤9%, Table S2†) and the growth step terminates either when the corral is completely filled (e.g.Fig. 3d) or when the adsorption–desorption equilibrium is reached, and there is a depletion of adsorbed QZ-C16 available for further growth. The largest domain observed on the CM-HOPG with low grafting density (∼5598 nm², Fig. 3i) suggests that under these experimental conditions the growth rate is at least 500 times larger than the rate of nucleation.

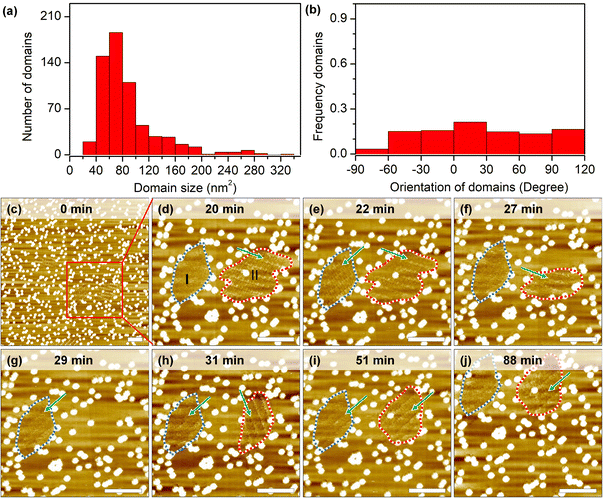
Dynamic process of assemblies under confinement space

Self-assembly processes are not static: borders of grafts prevent domain growth beyond a certain size, but continuous desorption–adsorption processes can result in partial/complete dissolution and nucleation of new 2D crystals. The measurement of growth and dissolution rates gives a wide range of estimations because of the stochastic nature and strong dependence on the scanning conditions of STM. Analysis of hundreds of short instances shows that domains larger than the estimated critical nucleus size (10.0 nm²) can still be destabilized under continuous scanning (Fig. 4a). In some cases, only minor fluctuations (∼2–4 nm²) are recorded at the domain periphery, while in other cases, i.e. in session 3 (marked by a lavender line in Fig. S8h, i and Table S6†), 90 seconds between consecutive images is long enough to completely dissolve a 260 nm² domain and to grow in its place a differently oriented 120 nm² 2D crystal.

Fig. 4 (a) Size distribution of domains which show dissolution–renucleation dynamics during continuous scanning. (b) Orientation distribution of domains during the dissolution–renucleation process. The orientation of domain is measured with respect to the horizontal direction, i.e. the orientation of domain I and II in (e) is −40 deg and 20 deg respectively. (c–j) Sequential STM images showing the dynamic processes of two domains under lateral confinement conditions over a period of 88 minutes. The blue and red dashed lines highlight domain I and II, the green arrow indicates the orientation of the domain. Scale bars: 10 nm. Imaging parameters: V_s = −0.8 V, I_t = 0.08 nA.

An examination of the orientation distribution histogram (Fig. 4b) did not reveal any preference for the dissolution–nucleation of domains with certain orientations in short scanning sessions (<10 min). Yet we often noticed that within the same area there are domains of similar size that vary in their stability. Longer imaging sessions allow showcasing this difference (Fig. 4c–j). In the first 20 min, domains are partially desorbed and adsorbed during the continuous scan at a large scale. Domain I (blurred structure with a size of 117 nm²) and domain II (containing packed rows with a size of 172 nm²) were marked with the blue dashed line and red dashed line in the zoomed-in image at 20 minutes (Fig. 4d). In the time span between minute 22 and minute 27, domain I shows a transition between a well-ordered structure and a metastable structure; later on (from minute 27 to minute 88), domain I remains blurred, which might result from the translational movement of the adsorbed molecules. The likelihood of observing similarly blurred domains increases on surfaces with very high grafting densities (>2050 pins/0.01 μm²). This could be explained as follows: on the one hand, these small domains are metastable phases whose molecular packing is difficult to distinguish; on the other hand, small domains might be more sensitive to STM tip scanning, resulting in increased mobility of the molecules in such areas.

Domain II shrank between minutes 20 to 27 and subsequently vanished completely at minute 29. Interestingly, a new domain with a different orientation formed immediately at the same location in the next scan. At minute 51, the orientation of the newly formed domain II changed again, adopting the same orientation as domain I, and remained unchanged until the end of experiment (another 36 minutes of continuous scanning). Effectively, here we have a case of self-organization⁴⁷ where, because of continuous energy input (STM scanning), there is a selection between otherwise energetically degenerate assemblies. Finally, we would like to mention that the specific configuration of grafted pins may be responsible for playing an important role not only in stabilizing domains but also to visualize dynamics. With the help of the laterally confined spaces realized by the engineered CM-HOPG surfaces, small metastable structures could be trapped and stabilized on the surface, and their dynamics could be followed.

Conclusions

In conclusion, we have applied ambient STM to investigate the early-stage self-assembly of QZ-C16 on defect-engineered HOPG. Metastable QZ-C16 domains could be stabilized on the CM-HOPG, even at very low concentration (<10⁻⁶ M), under conditions where essentially no stable structures are detected on bare HOPG. Our studies reveal that the compartmentalization of domains within randomly shaped “grafted molecular fences” significantly simplifies self-assembly behavior which, in this case, can be described by a Langmuir isotherm. By varying grafting density we found the critical nucleus size (∼10.4 nm² for self-assembly at a fixed concentration, 10⁻⁶ M) and a lower boundary estimate of the growth rate/nucleation rate ratio (>500 for self-assembly at 10⁻⁶ M). The use of the STM probe for continuous perturbation of molecular self-assembly allowed us to observe multiple dissolution–nucleation cycles of domains that are several times larger than the critical size. Interestingly, the degree of destabilization depends on the orientation of domains with respect to the scanning direction and probably on the specific configuration of covalent grafts surrounding the crystallization area. This work demonstrates our latest results in the use of engineered grafted substrates for the investigation of nucleation and growth of 2D crystals. Further investigation of the use of STM probes for directed self-organization of 2D crystals as well as the investigation of grafts that can chemo-selectively bind to molecular adsorbates are currently underway.

Data availability

The data that support the histograms and plots within this paper are available from the corresponding authors upon reasonable request.

Author contributions

All authors participated in the revision of the manuscript. Particularly, L.-H. Yu carried out all the experiments and wrote the original draft; Z.-F. Cai, L. Verstraete, and Y. Xia contributed to the discussion of the project; Y. Fang and L. Cuccia provided the compound, O. Ivasenko: contributed to the formal analysis, conceiving the manuscript; S. De Feyter: supervision, funding acquisition, and project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Tamara Rinkovec for insightful suggestions about the Langmuir isotherm modeling and design of experiments. We thank Brent Daelemans for the purification of solvent. We thank Gaolei Zhan for the helpful discussion. This work has received funding from the Research Foundation Flanders (FWO) (G081518N, G082218N, GF9118N (EOS 30489208), and G0E3422N), and KU Leuven – Internal Funds (C14/19/079). O. Ivasenko and Y. Fang acknowledge funding from Suzhou Key Laboratory of Functional Nano & Soft Materials, Collaborative Innovation Center of Suzhou Nano Science & Technology, the 111 Project, the National Natural Science Foundation of China (22102110) and Science Foundation of Jiangsu Province (BK20210700). L.-H. Yu gratefully acknowledges financial support through the China Scholarship Council (CSC 201908350094).

Notes and references

1. J. V. Barth, G. Costantini and K. Kern, in Nanoscience and Technology: A Collection of Reviews from Nature Journals, World Scientific, Singapore, 2009, vol. 437, pp. 67–78.
2. A. Langner, S. L. Tait, N. Lin, C. Rajadurai, M. Ruben and K. Kern, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17927–17930.
3. C. A. Palma, M. Cecchini and P. Samorí, Chem. Soc. Rev., 2012, 41, 3713–3730.
4. G. Zhan, Z. F. Cai, K. Strutyński, L. Yu, N. Herrmann, M. Martínez-Abadía, M. Melle-Franco, A. Mateo-Alonso and S. De Feyter, Nature, 2022, 603, 835–840.
5. M. Ruben, D. Payer, A. Landa, A. Comisso, C. Gattinoni, N. Lin, J. P. Collin, J. P. Sauvage, A. De Vita and K. Kern, J. Am. Chem. Soc., 2006, 128, 15644–15651.
6. C. A. Palma, J. Bjork, M. Bonini, M. S. Dyer, A. Llanes-Pallas, D. Bonifazi, M. Persson and P. Samorí, J. Am. Chem. Soc., 2009, 131, 13062–13071.
7. H. Cao and S. De Feyter, Nat. Commun., 2018, 9, 3416.
8. Z. F. Cai, G. Zhan, L. Daukiya, S. Eyley, W. Thielemans, K. Severin and S. De Feyter, J. Am. Chem. Soc., 2019, 141, 11404–11408.
9. B. Li, Y. Liu, Y. Tao, Y. Wang, X. Miao, X. Cheng and W. Deng, J. Phys. Chem. C, 2020, 124, 25396–25402.
10. Z. F. Cai, H. J. Yan, D. Wang and L. J. Wan, Nanoscale, 2018, 10, 3438–3443.
11. A. Ciesielski, P. J. Szabelski, W. Rzysko, A. Cadeddu, T. R. Cook, P. J. Stang and P. Samorì, J. Am. Chem. Soc., 2013, 135, 6942–6950.
12. C. A. Palma, M. Bonini, A. Llanes-Pallas, T. Breiner, M. Prato, D. Bonifazi and P. Samorì, Chem. Commun., 2008, 7345, 5289–5291.
13. S. Rana, J. Jiang, K. V. Korpany, U. Mazur and K. W. Hipps, J. Phys. Chem. C, 2021, 125, 1421–1431.
14. C. Liu, L. Yang, Y. Wang, S. Lei and W. Hu, J. Phys. Chem. C, 2018, 122, 12307–12314.
15. J. M. MacLeod, J. A. Lipton-Duffin, D. Cui, S. De Feyter and F. Rosei, Langmuir, 2015, 31, 7016–7024.
16. H. Yang, C. L. Song, Y. X. S. Lim, W. Chen and J. Y. Y. Heng, CrystEngComm, 2017, 19, 6573–6578.
17. S. A. Claridge, W. S. Liao, J. C. Thomas, Y. Zhao, H. H. Cao, S. Cheunkar, A. C. Serino, A. M. Andrews and P. S. Weiss, Chem. Soc. Rev., 2013, 42, 2725–2745.
18. D. L. Patrick and T. P. Beebe, Langmuir, 1994, 10, 298–302.
19. T. P. Beebe, D. L. Patrick, V. J. Cee and T. J. Purcell, Langmuir, 1996, 12, 1830–1835.
20. D. L. Patrick, V. J. Cee and T. P. Beebe, Science, 1994, 265, 231–234.
21. H. Chang and A. J. Bard, J. Am. Chem. Soc., 1990, 112, 4598–4599.
22. F. Stevens, D. Buehner and T. P. Beebe, J. Phys. Chem. B, 1997, 101, 6491–6496.
23. A. Tracz, A. Stabel and J. P. Rabe, Langmuir, 2002, 18, 9319–9326.
24. J. Greenwood, T. H. Phan, Y. Fujita, Z. Li, O. Ivasenko, W. Vanderlinden, H. Van Gorp, W. Frederickx, G. Lu, K. Tahara, Y. Tobe, H. Uji-I, S. F. L. Mertens and S. De Feyter, ACS Nano, 2015, 9, 5520–5535.
25. G. Ambrosio, A. Brown, L. Daukiya, G. Drera, G. Di Santo, L. Petaccia, S. De Feyter, L. Sangaletti and S. Pagliara, Nanoscale, 2020, 12, 9032–9037.
26. Y. Xia, C. Martin, J. Seibel, S. Eyley, W. Thielemans, M. van der Auweraer, K. S. Mali and S. De Feyter, Nanoscale, 2020, 12, 11916–11926.
27. A. M. Bragança, J. Greenwood, O. Ivasenko, T. H. Phan, K. Müllen and S. De Feyter, Chem. Sci., 2016, 7, 7028–7033.
28. N. Bilbao, Y. Yu, L. Verstraete, J. Lin, S. Lei and S. De Feyter, Chem. Commun., 2018, 54, 9905–9908.
29. A. M. Bragança, B. E. Hirsch, A. Sanz-Matias, Y. Hu, P. Walke, K. Tahara, J. N. Harvey, Y. Tobe and S. De Feyter, J. Phys. Chem. C, 2018, 122, 24046–24054.
30. E. Curcio, V. Curcio, G. Di Profi, E. Fontananova and E. Drioli, J. Phys. Chem. C, 2010, 114, 13650–13655.
31. Y. Diao, T. Harada, A. S. Myerson, T. A. Hatton and B. L. Trout, Nat. Mater., 2011, 10, 867–871.
32. A. M. Bragança, A. Minoia, R. Steeno, J. Seibel, B. E. Hirsch, L. Verstraete, O. Ivasenko, K. Müllen, K. S. Mali, R. Lazzaroni and S. De Feyter, J. Am. Chem. Soc., 2021, 143, 11080–11087.
33. L. Verstraete, B. E. Hirsch, J. Greenwood and S. De Feyter, Chem. Commun., 2017, 53, 4207–4210.
34. Y. Hu, A. M. Bragança, L. Verstraete, O. Ivasenko, B. E. Hirsch, K. Tahara, Y. Tobe and S. De Feyter, Chem. Commun., 2019, 55, 2226–2229.
35. L. Verstraete, J. Greenwood, B. E. Hirsch and S. De Feyter, ACS Nano, 2016, 10, 10706–10715.
36. J. Seibel, L. Verstraete, B. E. Hirsch, A. M. Braganca and S. De Feyter, J. Am. Chem. Soc., 2018, 140, 11565–11568.
37. Y. Fang, M. Cibian, G. S. Hanan, D. F. Perepichka, S. De Feyter, L. A. Cuccia and O. Ivasenko, Nanoscale, 2018, 10, 14993–15002.
38. Y. Fang, P. Nguyen, O. Ivasenko, M. P. Aviles, E. Kebede, M. S. Askari, X. Ottenwaelder, U. Ziener, O. Siri and L. A. Cuccia, Chem. Commun., 2011, 47, 11255–11257.
39. H. Malik, P. Saha, K. Patra, J. K. Bera and T. G. Gopakumar, Chem.–Asian J., 2021, 16, 1430–1437.
40. A. Della Pia, D. Luo, R. Blackwell, G. Costantini and N. Martsinovich, Faraday Discuss., 2017, 204, 191–213.
41. J. Hou, P. Lei, T. Meng, F. Zhao, H. Xu, X. Li, K. Deng and Q. Zeng, Langmuir, 2020, 36, 9810–9817.
42. L. K. S. von Krbek, C. A. Schalley and P. Thordarson, Chem. Soc. Rev., 2017, 46, 2622–2637.
43. A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825.
44. S. Yokoyama, T. Hirose and K. Matsuda, Chem. Commun., 2014, 50, 5964–5966.
45. O. Ochs, N. Martsinovich, W. M. Heckl and M. Lackinger, J. Phys. Chem. Lett., 2020, 11, 7320–7326.
46. K. V. Korpany, B. Chilukuri, K. W. Hipps and U. Mazur, J. Phys. Chem. C, 2020, 124, 18639–18649.
47. J. D. Halley and D. A. Winkler, Complexity, 2008, 14, 10–17.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc04599k

---