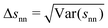Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrodynamic simulations of sedimenting dilute particle suspensions under repulsive DLVO interactions†
David
Jung
 ab,
Maximilian Johannes
Uttinger
cd,
Paolo
Malgaretti
ab,
Maximilian Johannes
Uttinger
cd,
Paolo
Malgaretti
 a,
Wolfgang
Peukert
a,
Wolfgang
Peukert
 cd,
Johannes
Walter
cd,
Johannes
Walter
 cd and
Jens
Harting
cd and
Jens
Harting
 *abe
*abe
aHelmholtz Institute Erlangen-Nürnberg for Renewable Energy, Forschungszentrum Jülich, Fürther Straße 248, 90429 Nürnberg, Germany
bDepartment of Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg, Fürther Straße 248, 90429 Nürnberg, Germany
cInstitute of Particle Technology (LFG), Friedrich-Alexander-Universität Erlangen Nürnberg (FAU), Cauerstraße 4, 91058 Erlangen, Germany
dInterdisciplinary Center for Functional Particle Systems (FPS), Friedrich-Alexander Universität Erlangen-Nürnberg, Haberstraße 9a, 91058 Erlangen, Germany
eDepartment of Chemical and Biological Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg, Fürther Straße 248, 90429 Nürnberg, Germany. E-mail: j.harting@fz-juelich.de
First published on 21st February 2022
Abstract
We present guidelines to estimate the effect of electrostatic repulsion in sedimenting dilute particle suspensions. Our results are based on combined Langevin dynamics and lattice Boltzmann simulations for a range of particle radii, Debye lengths and particle concentrations. They show a simple relationship between the slope K of the concentration-dependent sedimentation velocity and the range χ of the electrostatic repulsion normalized by the average particle–particle distance. When χ → 0, the particles are too far away from each other to interact electrostatically and K = 6.55 as predicted by the theory of Batchelor. As χ increases, K likewise increases as if the particle radius increased in proportion to χ up to a maximum around χ = 0.4. Over the range χ = 0.4–1, K relaxes exponentially to a concentration-dependent constant consistent with known results for ordered particle distributions. Meanwhile the radial distribution function transitions from a disordered gas-like to a liquid-like form. Power law fits to the concentration-dependent sedimentation velocity similarly yield a simple master curve for the exponent as a function of χ, with a step-like transition from 1 to 1/3 centered around χ = 0.6.
1 Introduction
The physics of sedimenting particles have proven to be surprisingly difficult to model despite many attempts over a large fraction of the 20th century. While a single particle slowly sedimenting in a sufficiently large container can be easily described by Stokes' law, the long-ranged nature of hydrodynamic interactions renders the dependence of the sedimentation speed on the particle concentration complicated to derive even in the dilute limit.For the purpose of brevity we refer to the case of uncharged particles interacting only via hydrodynamic and hard sphere interactions as the case of non-interacting particles throughout this paper. The theory of non-interacting particles reached a major breakthrough when in 1972 Batchelor1 derived the sedimentation velocity v at small particle volume fractions ϕ relative to the velocity v0 at infinite dilution as
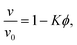 | (1) |
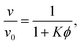 | (2) |
Especially for particles of nanometer scale neglecting any non-hydrodynamic interparticle interactions is a strict limitation though. Indeed, depending on the pH value, most types of colloidal particles tend to accumulate considerable surface charges when dissolved in water.5–7 This leads to strong electrostatic interactions which typically decay over a Debye length of the order of 10 nm. The Debye length in water can in principle reach hundreds of nanometers, though this requires high degrees of purity that are in practice difficult to achieve.
For this reason a majority of studies on the sedimentation of interacting particles focus on attractive potentials.8,9 In organic solvents such as ethanol, however, Debye lengths of around 800 nm have been reached in experiments.10
For particle suspensions with strong electrostatic interactions and weak screening (i.e. a Debye length λD large enough to be comparable to the average particle–particle distance) a strongly nonlinear decrease of the sedimentation velocity with concentration has been both predicted theoretically and observed experimentally10,11 even in the dilute limit where ϕ < 1%.
Early studies of electrostatic effects in particle sedimentation include the work of Booth12 in 1954. They developed the dipole moment of sedimenting charged particles as a power series in terms of the particle charge or zeta potential and managed to calculate the first two coefficients in the series. The theory is thus appropriate for sufficiently low surface charges/zeta potentials, although this limitation was removed in a numerical extension of Booth's work by Stigter in 1980.13 Both Booth's and Stigter's theories completely neglect hydrodynamic interactions between the particles and do not take changes in the RDF of the suspension into account.
A number of studies14–17 of sedimentation under both electrostatic and hydrodynamic particle–particle interactions have been performed using methods based on geometric cells to obtain the hydrodynamic component, either with the free-surface boundary condition by Happel18 or the zero vorticity condition by Kuwabara.19 While experimental results confirm the cell models as adequate to calculate the sedimentation potential,20 both the method by Happel and that of Kuwabara fail to correctly reproduce the sedimentation behavior of non-interacting particles in the dilute limit found by Batchelor about 14 years after the introduction of the method.1,18,19 Furthermore, the methods based on geometric cells cannot take into account changes in the RDF of the sedimenting suspension induced by the electrostatic interactions and they assume an electrically neutral unit cell, which may be a too rough simplification if Debye layers overlap strongly.21
Another promising approach in modeling charged particle sedimentation numerically was taken by Watzlawek and Nägele,22 though their approach is limited by the fact that it can only take into account pair-wise hydrodynamic interactions. Neglecting many-body hydrodynamic interactions was shown by Brady and Durlofsky2 to lead to a significant error in the sedimentation rate at volume fractions as low as 5%, though the result could be improved considerably by additionally neglecting stresslet contributions as per the Rotne–Prager approximation. Approximate many-body hydrodynamic interactions can be taken into account using the Stokesian dynamics method23 and advancements in recent years have improved its performance up to a linear scaling with the number of particles.24 Nonetheless, the handling of hydrodynamic interactions remains fundamentally approximate in Stokesian dynamics due to a truncated expansion of the mobility matrix. Furthermore, the method is limited in terms of its extensibility to non-zero Reynolds numbers and polydisperse or non-spherical particles. Parallelized Stokesian dynamics implementations scale efficiently to up to a few hundred CPUs25 and have been used to study the sedimentation of aggregates of thousands of polydisperse particles.26
Banchio et al. and Gapinski et al.,27–29 have previously employed the Stokesian dynamics method to numerically study suspensions under repulsive interactions. They obtained the structure factor of the suspension and the so-called hydrodynamic function H(q) for selected values of salt and particle concentrations. Though their results are focused more on modelling diffusivity, the hydrodynamic function contains the relative sedimentation speed of the suspension under a spatially constant force for q = 0. Comparison of experiments with the hydrodynamic function for a given concentration and as a function of q requires measuring the static structure factor, e.g. via X-ray scattering, as well as the collective diffusion function, e.g. via dynamic light scattering. Our approach of quantifying the functional shape and the mean slope of the sedimentation velocity as a function of concentration for a broad range of salt concentrations and different particle concentration ranges should lend itself to a more straightforward comparison to centrifugal sedimentation experiments. In fact we have recently applied an early version of our method described in this work in an experimental context.30
As an alternative to Stokesian dynamics one can model the sedimentation of particles in a fluid by coupling the discrete element method for the dynamics of the suspended particles to a Stokes or Navier–Stokes level hydrodynamics solver. Many different methods have been used for the latter, such as directly solving the Navier–Stokes equation using the finite element method,31 smoothed particle hydrodynamics,32 or stochastic rotation dynamics.33,34 In this work we employ the lattice Boltzmann method (LBM). It has been shown to be a viable tool to capture the full hydrodynamic interactions of large numbers of non-interacting sedimenting particles by Nguyen and Ladd in 2005,35 though there is similar work by Ladd with smaller particle numbers dating back to 1994.36 Later on the method has similarly been used to model particles with attractive interaction potentials.37 Several different algorithms for coupling particles to the LBM fluid exist, the method is numerically efficient and is not limited to low Reynolds number flows.38 For low Reynolds number flows the LBM has been found to give results consistent with the Stokesian dynamics method.39,40
In this paper we numerically study the impact of electrostatic interactions modeled by DLVO theory on sedimenting suspensions under varied particle size, concentration and Debye length. By simulating the interactions of a large number of particles and the resulting changes in the RDF explicitly and by including full hydrodynamic interactions using the LBM we improve upon previous studies and contribute to a clearer picture of how electrostatic interactions influence particle sedimentation.
2 Model and methodology
Each sedimentation simulation for a given set of concentration, particle size, and Debye length parameters consists of two major steps. First, a set of particle positions representative of an equilibrated bulk suspension of charged particles interacting via DLVO potentials is generated from a Langevin dynamics simulation. Second, the hydrodynamic interactions and the resulting sedimentation velocity under added constant acceleration (representing gravitational or centrifugal forces) are calculated for the particle positions obtained previously using the LBM. The final result is the particle velocity in the direction of the constant acceleration averaged over all particles.While in the first step both particle positions and particle velocities evolve in time, only the velocities are updated in the last step while the positions remain fixed. In this way we neglect changes in the RDF induced by hydrodynamic interactions and greatly reduce the convergence time and numerical cost of our hydrodynamic simulations. We consider this simplification to be justified in the limit of small Péclet numbers, where particle advection plays a small role compared to diffusion and drift fluxes induced by strong DLVO interactions. As we keep the particle positions fixed, neither advection nor diffusion occur in our hydrodynamic simulations so that the Péclet number is not obviously defined. However, by keeping the Reynolds number small (Re ≲ 5 × 10−6) we can consider the fluid flow velocity around the particles to be arbitrarily small. It follows that the Péclet number Pe ∝ Re/D calculated using the diffusivity D of the particles in the preceding Langevin simulation is likewise vanishingly small.
Ongoing research into the possible causes of an observed slow decay of sedimentation velocity fluctuations has led to the widespread assumption that subtle changes in the RDF may be taking place in sedimenting suspensions over long time spans up to several hours, even in the limit of small Pe.41,42 Reproducing this experimentally observed decay of velocity fluctuations accurately would require significantly longer simulation times43 and the presence of confinement44 with a geometry matching the experimental system.45 To our knowledge, however, no corresponding long term evolution of the mean sedimentation velocity has been observed so far in monodisperse suspensions.
2.1 Generating particle positions
In the first step, we initialize about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spherical particles with random positions ri without overlap in a 3D rectangular system with periodic boundary conditions. The particle positions are evolved in time t in each spatial dimension ι according to the Langevin equation
000 spherical particles with random positions ri without overlap in a 3D rectangular system with periodic boundary conditions. The particle positions are evolved in time t in each spatial dimension ι according to the Langevin equation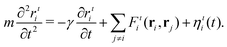 | (3) |
| 〈ηι(t)ηι(t′)〉 = 2kBTγδ(t − t′). | (4) |
2.2 Particle–fluid coupling
LB simulations are performed using our in-house code LB3D.46–48 In our LB implementation, fluid properties are calculated on a regular cubic lattice in three dimensions. On each lattice site 19 scalar populations fi are defined and the lattice constant is referred to as Δx. Each population is proportional to the fraction of fluid flowing in the velocity direction ci toward a neighboring lattice site or remaining at rest (c19 = 0) during that time step. In each time step Δt they are shifted to a neighboring lattice site according to| fi(r,t) → fi(r + ciΔt,t + Δt), | (5) |
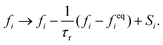 | (6) |
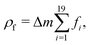 | (7) |
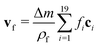 | (8) |
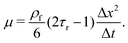 | (9) |
| Fs = −γ(vp − vf) = −γvΔ. | (10) |
Applying eqn (10) in the numerical model using γ = 6πμR and setting vf equal to the fluid velocity from the LBM interpolated to the particle position results in steady-state velocities vp = |vp| that are higher than the expected result from Stokes' theory. This is because vf in eqn (10) represents the fluid velocity without the Stokeslet contribution from the considered particle according to Stokes' law. We chose a particle radius equal to the LB grid spacing in order to have a relatively large radius while ensuring that the particle geometry remains comfortably within the extent of its stencil surrounding it. Furthermore we verified that the friction force densities remain smaller by more than an order of magnitude at all times compared to values deemed problematic in the lattice Boltzmann method. Fortunately, the contribution of the particle to its surrounding flow field can be easily subtracted by rescaling the friction coefficient, as shown by Ollila et al.55
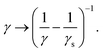 | (11) |
The sedimentation of particles with mass m in our LB simulations is triggered by a constant force Fg representing gravitational or centrifugal acceleration as well as the counteracting buoyancy. The same force Fg with opposite sign is distributed homogenously among all fluid sites in the system. This ensures global momentum conservation and mimics the backflow of displaced fluid occurring during sedimentation in a closed cell.
Assuming a constant vf, the particle velocity update by one time step due to the friction force alone can be written as
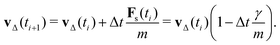 | (12) |
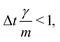 vp approaches vfvia an exponential decay. If
vp approaches vfvia an exponential decay. If 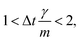 vp oscillates around vf due to discretization errors, but |vΔ| still decays to zero in time. If, however,
vp oscillates around vf due to discretization errors, but |vΔ| still decays to zero in time. If, however, 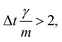 then |vΔ| diverges to infinity in an oscillating manner. The easiest way to avoid these discretization effects would be to choose the time step such that Δt < m/γ, or, at least, Δt < 2m/γ. However, large values of both γ and Δt are desirable when simulating a suspension at low Reynolds number. In order to avoid this issue, we analytically integrate the friction force Fs under the assumption of a constant vf but continuously varying vp and Fs over one time step, add the constant Fg, and calculate the average total force 〈FT〉Δt as
then |vΔ| diverges to infinity in an oscillating manner. The easiest way to avoid these discretization effects would be to choose the time step such that Δt < m/γ, or, at least, Δt < 2m/γ. However, large values of both γ and Δt are desirable when simulating a suspension at low Reynolds number. In order to avoid this issue, we analytically integrate the friction force Fs under the assumption of a constant vf but continuously varying vp and Fs over one time step, add the constant Fg, and calculate the average total force 〈FT〉Δt as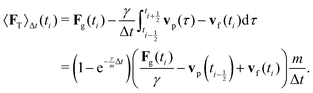 | (13) |
 shifted by half a time step with respect to positions and forces is readily available. The fluid velocity in eqn (13) is vf(ti) instead of vf
shifted by half a time step with respect to positions and forces is readily available. The fluid velocity in eqn (13) is vf(ti) instead of vf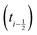 because we require the fluid velocity averaged over the time step from
because we require the fluid velocity averaged over the time step from 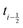 to
to 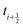 . In the overdamped limit, when m/γ ≪ Δt, eqn (13) gives the same acceleration from Fg as predicted by Brownian dynamics, plus advection by vf.
. In the overdamped limit, when m/γ ≪ Δt, eqn (13) gives the same acceleration from Fg as predicted by Brownian dynamics, plus advection by vf.
The averaged friction force acting on the fluid can be identified as −(〈FT〉Δt − Fg) and it is distributed to the fluid sites surrounding the particle on the same stencil on which the interpolation of takes place.
The LB simulations are considered converged when the slope of the sedimentation velocity over time relative to the velocity at infinite dilution and averaged over all particles and the last 1000 time steps falls below a threshold value of 5 × 10−8. This procedure usually requires between 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 LB time steps. We find that letting some simulations run up to about thirty times longer changes the final sedimentation velocity by less than 0.01%.
000 LB time steps. We find that letting some simulations run up to about thirty times longer changes the final sedimentation velocity by less than 0.01%.
2.3 DLVO interactions
The total force acting on a particle in the Langevin simulations is calculated with the same averaging of the friction force introduced in eqn (13) but setting the fluid velocity vf to zero and exchanging Fg with a sum of DLVO and hard sphere pair potentials, i.e.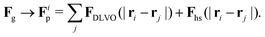 Each particle interacts only with particles within a numerical cutoff distance chosen according to the DLVO parameters of the simulation. The DLVO interactions consist of an attractive contribution stemming from van der Waals interactions and a repulsive contribution stemming from Coulomb repulsion screened by counterions: FDLVO = Fvdw + Fcoul. The van der Waals force of two spheres of equal radius R at a surface to surface distance ŝ = s/R in multiples of R is the derivative of the potential58
Each particle interacts only with particles within a numerical cutoff distance chosen according to the DLVO parameters of the simulation. The DLVO interactions consist of an attractive contribution stemming from van der Waals interactions and a repulsive contribution stemming from Coulomb repulsion screened by counterions: FDLVO = Fvdw + Fcoul. The van der Waals force of two spheres of equal radius R at a surface to surface distance ŝ = s/R in multiples of R is the derivative of the potential58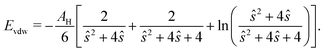 | (14) |
The repulsive component consists of a Coulomb interaction between like-charged spheres with an electrostatic potential ζ at the hydrodynamic slipping plane, which is exponentially screened over a decay length λD by the presence of dissolved ions in a solvent of dielectric permittivity ε58
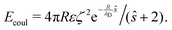 | (15) |
The simplified pair–wise interactions of DLVO theory are computationally efficient and allow us to reach large particle numbers with acceptable computational effort. However, this approach neglects the deformation of the Debye layer in the presence of a hydrodynamic flow. While taking this deformation into account could be achieved by coupling the solver for the fluid and particle dynamics to a solver for the Nernst–Planck equation,62,63 the influence of such ion advection effects becomes negligible when the ions' Péclet number λDv/Di is small.64 As established in Section 2, we are concerned in this work with systems of small particle Péclet number and Debye lengths comparable in size to the particle radius. The ions' Péclet number can be considered to be smaller still, owing to the smaller size and therewith larger diffusivity Di of the ions as compared to the particles. A fully resolved double layer would furthermore yield a reduction of the sedimentation velocity due to the restoring dipole force acting on the particle when it is accelerated by Fg out of the center of its ionic atmosphere.13,65,66 Because this so-called primary charge effect is also present in the sedimentation of a single particle, we assume its effect on the relative sedimentation speed v/v0 to be negligible.
In order to avoid strongly overlapping particles due to the divergence of Evdw at contact when λD is small and thermal fluctuations allow particles to cross the potential barrier posed by Ecoul, a hard sphere repulsion term of the form
| Ehs = k(2R − c)5/2 | (16) |
2.4 Validation
In order to check the accuracy of the particle–fluid coupling, we compare our simulations with known results for the sedimentation behavior of non-interacting particles. First we compute the velocity of a pair of neighboring particles under constant acceleration in Stokes flow. Two particles with a radius equal to the length of discretization of the LB solver are initialized in a fully periodic system. As described in Section 2.2, Fg is applied to each particle in the same direction and −2Fg is spread homogenously over all fluid lattice sites. The component of the final sedimentation velocity in direction of Fg and relative to the velocity of a single particle can be written as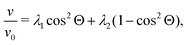 | (17) |
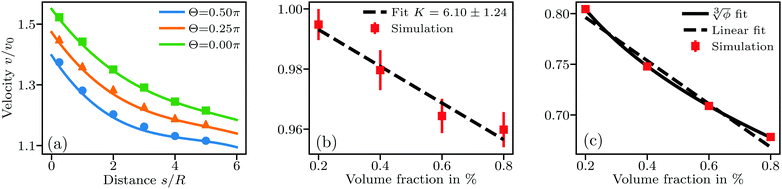 | ||
Fig. 1 Sedimentation velocity in three different types of systems. (a) A pair of particles at fixed distance and with Fg acting at angle Θ to the connecting line between the particles. Full lines show the theory prediction following eqn (17). (b) Suspension of non-interacting particles. Error bars stem from averaging over 6 simulations per concentration with different random particle placements. The dashed line shows the analytical solution by Batchelor.1 (c) Suspension under long-ranged repulsive DLVO interactions. The full line is a fit of the form 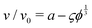 similar to eqn (18), giving a = 1.02 and ς = 1.71. The dashed line is a linear fit yielding K = 21.3. Error bars from averaging over 6 simulations are smaller than the symbols. similar to eqn (18), giving a = 1.02 and ς = 1.71. The dashed line is a linear fit yielding K = 21.3. Error bars from averaging over 6 simulations are smaller than the symbols. | ||
Next, we benchmark eqn (1) for the sedimentation velocity of non-interacting particles in bulk by simulating about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sedimenting particles in the same way as in the previous test. The corresponding results in Fig. 1(b) also show good agreement with eqn (1), with a measured K = 6.10 ± 1.24. Fig. 1(c) shows results from an identical set of sedimentation simulations with radius R = 100 nm and a Debye length λD = 950 nm. The long-ranged repulsive interactions in these simulations lead to a functional form of
000 sedimenting particles in the same way as in the previous test. The corresponding results in Fig. 1(b) also show good agreement with eqn (1), with a measured K = 6.10 ± 1.24. Fig. 1(c) shows results from an identical set of sedimentation simulations with radius R = 100 nm and a Debye length λD = 950 nm. The long-ranged repulsive interactions in these simulations lead to a functional form of 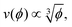 in agreement with theoretical expectations.10
in agreement with theoretical expectations.10
3 Results
We perform simulations for a range of Debye lengths from 5 nm to 950 nm with particle radii R set to 100, 200, 300, 450, and 600 nm. A Debye length of λD = 5 nm corresponds to a monovalent salt concentration of about 3.7 mM in water at room temperature, whereas 950 nm is close to the Debye length obtained in perfectly pure water solely by self-dissociation at a pH value of 7. We keep the zeta potential fixed at ζ = 50 mV regardless of the particle size.For the smallest Debye length of 5 nm combined with the largest particles of R = 600 nm, strong aggregation occurs, leading to negative values of K, as shown in Fig. 2. For smaller particles at the same Debye length, we observe K ≈ 6.55 and almost no aggregation. To understand this, first note that the van der Waals potential in eqn (14) does not depend on R for a given ŝ. The repulsive potential in eqn (15) on the other hand can be shown in a simple mathematical exercise to always decrease when R is increased as long as s > λD. The proof can be found in Section S3 of the ESI.† Thus, the attractive potential at distances beyond one Debye length is relatively stronger than the repulsion for larger particles. We exclude simulations showing extensive aggregation from further analysis.
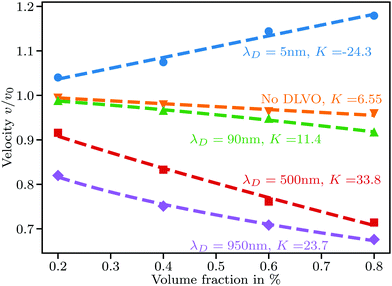 | ||
| Fig. 2 Sedimentation velocity in suspensions with particle radius R = 600 nm and various Debye lengths. Aggregation causes the large positive slope at λD = 5 nm. Dashed lines at λD = 500 nm and λD = 950 nm are nonlinear fits to eqn (18) giving ς = 16.54, 2.44 and ω = 1.2, 2.4, respectively. | ||
For small Debye lengths around 10 nm, the sedimentation velocity is predicted well by eqn (1) with K ≈ 6.55. As λD increases, the slope increases rapidly, meaning that mutual hindrance is increased. While particles close to each other sediment faster than a single particle, as shown in Fig. 1(a), at larger interparticle distances the effect of fluid backflow dominates and particles mainly slow down each other. An increase in λD leads directly to an increase in the mean distance between next neighbors due to a longer range of the repulsive potential.
When λD is sufficiently large so that the particles cannot fully escape the repulsive potential of their neighbors, v(ϕ) becomes distinctly nonlinear. The nonlinear regime begins to show in Fig. 2 for λD = 950 nm. According to calculations by Thies et al.,10 the sedimentation behavior in the limit of large λD should follow
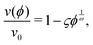 | (18) |
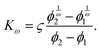 | (19) |
When λD is small enough for v(ϕ) to remain in the linear regime, K can be approximated for general interaction potentials Φ following Batchelor and Wen71 as K = 6.55 − 0.44α with
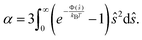 | (20) |
| KΦ(ξ) = 6.55 + 2.65(ξ2 + 2ξ). | (21) |
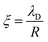 . However, as both the radius R and the zeta potential ζ influence the strength of the repulsive potential at a given distance s/R significantly (see Fig. S2 in the ESI†), we instead define ξ as the surface-to-surface distance in multiples of the radius at which EDLVO first exceeds kBT coming from infinity, thus constituting a significant potential barrier as compared to thermal energy. The exact choice of the threshold value makes relatively little difference in the resulting value of ξ due to the fast exponential decay of the repulsive potential. Because this measure depends on the charge state of the particle as well as its size, it encodes more information than the Debye length alone. In the dilute regime that we are focused on here, colloids are typically far apart. Hence, we can disregard the van der Waals contribution, eqn (14), and we can approximate the DLVO potential by the solely electrostatic interaction, eqn (15). Accordingly, the surface–surface dimensionless distance, ξ = ξ0, at which the colloid–colloid DLVO interaction is comparable to the thermal energy is obtained by numerically solving
. However, as both the radius R and the zeta potential ζ influence the strength of the repulsive potential at a given distance s/R significantly (see Fig. S2 in the ESI†), we instead define ξ as the surface-to-surface distance in multiples of the radius at which EDLVO first exceeds kBT coming from infinity, thus constituting a significant potential barrier as compared to thermal energy. The exact choice of the threshold value makes relatively little difference in the resulting value of ξ due to the fast exponential decay of the repulsive potential. Because this measure depends on the charge state of the particle as well as its size, it encodes more information than the Debye length alone. In the dilute regime that we are focused on here, colloids are typically far apart. Hence, we can disregard the van der Waals contribution, eqn (14), and we can approximate the DLVO potential by the solely electrostatic interaction, eqn (15). Accordingly, the surface–surface dimensionless distance, ξ = ξ0, at which the colloid–colloid DLVO interaction is comparable to the thermal energy is obtained by numerically solving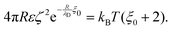 | (22) |
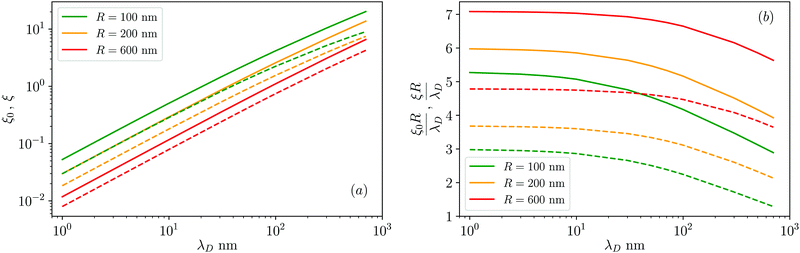 | ||
| Fig. 3 (a) Surface–surface dimensionless distance at which the colloid–colloid DLVO interaction is comparable to the thermal energy, ξ0 (defined in eqn (22), solid lines), and ten times the thermal energy, ξ (defined in eqn (25), dashed lines) as a function of the Debye length, λD, for various values of the particle radius, R = 100, 200, 600 nm (see legend) and for ζ = 50 mV. (b) Same data as in panel (a) but for ξR/λD and ξ0R/λD. | ||
Eqn (21) models the effect of the repulsive potential as an excluded volume around otherwise non-interacting and thus randomly distributed particles. A similar approach of modelling short-ranged DLVO interactions as an excluded volume, or alternatively an effective particle concentration, has been used previously for example by Gilleland et al.11 or Antonopoulou et al.72
The impact of the repulsive potential barrier at ŝ = ξ0 on the final particle distribution of course depends on the average particle–particle spacing, which in turn depends on the particle concentration ϕ. In order to account for this we furthermore introduce the naively calculated average interparticle spacing
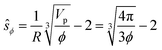 | (23) |
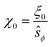 | (24) |
We have used the surface-surface distance ξ0 (see eqn (22)), and the associated value of χ0 (see eqn (24)), as the effective particle size in the hard-sphere model, eqn (21). However, the agreement is qualitatively good yet we admit some quantitative discrepancies. To address the role of the softness of the DLVO potential at distance ξ0, as compared to the hard-sphere interaction, we define ξ (and the associated χ) as the distance at which the DLVO potential ≃10kBT by numerically solving
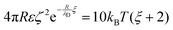 | (25) |
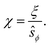 | (26) |
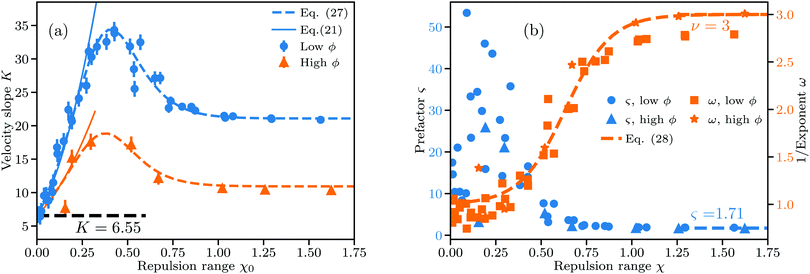 | ||
| Fig. 4 Linear and nonlinear fit parameters obtained for low ϕ (ϕ ∈ 0.2–0.8%) and high ϕ (ϕ ∈ 1–1.4%). χ = ξ/ŝϕ gives the range of the repulsive DLVO potential relative to the average interparticle distance. (a) Slope K from linear fits to v(ϕ)/v0. Dashed lines follow eqn (27) using identical fit parameters, and full lines follow eqn (21). (b) Parameters ς and ω from nonlinear fits of eqn (18) to v(ϕ)/v0. Dashed line follows eqn (28), fitted using low and high ϕ data combined. Uncertainties in the velocity v translate to a large variation in ς for low χ. | ||
The error bars in Fig. 4(a) account for variations due to the randomness involved in initial particle placement and the subsequent equilibration of particle distributions under thermal fluctuations. To estimate the error bars we repeat simulations up to 6 times at selected parameter combinations spanning the whole range of χ with different random number seeds and calculate the standard deviation of the resulting velocities as described in Section S4 of the ESI.† The error bars strongly depend on χ and are largest for non-interacting particles. Knowing χ and the concentration at which K is measured, we can predict the value of K to a decent accuracy both for small (viaeqn (21)) and large χ (viaeqn (19)). At intermediate χ an interpolating fit drawn in dashed lines in Fig. 4(a) matches the observed trend well.
This interpolating fit captures the transition from KΦ(ξ) (eqn (21)) to the constant value Kω given by eqn (19)via a sigmoid function
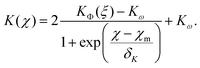 | (27) |
One can reformulate the fitted K(χ) from eqn (27) as a function of ϕ for fixed ξ and perform numerical integration to reconstruct the hindrance function v(ϕ)/v0 as shown in Section S5 in the ESI.† As shown in Fig. 4(a) we recover the case of non-interacting particles for χ → 0 and K → 6.55 as in eqn (1). Up to χ ≈ 0.3, K is well-approximated by eqn (21), which is shown as full lines in Fig. 4(a). Eqn (21) fails as a valid approximation when the particle distribution cannot be approximated as homogenous in space, i.e. when the RDF deviates from the step function expected for dilute hard spheres with an effective radius increased by Rξ/2.
Fig. 4(b) shows the obtained parameters ς and ω from nonlinear fits to eqn (18). While the nonlinear fit works well in the locally ordered regime at χ ≳ 0.4 and ω ≈ 1 is correctly reproduced even for χ → 0, there is a large uncertainty in ς at χ ≲ 0.4. As shown in Fig. 1(b) and (c), the uncertainty in the velocity in the disordered regime is much larger than in the locally ordered regime. According to eqn (18), v/v0 depends much more sensitively on the exponent ω than on the prefactor ς, in particular when ϕ is small. This can be seen from the ratio of the derivatives (∂v/∂ς)/(∂v/∂ω) = −ω2/(ς![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), which goes to zero for small ϕ. Accordingly, uncertainties in the velocity translate into much larger uncertainties in the values of ς than of ω, leading to the large spread in the obtained values of ς at low χ in Fig. 4(b). The exponent ω can be predicted well from χ via a fitted sigmoid function
ϕ), which goes to zero for small ϕ. Accordingly, uncertainties in the velocity translate into much larger uncertainties in the values of ς than of ω, leading to the large spread in the obtained values of ς at low χ in Fig. 4(b). The exponent ω can be predicted well from χ via a fitted sigmoid function
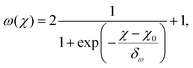 | (28) |
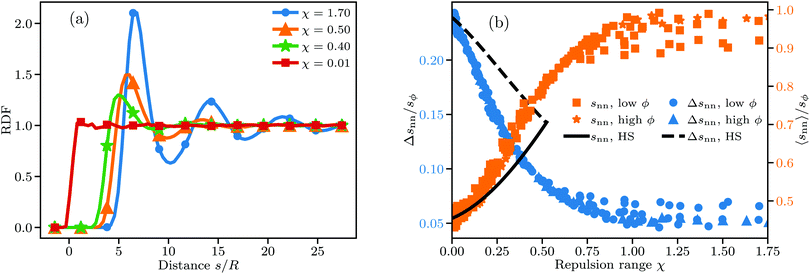
Fig. 5(a) shows the changes in the RDF leading in turn to the changes in K and ω. For small χ the RDF is a simple step function as expected for randomly distributed hard spheres. The first deviation from this idealized form is visible for χ = 0.4 in the form of a pronounced primary maximum next to the exclusion zone. The transition from a disordered to a locally ordered particle distribution is accompanied by an oscillatory component in the RDF, which becomes visible at χ ≈ 0.5. The length scale over which the oscillations decay can be interpreted as the length scale over which particle positions are correlated. Predictably, this length scale increases markedly as χ increases, with the RDF for χ = 1.7 showing visible correlation at distances well beyond 25 particle radii. Our results here qualitatively agree well with the RDF of charged sphere suspensions obtained in other works.10,11,28,29
Going to higher values of ϕ or χ than those we studied should lead to crystalline bcc or fcc particle distributions.73,74 Simulating crystalline systems would require great care though, because their very long-ranged order may be strongly affected by finite system sizes and take a long time to equilibrate.75 Furthermore, DLVO force models may be ill-suited for such systems, as they fail to properly model the experimentally observed coexistence of colloidal crystals with disordered phases in dilute suspensions at small salt concentration.76
In Fig. 5(b) we can see how changes in χ affect the average surface-to-surface interparticle distance 〈snn〉 as well as its standard deviation Δsnn within the particle configuration used in a given hydrodynamic simulation. Due to normalization by the average interparticle spacing sϕ the results for different ϕ again collapse rather well on a single curve. Unlike in Fig. 4(a) and (b), where each data point represents a group of simulations at different ϕ and otherwise identical parameters (with χ being averaged over ϕ), each data point here corresponds to a single simulation.
The full and dashed lines in Fig. 5(b) compare the simulation results with a homogenous suspension of particles interacting only via the step potential Φ = E0Θ(ξ − ŝ) with E0 → ∞ at ŝ = ξ – like hard spheres with a radius enlarged in proportion to χ. Because the particle distribution (derived in Section S6 of the ESI†) neglects particle–particle correlations beyond the range of the step potential, it is necessarily inaccurate when either ϕ or χ are large.
A substantial discrepancy between the simulation results for 〈snn〉 and the hard sphere distribution develops starting around χ = 0.3. This is consistent with the observation that the enlarged hard sphere model from eqn (21) predicts K(χ) well only up to χ ≈ 0.3, as shown in Fig. 4(a). Interestingly, Δsnn seems to diverge from the hard sphere distribution much faster though, showing that the microstructure of the DLVO suspension does differ noticeably from the hard sphere suspension for χ < 0.3, despite affecting sedimentation in much the same way as an increased hard sphere radius.
For χ ≳ 1, 〈snn〉 approaches the maximal average interparticle distance sϕ and Δsnn indicates a narrow distribution of next-neighbor distances as expected for a locally ordered particle distribution.
4 Conclusions
By simulating the hydrodynamic and DLVO interactions of large ensembles of particles we found seemingly universal trends in the sedimentation behavior for a wide range of Debye lengths and particle sizes. We quantified the effect of particle interactions depending on the range χ of electrostatic repulsion in our results either via the slope K or the exponent 1/ω of fits to the sedimentation velocity v(ϕ)/v0 across different ranges of ϕ.K is the slope extracted from a linear fit to v(ϕ)/v0 and appears to be described well by our fit to eqn (27) for any ϕ in the dilute limit. eqn (27) predicts K(χ) assuming that the electrostatic repulsion at χ ≲ 0.3 acts merely like an increase of the effective hard sphere radius, whereas at χ ≳ 1 sedimentation follows the known solution eqn (18) with ς ≈ 1.71 and ω = 3 for ordered particle arrays. The transition from one solution to another is approximated in eqn (27) using a simple sigmoid function.
Applying non-linear fits following eqn (18) to v(ϕ)/v0 instead we find clear nonlinearity (ω > 1) commencing around χ = 0.4, where K(χ) reaches its maximum. Near this transition point from linear to nonlinear the RDF shows a transition from a disordered gas-like state to a liquid-like state. ω(χ) is likewise describable by a sigmoid function, with a smoothened step-like transition from ω = 1 at χ → 0 to ω = 3 at χ ≳ 1. This coincides with the point where the average next-neighbor distance reaches its maximum possible value.
Both K(χ) following eqn (27) and ω(χ) following eqn (28) offer themselves as a potentially useful gauge to estimate the extent of electrostatic interactions (encoded by χ) in a suspension directly from experimental measurements of the sedimentation velocity under varied particle concentration. The approach of estimating χ via ω has the advantage that ω increases monotonously with χ and hence can in principle be inverted to obtain a mapping χ(ω). The downside of this approach is that the nonlinear fits tend to be more sensitive to noise in v(ϕ) than linear fits.
We note in conclusion that our results, while obtained under the assumption of a strongly repulsive DLVO potential at ζ = 50 mV, are in fact generally valid for any repulsive potential with a steep potential barrier at distance ξ = χŝϕ. The van der Waals interactions are strongly subdued in most of our parameter regime and the models we used to predict K at both small and large χ are not specific to details of the DLVO interaction.
In future work we aim to reproduce long-ranged electrostatic interactions in sedimentation velocity experiments for a broad parameter range and compare the experimental data directly to our simulations. In the experimental setup we wish to study model nanoparticle systems including a controlled degree of polydispersity. Other possible avenues of future research might include non-spherical, in particular rod-like charged particles, where orientation and rotation become important in addition to translational ordering.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Competence Network for Scientific and Technical High Performance Computing in Bavaria (KONWIHR) and has been further funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 416229255 – SFB 1411.Notes and references
- G. K. Batchelor, J. Fluid Mech., 1972, 52, 245–268 CrossRef.
- J. F. Brady and L. J. Durlofsky, Phys. Fluids, 1988, 31, 717–727 CrossRef CAS.
- B. Cichocki, M. L. Ekiel-Jeżewska, P. Szymczak and E. Wajnryb, J. Chem. Phys., 2002, 117, 1231–1241 CrossRef CAS.
- K. Benes, P. Tong and B. J. Ackerson, Phys. Rev. E, 2007, 76, 056302 CrossRef PubMed.
- D. J. Shaw, Introduction to Colloid and Surface Chemistry, Butterworths, 1980 Search PubMed.
- J. M. Horn and G. Y. Onoda, J. Am. Ceram. Soc., 1978, 61, 523–527 CrossRef CAS.
- K. Ohsawa, M. Murata and H. Ohshima, Colloid Polym. Sci., 1986, 264, 1005–1009 CrossRef CAS.
- A. M. Fiore, G. Wang and J. W. Swan, Phys. Rev. Fluids, 2018, 3, 063302 CrossRef.
- R. Sun, H. Xiao and H. Sun, Adv. Water Resour., 2018, 111, 406–422 CrossRef.
- D. M. E. Thies-weesie, A. P. Philipse, G. Nägele, B. Mandl and R. Klein, J. Colloid Interface Sci., 1995, 176, 43–54 CrossRef CAS.
- W. T. Gilleland, S. Torquato and W. B. Russel, J. Fluid Mech., 2011, 667, 403–425 CrossRef CAS.
- F. Booth, J. Chem. Phys., 1954, 22, 1956–1968 CrossRef CAS.
- D. Stigter, J. Phys. Chem., 1980, 84, 2758–2762 CrossRef CAS.
- S. Levine, G. Neale and N. Epstein, J. Colloid Interface Sci., 1976, 57, 424–437 CrossRef CAS.
- H. Ohshima, J. Colloid Interface Sci., 1998, 208, 295–301 CrossRef CAS PubMed.
- J. M. Ding and H. J. Keh, J. Colloid Interface Sci., 2001, 243, 331–341 CrossRef CAS.
- E. Lee, T.-S. Tong, M.-H. Chih and J.-P. Hsu, J. Colloid Interface Sci., 2002, 251, 109–119 CrossRef CAS PubMed.
- J. Happel, AIChE J., 1958, 4, 197–201 CrossRef CAS.
- S. Kuwabara, J. Phys. Soc. Jpn., 1959, 14, 527–532 CrossRef.
- B. J. Marlow and R. L. Rowell, Langmuir, 1985, 1, 83–90 CrossRef CAS.
- G. Nägele, M. Heinen, A. J. Banchio and C. Contreras-Aburto, Eur. Phys. J. Spec. Top., 2013, 222, 2855–2872 CrossRef.
- M. Watzlawek and G. Nägele, J. Colloid Interface Sci., 1999, 214, 170–179 CrossRef CAS PubMed.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- A. M. Fiore and J. W. Swan, J. Fluid Mech., 2019, 878, 544–597 CrossRef.
- F. Bülow, P. Hamberger, H. Nirschl and W. Dörfler, Comput. Phys. Commun., 2016, 204, 107–120 CrossRef.
- F. Bülow, H. Nirschl and W. Dörfler, Eur. J. Mech. B Fluids, 2015, 50, 19–26 CrossRef.
- A. J. Banchio, J. Gapinski, A. Patkowski, W. Häußler, A. Fluerasu, S. Sacanna, P. Holmqvist, G. Meier, M. P. Lettinga and G. Nägele, Phys. Rev. Lett., 2006, 96, 138303 CrossRef PubMed.
- J. Gapinski, A. Patkowski, A. J. Banchio, P. Holmqvist, G. Meier, M. P. Lettinga and G. Nägele, J. Chem. Phys., 2007, 126, 104905 CrossRef CAS PubMed.
- A. J. Banchio and G. Nägele, J. Chem. Phys., 2008, 128, 104903 CrossRef PubMed.
- M. J. Uttinger, D. Jung, N. Dao, H. Canziani, C. Lübbert, N. Vogel, W. Peukert, J. Harting and J. Walter, Soft Matter, 2011, 17, 2803 RSC.
- H. Gan, J. Chang, J. J. Feng and H. H. Hu, J. Fluid Mech., 2003, 481, 385–411 CrossRef.
- M. Robinson, S. Luding and M. M. Ramaioli, AIP Conf. Proc., 2013, 1542, 1079 CrossRef.
- C. A. Pérez, A. Moncho-Jordá, R. Hidalgo-Álvarez and H. Casanova, Mol. Phys., 2015, 113, 3587–3597 CrossRef.
- B. Schäfer, M. Hecht, J. Harting and H. Nirschl, J. Colloid Interface Sci., 2010, 349, 186–195 CrossRef PubMed.
- N.-Q. Nguyen and A. J. C. Ladd, J. Fluid Mech., 2005, 525, 73–104 CrossRef.
- A. J. C. Ladd, J. Fluid Mech., 1994, 271, 285 CrossRef CAS.
- J. J. Derksen, Int. J. Multiph. Flow, 2014, 58, 127–138 CrossRef CAS.
- H. Gao, H. Li and L.-P. Wang, Comput. Math. Appl., 2013, 65, 194–210 CrossRef.
- C. Binder, C. Feichtinger, H.-J. Schmid, N. Thürey, W. Peukert and U. Rüde, J. Colloid Interface Sci., 2006, 301, 155–167 CrossRef CAS PubMed.
- E. Schlauch, M. Ernst, R. Seto, H. Briesen, M. Sommerfeld and M. Behr, Comput. Fluids, 2013, 86, 199–209 CrossRef.
- D. L. Koch and E. S. G. Shaqfeh, J. Fluid Mech., 1991, 224, 275–303 CrossRef CAS.
- J. Möller and T. Narayanan, Phys. Rev. Lett., 2017, 118, 198001 CrossRef PubMed.
- A. J. C. Ladd, Phys. Rev. Lett., 2002, 88, 048301 CrossRef CAS PubMed.
- M. P. Brenner, Phys. Fluids, 1999, 11, 754–772 CrossRef CAS.
- S.-Y. Tee, P. J. Mucha, L. Cipelletti, S. Manley, M. P. Brenner, P. N. Segre and D. A. Weitz, Phys. Rev. Lett., 2002, 89, 054501 CrossRef PubMed.
- S. Schmieschek, L. Shamardin, S. Frijters, T. Krüger, U. D. Schiller, J. Harting and P. V. Coveney, Comput. Phys. Commun., 2017, 217, 149–161 CrossRef CAS.
- F. Janoschek, F. Toschi and J. Harting, Phys. Rev. E, 2010, 82, 056710 CrossRef CAS PubMed.
- J. Harting, J. Chin, M. Venturoli and P. V. Coveney, Philos. Trans. R. Soc., A, 2005, 363, 1895–1915 CrossRef PubMed.
- P. L. Bhatnagar, E. P. Gross and M. Krook, Phys. Rev., 1954, 94, 511–525 CrossRef CAS.
- R. Benzi, S. Succi and M. Vergassola, Phys. Rep., 1992, 222, 145 CrossRef.
- T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. M. Viggen, The Lattice Boltzmann Method: Principles and Practice, Springer International Publishing, 2017 Search PubMed.
- A. L. Kupershtokh, Proceeding of the 5th International EHD Workshop, 2004, pp. 241–246.
- A. L. Kupershtokh, D. A. Medvedev and D. I. Karpov, Comput. Math. Appl., 2009, 58, 965–974 CrossRef.
- P. Ahlrichs and B. Dünweg, Int. J. Mod. Phys. C, 1998, 1429–1438 CrossRef.
- S. Ollila, C. Smith, T. Ala-Nissila and C. Denniston, Multiscale Model. Simul., 2013, 11, 213–243 CrossRef.
- R. W. Nash, R. Adhikari and M. E. Cates, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 026709 CrossRef CAS PubMed.
- C. S. Peskin, Acta Numer., 2002, 11, 479–517 CrossRef.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, 2001 Search PubMed.
- M. L. Fielden, R. A. Hayes and J. Ralston, Phys. Chem. Chem. Phys., 2000, 2, 2623–2628 RSC.
- V. Valmacco, M. Elzbieciak-Wodka, C. Besnard, P. Maroni, G. Trefalt and M. Borkovec, Nanoscale Horiz., 2016, 1, 325–330 RSC.
- A. Watillon and A.-M. Joseph-Petit, Discuss. Faraday Soc., 1966, 42, 143–153 RSC.
- M. Kuron, G. Rempfer, F. Schornbaum, M. Bauer, C. Godenschwager, C. Holm and J. de Graaf, J. Chem. Phys., 2016, 145, 214102 CrossRef PubMed.
- N. Rivas, S. Frijters, I. Pagonabarraga and J. Harting, J. Chem. Phys., 2018, 148, 144101 CrossRef PubMed.
- A. S. Khair, Langmuir, 2018, 34, 876–885 CrossRef CAS PubMed.
- H. Ohshima, T. W. Healy, L. R. White and R. W. O'Brien, J. Chem. Soc., Faraday Trans. 2, 1984, 80, 1299–1317 RSC.
- F. Keller, M. Feist, H. Nirschl and W. Dörfler, J. Colloid Interface Sci., 2010, 344, 228–236 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon Press, 3rd edn, 1970, vol. 7 Search PubMed.
- M. Stimson and G. B. Jeffery, Philos. Trans. R. Soc., A, 1926, 111, 110–116 Search PubMed.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1966, 21, 1151–1170 CrossRef CAS.
- A. P. Philipse, Curr. Opin. Colloid Interface Sci., 1997, 2, 200–206 CrossRef CAS.
- G. K. Batchelor and C.-S. Wen, J. Fluid Mech., 1982, 124, 495–528 CrossRef CAS.
- E. Antonopoulou, C. F. Rohmann-Shaw, T. C. Sykes, O. J. Cayre, T. N. Hunter and P. K. Jimack, Phys. Fluids, 2018, 30, 030702 CrossRef.
- B. V. R. Tata and S. S. Jena, Solid State Commun., 2006, 139, 562–580 CrossRef CAS.
- Y. Monovoukas and A. P. Gast, J. Colloid Interface Sci., 1989, 128, 533–548 CrossRef CAS.
- J. Harting, H. J. Herrmann and E. Ben-Naim, EPL, 2008, 83, 30001 CrossRef.
- N. Ise and I. S. Sogami, Structure Formation in Solution, Springer, 2005 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: It includes several auxiliary plots and short derivations. See DOI: 10.1039/d1sm01294k |
| This journal is © The Royal Society of Chemistry 2022 |