Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cononsolvency of thermoresponsive polymers: where we are now and where we are going
Swaminath
Bharadwaj
 *a,
Bart-Jan
Niebuur†
*a,
Bart-Jan
Niebuur†
 b,
Katja
Nothdurft
b,
Katja
Nothdurft
 c,
Walter
Richtering
c,
Walter
Richtering
 c,
Nico F. A.
van der Vegt
c,
Nico F. A.
van der Vegt
 a and
Christine M.
Papadakis
a and
Christine M.
Papadakis
 b
b
aTechnical University of Darmstadt, Eduard-Zintl-Institut für Anorganische und Physikalische Chemie, Computational Physical Chemistry Group, 64287 Darmstadt, Germany. E-mail: bharadwaj@cpc.tu-darmstadt.de
bTechnical University of Munich, Physics Department, Soft Matter Physics Group, James-Franck-Str. 1, 85748 Garching, Germany
cRWTH Aachen University, Institut für Physikalische Chemie, Landoltweg 2, 52056 Aachen, Germany, European Union
First published on 14th March 2022
Abstract
Cononsolvency is an intriguing phenomenon where a polymer collapses in a mixture of good solvents. This cosolvent-induced modulation of the polymer solubility has been observed in solutions of several polymers and biomacromolecules, and finds application in areas such as hydrogel actuators, drug delivery, compound detection and catalysis. In the past decade, there has been a renewed interest in understanding the molecular mechanisms which drive cononsolvency with a predominant emphasis on its connection to the preferential adsorption of the cosolvent. Significant efforts have also been made to understand cononsolvency in complex systems such as micelles, block copolymers and thin films. In this review, we will discuss some of the recent developments from the experimental, simulation and theoretical fronts, and provide an outlook on the problems and challenges which are yet to be addressed.
1 Introduction
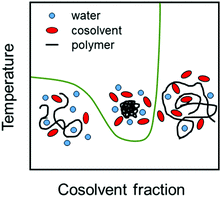
Cosolvents play an important role in determining properties of stimuli-responsive soft matter systems,1,2 manipulating the conformation of polypeptides3 and regulating the solubility of water-based formulations of drugs.4,5 Cononsolvency is a well known phenomenon in which a polymer in a good solvent phase separates with the progressive addition of a second good cosolvent leading to a miscibility gap (see Fig. 1). At the single chain level, the polymer exhibits coil–globule–coil transitions with increase in the cosolvent concentration as shown in Fig. 1. The cononsolvency effect has been employed in a wide range of applications such as sensing for detecting volatile organic compounds6 or enantiomeric excess,7 catalysis,8 hydrogel actuators,9 regulation of transport through nanopores,10 separation processes based on selective precipitation,11,12 and the formation of self-assembled nanostructures.13 Additionally, the cononsolvency effect of thermoresponsive polymer brushes has been utilized for the transportation of nanoparticles,14 and the development of surfaces with tunable friction.15–17 Cononsolvency has been observed in a wide variety of polymer and bio-macromolecular solutions, to different extents, with a broad range of cosolvents such as alcohols, acetone, dimethyl sulfoxide and dimethyl formamide. Some of the well known polymers which exhibit cononsolvency are poly(N-isopropylacrylamide) (PNIPAM), other poly(acrylamides),18 poly(n-propyl-2-oxazoline),19 poly(N-vinylcaprolactam)20,21 and elastin-like polypeptides.3 However other chemically similar polymers such as poly(2-cyclopropyl-2-oxazoline), do not feature cononsolvency,22 and the reasons have not been clarified yet.Although the cononsolvency phenomenon has been known for the past 30 years, there is still no consensus on the driving mechanism and the associated molecular interactions. An important aspect which has been studied alongside cononsolvency is the preferential accumulation of the cosolvent on the polymer. Intuitively, cosolvents which preferentially bind to the polymer would promote polymer swelling due to the presence of favorable polymer–cosolvent interactions. Conversely, cosolvents which deplete from the polymer surface would drive polymer collapse. However, several recent observations have shown that this simple picture is not generic and that preferential interactions with cosolvents,23–29 specific salts30–33 and cosolutes34–42 can trigger both polymer collapse and polymer swelling. Over the past 10 years, there have been numerous experimental, theoretical and simulation efforts to understand the cononsolvency phenomenon and its connection with the preferential adsorption of the cosolvent.
A number of experimental investigations have been reported, addressing different aspects of the phenomenon, such as cloud point variation,20–22,43–45 the energetics of the transition,46 the dynamics of certain segments of the side group or of the chain,47–49 the solvent dynamics,28,48,50 and the chain size.51,52 For studying these aspects, methods as different as differential scanning calorimetry (DSC),46 nuclear magnetic resonance spectroscopy (NMR),47 broadband dielectric spectroscopy (BDS),48 quasi-elastic neutron scattering (QENS),28,50 and fluorescence correlation spectroscopy (FCS)51 were used. Different polymers in large concentration ranges as well as different cosolvents were addressed; however, most studies focused on the PNIPAM/water/methanol system. Pressure was found to reverse cononsolvency.50,53–56 Recently, the effect of cononsolvency on complex systems was investigated as well, such as polypeptides,3 (micro)gels,2 block copolymers,57,58 thin films59 and grafted polymer brushes.15
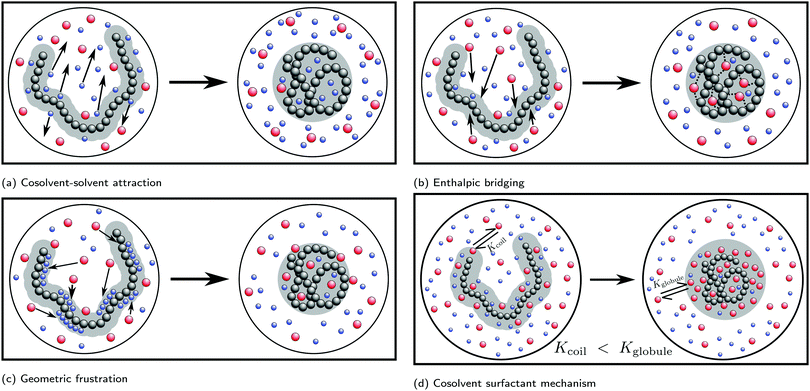
Simulation studies have predominantly focused on the cononsolvency and preferential adsorption in PNIPAM/water/alcohol mixtures. To understand the molecular driving forces, a wide variety of model systems ranging from generic bead-spring polymer solutions60–64 to fully atomistic models23,26,27,47,65–69 have been employed. In contrast to experiments, the simulation studies have focused primarily on the effects of the cosolvent on the single chain coil-to-globule transition. Such an approach is meaningful as it is known that the bulk phase behavior in the polymer solutions is coupled to the single chain coil-to-globule transition at low cosolvent concentrations.2,70 In the addition to simulations, significant efforts have been made to develop theoretical ideas, such as the adsorption–attraction model,71–73 scaled particle theory approach,74 Flory–Huggins type mean-field theory,75–77 field theory approach,78,79 and cooperative hydration,80–82 to understand and compliment the experimental and simulation results. Some of the prominent mechanisms which have been proposed in the literature are based on attractive solvent–cosolvent interactions, polymer–cosolvent bridging interactions, cosolvent-induced geometric frustration and cosolvent surfactant effects. These will be discussed in detail in the forthcoming sections.
Previous reviews addressed the cononsolvency behavior in aqueous PNIPAM solutions, comparing the behavior of microgels to the ones of homopolymers and macrogels.2 Mukherji et al. contrasted the cosolvency and the cononsolvency behavior in different polymer solutions.83 The cononsolvency in solutions of polymers, chemically different from PNIPAM, has also been discussed in a few earlier reviews.84,85 In attempting to understand cononsolvency of polymers chemically distinct from PNIPAM at a fundamental level, a combined use of experiments and simulations is required to obtain a complete picture of all relevant molecular interactions. While spectroscopic methods provide ways to probe these interactions, it is often difficult to separate their contributions in complex polymer/water/cosolvent systems where the various length scales pose additional problems. Molecular simulations provide complementary information at the atomic level that can aid the interpretation of experiments, but require the availability of well-balanced force fields. These should be sufficiently accurate to reproduce experimental data, such as the enthalpy of the coil–globule transition, which depends on the strength of the hydrogen bonds between polymer and water. While this accuracy has been achieved for PNIPAM,66,86 no further studies have been reported to our knowledge that validate force fields for responsive polymer systems based on different chemical constituents. Therefore, experiments and simulations should go hand in hand to investigate effects related to cononsolvency beyond the application to PNIPAM. As specific chemistry is used to tune swelling and collapse transitions in applications of the cononsolvency effect, a detailed understanding of all relevant interactions involved is needed.
Here, we summarize the recent experimental, simulation and theoretical developments, focusing on the connection between the preferential adsorption of the cosolvent and cononsolvency. A significant emphasis has also been placed on understanding the cononsolvency phenomenon in biomacromolecules and complex systems. In this review, we highlight the connections, or lack thereof, between the experimental findings and the simulation or theoretical observations. We also discuss aspects which are yet to be understood and provide an outlook to the associated problems and challenges. The review is structured as follows: We summarize experimental findings on interactions between the polymers, the solvent and the cosolvent and their effect on the chain conformation and dynamics. After a description of the PNIPAM/water/methanol system, we address the effect of other alcohols and the cononsolvency effect in other polymers. In the subsequent section, the mechanisms, proposed from simulation and theoretical studies, and the associated shortcomings are described. In the third section, further developments, such as studies on the effects of pressure on cononsolvency as well as the cononsolvency effect in polypeptide solutions, microgels, self-assembled micelles and thin films from thermoresponsive polymers are discussed.
2 Polymer–solvent/cosolvent interaction
This section focuses on the interactions between the polymer segments with the solvent and the cosolvent. In the first part, experimental findings are reviewed and discussed. The second part revisits the underlying thermodynamics and describes results from simulations.2.1 Experiments
Most experimental studies of the interactions between the polymer segments, water and the cosolvent with the aim of understanding the molecular origin of the cononsolvency effect were carried out on PNIPAM solutions in water/methanol mixtures. A few recent investigations are discussed in the first part of this section. Afterwards, we summarize findings from studies using alcohols other than methanol. Finally, the cononsolvency effect in solution from polymers chemically different from PNIPAM is described.The energetics of the phase transition of PNIPAM solutions in water–methanol mixtures were addressed by Grinberg et al. using differential scanning calorimetry (DSC) on solutions covering a wide range of polymer concentrations.46 Fundamentally different behavior was found for methanol molar fractions below and above xm = 0.35, where the transition temperature assumes a minimum. Below this value, the dependence of the transition temperature, the transition enthalpy and the width could be quantitatively explained by the Okada–Tanaka model (Fig. 2).80 The authors assign this finding to the importance of the cooperative hydro-solvation in the shell formed by water–methanol complexes. In contrast, at xm > 0.35, the behavior was found to be similar to that of polymer solutions in organic solvents, that feature Flory–Huggins type behavior.
 | ||
| Fig. 2 Results from DSC on PNIPAM solutions (2–150 mg ml−1) in different water/methanol mixtures. (a–d) Excess heat capacity functions of PNIPAM per monomer unit at the methanol weight fractions of (a) 5, (b) 10, (c) 20, and (d) 30% (symbols). Lines are calculated following the Okada–Tanaka model. (e) Symbols: resulting correlation between the measured calorimetric enthalpy of PNIPAM (per PNIPAM monomer unit) and the transition enthalpy corresponding to the polymer dehydration heat calculated on the basis of the Okada–Tanaka theory. Red line: linear fit. Adapted with permission from ref. 46. Copyright 2020. Reproduced with permission from The American Chemical Society. | ||
Using 1H nuclear magnetic resonance (NMR) spectroscopy, Mukherji et al. showed that the mobility of the side group of PNIPAM is reduced with increasing methanol content.47 It was suggested that the reduced mobility is due to the accumulation of side groups in the inner part of the globules, leading to an encapsulation of methanol inside the globules due to preferential adsorption of methanol at the side groups. This claim was supported by complementary molecular dynamics simulations. In a time-resolved NMR study of the osmosis of methanol through a membrane, that was impermeable for PNIPAM, information about the behavior of methanol could be obtained.47 For a molar fraction of methanol xm = 0.15 and a temperature of 25 °C, the amount of methanol in the compartment containing only the solvents decreased with time before it stabilized after ca. 150 h. This decrease was assigned to the preferential adsorption of methanol at the polymer, which was assumed to drive the polymer collapse observed for this solvent composition. Several studies indicate an enrichment of alcohol for the case of PNIPAM gels in binary water–alcohol mixtures, as will be discussed in more detail further below.87–89
It emerged recently that the dynamics of the chain and of the solvent molecules are sensitively affected by a cosolvent.28,48–50,90 Using broadband dielectric spectroscopy (BDS) on dilute solutions of PNIPAM in a series of water/methanol mixtures covering the entire composition range, Yang and Zhao identified a number of relaxation processes at room temperature.48 These comprise the global motion of the chain, the local motion of the backbone, the motion of the side group, and the dipole orientation of the solvent molecule. For xm increasing from 0 to 0.15, the PNIPAM chains collapse, and the solvation unit that solvates PNIPAM is composed of one water molecule (Fig. 3). For xm = 0.15–0.50, methanol molecules attach to the water molecules in the solvation unit. Since they attach mainly with their hydroxyl unit, a hydrophobic layer can be expected to be formed by the methyl groups on the surface of the solvated PNIPAM chain. These findings indicate that the PNIPAM chains are collapsed, even though they are immersed in a water-rich environment. For xm > 0.50, more and more methanol molecules participate in the solvation of PNIPAM by forming water–methanol clusters. This clustering reduces the hydrophobic effect and causes a reswelling of the chains. Finally, as xm = 1.0 is approached, the solvation unit is composed of three methanol molecules. The results highlight the importance of the composition of the solvation shell of the polymer for the cononsolvency effect.
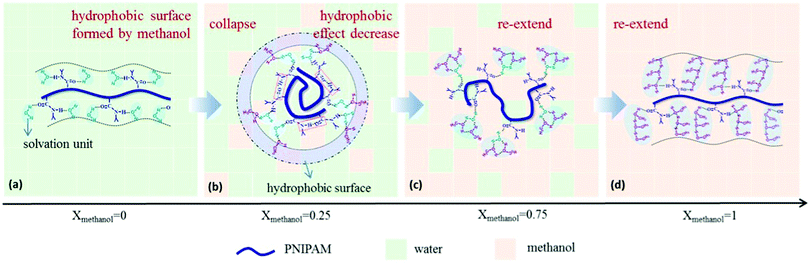 | ||
| Fig. 3 Results from BDS on a dilute solution of PNIPAM in a series of water/methanol mixtures having different compositions. The interactions between the solute PNIPAM and the solvation units (blue shadow) differ as the methanol content is increased, because the composition of the solvation unit changes from being water-rich to methanol-rich. For compositions in the miscibility gap, the surface of the solvated chain appears hydrophobic. Adapted with permission from ref. 48. Copyright 2017. Reproduced with permission by Wiley Periodicals Inc. | ||
Exploiting the possibilities for contrast variation in neutron scattering, the dynamics of the water molecules in the solvation shell are accessible using quasi-elastic neutron scattering (QENS). A concentrated solution of PNIPAM (25 wt%) in a mixture of H2O and fully deuterated methanol, CD3OD, with a volume fraction of CD3OD of 15% was investigated by Kyriakos et al. in dependence on temperature across the cloud point.28 For this choice of solvents, the scattering signal of H2O dominates, and two types of water could be distinguished, namely strongly arrested and weakly arrested water. Upon heating through the cloud point, the strongly arrested water is partially released from PNIPAM. In contrast, the dynamic properties of the weakly arrested water species are similar to the ones in the absence of PNIPAM. Above the cloud point, its residence time decreases, while its fraction increases. Overall, these two types of water behaved very similarly to water in a purely aqueous solution of PNIPAM. In a complementary QENS experiment, the dynamics of methanol was addressed in solutions of the same polymer having the same composition, now using a mixture of D2O and CH3OH as a solvent.28 Methanol was found to both form complexes with D2O and to be associated with the PNIPAM chains. Thus, methanol is present in the hydration shell of PNIPAM. Later, temperature-resolved QENS experiments by Niebuur et al. were carried out across the cloud point of a 25 wt% solution of PNIPAM in a mixture of H2O and CD3OD with a similar volume fraction of CD3OD, namely 20%.50 Converting the dynamic structure factor into the dynamic susceptibility revealed more detailed information on the dynamics of the hydration and the bulk water than the analysis of the dynamic structure factor, as carried out by Kyriakos et al.28 Especially, the dynamics of the hydration water can be clearly distinguished from the one of the bulk water. Far below the cloud point, the solvent phase was found to be enriched with water, thus methanol is preferentially adsorbed on the chains. Close to the cloud point, the effective solvent composition approaches the nominal ratio, i.e. preferential adsorption is diminished. A weakening effect of adsorbed methanol molecules on the binding strength of water with PNIPAM was observed. Moreover, the previously observed release of a part of the polymer-bound water at the cloud point could be confirmed. The interaction between the solvent molecules and the hydrophobic groups of PNIPAM were probed in complementary temperature-resolved Raman spectroscopy measurements across the cloud point, confirming that the hydration of the hydrophobic groups of PNIPAM in the presence of methanol below the cloud point is weaker than in a purely aqueous PNIPAM solution.50 Thus, it could be concluded that, below the cloud point, at the hydrophobic groups, a fraction of the hydration water is partially replaced by methanol.
In a combined dynamic light scattering (DLS) and neutron spin-echo (NSE) study, Raftopoulos et al. investigated the chain dynamics of PNIPAM dissolved in mixtures of D2O and fully deuterated methanol having different compositions (0–15 vol% of CD3OD).49 The polymer concentration was chosen at 9 and a 25 wt%. DLS revealed two dynamic processes (Fig. 4(a)). The fast diffusive process, that is also observed in the intermediate structure factor from NSE, was attributed to the relaxation of the chain segments within the blobs, with the corresponding diffusion coefficient decreasing with increasing methanol content. The corresponding dynamic correlation length of concentration fluctuations follows critical scaling with temperature, and the values of the exponent point to 3D Ising rather than mean-field behavior (Fig. 4(b)). The authors speculated that this is related to the additional observed slow dynamic process, which is due to large-scale dynamic heterogeneities (Fig. 4(a)). Since these are even more pronounced for the higher polymer concentration, they seem to be related to interchain interactions. These observations on the fast and the slow dynamic process point to the importance of methanol on the chain dynamics and the interchain interactions, resulting in strong large-scale heterogeneities.
 | ||
| Fig. 4 Results from DLS on a semidilute solution of PNIPAM (9 wt%) in mixtures of D2O and CD3OD having the CD3OD volume fractions given in (a).49 (a) Representative normalized intensity autocorrelation functions at 22 °C. (b) Dynamic correlation length from the fast mode of all solutions vs. Tc–T in a double-logarithmic representation, where Tc is the critical temperature. Same symbols as in (a). The lines have a slope of −0.63. | ||
To summarize, PNIPAM in water/methanol was investigated in a large range of PNIPAM concentrations and in a large range of solvent compositions. Methods addressing different aspects have been used: Various spectroscopies (NMR, Raman, BDS and NSE) and DLS gave information about the segment dynamics of PNIPAM in presence of the two solvents, QENS elucidates the fraction and dynamics of the hydration water and the cosolvent, while DSC allowed quantifying the energetics of the transition. The picture that emerges is that the cosolvent methanol is present near the chain and perturbs the hydration water shell. At larger length scales, the cosolvent has a strong effect, which points to an alteration of the interchain interaction.
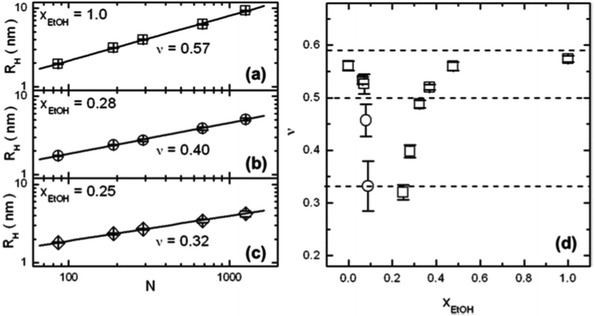 | ||
| Fig. 5 Results from FCS on extremely dilute PNIPAM solutions (10−9 M) in water/ethanol mixtures.51 (a–c) Double-logarithmic representations of the hydrodynamic radii RH of single PNIPAM chains as a function of the degree of polymerization, N, at molar fractions of ethanol, xEtOH of (a) 1.0, (b) 0.28 and (c) 0.25. Solid lines are linear fits. The fitted values of the Flory exponent ν are displayed. (d) The resulting ν values as a function of xEtOH. The three dashed lines denote the theoretical values of the static scaling index for a random coil (0.588), an undisturbed coil (0.5), and a compact globule (1/3). Copyright 2012. Reproduced with permission from The American Chemical Society. | ||
A dilute solution of PNIPAM in a series of mixtures of D2O and deuterated ethanol (d-ethanol) was investigated by Hore and Hammouda in dependence on temperature using small-angle neutron scattering.52 In this system, lower critical solution temperature (LCST) behavior is encountered at low d-ethanol fractions, a miscibility gap at intermediate compositions, and upper critical solution temperature (UCST) behavior at high d-ethanol fraction. Using the random phase approximation model and assuming an excluded volume chain conformation, the Flory–Huggins interaction parameters between the three components could be deduced from the shape of the scattering curves. It emerges that, for D2O fractions up to 40 vol%, interactions between PNIPAM and d-ethanol are favored over those between PNIPAM and D2O and between D2O and d-ethanol. The non-linear composition dependences of the interaction parameters led the authors to speculate that a competition between the formation of D2O/d-ethanol complexes and the solvation of the PNIPAM chains is at play and that the former may dominate in the intermediate composition range.
Analogs of PNIPAM were investigated with respect to the structure of the entire polymer (linear PNIPAM vs. 4-arm PNIPAM stars), the nature of the side groups (linear poly(N-n-propylacrylamide) vs. PNIPAM) and the hydrophobicity of the terminal groups.45 As solvent, mixtures of water and propanol were chosen. The critical solution temperature was found to be affected by the size and shape of the hydrophobic region of both the solvent and n-alkyl acrylamide monomer.
Poly(N-vinylcaprolactam) (PVCL) was reported by Kirsh et al. to feature peculiar behavior in different alcohols.20,21 Upon addition of methanol to aqueous PVCL solutions, the cloud point increases weakly up to a volume fraction of methanol of 40% and steeply above. The addition of ethanol, iso- or n-propanol or tert-propanol lowers the cloud point up to 10–20 mol% of the respective alcohol, while the cloud point increases sharply to >60–80 °C at higher mole fractions.
Complex behavior was found by Su et al. in poly[N-(4-vinylbenzyl)-N,N-diethylamine]: while it shows UCST behavior in pure isopropanol, it features a LCST transition in isopropanol/water mixtures having water contents higher than 15 wt%.43 In the latter mixtures, the cloud point decreases with increasing water content.
Pooch et al. investigated various poly(2-oxazoline) homopolymers in water/methanol mixtures (Fig. 6(a)).22 In water/methanol mixtures, a depression of the cloud point temperature was observed for poly(n-propyl-2-oxazoline) (PnPOx), which is most pronounced at a methanol content of 35 vol%, but this was not observed for poly(2-isopropyl-2-oxazoline) (PiPOx) or poly(2-cyclopropyl-2-oxazoline) (PcyPOx, Fig. 6(b)). By means of high-resolution 1H NMR spectroscopy, the bond rotations depicted in Fig. 6(c) were characterized. From the endotherms observed in calorimetric experiments at the cloud points (Fig. 6(d)–(f)) and by comparing them to the ones in the corresponding PNIPAM solutions, the authors identified a sharp and symmetric shape of the endotherm as a characteristic of a cooperative transition. By comparing the behavior of poly(n-propyl-2-oxazoline), that features cononsolvency, with the ones of of poly(2-isopropyl-2-oxazoline) or poly(2-cyclopropyl-2-oxazoline), which do not show a cononsolvency effect, they identified the extent of rotational freedom of the side group as a controlling factor determining the occurrence of cononsolvency by affecting the entropy/enthalpy balance. This aspect has so far not been considered in theoretical approaches.
 | ||
| Fig. 6 Behavior of various poly(2-oxazoline)s in water/methanol mixture.22 (a) Chemical structures of the polymers investigated. (b) Cloud points of the different polymers in water/methanol mixtures as a function of MeOH volume fraction, as determined using turbidimetry. Same colors as in (a). (c) Three-dimensional representation of one PcyPOx repeating unit. The slowly rotating bonds CO–N (α) and C–CO (β) are indicated. (d–f) Thermograms of (d) PnPOx, (e) PiPOx, and (f) PcyPOx in aqueous methanol solutions for the methanol volume fractions given. Copyright 2019. Reproduced with permission from The American Chemical Society. | ||
The thermoresponsiveness of the random copolymer poly(N-acryloylpiperidine-random-N-acryloylpyrrolidine) was investigated by Lucht et al. in mixtures of water with different mono- and bivalent alcohols.44 Depending on the nature of the alcohol, the cloud point is shifted upwards or downwards. The results were discussed in terms of polymer–additive as well as additive–water interactions: Hydrophobic interactions between the polymer and the hydrophobic part of ethanol and the resulting overall hydrophilic appearance of the polymer–ethanol complexes were suggested to be responsible for the increase of the cloud point. The authors speculated that the formation of hydrogen bonds with the OH-groups of the alcohols may result in an overall hydrophilic appearance, for instance for bivalent alcohols.
To summarize, these experiments gave valuable and detailed insight into molecular aspects like the composition of the solvation shell, the arrangement of the two solvents on the chain, their way of binding and their dynamics, the composition of the bulk solvent mixture, the role of the chemical nature of the segment and the energetics of the transition in solvent mixtures as well as on the dynamics of the chain and its segments in the solvent mixtures. Moreover, not only the solvent molecules being in direct contact with the polymer may play a role, but also those in the second and third solvation shells. These aspects have to be studied in atomistic simulations, which, to date, are limited to single, short chains. For most experimental methods, however, a certain polymer concentration is necessary to obtain sufficient signal.
Single-molecule experiments with atomic force microscopy or optical tweezers might fill this gap, such as those carried out by Kutnyanszky et al.91 and Kolberg et al.92 In the latter study, the force-extension behavior of single PNIPAM and poly(ethylene glycol) chains in aqueous environment was studied with AFM and molecular dynamics (MD) simulations, and the relation between hydration interactions and temperature-dependent effects was determined from the corresponding force-extension curves.92 Possibly, such experiments can in the future be used to provide information on the interactions of water and cosolvents with the polymer and the resulting chain conformation. Such results could be linked to simulations.
Further insight on the composition of the solvation shell as well as the dynamics and the interactions between the components may be gained from modern spectroscopy methods. For instance, ultrafast optical Kerr-effect spectroscopy allows characterizing the water dynamics in the solvation shell.93 A combination of Raman spectroscopy and Multivariate Curve resolution (MCR) techniques have been utilized to study the structure of the solvation shell and its dependence on perturbations such as addition of cosolutes and conformation change.94–96
2.2 Theory and simulations
Theoretical and simulation studies on cononsolvency have predominantly focused on the coil-to-globule transitions of short single polymer chains in water/alcohol mixtures.23,26,27,60,63–66,68,69 Understanding these single chain transitions can provide insights on the experimental results from bulk systems, as it has been shown that the transition temperatures of the coil-to-globule transition of linear PNIPAM chains or the volume phase transition of PNIPAM microgels coincide with the phase transition temperature in water/alcohol mixtures in the regime of low alcohol content.2,97 Additionally, the results from these simulations can be linked to observations from experiments on single molecules (atomic force microscopy) and dilute polymer solutions, as discussed in the previous section. An important point which has emerged from the experimental studies (see Section 2.1.1) is that alcohol molecules accumulate near the chain and significantly alter the local environment of the polymer. In agreement with these experimental findings, simulations studies have also shown that the cononsolvency behavior with amphiphilic cosolvents, such as alcohols and acetone, is accompanied by the preferential adsorption of the cosolvent.23,26,27,63,64,68 Although different mechanisms have been proposed to explain the cononsolvency phenomenon, its molecular origin remains incompletely understood.Before discussing the different mechanisms, it is important to understand the thermodynamic relations between polymer collapse and the preferential adsorption of the cosolvent. Aqueous solutions of polymers such as PNIPAM and poly(N,N-diethylacrylamide) (PDEAM) exhibit a LCST type phase transition which is experimentally observed to be first order (two state coil–globule equilibrium).98–102 Note that simulation studies, with short polymer chains, have shown that the coil-to-globule transitions in these systems also exhibit a two-state behavior.103–105 Given this two-state behavior, one can consider coil (C) and globule (G) chains as two distinct species which are in equilibrium,
| C ⇌ G | (1) |
| ΔμC→G2 = μG2 − μC2 | (2) |
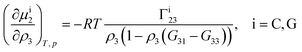 | (3) |
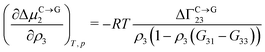 | (4) |
Note that Γi23 quantifies the effective polymer–cosolvent (relative to polymer–solvent) thermodynamic affinity but does not provide any information about the underlying intermolecular interactions involved. Although most of the proposed mechanisms satisfy the aforementioned thermodynamic necessities, they make different assumptions on the intermolecular interactions responsible for cononsolvency and preferential cosolvent adsorption. The different mechanisms will be discussed in detail in the forthcoming sections.
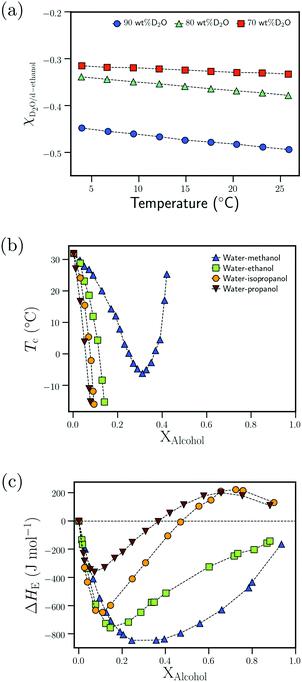 | ||
| Fig. 8 Attractive interactions in the bulk solvent–cosolvent mixture: (a) dependence of the Flory–Huggins interaction parameter, χD2O–d-ethanol, on the temperature for different D2O wt% from ref. 111 (b) Dependence of the cloud point temperature, Tc, on the alcohol molar fraction, XAlcohol, for different PNIPAM/water/alcohol mixtures from ref. 97 (c) Dependence of the excess enthalpy of mixing, ΔHE, on the alcohol molar fraction, XAlcohol, for different water/alcohol mixtures as measured at 25 °C from ref. 112 Data in (a) has been reprinted (adapted) from ref. 111 Copyright 2016. Reproduced with permission from The American Chemical Society. Data in (c) has been reprinted (adapted) from ref. 112 Copyright 1965. Reproduced with permission from The American Chemical Society. | ||
Based on the correlation between the concentration dependence of the LCST (in PNIPAM/water/alcohol mixtures) and the enthalpy of mixing in water/alcohol solutions (see Fig. 8(b) and (c)), Bischofberger et al. proposed that adding small amounts of alcohol to a solution of a thermoresponsive polymer in neat water leads to strengthening of the attractive energetic interactions in the bulk water/cosolvent mixture. This, in turn, would increase the solvation free energy of the polymer chain, thereby causing it to collapse.70,97 The cononsolvency behavior was then hypothesized to be dependent on the interplay between the attractive polymer–(co)solvent interactions in the solvation shell and the attractive energetic interactions in the bulk solvent/cosolvent mixture where the former favors the coil state and the latter the globule state.77 Based on this mechanism, it was hypothesized that PDEAM, due to its larger solvent accessible surface area (SASA), has stronger attractive interactions with the solvent/cosolvent mixture compared to PNIPAM, which overcompensates the enhanced attractive interactions in the bulk solvent/cosolvent mixture due to the addition of methanol. This might be the reason for the absence of cononsolvency in PDEAM/water/methanol systems.77
Although these mechanisms were able to rationalize the coil–globule–coil transitions with the addition of alcohols, they could not explain the preferential adsorption of alcohol molecules. In the FH mean-field theory, the cosolvent-induced polymer collapse leads to an increase in the solvation free energy (and chemical potential) of the polymer. From eqn (3), it can be seen that such a trend corresponds to the depletion of the cosolvent. This was observed in simulations involving a Lennard-Jones (LJ) polymer in an associating LJ solvent–cosolvent mixture.113 However, cononsolvency in alcohol/water mixtures is accompanied by preferential adsorption of the cosolvent which indicates that this mechanism may not be applicable in such systems.
Mukherji and Kremer performed atomistic simulations on PNIPAM/water/methanol solutions where, in agreement with experiments, they observed that the polymer size (radius of gyration, Rg) undergoes coil–globule–coil transitions with the progressive addition of methanol (see Fig. 9(a)).26 Further, through simulations of a NIPAM monomer in water/methanol solutions, they observed that the monomer-methanol Kirkwood–Buff integral is larger than the monomer-water Kirkwood–Buff integral, indicating a preferential accumulation of methanol around NIPAM. Based on these two observations, Mukherji and Kremer hypothesized that, at low methanol concentrations, the collapse of PNIPAM was driven by the formation of PNIPAM–methanol bridging interactions as shown in Fig. 9(a).
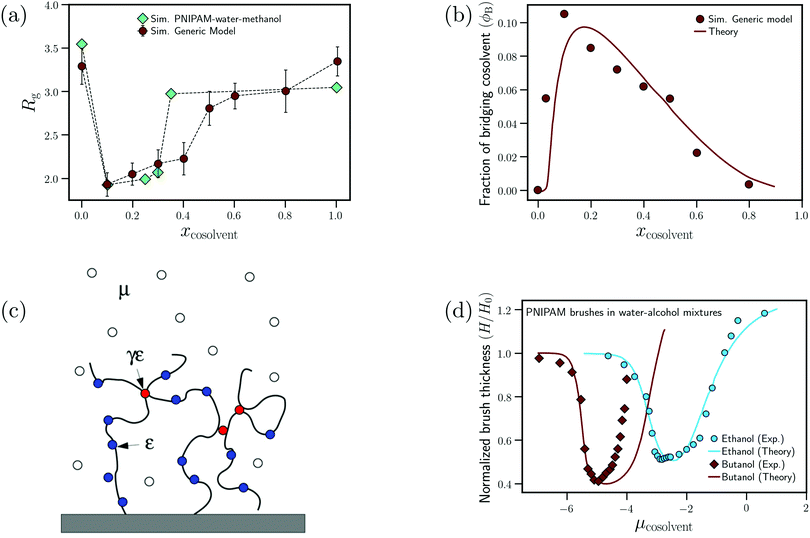 | ||
| Fig. 9 Enthalpic bridging: (a) dependence of the radius of gyration on the cosolvent mole fraction for the generic model proposed by Mukherji et al.60 and PNIPAM in water/methanol mixtures from ref. 26 and (b) dependence of the fraction of bridging cosolvent on the cosolvent mole fraction for the generic polymer model and the theoretical model from ref. 60. (c) Schematic showing the preferential adsorption and bridging aspects of the adsorption–attraction model from ref. 71. (d) Dependence of the normalized polymer brush height on the cosolvent chemical potential (increase in μcosolvent leads to increase in cosolvent concentration) for water/ethanol and water/butanol solutions from experiments and the adsorption–attraction model. The points represent the experimental data and the solid lines the theoretical fits.73 Data in (c) has been reprinted (adapted) from ref. 71 Copyright 2017. Reproduced with permission from The American Chemical Society. Data in (d) has been reprinted (adapted) from ref. 73 Copyright 2019. Reproduced with permission from The American Chemical Society. | ||
On the basis of these observations, Mukherji et al.60 studied the properties of a generic bead-spring polymer model in a Lennard-Jones solvent–cosolvent mixture. Based on the aforementioned assumption of polymer–cosolvent bridging interactions, only the monomer–cosolvent pair interaction was attractive and all other pair interactions (monomer–monomer, water–water, cosolvent–water and monomer–water) were strictly repulsive. In this model system, at low concentration, the cosolvent molecules preferentially adsorb on the polymer chain and bind distant monomers, via cosolvent bridging interactions, to induce polymer collapse (see Fig. 9(a)). On the other hand, at high concentration, there is a reduction in these bridging interactions due to large number of adsorbed cosolvent molecules which in turn leads to polymer swelling. In addition, they also proposed a simple theoretical model which predicted the fraction of bridging cosolvent particles.60 They then observed that the non-monotonic dependence (increase followed by decrease) of the fraction of bridging cosolvent on the cosolvent concentration predicted by the theory matches with the calculations from their generic model (see Fig. 9(b)). This bridging model has been employed alongside experiments to explain the effect of temperature and ethanol volume fraction on the phase diagram of PNIPAM-based microgels.114
On the theoretical front, models based on the statistical field theory of a dilute polymer (implicit solvent and explicit cosolvent)78 and random phase approximation115 showed that cononsolvency could be observed in two different regimes. The first regime involves a strongly interacting solvent–cosolvent mixture. Note that in an implicit solvent model, this would correspond to a repulsive polymer–cosolvent interaction.78 The mechanism here is similar to the one discussed in Section 8. The other regime involves strong polymer–cosolvent attractive interaction, where polymer collapse is induced by monomer–cosolvent bridging interactions.78 Budkov et al. further extended their statistical field theory to an explicit solvent–cosolvent mixture where, similar to model of Mukherji et al., the polymer–cosolvent attraction is dominant.116 Here they observed that the system exhibited cononsolvency and preferential adsorption, such that the extent of both increased with increase in the polymer–cosolvent attraction strength.116
Sommer71 proposed a theoretical framework which was able to capture the correlation between the polymer conformation and preferential adsorption of the cosolvent for systems, where polymer collapse is driven by polymer–cosolvent bridging interactions. The adsorption–attraction (AA) model proposed by Sommer71,72 combined the Alexander-de Gennes approach for polymer brushes and the polymer–cosolvent bridging interactions to understand the cononsolvency phenomenon for polymer brushes in mixed solvent solutions. The central assumption in the model was that a cosolvent molecule can be shared by two or more monomers which, because of the attractive monomer-cosolvent interaction, decreased the free energy of the total system and favored chain collapse at low cosolvent concentrations (see Fig. 9(c)). In his model, the contribution from the ![[m with combining low line]](https://www.rsc.org/images/entities/char_006d_0332.gif) onomer–
onomer–![[c with combining low line]](https://www.rsc.org/images/entities/char_0063_0332.gif) osolvent attractive interactions to the free energy is the following71
osolvent attractive interactions to the free energy is the following71
| fmc = −εmcϕ − 2γmcεmcϕ(1 − ϕ) | (5) |
In all the studies, the extended AA model assumes that the PNIPAM/alcohol combination has the ability to engage in enthalpic bridging interactions, γnipam–alcohol = 1. This assumption is based on the simulation studies of Mukherji and co-workers.26,47,60 However, this concept of PNIPAM–methanol bridging interactions is a poorly justified part of these models. Note that there are well-characterized systems in which bridging interactions have been observed. These include PNIPAM in urea/water mixtures and elastin-like polypeptides (ELPs) in water with guanidinium salts,30,34,41 where bivalent hydrogen bonding or electrostatic interactions energetically stabilize monomer–monomer contacts bridged by urea molecules or cation–anion pairs. Such type of bridging interactions has however not been observed for amphiphilic cosolvents such as alcohols. MD simulations have in fact shown that the effective NIPAM (monomer)–methanol attraction (i.e. the NIPAM–methanol potential of mean force) increases as a function of the temperature,47 indicating that it originates from entropic effects presumably related to hydrohobic interactions of methanol with the amphiphilic polymer chain.119 If, instead, PNIPAM–methanol hydrogen bonds or enthalpic bridging interactions would dominate the binding of methanol to the chain, an increase in temperature would lead to a decrease in methanol binding, contrary to what has been observed. Additionally, MD simulations on PNIPAM/water/methanol solutions by Dalgicdir et al.65,66 showed that, at low methanol concentrations, the polymer–methanol attractive interactions favored polymer swelling, which pointed to the absence of bridging interactions. Based on MD simulations of collapsed PNIPAM chains in water and in methanol/water solutions, Rodríguez-Ropero et al. showed that the configurational entropy, related to conformational fluctuations of the collapsed chain, is larger for collapsed chains in a solution with 10% methanol than in pure water.27 These authors also observed that the osmotic compressibility of collapsed chains in the solution with 10% methanol exceeds the corresponding compressibility in pure water, suggesting that hydrogen bonding and van der Waals interactions within the interior of globular chains become weaker when methanol is added to the solution.
 | ||
| Fig. 10 Cosolvent-induced geometric frustration: dependence of the (a) change in the PNIPAM–water interaction energy upon polymer collapse, ΔUC→Gpw, and (b) change in the PNIPAM–methanol interaction energy upon polymer collapse, ΔUC→Gpm, on the methanol mole fraction, XMeOH, from the atomistic simulations of Dalgicdir et al.65 Dependence of the (c) number of PNIPAM–water hydrogen bonds and (d) PNIPAM–ethanol hydrogen bonds on the temperature at XEtOH = 0.07 (mole fraction) from the simulations of Tavagnacco et al.68 Data in (a) and (b) has been reprinted (adapted) from ref. 65 Copyright 2017. Reproduced with permission from The American Chemical Society. Data in (c) and (d) has been reprinted from ref. 68 Copyright (2020), with permission from Elsevier. | ||
Interestingly, cosolvent-induced frustration of polymer–water interactions has also been shown to play a major role in the aggregation behavior of thermoresponsive core–shell micelles in water/alcohol mixtures. Using a combination of time-resolved small angle neutron scattering and the reversible association model, Kyriakos et al.58 studied the aggregation of thermoresponsive core–shell micelles with a PNIPAM shell in different water/alcohol mixtures. From the growth rate of the aggregates above the cloud point temperature, they obtained the effective interaction potential between aggregates, consisting of collapsed micelles, and observed that the aggregation tendency is higher in the presence of alcohols. Here, they hypothesised that the repulsion between the aggregates at short distances was due to the layers of structured water in the hydration shell of these aggregates. In water/alcohol mixtures, the alcohol molecules adsorbed on these aggregates and perturbed the formation of structured water layers in the hydration shell (see Fig. 16 in Section 3.3). This, in turn, diminished the repulsion between these micellar aggregates. They also pointed out that the attraction between aggregates may also occur due to the presence of alcohol mediated bridging interactions. However, this effect was expected to be weak, as a larger concentration of alcohol molecules would be needed to render bridging significant.
Dalgicdir et al. also calculated the potential of mean force (PMF) between two isolated NIPAM monomers at different methanol concentrations in water.65 This calculation provided information on changes in the solvent-mediated monomer–monomer attraction due to the change in solvent/cosolvent composition. It was observed that the depth of the first minimum in the PMF, corresponding to the contact interaction of the two monomers, monotonically decreased (i.e. became more shallow) as a function of the methanol concentration. Hence, the effective monomer–monomer interaction became weaker as methanol was introduced, indicating that the cononsolvency effect of PNIPAM cannot be rationalized at the individual monomer level. Based on these observations, Dalgicdir et al. concluded that cooperative solvation effects, related to the mechanism proposed by Okada and Tanaka,80 are important in understanding the cononsolvency phenomenon of PNIPAM in methanol/water solutions. In the cooperative hydration model, Okada and Tanaka proposed that water molecules form sequential hydrogen bonds (cooperative effects) with the polymer chain, i.e. the hydrogen bonding of a water molecule to an amide group of PNIPAM is facilitated by the water molecule hydrogen bonded to the neighbouring amide group. Tanaka et al. then hypothesised that the preferential adsorption of alcohol molecules blocked the formation of these cooperative PNIPAM–water hydrogen bond sequences and led to polymer collapse.81,82 Within the cooperative hydration model, the temperature-induced polymer collapse is accompanied by a sigmoidal decrease in the number of bound water molecules. Such trends were also seen in the simulation studies on both PNIPAM/water and PNIPAM/water/ethanol mixtures by Tavagnacco et al.68,120
The cosolvent-induced geometric frustration mechanism has only been studied in the context of aqueous alcohol solutions of PNIPAM, and its application to other systems such as PDEAM, which does not exhibit cononsolvency in water/methanol mixtures, is yet to be explored. Additionally, this model does not discuss the driving forces which lead to the preferential adsorption of the cosolvent. Polyvinylcaprolactam (PVCL) shows cononsolvency and preferential adsorption in water/2-propanol mixtures.121 Interestingly, the depth of the first minimum of the PMF between two vinylcaprolactam monomers exhibits a non-monotonic dependence, similar to cononsolvency, on the 2-propanol concentration, which indicates that cooperative effects may not play a dominant role for all polymer solutions.
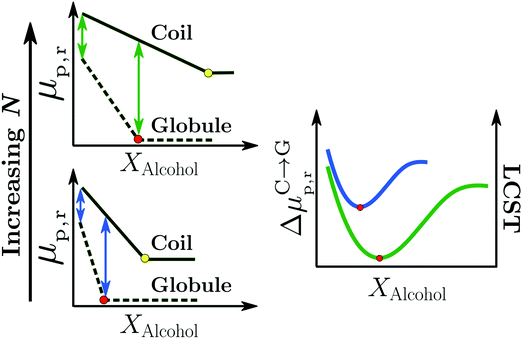 | ||
| Fig. 11 Surfactant mechanism: schematic illustration of the dependence of the free energy cost (μp,r) of creating a repulsive polymer–water/alcohol interface on the degree of polymerization N for the coil and globule states of the polymer (left panel). Amphiphilic cosolvents such as alcohols preferentially adsorb to both the coil and globule states, leading to a favorable decrease of μp,r as a function of the alcohol mole fraction, XAlcohol, in the bulk solution. This surfactant-type effect is analogous to the reduction of the air–water surface tension by alcohols and other amphiphilic organic compounds. The free energies (μp,r) decrease as a function of XAlcohol until the polymer surface is saturated with the cosolvent (indicated by red and yellow markers). The right panel shows the correlation between the LCST of PNIPAM/water/methanol solutions and the polymer collapse free energy, ΔμC→Gp,r, corresponding to the lengths of the arrows shown in the left panel, for short (blue) and long chains (green). The solvent accessible surface areas (SASA) of both the coil and globule states increase as a function of N due to which the alcohol concentration required to saturate them also increases. Note that μ(Coil)p,r − μ(Globule)p,r is an increasing function of N below the saturation point of the globule (the green arrows are longer than the blue arrows) because the SASA of the coil state (SASAC ∼ NαC) grows faster with N than that of the globule (SASAG ∼ NαG) state, αC > αG. These are the two aspects due to which the minimum in ΔμC→Gp,r, and thereby the minimum in the LCST, becomes deeper and shifts to higher alcohol concentration with increase in N, as observed experimentally.2,81 The data has been reproduced from ref. 63, licensed under a Creative Commons Attribution 4.0 International License. | ||
Bharadwaj et al. also showed that the surfactant-like effect was able to rationalize the effects of the cosolvent molecular size (methanol versus ethanol) and degree of polymerization, N, on the cononsolvency phenomenon.63 Specifically, they observed that the alcohol concentration Xc,min, corresponding to the minimum in ΔμC→Gp,r and LCST, was related to the concentration at which the solvation shell of the globule state is saturated by alcohol molecules (see red markers in the left panel of Fig. 11). Based on this observation, they proposed that higher alcohols would reduce Xc,min as the globule state could be saturated by the larger sized cosolvent molecules at relatively lower alcohol concentrations.63 This is in agreement with experimental LCST measurements which show that the minimum in the LCST, measured in PNIPAM/methanol/water solutions, shifts to lower cosolvent concentrations when higher alcohols such as ethanol and propanol are used to replace methanol.70 The cosolvent surfactant mechanism also explains the effect of N on the LCST in PNIPAM/water/methanol solutions.2,81 With increasing N, the collapse of the polymer chain leads to a larger reduction in the macromolecular surface area exposed to the solution. Correspondingly, the coil-to-globule transition will be driven by a larger gain in translational entropy leading to a deeper minimum in ΔμC→Gp,r and LCST for higher molecular weight chains (right panel in Fig. 11). Additionally, Xc,min will be shifted to higher alcohol concentrations because the macromolecular surface of the larger N globular chain requires more cosolvent molecules to reach saturation (see red markers in the Fig. 11). These predictions are in agreement with experimental results on PNIPAM/water/methanol mixtures, which show that the minimum in the LCST becomes deeper and shifts to higher alcohol concentrations with increase in PNIPAM molecular weight.2,81
Thus, the cosolvent surfactant-mechanism is able to rationalize the preferential adsorption and coil–globule–coil transitions in water/alcohol mixtures of acrylamide polymers. However, the ability of this model to explain the macroscopic phase separation in these systems is yet to be explored.
Another aspect which is yet to be studied is the coupling between the single chain coil-to-globule transition and the macroscopic bulk phase separation. Experimentally, it was observed that the LCST of PNIPAM decreases with the addition of alcohol at low alcohol concentration.2,70 In this concentration regime, the bulk phase separation brought on increase in the temperature beyond the LCST is accompanied by a coil-to-globule transition at the single chain level. This coupling between the bulk phase separation and the coil-to-globule transition at low methanol concentrations (xMeOH < 0.2) is also evident from the observation that the experimental trends in the transition enthalpy of PNIPAM in water/methanol solutions, from DSC measurements,46 are in agreement with the trends in the polymer collapse energies obtained from atomistic simulations of a single 40mer PNIPAM chain in water/methanol solutions.65,66 At high alcohol concentrations, the LCST increases with the addition of alcohol. However, in this regime, the bulk phase separation beyond the LCST is not accompanied by any coil-to-globule transition.2,70 Although atomistic single chain simulations show an increase in the polymer collapse energies with increasing methanol concentration (0.2< xMeOH < 0.6),65,66 such a trend is not observed in the transition enthalpy obtained from DSC measurements.46 In order to understand this coupling, one requires multi-scale models, which can predict the bulk phase behavior, while maintaining the effects from the molecular chemical details. Hybrid particle-field (HPF) simulations, which have been used to study a wide range of systems from binary liquid mixtures to polymer solutions, melts and biological phospholipids, in combination with atomistic simulations are ideal candidates for such problems.126–130 Additionally, these approaches may also be extended to simulate complex systems such as micelles, crosslinked gels and polymer brushes which will be discussed in Section 3.3.
3 Further developments
3.1 Effect of pressure on cononsolvency
Applying hydrostatic pressure changes the equilibrium state of a system to the one with the lowest overall volume, which alters the physical interactions. The phase behavior of ternary PNIPAM/water/cosolvent solutions in dependence on pressure was subject of several studies. As depicted in Fig. 12, the addition of a cosolvent (dimethyl sulfoxide, ethanol or methanol) shifts the maximum of the coexistence line in the pressure–temperature frame to higher pressures and temperatures.53,54,56 This implies that, at low pressures, the cloud point of PNIPAM in neat water is above the one of PNIPAM in water/methanol, while this behavior is reversed above the pressures where the coexistence lines overlap, i.e. the cononsolvency effect breaks down at high pressure. | ||
| Fig. 12 Temperature–pressure phase diagrams of poly(N-isopropylacrylamide) in water/DMSO (a) and water/methanol (b) at mole fractions of the cosolvent as indicated in the graph. (c) Chain solvation in the one-phase state in dependence on pressure, as determined using various methods.50,79,131,132 The data in (a) has been reprinted (adapted) from ref. 53 Copyright 2012. Reproduced with permission from The American Chemical Society. The data in (b) has been reprinted (adapted) from ref. 56 Copyright 2020. Reproduced with permission from The American Chemical Society. | ||
The experimental investigation of the origin of this behavior is still in its infancy, presumably due to the technological challenges regarding the design of high-pressure sample environments. Using small-angle X-ray scattering, it was found that, at high pressure, nanogels do not collapse at the volume phase transition temperature (VPTT), when methanol is present.55 Using Fourier-transform infrared spectroscopy (FTIR), this observation was related to the polymer–solvent interactions, namely the decrease of the fraction of methanol molecules attached to the carbonyl groups with increasing pressure, and thus an increase in their degree of hydration.
Small-angle neutron scattering on PNIPAM homopolymers in a mixture of water and methanol revealed that, in the one-phase region, the application of pressure leads to a contraction of the chains, indicating a weaker overall solvation of the chains.56 Relating the chain conformation to an effective Flory–Huggins interaction parameter between the polymer segments and the solvent mixture, it was found that local entropic effects, e.g. the hydrophobic effect, are significantly weakened at pressures above ∼150 MPa. Moreover, enthalpic polymer–solvent interactions are weakened at high pressure, pointing to a decrease in the amount of water molecules adsorbed at the chains.
Quasi-elastic neutron scattering elucidates the water dynamics. From the dynamic susceptibility spectra of a concentrated PNIPAM/water/methanol solution measured below the cloud point, it was found that, while at atmospheric pressure, methanol is preferentially adsorbed at the chains, nearly all methanol molecules are expelled from the chains at a pressure of 200 MPa.50 Complementary Raman spectroscopy experiments, specifically probing the hydrophobic groups of PNIPAM, indicate that, at atmospheric pressure, this replacement of water by methanol occurs at the hydrophobic groups. At high pressure, the overall solvent adsorption at the hydrophobic groups is weaker.
In large-scale molecular dynamics simulations, a change of chain conformation from a globular state at atmospheric pressure to an expanded chain conformation at 200 MPa was observed,131 and explained in terms of polymer–cosolvent bridging interactions (see Section 2.2.2): a decreased preferential presence of methanol in the solvation shell of PNIPAM was suggested to lead to the disruption of bridges, breaking down the cononsolvency effect.
Pica et al.132 explained the breakdown of the cononsolvency effect at high pressure in terms of cosolvent-induced geometric frustration, discussed in Section 2.2.3. At atmospheric pressure, the results indicate geometric frustrations caused by the competition between water and methanol to interact with the polymer. The chains cannot realize all attractive interactions that would be possible in pure water, leading to an overall reduction of the chain solvation, and, as a result, a collapsed conformation. The breakdown of the cononsolvency effect at high pressure was shown to result from (i) the reduction of the water-accessible surface area, which makes the chain collapse less favorable, and (ii) the trend towards replacement of methanol by water on the chains to enable a more efficient packing of solvent molecules around the chains. Thus, geometric frustrations are reduced at high pressure, because the competition between water and methanol on the chains is weakened.
The chain conformation of a polymer dissolved in a binary solvent mixture was determined using self-consistent field theory, taking only van der Waals and excluded volume interactions into account.79 Whereas at low pressure, the radius of gyration decreases with increasing mole fraction of the cosolvent, it stays constant at high pressure. Thus, excluded volume effects dominate over attractive interactions due to the increased density of the system at high pressure. Moreover, it was suggested, that the preferential adsorption of methanol at the chains observed at atmospheric pressure is lost at high pressure.
To conclude, a fairly consistent picture of the driving forces behind the breakdown of cononsolvency at high pressure emerges. Whereas the preferential adsorption of the organic cosolvent leads to a reduction of the overall chain solvation at atmospheric pressure, the loss of preferential cosolvent adsorption at high pressure enhances the chain solvation by two effects: firstly, the competition between the two solvents is reduced, which allows for more enthalpic interactions between the solvent molecules and the chain. Secondly, the solvent phase is enriched with the organic solvent, which weakens the hydrophobic effect driving the coil-to-globule transition.50 However, further experiments and especially theoretical work have to be carried out to substantiate these findings. At this, predictions on experimentally accessible parameters should be provided. Additionally, it emerges that the packing of solvent molecules is altered by pressure, and the focus of both theoretical and experimental work should, therefore, shift to the until now often overlooked volumetric properties of ternary polymer/water/cosolvent systems.
3.2 Cononsolvency in aqueous polypeptide solutions
Besides synthetic polymers, also polypeptides are a class of macromolecules, that may feature temperature responsiveness. In contrast to polymers, polypeptides have a complex local primary structure, i.e. the type and sequence of amino acids on the chain, and these control the phase behavior in solution.133 As a result, highly ordered secondary structures accompanying the phase transitions may be present.134 Only very recently, it was shown, that also certain polypeptides are susceptible to the cononsolvency effect (Fig. 13).3,135 It is expected that, in these systems, the local primary structure determines the solvent affinity of that particular segment. The sensitivity of different amino acids to water/alcohol mixtures may lead to changes in the secondary structure, which influences the phase behavior of the system.136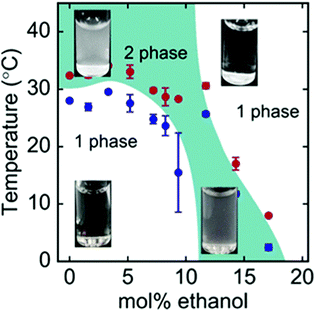 | ||
| Fig. 13 Phase diagram of the ternary ELP/water/ethanol system as determined using turbidimetry during cooling scans (blue symbols) and heating scans (red symbols).3 The images show the visual appearance of the solution at different temperatures and mol% of ethanol, which is turbid in the two-phase state and transparent in the one-phase state. The figure has been reprinted (adapted) from ref. 3 Copyright 2019. Reproduced with permission from The American Chemical Society. | ||
Polypeptides act as model systems for complex proteins,137 and allow to study the isolated effect of certain repeat unit sequences. In contrast to polymers, they are inherently biodegradable,134 and can be employed as building blocks for the formation of complex nanostructures, as they can adopt well-defined anisotropic chain conformations.138 The research on the effect of cosolvents, and cononsolvency specifically, in solutions of polypeptides is important for various reasons. For example, in biological systems, small organic molecules acting as cosolvents can alter the folding/unfolding equilibrium of proteins.139 Cononsolvency may be employed in separation processes based on selective precipitation,11,12 as not all macromolecules are subject to this effect. In addition, the effect can be employed to induce the self-assembly of nanostructures composed of biomacromolecules, similar to synthetic thermo-responsive polymers.13
A deeper understanding of the driving forces for cononsolvency in solutions of polypeptides was given by Zhao et al.140 Using molecular dynamics simulations, the interaction between cosolvents and ELPs was investigated. It was found, that ethanol preferentially binds with all peptide residues, leading to a strong cononsolvency effect. In the case of urea, however, the cononsolvency effect is much weaker. This was ascribed to weaker interactions of the cosolvent with especially glycine residues, which confirms that the local primary structure determines the solvent affinity.
Comprehensive experimental studies on the occurrence of the cononsolvency effect in aqueous solutions of polypeptides as well as in-depth studies aiming to elucidate the underlying mechanisms, are lacking. A better understanding of the phase behavior, interactions and structural properties of ternary polypeptide/water/alcohol systems will provide an important step forward in designing polypeptides for nanostructure formation, developing strategies for protein separation processes, and the understanding of the phase behavior of proteins in cells.
3.3 Complex systems
Besides linear chains of homopolymers, more complex systems have been investigated regarding their cononsolvency behavior such as cross-linked gels,29,55,114,141–146 block copolymer systems,13,57,58,147–149 thin films,59,150 and grafted polymer brushes.10,14,15,17,73,151,152 Microgels are macromolecular networks swollen by the solvent they are dissolved in. The size of the microgels networks is in the range of several micrometers down to nanometers (then sometimes called “nanogels”). They combine properties of flexible macromolecules, gels and particles:153 In the collapsed state, they may resemble hard colloids, but can still contain significant amounts of solvent. When swollen, they are soft, their interior is characterised by the mesh size of the network, and the surface is fuzzy with dangling chains. Structural integrity is provided by cross-links, and the degree of cross-linking determines the macromolecule-to-particle transition. Microgels can be synthesised such that they are colloidally stable even in the collapsed state, which is relevant for applications as, for instance, in catalysis.8,154 Furthermore, they allow probing the collapsed state in solvent mixtures without disturbances caused by aggregation/flocculation.57,90,155 Scattering methods have been used to determine the size and structure of microgels as a function of the solvent composition. It was found that the composition range, in which cononsolvency occurs, is almost independent of the cross-linking density of the PNIPAM gels.2 Furthermore, the influence of temperature on the cononsolvency behavior of PNIPAM microgels and the temperature-dependent swelling behavior in various water–alcohol mixtures were investigated by DLS.114,141 A decrease of the VPTT was found with increasing fraction of alcohol, until the behavior is temperature independent in alcohol-rich mixtures. Backes et al.114 combined DLS measurements of PNIPAM microgels and molecular simulations of linear chains. They concluded that, at T < VPTT, preferential binding of ethanol and the collective formation of ethanol bridges cause the collapse of the polymer network. In the temperature-dependent measurements, an unexpected reswelling of the PNIPAM microgels at higher temperature (T > 50 °C) in water–alcohol mixtures with intermediate alcohol volume fractions (e.g. 40 vol% MeOH, EtOH or iPrOH) was observed. They rationalized the reswelling at high temperatures by the addition of a good solvent (alcohol) to a poor solvent (water) for the polymer. Additionally, the effect of pressure on cononsolvency of PNIPAM nanogels was investigated using small-angle X-ray scattering (SAXS) and FTIR as described in Section 3.1.55Cononsolvency and the above-mentioned preferential adsorption of one of the solvents can lead to a different solvent composition inside the macromolecule as compared to the surrounding solvent mixture. Here, the rather well-defined size and shape of micro- and macrogels allows probing a local solvent composition, as it is easier to distinguish between “inside” and “outside” than for linear polymers. Various spectroscopic techniques were applied to quantify the solvent composition as well as to gain insights on local molecular interactions. Several studies have addressed that issue for the case of PNIPAM in binary water–alcohol mixtures, where a preferential adsorption of alcohol by strong interactions with the PNIPAM chain in the collapsed region was suggested.47,87–89,156
While Maeda et al.157 reported on the preferential adsorption of isopropanol to linear PNIPAM chains in water–isopropanol mixtures, the case of polymer gels provides the opportunity to distinguish between inside of the polymer and the polymer-free surroundings. For macroscopic PNIPAM gels in water–alcohol mixtures, evaluation of solvent partitioning in the ternary system was carried out by determining the composition of the surrounding and applying a mass balance to calculate the solvent composition inside the gels (Fig. 14).87,89,156 Raman microspectroscopy was applied to measure the Raman spectrum of the surrounding solvent mixture next to the macrogel.89 By spectral analysis using indirect hard modeling, the methanol fraction could be quantified. Combined with a mass balance, an enrichment of the alcohol was found. The extent of the accumulation is influenced by the hydrophobicity of the alcohol species. For example, a higher preferential adsorption was found for ethanol compared to methanol.87,89,156
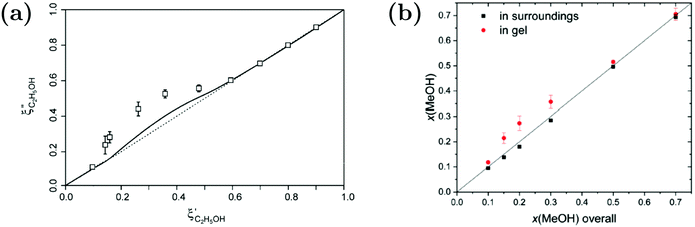 | ||
Fig. 14 Comparison of the solvent composition inside the gel vs. outside the gel. (a) Experimental results and predictions for the partitioning of ethanol between the poly N-isopropyl acrylamide hydrogel phase 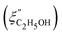 and the surrounding coexisting aqueous solutions of ethanol and the surrounding coexisting aqueous solutions of ethanol 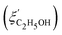 at 298 K. Experimental results (squares); predictions (line).87 (b) Experimental results for poly N-isopropyl acrylamide hydrogel in water–methanol.89 In both cases, the alcohol is enriched in the gel phase in the concentration range where the presence of alcohol results in a shrinking of the gel. (a) has been reprinted from ref. 87 Copyright (2004), with permission from Elsevier. (b) is reproduced from ref. 89. at 298 K. Experimental results (squares); predictions (line).87 (b) Experimental results for poly N-isopropyl acrylamide hydrogel in water–methanol.89 In both cases, the alcohol is enriched in the gel phase in the concentration range where the presence of alcohol results in a shrinking of the gel. (a) has been reprinted from ref. 87 Copyright (2004), with permission from Elsevier. (b) is reproduced from ref. 89. | ||
Further Raman measurements inside the PNIPAM gels additionally revealed insights into the molecular interactions, as the positions of certain methanol bands depend on the hydrogen bonding environment. Furthermore, variable-temperature 1H MAS NMR spectroscopy was applied to study preferential interactions of solvents with PNIPAM microgels.88 Here, the ternary systems of PNIPAM in water–methanol or in water–ethanol mixtures with 2.5 or 5 mol% alcohol were investigated. The coil-to-globule transition upon heating was observed as a sudden decrease in the intensity of the 1H resonance of PNIPAM. Peak splitting of the HOD signal and the methyl signal of the alcohol allowed the distinction between free solvent and confined solvent molecules bound inside the gel. Quantitative analysis of the peak splitting revealed a preferential adsorption of alcohol molecules within the collapsed polymer network.
Not only investigations of PNIPAM in water–alcohol mixtures, but also in mixtures of water and other organic solvents, such as N,N-dimethylformamide (DMF), acetone and dimethyl sulfoxide (DMSO), have been conducted.87,143,145,158 Zhu et al.145 described the cononsolvency of PNIPAM microgels in water–DMF mixtures. DLS measurements confirmed the typical dependence of the hydrodynamic radius on the DMF mole fraction for various temperatures. The cononsolvency effect was rationalized by the preferential adsorption and additional bridging of the DMF molecules in combination with mean-field approaches. Wang et al.143 discussed the necessity of preferential adsorption for cononsolvency by studying PNIPAM gels in water–acetone and water–DMSO mixtures at high water contents using NMR spectroscopy. Both cosolvents comprise the same hydrophobic group, and both water–cosolvent mixtures induce the cononsolvency effect of the PNIPAM gels. For both, the peak splitting in the 1H MAS (Magic Angle Spinning) NMR spectra above the VPTT and NOE (Nuclear Overhauser Effect) data below the VPTT were evaluated. In the case of acetone, more confined, thereby strongly adsorbed, acetone species were found similar to the results previously described for water–alcohol mixtures.88,143 In contrast, no preferential adsorption of DMSO was observed. Preferential adsorption of acetone and preferential exclusion of DMSO had also previously been reported.87,158 Thus, preferential adsorption is not a prerequisite for cononsolvency. This conclusion is in accordance with theoretical studies (see Section 2.2.1).113
Besides PNIPAM microgels, the cononsolvency of other polymer gels, e.g. comprising PDEAM, has been reported.29,142,155 In contrast to PNIPAM, PDEAM does not exhibit a cononsolvency effect in water–methanol and water–ethanol mixtures. The dependence on the solvent composition and temperature of PNIPAM, bearing a secondary amide group, was compared to PDEAM, which is a tertiary amide. For both systems, the phase transition broadens with increasing methanol fraction, until no more thermoresponsive behavior is observed. In case of PDEAM, this change of behavior occurs already at lower mole fractions than in case of PNIPAM. This suggests that methanol has a higher affinity towards PDEAM and is a better solvent compared to water. The transition temperatures in various water–methanol mixtures up to xMeOH = 0.25 were determined using DLS and DSC. The transition temperature drastically decreased with the methanol fraction in case of PNIPAM, which was explained by the exchange of polymer–solvent interactions by intra- and inter-molecular polymer–polymer hydrogen bonds. In case of PDEAM microgels, a slight increase of the transition temperature or an unchanged transition temperature were observed. As the monomer units only contain an H-bond acceptor function, no intramolecular hydrogen bonds can be formed, but hydrogen bonds with water are exchanged by hydrogen bonds with methanol.55 These findings stress the importance of the amide proton for the interactions with the solvents and thus the cononsolvency behavior.142 However, for alcohols with larger hydrophobic groups such as iso- or n-propanol, cononsolvency was also reported for PDEAM gels.29 Liu et al.29 pointed out the importance of the hydrophobicity of the alcohol and concluded that the amide proton is not the determining factor for the cononsolvency behavior. Note that atomistic simulations of PNIPAM in water/methanol mixtures have indicated that not the amide proton but instead the amide oxygen that plays a decisive role in the cononsolvency effect observed in this system (see Section 2.2.3).65–67 In line with the interpretation of Liu et al.,29 Bharadwaj et al. explained the cononsolvency in PDEAM solutions with higher alcohols based on the surfactant mechanism (see Section 2.2.4).63,64 Using variable-temperature 1H MAS NMR spectroscopy of PDEAM gels in mixtures with 2.5 or 5 mol% alcohol, Liu et al. reported an alcohol enrichment inside the high-temperature collapsed PDEAM network. As mentioned above, an increase in the hydrophobicity of the alcohol moiety also results in a higher enrichment of the alcohol inside the PDEAM gels.
The colloidal stability of microgels has been also exploited to study the kinetics of the collapse. While the collapse transition of large microgels and hydrogels can be detected in optical microscopy, the size evolution of small microgels can be detected by time-resolved small-angle scattering.
While the prominent theory of Tanaka and Fillmore159 suggests a rather simple behavior with the relaxation time (τ) scaling with the square of the final radius R2, the experimental studies concerning gels report very different types of behavior during the collapse transition, see e.g. references in Nothdurft et al.146 Recent studies used cononsolvency as a trigger for the collapse of small microgels and larger microgel beads and found two relaxation times.144,146 The first, fast process is responsible for the major part of the volume transition. During this transition, the microgel stays porous, and thus the process is not limited by the surface area, and the relaxation time τ is not proportional to R2. Computer simulations indicated that the collapse starts at the cross-links leading to a local collapse, while keeping the microgel porous (Fig. 15).144 In a second step, the collapsed regions form a dense shell at the surface of the microgel, which slows down further collapse. Recent experiments, employing much larger microgels and optical microscopy, confirmed the two-step process.146 Furthermore, a study by Wrede et al. on N-n-propylacrylamide microgels dissolved in water also reported a bi-exponential time dependence of the collapse transition in pressure jump experiments.160 Altogether, this indicates that the two-step collapse process of microgels is a generic feature.
 | ||
| Fig. 15 Results of mesoscale hydrodynamic simulations of the time-dependent structural evolution of a microgel. Snapshots illustrating the microgel structure at indicated times during the simulation: (left) 2D projection and (right) center slice. Adapted from ref. 144. | ||
Copolymers combine different repeating units within the polymer chain, leading to complex properties in solution. Cononsolvency effects have been studied with copolymers based on N,N-diethyl acrylamide (DEAM) and N-isopropyl acrylamide and with different compositions.25 Comparing results from various experimental techniques and quantum-chemical calculations revealed the relevance of the copolymer composition on the local solvation characteristics. Block copolymers from a hydrophobic and a thermoresponsive block often form core–shell micelles in aqueous solution. Below the cloud point of the shell-forming block, these are swollen, whereas above, the shell blocks collapse, and the micelles become hydrophobic and aggregate. Thus, the collapse of the shell and the subsequent aggregation cannot only be induced by raising the temperature above the cloud point, but also by addition of a cosolvent, exploiting cononsolvency. The pathway of aggregation upon addition of methanol to an aqueous micellar solution from PS-b-PNIPAM, where PS stands for polystyrene, was investigated using time-resolved small-angle neutron scattering along with a stopped-flow instrument.13 It was found that aggregates of a final size of only ∼50 nm form. While their growth initially followed diffusion-limited coalescence, in the late stage, the growth was slowed down by an energy barrier, having a height proportional to the aggregate radius. These stages were not observed in experiments on PNIPAM homopolymers, which formed very large aggregates within less than 0.1 s.13 In a later experiment, the effect of different cosolvents (methanol or ethanol) on the growth behavior of the same type of micellar solution was investigated after a rapid temperature change across the cloud point (Fig. 16(a)).58 After a certain time (0.5–40 s, depending on the cosolvent), aggregates started to form. Their growth rate increased from the solution in pure water over the one in water/methanol to the one in water/ethanol, i.e. with the molar volume of the solvent. The effect of the cosolvent was attributed to the interaction potential, which is related to the structured layer of hydration water around the aggregates (Fig. 16(b)). The latter may be perturbed by the cosolvent, which reduces the residual repulsive hydration force between the aggregates (Fig. 16(c)).
 | ||
| Fig. 16 Structural changes in micellar solutions of PS-b-PNIPAM diblock copolymers in water, water–methanol and water–ethanol mixtures (all solvents were fully deuterated) during a temperature jump across the cloud point from the one-phase to the two-phase region, as deduced from time-resolved SANS. Black squares: core radius rcore (fixed at the same value for all solvent mixtures during model fitting), reddish circles: micellar radius rmic, bluish diamonds: radius of gyration of large aggregates, ragg. Dark red and blue: pure water, medium red and blue: water/methanol, light red and blue: water/ethanol. The dashed lines mark the phase transition TCP. (b) Total interaction potential between two collapsed micelles in pure water, deduced from the behavior of ragg (full dark blue line), water/methanol (dashed medium blue line) and water/ethanol (dash-dotted light blue line). (c) Schematic drawing of the proposed model describing the final state. The collapsed core–shell micelles are depicted in black and brown, water molecules in blue and alcohol molecules in violet (not to scale). From.58 Copyright 2016. Reproduced with permission from Wiley-VCH Verlag. | ||
Diblock copolymers polyferrocenyldimethylsilane-b-poly(N-isopropylacrylamide) (PFS-b-PNIPAM) were found to form micelles in 2-propanol.147 Upon transfer of these micelles to water, extensive fragmentation of the micelles was observed, which was assigned to the loosely packed nature of the PFS blocks in the micelle core, but also to the cononsolvency effect of 2-propanol–water mixtures on the PNIPAM shell. In water, the micelle fragments retained their anticipated thermoresponsive behavior.
A diblock copolymer system PMPC-b-PNIPAM, where PMPC stands for the zwitterionic poly(2-(methacryloyloxy)-ethylphosphorylcholine), consisting of blocks that show cononsolvency in different composition ranges of the solvent mixture water/ethanol, was designed recently.148 While PMPC collapses at high ethanol mole fractions, PNIPAM does so at low ethanol mole fractions. For similar block lengths, a double-well conformational behavior was observed in computer simulations. In experiments, micelles were observed, and the block, that was insoluble at the given mixing ratio of the solvents, was supposed to form the core.
The effect of methanol on the micellar structures and the single chain conformations of aqueous solutions of a poly(methyl methacrylate)-b-poly(N-isopropylacrylamide) diblock copolymer at 20 °C were investigated by Ko et al. using synchrotron SAXS.149 In water-rich solvent mixtures, self-assembled spherical core–shell micelles are formed (Fig. 17). The internal structure of the micelles is adjusted by the solvent compositions in two ways: methanol softens the PMMA micellar core, while it causes the shrinkage of the PNIPAM micellar shell. In methanol-rich solvent mixtures beyond the miscibility gap, the copolymers are molecularly dissolved chains (Fig. 17). They are collapsed near the coexistence line, while they become random coils as the methanol content increases. It is proposed that the internal morphology of the micelles and the conformation of the dissolved chains depend strongly on the solvent composition, as a consequence of the superposed cononsolvency effect of PNIPAM and the overall enhanced solvation of PMMA, when adding methanol.
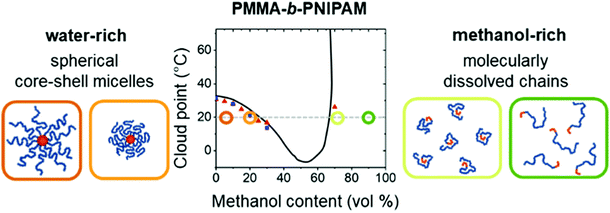 | ||
| Fig. 17 Phase diagram of a dilute solution of PMMA-b-PNIPAM diblock copolymers in water–methanol (small symbols). The full line guides the eye. Schematic representations of the micelles (left) and molecularly dissolved chains (right) at the points in the phase diagram having the same colors. From.149 Copyright 2021. Reproduced with permission from The American Chemical Society. | ||
Recently, the response dynamics of polymeric thin films to mixed water–methanol vapors were investigated.59,150 Time-resolved spectral reflectance, time-of-flight neutron reflectometry and FTIR measurements revealed a multistep response behavior of PMMA-b-PNIPAM films to an exchange from water vapor to a mixed water–methanol vapor. Additionally, differences were found for hydrated or deuterated solvents.59 The comparison of PNIPMAM films and zwitterionic poly(sulfobetaine) films showed that the kinetic response is governed by the specific nature of the polymer. While a two-step contraction was observed for PNIPMAM, only one step was found for the zwitterionic film.150
Furthermore, the cononsolvency behavior of PNIPAM-based polymer brushes was discussed in experimental and theoretical studies (see Section 2.2).10,14,15,17,73,151,152 These systems show high potential for separation and transfer of nanoparticles or as switchable nanopores, e.g. to regulate the translocation of DNA.10,14,151 Experimentally, the polymer chains are grafted from the surface with varying grafting density and chain length. The grafting density influences the swelling ratio of the brushes, but only exhibits a minor impact on the composition of the minimum brush height. Chen et al.15 observed a collapse from the top of the polymer brushes in unfavorable mixtures. The parts of the chains in contact with the cosolvent collapse, whereas the interior remains partly swollen. Combining the cononsolvency properties of polymer brushes with Förster resonant energy transfer functionality enables probing chain conformations and can be used to optically sense changes in liquid mixture compositions.161 While for thin films or polymer brushes grafted from planar surfaces, the swelling behavior can be derived from spectral reflectance, ellipsometry and AFM measurements, the characterization of polymer-decorated nanopores is more complicated. Very recently, Yong et al.10 presented a novel method the quantitatively evaluate the swelling state using the translocation of polymer in dilute solutions.
4 Conclusions
Cononsolvency is an intriguing phenomenon which has been widely researched through various experimental, simulation and theoretical methods as discussed in this review. Across literature, the cononsolvency phenomenon has been observed in several synthetic and biological polymer solutions, and a wide range of complex systems such as thin films, grafted polymer brushes, block copolymers and cross-linked gels. Over the last decade, several mechanisms, from both experimental and theoretical studies, have been proposed with a predominant emphasis on the connection between cononsolvency and the preferential adsorption of the cosolvent on the polymer. Additionally, significant progress has been made, on the experimental front, to understand the effect of cosolvents on polymer and solvent dynamics, though efforts on the simulation front have been limited.Although several mechanisms based on cosolvent–solvent attractive interactions, polymer–cosolvent bridging, geometric frustration and cosolvent surfactant effects have been proposed, there is still no consensus on the nature of the molecular interactions which drive cononsolvency. One of the major reasons for this lack of consensus is the predominant emphasis on cononsolvency in poly(N-isopropylacrylamide) (PNIPAM)/water/alcohol mixtures. Unlike PNIPAM, polymers such as poly(N,N-diethylacrylamide) (PDEAM) and poly(N-vinylcaprolactam) exhibit cononsolvency only in combination with certain alcohols indicating that mechanisms based purely on the observations in PNIPAM solutions may not be transferable to other systems. In this regard, one possible approach would be to extend simulation and experimental efforts to polymer solutions other than PNIPAM–water–alcohol mixtures. One major bottleneck in such an approach is the development of atomistic forcefields which can accurately reproduce the experimental data. Another closely related aspect is the development of methods and strategies for adequate sampling of polymer conformations in atomistic simulations of such systems. An important point to note is that most of the proposed mechanisms focus on specific interactions which are either related to polymer–cosolvent attractive interactions or clustering (or attractive interactions) in the bulk solvent–cosolvent mixture. As discussed in the theory and simulations section, each of these mechanisms are applicable to only certain systems indicating that the cononsolvency phenomenon depends on the interplay of the proposed specific interactions. Therefore, there is need for development of theoretical models which focus on the balance between polymer–(co)solvent and hydrophobic interactions and their effects on the polymer solvation shells.
Another aspect which is yet to be addressed is the connection between the coil-to-globule transition at the single chain level to the phase separation at the macroscopic level. Understanding this aspect is very important as the simulation studies predominantly focus on the coil–globule equilibrium of a single chain whereas the experimental studies are mostly on macroscopic (multiple chain) systems. As discussed in the experimental and theory sections, the coil-to-globule transition (temperature driven) and the phase separation are not coupled at all cosolvent concentrations. To understand this coupling, on the simulation front, there is a need for development of frameworks such as hybrid particle field simulations which can be used for simulating multi-chain systems and also be linked to the single chain coil-to-globule transitions. At the same time, single molecule experiments, using atomic force microscopy or optical tweezers, may provide new insights and can be more directly related to and supported by atomistic simulations.
Synthesis procedures for polymers have been tremendously improved over the last years providing better control of the sequence of repeating units along the chain as well as with respect to complex macromolecular architectures. Combining that with cononsolvency will allow preparing materials, where collapse transitions can be confined to compartments on different length scales. These locally collapsed regions have a different polarity as compared to their surroundings, which can be exploited, e.g. for sensing, scavenging or (bio-)chemical transformations.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank A. V. Berezkin, C.-H. Ko, K. Kyriakos, C.-H. Lin, P. Müller-Buschbaum, M. Nuber, K. N. Raftopoulos (all TU München), A. Miasnikova, C. Henschel and A. Laschewsky (Universität Potsdam), A. Schulte (University of Central Florida), C. Dalgicdir, F. Rodríguez-Ropero and D. Nayar (Indian Institute of Technology, Delhi). K. N. and W. R. thank the Deutsche Forschungsgemeinschaft (DFG) for funding within SFB 985 “Functional Microgels and Microgel Systems”. BJN thanks DFG for funding (PA 771/22-1). CP thanks DFG for funding (PA 771/4-1, PA 771/14-1, PA 771/22-1). SB and NvdV thank the DFG for funding within the Collaborative Research Center Transregio SFB TRR 146 “Multiscale Simulation Methods for Soft Matter Systems”.References
- F. M. Winnik, H. Ringsdorf and J. Venzmer, Macromolecules, 1990, 23, 2415–2416 CrossRef CAS.
- C. Scherzinger, A. Schwarz, A. Bardow, K. Leonhard and W. Richtering, Curr. Opin. Colloid Interface Sci., 2014, 19, 84–94 CrossRef CAS.
- C. E. Mills, E. Ding and B. D. Olsen, Biomacromolecules, 2019, 20, 2167–2173 CrossRef CAS PubMed.
- R. G. Strickley, Pharm. Res., 2004, 21, 201–230 CrossRef CAS PubMed.
- N. Seedher and M. Kanojia, Pharm. Dev. Technol., 2009, 14, 185–192 CrossRef CAS PubMed.
- Y. Zhang, W. S. Carvalho, C. Fang and M. J. Serpe, Sens. Actuators, B, 2019, 290, 520–526 CrossRef CAS.
- S. Nian and L. Pu, J. Org. Chem., 2019, 84, 909–913 CrossRef CAS PubMed.
- D. Kleinschmidt, K. Nothdurft, M. V. Anakhov, A. A. Meyer, M. Mork, R. A. Gumerov, I. I. Potemkin, W. Richtering and A. Pich, Mater. Adv., 2020, 1, 2983–2993 RSC.
- X. Wang, H. Huang, H. Liu, F. Rehfeldt, X. Wang and K. Zhang, Macromol. Chem. Phys., 2019, 220, 1800562 CrossRef.
- H. Yong, B. Molcrette, M. Sperling, F. Montel and J.-U. Sommer, Macromolecules, 2021, 54, 4432–4442 CrossRef CAS.
- E. Krieg and W. M. Shih, Angew. Chem., Int. Ed., 2018, 57, 714–718 CrossRef CAS PubMed.
- C. E. Mills, E. Ding and B. D. Olsen, Ind. Eng. Chem. Res., 2019, 58, 11698–11709 CrossRef CAS.
- K. Kyriakos, M. Philipp, J. Adelsberger, S. Jaksch, A. V. Berezkin, D. M. Lugo, W. Richtering, I. Grillo, A. Miasnikova, A. Laschewsky, P. Müller-Buschbaum and C. M. Papadakis, Macromolecules, 2014, 47, 6867–6879 CrossRef CAS.
- Y. Yu, R. A. Lopez de la Cruz, B. D. Kieviet, H. Gojzewski, A. Pons, G. Julius Vancso and S. de Beer, Nanoscale, 2017, 9, 1670–1675 RSC.
- Q. Chen, E. S. Kooij, X. Sui, C. J. Padberg, M. A. Hempenius, P. M. Schon and G. J. Vancso, Soft Matter, 2014, 10, 3134–3142 RSC.
- Y. Yu, M. Cirelli, B. D. Kieviet, E. S. Kooij, G. J. Vancso and S. de Beer, Polymer, 2016, 102, 372–378 CrossRef CAS.
- H. Wang and J. E. Pemberton, Langmuir, 2017, 33, 7468–7478 CrossRef CAS PubMed.
- M. Panayiotou, F. Garret-Flaudy and R. Freitag, Polymer, 2004, 45, 3055–3061 CrossRef CAS.
- H. M. L. Lambermont-Thijs, H. P. C. van Kuringen, J. P. W. van der Put, U. S. Schubert and R. Hoogenboom, Polymers, 2010, 2, 188–199 CrossRef CAS.
- Y. E. Kirsh, A. V. Krylov, T. A. Belova, C. G. Abdel'sadek and I. I. Pashkin, Russ. J. Phys. Chem. A, 1996, 70, 1302–1306 Search PubMed.
- N. A. Cortez-Lemus and A. Licea-Claverie, Progr. Polym. Sci., 2016, 53, 1–51 CrossRef CAS.
- F. Pooch, V. Teltevskij, E. Karjalainen, H. Tenhu and F. M. Winnik, Macromolecules, 2019, 52, 6361–6368 CrossRef CAS PubMed.
- J. Walter, J. Sehrt, J. Vrabec and H. Hasse, J. Phys. Chem. B, 2012, 116, 5251–5259 CrossRef CAS PubMed.
- J. Heyda, A. Muzdalo and J. Dzubiella, Macromolecules, 2013, 46, 1231–1238 CrossRef CAS.
- C. H. Hofmann, F. A. Plamper, C. Scherzinger, S. Hietala and W. Richtering, Macromolecules, 2013, 46, 523–532 CrossRef CAS.
- D. Mukherji and K. Kremer, Macromolecules, 2013, 46, 9158–9163 CrossRef CAS.
- F. Rodríguez-Ropero, T. Hajari and N. F. A. van der Vegt, J. Phys. Chem. B, 2015, 119, 15780–15788 CrossRef PubMed.
- K. Kyriakos, M. Philipp, L. Silvi, W. Lohstroh, W. Petry, P. Müller-Buschbaum and C. M. Papadakis, J. Phys. Chem. B, 2016, 120, 4679–4688 CrossRef CAS PubMed.
- B. Liu, J. Wang, G. Ru, C. Liu and J. Feng, Macromolecules, 2015, 48, 1126–1133 CrossRef CAS.
- J. Heyda, H. I. Okur, J. Hladílková, K. B. Rembert, W. Hunn, T. Yang, J. Dzubiella, P. Jungwirth and P. S. Cremer, J. Am. Chem. Soc., 2017, 139, 863–870 CrossRef CAS PubMed.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS PubMed.
- E. E. Bruce, P. T. Bui, B. A. Rogers, P. S. Cremer and N. F. A. van der Vegt, J. Am. Chem. Soc., 2019, 141, 6609–6616 CrossRef CAS PubMed.
- E. E. Bruce and N. F. A. van der Vegt, J. Am. Chem. Soc., 2019, 141, 12948–12956 CrossRef CAS PubMed.
- L. B. Sagle, Y. Zhang, V. A. Litosh, X. Chen, Y. Cho and P. S. Cremer, J. Am. Chem. Soc., 2009, 131, 9304–9310 CrossRef CAS PubMed.
- J. Wang, B. Liu, G. Ru, J. Bai and J. Feng, Macromolecules, 2016, 49, 234–243 CrossRef CAS.
- J. Mondal, G. Stirnemann and B. J. Berne, J. Phys. Chem. B, 2013, 117, 8723–8732 CrossRef CAS PubMed.
- J. Mondal, D. Halverson, I. T. S. Li, G. Stirnemann, G. C. Walker and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9270–9275 CrossRef CAS PubMed.
- Y.-T. Liao, A. C. Manson, M. R. DeLyser, W. G. Noid and P. S. Cremer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2479–2484 CrossRef CAS PubMed.
- F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2014, 118, 7327–7334 CrossRef PubMed.
- F. Rodríguez-Ropero and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2015, 17, 8491–8498 RSC.
- D. Nayar, A. Folberth and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2017, 19, 18156–18161 RSC.
- L. Sapir and D. Harries, Curr. Opin. Colloid Interface Sci., 2016, 22, 80–87 CrossRef CAS.
- Y. Su, M. Dan, X. Xiao, X. Wang and W. Zhang, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 4399–4412 CrossRef CAS.
- N. Lucht, S. Eggers and V. Abetz, Polym. Chem., 2017, 8, 1196–1205 RSC.
- X. Lang, E. X. Xu, Y. Wei, L. N. Walters and M. J. A. Hore, Polymer, 2019, 170, 190–197 CrossRef CAS.
- V. Y. Grinberg, T. V. Burova, N. V. Grinberg, A. P. Moskalets, A. S. Dubovik, I. G. Plashchina and A. R. Khokhlov, Macromolecules, 2020, 53, 10765–10772 CrossRef CAS.
- D. Mukherji, M. Wagner, M. D. Watson, S. Winzen, T. E. de Oliveira, C. M. Marques and K. Kremer, Soft Matter, 2016, 12, 7995–8003 RSC.
- M. Yang and K. Zhao, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1227–1234 CrossRef CAS.
- K. N. Raftopoulos, K. Kyriakos, M. Nuber, B.-J. Niebuur, O. Holderer, M. Ohl, O. Ivanova, S. Pasini and C. M. Papadakis, Soft Matter, 2020, 16, 8462–8472 RSC.
- B.-J. Niebuur, W. Lohstroh, C.-H. Ko, M.-S. Appavou, A. Schulte and C. M. Papadakis, Macromolecules, 2021, 54, 4387–4400 CrossRef CAS.
- F. Wang, Y. Shi, S. Luo, Y. Chen and J. Zhao, Macromolecules, 2012, 45, 9196–9204 CrossRef CAS.
- M. J. A. Hore and B. Hammouda, Macromolecules, 2013, 46, 7894–7901 CrossRef CAS.
- N. Osaka and M. Shibayama, Macromolecules, 2012, 45, 2171–2174 CrossRef CAS.
- B. Ebeling, S. Eggers, M. Hendrich, A. Nitschke and P. Vana, Macromolecules, 2014, 47, 2000–2007 CrossRef.
- C. H. Hofmann, S. Grobelny, M. Erlkamp, R. Winter and W. Richtering, Polymer, 2014, 55, 1462–1469 CrossRef.
- B.-J. Niebuur, C.-H. Ko, X. Zhang, K.-L. Claude, L. Chiappisi, A. Schulte and C. M. Papadakis, Macromolecules, 2020, 53, 3946–3955 CrossRef CAS.
- C. H. Hofmann, S. Grobelny, P. T. Panek, L. K. M. Heinen, A.-K. Wiegand, F. A. Plamper, C. R. Jacob, R. Winter and W. Richtering, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 532–544 CrossRef CAS.
- K. Kyriakos, M. Philipp, C.-H. Lin, M. Dyakonova, N. Vishnevetskaya, I. Grillo, A. Zaccone, A. Miasnikova, A. Laschewsky, P. Müller-Buschbaum and C. M. Papadakis, Macromol. Rapid Commun., 2016, 37, 420–425 CrossRef CAS PubMed.
- C. Geiger, J. Reitenbach, L. P. Kreuzer, T. Widmann, P. Wang, R. Cubitt, C. Henschel, A. Laschewsky, C. M. Papadakis and P. Müller-Buschbaum, Macromolecules, 2021, 54, 3517–3530 CrossRef CAS.
- D. Mukherji, C. M. Marques and K. Kremer, Nat. Commun., 2014, 5, 4882 CrossRef PubMed.
- D. Mukherji, C. M. Marques, T. Stühn and K. Kremer, J. Chem. Phys., 2015, 142, 114903 CrossRef PubMed.
- S. Bharadwaj, P. B. S. Kumar, S. Komura and A. P. Deshpande, Macromol. Theory Simul., 2017, 26, 1600073 CrossRef.
- S. Bharadwaj, D. Nayar, C. Dalgicdir and N. F. A. van der Vegt, Commun. Chem., 2020, 3, 165 CrossRef CAS.
- S. Bharadwaj, D. Nayar, C. Dalgicdir and N. F. A. van der Vegt, J. Chem. Phys., 2021, 154, 134903 CrossRef CAS PubMed.
- C. Dalgicdir, F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2017, 121, 7741–7748 CrossRef CAS PubMed.
- C. Dalgicdir and N. F. A. van der Vegt, J. Phys. Chem. B, 2019, 123, 3875–3883 CrossRef CAS PubMed.
- C. Dalgicdir, F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2019, 123, 955 CrossRef CAS PubMed.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, J. Mol. Liq., 2020, 297, 111928 CrossRef CAS.
- H. A. Pérez-Ramírez, C. Haro-Pérez, E. Vázquez-Contreras, J. Klapp, G. Bautista-Carbajal and G. Odriozola, Phys. Chem. Chem. Phys., 2019, 21, 5106–5116 RSC.
- I. Bischofberger, D. C. E. Calzolari and V. Trappe, Soft Matter, 2014, 10, 8288–8295 RSC.
- J.-U. Sommer, Macromolecules, 2017, 50, 2219–2228 CrossRef CAS.
- J.-U. Sommer, Macromolecules, 2018, 51, 3066–3074 CrossRef CAS.
- H. Yong, E. Bittrich, P. Uhlmann, A. Fery and J.-U. Sommer, Macromolecules, 2019, 52, 6285–6293 CrossRef CAS.
- A. Pica and G. Graziano, Phys. Chem. Chem. Phys., 2016, 18, 25601–25608 RSC.
- J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 143, 131101 CrossRef PubMed.
- J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2015, 142, 214906 CrossRef PubMed.
- S. Bharadwaj, P. B. S. Kumar, S. Komura and A. P. Deshpande, J. Chem. Phys., 2018, 148, 084903 CrossRef PubMed.
- Y. A. Budkov, A. L. Kolesnikov, N. Georgi and M. G. Kiselev, J. Chem. Phys., 2014, 141, 014902 CrossRef PubMed.
- Y. A. Budkov and A. L. Kolesnikov, Soft Matter, 2017, 13, 8362–8367 RSC.
- Y. Okada and F. Tanaka, Macromolecules, 2005, 38, 4465–4471 CrossRef CAS.
- F. Tanaka, T. Koga, H. Kojima, N. Xue and F. M. Winnik, Macromolecules, 2011, 44, 2978–2989 CrossRef CAS.
- F. Tanaka, T. Koga and F. M. C. M. Winnik, Phys. Rev. Lett., 2008, 101, 028302 CrossRef PubMed.
- D. Mukherji, C. M. Marques and K. Kremer, J. Phys.: Condens. Matter, 2018, 30, 024002 CrossRef PubMed.
- Q. Zhang and R. Hoogenboom, Progr. Polym. Sci., 2015, 48, 122–142 CrossRef CAS.
- D. Mukherji, C. M. Marques and K. Kremer, Annu. Rev. Condens. Matter Phys., 2020, 11, 271–299 CrossRef CAS.
- J. Polák, D. Ondo and J. Heyda, J. Phys. Chem. B, 2020, 124, 2495–2504 CrossRef PubMed.
- A. Hüther, X. Xu and G. Maurer, Fluid Ph. Equilibria, 2004, 219, 231–244 CrossRef.
- N. Wang, G. Ru, L. Wang and J. Feng, Langmuir, 2009, 25, 5898–5902 CrossRef CAS PubMed.
- K. Nothdurft, D. H. Müller, T. Brands, A. Bardow and W. Richtering, Phys. Chem. Chem. Phys., 2019, 21, 22811–22818 RSC.
- C. Scherzinger, O. Holderer, D. Richter and W. Richtering, Phys. Chem. Chem. Phys., 2012, 14, 2762–2768 RSC.
- E. Kutnyanszky, A. Embrechts, M. A. Hempenius and G. J. Vancso, Chem. Phys. Lett., 2012, 535, 126–130 CrossRef CAS.
- A. Kolberg, C. Wenzel, K. Hackenstrass, R. Schwarzl, C. Rüttiger, T. Hugel, M. Gallei, R. R. Netz and B. N. Balzer, J. Am. Chem. Soc., 2019, 141, 11603–11613 CrossRef CAS PubMed.
- G. Ramakrishnan, M. González-Jiménez, A. J. Lapthorn and K. Wynne, J. Phys. Chem. Lett., 2017, 8, 2964–2970 CrossRef CAS PubMed.
- K. Mochizuki, S. R. Pattenaude and D. Ben-Amotz, J. Am. Chem. Soc., 2016, 138, 9045–9048 CrossRef CAS PubMed.
- K. Mochizuki and D. Ben-Amotz, J. Phys. Chem. Lett., 2017, 8, 1360–1364 CrossRef CAS PubMed.
- D. Mendes de Oliveira and D. Ben-Amotz, J. Phys. Chem. Lett., 2021, 12, 355–360 CrossRef CAS PubMed.
- I. Bischofberger, D. C. E. Calzolari, P. De Los Rios, I. Jelezarov and V. Trappe, Sci. Rep., 2014, 4, 4377 CrossRef CAS PubMed.
- C. Wu and X. Wang, Phys. Rev. Lett., 1998, 80, 4092–4094 CrossRef CAS.
- X. Wang, X. Qiu and C. Wu, Macromolecules, 1998, 31, 2972–2976 CrossRef CAS.
- E. I. Tiktopulo, V. N. Uversky, V. B. Lushchik, S. I. Klenin, V. E. Bychkova and O. B. Ptitsyn, Macromolecules, 1995, 28, 7519–7524 CrossRef CAS.
- N. K. Li, S. Roberts, F. G. Quiroz, A. Chilkoti and Y. G. Yingling, Biomacromolecules, 2018, 19, 2496–2505 CrossRef CAS PubMed.
- F. G. Quiroz, N. K. Li, S. Roberts, P. Weber, M. Dzuricky, I. Weitzhandler, Y. G. Yingling and A. Chilkoti, Sci. Adv., 2019, 5, eaax5177 CrossRef CAS PubMed.
- V. Palivec, D. Zadrazil and J. Heyda, 2018, arXiv:1806.05592.
- M. Podewitz, Y. Wang, P. K. Quoika, J. R. Loeffler, M. Schauperl and K. R. Liedl, J. Phys. Chem. B, 2019, 123, 8838–8847 CrossRef CAS PubMed.
- Y. Zhao and K. Kremer, J. Phys. Chem. B, 2021, 125, 9751–9756 CrossRef CAS PubMed.
- J. Rösgen, B. M. Pettitt and D. W. Bolen, Biophys. J., 2005, 89, 2988–2997 CrossRef PubMed.
- P. E. Smith, J. Phys. Chem. B, 2004, 108, 18716–18724 CrossRef CAS.
- T. Amiya, Y. Hirokawa, Y. Hirose, Y. Li and T. Tanaka, J. Chem. Phys., 1987, 86, 2375–2379 CrossRef CAS.
- T. Zuo, C. Ma, G. Jiao, Z. Han, S. Xiao, H. Liang, L. Hong, D. Bowron, A. Soper, C. C. Han and H. Cheng, Macromolecules, 2019, 52, 457–464 CrossRef CAS.
- H. G. Schild, M. Muthukumar and D. A. Tirrell, Macromolecules, 1991, 24, 948–952 CrossRef CAS.
- D. Jia, T. Zuo, S. Rogers, H. Cheng, B. Hammouda and C. C. Hans, Macromolecules, 2016, 49, 5152–5159 CrossRef CAS.
- R. F. Lama and B. C.-Y. Lu, J. Chem. Eng. Data, 1965, 10, 216–219 CrossRef CAS.
- S. Bharadwaj and N. F. A. van der Vegt, Macromolecules, 2019, 52, 4131–4138 CrossRef CAS.
- S. Backes, P. Krause, W. Tabaka, M. U. Witt, D. Mukherji, K. Kremer and R. von Klitzing, ACS Macro Lett., 2017, 6, 1042–1046 CrossRef CAS.
- X. Zhang, J. Zong and D. Meng, Soft Matter, 2020, 16, 7789–7796 RSC.
- Y. A. Budkov, A. L. Kolesnikov, N. N. Kalikin and M. G. Kiselev, EPL, 2016, 114, 46004 CrossRef.
- A. Galuschko and J.-U. Sommer, Macromolecules, 2019, 52, 4120–4130 CrossRef CAS.
- H. Yong, H. Merlitz, A. Fery and J.-U. Sommer, Macromolecules, 2020, 53, 2323–2335 CrossRef CAS.
- N. F. A. van der Vegt and F. Rodriguez-Ropero, Soft Matter, 2017, 13, 2289–2291 RSC.
- L. Tavagnacco, E. Zaccarelli and E. Chiessi, Phys. Chem. Chem. Phys., 2018, 20, 9997–10010 RSC.
- K. Mochizuki, J. Phys. Chem. B, 2020, 124, 9951–9957 CrossRef CAS PubMed.
- G. Vazquez, E. Alvarez and J. M. Navaza, J. Chem. Eng. Data, 1995, 40, 611–614 CrossRef CAS.
- D. R. Lide, in CRC handbook of chemistry and physics, ed. D. R. Lide, Boca Raton, 89th edn, 2008 Search PubMed.
- N. F. A. van der Vegt, J. Phys. Chem. B, 2021, 125, 5191–5199 CrossRef CAS PubMed.
- A. Folberth, S. Bharadwaj and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2022, 24, 2080–2087 RSC.
- A. De Nicola, Y. Zhao, T. Kawakatsu, D. Roccatano and G. Milano, J. Chem. Theory Comput., 2011, 7, 2947–2962 CrossRef CAS PubMed.
- Z. Wu, A. Kalogirou, A. De Nicola, G. Milano and F. Müller-Plathe, J. Comput. Chem., 2021, 42, 6–18 CrossRef CAS PubMed.
- Z. Wu, G. Milano and F. Müller-Plathe, J. Chem. Theory Comput., 2021, 17, 474–487 CrossRef CAS PubMed.
- K. C. Daoulas and M. Müller, J. Chem. Phys., 2006, 125, 184904 CrossRef PubMed.
- J. Zhang, D. Mukherji, K. Kremer and K. C. Daoulas, Soft Matter, 2018, 14, 9282–9295 RSC.
- T. E. de Oliveira, P. A. Netz, D. Mukherji and K. Kremer, Soft Matter, 2015, 11, 8599–8604 RSC.
- A. Pica and G. Graziano, Biophys. Chem., 2017, 231, 34–38 CrossRef CAS PubMed.
- F. G. Quiroz and A. Chilkoti, Nat. Mater., 2015, 14, 1164–1171 CrossRef CAS PubMed.
- N. K. Li, F. G. Quiroz, C. K. Hall, A. Chilkoti and Y. G. Yingling, Biomacromolecules, 2014, 15, 3522–3530 CrossRef CAS PubMed.
- A. Nandakumar, Y. Ito and M. Ueda, J. Am. Chem. Soc., 2020, 142, 20994–21003 CrossRef CAS PubMed.
- D. W. Urry, M. M. Long, B. A. Cox, T. Ohnishi, L. W. Mitchell and M. Jacobs, Biochim. Biophys. Acta, 1974, 371, 597–602 CrossRef CAS.
- S. Roberts, M. Dzuricky and A. Chilkoti, FEBS Lett., 2015, 589, 2477–2486 CrossRef CAS PubMed.
- C. Chen, D. Y. W. Ng and T. Weil, Prog. Polym. Sci., 2020, 105, 101241 CrossRef CAS.
- D. R. Canchi and A. E. García, Annu. Rev. Phys. Chem., 2013, 64, 273–293 CrossRef CAS PubMed.
- Y. Zhao, M. K. Singh, K. Kremer, R. Cortes-Huerto and D. Mukherji, Macromolecules, 2020, 53, 2101–2110 CrossRef CAS PubMed.
- H. Kojima, F. Tanaka, C. Scherzinger and W. Richtering, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1100–1111 CrossRef CAS.
- C. Scherzinger, A. Balaceanu, C. Hofmann, A. Schwarz, K. Leonhard, A. Pich and W. Richtering, Polymer, 2015, 62, 50–59 CrossRef CAS.
- J. Wang, N. Wang, B. Liu, J. Bai, P. Gong, G. Ru and J. Feng, Phys. Chem. Chem. Phys., 2017, 19, 30097–30106 RSC.
- R. Keidel, A. Ghavami, D. M. Lugo, G. Lotze, O. Virtanen, P. Beumers, J. S. Pedersen, A. Bardow, R. G. Winkler and W. Richtering, Sci. Adv., 2018, 4, eaao7086 CrossRef PubMed.
- P.-W. Zhu and L. Chen, Phys. Rev. E, 2019, 99, 022501 CrossRef PubMed.
- K. Nothdurft, D. H. Müller, S. D. Mürtz, A. A. Meyer, L. P. B. Guerzoni, A. Jans, A. J. C. Kühne, L. De Laporte, T. Brands, A. Bardow and W. Richtering, J. Phys. Chem. B, 2021, 125, 1503–1512 CrossRef CAS PubMed.
- H. Zhou, Y. Lu, M. Zhang, G. Guerin, I. Manners and M. A. Winnik, Macromolecules, 2016, 49, 4265–4276 CrossRef CAS.
- D. Mukherji, M. D. Watson, S. Morsbach, M. Schmutz, M. Wagner, C. M. Marques and K. Kremer, Macromolecules, 2019, 52, 3471–3478 CrossRef CAS.
- C.-H. Ko, C. Henschel, G. P. Meledam, M. A. Schroer, R. Guo, L. Gaetani, P. Müller-Buschbaum, A. Laschewsky and C. M. Papadakis, Macromolecules, 2021, 54, 5825–5837 CrossRef CAS.
- L. P. Kreuzer, C. Lindenmeir, C. Geiger, T. Widmann, V. Hildebrand, A. Laschewsky, C. M. Papadakis and P. Müller-Buschbaum, Macromolecules, 2021, 54, 1548–1556 CrossRef CAS.
- C.-W. Li, H. Merlitz, C.-X. Wu and J.-U. Sommer, Macromolecules, 2018, 51, 6238–6247 CrossRef CAS.
- G. Park and Y. Jung, Soft Matter, 2019, 15, 7968–7980 RSC.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angew. Chem., Int. Ed., 2012, 51, 2229–2233 CrossRef CAS PubMed.
- C. Scherzinger, P. Lindner, M. Keerl and W. Richtering, Macromolecules, 2010, 43, 6829–6833 CrossRef CAS.
- K. Mukae, M. Sakurai, S. Sawamura, K. Makino, S. W. Kim, I. Ueda and K. Shirahama, J. Phys. Chem., 1993, 97, 737–741 CrossRef CAS.
- Y. Maeda, H. Yamamoto and I. Ikeda, Macromolecules, 2003, 36, 5055–5057 CrossRef CAS.
- H. Yamauchi and Y. Maeda, J. Phys. Chem. B, 2007, 111, 12964–12968 CrossRef CAS PubMed.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- O. Wrede, Y. Reimann, S. Lülsdorf, D. Emmrich, K. Schneider, A. J. Schmid, D. Zauser, Y. Hannappel, A. Beyer, R. Schweins, A. Gölzhäuser, T. Hellweg and T. Sottmann, Sci. Rep., 2018, 8, 13781 CrossRef PubMed.
- Q. A. Besford, H. Yong, H. Merlitz, A. J. Christofferson, J.-U. Sommer, P. Uhlmann and A. Fery, Angew. Chem., Int. Ed., 2021, 60, 16600–16606 CrossRef CAS PubMed.
Footnote |
| † Present address: INM - Leibniz Institute for New Materials, Campus D2 2, 66123 Saarbrücken, Germany. |
| This journal is © The Royal Society of Chemistry 2022 |