Open Access Article
Open Access ArticleNanoparticle anisotropy induces sphere-to-cylinder phase transition in block copolymer melts†
Javier
Diaz
 a,
Marco
Pinna
a,
Marco
Pinna
 *b,
Andrei
Zvelindovsky
*b,
Andrei
Zvelindovsky
 b and
Ignacio
Pagonabarraga
b and
Ignacio
Pagonabarraga
 acd
acd
aCECAM, Centre Européen de Calcul Atomique et Moléculaire, EPFL, École Polytechnique Fédérale de Lausanne, Batochime - Avenue Forel 2, 1015 Lausanne, Switzerland
bCentre for Computational Physics, University of Lincoln, Brayford Pool, Lincoln, LN6 7TS, UK. E-mail: mpinna@lincoln.ac.uk
cDepartament de Física de la Matèria Condensada, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
dUniversitat de Barcelona Institute of Complex Systems (UBICS), Universitat de Barcelona, 08028 Barcelona, Spain
First published on 6th May 2022
Abstract
Block copolymer nanocomposites including anisotropic nanoparticles have been previously found to co-assemble into complex structures with nanoparticle alignment. Anisotropic nanoparticles with large aspect ratios are found to modify the morphology of block copolymers at modest concentrations, inducing a sphere-to-cylinder phase transition by breaking the local symmetry in the vicinity of a solid particle. This transition takes place over a wide range of NP lengths comparable with the BCP spacing. Controlling the orientation of uniaxial nanoparticles provides additional control over the global orientation of the block copolymer, as previously reported by experiments.
Block copolymer (BCP) materials offer a perfect matrix to control the location and alignment of anisotropic nanoparticles (NPs).1 The convergence of several length scales2 along with tuning chemical BCP-NP interaction can result in hierarchical materials. For instance, anisotropic NPs can display orientational order with respect to the BCP matrix,3–6 or colloid-colloid ordered configurations.7–9 Achieving control over the BCP assembly and the global orientation is essential for applications where long-range ordered structures are required. On the other hand, anisotropic NPs such as semiconductive nanorods (NRs) mixed with polymer matrices have applications for photovoltaic devices.10 Additionally, the optical properties of NR/polymer mixtures can be controlled by the NR loading.11 To exploit the anisotropic properties of NRs, it is often desirable to achieve control over the NR alignment via external fields(electric12,13 and shear flow14), while the need for additional methods to control the NR orientation has been pointed out.15 While these works highlight the co-assembly possibilities of anisotropic NPs mixed with BCP, various computational,16–19 theoretical20 and experimental21,22 works have shown that the presence of NPs can modify the BCP nanostructure.
Previous experiments21 and simulations23 have shown NP-induced phase transition due to the change in the BCP effective composition using isotropic NPs. Contrary to that, this work reports a BCP phase transition driven by the aspect ratio of NPs, even at small NP loading (i.e. well below the corresponding nematic phase transition concentration for a given aspect ratio). Earlier experimental,4–6 theoretical24,25 and computational26 studies have demonstrated the alignment of anisotropic NPs in BCP domains. Nonetheless, the effect of a low concentration of anisotropic NPs in the BCP morphology has not been explored. This work reports a novel mechanism to control the BCP morphology induced by NP anisotropy. We present computational evidence of a body-centered cubic spheres (BCC) to hexagonally-ordered cylinders (HEX) phase transition driven by highly anisotropic majority-compatible NPs. Highly elongated NPs break the local symmetry, privileging an axial geometry, which in turn renders the spherical BCC morphology unstable against the HEX morphology, in the weak segregation regime. Previous experimental22 and computational27 works have described the circles-to-lamellar phase transition in two-dimensional BCP in the presence of anisotropic NPs acquiring nematic order, when NPs are compatible with the minority phase. This work, instead, reports the effect of a low concentration-well below the isotropic–nematic critical value-of NPs compatible with the majority phase of BCC-forming BCP.
In order to study the interplay between the NP anisotropy and the BCP morphology and its orientation it is essential to be able to simulate large systems containing several BCP domains. To this end, we develop and exploit a coarse grained model to cover the time evolution of the system over a large number of domains and over the time scales associated to the BCP domain reorganisation, which are relevant to the kinetic of phase separation.
A BCP melt with chain composition f0 = NA/(NA + NB) (i.e., A-monomer ratio) is described by the differential concentration field ψ(r, t) = ϕA(r, t) − ϕB(r, t) + (1 − 2f0), with diffusive dynamics, which is described through the Cahn–Hilliard equation28–30 and the thermodynamic state given by the standard Ohta–Kawasaki31 free energy, Fpol. The total free energy of the system, Ftot = Fpol + Fcc + Fcpl, includes two additional terms in the presence of Np number of NPs which account for the NP–NP purely repulsive interaction Fcc, and the energetic cost of embedding the NPs in the BCP matrix, Fcpl. The NP–NP interaction is a totally repulsive Yukawa-like potential that prevents NP overlapping. The coupling free energy can be expressed as32
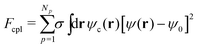 | (1) |
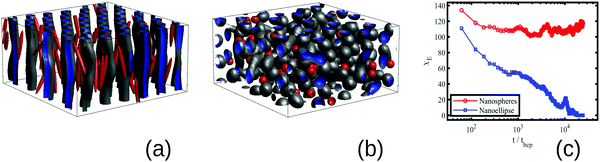
In order to capture the role of anisotropy, we compare the effect of anisotropic nanoellipses (NEs) and isotropic nanospheres (NSs) in the BCP morphology. In Fig. 1 a small volume fraction ϕp = 0.015 of NPs with an initially vertical orientation and random position is mixed with a sphere-forming BCP (f0 = 0.4, see ESI† for the rest of parameter details) in the disordered state (ie, ψ(r, t) is randomly initialised). In the absence of nanoscopic particles, the BCP is in the weak segregation regime and self-assembles into a BCC spherical structure. NPs are compatible with the majority phase of the BCP leading to the segregation of NPs in the continuous phase of the BCP for two distinct NP shapes: (a) NEs with aspect ratio e = 1/8 and (b) NSs with e = 1.
After relaxation, the BCP morphology is cylindrical in Fig. 1 (a) for NEs, and spherical for NSs in (b). The BCP HEX cylinders in (a) are oriented along the initial direction of the NEs with NEs maintaining their initial orientation in time, consistent with experimental results.35 The transition in the BCP driven by the anisotropic NPs can be quantified via the Euler characteristic χE of the BCP structure, in (c). This quantity provides information on the topology of the BCP mesophase.36 It takes values χE = 1 for an isolated sphere, χE = 0 for a torus, and negative values for highly connected structures. The large positive value of χE in the presence of NSs indicates that the BCP acquires a spherical morphology with a number χE of independent domains (further details on χE can be found in the Section B.3, ESI†). On the contrary, in the presence of NEs χE decreases monotonously until it vanishes, which indicates the formation of connected cylinders via the periodic boundary conditions(equivalent to a torus).
Radical change in the morphological metric χE with the NP anisotropy shows that highly anisotropic NPs induce a sphere-to-cylinder phase transition in the BCP, while isotropic spheres do not. This transition in the presence of anisotropic NPs can be rationalised assuming that the longer dimension of the NPs promotes the preferential orientation of the BCP microstructure, specially in the early stages of the phase separation. Given that the BCC sphere phase of the BCP does not have a preferential direction, it becomes unstable against the uniaxial HEX cylinder phase. In this context, given that NSs do not promote any preferential direction, the BCP phase remains BCC spheres. The promotion of anisotropic against isotropic phases in systems doped with anisotropic NPs has been previously reported in liquid crystals.37
The BCP kinetic pathway in the presence of NEs in Fig. 1(c) displays a monotonically decreasing Euler characteristic χE, consistent with the coalescence of several small spherical domains into larger cylinders. An intermediate increase in χE can be observed for a time of the order t/tbcp ∼ 104, which is correlated with domain breakage and coalescence: in Fig. 2(a) domains are developed, but defects in the BCP equilibrium HEX phase can be observed. In order to alleviate the energetic cost associated to the defects, the BCP undergoes a breakage and coalescence mechanism to eliminate defects (snapshot b and c), which leads to a temporal increase in the Euler number as more disconnected domains are created. This defect-removal mechanism occurs in a small time scale, consistent with the weak segregation regime of the BCP.38 Finally, in (d) the equilibrium HEX cylindrical phase is achieved, corresponding to χE = 0 in Fig. 1.
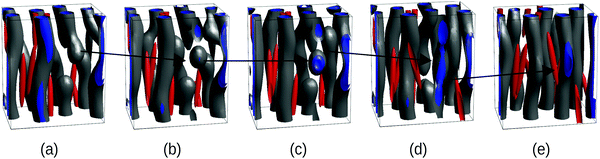 | ||
| Fig. 2 Kinetic pathway of the BCP domains during breakup and formation of cylinders via intermediate spherical domains, corresponding to the NE curve in Fig. 1(c) (blue squares). All parameters are the same as in Fig. 1(c) for the NE case, i.e., a = 1.333, b = c = 0.167. The snapshots correspond to a fraction of the full system and a black arrow indicates the evolution of a domain end defect. Snapshots correspond to times: t/tbcp = 8575 (a), 9800 (b), 11025 (c), 12250 (d) and 24500 (e). | ||
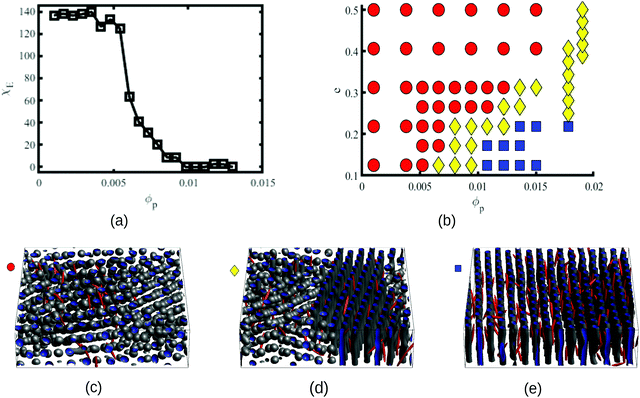
In order to characterise the sphere-to-cylinder phase transition we explore the concentration of NPs ϕp. Fig. 3(a) shows the role of a volume fraction ϕp of NEs with e = 1/8 in the BCP morphology, characterised by χE. The NE length-to-periodicity ratio is 2a/H0 = 1.44 where H0 is the BCP periodicity in the BCC morphology. Three regimes are clearly distinguishable, with a low concentration displaying BCC spheres 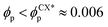 , quantified by χE ∼ 140, indicating many disconnected BCP domains, as shown in (c). For a higher concentration
, quantified by χE ∼ 140, indicating many disconnected BCP domains, as shown in (c). For a higher concentration 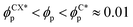 we observe a monotonic decay in χE as the system transitions from BCC spheres to elongated HEX cylinder domains. Visual inspection is consistent with coexistence between HEX and BCC phase occurring for this intermediate range, as shown in Fig. 3(d). For larger volume fractions the system acquires a global HEX phase with χE ∼ 0, as shown in Fig. 3(e). The coexistence regime can be rationalised as a consequence of the initial fluctuations in the local NP densities, with regions of relatively high local density
we observe a monotonic decay in χE as the system transitions from BCC spheres to elongated HEX cylinder domains. Visual inspection is consistent with coexistence between HEX and BCC phase occurring for this intermediate range, as shown in Fig. 3(d). For larger volume fractions the system acquires a global HEX phase with χE ∼ 0, as shown in Fig. 3(e). The coexistence regime can be rationalised as a consequence of the initial fluctuations in the local NP densities, with regions of relatively high local density 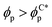 inducing a HEX phase, and relatively sparse regions inducing a BCC phase. After that, a process of HEX/BCC grain growth occurs in a slower time scale, until a phase coexistence regime is achieved as depicted in Fig. 3 (d), which is consistent with the slower kinetics shown in Fig. S2 (ESI†) and the snapshots in Fig. S3 (ESI†). Shorter NEs with 2a/H0 = 0.72 are shown to induce an equivalent phase transition in the BCP morphology, as plotted in Fig. S4 (ESI†). Furthermore, we can exploit the generality of the model to simulate cuboid-shaped NPs to observe the same BCC-HEX phase transition, indicating that the phase transition can be triggered in the presence of various generically anisotropic NPs, as shown in Fig. S5 (ESI†).
inducing a HEX phase, and relatively sparse regions inducing a BCC phase. After that, a process of HEX/BCC grain growth occurs in a slower time scale, until a phase coexistence regime is achieved as depicted in Fig. 3 (d), which is consistent with the slower kinetics shown in Fig. S2 (ESI†) and the snapshots in Fig. S3 (ESI†). Shorter NEs with 2a/H0 = 0.72 are shown to induce an equivalent phase transition in the BCP morphology, as plotted in Fig. S4 (ESI†). Furthermore, we can exploit the generality of the model to simulate cuboid-shaped NPs to observe the same BCC-HEX phase transition, indicating that the phase transition can be triggered in the presence of various generically anisotropic NPs, as shown in Fig. S5 (ESI†).
In order to quantify the combined role of the NP loading and the anisotropy we explore a concentration ϕp of NPs in a fixed f0 = 0.4 BCP, with an aspect ratio e. The volume per particle is kept constant while modifying the aspect ratio. In Fig. 3(b) we distinguish three phase regions: BCC spheres in red circles, yellow triangle for spheres/cylinder coexistence, and blue squares for HEX cylinder phase. A cylinder phase is found only for highly anisotropic NEs (e < 0.22) at the bottom-right region of the phase diagram, while weakly anisotropic NEs do not display a cylindrical phase, with χE ≫ 1. For relatively large concentrations ϕp ∼ 0.02 the coexistence phase can be seen to broaden, but visual inspection concludes that no hexagonal phase is present in the system. Instead, the presence of a high ϕp promotes several tubular domains. These results confirm the need of a critical concentration of particles ϕp that depends on the aspect ratio e, in order to trigger the sphere-to-coexistence and the coexistence-to-cylinder transition. It should be noted that the BCC-HEX phase transition for a given e occurs at a required concentration 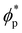 located well below the isotropic-nematic phase transition,39e.g. ϕI−Np ≈ 0.38 for e = 0.2 for hard ellipsoids.40
located well below the isotropic-nematic phase transition,39e.g. ϕI−Np ≈ 0.38 for e = 0.2 for hard ellipsoids.40
In order to address the metastability of the anisotropy-driven HEX phase, we consider initial configurations with disordered NEs' orientation. Fig. S7 (ESI†) shows that both the snapshots and χE display a different BCP morphology in the presence of a concentration ϕp = 0.015 of NEs and isotropic NSs, which shows that even initially randomised NEs promote the formation of elongated BCP phases, although a global hexagonal ordered is not achieved. The lack of a global ordering in the cylindrical phase can be thought of as consequence of the various initially seeded BCP orientations, which are not cooperating into a global director orientation. Instead, Fig. S8 (ESI†) shows that NEs with a global but random initial orientation lead to a clear χE ∼ 0 value characterising an equilibrated HEX BCP phase, with the initial orientation of NEs seeding the final global BCP axis, as previously shown in experiments.35 The initial orientation of the NEs does not influence the final HEX cylindrical morphology of the BCP (although it determines its orientation), which indicates the lack of system-shape dependence.
In order to address the role of the NP chemistry, in Fig. S10 (ESI†) a similar transition is explored for minority-compatible NEs. Contrary to majority-compatible NEs, χE decreases linearly with ϕp, indicating a progressive decrease in the total number of isolated domains. This indicates that minority-compatible NEs deform the hosting spherical domain and effectively increase the overall composition of the BCP, which is a well know behaviour.23 Contrary to that, majority-compatible NEs distort the BCP mesophase not by directly deforming BCP domains, but breaking the local symmetry around each NE.
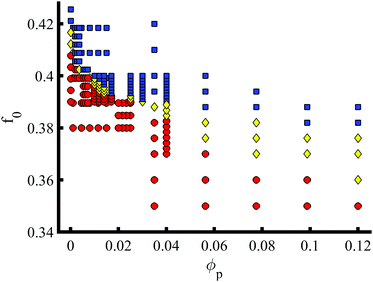
In addition to the NP properties (volume fraction, size, shape and chemistry), the phase transition can be characterised in terms of the BCP properties. The phase behaviour of pure BCP melts is controlled by the composition f0 along with the degree of segregation χN, the Flory-Huggins parameter. In Fig. 4f0 is explored against a volume fraction ϕp of e = 1/8 NEs. The transition from BCC (red circles) to HEX (blue squares) via a coexistence phase (yellow diamonds) is shown to occur over a wide range of BCP composition, well below the critical pure BCP composition fBCC-HEX0 = 0.412. At moderate volume fractions ϕp > 0.05 the coexistence is shown to broaden. The presence of NEs is shown to enhance the HEX phase by lowering the critical composition.
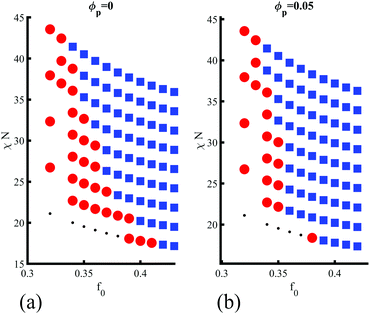
Finally, in Fig. 5(a and b) the role of the degree of segregation χN is studied to assert the effect of polymer–polymer incompatibility. Since modifying χN for a fixed value of f0 leads to changes in the critical composition (i.e., the BCP morphology), the complete phase diagram of the BCP is explored with and without NEs. The parameters used are the same as in Fig. 3(a). Beyond the weak segregation, the phase transition does not occur for χN > 39, as shown by comparing Fig. 5(a and b), respectively for no NEs and a volume fraction ϕp = 0.05. This can be rationalised by analysing the contributions to the free energy Ftot ≈ Fpol + Fcpl, assuming a negligible contribution from the repulsive colloid–colloid potential in the highly dilute regime that is considered in this work. In the weak segregation the BCP is not completely demixed, with |ψ| < 1 in the center of BCP domains. Therefore, a purely majority-coated NE with affinity ψ0 = 1 introduces a disturbance in the surrounding BCP profile, which is dictated by the NE shape, given by ψc (see eqn (1)). The morphology of the overall system is then controlled by the competition between the polymeric and the coupling free energy, which leads to the presented phase transition. On the other hand, in the strong segregation the coupling free energy becomes negligible (see Fig. S11a, ESI†), as ψ ≈ ψ0 within the continuous (majority) phase and the phase behaviour of the system is dominated by the pure-BCP free energy minimisation Ftot ≈ Fpol. Therefore, the origin of the sphere-to-cylinder phase transition can be placed in the entropic effect introduced by the anisotropic NPs, which break the local symmetry in the vicinity of the anisotropic NP, favouring unixial BCP morphologies. This entropic contribution dominates in the weak segregation of the BCP.
The role of NP anisotropy in BCP composites has shown that highly nonspherical particles can control the BCP mesophase, even in the dilute regime, for weakly segregated BCP melts. A mechanism to control the BCP morphology has been described which, contrary to previous works, is due to NP anisotropy. Highly anisotropic NPs are found to break the local symmetry in their vicinity, rendering uniaxial cylindrical domains stable against more isotropic spherical BCC domains. A small concentration of highly anisotropic NPs induced a sphere-to-cylinder transition which can result in a global hexagonally ordered cylinder morphology.
The BCP phase transition in the presence of anisotropic NPs highlights the complex behaviour of BCP/nanorod mixtures, where several length scales converge, leading to highly organised systems with emerging structures. Further work could explore the effect of oblate NPs with two main axis which can be tentatively better matched in a lamellar phase.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work has been performed under the project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the authors gratefully acknowledges the computer resources and technical support provided by Barcelona Supercomputing Center (BSC). I. P. acknowledges support from MINECO (Grant No. PGC2018-098373-B-100), DURSI (Grant No. 2017 SGR 884) and SNF Project No. 200021-175719. I. P. and J. D. thank the European Union’s Horizon 2020 Research and Innovation Programme project VIMMP under grant agreement No. 760907.Notes and references
- M. R. Bockstaller, Y. Lapetnikov, S. Margel and E. L. Thomas, J. Am. Chem. Soc., 2003, 125, 5276–5277 CrossRef CAS PubMed.
- R. Krishnamoorti and R. A. Vaia, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 3252–3256 CrossRef CAS.
- R. D. Deshmukh, Y. Liu and R. J. Composto, Nano Lett., 2007, 7, 3662–3668 CrossRef CAS PubMed.
- N. M. Krook, J. Ford, M. Maréchal, P. Rannou, J. S. Meth, C. B. Murray and R. J. Composto, ACS Macro Lett., 2018, 1400–1407 CrossRef CAS.
- K. Thorkelsson, A. J. Mastroianni, P. Ercius and T. Xu, Nano Lett., 2012, 12, 498–504 CrossRef CAS PubMed.
- K. Thorkelsson, N. Bronstein and T. Xu, Macromolecules, 2016, 49, 6669–6677 CrossRef CAS.
- E. Ploshnik, A. Salant, U. Banin and R. Shenhar, Phys. Chem. Chem. Phys., 2010, 12, 11885 RSC.
- E. Ploshnik, A. Salant, U. Banin and R. Shenhar, Adv. Mater., 2010, 22, 2774–2779 CrossRef CAS PubMed.
- K. Thorkelsson, J. H. Nelson, A. P. Alivisatos and T. Xu, Nano Lett., 2013, 13, 4908–4913 CrossRef CAS PubMed.
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295, 2425–2427 CrossRef CAS PubMed.
- G. Jiang, M. J. A. Hore, S. Gam and R. J. Composto, ACS Nano, 2012, 6, 1578–1588 CrossRef CAS PubMed.
- S. Gupta, Q. Zhang, T. Emrick and T. P. Russell, Nano Lett., 2006, 6, 2066–2069 CrossRef CAS PubMed.
- K. M. Ryan, A. Mastroianni, K. A. Stancil, H. Liu and A. P. Alivisatos, Nano Lett., 2006, 6, 1479–1482 CrossRef CAS PubMed.
- C. J. Murphy and C. J. Orendorff, Adv. Mater., 2005, 17, 2173–2177 CrossRef CAS.
- M. J. A. Hore and R. J. Composto, Macromolecules, 2014, 47, 875–887 CrossRef CAS.
- Z. Pan, L. He, L. Zhang and H. Liang, Polymer, 2011, 52, 2711–2721 CrossRef CAS.
- L. He, L. Zhang, A. Xia and H. Liang, J. Chem. Phys., 2009, 130, 144907 CrossRef PubMed.
- L. He, L. Zhang and H. Liang, Polymer, 2010, 51, 3303–3314 CrossRef CAS.
- Y. Zhao, M. Byshkin, Y. Cong, T. Kawakatsu, L. Guadagno, A. De Nicola, N. Yu, G. Milano and B. Dong, Nanoscale, 2016, 8, 15538–15552 RSC.
- M. A. Osipov, M. V. Gorkunov, A. V. Berezkin and Y. V. Kudryavtsev, Phys. Rev. E, 2018, 97, 042706 CrossRef CAS PubMed.
- C.-T. Lo, B. Lee, V. G. Pol, N. L. Dietz Rago, S. Seifert, R. E. Winans and P. Thiyagarajan, Macromolecules, 2007, 40, 8302–8310 CrossRef CAS.
- A. Halevi, S. Halivni, M. Oded, A. H. E. Müller, U. Banin and R. Shenhar, Macromolecules, 2014, 47, 3022–3032 CrossRef CAS.
- J. Huh, V. V. Ginzburg and A. C. Balazs, Macromolecules, 2000, 33, 8085–8096 CrossRef CAS.
- A. V. Berezkin, Y. V. Kudryavtsev, M. V. Gorkunov and M. A. Osipov, J. Chem. Phys., 2017, 146, 144902 CrossRef PubMed.
- M. A. Osipov and A. S. Ushakova, J. Mol. Liq., 2018, 267, 330–336 CrossRef CAS.
- L. He, L. Zhang, H. Chen and H. Liang, Polymer, 2009, 50, 3403–3410 CrossRef CAS.
- J. Diaz, M. Pinna, A. V. Zvelindovsky and I. Pagonabarraga, Adv. Theory Simul., 2022, 5, 2100433 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- J. W. Cahn, J. Chem. Phys., 1959, 30, 1121–1124 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1959, 31, 688–699 CrossRef CAS.
- T. Ohta and K. Kawasaki, Macromolecules, 1986, 19, 2621–2632 CrossRef CAS.
- M. Pinna, I. Pagonabarraga and A. V. Zvelindovsky, Macromol. Theory Simul., 2011, 20, 769–779 CrossRef CAS.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed.
- J. Diaz, M. Pinna, A. V. Zvelindovsky and I. Pagonabarraga, Macromolecules, 2019, 52, 8285–8294 CrossRef CAS.
- C. S. T. Laicer, T. Q. Chastek, T. P. Lodge and T. A. Taton, Macromolecules, 2005, 38, 9749–9756 CrossRef CAS.
- G. J. A. Sevink and A. V. Zvelindovsky, J. Chem. Phys., 2004, 121, 3864–3873 CrossRef CAS PubMed.
- M. V. Gorkunov and M. A. Osipov, Soft Matter, 2011, 7, 4348–4356 RSC.
- W. Li, P. F. Nealey, J. J. de Pablo and M. Müller, Phys. Rev. Lett., 2014, 113, 168301 CrossRef PubMed.
- P. Bolhuis and D. Frenkel, J. Chem. Phys., 1997, 106, 666–687 CrossRef CAS.
- G. Odriozola, J. Chem. Phys., 2012, 136, 134505 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sm00214k |
| This journal is © The Royal Society of Chemistry 2022 |