Open Access Article
Open Access ArticleSupramolecular structures of self-assembled oligomers under confinement†
Jarosław
Paturej
 *ab,
Kajetan
Koperwas
*ab,
Kajetan
Koperwas
 a,
Magdalena
Tarnacka
a,
Magdalena
Tarnacka
 a,
Karolina
Jurkiewicz
a,
Karolina
Jurkiewicz
 a,
Paulina
Maksym
a,
Paulina
Maksym
 c,
Joanna
Grelska
c,
Joanna
Grelska
 a,
Marian
Paluch
a and
Kamil
Kamiński
a,
Marian
Paluch
a and
Kamil
Kamiński
 a
a
aAugust Chełkowski Institute of Physics, University of Silesia in Katowice, 75 Pułku Piechoty 1, 41-500 Chorzów, Poland. E-mail: jaroslaw.paturej@us.edu.pl
bLeibniz-Institut für Polymerforschung, Dresden e.V., Hohe Str. 6, 01069 Dresden, Germany
cInstitute of Materials Engineering, University of Silesia, 75 Pułku Piechoty 1a, 41-500 Chorzow, Poland
First published on 7th June 2022
Abstract
We study the molecular origin of a prepeak (PP) observed at low q values in the structure factors of three oligomers in a bulk (poly(mercaptopropyl)methylsiloxane, PMMS, poly(methylmercaptopropyl)-grafted-hexylmethacrylate, PMMS-g-HMA, and poly(methylphenyl)siloxane, PMPS) in order to understand the lowering of the PP intensity detected for oligomers confined in cylindrical pores with low diameter. For this purpose, we use a combination of X-ray diffraction measurements and coarse-grained bead-spring molecular dynamics simulations. Our molecular modelling demonstrated that the planarity of the pendant groups triggers the self-association of oligomers into nanoaggregates. However, the formation of oligomeric nanodomains is not sufficient for building-up the PP. The latter requires spatial disturbance in the arrangement of the side groups of oligomers within clusters. Importantly, our numerical analysis revealed that the increasing degree of the confinement of oligomers limits their aggregation and consequently lowers the amplitude of the PP observed in the experimental data.
Supramolecular self-assembly is one of the most fascinating processes occurring in nature. This phenomenon originates from the presence of characteristic moieties in the chemical structures, i.e., hydroxyl, phenyl or ionic groups, which determine the formation of various (nano)aggregates held together by noncovalent bonds. The population of aggregates and their microstructure are key factors controlling the macroscopic physicochemical properties of associated materials. Therefore, self-assembly is a powerful tool in the fabrication of advanced functional materials revealing unique properties, such as self-healing1–3 and shape-memory,4,5 which are highly desired by a number of target industrial applications. Consequently, a great effort is being made towards the exploration of the molecular origin of the self-assembly in materials and the correlations of this phenomenon with their chemical structure.
One of the most characteristic structural fingerprints of the molecular self-assembly and organization at the nanoscale is the presence of a pre-peak (PP) in X-ray, neutron or electron scattering patterns, observed at much lower values of the scattering vector, q, as compared to the main amorphous halo.6 The appearance of the PP was reported for several monohydroxy alcohols, ionic liquids with medium-long alkyl chains or some active pharmaceutical ingredients.7–11 The origin of the PP is typically related to either the self-assembly into aggregates or the existence of spatial heterogeneity.12,13 Recent studies on hydrogen-bonding alcohols have revealed that the existence of the PP in these systems is the result of the self-assembly of molecules into clusters which leads to a medium-range order (MRO).12–14 For ionic liquids, the asymmetry caused by longer cationic alkyl tails gives rise to packing patterns with characteristic short and long separations between neighboring polar groups. Longer cationic alkyl tails tend to aggregate, and anionic heads associate, resulting in a strong MRO and the appearance of two PPs in the diffraction pattern.9,10,15,16
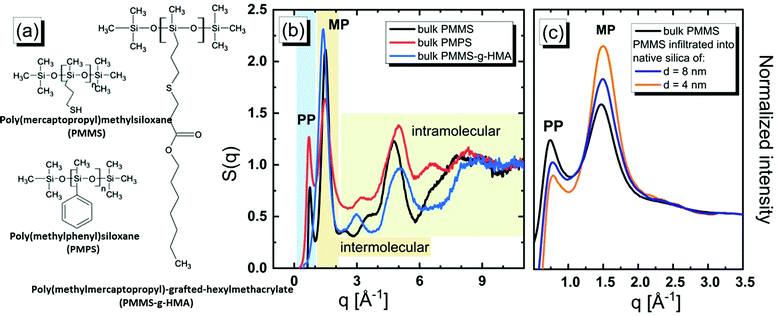
In order to unravel the origin of the diffraction PPs and understand the self-assembly phenomenon in many systems of varying complexity, different experimental strategies relying on the application of high pressure, electric and magnetic fields or mechanical stress were considered.17–21 Recently, a confinement at the nanometer-scale (i.e. comparable to the radius of gyration of individual molecules) has gained attention as a promising approach to elucidate the behavior of associated materials. Interestingly, the majority of studies reported that the nanospatial geometrical restrictions disarrange the supramolecular organization and suppress the MRO.22–27 As demonstrated in the case of tert-butanol (tB), which is able to form supramolecular clusters, the PP is not detectable for this material under confinement. Initially, it was hypothesized that the absence of the PP is due to the suppression of the spatial correlations associated with micellar-like clusters by the applied geometrical constraints.25 However, more recent molecular dynamics (MD) simulations of tB have shown that this might not be the case. It was demonstrated that the supramolecular clusters in tB survive in cylindrical silica nanopores, despite the absence of the PP.14,28,29 It should also be mentioned that for some van der Waals materials, the spatial geometrical restrictions induce peculiar molecular arrangements, which are not observed in the bulk state.30–34 The above examples demonstrate that depending on the system under probe the imposed confinement impacts in various ways the supramolecular structures and MRO, and that these structural alterations may or may not be manifested by either an increase or a decrease of the PP. This naturally implies that to understand the physical origin of the supramolecular self-assembly extensive computer modeling is required. Summarizing this discussion one can easily find that as far as there are numerous studies on the formation of self-assemblies and connection of this phenomenon with the structural modification (the presence of the PP at low q values in the structure factor) much less is known in the case of polymers. In fact, the presence or lack of the PP in the diffraction pattern of polymer materials in the bulk or under confinement seems to be sparse in the literature from both the experimental and simulation perspectives.35–38 In this paper, we explore this issue in more detail. As model substances, we selected poly(mercaptopropyl)methylsiloxane (PMMS) of molecular weight Mn = 2400 g mol−1, poly(methylmercaptopropyl)-grafted-hexylmethacrylate (PMMS-g-HMA) of molecular weight Mn = 4400 g mol−1, and poly(methylphenyl)siloxane (PMPS) of molecular weight Mn = 2500 g mol−1. The chemical structures of all examined oligomers are presented in Fig. 1(a). The more detailed information of all studied substances can be found in the ESI.† As it will be presented below, the differences in the molecular architecture of oligomers imply various behaviors of the molecules in the bulk system. Namely, PMMS has the ability to form H-bonding via thiol moieties that are attached to its backbone.39 In contrast, PMMS-g-HMA is a graft copolymer based on PMMS and extended with the hexylmethacrylate (HMA) group, which forbids the formation of H-bonding between these oligomers (see Fig. 1(a) and Fig. S1, ESI†). Thus, one can expect that the side groups of PMMS cannot freely rotate around backbones, which are due to H-bonds occurring between neighboring oligomers, whereas the rotation of the side groups of PMM-g-HMA is not restricted. Alternatively, PMPS is characterized by the substantial size of side groups,40–43 which also limits their rotation. The above selection of different types of oligomers allows us to examine the impact of spatial restrictions imposed on the oligomeric side groups (rigidity and planarity) on the local molecular arrangements of oligomers and on the building-up of the PP in the structure factor. It should be noted that tuning molecular rigidity is known as an important factor controlling the local ordering (microcrystallinity) of molecular, liquid-crystal and colloidal assemblies.44–46
The experimental XRD data in the form of the structure factor, S(q), defined in the ESI,† for the bulk polymer recorded at room temperature are presented in Fig. 1(b).
We observe that the results obtained for PMMS and PMPS distinctly differ than those determined for PMMS-g-HMA. The structure factors for PMMS and PMPS reveal two peaks in the low q range, i.e. the main peak (MP) and the PP, whereas S(q) for PMMS-g-HMA exhibits only a single MP. The MP is the so-called ‘amorphous halo’ which here is observed at qMP ≈ 1.5 Å−1 reflecting the short-range intermolecular correlations.47 The corresponding average intermolecular separation distance is dMP = 2π/qMP ≈ 4.2 Å. On the other hand, the PP at q ≈ 0.75 Å−1 indicates the presence of a MRO with two times larger spatial periodicity, dPP = 2π/qPP ≈ 8.4 Å. The latter observation might signal the formation of locally ordered microstructures as it usually assumed in the case of low molecular weight liquids.48 In Fig. 1(c), we display the experimental S(q) for PMMS melt confined in the cylindrical silica pores of different diameters of d ≈ 4 and 8 nm. We observe that increased geometrical restrictions imposed on PMMS result in decreasing of the amplitude of the PP. The questions that arise from our XRD experiments are as follows: Is the presence of the PP for polymers related to the formation of locally ordered microstructures as suggested for low molecular weight samples? Is the planarity of the side groups crucial for the occurrence of the PP, and consequently what is the molecular origin of the PP? Why the intensity of the PP decreases for PMMS subjected to confinement?
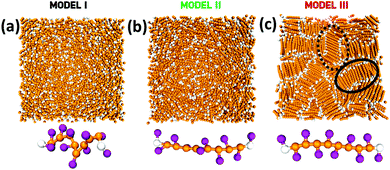
To address the above questions and gain a more thorough insight into the local structure of studied oligomers in the bulk phase and under nanoconfinement, we have used MD simulations of three different coarse-grained molecular architectures. Namely, we investigated oligomers with flexible backbones and flexible side beads (model I), stiff backbones and flexible side beads (model II), and stiff backbones and constrained side beads (model III). Note that in the latter model side beads maintain the planarity of the backbone. A detailed description of all models and simulation methodology can be found in the corresponding section of the ESI.†
The overview of the conformations of individual oligomers and corresponding equilibrium bulk morphologies for each model is displayed in Fig. 2. Interestingly, model III exhibits a substantial increase in the spatial molecular organization as compared to models I and II, which is manifested by the formation of the supramolecular domains with a preferred orientation of polymeric chains.
The differences in the molecular morphology of all examined molecular models are quantitatively analyzed in Fig. 3 where we display the corresponding static structure factors S(q), cf. definition in eqn (S5) in the ESI.†S(q) for oligomers with flexible backbone and side beads (black dotted line) has a characteristic form known from the bead-spring simulations of linear polymers in a melt state.49 The first peak at q ≈ 7σ−1 corresponds to the most probable distance between beads ≈2πσ/7 ≈ 0.9σ,29,50 which is comparable with an average bond length of ≈0.96σ. Note that the mismatch in size between the most probable distance and the average bond length indicates the amorphous structure of melts composed of flexible macromolecules,16 see Fig. 3(a). S(q) for stiff oligomers with flexible side beads (green dashed line) is qualitatively the same. The only difference is more pronounced peak, which is due to the stronger intramolecular correlation of the backbone monomers.51 Hence, the presence of flexible side beads grafted onto a stiff linear backbone favors the disordered bulk morphology (Fig. 3(a)). In the independent set of simulations, we verified that the melts of stiff linear oligomers (i.e., without side beads) undergo expected nematic ordering.52
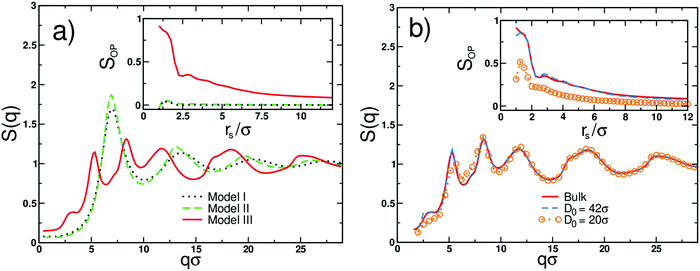 | ||
| Fig. 3 (a) The static structure factor S(q) obtained from simulations of different molecular models of bulk oligomers with flexible backbone and side beads (black dotted line), stiff backbone and flexible side beads (green dashed line) and stiff backbone with planar side beads (red solid line), as indicated. The inset displays the local structure order parameter SOP for all models as a function of the radius rs that encompasses the center of the mass of the reference backbone with respect to which SOP is calculated; see definition and detailed description in the ESI.† (b) The static structure factor S(q) obtained from simulations of the cylindrically confined melts of oligomers with stiff backbones and planar side beads. The results are for different effective cylinder diameters D0. The blue dashed line and orange circles are for D0 = 42 and 20σ, respectively. The reference bulk S(q) is displayed by the solid red line. The inset presents the local structure order parameter SOP. | ||
However, in contrast to models I and II, S(q) for oligomers with stiff backbones and planar side beads (the red solid line in Fig. 3(a)) exhibits an entirely different structural behavior. Here, the main peak splits into two smaller peaks located at q ≈ 5.2σ−1 and 8.3σ−1, respectively. The position of the second peak corresponds to the average bond length, which for this system is ≈0.77σ. Taking into account that the distances between molecules’ centers of masses are not smaller than 1.2σ (see the inset in Fig. 3a), we identify the position of the first peak, 5.2σ−1 ≈ 2π/1.2σ, with the intermolecular distances, which separate the subsequent layers of the supramolecular structures. Hence, the first peak reflects the periodicity between molecules belonging to neighboring parallel layers within the lamellar-like aggregate. However, the most interesting feature of S(q) for model III is the two-step decay separated by the narrow plateau between ≈2.7 and 3.7σ−1, which indicates increased bulk periodicity at larger length scales, i.e., up to ≈2.5σ. The beginning of the plateau corresponds to a distance of ≈2.3σ, which is approximately twice larger than the distance between neighboring layers. In model III, oligomers by design possess side beads that are alternately connected to the backbone (cf. the bottom of Fig. 2c). Consequently, two molecular arrangements of oligomers are possible within the subsequent layers of aggregate. The molecules can either ideally stack on each other (cf. the black solid region in Fig. 2c) or can randomly flipped along the backbone axis. The crucial difference between these two arrangements is in the periodicity of side beads between layers. In the former case, the side beads are exactly on top of each other in every subsequent layer, whereas, in the latter case, this periodicity is disturbed. Note that the second arrangement also occurs when the molecule is shifted along the backbone axis of the neighboring oligomer (cf. the black dotted region in Fig. 2c). In this case, the periodicity in the side bead positions takes place in every second subsequent layer. Consequently, the respective distance between side beads is twice as large as the distance between layers. This gives additional contribution to S(q) and is observed in the form of plateau in Fig. 3a (red solid line). Note that S(q) for model III qualitatively corroborates our experimental findings for the bulk PMMS and PMPS (see Fig. 1(b)). The MP and PP observed for the experimental S(q) of PMMS and PMPS correspond to the numerically derived MP and plateau obtained from model III. The difference between the evident PP observed in our diffraction data for PMMS and the plateau derived from MD simulations is due to the coarse-grained characteristic of our modeling.
To quantify the structural order between oligomeric backbones, we calculate the local order parameter SOP defined as follows:
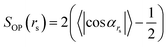 | (1) |
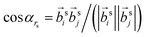 is the angle between a pair of vectors connecting the center of the mass of the oligomer backbone (
is the angle between a pair of vectors connecting the center of the mass of the oligomer backbone (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) cmi) with its closest (own) side bead
cmi) with its closest (own) side bead ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) si, i.e.
si, i.e. ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) si = (
si = (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) si −
si − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) cmi). The angle cos
cmi). The angle cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αrs is averaged for all i and j pairs of oligomers within a sphere of radius rs. It should be noted that the parallel (αrs = 0) and antiparallel (αrs = π) orientations of the unit vectors yield comparable structural orders. Consequently, in the definition given by (eqn (1)), we used the absolute value of cos
αrs is averaged for all i and j pairs of oligomers within a sphere of radius rs. It should be noted that the parallel (αrs = 0) and antiparallel (αrs = π) orientations of the unit vectors yield comparable structural orders. Consequently, in the definition given by (eqn (1)), we used the absolute value of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αrs. The values of SOP vary between 0, which represents the entirely disordered structure, and 1, which corresponds to the perfectly arranged oligomeric layers.
αrs. The values of SOP vary between 0, which represents the entirely disordered structure, and 1, which corresponds to the perfectly arranged oligomeric layers.
In the inset of Fig. 3(a), we display the values of SOP plotted as a function of rs for all considered molecular models. We observe a striking difference between the values of SOP calculated for a melt constituted of stiff oligomers with constrained side beads (model III) and two other models (models I and II). In the former case, high values of SOP suggest an ordering of up to ≈3.0σ, which is larger than the distance between three subsequent layers (solid line). At larger length scales, a gradual transition to a disordered morphology takes place. Low values of SOP ≈ 0 observed for models I and II (dashed and dotted lines) suggest the disordered structure in a wide range of length scales.
In what follows, we focus on the structure of a melt of stiff oligomers with planar side beads (model III) under nanoconfinement. In Fig. 3(b), we display numerical structure factors for this melt confined in cylindrical pores of a different effective diameter D0. We compare two cases of nanochannels with large and small D0 (as compared to the average end-to-end distance of oligomers in an unconstrained melt R of ≈ 7σ). S(q) for the melt infiltrated within the nanocylinder of large pore sizes (D0 = 42σ) is barely affected by the presence of confinement as compared to the S(q) for the bulk polymer (dashed blue and red solid lines, respectively). This is supported by the values of the order parameter SOP presented in the inset of Fig. 3(b). In contrast, the melt trapped in the nanocylinder with a smaller pore size (D0 = 20σ) reveals a remarkable effect of geometrical restrictions on the intermolecular structure (orange circles in Fig. 3b). As a result of confinement, the first peak in S(q) decreases, and the plateau turns into a gentle decay. The shift in the position of the first S(q) peak towards slightly larger q values observed in simulations for the melt under confinement is in agreement with the changes observed in the experimental diffraction data (Fig. 1(c)). The striking difference between the local arrangements of oligomers in large and small pores is also clearly visible from the calculated values of SOP (see the inset of Fig. 3b). Clearly, with the increasing degree of confinement, the MRO of oligomers is reduced (but not entirely suppressed) as compared to the bulk material. These observations suggest that narrow channels diminish the domain-like aggregation of PMMS oligomers and affect the intensity of the PP.
In conclusion, we report on the structural properties of oligomeric PMMS, PMPS, and PMMS-g-HMA in the bulk and under confinement in cylindrical pores. Our modelling revealed that the formation of lamellar-like nanoaggregates in the bulk yields the presence of the PP in the structure factor, which is also observed in our experimental XRD data for PMMS and PMPS but it was not detected in the PMMS-g-HMA sample. The molecular origin of the PP is the specific periodic arrangement of individual oligomers which form layers within nanodomains. Our finding suggests that the existence of the supramolecular structures does not necessarily result in building up of the PP in the structure factor. In particular, the lamellar-like organization of oligomers is not a sufficient condition for the presence of the PP. The necessary condition is the specific mutual orientation of oligomers within the aggregate. The performed MD simulations disclosed that the PP is due to the spatial correlations between oligomers’ side beads occupying positions in every second layer. These correlations are favoured by the planar arrangement of side beads with respect to backbones. Moreover, our results for a melt subjected to confinement indicate that the amplitude of the PP decreases upon decreasing the nanochannel diameter. Consequently, we observe that an increase in geometrical restrictions imposed on the melt diminishes the local ordering of oligomers in clusters and, thus, partially blights their aggregation. Therefore, our work presents valuable insights into the structure of self-assembled polymers in the bulk and under confinement.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
J. P. acknowledges the financial support from the Polish National Science Center (grant no. 2018/30/E/ST3/00428) and the computational time at PL-Grid (Poland). K. K. and M. P. are grateful for financial support from the Polish National Science Center within the framework of the Maestro 10 project (Grant No. UMO-2018/30/A/ST3/00323). M. T. and K. K. are thankful for financial support from the Polish National Science Centre within OPUS project (Dec. no. 2019/33/B/ST3/00500).References
- N. R. Sottos and J. S. Moore, Spot-on healing, Nature, 2011, 472(7343), 299–300, DOI:10.1038/472299a.
- M. Burnworth, L. Tang, J. R. Kumpfer, A. J. Duncan, F. L. Beyer, G. L. Fiore, S. J. Rowan and C. Weder, Optically healable supramolecular polymers, Nature, 2011, 472(7343), 334–337, DOI:10.1038/nature09963.
- T. Yan, K. Schröter, F. Herbst, W. H. Binder and T. Thurn-Albrecht, Unveiling the molecular mechanism of self-healing in a telechelic, supramolecular polymer network, Sci. Rep., 2016, 6(1), 32356, DOI:10.1038/srep32356.
- T. Xie, Tunable polymer multi-shape memory effect, Nature, 2010, 464(7286), 267–270, DOI:10.1038/nature08863.
- H. Meng and G. Li, A review of stimuli-responsive shape memory polymer composites, Polymer, 2013, 54(9), 2199–2221, DOI:10.1016/j.polymer.2013.02.023.
- H. E. Fischer, A. C. Barnes and P. S. Salmon, Neutron and X-ray diffraction studies of liquids and glasses, Rep. Prog. Phys., 2006, 69(1), 233–299, DOI:10.1088/0034-4885/69/1/R05.
- K. Jurkiewicz, S. Kołodziej, B. Hachuła, K. Grzybowska, M. Musiał, J. Grelska, R. Bielas, A. Talik, S. Pawlus, K. Kamiński and M. Paluch, Interplay between structural static and dynamical parameters as a key factor to understand peculiar behaviour of associated liquids, J. Mol. Liq., 2020, 319, 114084, DOI:10.1016/j.molliq.2020.114084.
- A. Nowok, K. Jurkiewicz, M. Dulski, H. Hellwig, J. G. Małecki, K. Grzybowska, J. Grelska and S. Pawlus, Influence of molecular geometry on the formation, architecture and dynamics of H-bonded supramolecular associates in 1-phenyl alcohols, J. Mol. Liq., 2021, 326, 115349, DOI:10.1016/j.molliq.2021.115349.
- M. Y. Ivanov, S. A. Prikhod’ko, N. Y. Adonin, I. A. Kirilyuk, S. V. Adichtchev, N. V. Surovtsev, S. A. Dzuba and M. V. Fedin, Structural anomalies in ionic liquids near the glass transition revealed by pulse EPR, J. Phys. Chem. Lett., 2018, 9(16), 4607–4612, DOI:10.1021/acs.jpclett.8b02097.
- M. Y. Ivanov, S. A. Prikhod’ko, N. Y. Adonin and M. V. Fedin, Structural anomalies in binary mixtures of ionic liquid [Bmim]BF 4 with water studied by EPR, J. Phys. Chem. B, 2019, 123(46), 9956–9962, DOI:10.1021/acs.jpcb.9b08933.
- M. Tarnacka, K. Adrjanowicz, E. Kaminska, K. Kaminski, K. Grzybowska, K. Kolodziejczyk, P. Wlodarczyk, L. Hawelek, G. Garbacz, A. Kocot and M. Paluch, Molecular dynamics of itraconazole at ambient and high pressure, Phys. Chem. Chem. Phys., 2013, 15(47), 20742–20752, 10.1039/c3cp52643g.
- M. Požar, B. Lovrinčević, L. Zoranić, T. Primorać, F. Sokolić and A. Perera, Micro-heterogeneity versus clustering in binary mixtures of ethanol with water or alkanes, Phys. Chem. Chem. Phys., 2016, 18(34), 23971–23979, 10.1039/C6CP04676B.
- I. Essafri and A. Ghoufi, Microstructure of nonideal methanol binary liquid mixtures, Phys. Rev. E, 2019, 99(6), 062607, DOI:10.1103/PhysRevE.99.062607.
- A. Ghoufi, Molecular origin of the prepeak in the structure factor of alcohols, J. Phys. Chem. B, 2020, 124(50), 11501–11509, DOI:10.1021/acs.jpcb.0c09302.
- H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, What is the origin of the prepeak in the X-ray scattering of imidazolium-based room-temperature ionic liquids?, J. Phys. Chem. B, 2010, 114(50), 16838–16846, DOI:10.1021/jp108545z.
- O. D. Bakulina, M. Y. Ivanov, S. A. Prikhod’ko, S. Pylaeva, I. V. Zaytseva, N. V. Surovtsev, N. Y. Adonin and M. V. Fedin, Nanocage formation and structural anomalies in imidazolium ionic liquid glasses governed by alkyl chains of cations, Nanoscale, 2020, 12(38), 19982–19991, 10.1039/D0NR06065H.
- D. Fragiadakis, C. M. Roland and R. Casalini, Insights on the origin of the Debye process in monoalcohols from dielectric spectroscopy under extreme pressure conditions, J. Chem. Phys., 2010, 132(14), 144505, DOI:10.1063/1.3374820.
- S. Bauer, K. Burlafinger, C. Gainaru, P. Lunkenheimer, W. Hiller, A. Loidl and R. Böhmer, Debye relaxation and 250 K anomaly in glass forming monohydroxy alcohols, J. Chem. Phys., 2013, 138(9), 094505, DOI:10.1063/1.4793469.
- C. Gainaru, M. Wikarek, S. Pawlus, M. Paluch, R. Figuli, M. Wilhelm, T. Hecksher, B. Jakobsen, J. C. Dyre and R. Böhmer, Oscillatory shear and high-pressure dielectric study of 5-methyl-3-heptanol, Colloid Polym. Sci., 2014, 292(8), 1913–1921, DOI:10.1007/s00396-014-3274-0.
- K. Adrjanowicz, B. Jakobsen, T. Hecksher, K. Kaminski, M. Dulski, M. Paluch and K. Niss, Communication: Slow supramolecular mode in amine and thiol derivatives of 2-ethyl-1-hexanol revealed by combined dielectric and shear-mechanical studies, J. Chem. Phys., 2015, 143(18), 181102, DOI:10.1063/1.4935510.
- S. Pawlus, M. Wikarek, C. Gainaru, M. Paluch and R. Böhmer, How do high pressures change the Debye process of 4-methyl-3-heptanol?, J. Chem. Phys., 2013, 139(6), 064501, DOI:10.1063/1.4816364.
- G. H. Findenegg, S. Jähnert, D. Akcakayiran and A. Schreiber, Freezing and melting of water confined in silica nanopores, ChemPhysChem, 2008, 9(18), 2651–2659, DOI:10.1002/cphc.200800616.
- L. Liu, A. Faraone, C.-Y. Mou, C.-W. Yen and S.-H. Chen, Slow dynamics of supercooled water confined in nanoporous silica materials, J. Phys.: Condens. Matter, 2004, 16(45), S5403–S5436, DOI:10.1088/0953-8984/16/45/007.
- F. Mallamace, M. Broccio, C. Corsaro, A. Faraone, D. Majolino, V. Venuti, L. Liu, C.-Y. Mou and S.-H. Chen, Evidence of the existence of the low-density liquid phase in supercooled, confined water, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(2), 424–428, DOI:10.1073/pnas.0607138104.
- D. Morineau and C. Alba-Simionesco, Does molecular self-association survive in nanochannels?, J. Phys. Chem. Lett., 2010, 1(7), 1155–1159, DOI:10.1021/jz100132d.
- W. K. Kipnusu, M. Elsayed, W. Kossack, S. Pawlus, K. Adrjanowicz, M. Tress, E. U. Mapesa, R. Krause-Rehberg, K. Kaminski and F. Kremer, Confinement for more space: A larger free volume and enhanced glassy dynamics of 2-ethyl-1-hexanol in nanopores, J. Phys. Chem. Lett., 2015, 6(18), 3708–3712, DOI:10.1021/acs.jpclett.5b01533.
- A. Talik, M. Tarnacka, M. Geppert-Rybczyńska, B. Hachuła, R. Bernat, A. Chrzanowska, K. Kaminski and M. Paluch, Are hydrogen supramolecular structures being suppressed upon nanoscale confinement? The case of monohydroxy alcohols, J. Colloid Interface Sci., 2020, 576, 217–229, DOI:10.1016/j.jcis.2020.04.084.
- A. Ghoufi, I. Hureau, R. Lefort and D. Morineau, Hydrogen-bond-induced supermolecular assemblies in a nanoconfined tertiary alcohol, J. Phys. Chem. C, 2011, 115(36), 17761–17767, DOI:10.1021/jp205943p.
- A. Ghoufi, I. Hureau, D. Morineau, R. Renou and A. Szymczyk, Confinement of tert-butanol nanoclusters in hydrophilic and hydrophobic silica nanopores, J. Phys. Chem. C, 2013, 117(29), 15203–15212, DOI:10.1021/jp404702j.
- S. Chattopadhyay, A. Datta, A. Giglia, N. Mahne, A. Das and S. Nannarone, Intramolecular and intermolecular rearrangements in nanoconfined polystyrene, Macromolecules, 2007, 40(25), 9190–9196, DOI:10.1021/ma071392y.
- K. Shin, E. Woo, Y. G. Jeong, C. Kim, J. Huh and K.-W. Kim, Crystalline structures, melting, and crystallization of linear polyethylene in cylindrical nanopores, Macromolecules, 2007, 40(18), 6617–6623, DOI:10.1021/ma070994e.
- M. Beiner, G. T. Rengarajan, S. Pankaj, D. Enke and M. Steinhart, Manipulating the crystalline state of pharmaceuticals by nanoconfinement, Nano Lett., 2007, 7(5), 1381–1385, DOI:10.1021/nl0705081.
- P. A. Wiggins, K. C. Cheveralls, J. S. Martin, R. Lintner and J. Kondev, Strong intranucleoid interactions organize the Escherichia coli chromosome into a nucleoid filament, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(11), 4991–4995, DOI:10.1073/pnas.0912062107.
- A. Ananiadou, G. Papamokos, M. Steinhart and G. Floudas, Effect of confinement on the dynamics of 1-propanol and other monohydroxy alcohols, J. Chem. Phys., 2021, 155(18), 184504, DOI:10.1063/5.0063967.
- M. Daoud and P. G. De Gennes, Statistics of macromolecular solutions trapped in small pores, J. Phys., 1977, 38(1), 85–93, DOI:10.1051/jphys:0197700380108500.
- A. Milchev and K. Binder, Cylindrical confinement of solutions containing semiflexible macromolecules: Surface-induced nematic order versus phase separation, Soft Matter, 2021, 17(12), 3443–3454, 10.1039/D1SM00172H.
- J. M. Y. Carrillo and B. G. Sumpter, Structure and dynamics of confined flexible and unentangled polymer melts in highly adsorbing cylindrical pores, J. Chem. Phys., 2014, 141(7), 074904, DOI:10.1063/1.4893055.
- J. Paturej, A. Milchev, S. A. Egorov and K. Binder, Star polymers confined in a nanoslit: A simulation test of scaling and self-consistent field theories, Soft Matter, 2013, 9(44), 10522–10531, 10.1039/c3sm51275d.
- M. Tarnacka, K. Jurkiewicz, B. Hachuła, Z. Wojnarowska, R. Wrzalik, R. Bielas, A. Talik, P. Maksym, K. Kaminski and M. Paluch, Correlation between locally ordered (hydrogen-bonded) nanodomains and puzzling dynamics of polymethysiloxane derivative, Macromolecules, 2020, 53(22), 10225–10233, DOI:10.1021/acs.macromol.0c01289.
- W. Tu, K. L. Ngai, M. Paluch and K. Adrjanowicz, Dielectric study on the well-resolved sub-rouse and JG β-relaxations of poly(methylphenylsiloxane) at ambient and elevated pressures, Macromolecules, 2020, 53(5), 1706–1715, DOI:10.1021/acs.macromol.9b02332.
- T. Chen, M. Li and J. Liu, π–π Stacking interaction: A nondestructive and facile means in material engineering for bioapplications, Cryst. Growth Des., 2018, 18(5), 2765–2783, DOI:10.1021/acs.cgd.7b01503.
- S. M. Melikova, A. P. Voronin, J. Panek, N. E. Frolov, A. V. Shishkina, A. A. Rykounov, P. Y. Tretyakov and M. V. Vener, Interplay of π-stacking and inter-stacking interactions in two-component crystals of neutral closed-shell aromatic compounds: Periodic DFT Study, RSC Adv., 2020, 10(47), 27899–27910, 10.1039/d0ra04799f.
- J. H. Deng, J. Luo, Y. L. Mao, S. Lai, Y. N. Gong, D. C. Zhong and T. B. Lu, π–π Stacking interactions: Non-negligible forces for stabilizing porous supramolecular frameworks, Sci. Adv., 2020, 6(2), eaax9976, DOI:10.1126/sciadv.aax9976.
- S. C. Glotzer and M. J. Solomon, Anisotropy of building blocks and their assembly into complex structures, Nat. Mater., 2007, 6(8), 557–562, DOI:10.1038/nmat1949.
- E. M. King, M. A. Gebbie and N. A. Melosh, Impact of rigidity on molecular self-assembly, Langmuir, 2019, 35(48), 16062–16069, DOI:10.1021/acs.langmuir.9b01824.
- M. Y. Ben Zion, X. He, C. C. Maass, R. Sha, N. C. Seeman and P. M. Chaikin, Self-assembled three-dimensional chiral colloidal architecture, Science, 2017, 358(6363), 633–636, DOI:10.1126/science.aan5404.
- A. Arbe, F. Alvarez and J. Colmenero, Neutron scattering and molecular dynamics simulations: Synergetic tools to unravel structure and dynamics in polymers, Soft Matter, 2012, 8(32), 8257, 10.1039/c2sm26061a.
- N. S. Murthy, H. Minor, C. Bednarczyk and S. Krimm, Structure of the amorphous phase in oriented polymers, Macromolecules, 1993, 26(7), 1712–1721, DOI:10.1021/ma00059a034.
- J. Baschnagel, C. Bennemann, W. Paul and K. Binder, Dynamics of a supercooled polymer melt above the mode-coupling critical temperature: Cage versus polymer-specific effects, J. Phys.: Condens. Matter, 2000, 12(29), 6365–6374, DOI:10.1088/0953-8984/12/29/308.
- K. Binder and W. Kob, Glassy Materials and Disordered Solids, World Scientific, 2011 DOI:10.1142/7300.
- M. Bulacu and E. van der Giessen, Effect of bending and torsion rigidity on self-diffusion in polymer melts: A molecular-dynamics study, J. Chem. Phys., 2005, 123(11), 114901, DOI:10.1063/1.2035086.
- S. A. Egorov, A. Milchev, P. Virnau and K. Binder, A new insight into the isotropic-nematic phase transition in lyotropic solutions of semiflexible polymers: Density-functional theory tested by molecular dynamics, Soft Matter, 2016, 12(22), 4944–4959, 10.1039/c6sm00778c.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00343k |
| This journal is © The Royal Society of Chemistry 2022 |