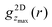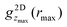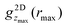Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Layering and packing in confined colloidal suspensions
Alejandro
Villada-Balbuena†
 a,
Gerhard
Jung†
a,
Gerhard
Jung†
 bc,
Angel B.
Zuccolotto-Bernez
a,
Thomas
Franosch
bc,
Angel B.
Zuccolotto-Bernez
a,
Thomas
Franosch
 b and
Stefan U.
Egelhaaf
b and
Stefan U.
Egelhaaf
 *a
*a
aCondensed Matter Physics Laboratory, Heinrich Heine University, Universitätsstraße 1, 40225 Düsseldorf, Germany. E-mail: stefan.egelhaaf@uni-duesseldorf.de
bInstitut für Theoretische Physik, Universität Innsbruck, Technikerstraße 21A, 6020 Innsbruck, Austria
cLaboratoire Charles Coulomb (L2C), Université de Montpellier, CNRS, 34095 Montpellier, France
First published on 7th June 2022
Abstract
Confinement modifies the properties of a fluid. The particle density is no longer uniform but depends on the distance from the walls; parallel to the walls, layers with different particle densities form. This affects the particle packing in the layers. We investigated colloidal fluids with volume fractions between 0.19 and 0.32 confined between rough walls. The particle–particle interactions were dominated by hard-sphere interactions but also contained some electrostatic interactions. The particle locations were determined using confocal microscopy and served to calculate the density profile, radial distribution function, anisotropic and generalized structure factors but also to characterize the arrangement of the wall particles leading to the roughness of the walls. The experiments are complemented by molecular dynamics simulations and fundamental-measure theory. While the particle arrangements are mainly controlled by hard-core interactions, electrostatic interactions become more important as the volume fraction decreases. Furthermore, the structure of the rough walls was varied and found to have a significant effect on the fluid structure. An appropriate representation of the rough walls in the simulations is thus crucial to successfully mimic the experiments.
1 Introduction
The properties of fluids are modified by physical confinement. Confinement changes, for example, the structure and phase behaviour,1–12 dynamics and viscoelasticity,12–16 and glass transition.17–24 It affects atomic, molecular, as well as colloidal fluids. Correspondingly, confinement is relevant for many areas, ranging from physics, chemistry, biology, and medicine to environmental and material sciences as well as technology. Applications include, e.g., nanopatterning and nanofabrication, coatings, tribology including lubrication and friction, micro- and nanofluidics, molecular sieving, liquids in porous media or the interiors of cells, blood components in vessels and channels in biological membranes.A bulk fluid is isotropic and disordered except for a local structure characterized by short-ranged density variations.25 A wall, however, leads to wetting and results in a nonuniform density profile with layers parallel to the wall.26 The density profile perpendicular to the wall hence shows modulations. The length scale of the modulations corresponds to the particle size. The modulations extend from the wall into the fluid over a range governed by the position correlations in the fluid structure. Confinement between two walls similarly breaks translational symmetry. It leads to anisotropic ordering with distinct layers parallel to the walls and transport properties that differ from those found in bulk.5–8,12,14,27–36 The incompatibility between the isotropic structure of bulk fluids and the anisotropic layering imposed by confinement results in density variations that are particularly pronounced when both effects are commensurate and hence mutually reinforce each other.27 The packing of spheres in layers is particularly efficient, and hence the layering most pronounced, for wall separations slightly less than an integer multiple of the particle diameter. Upon increasing the wall separation, an alternating sequence of highly anisotropic layering and a more isotropic local order is observed.
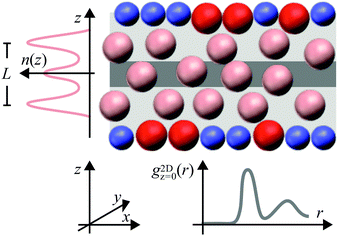
The density modulations perpendicular to the walls can be quantified by the density profile n(z), where the z direction is defined perpendicular to the walls with z = 0 in the centre of the slit (Fig. 1). The modulations extend throughout the whole slit if the wall separation is small, up to a few times the particle size, and the particle concentration is high enough, such that the particle–particle and particle–wall interactions are important. Correspondingly, the packing within the layers depends on the wall separation and the distance to the walls. In the layers parallel to the walls, a pronounced local order with significant density modulations can develop28 and, in concentrated systems, a fluid–crystal transition can occur.2 The packing of particles parallel to the walls can be characterized by the distribution of particles around a specific particle and is quantified by the two-dimensional positions of particles in a slab parallel to the walls, the two-dimensional radial distribution function (2D-RDF) g2Dz(r) (Fig. 1). The radial distribution functions can be strongly anisotropic and show a pronounced dependence on the position within the slit, z.6,29,30 Both, layering and packing, have together been described by the local density correlation function8,27–31 or the structure factor S(q).8,18–20,29,30,37 Due to the symmetry of the confined fluid, the fluid structure can be fully characterized in dependence of two parameters, the distance to the central plane, z, and the particle–particle distance within a plane parallel to the walls, r = (x2 + y2)1/2 (Fig. 1). Similarly, the structure factor is studied in dependence of the magnitudes of the wavevectors parallel, q‖, and perpendicular, q⊥, to the walls.
Particles with a variety of shapes and differently-shaped cavities have been investigated.9–11,13 However, the simplest possible system consists of hard-spheres confined by hard walls. This situation has been investigated using computer simulations, density-functional theory and integral-equation theory5,6,12,27,31,32,38 and experiments based on force measurements,39–42 scattering methods6,29,30,33–35,43–50 as well as conventional and confocal microscopy.51–58 In addition, the effects of charges on the particles and walls have been studied, for example their effects on the phase behaviour59 and packing.33–35,45,48,49 In both cases, hard and charged walls, the walls are in general isotropic in the plane of the wall. Randomly structured, e.g. patchy or rough, walls have been less studied and, if so, the emphasis has been on the particle dynamics in confinement60–69 or close to individual rough walls.22,70,71
Using experiments, simulations and theoretical calculations, we investigate the effects of confinement by rough walls on moderately dense fluids. We consider spherical colloids. The particle–particle as well as the particle–wall interactions were dominated by hard-core interactions but also contained some electrostatic contribution. The amplitude of the roughness, that is the typical variation in the wall relief, has been chosen small enough to still allow for layering and for an unambiguous definition of the slit width, but large enough to have an effect on the arrangement of the particles. This implies an amplitude of the roughness smaller than but similar to the particle diameter. Roughness is introduced by decorating the walls with particles that are similar to the particles forming the fluid.
The experimental system consisted of micron-sized poly(methyl methacrylate) (PMMA) spheres with, mainly, hard-sphere-like interactions but also a small amount of residual charges. Their volume fraction covered a range 0.19 ≲ ϕ ≲ 0.32. They are confined between two walls formed by randomly-arranged fixed particles and immobile fluid particles. The wall separation is quantified by the confinement length L corresponding to the separation between the outermost maxima of the density profile n(z) (Fig. 1). The confinement length L has been varied. The colloidal size allowed us to image the samples using confocal microscopy. This yields the location of each particle and thus permits for a quantitative analysis on an individual particle level. Thus, a detailed characterization of the confined fluid as well as the particles forming the rough walls is possible. The focus is on the density profile n(z), the two-dimensional radial distribution function g2Dz(r) and the anisotropic, S(q‖,q⊥), as well as the generalized, Sμν(q‖), structure factors. Although the samples are investigated by confocal microscopy and hence real space information on each single particle is obtained, also the structure factors are considered because they provide complementary and detailed information on the particle arrangement and allow for a comparison with scattering experiments and theoretical predictions.
The experimental systems are mimicked in molecular dynamics simulations. The simulation results quantitatively agree with the experimental findings. The experimental findings and simulation results are moreover compared to predictions from fundamental-measure theory for hard-spheres confined by flat soft walls. Thus, the experimental findings can be compared with simulation results as well as theoretical predictions. The main aims are to quantify the effects of a moderate particle charge and of the roughness of the walls and to faithfully implement the roughness of the walls in the simulations to be able to mimic the experiments. While the fluid structure is dominated by excluded-volume effects, i.e. hard-core interactions, the electrostatic interactions are found to become more important at low volume fractions. Moreover, the effects of the wall roughness are investigated by simulations employing different rough and flat walls. Our findings indicate that the structure of the fluid significantly depends on the details of the rough walls. They also show that a detailed determination of the roughness, as accessible through confocal microscopy, as well as a subsequent realistic representation of the roughness of the walls in the simulations is crucial to achieve quantitative agreement with the experimental findings.
2 Materials and methods
2.1 Sample preparation and imaging
The particles have a mean diameter σp = 1.85 μm as determined by confocal differential dynamic microscopy.78 Within the expected uncertainty, this diameter is consistent with results from static light-scattering experiments79 that yielded a mean diameter of 1.80 μm and a polydispersity δp = 4.8%.
 | ||
| Fig. 2 Layer of fixed wall particles (blue) and immobile fluid particles (red) schematically represented in side view (a) and bottom view (b), where the images were created using Ovito,80 as well as the corresponding confocal microscopy images (c). The variations in the wall coverage are caused by slight differences in the preparation procedure but not by the volume fraction of the sample, here ϕ = 0.32, or the confinement length L, here L = 1.9σp (left), 2.4σp (middle), 4.4σp (right). The scale bar represents 20 μm. | ||
Finally, approximately 4 μl of sample was placed on the circular monolayer of the larger cover glass and covered by the smaller cover glass with its circular monolayer and spacer facing the layer and spacer of the larger cover glass. Once the sample had spread throughout the whole volume, the edges were sealed with glue (All Purpose Adhesive Super, UHU). The glue was left to dry for 48 h. Thus the sample was contained in a narrow, wedge-shaped slit with a maximum height of 20 to 30 μm. This implies a very small inclination angle of less than 0.1°. Thus different wall separations could be investigated using the same sample cell while the wall separation was almost constant in one particular field of view. The difference in slit height that occurs in one direction across the field of view due to the inclination angle depends on the imaging conditions (Section 2.1.3) but was always smaller than 0.1 μm and hence more than an order of magnitude smaller than the mean particle diameter. The samples were kept and investigated at a temperature between 19 °C and 20 °C.
At different positions in the samples corresponding to different wall separations, image stacks were obtained. The stacks consisted of individual slices with 512 × 512 pixels. The stacks covered the whole slit and were collected from the bottom to the top of the slit in steps of 0.25 μm. To scan one stack took 4 to 6 s depending on the wall separation. For each position between 3000 (large widths) and 5000 (small widths) stacks were recorded resulting in a total measurement time per position of about 5 h.
From the stacks, particle locations were extracted using standard algorithms implemented using interactive data language (IDL).81 To detect the fluid particles, a reconstruction diameter between 1.8 and 2.0 μm was used whereas a reliable detection of the fixed wall particles required to reduce the reconstruction diameter to 0.6 μm because of the loss of dye in these particles during the preparation of the sample cell. The obtained particle locations were analyzed as described below (Section 2.4) using Python routines.82
2.2 Molecular dynamics simulations
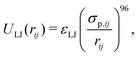 | (1) |
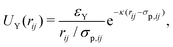 | (2) |
The simulation units are given by the energy scale ε, the charge e, the length scale σ and the time scale τ. They can be translated into SI units by comparison to the experimental parameters. The unit of energy ε is given by the thermal energy kBT = T*ε with T* = 1 in the simulations. Since the experiments were performed at room temperature, the energy scale ε = 4.1 × 10−21 J. The unit of charge e can directly be identified with the elementary charge e = 1.602 × 10−19 C. The unit of length σ is defined by σ = σp = 1.85 μm. The unit of time, τ, was not mapped since only static properties are of interest here.
The system is integrated in the canonical ensemble using a Langevin thermostat to maintain constant temperature (relaxation time scale τL = τ). Since we aim to extract static properties only, we have chosen this approach although it does not include hydrodynamics. The time step was set to Δt = 10−4τ and the particle mass to m = 0.25ετ2σ−2. The size of the simulated system corresponds to the experimental observation volume; approximately 30 × 30 particles parallel to the walls and 3 to 6 particle layers across the slit where periodic boundary conditions were applied in both directions parallel to the walls. This results in approximately 2700 to 5600 particles depending on the confinement length L. The systems were equilibrated before measurements were started.
The simulations were initialized with configurations taken from confocal microscopy images that contained all particles, i.e. mobile and immobile fluid particles and fixed wall particles. The different kinds of particles were classified based on the experimental density profiles n(z) containing mobile and, for this analysis of the wall particles, also immobile fluid particles and fixed wall particles (Section 2.4.1). Particles were identified as fixed wall particles if they are located within a distance Lw = 0.35σp from the outermost maxima of the density profile. Immobile fluid particles are larger than fixed wall particles and hence are expected further from the outermost maxima but they are part of the rough wall and hence are closer to the outermost maxima than the fluid particles. Thus, particles within a range Lw = 0.35σp to Lim = 0.81σp from the outermost maxima are considered immobile fluid particles if, in addition, they do not overlap with fixed wall particles. All other particles are defined as (mobile) fluid particles. (Note that the monolayers next to the walls, which contain only fixed wall and immobile fluid particles, are only taken into account here but not in the further analysis; Section 2.4.) The results are not significantly altered if the values of Lw and Lim are changed within reason. This procedure resulted in a full coverage of the walls (Fig. 2a and b). It also takes into account experimental variations, such as the exact coverage with fixed wall particles and their arrangement (Fig. 2c). This is important because the coverage and arrangement depend on minute details of the experimental preparation procedure followed to coat the cover slips (Section 2.1.2) and are hence difficult to precisely and consistently reproduce in the experiments. The coverage and arrangement do not directly but implicitly depend on the parameters varied in this study, such as the wall separation and the volume fraction of the sample.
The values of the inverse Debye length were determined to κ ≈ 19σp−1 = 10 μm−1 with some variations between the samples (Table 1). The variations are attributed to, e.g., the low solubility of the salt and solvent evaporation during sample preparation which was difficult to avoid due to the relatively large surface area of the sample during its spreading on the cover slip. The magnitude of the Debye length κ−1 ≈ 100 nm is within the range previously reported for similar systems.73,83
| ϕ | κσ p | ε Y/ε | ε wY/ε | Z | Z w |
|---|---|---|---|---|---|
| 0.19 | 14.8 | 34 | 204 | 702 | 1670 |
| 0.20 | 15.7 | 23 | 115 | 691 | 1320 |
| 0.28 | 24.0 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 64 |
599 | 1440 |
| 0.32 | 20.3 | 16 | 112 | 602 | 1640 |
Since the fixed wall particles underwent extended handling, including prolonged exposure to air, their charge and Yukawa-energy scale is expected to be higher than the ones of the mobile and immobile fluid particles. Thus, the value of the Yukawa-energy scale was separately adjusted for the mobile and immobile fluid particles, εY, and the fixed wall particles, εwY (Table 1).
Based on the values of the inverse Debye length κ, the Yukawa-energy scales, εY and εwY, the particle diameters, σp and σwp, and the Bjerrum length in CHB6, λB = 7 nm, the number of elementary charges of the fluid particles,
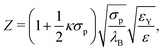 | (3) |
2.3 Fundamental-measure theory and Ornstein–Zernicke equation
Density profiles were calculated using fundamental-measure theory (FMT). They were also used as input for the integral-equation theory of inhomogeneous fluids to determine radial-distribution functions and structure factors.FMT is similarly applied as previously84 but extended to soft walls. It is based on density-functional theory and as such also minimizes the functional for the grand potential. The minimization directly leads to85,86
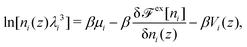 | (4) |
 of a mixture of hard-spheres. To determine the density profiles ni(z), eqn (4) is self-consistently solved in an iterative procedure.86 In each iteration, the chemical potential μi is adapted such that the number distribution of sizes is Gaussian with mean σp and standard deviation δp.84
of a mixture of hard-spheres. To determine the density profiles ni(z), eqn (4) is self-consistently solved in an iterative procedure.86 In each iteration, the chemical potential μi is adapted such that the number distribution of sizes is Gaussian with mean σp and standard deviation δp.84
The potential Vi(z) is not a hard wall potential, as in ref. 84, but describes a slit with soft walls, similar but not identical to ref. 88, and is given by
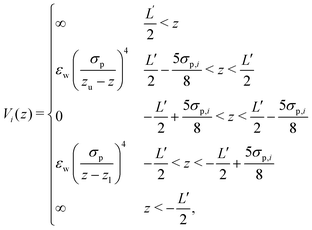 | (5) |
Based on the density profile 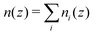 structural properties can be calculated using a confined version of the Ornstein–Zernicke equation89 in combination with a Percus–Yerwick closure. In particular, based on the direct correlation function hz(r), the two-dimensional radial distribution function g2Dz(r) = hz(r) + 1 (Section 2.4.2) can be calculated. Details of the algorithm are given in ref. 37 and 90. This algorithm requires monodisperse particles and hence, in this step of the theoretical calculation, polydispersity is neglected.
structural properties can be calculated using a confined version of the Ornstein–Zernicke equation89 in combination with a Percus–Yerwick closure. In particular, based on the direct correlation function hz(r), the two-dimensional radial distribution function g2Dz(r) = hz(r) + 1 (Section 2.4.2) can be calculated. Details of the algorithm are given in ref. 37 and 90. This algorithm requires monodisperse particles and hence, in this step of the theoretical calculation, polydispersity is neglected.
2.4 Relevant observables
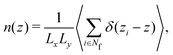 | (6) |
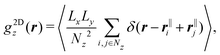 | (7) |
In the case of FMT, the 2D-RDFs were calculated from the direct correlation function hz(r) according to g2Dz(r) = hz(r) + 1 (Section 2.3).
The anisotropic structure factor has previously been determined in scattering experiments with confined samples.8,29,30 It is defined as
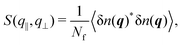 | (8) |
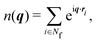 | (9) |
The generalized structure factor takes into account the broken translational invariance. Thus it is described by two discrete modes
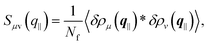 | (10) |
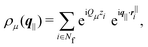 | (11) |
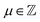 .
.
Both structure factors are complementary. The anisotropic structure factor S(q‖,q⊥) is often experimentally easier or solely accessible while the generalized structure factor Sμν(q‖) contains additional information. To illustrate this, the density-density correlation function G(r‖,z,z′)91 is represented in terms of the generalized structure factor Sμν(q‖),
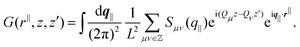 | (12) |
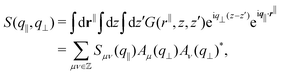 | (13) |
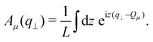 | (14) |
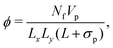 | (15) |
3 Results and discussion
The effects of confinement on colloidal fluids with moderate volume fractions were investigated. The fluids were confined by rough walls. The roughness is due to particles attached to the walls; ‘fixed wall particles’ and ‘immobile fluid particles’. The immobile fluid particles are identical to the (mobile) fluid particles except that they form part of the rough wall for an extended period of time and hardly move, whereas the fixed wall particles are slightly smaller and carry a higher charge than the fluid particles and are permanently part of the rough wall (Sections 2.1.2 and 2.2.2). The proportion of fixed wall particles and immobile fluid particles as well as their arrangement affect the roughness. Since the coverage and arrangement depend on minute details of the experimental preparation procedure, which are difficult to consistently perform (Section 2.1.2, Fig. 2), the roughness shows moderate variations and hence implicitly depends on the parameters varied in this study, namely the slit width and the volume fraction, although the coverage and arrangement do not directly depend on these parameters.The slit width is the central parameter in the present study. Because the specific thickness of the monolayer of fixed wall particles and immobile fluid particles depends on the details of the preparation, it is not useful to refer to the separation of the surfaces to which they are attached. Instead, we consider the distance L between the outermost peaks in the density profile of the fluid particles, i.e. not considering the fixed wall particles and immobile fluid particles, which is the separation of the two layers next to the fixed wall particles and immobile fluid particles at the bottom and at the top of the sample (Fig. 1). In the limit of flat walls, corresponding to uncovered walls and hence an infinitely thin layer of fixed wall particles and immobile fluid particles, this definition corresponds to the previously defined accessible slit width.18,23 In the following we will refer to L as the confinement length. The mentioned values of L are nominal values because the experimental and simulation values slightly differ.
In this study we varied the confinement length L and the volume fraction ϕ and investigated the effects of these parameters on the structure of the confined fluid. The particle arrangement in the slit is quantified by the density profile n(z), which characterizes the distribution perpendicular to the walls (Fig. 1, Section 3.1), and the two-dimensional radial distribution function g2Dz(r), which characterizes the arrangement parallel to the walls and is determined at wall distances corresponding to maxima in the density profile, zmax (Section 3.2). In addition, the anisotropic structure factor S(q‖,q⊥) and the generalized structure factor Sμν(q‖) provide information on the arrangement perpendicular and parallel to the walls (Section 3.3). The discussion of these parameters focuses on the most dilute, ϕ = 0.19, and most dense, ϕ = 0.32, samples because the results for intermediate volume fractions, ϕ = 0.20 and 0.28, lie in between these two cases and do not show qualitatively different behaviour.
3.1 Density profiles – layering
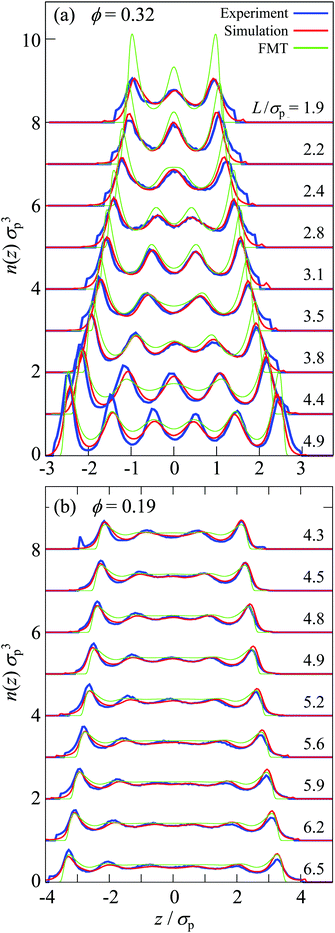
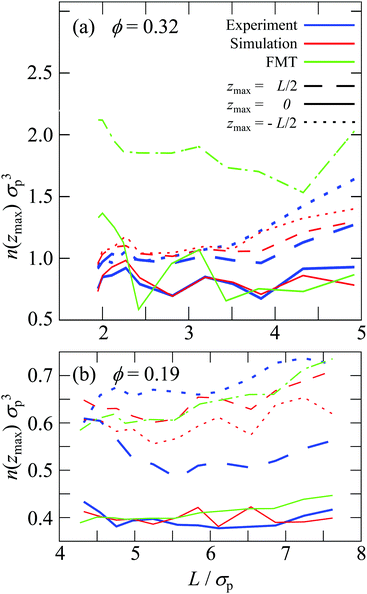
Perpendicular to the walls, the confinement leads to density variations. They are quantified by the density profile n(z) (eqn (6), Fig. 1) which was determined in experiments, simulations, and theory for different confinement lengths L and volume fractions ϕ. The density profile n(z) is only based on the mobile fluid particles thus disregarding the layers of fixed wall particles and immobile fluid particles.The sample with the highest volume fraction ϕ = 0.32 exhibits pronounced density variations (Fig. 3a). For the smallest confinement length L ≈ 2σp, the density profile n(z) shows three peaks. With increasing confinement length L, the central peak becomes more pronounced, then decreases and broadens to subsequently split into two distinct peaks. This sequence of increase, decrease and splitting of the central peak(s) is repeated upon further increasing the confinement length L. This is reflected in the height of the central peak or, in the case of two central peaks, the peak with z ≳ 0. It shows a non-monotonic dependence on the confinement length L (Fig. 4a, solid lines). The period of these oscillations is approximately one particle diameter σp. In contrast, the heights of the outermost peaks steadily increase with confinement length L (Fig. 4a, dashed and dotted lines) which might also be caused by accidental variations in the wall coverage (Fig. 2), as discussed below (Section 3.3.1). The sample with the lowest volume fraction, ϕ = 0.19, shows similar density variations which, however, are significantly less pronounced with respect to the amplitude of the modulations in n(z) as well as the non-monotonic dependence of the height of the central peak and the increase of the height of the outermost peaks (Fig. 3b and 4b).
The density profiles determined in experiments and simulations quantitatively agree, despite the complex boundaries and interaction potential. For all data sets of each sample, i.e. all confinement lengths L, only three adjustable parameters are involved, namely the inverse Debye length κ, the Yukawa-energy scale of the fluid particles, εY, and of the fixed wall particles, εwY (Section 2.2.3 with Table 1). Small deviations are observed for the outermost peaks, which are attributed to the empirical description and identification of the fixed wall particles and immobile fluid particles. In addition, there is a small bump in the experimental density profile for ϕ = 0.19 and L/σp = 4.3 at z/σp ≈ −3 which is due to misidentified immobile particles just outside the chosen range for immobile particles, ranging from Lw to Lim (Section 2.2.2). At large confinement length L and particularly for the largest volume fraction, ϕ = 0.32, also the other peaks show some differences between experiments and simulations. The simulations yield more symmetric density profiles whereas the experiments tend to show higher peaks at the bottom of the slit than at the top of the slit (compare the dashed and dotted lines in Fig. 4). This is attributed to moderate sedimentation during the experiments which has a stronger effect in thicker samples, i.e. larger L. While the tendency for sedimentation increases with particle size, a fractionation by particle size was not observed. Although the samples were carefully density matched (Section 2.1.1), a small density mismatch is sufficient to cause noticeable sedimentation due to the large particle size. For example, evaporation during the sample preparation might have caused not only a slight increase in volume fraction (which is taken into account, see Section 2.4.4) but, together with different evaporation rates of cis-decalin and CHB6, can change the composition of the solvent mixture and hence its density. In addition, due to different thermal expansion coefficients of the particles and the solvent mixture, small temperature variations might have led to minute density differences between the particles and the solvent mixture.
The density profile was also studied using fundamental-measure theory (FMT). It is based on a simplified soft wall potential and hard-sphere particle–particle interactions, thus disregarding the roughness of the wall and the electrostatic interactions (Section 2.3). Quantitative agreement is therefore not expected. Nevertheless, the behaviour qualitatively agrees with the experimental and simulation findings (Fig. 3) as well as previous theoretical and experimental results.6,27,29,33–35,45,58 For the highest volume fraction, ϕ = 0.32, strong modulations of the density profiles are observed which qualitatively agree with the experimental and simulation results (Fig. 3a) and are consistent with observations in previous studies comparing hard-spheres and charged spheres.33–35,45 However, for the lowest volume fraction, ϕ = 0.19, only moderate modulations of the density profiles are predicted (Fig. 3b). They are weaker than observed in experiments and simulations, which is attributed to the missing electrostatic interactions. Furthermore, the height of the central peak as determined by FMT shows variations with the confinement length L. The period of the variations is also approximately a particle diameter σp but the amplitude of the variations is more pronounced (Fig. 4a, green solid line).
3.2 Radial distribution function – packing
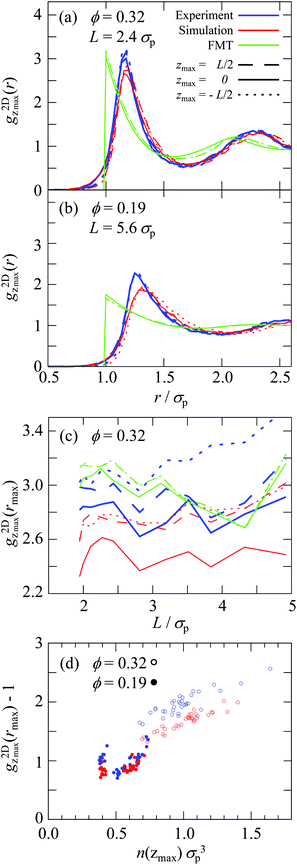
Having analyzed the density profiles describing the layering, we now turn to the packing within the layers. The packing is quantified by the two-dimensional radial distribution function (2D-RDF) g2Dz(r) in planes parallel to the walls and at different positions within the slit, z, where the packing around the maxima in the density profile are of particular interest (eqn (7), Fig. 1). The 2D-RDF was determined based on confocal microscopy images. Confocal microscopy provides the necessary spatial resolution in z direction. This allows to identify the layers parallel to the walls and avoids averaging in z direction and hence mixing the different layers.For all volume fractions ϕ, confinement lengths L and positions z, the g2Dz(r) are qualitatively similar and indicate well-developed shells. Representative g2Dz(r) are shown in Fig. 5a and b. The g2Dz(r) determined by experiments and simulations are very similar with only small but significant differences. In particular, in the simulations the first peak is slightly lower and broader, especially for the less dense sample (Fig. 5a and b). This indicates a slightly less pronounced order but a very similar number of particles in the first shell, variations are found to be smaller than 3%. This is most likely due to the modelling of the electrostatic interactions (Section 2.2.1), consistent with the stronger discrepancy in the less dense sample in which electrostatic interactions are more important.
For the highest volume fraction, ϕ = 0.32, the first maximum of 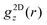 , that is
, that is 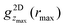 , is smaller in the center of the samples, zmax = 0, than next to the walls, zmax = ±L/2, (Fig. 5a and c) whereas for the lowest volume fraction, ϕ = 0.19, no significant dependence on the position z has been observed beyond the expected statistical uncertainty (Fig. 5b). Also for ϕ = 0.32 the differences are small but significant and observed for all confinement lengths L in experiments and simulations. Furthermore, for all positions z, the height of the first maximum shows modulations with a period of approximately one particle diameter σp. Although these modulations are clearly visible, their amplitude is relatively small. The difference between the central, z = 0, and outermost, z = ±L/2, layers as well as the non-monotonic behavior as a function of the confinement length L resemble the behaviour of the density profiles (Fig. 4a). This indicates that the packing strongly depends on the local density.
, is smaller in the center of the samples, zmax = 0, than next to the walls, zmax = ±L/2, (Fig. 5a and c) whereas for the lowest volume fraction, ϕ = 0.19, no significant dependence on the position z has been observed beyond the expected statistical uncertainty (Fig. 5b). Also for ϕ = 0.32 the differences are small but significant and observed for all confinement lengths L in experiments and simulations. Furthermore, for all positions z, the height of the first maximum shows modulations with a period of approximately one particle diameter σp. Although these modulations are clearly visible, their amplitude is relatively small. The difference between the central, z = 0, and outermost, z = ±L/2, layers as well as the non-monotonic behavior as a function of the confinement length L resemble the behaviour of the density profiles (Fig. 4a). This indicates that the packing strongly depends on the local density.
To investigate the relation between the packing and local density, the correlation between 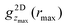 and n(zmax) is investigated. A correlation is indeed found (Fig. 5d). Irrespective of the volume fraction ϕ, confinement length L and position zmax, a general dependence of the packing, quantified by
and n(zmax) is investigated. A correlation is indeed found (Fig. 5d). Irrespective of the volume fraction ϕ, confinement length L and position zmax, a general dependence of the packing, quantified by 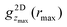 , and the local density, quantified by n(zmax), is observed, except for the above-mentioned slightly lower (and broader) peak in the simulations.
, and the local density, quantified by n(zmax), is observed, except for the above-mentioned slightly lower (and broader) peak in the simulations.
The FMT allows for a direct evaluation of g2Dz(r) based on the direct correlation function (Section 2.3). Since only hard-sphere particle–particle interactions and a flat soft wall instead of a rough wall are considered, no quantitative agreement with the results from experiments and simulations is expected. In particular, the pure hard-sphere interactions lead to the jump of g2Dz(r) at contact, i.e. r = σp. The g2Dz(r) of FMT is closer to the experimental and simulation findings for the sample with the high volume fraction, ϕ = 0.32, in which hard-sphere interactions dominate, than the less dense sample, ϕ = 0.19, in which electrostatic interactions are more important. This particularly concerns the height of the first maximum and the relative heights in the central and outermost layers, although the difference between the central and outermost layers is much smaller (Fig. 5a–c). The slightly stronger packing in the central compared to the outermost layers predicted for the low volume fraction (Fig. 5b) is due to the fact that, at the positions of the outermost layers, the direct correlation function has already considerably decayed due to the rapid decay of the density to zero (Fig. 3b), and therefore is a technical artifact and also prohibits a reliable determination of 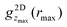 as a function of n(zmax) (Fig. 5d).
as a function of n(zmax) (Fig. 5d).
3.3 Structure factors – layering and packing
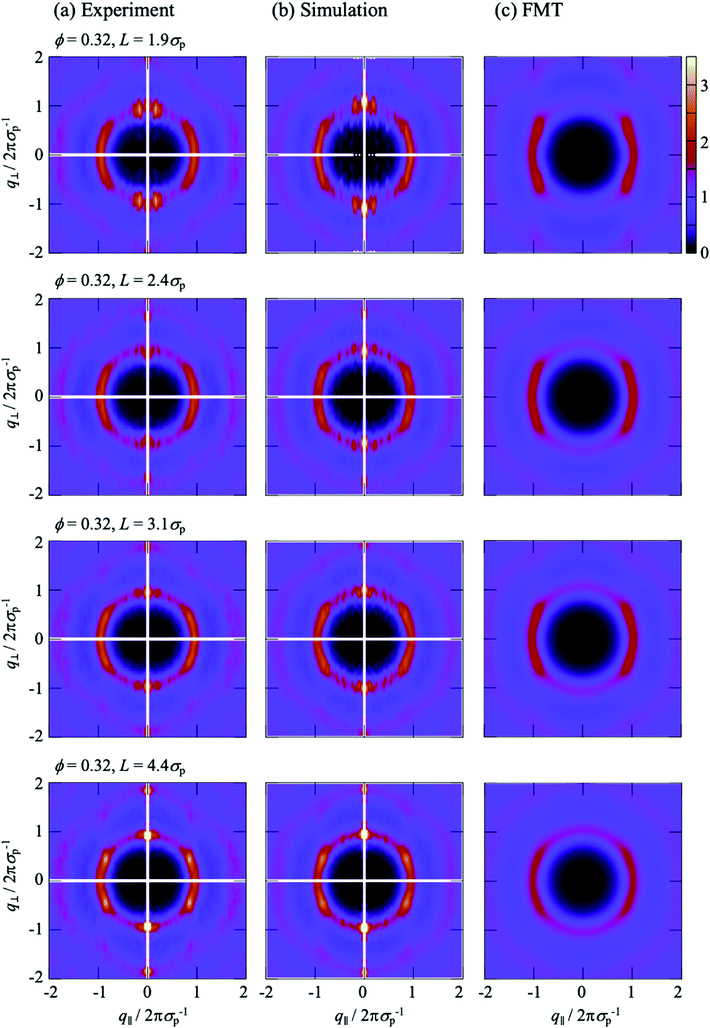
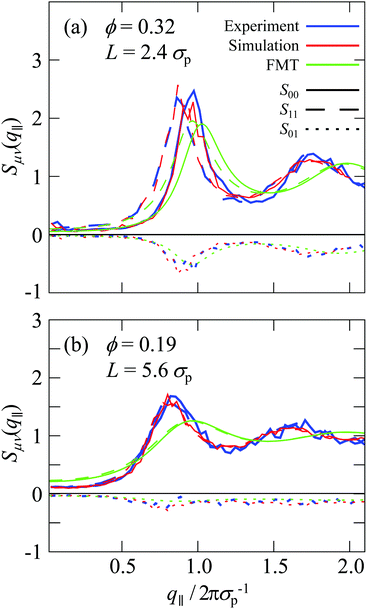
All experimental results were obtained using imaging and hence in real space. Nevertheless, in the following we will consider the effects of confinement on the particle arrangement in terms of the structure factor, which characterizes the arrangement in wavevector space and provides an average across the slit. It is usually determined in scattering experiments. Typically the anisotropic structure factor S(q‖,q⊥) is obtained. In addition, we calculate the generalized structure factor Sμν(q‖) (Section 2.4.3). The structure factor enables a direct comparison with results from scattering experiments and highlights aspects of the packing that are less obvious in real space. As for the density profile n(r) and the 2D-RDF g2Dz(r), only the Nf mobile fluid particles are taken into account whereas the fixed wall particles and the immobile fluid particles are not considered (Section 2.4).The experimental and simulation results quantitatively agree with each other (Fig. 6a, b and 7a, b). They, however, refer to a more complex situation than considered with FMT due to the combination of hard-sphere and electrostatic interactions and especially due to the roughness of the walls. Nevertheless, there are several similarities. Most prominent, the S(q‖,q⊥) from experiments and simulations also show two extended peaks for (q‖,q⊥) ≈ (±2πσp−1,0) indicating pronounced order parallel to the walls. With increasing confinement length L and decreasing volume fraction ϕ, the two peaks evolve towards modulated rings, similar to previous observations in a similar system.29 This corresponds to the pronounced and z independent shell structure indicated by the 2D-RDF g2Dz(r) (Fig. 5a–c), as described above for the FMT data.
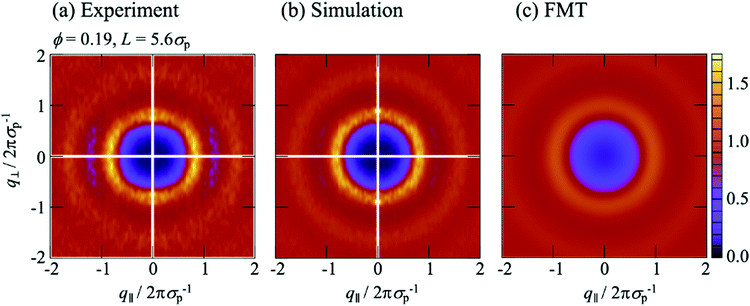
The S(q‖,q⊥) from experiments and simulations also show modulations perpendicular to the walls at q⊥ = 2πσp−1 and 4πσp−1, similar to the S(q‖,q⊥) from FMT and in agreement with the density profiles n(z) (Fig. 3). There are, however, also additional features. Pronounced peaks are observed at (q‖,q⊥) ≈ (0,±2πσp−1) for all confinement lengths L and, although with different intensities, also for all volume fractions ϕ. Further peaks at (0,±4πσp−1) are visible at least for the highest volume fraction ϕ = 0.32. For L = 1.95σp and less so for L = 2.43σp, these peaks at very small q‖≈0 are accompanied by peaks at larger but still small q‖, approximately (±0.2 × 2πσp−1,±2πσp−1). These peaks at very small and small q‖ have not been reported before, possibly because the diffraction from the confining walls masks them in scattering experiments or because practically flat walls were investigated.6,29 Since these peaks occur in experiments and simulations with rough walls (Fig. 6a, b and 7a, b) but not in the presence of flat walls (Fig. 6c and 7c), they are believed to be due to the roughness of the walls.
To investigate the effects of the wall roughness, S(q‖,q⊥) was determined in simulations for the experimental walls as well as increasingly modified walls (Fig. 8a). In the experiments, the walls are formed by fixed wall particles and immobile fluid particles (Section 2.2.2). The roughness, especially its range of length scales, depends on the ratio of fixed wall particles to immobile fluid particles since their sizes and charges are different (Section 2.2.3 with Table 1). Two cases are investigated; a similar fraction of both species and hence a particularly rough wall with a roughness on a broad range of length scales (Fig. 2, left; Fig. 8b) and mainly fixed wall particles and hence a more homogeneous rough wall with a roughness on a limited range of length scales (Fig. 2, right; Fig. 8c). (Note that the link between the roughness and the confinement length L is accidental.) The experimental findings (Fig. 8b and c, top left quadrant; identical to Fig. 6a, top and bottom respectively; note that all four quadrants in Fig. 6 refer to the same conditions) are well reproduced by the simulations (Fig. 8b and c, top right quadrant; identical to Fig. 6b, top and bottom respectively), as already discussed in the context of Fig. 6a and b. First the particularly rough wall is modified (Fig. 8b). The fixed wall particles are retained but the immobile fluid particles are replaced by mobile fluid particles (Fig. 8b, bottom right quadrant). The pronounced peak at very small q‖ is now weaker and the peak at small q‖ disappeared. This indicates that the roughness-related order on the smaller length scale, which still corresponds to a few particle sizes, is reduced while the order on a larger length scale is essentially unaffected. This is attributed to the replacement of immobile fluid particles that represent a fixed roughness by mobile fluid particles that result in a time-averaged, reduced roughness. In addition, the heterogeneity on a larger length scale, caused by the presence of fixed wall particles and mobile fluid particles, essentially remains. This is consistent with the case of the less rough walls (Fig. 8c); only a few immobile fluid particles are present and, correspondingly, no pronounced peak at small q‖ is observed whereas a pronounced peak is detected at very small q‖. In addition, the better agreement of the experimental data with the simulation data obtained in the presence of immobile particles indicates that describing the fluid particles in the uncovered regions as immobile is justified (Section 2.2.2).
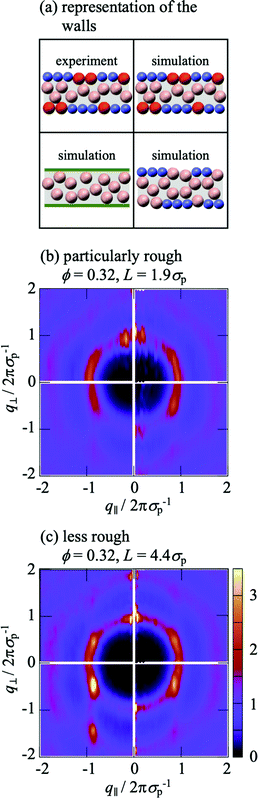 | ||
| Fig. 8 Anisotropic structure factor S(q‖,q⊥) as a function of the magnitudes of the wavevector components in parallel, q‖, and perpendicular, q⊥, direction to the walls normalized by the particle diameter σp. As indicated in (a), experimental data are shown in the top left quadrant, whereas the other quadrants show simulation data. The top right quadrant shows the results of the simulations that mimic the experimental situation with fluid particles (pink) confined by fixed wall particles (blue) and immobile fluid particles (red); the bottom right quadrant shows the results of the simulations that omit the immobile fluid particles and hence the fluid particles are confined by fixed wall particles and the gaps are filled by mobile fluid particles; the bottom left quadrant shows the results of simulations omitting the immobile fluid particles and the fixed wall particles and hence the fluid particles are confined by flat hard walls (green); The walls in the experiments are (b) particularly rough, i.e. heterogeneous due to a large fraction of immobile fluid particles (Fig. 2, left), and (c) less rough, i.e. more homogeneous due to a small fraction of immobile fluid particles (Fig. 2, right). The volume fraction ϕ = 0.32. | ||
If the fixed wall particles are successively removed, the peaks at small and very small q‖ gradually vanish in the case of both, the particularly rough and less rough wall (data not shown). Once all fixed wall particles are replaced by a flat hard wall (Fig. 8a, bottom left quadrant), all peaks at small and very small q‖ vanish and the obtained S(q‖,q⊥) (Fig. 8b and c, bottom left quadrant) resembles the one theoretically predicted for a flat wall (Fig. 6c). In summary, these observations indicate that the roughness of the wall is indeed responsible for the arrangement of the mobile fluid particles that results in the additional peaks. The peak at small q‖ seems to reflect the particle arrangement induced by the roughness due to the immobile fluid particles. In contrast, the peak at very small q‖ is mainly due to the longer-range heterogeneity of the fixed wall particles. Moreover, a comparison of the effects of a particularly rough and a less rough wall (Fig. 8b and c) reveals that the roughness mainly affects the ordering in the layers parallel to the walls, i.e. the dependence of S(q‖,q⊥) on q‖, whereas the layering perpendicular to the walls is only affected by the details of the roughness if the roughness is only moderate. These results also illustrate that a faithful representation of the experimental wall in the simulations requires to carefully take into account the fixed wall particles as well as the immobile fluid particles.
Beyond the diagonal element, the generalized structure factor Sμν(q‖) also reflects the broken translational invariance perpendicular to the walls, which is not reflected in the anisotropic structure factor S(q‖,q⊥). The lowest mode that highlights this effect is S01(q‖) which is given by (eqn (10) and (11))
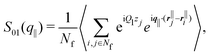 | (16) |
4 Conclusions
The structure of colloidal fluids confined between rough walls has been investigated. The colloids were imaged using confocal microscopy and the experimental situation mimicked in computer simulations. The results from experiments and simulations were compared to predictions based on fundamental-measure theory for a more basic situation, namely hard-spheres confined between flat soft walls. For a detailed description of the fluid structure, several structural parameters were determined that describe the layering and packing. Specifically, the layering is characterized by the density profile perpendicular to the walls, n(z), the packing within these layers is quantified by the two-dimensional radial distribution function g2Dz(r) in layers parallel to the walls and both is contained in the anisotropic, S(q‖,q⊥), as well as the generalized, Sμν(q‖), structure factors. Although an imaging technique was used and hence real-space information was obtained, the structure factors were determined to achieve a more detailed characterization of the fluid structure but also to allow for a better comparison to previous experimental, simulation and theoretical work.The structure of the fluid is dominated by excluded volume effects and hence the hard-sphere particle–particle interactions. However, charges are found to significantly contribute in the lower-volume-fraction samples, where excluded volume effects are less prominent. Electrostatic interactions particularly affect the packing whereas the layering is less affected. This is indicated by the agreement between theory, which neglects electrostatic interactions, and experiments as well as simulations, which is better for the density profile n(z) than the two-dimensional radial distribution function g2Dz(r).
The structure of the confined fluid was shown to strongly depend on the details of the confining walls. Compared to flat walls, rough walls lead to distinct peaks in the structure factor and hence a more pronounced arrangement. By modifying the walls and their roughness, the peaks could be related to the properties of the rough wall. The properties of the walls could hence be linked to the fluid structure that they impose. The strong and complex effects of the wall furthermore imply that it is crucial to accurately mimic the experimental situation in simulations. The agreement between experiments and simulations provides confidence in the procedure applied in our simulations. The developed experimental protocol and computer model can now be exploited to investigate the dynamics of confined fluids, including denser systems.
Author contributions
T. F. and S. U. E. conceived the project. A. V. B. performed and analyzed the experiments and provided input to the simulations, A. B. Z. B. contributed to the sample preparation and experimental realization, and G. J. performed and analyzed the simulations and FMT calculations. All authors contributed to the interpretation of the data and the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Manuel A. Escobedo-Sánchez for the synthesis of the particles and his expert help with their handling. We gratefully acknowledge funding by the Fonds zur Förderung der wissenschaftlichen Forschung (FWF, Austrian Science Fund, grant I5257-N) and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, grant EG 269/7-1, project number 383534318) as well as the Federal Ministry for Economic Affairs and Energy (BMWi) and the German Aerospace Center (DLR) through project SoMaDy-II (50WM1946). AVB acknowledges financial support provided by Conacyt (No. CVU 417675).References
- M. Schmidt and H. Löwen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 7228 CrossRef CAS.
- A. Fortini and M. Dijkstra, J. Phys.: Condens. Matter, 2006, 18, L371–L378 CrossRef CAS PubMed.
- H. Löwen, J. Phys.: Condens. Matter, 2009, 21, 474203 CrossRef PubMed.
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed.
- B. Götzelmann and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 2993 CrossRef.
- K. Nygård, R. Kjellander, S. Sarman, S. Chodankar, E. Perret, J. Buitenhuis and J. F. van der Veen, Phys. Rev. Lett., 2012, 108, 037802 CrossRef PubMed.
- K. Nygård, Curr. Opin. Colloid Interf. Sci., 2016, 22, 30 CrossRef.
- K. Nygård, S. Sarman, K. Hyltegren, S. Chodankar, E. Perret, J. Buitenhuis, J. F. van der Veen and R. Kjellander, Phys. Rev. X, 2016, 6, 011014 Search PubMed.
- D. Wang, M. Hermes, R. Kotni, Y. Wu, N. Tasios, Y. Liu, B. de Nijs, E. B. van der Wee, C. B. Murray, M. Dijkstra and A. van Blaaderen, Nat. Commun., 2018, 9, 2228 CrossRef PubMed.
- S. Mizani, R. Aliabadi, H. Salehi and S. Varga, Phys. Rev. E, 2019, 100, 032704 CrossRef CAS PubMed.
- X. Yao and J. Z. Y. Chen, Phys. Rev. E, 2020, 101, 062706 CrossRef CAS PubMed.
- J. Mittal, T. M. Truskett, J. R. Errington and G. Hummer, Phys. Rev. Lett., 2008, 100, 145901 CrossRef PubMed.
- A. Patti and A. Cuetos, Phys. Fluids, 2021, 33, 097103 CrossRef CAS.
- J. Mittal, J. R. Errington and T. M. Truskett, Phys. Rev. Lett., 2006, 96, 177804 CrossRef PubMed.
- S. Granick, Science, 1991, 253, 1374 CrossRef CAS PubMed.
- S. Lang, R. Schilling, V. Krakoviack and T. Franosch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021502 CrossRef PubMed.
- M. Alcoutlabi and G. B. McKenna, J. Phys.: Condens. Matter, 2005, 17, R461 CrossRef CAS.
- S. Lang, V. Botan, M. Oettel, D. Hajnal, T. Franosch and R. Schilling, Phys. Rev. Lett., 2010, 105, 125701 CrossRef PubMed.
- S. Mandal, S. Lang, M. Gross, M. Oettel, D. Raabe, T. Franosch and F. Varnik, Nat. Commun., 2014, 5, 4435 CrossRef CAS PubMed.
- F. Varnik and T. Franosch, J. Phys.: Condens. Matter, 2016, 28, 133001 CrossRef PubMed.
- L. Schrack and T. Franosch, Philos Mag., 2020, 100, 1032–1057 CrossRef CAS PubMed.
- K. H. Nagamanasa, S. Gokhale, A. K. Sood and R. Ganapathy, Nat. Phys., 2015, 11, 403 Search PubMed.
- G. Jung, M. Caraglio, L. Schrack and T. Franosch, Phys. Rev. E, 2020, 102, 012612 CrossRef CAS PubMed.
- G. Jung, L. Schrack and T. Franosch, Phys. Rev. E, 2020, 102, 032611 CrossRef CAS PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 3rd edn, 2006 Search PubMed.
- K. Binder, Annu. Rev. Mater. Res., 2008, 38, 123 CrossRef CAS.
- R. Kjellander and S. Sarman, J. Chem. Soc. Farad. Trans., 1991, 87, 1869–1881 RSC.
- K. Nygård, S. Sarman and R. Kjellander, J. Chem. Phys., 2014, 141, 094501 CrossRef PubMed.
- K. Nygård, S. Sarman and R. Kjellander, J. Chem. Phys., 2013, 139, 164701 CrossRef PubMed.
- K. Nygård, Phys. Chem. Chem. Phys., 2017, 19, 23632–23641 RSC.
- R. Kjellander and S. Sarman, Mol. Phys., 1991, 74, 665–688 CrossRef CAS.
- R. Kjellander and S. Sarman, Mol. Phys., 1990, 70, 215–237 CrossRef CAS.
- O. Bunk, A. Diaz, F. Pfeiffer, C. David, B. Schmitt, D. K. Satapathy and J. F. van der Veen, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 306–314 CrossRef CAS PubMed.
- O. Bunk, A. Diaz, F. Pfeiffer, C. David, C. Padeste, H. Keymeulen, P. R. Willmott, B. D. Patterson, B. Schmitt, D. K. Satapathy, J. F. van der Veen, H. Guo and G. H. Wegdam, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021501 CrossRef PubMed.
- O. Bunk, D. K. Satapathy, F. Pfeiffer, A. Diaz, C. David, K. Nygård, E. Perret, C. Padeste, P. R. Willmott, B. D. Patterson, B. Schmitt and J. F. van der Veen, Chimia, 2008, 62, 789–792 CrossRef CAS.
- R. Kjellander and S. Sarman, Chem. Phys. Lett., 1988, 149, 102 CrossRef CAS.
- C. F. Petersen, L. Schrack and T. Franosch, J. Stat. Mech. Theo. Exp., 2019, 2019, 083216 CrossRef.
- D. Henderson, S. Sokolowski and D. Wasan, J. Stat. Phys., 1997, 89, 233–247 CrossRef.
- R. G. Horn and J. N. Israelachvili, J. Chem. Phys., 1981, 75, 1400 CrossRef CAS.
- J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 4722–4724 CrossRef CAS.
- S. Klapp, Y. Zeng, D. Qu and R. von Klitzing, Phys. Rev. Lett., 2008, 100, 118303 CrossRef PubMed.
- M. Heuberger, M. Zäch and N. D. Spencer, Science, 2001, 292, 905 CrossRef CAS PubMed.
- O. H. Seeck, K. Hyunjung, D. R. Lee, D. Shu, I. D. Kaendler, J. K. Basu and S. K. Sinha, Europhys. Lett., 2002, 60, 376–382 CrossRef CAS.
- M. J. Zwanenburg, H. H. Bongaerts, J. F. Peters, D. O. Riese and J. F. van der Veen, Phys. Rev. Lett., 2000, 85, 5154 CrossRef CAS PubMed.
- D. K. Satapathy, O. Bunk, K. Jefimovs, K. Nygård, H. Guo, A. Diaz, E. Perret, F. Pfeiffer, C. David, G. H. Wegdam and J. F. van der Veen, Phys. Rev. Lett., 2008, 101, 136103 CrossRef CAS PubMed.
- K. Nygård, D. K. Satapathy, O. Bunk, A. Diaz, E. Perret, J. Buitenhuis, F. Pfeiffer, C. David and J. F. van der Veen, Opt. Exp., 2008, 16, 20522–20529 CrossRef PubMed.
- K. Nygård, D. K. Satapathy, O. Bunk, E. Perret, J. Buitenhuis, C. David and J. F. van der Veen, J. Appl. Cryst., 2009, 42, 1129–1138 CrossRef.
- D. K. Satapathy, K. Nygård, O. Bunk, K. Jefimovs, E. Perret, A. Diaz, F. Pfeiffer, C. David and J. F. van der Veen, Europhys. Lett., 2009, 87, 34001 CrossRef.
- K. Nygård, D. K. Satapathy, J. Buitenhuis, E. Perret, O. Bunk, C. David and J. F. van der Veen, Europhys. Lett., 2009, 86, 66001 CrossRef.
- K. Nygård, J. Buitenhuis, M. Kagias, K. Jefimovs, F. Zontone and Y. Chushkin, Phys. Rev. E, 2017, 95, 062601 CrossRef PubMed.
- P. Pieranski, L. Strzelecki and B. Pansu, Phys. Rev. Lett., 1983, 50, 900 CrossRef CAS.
- D. H. Van Winkle and C. A. Murray, J. Chem. Phys., 1988, 89, 3885 CrossRef.
- C. A. Murray and D. G. Grier, Annu. Rev. Phys. Chem., 1996, 47, 421 CrossRef CAS.
- A. Barreira Fontecha, H. J. Schöpe, H. König, T. Palberg, R. Messina and H. Löwen, J. Phys.: Condens. Matter, 2005, 17, S2779–S2786 CrossRef.
- A. Barreira Fontecha, T. Palberg and H. J. Schöpe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 050402R CrossRef PubMed.
- C. R. Nugent, K. V. Edmond, H. N. Patel and E. R. Weeks, Phys. Rev. Lett., 2007, 99, 025702 CrossRef PubMed.
- K. V. Edmond, C. R. Nugent and E. R. Weeks, Eur. Phys. J. Special Topics, 2010, 189, 83–93 CrossRef CAS.
- K. V. Edmond, C. R. Nugent and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041401 CrossRef PubMed.
- H. Serna, W. T. Gozdz and E. G. Noya, Int. J. Mol. Sci., 2021, 22, 11050 CrossRef PubMed.
- P. Scheidler, W. Kob and K. Binder, J. Phys. IV France, 2000, 10, 33–36 Search PubMed.
- P. Scheidler, W. Kob and K. Binder, Europhys. Lett., 2000, 52, 277 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, Europhys. Lett., 2002, 59, 701–707 CrossRef CAS.
- P. Scheidler, W. Kob and K. Binder, Eur. Phys. J. E, 2003, 12, 5–9 CrossRef CAS PubMed.
- P. Scheidler, W. Kob and K. Binder, J. Phys. Chem. B, 2004, 108, 6673–6686 CrossRef CAS.
- J. Koppensteiner, W. Schranz and M. R. Puica, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054203 CrossRef.
- H. B. Eral, D. van der Ende, F. Mugele and M. H. G. Duits, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061403 CrossRef CAS PubMed.
- W. P. Krekelberg, V. K. Shen, J. R. Errington and T. M. Truskett, J. Phys. Chem., 2011, 135, 154502 CrossRef PubMed.
- B. Mei, Y. Lu, L. An, H. Li and L. Wang, Phys. Rev. E, 2017, 95, 050601R CrossRef PubMed.
- B. M. G. D. Carter, C. P. Royall, J. C. Dyre and T. S. Ingebrigtsen, Soft Matter, 2021, 17, 8662 RSC.
- H. B. Eral, F. Mugele and M. H. G. Duits, Langmuir, 2011, 27, 12297–12303 CrossRef CAS PubMed.
- C. Cao, X. Huang and C. B. Roth, J. Chem. Phys., 2017, 147, 224505 CrossRef PubMed.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78 CrossRef CAS.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- G. N. Smith, J. E. Hallett and J. Eastoe, Soft Matter, 2015, 11, 8029–8041 RSC.
- M. N. van der Linden, J. C. P. Stiefelhagen, G. Heessels-Guürboga, J. E. S. van der Hoeven, N. A. Elbers, M. Dijkstra and A. van Blaaderen, Langmuir, 2015, 31, 65–75 CrossRef CAS PubMed.
- U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Science, 2001, 292, 258–262 CrossRef CAS PubMed.
- W. Schaertl and H. Sillescu, J. Stat. Phys., 1994, 77, 1007–1025 CrossRef.
- P. J. Lu, F. Giavazzi, T. E. Angelini, E. Zaccarelli, F. Jargstorff, A. B. Schofield, J. N. Wilking, M. B. Romanowsky, D. A. Weitz and R. Cerbino, Phys. Rev. Lett., 2012, 108, 218103 CrossRef PubMed.
- C. Urban and P. Schurtenberger, J. Colloid Interface Sci., 1998, 207, 150–158 CrossRef CAS PubMed.
- A. Stukowski, Modelling Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- D. B. Allan, T. Caswell, N. C. Keim and C. M. van der Wel, soft-matter/trackpy: Trackpy v0.4.2, 2019 DOI:10.5281/zenodo.3492186.
- C. P. Royall, W. C. K. Poon and E. R. Weeks, Soft Matter, 2013, 9, 17–27 RSC.
- G. Jung and C. F. Petersen, Phys. Rev. Res., 2020, 2, 033207 CrossRef CAS.
- Y. Rosenfeld, Phys. Rev. Lett., 1989, 63, 980–983 CrossRef CAS PubMed.
- R. Roth, J. Phys.: Condens. Matter, 2010, 22, 063102 CrossRef PubMed.
- D. M. Heyes and A. Santos, J. Chem. Phys., 2018, 148, 214503 CrossRef PubMed.
- D. Deb, A. Winkler, M. H. Yamani, M. Oettel, P. Virnau and K. Binder, J. Chem. Phys., 2011, 134, 214706 CrossRef PubMed.
- Fundamentals of Inhomogeneous Fluids, ed. D. Henderson, Marcel Dekker, Inc., New York, NY, 1992 Search PubMed.
- S. Lang, Glass transition in confined geometries described by mode-coupling theory, Diploma thesis, Johannes Gutenberg-Universität Mainz, 2010.
- S. Lang, T. Franosch and R. Schilling, J. Chem. Phys., 2014, 140, 104506 CrossRef PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |