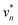Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Collapse of a hemicatenoid bounded by a solid wall: instability and dynamics driven by surface Plateau border friction†
Christophe
Raufaste
 a,
Simon
Cox
a,
Simon
Cox
 b,
Raymond E.
Goldstein
b,
Raymond E.
Goldstein
 c and
Adriana I.
Pesci
d
c and
Adriana I.
Pesci
d
aUniversité Côte d'Azur, CNRS, Institut de Physique de Nice (INPHYNI), 06100 Nice, France and Institut Universitaire de France (IUF), 75005 Paris, France. E-mail: christophe.raufaste@univ-cotedazur.fr
bDepartment of Mathematics, Aberystwyth University, Aberystwyth, Ceredigion, SY23 3BZ, UK. E-mail: simon.cox@aber.ac.uk
cDepartment of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK. E-mail: r.e.goldstein@damtp.cam.ac.uk
dDepartment of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK. E-mail: a.i.pesci@damtp.cam.ac.uk
First published on 22nd June 2022
Abstract
The collapse of a catenoidal soap film when the rings supporting it are moved beyond a critical separation is a classic problem in interface motion in which there is a balance between surface tension and the inertia of the surrounding air, with film viscosity playing only a minor role. Recently [Goldstein et al., Phys. Rev. E, 2021, 104, 035105], we introduced a variant of this problem in which the catenoid is bisected by a glass plate located in a plane of symmetry perpendicular to the rings, producing two identical hemicatenoids, each with a surface Plateau border (SPB) on the glass plate. Beyond the critical ring separation, the hemicatenoids collapse in a manner qualitatively similar to the bulk problem, but their motion is governed by the frictional forces arising from viscous dissipation in the SPBs. We present numerical studies of a model that includes classical laws in which the frictional force fv for SPB motion on wet surfaces is of the form fv ∼ Can, where Ca is the capillary number. Our experimental data on the temporal evolution of this process confirms the expected value n = 2/3 for mobile surfactants and stress-free interfaces. This study can help explain the fragmentation of bubbles inside very confined geometries such as porous materials or microfluidic devices.
1 Introduction
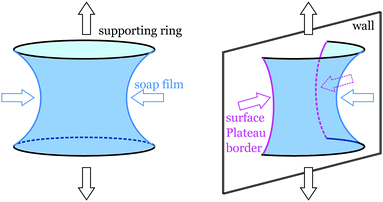
Free-boundary problems involving the collapse of unstable minimal surfaces generally fall into two main categories: either the ultimate singularity and surface reconnection occur in the bulk, far from any supporting boundaries, or they occur at the boundary itself. A bulk singularity is found in the classical problem of a collapsing catenoid supported by two rings, which was first studied by Plateau1 and Maxwell2 in the XIXth century, whereas boundary singularities were only studied recently in the context of collapsing soap films with more exotic topologies.3–5 A typical example of a boundary singularity is found in the collapse of a Möbius strip soap film,3 first studied by Courant.6In all of these problems, the boundaries of the soap film are rigid “frames” that are fixed in position or subjected to infinitesimal changes to induce the collapse. In this paper, we study a distinct class of dynamics where part of the boundary of the film moves as a consequence of the surface evolution. In this context, the moving boundary problem gives rise to a boundary singularity. Specifically, we study a problem introduced briefly in earlier work7 consisting of a catenoid film supported in the usual way by two circular rings, but which is split into two hemicatenoids by a glass plate oriented perpendicularly to the rings, as in Fig. 1. The closed boundary of each half of the film thus consists of two rigid, stationary semicircular frames and two curved, movable surface Plateau borders (SPBs) connecting the intersections of those frames with the glass plate. The geometry of this system allows for a detailed experimental and computational study of the interplay between friction, three-dimensionality and singularity formation of moving fluid films. In particular, we show that wall friction, by determining a maximum sliding velocity of the film, prevents the divergence of velocity that would normally occur in the equivalent unbounded film. The computational support for this observation consists of the first numerical studies of 3D soap film motion in the presence of wall friction. Our computations are reminiscent of recent work on bulk dynamics of drops experiencing wall friction,8 but with a distinct rule for the relation between the motion of the soap film contact line and the contact angle.9
This is precisely of the class of problems studied by Courant10 as a generalization of the work of Douglas11,12 on the existence of minimal surfaces bounded completely by Jordan curves. It is one of a class of problems involving equilibrium capillary surfaces in contact with a wall, subject to various boundary conditions,13–15 as well as dynamical problems such as the motion of bubbles in tubes.16 As shown in cross section in Fig. 2, the lateral balance of forces that occurs in the surface Plateau borders involves the component of the force fγ parallel to the wall due to surface tension γ and the frictional force fv due to motion of the film at velocity v. In the case of a minimal surface, we know from Plateau's laws that the contact angle Ψ = π/2 and corresponds to equilibrium, i.e. v = 0. The dependence of fv on the sliding velocity v is a well-studied problem in foam rheology17,18 and is strongly correlated with the nature of the gas–liquid interfaces, whose properties lie between the limiting cases of a stress-free surface and an incompressible surface covered with surfactants.9 Here, in contrast to the case of foams, it is the three-dimensional shape of the soap film that drives the surface Plateau border motion and thereby controls the dynamics.
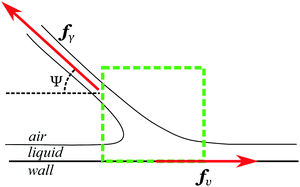 | ||
| Fig. 2 Momentum balance in a plane perpendicular to a surface Plateau border (region inside dashed green square) in contact with a wall. The thin soap film with contact angle Ψ relative to the wall experiences a surface tension force fγ parallel to itself and a frictional force fv opposing its motion due to the presence of the wall. After Cantat.9 | ||
The experimental setup in Fig. 1 is related to the general problem of a triple line that becomes unstable. Examples include the collapse of liquid or air bridges during dewetting19,20 and air entrainment in dynamic wetting.21–23 These situations are characterized by small bubbles and droplets, respectively, that are left behind on the substrate. The instability of liquid bridges is also central to the detachment of droplets from moving drops24–27 or liquid bridges.28–30 In each case, the dynamics is essentially that of a hemicatenoid in contact with a solid wall. For the case of soap films, the dynamics of a collapsing hemicatenoid is also relevant to bubble fragmentation inside foams confined in porous media31,32 or in microfluidic devices.33
We study the collapse of hemicatenoids in the geometry of Fig. 1, and compare the experimental measurements with a numerical model for the film evolution that incorporates the friction laws for surface Plateau border motion. The model exploits the separation of time scales between the fast film motion and the slow creep of the SPBs. Given this time-scale separation, the film can be approximated by a minimal surface that spans the support rings and the Plateau borders, and its local contact angle with the plate determines the SPB speed. This situation is similar to the retraction of a soap films inside an elastic ring,34 whose shape and dynamics are linked to surface tension on one side as well as on the elastic and inertial properties of the ring on the other side. In that spirit, the properties of the ring are replaced here by the frictional properties of the surface Plateau border.
In Section 2 of this paper we summarize the experimental methods used both in the study of hemicatenoid collapse and also in the related problem of SPB reconnection on surfaces described in the Discussion. The main experimental results are presented in Section 3, while the formulation of the dynamical model used in numerical studies is given in Section 4. Section 5 presents results of those studies and a comparison with experiments. The concluding discussion Section 6 connects these results to surface Plateau border reconnection and other problems in foams.
2 Experimental methods
As in previous work,7 soap solutions were obtained by dissolving tetradecyl trimethyl ammonium bromide (TTAB) into deionized water and adding glycerol in order to vary the viscosity. The concentration of TTAB was 3 g L−1 for the aqueous solution containing no glycerol and was raised to 6 g L−1 for the solutions containing glycerol to enhance the stability of the soap films. The viscosity η varies from 1.0 to 77 mPa s over the range of glycerol concentrations, while the surface tension is nearly constant at 35–38 mPa m.35,36 Fluorescein was added to aid visualization.In the experiments on hemicatenoids, a full catenoid is first formed between two coaxial circular rings of radius R = 4 cm, whose distance apart is adjusted with a micrometric linear stage. A glass plate of width slightly less than 2R and thickness of 1 mm was introduced and passes through the diameters of both rings. In this way we create two independent hemicatenoids that become unstable once the distance 2d between the rings becomes larger than a critical value.
In separate experiments on SPB reconnection discussed in Section 6, we used a different soap film chemistry to slow down the dynamics3 for accurate visualization. We used deformable, transparent tubing with a large diameter (6.4 mm) and a SLES/CAPB/SLES mixture37 known for its high dissipative properties.38 We mixed 6.6% of sodium lauryl ether sulfate (SLES) and 3.4% of cocamidopropylbetaine (CAPB) by weight in ultra pure water, and then dissolved 0.4% by weight of myristic acid (MAc), by stirring and heating at 60 °C for one hour. We then diluted this solution by a factor of 20 with water containing fluorescein at a concentration of 0.5 g L−1.
The dynamics of the collapsing soap films were recorded using a color high speed camera (Phantom V641, Ametek) at speeds up to 4000 frames per second while the films were illuminated from multiple directions with arrays of cyan LEDs. The ESI† includes a video of the collapse of a 3d catenoid and videos of collapsing hemicatenoids with η = 9.6 and 77 mPa s.
3 Experimental results
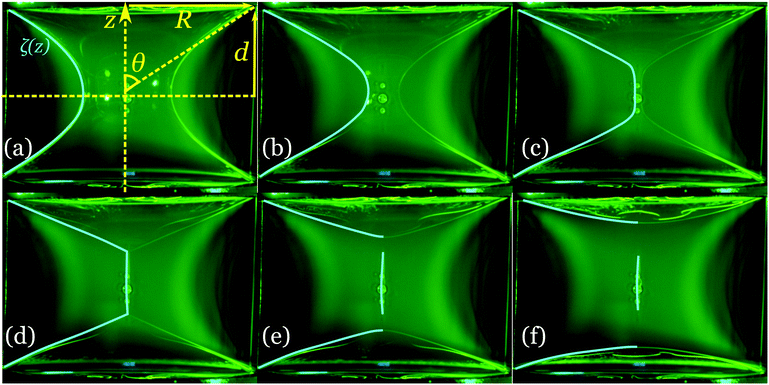
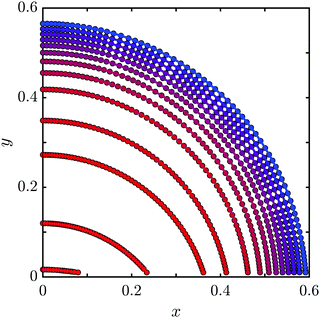
As is well known, a full catenoid spanning two circular frames a distance 2d apart becomes unstable when d/R exceeds the critical value 0.663…7 Using the setup shown schematically in Fig. 1, we found experimentally that essentially the same threshold exists in the case of a hemicatenoid. In capturing images of this process with a high-speed camera aimed along the normal to the plate, we naturally see two hemicatenoids, one in front and the other behind the plate. It is inevitable that they are slightly different due to imperfections in the setup, and therefore they tend to collapse at slightly different times. We therefore introduced a deliberate, infinitesimal bias in the position of the plate in order to assure that the hemicatenoid facing the camera would collapse last. The consequence of this is seen in Fig. 3, where the bubbles in the central region of the images are the satellite bubbles left over after the collapse of the hemicatenoid that was behind the plate. The cyan tracings in Fig. 3 indicate one of the two surface Plateau borders of the hemicatenoid facing the camera.The sequence of shapes of the SPB is strikingly similar to the equivalent sequence for three-dimensional catenoids obtained by taking longitudinal cross-sections in the plane of symmetry.7 We note in particular the evolution toward a shape consisting of two conical films connected by a quasi-cylindrical region (panel (c)), with a characteristic angle θ* ≃ 67.5° at the pinchoff time tp (panel (d)). After pinchoff, the two disjoint films still attached to the frame relax towards two half discs spanning the wire loops, while the remnants of the central cylinder slowly round up to form satellite bubbles, as seen in panel (f).
In quantifying the observed film shapes, we label the SPB location as ζ(z), and define7 the dimensionless radius r = ζ/a, where a = 0.5524R is the critical catenoid waist radius. Similarly, we use the half disc area to define the dimensionless film area ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = A/πR2, with
= A/πR2, with ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≃ 1.199… for the critical hemicatenoid and
≃ 1.199… for the critical hemicatenoid and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = 1 for the configuration with two hemidiscs. The area is calculated from the catenoid contour assuming axisymmetry. This requires that the contact angle on the glass is close to 90°, as observed in experiments. While we know that this is not strictly fulfilled at all space-time points in the experiments, it is a convenient simplification for the measurements. We have used the same assumption in the simulations to enable direct comparison of the two; the error in this approximation increases as the contact angle Ψ decreases away from 90° and pinchoff is approached.
= 1 for the configuration with two hemidiscs. The area is calculated from the catenoid contour assuming axisymmetry. This requires that the contact angle on the glass is close to 90°, as observed in experiments. While we know that this is not strictly fulfilled at all space-time points in the experiments, it is a convenient simplification for the measurements. We have used the same assumption in the simulations to enable direct comparison of the two; the error in this approximation increases as the contact angle Ψ decreases away from 90° and pinchoff is approached.
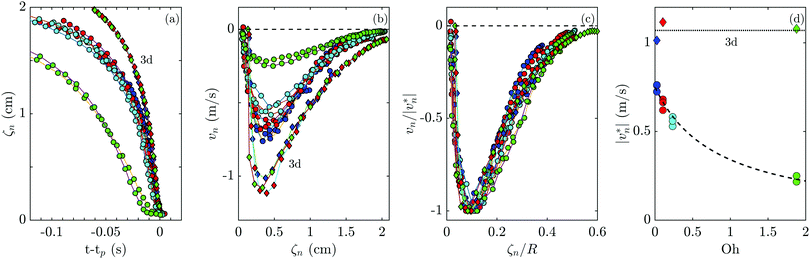
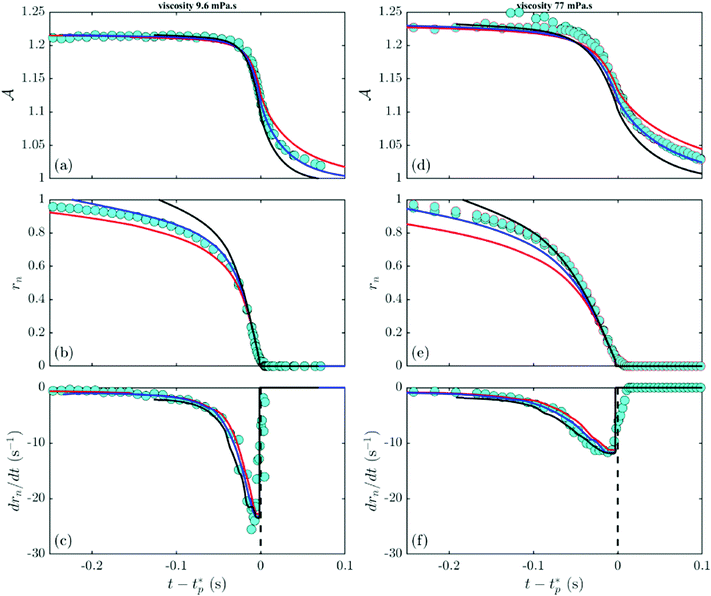
From the measured SPB locations we determine the time evolution of ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (t), the minimum neck radius ζn(t), and the neck contraction speed vn = dζn/dt for hemicatenoids and full catenoids (also with ring radius R = 4 cm). The data for ζn shown in Fig. 4a, for the four different values of the film viscosity indicated in the caption, illustrate how the contraction dynamics of even the least-viscous hemicatenoids is slower than the 3d case, and that the hemicatenoid dynamics progressively slows down with increasing viscosity. In contrast, the 3d data shows little if any dependence on viscosity, implying that the 3d balance of forces is between surface tension and air inertia.
(t), the minimum neck radius ζn(t), and the neck contraction speed vn = dζn/dt for hemicatenoids and full catenoids (also with ring radius R = 4 cm). The data for ζn shown in Fig. 4a, for the four different values of the film viscosity indicated in the caption, illustrate how the contraction dynamics of even the least-viscous hemicatenoids is slower than the 3d case, and that the hemicatenoid dynamics progressively slows down with increasing viscosity. In contrast, the 3d data shows little if any dependence on viscosity, implying that the 3d balance of forces is between surface tension and air inertia.
Fig. 4b plots the neck contraction speed vn as a function of the neck radius. From this we see that all the data sets display a maximum contraction speed at a neck radius 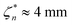 , independent of the film viscosity. This is clearly associated with the incipient formation of a central satellite droplet. The lack of variation with η, and the presence of the central plate, indicates that it is a geometric effect in the sense that
, independent of the film viscosity. This is clearly associated with the incipient formation of a central satellite droplet. The lack of variation with η, and the presence of the central plate, indicates that it is a geometric effect in the sense that 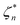 should scale with the loop radius R. This hypothesis is borne out by comparison with numerical studies of inviscid capillary breakup,39 where the maximum contraction speed is reached for ζn/R ≈ 0.1. While the radius of maximum contraction speed is common to both 3d catenoids and hemicatenoids, the neck radius at which the speed vanishes for hemicatenoids is approximately one half of that for the 3d case. This difference arises from the very different local geometries of the collapsing necks in the two cases. Whereas the 3d catenoid maintains axisymmetry during collapse, the hemicatenoids do not, as discussed in Section 4 below. When scaled by the maximum contraction speed
should scale with the loop radius R. This hypothesis is borne out by comparison with numerical studies of inviscid capillary breakup,39 where the maximum contraction speed is reached for ζn/R ≈ 0.1. While the radius of maximum contraction speed is common to both 3d catenoids and hemicatenoids, the neck radius at which the speed vanishes for hemicatenoids is approximately one half of that for the 3d case. This difference arises from the very different local geometries of the collapsing necks in the two cases. Whereas the 3d catenoid maintains axisymmetry during collapse, the hemicatenoids do not, as discussed in Section 4 below. When scaled by the maximum contraction speed 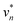 , the data for both 3d catenoids and hemicatenoids show an approximate collapse, as shown in Fig. 4(c).
, the data for both 3d catenoids and hemicatenoids show an approximate collapse, as shown in Fig. 4(c).
We can understand the crossover between inertial and viscous effects in film collapse by means of a scaling argument for characteristic film speeds U. Under inertial dynamics, we expect the Keller–Miksis40 scaling U ∼ (γ/Rρa)1/2 to hold, where ρa is the density of air, while in the viscous limit the speed U ∼ γ/η is associated with a capillary number of order unity.9 The ratio of these velocities defines the Ohnesorge number of this problem 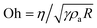 , where large (small) values correspond to frictional (inertial) dynamics, respectively. Fig. 4(d) shows the maximum contraction speed as a function of Oh. Note that for 3d catenoids there is no dependence on Oh, confirming that film viscosity plays no measurable role for this configuration. By contrast, for hemicatenoids there is a strong decrease with Oh, and the critical viscosity ηc for a balance between the two effects is at Oh ≃ 0.5, where the contraction speed is approximately half of the 3d value.
, where large (small) values correspond to frictional (inertial) dynamics, respectively. Fig. 4(d) shows the maximum contraction speed as a function of Oh. Note that for 3d catenoids there is no dependence on Oh, confirming that film viscosity plays no measurable role for this configuration. By contrast, for hemicatenoids there is a strong decrease with Oh, and the critical viscosity ηc for a balance between the two effects is at Oh ≃ 0.5, where the contraction speed is approximately half of the 3d value.
4 Model and simulations
A moving meniscus in contact with a wall (an SPB) experiences a frictional force per unit length whose form depends on the spatial distribution of dissipation, which itself depends on the stress and physical chemistry at the liquid–air interface. This dissipation can be written as the sum of two terms,9 both of which depend on the capillary number Ca = ηv/γ. The first term represents the contribution from dissipation inside the wetting film, and scales as Ca1/3, while the second is the contribution from dissipation inside the SPB, and scales as Ca2/3. The latter contribution is associated with mobile surfactants and stress-free interfaces. In general, both contributions are present and over a large range of Ca this combined frictional law can be approximated as fv ∼ Can with n in the range 1/2–2/3. This empirical law holds for other systems in which the frictional force is the dominant one in the balance with the capillary driving force, such as liquid and air bridges.The model we study here rests on this assumption, namely that the capillary forces are balanced by the viscous friction at the contact between the soap film and the glass plate. That contact consists of an SPB41 that connects the wetting film on the plate to the soap film. A slice through a plane perpendicular to this SPB (Fig. 2) shows that the driving force density is fγ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ, with fγ = 2γ. Balancing against the frictional force fv = AγCan, with A a dimensionless constant, we obtain
Ψ, with fγ = 2γ. Balancing against the frictional force fv = AγCan, with A a dimensionless constant, we obtain
v = v0(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ)1/n, Ψ)1/n, | (1) |
To apply this law to the evolution of hemicatenoids toward collapse, we exploit the separation of time scales between the motion of the bulk surface, resisted only by the inertia of the surrounding air, and that of the contact lines, and view the surface spanning the moving contact lines and the two half-rings as in quasi-equilibrium. It is therefore a minimal surface at any instant of time, but does not necessarily meet the glass plate with Ψ = π/2, as would be the case in static equilibrium in accordance with Plateau's laws. Instead, the contact line acts like a constraining wire, and the surface meets it at the angle that yields a minimal surface. Fig. 5 shows an experimental realization of this concept, where 3D printed frames, consisting of two half-circular loops connected by contours obtained from the numerical studies below, support minimal surfaces with contact angle Ψ < π/2.
The dynamics of evolving hemicatenoids obeying the laws specified above were obtained using Surface Evolver.42 We nondimensionalize lengths with the loop radius R and scale speeds with v0, leaving R/v0 as a characteristic time scale in the motion. Therefore, changing R in the initial conditions or v0 in (1) corresponds to a dilation in time and all simulations can be rescaled with respect to time. Hence, for a given power-law exponent n, there is only a single simulation needed for each initial stretching factor. The updating algorithm involves advecting each part of the SPB in the plane along its projected normal by a distance d![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = vdt, with v determined by the local angle Ψ. The updated shape of the catenoid is obtained by finding a minimal surface with the new position of the contact lines, which then yields the updated Ψ along the SPBs, and the velocity for the next time step.
= vdt, with v determined by the local angle Ψ. The updated shape of the catenoid is obtained by finding a minimal surface with the new position of the contact lines, which then yields the updated Ψ along the SPBs, and the velocity for the next time step.
By symmetry, we need only simulate one quarter of the hemicatenoid. We fix the plate thickness at 0.008R and first create a stable catenoid with d = 0.65R, close to the critical value for three-dimensional catenoids, and a triangulation in which triangle side lengths lie in the range 0.004–0.06R. To begin the evolution, we stretch the catenoid by a few percent and fix all points along the SPB. Motion then proceeds in time steps of dt = 1 × 10−3 using the algorithm outlined above, where the relaxation to a minimal surface is done to 7 significant figures. The initial stretching is needed to match the initial area in experiments: stretches of 5% and 7.2% correspond to the experiments with η = 9.6 and 77 mPa s respectively.
In the numerics, several quantities are calculated as functions of time: the dimensionless area ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , the dimensionless neck radius rn as defined in Section 3, and the tangent angle θ at the junction of the contact line and the supporting half-ring. As in the presentation of the experimental results, we define the zero of time as the moment when the apparent neck radius vanishes and the topological transition occurs. In simulations, a cutoff radius of 0.02R is introduced to trigger the transition. This choice is not critical in the analysis since the radius goes to zero in a finite time and the transition is well defined, as seen in Fig. 8.
, the dimensionless neck radius rn as defined in Section 3, and the tangent angle θ at the junction of the contact line and the supporting half-ring. As in the presentation of the experimental results, we define the zero of time as the moment when the apparent neck radius vanishes and the topological transition occurs. In simulations, a cutoff radius of 0.02R is introduced to trigger the transition. This choice is not critical in the analysis since the radius goes to zero in a finite time and the transition is well defined, as seen in Fig. 8.
5 Comparison of experimental and numerical results
We now describe the key results obtained with the numerical implementation of the model described in Section 4. The full temporal evolution of a collapsing hemicatenoid is shown in Fig. 6 (and in a video in the ESI†), while Fig. 7 shows the cross-sectional shapes of the narrowest part of the neck. We observe that the initial cross-section is nearly circular, with the angle Ψ ≈ π/2, as expected for a minimal surface. However, as the collapse sequence progresses, the neck becomes ever flatter and Ψ tends to zero. Within the assumptions of the model (1), this implies that the neck contraction speed dζn/dt tends to the extremal value – v0 before pinchoff. As in collapsing three-dimensional catenoids,7 we observe that the film shape connecting the pinchoff region to the supporting wire loops is close to a (half) cone.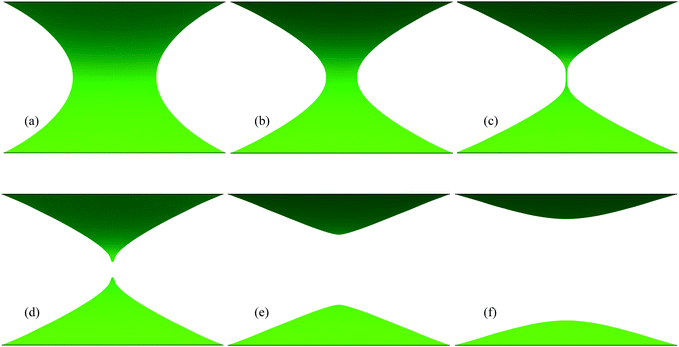 | ||
| Fig. 6 Image sequence in simulation (n = 2/3, stretching factor 5%), corresponding to the times at which the images in Fig. 3 were recorded, namely t − tp = −51 ms, −16 ms, −6 ms, 0 ms, 10 ms, 35 ms, where tp is the pinchoff time. | ||
The experimental data shown in Fig. 4 for the neck radius and neck contraction speed, as well as the experimental film area are plotted in Fig. 8 along with the numerical results obtained for three different values of the exponent n of the friction law (1). Simulations are rescaled with respect to experiments using the curves of the neck contraction speed as a function of time. The value of v0 in simulations is set, for each viscosity η, by the maximum contraction speed observed in experiments. This sets the time axis up to an additive constant. There is a noticeable difference between experiments and simulations close to pinchoff. In simulations, the neck contraction speed remains constant in the last instants before pinchoff at its extremal value – v0. In experiments, the neck contraction speed reaches a maximum, used to infer v0, and decreases thereafter to zero. As mentioned previously, this is associated with the complex dynamics close to pinchoff due to the air trapped in the neck, as observed in 3D catenoids. As a consequence, we define 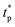 as the hypothetical pinchoff time assuming that the neck contraction speed maintains its extremal value (note that
as the hypothetical pinchoff time assuming that the neck contraction speed maintains its extremal value (note that 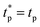 in simulations) and plot all the data as a function of
in simulations) and plot all the data as a function of 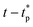 in Fig. 8. This allows a quantitative comparison between experiments and simulations. For the two viscosities studied in Fig. 8, we see a clear tendency to favour the exponent 2/3 over 1/2 and 1. This nonlinear friction law thus seems consistent not only with the presence of mobile surfactants and stress-free interfaces, but also implies that dissipation occurs within the SPBs.
in Fig. 8. This allows a quantitative comparison between experiments and simulations. For the two viscosities studied in Fig. 8, we see a clear tendency to favour the exponent 2/3 over 1/2 and 1. This nonlinear friction law thus seems consistent not only with the presence of mobile surfactants and stress-free interfaces, but also implies that dissipation occurs within the SPBs.
The value of the prefactor A in the frictional force law (1) can be inferred from the experimental measurements of v0, using the exponent n = 2/3 that is most consistent with the data. For the data of Fig. 8, we find for η = 9.6 and 77 mPa s that v0 = 0.52 and 0.26 m s−1, respectively. These yield A ≈ 7.3 and 2.9, respectively, in agreement with the prediction A ∼ 5–7 from lubrication theory in a simpler geometry.9 For the two other viscosities (η = 1.0 and 4.3 mPa s), the dynamics can not be described with the same approach since both viscous and inertial effects are present.
In previous work,7 we have referred to the conical film shape as the “Martini glass” configuration, and detailed a method to determine its appearance based on the shape of the film near the supporting ring. The method involves finding, within the time sequence, that contour whose shape displays the minimum standard deviation in a fit to a straight line. The critical vertex angle is then θ* = π/2 − arctan(m), where m is the associated slope of the line. For the case of 3D catenoids, whose dynamics are driven by inertia, we found θ* = 68°. For hemicatenoids bounded by a solid wall, our measurements are reported in Table 1. In experiment, this configuration is observed when the neck pinches. The stated uncertainties are estimated either over repeated experiments or by assuming a 10% allowance on the standard deviation to find its minimum value. Both estimates give typical errors around 1°. In the simulations, this configuration occurs slightly after the pinchoff time and for larger n it occurs later, and yields a larger θ*.‡ In the simulations, the error bars are determined with the same 10% criterion.
| Experiments | ||||
|---|---|---|---|---|
| η (mPa s) | 1.0 | 4.3 | 9.6 | 77 |
| θ* (deg) | 68.0 ± 1.0 | 68.0 ± 1.0 | 67.5 ± 1.0 | 66.6 ± 1.0 |
| Simulations | |||
|---|---|---|---|
| n | 1/2 | 2/3 | 1 |
| θ* (deg) | 65.8 ± 0.6 | 68.2 ± 0.7 | 72.1 ± 1.1 |
We find that θ* is almost constant in experiments and very close to what was observed experimentally with 3D catenoids,7 and which was found to be a consequence of the fact that the first few active modes dominate the dynamics near the rigid frames. A slight decrease is apparent as the viscosity increases, but it is difficult to give strong statements given the error bars. Note that the value of θ* obtained with η = 9.6 mPa s is consistent with a 2/3 exponent. For η = 77 mPa s, the value lies between what is obtained with exponents 1/2 and 2/3 in simulation, but this method to discuss the exponent is not as robust as the comparison through the whole time sequence as presented in Fig. 8 and is more sensitive to the complex dynamics around the pinchoff time.
6 Discussion
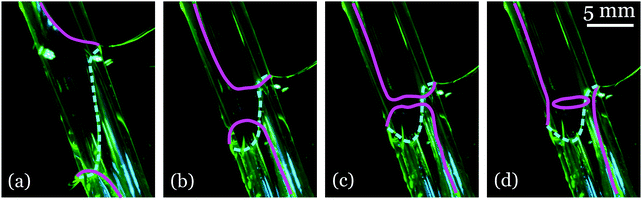
In this work, we have studied the dynamics of surface Plateau borders that are driven by unstable soap films. Unlike in the case of collapsing three-dimensional catenoidal films, the motion of hemicatenoids bounded by solid walls is dominated by dissipation localized in the moving SPBs. Whereas the film viscosity plays essentially no observable role in the collapse of 3d catenoids, we observe a strong dependence on viscosity of the collapse dynamics of hemicatenoids. Through comparisons between experimental observations and numerical simulations of a model that incorporates the widely used nonlinear friction law f ∼ Can for the viscous force f as a function of capillary number Ca, we found consistency with the exponent n = 2/3 associated with mobile surfactants and stress-free interfaces. Despite this effect on the dynamics, the large-scale shapes of the collapsing films are insensitive to the film viscosity, a fact that highlights the crucial role played by intrinsic geometric features.Surface Plateau border motion is also present in certain exotic topological transitions involving soap films. For example, in previous work3–5 we studied the interconversion of a soap-film Möbius strip to a two-sided surface, and showed that the singularity associated with that topological transition occurs at the boundary of the film and involves reconnection of the SPB. Fig. 9 shows a close-up of the region of the incipient singularity, in which we see that the film evolves in such a way as to make the SPB twist ever more tightly around the tube, until two sections of the film touch each other and reconnect. While this is similar to the neck of a half catenoid, which collapses with the formation of a satellite droplet, the detailed dynamics of the twist-driven reconnection event and associated change in the orientation of the SPB in Fig. 9 remain to be understood.
The dynamics that we describe here, driven by the shape of the interface and the motion of the associated SPB, is found more widely during the motion of surfactant–laden interfaces. In flow through porous media, for example during foam enhanced oil recovery,41 lamellae are forced under a pressure gradient through narrow pore throats between solid surfaces. The collision of two SPBs leads to processes such as pinch-off,33 in which two interfaces separate in the way that the hemicatenoid does, snap-off and lamella-division.32 These process lead to variations in bubble size, which then requires an adjustment to the pressure gradient required to mobilize the foam. SPB friction therefore controls the rate at which foam is generated in porous media.
Author contributions
All authors designed and performed the research, analyzed the results and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to K. Brakke for provision and support of the Surface Evolver software and to Médéric Argentina and Keith Moffatt for enlightening discussions. This work was supported in part by the National Research Agency (ANR-20-CE30-0019) and by the French government, through the UCAJEDI Investments in the Future project of the National Research Agency (ANR-15-IDEX-01) (CR), with additional support from the Engineering and Physical Sciences Research Council (EP/N002326/1 to SC; Established Career Fellowship EP/M017982/1 to REG & AIP), from the Schlumberger Chair Fund (REG), and the European Space Agency (4000129502) (SC).Notes and references
- J. Plateau, Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires [Experimental and theoretical statics of liquids subject to only molecular forces] (in French), Gauthier-Villars, Paris, France, 1873 Search PubMed.
- J. C. Maxwell, The Scientific Papers of James Clerk Maxwell, ed. W. D. Niven, Cambridge University Press, Cambridge, 1890, vol. 2 Search PubMed.
- R. E. Goldstein, H. K. Moffatt, A. I. Pesci and R. L. Ricca, Soap-film Möbius strip changes topology with a twist singularity, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21979–21984 CrossRef CAS.
- R. E. Goldstein, J. McTavish, H. K. Moffatt and A. I. Pesci, Boundary singularities produced by the motion of soap films, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8339–8344 CrossRef CAS PubMed.
- A. I. Pesci, R. E. Goldstein, G. P. Alexander and H. K. Moffatt, Instability of a Möbius strip minimal surface and a link with systolic geometry, Phys. Rev. Lett., 2015, 114, 127801 CrossRef PubMed.
- R. Courant, Soap film experiments with minimal surfaces, Am. Math. Mon., 1940, 47, 167–174 CrossRef.
- R. E. Goldstein, A. I. Pesci, C. Raufaste and J. D. Shemilt, Geometry of catenoidal soap film collapse induced by boundary deformation, Phys. Rev. E, 2021, 104, 035105 CrossRef CAS PubMed.
- Z. Solomenko, P. D. M. Spelt and P. Alix, A level-set method for large-scale simulations of three-dimensional flows with moving contact lines, J. Comput. Phys., 2017, 348, 151–170 CrossRef CAS.
- I. Cantat, Liquid meniscus friction on a wet plate: Bubbles, lamellae, and foams, Phys. Fluids, 2013, 25, 031303 CrossRef.
- R. Courant, The existence of a minimal surface of least area bounded by prescribed Jordan arcs and prescribed surfaces, Proc. Natl. Acad. Sci. U. S. A., 1938, 24, 97–101 CrossRef CAS PubMed.
- J. Douglas, Some new results in the problem of Plateau, J. Math. Phys., 1936, 15, 55–64 CrossRef.
- J. Douglas, Minimal surfaces of general topological structure with any finite number of assigned boundaries, J. Math. Phys., 1936, 15, 105–123 CrossRef.
- J. B. Bostwick and P. H. Steen, Stability of constrained capillary surfaces, Annu. Rev. Fluid Mech., 2015, 47, 539–568 CrossRef.
- A. Akbari and R. J. Hill, Liquid-bridge stability and breakup on surfaces with contact-angle hysteresis, Soft Matter, 2016, 12, 6868–6882 RSC.
- A. Akbari, R. J. Hill and T. G. M. van de Ven, Catenoid stability with a free contact line, SIAM J. Appl. Math., 2015, 75, 2110–2127 CrossRef.
- F. P. Bretherton, The motion of long bubbles in tubes, J. Fluid Mech., 1961, 10, 166–188 CrossRef.
- N. D. Denkov, V. Subramanian, D. Gurovich and A. Lips, Wall slip and viscous dissipation in sheared foams: effect of surface mobility, Colloids Surf., A, 2005, 263, 129–145 CrossRef CAS.
- N. D. Denkov, S. Tcholakova, K. Golemanov, V. Subramanian and A. Lips, Foam-wall friction: Effect of air volume fraction for tangentially immobile bubble surface, Colloids Surf., A, 2006, 282, 329–347 CrossRef.
- G. Reiter, Dewetting of thin polymer films, Phys. Rev. Lett., 1992, 68, 75–78 CrossRef CAS PubMed.
- G. Reiter, Unstable thin polymer films: Rupture and dewetting processes, Langmuir, 1993, 9, 1344–1351 CrossRef CAS.
- T. D. Blake and K. J. Ruschak, A maximum speed of wetting, Nature, 1979, 282, 489–491 CrossRef.
- H. Benkreira and M. I. Khan, Air entrainment in dip coating under reduced air pressures, Chem. Eng. Sci., 2008, 63, 448–459 CrossRef CAS.
- R. Burley and B. S. Kennedy, An experimental study of air entrainment at a solid/liquid/gas interface, Chem. Eng. Sci., 1976, 31, 901–911 CrossRef CAS.
- S. Engelnkemper, M. Wilczek, S. V. Gurevich and U. Thiele, Morphological transitions of sliding drops: Dynamics and bifurcations, Phys. Rev. Fluids, 2016, 1, 073901 CrossRef.
- N. Le Grand, A. Daerr and L. Limat, Shape and motion of drops sliding down an inclined plane, J. Fluid Mech., 2005, 541, 293–315 CrossRef.
- W. Liang and S. Tietze, Pearls in running drops on an inclined glass substrate excited by Lamb waves, Sci. Rep., 2017, 7, 14164 CrossRef PubMed.
- T. Podgorski, J.-M. Flesselles and L. Limat, Corners, cusps, and pearls in running drops, Phys. Rev. Lett., 2001, 87, 036102 CrossRef CAS PubMed.
- P. Beltrame, E. Knobloch, P. Hänggi and U. Thiele, Rayleigh and depinning instabilities of forced liquid ridges on heterogeneous substrates, Phys. Rev. E, 2011, 83, 016305 CrossRef PubMed.
- J. A. Diez, A. G. González and L. Kondic, Instability of a transverse liquid rivulet on an inclined plane, Phys. Fluids, 2012, 24, 032104 CrossRef.
- R. K. Singh, J. E. Galvin, G. A. Whyatt and X. Sun, Breakup of a liquid rivulet falling over an inclined plate: Identification of a critical Weber number, Phys. Fluids, 2017, 29, 052101 CrossRef.
- B. Géraud, S. A. Jones, I. Cantat, B. Dollet and Y. Méheust, The flow of a foam in a two-dimensional porous medium, Water Res. Res., 2016, 52, 773–790 CrossRef.
- B. Géraud, Y. Méheust, I. Cantat and B. Dollet, Lamella division in a foam flowing through a two-dimensional porous medium: A model fragmentation process, Phys. Rev. Lett., 2017, 118, 098003 CrossRef PubMed.
- R. Liontas, K. Ma, G. J. Hirasaki and S. L. Biswal, Neighbor-induced bubble pinch-off: Novel mechanisms of in situ foam generation in microfluidic channels, Soft Matter, 2013, 9, 10971 RSC.
- F. Box, O. Kodio, D. O'Kiely, V. Cantelli, A. Goriely and D. Vella, Dynamic buckling of an elastic ring in a soap film, Phys. Rev. Lett., 2020, 124, 198003 CrossRef CAS PubMed.
- A. Cohen, N. Fraysse, J. Rajchenbach, M. Argentina, Y. Bouret and C. Raufaste, Inertial mass transport and capillary hydraulic jump in a liquid foam microchannel, Phys. Rev. Lett., 2014, 112, 218303 CrossRef.
- A. Cohen, N. Fraysse and C. Raufaste, Drop coalescence and liquid flow in a single Plateau border, Phys. Rev. E, 2015, 91, 053008 CrossRef PubMed.
- K. Golemanov, N. D. Denkov, S. Tcholakova, M. Vethamuthu and A. Lips, Surfactant Mixtures for Control of Bubble Surface Mobility in Foam Studies, Langmuir, 2008, 24, 9956–9961 CrossRef CAS PubMed.
- N. D. Denkov, S. Tcholakova, K. Golemanov, K. P. Ananthpadmanabhan and A. Lips, The role of surfactant type and bubble surface mobility in foam rheology, Soft Matter, 2009, 5, 3389–3408 RSC.
- Y.-J. Chen and P. H. Steen, Dynamics of inviscid capillary breakup: collapse and pinchoff of a film bridge, J. Fluid Mech., 1997, 341, 245–267 CrossRef.
- J. B. Keller and M. J. Miksis, Surface tension driven flows, SIAM J. Appl. Math., 1983, 43, 268–277 CrossRef.
- I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Foams: Structure and Dynamics, Oxford University Press, Oxford, 2013 Search PubMed.
- K. Brakke, The Surface Evolver, Exp. Math., 1992, 1, 141–165 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Videos from experiments and simulations. See DOI: https://doi.org/10.1039/d2sm00516f |
| ‡ For n = 1 the local minimum is less pronounced. We have tested a simulation with n = 4/3 (data not shown). In this case, the local minimum does not exist as emphasized by the absence of a curvature inversion in the corresponding movie/image sequence (data not shown). |
| This journal is © The Royal Society of Chemistry 2022 |