Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of solvent isomers on the gelation properties of tri-aryl amine organogels and their hybrid thermoreversible gels with poly[vinyl chloride]†
Yao
Xiao
,
Collin
Dominique
,
Gavat
Odile
,
Carvalho
Alain
,
Moulin
Emilie
 ,
Giuseppone
Nicolas
,
Giuseppone
Nicolas
 and
Guenet
Jean-Michel
and
Guenet
Jean-Michel
 *
*
Institut Charles Sadron CNRS-Université de Strasbourg 23 rue du Loess, BP84047 67034 STRASBOURG, Cedex2, France. E-mail: jean-michel.guenet@ics-cnrs.unistra.fr
First published on 5th July 2022
Abstract
The gelation properties of tri-aryl amine (TATA) in two isomers of dichlorobenzene, namely ortho-dichlorobenzene (o-DCB) and meta-dichlorobenzene (m-DCB), have been studied by calorimetry for mapping out the temperature–concentration phase diagram. It is shown that both systems behave differently, yet both form molecular compounds. The occurrence of these compounds is further demonstrated by neutron diffraction in o-DCB. Depending on the isomer used, X-ray investigations highlight a difference in the position of the diffraction peaks. The morphology observed by scanning electron microscopy reveals fibrillar systems in both cases, yet the fibrils’ cross-sections are far larger in m-DCB with respect to o-DCB. The body of these results is discussed in light of current opinions on the role of the solvent. Ternary gels obtained with PVC have also been investigated by means of the same experimental approach. Calorimetry investigations and X-ray diffraction data show no significant difference for the behavior of the TATA moiety. The morphology studied by scanning electron microscopy allows one to distinguish clearly the TATA fibrils and the PVC network. This again confirms the possibility of preparing functional materials with an organogelator and a polymer through the making of hybrid gels.
Introduction
The phenomenon of organogelation is a topical subject as it raises many questions as to the mechanisms responsible for the formation of a three-dimensional network that can retain up to 99% of solvent.1–5 Also, their potential applications in various domains arise continuously growing interest.6,7 The term “network” is important as it conveys the notion of a morphology made up with elongated structures such as fibrils.4The possibility of predicting whether a given molecule is to produce a gel in a given solvent8–13 stands among the different concerns frequently expressed. As suggested by Guenet,4 a potential organogelator must be a “chimera type” molecule, namely a molecule bearing different types of interactions such as hydrogen bonding, van der Waals interaction, π–π interaction, and the like. This can favour the much faster growth of one of the crystalline faces, which generates fibrils instead of 3-D crystals. For instance, in the case of OPV molecules the gel fibrillar structures are produced by the fastest growth of the face involving the π–π interaction.4,7
The other player in the gelation process is the solvent. Recently, the Hansen parameter has been used abundantly in an attempt to predict whether a gel will form or not in a given solvent.8–13 Although this parameter can indicate whether a solvent is not too good so as to allow structure formation, nor too bad thus preventing solubilization, it does not give indications on the gel thermodynamic properties nor on its morphology. An example is given by triarylamine tris-amide (TATA) organogels obtained in two solvents of very close Hansen parameters,13 namely bromobenzene (20.3) and tetrachloroethane (19.8),8 which possess melting temperatures some 40–60 °C apart.14,15 Also, the occurrence of TATA molecular compounds has recently been demonstrated in these solvents.16 The Hansen parameter cannot predict the formation of molecular compounds between the solvent and the organogelator, something reminiscent of the case of polymer thermoreversible gels where the Flory's parameter is also not relevant. Indeed, poor solvents, such as trans-decahydronaphthalene, unexpectedly produce molecular compounds with syndiotactic polystyrene and isotactic polystyrene.17 In fact, the shape of the solvent can be a decisive factor, as particularly revealed first in the case of polyethylene oxide compounds that form with para-dihalogenobenzene18,19 but not with meta-dihalogenobenzene nor ortho-dihalogenobenzene.
Clearly, the organogelation phenomenon is more complex than anticipated, and therefore requires a deeper investigation into the role of the solvent.20,21 For this purpose, we report here on the effect of the shape of the solvent on the gelation of triarylamine tris-amide (TATA) in two isomers of dichlorobenzene, namely ortho-dichlorobenzene and meta-dichlorobenzene. It is shown that these solvents of the same Hansen solubility parameter produce organogels with differing thermodynamic properties, molecular structures and morphologies. The case of hybrid materials made up with PVC thermoreversible gels and TATA organogels in these isomers is also tackled.
Experimental section
Materials
The fibrillar organogels were obtained from solutions of tri-aryl tri-amines designated as TATA in what follows (see Fig. 1). The synthesis and properties of these molecules are extensively described in ref. 22–25.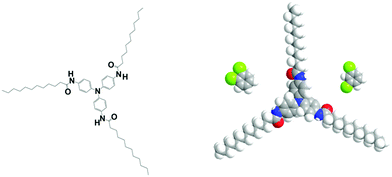 | ||
| Fig. 1 left: Chemical structure of the tris-amide triarylamine C11 in its completely extended conformation with the phenyl group tilting.22 This molecule can be inscribed in a cylinder of radius r ≈ 2.1 nm. Right space-filling model of the same molecule together with the two conformers of dichlorobenzene at the same scale; left, ortho-dichlorobenzene (oDCB) and right, meta-dichlorobenzene (m-DCB). | ||
Of particular interest are the conductivity properties of its organogels, especially in chlorinated solvents.23,24 Also, it has been shown that small amounts of TATA to PVC thermoreversible gels increase drastically the elastic modulus beyond Voigt's upper limit.14
The poly[vinyl chloride], PVC, used for the preparation of the hybrid systems was purchased from Sigma-Aldrich and was used without further purification. From SEC in THF at 25 °C (universal calibration) the weight average molecular weight was found to be Mw = 7.9 × 104 g mol−1 with a polydispersity index Mw/Mn = 1.87. The fractions of tetrads were found to be sss = 41% ssi, iss, sis,… = 39% and iii = 19% as determined from 13C-NMR.
Ortho-Dichlorobenzene (o-DCB), meta-dichlorobenzene (m-DCB) were purchased from Sigma-Aldrich (purity grade 99.5%), and were used as-received. Deuterated ortho-dichlorobenzene (o-DCBD) was purchased from Eurisotop, and also used as-received.
The preparation of the binary TATA/DCB gels and of the hybrid networks (PVC/TATA/DCB) consists in preparing mixtures at the desired concentration and composition, and then heating them up to 120–160 °C until clear, homogeneous solutions are obtained. Gels are produced by quenching these solutions at low temperature (0 °C down to −20 °C).
TATA concentration was varied from 0.5 × 10−2 g cm−3 (or 0.004 g g−1) to 1.04 × 10−2 g cm−3 (or 0.065 g g−1). Three PVC concentrations have been studied: 4.82 × 10−2 g cm−3 (or 3.0 × 10−2 in g g−1), designated as PVC5%, 9.3 × 10−2 g cm−3 (or 5.8 × 10−2 in g g−1) designated as PVC10%, and 0.135 g cm−3 (or 0.10 in g g−1) designated as PVC15%.
About 30–40 mg of gel were introduced into stainless steel pans that were hermetically sealed by means of an o-ring. A first run was systematically performed for erasing the sample history, as well as to suppress parasitic mechanical effects at the gel melting. The weight of the sample was systematically checked after the different cycles in order to evaluate any solvent loss.
Although PVC gel formation arises from the crystallization of the longest syndiotactic sequences, the thermal behaviour of its gels is not detectable by DSC, an observation already reported in several papers.26,27 Only the first run gives the melting range, while the enthalpy is highly overestimated. Consequently, PVC gel formation was determined by the tube tilting. This further implies that the first order transition observed by DCS on the hybrid systems arise from the only TATA moiety.
Scanning electron microscopy
A piece of a gel from PVC/DCB or PVC/TATA/DCB was placed onto a cryo-holder and quenched by a plunge into a nitrogen slush. After transfer of the sample into the Quorum PT3010 chamber attached to the microscope, the sample was coated by sputter deposition with a thin Pt layer, and then fractured with a razor blade. Subsequent etching was performed at T = −70 °C so as to expose the details of the morphology. Samples were eventually transferred in the FEG-cryoSEM (Hitachi SU8010). Images were taken with the SE-in lens detector at 1 keV and at T = −150 °C.X-Ray diffraction
X-Ray diffraction experiments were performed using a diffractometer developed by the Institut Charles Sadron DiffériX platform. The instrument operates with a pinhole collimator and a hybrid photon counting detector (HPC-Dectrics Pilatus®3 R 300 K). The monochromatic beam (λ = 0.154 nm) is obtained by reflection of the primary beam produced by means of an X-ray generator from Rigaku (Micromax 007HF) onto a confocal mirror with multilayer coating (Confocal Max-Flux™ Optic, Rigaku). The size of the beam incident on the sample is about 800 μm. The distance between the sample and the detector is set in such a way as to access scattering vectors q = 4πsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (θ/2)/λ(θ = diffraction angle) ranging from q = 0.4 to 10 nm−1. Data reduction is performed following the standard procedure for isotropic scattering. Calibration of the scattering vector range is performed with a silver behenate sample. Sample holders consist of cells of 1 mm thick with calibrated mica windows. Typical counting times are about 10 mins.
(θ/2)/λ(θ = diffraction angle) ranging from q = 0.4 to 10 nm−1. Data reduction is performed following the standard procedure for isotropic scattering. Calibration of the scattering vector range is performed with a silver behenate sample. Sample holders consist of cells of 1 mm thick with calibrated mica windows. Typical counting times are about 10 mins.
Neutron diffraction
Neutron diffraction experiments were carried out at Institut Laue–Langevin on the D16 camera.28 This camera is equipped with a helium detector of 320 × 320 mm2 with 1 × 1 mm2 pixels. The detector can rotate so as to access larger q values. In these experiments three angles were used: 0° for the transmission measurements, and 10.8° and 27° for the determination of the diffracted intensities. The neutron wavelength is selected by reflection by a focussing pyrolytic graphite monochromator. Experiments reported herein were obtained with a neutron wavelength of λ = 0.4454 nm, providing the following q-range with the two-angle set-up: 0.6 nm−1 ≤ q ≤ 9 nm−1 (further details are available at https://www.ill.eu/users/instruments/instruments-list/d16/characteristics). The sample holder temperature can be controlled with an external bath. Four temperatures were used: T = 20 °C, T = 50 °C, T = 70 °C, and T = 85 °C.The samples were prepared in closed quartz cells of 2 mm thickness purchased from B. Thuet (Blodelsheim, France). The required amounts of TATA and PVC powders are first introduced, and then mixed by stirring vigorously prior to the addition of the solvent. The mixture is finally heated up to 160 °C. This procedure allows one to prepare more easily homogeneous solutions within a few minutes. Gels were formed by cooling the solutions in a fridge kept at 4 °C. Gel samples were systematically prepared in the same way with hydrogenous o-dichlorobenzene and perdeuterated o-dichlorobenzene for testing the existence of TATA/o-dichlorobenzene molecular compounds. These experiments were restricted to o-DCB as deuterated m-DCB was not available.
Results and discussion
(1) Thermodynamic properties of tri-aryl-triamine binary gels
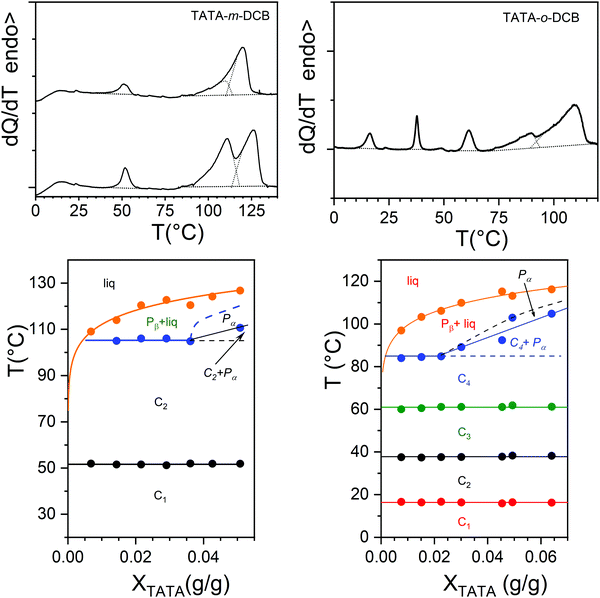
The thermodynamic properties have been studied by DSC. Typical thermograms for TATA/o-DCB and TATA/m-DCB are displayed in Fig. 2. These thermograms differ significantly with the DCB isomer.In the case of m-DCB, a maximum of three endotherms is observed while up to five endotherms are seen with o-DCB. From the endotherms the temperature–concentration phase diagrams have been mapped out as shown in Fig. 2. They reveal in m-DCB that the endotherm at T = 50 ± 1 °C is a non-variant event. The endotherm at T = 109 ± 1 °C is also a non-variant event up to XTATA = 0.036, and then increases. As to the terminal endotherm, it increases monotonously with TATA concentration.
In the case of o-DCB the endotherms at T = 16 ± 1 °C, T = 37 ± 1 °C and T = 61 ± 1 °C represent non-variant events, while the terminal endotherm, which corresponds to the gel macroscopic melting, increases with TATA concentration as also observed with m-DCB.
The endotherm at T = 85 °C is a non-variant event up to XTATA = 0.022, and then also increases beyond this concentration. It is worth noting that the terminal gel melting is some 10 °C higher in m-DCB than in o-DCB. As is customary, the dotted lines in both phase diagrams as well as the italics stand for possible extensions and for plausible phases that fulfil Gibbs phase rules.29
In the case of TATA/o-DCB systems, the melting enthalpies ΔH related to the non-variant events are about the same irrespective of the transition, but are relatively low with respect to those of the terminal melting ΔHf, which are about five times larger (see Fig. S1, ESI†). Extrapolation of ΔHf to XTATA = 1 yields ΔHf = 41 J g−1, a value about 25% lower than that measured in the solid state.15 This would be consistent with a molecular compound rather than a solid phase. Note that these enthalpies are not heating-rate dependent in both systems, which emphasizes the absence of any noticeable kinetic effects. We further observe that the terminal melting enthalpies are larger in m-DCB than in o-DCB (see Fig. S1, ESI†).
The shapes of the phase diagrams suggest that the non-variant events correspond to the transformations of molecular compounds.19,29 This assumption will receive further confirmation in what follows. In m-DCB, compound C1 transforms into compound C2 at T = 51.5 °C, which is likely to be related to a change of the solvation degree, or in other words to a change of the compound stoichiometry. The same comments apply to TATA/o-DCB gels with the occurrence of 4 molecular compounds. The following sequence takes place C1 ⇒ C2 at T = 16 ± 1 °C, C2 ⇒ C3 at T = 37 ± 1 °C and C3 ⇒ C4 at T = 61 ± 1 °C. The stoichiometries of the different compounds cannot be inferred from the present data. In view of the size of the solvent molecules with respect to the space between the aliphatic arms, the number of DCB molecules per TATA moiety is likely to be high. There might be two types of solvent molecules, those tightly bound close to the TATA core, and those loosely bound located at the edge.
In both cases, the last non-variant event at T = 106 °C for TATA/m-DCB gels and T = 84 °C for TATA/o-DCB gels may be assigned to a metatectic transition18 corresponding to the phases Pα and Pβ (see Fig. S2, ESI†). The metatectic concentration where three phases are supposed to coexist, namely Pα and Pβ, and C4, is about CTATA ≈ 0.025 g g−1 in o-DCB and CTATA ≈ 0.036 g g−1 in m-DCB. Assuming metatectic transitions at 85 °C for TATA/o-DCB and at 105 °C for TATA/m-DCB relies on the existence of several crystalline forms of TATA in the solid state (see Fig. S3, ESI†) so that Pα and Pβ could correspond to the recently reported structure II and III,15 respectively. Yet, at this stage, we cannot completely disregard their possible molecular compound status.
(2) Molecular structure of tri-aryl-triamine binary gels
The molecular structure of TATA/o-DCB gels has been chiefly investigated by neutron diffraction as this technique is well-suited to the case of molecular compounds.30–34 Complementary X-ray diffraction investigations have also been performed.The intensity diffracted by any kind of radiation for a binary system is written:
| I(q) = Ā2i (q)Si(q) + Ā2j(q)Sj(q) + 2Āi(q)Āj(q)Sij(q) | (1) |
If the system forms a solid phase, then I(q) reduces to:
| I(q) = ĀTATA2(q)STATA(q) + ĀoDCB2(q)SoDCB(q). | (2) |
This implies that altering the value of ĀoDCB is not to modify the diffraction pattern of the crystalline TATA fibrils. In other words, the relative intensity of the peaks with respect to one another will not change as So-DCB(q) is chiefly featureless except for a broad maximum.
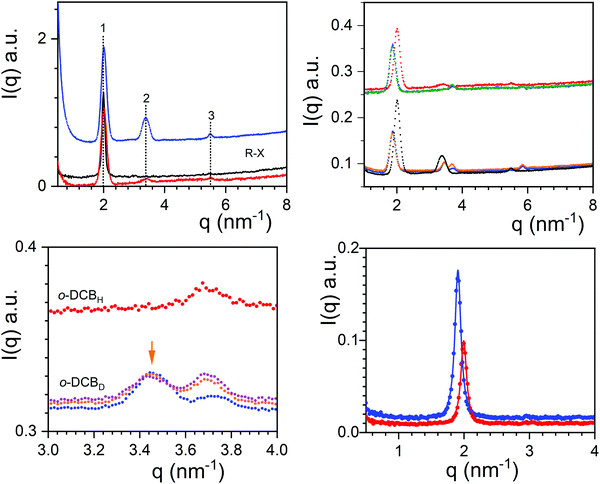
Conversely, if a molecular compound is formed, then the cross-term in relation (1) cannot be discarded any longer. As a result, if one can modify the solvent contrast, Āsolv the diffraction pattern will be altered.31–33 Testing the occurrence of molecular compounds can be achieved by means of neutron diffraction by comparing the diffraction pattern obtained in hydrogenous and in deuterated solvents as the scattering length of hydrogen (aH = −0.375 × 10−12 cm) differs drastically from that of deuterium (aD = 0.670 × 10−12 cm).34 The neutron diffraction peak intensity can therefore vary significantly with the solvent labelling. In this paper, only systems in o-DCB have been considered since deuterated m-DCB was not commercially available (see Table ST1, ESI†).
The neutron diffraction patterns for TATA/o-DCBH and TATA/o-DCBD are given in Fig. 3 together with the X-ray diffraction pattern obtained for TATA/o-DCBH. For the neutron diffraction patterns, three peaks are observed at q1 = 2.00 nm−1, q2 = 3.38 nm−1, and q3 = 5.49 nm−1 with intensities that differ as to whether hydrogenous or deuterated o-dichlorobenzene is used. The intensity ratio of peaks 1 and 2 is I2/I1 = 0.315 for TATA/o-DCBD against I2/I1 = 0.053 for TATA/o-DCBH, which confirms the occurrence of the molecular compound C2 in agreement with the conclusions drawn from the phase diagram. The X-ray diffraction pattern is nearly identical to the TATA/o-DCBH system as it shows only the peak located at q1 = 1.99 nm−1.
A tentative model of the clathrate type35,36 is shown in Fig. S6 (ESI†) as a basis for discussion. It relies on previous calculations that suggested that TATA helices arrange in rows.15 At the present resolution level, the helical structure scatters as a hollow solid cylinder. The intensity diffracted by an array of such cylinders is written:37–39
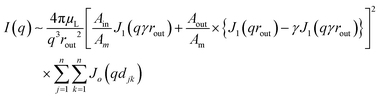 | (3) |
By considering helices arranged in rows instead of hexagonally assembled, one can reproduce fairly well the peak at q1 = 2.00 nm−1 with a close FWHM value by taking rout = 1.7 nm, γ = 0.41, n = 20, and the distance between adjacent helices d = 3.4 nm (see Fig. S4, ESI†). The value of rout which is lower than the value expected for the all-extended structures (2.1 nm), suggests therefore some disorganization of the aliphatic arms.
The additional peaks observed with the deuterated solvent imply an organization of the solvent differing from that of the TATA helices. It is, however, not possible to elaborate further with the present data.
Neutron diffraction patterns for TATA/o-DCBH and TATA/o-DCBD as a function of temperature are displayed in Fig. 3. As will be further discussed below, the results at T = 50 °C, 70 °C and 85 °C are all consistent with the existence of molecular compounds.
A conspicuous change of the diffraction pattern is seen after transforming C2 into C3. Peak q1 shifts to a lower q value (from q = 2.00 nm−1 to 1.872 nm−1) while peaks q2 and peak q3 shift to higher q values (from 3.380 nm−1 to 3.439 nm−1, and from 5.846 nm−1 to 5.497 nm−1). Also, a new peak occurs at q = 3.704 nm−1. The most prominent peak, here q1, is generally related to the distance between first neighbours, namely between TATA helices in the present case. Its shift to lower q values therefore suggests an increase of this distance. This may suggest that the stoichiometry, namely the number of solvent molecules per TATA moiety, increases at the C2 ⇒ C3 transition instead of decreasing as is usually observed. In other words, the structure would absorb instead of releasing solvent molecules. The slight decrease of turbidity detected at this transition is consistent with this assumption (see Fig. S5, ESI†) as raising the compound stoichiometry is likely to bring the refractive index of the TATA fibrils closer to that of the surrounding solvent.
The transformations C3 ⇒ C4, and C4 ⇒ Pα do not entail a modification of the positions of the peaks of the diffraction pattern. The changes only occur at the intensity level, particularly the ratio of the intensities of the peak at q = 3.439 nm−1vs. the peak at q = 3.704 nm−1, I(3.704)/I(3.439) for the system TATA/o-DCBD (see Fig. 3c upper right, and Fig. S6, ESI†). This effect is possibly related to a change of stoichiometry that occurs without alteration of the molecular arrangement.
Comparison of the diffraction patterns obtained at 85 °C for o-DCBH and o-DCBD is consistent with the existence of a compound. Yet, it seems difficult to conclude that phase Pβ is a molecular compound as the presence of compound C4 cannot be excluded. Due to technical constraints we could not increase the temperature above 85 °C, which would have been the only way to settle this issue.
Finally, X-ray diffraction patterns show a slight difference in peak positions between gels in o-DCB and m-DCB (see Fig. 3). The intense peak q1 stands at a slightly lower q for m-DCB (q = 1.905 nm−1) than for o-DCB (q = 1.99 nm−1). This therefore suggests a slightly different packing in each isomer, which is in line with the discrepancies observed in the temperature–concentration phase diagram.
Note that in all the diffraction patterns shown here, the full-width at half maximum (FWHM) of the first peak is about 0.1–0.12 which suggests a rather low degree of disorganization as the correlation length is about 2π/FWHM ≈ 60–50 nm.
(3) Morphology of tri-aryl-triamine binary gels
Morphologies obtained by means of scanning electron microscopy are shown in Fig. 4. Again, as already reported for the thermodynamic properties, the solvent isomer has a marked impact on the microscopic framework of TATA/DCB gels. TATA/m-DCB gels consist of a jumble of flat, chipped laths of width somewhere between 0.5–3 μm (Fig. 4a). Most of the laths are not connected nor branched to one another. TATA/o-DCB gels are made up with needles of cross-section somewhere between 0.06–0.4 μm, that, too, display no interconnections (Fig. 4b). Therefore, gels in DCB possess a similar network architecture, yet with sizes differing by one order of magnitude depending upon the isomer used.In principle, TATA helices are supposed to be aligned along the length of the laths/needles.23 The smaller width observed in o-DCB with respect to m-DCB may be related to their disparate molecular compounds, whose aggregation of their solvated helices could be rapidly arrested by accumulation of packing defects. Another possibility could be that helix growth is much faster than the helix–helix aggregation, in which case the material is rapidly consumed thus limiting the lateral dimensions.
(4) The ternary gels PVC/TATA/DCB
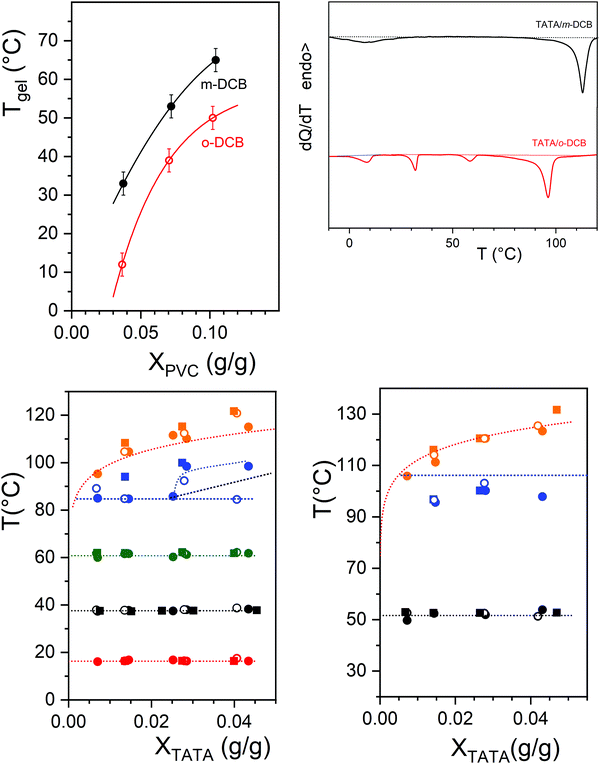
As was already described in previous papers, the gelation temperature Tgel of PVC gels cannot be straightforwardly determined by DSC. The tilting tube method has been used in this study for accessing this parameter.15 As can be seen in Fig. 5 upper left, the gelation temperature depends significantly upon the DCB isomer, about 15–20 °C higher in m-DCB than in o-DCB. The PVC gel morphology is also affected by the DCB isomer as can be seen in Fig. 5c and d, but appears basically as a network of connected fibrils. In m-DCB, the mesh size is in the submicron range (about 0.1–0.2 μm) while the fibril cross-section is a few tens of nm (around 40 nm). In o-DCB, the mesh size is smaller (about 0.1 μm) while the fibril cross-section looks about the same at the current resolution.The TATA gel formation temperature is substantially higher in both isomers than that of the PVC gels for all the investigated range of PVC compositions (Fig. 5 upper right). This implies that the TATA network is likely to form before the PVC's during the cooling process of the ternary systems. The morphology of the hybrid systems shown in micrographs 5e and 5f confirm this statement as the TATA fibrils can be distinctly discriminated from the PVC network. Clearly, the PVC gel grows within the TATA network.
The temperature–concentration phase diagrams determined for the different PVC compositions are displayed in Fig. 5 where the dotted lines stand for the transition determined for TATA/DCB binary gels. As a rule, the temperatures of the first-order thermal events associated with the TATA moiety are virtually unaltered by the PVC chains. Yet, the metatectic line is not so well-defined for the TATA/PVC/m-DCB system, and appears to be shifted downwards by about 10 °C.
While the temperature–concentration phase diagrams of the ternary systems are virtually unchanged with respect to the TATA binary gels, the associated enthalpies turn out to be lower and their values are highly scattered (see Fig. S7, ESI†). This implies that a fraction of the TATA molecules does not gel. Since the TATA network forms first, it is surmised that these TATA molecules establish a privileged interaction with PVC chains that prevents them from aggregating.
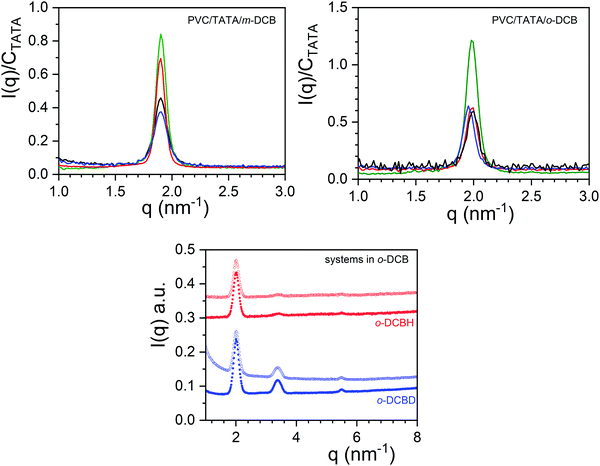
The existence of isolated TATA molecules is further confirmed by the X-ray diffraction patterns obtained on the hybrid gels at room temperature (see Fig. 6). While there is no change as to the position of the peaks for the different PVC compositions, the intensities differ significantly. For PVC/TATA/o-DCB systems the intensity is about half the value of that in the binary gels independent of the PVC composition. Conversely, the intensity decreases with increasing PVC composition for PVC/TATA/m-DCB systems.
As expected in view of the temperature–concentration phase diagrams, molecular compound C2 is still present in the ternary PVC/TATA/o-DCB hybrid gels as ascertained by neutron diffraction data in Fig. 6. Peaks remain at the same positions, and the intensity ratios are the same. Only an upturn is seen for the PVC/TATA/o-DCBD sample due to the PVC coherent scattering.
Concluding remarks
Results presented herein show the significant effect of the solvent isomer on the thermodynamic properties, the morphology, and to a lesser extent the molecular structure of TATA organogels. Molecular compounds are, however, formed for both solvents with different stoichiometries. These results highlight the complexity of the phenomenon of organogelation. In the present case, the Hansen parameters are the same for o-DCB and m-DCB13 (h = 20.5), and yet the thermodynamic properties differ considerably. Clearly, the Hansen solubility parameter chiefly indicates whether structure formation is possible or not. Yet, it cannot predict the morphology, particularly whether structures that comply to the definition of a network are generated. For instance, when spherulites are formed40 the gel status can be legitimately questioned. Note that relying on routine rheological experiments where G′ > G′′ can be deceiving.41,42 Indeed, the rheological definition of a true gel states that an elastic modulus at 0 frequency (or infinite time) should be observed. Recent observation by Collin et al.42 for organogels, but also former investigations on polymer thermoreversible gels41 report that this condition is not always fulfilled.This investigation therefore opens up new questions such as resolving the structure of the solvent in the TATA molecular compounds. One may wonder whether there is simply a solvent shell around the 201 TATA helix reported earlier,23 or a new helical form that can accommodate the solvent molecules through intercalation, has to be considered.
It is here further observed that the TATA molecules keep their properties when imbedded in a PVC matrix. This again confirms previous results14,15 that show the possibility of preparing functional materials with an organogelator and a polymer by making hybrid gels.
Finally, the recent reports on other systems suggest that the occurrence of molecular compounds with other self-assembling systems may be a more general trend.43,44
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors are indebted to G. Fleith for experimental assistance in X-ray diffraction experiments, and C. Saettel for DSC data acquisition. The authors are indebted to ILL for providing access to D16, together with financial support, as well as to Dr B. Démé for continuous assistance during the experiments. Data are accessible under http://10.5291/ILL-DATA.9-11-2058.References
- P. Terech and R. G. Weiss, Low molecular mass gelators of organic liquids and the properties of their gels, Chem. Rev., 1997, 97, 3133–3159 CrossRef CAS PubMed.
- In Molecular Gels: Materials with Self-Assembled Fibrillar Networks, ed. P. Terech and R. G. Weiss, Springer Verlag, 2006 Search PubMed.
- R. G. Weiss, The past, present and future of molecular gels. What is the status of the field, and where is it going?, J. Am. Chem. Soc., 2014, 136, 7519–7530 CrossRef CAS PubMed.
- J. M. Guenet, Organogels: thermodynamics, structure, solvent role and properties, Springer International Publishing, N.Y., 2016. According to the dictionary: a network is “a large system of lines, tubes, wires, etc. that cross one another or are connected with one another” Search PubMed.
- In Molecular Gels, Structure and Dynamics, ed., R. G. Weiss, Monograph in Supramolecular Chemistry, Royal Society of Chemistry, London, 2018 Search PubMed.
- X. L. Liu and J. L. Li, Soft Fibrillar Materials: Fabrication and Applications, Wiley-VCH, 2013 Search PubMed.
- S. S. Babu, V. K. Praveen and A. Ajayaghosh, Functional π-Gelators and Their Applications, Chem. Rev., 2014, 114, 1973–2129 CrossRef CAS PubMed.
- C. M. Hansen, Hansen Solubility Parameter, Users’ Handbook, CRC Press, London, 2nd edn, 2007; The three Hansen parameters are: δd = 18, δp = 4.4, δH = 4.2 for tetrachloroethane, δd = 19.2, δp = 5.5, δH = 4.1 for bromobenzene. For the solvents used here, δd = 19.2, δp = 6.3, δH = 3.3 for o-DCB, and δd = 19.2, δp = 6.3, δH = 3.3 for m-DCB, the resulting h is 20.5 Search PubMed.
- R. F. Fedors, A method for estimating both the solubility parameters and the molar volume of liquids, Polym. Eng. Sci., 1974, 14, 147 CrossRef CAS.
- M. Raynal and L. Bouteiller, Organogel formation rationalized by Hansen solubility parameters, Chem. Commun., 2011, 47, 8271 RSC.
- N. Yan, Z. Xu, K. K. Diehn, S. R. Raghavan, Y. Fang and R. G. Weiss, How do liquid mixtures solubilize insoluble gelators? Self-assembly properties of pyrenyl-glucono gelators in tetrahydrofuran-water mixtures, J. Am. Chem. Soc., 2013, 135, 8989 CrossRef CAS PubMed.
- J. Bonnet, G. Suissa, M. Raynal and L. Bouteiller, Organogel formation rationalized by Hansen solubility parameters: dos and don'ts, Soft Matter, 2014, 10, 3154 RSC.
- C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, Boca Raton, 2nd edn, 2007 Search PubMed.
- B. Kiflemariam, D. Collin, O. Gavat, A. Carvalho, E. Moulin, N. Giuseppone and J. M. Guenet, Hybrid materials from tri-aryl amine organogelators and poly[vinyl chloride] networks, Polymer, 2020, 207, 122814 CrossRef CAS.
- P. Talebpour, B. Heinrich, O. Gavat, A. Carvalho, E. Moulin, N. Giuseppone and J. M. Guenet, Modulation of the Molecular Structure of Tri-aryl Amine Fibrils in Hybrid Poly[vinyl chloride] Gel/Organogel Systems, Macromolecules, 2021, 54, 8104 CrossRef CAS.
- J.-M. Guenet, B. Demé, O. Gavat, E. Moulin and N. Giuseppone, Evidence by neutron diffraction of molecular compounds in triarylamine tris-amide organogels and in their hybrid thermoreversible gels with PVC, Soft Matter, 2022, 18, 2851 RSC.
- J. M. Guenet, Polymer_solvent molecular compounds, Elsevier, London, 2008 Search PubMed.
- J. J. Point and C. Coutelier, Linear high polymers as host in intercalates. Introduction and example, J. Polym. Sci., Part B: Polym. Phys., 1985, 23, 231 CAS.
- J. J. Point, C. Coutelier and D. Villers, Intercalates with linear polymer host. Part 4. Structure of p-C6H4XY-polyoxyethylene) intercalates from unit-cell determination and energy minimization, J. Phys. Chem., 1986, 90, 3277 CrossRef CAS.
- L. Feng and K. A. Cavicchi, Investigation of the relationships between the thermodynamic phase behavior and gelation behavior of a series of tripodal trisamide compounds, Soft Matter, 2012, 8, 6483 RSC.
- J. M. Guenet, Physical Aspects of Organogelation: A Point of View, Gels, 2021, 7, 65 CrossRef CAS PubMed.
- E. Moulin, F. Niess, M. Maaloum, E. Buhler, L. Nyrkova and N. Giuseppone, The hierarchical self-assembly of charge nanocarriers: a highly cooperative process promoted by visible light, Angew. Chem., Int. Ed., 2010, 49, 6974 CrossRef CAS PubMed.
- J. J. Armao IV, M. Maaloum, T. Ellis, G. Fuks, M. Rawiso, E. Moulin and N. Giuseppone, Healable supramolecular polymers as organic metals, J. Am. Chem. Soc., 2014, 136, 11382 CrossRef PubMed.
- L. Nyrkova, E. Moulin, J. J. Armao IV, M. Maaloum, B. Heinrich, M. Rawiso, F. Niess, J. J. Cid, N. Jouault, E. Buhler, A. Semenov and N. Giuseppone, Supramolecular self-assembly and radical kinetics in conducting self-replicating nanowires, ACS Nano, 2014, 8, 10111 CrossRef PubMed.
- E. Moulin, J. J. Armao IV and N. Giuseppone, Triaryl amine-based supramolecular polymers: structure, dynamics, and functions, Acc. Chem. Res., 2019, 52, 975 CrossRef CAS PubMed.
- Y. C. Yang and P. H. Geil, Morphology and properties of PVC/solvent gels, J. Macromol. Sci., Part B: Phys., 1983, 22, 463 CrossRef.
- P. H. Mutin and J. M. Guenet, Physical gels from PVC: ageing and solvent effect on thermal behavior, swelling and compression modulus, Macromolecules, 1989, 22, 843 CrossRef CAS.
- V. Cristiglio, B. Giroud, L. Didier and B. Demé, D16 is back to business: more neutrons, more space, more fun, J. Neutron Res., 2015, 26, 23 Search PubMed.
- See for instance: A. Reisman, Phase Equilibria: Basic Principles, Applications, experimental Techniques, Acad. Press, London, 1970 Search PubMed.
- R. E. Rundle, C. G. Schull and E. O. Wollan, The crystal structure of thorium and zirconium dihydrides by X-ray and neutron diffraction, Acta Crystallogr., 1952, 5, 22 CrossRef CAS.
- J. J. Point, P. Damman and J. M. Guenet, Neutron diffraction study of poly(ethylene oxide) p dihalogenobenzene crystalline complexes, Polym. Commun., 1991, 32, 477 CAS.
- C. Daniel, A. Menelle, A. Brulet and J. M. Guenet, Thermoreversible Gelation of Syndiotactic Polystyrene in Toluene and Chloroform, Polymer, 1997, 38, 4193 CrossRef CAS.
- F. Kaneko, N. Seto, S. Sato, A. Radulescu, M. M. Schiavone, J. Allgaier and K. Ute, Development of a Simultaneous SANS/FTIR Measuring System, Chem. Lett., 2015, 44, 497 CrossRef CAS.
- G. E. Bacon, Coherent neutron-scattering amplitudes, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1972, A28, 357 CrossRef.
- H. Tadokoro, Y. Chatani, T. Yoshihara, S. Tahara and S. Murahashi, Structural studies on polyethers, [–(CH2)m–O–]n. II. Molecular structure of polyethylene oxide, Makromol. Chem., 1964, 73, 109 CrossRef CAS.
- A. Chenite and F. Brisse, Structure and conformation of poly(ethylene oxide), PEO, in the trigonal form of the PEO-urea complex at 173 K, Macromolecules, 1991, 24, 2221 CrossRef CAS.
- O. A. Pringle and P. W. Schmidt, Small-Angle X-Ray Scattering from Helical Macromolecules, J. Appl. Crystallogr., 1971, 4, 290 CrossRef CAS.
- G. Oster and D. P. Riley, Scattering from Cylindrically Symmetric Systems, Acta Cryst., 1952, 5, 272 CrossRef CAS.
- P. Mittelbach and G. Porod, Zur Röntgenkleinwinkelstreuung verdünnter kolloiden Systeme, Acta Phys. Austriaca, 1961, 14, 185 CrossRef CAS.
- M. Lescanne, A. Colin, O. Mondain-Monval, F. Fages and J. L. Pozzo, Structural Aspects of the Gelation Process Observed with Low Molecular Mass Organogelators, Langmuir, 2003, 19, 2013 CrossRef CAS.
- J. M. Guenet and G. B. McKenna, The concentration dependence of the compression modulus of iPS/cis decalin gels, J. Polym. Sci., Polym. Phys. Ed., 1986, 24, 2499 CrossRef CAS.
- D. Collin, R. Covis, F. Allix, B. Jamart-Grégoire and P. Martinoty, Jamming transition in solutionscontaining organogelator molecules of amino-acid type: rheological and calorimetry experiments, Soft Matter, 2013, 9, 2947 RSC.
- K. K. Kartha, S. S. Babu, S. Srinivasan and A. Ajayaghosh, Attogram Sensing of Trinitrotoluene with a Self-Assembled Molecular Gelator, J. Am. Chem. Soc., 2012, 134, 4834 CrossRef CAS PubMed.
- G. Ghosh, A. Chakraborty, P. Pal, B. Jana and S. Ghosh, Direct Participation of Solvent Molecules in the Formation of Supramolecular Polymers, Chem. – Eur. J., 2022 DOI:10.1002/chem.202201082.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00563h |
| This journal is © The Royal Society of Chemistry 2022 |