Open Access Article
Open Access ArticleAnnealing and melting of active two-dimensional soliton lattices in chiral nematic films†
Yuan
Shen
 and
Ingo
Dierking
and
Ingo
Dierking
 *
*
Department of Physics and Astronomy, School of Natural Sciences, University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: ingo.dierking@manchester.ac.uk
First published on 19th August 2022
Abstract
In this work, thousands of electrically driven dissipative solitons, called directrons, are generated in a chiral nematic liquid crystal. The directrons start with random motions but soon synchronize their motions and self-organize into a two-dimensional hexagonal lattice. The directron lattice moves collectively and forms a hexatic phase. By increasing the applied voltage, the lattice exhibits a first-order hexatic-to-liquid phase transition.
Soft materials in which constituent building elements dissipate ambient free energy and convert it into mechanical work are generally referred to as active matter.1 Distinct from conventional thermal systems in which self-organization usually arises from the coupling between entropy and potential interactions, the thermal energy is negligible for active matter and various complicated self-organization and collective motion stems from its primitive rules of propulsion and inter-particle interactions. Examples include large-scale vortices in bacteria suspensions,2–4 sperm cells,5 driven filaments6–8 and artificial active particles,9–11 nematic order in vibrated rods12 and cell swarms,13 active crystallization of bacteria14 and colloidal particles,15–18 clustering and phase separation of self-propelled particles,19–21etc. However, self-organization of large scale ordered structure that experiences directional collective motion has rarely been reported so far.22
Solitons are self-sustained localized packets of waves in nonlinear media that propagate without changing shape, such as water waves in a canal.23 They are ubiquitous and exist in many areas of physics including nonlinear photonics,24 Bose–Einstein condensates,25 superconductors,26 magnetic materials27 and liquid crystals.28 The investigations of solitons in liquid crystals have been carried out for over 5 decades. Various kinds of solitons have been reported, including different types of inversion walls,29–31 propagating solitary waves,32,33 individual convective rolls34 and local convective domains,35 discommensurations36,37 and breathers,38 nematicons,39 skyrmions and torons,28 swallow-tail solitons,40etc. In 1997, Brand et al. reported an electrically driven butterfly-like soliton which moves easily and rapidly throughout the uniform nematic bulk,41 which was recently recognized as the three-dimensional (3D) dissipative solitary waves coined as “director bullets” or “directrons” by Li et al.42–45 and received increasing attention due to their intriguing nonlinear dynamic properties and potential applications in various areas such as microfluidics and optics.46–48 These directrons represent topological trivial particle-like localized dissipative solitary director waves. They behave like active particles in so far that they convert the applied electric energy into translational motions and repel each other during collisions.
Here, we show that hundreds and thousands of directrons are created in a chiral nematic film by applying an electric field. The directrons start with random motions but then synchronize their motions through many-body interactions and self-organize into an active two-dimensional (2D) hexagonal lattice which moves in a direction selected by spontaneous symmetry breaking. The lattice anneals with time from a disordered liquid phase to an ordered hexatic phase through the motion and collisions of the directrons. By increasing the applied voltage, individual directrons perform random walks, leading to a first-order hexatic-to-liquid melting transition of the 2D lattice.
A chiral nematic film is prepared by capillary filling a mixture of the nematic liquid crystal ZLI-2806 (Merck) and chiral dopant ZLI-811 (Xianhua, China) into a commercial cell (AWAT, Poland). The ZLI-2806 has a negative dielectric anisotropy and a positive conductivity anisotropy.46 The pitch of the LC mixture p ∼ 2 μm is calculated according to the equation p = 1/(HTP × c), where c is the weight concentration of the chiral dopant, and HTP = −8.3 μm−1 represents the helical twisting power of the chiral dopant.46 The inner surfaces of the cell are covered with transparent indium tin oxide (ITO) layers to act as electrodes and are coated with rubbed polyimide layers to produce a homogeneous alignment. The rubbing direction is along the x-axis. The cell gap d ∼ 9.5 μm is measured by the thin-film interference method.49 The sample is kept at 80 °C and an alternating-current (AC) electric field (E) is applied perpendicular to the cell substrates. By increasing the voltage (U) to a threshold value, thousands of directrons emerge and move in random directions.
The directrons are the same as the ones reported before,50 which show a quadrupolar symmetric texture in polarized optical microscopy (Fig. S1, ESI†). Outside the directrons, the helical director field aligns homogeneously with its helix parallel to the electric field along the z-axis. Within the directron, the director deviates from the homogeneous state due to the transverse Coulomb forces provided by space charges as well as the flexoelectric polarization.46 The director distortion reaches the maximum in the middle plane of the cell, but gradually decreases as one moves toward the top and bottom cell substrates.42 This is due to the competition between the flexoelectric torque and the homogeneous surface anchoring. The structure of the directrons changes periodically with the frequency of the applied electric field, indicating the periodic oscillation of the director field within the directrons due to the flexoelectric effect (Fig. S2, ESI†).46 Once the symmetric structure of the directrons is broken due to, for instance, thermal fluctuations, such oscillations of the director field produces polarized flows which drive the directrons move forward.42,46 The formation mechanism of the directrons is relatively complicated which involves many different factors, such as space charges, ion injection, flexoelectric effect, electro-convection effect, etc., and has not been completely understood yet. In our opinion, the formation of the directrons is mainly attributed to the coupling between the space charges and the flexoelectric effect.50 Unlike topological solitons, such as skyrmions,51 whose stability is topologically protected and cannot be continuously transformed into the uniform state, the directrons are topologically trivial and immediately disappear once the applied electric field is below the threshold values.
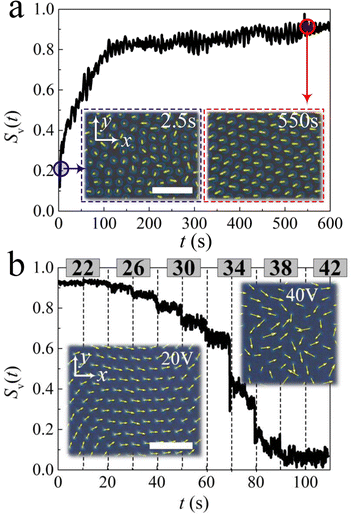
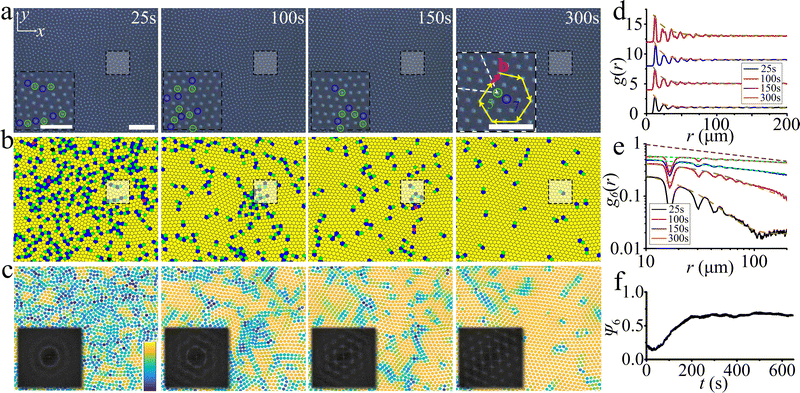
Millions of directrons start from random motions but soon synchronize their motions through interactions with each other (Fig. 1a). The velocity order parameter 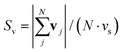 , where N is the total number of directrons in the field of view and vs is the absolute value of the velocity of coherently moving directrons,52 gradually increases from 0.1 to 0.8 and eventually saturates at Sv ≈ 0.9 (Fig. 1a). The directrons are uniformly distributed throughout the sample and gradually self-organize into an ordered 2D hexagonal lattice with time (Fig. 2a and Movie S1, ESI†). Within the lattice, dislocations composed of a pair of five-and sevenfold coordinated directrons, also called disclinations, are formed randomly (Fig. 2a inset). The magnitude and direction of an isolated dislocation is given by the Burgers vector, b, along which the translational order of the lattice is decreased. The formation of dislocations usually costs huge amounts of free energy and destroys the translational order of the crystal.53 To better visualize the dislocations, the directron lattice is characterized by the Voronoi construction (Fig. 2b). As one can see, a large amount of topological defects, dislocations and dislocation pairs, are formed right after the generation of directrons, which assemble into grain boundaries and clusters. As the directrons keep moving and colliding with each other, they gradually synchronize their motion. As a result, the defects annihilate with each other and the lattice becomes more and more ordered. After approximately 300 seconds, there are only small amounts of dislocations left which are sparsely distributed within the lattice (Movie S2, ESI†). To quantify the effects of the motion on the orientational ordering, we have characterized the local (ψ6(rj) for soliton j) and global (Ψ6) hexatic bond orientational order parameters, respectively. The magnitude of the local bond-orientational order parameter |ψ6(rj)| varies from 0 to 1 and measures how the neighbors of soliton j fit locally on a hexagonal lattice (Fig. 2c). Ψ6 changes with time which gradually increases and eventually saturates at late times (Fig. 2f). While the radial distribution function g(r) decays exponentially to one within several peaks, it becomes more and more long-range with time, indicating the increase of the translational order of the lattice (Fig. 2d and Fig. S3, ESI†). On the other hand, the bond orientational correlation function decays exponentially (g6(r) ∝ e−r/ξ6) at early times, but decays algebraically (g6(r) ∝ r−η6) at late times (Fig. 2e and Fig. S3, ESI†). The exponent η6 is 0.22 at t = 150 s and 0.09 at t = 300 s. In 2D systems, the existence of a solid featuring long-range positional order is absent due to the Mermin–Wagner theorem54 and the transition from the solid to the liquid phase experiences two continuous phase transitions according to the Kosterlitz–Thouless–Halperin–Nelson–Young (KTHNY) theory.55–58 The first transition driven by the dissociation of bound dislocation pairs is from the crystal with quasi-long-range positional order and long-range orientational order to the so-called hexatic phase with short-range positional order and quasi-long-range orientational order. The second transition driven by the dissociation of isolated dislocations is from the hexatic phase to a liquid phase in which both positional and orientational order show short-range correlations. While the radial distribution function (g(r)) decays exponentially in both liquid and hexatic phases, the bond orientational correlation function (g6(r)) decays exponentially in the liquid phase but algebraically in the hexatic phase. At the hexatic-liquid transition point, g6(r) decays algebraically with the exponent η6 = 0.25, i.e., g6(r) ∝ r−0.25.59 As a result, according to the KTHNY theory, the 2D directron lattice shows a liquid phase at early time stages and transforms into a hexatic phase at t = 150 s. At t = 300 s, the directron lattice is deep into the hexatic phase and well ordered. One may suspect it represents a crystal phase at t = 300 s, however, the exponentially decaying radial distribution function (Fig. 2d) and the divergence of the dynamic Lindemann parameter (L2) (Fig. S4, ESI†) exclude this possibility. The sparsely distributed free dislocations shown in Fig. 2b destroys the translational order of the lattice according to the KTHNY theory.60 The dynamic Lindemann parameter as an improved criterion of 2D melting stays finite below a critical value Lc2 = 0.033 in a crystal but diverges in the hexatic and liquid phases.61 The insets in Fig. 2c show the 2D structure factors of the directron lattice at different moments which are obtained by Fourier transforming the 2D radial distribution functions before azimuthally averaging them. It transforms gradually with time from a pattern of continuous concentric rings which is typical for an isotropic liquid phase to a sixfold angular symmetric diffraction pattern which is a necessary but not sufficient condition of a hexatic phase.62
, where N is the total number of directrons in the field of view and vs is the absolute value of the velocity of coherently moving directrons,52 gradually increases from 0.1 to 0.8 and eventually saturates at Sv ≈ 0.9 (Fig. 1a). The directrons are uniformly distributed throughout the sample and gradually self-organize into an ordered 2D hexagonal lattice with time (Fig. 2a and Movie S1, ESI†). Within the lattice, dislocations composed of a pair of five-and sevenfold coordinated directrons, also called disclinations, are formed randomly (Fig. 2a inset). The magnitude and direction of an isolated dislocation is given by the Burgers vector, b, along which the translational order of the lattice is decreased. The formation of dislocations usually costs huge amounts of free energy and destroys the translational order of the crystal.53 To better visualize the dislocations, the directron lattice is characterized by the Voronoi construction (Fig. 2b). As one can see, a large amount of topological defects, dislocations and dislocation pairs, are formed right after the generation of directrons, which assemble into grain boundaries and clusters. As the directrons keep moving and colliding with each other, they gradually synchronize their motion. As a result, the defects annihilate with each other and the lattice becomes more and more ordered. After approximately 300 seconds, there are only small amounts of dislocations left which are sparsely distributed within the lattice (Movie S2, ESI†). To quantify the effects of the motion on the orientational ordering, we have characterized the local (ψ6(rj) for soliton j) and global (Ψ6) hexatic bond orientational order parameters, respectively. The magnitude of the local bond-orientational order parameter |ψ6(rj)| varies from 0 to 1 and measures how the neighbors of soliton j fit locally on a hexagonal lattice (Fig. 2c). Ψ6 changes with time which gradually increases and eventually saturates at late times (Fig. 2f). While the radial distribution function g(r) decays exponentially to one within several peaks, it becomes more and more long-range with time, indicating the increase of the translational order of the lattice (Fig. 2d and Fig. S3, ESI†). On the other hand, the bond orientational correlation function decays exponentially (g6(r) ∝ e−r/ξ6) at early times, but decays algebraically (g6(r) ∝ r−η6) at late times (Fig. 2e and Fig. S3, ESI†). The exponent η6 is 0.22 at t = 150 s and 0.09 at t = 300 s. In 2D systems, the existence of a solid featuring long-range positional order is absent due to the Mermin–Wagner theorem54 and the transition from the solid to the liquid phase experiences two continuous phase transitions according to the Kosterlitz–Thouless–Halperin–Nelson–Young (KTHNY) theory.55–58 The first transition driven by the dissociation of bound dislocation pairs is from the crystal with quasi-long-range positional order and long-range orientational order to the so-called hexatic phase with short-range positional order and quasi-long-range orientational order. The second transition driven by the dissociation of isolated dislocations is from the hexatic phase to a liquid phase in which both positional and orientational order show short-range correlations. While the radial distribution function (g(r)) decays exponentially in both liquid and hexatic phases, the bond orientational correlation function (g6(r)) decays exponentially in the liquid phase but algebraically in the hexatic phase. At the hexatic-liquid transition point, g6(r) decays algebraically with the exponent η6 = 0.25, i.e., g6(r) ∝ r−0.25.59 As a result, according to the KTHNY theory, the 2D directron lattice shows a liquid phase at early time stages and transforms into a hexatic phase at t = 150 s. At t = 300 s, the directron lattice is deep into the hexatic phase and well ordered. One may suspect it represents a crystal phase at t = 300 s, however, the exponentially decaying radial distribution function (Fig. 2d) and the divergence of the dynamic Lindemann parameter (L2) (Fig. S4, ESI†) exclude this possibility. The sparsely distributed free dislocations shown in Fig. 2b destroys the translational order of the lattice according to the KTHNY theory.60 The dynamic Lindemann parameter as an improved criterion of 2D melting stays finite below a critical value Lc2 = 0.033 in a crystal but diverges in the hexatic and liquid phases.61 The insets in Fig. 2c show the 2D structure factors of the directron lattice at different moments which are obtained by Fourier transforming the 2D radial distribution functions before azimuthally averaging them. It transforms gradually with time from a pattern of continuous concentric rings which is typical for an isotropic liquid phase to a sixfold angular symmetric diffraction pattern which is a necessary but not sufficient condition of a hexatic phase.62
The dynamics of the directrons depends on the applied voltage. By increasing the voltage, the velocity order parameter Sv continuously decreases from 0.9 to 0 and the collective motion of the directrons gradually transforms to a chaotic incoherent motion (Fig. 1b and Movie S3, ESI†). In our opinion, there are two possible reasons which induce such an order–disorder transition. The first possibility is that the director structure of directrons is distorted by increasing voltages, and such a distortion changes randomly and breaks the symmetry of directrons with the frequency of the applied electric field. The second possibility is due to the formation of isotropic electro-hydrodynamic flows at high voltages.
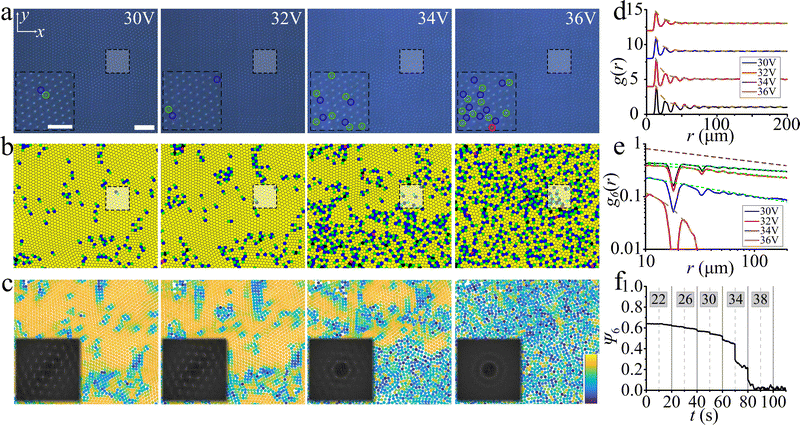
As a result, the directron lattice gradually melts from the hexatic phase to the liquid phase (Fig. 3 and Movie S3, ESI†). As the voltage gradually increases from 20 V to 32 V, the topological defects gradually increase and form grain boundaries (Fig. 3b and Movie S4, ESI†). At the same time, the global orientational order parameter, Ψ6, continuously decreases (Fig. 3f). However, the directron lattice stays in the hexatic phase. This is indicated by the exponentially decaying radial distribution function and the algebraically decaying orientational correlation function whose exponent η6 is smaller than 0.25 (Fig. 3d and e and Fig. S5, ESI†). To get a better insight into the degree of local orientational ordering, we investigate the magnitude of the projection of ψ6(rj) onto the mean local orientational field, 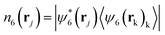 , where k represents the nearest neighbours of directron j, which takes the second nearest neighbours into account and determines how the orientation of directron j fits into the orientation of its neighbours.63 It was shown by Larsen and Grier that the joint distribution P(|ψ6|, n6) is unimodal if the system shows a pure phase,64 whereas a bimodal distribution is found if the system exhibits coexistence of different phases.65 A directron with |ψ6| + n6 > 1 is classified as belonging to the crystal phase, otherwise, it is assigned to the liquid phase. Fig. 4 gives the probability distribution for the directron lattice in the |ψ6| − n6-plane at different voltages. It is noted that most of the directrons have |ψ6| + n6 > 1 and form a unimodal distribution at U = 30 V and 32 V, indicating a pure hexatic phase (Fig. 4a and b). The defects significantly increase and form chains and clusters at U = 34 V with a drastic decrease of global bond orientational order, Ψ6 (Fig. 3f). At the same time, g6(r) decays algebraically with an exponent η6 = 0.34 > 0.25, which indicates the occurrence of a phase transition (Fig. 3e). This is inconsistent with the KTHNY theory where a continuous hexatic-to-liquid phase transition is driven by the unbinding of individual dislocations into free disclinations.56,58 Instead, the “condensation” of defects observed in Fig. 3 is, to some extent, in qualitative agreement with the grain-boundary-induced melting theory proposed by Chui.66 Moreover, the joint distribution P(|ψ6|, n6) in Fig. 4c shows a bimodal distribution indicating that the system is in a state of coexistence between hexatic and liquid phases. Such a hexatic-liquid phase separation can also be clearly observed from the colormap of |ψ6| (Fig. 3c). The KTHNY theory is not a thermodynamically consistent theory of 2D melting and different particle-particle interactions may lead to different melting phenomena.67 Such a first-order phase transition is similar to the motility-induced phase separation (MIPS) of active Brownian particles reported by R. Digregorio, et al.68 Further increase of voltage leads to an isotropic liquid phase with Ψ6 decaying to zero (Fig. 3f). Both the radial distribution function and the orientational correlation function decay exponentially (Fig. 3d and e). The joint distribution P(|ψ6|, n6) exhibits a unimodal distribution with most of the directrons showing |ψ6| + n6 < 1 (Fig. 4d), which demonstrates that the local sixfold order up to the second shell is lost.
, where k represents the nearest neighbours of directron j, which takes the second nearest neighbours into account and determines how the orientation of directron j fits into the orientation of its neighbours.63 It was shown by Larsen and Grier that the joint distribution P(|ψ6|, n6) is unimodal if the system shows a pure phase,64 whereas a bimodal distribution is found if the system exhibits coexistence of different phases.65 A directron with |ψ6| + n6 > 1 is classified as belonging to the crystal phase, otherwise, it is assigned to the liquid phase. Fig. 4 gives the probability distribution for the directron lattice in the |ψ6| − n6-plane at different voltages. It is noted that most of the directrons have |ψ6| + n6 > 1 and form a unimodal distribution at U = 30 V and 32 V, indicating a pure hexatic phase (Fig. 4a and b). The defects significantly increase and form chains and clusters at U = 34 V with a drastic decrease of global bond orientational order, Ψ6 (Fig. 3f). At the same time, g6(r) decays algebraically with an exponent η6 = 0.34 > 0.25, which indicates the occurrence of a phase transition (Fig. 3e). This is inconsistent with the KTHNY theory where a continuous hexatic-to-liquid phase transition is driven by the unbinding of individual dislocations into free disclinations.56,58 Instead, the “condensation” of defects observed in Fig. 3 is, to some extent, in qualitative agreement with the grain-boundary-induced melting theory proposed by Chui.66 Moreover, the joint distribution P(|ψ6|, n6) in Fig. 4c shows a bimodal distribution indicating that the system is in a state of coexistence between hexatic and liquid phases. Such a hexatic-liquid phase separation can also be clearly observed from the colormap of |ψ6| (Fig. 3c). The KTHNY theory is not a thermodynamically consistent theory of 2D melting and different particle-particle interactions may lead to different melting phenomena.67 Such a first-order phase transition is similar to the motility-induced phase separation (MIPS) of active Brownian particles reported by R. Digregorio, et al.68 Further increase of voltage leads to an isotropic liquid phase with Ψ6 decaying to zero (Fig. 3f). Both the radial distribution function and the orientational correlation function decay exponentially (Fig. 3d and e). The joint distribution P(|ψ6|, n6) exhibits a unimodal distribution with most of the directrons showing |ψ6| + n6 < 1 (Fig. 4d), which demonstrates that the local sixfold order up to the second shell is lost.
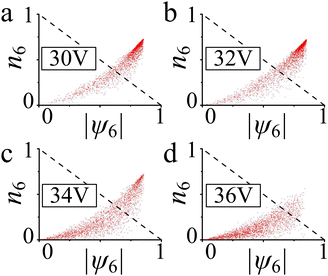 | ||
| Fig. 4 Probability distributions of |ψ6| versus n6 of the soliton lattice at different Voltages. (a) 30 V. (b) 32. (c) 34 V. (d) 36 V. The black-dashed line shows n6 + |ψ6| = 1. | ||
Conclusions
To conclude, we show that an active system formed by microscopic particle-like solitonic field configurations exhibit emergent collective dynamics inaccessible to their atomic and molecular counterparts, providing a tuneable model for studying out-of-equilibrium self-organization and order–disorder transitions. The large scale polar order and directional collective motion of the directrons share similarities with classical flocking models such as the Vicsek69 and Toner–Tu modes70,71 and is analogous to other active systems such as active colloidal particles.72 Although it is predicted that phases known in thermodynamic equilibrium systems have their counterparts in out-of-equilibrium systems,73 only several phases have been observed so far.15,19,73,74 Recently, the formation of an active hexatic phase has been demonstrated in different numerical simulation systems.68,75–77 However, the experimental counterpart has rarely been reported.78,79 Our results show that dynamic directrons can self-organize into an active hexatic phase which thus extends the scenarios of 2D melting developed for a description of thermodynamic equilibrium systems to non-equilibrium systems. The facile fabrication, control and observation of our system also make it potentially promising for studying many other forms of out-of-equilibrium behaviour, such as collective motion,80 motility-induced phase separation,81 phase transition in non-equilibrium systems,82etc.Author contributions
Y. S. conceived and carried out the experimental investigations, analysed the results and wrote the manuscript. I. D. supervised the investigation and contributed through discussion and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Notes and references
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- H. Zhang, A. Be'Er, R. S. Smith, E.-L. Florin and H. L. Swinney, EPL, 2009, 87, 48011 CrossRef.
- H. Wioland, F. G. Woodhouse, J. Dunkel, J. O. Kessler and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 268102 CrossRef PubMed.
- E. Lushi, H. Wioland and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9733–9738 CrossRef CAS PubMed.
- I. H. Riedel, K. Kruse and J. Howard, Science, 2005, 309, 300–303 CrossRef CAS PubMed.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- V. Schaller and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4488–4493 CrossRef.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- A. Bricard, J.-B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 7470 CrossRef CAS PubMed.
- G. Kokot and A. Snezhko, Nat. Commun., 2018, 9, 1–7 CrossRef CAS PubMed.
- Z. T. Liu, Y. Shi, Y. Zhao, H. Chaté, X.-Q. Shi and T. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104724118 CrossRef CAS PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- G. Duclos, S. Garcia, H. Yevick and P. Silberzan, Soft Matter, 2014, 10, 2346–2353 RSC.
- A. P. Petroff, X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2015, 114, 158102 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- B. A. Grzybowski, H. A. Stone and G. M. Whitesides, Nature, 2000, 405, 1033–1036 CrossRef CAS PubMed.
- G. A. Voth, B. Bigger, M. Buckley, W. Losert, M. Brenner, H. A. Stone and J. Gollub, Phys. Rev. Lett., 2002, 88, 234301 CrossRef PubMed.
- M. Baron, J. Bławzdziewicz and E. Wajnryb, Phys. Rev. Lett., 2008, 100, 174502 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095–1099 CrossRef CAS PubMed.
- H. R. Sohn and I. I. Smalyukh, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 6437–6445 CrossRef CAS PubMed.
- T. Dauxois and M. Peyrard, Physics of solitons, Cambridge University Press, 2006 Search PubMed.
- L. Du, A. Yang, A. V. Zayats and X. Yuan, Nat. Phys., 2019, 15, 650–654 Search PubMed.
- M. W. Ray, E. Ruokokoski, S. Kandel, M. Möttönen and D. Hall, Nature, 2014, 505, 657–660 CrossRef CAS.
- K. Harada, T. Matsuda, J. Bonevich, M. Igarashi, S. Kondo, G. Pozzi, U. Kawabe and A. Tonomura, Nature, 1992, 360, 51–53 CrossRef.
- X. Yu, Y. Onose, N. Kanazawa, J. Park, J. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465, 901–904 CrossRef CAS PubMed.
- I. I. Smalyukh, Y. Lansac, N. A. Clark and R. P. Trivedi, Nat. Mater., 2009, 9, 139 CrossRef PubMed.
- W. Helfrich, Phys. Rev. Lett., 1968, 21, 1518–1521 CrossRef CAS.
- L. Leger, Solid State Commun., 1972, 10, 697–700 CrossRef CAS.
- K. B. Migler and R. B. Meyer, Phys. Rev. Lett., 1991, 66, 1485–1488 CrossRef CAS PubMed.
- Z. Guozhen, Phys. Rev. Lett., 1982, 49, 1332–1335 CrossRef CAS.
- L. Lei, S. Changqing, S. Juelian, P. M. Lam and H. Yun, Phys. Rev. Lett., 1982, 49, 1335–1338 CrossRef CAS.
- R. Ribotta, Phys. Rev. Lett., 1979, 42, 1212–1215 CrossRef CAS.
- A. Joets and R. Ribotta, Phys. Rev. Lett., 1988, 60, 2164–2167 CrossRef CAS PubMed.
- M. Lowe and J. P. Gollub, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 3893–3897 CrossRef CAS PubMed.
- M. Lowe, J. P. Gollub and T. C. Lubensky, Phys. Rev. Lett., 1983, 51, 786–789 CrossRef CAS.
- O. A. Skaldin, V. A. Delev and E. S. Shikhovtseva, JETP Lett., 2013, 97, 92–97 CrossRef CAS.
- M. Peccianti and G. Assanto, Phys. Rep., 2012, 516, 147–208 CrossRef.
- Y. Shen and I. Dierking, Mater. Adv., 2021, 2, 4752–4761 RSC.
- H. R. Brand, C. Fradin, P. L. Finn, W. Pesch and P. E. Cladis, Phys. Lett. A, 1997, 235, 508–514 CrossRef CAS.
- B.-X. Li, V. Borshch, R.-L. Xiao, S. Paladugu, T. Turiv, S. V. Shiyanovskii and O. D. Lavrentovich, Nat. Commun., 2018, 9, 2912 CrossRef PubMed.
- B.-X. Li, R.-L. Xiao, S. Paladugu, S. V. Shiyanovskii and O. D. Lavrentovich, Nat. Commun., 2019, 10, 3749 CrossRef PubMed.
- B.-X. Li, R.-L. Xiao, S. V. Shiyanovskii and O. D. Lavrentovich, Phys. Rev. Res., 2020, 2, 013178 CrossRef CAS.
- O. D. Lavrentovich, Liq. Cryst. Rev., 2020, 8, 59–129 CrossRef CAS PubMed.
- Y. Shen and I. Dierking, Commun. Phys., 2020, 3, 1 CrossRef.
- Y. Shen and I. Dierking, Soft Matter, 2020, 16, 5325 RSC.
- S. Aya and F. Araoka, Nat. Commun., 2020, 11, 1–10 CrossRef.
- A. M. Goodman, Appl. Opt., 1978, 17, 2779–2787 CrossRef CAS PubMed.
- Y. Shen and I. Dierking, Nat. Commun., 2022, 13, 1–12 Search PubMed.
- J.-S. Wu and I. I. Smalyukh, Liq. Cryst. Rev., 2022, 1–91 Search PubMed.
- Y. Shen and I. Dierking, Phys. Rev. Appl., 2021, 15, 054023 CrossRef CAS.
- U. Gasser, C. Eisenmann, G. Maret and P. Keim, Chem. Phys. Chem., 2010, 11, 963–970 CrossRef CAS PubMed.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133 CrossRef CAS.
- J. M. Kosterlitz and D. J. Thouless, J. Phys. C-Solid State Phys., 1973, 6, 1181 CrossRef CAS.
- D. R. Nelson and B. I. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys, 1979, 19, 2457–2484 CrossRef CAS.
- A. P. Young, Phys. Rev. B: Condens. Matter Mater. Phys, 1979, 19, 1855–1866 CrossRef CAS.
- B. Halperin and D. R. Nelson, Phys. Rev. Lett., 1978, 41, 121 CrossRef CAS.
- K. J. Strandburg, Rev. Mod. Phys., 1988, 60, 161 CrossRef CAS.
- W. Brinkman, D. S. Fisher and D. Moncton, Science, 1982, 217, 693–700 CrossRef CAS PubMed.
- K. Zahn, R. Lenke and G. Maret, Phys. Rev. Lett., 1999, 82, 2721 CrossRef CAS.
- A. H. Marcus and S. A. Rice, Phys. Rev. Lett., 1996, 77, 2577 CrossRef CAS PubMed.
- P. Dillmann, G. Maret and P. Keim, J. Phys.: Condens. Matter, 2012, 24, 464118 CrossRef PubMed.
- A. E. Larsen and D. G. Grier, Phys. Rev. Lett., 1996, 76, 3862 CrossRef CAS PubMed.
- A. H. Marcus and S. A. Rice, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 637 CrossRef CAS.
- S. Chui, Phys. Rev. B: Condens. Matter Mater. Phys, 1983, 28, 178 CrossRef.
- P. Karnchanaphanurach, B. Lin and S. A. Rice, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4036 CrossRef CAS PubMed.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226 CrossRef CAS PubMed.
- J. Toner and Y. Tu, Phys. Rev. Lett., 1995, 75, 4326 CrossRef CAS PubMed.
- J. Toner and Y. Tu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 4828 CrossRef CAS.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- J. Toner, Y. Tu and S. Ramaswamy, Ann. Phys., 2005, 318, 170–244 CAS.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- J. U. Klamser, S. C. Kapfer and W. Krauth, Nat. Commun., 2018, 9, 1–8 CrossRef CAS PubMed.
- M. James, D. A. Suchla, J. Dunkel and M. Wilczek, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed.
- S. Paliwal and M. Dijkstra, Phys. Rev. Res., 2020, 2, 012013 CrossRef CAS.
- J. Olafsen and J. Urbach, Phys. Rev. Lett., 2005, 95, 098002 CrossRef CAS PubMed.
- R. Seshadri and R. Westervelt, Phys. Rev. B: Condens. Matter Mater. Phys, 1992, 46, 5150 CrossRef PubMed.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- J. Bialké, T. Speck and H. Löwen, Phys. Rev. Lett., 2012, 108, 168301 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00815g |
| This journal is © The Royal Society of Chemistry 2022 |