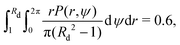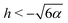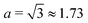DOI:
10.1039/D2SM00907B
(Paper)
Soft Matter, 2022,
18, 8931-8944
Microswimmers in vortices: dynamics and trapping
Received
4th July 2022
, Accepted 9th November 2022
First published on 21st November 2022
Abstract
Biological and artificial microswimmers often self-propel in external flows of vortical nature; relevant examples include algae in small-scale ocean eddies, spermatozoa in uterine peristaltic flows and bacteria in microfluidic devices. A recent experiment has shown that swimming bacteria in model vortices are expelled from the vortex all the way to a well-defined depletion zone (A. Sokolov and I. S. Aranson, Rapid expulsion of microswimmers by a vortical flow. Nat. Commun., 2016, 7, 11114). In this paper, we propose a theoretical model to investigate the dynamics of elongated microswimmers in elementary vortices, namely active particles in two- and three-dimensional rotlets. A deterministic model first reveals the existence of bounded orbits near the centre of the vortex and unbounded orbits elsewhere. We further discover a conserved quantity of motion that allows us to map the phase space according to the type of the orbit (bounded vs unbounded). We next introduce translational and rotational noise into the system. Using a Fokker–Planck formalism, we quantify the quality of trapping near the centre of the vortex by examining the probability of escape and the mean time of escape from the region of deterministically bounded orbits. We finally show how to use these findings to formulate a prediction for the radius of the depletion zone, which compares favourably with the experiments (A. Sokolov and I. S. Aranson, Rapid expulsion of microswimmers by a vortical flow. Nat. Commun., 2016, 7, 11114).
1 Introduction
Motile microorganisms, ubiquitous in nature, have been shown to exploit a wide range of physical mechanisms to self propel through their fluid environment.1,2 These swimming microorganisms must not only ensure successful propulsion but also navigate against external flows.3–7 The novel dynamics that arises from the interaction of motile microorganisms and external flows is commonly known as the rheotaxis.
Perhaps the most famous example of rheotaxis is the hydrodynamic focusing of bottom-heavy algae in downward flows as observed in both laboratory experiments and oceanic flows.8–12 This focusing results from a combination of hydrodynamic interactions with external flows and the gravitational alignment of the bottom-heavy algae with the vertical direction; as a result, it is often known as gyrotaxis. Further examples of motile cells that show a rheotactic response include bacteria13–17 and mammalian spermatozoa.18–22 Unsurprisingly, bio-inspired artificial microswimmers are faced with similar rheotactic challenges.23–28
To understand the essential physics of rheotaxis, minimal mathematical models of motile cells in flows have recently been proposed.29–32 In the simplest model, the swimmer is an active particle of fixed shape advected by the flow while swimming with a prescribed speed along a fixed direction in the swimmer's frame. The flow changes not only the location of the swimmer (advection) but also its swimming direction (reorientation). For spherical swimmers, the minimal model can have closed-form solutions, as long as the swimmer is assumed to move through an infinite fluid. Indeed, in that case the equations of motion are exact, with interactions with the flow following from Faxén's laws.33 Fundamental solutions exist then for swimming in simple linear flows such as the solid-body rotation, shear and extensional flows.2,34 In the more complex case of swimming in a Poiseuille flow, but perhaps one more relevant to applications, the dynamics of a spherical swimmer cannot be exactly integrated but it was shown to have an underlying Hamiltonian structure.35
A more realistic version of the minimal model consider the swimmers to have the shapes of elongated spheroids. This allows the model to capture phenomena arising from the elongated form of real cells, as relevant for example for flagellated bacteria and spermatozoa.2 In turn, this assumption makes analytical predictions more complex unless additional assumptions are made. Focusing on flows that have a typical gradient length scale much larger than the size of the swimmer, the equations of motion can be approximated using the classical Jeffery's equations36 that exactly describe the behaviour of passive spheroids in a shear flow. For example, eddies in the ocean relevant for microorganisms have sizes on the order of millimetres, thus always much larger than the micro-algae that populate them (tens of microns). The validity of Jeffery's equations as applied to elongated biological organisms has been further verified using direct experiments with the bacterium E. coli in microfluidic channels.13 Note that using Jeffery's equations, classical work has been carried out on the dynamics of passive elongated particles in external flows37–39 as well as some recent work on active elongated swimmers in linear40 and pressure-driven flows.35,41 In a Poiseuille flow, and in contrast to the case of a spherical swimmer, the equations of motion for an elongated swimmer no longer have the Hamiltonian structure but a conserved quantity still exists42 and two types of trajectories are seen in this case: upstream swinging motion around the middle of the channel or downstream tumbling closer to the channel walls. Both types of trajectories were confirmed experimentally for motile bacteria.43
In this work, we focus on the behaviour of elongated microswimmers in elementary vortical flows. A well-known example where biological microswimmers have to self-propel in vortices are algae and bacteria swimming in small-scale ocean eddies.44–47 Other relevant examples include spermatozoa swimming in uterine peristaltic flows4 and recirculation flows generically occurring in standard microfluidic devices.48,49 Motivated by this fundamental problem, a recent experimental study on swimming bacteria reported the existence of a cell depletion zone in a vortical flow created by an externally rotated body.50 This depletion zone forms around the body after it is forced into rotation in an otherwise uniform, dilute suspension of swimming bacteria. In contrast, recent theoretical work predicted a zone around the centre of a vortex with bounded orbits.51
In this paper, we use a theoretical treatment to reconcile the experimentally-observed depletion50 with the theoretically-predicted trapping.51 Specifically, we consider the dynamics of model swimmers in two- and three-dimensional rotlets, i.e. the rotational flows that exactly represent the flow of rotating bodies (cylinders and spheres) in a bulk fluid at low Reynolds number33 (setup described in Section 2). We mathematically determine the trapped orbits of swimmers in both types of singular vortices, in the absence of any noise in the system (spherical swimmers in Section 3 and elongated swimmers in Section 4). Next, we include translation and rotation noise and show how to quantify trapping in these vortices (Section 5). Finally, we use our mathematical model to formulate a prediction for the radius of the depletion zone, which we show compares favourably with experimental observations in ref. 50 (Section 6).
2 Setup and deterministic model
In order to address the physical behaviour of swimming cells in external flows, we consider the fundamental elongated ‘active particle’ model. A swimming cell is modelled as a prolate spheroid, of fixed aspect ratio a ≥ 1 and major axis d, which is being advected and rotated by the steady external flow u(r). In addition to the flow advection, the cell swims with velocity V0p of fixed magnitude V0 in the direction of the major axis of the spheroid (unit vector p in that direction). Using the aforementioned Faxén's laws and neglecting the size d of the swimmer relative to the typical length scale characterising the flow gradients,2 the position r(t) of the cell evolves in time as
Following the classical result of Jeffery,36 and using the same assumption on the size of the swimmer, we may model the rotation of the swimmer as that of a passive spheroid in a linear flow, given by the equation
| | 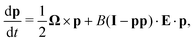 | (2) |
where
I is the identity tensor,
E = (∇
u + ∇
uT)/2 is the symmetric rate of strain tensor of the external flow,
Ω = ∇ ×
u is its vorticity and
B = (
a2 − 1)/(
a2 + 1) ∈ [0,1) is the swimmer's shape factor (
B = 0 for a sphere and
B → 1 for an elongated rod). Using this fundamental active particle model, we investigate below the dynamics of swimmers in external vortical flows.
3 Spherical swimmers in vortices
We start by the simplest case of spherical swimmers, i.e. with B = 0 in eqn (2). We mathematically demonstrate the existence of two classes of deterministic trajectories, bounded and unbounded, using a theoretical approach that will be exploited further in the case of elongated cells (B > 0, Section 4). We focus on the case where the flow is the three-dimensional (3D) Stokes flow u created by a sphere of radius R rotating with angular velocity ω = ωẑ, namely| | 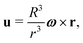 | (3) |
where r = |r|. This solution is also known at the 3D rotlet, i.e. the flow created by a point torque L = 8πμR3ω located at the origin. In later sections of this paper, we will investigate the two-dimensional (2D) version of this singular vortex flow, i.e. the 2D rotlet. That flow can be realised as the Stokes flow around a rotating, infinitely long cylinder. However, since the 2D rotlet has no vorticity (see Section 4.2), it does not affect the dynamics of spherical swimmers, hence our focus on the 3D case here.
We confine the swimmer to move in the sphere's equatorial plane (through its centre and perpendicular to ẑ, see illustration in Fig. 1A). We describe the location of the swimmer in the plane using the planar polar coordinates (r,ϕ) and its orientation using the angle ψ between its orientation vector p and the radial unit vector r/r at its position (see Fig. 1C).
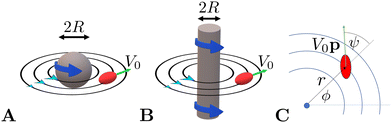 |
| | Fig. 1 Illustration of the model swimmer in a 3D rotlet flow, i.e. the flow outside a rotating sphere (A), and in a 2D rotlet flow outside a rotating cylinder (B). The swimmer is sketched as a red spheroid and black lines show the flow streamlines. (C) Notation used throughout this paper with the location of the swimmer described using planar polar coordinates (r,ϕ) and its orientation using the angle ψ. | |
Using this notation, the equations of motion, eqn (1) and (2), take the form
| | ṙ = V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, ψ, | (4a) |
| | 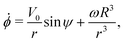 | (4b) |
| | 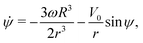 | (4c) |
After nondimensionalising these equations using
R as the relevant length scale and
ω−1 as time scale, a straightforward manipulation of
eqn (4a) and (4c) show that there exists a constant of motion in this dynamical system. Specifically, if we define
| | 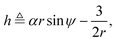 | (5) |
where
α =
V0/
ωR is the non-dimensional swimming speed, we see that
ḣ = 0.
Next, using the fact that ṙ2 = α2(1 − sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ) we can express sin
ψ) we can express sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ(r) = h/αr + 3/2αr2 from eqn (5) to notice that
ψ(r) = h/αr + 3/2αr2 from eqn (5) to notice that
| | 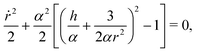 | (6) |
and thus
r behaves as if it was under the influence of an effective potential
| | 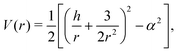 | (7) |
with an energy-like quantity
E =
ṙ2/2 +
V(
r) equal to 0 for all times.
Since the effective potential V has limits V → −α2/2 as r → ∞ and V → +∞ as r → 0, the entrapment relies on the existence of a local maximum of V(r) > 0 to prevent the swimmer from escaping to infinity. Taking the derivative, we see that the condition dV/dr = 0 is equivalent to rh = −3/2 or rh = −3. Clearly, if h ≥ 0, then the potential is monotonic and the swimmer escapes. On the other hand, if h < 0, then we obtain that at r = −3/2h we have a minimum of the potential, with Vmin = −α2/2 while at r = −3/h there is a local maximum Vmax = (h4 − 36α2)/72. Thus, we predict theoretically that the swimmer will be trapped if and only if r0 < −3/h and Vmax > 0 so that 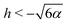 .
.
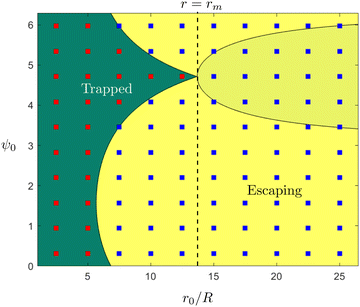
These theoretical predictions can be used to validate direct finite-difference simulations of the equations of motion in eqn (4a)–(4c); these simulations will then be used in the rest of the paper when exact theoretical predictions are harder to make. Results are shown in Fig. 2 and we obtain excellent agreement between simulations and theoretical predictions. Using the initial position and orientation of the swimmer (r0,ψ0), we note that the theoretical conditions condense to a single equation, 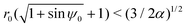 ; this is the equation of the separatrix of this dynamical system, i.e. the interface between the light yellow and dark green regions in Fig. 2. An important feature of this phase map that we will use later is the maximal radial distance r = rm for which a trapped state exists, given by rm = (3/2α)1/2.
; this is the equation of the separatrix of this dynamical system, i.e. the interface between the light yellow and dark green regions in Fig. 2. An important feature of this phase map that we will use later is the maximal radial distance r = rm for which a trapped state exists, given by rm = (3/2α)1/2.
 |
| | Fig. 2 Trapping of a spherical swimmer in a 3D rotlet: a map of the parameter space of the initial position (r0/R) and orientation angle (ψ0), in the case α = 0.008. Yellow and green regions indicate theoretical predictions of open and bounded orbits, respectively. Shaded and unshaded yellow regions are only there to illustrate different theoretical conditions for escape, namely 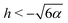 (shaded) and r0 < −3/h (unshaded). Square symbols represent the outcomes of numerical simulations: red – bounded orbits; blue – open orbits. (shaded) and r0 < −3/h (unshaded). Square symbols represent the outcomes of numerical simulations: red – bounded orbits; blue – open orbits. | |
In a recent theoretical study,51 based on the same model equations as the current work, it has been noted that in a general axisymmetric flow of the form u(r)eϕ the equations of motion for a spherical swimmer can be transformed to take a Hamiltonian form. Indeed, under the transformation
then
eqn (4a) and (4b) become equivalent to a set of Hamilton's equations
| | 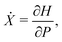 | (9a) |
| | 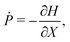 | (9b) |
for the “position”
X and the “momentum”
P with the Hamiltonian
H given by
| | 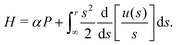 | (10) |
Since the Hamiltonian
H has no explicit time dependence, it is a conserved quantity of motion and so we expect it to be a function of the conserved quantity
h derived above. For the case of a 3D rotlet that we consider here, it is simple to integrate and express
H as a function of
r and
ψ only as
| | 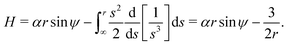 | (11) |
In other words,
H =
h, so the Hamiltonian is equal to the conserved quantity found above in
eqn (5).
4 Elongated swimmers in vortices
So far we only considered the case of spherical swimmers. In contrast, most biological or artificial swimmers have anisotropic shapes and are often elongated in the direction of swimming. When in an external flow, spherical swimmers are not influenced by the local rate of strain of the fluid flow, while an elongated swimmer experiences an additional torque aligning it with the principal axes of the local rate of strain. Thus, the rotational dynamics can be drastically different for elongated swimmers, which could lead to qualitatively different behaviour in external flows. Therefore, we now consider the case of elongated swimmers in vortices. By deriving the conserved quantity of motion for elongated swimmers in 3D and 2D rotlet flows, we show the existence of a similar phase diagram as for spherical swimmers, but with a different separatrix between the region of trapped and unbounded orbits.
4.1 Prolate spheroid in the equatorial plane of a 3D rotlet
Let the swimmer be a prolate spheroid of aspect ratio a ≥ 1 swimming in the same external flow as above, i.e.u = ω × rR3/r3. Using same notation as above, the non-dimensional equations of motion become| | ṙ = α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, ψ, | (12a) |
| | 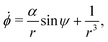 | (12b) |
| | 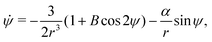 | (12c) |
where we recall that B = (a2 − 1)/(a2 + 1) ∈ (0,1) is the shape factor of the spheroid. If we introduce u = αr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ we can combine the radial and ψ equations of motion to obtain
ψ we can combine the radial and ψ equations of motion to obtain| | 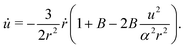 | (13) |
By introducing x = Bα−2r−3 and solving for u(x), the equation above becomes| | 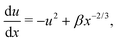 | (14) |
where β = (1 + B)α2/3B−1/3/2. This is a classical Riccati equation and we can transform it to the modified Bessel equation by first introducing s(x) such that 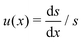 , then defining z = 3β1/2x3/2/2 and ω(z) such that s(x) = z3/4ω(z). This transformation leaves us with solving the modified Bessel equation
, then defining z = 3β1/2x3/2/2 and ω(z) such that s(x) = z3/4ω(z). This transformation leaves us with solving the modified Bessel equation| | | z2ω′′ + zω′ − (z2 + 9/16)ω = 0, | (15) |
whose solutions are ω(z) = c1I3/4(z) + c2K3/4(z), where I, K are the modified Bessel functions of the first kind and c1 and c2 are constants. Hence we obtain| | 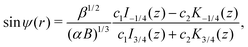 | (16) |
where z = 3β1/2B2/3α−4/3r−2/2. Then, h = c1/c2 is a conserved quantity of the motion and it is expressed as| | 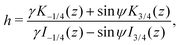 | (17) |
where γ = β1/2(αB)−1/3 = ((B + 1)/2B)1/2 ≥ 1. Note that 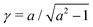 represents the inverse of the eccentricity of the elliptical cross-section of the swimmer.
represents the inverse of the eccentricity of the elliptical cross-section of the swimmer.
Finally, we may now investigate the conditions for entrapment in case of a prolate swimmer in the equatorial plane of a 3D rotlet. For comparison, we perform agent based simulations of swimmers starting from various initial conditions (r,ψ) (or equivalently (r,h)) and plot the symbols in Fig. 3A according to the type of the orbit that we find: blue empty circles represent unbounded orbits while and red filled squares are used for bounded ones. As opposed to the spherical case, it is less straightforward to examine the features of the effective radial potential analytically, so we introduce a different approach by considering orbits in the r−h space. Swimmers will clearly be moving along the constant-h lines but not all of the r−h space is physically feasible. Inspecting eqn (17) we can see that for a given r (i.e. a given z), h can only vary between hmin(r) and hmax(r), where
| | 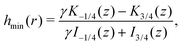 | (18a) |
| | 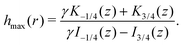 | (18b) |
We claim that a swimmer is certain to be trapped if it starts from a point in the
r−
h space such that its constant-
h line has two intersections with any of the
h =
hmin(
r) or
h =
hmax(
r) lines (see illustration in
Fig. 3A). Otherwise, it will escape due to the fact that
ṙ ∝ cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ. Specifically, if the swimmer starts with cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ > 0 it will always advance in
r since
ṙ ∝ cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ and the change in the sign of cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ can only happen when sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ = ±1, which are exactly the
hmin and
hmax lines that the swimmer cannot approach. If initially cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ < 0, then the swimmer will certainly reach the
hmin or
hmax line and the unboundedness of the orbit will depend on whether the point of interception with these lines is stationary and stable or not. In the dynamical system that we consider here, there is only one stationary point on
hmin and
hmax but it is unstable so the swimmer will turn around and escape.
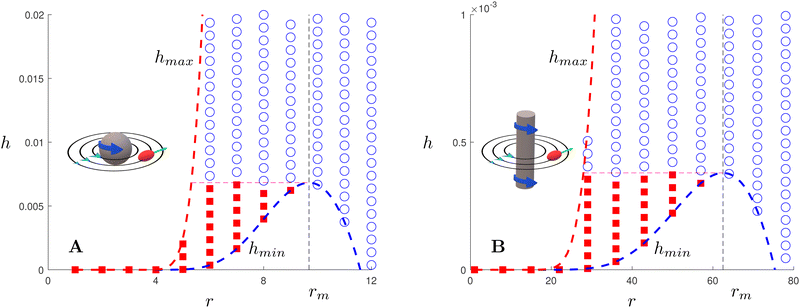 |
| | Fig. 3 Trapping of elongated swimmers in a 3D rotlet flow (A) and a 2D rotlet (B). In both cases, we display a map in the r−h parameter space in the case B = 0.5 (corresponding to a swimmer of aspect ratio 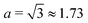 ) and α = 0.008. Scattered symbols represent the outcomes of numerical simulations; red filled squares stand for bounded orbits and blue empty circles for unbounded ones. The dashed red and blue lines represent, respectively, the functions hmax(r) and hmin(r) derived analytically; the dashed black line shows the location of r = rm while the dashed pink line shows h = hmin(rm). ) and α = 0.008. Scattered symbols represent the outcomes of numerical simulations; red filled squares stand for bounded orbits and blue empty circles for unbounded ones. The dashed red and blue lines represent, respectively, the functions hmax(r) and hmin(r) derived analytically; the dashed black line shows the location of r = rm while the dashed pink line shows h = hmin(rm). | |
As can be seen from Fig. 3A, the function hmax(r) is monotonically increasing (this is easily verified analytically) but hmin has a maximum, which we find occurs analytically at the remarkably simple expression rm = [3(1 − B)/2α]1/2. Thus, the prolate swimmer will be trapped in a 3D rotlet vortex flow if and only if both r0 < rm initially and h(r0,ψ0) < hmin(rm). Note that in the limit of spherical swimmers B → 0 we have rm = (3/2α)1/2 which agrees with the result for a sphere in Section 3.
4.2 Prolate spheroid in a 2D rotlet
We now consider the case of a two-dimensional (2D) Stokes flow created by the rotation of an infinitely long cylinder of radius R and angular velocity (along its axis) ω, i.e.| | 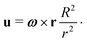 | (19) |
Interestingly, this flow has no vorticity so spherical swimmers are not rotated by this flow. Thus, we focus on the prolate swimmers with shape factor B > 0 for which the non-dimensional equations of motion are| | ṙ = α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, ψ, | (20a) |
| | 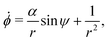 | (20b) |
| | 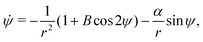 | (20c) |
with the same notation as above. Following a similar method to that for the 3D rotlet we obtain a conserved quantity| | 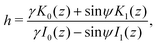 | (21) |
with β = (1 + B)/2, 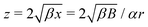 and γ = (β/B)1/2 = ((B + 1)/2B)1/2 ≥ 1. Using the same method as in case of a 3D rotlet we come to a similar conclusion that a swimmer will be trapped in a 2D rotlet if and only if initially r0 < rm = (1 − B)/α and h(r0,ψ0) < hmin(rm). We compare in Fig. 3B this theoretical prediction with numerical computations, and again obtain excellent agreement.
and γ = (β/B)1/2 = ((B + 1)/2B)1/2 ≥ 1. Using the same method as in case of a 3D rotlet we come to a similar conclusion that a swimmer will be trapped in a 2D rotlet if and only if initially r0 < rm = (1 − B)/α and h(r0,ψ0) < hmin(rm). We compare in Fig. 3B this theoretical prediction with numerical computations, and again obtain excellent agreement.
4.3 The trapping separatrix in the rod-like limit
In order to better understand the extent of trapping in vortical flows, we next investigate the boundary between the regions of bounded and unbounded orbits in the r − ψ space (i.e. the separatrix). This separatrix can only be implicitly defined as h(r,ψ) = h(rm,3π/2), since the bounded orbits are found in r < rm,h < hmin(rm) = h(rm,ψ = 3π/2) part of the r−h space, as argued above. This implicit definition can be turned into an explicit one in the limit of swimmers with large aspect ratios, a ≫ 1. This rod-like limit is relevant not only for slender artificial microswimmers25 but also for various types of bacteria.52
Focusing on the 3D rotlet (the calculation in the 2D rotlet case is analogous), this implicit formulation takes the following form
| | 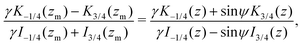 | (22) |
where
z = 3
γB/2
αr2 and where
zm =
γ/2(
γ2 − 1) is the corresponding value of
z for
r =
rm. Again, this equality is difficult to invert into an explicit formula
r(
ψ); however, in the limit of the swimmers that are very prolate (
B → 1
i.e. γ = [(
B + 1)/2
B]
1/2 → 1), it is possible to find an asymptotic expression for
z(
ψ). In this limit, the maximal radius that the separatrix reaches is
rm so the minimal
z is
zm ≫ 1. Thus we can assume
z ≫ 1 along the separatrix and we can use the well-known asymptotic expansion of the modified Bessel functions
53| | 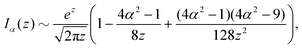 | (23) |
| | 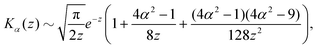 | (24) |
to find an approximate explicit expression for the separatrix. In the aforementioned limit, the expanded implicit formulation from
eqn (22) takes the form
| | 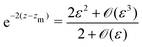 | (25) |
| | 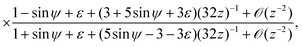 | (26) |
with
ε =
γ − 1 ≪ 1. As the balance of the dominant terms is different depending on sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ, we further investigate each of these cases separately. In the |sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ ± 1| ≫
ε case, the balance of dominant terms becomes
| | 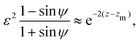 | (27) |
and thus we can approximate
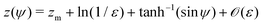
. Now, if instead sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ = 1 −
εζ, with
ζ ∼
O(1), the balance reads
| | 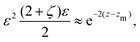 | (28) |
and the explicit formulation of the separatrix in this region is asymptotically
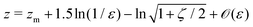
. Finally, if sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ
ψ = −1 +
ε2ζ, with
ζ ∼
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1) we expect an
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(1) correction of the form
z =
zm +
F(
ζ) that must satisfy
| | 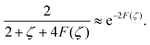 | (29) |
Solving this gives us 2
F(
ζ) = −1 −
ζ/2 −
W−1[−exp(−1 −
ζ/2)], where
W−1 is a branch of the Lambert
W function.
An important result of this calculation is the value of the minimal radius that the separatrix reaches rmin, or equivalently, the value zmax of the maximal z. It is attained for ψ = π/2, thus it can be approximated as
| | 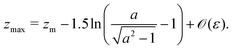 | (30) |
In
Fig. 4 we show the results of numerical computations for the value of
zmax together with the theoretical predictions based on
eqn (30) for various values of the aspect ratio
a of the swimmer. We obtain excellent agreement across a large range of biologically relevant aspect ratios.
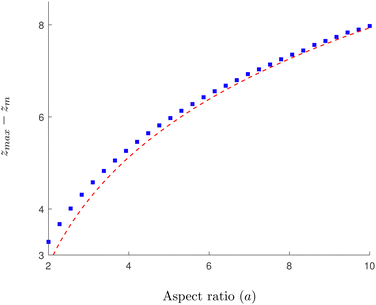 |
| | Fig. 4 Numerical verification of the asymptotic expression for zmax in a 3D rotlet flow. Solid, blue squares show a numerical approximation obtained by inverting eqn (22) at ψ = π/2 for various values of the aspect ratio of the swimmers a. The red, dashed line follows the theoretical prediction based on eqn (30), while neglecting the O(ε) terms. | |
5 Impact of noise on trapping
The deterministic calculations in the previous sections provided insights into the behaviour of microswimmers in vortices. However, the existence of bounded orbits seems to be at odds with the depletion zones observed experimentally.50 In order to capture this experimentally observed phenomena, we include in our model the effects of Brownian (translational and rotational) noise.
5.1 Mathematical modelling
We add to our mathematical model delta-correlated white noise with rotational and translational diffusion coefficients denoted by Dr and Dt, respectively; in addition to thermal noise, this allows us to also capture the effective impact of variability in the translational velocity of biological swimmers. For simplicity, we focus here on swimmers in the flow due to a rotating sphere (i.e. the 3D rotlet) in the rest of this section; results follow similarly for the 2D rotlet case.
The stochastic form of the dimensionless governing eqn (12a)–(12c) now takes the following Langevin form
| | 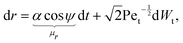 | (31a) |
| | 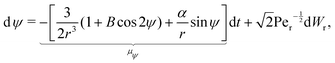 | (31b) |
where
Wt and
Wr are two independent Wiener processes, Pe
t =
ωR2/
Dt is the translational Péclet number and Pe
r =
ω/
Dr is the rotational Péclet number. The drifts
μr and
μψ defined in these equations represent the deterministic rates of change of
r and
ψ, respectively. It should be noted that translational noise impacts the evolution of
ψ as well, since
ψ changes as the swimmer translates tangentially to the circles of constant
r. For a swimmer of typical size
d, it holds that Pe
r/Pe
t =
Dt/
R2Dr = (
d/
R)
2 ≪ 1
32 and hence we can neglect translational noise in the dynamics of
ψ relative to the rotational noise. It is known that anisotropic particles, such as the prolate spheroids considered here, experience anisotropic diffusion due to their different hydrodynamic mobilities along and perpendicular to its axis of symmetry.
33 Since we only consider here a two-dimensional geometry (
i.e. the cells are restricted to move within a plane), this impacts translational, but not rotational, diffusion. The anisotropy in mobility means that, strictly speaking, the translational Péclet number is a function of the cell orientation,
ψ (this is a weak dependance since the maximum ratio in mobilities is known to be two, obtained for slender shapes). For simplicity, here we assume that the Péclet number remains a constant, an assumption consistent with the fact that we obtain no significant dependence of our results on its exact value.
5.2 Quantifying the quality of trapping
Since eqn (31a) and (31b) are coupled, it is difficult to extract statistical properties, such as mean square displacement. However, since noise is now included in the model, it is unlikely (i.e. of probability zero) that swimmers starting on a bounded trajectory will remain trapped indefinitely. In order to quantify the quality of trapping, we thus focus our attention on finding the average time swimmers take to escape.
This brings a few questions to consider. First, what does it mean exactly for a swimmer to escape? A natural choice would be to qualify the swimmers as escaped once they cross the (implicit) separatrix that delineates the regions of bounded and open orbits obtained above. However, as a swimmer gets further from the rotating body, noise becomes dominant over the effects of the flow and thus we expect swimmers to return infinitely many times to the region of deterministically trapped orbits. Having the separatrix as the classifying boundary has therefore limited physical significance. Instead, since there are no deterministically trapped orbits with r > rm, we set r = rm as the qualifying boundary.
Another important point is what exactly happens once a swimmer reaches the rotating body located at r = 1 (in dimensionless units)? The exact physics of the encounter between a microswimmer and a solid rotating body depends of course on the microscopic details of both the swimmer and the surface. In the specific case of bacteria Bacillus subtilis used in the experiments in ref. 50, the cells have been observed to stick to the surface of solid spheres. Thus, it is appropriate to treat r = 1 as an absorbing boundary.
For a swimmer that starts from (r,ψ) = (r0,ψ0) at time t = 0, we thus aim to determine the mean time T(r0,ψ0) that it would take to reach either r = rm (escape from the vortex from the outside) or r = 1 (reaching the surface of the rotating body). While the mean first passage time (MFPT) T(r0,ψ0) is a useful measure for quantifying the quality of trapping, it does not allow us to distinguish between the two types of escapes (away from the body vs. sticking to it). Thus, we will also introduce the probability P(r0,ψ0) the a swimmer will reach r = rm (and thus escapes) before hitting the rotating body, as the second important statistical property of the problem.
5.3 Fokker–Planck formalism
A common approach to solving such drift-diffusion problems is to introduce the Fokker–Planck equation| | 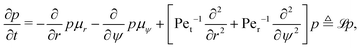 | (32) |
that governs the evolution of the probability distribution p(r,ψ,t|r0,ψ0) for a swimmer located at (r,ψ) at time t starting from (r0,ψ0) at t = 0 (e.g. see ref. 54). To determine statistics of the system, such as the MFPT or the escape probability, we need to introduce the adjoint of the Fokker–Planck equation.55,56 Using ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) to denote the Fokker–Planck operator from eqn (32), its adjoint
to denote the Fokker–Planck operator from eqn (32), its adjoint ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) † is defined on the space of the initial conditions (r0,ψ0) as the unique operator satisfying
† is defined on the space of the initial conditions (r0,ψ0) as the unique operator satisfying| | 〈![[script L]](https://www.rsc.org/images/entities/char_e144.gif) f,g〉 = 〈f, f,g〉 = 〈f,![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †g〉, †g〉, | (33) |
for any two functions f and g, where 〈·,·〉 denotes the standard integral inner product defined as| | 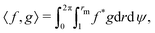 | (34) |
where f* is the complex conjugate of the function f. Following standard algebra, we thus obtain ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) † as
† as| | 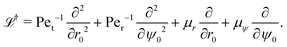 | (35) |
Using the adjoint operator, it is a classical results that the mean first passage time T and the probability of escape are known to satisfy the partial differential equations54
| | ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †T = −1 with T = 0 at r0 = 1 and r0 = rm, †T = −1 with T = 0 at r0 = 1 and r0 = rm, | (36) |
| | ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †P = 0 with P = 0 at r0 = 1 and P = 1 at r0 = rm. †P = 0 with P = 0 at r0 = 1 and P = 1 at r0 = rm. | (37) |
5.4 Solution of Fokker–Planck model and validation
We solve eqn (36) and (37) numerically using the open-source FreeFem++57 solver, based on the finite element method. The results for the mean first passage time T(r0,ψ0) are shown in Fig. 5A (in units of ω−1) while the probability of escape P(r0,ψ0) is plotted in Fig. 5B. To verify the results of our numerical integration, we also compare it with ensemble averages of a large number of realisations of direct numerical time-stepping of the Langevin model in eqn (31a) and (31b) using the Runge–Kutta fourth-order method. These results are plotted in Fig. 5C and D below the corresponding Fokker–Planck result, where we obtain excellent quantitative agreement.
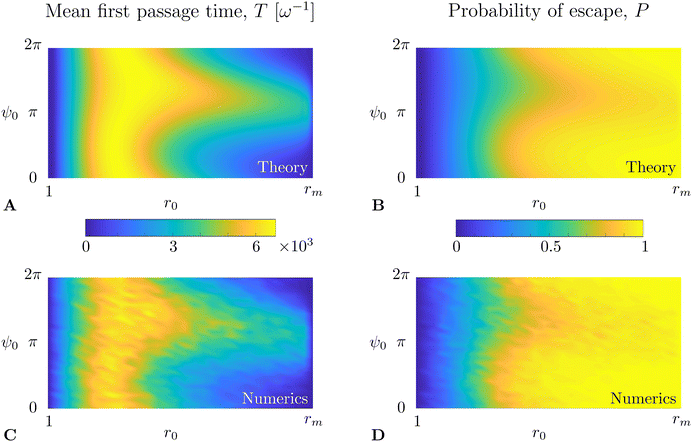 |
| | Fig. 5 Comparison between theory and simulations for the mean first passage time T(r0,ψ0) (A and C, in units of ω−1) and probability of escape P(r0,ψ0) (B and D). (A) and (B) are obtained by direct integration of the adjoint Fokker–Planck equations, eqn (36) and (37), while (C and D) are results of direct numerical simulations of the Langevin swimming model in eqn (31a) and (31b). Results shown are for Pet−1 = 0.045, Per−1 = 0.05, B = 0 and α = 0.008. | |
Apart from the obvious observations that MFPT is small next to the boundaries and larger in between, we observe that the region of high MFPT extends significantly close to the r = rm boundary along a ψ ∼ π direction (see Fig. 5A or C). Intuitively, this can be explained by noting that ψ ∼ π means that the swimmer is directed towards the decreasing r direction; a swimmer close to r = rm has therefore a high chance of escaping through that boundary (see Fig. 5B or D) and will take a long time to turn around and escape.
Following the same logic, one would expect a region of low MFPT to extend from the r = 1 boundary along the ψ ∼ π direction. However, in that region, the flow vorticity is strong and rotates the swimmers rapidly; the radial swimming vanishes thus on average there and escape is instead dominated by translational diffusion, which is independent of the swimmers’ orientation. Based on the same arguments, we can expect the probability of escape to be lower for ψ ∼ π in the region close to r = rm and independent of ψ close to r = 1, in agreement with results in Fig. 5B and D.
5.5 Parameter sweep
Next, we explore the phase space of the four dimensionless parameters of the problem: (i) the relative swimming speed α, (ii) the swimmer's shape factor B and the two Péclet numbers (iii) Pet and (iv) Per. In order to quantify the overall quality of trapping as a function of the parameters, we consider some scalar moments of the continuum solutions for the MFPT T(r0,ψ0) and the probability of escape P(r0,ψ0). A natural first choice is the average probability of escaping 〈P〉, taken over the range r ∈ [1,rm]. Note that we want the swimmers to initially be uniformly distributed in space i.e. according to a linear distribution in r, fU(r0,ψ0) = r0/π(rm2 − 1) so that| | 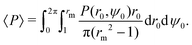 | (38) |
Additionally, we measure the maximal MFPT, denoted by ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , which sets a timescale for the emergent dynamics of the ensemble of swimmers.
, which sets a timescale for the emergent dynamics of the ensemble of swimmers.
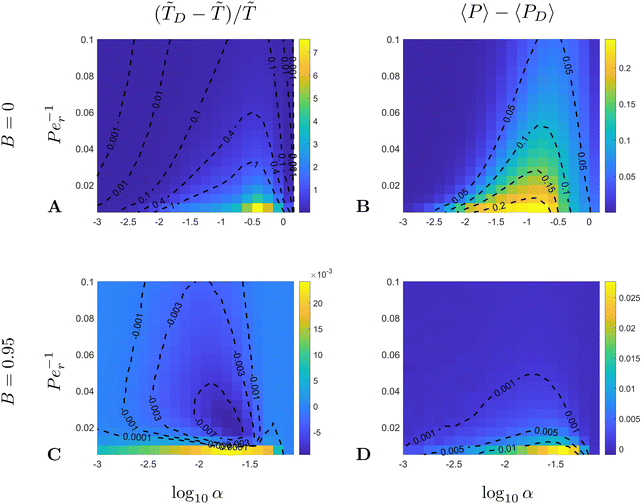
In computations, we fix the ratio between the translational Péclet number and the rotational one to Pet/Per = 4; the exact value for this ratio turns out to not affect the qualitative features of our results, as confirmed in our computations (not shown). We then explore the rest of the parameter space by fixing the shape parameter B and then sweeping among the values for the pair (α,Per). In Fig. 6 we show results for two limiting values of B: spherical swimmers with B = 0 (Fig. 6A and B) and rod-like swimmers with B = 0.95 (Fig. 6C and D).
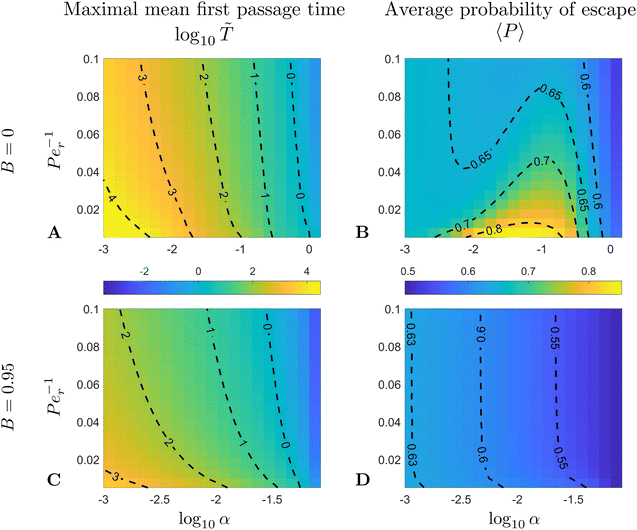 |
| | Fig. 6 (A and C) Maximal MFPT, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , and average probability of escape, 〈P〉, for two different values of the shape parameter B = 0 (spherical limit; A and B) and B = 0.95 (elongated swimmer; C and D), as a function of the dimensionless swimming speed, α, and the rotational Péclet number, Per. , and average probability of escape, 〈P〉, for two different values of the shape parameter B = 0 (spherical limit; A and B) and B = 0.95 (elongated swimmer; C and D), as a function of the dimensionless swimming speed, α, and the rotational Péclet number, Per. | |
The maximal MFPT (![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ) behaves qualitatively as expected. The faster the swimmers and the stronger the noise, the easier it is to escape and thus
) behaves qualitatively as expected. The faster the swimmers and the stronger the noise, the easier it is to escape and thus ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) takes smaller values. The difference in maximal MFPT between the two values of the shape factor B can be understood by realising that the trapping domain is different for distinct values of B and α. Indeed, the trapping domain is given by r ∈ [1,rm] where rm = [3(1 − B)/2α]1/2 so it is significantly smaller for rod-like swimmers (B → 1) than for spherical ones (B = 0). The size of the trapping region indicates that more elongated swimmers are more difficult to trap, which is reflected in the fact that MFPT is shorter for elongated swimmers.
takes smaller values. The difference in maximal MFPT between the two values of the shape factor B can be understood by realising that the trapping domain is different for distinct values of B and α. Indeed, the trapping domain is given by r ∈ [1,rm] where rm = [3(1 − B)/2α]1/2 so it is significantly smaller for rod-like swimmers (B → 1) than for spherical ones (B = 0). The size of the trapping region indicates that more elongated swimmers are more difficult to trap, which is reflected in the fact that MFPT is shorter for elongated swimmers.
Regarding the average probability of escape, we notice in Fig. 6B and D that for strong noise (large Per−1) the value of 〈P〉 is decreasing with α. This is also due to the fact that the decrease in α leads to an increase in rmi.e. the size of the trapping domain. Recall that the swimmers are initially distributed uniformly in space, so they follow a linear distribution in fU ∼ r0 and the average probability of escape is weighted towards larger values of the initial position r0 (see eqn (38)). With strong noise, the increase in rm leads to even more weight towards r0 = rm and a larger escape probability (this is also captured by eqn (40b) below).
Interestingly, we note that in Fig. 6B and D, the value of 〈P〉 appears to always be in the range 0.6–0.7 for small values of the non-dimensional swimming speed α. To rationalise this observation, we can use an analysis in the diffusion-dominated regime. When locomotion is negligible (i.e. α ≪ 1), the adjoint system of equations, eqn (36) and (37), admits simple solutions given by
| | 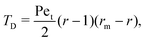 | (39a) |
| | 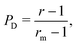 | (39b) |
with the subscript D used to indicate this is the diffusion-dominated solution. This in turn allows to compute the two trapping measures as
| | 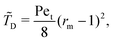 | (40a) |
| | 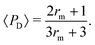 | (40b) |
Since
rm = [3(1 −
B)/2
α]
1/2, small values of
α correspond to
rm ≫ 1, leading to the approximate solution 〈
PD〉 ≈ 2/3. The small-
α limits in
Fig. 6B and D correspond therefore a constant probability of 2/3.
In Fig. 7 we further compare the computational results from Fig. 6 with the diffusion-dominated predictions in eqn (40). The dark blue regions are those for which the simulations are in line with the no-swimming predictions, and we observe a systematic agreement for small values of α. We also note a significant deviation from these predictions around the α ∼ 0.1, Per−1 ∼ 0.01 region where the maximal MFPT can become up to 10 times smaller than the pure diffusion value. It is also notable that it takes a much stronger noise to overcome swimming for spherical swimmers (Fig. 7A and B) than it does for rod-like swimmers (Fig. 7C and D). Here again this is due to the fact that the trapping region is smaller for more elongated particles.
 |
| | Fig. 7 Comparison between numerical results (from Fig. 6) for the maximal MFPT, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (A and C), and the average probability of escape, 〈P〉 (B and D), and the theoretical predictions in the diffusion dominated regime, (A and C), and the average probability of escape, 〈P〉 (B and D), and the theoretical predictions in the diffusion dominated regime, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) D and 〈PD〉, eqn (40). (A and B) Spherical swimmers B = 0; (C and D) rod-like swimmers B = 0.95. D and 〈PD〉, eqn (40). (A and B) Spherical swimmers B = 0; (C and D) rod-like swimmers B = 0.95. | |
Importantly, the results in Fig. 7 indicate that the region where the maximal MFPT ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) is significantly less than
is significantly less than ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) D coincides roughly with the region where the average probability of escape is significantly greater than the diffusion dominated prediction, a result that appears to hold for both limiting values of the shape factor B. Consequently, swimming not only promotes faster migration from the trapping region but it does so by increasing the chance of escape and not by making more particles stick to the rotating body.
D coincides roughly with the region where the average probability of escape is significantly greater than the diffusion dominated prediction, a result that appears to hold for both limiting values of the shape factor B. Consequently, swimming not only promotes faster migration from the trapping region but it does so by increasing the chance of escape and not by making more particles stick to the rotating body.
6 Depletion zone and comparison with experiments
In this section, we show how the theoretical framework developed above can explain the formation of the depletion of swimming bacteria around a rotating sphere reported in ref. 50; these experiments are reproduced in Fig. 8, with the initial distribution of bacteria shown in Fig. 8A and the depletion (shown in a lighter colour, corresponding to a lower concentration) visualised in Fig. 8B.
 |
| | Fig. 8 Formation of a depletion zone of swimming bacteria around a rotating sphere. (A) Initial distribution of bacteria. (B) Depletion zone formed (lighter colour, lower concentration) after 50 s of rotation at 5 Hz. Adapted with permission from ref. 50, licenced under CC BY 4.0. | |
The original study included a theoretical model, with bacteria modelled as self-propelled rods (B = 1) swimming in a 2D rotlet flow.50 The comparison with the experiments was then done by performing the numerical integration of the Fokker–Plank equations with a reflecting boundary condition at the surface of the rotating object. Although the agreement between the theoretical predictions from ref. 50 and their experimental results appear good, one assumption of their model disagrees qualitatively with observations. It was noted that, experimentally, about 40% of bacteria initially located in what becomes the depletion zone end up stuck to the surface of the rotating body; this clearly contradicts the assumption that the surface of the body is reflective.
Thus, to predict the experimental results, we propose here that the more appropriate boundary condition at the surface of the rotating body is for it to be absorbing. We also consider a more realistic value of the shape factor (B < 1); the rest of the model is similar to the one in ref. 50. Instead of solving the Fokker–Plank equations, we estimate the concentration profile by using a Monte Carlo method based on the agent based simulations of the corresponding evolution equations.
To confirm that altering the boundary condition from reflecting to absorbing does not prevent the depletion zone from forming, we start by carrying out direct swimming simulations on an ensemble of prolate swimmers by numerically time-stepping eqn (31a) and (31b). As a test case, we choose a frequency of rotation of f = 20 Hz, cells of shape factor B = 0.85 (corresponding to aspect ratio a ≈ 3.51) and take the values for the average swimming speed and diffusion coefficients from the data in ref. 50. Note that the particular value of B was chosen to reflect the aspect ratio of bacteria used in ref. 50. However, additional simulations (not shown) reveal that that the results are not particularly sensitive to the choice of B. We initialise a uniform distribution of 3112 non-interacting swimmers in the region 1 ≤ r ≤ L, where L ≫ Rd with Rd being the radius of the depletion zone reported experimentally for f = 20 Hz. Here the boundary at r = 1 (i.e. the rotating sphere) is set to be absorbing while r = L is taken to be reflective. Note that a spatially uniform distribution of bacteria implies a linear distribution in r in the (r,ψ) space, i.e. a uniform distribution fU(r,ψ) = rπ−1(L2 − 1)−1.
We carry out these computations until a steady distribution of swimmers is obtained, which in our simulations happens before T = 8000 (in units of ω−1), so this is when we stop our computations. The resulting distribution, averaged over the angle ψ, and denoted by fSS, is shown in Fig. 9A relative to a uniform distribution fU. We see the clear emergence of a depletion region at r < Rd where the concentration of cells is significantly less than its initial value (recall that Rd is the radius of the depletion zone from experiments). In Fig. 9B we show snapshots of the particular realisation of the ensemble simulations at times t = 0, T/2, T; here again the depletion zone is apparent at t = T. Since all the parameters were taken from the experiments, including the depletion radius Rd, we conclude that our Langevin approach correctly captures the steady-state depletion of swimming bacteria in the experiments.
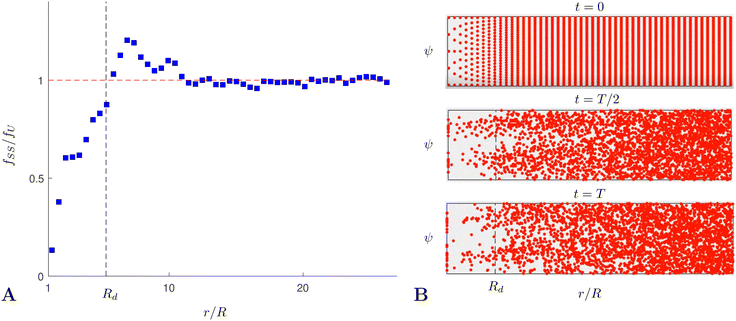 |
| | Fig. 9 Numerical verification of the emergence of the depletion zone in our theoretical model. (A) Steady-state distribution fSS of an ensemble of non-interacting swimmers following the stochastic model in eqn (31a) and (31b), normalized to the uniform distribution and averaged over the angle ψ. (B) Snapshots from the simulations used to obtain data for A; shown at the start (t = 0), midway through (t = T/2) and at the end of the simulation (t = T). The ensemble contains 3112 swimmers and the total simulation time is T = 8000, in units of ω−1. | |
Using additional simulations (not shown), we have also confirmed the emergence of the depletion zone for various values of the probability pst of the swimmer sticking to the rotating body after each encounter, from pst = 0 (perfectly reflective surface) to pst = 1 (perfectly absorbing surface). We have found that the size of the depletion zone varies weakly with the value of pst. This result is consistent with the model in ref. 50 that assumed a reflective surface and still recovered the emergence of the depletion. The escape away from the rotating body is therefore the critical component in the establishment of the depletion zone.
With the emergence of the depletion zone confirmed quantitatively in the model, we can now compare our theoretical predictions for Rd with the experimental measurements. To estimate the value of Rd, we use the experimental observation that roughly 40% of bacteria from the depletion zone get stuck at the rotating body. Thus, we can use the probability of escape P(r,ψ) described above to define the depletion zone radius Rd as the solution
| | 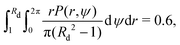 | (41) |
i.e. as the radius
Rd such that the swimmers that start closer than
Rd to the rotating body have a 60% probability of escape, or equivalently, 40% probability of getting stuck to the rotating body. With
B = 0.85 and taking all parameters from the experiments, we compare in
Table 1 our prediction for the depletion radius
Rd (in units of the sphere radius
R) with the experimentally measured values in ref.
50 for four rotation frequencies of the sphere (from 10 Hz to 40 Hz). We obtain excellent quantitative agreement between the experiments and our Fokker–Planck continuum predictions in all cases.
Table 1 Comparison of the experimental50 and theoretical results for the radius of the depletion zone Rd in the units of the bead radius R. Theoretical predictions are calculated under the assumption B = 0.85 (i.e. for a cell with effective aspect ratio a = 3.51)
| Bead frequency [Hz] |
Experiments ref. 50 |
Theory |
| 3.0 |
2.5 ± 0.3 |
2.0 |
| 10 |
4.1 ± 0.4 |
3.6 |
| 20 |
5.1 ± 0.5 |
5.0 |
| 40 |
6.5 ± 0.5 |
6.9 |
Finally, by using the continuum model computations of the first passage time and the probability of escape, as described in the previous section, we may investigate how the quality of trapping changes with the dimensional parameters of the experiment, namely the frequency of rotation ω and the shape factor of the swimmers B. As opposed to the parameter sweep done in Section 5.5, we vary here only these two parameters since: (i) the frequency ω is the only directly controllable parameter of the problem and (ii) B is an effective shape parameter that is not easily measured for a population of microorganisms. As argued above, the quality of trapping is well described by the maximal MFPT and the average probability of escape. In Fig. 10 we plot the relevant results as derived from the data obtained by numerically solving the Fokker–Planck model in eqn (36) and (37). The quality of trapping is seen to increase with the frequency of rotation, with the vortex flow able to overpower both swimming and noise. However, trapping becomes more difficult as the swimmers become more elongated (i.e. when B increases); this is due to persistence in swimming orientation for elongated swimmers, which promotes a faster escape. Note that the typical time-scale of the maximal MFPT is predicted to be around 50 s, a value which agrees with the observed time of formation of the depletion zone.50
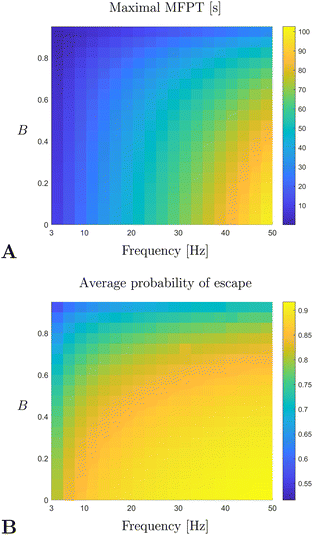 |
| | Fig. 10 Maximal MFPT (A) and average probability of escape (B) as a function of the rotation frequency of the sphere, ω, and of the shape factor of the swimmer B. All parameters of the problem were fixed according to experimental data from ref. 50 and the MFPT is given in units of seconds [s]. | |
7 Conclusions
In this paper, we investigate the behaviour of microswimmers in elementary vortices, namely in two- and three-dimensional rotlet flows. In the absence of noise, a mathematical approach reveals the existence of deterministically bounded orbits near the centre of the vortex and unbounded ones further away. For elongated microswimmers, we discover a conserved quantity of motion that allows us to easily map the regions of phase space according to the type of the orbit (bounded/unbounded). Next, we introduce translational and rotational noise into the system, modelling both thermal noise as well as active biological fluctuations. We quantify the quality of trapping in the deterministically bounded orbits near the centre of the vortex by examining the probability of escape and mean escape time of the swimmers starting on said deterministically bounded orbits. We show how to use these findings to formulate a prediction for the radius of the depletion zone (see Fig. 8), which compares favourably with the experiments.50
In the case of spherical swimmers, the equations in our model were found to have a Hamiltonian structure. The axial symmetry of the flow also leads to a conserved quantity of motion for elongated swimmers, even though the system is no longer Hamiltonian. Interestingly, a similar behaviour was reported for swimmers in Poiseuille flow,42 suggesting an underlying fundamental behaviour in the two-dimensional swimming of elongated microswimmers in Stokes flows.
Throughout this paper, we have assumed the motion to remain two-dimensional. This simplification is supported by the experimental setup in ref. 50 in which bacteria are hydrodynamically attracted to, and thus gather on, a horizontal surface below the rotating sphere. Allowing swimmers to explore the third dimension in the model of the three-dimensional rotlet, or performing similar experiments but in bulk fluid, could potentially lead to new behaviour not seen within the two-dimensional assumption. In this paper, we demonstrated that the swimmers that are relatively close to the rotating body would be deterministically trapped in the plane orthogonal to the axis of rotation of the body. Allowing motion in the third dimension would represent an important extension of the current work as it could result in plumes of swimmers escaping along the axis of rotation, and therefore an interesting new instance of collective motion.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This project has received funding from the European Research Council under the European Union's Horizon 2020 research and innovation program (Grant No. 682754 to E. L.). It was also funded by Trinity College, Cambridge (IGS scholarship to I. T.).
References
-
J. Lighthill, Mathematical Biofluiddynamics, SIAM, Philadelphia, 1975 Search PubMed.
-
E. Lauga, The Fluid Dynamics of Cell Motility, Cambridge University Press, UK, 2020 Search PubMed.
- J. D. Wheeler, E. Secchi, R. Rusconi and R. Stocker, Annu. Rev. Cell Dev. Biol., 2019, 35, 213–237 CrossRef PubMed.
- L. J. Fauci and R. Dillon, Annu. Rev. Fluid Mech., 2006, 38, 371–394 CrossRef.
- J. S. Guasto, R. Rusconi and R. Stocker, Annu. Rev. Fluid Mech., 2012, 44, 373–400 CrossRef.
- T. J. Pedley and J. O. Kessler, Annu. Rev. Fluid Mech., 1992, 24, 313–358 CrossRef.
- R. Rusconi and R. Stocker, Curr. Opin. Microbiol., 2015, 25, 1–8 CrossRef PubMed.
- J. O. Kessler, Nature, 1985, 313, 218–220 CrossRef.
- T. J. Pedley and J. O. Kessler, J. Fluid Mech., 1990, 212, 155–182 CrossRef CAS PubMed.
- F. D. Lillo, M. Cencini, W. M. Durham, M. Barry, R. Stocker, E. Climent and G. Boffetta, Phys. Rev. Lett., 2014, 112, 044502 CrossRef PubMed.
- F. Santamaria, F. D. Lillo, M. Cencini and G. Boffetta, Phys. Fluids, 2014, 26, 111901 CrossRef.
- K. Gustavsson, F. Berglund, P. R. Jonsson and B. Mehlig, Phys. Rev. Lett., 2016, 116, 108104 CrossRef CAS PubMed.
- T. Kaya and H. Koser, Phys. Rev. Lett., 2009, 103, 138103 CrossRef PubMed.
- T. Kaya and H. Koser, Biophys. J., 2012, 102, 1514–1523 CrossRef CAS.
- Marcos, H. C. Fu, T. R. Powers and R. Stocker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4780–4785 CrossRef CAS.
- N. Figueroa-Morales, G. Leonardo Miño, A. Rivera, R. Caballero, E. Clément, E. Altshuler and A. Lindner, Soft Matter, 2015, 11, 6284–6293 RSC.
- A. Dehkharghani, N. Waisbord, J. Dunkel and J. S. Guasto, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11119–11124 CrossRef CAS.
- A. M. Roberts, Nature, 1970, 228, 375–376 CrossRef CAS PubMed.
- V. Kantsler, J. Dunkel, M. Blayney and R. E. Goldstein, eLife, 2014, 3, e02403 CrossRef PubMed.
- M. Kumar and A. M. Ardekani, Soft Matter, 2019, 15, 6269–6277 RSC.
- L. J. Fauci and R. Dillon, Annu. Rev. Fluid Mech., 2006, 38, 371–394 CrossRef.
- K. Miki and D. E. Clapham, Curr. Biol., 2013, 23, 443–452 CrossRef.
-
M. Kim and A. A. Julius, Micro and Nano Technologies, Elsevier, 2012 Search PubMed.
- J. Palacci, S. Sacanna, A. Abramian, J. Barral, K. Hanson, A. Y. Grosberg, D. J. Pine and P. M. Chaikin, Sci. Adv., 2015, 1, e1400214 CrossRef.
- R. Baker, J. E. Kauffman, A. Laskar, O. E. Shklyaev, M. Potomkin, L. Dominguez-Rubio, H. Shum, Y. Cruz-rivera, I. S. Aranson, A. C. Balazs and A. Sen, Nanoscale, 2019, 11, 10944–10951 RSC.
- L. Ren, D. Zhou, Z. Mao, P. Xu, T. J. Huang and T. E. Mallouk, ACS Nano, 2017, 11, 10591–10598 CrossRef CAS PubMed.
- M. Potomkin, A. Kaiser, L. Berlyand and I. Aranson, New J. Phys., 2017, 19, 115005 CrossRef.
- W. E. Uspal, M. N. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 6613–6632 RSC.
- Y. Hatwalne, S. Ramaswamy, M. Rao and R. A. Simha, Phys. Rev. Lett., 2004, 92, 118101 CrossRef.
- C. Torney and Z. Neufeld, Phys. Rev. Lett., 2007, 99, 078101 CrossRef.
- B. T. Hagen, S. V. Teeffelen and H. Löwen, J. Phys.: Condens. Matter, 2011, 23, 194119 CrossRef PubMed.
- H. Stark, Eur. Phys. J.-Spec. Top., 2016, 225, 2369–2387 CrossRef.
-
S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Courier Corporation, North Chelmsford, MA, 2013 Search PubMed.
- M. Sandoval, N. K. Marath, G. Subramanian and E. Lauga, J. Fluid Mech., 2014, 742, 50–70 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2012, 108, 218104 CrossRef.
- G. B. Jeffery and L. N. G. Filon, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 Search PubMed.
- R. C. Binder, J. Appl. Phys., 1939, 10, 711–713 CrossRef.
- R. Simha, J. Phys. Chem., 1940, 44, 25–34 CrossRef CAS.
- L. G. Leal and E. J. Hinch, J. Fluid Mech., 1971, 46, 685–703 CrossRef.
- S. A. Berman, J. Buggeln, D. A. Brantley, K. A. Mitchell and T. H. Solomon, Phys. Rev. Fluids, 2021, 6, L012501 CrossRef.
- B. Ezhilan and D. Saintillan, J. Fluid Mech., 2015, 777, 482–522 CrossRef.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 4 CrossRef.
- R. Rusconi, J. S. Guasto and R. Stocker, Nat. Phys., 2014, 10, 212–217 Search PubMed.
- N. Khurana, J. Blawzdziewicz and N. T. Ouellette, Phys. Rev. Lett., 2011, 106, 198104 CrossRef PubMed.
- N. Khurana and N. T. Ouellette, Phys. Fluids, 2012, 24, 091902 CrossRef.
- J. R. N. Lazier and K. H. Mann, Deep-Sea Res., Part A, 1989, 36, 1721–1733 CrossRef CAS.
- M. Borgnino, K. Gustavsson, F. De Lillo, G. Boffetta, M. Cencini and B. Mehlig, Phys. Rev. Lett., 2019, 123, 138003 CrossRef CAS PubMed.
- Marcos and R. Stocker, Limnol. Oceanogr.: Methods, 2006, 4, 392–398 CrossRef.
- S.-W. Li, P.-H. Lin, T.-Y. Ho, C.-H. Hsieh and C.-L. Sun, Sci. Rep., 2021, 11, 11105 CrossRef CAS.
- A. Sokolov and I. S. Aranson, Nat. Commun., 2016, 7, 11114 CrossRef CAS PubMed.
- J. A. Arguedas-leiva and M. Wilczek, New J. Phys., 2020, 22, 053051 CrossRef CAS.
- M. F. Velho Rodrigues, M. Lisicki and E. Lauga, PLoS One, 2021, 16, 1–80 CrossRef PubMed.
-
M. Abramowitz and I. A. Stegun, Handbook of mathematical functions with formulas, graphs, and mathematical tables, US Government printing office, 1964, vol. 55 Search PubMed.
-
C. W. Gardiner
et al.
, Handbook of stochastic methods, Springer, Berlin, 1985, vol. 3 Search PubMed.
- A. J. F. Siegert, Phys. Rev., 1951, 81, 617–623 CrossRef.
-
S. Redner, A Guide to First-Passage Processes, Cambridge University Press, 2001 Search PubMed.
- F. Hecht, J. Numer. Math., 2012, 20, 251–265 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Eric
Lauga
* and
Eric
Lauga

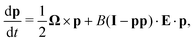
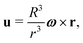
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ,
ψ,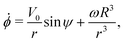
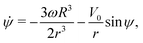
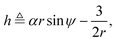
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ) we can express sin
ψ) we can express sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ(r) = h/αr + 3/2αr2 from eqn (5) to notice that
ψ(r) = h/αr + 3/2αr2 from eqn (5) to notice that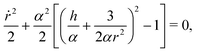
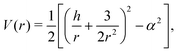
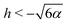 .
.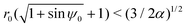 ; this is the equation of the separatrix of this dynamical system, i.e. the interface between the light yellow and dark green regions in Fig. 2. An important feature of this phase map that we will use later is the maximal radial distance r = rm for which a trapped state exists, given by rm = (3/2α)1/2.
; this is the equation of the separatrix of this dynamical system, i.e. the interface between the light yellow and dark green regions in Fig. 2. An important feature of this phase map that we will use later is the maximal radial distance r = rm for which a trapped state exists, given by rm = (3/2α)1/2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + y
ϕ + y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,
ϕ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + y
ϕ + y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,
ϕ,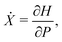
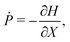
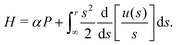
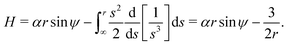
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ,
ψ,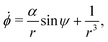
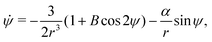
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ we can combine the radial and ψ equations of motion to obtain
ψ we can combine the radial and ψ equations of motion to obtain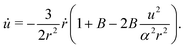
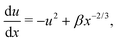
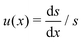 , then defining z = 3β1/2x3/2/2 and ω(z) such that s(x) = z3/4ω(z). This transformation leaves us with solving the modified Bessel equation
, then defining z = 3β1/2x3/2/2 and ω(z) such that s(x) = z3/4ω(z). This transformation leaves us with solving the modified Bessel equation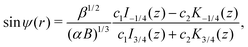
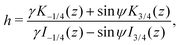
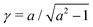 represents the inverse of the eccentricity of the elliptical cross-section of the swimmer.
represents the inverse of the eccentricity of the elliptical cross-section of the swimmer.
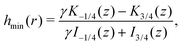
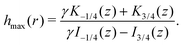
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ. Specifically, if the swimmer starts with cos
ψ. Specifically, if the swimmer starts with cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ > 0 it will always advance in r since ṙ ∝ cos
ψ > 0 it will always advance in r since ṙ ∝ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ and the change in the sign of cos
ψ and the change in the sign of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ can only happen when sin
ψ can only happen when sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ = ±1, which are exactly the hmin and hmax lines that the swimmer cannot approach. If initially cos
ψ = ±1, which are exactly the hmin and hmax lines that the swimmer cannot approach. If initially cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ < 0, then the swimmer will certainly reach the hmin or hmax line and the unboundedness of the orbit will depend on whether the point of interception with these lines is stationary and stable or not. In the dynamical system that we consider here, there is only one stationary point on hmin and hmax but it is unstable so the swimmer will turn around and escape.
ψ < 0, then the swimmer will certainly reach the hmin or hmax line and the unboundedness of the orbit will depend on whether the point of interception with these lines is stationary and stable or not. In the dynamical system that we consider here, there is only one stationary point on hmin and hmax but it is unstable so the swimmer will turn around and escape.
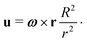
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ,
ψ,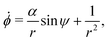
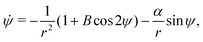
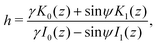
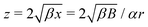 and γ = (β/B)1/2 = ((B + 1)/2B)1/2 ≥ 1. Using the same method as in case of a 3D rotlet we come to a similar conclusion that a swimmer will be trapped in a 2D rotlet if and only if initially r0 < rm = (1 − B)/α and h(r0,ψ0) < hmin(rm). We compare in Fig. 3B this theoretical prediction with numerical computations, and again obtain excellent agreement.
and γ = (β/B)1/2 = ((B + 1)/2B)1/2 ≥ 1. Using the same method as in case of a 3D rotlet we come to a similar conclusion that a swimmer will be trapped in a 2D rotlet if and only if initially r0 < rm = (1 − B)/α and h(r0,ψ0) < hmin(rm). We compare in Fig. 3B this theoretical prediction with numerical computations, and again obtain excellent agreement.
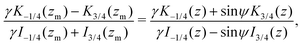
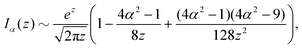
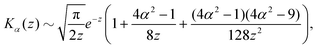
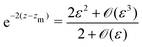
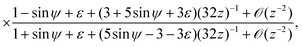
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ, we further investigate each of these cases separately. In the |sin
ψ, we further investigate each of these cases separately. In the |sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ ± 1| ≫ ε case, the balance of dominant terms becomes
ψ ± 1| ≫ ε case, the balance of dominant terms becomes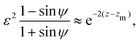
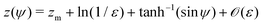 . Now, if instead sin
. Now, if instead sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ = 1 − εζ, with ζ ∼ O(1), the balance reads
ψ = 1 − εζ, with ζ ∼ O(1), the balance reads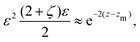
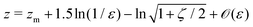 . Finally, if sin
. Finally, if sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ψ = −1 + ε2ζ, with ζ ∼
ψ = −1 + ε2ζ, with ζ ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) we expect an
(1) we expect an ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) correction of the form z = zm + F(ζ) that must satisfy
(1) correction of the form z = zm + F(ζ) that must satisfy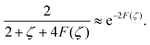
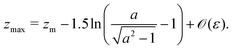

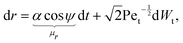
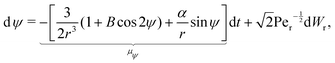
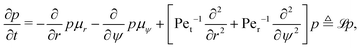
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) to denote the Fokker–Planck operator from eqn (32), its adjoint
to denote the Fokker–Planck operator from eqn (32), its adjoint ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) † is defined on the space of the initial conditions (r0,ψ0) as the unique operator satisfying
† is defined on the space of the initial conditions (r0,ψ0) as the unique operator satisfying![[script L]](https://www.rsc.org/images/entities/char_e144.gif) f,g〉 = 〈f,
f,g〉 = 〈f,![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †g〉,
†g〉,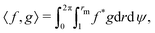
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) † as
† as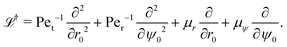
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †T = −1 with T = 0 at r0 = 1 and r0 = rm,
†T = −1 with T = 0 at r0 = 1 and r0 = rm,![[script L]](https://www.rsc.org/images/entities/char_e144.gif) †P = 0 with P = 0 at r0 = 1 and P = 1 at r0 = rm.
†P = 0 with P = 0 at r0 = 1 and P = 1 at r0 = rm.
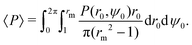
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) , which sets a timescale for the emergent dynamics of the ensemble of swimmers.
, which sets a timescale for the emergent dynamics of the ensemble of swimmers.
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ) behaves qualitatively as expected. The faster the swimmers and the stronger the noise, the easier it is to escape and thus
) behaves qualitatively as expected. The faster the swimmers and the stronger the noise, the easier it is to escape and thus ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) takes smaller values. The difference in maximal MFPT between the two values of the shape factor B can be understood by realising that the trapping domain is different for distinct values of B and α. Indeed, the trapping domain is given by r ∈ [1,rm] where rm = [3(1 − B)/2α]1/2 so it is significantly smaller for rod-like swimmers (B → 1) than for spherical ones (B = 0). The size of the trapping region indicates that more elongated swimmers are more difficult to trap, which is reflected in the fact that MFPT is shorter for elongated swimmers.
takes smaller values. The difference in maximal MFPT between the two values of the shape factor B can be understood by realising that the trapping domain is different for distinct values of B and α. Indeed, the trapping domain is given by r ∈ [1,rm] where rm = [3(1 − B)/2α]1/2 so it is significantly smaller for rod-like swimmers (B → 1) than for spherical ones (B = 0). The size of the trapping region indicates that more elongated swimmers are more difficult to trap, which is reflected in the fact that MFPT is shorter for elongated swimmers.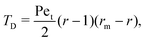
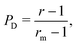
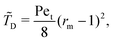
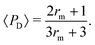

![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (A and C), and the average probability of escape, 〈P〉 (B and D), and the theoretical predictions in the diffusion dominated regime,
(A and C), and the average probability of escape, 〈P〉 (B and D), and the theoretical predictions in the diffusion dominated regime, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) D and 〈PD〉, eqn (40). (A and B) Spherical swimmers B = 0; (C and D) rod-like swimmers B = 0.95.
D and 〈PD〉, eqn (40). (A and B) Spherical swimmers B = 0; (C and D) rod-like swimmers B = 0.95.![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) is significantly less than
is significantly less than ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) D coincides roughly with the region where the average probability of escape is significantly greater than the diffusion dominated prediction, a result that appears to hold for both limiting values of the shape factor B. Consequently, swimming not only promotes faster migration from the trapping region but it does so by increasing the chance of escape and not by making more particles stick to the rotating body.
D coincides roughly with the region where the average probability of escape is significantly greater than the diffusion dominated prediction, a result that appears to hold for both limiting values of the shape factor B. Consequently, swimming not only promotes faster migration from the trapping region but it does so by increasing the chance of escape and not by making more particles stick to the rotating body.