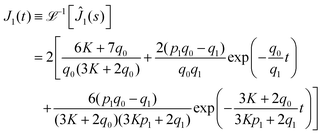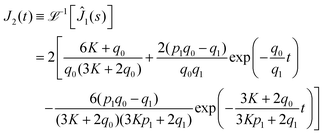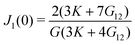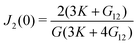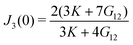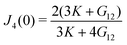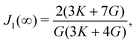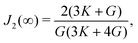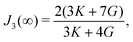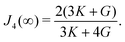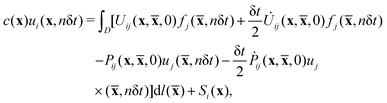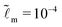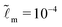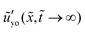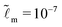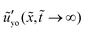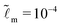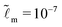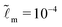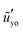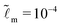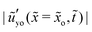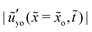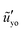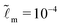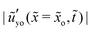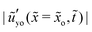DOI:
10.1039/D2SM00913G
(Paper)
Soft Matter, 2022,
18, 7280-7290
The growth and the decay of a visco-elastocapillary ridge by localized forces†
Received
6th July 2022
, Accepted 28th August 2022
First published on 29th August 2022
Abstract
A soft solid layer develops a ridge-like deformation below the contact line due to the pulling force of the liquid–air surface tension when a droplet is in contact with it. We investigate the growth and the decay of a viscoelastic wetting ridge. The global features, e.g. the ridge height, evolve with time scales corresponding to the relaxation of the viscoelastic material. In contrast, we show that locally around the tip of the ridge, the surface tensions not only determine the equilibrium shape, but also have a significant impact on the dynamics, for which the relaxation has a characteristic spreading velocity depending on the solid surface tension. The relaxation time to an equilibrium state depends on the distance from the contact line, which can be much smaller than the long-term relaxation time scale of the viscoelastic material. The different dynamics between the global features of the ridge and the tip morphology suggests an alternative focus when investigating the contact line dynamics in soft wetting, such as stick-slip motion.
1 Introduction
A liquid droplet in contact with a soft substrate, such as elastomers, gels and rubbers, can deform the substrate due to the localized force acted upon by the liquid on the solid at the contact line.1,2 This morphological change in soft solids has a significant impact on the shape of the droplet,3 as well as the dynamical process when the droplet is in motion.4–8 Apart from the scenario of droplets interacting with a soft solid, studying how soft solids respond to external localized stresses is important to the understanding of industrial and biological systems such as soft adhesion,9,10 and the functions of cells and tissues.11,12
The deformation of soft solids below the contact line appears as a ridge-like shape, which has been measured, for example, using X-ray microscopy.1 The equilibrium shape of the ridge is critically determined by the elastic properties of the soft solid,2,13–15 as well as the forces acting on it. An apparent normal force pulling the solid upwards by the liquid at the contact line is the tension with a magnitude equal to γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,16 here γ is the liquid–air surface tension and θ is the liquid equilibrium contact angle. A length scale named the elastocapillary length γ/G can be constructed, with the shear modulus G serving as a resistance to deformation.15 Earlier computations of the equilibrium shape of the wetting ridge date back to the studies by Lester17 and Rusanov,18 in which a droplet is in contact with a soft semi-infinitely thick substrate. Later, more investigations were done for a soft solid layer of finite thickness H attached to a rigid substrate.19,20 All these studies point to a conclusion that both length scales γ/G and H play a crucial role in solid deformation.
θ,16 here γ is the liquid–air surface tension and θ is the liquid equilibrium contact angle. A length scale named the elastocapillary length γ/G can be constructed, with the shear modulus G serving as a resistance to deformation.15 Earlier computations of the equilibrium shape of the wetting ridge date back to the studies by Lester17 and Rusanov,18 in which a droplet is in contact with a soft semi-infinitely thick substrate. Later, more investigations were done for a soft solid layer of finite thickness H attached to a rigid substrate.19,20 All these studies point to a conclusion that both length scales γ/G and H play a crucial role in solid deformation.
Remarkably, recent studies15,21–24 have demonstrated that when including the contribution of solid surface tension γs to the elastic model, the agreement with the experimentally measured ridge profiles turns out to be promising. The solid surface tension suppresses the deformation and regularizes the singularity at the contact line.21 The solid angle formed at the contact line follows the balance between the surface forces, or named Neumann's relation.3,25 Neumann's relation has also been validated by studies using nonlinear elastic constitutive models26 and experimentally by measurements using confocal microscopy.9 When γ/G is very small, i.e. rigid solids, one expects the liquid contact angle at the contact line to follow the Young's relation. By including a microscopic length scale lm characterizing the width of the liquid–air interface,27 it is shown that the transition from Neumann's relation to Young's relation occurs when γ/G ∼ lm.28,29 Young's relation is recovered for γ/G ≪ lm. The crossover from the Neumann's relation to Young's law has also been demonstrated in studies using the molecular dynamics simulations.30
Apart from the elastic properties, many soft solids like tissues and gels also demonstrate viscoelastic features. When a droplet is placed in contact with such smooth soft substrates, the flat surface of the solid around the contact line starts to deform and gradually form a wetting ridge. Both experimental1,6 and theoretical6 studies find that a sharp tip has developed even at the early stage of ridge formation. Another study31 investigated the relaxation of a deformed viscoelastic half-space subsequent to the removal of the point load. It was shown that solid surface tension reduces the local elastic deformation and stress field near the load point.
As we mentioned above, the dynamic response of a viscoelastic solid to a time-dependent localized force has been demonstrated by some previous studies. Nevertheless, how different regions of a viscoelastic solid respond in time during the growth and the decay of the ridge has not been fully investigated and described in the literature, in particular the role played by the solid surface tension, which is crucial for the understanding of phenomena such as stick-slip motion of contact lines;7,32 droplet evaporation5,33,34 and soft electrowetting.35 In this study, we examine both the growth and the decay of a ridge and show how the solid interface and the characteristic features of the ridge change with time. Importantly, we focus on the tip region of the ridge and show that the solid material in that region relaxes in a different dynamical way from the remaining part of the ridge. To describe the viscoelastic properties of the soft material, the standard solid model will be implemented. The solutions are computed using the approach of the boundary element method (BEM), which has been used widely to study droplet36–38 and solid deformation.39,40 The BEM can be extended to study problems involving viscoelastic deformation coupled with fluid flow such as in wet adhesion.
2 Formulation
We consider that a droplet is placed in contact with a layer of isotopic viscoelastic solid with thickness H which is attached to a rigid solid. We denote the displacement at any position x = x![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + yŷ + zẑ of the undeformed viscoelastic solid and time t as u(x,t) = ux(x,t)
+ yŷ + zẑ of the undeformed viscoelastic solid and time t as u(x,t) = ux(x,t)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + uy(x,t)ŷ + uz(x,t)ẑ. In index notations, we write the component as ui where i = x, y or z. In the following, the subscripts i, j and k take either one of the components in rectangular coordinates. The repeated indices conform to the Einstein summation convention, i.e., they are summed over the three components. For viscoelastic materials made of polymers such as elastomers and gels, we assume that the bulk modulus K can be considered as a constant, independent of time. We further assume that the strain is small, namely the strain tensor εij(x,t) = (∂ui/∂xj + ∂uj/∂xi)/2 ≪ 1. Hence, the stress tensor σij(x,t) and the strain tensor follow the linear constitutive relation given as
+ uy(x,t)ŷ + uz(x,t)ẑ. In index notations, we write the component as ui where i = x, y or z. In the following, the subscripts i, j and k take either one of the components in rectangular coordinates. The repeated indices conform to the Einstein summation convention, i.e., they are summed over the three components. For viscoelastic materials made of polymers such as elastomers and gels, we assume that the bulk modulus K can be considered as a constant, independent of time. We further assume that the strain is small, namely the strain tensor εij(x,t) = (∂ui/∂xj + ∂uj/∂xi)/2 ≪ 1. Hence, the stress tensor σij(x,t) and the strain tensor follow the linear constitutive relation given as| |
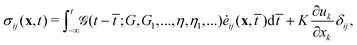 | (1) |
where the deviatoric part of the strain tensor 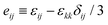 , ėij ≡ ∂eij/∂
, ėij ≡ ∂eij/∂![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is the shear relaxation function which depends on the viscoelastic model characterized by the parameters G, G1,… and η, η1,…. We assume the dynamics of the solid deformation is slow enough so that the net force on a soft solid element vanishes which gives the governing equation
is the shear relaxation function which depends on the viscoelastic model characterized by the parameters G, G1,… and η, η1,…. We assume the dynamics of the solid deformation is slow enough so that the net force on a soft solid element vanishes which gives the governing equation| |
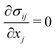 | (2) |
when body forces such as gravity are neglected.
The range of solid deformation depends on the elastocapillary length γ/G and the thickness of the soft layer H. In this study, we assume that both the elastocapillary length and the thickness of the soft layer are much smaller than the contact radius R of the droplet, i.e., γ/G ≪ R and H ≪ R, meaning that the solid deformation is localized around the edge of the droplet. In this limit, it is justified to assume that the deformation of a solid behaves as the case of plane strain, for which ux and uy are a function of x and y only, and uz is a constant, and so the governing eqn (1) can be simplified due to the conditions of the vanishing of the following quantities, namely
| |
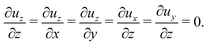 | (3) |
In the plane strain situation, the domain of the soft solid layer that we consider is a rectangle with thickness H and length L ≫ H. Fig. 1 shows the schematic of the setup. The soft layer is attached to a rigid solid, hence at the bottom boundary (y = −H) of the domain where the soft and the rigid solids are in contact, the displacement
At the two other ends of the domain, we also assume the displacements are zero,
i.e.| |
| ui(x = −L/2,y,t) = ui(x = L/2,y,t) = 0. | (5) |
The boundary conditions at the solid/fluid interfaces require more discussions. As it has been shown that the solid surface tension plays an important role in the deformation of the wetting ridge, we include this specific property in our model. For soft solids, we have to distinguish between surface energy and surface stress due to the Shuttleworth effect.
41–43 In this study, for the simplicity of modelling, we neglect this effect and hence the tension force at the solid interface is independent of the stretching of the solid. We also assume that the surface tensions are the same for the solid/liquid and the solid/air interfaces, hence the tension is described by a constant
γs along the whole solid interface, and the liquid contact angle
θ = 90°. We now consider the forces acting on an element of the interface. We first define the traction in the soft solid as
fi ≡
σijnj, where
nj is the normal vector of a surface pointing outward from an element. We assume that the external force acting on the soft solid only has the out-of-plane component (
i.e., the
y-component). Suppose the external force per unit area acting on the interface is given by
fexti(
x,
t), for small interface slope due to small deformation ∂
uy/∂
x ≪ 1, we have the force balance on the interface as
and
| |
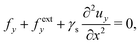 | (7) |
where the normal force balance
eqn (7) includes the contribution of the solid surface tension
γs.
15,22,23 Here we have adopted the approximation for the curvature of the interface,
i.e.,
κ = ∂
2uy/∂
x2, when the slope is small.
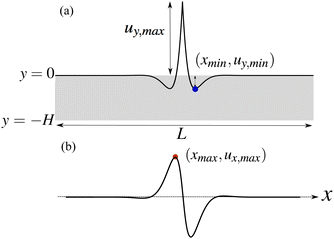 |
| | Fig. 1 Schematic of the setup. (a) The gray region represents the undeformed soft layer with a width L and a thickness H. The solid curve shows an out-of-plane displacement profile at the solid surface. The maximum is denoted by uy,max and the local minimum (indicated by a blue circle) is denoted by uy,min at x = xmin. (b) The solid curve shows an in-plane displacement profile at the solid surface. The maximum (indicated by a red circle) is denoted by ux,max at x = xmax. | |
To model the localized external traction, we use the Gaussian function to describe the spatial distribution of the normal traction, i.e., 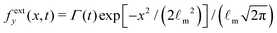 , where
, where ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is the microscopic length such that
m is the microscopic length such that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m ≪ H. In the limit that
m ≪ H. In the limit that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m → 0, the traction fexty(x,t) = Γ(t)δ(x), where δ(x) is the Dirac delta function, which is also used in some other studies.6 The strength of the external force Γ(t) is a function of time. In this study, we will use two different functional forms, respectively, to investigate the growth and the decay of the ridge, namely case 1: Γ(t) = γ
m → 0, the traction fexty(x,t) = Γ(t)δ(x), where δ(x) is the Dirac delta function, which is also used in some other studies.6 The strength of the external force Γ(t) is a function of time. In this study, we will use two different functional forms, respectively, to investigate the growth and the decay of the ridge, namely case 1: Γ(t) = γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t) and case 2: Γ(t) = γ[1 −
(t) and case 2: Γ(t) = γ[1 − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t)] = γ − γ
(t)] = γ − γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t). Here
(t). Here ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t) is the Heaviside step function. As the governing equations are linear, the solution for case 2 (decay case) will be obtained by combining the steady solution (at t → ∞) of case 1 and the solution obtained when using Γ(t) = −γ
(t) is the Heaviside step function. As the governing equations are linear, the solution for case 2 (decay case) will be obtained by combining the steady solution (at t → ∞) of case 1 and the solution obtained when using Γ(t) = −γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t).
(t).
There are different types of viscoelastic models which have been used to describe the behavior of different viscoelastic materials. The simplest models are the Kelvin–Voigt model or the Maxwell model which consists of a spring and a viscous damper connected in parallel or in series respectively. In this study, we assume the response of the soft material follows the standard solid (Zener) model which consists of a spring (characterized by G) connected in parallel with a Maxwell element, i.e., a spring (characterized by G1) connected in series with a viscous damper (characterized by η), which is relatively simple but can describe both stress relaxation and creep. The standard solid model has been used to describe the viscoelastic behavior of elastomers. We note that our approach can be used for other linear viscoelastic models. Please refer to the Appendix for the details of the description of the viscoelastic model. Here we point out that for our viscoelastic model, the initial instantaneous shear modulus is G + G1 and the static (long-term) shear modulus is G. Since many soft solids can be considered as incompressible, we will take the incompressible limit, i.e. K ≫ (G + G1).
2.1 The boundary element method (BEM)
To solve the governing eqn (1) and (2) with the plane strain conditions (eqn (3)) and the boundary conditions given by eqn (4)–(7), we implement the approach of the boundary element method (BEM) in the time domain.39,44–46 We denote the closed contour of the boundary of the domain as D, the position vector of a point on the contour as ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) and
and 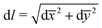 as the differential length on the contour. The governing eqn (1)–(3) are formulated as boundary integral equations (see the Appendix for the details of derivation) which read
as the differential length on the contour. The governing eqn (1)–(3) are formulated as boundary integral equations (see the Appendix for the details of derivation) which read| |
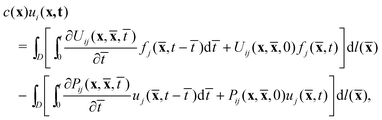 | (8) |
where| |
 | (9) |
The expression of the tensor components Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) and Uij(x,
,t) and Uij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) depends on the specific viscoelastic model as for the shear relaxation function
,t) depends on the specific viscoelastic model as for the shear relaxation function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) . In the Appendix, we derive the expressions for the standard solid (Zener) model. We note that Pij and Uij are singular at x =
. In the Appendix, we derive the expressions for the standard solid (Zener) model. We note that Pij and Uij are singular at x = ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ; the integral over the singular point is thus computed analytically by expanding the tensor components in series around x =
; the integral over the singular point is thus computed analytically by expanding the tensor components in series around x = ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) .
.
To solve the boundary integral equations numerically, we implement a time marching scheme39,44–46 and discretize the boundary of the domain D as follows: we have evenly distributed marker points for the two side boundaries at x = −L/2 and x = L/2, and the bottom boundary at y = −H. The number of marker points, respectively, equals to 50, 50 and 200. For the top boundary at y = 0, we use 400 marker points and distribute them with a separation increasing exponentially from the center. The distance dm between two marker points at the center is as small as dm/H = 10−6 so that we can resolve the fine structures around the contact line where the localized force is imposed. We take a constant time step δt. At any time t = nδt, the boundary integral eqn (8) is discretized in the following way (using trapezoidal rule for the time integral):
where
![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) ij
ij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
t) = ∂
Uij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
t)/∂
t,
Ṗij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
t) = ∂
Pij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
t)/∂
t and
Si(
x) is the term corresponding to the history of responses, which can be written as
| |
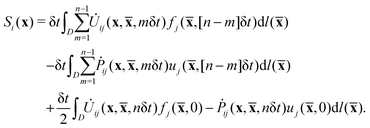 | (10) |
Regarding the rescalings, unless specified differently, we will divide all the lengths by the thickness of the soft layer H, the stresses by γs/H and the time by η/G; we end up with the following independent dimensionless control parameters (with a tide):
| |
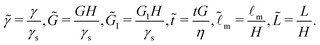 | (11) |
3 Results
We consider that the width of the soft layer L is much larger than its thickness H, and the microscopic length scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is much smaller than the thickness of the soft layer. We take
m is much smaller than the thickness of the soft layer. We take ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and
= 50 and 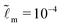 (e.g. consider a liquid/air interface of nanometric thickness and a 10 micron thick soft solid layer). We present the results in three main parts. In Section 3.1, we focus on the evolution of the global features of the ridge. In Section 3.2.1, we discuss at how the static solid interface profile depends on the parameters. In Sections 3.2.2 and 3.2.3, the role of the solid surface tension and the relaxation at the tip region is explored in detail.
(e.g. consider a liquid/air interface of nanometric thickness and a 10 micron thick soft solid layer). We present the results in three main parts. In Section 3.1, we focus on the evolution of the global features of the ridge. In Section 3.2.1, we discuss at how the static solid interface profile depends on the parameters. In Sections 3.2.2 and 3.2.3, the role of the solid surface tension and the relaxation at the tip region is explored in detail.
3.1 Shape evolution of the wetting ridge
3.1.1 Profiles of the wetting ridge during the growth and the decay.
We look at how a wetting ridge grows when 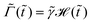 and how the ridge decays when
and how the ridge decays when 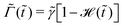 , with
, with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2. As our viscoelastic model is linear, which assumes small solid interfacial slopes (small strains), we thus pick the value of
= 0.2. As our viscoelastic model is linear, which assumes small solid interfacial slopes (small strains), we thus pick the value of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) to be significantly smaller than 1. Note that the solid interfacial slope around the contact line increases with
to be significantly smaller than 1. Note that the solid interfacial slope around the contact line increases with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) based on the Neumann's relation. The time series of
based on the Neumann's relation. The time series of 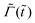 is plotted in Fig. 2(a) and (b). We take
is plotted in Fig. 2(a) and (b). We take ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. Fig. 2(c) and (d) show the out-of-plane displacement ũyo ≡ ũy(
1 = 102. Fig. 2(c) and (d) show the out-of-plane displacement ũyo ≡ ũy(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ = 0,
,ỹ = 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at different times. Fig. 2(e) and (f) show the corresponding in-plane displacement ũxo ≡ ũx(
) at different times. Fig. 2(e) and (f) show the corresponding in-plane displacement ũxo ≡ ũx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ = 0,
,ỹ = 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). At
). At ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+, there is an instantaneous elastic deformation with shear modulus equal to
= 0+, there is an instantaneous elastic deformation with shear modulus equal to ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) +
+ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1. As
1. As ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 is large, the initial solid surface deflection is tiny. The ridge shape, described by ũyo, is symmetric along the central axis (
1 is large, the initial solid surface deflection is tiny. The ridge shape, described by ũyo, is symmetric along the central axis (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) while the in-plane displacement ũxo is anti-symmetric. A significant difference between the growth and the decay of the ridge is that, during the growth, a sharp tip (around
= 0) while the in-plane displacement ũxo is anti-symmetric. A significant difference between the growth and the decay of the ridge is that, during the growth, a sharp tip (around ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) is maintained from the early stage of the growth. For the decay, when the localized external stress vanishes (at
= 0) is maintained from the early stage of the growth. For the decay, when the localized external stress vanishes (at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0), the sharp tip quickly relaxes to round shapes with a much smaller curvature as can be seen in Fig. 2(d). Note that the profiles at
= 0), the sharp tip quickly relaxes to round shapes with a much smaller curvature as can be seen in Fig. 2(d). Note that the profiles at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0− in Fig. 2(d) and (f) are the steady profiles before the external stress vanishes.
= 0− in Fig. 2(d) and (f) are the steady profiles before the external stress vanishes.
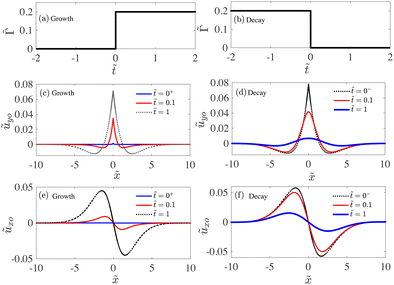 |
| | Fig. 2 (a and b) The time series of the strength of the external stress  . The growth (c) and (e) and decay (d) and (f) of a wetting ridge. (c and d) The out of plane displacement at the solid–fluid interface ũyo as a function of . The growth (c) and (e) and decay (d) and (f) of a wetting ridge. (c and d) The out of plane displacement at the solid–fluid interface ũyo as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for different rescaled times. (e and f) The in-plane displacement at the solid–liquid interface ũxo as a function of for different rescaled times. (e and f) The in-plane displacement at the solid–liquid interface ũxo as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . Parameters: . Parameters: ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1, = 10−1, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102, 1 = 102, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and = 50 and  . . | |
3.1.2 Evolution of the characteristic quantities.
There are several features of the ridge that we can describe here. First, the maximum out-of-plane displacement ũy,max ≡ ũyo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0,
= 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) of the solid surface or called the ridge height is at the center
) of the solid surface or called the ridge height is at the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0. Second, the out-of-plane displacement decreases from the center and a minimum value ũy,min ≡ ũyo(
= 0. Second, the out-of-plane displacement decreases from the center and a minimum value ũy,min ≡ ũyo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min,
min,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is achieved at
) is achieved at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min (and
min (and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = −
= −![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min), where a clear dimple is formed with a negative out-of-plane displacement. Third, for the in-plane displacement ũxo, we see from Fig. 2(e) and (f) that around the center
min), where a clear dimple is formed with a negative out-of-plane displacement. Third, for the in-plane displacement ũxo, we see from Fig. 2(e) and (f) that around the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0, the solid material is compressed (with a negative slope shown in the plot, i.e., ∂ũxo/∂
= 0, the solid material is compressed (with a negative slope shown in the plot, i.e., ∂ũxo/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) < 0, and there is a maximum ũx,max ≡ ũxo(
< 0, and there is a maximum ũx,max ≡ ũxo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max,
max,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at the negative side of
) at the negative side of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . These characteristic quantities are also indicated in the schematic of the setup in Fig. 1.
. These characteristic quantities are also indicated in the schematic of the setup in Fig. 1.
Now we look at the evolution of the characteristic quantities. In Fig. 3(a) and (b), we plot ũy,max, |ũy,min| and ũx,max as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , respectively, during the growth and the decay of the ridge. All these quantities increase/decrease monotonically with time and saturate to a steady value during the growth/decay of the ridge. Next, we look at the time series of the magnitudes of the positions |
, respectively, during the growth and the decay of the ridge. All these quantities increase/decrease monotonically with time and saturate to a steady value during the growth/decay of the ridge. Next, we look at the time series of the magnitudes of the positions |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min| and |
min| and |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max| as plotted in Fig. 3(c) and (d). Both |
max| as plotted in Fig. 3(c) and (d). Both |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min| and |
min| and |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max| equal to unity at
max| equal to unity at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ (instantaneous elastic response). This means that for a large
= 0+ (instantaneous elastic response). This means that for a large ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1, these two positions are equal to the thickness of the soft substrate. They increase with time during the growth. However, during the decay of the ridge, instead of decreasing, the positions still increase with time. This feature can also be observed from the profiles shown in Fig. 2(d) and (f).
1, these two positions are equal to the thickness of the soft substrate. They increase with time during the growth. However, during the decay of the ridge, instead of decreasing, the positions still increase with time. This feature can also be observed from the profiles shown in Fig. 2(d) and (f).
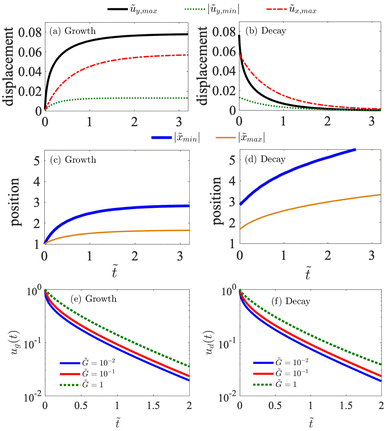 |
| | Fig. 3 (a and b) The rescaled ridge height ũy,max, the absolute value of the rescaled minimum out-of-plane displacement |ũy,min| and the rescaled maximum in-plane displacement ũx,max as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) . (c and d) The absolute value of . (c and d) The absolute value of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min and min and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max as a function of the rescaled time max as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) . For (a–d), . For (a–d), ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1. (e and f) The rescaled ridge height ũg in (e) and ũd in (f) as a function of the rescaled time = 10−1. (e and f) The rescaled ridge height ũg in (e) and ũd in (f) as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) for different values of for different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Parameters: . Parameters: ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102, 1 = 102, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and = 50 and 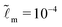 . . | |
To characterize the dynamics of the whole wetting ridge, we here focus on the evolution of the ridge height ũy,max. For both the growth and the decay, we find that, a rescaled ridge height relaxes exponentially to the steady states at late times. The rescaled ridge heights are defined as 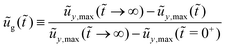 for the growth and
for the growth and 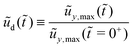 for the decay. In Fig. 3(e) and (f), the rescaled ridge heights are respectively plotted as a function of
for the decay. In Fig. 3(e) and (f), the rescaled ridge heights are respectively plotted as a function of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) for different values of
for different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . We find that both ũg(
. We find that both ũg(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) and ũd(
) and ũd(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) relax the same way, i.e., ũg(
) relax the same way, i.e., ũg(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) or ũd(
) or ũd(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), scales as ∼exp(−1.15
), scales as ∼exp(−1.15![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at late times. The late time ridge evolution possesses the same time scale as the relaxation of the viscoelastic material in our standard solid model, i.e., η/G.
) at late times. The late time ridge evolution possesses the same time scale as the relaxation of the viscoelastic material in our standard solid model, i.e., η/G.
3.2 The role of the solid surface tension
3.2.1 Static profiles: from the soft regime to the stiff regime.
Before we look at the dynamic response of the soft solid at the tip region of the ridge, it is insightful to see how the static shape (purely elastic) of solid deformation at the tip region varies when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) is changed. Note that the static shape is the same as the shape at
is changed. Note that the static shape is the same as the shape at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞ in the growth case. From the scaling with
→ ∞ in the growth case. From the scaling with ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , we will also deduce the dependence on the shear modulus G and the soft layer thickness H, which are dimensional quantities of physical and practical importance. Before we focus on the tip region, let us first look at the ridge height ũy,max(
, we will also deduce the dependence on the shear modulus G and the soft layer thickness H, which are dimensional quantities of physical and practical importance. Before we focus on the tip region, let us first look at the ridge height ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞), which is plotted in Fig. 4(a) as a function of
→ ∞), which is plotted in Fig. 4(a) as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . As one might expect, the ridge height increases with decreasing
. As one might expect, the ridge height increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Moreover, when
. Moreover, when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≫ 1 or in other words, when the soft layer thickness is much larger than the elastocapillary length γs/G, we find that ũy,max(
≫ 1 or in other words, when the soft layer thickness is much larger than the elastocapillary length γs/G, we find that ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) ∼
→ ∞) ∼ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) −1. This scaling implies that the dimensional ridge height uy,max(
−1. This scaling implies that the dimensional ridge height uy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) scales linearly with the elastocapillary length and is independent of the soft layer thickness. The confinement (thickness) of the soft layer plays no role in this regime. When
→ ∞) scales linearly with the elastocapillary length and is independent of the soft layer thickness. The confinement (thickness) of the soft layer plays no role in this regime. When ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) becomes smaller (≲10), we see that ũy,max(
becomes smaller (≲10), we see that ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) scales as
→ ∞) scales as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) α locally with −1 < α < 0. Hence uy,max(
α locally with −1 < α < 0. Hence uy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) increases with decreasing G and increasing H.
→ ∞) increases with decreasing G and increasing H.
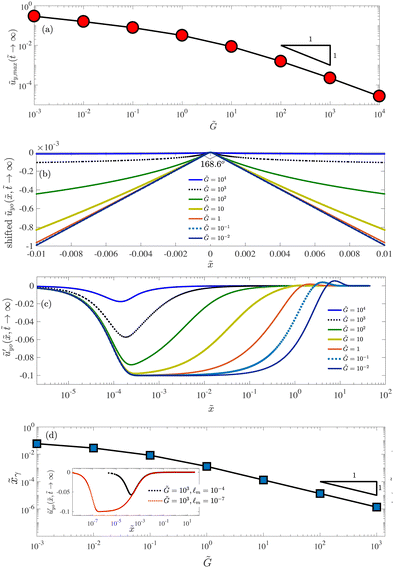 |
| | Fig. 4 Static states: solutions for the growth case when ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞. (a) The static ridge height ũy,max( → ∞. (a) The static ridge height ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) as a function of → ∞) as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . (b) The static solid interface profile ũyo( . (b) The static solid interface profile ũyo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , ,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) shifted by the static ridge height as a function of → ∞) shifted by the static ridge height as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for a wide range of for a wide range of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . (c) The slope of the static solid interface . (c) The slope of the static solid interface 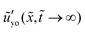 vs. vs. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . (d) The size of the constant-slope region . (d) The size of the constant-slope region ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ as a function of γ as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Here . Here 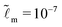 , we increase the numerical resolution around the contact line by having the smallest separation of marker points ≈10−9. Inset: The slope of the static solid interface , we increase the numerical resolution around the contact line by having the smallest separation of marker points ≈10−9. Inset: The slope of the static solid interface 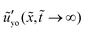 vs. vs. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for for 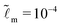 and and 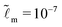 and a fixed value of and a fixed value of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103. Parameters: = 103. Parameters: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50, and = 50, and 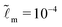 for (a–c). for (a–c). | |
In the following, we focus on the tip region. In Fig. 4(b), we plot the static out-of-plane displacement ũyo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) in the region of −0.01 <
→ ∞) in the region of −0.01 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) < 0.01, for a wide range of
< 0.01, for a wide range of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2–104. Note that the profiles are shifted by the ridge height ũy,max(
= 10−2–104. Note that the profiles are shifted by the ridge height ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) so that all the tips are at the same position. For
→ ∞) so that all the tips are at the same position. For ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≤ 10, we see the solid interfaces form the same solid angle θs = 168.6°. The solid angle can be understood by the force balance between the solid surface tensions and the external liquid–air surface tension, namely γ = 2γs
≤ 10, we see the solid interfaces form the same solid angle θs = 168.6°. The solid angle can be understood by the force balance between the solid surface tensions and the external liquid–air surface tension, namely γ = 2γs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θs/2). For
cos(θs/2). For ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) > 10, the interface profiles have a solid angle getting closer to 180° as
> 10, the interface profiles have a solid angle getting closer to 180° as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) increases. This shows how the solid deformation at the tip region varies from a soft regime to a stiff regime which are consistent with Neumann's relation and Young's relation, respectively, in the two different limits.
increases. This shows how the solid deformation at the tip region varies from a soft regime to a stiff regime which are consistent with Neumann's relation and Young's relation, respectively, in the two different limits.
To show clearly how the slope of the solid interface varies with the distance from the center at different length scales, we plot the interfacial slope 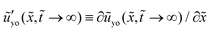 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) in Fig. 4(c). For the stiffer case we have computed here, e.g.
(in log scale) in Fig. 4(c). For the stiffer case we have computed here, e.g. ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 104, the magnitude of the slope is small. The whole solid interface maintains close to a flat surface even though being exerted by a localized external force. As
= 104, the magnitude of the slope is small. The whole solid interface maintains close to a flat surface even though being exerted by a localized external force. As ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) decreases, the magnitude of the slope increases. There appear overlapping regions of the curves for different
decreases, the magnitude of the slope increases. There appear overlapping regions of the curves for different ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) values. The size of the overlapping region increases with decreasing
values. The size of the overlapping region increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . The overlapping of the curves means that the solid deformation in that region is independent of
. The overlapping of the curves means that the solid deformation in that region is independent of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , and hence the solid surface tension dominates over the elastic stress. Moreover, we also see that there is a region of a constant slope −0.1 for
, and hence the solid surface tension dominates over the elastic stress. Moreover, we also see that there is a region of a constant slope −0.1 for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) < 10. Note that the slope −0.1 means that the solid angle θs = 168.6°. Indeed the constant-slope region is what we have plotted in Fig. 4(b). At distances from the center
< 10. Note that the slope −0.1 means that the solid angle θs = 168.6°. Indeed the constant-slope region is what we have plotted in Fig. 4(b). At distances from the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) smaller than
smaller than 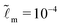 , the distribution of external stress plays a role, the slope of the interface is not −0.1, although the solid surface tension dominates over the elastic stress (for
, the distribution of external stress plays a role, the slope of the interface is not −0.1, although the solid surface tension dominates over the elastic stress (for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≤ 10). It is important to point out that
≤ 10). It is important to point out that 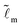 plays a role for the existence of a region where Neumann's relation is valid. When taking
plays a role for the existence of a region where Neumann's relation is valid. When taking 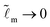 , there always exists a region close enough to
, there always exists a region close enough to ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0 where the Neumann's relation is valid for any
= 0 where the Neumann's relation is valid for any ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) values. For example, in the inset of Fig. 4(d), we plot
values. For example, in the inset of Fig. 4(d), we plot 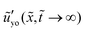 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for both
for both 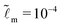 and
and 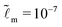 , and a fixed value of
, and a fixed value of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103. We find that when approaching the contact line (
= 103. We find that when approaching the contact line (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) from a large distance, the curves of
= 0) from a large distance, the curves of 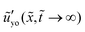 for
for 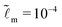 and
and 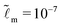 overlap until
overlap until ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−4 where
≈ 3 × 10−4 where 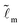 starts to play a role. In the case of
starts to play a role. In the case of 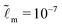 , the magnitude of the interfacial slope keeps increasing until
, the magnitude of the interfacial slope keeps increasing until ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−7 for which
≈ 3 × 10−7 for which 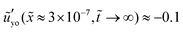 and a constant-slope region is observed around
and a constant-slope region is observed around ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−7. In reality, the thickness of the interface (i.e.
≈ 3 × 10−7. In reality, the thickness of the interface (i.e. ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m) is in the nanometric scales, that means when
m) is in the nanometric scales, that means when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) is larger than a certain value, Neumann's relation cannot be observed at any distance from the contact line. Instead, the solid interface maintains as a flat surface as we have shown in Fig. 4(b) and (c).
is larger than a certain value, Neumann's relation cannot be observed at any distance from the contact line. Instead, the solid interface maintains as a flat surface as we have shown in Fig. 4(b) and (c).
How does the size of the constant-slope region depend on ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ? To address this issue, we introduce the boundary of the constant-slope region as follows. We define
? To address this issue, we introduce the boundary of the constant-slope region as follows. We define ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ as the largest value of |
γ as the largest value of |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | such that
| such that 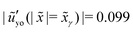 . Thus when
. Thus when 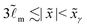 , we have
, we have 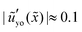 , which defines the range of the constant-slope region. Since the constant-slope-region disappears for large
, which defines the range of the constant-slope region. Since the constant-slope-region disappears for large ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) when
when 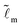 is not small enough, we here use
is not small enough, we here use 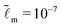 in our computations. In Fig. 4(d), we plot
in our computations. In Fig. 4(d), we plot ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ as a function of
γ as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . As we have demonstrated already in Fig. 4(c), we find that
. As we have demonstrated already in Fig. 4(c), we find that ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ increases with decreasing
γ increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Similar to the scaling of the ridge height, when
. Similar to the scaling of the ridge height, when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≫ 1, the size of the constant-slope region
≫ 1, the size of the constant-slope region ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ ∼
γ ∼ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) −1, which implies that the dimensional quantity xγ scales linearly with the elastocapillary length γs/G and is independent of the soft layer thickness. When
−1, which implies that the dimensional quantity xγ scales linearly with the elastocapillary length γs/G and is independent of the soft layer thickness. When ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≲ 1, we see that
≲ 1, we see that ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ scales as
γ scales as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) β locally with −1 < β < 0. Hence the dimensional size xγ increases with decreasing G and increasing H. We end this section with an example to estimate the dimensional size of the constant-slope region. Taking the shear modulus G = 1 kPa, the thickness of the soft layer H = 10 μm, the solid surface tension γs = 0.01 N m−1 and γ = 0.002 N m−1, we get
β locally with −1 < β < 0. Hence the dimensional size xγ increases with decreasing G and increasing H. We end this section with an example to estimate the dimensional size of the constant-slope region. Taking the shear modulus G = 1 kPa, the thickness of the soft layer H = 10 μm, the solid surface tension γs = 0.01 N m−1 and γ = 0.002 N m−1, we get ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 1. From Fig. 4(d), we obtain
= 1. From Fig. 4(d), we obtain ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ ≈ 10−3, i.e., xγ ≈ 10 nm. No constant-slope-region can be observed when xγ ≲ 3
γ ≈ 10−3, i.e., xγ ≈ 10 nm. No constant-slope-region can be observed when xγ ≲ 3![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m.
m.
3.2.2 Dynamic response at the tip region during the growth.
We first look at the growth case. We take ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. In Fig. 5(a), the interfacial slope
1 = 102. In Fig. 5(a), the interfacial slope 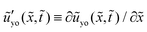 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) is plotted for different times. At
(in log scale) is plotted for different times. At ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+, the solid responds by an instantaneous elastic deformation. As time goes on, we observe that there is a region around the tip where the interfacial slope is independent of the time after. The size of this region grows with time. For example, this region has a range 0 <
= 0+, the solid responds by an instantaneous elastic deformation. As time goes on, we observe that there is a region around the tip where the interfacial slope is independent of the time after. The size of this region grows with time. For example, this region has a range 0 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≲ 10−4 at
≲ 10−4 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ and 0 <
= 0+ and 0 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≲ 10−3 at
≲ 10−3 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0.02. To understand this result, we note that the shear modulus relaxes from
= 0.02. To understand this result, we note that the shear modulus relaxes from ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) +
+ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 to
1 to ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for our viscoelastic model. We have also shown in Fig. 4(c) and (d) that there exists a surface-tension-dominated region with a size increasing with decreasing
for our viscoelastic model. We have also shown in Fig. 4(c) and (d) that there exists a surface-tension-dominated region with a size increasing with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Hence, once a solid element relaxes to within the surface-tension-dominated region, the solid element is in an equilibrium state. The time taken to relax to an equilibrium state thus depends on the distance from the center. The solid relaxes to an equilibrium state in a shorter time for materials closer to the center as we have shown in Fig. 5(a). In contrast, for stiffer solid materials for which no surface-tension-dominated region exists, all the solid elements relax in the same time scale η/G as shown in one example in Fig. 5(b) in which
. Hence, once a solid element relaxes to within the surface-tension-dominated region, the solid element is in an equilibrium state. The time taken to relax to an equilibrium state thus depends on the distance from the center. The solid relaxes to an equilibrium state in a shorter time for materials closer to the center as we have shown in Fig. 5(a). In contrast, for stiffer solid materials for which no surface-tension-dominated region exists, all the solid elements relax in the same time scale η/G as shown in one example in Fig. 5(b) in which ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103 and
= 103 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 104.
1 = 104.
 |
| | Fig. 5 The slope of solid interface 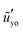 vs. vs. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for different rescaled times for different rescaled times ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) during the growth of the ridge for during the growth of the ridge for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1, = 10−1, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102 in (a) and for 1 = 102 in (a) and for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103, = 103, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 104 in (b). Other parameters: 1 = 104 in (b). Other parameters: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and = 50 and 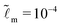 . (c and d) The slope . (c and d) The slope 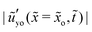 as a function of the rescaled time as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) / /![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Here . Here ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2. Other parameters: o = 10−2. Other parameters: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102 for (c) and 1 = 102 for (c) and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2 for (d). (e) The slope = 10−2 for (d). (e) The slope 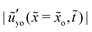 rescaled by rescaled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2 as a function of the rescaled time /2 as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) / /![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for different for different ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . Inset: The slope . Inset: The slope 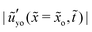 vs. vs. ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) / /![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for different for different ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . Other parameters: . Other parameters: ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and = 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. 1 = 102. | |
How does the relaxation at the tip region depend on material parameters? To address this question, we pick a position ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and study how the solid interface slope at this position varies with time for different values of
o = 10−2 and study how the solid interface slope at this position varies with time for different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ,
, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 and
1 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . We find that the slope relaxation is independent of
. We find that the slope relaxation is independent of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) when plotting
when plotting 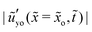 as a function of the rescaled time
as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) as shown in Fig. 5(c). In other words, the relaxation at the tip region is much shorter than the long-term relaxation of the ridge. Note that
as shown in Fig. 5(c). In other words, the relaxation at the tip region is much shorter than the long-term relaxation of the ridge. Note that ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = tγs/ηH. On the other hand, the short-term shear modulus
= tγs/ηH. On the other hand, the short-term shear modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 does play a role as shown in Fig. 5(d). It is interesting to see how the surface tensions determine the tip relaxation. In Fig. 5(e), we plot
1 does play a role as shown in Fig. 5(d). It is interesting to see how the surface tensions determine the tip relaxation. In Fig. 5(e), we plot 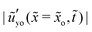 recalled by
recalled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2 as a function of
/2 as a function of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for different values of
for different values of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ; all curves collapse on each other. Hence we find that
; all curves collapse on each other. Hence we find that 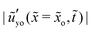 scales linearly with
scales linearly with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . From the results we have shown, the relaxation of the slope can be written as
. From the results we have shown, the relaxation of the slope can be written as 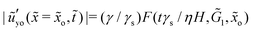 , with the functional form of F undetermined. The physical interpretation is as follows: the ratio γ/γs determines the equilibrium slope (solid angle). The relaxation time scale is determined by the solid surface tension γs and the short-term relaxation time of the viscoelastic material. The relaxation is characterized by a spreading velocity γs/η.
, with the functional form of F undetermined. The physical interpretation is as follows: the ratio γ/γs determines the equilibrium slope (solid angle). The relaxation time scale is determined by the solid surface tension γs and the short-term relaxation time of the viscoelastic material. The relaxation is characterized by a spreading velocity γs/η.
3.2.3 Dynamic response at the tip region during the decay.
Once the external force disappears, the sharp tip relaxes immediately. How does the tip region relax during the decay of the ridge? In Fig. 6(a), we show the slope 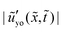 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) for different times during the decay. As there is an instantaneous elastic response at
(in log scale) for different times during the decay. As there is an instantaneous elastic response at 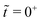 , the constant-slope-region may disappear as early as at
, the constant-slope-region may disappear as early as at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ as shown in Fig. 6(a) for which
= 0+ as shown in Fig. 6(a) for which ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. Since the static shape at the tip region is determined by the surface tensions (in the soft regime), one may expect the tip region relaxes differently from the rest part of the ridge during the decay, as we have observed for the growth case. To address this question, we pick two positions, i.e.
1 = 102. Since the static shape at the tip region is determined by the surface tensions (in the soft regime), one may expect the tip region relaxes differently from the rest part of the ridge during the decay, as we have observed for the growth case. To address this question, we pick two positions, i.e. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and
o = 10−2 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1, and study how the solid interface slope
o = 1, and study how the solid interface slope 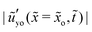 at these two positions varies with time for two different values of
at these two positions varies with time for two different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , namely
, namely ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2. Note that from Fig. 4(d),
= 10−2. Note that from Fig. 4(d), ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 ≲
o = 10−2 ≲ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ and
γ and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 ≫
o = 1 ≫ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ. In Fig. 6(b), we see that at
γ. In Fig. 6(b), we see that at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2, the evolution of the interfacial slope is the same for
o = 10−2, the evolution of the interfacial slope is the same for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2. However, at
= 10−2. However, at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1, the slope evolves differently as we can see in Fig. 6(c), and the time scale depends on η/G, which is much larger than the relaxation time at the tip region. On the other hand, the slope scales with
o = 1, the slope evolves differently as we can see in Fig. 6(c), and the time scale depends on η/G, which is much larger than the relaxation time at the tip region. On the other hand, the slope scales with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) for both
for both ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and
o = 10−2 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 as we have shown in Fig. 6(d) and (e), in which the y-axis is
o = 1 as we have shown in Fig. 6(d) and (e), in which the y-axis is 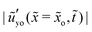 rescaled by
rescaled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2. This is because the out-of-plane displacement depends linearly with γ for the whole ridge, and hence the ratio γ/γs determines the interfacial slope.
/2. This is because the out-of-plane displacement depends linearly with γ for the whole ridge, and hence the ratio γ/γs determines the interfacial slope.
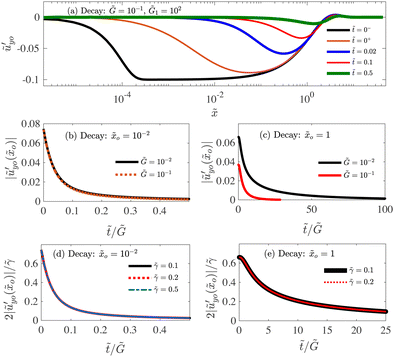 |
| | Fig. 6 (a) The slope of solid interface 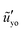 vs. vs. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for different rescaled times for different rescaled times ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) during the decay of the ridge for during the decay of the ridge for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and = 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. Other parameters: 1 = 102. Other parameters: ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2, = 0.2, ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and = 50 and 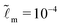 . (b and c) The magnitude of the slope . (b and c) The magnitude of the slope 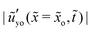 as a function of the rescaled time as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) / /![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Here . Here ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 in (b) and o = 10−2 in (b) and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 in (c). Other parameters: o = 1 in (c). Other parameters: ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102 and 1 = 102 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2. (d and e) The slope = 0.2. (d and e) The slope 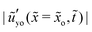 rescaled by rescaled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2 as a function of the rescaled time /2 as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) / /![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for different for different ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . Here . Here ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 in (d) and o = 10−2 in (d) and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 in (e). Other parameters: o = 1 in (e). Other parameters: ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2 and = 10−2 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. 1 = 102. | |
4 Discussion and conclusions
In summary, we study the dynamic response of an incompressible viscoelastic solid being acted upon by a localized surface force. The responses of the global features of the wetting ridge, e.g., the growth and the decay of the ridge height, depend on the rheological properties of the solid material. For the standard solid model we implement in this study, the ridge height relaxes exponentially at late time with a time scale given by η/G. Some other studies use the Chasset-Thirion model to describe the viscoelastic behavior of silicone gels;6 the relaxation of the ridge is found to follow a power law with time. The dynamic around the tip, on the other hand, is different from the remaining part of the soft solid during both the growth and the decay. For the growth, the equilibrium state of a solid element is achieved when it is within the surface-tension-dominated region, which has a size increasing with time due to viscoelastic properties of the solid. Hence an equilibrium can be achieved within a time scale much shorter than the relaxation time of the shear modulus of the viscoelastic material (η/G). Similarly for the decay, the tip region relaxes with time scales that depend significantly on the solid surface tension, namely the relaxation has a characteristic spreading velocity γs/η. Although the results presented in this study are obtained using the standard solid model, the existence of the surface-tension-dominated region at the ridge tip is expected to be universal. Hence the features of the dynamics at the tip region shown in this study can be compared with experimental measurements given that the viscoelastic properties of the solid material are determined.
How does the dynamic response of a soft solid play a role when a droplet is in motion? Current models4,6,47 assume dissipation being dominated by the viscoelastic effects in the soft solid and neglect flow in the fluids, and consider a constant contact line velocity. On the other hand, experimental studies observe the stick-slip motion of the contact line.7 The interplay between the fluid flow and the time-dependent morphological changes of the wetting ridge is expected to be crucial for the dynamics of the contact line and the droplet motion, which remains a challenging topic to be explored. Our findings show the features of the local morphological changes at the ridge tip during both growth and relaxation, which provide an important fundamental knowledge for investigating a contact line moving over a soft surface.
Conflicts of interest
There are no conflicts to declare.
Appendix A1. Derivation of the boundary integral equation in time domain for linear viscoelastic models (plane strain cases)
We here decompose the stress σij(x,t) and the strain εij(x,t) tensors into the hydrostatic and deviatoric parts. Namely, we write| |
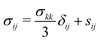 | (12) |
and| |
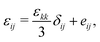 | (13) |
with the strain tensor defined as| |
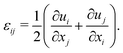 | (14) |
For isotropic linear viscoelastic materials, the constitutive relations can be written in the generalized differential forms which read
| |
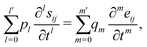 | (15) |
and
| |
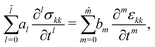 | (16) |
where
pl,
qm,
al and
bm are coefficients that depend on the specific viscoelastic model. Applying Laplace transform to the constitutive
relations (15) and (16), with Laplace transform of a function
f(
t) defined as
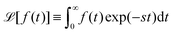
, the constitutive relation can be written as
44| |
Σij(x,s) = ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (s)Ekk(x,s)δij + 2Ĝ(s)Eij(x,s), (s)Ekk(x,s)δij + 2Ĝ(s)Eij(x,s), | (17) |
where
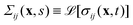
,
Ekk(
x,
s) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
[
εkk(
x,
t)] and
Eij(
x,
s) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
[
eij(
x,
t)]. The expressions in Laplace space of the bulk modulus
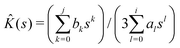
and the shear modulus
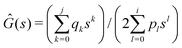
. In Appendix A2 we show how to obtain them for the standard solid (Zener) model.
Eqn (17) has the same form as the linear elastic constitutive relation. Hence by following the same approach of deriving the boundary integral equation for a purely linear elastic material in the quasi-static state (∂
σij/∂
xj = 0), we can obtain the boundary integral equations for linear viscoelastic models in the Laplace space. Here we consider plane strain cases, for which the boundary integral equation in Laplace space is given as
45| |
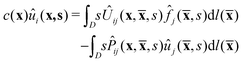 | (18) |
where
| |
 | (19) |
ûj(
x,s) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
[
uj(
x,
t)],
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) j
j(
x,
s) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
[
σij(
x,
t)
nj(
x)], with
n being the normal vector pointing outward the soft solid domain, and the line integrals on the right hand side are carried out along the closed contour
D of the boundary of the domain with d
l(
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
) denoting the differential length of
D and
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
=
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
+
ȳŷ being the position vector of a point on the contour. The functions
Ûij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
s) and
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij
ij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
s) are given by
45,46| |
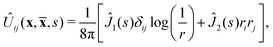 | (20) |
| |
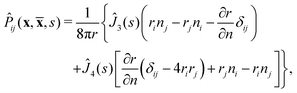 | (21) |
where
r = [(
x −
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
)
2 + (
y −
ȳ)
2]
1/2,
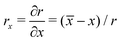
,
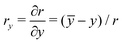
and
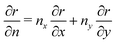
. The functions
Ĵ1(
s),
Ĵ2(
s),
Ĵ3(
s) and
Ĵ4(
s) are given as
| |
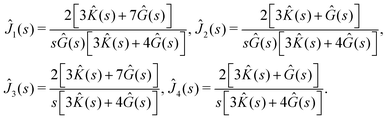 | (22) |
To obtain the boundary integral equation in the time domain,39,44–46 we perform an inverse Laplace transform ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1 to eqn (18) and obtain
−1 to eqn (18) and obtain
| |
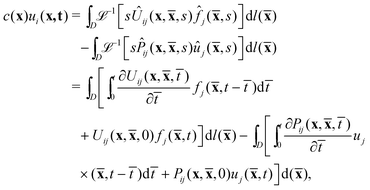 | (23) |
where
ûij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1
−1[
Ûij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
s)] and
Pij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif)
) ≡
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1
−1[
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij
ij(
x,
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif)
,
s)]. Here we have used the convolution and the derivative properties of the Laplace transform.
45,46
Appendix A2. The fundamental solutions in the time domain for the standard solid model
Here we show how to obtain the expressions of the fundamental solutions in the time domain, namely Uij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Pij(x,
) and Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). As shown in Appendix A1, the stress σij and the strain εij tensors are decomposed into the hydrostatic and deviatoric parts. For viscoelastic materials made of polymers such as elastomers and gels, the response to the hydrostatic pressure acts like purely elastic materials. We thus writefor the hydrostatic part.
). As shown in Appendix A1, the stress σij and the strain εij tensors are decomposed into the hydrostatic and deviatoric parts. For viscoelastic materials made of polymers such as elastomers and gels, the response to the hydrostatic pressure acts like purely elastic materials. We thus writefor the hydrostatic part.
We consider the standard solid (Zener) model which consists of a spring connected in parallel with a Maxwell element (a spring connected in series with a viscous damper). That means we can construct the following relations between the different components of stresses and strains. The superscript ‘Ma’ is used to represent the Maxwell element; ‘e2’ and ‘η’ are respectively for the elastic and the viscous component of the Maxwell element, and ‘e1’ for the elastic part that is connected in series with the Maxwell element. Hence for the deviatoric part we have
and
The Maxwell element gives the following relations as
| |
| eMaij = ee2ij + eηij. | (28) |
The constitutive relations for each component are given as
| |
| se1ij = 2Gee1ij, se2ij = 2G1ee2ij, sηij = 2ηėηij. | (29) |
Using the above relations we end up with the constitutive relation for the whole deviatoric part of the Zener model given as
| |
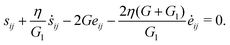 | (30) |
In terms of the generalized differential form of the constitutive relation in
eqn (15), we get for the Zener model
| |
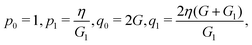 | (31) |
and the other coefficients of
pl and
qm being vanishing. Next, we impose the Laplace transform to the differential form of the constitutive relation
(30), we end up with the constitutive relation in Laplace space given as
| |
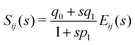 | (32) |
where
| |
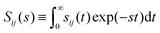 | (33) |
and
| |
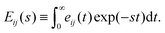 | (34) |
Including the hydrostatic part, we have the full constitutive relation in the Laplace space
| |
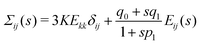 | (35) |
where
| |
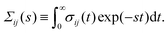 | (36) |
Hence we can define the bulk modulus and the shear modulus in Laplace space as
| |
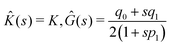 | (37) |
To obtain the fundamental solutions Uij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) ≡
,t) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[Ûij(x,
−1[Ûij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)] and Pij(x,
,s)] and Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) ≡
,t) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[
−1[![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij(x,
ij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)], what we need to do is to perform the inverse Laplace transform of Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) using the expressions of
,s)], what we need to do is to perform the inverse Laplace transform of Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) using the expressions of ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (s) and Ĝ(s) in (37), we then obtain
(s) and Ĝ(s) in (37), we then obtain
| |
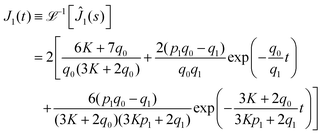 | (38) |
| |
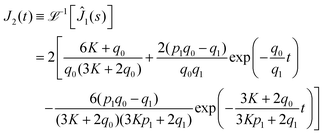 | (39) |
| |
 | (40) |
| |
 | (41) |
At
t = 0, the functions are given as
| |
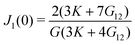 | (42) |
| |
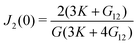 | (43) |
| |
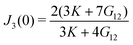 | (44) |
| |
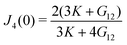 | (45) |
where
G12 ≡
G +
G1.
When t → ∞, we have
| |
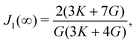 | (46) |
| |
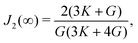 | (47) |
| |
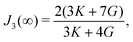 | (48) |
| |
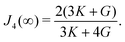 | (49) |
Acknowledgements
TSC gratefully acknowledges financial support from the Research Council of Norway (Project No. 315110). TSC thanks Christian Pedersen for the fruitful discussions and the referees of the paper for the inspiring comments to help to improve the manuscript.
References
- S. J. Park, B. M. Weon, J. S. Lee, J. Lee, J. Kim and J. H. Je, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
- R. W. Style and E. R. Dufresne, Soft Matter, 2012, 8, 7177–7184 RSC.
- A. Carré, J.-C. Gastel and M. E. R. Shanahan, Nature, 1996, 379, 432–434 CrossRef.
- T. Kajiya, A. Daerr, T. Narita, L. Royon, F. Lequeux and L. Limat, Soft Matter, 2013, 9, 454–461 RSC.
- S. Karpitschka, S. Das, M. Van Gorcum, H. Perrin, B. Andreotti and J. H. Snoeijer, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- M. Van Gorcum, B. Andreotti, J. H. Snoeijer and S. Karpitschka, Phys. Rev. Lett., 2018, 121, 208003 CrossRef CAS.
- S. I. Tamim and J. B. Bostwick, Phys. Rev. E, 2021, 104, 1–10 CrossRef PubMed.
- R. W. Style, R. Boltyanskiy, Y. Che, J. S. Wettlaufer, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2013, 110, 1–5 CrossRef PubMed.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 046601 CrossRef PubMed.
- B. Corominas-Murtra and N. I. Petridou, Front. Phys., 2021, 9, 1–17 Search PubMed.
- X. Shi, Z. Liu, L. Feng, T. Zhao, C.-Y. Hui and S. Zhang, Phys. Rev. X, 2022, 12, 021053 CAS.
- R. Pericet-Cámara, A. Best, H. J. Butt and E. Bonaccurso, Langmuir, 2008, 24, 10565–10568 CrossRef.
- Y. S. Yu, Appl. Math. Mech. (Engl. Ed.), 2012, 33, 1095–1114 CrossRef.
- R. W. Style, A. Jagota, C. Y. Hui and E. R. Dufresne, Annu. Rev. Condens. Matter Phys., 2017, 8, 99–118 CrossRef CAS.
- J. C. Fernandez-Toledano, T. D. Blake, P. Lambert and J. De Coninck, Adv. Colloid Interface Sci., 2017, 245, 102–107 CrossRef CAS PubMed.
- G. R. Lester, J. Colloid Sci., 1961, 16, 315–326 CrossRef CAS.
- A. I. Rusanov, Colloid J. USSR, 1975, 37(4), 614–622 Search PubMed.
- Y. S. Yu and Y. P. Zhao, J. Colloid Interface Sci., 2009, 339, 489–494 CrossRef CAS PubMed.
- R. Pericet-Camara, G. K. Auernhammer, K. Koynov, S. Lorenzoni, R. Raiteri and E. Bonaccurso, Soft Matter, 2009, 5, 3611–3617 RSC.
- E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 1–4 CrossRef PubMed.
- L. Limat, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–13 CrossRef PubMed.
- J. Bico, É. Reyssat and B. Roman, Annu. Rev. Fluid Mech., 2018, 50, 629–659 CrossRef.
- R. W. Style and Q. Xu, Soft Matter, 2018, 14, 4569–4576 RSC.
- A. Marchand, S. Das, J. H. Snoeijer and B. Andreotti, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef.
- A. Pandey, B. Andreotti, S. Karpitschka, G. J. Van Zwieten, E. H. Van Brummelen and J. H. Snoeijer, Phys. Rev. X, 2020, 10, 31067 CAS.
- C. Y. Hui and A. Jagota, Proc. R. Soc. A, 2014, 470, 20140085 CrossRef.
- L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, J. Fluid Mech., 2014, 747, R1 CrossRef CAS.
- J. Dervaux and L. Limat, Proc. R. Soc. A, 2015, 471, 20140813 CrossRef.
- Z. Cao and A. V. Dobrynin, Macromolecules, 2015, 48, 443–451 CrossRef CAS.
- C. Y. Hui and A. Jagota, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 274–280 CrossRef CAS.
- D. Guan, E. Charlaix and P. Tong, Phys. Rev. Lett., 2020, 124, 188003 CrossRef CAS PubMed.
- G. Pu and S. J. Severtson, Langmuir, 2012, 28, 10007–10014 CrossRef CAS PubMed.
- M. C. Lopes and E. Bonaccurso, Soft Matter, 2012, 8, 7875–7881 RSC.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS.
-
C. Pozrikidis, Boundary Integral and singularity methods for linearized flow, Cambridge University Press, Cambridge, 1992 Search PubMed.
- J. D. McGraw, T. S. Chan, S. Maurer, T. Salez, M. Benzaquen, E. Raphaël, M. Brinkmann and K. Jacobs, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1168 CrossRef CAS PubMed.
- T. S. Chan, J. D. McGraw, T. Salez, R. Seemann and M. Brinkmann, J. Fluid Mech., 2017, 828, 271–288 CrossRef CAS.
- X. Y. Zhu, W. Q. Chen, Z. Y. Huang and Y. J. Liu, Eng. Anal. Bound Elem., 2011, 35, 170–178 CrossRef.
- C. G. Panagiotopoulos, V. Mantič and T. Roubíček, Int. J. Solids Struct., 2014, 51, 2261–2271 CrossRef.
- R. Shuttleworth, Proc. Phys. Soc. Sect. A, 1950, 63, 444 CrossRef.
- B. Andreotti and J. H. Snoeijer, EPL, 2016, 113, 66001 CrossRef.
- R. Masurel, M. Roché, L. Limat, I. Ionescu and J. Dervaux, Phys. Rev. Lett., 2019, 122, 1–6 CrossRef.
- M. Schanz and L. Gaul, Appl. Mech. Rev., 1993, 46, S41–S46 CrossRef.
- S. S. Lee, Y. S. Sohn and S. H. Park, Eng. Anal. Bound Elem., 1994, 13, 211–217 CrossRef.
- S. Syngellakis, Eng. Anal. Bound Elem., 2003, 27, 125–135 CrossRef.
- J. Dervaux, M. Roché and L. Limat, Soft Matter, 2020, 16, 5157–5176 RSC.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,16 here γ is the liquid–air surface tension and θ is the liquid equilibrium contact angle. A length scale named the elastocapillary length γ/G can be constructed, with the shear modulus G serving as a resistance to deformation.15 Earlier computations of the equilibrium shape of the wetting ridge date back to the studies by Lester17 and Rusanov,18 in which a droplet is in contact with a soft semi-infinitely thick substrate. Later, more investigations were done for a soft solid layer of finite thickness H attached to a rigid substrate.19,20 All these studies point to a conclusion that both length scales γ/G and H play a crucial role in solid deformation.
θ,16 here γ is the liquid–air surface tension and θ is the liquid equilibrium contact angle. A length scale named the elastocapillary length γ/G can be constructed, with the shear modulus G serving as a resistance to deformation.15 Earlier computations of the equilibrium shape of the wetting ridge date back to the studies by Lester17 and Rusanov,18 in which a droplet is in contact with a soft semi-infinitely thick substrate. Later, more investigations were done for a soft solid layer of finite thickness H attached to a rigid substrate.19,20 All these studies point to a conclusion that both length scales γ/G and H play a crucial role in solid deformation.![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + yŷ + zẑ of the undeformed viscoelastic solid and time t as u(x,t) = ux(x,t)
+ yŷ + zẑ of the undeformed viscoelastic solid and time t as u(x,t) = ux(x,t)![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + uy(x,t)ŷ + uz(x,t)ẑ. In index notations, we write the component as ui where i = x, y or z. In the following, the subscripts i, j and k take either one of the components in rectangular coordinates. The repeated indices conform to the Einstein summation convention, i.e., they are summed over the three components. For viscoelastic materials made of polymers such as elastomers and gels, we assume that the bulk modulus K can be considered as a constant, independent of time. We further assume that the strain is small, namely the strain tensor εij(x,t) = (∂ui/∂xj + ∂uj/∂xi)/2 ≪ 1. Hence, the stress tensor σij(x,t) and the strain tensor follow the linear constitutive relation given as
+ uy(x,t)ŷ + uz(x,t)ẑ. In index notations, we write the component as ui where i = x, y or z. In the following, the subscripts i, j and k take either one of the components in rectangular coordinates. The repeated indices conform to the Einstein summation convention, i.e., they are summed over the three components. For viscoelastic materials made of polymers such as elastomers and gels, we assume that the bulk modulus K can be considered as a constant, independent of time. We further assume that the strain is small, namely the strain tensor εij(x,t) = (∂ui/∂xj + ∂uj/∂xi)/2 ≪ 1. Hence, the stress tensor σij(x,t) and the strain tensor follow the linear constitutive relation given as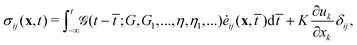
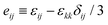 , ėij ≡ ∂eij/∂
, ėij ≡ ∂eij/∂![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) and
and ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is the shear relaxation function which depends on the viscoelastic model characterized by the parameters G, G1,… and η, η1,…. We assume the dynamics of the solid deformation is slow enough so that the net force on a soft solid element vanishes which gives the governing equation
is the shear relaxation function which depends on the viscoelastic model characterized by the parameters G, G1,… and η, η1,…. We assume the dynamics of the solid deformation is slow enough so that the net force on a soft solid element vanishes which gives the governing equation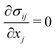
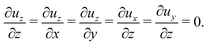
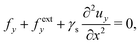
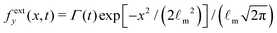 , where
, where ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is the microscopic length such that
m is the microscopic length such that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m ≪ H. In the limit that
m ≪ H. In the limit that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m → 0, the traction fexty(x,t) = Γ(t)δ(x), where δ(x) is the Dirac delta function, which is also used in some other studies.6 The strength of the external force Γ(t) is a function of time. In this study, we will use two different functional forms, respectively, to investigate the growth and the decay of the ridge, namely case 1: Γ(t) = γ
m → 0, the traction fexty(x,t) = Γ(t)δ(x), where δ(x) is the Dirac delta function, which is also used in some other studies.6 The strength of the external force Γ(t) is a function of time. In this study, we will use two different functional forms, respectively, to investigate the growth and the decay of the ridge, namely case 1: Γ(t) = γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t) and case 2: Γ(t) = γ[1 −
(t) and case 2: Γ(t) = γ[1 − ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t)] = γ − γ
(t)] = γ − γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t). Here
(t). Here ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t) is the Heaviside step function. As the governing equations are linear, the solution for case 2 (decay case) will be obtained by combining the steady solution (at t → ∞) of case 1 and the solution obtained when using Γ(t) = −γ
(t) is the Heaviside step function. As the governing equations are linear, the solution for case 2 (decay case) will be obtained by combining the steady solution (at t → ∞) of case 1 and the solution obtained when using Γ(t) = −γ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (t).
(t).![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) and
and 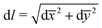 as the differential length on the contour. The governing eqn (1)–(3) are formulated as boundary integral equations (see the Appendix for the details of derivation) which read
as the differential length on the contour. The governing eqn (1)–(3) are formulated as boundary integral equations (see the Appendix for the details of derivation) which read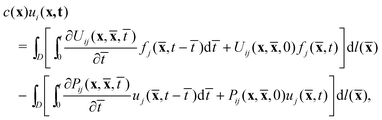

![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) and Uij(x,
,t) and Uij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) depends on the specific viscoelastic model as for the shear relaxation function
,t) depends on the specific viscoelastic model as for the shear relaxation function ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) . In the Appendix, we derive the expressions for the standard solid (Zener) model. We note that Pij and Uij are singular at x =
. In the Appendix, we derive the expressions for the standard solid (Zener) model. We note that Pij and Uij are singular at x = ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ; the integral over the singular point is thus computed analytically by expanding the tensor components in series around x =
; the integral over the singular point is thus computed analytically by expanding the tensor components in series around x = ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) .
.![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) ij(x,
ij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) = ∂Uij(x,
,t) = ∂Uij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t)/∂t, Ṗij(x,
,t)/∂t, Ṗij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) = ∂Pij(x,
,t) = ∂Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t)/∂t and Si(x) is the term corresponding to the history of responses, which can be written as
,t)/∂t and Si(x) is the term corresponding to the history of responses, which can be written as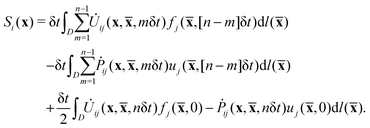
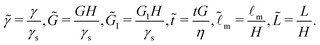
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m is much smaller than the thickness of the soft layer. We take
m is much smaller than the thickness of the soft layer. We take ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) = 50 and
= 50 and 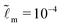 (e.g. consider a liquid/air interface of nanometric thickness and a 10 micron thick soft solid layer). We present the results in three main parts. In Section 3.1, we focus on the evolution of the global features of the ridge. In Section 3.2.1, we discuss at how the static solid interface profile depends on the parameters. In Sections 3.2.2 and 3.2.3, the role of the solid surface tension and the relaxation at the tip region is explored in detail.
(e.g. consider a liquid/air interface of nanometric thickness and a 10 micron thick soft solid layer). We present the results in three main parts. In Section 3.1, we focus on the evolution of the global features of the ridge. In Section 3.2.1, we discuss at how the static solid interface profile depends on the parameters. In Sections 3.2.2 and 3.2.3, the role of the solid surface tension and the relaxation at the tip region is explored in detail.
 and how the ridge decays when
and how the ridge decays when  , with
, with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) = 0.2. As our viscoelastic model is linear, which assumes small solid interfacial slopes (small strains), we thus pick the value of
= 0.2. As our viscoelastic model is linear, which assumes small solid interfacial slopes (small strains), we thus pick the value of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) to be significantly smaller than 1. Note that the solid interfacial slope around the contact line increases with
to be significantly smaller than 1. Note that the solid interfacial slope around the contact line increases with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) based on the Neumann's relation. The time series of
based on the Neumann's relation. The time series of 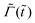 is plotted in Fig. 2(a) and (b). We take
is plotted in Fig. 2(a) and (b). We take ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. Fig. 2(c) and (d) show the out-of-plane displacement ũyo ≡ ũy(
1 = 102. Fig. 2(c) and (d) show the out-of-plane displacement ũyo ≡ ũy(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ = 0,
,ỹ = 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at different times. Fig. 2(e) and (f) show the corresponding in-plane displacement ũxo ≡ ũx(
) at different times. Fig. 2(e) and (f) show the corresponding in-plane displacement ũxo ≡ ũx(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,ỹ = 0,
,ỹ = 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ). At
). At ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+, there is an instantaneous elastic deformation with shear modulus equal to
= 0+, there is an instantaneous elastic deformation with shear modulus equal to ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) +
+ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1. As
1. As ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 is large, the initial solid surface deflection is tiny. The ridge shape, described by ũyo, is symmetric along the central axis (
1 is large, the initial solid surface deflection is tiny. The ridge shape, described by ũyo, is symmetric along the central axis (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) while the in-plane displacement ũxo is anti-symmetric. A significant difference between the growth and the decay of the ridge is that, during the growth, a sharp tip (around
= 0) while the in-plane displacement ũxo is anti-symmetric. A significant difference between the growth and the decay of the ridge is that, during the growth, a sharp tip (around ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) is maintained from the early stage of the growth. For the decay, when the localized external stress vanishes (at
= 0) is maintained from the early stage of the growth. For the decay, when the localized external stress vanishes (at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0), the sharp tip quickly relaxes to round shapes with a much smaller curvature as can be seen in Fig. 2(d). Note that the profiles at
= 0), the sharp tip quickly relaxes to round shapes with a much smaller curvature as can be seen in Fig. 2(d). Note that the profiles at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0− in Fig. 2(d) and (f) are the steady profiles before the external stress vanishes.
= 0− in Fig. 2(d) and (f) are the steady profiles before the external stress vanishes.
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0,
= 0,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) of the solid surface or called the ridge height is at the center
) of the solid surface or called the ridge height is at the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0. Second, the out-of-plane displacement decreases from the center and a minimum value ũy,min ≡ ũyo(
= 0. Second, the out-of-plane displacement decreases from the center and a minimum value ũy,min ≡ ũyo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min,
min,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) is achieved at
) is achieved at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min (and
min (and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = −
= −![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min), where a clear dimple is formed with a negative out-of-plane displacement. Third, for the in-plane displacement ũxo, we see from Fig. 2(e) and (f) that around the center
min), where a clear dimple is formed with a negative out-of-plane displacement. Third, for the in-plane displacement ũxo, we see from Fig. 2(e) and (f) that around the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0, the solid material is compressed (with a negative slope shown in the plot, i.e., ∂ũxo/∂
= 0, the solid material is compressed (with a negative slope shown in the plot, i.e., ∂ũxo/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) < 0, and there is a maximum ũx,max ≡ ũxo(
< 0, and there is a maximum ũx,max ≡ ũxo(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max,
max,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at the negative side of
) at the negative side of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) . These characteristic quantities are also indicated in the schematic of the setup in Fig. 1.
. These characteristic quantities are also indicated in the schematic of the setup in Fig. 1.
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , respectively, during the growth and the decay of the ridge. All these quantities increase/decrease monotonically with time and saturate to a steady value during the growth/decay of the ridge. Next, we look at the time series of the magnitudes of the positions |
, respectively, during the growth and the decay of the ridge. All these quantities increase/decrease monotonically with time and saturate to a steady value during the growth/decay of the ridge. Next, we look at the time series of the magnitudes of the positions |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min| and |
min| and |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max| as plotted in Fig. 3(c) and (d). Both |
max| as plotted in Fig. 3(c) and (d). Both |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) min| and |
min| and |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) max| equal to unity at
max| equal to unity at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ (instantaneous elastic response). This means that for a large
= 0+ (instantaneous elastic response). This means that for a large ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1, these two positions are equal to the thickness of the soft substrate. They increase with time during the growth. However, during the decay of the ridge, instead of decreasing, the positions still increase with time. This feature can also be observed from the profiles shown in Fig. 2(d) and (f).
1, these two positions are equal to the thickness of the soft substrate. They increase with time during the growth. However, during the decay of the ridge, instead of decreasing, the positions still increase with time. This feature can also be observed from the profiles shown in Fig. 2(d) and (f).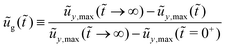 for the growth and
for the growth and 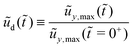 for the decay. In Fig. 3(e) and (f), the rescaled ridge heights are respectively plotted as a function of
for the decay. In Fig. 3(e) and (f), the rescaled ridge heights are respectively plotted as a function of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) for different values of
for different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . We find that both ũg(
. We find that both ũg(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) and ũd(
) and ũd(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) relax the same way, i.e., ũg(
) relax the same way, i.e., ũg(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) or ũd(
) or ũd(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ), scales as ∼exp(−1.15
), scales as ∼exp(−1.15![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) at late times. The late time ridge evolution possesses the same time scale as the relaxation of the viscoelastic material in our standard solid model, i.e., η/G.
) at late times. The late time ridge evolution possesses the same time scale as the relaxation of the viscoelastic material in our standard solid model, i.e., η/G.![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) is changed. Note that the static shape is the same as the shape at
is changed. Note that the static shape is the same as the shape at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞ in the growth case. From the scaling with
→ ∞ in the growth case. From the scaling with ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , we will also deduce the dependence on the shear modulus G and the soft layer thickness H, which are dimensional quantities of physical and practical importance. Before we focus on the tip region, let us first look at the ridge height ũy,max(
, we will also deduce the dependence on the shear modulus G and the soft layer thickness H, which are dimensional quantities of physical and practical importance. Before we focus on the tip region, let us first look at the ridge height ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞), which is plotted in Fig. 4(a) as a function of
→ ∞), which is plotted in Fig. 4(a) as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . As one might expect, the ridge height increases with decreasing
. As one might expect, the ridge height increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Moreover, when
. Moreover, when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≫ 1 or in other words, when the soft layer thickness is much larger than the elastocapillary length γs/G, we find that ũy,max(
≫ 1 or in other words, when the soft layer thickness is much larger than the elastocapillary length γs/G, we find that ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) ∼
→ ∞) ∼ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) −1. This scaling implies that the dimensional ridge height uy,max(
−1. This scaling implies that the dimensional ridge height uy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) scales linearly with the elastocapillary length and is independent of the soft layer thickness. The confinement (thickness) of the soft layer plays no role in this regime. When
→ ∞) scales linearly with the elastocapillary length and is independent of the soft layer thickness. The confinement (thickness) of the soft layer plays no role in this regime. When ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) becomes smaller (≲10), we see that ũy,max(
becomes smaller (≲10), we see that ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) scales as
→ ∞) scales as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) α locally with −1 < α < 0. Hence uy,max(
α locally with −1 < α < 0. Hence uy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) increases with decreasing G and increasing H.
→ ∞) increases with decreasing G and increasing H.
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ,
,![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) in the region of −0.01 <
→ ∞) in the region of −0.01 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) < 0.01, for a wide range of
< 0.01, for a wide range of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2–104. Note that the profiles are shifted by the ridge height ũy,max(
= 10−2–104. Note that the profiles are shifted by the ridge height ũy,max(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) → ∞) so that all the tips are at the same position. For
→ ∞) so that all the tips are at the same position. For ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≤ 10, we see the solid interfaces form the same solid angle θs = 168.6°. The solid angle can be understood by the force balance between the solid surface tensions and the external liquid–air surface tension, namely γ = 2γs
≤ 10, we see the solid interfaces form the same solid angle θs = 168.6°. The solid angle can be understood by the force balance between the solid surface tensions and the external liquid–air surface tension, namely γ = 2γs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θs/2). For
cos(θs/2). For ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) > 10, the interface profiles have a solid angle getting closer to 180° as
> 10, the interface profiles have a solid angle getting closer to 180° as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) increases. This shows how the solid deformation at the tip region varies from a soft regime to a stiff regime which are consistent with Neumann's relation and Young's relation, respectively, in the two different limits.
increases. This shows how the solid deformation at the tip region varies from a soft regime to a stiff regime which are consistent with Neumann's relation and Young's relation, respectively, in the two different limits.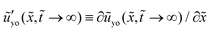 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) in Fig. 4(c). For the stiffer case we have computed here, e.g.
(in log scale) in Fig. 4(c). For the stiffer case we have computed here, e.g. ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 104, the magnitude of the slope is small. The whole solid interface maintains close to a flat surface even though being exerted by a localized external force. As
= 104, the magnitude of the slope is small. The whole solid interface maintains close to a flat surface even though being exerted by a localized external force. As ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) decreases, the magnitude of the slope increases. There appear overlapping regions of the curves for different
decreases, the magnitude of the slope increases. There appear overlapping regions of the curves for different ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) values. The size of the overlapping region increases with decreasing
values. The size of the overlapping region increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . The overlapping of the curves means that the solid deformation in that region is independent of
. The overlapping of the curves means that the solid deformation in that region is independent of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , and hence the solid surface tension dominates over the elastic stress. Moreover, we also see that there is a region of a constant slope −0.1 for
, and hence the solid surface tension dominates over the elastic stress. Moreover, we also see that there is a region of a constant slope −0.1 for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) < 10. Note that the slope −0.1 means that the solid angle θs = 168.6°. Indeed the constant-slope region is what we have plotted in Fig. 4(b). At distances from the center
< 10. Note that the slope −0.1 means that the solid angle θs = 168.6°. Indeed the constant-slope region is what we have plotted in Fig. 4(b). At distances from the center ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) smaller than
smaller than 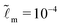 , the distribution of external stress plays a role, the slope of the interface is not −0.1, although the solid surface tension dominates over the elastic stress (for
, the distribution of external stress plays a role, the slope of the interface is not −0.1, although the solid surface tension dominates over the elastic stress (for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≤ 10). It is important to point out that
≤ 10). It is important to point out that 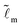 plays a role for the existence of a region where Neumann's relation is valid. When taking
plays a role for the existence of a region where Neumann's relation is valid. When taking  , there always exists a region close enough to
, there always exists a region close enough to ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0 where the Neumann's relation is valid for any
= 0 where the Neumann's relation is valid for any ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) values. For example, in the inset of Fig. 4(d), we plot
values. For example, in the inset of Fig. 4(d), we plot 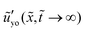 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) for both
for both 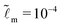 and
and 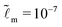 , and a fixed value of
, and a fixed value of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103. We find that when approaching the contact line (
= 103. We find that when approaching the contact line (![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0) from a large distance, the curves of
= 0) from a large distance, the curves of 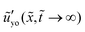 for
for 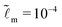 and
and 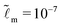 overlap until
overlap until ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−4 where
≈ 3 × 10−4 where 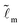 starts to play a role. In the case of
starts to play a role. In the case of 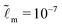 , the magnitude of the interfacial slope keeps increasing until
, the magnitude of the interfacial slope keeps increasing until ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−7 for which
≈ 3 × 10−7 for which 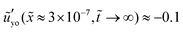 and a constant-slope region is observed around
and a constant-slope region is observed around ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≈ 3 × 10−7. In reality, the thickness of the interface (i.e.
≈ 3 × 10−7. In reality, the thickness of the interface (i.e. ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m) is in the nanometric scales, that means when
m) is in the nanometric scales, that means when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) is larger than a certain value, Neumann's relation cannot be observed at any distance from the contact line. Instead, the solid interface maintains as a flat surface as we have shown in Fig. 4(b) and (c).
is larger than a certain value, Neumann's relation cannot be observed at any distance from the contact line. Instead, the solid interface maintains as a flat surface as we have shown in Fig. 4(b) and (c).![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ? To address this issue, we introduce the boundary of the constant-slope region as follows. We define
? To address this issue, we introduce the boundary of the constant-slope region as follows. We define ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ as the largest value of |
γ as the largest value of |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | such that
| such that 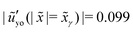 . Thus when
. Thus when 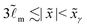 , we have
, we have 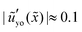 , which defines the range of the constant-slope region. Since the constant-slope-region disappears for large
, which defines the range of the constant-slope region. Since the constant-slope-region disappears for large ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) when
when  is not small enough, we here use
is not small enough, we here use  in our computations. In Fig. 4(d), we plot
in our computations. In Fig. 4(d), we plot ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ as a function of
γ as a function of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . As we have demonstrated already in Fig. 4(c), we find that
. As we have demonstrated already in Fig. 4(c), we find that ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ increases with decreasing
γ increases with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Similar to the scaling of the ridge height, when
. Similar to the scaling of the ridge height, when ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≫ 1, the size of the constant-slope region
≫ 1, the size of the constant-slope region ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ ∼
γ ∼ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) −1, which implies that the dimensional quantity xγ scales linearly with the elastocapillary length γs/G and is independent of the soft layer thickness. When
−1, which implies that the dimensional quantity xγ scales linearly with the elastocapillary length γs/G and is independent of the soft layer thickness. When ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ≲ 1, we see that
≲ 1, we see that ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ scales as
γ scales as ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) β locally with −1 < β < 0. Hence the dimensional size xγ increases with decreasing G and increasing H. We end this section with an example to estimate the dimensional size of the constant-slope region. Taking the shear modulus G = 1 kPa, the thickness of the soft layer H = 10 μm, the solid surface tension γs = 0.01 N m−1 and γ = 0.002 N m−1, we get
β locally with −1 < β < 0. Hence the dimensional size xγ increases with decreasing G and increasing H. We end this section with an example to estimate the dimensional size of the constant-slope region. Taking the shear modulus G = 1 kPa, the thickness of the soft layer H = 10 μm, the solid surface tension γs = 0.01 N m−1 and γ = 0.002 N m−1, we get ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 1. From Fig. 4(d), we obtain
= 1. From Fig. 4(d), we obtain ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ ≈ 10−3, i.e., xγ ≈ 10 nm. No constant-slope-region can be observed when xγ ≲ 3
γ ≈ 10−3, i.e., xγ ≈ 10 nm. No constant-slope-region can be observed when xγ ≲ 3![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m.
m.![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. In Fig. 5(a), the interfacial slope
1 = 102. In Fig. 5(a), the interfacial slope 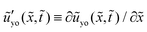 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) is plotted for different times. At
(in log scale) is plotted for different times. At ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+, the solid responds by an instantaneous elastic deformation. As time goes on, we observe that there is a region around the tip where the interfacial slope is independent of the time after. The size of this region grows with time. For example, this region has a range 0 <
= 0+, the solid responds by an instantaneous elastic deformation. As time goes on, we observe that there is a region around the tip where the interfacial slope is independent of the time after. The size of this region grows with time. For example, this region has a range 0 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≲ 10−4 at
≲ 10−4 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ and 0 <
= 0+ and 0 < ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≲ 10−3 at
≲ 10−3 at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0.02. To understand this result, we note that the shear modulus relaxes from
= 0.02. To understand this result, we note that the shear modulus relaxes from ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) +
+ ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 to
1 to ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for our viscoelastic model. We have also shown in Fig. 4(c) and (d) that there exists a surface-tension-dominated region with a size increasing with decreasing
for our viscoelastic model. We have also shown in Fig. 4(c) and (d) that there exists a surface-tension-dominated region with a size increasing with decreasing ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) . Hence, once a solid element relaxes to within the surface-tension-dominated region, the solid element is in an equilibrium state. The time taken to relax to an equilibrium state thus depends on the distance from the center. The solid relaxes to an equilibrium state in a shorter time for materials closer to the center as we have shown in Fig. 5(a). In contrast, for stiffer solid materials for which no surface-tension-dominated region exists, all the solid elements relax in the same time scale η/G as shown in one example in Fig. 5(b) in which
. Hence, once a solid element relaxes to within the surface-tension-dominated region, the solid element is in an equilibrium state. The time taken to relax to an equilibrium state thus depends on the distance from the center. The solid relaxes to an equilibrium state in a shorter time for materials closer to the center as we have shown in Fig. 5(a). In contrast, for stiffer solid materials for which no surface-tension-dominated region exists, all the solid elements relax in the same time scale η/G as shown in one example in Fig. 5(b) in which ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 103 and
= 103 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 104.
1 = 104.
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and study how the solid interface slope at this position varies with time for different values of
o = 10−2 and study how the solid interface slope at this position varies with time for different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ,
, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 and
1 and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . We find that the slope relaxation is independent of
. We find that the slope relaxation is independent of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) when plotting
when plotting 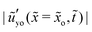 as a function of the rescaled time
as a function of the rescaled time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) as shown in Fig. 5(c). In other words, the relaxation at the tip region is much shorter than the long-term relaxation of the ridge. Note that
as shown in Fig. 5(c). In other words, the relaxation at the tip region is much shorter than the long-term relaxation of the ridge. Note that ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = tγs/ηH. On the other hand, the short-term shear modulus
= tγs/ηH. On the other hand, the short-term shear modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 does play a role as shown in Fig. 5(d). It is interesting to see how the surface tensions determine the tip relaxation. In Fig. 5(e), we plot
1 does play a role as shown in Fig. 5(d). It is interesting to see how the surface tensions determine the tip relaxation. In Fig. 5(e), we plot 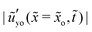 recalled by
recalled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2 as a function of
/2 as a function of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) /
/![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) for different values of
for different values of ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ; all curves collapse on each other. Hence we find that
; all curves collapse on each other. Hence we find that 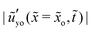 scales linearly with
scales linearly with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) . From the results we have shown, the relaxation of the slope can be written as
. From the results we have shown, the relaxation of the slope can be written as 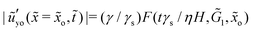 , with the functional form of F undetermined. The physical interpretation is as follows: the ratio γ/γs determines the equilibrium slope (solid angle). The relaxation time scale is determined by the solid surface tension γs and the short-term relaxation time of the viscoelastic material. The relaxation is characterized by a spreading velocity γs/η.
, with the functional form of F undetermined. The physical interpretation is as follows: the ratio γ/γs determines the equilibrium slope (solid angle). The relaxation time scale is determined by the solid surface tension γs and the short-term relaxation time of the viscoelastic material. The relaxation is characterized by a spreading velocity γs/η.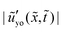 as a function of
as a function of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (in log scale) for different times during the decay. As there is an instantaneous elastic response at
(in log scale) for different times during the decay. As there is an instantaneous elastic response at  , the constant-slope-region may disappear as early as at
, the constant-slope-region may disappear as early as at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0+ as shown in Fig. 6(a) for which
= 0+ as shown in Fig. 6(a) for which ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) 1 = 102. Since the static shape at the tip region is determined by the surface tensions (in the soft regime), one may expect the tip region relaxes differently from the rest part of the ridge during the decay, as we have observed for the growth case. To address this question, we pick two positions, i.e.
1 = 102. Since the static shape at the tip region is determined by the surface tensions (in the soft regime), one may expect the tip region relaxes differently from the rest part of the ridge during the decay, as we have observed for the growth case. To address this question, we pick two positions, i.e. ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and
o = 10−2 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1, and study how the solid interface slope
o = 1, and study how the solid interface slope 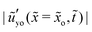 at these two positions varies with time for two different values of
at these two positions varies with time for two different values of ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) , namely
, namely ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2. Note that from Fig. 4(d),
= 10−2. Note that from Fig. 4(d), ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 ≲
o = 10−2 ≲ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ and
γ and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 ≫
o = 1 ≫ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) γ. In Fig. 6(b), we see that at
γ. In Fig. 6(b), we see that at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2, the evolution of the interfacial slope is the same for
o = 10−2, the evolution of the interfacial slope is the same for ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−1 and
= 10−1 and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) = 10−2. However, at
= 10−2. However, at ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1, the slope evolves differently as we can see in Fig. 6(c), and the time scale depends on η/G, which is much larger than the relaxation time at the tip region. On the other hand, the slope scales with
o = 1, the slope evolves differently as we can see in Fig. 6(c), and the time scale depends on η/G, which is much larger than the relaxation time at the tip region. On the other hand, the slope scales with ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) for both
for both ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 10−2 and
o = 10−2 and ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) o = 1 as we have shown in Fig. 6(d) and (e), in which the y-axis is
o = 1 as we have shown in Fig. 6(d) and (e), in which the y-axis is 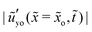 rescaled by
rescaled by ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /2. This is because the out-of-plane displacement depends linearly with γ for the whole ridge, and hence the ratio γ/γs determines the interfacial slope.
/2. This is because the out-of-plane displacement depends linearly with γ for the whole ridge, and hence the ratio γ/γs determines the interfacial slope.
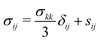
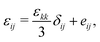
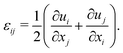
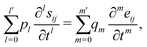
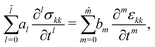
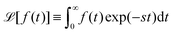 , the constitutive relation can be written as44
, the constitutive relation can be written as44![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (s)Ekk(x,s)δij + 2Ĝ(s)Eij(x,s),
(s)Ekk(x,s)δij + 2Ĝ(s)Eij(x,s),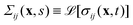 , Ekk(x,s) ≡
, Ekk(x,s) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) [εkk(x,t)] and Eij(x,s) ≡
[εkk(x,t)] and Eij(x,s) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) [eij(x,t)]. The expressions in Laplace space of the bulk modulus
[eij(x,t)]. The expressions in Laplace space of the bulk modulus 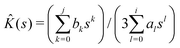 and the shear modulus
and the shear modulus 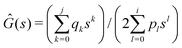 . In Appendix A2 we show how to obtain them for the standard solid (Zener) model. Eqn (17) has the same form as the linear elastic constitutive relation. Hence by following the same approach of deriving the boundary integral equation for a purely linear elastic material in the quasi-static state (∂σij/∂xj = 0), we can obtain the boundary integral equations for linear viscoelastic models in the Laplace space. Here we consider plane strain cases, for which the boundary integral equation in Laplace space is given as45
. In Appendix A2 we show how to obtain them for the standard solid (Zener) model. Eqn (17) has the same form as the linear elastic constitutive relation. Hence by following the same approach of deriving the boundary integral equation for a purely linear elastic material in the quasi-static state (∂σij/∂xj = 0), we can obtain the boundary integral equations for linear viscoelastic models in the Laplace space. Here we consider plane strain cases, for which the boundary integral equation in Laplace space is given as45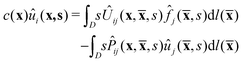

![[script L]](https://www.rsc.org/images/entities/char_e144.gif) [uj(x,t)],
[uj(x,t)], ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) j(x,s) ≡
j(x,s) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) [σij(x,t)nj(x)], with n being the normal vector pointing outward the soft solid domain, and the line integrals on the right hand side are carried out along the closed contour D of the boundary of the domain with dl(
[σij(x,t)nj(x)], with n being the normal vector pointing outward the soft solid domain, and the line integrals on the right hand side are carried out along the closed contour D of the boundary of the domain with dl(![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ) denoting the differential length of D and
) denoting the differential length of D and ![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) =
= ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + ȳŷ being the position vector of a point on the contour. The functions Ûij(x,
+ ȳŷ being the position vector of a point on the contour. The functions Ûij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s) and
,s) and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij(x,
ij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s) are given by45,46
,s) are given by45,46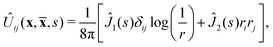
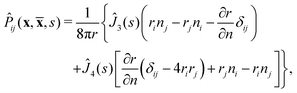
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) )2 + (y − ȳ)2]1/2,
)2 + (y − ȳ)2]1/2, 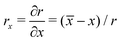 ,
, 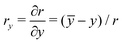 and
and 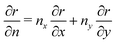 . The functions Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) are given as
. The functions Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) are given as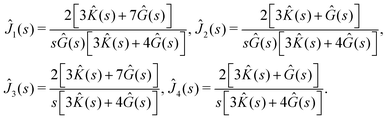
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1 to eqn (18) and obtain
−1 to eqn (18) and obtain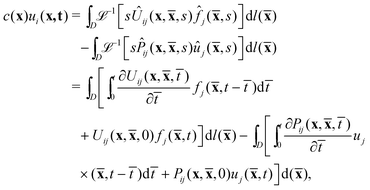
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) ≡
) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[Ûij(x,
−1[Ûij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)] and Pij(x,
,s)] and Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) ≡
) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[
−1[![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij(x,
ij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)]. Here we have used the convolution and the derivative properties of the Laplace transform.45,46
,s)]. Here we have used the convolution and the derivative properties of the Laplace transform.45,46
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ) and Pij(x,
) and Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,
,![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) ). As shown in Appendix A1, the stress σij and the strain εij tensors are decomposed into the hydrostatic and deviatoric parts. For viscoelastic materials made of polymers such as elastomers and gels, the response to the hydrostatic pressure acts like purely elastic materials. We thus write
). As shown in Appendix A1, the stress σij and the strain εij tensors are decomposed into the hydrostatic and deviatoric parts. For viscoelastic materials made of polymers such as elastomers and gels, the response to the hydrostatic pressure acts like purely elastic materials. We thus write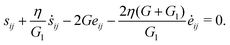
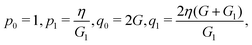
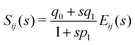
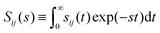
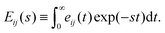
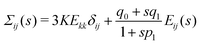
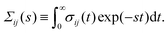
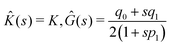
![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) ≡
,t) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[Ûij(x,
−1[Ûij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)] and Pij(x,
,s)] and Pij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,t) ≡
,t) ≡ ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) −1[
−1[![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ij(x,
ij(x,![[x with combining macron]](https://www.rsc.org/images/entities/b_char_0078_0304.gif) ,s)], what we need to do is to perform the inverse Laplace transform of Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) using the expressions of
,s)], what we need to do is to perform the inverse Laplace transform of Ĵ1(s), Ĵ2(s), Ĵ3(s) and Ĵ4(s) using the expressions of ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (s) and Ĝ(s) in (37), we then obtain
(s) and Ĝ(s) in (37), we then obtain