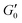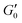Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The elastic response of graphene oxide gels as a crumpling phenomenon
Sebastian
Barwich
 and
Matthias E.
Möbius
and
Matthias E.
Möbius
 *
*
School of Physics, AMBER and CRANN Research Centres, Trinity College Dublin, Dublin 2, Ireland. E-mail: mobiusm@tcd.ie; Tel: +353-01-896-1055
First published on 25th October 2022
Abstract
The broad spectrum of chemical and electronic properties of 2D nanomaterials makes them attractive in a wide range of applications, especially in the context of printed electronics. Therefore, understanding the rheological properties of nanosheet suspensions is crucial for many additive manufacturing techniques. Here, we study the viscoelastic properties of aqueous suspensions of graphene oxide nanosheets. We show that in the gel phase, the magnitude of the elastic response and its scaling with volume fraction is independent of the lateral size of the particles and the interaction strength between them. We explain this behavior by modelling the elasticity of these gels as a crumpling phenomenon where the magnitude of the response is determined by the bending stiffness and thickness of the sheets. Due to their low bending stiffness these nanosheets crumple upon deformation and may therefore be considered soft colloids. Furthermore, we provide an explanation why the yield strain decreases with packing fraction for these gels.
Suspensions of attractive, colloidal particles form a stress-bearing, solid-like microstructure beyond a critical particle volume fraction ϕc. The magnitude of the elastic response of these particulate gels is an important characteristic and crucial for many industrial processes. In general, the shear modulus G increases with the particle volume fraction ϕ. The two most common scalings observed are G ∝ ϕn where the prefactor and exponent is usually governed by the interaction potential between the particles and the microstructure of the arrested state,1–6 and a percolation-type scaling G ∝ (ϕ − ϕc)n which has been seen in suspensions of carbon nanotubes,7 few layer graphene,8 clays9 and graphene oxide.10 In the case of sheets of nanometric thickness (nanosheets) such as graphene8 and graphene oxide10–12 the scaling exponent n is between 2.7 and 3.0, though the origin of this scaling remains unknown. Due to their low bending stiffness and high aspect ratio (lateral size/thickness), nanosheets can easily fold and crumple13–15 and may therefore be considered soft particles. We address the deformable nature of nanosheets which so far has not been considered in the modelling of the elastic response of gels formed by these particles.
Here we show that the strength of the elastic response of nanosheet gels is dominated by the mechanical properties of the nanosheet rather than the interaction between the particles. We find that the scaling exponent of the elastic response with volume fraction is consistent with a crumpling process. Furthermore the magnitude of the elastic response is independent of the lateral size of the particles and the interactions strength between them which is consistent with a crumpling process in which the elastic response is solely governed by the bending stiffness and thickness of the sheets. We show that this model is also consistent with the elastic response of graphene8 and LAPONITE® suspensions.9 Finally, we develop a model that explains the decrease of the yield strain with volume fraction and links it to the cohesive energy between particles. This result provides an important insight into the rheology of nanosheet gels as it connects the macroscopic response of the gel to the mechanical properties of single nanosheets which can be considered soft colloids.
We investigate the rheological properties of aqueous graphene oxide (GO) gels as a function of particle volume fraction ϕ and interaction potential which can be changed via the addition of NaCl. Graphene oxide is an oxidised graphene monolayer that is usually chemically exfoliated via the Hummers’ method.16 These nanosheets can be produced in a wide range of lateral sizes, ranging from approximately 10 nm to several 100 microns, and can have different level of oxidation depending on the preparation method.17 GO is easily dispersed in water due to the presence of the oxide groups. We obtained aqueous GO stock solution from Graphenea with a concentration of 25 g l−1 and a monolayer content >95%. The GO monolayers have a thickness of h = 0.8 ± 0.2 nm16 and a lateral size of L0 = 15 ± 5 μm, which we verified with SEM, giving rise to an aspect ratio α = L0/h = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750. One day prior to the rheological measurements we dilute the stock solution to the desired concentration and keep the pH neutral for enhanced stability18,19 by adding appropriate amounts of 0.5 M NaOH. In this work we investigated volume fractions between ϕ = 0.001 and 0.01 that we calculated using 2000 kg m−3 as the density of GO. The samples are sonicated for 30 minutes and allowed to rest for 24 hours. After loading the samples into the rheometer we wait for one hour before measurements commence. All rheology measurements are performed in a 5 cm diameter plate–plate geometry at a 0.5 mm gap with roughened plates and a solvent trap to prevent slip and evaporation. We do not preshear the sample as the rheology of GO gels is highly dependent on the flow history.20,21
750. One day prior to the rheological measurements we dilute the stock solution to the desired concentration and keep the pH neutral for enhanced stability18,19 by adding appropriate amounts of 0.5 M NaOH. In this work we investigated volume fractions between ϕ = 0.001 and 0.01 that we calculated using 2000 kg m−3 as the density of GO. The samples are sonicated for 30 minutes and allowed to rest for 24 hours. After loading the samples into the rheometer we wait for one hour before measurements commence. All rheology measurements are performed in a 5 cm diameter plate–plate geometry at a 0.5 mm gap with roughened plates and a solvent trap to prevent slip and evaporation. We do not preshear the sample as the rheology of GO gels is highly dependent on the flow history.20,21
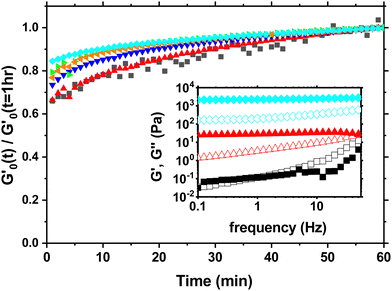
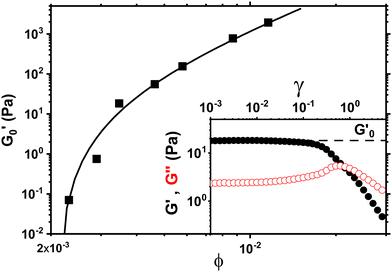
During that 1 hr waiting time we monitor the evolution of the storage modulus G′ through small amplitude oscillations in the linear viscoelastic regime to investigate the aging process as shown in Fig. 1. The storage modulus G′ is frequency independent and larger than the loss modulus G′′ at low frequencies indicating solid like behavior (inset Fig. 1). During the waiting time G′ increases between 35% to 20% depending on the concentration with the largest increase occuring in the first 30 minutes. The slight increase in the modulus beyond 60 minutes is negligible for the subsequent measurements and analysis.
In order to measure the elastic response of the GO gel we perform strain sweeps from which we infer the storage modulus 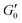 plateau in the linear viscoelastic regime which corresponds to the shear modulus. The inset in Fig. 2 shows a typical strain sweep where the storage modulus G′ is constant and larger than the loss modulus G′′ in linear response. Beyond the yield strain, the microstructure disintegrates and the suspensions fluidizes when G′′ > G′. Fig. 2 shows the shear modulus at different volume fractions which does not follow a simple power law ∝ ϕn but instead is well fit by G ∝ (ϕ − ϕc)n, with an exponent n = 2.7 ± 0.1 and ϕc = 0.0021. This exponent is consistent with previous rheological experiments on aqueous GO gels10–12 which are shown Fig. 3A together with our data. Interestingly, not only is the exponent the same, but also the prefactor of this power law despite the fact the lateral size of the GO particles differs by two orders of magnitude between the data sets ranging from 0.6 μm (Valles et al.12) to 64 μm (Corker et al.11).
plateau in the linear viscoelastic regime which corresponds to the shear modulus. The inset in Fig. 2 shows a typical strain sweep where the storage modulus G′ is constant and larger than the loss modulus G′′ in linear response. Beyond the yield strain, the microstructure disintegrates and the suspensions fluidizes when G′′ > G′. Fig. 2 shows the shear modulus at different volume fractions which does not follow a simple power law ∝ ϕn but instead is well fit by G ∝ (ϕ − ϕc)n, with an exponent n = 2.7 ± 0.1 and ϕc = 0.0021. This exponent is consistent with previous rheological experiments on aqueous GO gels10–12 which are shown Fig. 3A together with our data. Interestingly, not only is the exponent the same, but also the prefactor of this power law despite the fact the lateral size of the GO particles differs by two orders of magnitude between the data sets ranging from 0.6 μm (Valles et al.12) to 64 μm (Corker et al.11).
 | ||
Fig. 3 (A) Storage modulus plateau 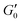 versus reduced volume fraction (ϕ − ϕc) for different aqueous GO gels. Black line is eqn (1) with cκ/h3 = 0.45 GPa. Our data with L0 = 15 μm: (■) without NaCl, ϕc = 0.00207, ( versus reduced volume fraction (ϕ − ϕc) for different aqueous GO gels. Black line is eqn (1) with cκ/h3 = 0.45 GPa. Our data with L0 = 15 μm: (■) without NaCl, ϕc = 0.00207, ( ) 0.1 M NaCl, ϕc = 0.0011. Literature data: ( ) 0.1 M NaCl, ϕc = 0.0011. Literature data: ( ) Valles et al.,12L0 = 0.6 μm, ϕc = 0.0003, ( ) Valles et al.,12L0 = 0.6 μm, ϕc = 0.0003, ( ) Data from supplementary information of Naficy et al.,10L0 = 50 μm, ϕc = 0.00023, ( ) Data from supplementary information of Naficy et al.,10L0 = 50 μm, ϕc = 0.00023, ( ) Corker et al.,11L0 = 64 μm, ϕc = 0.0008. Inset: Normalised size of the average particle free volume at ϕc for the data shown in main panels (A and B) (same symbols as in main panels). Black dashed line corresponds to overlap concentration (OC) Lc/L0 = 1.01 and blue dotted line to random contact equation (RCE) prediction Lc/L0 = 0.51, solid black line is a guide to the eye Lc/L0 = 5.5α−0.25. (B) ) Corker et al.,11L0 = 64 μm, ϕc = 0.0008. Inset: Normalised size of the average particle free volume at ϕc for the data shown in main panels (A and B) (same symbols as in main panels). Black dashed line corresponds to overlap concentration (OC) Lc/L0 = 1.01 and blue dotted line to random contact equation (RCE) prediction Lc/L0 = 0.51, solid black line is a guide to the eye Lc/L0 = 5.5α−0.25. (B)  versus reduced volume fraction (ϕ − ϕc) for different nanosheet gels. Black line is eqn (1) with cκ/h3 = 0.45 GPa, red line is eqn (1) with cκ/h3 = 0.1 GPa. ( versus reduced volume fraction (ϕ − ϕc) for different nanosheet gels. Black line is eqn (1) with cκ/h3 = 0.45 GPa, red line is eqn (1) with cκ/h3 = 0.1 GPa. ( ) 3-layer graphene in NMP,8h = 1 nm, L0 = 1 ± 0.5 μm, ϕc = 0.002. Aqueous LAPONITE® clay9 (h = 1 nm, L0 = 30 nm) at different NaCl concentrations: (●) 10 mM, ϕc = 0.0012, (△) 6 mM, ϕc = 0.0017, (◊) 5 mM, ϕc = 0.0023, (▷) 3 mM, ϕc = 0.0054, (◁) 0.1 mM, ϕc = 0.0074. Upper inset: Literature values for the bending stiffness κLitversus cκ from fits to eqn (1). ( ) 3-layer graphene in NMP,8h = 1 nm, L0 = 1 ± 0.5 μm, ϕc = 0.002. Aqueous LAPONITE® clay9 (h = 1 nm, L0 = 30 nm) at different NaCl concentrations: (●) 10 mM, ϕc = 0.0012, (△) 6 mM, ϕc = 0.0017, (◊) 5 mM, ϕc = 0.0023, (▷) 3 mM, ϕc = 0.0054, (◁) 0.1 mM, ϕc = 0.0074. Upper inset: Literature values for the bending stiffness κLitversus cκ from fits to eqn (1). ( ) range of bending angle dependent κ for 3-layer graphene,22 ( ) range of bending angle dependent κ for 3-layer graphene,22 ( ) GO value from Poulin et al.,23 ( ) GO value from Poulin et al.,23 ( ) GO(2 ) GO(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydroxyl/epoxide ratio) minimum and maximum value from Liu et al.,24 (▼) GO minimum and maximum value from Incze et al.,25 ( 1 hydroxyl/epoxide ratio) minimum and maximum value from Liu et al.,24 (▼) GO minimum and maximum value from Incze et al.,25 ( ) range of curvature dependent κ for Montmorillonite (h = 1 nm) from Fu et al. (using κ ≈ 2rc2Eb, where rc is the radius of curvature and Eb the bending energy/area), ( ) range of curvature dependent κ for Montmorillonite (h = 1 nm) from Fu et al. (using κ ≈ 2rc2Eb, where rc is the radius of curvature and Eb the bending energy/area), ( ) F-hectorite (h = 1 nm), black and dotted lines denote κLit = (15 ± 10)cκ. Lower inset: ) F-hectorite (h = 1 nm), black and dotted lines denote κLit = (15 ± 10)cκ. Lower inset: 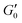 versus ϕ for ( versus ϕ for ( ) 3-layer graphene and (●) 10 mM NaCl LAPONITE® with fits to eqn (1) with the same fit parameters as in main panel. ) 3-layer graphene and (●) 10 mM NaCl LAPONITE® with fits to eqn (1) with the same fit parameters as in main panel. | ||
The elastic response of GO gels is similar to other suspensions of nanosheets with a thickness of 1 nm. Both aqueous LAPONITE® clay at different salt concentrations9 (α = 30) and 3-layer graphene in NMP8 (α = 1000) do not follow a simple power law either (lower inset Fig. 3B) but are well described by G ∝ (ϕ − ϕc)n with the same exponent (n = 2.7) as GO (Fig. 3B), though the best fit for LAPONITE® is slightly lower (n = 2.35).9
While the elastic response of GO gels appears to be independent of lateral size of the particles, the critical concentration ϕc at which gelation occurs does depend on it and usually decreases with increasing aspect ratio.26 In order to quantify the microstructure at ϕc, we look at the average free volume Vf per particle, which is defined as ϕ = L02h/Vf. Approximating this volume as a simple cube, the size of the free volume L = Vf1/3 normalised by the lateral size of the particle gives Lc/L0 = 1/(ϕcα)1/3 at the gelation point, where α = L0/h is the aspect ratio of the particles. Two common models to predict ϕc are the overlap concentration (OC)8,27 and the random contact equation (RCE).26 OC approximates the gelation point as a random packing of imaginary spheres in which the sheets are embedded and can freely rotate in, which leads to ϕc = 3ϕRCP/(2α). Using the random close pack density of spheres ϕRCP = 0.64, OC predicts Lc/L0 = 1.01 at the gelation point ϕc. The RCE is based on the orientational average of the excluded volume and predicts for discs that ϕc = 2 〈z〉/(πα), where 〈z〉 is the average contact number per particle. For a random packing of ellipsoids the maximum value is 〈z〉 = 12,28 leading to Lc/L0 = 0.51. The inset of Fig. 3A shows Lc/L0, the normalized size of the free volume at ϕc for the different aspect ratios of the particles shown in the main panels and the predictions made by OC and RCE. Note that for LAPONITE® clays, ϕc decreases significantly with salt with a corresponding increase of Lc/L0 from 1.6 to 3 as the increased particle attraction from the addition of salt leads to more porous structures.29–31Lc/L0 decreases from 2.3 ± 0.7 (LAPONITE®) to 0.25 for the largest aspect ratio GO particle gel which is just below the RCE prediction for a glassy, random packing of ellipsoids. The value of Lc/L0 for non-aqueous 3-layer graphene gel is consistent with this overall trend. This shows that the microstructure is not only affected by the particle interactions but also by the aspect ratio.32 The overall decrease of Lc/L0 with α (Lc/L0 ∼ α−0.25) explains why ϕc for all the gels shown only differ by a factor of ≈30 at most across 4 orders of magnitude in aspect ratio as ϕc = (Lc/L0)−3α−1 ∼ α−0.25. Since the low aspect ratio GO gel (α = 750) is significantly more porous (L/L0 = 1.6) compared to the high aspect ratio GO gels (L/L0 ≈ 0.3) with α > 104, the microstructure of GO gels does not appear to play a dominant role in determining the prefactor and exponent of the power law fit to the elastic response in Fig. 3A.
Next, we added NaCl to the suspension in order to increase the interaction between the particles and investigate its effect on the storage modulus plateau of the gel. Adding salt decreases the electrostatic repulsion and makes the potential well between particles deeper up to the critical coagulation concentration (CCC). While the CCC for aqueous GO can be predicted from DLVO theory,19 DLVO alone may not give a complete description of the interparticle potential.33,34 Here, the salt concentration was 0.1 M, below the CCC of our gel. The addition of NaCl lowers the critical volume fraction from 0.00207 to 0.0011 analogous to what has been found in LAPONITE® clays9 (inset Fig. 3A) and consistent with an increased attraction between the particles.29,30 However, 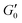 still follows the power law with the same exponent and prefactor as shown in Fig. 3A. Therefore the increased interaction leads to changes in microstructure indicated by the change of ϕc but does not alter the overall strength and scaling of the elastic response.
still follows the power law with the same exponent and prefactor as shown in Fig. 3A. Therefore the increased interaction leads to changes in microstructure indicated by the change of ϕc but does not alter the overall strength and scaling of the elastic response.
Existing models1–6 for gel elasticity cannot account for this observation as the magnitude of the elastic response in these models scales with the bond stiffness between the particles. These models assume that particles are stiff and the elasticity arises solely from the interaction between the particles and the overall microstructure. However, GO particles cannot be considered stiff.34
While GO has a relatively high 2D Young's modulus, Y2D ≈ 300 N m−1,35 its bending stiffness κ is low though there is a considerable spread of values for κ in the literature. The only experimental value is 0.025 eV,24 a factor of ∼40 lower than graphene and three orders of magnitude smaller than simulation results (up to 40 eV).24,25 Therefore, the ratio of stretching to bending energies Y2DL02/κ, the Föppl–von Kármán number,13 is at least 1010 which means that GO and other nanosheets can easily crumple and wrinkle.14 The elastic response of the GO gel may therefore originate from the stored elastic energy of wrinkles and ridges in the GO rather than the bond stiffness between the particles.
In general, the elastic energy of a crumpled sheet is stored mostly in the ridges35,36 and can be approximated as a summation of all the ridge energies in a crumpled sheet E = Nκ(X/h)1/3, where N is the number of facets, κ the bending stiffness, X the characteristic size of the ridge and h the thickness of the sheet. The number of facets is simply the area of the sheet divided by the area of the facet N ∼ L02/X2 and the random orientation of the facets implies that N ∼ V/X3, where V is the volume which the sheet is confined in. Finally, the volume fraction for a single sheet is given by ϕs = L02h/V. These relations lead to an energy density ε = E/V ∼ (κ/h3)ϕs8/3.36 The Young's modulus Y scales with the energy density. Treating the crumpled sheet as an elastic, isotropic medium, the shear modulus G is proportional to the Young's modulus with a prefactor of order 1 that depends on the Poisson ratio. Therefore G ∼ Y ∼ ε. We now model the gel as a suspension of crumpled nanosheets. In such a system crumpling only occurs beyond the gelation threshold ϕc, at which the particles touch and form a stress bearing microstructure. Therefore we replace ϕs with (ϕ − ϕc) and the shear modulus of the gel can be written as
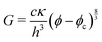 | (1) |
Eqn (1) provides an excellent fit to the data shown in Fig. 3A and is consistent with the observation that the prefactor and exponent is independent of the lateral size and interaction potential. We find that the prefactor cκ/h3 = 0.45 ± 0.5 GPa, which corresponds to a bending stiffness κ = 1.4 ± 0.2 eV for h = 0.8 nm assuming c = 1, which is similar to graphene and inbetween the literature values.24,25,33 Fitting eqn (1) to 3-layer graphene and LAPONITE® gels (Fig. 3B) yields 0.63 ± 0.15 eV and 2.8 ± 0.8 eV for cκ, respectively. The literature value for 3-layer graphene is between 3 and 19 eV depending on the bending angle.23 There are no literature values for LAPONITE®, but κ for other 1 nm thin clay particles from the smectite family range from 22 eV (f-hectorite39) up to to 73 eV (montmorrilonite40). It may seem surprising that bending should play a role for low aspect ratio LAPONITE® (α = 30). However, clay platelets are very compliant and readily conform to nanoscale features.15 Kinks with radii of curvature as lows as 3 nm have been observed40 and the energy to create a fold is independent of the lateral particle size. In the case of GO, MD simulations of small GO flakes interacting in water (α = 13) have shown significant bending.41
While there is considerable spread in κ for each type of nanosheet,42 the trend is consistent with the literature values being proportional to cκ inferred from eqn (1) as shown in the upper inset of Fig. 3B though the experimental value for GO24 is an outlier. This allows us to constrain the value of the constant c = (15 ± 10)−1 = 0.066 ± 0.044 in eqn (1) from the fit κLit = (15 ± 10)cκ. This leads to a bending stiffness of 21 ± 14 eV for GO similar to simulation results,24,25 while for 3-layer graphene and LAPONITE® we obtain 9.5 ± 6.3 eV and 42 ± 28 eV, respectively.
In order to gain further insight into the microstructure of the stress-bearing network we measured yield strain as a function of volume fraction. We define the yield strain γy to be the point at which G′ has decreased a factor of 10 from its plateau value at low strain amplitudes. At this point the gel has lost most of its elasticity due to the strain induced breakage of the microstructure. We rescale the storage moduli from oscillatory strain sweeps by their plateau value 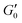 and yield strain as shown in Fig. 4. The yield strain is decreasing with increasing volume fraction for gels with and without NaCl. Note that a similar trend has been observed in graphene gels8 and also for carbon nanotube suspensions.7
and yield strain as shown in Fig. 4. The yield strain is decreasing with increasing volume fraction for gels with and without NaCl. Note that a similar trend has been observed in graphene gels8 and also for carbon nanotube suspensions.7
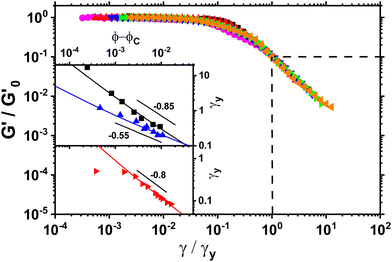 | ||
Fig. 4
G′ normalised by its plateau value 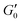 versus the strain amplitude γ normalised by the yield strain γy at f = 1 Hz as shown in inset. Data shown from gels without NaCl. versus the strain amplitude γ normalised by the yield strain γy at f = 1 Hz as shown in inset. Data shown from gels without NaCl. 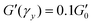 as indicated by the dotted lines. (■) 0.00232, ( as indicated by the dotted lines. (■) 0.00232, ( ) 0.0029, ( ) 0.0029, ( ) 0.00348, ( ) 0.00348, ( ) 0.00463, ( ) 0.00463, ( ) 0.00579, ( ) 0.00579, ( ) 0.0087, ( ) 0.0087, ( ) 0.0116. Upper inset: The yield strain versus (ϕ − ϕc). (■) without NaCl, ( ) 0.0116. Upper inset: The yield strain versus (ϕ − ϕc). (■) without NaCl, ( ) with 0.1 M NaCl. The short black lines denote the logarithmic slopes as shown. The lines are fits to eqn (2) with σ = 1.1 ± 0.2 mJ m−2, x = 0.66 ± 0.05 without NaCl and σ = 11 ± 2 mJ m−2 and x = 1.33 ± 0.05 for 0.1 M NaCl using cκ/h3 = 0.45 GPa for both fits. Lower inset: The yield strain versus (ϕ − ϕc) for 3-layer graphene in NMP gel8 ( ) with 0.1 M NaCl. The short black lines denote the logarithmic slopes as shown. The lines are fits to eqn (2) with σ = 1.1 ± 0.2 mJ m−2, x = 0.66 ± 0.05 without NaCl and σ = 11 ± 2 mJ m−2 and x = 1.33 ± 0.05 for 0.1 M NaCl using cκ/h3 = 0.45 GPa for both fits. Lower inset: The yield strain versus (ϕ − ϕc) for 3-layer graphene in NMP gel8 ( ). The line is a fit to eqn (2) with σ = 7 ± 0.2 μJ m−2, x = 0.7 ± 0.05 using cκ/h3 = 0.1 GPa. ). The line is a fit to eqn (2) with σ = 7 ± 0.2 μJ m−2, x = 0.7 ± 0.05 using cκ/h3 = 0.1 GPa. | ||
This decrease in γy is also seen in gels with fractal microstructures, where theory32,39 predicts that 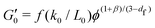 and γy ∝ ϕ(1−β)/(3−df) assuming stiff particles. Here, β and df are related to the fractal dimensions of the elastic backbone and the flocs, respectively, k0 is the bond rigidity and f a prefactor. Far from ϕc we find that the exponent of the yield strain is −0.55 (−0.85) for the GO gels with (and without) salt. Using
and γy ∝ ϕ(1−β)/(3−df) assuming stiff particles. Here, β and df are related to the fractal dimensions of the elastic backbone and the flocs, respectively, k0 is the bond rigidity and f a prefactor. Far from ϕc we find that the exponent of the yield strain is −0.55 (−0.85) for the GO gels with (and without) salt. Using 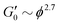 this results in β = 1.5(1.9) and df = 2.1(1.9) which is similar to what has been found in other gels.22 However, the addition of salt should increase the bond rigidity k0 and thereby
this results in β = 1.5(1.9) and df = 2.1(1.9) which is similar to what has been found in other gels.22 However, the addition of salt should increase the bond rigidity k0 and thereby 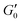 , which is not what we observe. Also, consistency with Fig. 3A would require fk0 to be proportional to the particle size L0 across two orders of magnitude change in L0. Finally, the low aspect ratio GO gel12 is much more porous (Lc/L0 = 1.6) than the high aspect ratio GO gel (Lc/L0 = 0.3), yet
, which is not what we observe. Also, consistency with Fig. 3A would require fk0 to be proportional to the particle size L0 across two orders of magnitude change in L0. Finally, the low aspect ratio GO gel12 is much more porous (Lc/L0 = 1.6) than the high aspect ratio GO gel (Lc/L0 = 0.3), yet 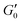 scales with the same microstructure-dependent exponent for both gels.
scales with the same microstructure-dependent exponent for both gels.
In order to understand this behaviour of γy in the context of the crumpling model, we consider the elastic deformation of the gel up to yield point. The stored elastic energy at the yield point 0.5Gγy2. We relate this to the energy it takes to break the contacts between neighboring crumpled nanosheets. We propose a simple relaxation dissipation model43 to describe the yielding process. The stored elastic energy density at the yield point can be related to the energy stored in the bonds that get broken during the yielding process. In contrast to hard spheres it is difficult to characterise the bond energy between crumpled sheets in terms of bond stiffness and coordination number as these contacts will most likely have a wide range of contact areas and therefore bond energies due to the disordered shape of crumpled sheets. Instead we introduce the area fraction a = m(ϕ − ϕc)x which denotes the fraction of the area of the free volume Vf occupied by a single sheet that is in contact with neighboring sheets with an unknown exponent x which must be positive. Since ϕc ≪ 1 for high aspect ratio particle suspensions,22,32 the area fraction a should go to 1 in the theoretical limit of ϕ = 1. Therefore the prefactor m is set to 1. The average free volume per sheet is just Vf = L02h/ϕ with a corresponding area Af = Vf2/3.
In order to model the process we equate the stored elastic energy density at the yield point to the bond energy density. If σ is the cohesive energy per area between two graphene oxide sheets in water, then the bond energy density is given by σaAf/2Vf. This bond density only includes bonds between neighboring sheets and not internal bonds within a crumpled sheet. The factor 2 accounts for the fact the a bond is shared by two particles. Solving for the yield strain we obtain
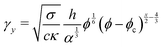 | (2) |
In conclusion we find that the elasticity of particulate gels from GO and other nanosheet suspensions arise from the mechanical properties of the sheets rather than the interaction between them. Therefore these particle can be considered soft colloids. Our model based on crumpling gives the correct exponent with a prefactor that solely depends on the bending stiffness κ and thickness of the nanosheet but not on the lateral size of the particles. From the rheology we infer κ = 21 ± 14 eV for GO which is close to simulation results.25,33 The microstructure, which is an important parameter in modelling gel elasticity, only enters the model via the gelation point ϕc. This model should only apply to particles with nanometric thickness. It remains an open question at what bending stiffness the particles can be considered stiff such that the gel elasticity is dominated by the bond rigidity.
Author contributions
S. B. carried out the experiments and M. E. M. designed the project. Both authors analysed the data and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was supported by the grant SFI 17/CDA/4704 and SFI AMBER2 12/RC/2278. We thank T. Witten and J. Coleman for fruitful discussions.Notes and references
- A. Zaccone, H. Wu and E. Del Gado, Phys. Rev. Lett., 2009, 103, 208301 CrossRef PubMed.
- K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Nat. Commun., 2019, 10, 1–8 CrossRef CAS.
- W. H. Shih, W. Y. Shih, S. I. Kim, J. Liu and I. A. Aksay, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4772–4779 CrossRef CAS.
- H. Wu and M. Morbidelli, Langmuir, 2001, 17, 1030–1036 CrossRef CAS.
- S. Romer, H. Bissig, P. Schurtenberger and F. Scheffold, EPL, 2014, 108, 48006 CrossRef.
- P. B. Laxton and J. C. Berg, Colloids Surf., A, 2007, 301, 137–140 CrossRef CAS.
- L. A. Hough, M. F. Islam, P. A. Janmey and A. G. Yodh, Phys. Rev. Lett., 2004, 93, 168102 CrossRef CAS.
- S. Barwich, J. N. Coleman and M. E. Möbius, Soft Matter, 2015, 11, 3159–3164 RSC.
- A. Mourchid, E. Lecolier, H. Van Damme and P. Levitz, Langmuir, 1998, 14, 4718–4723 CrossRef CAS.
- S. Naficy, R. Jalili, S. H. Aboutalebi, R. A. Gorkin III, K. Konstantinov, P. C. Innis, G. M. Spinks, P. Poulin and G. G. Wallace, Mater. Horiz., 2014, 10, 1039 Search PubMed.
- A. Corker, H. C.-H. Ng, R. J. Poole and E. Garca-Tuñón, Soft Matter, 2019, 15, 1444–1456 RSC.
- C. Vallés, R. J. Young, D. J. Lomax and I. A. Kinloch, J. Mater. Sci., 2014, 49, 6311–6320 CrossRef.
- M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill, P. Y. Huang, A. R. Ruyack, J. W. Kevek, B. Kobrin and D. A. Muller, et al. , Nature, 2015, 524, 204–207 CrossRef PubMed.
- M. Fokker, S. Janbaz and A. Zadpoor, RSC Adv., 2019, 9, 5174–5188 RSC.
- R. D. Piner, T. T. Xu, F. T. Fisher, Y. Qiao and R. S. Ruoff, Langmuir, 2003, 19, 7995–8001 CrossRef CAS.
- S. Gambhir, R. Jalili, D. L. Officer and G. G. Wallace, NPG Asia Mater., 2015, 7, e186 CrossRef CAS.
- K. P. Loh, Q. Bao, G. Eda and M. Chhowalla, Nat. Chem., 2010, 2, 1015–1024 CrossRef CAS PubMed.
- C.-J. Shih, S. Lin, R. Sharma, M. S. Strano and D. Blankschtein, Langmuir, 2012, 28, 235–241 CrossRef CAS PubMed.
- L. Wu, L. Liu, B. Gao, R. Muñoz-Carpena, M. Zhang, H. Chen, Z. Zhou and H. Wang, Langmuir, 2013, 29, 15174–15181 CrossRef CAS PubMed.
- F. Del Giudice and A. Q. Shen, Curr. Opin. Chem. Eng., 2017, 16, 23–30 CrossRef.
- F. D. Giudice, B. V. Cunning, R. S. Ruoff and A. Q. Shen, Rheol. Acta, 2018, 57, 293–306 CrossRef.
- E. Han, J. Yu, E. Annevelink, J. Son, D. A. Kang, K. Watanabe, T. Taniguchi, E. Ertekin, P. Y. Huang and A. M. van der Zande, Nat. Mater., 2020, 19, 305–309 CrossRef PubMed.
- P. Poulin, R. Jalili, W. Neri, F. Nallet, T. Divoux, A. Colin, S. H. Aboutalebi, G. Wallace and C. Zakri, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 11088–11093 CrossRef.
- L. Liu, X. Li, Z. Liu, S. Dai, X. Huang and J. Zhao, Nanoscale, 2020, 12, 1623–1628 RSC.
- A. Incze, A. Pasturel and P. Peyla, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 212103 CrossRef.
- (a) A. P. Philipse, Langmuir, 1996, 12, 1127–1133 CrossRef CAS; (b) A. P. Philipse, Langmuir, 1996, 12, 5971 CrossRef CAS.
- H. King Jr, S. T. Milner, M. Y. Lin, J. P. Singh and T. Mason, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021403 CrossRef CAS.
- M. van Hecke, J. Phys.: Condens. Matter, 2010, 22, 033101 CrossRef CAS PubMed.
- V. Trappe and P. Sandkühler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500 CrossRef CAS.
- H. Tanaka, J. Meunier and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 031404 CrossRef.
- M. J. Solomon and P. T. Spicer, Soft Matter, 2010, 6, 1391–1400 RSC.
- P.-K. Kao, M. J. Solomon and M. Ganesan, Soft Matter, 2022, 18, 1350–1363 RSC.
- S. Lin, C.-J. Shih, V. Sresht, A. G. Rajan, M. S. Strano and D. Blankschtein, Adv. Colloid Interface Sci., 2017, 244, 36–53 CrossRef PubMed.
- J. L. Suter and P. V. Coveney, Sci. Rep., 2021, 11, 1–11 CrossRef PubMed.
- K. Matan, R. B. Williams, T. A. Witten and S. R. Nagel, Phys. Rev. Lett., 2002, 88, 076101 CrossRef PubMed.
- T. A. Witten, Rev. Mod. Phys., 2007, 79, 643 CrossRef.
- G. Wang, Z. Dai, J. Xiao, S. Z. Feng, C. Weng, L. Liu, Z. Xu, R. Huang and Z. Zhang, Phys. Rev. Lett., 2019, 123, 116101 CrossRef CAS PubMed.
- Y.-T. Fu, G. D. Zartman, M. Yoonessi, L. F. Drummy and H. Heinz, J. Phys. Chem. C, 2011, 115, 22292–22300 CrossRef CAS.
- R. De Rooij, D. Van den Ende, M. H. Duits and J. Mellema, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 3038 CrossRef CAS PubMed.
- D. A. Kunz, E. Max, R. Weinkamer, T. Lunkenbein, J. Breu and A. Fery, Small, 2009, 5, 1816–1820 CrossRef CAS PubMed.
- L. Liu, J. Zhang, J. Zhao and F. Liu, Nanoscale, 2012, 4, 5910–5916 RSC.
- A. G. Kelly, D. O’Suilleabhain, C. Gabett and J. N. Coleman, Nat. Rev. Mater., 2022, 7, 217–234 CrossRef CAS.
- T. A. Witten and P. A. Pincus, Structured fluids, Oxford University Press, 2004 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |