Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Beating Poisson stochastic particle encapsulation in flow-focusing microfluidic devices using viscoelastic liquids†
Keshvad
Shahrivar
and
Francesco
Del Giudice
 *
*
Department of Chemical Engineering, School of Engineering and Applied Science, Faculty of Science and Engineering, Swansea University, Swansea, SA1 8EN, UK. E-mail: francesco.delgiudice@swansea.ac.uk
First published on 29th July 2022
Abstract
The encapsulation and co-encapsulation of particles in microfluidic flows is essential in applications related to single-cell analysis and material synthesis. However, the whole encapsulation process is stochastic in nature, and its efficiency is limited by the so-called Poisson limit. We here demonstrate particle encapsulation in microfluidic devices having flow-focusing geometries with efficiency up to 2-fold larger than the stochastic limit imposed by the Poisson statistics. To this aim, we exploited the recently observed phenomenon of particle train formation in viscoelastic liquids, so that particles could approach the encapsulation area with a constant frequency that was subsequently synchronised to the constant frequency of droplet formation. We also developed a simplified expression based on the experimental results that can guide optimal design of the microfluidic encapsulation system. Finally, we report the first experimental evidence of viscoelastic co-encapsulation of particles coming from different streams.
The compartmentalisation of particles in picoliter droplets obtained using microfluidic devices finds application across several fields of science,1 with some examples being single-cell analysis2 and material synthesis.3,4 The compartmentalisation process is driven by the same principle of droplet formation in microfluidic devices: a continuous phase ‘meets’ at a junction the dispersed phase containing particles or cells, and a droplet is formed as a result of a combination among interfacial, viscous, inertial and elastic forces (to form the droplet, the two fluids must not be miscible with each other).5 The microfluidic junction can present different shapes, for instance coaxial, T-shaped or flow-focusing.5,6 The process of encapsulating objects in droplets is stochastic and it is governed by the Poisson limit.7 The stochastic nature of the encapsulation process finds its origin in the fact that objects approaching the encapsulation area do not arrive with a constant frequency, at variance with the droplet formation process where the frequency of droplet formation is constant and can be tuned by changing the values of the volumetric flow rate for both continuous and dispersed phase.5,8 To ‘beat’ the stochastic encapsulation limit (that for single particle encapsulation is at around 30%, while for co-encapsulation is around 10%), it is possible to take advantage of the formation of strings of equally-spaced particles (also called particle trains) in microfluidic geometries thanks to either inertial9–16 or viscoelastic17–21 forces. In this way, the constant frequency of particles approaching the encapsulation area fp can be synchronised to the frequency of droplet formation fd, i.e., fp = fd, to overcome the Poisson stochastic limit. This approach has been successfully used in inertial microfluidics22–24 for a variety of microfluidic channel designs. Very recently, we employed a viscoelastic shear-thinning fluid to demonstrate the controlled encapsulation of rigid particles in a T-junction microfluidic device taking advantage of the viscoelasticity-driven particle train formation phenomenon.25 So far, this has been the only study on the subject and it was restricted to single particle encapsulation in a commercially available microfluidic device.
We here demonstrate controlled viscoelastic encapsulation and co-encapsulation of particles in flow-focusing microfluidic devices, achieving encapsulation and co-encapsulation efficiency up to 2-folds larger than the stochastic value, thus beating the Poisson limit. In practical terms, this work represents an extension of our previous one25 featuring controlled viscoelastic encapsulation in T-junction devices. This step is not straightforward, as the operational parameters for droplet formation in flow-focusing geometries are different from the ones in T-junction devices.5 Furthermore, the flow-focusing geometry is generally more common than the T-junction for the high-throughput production of droplets.
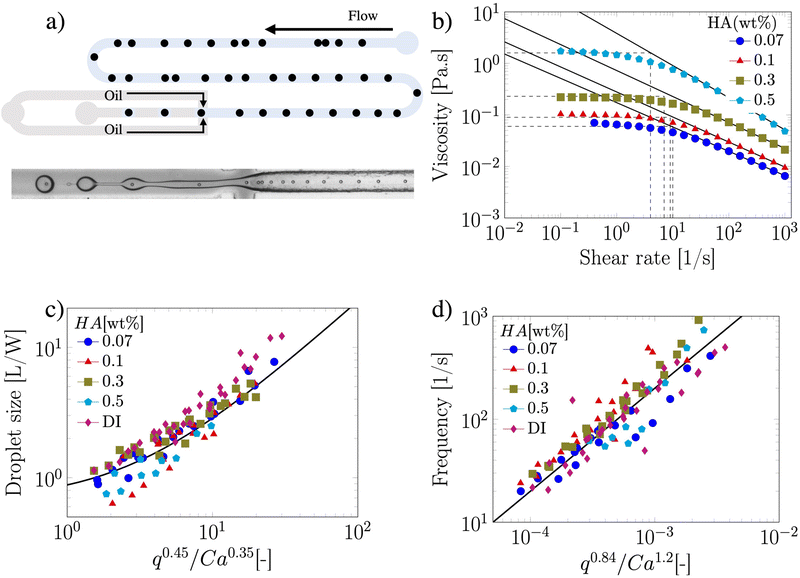
The suspension containing particles flowed in a polymethylmethacrylate (PMMA) square-shaped microchannel with lateral side H = 100 μm, width W = 100 μm and length of 30 cm, bonded on a glass coverslip using double-sided tape (Adhesive Research). The channel length was selected such that the 20 ± 2 μm particles (Polysciences Inc.) employed here at a bulk concentration of 0.4 wt% self-ordered in a particle train thanks to the viscoelastic properties of the suspending liquid18,21,26 before approaching the encapsulation area (Fig. 1a). The width of the section following the encapsulation area was W = 120 μm, while the height remained unchanged at H = 100 μm. Mineral oil (Sigma Aldrich UK, viscosity of 29 mPa s) was used as the continuous phase to form the viscoelastic droplets. The PMMA microchannel was fabricated using the same procedure reported elsewhere.18 As viscoelastic suspending liquid, we selected several aqueous polymer solutions of hyaluronic acid (HA, molecular weight Mw = 1.5–1.8 MDa, Sigma Aldrich, UK) displaying different amount of shear-thinning (Fig. 1b). The fluids displayed strong elastic properties (Fig. S1, ESI†), with longest relaxation time values estimated from the viscosity data of Fig. 1b, by determining the intersection between the power-law region and the zero-shear plateau region of the curve. Relaxation time values of 0.10, 0.11, 0.143 and 0.25 s were obtained for the HA concentrations 0.07, 0.1, 0.3 and 0.5 wt%, respectively. The interfacial tension values between the HA solutions and the mineral oil measured using a force tensiometer (Sigma 702, Biolin Scientific) were γ = 3.63 ± 0.07, 3.64 ± 0.05, 3.04 ± 0.16, and 1.65 ± 0.08 mN m−1 for the HA concentrations 0.07, 0.1, 0.3 and 0.5 wt%, respectively. We used a fast camera (Photron Mini UX50) mounted on a inverted Zeiss Axiovert A1 microscope; videos of recorded droplets were analysed using a Matlab subroutine employed in our previous study.25 The flow rate of the two liquids was controlled using a syringe pump (KD Scientific).
We first demonstrated the principle of controlled viscoelastic encapsulation using the flow-focusing microfluidic device schematised in Fig. 1a. Similarly to our previous work,25 we first studied the droplet formation phenomenon (Fig. 1(c and d)) to verify whether the experimental data could be described using a single scaling argument. The droplet formation phenomenon generally depends upon a series of parameters,5,6 including the flow rate ratio q = Qd/Qc, where Qd is the flow rate of the dispersed phase (HA solutions) and Qc that of the continuous phase (mineral oil), and the Capillary number Ca = μcUc/γ, where Uc = Qc/(WH) is the average velocity of continuous phase fluid, μc is the viscosity of the continuous phase and γ is the interfacial tension. In our experiments, the flow rate Qc was changed in range of 0.1–10 μL min−1 corresponding to capillary number in the range of Ca ∈ [0.001–0.1]. For this range of control parameters, the largest value of the Reynolds number of the continuous phase Re = ρcUcW/μc was Re = 6.4 × 10−2, hence, inertial effects were negligible. We found that, regardless of the polymer concentration, the viscoelastic droplets collapsed on the mastercurve given by the expression recently reported by Chen et al.,27L/W = a + ε(qb/Cac), with fitting parameters a = 0.66 ± 0.02, b = 0.45 ± 0.01 and c = 0.35 ± 0.01, respectively (Fig. 1c). It is worth noticing that the expression by Chen et al.27 was developed for Newtonian droplets surrounded by a continuous shear-thinning phase, a somehow opposite situation to the one investigated here. In other words, the fact that the data followed the scaling for Newtonian droplets may indicate that the droplet size is not significantly affected by the fluid elasticity. We observed a similar phenomenon in our recent work featuring viscoelastic droplets in T-junction microfluidic devices,25 thus suggesting that fluid viscoelasticity impacts more the dynamics of droplet formation rather than the final size, in agreement with other studies.8,28–33 Similarly to the droplet size, we also observed that the frequency of droplet formation fd scaled according to a mastercurve dependent upon the flow rate ratio q and the Capillary number Ca (Fig. 1d), with expression:
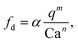 | (1) |
The results presented lay the foundation to demonstrate the controlled encapsulation principle in flow-focusing geometries thanks to the viscoelasticity of the dispersed suspending phase. When the process of loading particles into drops is purely random, the Poisson statistics predicts that the probability P of droplets containing n particles is given by:
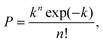 | (2) |
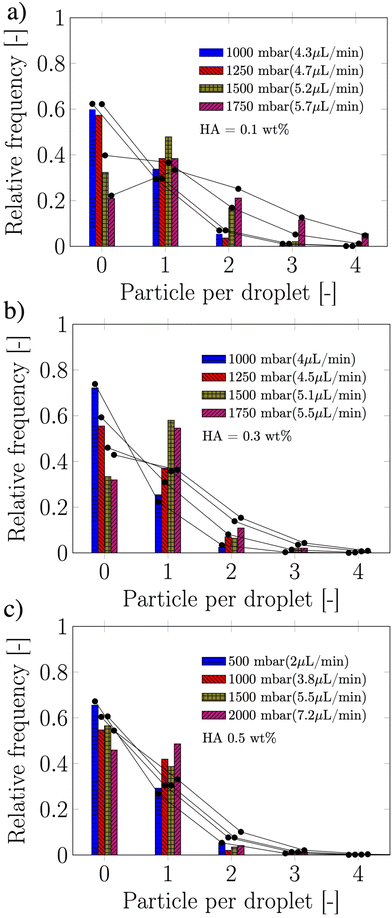
Owing the combination of the viscoelasticity-driven particle ordering and droplet formation, we observed a single particle encapsulation efficiency value above the Poisson stochastic limit for all the viscoelastic fluids employed (Fig. 2(a–c)). For each HA concentration, we observed a non-monotonic behaviour for the encapsulation efficiency, with a unique combination of parameters in which the single encapsulation efficiency was the highest possible. This is clearly expected as the optimal encapsulation conditions are only observed when fd = fp. Please note that the frequency of droplet formation, fd, changes with different values of the flow rate of the dispersed phase,5,6 while the frequency of particle approaching the encapsulation area, fp, does not depend significantly on the volumetric flow rate.18,21 This is also in good agreement with our previous work on viscoelastic particle encapsulation in T-junction25 and other works on inertial encapsulation.22 We also derived an expression that can guide the choice of experimental parameters aimed at obtaining a controlled encapsulation. In an ideal particle train with local concentration ϕl = Nd/L, where N is the number of particle observed in a video frame, d is the particle diameter and L is the length of the video frame, particles are equally spaced with a constant inter-particle distance.18,21 The expression for the frequency of particles approaching the encapsulation area is fp = uϕl/d,25 where u is the particle velocity. The use of ϕl over the bulk particle concentration is motivated by the fact that ϕl accounts for fluctuations in the local particle concentration, while the bulk particle concentration does not.11,21,25 (The relation between ϕl and the bulk concentration ϕb is18,25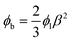 , where β = d/H is the confinement ratio for square-shaped geometries). By combining the expression for fp with the expression for fd (eqn (1)), the optimal encapsulation condition (fd = fp) is:
, where β = d/H is the confinement ratio for square-shaped geometries). By combining the expression for fp with the expression for fd (eqn (1)), the optimal encapsulation condition (fd = fp) is:
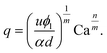 | (3) |
Being n ≈ m ≈ 1 (from the fitting of eqn (1)), an approximated expression of eqn (3) is:
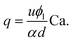 | (4) |
Note that eqn (4) is very similar to the equation we previously found in T-junction geometry, when using xanthan gum as viscoelastic liquid.25
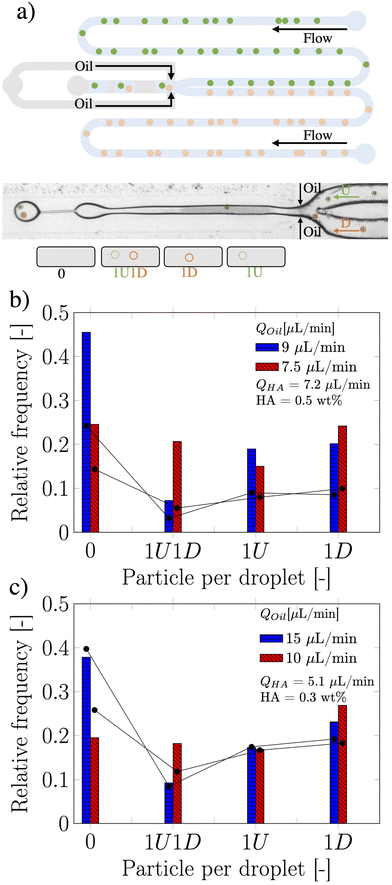
While single particle encapsulation is important in the context of optimising compartmentalisation efficiency,1 a step further aimed at targeting single-cell analysis applications is the co-encapsulation of particles and cells arriving from two different flow streams. For instance, this is extremely relevant for Drop-seq applications,2 where flowing cells need to be encapsulated together with functionalised beads in the same droplet in order to extract the genome of the cell. This application certainly benefits from a controlled encapsulation perspective, as the number of unused beads decreases while the number of analysed cells in a single run increases.23 Motivated by the success in achieving a controlled single particle encapsulation in a flow-focusing device, we investigated the possibility of overcoming the Poisson stochastic limit in co-encapsulation applications using viscoelastic liquids. Here, the co-encapsulation of particles was studied by introducing a second inlet to the original single encapsulation design (see Fig. 3a).
The two streams of dispersed phase, here referred as type U and type D (representing “up” and “down” stream from a top view of the device), met at the junction, while the continuous mineral oil phase did cut the HA dispersed phase to form viscoelastic droplets containing particles coming from the two streams. The Poisson probability for the co-encapsulation in a droplet containing nD particles of type D and nU particles of type U is given by the product of the two independent Poisson probabilities as:
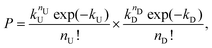 | (5) |
In summary, we here demonstrated controlled encapsulation and co-encapsulation of particles in flow focusing geometries using viscoelastic fluids, achieving efficiency up to 2-fold larger compared to the Poisson value. The results presented here are an extension of our previous work on T-junction geometries.25 Future work should extend our findings further to include different particle diameters as well as experiments on cells. With regards to the second point, this is not straightforward as cells require phosphate buffer saline (or cell media) to survive in solution: being HA a polyelectrolyte, addition of salt to a fixed polymer concentration would alter the rheological properties by decreasing both the elasticity and the shear-thinning properties:35,36 both conditions are required to observe self-assemble of viscoelastic particle trains in microchannels.18 It is important to stress the fact that similar results may potentially be achieved using a different set of polymer solutions, including polyethylene oxide and polyacrylamide, as long as the resulting solutions display shear-thinning properties to enable particle ordering.18 In such cases, the experimental parameters to obtain a controlled encapsulation are likely to be different from the ones employed here due to the complexity of the droplet formation mechanisms5 and of the ordering phenomenon.18
F.D.G acknowledges support from EPSRC New Investigator Award, grant EP/S036490/1. The data that support the findings of this study are available from the corresponding author upon reasonable request.
Author contributions
F. D. G. designed the study. K. S. performed the experiments and analysed the data. Both authors wrote the manuscript and approved the final submission.Conflicts of interest
The results presented in this manuscript have also been submitted as part of a patent application.References
- F. Del Giudice, G. D’Avino and P. L. Maffettone, Lab Chip, 2021, 21, 2069–2094 RSC.
- E. Z. Macosko, A. Basu, R. Satija, J. Nemesh, K. Shekhar, M. Goldman, I. Tirosh, A. R. Bialas, N. Kamitaki and E. M. Martersteck, et al. , Cell, 2015, 161, 1202–1214 CrossRef CAS PubMed.
- V. A. Turek, Y. Francescato, P. Cadinu, C. R. Crick, L. Elliott, Y. Chen, V. Urland, A. P. Ivanov, L. Velleman and M. Hong, et al. , ACS Photonics, 2016, 3, 35–42 CrossRef CAS.
- G.-R. Yi, T. Thorsen, V. N. Manoharan, M.-J. Hwang, S.-J. Jeon, D. J. Pine, S. R. Quake and S.-M. Yang, Adv. Mater., 2003, 15, 1300–1304 CrossRef CAS.
- J. Nunes, S. Tsai, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 CrossRef PubMed.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446 RSC.
- E. W. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. Van Den Berg, Lab Chip, 2012, 12, 2881–2887 RSC.
- W. Du, T. Fu, Q. Zhang, C. Zhu, Y. Ma and H. Z. Li, Chem. Eng. Sci., 2016, 153, 255–269 CrossRef CAS.
- J.-P. Matas, V. Glezer, É. Guazzelli and J. F. Morris, Phys. Fluids, 2004, 16, 4192–4195 CrossRef CAS.
- K. J. Humphry, P. M. Kulkarni, D. A. Weitz, J. F. Morris and H. A. Stone, Phys. Fluids, 2010, 22, 081703 CrossRef.
- S. Kahkeshani, H. Haddadi and D. Di, Carlo, J. Fluid Mech., 2016, 786, R3-1–R3-11 Search PubMed.
- W. Lee, H. Amini, H. A. Stone and D. Di Carlo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22413–22418 CrossRef CAS PubMed.
- Y. Gao, P. Magaud, L. Baldas, C. Lafforgue, M. Abbas and S. Colin, Microfluid. Nanofluid., 2017, 21, 1–10 CrossRef CAS.
- C. Dietsche, B. R. Mutlu, J. F. Edd, P. Koumoutsakos and M. Toner, Microfluid. Nanofluid., 2019, 23, 1–8 CrossRef.
- X. Hu, J. Lin, D. Chen and X. Ku, Microfluid. Nanofluid., 2020, 24, 1–12 CrossRef.
- J. Liu and Z. Pan, Phys. Fluids, 2022, 34, 023309 CrossRef CAS.
- G. D’Avino, M. A. Hulsen and P. L. Maffettone, Comput. Fluids, 2013, 86, 45–55 CrossRef.
- F. Del Giudice, G. D’Avino, F. Greco, P. L. Maffettone and A. Q. Shen, Phys. Rev. Appl., 2018, 10, 064058 CrossRef CAS.
- G. D’Avino and P. L. Maffettone, Microfluid. Nanofluid., 2019, 23, 82 CrossRef.
- G. D’Avino and P. L. Maffettone, Meccanica, 2020, 55, 317–330 CrossRef.
- A. Jeyasountharan, K. Shahrivar, G. D’Avino and F. Del Giudice, Anal. Chem., 2021, 93, 5503–5512 CrossRef CAS PubMed.
- J. F. Edd, D. Di Carlo, K. J. Humphry, S. Köster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262–1264 RSC.
- L. Li, P. Wu, Z. Luo, L. Wang, W. Ding, T. Wu, J. Chen, J. He, Y. He and H. Wang, et al. , ACS Sens., 2019, 4, 1299–1305 CrossRef CAS PubMed.
- J. Harrington, L. B. Esteban, J. Butement, A. F. Vallejo, S. I. Lane, B. Sheth, M. S. Jongen, R. Parker, P. S. Stumpf and R. C. Smith, et al. , Lab Chip, 2021, 21, 3378–3386 RSC.
- K. Shahrivar and F. Del Giudice, Soft Matter, 2021, 17, 8068–8077 RSC.
- A. Jeyasountharan, G. D’Avino and F. Del Giudice, Phys. Fluids, 2022, 34, 042015 CrossRef CAS.
- Q. Chen, J. Li, Y. Song, D. M. Christopher and X. Li, Heat Mass Transfer, 2020, 56, 2711–2723 CrossRef.
- B. Rostami and G. L. Morini, Int. J. Multiphase Flow, 2018, 105, 202–216 CrossRef CAS.
- M. Fatehifar, A. Revell and M. Jabbari, Polymers, 2021, 13, 1915 CrossRef CAS PubMed.
- V.-L. Wong, K. Loizou, P.-L. Lau, R. S. Graham and B. N. Hewakandamby, Chem. Eng. Sci., 2017, 174, 157–173 CrossRef CAS.
- Y. Ren, Z. Liu and H. C. Shum, Lab Chip, 2015, 15, 121–134 RSC.
- Q. Chen, J. Li, Y. Song, B. Chen, D. M. Christopher and X. Li, Int. J. Multiphase Flow, 2021, 140, 103648 CrossRef CAS.
- C.-D. Xue, X.-D. Chen, Y.-J. Li, G.-Q. Hu, T. Cao and K.-R. Qin, Micromachines, 2020, 11, 406 CrossRef PubMed.
- T. P. Lagus and J. F. Edd, RSC Adv., 2013, 3, 20512–20522 RSC.
- F. Del Giudice, V. Calcagno, V. Esposito Taliento, F. Greco, P. A. Netti and P. L. Maffettone, J. Rheol., 2017, 61, 13–21 CrossRef CAS.
- R. H. Colby, Rheol. Acta, 2010, 49, 425–442 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00935h |
| This journal is © The Royal Society of Chemistry 2022 |