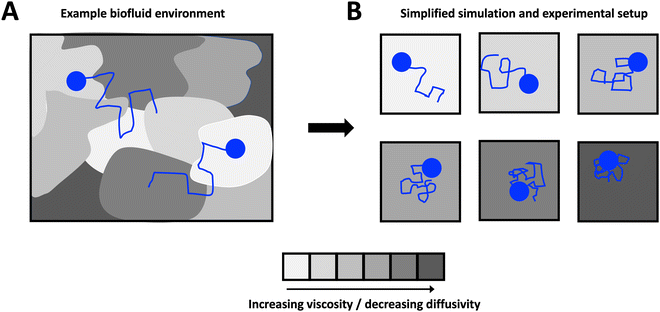
Open Access Article
Open Access ArticleDistributed medium viscosity yields quasi-exponential step-size probability distributions in heterogeneous media
Nicole A.
Bustos
 a,
Chadi M.
Saad-Roy
a,
Chadi M.
Saad-Roy
 bcd,
Andrey G.
Cherstvy
bcd,
Andrey G.
Cherstvy
 e and
Caroline E.
Wagner
e and
Caroline E.
Wagner
 *f
*f
aDepartment of Mechanical Engineering, MIT, Cambridge, MA 02139, USA
bLewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ 08540, USA
cMiller Institute for Basic Research in Science, University of California, Berkeley, Berkeley, CA 94720, USA
dDepartment of Integrative Biology, University of California, Berkeley, Berkeley, CA 94720, USA
eInstitute for Physics and Astronomy, University of Potsdam, 14476 Potsdam-Golm, Germany
fDepartment of Bioengineering, McGill University, Montreal, QC H3A 0E9, Canada. E-mail: caroline.wagner@mcgill.ca
First published on 14th November 2022
Abstract
The analysis of the statistics of random walks undertaken by passive particles in complex media has important implications in a number of areas including pathogen transport and drug delivery. In several systems in which heterogeneity is important, the distribution of particle step-sizes has been found to be exponential in nature, as opposed to the Gaussian distribution associated with Brownian motion. Here, we first develop a theoretical framework to study a simplified version of this problem: the motion of passive tracers in a range of sub-environments with different viscosity. We show that in the limit of a large number of equi-distributed sub-environments spanning a broad viscosity range, an exact analytical expression for the underlying particle step-size distribution can be derived, which approaches an exponential distribution when step sizes are small. We then validate this using a simple experimental system of glycerol–water mixtures, in which the volume fraction of glycerol is systematically varied. Overall, the assumption of exponentially distributed step sizes may substantially over-estimate the incidence of large steps in heterogeneous systems, with important implications in the analysis of various biophysical processes.
1 Introduction
Understanding the motion of small particles in complex media has important applications in a number of biophysical fields, including drug delivery,1 pathogen transport,2 and material characterization (i.e. microrheology).3 In simple homogeneous Newtonian media, passive particles undergo normal diffusion due to random collisions with solvent molecules; the well-understood phenomenon of Brownian motion. Normal diffusive processes are characterised by a Gaussian distribution in particle step-sizes and a linear increase in the particle mean-squared displacement (MSD) with time.4 In biophysical systems, however, many of the assumptions underlying Brownian motion may be violated, leading to the emergence of anomalous diffusive behaviour for passive particles. Examples include, but are not limited to, binding interactions between the particle and components of the medium,5 medium viscoelasticity including particle confinement by a polymer network,6 polydispersity of the tracers,7 and environmental heterogeneity.8The underlying distribution of particle step sizes, in combination with the distribution of waiting times between successive particle jumps (possibly arising as a result of, say, binding between the particle and medium components) are the two features that dictate the evolution of the displacement of particles undergoing the generalised process of a continuous-time random walk (CTRW),4 which can be used to describe the motion of particles in complex media. As a result, analyzing distributions of particle step sizes, or van Hove distributions, is a frequently used readout to explore physicochemical factors in a given particle—medium system that may be resulting in deviations from normal diffusion.
One step-size distribution that has been documented to emerge in several systems is an exponential distribution, as a opposed to the Gaussian distribution associated with Brownian motion. A common unifying feature to many—if not all—of these systems is either spatial or temporal heterogeneity in the behaviour of the individual tracers. For example, Wagner et al.8,9 observed exponential step-size distributions for a subset of particles in MUC5AC mucin gels, which were thought to have mesoscopically phase-separated under the acidic experimental conditions. These distributions have also been reported in a number of other biological systems including particle motion in agarose gels,10 tumor-cell migration in two and three dimensions,11 the motion of acetylcholine receptors on muscle-cell membranes,12 the diffusion of doxorubicin drug molecules in silica nanoslits,13 colloidal beads diffusing on lipid tubes,14 and nanospheres diffusing in entangled F-actin networks.14 This phenomenon has also been observed in non-biological materials close to glass or jamming transitions.15 Indeed, in at least two of these studies12,14 it has been conjectured that these exponential distributions may emerge as a result of the aggregation of a series of Gaussian distributions with different variances that describe the motion of individual tracers, but not of the ensemble.
Here, we develop theory, which we support with the results from both numerical simulations and experiments, to investigate the origin of reported exponentially distributed particle step sizes in heterogeneous media. We consider a theoretical scenario in which we simplify heterogeneous complex media, shown schematically in Fig. 1A, as a series of homogeneous Newtonian sub-environments of varying viscosity (Fig. 1B). We show that, despite the step-size distributions of particles in a single sub-environment being Gaussian, the combined distribution when particle steps are pooled across all sub-environments is no longer normal. In Section 3.1, we derive an exact analytical expression for the underlying particle step-size distribution in the limit of a large number of sub-environments linearly spanning a broad range of particle diffusivities, which we confirm with numerical simulations in Section 3.2. We show that for small step sizes only, this expression approaches an exponential distribution, but that the incidence of large steps may be substantially over-estimated if an exponential relationship is assumed. We then validate these results in a simplified glycerol–water system in Section 3.3, and provide concluding remarks in Section 4.
2 Materials and methods
Samples for single-particle tracking (SPT) experiments were prepared by combining 30 μL of a sample of glycerol (Sigma, Catalog No. G9012-2L)–water mixture ranging from 0% to 88.6% glycerol by volume with 0.5 μL of a solution of 0.19 μm diameter, fluorescent, negatively charged (carboxylated) microspheres (Magsphere Inc., Catalog No. CAF-200NM) in deionised water at a dilution ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 by volume (resulting in an overall dilution ratio of 1
200 by volume (resulting in an overall dilution ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the microspheres). Specimens were subsequently vortexed to ensure adequate mixing and then loaded via pipet into borosilicate square capillaries ≈0.9 mm × 0.9 mm × 15 mm in dimension (Vitrocom 8290). The capillaries were sealed on either end using a 1
000 for the microspheres). Specimens were subsequently vortexed to ensure adequate mixing and then loaded via pipet into borosilicate square capillaries ≈0.9 mm × 0.9 mm × 15 mm in dimension (Vitrocom 8290). The capillaries were sealed on either end using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of Vaseline, lanolin, and paraffin to prevent evaporation and then mounted onto microscope slides for imaging.
1 mixture of Vaseline, lanolin, and paraffin to prevent evaporation and then mounted onto microscope slides for imaging.
Imaging was performed at ≈30 frames per second for 10 s at room temperature with an Axio Observer D.1 inverted microscope using a Zeiss LD Plan-Apochromat 100×/1.4 Oil Ph3 objective lens and a Hamamatsu Flash 4.0 C1144022CU camera. For each resulting image frame, particles were identified using publicly available Matlab16 code, which identifies candidate features using high-intensity matches and filters them using criteria such as maximum feature eccentricity and radius of gyration.
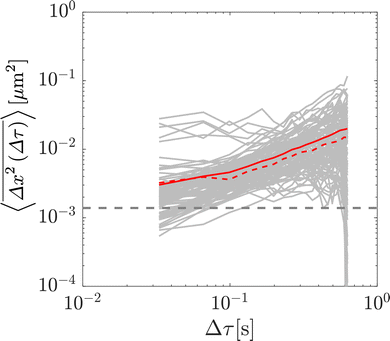
As a result of the substantial increase in medium viscosity with increasing glycerol concentration, the duration of the particle trajectories was, on average, longer at higher glycerol concentrations (due to slower diffusion in media of higher viscosity). Therefore, to guarantee an equal number particle steps at each glycerol concentration, all accepted trajectories were restricted to 20 frames: longer trajectories were shortened, and shorter trajectories were discarded. Although this discarding may bias the inferred medium rheological properties in heterogeneous media by retaining trajectories corresponding to particles in more viscoelastic subregions,9,17 in these simple Newtonian solutions shorter trajectories simply correspond to particles that were in focus for a shorter duration, and as such overall particle statistics are not affected. In addition to the average trajectory length varying with medium concentration, a larger number of particles were also successfully identified and tracked for higher concentrations of glycerol. As such, for all glycerol concentrations, a subset of 107 particles, corresponding to the number of particle tracks at 0% glycerol, were randomly selected for analysis. In summary, for each glycerol concentration, 107 particle trajectories 20 frames in length were retained for analysis.
The x and y positions of every retained particle were recorded using the same publicly available MATLAB code by the center of mass of the localised image intensity. A drift-correction code from a publicly available source18 was subsequently applied to all SPT data. This correction subtracts the center of mass motion of all of the particles in a given frame from each individual trajectory. Using these drift-corrected data, the time-averaged mean-squared displacement (TAMSD; in one dimension) of the jth particle for a movie M images in length is given by
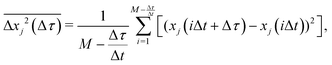 | (1) |
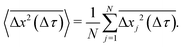 | (2) |
3 Results
3.1 Derivation of the theoretical probability distribution function
The quantitative description of the statistical walk undertaken by a tracer particle in a Newtonian liquid of viscosity μ undergoing regular Brownian motion is well known.4 In 1-D, the ensemble-averaged particle MSD as a function of experimental lag time Δτ, denoted by 〈Δx2(Δτ)〉, scales linearly with the lag time via the relationship| 〈Δx2(Δτ)〉 = 2DΔτ, | (3) |
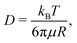 | (4) |
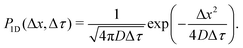 | (5) |
As described in Section 1, exponential step-size distributions have been documented to emerge in a number of systems. In some cases, this has been attributed to variations in the diffusion coefficients between individual tracers,12,14 reflecting medium heterogeneity. However, these distributions have also been observed to arise via different mechanisms in other model systems, including due to temporal (in addition to spatial) heterogeneity in the motion of individual tracers.11,13 Following ref.8, we can express the associated PDF for this distribution as
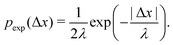 | (6) |
Assume that we are tracking the motion of N particles, which are evenly distributed within n Newtonian sub-environments characterised by distinct viscosities and hence diffusion coefficients. The particles are assumed to be evenly distributed such that there are N/n particles in each sub-environment. In reality, in the limit of long times a quasi-equilibrium would be expected to be reached experimentally, where particles would predominantly occupy the regions of slower diffusivity (or higher viscosity).
However, if the measurements are being taken on particles initially evenly spread between the sub-environments with different viscosities and tracked for considerably shorter times, then this assumption indeed reflects a realistic experimental scenario. For simplicity, note that the variance of each Gaussian PDF is given by σ2 = 2DΔτ, such that eqn (5) can be expressed as
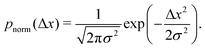 | (7) |
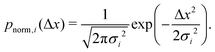 | (8) |
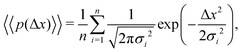 | (9) |
Assume further than the viscosities of the sub-environments vary between values of μ and μ/ε, where ε ≪ 1. Therefore, μ/ε describes the viscosity of the most viscous sub-environment. From eqn (4), assumed to be valid across regions of all viscosities, the diffusion coefficients then vary between εD and D, where D describes the diffusion coefficient in the least viscous region. The variances of the Gaussian PDFs associated with the step-size distributions in each sub-environment then also vary between εσ2 and σ2.
For mathematical tractability, suppose that the sub-environments are chosen such that the diffusion coefficients vary linearly between εD and D. This allows us to derive an expression for the variance of the step-size PDF in each sub-environment. In particular, we obtain
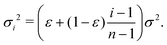 | (10) |
The aggregate PDF from eqn (9) can then be written as
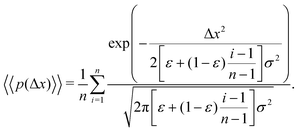 | (11) |
We note that more generally, as in ref. 14, the aggregate PDF across particles divided into n sub-environments, for which the step-size distribution in each i-th sub-environment is given by pnorm,i(Δx), can be written as
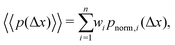 | (12) |
Returning to our scenario and eqn (11), we can simplify notation by letting Δx → x such that we obtain
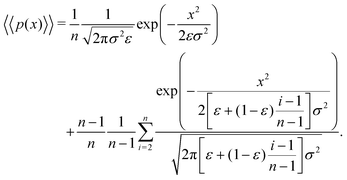 | (13) |
Letting j = i − 1 and m = n − 1, eqn (13) can be written as
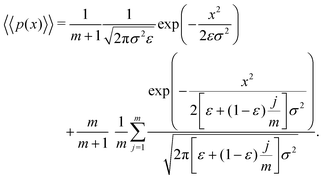 | (14) |
In the limit of n → ∞, i.e. a very large number of sub-environments, then m → ∞ and the first term of eqn (14) approaches 0. Further, the second term approaches the integral
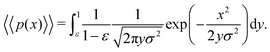 | (15) |
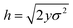 , such that
, such that 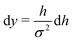 . Substituting this into eqn (15) we obtain
. Substituting this into eqn (15) we obtain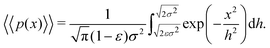 | (16) |
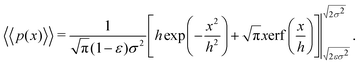 | (17) |
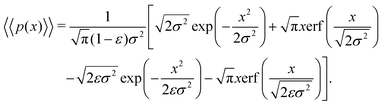 | (18) |
Eqn (18) can be simplified under various limiting scenarios. In the limit of ε → 0, relevant in highly heterogeneous biological media in which the sub-environments may vary from pure water to a dense protein gel, the third term in square brackets in eqn (18) will tend to 0, while the error function in the fourth term will quickly saturate to a value of ±1 depending on the sign of x, such that the fourth term will tend to 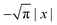 . We therefore simplify expression (18) to
. We therefore simplify expression (18) to
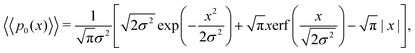 | (19) |
Using Taylor expansions for the exponential and error functions, we can write eqn (19) for small values of displacements x as
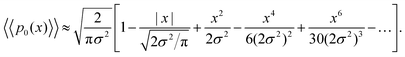 | (20) |
On the other hand, the exponential PDF in eqn (6) can similarly be expanded to yield
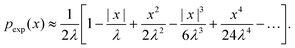 | (21) |
Interestingly, for small x, the two expansions in eqn (20) and (21) do indeed possess the same functional dependencies, albeit with different coefficients, as can be seen by the terms up to second order in x. However, beyond this the expansions differ, and an exponential PDF is not recovered exactly. Both expansions feature alternating positive and negative terms, although notably there are no odd terms other than the first term in |x| in the expansion of eqn (20). The step-size PDF in eqn (20)—equivalent for small x to an exponential PDF—is therefore a fundamental consequence of sampling an ensemble of heterogeneous sub-environments in the model.
3.2 Numerical simulations
We simulate a simple Brownian motion for N = 1000 particles in one dimension, where the particles are randomly and equally divided among the two sub-environments. We perform the simulation for 500 steps which are assumed to occur at time intervals of 1/30 s. At each time step, we draw a particle step-size in the x direction from the Gaussian PDF in eqn (5) depending on the sub-environment assigned to that particle. In this way, the simulation does not assign a true spatial organization to sub-environments, it simply records the position of the particles that remain in their assigned sub-environment for all times considered. The variance of the Gaussian PDF in each sub-environment is set by the local viscosity and, hence, particle diffusion coefficient. In Fig. 2A, we plot the individual particle TAMSDs as the thin grey lines. TAMSD clustering by sub-environment is clearly demonstrated, and the solid grey circles denote the ensemble-averaged TAMSDs in each sub-environment. The solid blue circles are the ensemble-averaged TAMSD at each lag time across all particles. Intuitively, this result is well-described by eqn (3), when the diffusivity is taken to be the average diffusivity across both regions (the dashed black line).
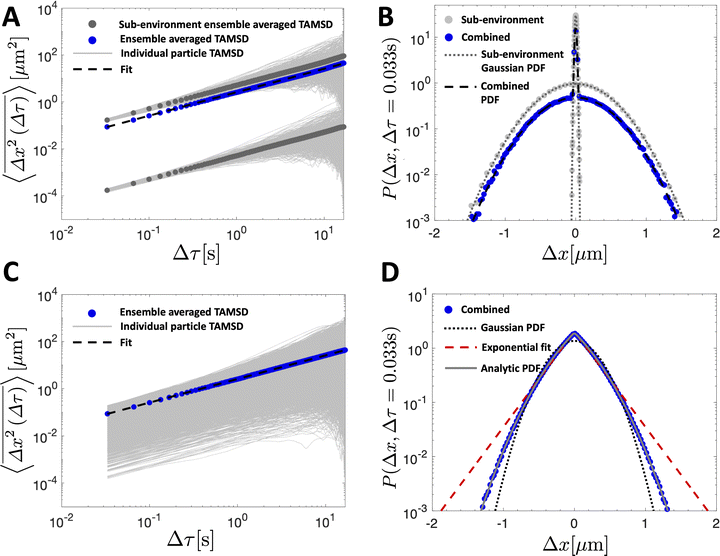 | ||
Fig. 2 TAMSDs and van Hove distributions from numerical simulations of particle trajectories in various numbers of sub-environments. In all panels, the least viscous sub-environment has the viscosity of water at room temperature, i.e. T = 298 K and μ1 = 8.9 × 10−4 Pa s, and the particle diameter is set to be 2R = 0.19 μm. The parameter ε = 0.001 sets the viscosities and diffusivities of the other sub-environments, eqn (10). In (A and B), 1000 particles are simulated for 500 frames assumed to be spaced by 1/30 s in 2 sub-environments. The TAMSDs are shown in (A), with thin grey lines showing individual particle TAMSDs, solid grey dots showing the ensemble-averaged TAMSD of each sub-environment, and the solid blue dots correspond to the ensemble-averaged TAMSD over all particles. The dashed black curve is given by eqn (3) with D taken to be the average diffusivity across both sub-environments. The corresponding step-size distributions at Δτ = 0.033 s are shown in (B). The solid grey circles are the step-size distributions of particles in each sub-environment, and the solid blue circles denote the distribution for all particles. The dotted dark grey line is eqn (5) with the diffusivity of each sub-environment, and the dashed black curve corresponds to eqn (9) with 2 sub-environments. In (C and D), 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles are simulated for 500 frames assumed to be spaced by 1/30 s in 1000 sub-environments. In (C), the thin grey lines show individual particle TAMSDs, and the solid blue dots correspond to the ensemble-averaged TAMSD over all particles. The dashed black curve is given by eqn (3) with D taken to be the average diffusivity across all sub-environments. The corresponding step-size distribution across all particles at Δτ = 0.033 s is shown in (D) (solid blue dots). The dotted black line is eqn (5) with the average diffusivity across all sub-environments. The dashed red line is a best fit of eqn (6) to the step-size distribution. The solid grey curve, nearly superimposing with the blue dots, is the exact analytic result of eqn (18). 000 particles are simulated for 500 frames assumed to be spaced by 1/30 s in 1000 sub-environments. In (C), the thin grey lines show individual particle TAMSDs, and the solid blue dots correspond to the ensemble-averaged TAMSD over all particles. The dashed black curve is given by eqn (3) with D taken to be the average diffusivity across all sub-environments. The corresponding step-size distribution across all particles at Δτ = 0.033 s is shown in (D) (solid blue dots). The dotted black line is eqn (5) with the average diffusivity across all sub-environments. The dashed red line is a best fit of eqn (6) to the step-size distribution. The solid grey curve, nearly superimposing with the blue dots, is the exact analytic result of eqn (18). | ||
The step-size distributions, or van Hove plots, at the earliest lag time of Δτ = 1/30 s for the two sub-environment scenario is shown in Fig. 2B. As can be seen, the van Hove distributions of each sub-environment (solid grey circles) are Gaussian, and excellent agreement with eqn (5) is recovered (dotted dark grey lines) when the appropriate sub-environment diffusivity is accounted for. The step-size distribution across both sub-environments, however, is clearly not described by a Gaussian curve (solid blue circles). The pronounced peak in the PDF is due to particles diffusing very slowly in the highly viscous sub-environment. However, excellent agreement with eqn (9), which takes the weighted sum of both Gaussian distributions, is observed (the dashed black curve).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and set the number of sub-environments to n = 1000. We keep all other parameters identical to those described in the simulations with 2 sub-environments. In this more involved case, the particle diffusivity in each sub-environment is given by D1 = εD and
000 and set the number of sub-environments to n = 1000. We keep all other parameters identical to those described in the simulations with 2 sub-environments. In this more involved case, the particle diffusivity in each sub-environment is given by D1 = εD and 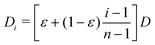 for i = 2…n, where D is the diffusivity in the least viscous sub-environment.
for i = 2…n, where D is the diffusivity in the least viscous sub-environment.
In Fig. 2C, we plot the individual particle TAMSDs as the thin grey lines, and the ensemble-averaged TAMSD across all sub-environments as the solid blue circles. Once again, the ensemble-averaged TAMSD is simply set by the average diffusivity of all sub-environments and eqn (3). In Fig. 2D, we plot the van Hove distribution across all particles, again at the earliest lag time of Δτ = 1/30 s, as the solid blue circles. As can be seen, in this limiting case of a large number of sub-environments with linearly-spaced diffusivities, excellent agreement with the theoretical analytic result (18) is recovered (the solid grey curve). Conversely, a Gaussian curve using eqn (5) and the average diffusivity across all sub-environments (dotted black curve) underestimates the incidence of small steps (from high viscosity regions) and large steps (from low viscosity regions). Finally, an exponential fit following eqn (6) to the step-size PDF is shown as the dashed red curve. Although this approximation is quite accurate for small step sizes, the exponential curve overestimates the incidence of large steps. This is consistent with the agreement between the exponential (eqn (21)) and exact analytic (eqn (20)) series expansions only occurring for small Δx.
3.3 Experimental data
To validate the numerical results, we tracked the motion of tracer particles with diameter 0.19 μm in 10 distinct glycerol–water mixtures that were systematically chosen to produce 10 approximately linearly-spaced particle diffusivities. More explicitly then, each experimental sub-environment was created in a distinct experimental setup, and therefore particles were incapable of experimentally sampling numerous sub-environments. The diffusivity of each glycerol–water mixture was determined by fitting the ensemble-averaged TAMSD for each mixture (Fig. 3A) between two specific time points (shown as the grey asterisks in Fig. 3A) with eqn (3). For 9 of the 10 solutions, earlier lag times were used to fit eqn (3). However, for the most viscous solution, 88.6% glycerol, later lag times were used to perform the fitting, as a result of a slope change in the early portion (Δτ ≲ 0.1 s) of the TAMSD.To understand the origin of this behaviour, in Fig. 4, we plot not only the ensemble-averaged TAMSD for this sub-environment (the solid red curve), but also the individual particle TAMSDs (solid grey curves) and the ensemble-averaged MSD (not time-averaged; the dashed red line). At short lag times, the particle TAMSDs approach the static error of the experimental setup (dashed grey curve), which may contribute to experimental error. Additionally, a minority of curves are characterised by relatively flat TAMSDs that are substantially greater than the remaining curves, particularly at short lag times. We suspect that this behaviour may have arisen as a tracking artifact in this highly viscous environment, in which particle displacement is relatively small. For instance, these particles may have been located substantially outside of the experimental focal plane, yet their minimal displacement in this highly viscous environment may have allowed for them to be ‘tracked’ for a sufficiently long period by the analysis code. In contrast, in less viscous environments, the motion of out of plane particles is quickly lost as they diffuse away from the experimental focal plane, see also the discussion in ref. 9.
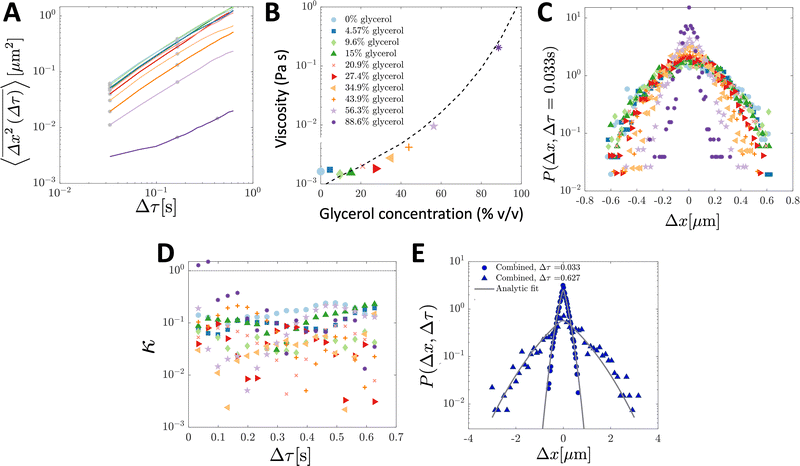 | ||
| Fig. 3 Ensemble-averaged TAMSDs and van Hove distributions from SPT experiments of tracer particles in various glycerol–water mixtures. For analysis, 107 particle trajectories 20 frames in length were retained for each mixture. In (A), the ensemble-averaged TAMSDs for each mixture are shown as solid colored lines. The colors in (A) correspond to the legend in (B), and the same color and marker schemes from (B) are used in (C and D). Grey asterisks denote where eqn (3) was fitted for each mixture to extract its corresponding diffusivity. The fit was performed at later lag times for the most viscous solution (88.6% glycerol) as discussed and further analysed in Fig. 4. In (B), the viscosity for each mixture was determined from eqn (4) using room temperature, T = 298 K, the particle diameter, 2R = 0.19 μm (as in the simulations), and the extracted diffusivity. The black dashed line denotes the expected viscosity for each glycerol–water mixture obtained from ref. 19 and 20. In (C), the van Hove distribution for each mixture is shown at Δτ = 0.033 s. In (D), the corresponding non-Gaussian parameter κ (eqn (23)) associated with the van Hove distributions for each mixture as a function of lag time are plotted. The thin dotted line denotes κ = 1. In (E), the combined van Hove distribution for particles across all 10 sub-environments at Δτ = 0.033 s and Δτ = 0.627 s is shown (solid blue dots and triangles, respectively). The solid grey curves are the exact analytic result from eqn (18) at both lag times, with D corresponding to the measured diffusion coefficient in the least viscous sub-environment, water (i.e. 0% glycerol), and ε = 0.0079 determined by the viscosity of the sub-environment with the highest glycerol concentration (88.6%). | ||
Using T = 298 K, the known particle diameter, and the extracted diffusivity, a viscosity for each mixture was determined from eqn (4) (plotted in Fig. 3B). The calculated viscosities (colored symbols) follow the expected viscosity of glycerol–water mixtures (dashed lines), determined using ref. 19 and 20. In these experiments, the most viscous sub-environment, 88.6% glycerol, was approximately 100 times more viscous than water, the least viscous sub-environment. Specifically, this corresponded to ε = 0.0079 (see Section 3.1 for additional details). We note that this degree of variation is in line with the viscosity heterogeneities encountered in important biological systems. For instance, the viscosity of the cell cytoplasm has been estimated to be approximately 3 times that of water (ref. 21, in CHO cells), while that of the cell membrane has been reported to be approximately 950 times that of water in Escherichia coli22 and approximately 270 times that of water in the plasma membrane of SK-OV-3 cells.23 The process of viscoelastic phase separation and the mobility of the distinct phases in biological cells has recently been explored in detail in ref. 24.
The step-size distributions at the earliest lag time Δτ = 1/30 s for each of the sub-environments is shown in Fig. 3C. For a Gaussian distribution, the kurtosis β (the ratio of the fourth to the second moment of the distribution) of the van Hove distribution can be shown to be8
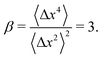 | (22) |
Therefore, we can define a non-Gaussian parameter κ as in ref. 8 as
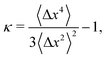 | (23) |
Finally, in Fig. 3E, the combined step-size distribution across all 10 sub-environments is shown for two lag times, Δτ = 0.033 s (circles, κ = 0.18) and Δτ = 0.627 s (triangles, κ = 0.18). We fit the van Hove distributions at both lag times with the exact analytic expression from eqn (18) using the diffusivity obtained from the least viscous sub-environment (water, i.e. 0% glycerol). Further, the parameter ε is obtained from the ratios of the viscosities in the least and most (88.6% glycerol) viscous sub-environments, yielding ε = 0.0079. Excellent agreement with the exact analytic result is observed at both lag times.
4 Discussion and conclusion
Interpreting the motion of small passive particles in soft-matter systems has numerous important applications across a range of biophysical systems including those involved in material characterization, drug delivery, and pathogen transport. The complexity of either or both of the particles and fluid environments frequently result in the observation of anomalous, non-Brownian, diffusive motion in these systems. This may manifest in terms of the distribution of step sizes taken by the particles, the scaling relationship between the MSD and lag time, and/or the distribution of waiting times between successive particle steps. Here, we focus on the well-documented emergence of non-Gaussian step-size distributions in heterogeneous media, which are frequently reported to be exponential in nature. We show analytically that when particles are distributed across sub-environments with a broad, linearly distributed range of diffusivities, analyzing their step-size distributions in a cumulative fashion indeed results in a distribution that approaches an exponential for small step sizes.However, the exact result is not exponential, and the assumption of an exponential distribution may substantially over-estimate the frequency of large steps. We subsequently validate this result numerically and experimentally in a Newtonian glycerol–water system in which we sequentially increase the viscosity of sub-environments by increasing the concentration of glycerol.
As a further development, particle diffusion-coefficient distributions other than linear ones can be considered rather straightforwardly, and their effect on step-size distributions examined. Similarly, scenarios with time-varying particle diffusivities, or sub-environment viscosities, could be considered, such as those explored in models of “diffusing diffusivity”.26–29
To explore the effect of heterogeneity explicitly, we make several simplifying assumptions in our analysis that are likely highly relevant to several biophysical systems. We assume that each sub-environment is a purely Newtonian liquid with a unique viscosity, when in reality many biofluids are viscoelastic. Even in the absence of heterogeneity, anomalous diffusive motion may be encountered in viscoelastic media, such as non-linear dependencies of the TAMSD on lag time. This is not accounted for in the simulations performed here, and we would not expect to observe such effects experimentally in the Newtonian glycerol–water system chosen. Beyond viscoelasticity, other factors relevant to several biophysical systems that we omit in the current analysis include processes such as particle-polymer binding, which may alter the distribution of waiting times taken by the particle and consequently the statistics of the walk. Therefore, while we focus here on spatial heterogeneity leading to non-Gaussian step-size distributions, in reality several other processes of biophysical relevance may also contribute to this phenomenon.
Medium heterogeneity may introduce numerous complexities into the analysis of SPT datasets of diffusion of passive particles. Notably, the ability to generalise the Stokes–Einstein relationship, in order to relate particle motion to the bulk rheological properties of the medium, may fail under heterogeneous conditions.30 This highlights the importance of numerical tools for recognising when heterogeneity may be important in different systems, and developing analytical methods to interpret particle motion accurately given heterogeneous micro-environments. Here, we provide a preliminary study to explore the conjectured emergence of exponential particle step-size distributions in heterogeneous environments. Even in the absence of more complex phenomena such as particle binding or viscoelasticity, we show that particle step-size distributions can deviate from the expected Brownian–Gaussian result. In particular, for the special case of inert particles distributed between Newtonian sub-environments with a broad range of linearly distributed diffusivities, we show that an exact analytical result for the distribution of particle step sizes can be derived and experimentally validated, which only approaches an exponential distribution for small steps.
Overall, our work sheds light on simple mechanisms leading to deviations from normal diffusion that are frequently reported in heterogeneous media. The experimental results and exact analytical expression presented here are likely relevant to a range of soft matter systems, and may be useful for interpreting particle motion associated with numerous biophysical processes taking place in heterogeneous media with distributed viscosities.
Author contributions
CEW conceived of the presented idea. CEW and CMSR derived the mathematical theory. NAB performed the experiments. CEW performed the simulations. CEW, NAB, and AGC analysed the experimental and simulation results. All authors participated in writing and editing the manuscript.Conflicts of interest
The authors report no conflicts of interest.Acknowledgements
We thank K. Ribbeck for generous use of experimental equipment. We thank S. Huberman for helpful ideas and discussions. NAB gratefully acknowledges support from the NSF under award PHY-2033046 (to K. Ribbeck). CMSR gratefully acknowledges funding from the Natural Sciences and Engineering Research Council of Canada through a Postgraduate Doctoral Scholarship, from a Charlotte Elizabeth Procter Fellowship of Princeton University, and a Miller Research Fellowship from the Miller Institute for Basic Research in Science of UC Berkeley.References
- B. S. Schuster, J. S. Suk, G. F. Woodworth and J. Hanes, Nanoparticle diffusion in respiratory mucus from humans without lung disease, Biomaterials, 2013, 34(13), 3439–3446, DOI:10.1016/j.biomaterials.2013.01.064.
- L. Kaler, E. Iverson, S. Bader, D. Song, M. A. Scull and G. A. Duncan, Influenza A virus diffusion through mucus gel networks, Commun. Biol., 2022, 5(1), 249, DOI:10.1038/s42003-022-03204-3.
- E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2018 Search PubMed.
- R. Metzler, J. H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16(44), 24128–24164, 10.1039/c4cp03465a.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(16), 6438–6443, DOI:10.1073/pnas.1016325108.
- I. Y. Wong, et al., Anomalous diffusion probes microstructure dynamics of entangled F-actin networks, Phys. Rev. Lett., 2004, 92(17), 178101, DOI:10.1103/PhysRevLett.92.178101.
- T. Kalwarczyk, et al., Apparent anomalous diffusion in the cytoplasm of human cells: The effect of probes’ polydispersity, J. Phys. Chem. B, 2017, 121(42), 9831–9837, DOI:10.1021/acs.jpcb.7b07158.
- C. E. Wagner, B. S. Turner, M. Rubinstein, G. H. McKinley and K. Ribbeck, A rheological study of the association and dynamics of MUC5AC gels, Biomacromolecules, 2017, 18(11), 3654–3664, DOI:10.1021/acs.biomac.7b00809.
- A. G. Cherstvy, S. Thapa, C. E. Wagner and R. Metzler, Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels, Soft Matter, 2019, 15(12), 2526–2551, 10.1039/c8sm02096e.
- M. T. Valentine, et al., Investigating the microenvironments of inhomogeneous soft materials with multiple particle tracking, Phys. Rev. E, 2001, 64(6), 061506, DOI:10.1103/PhysRevE.64.061506.
- C. Metzner, C. Mark, J. Steinwachs, L. Lautscham, F. Stadler and B. Fabry, Superstatistical analysis and modelling of heterogeneous random walks, Nat. Commun., 2015, 6, 7516, DOI:10.1038/ncomms8516.
- W. He, et al., Dynamic heterogeneity and non-Gaussian statistics for acetylcholine receptors on live cell membrane, Nat. Commun., 2016, 7, 11701, DOI:10.1038/ncomms11701.
- A. Díez Ferńandez, P. Charchar, A. G. Cherstvy, R. Metzler and M. W. Finnis, The diffusion of doxorubicin drug molecules in silica nanoslits is non-Gaussian, intermittent and anticorrelated, Phys. Chem. Chem. Phys., 2020, 22(48), 27955–27965, 10.1039/d0cp03849k.
- B. Wang, S. M. Anthony, C. B. Sung and S. Granick, Anomalous yet Brownian, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(36), 15160–15164, DOI:10.1073/pnas.0903554106.
- P. Chaudhuri, L. Berthier and W. Kob, Universal nature of particle displacements close to glass and jamming transitions, Phys. Rev. Lett., 2007, 99(6), 060604, DOI:10.1103/PhysRevLett.99.060604.
- E. M. Furst, Particle tracking with Matlab, http://lem.che.udel.edu/wiki/index.php?n=Main.Microrheology.
- C. E. Wagner, Micro- and macro-rheological studies of the structure and association dynamics of biopolymer gels, PhD dissertation, Massachusetts Institute of Technology, 2018, p. 205 Search PubMed.
- V. Pelletier and M. Kilfoil, Software Research Tools, Kilfoil Lab, 2007, http://people.umass.edu/kilfoil/downloads.html.
- N. Cheng, Formula for the viscosity of a glycerolwater mixture, Ind. Eng. Chem. Res., 2008, 47(9), 3285–3288, DOI:10.1021/ie071349z.
- A. Volk and C. J. Kähler, Density model for aqueous glycerol solutions, Exp. Fluids, 2018, 59(5), 75, DOI:10.1007/s00348-018-2527-y.
- R. Swaminathan, C. P. Hoang and A. S. Verkman, Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: Cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion, Biophys. J., 1997, 72(4), 1900–1907, DOI:10.1016/S0006-3495(97)78835-0.
- J. T. Mika, et al., Measuring the viscosity of the Escherichia coli plasma membrane using molecular rotors, Biophys. J., 2016, 111(7), 1528–1540, DOI:10.1016/j.bpj.2016.08.020.
- I. López-Duarte, T. Truc Vu, M. A. Izquierdo, J. A. Bull and M. K. Kuimova, A molecular rotor for measuring viscosity in plasma membranes of live cells, Chem. Commun., 2014, 50(40), 5282–5284, 10.1039/c3cc47530a.
- H. Tanaka, Viscoelastic phase separation in biological cells, Commun. Phys., 2022, 5(1), 167, DOI:10.1038/s42005-022-00947-7.
- T.-H. Kim and H. White, On more robust estimation of skewness and kurtosis, Finance Res. Lett., 2004, 1(1), 56–73, DOI:10.1016/S1544-6123(03)00003-5.
- W. Wang, et al., Fractional Brownian motion with random diffusivity: Emerging residual nonergodicity below the correlation time, J. Phys. A: Math. Theor., 2020, 53(47), 474001, DOI:10.1088/1751-8121/aba467.
- Y. Lanoiselée and D. S. Grebenkov, Non-Gaussian diffusion of mixed origins, J. Phys. A: Math. Theor., 2019, 52(30), 304001, DOI:10.1088/1751-8121/ab2826.
- M. V. Chubynsky and G. W. Slater, Diffusing diffusivity: A model for anomalous, yet Brownian, diffusion, Phys. Rev. Lett., 2014, 113(9), 098302, DOI:10.1103/PhysRevLett.113.098302.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Brownian yet non-Gaussian diffusion: From superstatistics to subordination of diffusing diffusivities, Phys. Rev. X, 2017, 7(2), 021002, DOI:10.1103/PhysRevX.7.021002.
- T. M. Squires and T. G. Mason, Fluid mechanics of microrheology, Annu. Rev. Fluid Mech., 2010, 42, 413–438, DOI:10.1146/annurevfluid-121108-145608.
| This journal is © The Royal Society of Chemistry 2022 |