C₃ production from CO₂ reduction by concerted *CO trimerization on a single-atom alloy catalyst

Abstract

The direct electroreduction of carbon dioxide (CO₂) and carbon monoxide (CO) to C₃ products is challenging. The main reason is the competitive C₂ production resulting from a traditional sequential C–C coupling mechanism. As a result, most catalysts could not facilitate C₃ products since the carbon chain growth from C₂ to C₃ competes with C₂ desorption. In this work, we carried out Density Functional Theory (DFT) calculations with implicit solvation effects on densely arrayed Cu nanopyramids (Cu-DANs). We demonstrate that the co-adsorption energy of three *CO intermediates (ΔG_3*CO; from the CO₂ or CO reactant) is a descriptor for C₃ activity. An activity volcano plot was constructed based on this discovery, which can be used to predict the optimal range for ΔG_3*CO adsorption strength. We demonstrate that by applying the single-atom alloy catalyst strategy, i.e. embedding Ag single metal onto Cu-DANs, we could successfully tune the ΔG_3*CO strength toward the optimal range. In addition, the adsorbed *CO could form a long carbon chain on such a structure via a one-step concerted trimerization mechanism to form the key C₃ reaction intermediate, avoiding the competitive C₂ desorption pathway. Furthermore, Ag-doped Cu-DANs could effectively retain oxygen atoms in the hydroxyl group, which enabled a pathway towards direct electrosynthesis of a new C₃ product (C₃H₈O₂; 1,2-PDO) beyond the only available n-propanol. Our newly discovered concerted trimerization mechanism in combination with single-atom alloy catalysts paves the way for materials design toward more long-chain oxygenate generation.

---

Introduction

The electrocatalytic CO₂ reduction reaction (CO₂RR) to chemicals and fuels is appealing due to the reuse of CO₂ for decreased overall carbon emission and the compatibility with renewable energy systems.¹ This allows for sustainable energy storage and a reduced carbon footprint. During the CO₂RR, renewable energy is converted to chemical energy – by reorganizing the molecular bonds within CO₂ to form molecules containing one or two carbon atoms or long carbon-chains, corresponding to C₁, C₂, or C₃₊ products, respectively.

Among the possible CO₂RR products, propanediol (C₃H₆(OH)₂, PDO) is the simplest linear polyol and a vital commodity chemical with broad applications in the cosmetic, pharmaceutical and polymer industries.² Currently, industrial PDO production mainly relies on the selective oxidation of petroleum-derived propylene, which is energy and cost-intensive, thereby not environmentally and economically sustainable. Therefore, it is worthwhile to explore alternative means of increasing selectivity toward electrochemical PDO production. With CO₂-to-CO conversion well established^3–5 and efficient C₂₊ production fast improved,^6–8 a subsequent electrocatalytic CO-to-PDO conversion offers a promising and attractive alternative to the conventional petroleum-based process.^9,10 However, the selectivity remains extremely low with existing catalysts^11,12 due to two challenges. They are (1) the intrinsically lower selectivity toward oxygenates relative to hydrocarbons^13,14 and (2) the low rate of C–C bond formation for both preliminary coupling and subsequent carbon chain elongation.^15,16 The key to achieving a higher CO₂RR selectivity toward PDO and other linear polyols lies in designing a novel catalyst that can simultaneously address these challenges.

In the past, several studies attempted to address the underlying origins of the first challenge: a low oxygenate selectivity.^17–19 Meanwhile, researchers proposed different material engineering strategies to increase oxygenate selectivity including crystal phase engineering,²⁰ molecule modification,²¹ vacancy engineering²² and compressive strain.²³ Different from these strategies, we recently proposed an alternative approach – formation of densely arrayed copper nanopyramids (Cu-DANs) – and proved their efficacy in significantly improving the selectivity toward diols.¹⁷ The selectivity enhancement was attributed to the unique spatial confinement effect to preserve O atoms in the hydroxyl group. The strategy is most likely extendable to the electrosynthesis of PDO.

About the second challenge, the formation of long carbon-chain products generally involves multi-step sequential C–C coupling reactions, which are the preliminary coupling C₁ + C₁ → C₂ and subsequent carbon chain elongation, i.e., C₁ + C₂ → C₃.^24–26 However, both theoretical^{16,17,27–32} and experimental studies^11,22 suggest sluggish C–C coupling kinetics on pristine Cu surfaces, in terms of initial C₁–C₁ coupling and the subsequent C₁–C₂ coupling. The kinetic-thermodynamic linear scaling relationship restricts initial C₁–C₁ coupling activity.^16,33,34 The C₁–C₂ coupling is less selective and needs to compete with many alternative by-products, especially C₂ product desorption. Consequently, C₃ selectivity via this two-step C–C coupling is low with sluggish kinetics. The secondary coupling between *C₁ and *C₂ intermediates is regarded as the rate-limiting step with a high activation barrier in C₃ electrosynthesis.³⁵

With all these considerations, the design of a highly selective catalyst for linear polyols will benefit from a new mechanism to bypass the sluggish multi-step sequential C–C coupling reactions. Selecting PDO as an example, we performed Density Functional Theory (DFT) calculations to examine the co-adsorption of three surface-bound *CO intermediates on Cu-DANs. Our results identified an adequate descriptor for C₃ activity – the co-adsorption free energy of three *CO (ΔG_3*CO). Based on this descriptor, we constructed a volcano plot to identify the optimal ΔG_3*CO range (between −1.2 eV and −1.0 eV). We also found that *CO with appropriate adsorption strength could enable C₃ production via a concerted trimerization mechanism, avoiding the energy-intensive dimer formation step.

Based on the finding of optimal *CO adsorption strength, we introduced single Ag atom doping onto the Cu-DAN structure to adjust *CO adsorption toward the optimal range. Ag was chosen for three reasons, (1) Ag has a weak CO adsorption strength, which will finetune the interaction between the *CO intermediate and the catalyst toward C₃ production.¹³ (2) Ag-doped Cu was reported to offer high activity for both C₁–C₁ and C₁–C₂ coupling due to the combination of strain and ligand effects,²³ which thus is expected to play the same role on our structure. (3) Ag-doping is possible to increase *CO coverage. It was reported that the alloying of CO-producing Ag leads to accumulated *CO, which then diffuses to the neighbouring reaction sites for C–C coupling.⁷ This effect might offset the adverse effects of lowering *CO coverage due to weakening *CO adsorption. We further validate the single metal doping strategy by exploring the complete pathway toward propanediol production, with a low onset potential of −0.74 V. This study creates a new avenue for engineering highly active and selective copper catalysts for the CO₍₂₎RR toward linear polyols by a single-atom alloy catalyst.

Methods and models

Computational methods

DFT computations were performed with the Vienna Ab Initio Simulation Package (VASP) code.³⁶ The Perdew–Burke–Ernzerhof (PBE) was employed for the electron exchange-correlation.³⁷ Projector augmented wave (PAW) potentials were used to describe the ionic cores.³⁸ The atomic relaxations were carried out with the quasi-Newton minimization scheme until the maximum force on any atom was below 0.03 eV Å⁻¹. Geometry optimizations were performed with a plane-wave cut-off of 400 eV. An irreducible 2 × 2 × 1 Monkhorst–Pack k-point grid was used,³⁹ with the centre shifted to the gamma point. The Fermi level was smeared with the Methfessel–Paxton approach with a smearing of 0.1 eV. Dipole corrections were included in all the calculations to minimize the inaccuracies in the total energy due to the simulated slab interactions. The dipole moment was calculated parallel to the z-direction.

An elementary electroreduction reaction step can be described by the following equation

*A + H⁺ + e⁻ = *AH (1)

in which the asterisk denotes surface bound species. Potential-dependent free energy change ΔG for such reaction can be determined by the linear free energy method under the Computational Hydrogen Electrode (CHE) assumption⁴⁰

ΔG = G_*AH − G_*A − [G_H2/2 − eU] (2)

where G denotes free energy for different states, U is the applied potential and G_H2 is the free energy of a hydrogen molecule (energy values for relevant gas phase species are listed in Table S1†). To calculate the free energy at room temperature (300 K), Zero Point Energy (ZPE), heat capacity and entropy were computed with standard methods.⁴¹ All energy values were acquired in a neutral environment (pH = 7).

The co-adsorption free energy of 3*CO (ΔG_3*CO) without applied potential (U = 0) was calculated as

ΔG_3*CO = G_3*CO − 3G_CO − G_* (3)

where G_CO is the free energy of a CO molecule, and G_* is the free energy of the bare surface. The formation free energy of *CO–CO–COH (ΔG_{*CO–CO–COH}, via 3*CO + H⁺ + e⁻ → *CO–CO–COH) was calculated as

ΔG_{*CO–CO–COH} = G_{*CO–CO–COH} − (G_3*CO + G_H2/2) (4)

where G_3*CO and G_{*CO–CO–COH} is the free energy of a surface with adsorbed 3*CO and *CO–CO–COH, respectively, and G_H2 is the free energy of a hydrogen molecule.

The formation energy of *CO–CO–COH (ΔE_{*CO–CO–COH}) was calculated as

ΔE_{*CO–CO–COH} = E_{*CO–CO–COH} − (E_3*CO + E_H2/2) (5)

where E_{*CO–CO–COH} is the energy of a surface with adsorbed *CO–CO–COH, E_3*CO is the energy of a surface with three adsorbed *CO, and E_H2 is the energy of a hydrogen molecule.

Limiting potential (U_limiting) was applied to describe the lowest energy requirement to eliminate the free energy change of the potential-determining step (PDS), as described in eqn (6),^43–46

U_limiting = −ΔG_PDS/e (6)

Activation energy barriers (E_a) were calculated using the nudged elastic band (NEB) approach.⁴² The total energy and force thresholds for geometry optimizations were 1 × 10⁻⁵ eV and 0.05 eV Å⁻¹, respectively. The minimum energy pathway (MEP) was examined using six images during the transition stage search. Each transition state was confirmed to have a single imaginary vibrational frequency along the reaction coordinate.

Models

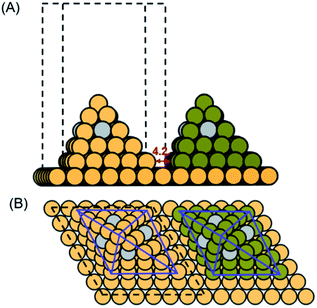
The lattice constant of Cu is optimized to be 3.64 Å in its fcc crystal structure. The computational models were constructed based on the [111] Cu diamond nanopyramid⁶ (Fig. S1A†) and derived densely arrayed nanopyramids¹⁷ (Fig. S1B and C†), which were sitting on a 6 × 6 × 1 Cu (111) surface with 4.2 Å space from adjacent Cu nanopyramids to represent the dense-array. The single atom Ag-doped Cu-DAN model was established by randomly anchoring one silver atom on each side surface of the nanopyramid as shown in Fig. 1. In this way, the single-atom alloy catalyst (SAAC) was achieved in which small amounts of isolated Ag atoms are present in the surface layer of a Cu metal host.⁴⁴ The presence of oxygen on oxide-derived Cu electrodes is a controversial issue.⁴⁵ We did not include subsurface O in our models because previous work has shown that surface O is more stable on Cu than Ag.⁴⁶ Neither did we include the effects of surface O in our calculations as previous studies also show that it is unlikely for surface O to be on Cu and Ag surfaces under negative potentials needed for the CO₍₂₎RR.⁴⁷

Fig. 1 (A) Side view and (B) top view of the atomic structure of Ag-doped Cu-DAN. The computational model is constructed based on a 6 × 6 × 1 Cu (111) surface with a 4.2 Å space between adjacent Cu nanopyramids (in green) to represent the dense-array, with one Ag atom doped to each sidewall. Colour codes: Cu, orange and green; Ag, silver. Solid blue lines serve as visual guides to show the Cu atoms on the edge. Black dashed lines depict the unit cell.

The base layers for all models were fixed while nanopyramids and adsorbates were allowed to fully relax in all configurations. The vertical separation between periodically repeated images was set to be at least 10 Å in all cases, to ensure no interaction between images. The implicit solvent effect was considered by using VASPsol, which implicitly involves counter charges in the system through solving the linearized Poisson–Boltzmann equation.⁴⁸ Within this model, the solvent dielectric constant was set to be 78.4 F m⁻¹, with the width of the dielectric cavity being 0.6 Å, cut-off charge density being 2.5 × 10⁻³ C m⁻³, and the effective surface tension being 5.25 × 10⁻⁴ N m⁻¹.

Results and discussion

C₃ active site screening on pristine Cu-DANs

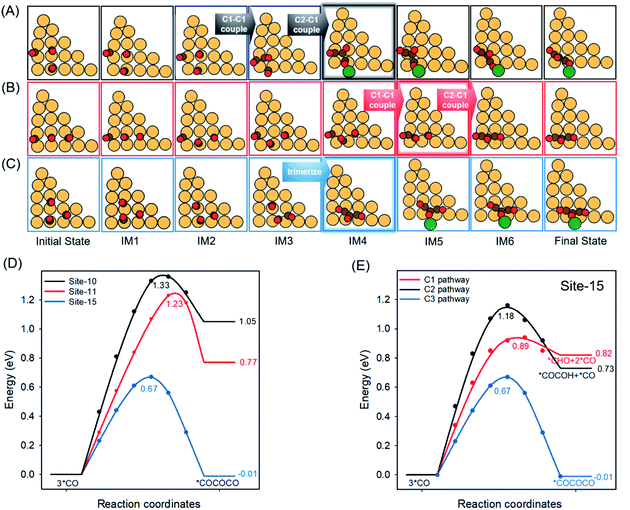
*CO–COH was experimentally identified as the stable hydrogenated dimer intermediate during C–C coupling.^49,50 Due to the abundance of *CO species on the surface when using CO as the feedstock in the CORR, the coupling between *CO and *CO–COH is a possible C₃ pathway as suggested in previous studies.^51–53 We, therefore, used the formation energy of *CO–CO–COH (ΔE_{*CO–CO–COH}) as the indicator for C₃ formation. Our previous research calculated single *CO adsorption energies (ΔE_*CO) for all possible active sites on Cu-DANs as summarized in Table S2.†⁶ Here, we picked in total 17 configurations on Cu-DANs which might geometrically facilitate C₃ formation, and divided them into three groups according to different features of *CO adsorption (Fig. 2A and S2–S18†). We then assessed the ΔE_{*CO–CO–COH} on these reaction sites by DFT calculations to examine how the *CO adsorption impacts the C₃ production.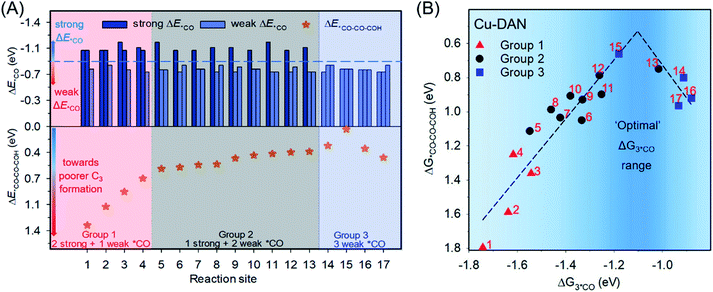

Fig. 2 (A) Individual *CO adsorption energies⁶ (upper panel) and corresponding *CO–CO–COH formation energies (lower panel) on 17 reaction sites on Cu-DANs. These 17 reaction sites are classified into three groups according to the individual *CO adsorption strength. The blue dashed line in the upper panel indicates the benchmark between strong and weak *CO adsorption (−0.87 V).⁵³ Detailed atomic structures, and *CO and *CO–CO–COH adsorption configurations can be found in Table S3 and Fig. S2–S18.† (B) Activity volcano plot between *CO adsorption free energy (ΔG_3*CO) and corresponding *CO–CO–COH formation free energy (ΔG_{*CO–CO–COH}) on the 17 reaction sites (numbered in red) of Cu-DAN. The optimal range for *CO adsorption toward *CO–CO–COH formation is highlighted in dark blue.

Fig. 2A shows that the activity toward C₃ formation improves from group-1 (2 strong + 1 weak *CO; for the definition of strong/weak adsorption please refer to Fig. 2A caption) through group-2 (1 strong + 2 weak *CO) to group-3 sites (3 weak *CO). This phenomenon is somewhat contradictory to the previous observation about C₁–C₁ coupling according to the extended square principle, that thermodynamically facile *CO dimerization should preferably precede between one strongly and one weakly surface-bound *CO within an under-coordinated surface square site.³¹ The fact that group-3 sites exhibit weak adsorption for all three *CO while still promoting C₃ production suggests the existence of a distinctive mechanism for long carbon-chain formation in the presence of all weak ΔE_*CO.

To gain a fundamental understanding of the nature of C₃ active sites on Cu-DANs, we investigated the theoretical C₃ activity as a function of the co-adsorption free energy of three *CO (ΔG_3*CO) by DFT calculations. A volcano-type relationship between ΔG_3*CO and corresponding ΔG_{*CO–CO–COH} was identified (Fig. 2B and Table S3†), which is rationalized as below. Reaction sites on the left side of the volcano possess strong adsorption energy, and then the strongly bound *CO is inert to coupling with as-formed *C₂. Reaction sites on the right side of the volcano exhibit a lower *CO binding energy, but are too weak to stabilize *C₂ on the surface which easily desorbs from the surface as C₂ products. Consequently, as per the Sabatier principle, optimal co-adsorption energies of three *CO which could improve long carbon-chain formation for C₃ products are identified to be between −1.2 and −1.0 eV (highlighted in dark blue, Fig. 2B).

Mechanism of *CO trimerization

Carbon chain growth of C₃ was previously believed to involve two-step sequential C–C coupling processes (C₁ + C₁ → C₂ and C₂ + C₁ → C₃).^23–25 Therefore at least one strong *CO adsorption energy is necessary to facilitate the preliminary C–C coupling (C₁ + C₁ → C₂) according to the extended square principle.³¹ However, our computational results show that site-15 without any strong *CO adsorption energy exhibits the best C₃ activity among all 17 sites (Fig. 2A). This anomalous activity could be explained by a new carbon chain growth mechanism as following.

*CO + *CO + *CO → *CO–CO–CO is studied in this section, as it is the most direct way of investigating carbon chain growth under the CORR conditions.^24,52 The choice is slightly different with the *CO–CO–COH formation in previous sections, due to consideration of producing comparable results with published results, and to simplify the problem by taking out the impact of protonation position. The MEPs for this process on sites-10, 11 and 15 were calculated and are presented in Fig. S19 and Table S4.† The selection of these three sites is based on the following considerations. Site-15 provides the best C₃ activity among all 17 sites despite three weak *CO adsorptions of −0.77, −0.77 and −0.77 eV (Fig. S16†), respectively. Site-10 has a similar *CO co-adsorption geometry to that on site-15, namely three surface-bound CO are angularly aligned on the surfaces (Fig. S11†), while site-11 takes another *CO co-adsorption geometry of linear alignment (Fig. S12†). Both sites-10 and 11 exhibit one strong and two weak *CO adsorption energies. The atomic structure evolution from the initial state to the final state for these three sites is presented in Fig. 3A–C.

Fig. 3 (A–C) Atomic configurations of images along the MEP on site-10 (A), site-11 (B) and site-15 (C) of the Cu-DAN. Colour codes: Cu, orange and green (adjacent nanopyramid); C, brown; O, red. IM is the abbreviation of ‘image’. (D) Energy profile of three MEPs for carbon chain growth reaction *CO + *CO + *CO → *CO–CO–CO. (E) Energy profile for C₁, C₂ and C₃ trifurcation reactions 3*CO + *H → *CHO + 2*CO, 3*CO + *H → *CO–COH + *CO, and 3*CO → *CO–CO–CO on site-15, respectively. The reference energy level is set to be 3*CO adsorption energy.

As shown in Fig. 3D, C₃ carbon chain growth on site-15 is both thermodynamically more stable and kinetically more facile than that on site-10 (ΔE: −0.01 eV vs. 1.05 eV; E_a: 0.67 eV vs. 1.33 eV). We noticed that the carbon chain growth on these two sites experiences distinctive atomic structure evolution (Fig. 3A and C). On site-15, three *CO move closer to each other and then trimerize to *CO–CO–CO following a concerted mechanism, whereas on site-10 a weakly bound CO approaches and couples with a strongly bound *CO first (C₁–C₁ coupling), followed by a subsequent intermolecular coupling between the dimer and another *CO (C₂–C₁ coupling). In addition, site-11 experiences a similar atomic structure evolution to site-10 and a comparable activation barrier (1.23 eV). The difference between sites 10 and 11 is where the barrier is located; on site-10, the transition state is the C₂–C₁ coupling step; while on site-11 the *CO dimerization is the transition state (Fig. S19B and C†). In consequence, we ascribe the discrepancy of C₃ activity between the presence and absence of strong *CO adsorption to an alternative carbon chain growth pathway where three *CO are concertedly coupled as a C₃ trimer in one-step as site-15 takes (Fig. 3C). This novel one-step *CO trimerization would avoid the sluggish kinetics of sequential C–C coupling (C₁–C₁ then C₂–C₁) as site-10 and site-11 experience, leading to a significantly lowered reaction barrier.

To further justify that weaker *CO adsorption promotes C₃ production, we compared the C₃ selectivity with competing C₁ and C₂ pathways on the most promising site-15. Fig. 3E compares the reaction energetics of C₃ formation with the reduction of surface-bound *CO to *CHO and *CO–COH (MEPs shown in Fig. S20 and S21,† respectively). The selective formation of *CHO, *CO–COH or *CO–CO–CO was found to be critical in trifurcating to C₁, C₂ and C₃ pathways.^28,53 Our computation results reveal that the C₂ production via *CO dimerization is difficult to carry out given all *CO are weakly adsorbed, because the condition of the extended square principle can hardly be met. Direct hydrogenation of weakly adsorbed *CO to the C₁ product is also unfavourable with a high E_a of 0.89 eV. Comparatively, the E_a for the formation of *CO–CO–CO remains low (0.67 eV), making this C₃ pathway more selective. Therefore, we attribute the energetically preferential reduction toward C₃₊ products to a concerted *CO trimerization process, which occurs due to weaker *CO co-adsorption. This new reaction mechanism leads to significantly lowered reaction energetics, which boosts the selectivity to the C₃ pathway instead of the conventional C₁ and C₂ pathway.

C₃ promotion through Ag doping

Using calculated adsorption energy of a key intermediate as the descriptor can provide mechanistic insight into a catalytic reaction. This strategy is well established as a convenient theoretical tool for fast catalyst screening.⁵⁴ From above, we identified that the co-adsorption energy of three *CO can be used as a descriptor for C₃ activity on Cu-DANs, in which the moderate to weak ΔG_3*CO (approximately between −1.2 and −1.0 eV) effectively promotes long carbon-chain formation via a concerted *CO trimerization mechanism. Nonetheless, the reaction sites with the optimal *CO adsorption energies are in lack on pristine Cu-DAN surfaces (two out of 17, ratio ≈ 12%), which probably explains the experimental observation that C₃ yields are extremely low.^22,55 Also the optimum balance of binding energy (i.e., the peak of activity volcano) is not achieved. We carried out further studies to improve the amount of C₃ active sites, based on a doping strategy.

Single-atom alloy construction has been demonstrated as a successful strategy for circumventing the scaling relationship.^44,51 Inspired by this, we propose that by doping single Ag atoms, the interaction between *CO intermediates and Cu can be tuned toward C₃ production. Accordingly, we studied an Ag-doped Cu-DAN model (Ag/Cu-DAN) as shown in Fig. 1. We propose that such structure can be experimentally synthesized by an electrodeposition method.⁵⁶ Moreover, the proposed Ag/Cu-DAN models show electrochemical stability as analyzed in ESI Fig. S22 and Note 1.†

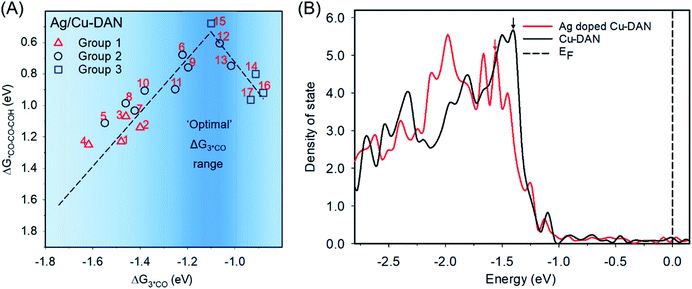
In such a model, due to the larger lattice constant, Ag doping induces inter-atomic strain. The bond length of Cu–Cu adjacent to the Ag dopant decreases from 2.56 Å to 2.44 Å (Fig. S23†). After surface Ag doping, the free energy for *H formation on the Cu-DAN surface increases by 0.12 eV (Fig. S24†), indicating a significant inhibition of the competing hydrogen evolution reaction (HER).^23,57 In the meantime, we traced the difference in *CO co-adsorption energetics upon doping of adjacent Ag atoms (Table S3†) and found that they were optimized with more reaction sites moving inside the desired co-adsorption region (five out of 17, ratio ≈ 30%), as shown in Fig. 4A.

Fig. 4 (A) Activity volcano plot between the *CO adsorption free energy (ΔG_3*CO) and the corresponding *CO–CO–COH formation free energy (ΔG_{*CO–CO–COH}) on the investigated 17 reaction sites (numbered in red) of the Cu-DAN with surface Ag doping (Ag/Cu-DAN). The optimal range for *CO adsorption toward *CO–CO–COH formation is highlighted in dark blue. (B) d-Projected DOS of Cu in the Cu-DAN with or without surface Ag doping. The arrows indicate the first peak on DOS adjacent to the Fermi level (E_F), which is identified as an indicator for intermediate binding strength.

The underlying mechanism for the weakened adsorption energy by Ag doping can be explained by electronic structure analysis. According to the d-band theory, the behaviour of the occupied d orbital projected on the catalyst surface correlates with the local electron transfer and surface chemisorption.⁵⁸ To further explain the different electrocatalytic behaviours of our catalysts, we calculated the projected density of states (DOS) of d orbitals and the d-band centre of Cu atoms. Fig. 4B illustrates that the Ag doping shifts the first peak under the Fermi level for Cu on d-projected DOS to a lower energy level (further from the Fermi level), which has been reported to result in a weaker binding of reaction intermediates with the substrate.^59,60 Meanwhile, a more negative d-band centre of Cu relative to the Fermi level is observed for the structure after Ag doping (−2.14 eV vs. −2.01 eV).

Because of the downshift in d-band electrons, the anti-bonding states derived from the coupling between the Cu atom and C atom of *CO would be downshifted and thus more filled, and weakens the Cu–C bonding. As a result, the *CO adsorption on the investigated reaction sites – most of them are adjacent to Ag dopants and experience a stronger impact from doping – are modulated in favour of *CO–CO–COH formation. These findings are analogous to the enhanced C–C coupling on two neighbouring Cu atoms induced by adjacent Ag doping proposed by Sargent and co-workers.²³ We conclude that through Ag doping, the co-adsorption energies of three *CO are further optimized in favour of C₃ formation, and the competing hydrogen evolution reaction is suppressed. This is attributed to the intrinsic electronic interaction between Ag and Cu, as well as the Ag doping-induced compressive strain among Cu atoms.

Propanediol pathway

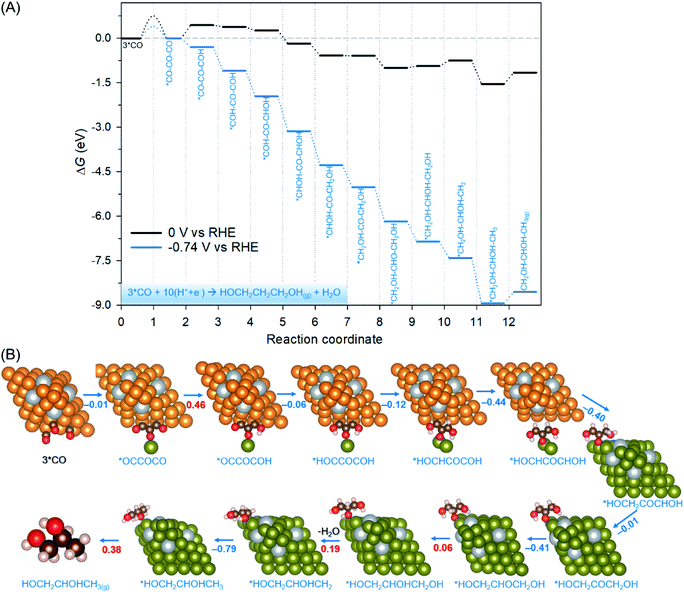
As the last part of our study, we obtained the further reduction pathway following 3*CO co-adsorption on the Ag-doped Cu-DAN (Fig. 5). Fig. 5A depicts the pathway and associated reaction energetics for 1,2-propanediol production at 0 V and −0.74 V vs. RHE. The atomic structures of the most favourable reduction path and the relevant energetics are depicted in Fig. 5B. A more detailed thermodynamic profile regarding all reaction intermediates is given in Tables S5 and S6.† Due to the unique spatial-confinement provided by a dense-array of Cu nanopyramids, there is an O–Cu bond between the trimer intermediate *CO–CO–COH and the adjacent Cu nanopyramids. The spatial confinement effectively protects O atoms against further hydrogenation and subsequent dihydroxylation as revealed by our previous research.¹⁷

Fig. 5 Reduction of *CO to 1,2-propanediol on the Ag-doped Cu-DAN. (A) Preferred pathway and associated reaction energetics identified for the production of 1,2-propanediol starting with 3*CO on the Ag-doped Cu-DAN surface at 0 V and −0.74 V (corresponding to the 0.40 eV barrier threshold) vs. RHE (B) atomic structures of the reaction intermediates along the pathway. In the upper panel, one or two Cu atoms bonded with O denote the adjacent nanopyramids (in green), after the formation of *CHOH–CO–CHOH, intermediates have completely adsorbed on the adjacent nanopyramids. Free energy change (ΔG) values are in eV. Blue and red values denote the exergonic and endergonic processes, respectively. Colour code: Cu, orange and green; C, brown; O, red; H, pink.

Consequently, as suggested by Fig. 5 and Table S5,† the reaction pathway on Ag-doped Cu-DANs prefers selective hydrogenation on C to preserve the O atom in the hydroxyl group. For example, the ninth proton-coupled electron transfer (PCET) step has two options: (1) protonation of O and subsequent dehydroxylation to *C–CO–COH (via *COH–CO–COH + H⁺ + e⁻ → *C–CO–COH + H₂O) and (2) direct protonation of C to *COH–CO–CHOH (*COH–CO–COH + H⁺ + e⁻ → *COH–CO–CHOH). Our calculation shows the former process is uphill by 1.2 eV. Meanwhile the direct protonation of C is exergonic by −0.12 eV. The same holds for all the subsequent steps: the H⁺/e⁻ pair prefers to continuously attack the C atoms until they are saturated, instead of the O atoms in the hydroxyl group which is followed by dehydroxylation. By the preferential hydrogenation of carbon, O atoms are mostly retained in hydroxyl groups toward the formation of 1,2-propanediol (CH₂OH–CHOH–CH₃). In addition, the desorption of 1,2-propanediol from the Ag-doped Cu-DAN surface is slightly endothermic at 0.38 eV, and can be readily overcome.

After applying an onset potential of −0.74 V, the kinetic barrier for the key *CO dimerization step was reduced to 0.40 eV, which can be overcome to give appreciable production rates at room temperature. We also note that most of the elementary reaction steps become exergonic under the onset potential, suggesting the Ag-doped Cu-DAN to be a promising electrocatalyst for CO reduction to propanediols. This propanediol production pathway confirms that the optimized *CO co-adsorption can facilitate a novel *CO trimerization process on the Ag-doped Cu-DAN surface for the selective formation of 1,2-propanediol without the energy-intensive formation of the *CO–CO intermediate.

Conclusions

Aiming at effective CO₍₂₎RR toward linear polyol production, we first identified the co-adsorption energy of three *CO as an effective descriptor for C₃ activity on Cu-DANs. The derived activity volcano indicated the optimal co-adsorption energies of three *CO for long carbon-chain formation. Subsequent exploration of reaction mechanisms for the CO₍₂₎RR to 1,2-propanediol on Cu-DANs shows that there exists an alternative and more favourable reaction pathway, i.e. *CO trimerization in a concerted mechanism. Unlike the conventional pathways which normally involve a two-step coupling process – two *CO dimerization to the C₂ intermediate followed by further coupling with the C₁ intermediate, this new pathway proceeds towards the selective formation of 1,2-propanediol via concerted *CO trimerization, which greatly improves the selectivity toward C₃ products. Such a trimerization pathway was confirmed for single metal Ag-doped Cu-DANs, owing to the optimized *CO co-adsorption energies. Our findings will be of immediate benefit in the design of selective electrocatalysts for CO₂ reduction to C₃ products via a newly discovered trimerization mechanism in combination with the single-atom alloy catalyst concept.

Author contributions

L. C. carried out the theoretical simulation and data analysis. C. T., Y. Z. and E. S. carried out part of the data analysis. Y. J. and C. T. conceived and supervised the research. Y. J. and E. S. designed the theoretical simulation, and directed the manuscript – writing and revision. All co-authors assisted in writing and revising the manuscript. All co-authors read and approved the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support by the Australian Research Council (FT190100636 and DP190103472), and the Icelandic Research Fund (Grant No. 207283-051). DFT computations were supported by computational resources provided by the Australian Government through NCI under the National Computational Merit Allocation Scheme, and the Phoenix High Performance Compute (HPC) Service at The University of Adelaide.

References

1. Y. Zheng, A. Vasileff, X. Zhou, Y. Jiao, M. Jaroniec and S. Qiao, J. Am. Chem. Soc., 2019, 141, 7646–7659.
2. X. Zhang, G. Cui and M. Wei, Ind. Eng. Chem. Res., 2020, 59, 12999–13006.
3. H. Xiao, T. Cheng, W. A. Goddard III and R. Sundararaman, J. Am. Chem. Soc., 2016, 138, 483–486.
4. M. Ma, B. J. Trześniewski, J. Xie and W. A. Smith, Angew. Chem., Int. Ed., 2016, 55, 9748–9752.
5. J. P. Birat and D. Maizières-lès-Metz, UNIDO Global Technology Roadmap for CCS in Industry-Sectoral Experts Meeting, Amsterdam, 2010.
6. L. Chen, C. Tang, Y. Jiao and S. Z. Qiao, ChemSusChem, 2020, 14, 671–678.
7. C. Tang, Y. Zheng, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2021, 60, 19572–19590.
8. X. Zheng, P. D. Luan, F. P. G. de Arquer, B. Zhang, N. R. M. B. Becknell, Y. Li, M. N. Banis, Y. Li, M. Liu, O. Voznyy, C. T. Dinh, T. Zhuang, P. Stadler, X. Du, P. Yang and E. H. Sargent, Joule, 2017, 1, 794–805.
9. F. P. Garcia de Arquer, O. S. Bushuyev, P. De Luna, C.-T. Dinh, A. Seifitokaldani, M. Saidaminov, C.-S. I Tan, L. N. Quan, A. Proppe, M. G. Kibria, S. O. Kelly, D. Sinto and E. H. Sargent, Adv. Mater., 2018, 30(38), 1802858.
10. N.-T. Suen, Z.-R. Kong, C.-S. Hsu, H.-C. Chen, C.-W. Tung, Y.-R. Lu, C.-L. Dong, C.-C. Shen, J.-C. Chung and H. M. Chen, ACS Catal., 2019, 9(6), 5217–5222.
11. C. W. Li, J. Ciston and M. W. Kanan, Nature, 2014, 508, 504.
12. J. Shan, H. Liu, K. Lu, S. Zhu, J. Li, J. Wang and W. Fan, J. Catal., 2020, 383, 13–23.
13. M. Luo, Z. Wang, Y. C. Li, F. Li, Y. Lum, D.-H. Nan, B. Chen, J. Wicks, A. Xu, T. Zhuang, W. R. Leow, Z. Wang, X.-T. Dinh, Y. Wang, D. Sinton and E. H. Sargent, Nat. Commun., 2019, 10, 5814.
14. D. Gao, I. Sinev, F. O. Scholten, R. Aran-Ais, J. A. Divins, K. Kvashnina, J. Timoshenko and B. R. Cuenya, Angew. Chem., Int. Ed., 2019, 58, 17047–17053.
15. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Norskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672.
16. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Norskov, Nat. Commun., 2017, 8, 15438.
17. L. Chen, C. Tang, K. Davey, Y. Zheng, Y. Jiao and S. Qiao, Chem. Sci., 2021, 12, 8079–8087.
18. Q. Zhu, X. Sun, D. Yang, J. Ma, X. Kang, L. Zheng, J. Zhang, Z. Wu and B. Han, Nat. Commun., 2019, 10, 3851.
19. H. Li, X. Qin, T. Jiang, X.-Y. Ma, K. Jiang and W.-B. Cai, ChemCatChem, 2019, 11, 6139–6146.
20. Y. Chen, Z. Fan, J. Wang, C. Ling, W. Nie, Z. Huang, G. Liu, B. Chen, Z. Lai, X. Liu, B. Li, Y. Zong, L. Gu, J. Wang, X. Wang and H. Zhang, J. Am. Chem. Soc., 2020, 142(29), 12760–12766.
21. C. G. Morales-Guio, E. R. Cave, S. A. Nitopi, J. T. Feaster, L. Wang, K. P. Kuhl, A. Jackson, N. C. Johnson, D. N. Abram, T. Hatsukade, C. Hahn and T. F. Jaramillo, Nat. Catal., 2018, 1(10), 764–771.
22. T.-T. Zhang, Z.-Q. Liang, A. Seifitokaldani, P. De Luna, T. Burdyny, F. Che, F. Meng, Y. Min, R. Quintero-Bermudez, C. T. Dinh, Y. Pang, M. Zhong, B. Zhang, J. Li, P.-N. Chen, X.-L. Zheng, H. Liang, W.-N. Ge, B.-J. Ye, D. Sinton, S.-H. Yu and E. H. Sargent, Nat. Catal., 2018, 1(6), 421–428.
23. X. Wang, Z. Wang, T.-T. Zhuang, C.-T. Dinh, J. Li, D.-H. Nam, F. Li, C.-W. Huang, C.-S. Tan, Z. Chen, M. Chi, C. M. Gabardo, A. Seifitokaldani, P. Todorovic, A. Proppe, Y. Pang, A. R. Kirmani, Y. Wang, A. H. IP, L. J. Richter, B. Scheffel, A. Xu, S.-C. Lo, S. O. Kelley, D. Sinton and E. H. Sargent, Nat. Commun., 2019, 10, 5186.
24. T. T. Zhuang, Y. Pang, Z.-Q. Liang, Z. Wany, Y. Li, C.-S. Tan, J. Li, C. T. Dinh, P. De Luna, P. L. Hsieh, T. Burdyny, H.-H. Li, M. Liu, Y. Wang, F. Li, A. Proppe, A. Johnston, D.-H. Nam, Z.-Y. Wu, Y.-R. Zheng, H. A. Ip, H. Tan, L.-J. Chen, S.-H. Yu, S. O. Kelly, D. Sinton and E. H. Sargent, Nat. Catal., 2018, 1, 946–951.
25. H. Xiao, T. Cheng and W. A. Goddard, J. Am. Chem. Soc., 2017, 139, 130–136.
26. K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5(5), 7050–7059.
27. J. Hussain, H. Jonsson and E. Skúlason, ACS Catal., 2018, 8, 5240–5249.
28. T. Cheng, H. Xiao and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(8), 1795–1800.
29. W. Luo, X. Nie, M. J. Janik and A. Asthagiri, ACS Catal., 2016, 6, 219–229.
30. J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477.
31. T. Cheng, H. Xiao and W. A. Goddard III, J. Am. Chem. Soc., 2017, 139, 11642–11645.
32. J. A. Garza, T. A. Bell and M. Head-Gardon, ACS Catal., 2018, 8, 1490–1499.
33. K. Jiang, B. R. Sandberg, J. A. Akey, X. Liu, D. C. Bell, J. K. Norskov, K. Chan and H. Wang, Nat. Catal., 2018, 1, 111–119.
34. F. Li, Y. C. Li, Z. Wang, J. Li, D.-H. Nam, Y. Lum, M. Luo, X. Wang, A. Ozden, S.-F. Hung, B. Chen, Y. Wang, J. Wicks, Y. Xu, Y. Li, C. M. Gabardo, C.-T. Dinh, Y. Wang, T.-T. Zhuang, D. Sinton and E. H. Sargent, Nat. Catal., 2020, 3, 75–82.
35. Y. Pang, J. Li, Z. Wang, C.-S. Tan, P.-L. Hsieh, T.-T. Zhuang, Z.-Q. Liang, C. Zou, X. Wang, P. De Luna, J. P. Edwards, Y. Xu, F. Li, C.-T. Dinh, M. Zhong, Y. Lou, D. Wu, L.-J. Chen, E. H. Sargent and D. Sinton, Nat. Catal., 2019, 2, 251–258.
36. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
38. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1758.
39. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
40. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem., 2004, 108, 17886–17892.
41. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315.
42. G. Henkelman and H. J. Jónsson, Chem. Phys., 2000, 113, 9978–9985.
43. Y. Ouyang, L. Shi, X. Bai, Q. Li and J. Wang, Chem. Sci., 2020, 11, 1807.
44. R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088.
45. M. Fields, X. Hong, J. K. Nørskov and K. Chan, J. Phys. Chem. C, 2018, 122, 16209–16215.
46. L. R. L. Ting, O. Pique, S. Y. Lim, M. Tanhaei, F. Calle-Vallejo and B. S. Yeo, ACS Catal., 2020, 10, 4059–4069.
47. A. Bagger, R. M. Aran-Ais, J. Halldin Stenlid, E. Campos dos Santos, L. Arnarson, K. Degn Jensen, M. Escudero-Escribano, B. Roldan Cuenya and J. Rossmeisl, ChemPhysChem, 2019, 20, 3096–3105.
48. K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106.
49. F. Calle-Vallejo and M. T. M. Koper, Angew. Chem., Int. Ed., 2013, 52(28), 7282–7285.
50. E. Perez-Gallent, M. C. Figueiredo, F. Calle-Vallejo and M. T. M. Koper, Angew. Chem., Int. Ed., 2017, 56, 3621–3624.
51. G. Sun, Z. J. Zhao, R. Mu, S. Zha, L. Li, S. Chen, K. Zang, J. Luo, Z. Li, S. C. Purdy, A. J. Kropf, J. T. Miller, L. Zeng and J. Gong, Nat. Commun., 2018, 9, 4454.
52. J. Li, F. Chen, Y. Pang, C. Zou, J. Y. Howe, T. Burdyny, J. P. Edwards, Y. Wang, F. Li, Z. Wang, P. De Luna, C.-T. Dinh, T.-T. Zhuang, M. I. Saidaminov, S. Cheng, T. Wu, Y. Z. Finfrock, L. Ma, S.-H. Hsieh, Y.-S. Liu, G. A. Botton, W.-F. Pong, X. Du, J. Guo, T.-K. Sham, E. H. Sargent and D. Sinton, Nat. Commun., 2018, 9, 4614.
53. K. Jiang, Y. Huang, G. Zeng, F. M. Toma, W. A. Goddard and A. T. Bell, ACS Energy Lett., 2020, 5, 1206–1214.
54. Y. Feng, W. An, Z. Wang, Y. Wang, Y. Men and Y. Du, ACS Sustainable Chem. Eng., 2020, 8, 210–222.
55. D. Kim, C. S. Kley, Y. Li and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10560–10565.
56. Y. Han, X. Zhang and G. Leach, Langmuir, 2014, 30, 3589–3598.
57. J. A. Z. Zeledon, M. B. Stevens, G. T. K. K. Gunasooriya, A. Gallo, A. T. Landers, M. E. Kreider, C. Hahn, J. K. Nørskov and T. F. Jaramillo, Nat. Commun., 2021, 12, 620.
58. T. Bligaard and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5512–5516.
59. J. J. Gao, H. B. Yang, X. Huang, S. F. Hung, W. Z. Cai, C. M. Jia, S. Miao, H. M. Chen, X. F. Yang, Y. Q. Huang, T. Zhang and B. Liu, Chem, 2020, 6(3), 658–674.
60. Y. Zheng, Y. Jiao, Y. H. Zhu, Q. R. Cai, A. Vasileff, L. H. Li, Y. Han, Y. Chen and S. Z. Qiao, J. Am. Chem. Soc., 2017, 139(9), 3336–3339.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta09608g

---