Using machine learning to screen non-graphite carbon materials based on Na-ion storage properties†
Xiaoxu
Liu
 *a,
Tian
Wang
a,
Tianyi
Ji
*a,
Hui
Wang
b,
Hui
Liu
*a,
Tian
Wang
a,
Tianyi
Ji
*a,
Hui
Wang
b,
Hui
Liu
 a,
Junqi
Li
a,
Junqi
Li
 a and
Dongliang
Chao
*c
a and
Dongliang
Chao
*c
aSchool of Material Science and Engineering, Shaanxi Key Laboratory of Green Preparation and Functionalization for Inorganic Materials, Shaanxi University of Science and Technology, Xi'an, 710021, China. E-mail: xaoxuliu@sust.edu.cn
bDivision of Physics and Applied Physics, School of Physical and Mathematical Sciences, Nanyang Technological University, 637371, Singapore
cLaboratory of Advanced Materials, Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, Fudan University, Shanghai, 200433, China
First published on 26th February 2022
Abstract
Non-graphite carbon materials are composed of basic carbon layer units, such as soft carbon, hard carbon, and reduced oxide graphene, and an increasing number of studies on various non-graphite carbon materials are being performed in sodium-ion batteries (SIBs). However, it is difficult to relate the different non-graphite anodes, and a systematic analysis of the correlation between the non-graphite carbon structure and sodium storage properties is lacking. Moreover, there is no strategy to screen for high-performance electrode materials by using the database from the Web of Science. In this study, the effects of crystallinity, an essential attribute of basic microstructural units, on the sodium storage properties have been identified and analyzed. The key structural parameters characterizing the crystallinity were explored. A structure–property database was built based on these parameters (La, Lc, d002, and ID/IG) and the main performance data. The data analysis results were used in conjunction with thermodynamic and kinetic analysis to systematically evaluate the effects of these parameters on the sodium storage performance. Finally, machine learning was used to effectively screen for optimal structural parameters, and a standardized process was proposed for the preparation of high-performance electrode materials programmatically, enabling the continuously updated database to effectively guide the scientific research and engineering application of non-graphite carbon materials.
1 Introduction
Non-graphite carbon materials, such as soft carbon, hard carbon and reduced graphene oxide (rGO), are cutting-edge electrode materials used in the research and commercial application of secondary batteries.1–3 All types of non-graphite carbon material have been widely studied as anodes of sodium-ion batteries (SIBs). In particular, soft carbon has been used as a commercial anode material for SIBs on a certain scale, because of its abundant resources, low cost and environment friendliness.4 More importantly, non-graphite carbon materials with low crystallinity generally have high Na+ (de)intercalation ability in ester electrolytes. Extensive studies on various precursors and different heat treatment temperatures (HTTs) have shown that non-graphite carbon materials generally exhibit excellent sodium storage performance; additionally, some types of hard carbon can be used as self-supporting or flexible electrodes, which is expected to be applied in flexible devices in the future.5,6 For example, Hou et al.7 synthesized self-supporting hard carbon paper with a disordered carbon layer arrangement and extended interlayer spacing, and found that the material had an initial coulombic efficiency (ICE) higher than 90% and a reversible capacity up to 200 mA h g−1; the paper could deliver 170 mA h g−1 even at 2 A g−1. Subsequently, Sun et al.8 used the relationship between the carbon layer structure and sodium storage mechanisms to classify the microstructure of hard carbon into three types, i.e., highly disordered carbon, pseudo-graphitic carbon and graphitic carbon. The proportion of the three types can be adjusted by HTT to optimize the sodium storage performance. However, the sodium storage mechanism and performance remain quite different for hard carbon obtained from different precursors and heat treatment processes, which is confusing for further research. Soft carbon and rGO also have a high sodium storage capacity. Jian et al.9,10 prepared soft carbon at a low temperature that exhibited a stable capacity and rate performance, and its charge–discharge curves had a clear slope and a higher voltage plateau than that of hard carbon. In 2018, Zhao et al. prepared porous rGO and proved that an enlarged carbon interlayer spacing and a large number of pores enhance the Na+ (de)intercalation rate performance.11 Although this material delivers 365 mA h g−1 at 0.1 A g−1, the charge–discharge curves have a clear slope, indicating a distinctly different sodium storage mechanism from that of hard carbon. Overall, non-graphite carbon materials represented by soft carbon, hard carbon and rGO are expected to be prime candidates for sodium storage anode materials, and numerous researchers have extensively investigated the sodium storage law of different carbon anodes.An in-depth analysis of many studies clearly shows that various carbon materials have been widely researched. However, structures and sodium storage properties have only been intensively studied within a single material system, and systematic classification and an in-depth analysis have not been carried out between the structures and sodium storage properties of various non-graphite carbon materials. Specific problems remain with using non-graphite carbon materials as SIB anodes. (i) A systematic analysis of the sodium storage mechanism and performance has not been performed for all the types of available non-graphite carbon material based on the intrinsic carbon layer units (crystallinity). (ii) The key structural parameters need to be explored and classified, and a structure–property database based on the structure and performance needs to be constructed. (iii) Most studies on the sodium storage characteristics have been limited to isolated systems (such as isolated hard carbon or rGO systems), and a strategy for using the Web of Science database to screen for high-performance carbon-based anodes has not been developed.
In response to these problems, many studies have been analyzed and summarized about sodium storage of non-graphite carbon materials in the Web of Science database in this work (retrieval form and results are shown in Fig. S1, ESI†). To systematically determine how the structural parameters affect the sodium storage mechanism and performance, intrinsic non-graphite carbon materials (without foreign dopants) with relatively ideal and simple structures were selected as a research subject. Furthermore, we systematically searched the quantitative data of key structural parameters (d002, La, Lc, and ID/IG) characterizing the crystallinity of non-graphite carbon materials (as depicted in Fig. S2, ESI†), and obtained the capacity, rate performance, average discharge voltage plateau and other sodium storage data from previous studies. Then, a structure–property relationship database was established based on the key structural parameters and main sodium storage performance. The crystallinity of the carbon layer was used to analyze all the non-graphite carbon materials and thereby relate different systems, which can be used to identify a relatively universal structure–property relationship. Finally, the structure–property database of non-graphite carbon materials was used in conjunction with machine learning to design suitable models to effectively screen for reasonable structural parameters that produce optimal sodium storage performance. The database and its construction method represent a new direction for the application of structure–property data in the literature, as well as a paradigm for the engineering application of test data, enabling the large quantity of available research data to effectively guide future scientific research and engineering applications.
2 Sodium storage mechanism and performance of non-graphite carbon materials
2.1 Overview of the structure and data extraction
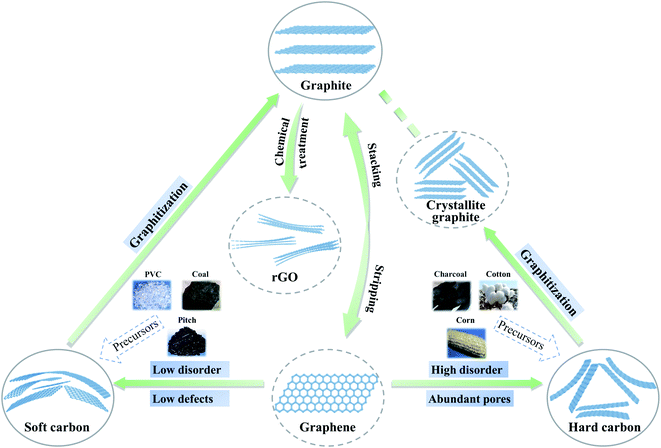
Over the past decade, some non-graphite carbon materials, such as soft carbon, hard carbon and rGO, have generally exhibited interesting sodium storage properties.12 In order to clarify the structural characteristics of various carbon materials, the evolution of the carbon layer stacking form is shown in Fig. 1. Two-dimensional carbon layers with different crystallization and stacking can form amorphous layered carbon materials with different morphologies including graphite, graphene, soft carbon, hard carbon, etc. With graphite as a raw material, expanded graphite can be obtained when the graphite layers are slightly oxidized and uniformly expanded; if the graphite layers are strongly oxidized, graphene oxide can be obtained via exfoliation, and rGO can be synthesized via reduction.13,14 At the same time, monolayer graphene can be obtained from a graphite precursor by mechanical exfoliation and other methods.15 Taking graphite as the standard, if a precursor can be transformed into an (artificial) graphite structure during heat treatment, it is called soft carbon, otherwise it is called hard carbon. Compared with hard carbon materials, soft carbon materials have a relatively higher ordering of carbon layers and are usually obtained by carbonizing precursors such as polyvinyl chloride (PVC), petroleum coke, pitch, coal, polyvinyl acetate (PVA) and benzene.16 Additionally, the carbon layers still have a certain number of defects (including cavities, edge structures, five-membered or seven-membered rings that cause the carbon material to bend and wrinkle, heteroatoms such as oxygen, etc.).17 The hard carbon is mainly obtained by a thermal or chemical process involving organic compounds and biomass, such as resin and sucrose.5 Hard carbon generally has a low-degree ordering, which is reflected in the large interlayer spacing, small crystallite size and abundant pore structures. The carbon layers also contain hydrogen, oxygen and other heteroatoms, which further leads to a decrease in the crystallinity of hard carbon.18 After high temperature treatment (>∼2000 °C), hard carbon can be transformed into crystallite graphite structurally, but its carbon layer size is much smaller than that of graphite. While non-graphite carbon materials are widely applied in SIB anodes, the sodium storage mechanisms and performances are quite different for various carbon materials and difficult to relate to each other. A systematic exploration and quantitative analysis of the crystallinity of non-graphite carbon materials are still lacking, which hinders the in-depth understanding of the relationship between structure and property.Based on a large number of experimental studies, XRD is a common experimental method to analyze the crystal structure of two-dimensional carbon layers. The interlayer spacing d002 (eqn (1)) can be obtained through Bragg's law. The dimensions along the a-axis (La) and the c-axis (Lc) are calculated using the Debye–Scherrer formula (eqn (2)).19–21
2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ θ = nλ | (1) |
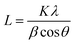 | (2) |
Additionally, the precursor and HTT have an important influence on the molecular structure of non-graphite carbon materials, especially for hard and soft carbon. Firstly, the formation and arrangement of carbon layers are influenced by the precursor structure and atom type, and secondly, non-graphite carbon materials are formed by many carbon layer units with a disordered arrangement. In both cases, the main defects in carbon materials are intrinsic heteroatoms and stacking disorder. Raman spectroscopy has become a key technology for characterizing various carbon allotropes and disordered structures, because it has high resolution and sensitivity to local changes in the carbon structure.22–24 In the Raman spectra, layered carbons have two main features, i.e., the G and D bands. The G band is related to the bond stretching of sp2 atoms in both rings and chains (E2g symmetry), while the D band is related to the breathing modes of sp2 atoms in rings (A1g symmetry). The intensity ratio between the D and G bands (ID/IG) is generally used to evaluate the defect level of carbon materials, which is often used in many literature reports.25–27
In summary, the crystallinity of the carbon layers is the key structural factor for non-graphite carbon materials and has an important effect on sodium storage properties. A quantification of crystallinity is helpful to obtain universal structure–property rules. By XRD and Raman, these key structural parameters can be easily obtained to identify the crystallinity levels of different non-graphite carbon materials. However, as for the doped or composite carbon materials, there are too many interference factors on the key structural parameters, resulting in complexity in the thermodynamics or kinetics.28 Therefore, because of the relatively ideal and simple structures, intrinsic non-graphite carbon materials are selected as the research object to study how the crystallinity systematically determines the sodium storage mechanism and performance. The specific process of data extraction is as follows. Firstly, for the structural parameters, XRD data were carefully extracted from the figures in the literature by using a figure digitization tool. The peak position and FWHM data were immediately analyzed according to the unified rules. Further, the grain size (La and Lc) and interlayer spacing (d002) are calculated using eqn (1) and (2). For Raman data, the figure information in the literature was also transformed into data, and the ID/IG was calculated from the peak intensity ratio. Secondly, for performance data, the capacity was taken from the specific capacity at a current density of 100 mA g−1. The rate factor was obtained by uniform processing: the capacity under different current densities was taken, and the slope was fitted. The reciprocal of the slope was taken to express the rate performance. The higher the value was, the better the rate performance. The working plateau was the average working voltage in the main discharge range. To avoid interference from other factors, all SIB electrolytes for non-graphite carbon materials are ester solvents (intercalation or other behaviors of Na+ alone), and the counter electrode is sodium metal. By sorting the key structural and performance parameters of pure layered carbon anodes, a database is established to represent the structure–property relationship for sodium storage (see Section S1, ESI†).
2.2 Hard carbon
Different from the orderly carbon layer arrangement of graphite, hard carbon has a small carbon layer size (usually below 10 nm) with a random arrangement, causing abundant defects and pore structures.29 Non-graphitizable hard carbon has many kinds of precursor and a changeable structure at different HTTs. Therefore, there are many studies on the sodium storage properties of hard carbon. In order to fully understand the structure–property relationship, we first analyzed the sodium storage mechanism of hard carbon. Previous studies on hard carbon are shown in Fig. S3 (ESI†). Sodium storage behaviors of hard carbon can be divided into three kinds: pseudocapacitive adsorption, intercalation, and pore-filling (as shown in Fig. S3a, ESI†), which dominate the sodiation process.30–34 So far, a variety of sodium storage mechanisms and models have been proposed. In fact, the hard carbon derived from various precursors and HTTs can be described by a “house of cards”, but this model is not enough to accurately reflect its microstructure, so the sodium storage mechanism for different structural parameters has been verified. Meanwhile, extensive studies have found that hard carbon has excellent sodium storage performance and is expected to become a commercial anode. Although hard carbon has been extensively studied, the change trends of sodium storage properties with crystallinity are likely very complex. Thus, there is an even greater need to develop the analysis of the key structural factors and sodium storage properties to discover the laws and reveal the relationship.In this section, the effect of key structural parameters on the performance is analyzed. Moreover, we also added specific surface area (SSA, read directly in the literature) as an adjustment factor since the pseudocapacitive behavior and ICE are closely related to the SSA. Hence, important structural parameters (d002, La, Lc, ID/IG, and SSA) and main performance data (capacity, rate, working plateau, and ICE) are sorted and listed in Table 1. The comprehensive impact of multiple structural parameters on performance is difficult to be pinpointed experimentally. Therefore, we tried to introduce big data analysis to determine the relationship between the structure and performance. In statistics, the Spearman rank correlation test is a nonparametric technique used to evaluate the correlation between two independent variables. It requires that the two variables be pairs of rating data, or ranked data converted from continuous variable observations, without considering the overall distribution of the two variables and the size of the sample.35 When the data does not follow a normal distribution or the population distribution is unknown, Spearman correlation should be used. The Spearman rank correlation coefficient between random variables is defined as follows:
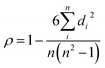 | (3) |
| HTT (°C) | Precursor | d 002 [nm] | L a [nm] | L c [nm] | I D/IG | SSABET [m2 g−1] | Rate factor | Initial CE [%] | Capacity [mA h g−1] | Working plateau [V] |
|---|---|---|---|---|---|---|---|---|---|---|
| a The values of d002, La, and Lc are derived from XRD. ID/IG is the intensity ratio between the D and G bands. The capacity is taken from the specific capacity at a current density of 100 mA g−1. The rate factor is obtained by uniform processing: the capacity under different current densities is taken, and the slope is fitted. The reciprocal of the slope is taken to express the rate performance. The higher the value is, the better the rate performance. The working plateau is the average working voltage in the main discharge range. | ||||||||||
| 600 | Peat moss39 | 0.384 | 2.09 | 1.08 | 0.86 | 369 | 0.23 | 44 | 189 | 1.02 |
| 600 | Waste tea bag40 | 0.389 | 1.61 | 0.67 | 0.95 | 415 | 0.33 | 58 | 170 | 0.54 |
| 700 | Pomelo peel18 | 0.371 | 1.84 | 0.88 | 1.04 | 1272 | 0.16 | 27 | 203 | 0.79 |
| 700 | Platanus bark41 | 0.372 | 1.62 | 0.76 | 0.84 | 602 | 0.19 | 34 | 234 | 0.87 |
| 700 | Sepals42 | 0.333 | 2.33 | 0.78 | 0.94 | 183 | 0.14 | 70 | 202 | 0.63 |
| 800 | Banana peel43 | 0.380 | 4.51 | 1.58 | 1.48 | 217 | 0.14 | 61 | 275 | 0.77 |
| 800 | Mangosteen shell44 | 0.367 | 2.71 | 1.04 | 0.97 | 540 | 1.17 | 22 | 50 | 0.59 |
| 800 | Shaddock peel45 | 0.386 | 1.91 | 0.81 | 0.95 | 25.5 | 0.16 | 62 | 216 | 0.73 |
| 800 | Cedarwood bark46 | 0.402 | 2.25 | 0.68 | 0.95 | 441 | 0.23 | 44 | 254 | 0.69 |
| 900 | Peat moss39 | 0.387 | 2.36 | 1.08 | 0.98 | 271 | 0.17 | 50 | 207 | 0.78 |
| 900 | Apricot shell47 | 0.377 | 1.93 | 0.67 | 1.01 | 27.9 | 0.23 | 73 | 282 | 0.63 |
| 900 | Reed straw48 | 0.394 | 1.95 | 0.77 | 1.01 | 325.3 | 0.22 | 49 | 116 | 0.62 |
| 900 | Water caltrop shell49 | 0.385 | 1.82 | 0.83 | 1.01 | 48.1 | 0.14 | 76 | 257 | 0.70 |
| 900 | Bio-oil50 | 0.359 | 1.70 | 0.86 | 1.09 | 820 | 0.23 | 56 | 200 | 0.93 |
| 950 | Sugarcane bagasse51 | 0.369 | 3.43 | 0.81 | 0.97 | 3 | 0.19 | 70 | 232 | 0.58 |
| 1000 | Cellulose52 | 0.375 | 2.72 | 0.83 | 1.05 | 377 | 0.13 | 59 | 235 | 0.68 |
| 1000 | Shaddock peel45 | 0.382 | 2.25 | 0.79 | 0.99 | 68 | 0.12 | 63 | 281 | 0.65 |
| 1000 | Switchgrass53 | 0.368 | 1.93 | 1.07 | 1.16 | 619 | 0.13 | 42 | 199 | 0.59 |
| 1000 | Lotus seedpods54 | 0.377 | 2.57 | 0.90 | 1.08 | 751.6 | 0.11 | 45 | 222 | 0.88 |
| 1000 | Cherry petals55 | 0.404 | 1.65 | 0.63 | 1.02 | 2 | 0.13 | 67 | 235 | 0.54 |
| 1100 | Peat moss39 | 0.374 | 3.49 | 0.87 | 0.99 | 197 | 0.12 | 57 | 281 | 0.63 |
| 1100 | Sucrose56 | 0.412 | 3.33 | 0.56 | 1.30 | 7 | 0.10 | 84 | 151 | 0.62 |
| 1100 | Rice husk57 | 0.395 | 2.75 | 0.86 | 1.01 | 3 | 0.16 | 64 | 332 | 0.58 |
| 1100 | Apricot shell47 | 0.385 | 2.29 | 0.72 | 1.03 | 56.7 | 0.18 | 77 | 328 | 0.65 |
| 1100 | Reed straw48 | 0.394 | 1.94 | 0.76 | 1.02 | 82 | 0.11 | 73 | 260 | 0.68 |
| 1200 | Shaddock peel45 | 0.390 | 2.60 | 0.73 | 1.00 | 82 | 0.08 | 67 | 315 | 0.60 |
| 1200 | Lotus stem58 | 0.371 | 2.36 | 0.48 | 1.06 | 25.8 | 0.19 | 69 | 194 | 0.54 |
| 1200 | Lotus seedpods54 | 0.386 | 2.69 | 0.86 | 1.04 | 140.7 | 0.08 | 50 | 279 | 0.81 |
| 1200 | Tamarind shell59 | 0.392 | 2.50 | 0.73 | 1.02 | 11.3 | 0.08 | 70 | 270 | 0.62 |
| 1300 | Mangosteen shell44 | 0.364 | 3.33 | 1.12 | 1.28 | 82 | 0.20 | 74 | 182 | 0.56 |
| 1300 | Rice husk57 | 0.388 | 3.08 | 0.93 | 0.99 | 0.3 | 0.13 | 66 | 365 | 0.59 |
| 1300 | Reed straw48 | 0.397 | 2.26 | 0.75 | 1.03 | 36 | 0.09 | 77 | 237 | 0.62 |
| 1300 | Walnut shell60 | 0.363 | 2.83 | 0.98 | 1.13 | 154 | 0.16 | 46 | 166 | 0.59 |
| 1300 | Lignin61 | 0.364 | 3.11 | 1.26 | 1.11 | 10.8 | 0.06 | 79 | 283 | 0.61 |
| 1400 | Peat moss39 | 0.373 | 4.19 | 0.99 | 1.03 | 92 | 0.11 | 60 | 240 | 0.50 |
| 1400 | Sucrose62 | 0.403 | 2.99 | 0.74 | 1.05 | 8 | 0.10 | 82 | 206 | 0.60 |
| 1400 | Peat63 | 0.339 | 3.38 | 2.19 | 0.98 | 6 | 0.08 | 80 | 303 | 0.51 |
| 1400 | Shaddock peel45 | 0.383 | 3.27 | 0.84 | 1.69 | 39 | 0.09 | 69 | 223 | 0.58 |
| 1500 | Mangosteen shell44 | 0.359 | 3.87 | 1.17 | 1.40 | 8.96 | 0.14 | 83 | 134 | 0.55 |
| 1500 | RF resin64 | 0.390 | 2.88 | 0.78 | 1.07 | 450 | 0.13 | 57 | 69 | 0.73 |
| 1500 | Reed straw48 | 0.381 | 2.99 | 0.90 | 1.05 | 23.9 | 0.09 | 79 | 210 | 0.62 |
| 1500 | Water caltrop shell49 | 0.376 | 3.25 | 0.95 | 1.01 | 7.4 | 0.11 | 86 | 236 | 0.56 |
| 1600 | Sucrose62 | 0.395 | 3.95 | 0.88 | 1.17 | 5 | 0.09 | 85 | 275 | 0.60 |
| 1600 | Cellulose65 | 0.386 | 4.03 | 0.79 | 1.16 | 2 | 0.12 | 81 | 51 | 0.52 |
| 1600 | Lotus stem58 | 0.350 | 2.73 | 1.21 | 1.24 | 23.7 | 0.08 | 56 | 240 | 0.49 |
| 1600 | Corn straw piths66 | 0.360 | 2.19 | 0.72 | 0.93 | 10 | 0.15 | 55 | 180 | 0.76 |
| 2050 | Switchgrass53 | 0.352 | 3.07 | 1.48 | 1.05 | 23 | 0.21 | 64 | 204 | 0.56 |
Let X and Y be the two variables, and they both have n elements. The i-th (1 ≤ i ≤ n) value of the two variables is expressed as Xi, Yi. Subsequently, xi and yi can be obtained after rearrangement of Xi and Yi in ascending or descending order, where element xi is the rank of Xi in X, and yi is the rank of Yi in Y. And then, a new set d can be obtained by subtracting the corresponding elements of xi and yi (di = xi − yi, 1 ≤ i ≤ n).
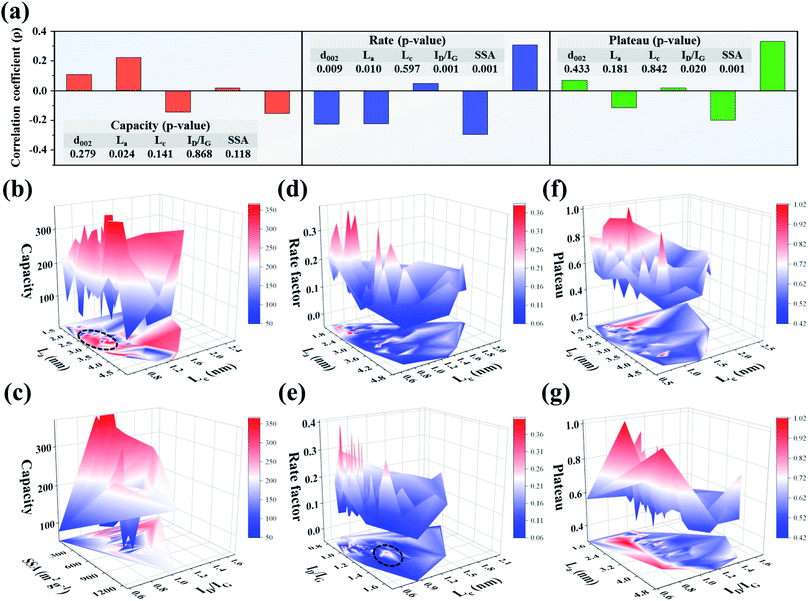
According to the structure–property data characteristics (independent, abnormal distribution), we chose the Spearman rank correlation test to analyze the correlation between variables. The significance (two-tailed) p value represents the reliability degree of the data. A small p-value (approaching 0) is generally considered as high significance, indicating that the correlation can be extended from the sample to the whole. The correlation coefficient ρ value represents the degree of correlation. The closer the absolute value of the correlation coefficient is to 1, the more significant the correlation, and a negative value indicates a negative correlation.36,37 After the Spearman rank correlation test, Fig. 2a shows the correlation degree between key structural parameters and performances (capacity, rate, and plateau). Each sodium storage performance is found to be mainly affected by one key structural parameter. The main impact factor for capacity is La (ρ = 0.223, p = 0.024). The rate and plateau are highly correlated with ID/IG with correlation coefficients of 0.296 and 0.201 (significances of 0.001 and 0.02), respectively. Considering the migration and diffusion mechanism of alkali metal ions, different energy storage performances reflect the different motion states in the carbon layer. The data analysis results above indicate that the motion state is closely related to the structure information. Hence, the effective extraction of key structural parameters is helpful in establishing the structure–property relationship. For example, by improving the morphology, intercalation routes could be controlled; adsorption behavior could be optimized by adjusting the pore structure and so on.38 Consequently, it is significant to establish the structure–property relationship for designing carbon materials with excellent sodium storage performance.
In fact, a certain sodium storage performance is affected by many structural parameters; for example, the size of the carbon layer (La and Lc) has a great influence on the diffusion kinetics of Na+. Single-factor analysis cannot reasonably reveal the change laws of non-graphite carbon with great structural differences. According to the thermodynamic and kinetic analysis for structure and performance in previous studies, a certain structural parameter can be mainly related to a corresponding performance parameter. For example, intercalation potential could be calculated using the Nernst equation, and diffusion barrier using density functional theory. Similarly, the ion diffusion rate can be studied by kinetic theory and is closely related to specific structural parameters, such as ionic diffusion coefficient and pseudocapacitive contribution (see the ESI† for a detailed description). Generally, the SSA is closely related to the ICE, and similarly for ID/IG and adsorption behavior.67 Therefore, based on the data analysis as well as thermodynamic and kinetic investigations, we found and analyzed the two structural factors that have the main impact on a certain performance parameter (as shown in Fig. 2b–g). Fig. 2b shows the influence of structural factors (La and Lc) on the sodium storage capacity. A small Lc and large La could mainly facilitate stable (de)intercalation of Na+ and provide a relatively large capacity (as shown in the dotted line area of Fig. 2b). A small Lc size favors reducing the number of layers, making it easy for hard carbon to form the “house of cards” structure. Meanwhile, the pore structure will be rich and diverse with the decrease of Lc, which increases the pore-filling sites and promotes the capacity eventually. Another high-capacity region in Fig. 2b is located in the large La (3–4.8 nm) and Lc (1.4–2.4 nm) region, which reflects different energy storage processes. A large carbon layer size will bring about more intercalation sites, but it is not conducive to the dynamics. Therefore, a large La can cause Na+ to (de)intercalate in the carbon layers at a low current density so that the reversible capacity is high. Additionally, the influence of the other two key structural parameters on the capacity is also evaluated. As shown in Fig. 2c, the reversible capacity is high in the region with medium SSA and high ID/IG, which is consistent with most of the reports.68 But the plateau capacity is low when SSA is high (600–1200 m2 g−1). The main energy storage behavior of hard carbon is dominated by the surface adsorption process as the SSA is high, which leads to the rise of working voltage plateau.18,50 Finally, the energy density lowers to a certain extent and irreversible capacity loss occurs inevitably.
The rate performance depends on the kinetic process. A high rate performance requires the microstructure to be conducive to large-scale ion diffusion. According to many research results, La and d002 determine the “length and width” of the Na+ diffusion process. Within a certain range, the smaller the carbon layer size is, the shorter is the ion intercalation path, which reduces the energy barrier and overpotential for Na+ diffusion. Moreover, the interlayer spacing of hard carbon is generally large, which is also helpful in the ion diffusion process. On the other hand, big data analysis shows that ID/IG has a significant negative correlation with the rate performance. According to the above analysis, the law between the rate performance and the two structural parameters is summarized. First, according to the variation law of rate performance versus changing La and Lc (as shown in Fig. 2d), small La and Lc values contribute to the rate performance over a certain range, but the mechanism is complicated, involving electron transfer and charge migration processes. In the results of Balogun et al., when alkali metal ions diffuse through etched carbon cloth (with increases in the pore content and diffraction intensity of the (100) crystal plane), the diffusion energy barrier rapidly decreases.69 The larger the La size is, the longer is the intercalation path, which is not conducive to high rate performance. Next, the influence rule of Lc and ID/IG on rate performance is shown in Fig. 2e. A carbon layer structure with a moderate ID/IG (0.8–1.0) and small Lc (<∼0.8 nm) is more conducive to high rate performance. The ID/IG value is closely related to the structural defects of the carbon layer. In general, DFT is an important research method, and the adsorption and diffusion processes of alkali metal ions at defect or edge sites can be explained based on DFT.70,71 The adsorption behavior will occur before the intercalation process due to the relatively smaller energy barrier. The increase in defects (decrease of crystallinity) enhances the adsorption behavior, which improves the rate performance but simultaneously leads to obvious sloping charge–discharge curves.5,72 However, there are some high rate values in the slightly large ID/IG (1.1–1.3) and small Lc (0.8–1.1 nm) regions (the dotted line area in Fig. 2e), which may correspond to different structural characteristics and sodium storage processes, and need to be further explored.
As shown in Fig. 2f, La and Lc have a relatively significant impact on the plateau. A slightly large La (1.6–2.3 nm) and a small Lc (<∼1.5 nm) make the plateau lower than those in other areas. Based on the analysis for the sodium storage mechanism, intercalation and pore-filling behaviors exhibit a very low plateau. Those behaviors could be promoted with large La and small Lc, which lower the working plateau. Similarly, as shown in Fig. 2g, the large ID/IG value also reflects the disorder of carbon layer arrangement. To a certain extent, the increase of defects caused by micropores is conducive to the pore-filling process, and thus the working plateau decreases. Therefore, Na+ can be stably intercalated and filled into the microstructure with a low working voltage plateau by adjusting the carbon layer size and defect degree. In anode material research, the low working plateau plays a significant role in improving the energy density of the battery.5 Hence, it is significant to design the structure to keep high capacity and rate performance while lowering the working plateau. According to the above results, La and Lc have a very significant effect on the performance, but the data range and overall regularity is not integral.
In summary, with a disordered structure and low crystallinity, hard carbon has been widely studied due to its high rate performance and highly adjustable microstructure. Although hard carbon has been widely studied in recent years, the complex “house of cards” structure is difficult to be quantitatively described due to its low crystallinity. The structure and sodium storage properties of hard carbon are easily affected by different precursors and HTTs, so the structure analysis is complex. Therefore, in this section, the key structural parameters and performance data were extracted, and the structure–property relationship of hard carbon for sodium storage was described quantitatively by a data analysis method. The excellent rate performance may be owed to the small carbon layer size and many defects. Such a structure is favorable for maintaining a stable microcrystalline structure, avoiding the structural damage caused by excessive volume expansion and improving the (de)intercalation process simultaneously. In addition, pore-filling behavior is also promoted owing to the high pore content and reduced Na+ diffusion distance. Therefore, fast and stable charge–discharge can be achieved. Although many efforts have been made to improve the performance, the energy storage process is still complex. According to the research results, further regulation of carbon layer size can effectively improve the sodium storage performance and exploring new preparation processes will be conducive to achieving this goal.
2.3 Soft carbon
Compared with hard carbon, soft carbon has a relatively higher ordering structure with reduced pores at the same HTT. Soft carbon can be graphitized at high temperature (artificial graphite). When the HTT is ∼1000 °C, the microstructure of the soft carbon contains some disorder region, which provides sites for the Na+ adsorption; when the HTT is higher than 1200 °C, the arrangement of the carbon layer gradually becomes regular with obvious lattice fringes, which is significantly different from that of hard carbon. As a result, the sodium storage mechanism and performance of soft carbon are quite different from those of hard carbon. As shown in Fig. S4 (ESI†), during the processes of sodiation/desodiation, the soft carbon only shows a certain slope with no extended plateau area in the charge–discharge curve. The sodium storage behavior has the following rules: firstly, sodium storage in the sloping region has better reversibility than that of hard carbon. But with many more defects, soft carbon has higher overall potential for sodium storage than hard carbon. Secondly, when Na+ ions are inserted into the carbon layers of soft carbon, local structural expansion will occur and some of the Na+ ions are trapped in the carbon layer, resulting in irreversible capacity loss.10,73–75 Certainly, the carbon layer crystallinity of soft carbon has a great influence on its sodium storage properties. Exploring the relationship between the key structural parameters and sodium storage properties will further promote the understanding and application of soft carbon.The structural and performance data of soft carbon synthesized with different precursors and HTTs are shown in Table 2. Compared with hard carbon, the carbon layer size of soft carbon is larger at the same HTT. The changes in these structural parameters lead to even greater differences in sodium storage performance. This section continues to explore the effect of key structural parameters on performance. The structure–property relationship is directly analyzed for soft carbon according to the existing data because of the small amount of data.
| HTT (°C) | Precursor | d 002 [nm] | L a [nm] | L c [nm] | I D/IG | SSABET [m2 g−1] | Rate factor | Initial CE [%] | Capacity [mA h g−1] | Working plateau [V] |
|---|---|---|---|---|---|---|---|---|---|---|
| a — indicates missing data. The values of d002, La, and Lc are derived from XRD. ID/IG is the intensity ratio between the D and G bands. The capacity is taken from the specific capacity at a current density of 100 mA g−1 unless otherwise stated. The rate factor is obtained by uniform processing: the capacity under different current densities is taken, and the slope is fitted. The reciprocal of the slope is taken to express the rate performance. The higher the value is, the better the rate performance. The working plateau is the average working voltage in the main discharge range. | ||||||||||
| 500 | NTCDA76 | 0.357 | 3.11 | 1.10 | 0.94 | 15 | 0.43 | 46 | 75.5 | 0.82 |
| 550 | Copolymer77 | 0.383 | 3.73 | 0.63 | 0.97 | 1106 | 0.18 | 71 | 215 | — |
| 700 | PTCDA9 | 0.362 | — | 1.52 | — | 13.6 | 0.19 | 62.6 | 171 | — |
| 700 | Pitch78 | 0.351 | 3.41 | 1.15 | 0.87 | 0.1 | 0.15 | 66 | 139 | 0.62 |
| 800 | PTCDA79 | 0.348 | 2.87 | 1.56 | 1.52 | 471 | 0.17 | 29 | 197 | 0.69 |
| 800 | Polymerized acetone80 | 0.369 | 2.22 | 0.81 | — | 467 | 0.12 | 34 | — | 0.73 |
| 800 | Pitch81 | 0.353 | 3.85 | 1.05 | 1.04 | 3 | 0.12 | 71 | 224 | 0.77 |
| 800 | Pitch81 | 0.349 | 2.97 | 1.43 | 0.91 | 113 | 0.11 | 45 | 135 | 0.64 |
| 900 | PTCDA9 | 0.356 | 3.69 | 1.92 | — | 20 | 0.30 | 67.6 | 167 | 0.59 |
| 900 | PTCDA82 | 0.356 | 3.84 | 1.41 | 1.04 | 14 | 0.21 | 80 | — | 0.91 |
| 1100 | PTCDA9 | 0.353 | 4.59 | 2.43 | — | 32 | 0.56 | 60.5 | 95 | — |
| 1000 | HC-SC83 | 0.356 | 1.66 | 1.11 | 0.94 | 589 | 0.38 | 57 | 240 (at 60 mA g−1) | 1.43 |
| 1000 | MP/THF84 | 0.363 | 2.80 | 1.27 | 0.87 | 59 | 0.12 | 80 | 260 | 0.63 |
| 1300 | MP/THF84 | 0.352 | 3.62 | 1.74 | 0.90 | 89 | 0.16 | 72 | 211 | — |
| 1300 | Coal38 | 0.371 | 2.63 | 0.89 | 1.02 | 4.53 | 0.08 | 79.5 | 155 | 0.58 |
| 1400 | Pitch/lignin85 | 0.37 | 3.74 | 1.17 | 1.09 | 1.3 | 0.16 | 82 | 245 (at 60 mA g−1) | 0.48 |
| 1400 | Pitch/phenolic resin86 | 0.39 | 3.27 | 0.92 | 1.17 | 3 | 0.08 | 88 | 255 (at 60 mA g−1) | 0.51 |
| 1500 | MP/THF84 | 0.352 | 4.65 | 1.97 | 1.35 | 32 | 0.12 | 74 | 241 | — |
| 1500 | Pitch87 | 0.354 | 2.95 | 1.75 | 1.07 | 119 | 0.24 | 60 | 189 | 0.64 |
| 1600 | PTCDA9 | 0.346 | 5.53 | 5.27 | — | 26 | 0.68 | 47.5 | 68 | — |
The effect rules of two structural parameters on the sodium storage performance are shown in Fig. 3a–f. As shown in Fig. 3a, high capacity mainly corresponds to a region of medium La (∼3.5–4.7 nm) and small Lc (0.5–1.8 nm). Meanwhile, a small SSA (<300 m2 g−1) and medium La (2.75–4 nm), as shown in Fig. 3b, is beneficial for obtaining high reversible capacity. The analysis shows that the carbon layer size is closely related to the capacity. Alvin et al.33 also reported a positive correlation between La and the plateau capacity. In the case of medium La size, both the sloping and plateau regions can provide high capacity. A small Lc will increase the disorder degree of the carbon layer, which also leads to a high reversible capacity mainly contributed by the adsorption process. Therefore, the data demonstrate the rationality and highlight the change regularity of the structure–property relationship. As a result, it is important to choose the appropriate carbon layer size to improve the sodium storage capacity. Additionally, there are still many blank areas in the figure to be further explored to reveal the law. There are still lots of unexplored areas for La and Lc, and further research is required to reveal the law.
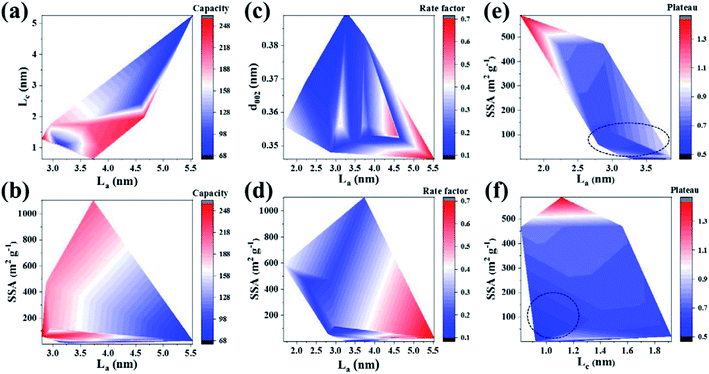 | ||
| Fig. 3 Contour maps of change trends for dual structural parameters and sodium storage performance. (a and b) Capacity; (c and d) rate; (e and f) plateau. | ||
Regarding the rate performance, La and d002 are two main influencing factors. As shown in Fig. 3c, large La (4.3–5.5 nm) and medium d002 (∼0.345–0.355 nm) values contribute to the rate performance over a certain range. It can also be seen from the influence of SSA and La on the rate performance (as shown in Fig. 3d) that the carbon layer structure with small SSA (<∼400 m2 g−1) and large La (4.0–5.5 nm) is associated with high rate performance. Inspired by the research results of Qiu et al., the diffusion energy barrier of Na+ will decrease significantly in the carbon layer with moderate interlayer spacing.88 As a result, medium d002 is helpful to promote Na+ reversible (de)intercalation at high rate and alleviate the volume expansion. The large La and medium d002 should be to obtain the optimum rate performance. However, large La may make the adsorption behavior dominant, because of the large resistance to Na+ intercalation. Although large La is associated with high rate performance, the rate factor obtained by uniform processing does not reflect the capacity value. Hence, combined with the analysis for capacity, medium d002 (∼0.345–0.355 nm) and moderate La (∼3.5–4.5 nm) are helpful to obtain high capacity at large current density. The impact mechanism of soft carbon is different from that of hard carbon, and the effect of the carbon layer size still needs to be further explored in order to fill the gaps in the current experiment, so as to improve the structure–property relationship.
As shown in Fig. 3e, La and SSA have a relatively significant impact on the plateau. A larger La and a smaller SSA make the plateau lower than those in other areas (as shown in the dotted line area of Fig. 3e), which are consistent with the effect of the structure on the rate performance. A large La will increase active sites, and low SSA does reduce the contribution of adsorption behavior to capacity, thus effectively lowering the plateau. But the effect rules, as shown in Fig. 3f, are not obvious for Lc on a plateau, and the low plateau area is widely distributed. The plateau performance is relatively low in the area of small Lc and SSA (as shown in the dotted line in Fig. 3f). On the one hand, there are many research studies on low-temperature soft carbon. The adsorption behavior is enhanced due to the poor crystallinity and many defects, and so the average working voltage plateau will rise. On the other hand, according to thermodynamics, the entropy change will be significant in the energy storage process on the basis of Boltzmann's entropy equation:
S = k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω Ω | (4) |
In conclusion, with different precursors and HTTs, the crystallinity of soft carbon changes in a certain range. The Na+ storage behavior of soft carbon has been changed owing to the distinction of key structural parameters. The main mechanism of soft carbon is interlayer intercalation, and most of the expansion is reversible. The results of data analysis show that the low-temperature soft carbon has high rate performance, which benefits from moderate expansion of interlayer spacing and disordered structure. The available data show that the medium La (∼3.5–4.5 nm) size is helpful to improve the three performances at the same time. It is still worth studying how to adjust the carbon layer structure of high-temperature soft carbon to optimize the comprehensive sodium storage performance.
Based on the relevant thermodynamic analysis, the statistical analysis of the structure–property data shows that the structure has a significant effect on the performance. The existing data point out that when the key structural parameters are in a specific range, comprehensive performance would be generally excellent. For example, when La is large (∼1.6–4.8 nm) and Lc is slightly small (<∼2.4 nm) for hard carbon, the comprehensive performance is generally outstanding. Similarly, when the range of La and Lc is ∼2–5.5 nm and ∼0.5–1.8 nm, respectively, most of the performance is usually good. Although there is a certain law when selecting two highly correlated parameters to analyze the performance data, here are also large errors and the laws are still complex. The influence of other structural parameters cannot be ignored. Therefore, it is necessary to use an accurate machine learning model to analyze the influence of all structural parameters on sodium storage performance.
3 Structure–property relationship and structure prediction
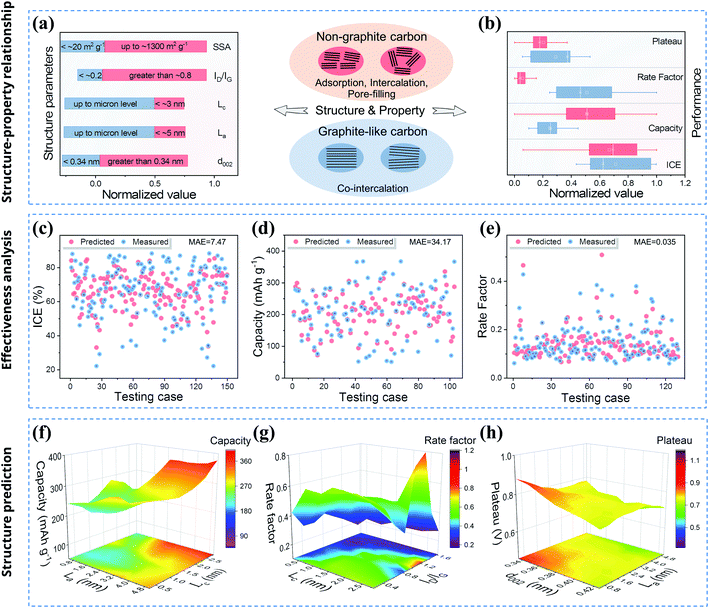
From the analysis of non-graphite carbon materials, the key structural parameters characterizing the crystallinity are the key factors affecting the sodium storage properties. However, various factors including structure and test conditions will affect the sodium storage mechanism and performance, and they are coupled with each other. Thus, the mechanisms that lead to changes in performance are very complicated. It is also difficult to use traditional research methods to analyze the influence of multiple structural parameters on a performance parameter at the same time. Previous research methods can only identify some influencing mechanisms, and the method of regulating and predicting the sodium storage performance through traditional structural research not only lacks accuracy but also has a certain lag.91 In addition, Section 2 of this work also shows that the rules of sodium storage based on the big data analysis are not accurately predicted. Large amounts of information about material structure and performance are stored in the databases, which currently cannot play a substantial guiding role, causing a serious waste of information resources. Most noteworthily, based on research advances in recent years, machine learning is currently undergoing a massive development that is affecting many areas of science and engineering, including catalysis and energy storage.92,93 In this work, in order to predict and screen the data of structural parameters with potentially excellent sodium storage performance, the model will be established in the basis of the structure–property database (Section S1, ESI†). The model makes it possible to predict different sodium storage performances with multiple structural parameters. Therefore, this research work aims to combine material structure–property data with machine learning technology to promote the development of high-performance electrode materials, so as to contribute to solving problems for scientific research and enterprises.Firstly, we summarized the structure and properties of non-graphite carbon materials. Furthermore, to facilitate a comprehensive understanding of the structure–property relationship, we comprehensively sorted out the structural and performance data of non-graphite (hard carbon, soft carbon, and rGO) and graphite-like (graphite, few-layer graphene and expanded graphite) carbon materials for sodium storage (Tables S1 and S2 in the ESI†). As shown in Fig. 4a, for graphite-like carbon materials, there are few structural defects and low heteroatom content, and regularly arranged carbon layers. Graphite-like carbon materials show significantly small interlayer spacing as well as micron-scale La and Lc which are much larger than those of non-graphite carbon materials. On the one hand, non-graphite carbon materials have short range order with an amorphous structure, and the carbon layer structure gradually forms with the rearrangement, assembly of carbon atoms and escape of unstable heteroatoms during the thermal treatment process. Due to the structural stress/strain, the layer-to-layer arrangement gradually becomes compact and flat with increasing HTT. On the other hand, under the influence of various precursors and HTTs, the carbon layer will form a large number of disordered regions, and the residual heteroatoms constitute intrinsic doping defects and cause local structural changes. Regardless of whether it is prepared from top-down or bottom-up, a specific evolution law can be applied to the carbon material, such as for soft carbon and hard carbon. For non-graphite carbon materials, the interlayer spacing is larger than that of graphite, and the ID/IG also increases to a certain extent, but the carbon layer sizes of La and Lc are much smaller (within tens of nanometers) than those of graphite-like carbon materials.
Next, the performance comparison of the two types of layered carbon material is clearly shown in Fig. 4b. The results show that the graphite-like carbon materials have excellent rate performance but a high plateau, which is mainly due to the co-intercalation mechanism in ether electrolyte.94 However, in the ester electrolyte system, the capacity performance of non-graphite carbon materials shows obvious advantages, and the plateau is also significantly reduced. This is because the sodium storage mechanism is mainly controlled by adsorption, intercalation and pore-filling. As for the ICE, it is mainly related to the electrolyte reduction on the electrode surface and the Na+ storage behavior inside the carbon layer, so the average value of the ICE is at a similar level for the two types of layered carbon material. Through comparative analysis, it can be found that the non-graphite carbon materials with low crystallinity have obvious advantages in the capacity and plateau performance, and there is still significant room to improve the high-rate capacity and ICE. Therefore, the reasonable design for carbon material structure plays a decisive role in improving its sodium storage performance. Importantly, it is necessary to predict the performance from the time when the structure is designed. Therefore, we tried to establish models and use computers to understand the change rules between the structural parameters and the sodium storage performance, and to consequently predict the performances. For several performance data, different basic models were selected to preliminarily verify the effect of machine learning according to previous research (see Section S2 for details, ESI†).95,96 The R2 and root mean squared error (RMSE) are displayed in Fig. S5 of the ESI† and there are some relatively good models with high R2 and low RMSE (bagging model for ICE, XGBoost for capacity and gradient boosting for rate). The prediction value and mean absolute error (MAE) are given in Fig. 4c–e, respectively. Overall, the results show that the predicted values are in good agreement with the measured values and the deviations are within the acceptable range. The predicted results indicate that the effectiveness of basic models is generally satisfactory. At the same time, the feature importance analysis also points out the degree of influence for different structural parameters (Fig. S6, ESI†). The above analysis urges us to establish accurate models to reduce errors for guiding future research.
Based on the structure–property database and machine learning, we planned to predict the structural parameters required to obtain the optimal performance. According to the existing value range of structure–property data for each performance, the ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sets of artificially constructed structure data were successfully built through permutation and combination (as depicted in Section S3 of the ESI†). Now the machine learning modeling for the above complete structure–property database is continued. The computer code reads in ∼100 sets of existing data for each performance parameter first, and the original data are divided into a training set and a testing set at a ratio of 8
000 sets of artificially constructed structure data were successfully built through permutation and combination (as depicted in Section S3 of the ESI†). Now the machine learning modeling for the above complete structure–property database is continued. The computer code reads in ∼100 sets of existing data for each performance parameter first, and the original data are divided into a training set and a testing set at a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Then, a suitable model could be established by analyzing the rules of the original data through multiple iterations (see the ESI† for the source code). Finally, prediction models are trained and tested. The results of ∼20
2. Then, a suitable model could be established by analyzing the rules of the original data through multiple iterations (see the ESI† for the source code). Finally, prediction models are trained and tested. The results of ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sets of artificially constructed structural data are substituted into the model to obtain the final prediction data. The prediction results are shown in Fig. 4f–h after filtering out the data that do not conform to the thermodynamic or kinetic results. Then, two key structural parameters were selected to illustrate the change rules for obtaining a specific structure and performance. As shown in Fig. 4f, high-capacity values are concentrated around the large La and Lc area, which are the same as the results described above. This carbon layer structure provides a substantial number of sites for Na+ intercalation but also has a certain hindrance effect on the diffusion kinetics. As for the rate performance (Fig. 4g), the high values are concentrated in the region with slightly large ID/IG (1.0–1.2) and large Lc (2.5–2.8 nm), which may correspond to the sodium storage mechanism of adsorption and pore-filling. However, the kinetic differences between different sodium storage mechanisms still need to be further explored. Finally, as shown in Fig. 4h, the La shows a significant impact on the plateau, and the large La area (4.0–5.0 nm) corresponds to the low value of the plateau. As for d002, the small d002 (<0.35 nm) significantly increases the plateau, and the plateau decreases as d002 increase (∼0.35–0.42 nm). Like the above research results, the large d002 and La also reflect the disorder of the carbon layer, which is helpful for Na+ intercalation and pore-filling to a certain degree, thus reducing the plateau. The above results show that the prediction is kinetically and thermodynamically reasonable, which also indicates the effectiveness of the predictions.
000 sets of artificially constructed structural data are substituted into the model to obtain the final prediction data. The prediction results are shown in Fig. 4f–h after filtering out the data that do not conform to the thermodynamic or kinetic results. Then, two key structural parameters were selected to illustrate the change rules for obtaining a specific structure and performance. As shown in Fig. 4f, high-capacity values are concentrated around the large La and Lc area, which are the same as the results described above. This carbon layer structure provides a substantial number of sites for Na+ intercalation but also has a certain hindrance effect on the diffusion kinetics. As for the rate performance (Fig. 4g), the high values are concentrated in the region with slightly large ID/IG (1.0–1.2) and large Lc (2.5–2.8 nm), which may correspond to the sodium storage mechanism of adsorption and pore-filling. However, the kinetic differences between different sodium storage mechanisms still need to be further explored. Finally, as shown in Fig. 4h, the La shows a significant impact on the plateau, and the large La area (4.0–5.0 nm) corresponds to the low value of the plateau. As for d002, the small d002 (<0.35 nm) significantly increases the plateau, and the plateau decreases as d002 increase (∼0.35–0.42 nm). Like the above research results, the large d002 and La also reflect the disorder of the carbon layer, which is helpful for Na+ intercalation and pore-filling to a certain degree, thus reducing the plateau. The above results show that the prediction is kinetically and thermodynamically reasonable, which also indicates the effectiveness of the predictions.
Furthermore, a part of the excellent predicted data is presented in Table 3. Notably, those data were carefully screened according to the results of statistical analysis based on the thermodynamic and kinetic results in Section 2. Therefore, we predicted and screened the specific structural parameters with potentially excellent sodium storage performance according to the results of machine learning and data analysis. Taken together, a structure with integrated excellent performance should have the following features, and the origin of each optimal range is revealed from the view of the sodium storage mechanism: d002 is slightly large (mainly 0.36–0.4 nm), which enables the intercalation behavior;88La should be in the range of 2.5–5 nm and Lc 1.5–2.5 nm, which promotes the stable intercalation process and fast rate capacity; and ID/IG ought to be medium (0.8–1.5) and SSA small (below ∼300 m2 g−1) to avoid excessive plateau and reduced ICE.67,97 Thus, the sodium storage mechanism of such carbon material should be dominated by intercalation behavior and include partial adsorption and pore filling behaviors. The moderate crystallinity ensures that the carbon material has high capacity and a low plateau, and the medium defect degree promotes the rapid (de)intercalation of Na+ and maintains the structural stability during the cycling. These data show that excellent sodium storage performance can be obtained by designing the carbon layer size, interlayer spacing and defect degree. Unfortunately, these layered pure carbon materials with excellent sodium storage performance have not yet been confirmed by researchers. However, this study provides future directions for designing carbon anodes, as well as an effective demonstration of machine learning in the performance prediction for other scientific areas. Additionally, if more data are available in the future, then reliable predictions can be made. Therefore, it is a useful exploration to analyze the existing data by machine learning, which not only fills the gaps in existing research but also predicts the specific structural parameters that may have the optimal sodium storage performance. The present study provides a promising route for the development of high-performance carbon materials. Both the material database and machine learning will contribute to the development of new energy materials for scientific research and enterprise.
| d 002 [nm] | L a [nm] | L c [nm] | I D/IG | SSABET [m2 g−1] | Rate factor | Initial CE [%] | Capacity [mA h g−1] | Working plateau [V] |
|---|---|---|---|---|---|---|---|---|
| 0.365 | 3.5 | 2.3 | 0.43 | 2 | 0.43 | 89 | 380 | 0.75 |
| 0.365 | 4 | 1.8 | 0.83 | 2 | 0.25 | 96 | 326 | 0.56 |
| 0.365 | 4 | 1.8 | 1.03 | 2 | 0.19 | 94 | 355 | 0.57 |
| 0.365 | 4.5 | 1.8 | 0.63 | 2 | 0.37 | 97 | 310 | 0.80 |
| 0.365 | 5 | 0.8 | 0.83 | 2 | 0.19 | 86 | 361 | 0.72 |
| 0.38 | 2.5 | 1.8 | 1.63 | 325 | 0.13 | 85 | 392 | 0.70 |
| 0.38 | 1.5 | 1.8 | 1.23 | 325 | 0.09 | 85 | 388 | 0.64 |
| 0.38 | 1.5 | 1.8 | 1.63 | 587 | 0.12 | 98 | 391 | 0.71 |
| 0.38 | 3 | 1.8 | 1.63 | 160 | 0.13 | 87 | 381 | 0.72 |
| 0.38 | 3.5 | 1.8 | 0.83 | 2 | 0.27 | 87 | 379 | 0.51 |
| 0.38 | 4.5 | 1.8 | 1.63 | 2 | 0.15 | 94 | 352 | 0.75 |
| 0.38 | 5 | 1.8 | 1.63 | 2 | 0.15 | 98 | 328 | 0.72 |
| 0.395 | 3.5 | 1.8 | 1.63 | 160 | 0.15 | 87 | 399 | 0.77 |
| 0.395 | 2.5 | 1.3 | 1.63 | 160 | 0.13 | 93 | 309 | 0.65 |
| 0.395 | 2 | 1.3 | 1.63 | 325 | 0.13 | 93 | 316 | 0.66 |
It must be recognized that the research of the structure–property database is still in its infancy, the reliability of the machine learning model in this work still needs to be improved, and equal attention should be paid to other structural information, such as porosity and defect sites. To prepare high-performance electrode materials efficiently and flexibly through big-data analysis and material design, the potential of the structure–property database might be jointly developed by interdisciplinary researchers. Herein, we call for a standardized test specification for material research, and a proposed process is presented for the preparation of high-performance electrode materials programmatically (as depicted in Fig. 5): firstly, we suggest a standardized data processing method: based on the main material characterization technologies (including XRD, Raman, BET, etc.), the key structural parameters and energy storage performance data of layered carbon materials can be obtained through a standardized processing method. The La and Lc should be calculated by fitting the FWHM of XRD and the d002 from Bragg's law. The ID/IG, pore size distribution and SSA should be obtained from Raman and BET results, respectively. It is also suggested that the electrochemical performance be standardized. The ICE, capacity and plateau data should be tested at low current density (e.g. 100 mA g−1 in this work). For rate performance, each current density should be cycled for a specified number of times (the battery could be cycled ten times at each current density). Furthermore, the cycle performance might be tested for a long time at low and high current density, respectively. Following the standardized testing and data processing methods, secondly, these structure parameters and performance data of future research will be integrated into the structure–property database established in this work, forming a constantly updated database to gain a comprehensive understanding of various non-graphite carbon materials; lastly, at the design end and implementation end, machine learning is supplemented to further update and improve the prior experience. Thus, the optimal structural parameters could be predicted precisely to achieve the screening effect for electrode materials and finally guide the future material design.
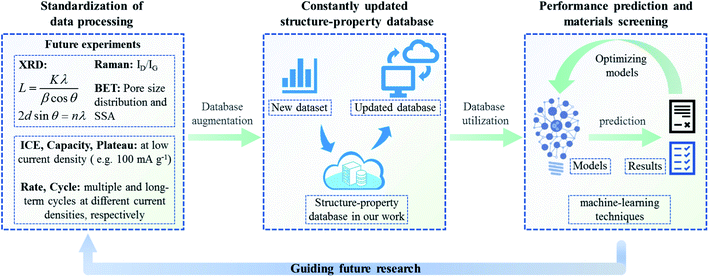 | ||
| Fig. 5 The proposed content of standardization data processing for non-graphite carbon materials, and the ideas for updating the structure–property database and optimizing machine learning. | ||
4 Summary and prospects
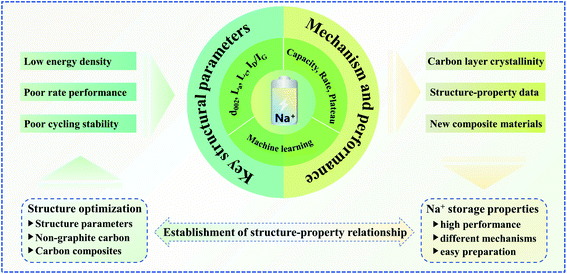
In summary, based on the crystallinity of the carbon layer, this research work clearly defines the microstructure relationship of non-graphite carbon materials. As illustrated in Fig. 6, the microstructure information (La, Lc, d002, ID/IG, and SSA) and sodium storage performance data (ICE, capacity, rate factor, and plateau) of non-graphite carbon materials in the existing literature are comprehensively sorted out, and a structure–property relationship database is preliminarily established, which can be supplemented and updated by subsequent research data. At the same time, we also call for a standardized processing specification for microstructure and sodium storage performance tests, so as to improve and update the sodium storage structure–property relationship database of non-graphite carbon materials in the future. Moreover, a data analysis method is used in conjunction with thermodynamic and kinetic analysis to clarify the correlation between sodium storage performance and structural parameters, and the relatively universal structure–property relationship of non-graphite carbon materials is also summarized. The sodium storage mechanism of hard carbon, soft carbon, rGO and other non-graphite carbon materials with poor crystallinity is mainly dominated by adsorption, intercalation and pore filling to different degrees. A small carbon layer, large interlayer spacing and high defect degree lead to different sodium storage properties for non-graphite carbon materials. The sodium storage mechanism and performance of different carbon materials change in a well-defined way with the structural evolution. Machine learning exploits this regularity to predict the sodium storage performance from the structural parameters. Furthermore, machine learning is employed to successfully screen for key structural parameters to achieve excellent comprehensive sodium storage performance, which can be used to guide the design of novel carbon-based materials. Finally, the following research directions on the sodium storage of carbon-based anodes are identified based on the synopsis provided here.(I) For non-graphite carbon materials, only low HTT performance has been considered, and few detailed studies have been performed on the structure and properties of high HTTs. Although a low HTT increases the number of active sites, a high HTT does not cause the dynamic process to completely deteriorate. The gaps in the sodium storage properties of non-graphite carbon materials at high HTTs still remain to be understood. Lastly, more comprehensive structural parameters of soft and hard carbon obtained through machine learning can lead to a better understanding of the effect of structure on performance.
(II) According to the statistical analysis of data, the carbon layer size (La and Lc) should have an important influence on the sodium storage mechanism and performance. However, most previous studies focused on how the interlayer spacing and defect types influence the sodium storage performance of layered carbon materials. Non-graphite carbon materials with large nanosized carbon layers may have distinctly different sodium storage properties. Exploring the influence of carbon layer size combined with machine learning will provide a new idea for seeking the balance of performance. The effects of the carbon layer size will be studied at nanometer to submicron regions to improve the understanding of non-graphite carbon materials and promote commercial application of these materials.
(III) The machine learning model can be optimized to guarantee the accuracy of the predicted structure by expanding the amount of data and enriching structural parameters. Some key technologies, such as natural language processing and image recognition, can be applied to obtain rich structural information (like the pore structure and heteroatom type) and reduce errors. Furthermore, to increase the utilization efficiency of data, we call for a standardized data processing method on the carbon material structure and sodium storage performance. With the help of accurate machine learning models, the constantly updated structure–property database can be used to guide the preparation of high-performance electrode materials programmatically.
In this work, the essential nature of crystallinity is shown to be the key structural information required for systematically developing an understanding of sodium storage mechanism and performance for non-graphite carbon materials. We constructed a database containing key structural parameters and main sodium storage performance to explore their relationships, resulting in an overall understanding of structure and performance. Then, big data analysis and basic theories were used to illustrate the effect of structure on the sodium storage performance and its mechanism, which can provide important guidance in the field. Finally, with the help of machine learning, the structure–property relationship was revealed to predict and screen the optimal structure for the best sodium storage performance, thus filling the gaps in experimental results and identifying research directions. Therefore, the database collected from the previous reports can be combined with machine learning to identify the structure–property relationship, which promotes the design and application of novel electrode materials and provides a new paradigm for researching other materials.
Conflicts of interest
There are no conflicts to declare.References
- S. Rothermel, P. Meister, G. Schmuelling, O. Fromm, H. Meyer, S. Nowak, M. Winter and T. Placke, Energy Environ. Sci., 2014, 7, 3412–3423 RSC.
- X. K. Wang, J. Shi, L. W. Mi, Y. P. Zhai, J. Y. Zhang, X. M. Feng, Z. J. Wu and W. H. Chen, Rare Metals, 2020, 39(9), 1053–1062 CrossRef CAS.
- Y. Li, Y. S. Hu, M. M. Titirici, L. Chen and X. Huang, Adv. Energy Mater., 2016, 6, 1600659 CrossRef.
- Y. Qi, Y. Lu, F. Ding, Q. Zhang, H. Li, X. Huang, L. Chen and Y. S. Hu, Angew. Chem., Int. Ed., 2019, 58, 4361–4365 CrossRef CAS PubMed.
- X. Dou, I. Hasa, D. Saurel, C. Vaalma, L. Wu, D. Buchholz, D. Bresser, S. Komaba and S. Passerini, Mater. Today, 2019, 23, 87–104 CrossRef CAS.
- L. Liu, Z. Ji, S. Zhao, Q. Niu and S. Hu, J. Mater. Chem. A, 2021, 9, 6172–6179 RSC.
- B. H. Hou, Y. Y. Wang, Q. L. Ning, W. H. Li, X. T. Xi, X. Yang, H. J. Liang, X. Feng and X. L. Wu, Adv. Mater., 2019, 31, e1903125 CrossRef PubMed.
- N. Sun, Z. Guan, Y. Liu, Y. Cao, Q. Zhu, H. Liu, Z. Wang, P. Zhang and B. Xu, Adv. Energy Mater., 2019, 9, 1901351 CrossRef.
- W. Luo, Z. Jian, Z. Xing, W. Wang, C. Bommier, M. M. Lerner and X. Ji, ACS Cent. Sci., 2015, 1, 516–522 CrossRef CAS PubMed.
- Z. Jian, C. Bommier, L. Luo, Z. Li, W. Wang, C. Wang, P. A. Greaney and X. Ji, Chem. Mater., 2017, 29, 2314–2320 CrossRef CAS.
- J. Zhao, Y. Z. Zhang, F. Zhang, H. Liang, F. Ming, H. N. Alshareef and Z. Gao, Adv. Energy Mater., 2019, 9, 1803215 CrossRef.
- E. Goikolea, V. Palomares, S. Wang, I. R. de Larramendi, X. Guo, G. Wang and T. Rojo, Adv. Energy Mater., 2020, 10, 2002055 CrossRef CAS.
- T. Kuila, A. K. Mishra, P. Khanra, N. H. Kim and J. H. Lee, Nanoscale, 2013, 5, 52–71 RSC.
- J. Tianyi, L. Xiaoxu, Z. Jiupeng and L. Yao, Chem. J. Chin. Univ., 2020, 41, 821–828 Search PubMed.
- K. S. Novoselov, V. Fal, L. Colombo, P. Gellert, M. Schwab and K. Kim, Nature, 2012, 490, 192–200 CrossRef CAS PubMed.
- D. Saurel, B. Orayech, B. Xiao, D. Carriazo, X. Li and T. Rojo, Adv. Energy Mater., 2018, 8, 1703268 CrossRef.
- R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279 CrossRef CAS PubMed.
- K.-l. Hong, L. Qie, R. Zeng, Z.-q. Yi, W. Zhang, D. Wang, W. Yin, C. Wu, Q.-j. Fan and W.-x. Zhang, J. Mater. Chem. A, 2014, 2, 12733–12738 RSC.
- A. K. Kercher and D. C. Nagle, Carbon, 2003, 41, 15–27 CrossRef CAS.
- H. Fujimoto, Carbon, 2003, 41, 1585–1592 CrossRef CAS.
- F. Tai, C. Wei, S. Chang and W. Chen, J. Raman Spectrosc., 2010, 41, 933–937 CrossRef CAS.
- A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- J.-B. Wu, M.-L. Lin, X. Cong, H.-N. Liu and P.-H. Tan, Chem. Soc. Rev., 2018, 47, 1822–1873 RSC.
- X. Wang, S.-C. Huang, S. Hu, S. Yan and B. Ren, Nat. Rev. Phys., 2020, 2, 253–271 CrossRef.
- D.-W. Kim, H.-S. Kil, J. Kim, I. Mochida, K. Nakabayashi, C. K. Rhee, J. Miyawaki and S.-H. Yoon, Carbon, 2017, 121, 301–308 CrossRef CAS.
- T. Xing, L. H. Li, L. Hou, X. Hu, S. Zhou, R. Peter, M. Petravic and Y. Chen, Carbon, 2013, 57, 515–519 CrossRef CAS.
- H. Badenhorst, Carbon, 2014, 66, 674–690 CrossRef CAS.
- L. Su, J. Hei, X. Wu, L. Wang and Z. Zhou, Adv. Funct. Mater., 2017, 27, 1605544 CrossRef.
- D. Stevens and J. Dahn, J. Electrochem. Soc., 2000, 147, 1271 CrossRef CAS.
- Q. Jin, K. Wang, P. Feng, Z. Zhang, S. Cheng and K. Jiang, Energy Storage Mater., 2020, 27, 43–50 CrossRef.
- Z. E. Yu, Y. Lyu, Y. Wang, S. Xu, H. Cheng, X. Mu, J. Chu, R. Chen, Y. Liu and B. Guo, Chem. Commun., 2020, 56, 778–781 RSC.
- G. Yang, X. Li, Z. Guan, Y. Tong, B. Xu, X. Wang, Z. Wang and L. Chen, Nano Lett., 2020, 20, 3836–3843 CrossRef CAS PubMed.
- S. Alvin, H. S. Cahyadi, J. Hwang, W. Chang, S. K. Kwak and J. Kim, Adv. Energy Mater., 2020, 10, 2000283 CrossRef CAS.
- Z. Li, C. Bommier, Z. S. Chong, Z. Jian, T. W. Surta, X. Wang, Z. Xing, J. C. Neuefeind, W. F. Stickle, M. Dolgos, P. A. Greaney and X. Ji, Adv. Energy Mater., 2017, 7, 1602894 CrossRef.
- T. D. Gauthier, Environ. Forensics, 2001, 2, 359–362 CrossRef CAS.
- J. H. Zar, J. Am. Stat. Assoc., 1972, 67, 578–580 CrossRef.
- Q. Liu, C. Li, V. Wanga and B. E. Shepherd, Biometrics, 2018, 74, 595–605 CrossRef PubMed.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Chem. Soc. Rev., 2019, 48, 4655–4687 RSC.
- J. Ding, H. Wang, Z. Li, A. Kohandehghan, K. Cui, Z. Xu, B. Zahiri, X. Tan, E. M. Lotfabad, B. C. Olsen and D. Mitlin, ACS Nano, 2013, 7, 11004–11015 CrossRef CAS PubMed.
- A. A. Arie, B. Tekin, E. Demir and R. Demir-Cakan, Mater. Technol., 2019, 34, 515–524 CrossRef CAS.
- X.-K. Wang, J. Shi, L.-W. Mi, Y.-P. Zhai, J.-Y. Zhang, X.-M. Feng, Z.-J. Wu and W.-H. Chen, Rare Met., 2020, 39, 1053–1062 CrossRef CAS.
- D. Damodar, S. Ghosh, M. Usha Rani, S. K. Martha and A. S. Deshpande, J. Power Sources, 2019, 438, 227008 CrossRef CAS.
- E. M. Lotfabad, J. Ding, K. Cui, A. Kohandehghan, W. P. Kalisvaart, M. Hazelton and D. Mitlin, ACS Nano, 2014, 8, 7115–7129 CrossRef CAS PubMed.
- Z. Wang, W. He, X. Zhang, Y. Yue, G. Yang, X. Yi, Y. Wang and J. Wang, ChemElectroChem, 2017, 4, 671–678 CrossRef CAS.
- N. Sun, H. Liu and B. Xu, J. Mater. Chem. A, 2015, 3, 20560–20566 RSC.
- M. Lu, Y. Huang and C. Chen, Energy Fuels, 2020, 34, 11489–11497 CrossRef CAS.
- Y. Zhu, M. Chen, Q. Li, C. Yuan and C. Wang, Carbon, 2018, 129, 695–701 CrossRef CAS.
- J. Wang, L. Yan, Q. Ren, L. Fan, F. Zhang and Z. Shi, Electrochim. Acta, 2018, 291, 188–196 CrossRef CAS.
- W. Cao, E. Zhang, J. Wang, Z. Liu, J. Ge, X. Yu, H. Yang and B. Lu, Electrochim. Acta, 2019, 293, 364–370 CrossRef CAS.
- R. Muruganantham, T.-H. Hsieh, C.-H. Lin and W.-R. Liu, Mater. Today Energy, 2019, 14, 100346 CrossRef.
- P. C. Rath, J. Patra, H. T. Huang, D. Bresser, T. Y. Wu and J. K. Chang, ChemSusChem, 2019, 12, 2302–2309 CrossRef CAS PubMed.
- W. Luo, J. Schardt, C. Bommier, B. Wang, J. Razink, J. Simonsen and X. Ji, J. Mater. Chem. A, 2013, 1, 10662–10666 RSC.
- F. Zhang, Y. Yao, J. Wan, D. Henderson, X. Zhang and L. Hu, ACS Appl. Mater. Interfaces, 2017, 9, 391–397 CrossRef CAS PubMed.
- F. Wu, M. Zhang, Y. Bai, X. Wang, R. Dong and C. Wu, ACS Appl. Mater. Interfaces, 2019, 11, 12554–12561 CrossRef CAS PubMed.
- Z. Zhu, F. Liang, Z. Zhou, X. Zeng, D. Wang, P. Dong, J. Zhao, S. Sun, Y. Zhang and X. Li, J. Mater. Chem. A, 2018, 6, 1513–1522 RSC.
- Z. Li, L. Ma, T. W. Surta, C. Bommier, Z. Jian, Z. Xing, W. F. Stickle, M. Dolgos, K. Amine, J. Lu, T. Wu and X. Ji, ACS Energy Lett., 2016, 1, 395–401 CrossRef CAS.
- Q. Wang, X. Zhu, Y. Liu, Y. Fang, X. Zhou and J. Bao, Carbon, 2018, 127, 658–666 CrossRef CAS.
- Y. Xu, C. Zhang, M. Zhou, Q. Fu, C. Zhao, M. Wu and Y. Lei, Nat. Commun., 2018, 9, 1–11 CrossRef PubMed.
- K. Yu, H. Zhao, X. Wang, M. Zhang, R. Dong, Y. Li, Y. Bai, H. Xu and C. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 10544–10553 CrossRef CAS PubMed.
- S. Zhang, Y. Li and M. Li, Jom, 2018, 70, 1387–1391 CrossRef CAS.
- X. Yu, B. Yu, J. Zhang, Y. Zhang, J. Zeng, M. Chen and C. Wang, ChemistrySelect, 2018, 3, 9518–9525 CrossRef CAS.
- C. Bommier, T. W. Surta, M. Dolgos and X. Ji, Nano Lett., 2015, 15, 5888–5892 CrossRef CAS PubMed.
- A. Adamson, R. Väli, M. Paalo, J. Aruväli, M. Koppel, R. Palm, E. Härk, J. Nerut, T. Romann, E. Lust and A. Jänes, RSC Adv., 2020, 10, 20145–20154 RSC.
- Q. Zhang, X. Deng, M. Ji, Y. Li and Z. Shi, Ionics, 2020, 26, 4523–4532 CrossRef CAS.
- C. Bommier, D. Leonard, Z. Jian, W. F. Stickle, P. A. Greaney and X. Ji, Adv. Mater. Interfaces, 2016, 3, 1600449 CrossRef.
- Y.-E. Zhu, H. Gu, Y.-N. Chen, D. Yang, J. Wei and Z. Zhou, Ionics, 2018, 24, 1075–1081 CrossRef CAS.
- H. He, D. Sun, Y. Tang, H. Wang and M. Shao, Energy Storage Mater., 2019, 23, 233–251 CrossRef.
- H. Alptekin, H. Au, A. C. Jensen, E. Olsson, M. Goktas, T. F. Headen, P. Adelhelm, Q. Cai, A. J. Drew and M.-M. Titirici, ACS Appl. Energy Mater., 2020, 3, 9918–9927 CrossRef CAS.
- M.-S. Balogun, H. Yang, Y. Luo, W. Qiu, Y. Huang, Z.-Q. Liu and Y. Tong, Energy Environ. Sci., 2018, 11, 1859–1869 RSC.
- L. Fu, R. Wang, C. Zhao, J. Huo, C. He, K.-H. Kim and W. Zhang, Chem. Eng. J., 2021, 414, 128857 CrossRef CAS.
- H. Yang, C. He, L. Fu, J. Huo, C. Zhao, X. Li and Y. Song, Chin. Chem. Lett., 2021, 32, 3202–3206 CrossRef CAS.
- C. Xu, B. Xu, Y. Gu, Z. Xiong, J. Sun and X. Zhao, Energy Environ. Sci., 2013, 6, 1388–1414 RSC.
- M. M. Doeff, Y. Ma, S. J. Visco and L. C. De Jonghe, J. Electrochem. Soc., 1993, 140, L169–L170 CrossRef CAS.
- R. Alcántara, F. F. Madrigal, P. Lavela, J. Tirado, J. J. Mateos, C. G. De Salazar, R. Stoyanova and E. Zhecheva, Carbon, 2000, 38, 1031–1041 CrossRef.
- R. Alcántara, P. Lavela, G. F. Ortiz, J. L. Tirado, R. Menéndez, R. Santamaría and J. M. Jimenez-Mateos, Carbon, 2003, 41, 3003–3013 CrossRef.
- W. Li, M. Zhou, H. Li, K. Wang, S. Cheng and K. Jiang, Energy Environ. Sci., 2015, 8, 2916–2921 RSC.
- L. Yu, H. Song, Y. Li, Y. Chen, X. Chen, J. Zhou, Z. Ma, X. Wan, P. Tian and J. Wu, Electrochim. Acta, 2016, 218, 285–293 CrossRef CAS.
- L.-J. Song, S.-S. Liu, B.-J. Yu, C.-Y. Wang and M.-W. Li, Carbon, 2015, 95, 972–977 CrossRef CAS.
- X. Yao, Y. Ke, W. Ren, X. Wang, F. Xiong, W. Yang, M. Qin, Q. Li and L. Mai, Adv. Energy Mater., 2018, 9, 1803260 CrossRef.
- H. Hou, C. E. Banks, M. Jing, Y. Zhang and X. Ji, Adv. Mater., 2015, 27, 7861–7866 CrossRef CAS PubMed.
- B. Cao, H. Liu, B. Xu, Y. Lei, X. Chen and H. Song, J. Mater. Chem. A, 2016, 4, 6472–6478 RSC.
- L. Fan, Q. Liu, S. Chen, Z. Xu and B. Lu, Adv. Energy Mater., 2017, 7, 1602778 CrossRef.
- Y. Xue, M. Gao, M. Wu, D. Su, X. Guo, J. Shi, M. Duan, J. Chen, J. Zhang and Q. Kong, ChemElectroChem, 2020, 7, 4010–4015 CrossRef CAS.
- F. Xie, Z. Xu, A. C. S. Jensen, H. Au, Y. Lu, V. Araullo-Peters, A. J. Drew, Y. S. Hu and M. M. Titirici, Adv. Funct. Mater., 2019, 29, 1901072 CrossRef.
- Y. Li, Y.-S. Hu, H. Li, L. Chen and X. Huang, J. Mater. Chem. A, 2016, 4, 96–104 CAS.
- Y. Li, L. Mu, Y.-S. Hu, H. Li, L. Chen and X. Huang, Energy Storage Mater., 2016, 2, 139–145 CrossRef.
- D. Qiu, T. Cao, J. Zhang, S.-W. Zhang, D. Zheng, H. Wu, W. Lv, F. Kang and Q.-H. Yang, J. Energy Chem., 2019, 31, 101–106 CrossRef.
- S. Qiu, L. Xiao, M. L. Sushko, K. S. Han, Y. Shao, M. Yan, X. Liang, L. Mai, J. Feng and Y. Cao, Adv. Energy Mater., 2017, 7, 1700403 CrossRef.
- J. Sun, H.-W. Lee, M. Pasta, H. Yuan, G. Zheng, Y. Sun, Y. Li and Y. Cui, Nat. Nanotechnol., 2015, 10, 980–985 CrossRef CAS PubMed.
- J. Sun, G. Zheng, H.-W. Lee, N. Liu, H. Wang, H. Yao, W. Yang and Y. Cui, Nano Lett., 2014, 14, 4573–4580 CrossRef CAS PubMed.
- S. Ma and Z.-P. Liu, ACS Catal., 2020, 10, 13213–13226 CrossRef CAS.
- A. Chen, X. Zhang and Z. Zhou, InfoMat, 2020, 2, 553–576 CrossRef CAS.
- X. Chen, X. Liu, X. Shen and Q. Zhang, Angew. Chem., Int. Ed., 2021, 60, 24354–24366 CrossRef CAS PubMed.
- H. Kim, J. Hong, G. Yoon, H. Kim, K.-Y. Park, M.-S. Park, W.-S. Yoon and K. Kang, Energy Environ. Sci., 2015, 8, 2963–2969 RSC.
- A. Chen, X. Zhang, L. Chen, S. Yao and Z. Zhou, J. Phys. Chem. C, 2020, 124, 22471–22478 CrossRef CAS.
- L. Chen, X. Zhang, A. Chen, S. Yao, X. Hu and Z. Zhou, Chin. J. Catal., 2022, 43, 11–32 CrossRef CAS.
- X. Liu, T. Ji, H. Guo, H. Wang, J. Li, H. Liu and Z. Shen, Electrochem. Energy Rev., 2021 DOI:10.1007/s41918-021-00114-6.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta10588d |
| This journal is © The Royal Society of Chemistry 2022 |