In optimized rubrene-based nanoparticle blends for photon upconversion, singlet energy collection outcompetes triplet-pair separation, not singlet fission

Abstract

The conversion of near-infrared photons to visible light through triplet–triplet annihilation upconversion offers an enticing strategy for significantly boosting the efficiency of conventional solar cell technology. Rubrene is widely employed as the acceptor molecule for realising such upconversion, yet in the solid state, the reverse process of singlet fission is believed to hinder efficient upconversion. Consequently, rubrene is sometimes doped at low concentration (0.5 mol%) with the singlet energy collector tetraphenyldibenzoperiflanthene (DBP) which harvests singlet energy via Förster transfer. Although singlet fission is a multi-step process involving various intermediate triplet-pair states, the interplay between it, triplet recombination and singlet energy collection has not been studied in detail to date. Here we use both transient absorption and time-resolved fluorescence spectroscopy to investigate the dynamics of both singlet and triplet species in rubrene-based nanoparticle films. Strikingly, we find that energy transfer from rubrene to DBP does not outcompete the formation of triplet-pairs through singlet fission, despite the fact that DBP doping increases the photoluminescence quantum yield of the nanoparticle films from 3% to 61%. We rationalise this surprising result in the context of the well-known effects of triplet fusion and triplet-quenching defects on the photoluminescence yield of crystalline rubrene.

---

Introduction

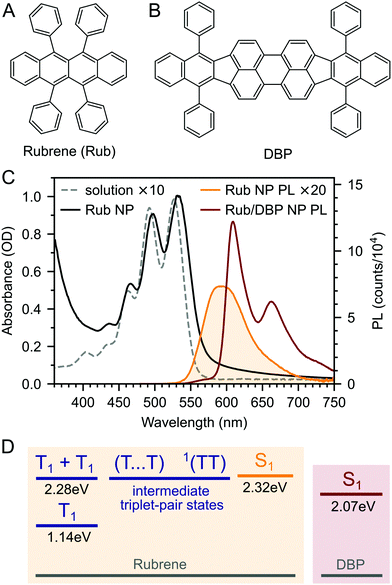
Triplet–triplet annihilation upconversion (TTA-UC) provides an attractive mechanism for converting near-infrared photons into visible photons.^1–3 Triplet excitons created on donor species following photon absorption are transferred to acceptor molecules via Dexter transfer.⁴ The subsequent annihilation of two sensitised triplets yields one singlet state which fluoresces, giving upconverted emission. TTA-UC has received a great deal of interest in recent years due to its potential to significantly enhance the power conversion efficiency of photovoltaics cells.^5–9 In addition, TTA-UC also has a variety of biomedical applications^10,11 including optogenetics¹² and targeted drug delivery.¹³

In order to maximise the photon energy gain (anti-Stokes shift) during TTA-UC, it is desirable for the singlet energy level of the annihilator molecule to be as close as possible to twice the triplet energy. Rubrene fulfils this criterion,¹⁴ which partly explains its widespread use as the acceptor molecule for near-infrared-to-visible TTA-UC.^1,3,15–21 For example, a TTA-UC efficiency of 8% (out of a maximum 50%) has been reported for rubrene-mediated TTA-UC in solution.²² However, photovoltaic and biomedical applications demand solid state TTA-UC material systems. In this case, the beneficial energy level alignment between S₁ and twice T₁ can become a hindrance to efficient upconversion. This is because the singlet states populated by TTA can undergo the reverse process of singlet fission,^23,24 whereby they split into pairs of triplet excitons, rather than emitting their energy radiatively.^18,25–28

As a result, several strategies have recently been reported to mitigate the effects of singlet fission in solid rubrene-based TTA-UC systems. The addition of bulky side groups to increase intermolecular distances has been shown to improve the PLQY of rubrene several-fold,^26,29,30 though the benefit to TTA-UC is severely tempered by reduced triplet diffusivity.³⁰ More commonly, rubrene is doped with the singlet energy collector tetraphenyldibenzoperiflanthene (DBP), which can harvest singlet energy from rubrene by Förster resonance energy transfer (FRET).^18,26–28 The effectiveness of this strategy appears to vary significantly with the type of sample studied. For example Wu et al. reported a 19-fold increase in the upconversion quantum yield upon doping with DBP,¹⁸ whilst Wieghold et al. reported that it had little effect.²⁸

Previous studies of rubrene–DBP TTA-UC systems include in some form the assertion that FRET from rubrene to DBP outcompetes singlet fission.^18,26–28 This simple statement appears to overlook the complexity of singlet fission and triplet fusion that occurs in solid rubrene, dynamics that have been extensively studied in vapour-grown orthorhombic single crystals^31–45 and to a lesser degree in more complex thin films.^{25,30,46–51}

Furthermore, transient absorption spectroscopy of rubrene single crystals has shown that S₁ → ¹(TT) occurs extremely rapidly, with reported time constants varying from 25 fs^35,36 to 2 ps.^33,34 FRET from rubrene to DBP is therefore very unlikely to outcompete this first singlet fission step for the majority of excitons. In ESI,‡ Section S11, we estimate the rubrene–DBP FRET rate to be 1.5 ps for nearest neighbours based on previous calculations of the Förster radius.⁵² We also demonstrate that, since the DBP concentration is low (1 in 200),^26,27 the majority of photo-excited rubrene singlets will undergo singlet fission well before diffusing far enough to encounter a DBP molecule. If energy transfer from rubrene to DBP is not competitive with singlet fission, what role does DBP play that enables it to increase the PLQY of solid rubrene by such a large factor?^18,26,53

In order to answer this question, we probe the excited-state dynamics of some of the most highly emissive solid-state rubrene samples developed to date,^27,53 both with and without the DBP dopant. This new material system consists of solid rubrene nanoparticles prepared by reprecipitation and dispersed in an oxygen-blocking poly(vinyl alcohol) (PVA) matrix.^27,53 The nanoparticles are smooth and spherical with an average diameter of 220 nm and give no peaks in X-ray diffraction measurements,⁵³ indicating a lack of any long-range molecular ordering. These rubrene nanoparticle films have proven to be an effective and versatile platform for realising in-air TTA-UC in solid rubrene, reaching an upconversion quantum efficiency of more than 2% when doped with an optimum 0.5 mol% DBP.²⁷ Perhaps most strikingly, the reported PLQY value of 84% for the rubrene–DBP nanoparticles²⁷ is several times greater than the 15% measured for equivalently doped polycrystalline films.²⁶

In rubrene–DBP systems, the details of exciton dynamics is yet to be discussed in terms of the triplet-pair intermediates and the concurrent nature of singlet fission and triplet fusion in rubrene. Here we use the high-performing rubrene NP films as a model system, combined with transient absorption and time-resolved photoluminescence spectroscopy, to explore and understand the true role of the DBP dopant. We also compare our results against a polycrystalline film reference. We begin by characterising the singlet fission and triplet fusion dynamics of pure rubrene NPs, allowing us to next identify which processes are affected by the addition of DBP. We find that FRET from rubrene to DBP does not outcompete the formation of triplet-pairs via singlet fission, but instead partially outcompetes triplet-pair separation. We further highlight the crucial effects of energy cycling through triplet fusion in the high PLQY of DBP-doped rubrene.

Singlet fission and triplet fusion in rubrene: a brief review

Before presenting our results, it is useful to briefly review the extensive existing literature on singlet fission and triplet fusion in rubrene crystals and films. We begin with the best studied material system: vapour-grown orthorhombic single crystals.^31,32

In orthorhombic rubrene crystals, the electronic coupling between S₁ and ¹(TT) vanishes by symmetry.⁵⁴ As a result, some form of symmetry breaking is responsible for the first fission step, S₁ → ¹(TT), though the mechanism is debated.^35,36,55 As stated above, reported time constants for this first step range from 25 fs^35,36 to 2 ps.^33,34

Next, ¹(TT) separates into (T⋯T) over tens of picoseconds,^33–36 a process thought to occur by thermally-activated triplet hopping.^56–59 The overall singlet fission process is therefore commonly written as^60,61

S₁ → ¹(TT) → (T⋯T) → T₁ + T₁, (1)

where (T⋯T) denotes spatially separated triplet-pair states that retain their spin interactions⁶² before eventually decohering into independent triplet excitons.

Observations of quantum beats in the delayed fluorescence⁴² confirm the existence of ¹(T⋯T): a spatially separated triplet-pair state that retains its spin-0 singlet character.^63–661(T⋯T) subsequently undergoes spin evolution,⁴⁶ resulting in the formation of mixed-spin triplet-pair states (T⋯T)^l, whose presence is confirmed by the observation of changes in PL with applied magnetic field.⁶⁷ The final products of singlet fission in rubrene single crystals are independent triplet excitons, which are formed with near-unity quantum yield.^38,40 These triplets possess a long excited state lifetime of 100 μs,³⁸ enabling them to diffuse across distances of several microns.^39,41

Geminate and non-geminate fusion of triplet-pairs and triplets respectively results in pronounced delayed PL.^38,40,43,44 Geminate fusion of separated triplet-pairs gives rise to distinct power-law dynamics in the delayed PL, with exponents that depend on the dimensionality and anisotropy of the triplet diffusion.^43,44 Overall, triplet fusion in rubrene crystals is extremely efficient and can contribute more than 90% of the total photoluminescence quantum yield (PLQY).⁴⁰ The long diffusion length of the triplet excitons, coupled with dominant contribution of triplet fusion to the total PL, means that the PLQY of rubrene single crystals is extremely sensitive to triplet-quenching defects.⁴⁵

Rubrene single crystals are impractical for technological applications. Instead, rubrene-based TTA-UC systems are often based on thin film morphologies.^18,26,28 Similar to single crystals, singlet fission dynamics and delayed PL arising from triplet fusion have been reported in rubrene thin films, though the time constants measured vary widely and there is a clear dependence on sample morphology.^{25,30,46–51} In particular, truly amorphous thin films show no evidence of singlet fission: the photoluminescence decays exponentially with a time constant of 15.2 ns,⁴⁸ matching the radiative lifetime of singlet excitons in solution.⁶⁸ Even thin films that give no peaks in X-ray diffraction experiments exhibit singlet fission dynamics,^46,47 suggesting that favourable molecular packing on a local scale can give rise to site-specific singlet fission.⁴⁷

Results and discussion

We prepared rubrene and rubrene–DBP nanoparticles (NPs) using the reprecipitation method, dispersed them in a PVA matrix and cast them onto glass substrates as described in the Experimental section and ref. 27 and 53. Nanoparticle films prepared in this way have been characterised previously: the nanoparticles are spherical with an average diameter of 220 nm and there are no sharp peaks apparent in X-ray diffraction patterns indicating a lack of any long-range crystalline order.^27,53 We might therefore expect the NPs to behave differently to rubrene crystals.

We measured the absolute PLQY of our pure rubrene NP films to be 2.9–3.6%, and rising to 61% when doped with an optimum²⁷ 0.5 mol% DBP (Fig. 1B). 61% is lower than previously reported values²⁷ and we found that the absolute PLQY values exhibited a small degree of sample-to-sample variation and dropped slightly over more than one year of sample storage in inert atmosphere. For example, we measured a PLQY of 46% for DBP-doped rubrene NPs 18 months after fabrication. The reason for the sample-to-sample variation is unclear, but may be due to the different states of the compounds and nanoparticles or the batch and purity of rubrene. These small variations are discussed in ESI,‡ Section S3, but we highlight that the photophysical behaviour did not change significantly with storage time (ESI,‡ Fig. S4 and S5).

Fig. 1 Molecular structures of rubrene (A) and DBP (B). (C) Absorption spectra of rubrene dissolved in anhydrous toluene (10⁻⁴ M) and as a nanoparticle (NP) film. The emission spectrum for the pure rubrene NP film (orange) is affected by self-absorption due to its high optical density. When 0.5 mol% DBP is added, almost all of the PL comes from the DBP (red). (D) The S₁ and triplet-pair energy levels in rubrene are almost isoenergetic, allowing for concurrent singlet fission and triplet fusion via various triplet-pair intermediates. The S₁ state of DBP lies approximately 200 meV lower.

The dramatic rise in PLQY upon doping with DBP is reflected in the steady-state PL spectra (Fig. 1C). As described previously,^18,26–28 for the DBP-doped NPs, almost all of the emission comes from DBP, with only a small residual contribution from rubrene. The absolute PLQY of our rubrene NP films is towards the higher end of values typically reported for polycrystalline rubrene films,^26,29 for which the relatively low quantum yield has been attributed to the rapid formation of triplets through efficient singlet fission.^29,46 Previous works that saw a similar enhancement in PL yield upon doping with DBP attributed it to FRET outcompeting singlet fission.^18,26–28 As discussed in ESI,‡ Section S11, this seems unlikely given that singlet fission is expected to be considerably faster than FRET in rubrene–DBP systems at optimal DBP concentrations.^33–36,52

To investigate the role of the DBP dopant in our rubrene NPs, we begin by characterising the singlet fission and triplet fusion processes in pure rubrene NPs. This gives us rate constants for all of the steps in the singlet fission process (eqn (1)), thereby allowing us to understand which processes are affected by the presence of DBP.

Photophysics of pure rubrene nanoparticle films

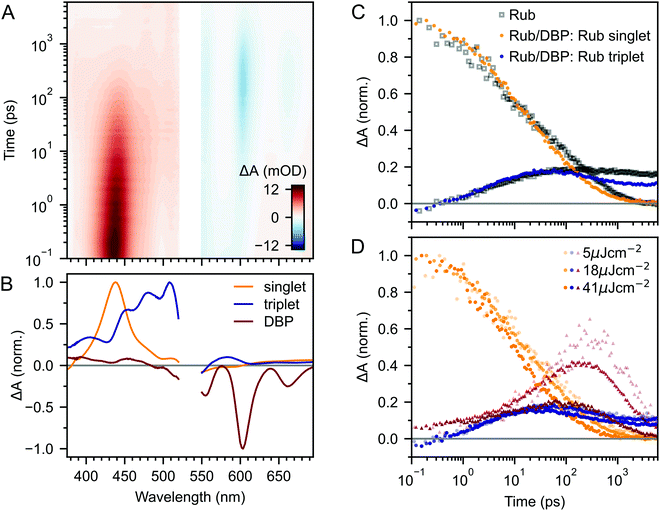
Fig. 2A–C(i) shows ultrafast transient absorption (TA) spectroscopy of a rubrene nanoparticle film, which we compare against data taken for a dilute solution (ii) and a spin-coated 50 nm thick polycrystalline film (iii) under the same experimental conditions. Transient absorption data has been measured previously for rubrene in solution,^33,51 films^30,49,51 and crystals^33–36 and we include them here simply as references.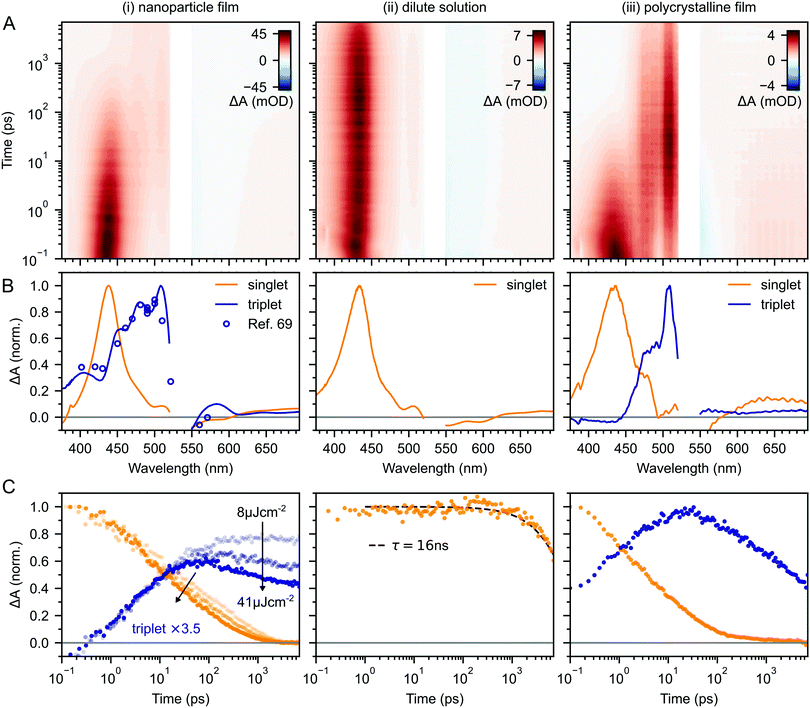

Fig. 2 (A) False-colour maps of the transient absorption of rubrene as PVA-dispersed NPs (i), dilute (1 × 10⁻⁴ M) toluene solution (ii) and polycrystalline film (iii). The excitation intensity was 41 μJ cm⁻² and the pump pulses were centred at 532 nm with a FWHM of 16 nm. Data in the spectral region of the pump have been removed. (B) Transient absorption spectra of singlets (orange) and triplets (blue) in rubrene, extracted via MCR-ALS in (i) and (iii). The singlet and triplet excited state absorption spectra in the NPs are very similar to those of rubrene in solution.⁶⁹ (C) Dynamics of singlets and triplets in rubrene, normalised to the initial singlet population.

In the rubrene NP film (Fig. 2A–C(i)) we find signatures of singlet fission.³³ An extraction of the two components using Multivariate Curve Resolution Alternating Least Squares (MCR-ALS)^70,71 (full details in ESI,‡ Section S6) results in spectra (Fig. 2B(i)) that closely match the excited state absorption (ESA) spectra of singlet and triplet excitons in solution.^51,69,72 From the extracted dynamics (Fig. 2C(i)), we see that the singlet exciton lifetime is dramatically reduced from the 16 ns value measured in solution (Fig. 2C(ii)). In the NP film, the singlet population initially decays exponentially with a time constant of 5 ps to half of its initial value, accompanied by a corresponding exponential rise in the triplet population, also with a time constant of 5 ps (ESI,‡ Fig. S1). These dynamics indicate (in the absence of rapid nonradiative decay to the ground state) that a roughly 50 : 50 equilibrium between S₁ and triplet-pair states is established within the first 10 ps. In addition, similar to rubrene single crystals,³³ we find an isosbestic point between the singlet and triplet ESA spectra (ESI,‡ Fig. S3), indicating a single singlet to triplet transformation.³³ Taken together, these data suggest that the first step of singlet fission, S₁ ↔ ¹(TT) occurs in the nanoparticles with a time constant of 10 ps, and that the triplet yield is high, as it is in single crystals.^33,40

Given the similarity between the singlet fission dynamics of our rubrene NP films and rubrene single crystals,^33,48 it is surprising that the singlet and triplet ESA spectra of the NPs so closely resemble those of rubrene in solution, and that the triplet ESA is four times weaker in the NPs than the polycrystalline film, relative to the initial singlet ESA. Since the spectra are similar, we estimated the triplet yield in our rubrene NP films from the ESA cross-sections previously measured in solution.⁷² This procedure gives a yield of ∼40% (out of a maximum of 200%), which would imply that only 1 in 5 singlet excitons undergoes fission. This is inconsistent with the population dynamics however: 50% of the initial S₁ population is lost within the first 10 ps, with an exponential decay that matches the rise of the triplet signal. The reasons for the similarities and differences in ESA spectral shapes and cross sections between solution, crystals and NPs therefore remain unclear.

Moving beyond the first 10 ps, the triplet signal in the rubrene NP films continues to rise, accompanied by a reduction in singlet population (Fig. 2C(i)). This could be a sign of the next step in the singlet fission process: the formation of spatially separated triplet-pairs from ¹(TT).^36,56,61 There are alternative explanations for two-stage singlet fission dynamics, such as the co-existence of a direct parallel pathway S₁ → ¹(T⋯T) or exciton migration to singlet fission sites.⁶⁶ In ESI,‡ Section S2 we explain, with the help of further experimental evidence, why these are less likely than the simple sequential S₁ → ¹(TT) → ¹(T⋯T) pathway that has been well established for rubrene single crystals.^33–37 We show below that this sequential pathway quantitatively explains our experimental data with physically reasonable rate constants. Finally, we find a slight dependence of the singlet and triplet dynamics on excitation pulse energy, demonstrating that a small amount of singlet–singlet annihilation (SSA) is taking place. As shown in Fig. S16 (ESI‡), SSA principally affects the dynamics within the first 10 ps, though this is somewhat unclear in the normalised dynamics of Fig. 2C(i).

Given that initial singlet fission (∼10 ps) and triplet-pair separation (∼100 ps) are orders of magnitude faster than radiative decay (16 ns), triplet fusion must contribute significantly to the absolute PLQY of the rubrene nanoparticles, just as it does for rubrene single crystals.⁴⁰ We therefore turn to time-resolved measurements on nanosecond–millisecond timescales in order to investigate the triplet fusion dynamics in the rubrene NP films.

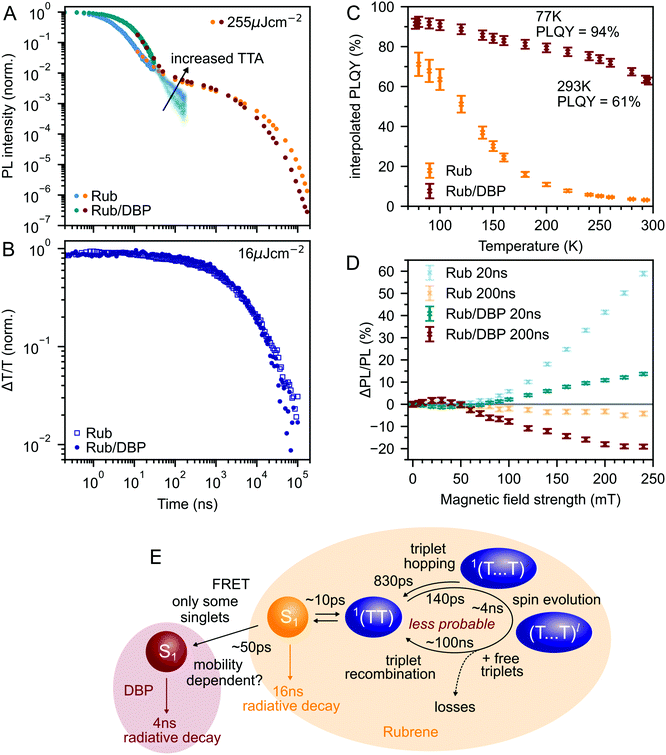
Fig. 3A shows the photoluminescence decay (wavelength-integrated since the spectrum is time-independent) of the rubrene NPs measured using a combination of time-correlated single photon counting (TCSPC) and an electronically gated iCCD (see Experimental section). Three regions are apparent. Following photoexcitation, the PL decays exponentially with an apparent time constant of 3 ns, though our TCSPC measurement does not have sufficient time resolution to give an accurate value. This subsequently gives way to a power law decay with an exponent of −1.3. On timescales of several hundred nanoseconds we find the onset of an enhancement to the delayed PL which grows with increasing excitation density. This latter region matches the triplet excited state dynamics shown in Fig. 3B, measured using transient absorption spectroscopy. Beyond 100 ns, the slow decrease in triplet population is replaced by a more rapid decay, which gets faster with increasing excitation density. This is characteristic of non-geminate TTA,⁷³ which here repopulates the S₁ state.

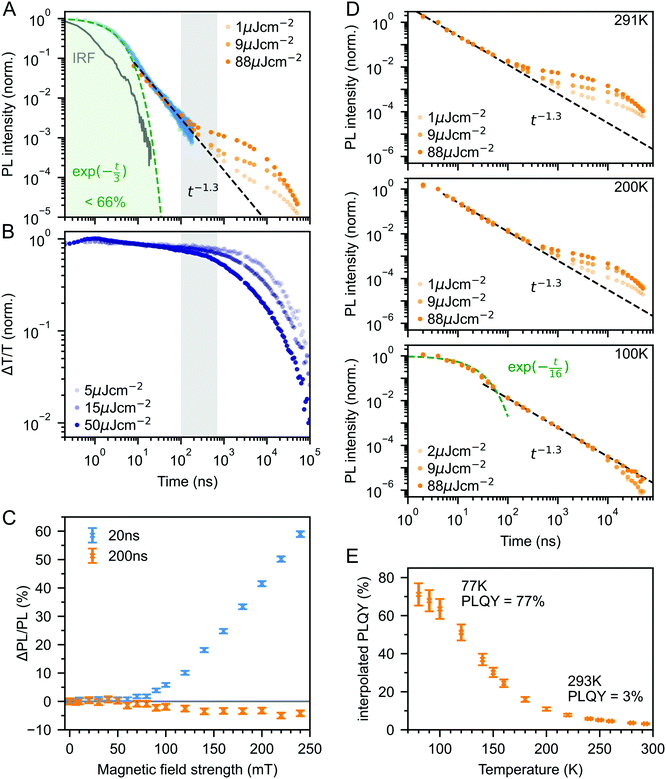Fig. 3 (A) Wavelength-integrated TRPL dynamics of rubrene NP films comprising TCSPC (blue, 470 nm excitation, IRF in grey) and intensified gated CCD (orange, 532 nm excitation) measurements. The power-law behaviour is characteristic of geminate fusion of ¹(TT) and (T⋯T).^43,44 We find an excitation density dependent enhancement to the delayed PL beyond 100 ns, that corresponds to the onset of bimolecular TTA determined by monitoring the triplet transient absorption signal at 510 nm (B). (C) Magnetic field effect on fluorescence at two different time delays. Error bars reflect the difference between sweeping up and down in magnetic field. (D) As the temperature is decreased, the contribution of non-geminate triplet fusion to the total PL reduces. At 100 K, all the triplet fusion is geminate, evidenced by the power-law decay. This is accompanied by a large increase in the PLQY (E). We calculated the interpolated PLQY values by normalising the integrated PL as a function of temperature to the measured absolute PLQY. Error bars reflect the discrepancy between normalising to the PLQY measured at 77 K and room temperature.

The intermediate power law dynamics that we observe in the NP films are characteristic of geminate fusion of associated and separated triplet-pair states,^43,44,74i.e.¹(TT) and (T⋯T). A random walk model for the triplet diffusion between fission and geminate fusion events predicts an exponent of −1.5 in the limits of 3D and 1D diffusion and −1 for 2D diffusion.^44,74 For example, Wolf et al.⁴³ have shown that a change in the power law exponent from −1.18 to −1.66 measured in rubrene single crystals is associated with a transition from 2D to 3D triplet diffusion. Our exponent lies in between these values, suggesting a mixture of 2D and 3D triplet diffusion occurs in the NP films on timescales of tens of nanoseconds.

We can estimate a lower bound on the contribution that triplet fusion makes to the total PL by integrating under the PL decay in Fig. 3A. We find that the ‘prompt’ exponential part contributes at most 66% of the total emitted light if no non-geminate TTA takes place, and much less otherwise. The exponential region itself must contain contributions from ¹(TT) fusion since the singlet fission rate is 10 ps, thus ours is a conservative estimate. Triplet fusion following singlet fission therefore makes a very substantial contribution to the total PL emitted by the rubrene NP films, similar to rubrene single crystals in which more than 90% of the PLQY comes from triplet fusion.⁴⁰

To gain further insight into the nature of the triplet-pair intermediates in the rubrene NP films, we measured the effects of an applied magnetic field on the PL at two different time delays. These results are presented in Fig. 3C. At a delay of 20 ns, we observe an enhancement of the PL for fields >70 mT. This is characteristic of the formation of weakly exchange-coupled triplet-pair states.^46,75,76 These triplet-pair states are not eigenstates of the total spin operator, thus spin is no longer a good quantum number and they instead possess mixed spin character. At zero applied field, three of the nine possible triplet-pair states have a degree of singlet character.⁷⁵ This falls to two at higher fields,⁷⁵ thus reducing the probability that singlet energy is lost and increasing the measured PL. At a delay of 200 ns the magnetic field effect (MFE) is inverted, showing that fusion of mixed spin triplet-pair states dominates on this timescale. We note that the magnitude of the time-gated MFEs depends sensitively on the gate time and width in a non-trivial way, and it is the shapes and signs that are important here.

We further investigate the effects of triplet-pair dynamics on the NP photoluminescence through measurements of the PL decay as a function of temperature and excitation density, as shown in Fig. 3D. The PL dynamics at 100 K are considerably different to those at 200 K and room temperature. Firstly, we find that the initial decay becomes noticeably exponential with a time constant of 16 ns, matching the radiative rate of singlet excitons in rubrene.^48,68 A very similar feature is seen in the PL decay of rubrene single crystals at room temperature,⁴⁴ where it corresponds to emission from the small percentage of singlet excitons that do not undergo fission.⁴³ Secondly, we find no dependence of the PL decay on excitation density, in stark contrast to the behaviour at room temperature and 200 K. Instead, the power law behaviour persists for many tens of microseconds, demonstrating that all subsequent triplet fusion is geminate at this temperature. Similar effects have been observed in tetracene derivatives⁷⁷ and anthradithiophene films.⁷⁸

The reduction in non-geminate triplet fusion with temperature implies that the triplet diffusion length is reduced at low temperature. This could be due to changes in the diffusion constant or the lifetime. The triplet lifetime in rubrene films shows little dependence on temperature.⁵⁰ In contrast, the hole mobility (mediated by a 1-electron Dexter transfer) in rubrene single crystals reduces by a factor of 30 on cooling from room temperature to 100 K.⁷⁹ Since triplet transfer is a 2-electron Dexter transfer process, we might expect the reduction in triplet mobility to be even greater. In rubrene thin films, the triplet hopping rate has been reported to decrease by approximately one order of magnitude over the same temperature range.⁸⁰

These low-temperature dynamics, caused by reduced triplet mobility, are accompanied by a striking 20-fold increase in the PLQY, shown in Fig. 3E. At 77 K, 77% of absorbed photons are re-emitted as PL. Singlet fission is still occurring at these temperatures since we observe significant delayed PL arising from geminate triplet fusion. Subsequent triplet-pair separation, which is reported to be thermally activated in rubrene³⁵ may also be reduced at low temperature.

The dramatic increase in PLQY accompanied by reduced triplet diffusion as the temperature is decreased suggests that substantial losses are associated with the formation of separated triplets following singlet fission, such as triplet quenching⁸¹ and trapping,^82,83 but that these losses are minimal at low temperature when triplet migration is inhibited. These results for our rubrene NP films are similar to reported single crystal measurements which show a reduction in the PL yield as the defect density is increased, attributed to the long diffusion lengths of triplet excitons and their dominant contribution to the total PL.⁴⁵ Confirming this idea, Fig. S10 (ESI‡) shows how a faster decay of the total triplet population, and hence increased triplet losses in our polycrystalline rubrene films dramatically reduce their emitted PL compared to the NP samples.

Putting our results together, we arrive at the description of rubrene NP photophysics shown in Fig. 4A which, with the addition of singlet–singlet annihilation, quantitatively reproduces the picosecond singlet and triplet dynamics as shown in Fig. 4B. The kinetic scheme is consistent with the picture built up through measurements of crystalline rubrene^{33–36,38,40,43–45,48} which we reviewed in the introduction. Here we focus on the rate constants of the different steps, which will be important when we come to consider the effect of the singlet energy collector DBP in the following section.

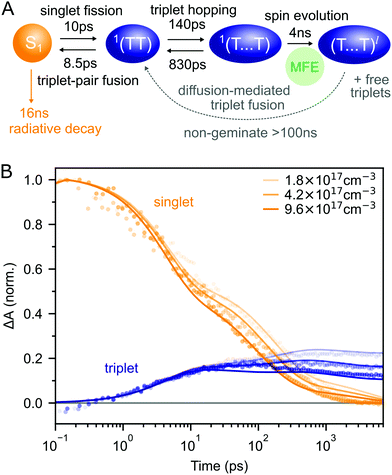Fig. 4 (A) Schematic diagram summarising the photophysics of rubrene nanoparticles. (B) The kinetic scheme in (A) provides a good description of the singlet and triplet dynamics (residuals are shown in ESI,‡ Fig. S12). We have neglected the >100 ns triplet fusion and included singlet–singlet annihilation (k = 3 × 10⁻⁸ cm³ s⁻¹) in the simulation.

Interconversion between S₁ and ¹(TT) occurs within 10 ps. ¹(TT) subsequently separates into ¹(T⋯T) with a time constant of approximately 140 ps. This triplet hopping rate is consistent with the bimolecular triplet annihilation constant of 5 × 10⁻¹² cm³ s⁻¹ measured for rubrene single crystals⁴⁰ (see ESI,‡ Section S4). The rate of fusion from ¹(T⋯T) to ¹(TT) is roughly six times slower which is expected for triplet hopping in three dimensions. Spin evolution on a timescale of several nanoseconds results in triplet-pairs with mixed spin character. Not included in the simulation is the complicated diffusion-mediated triplet fusion that occurs on nanosecond timescales.^43,44

The addition of DBP does not suppress initial singlet fission

In the previous section we showed that the PLQY of the rubrene NPs depends heavily on triplets, as it does for rubrene single crystals.⁴⁰ To investigate the effect of the DBP dopant on the photophysics of rubrene, we compare transient absorption measurements of DBP-doped NP films with those of pure rubrene NPs, recorded under the same experimental conditions.

Fig. 5A and B shows ultrafast transient absorption data for rubrene NPs containing 0.5 mol% DBP. In addition to the spectral features corresponding to the singlet and triplet excited states of rubrene, we observe a new, negative feature that grows in over several tens of picoseconds. This feature closely matches the TA spectrum of DBP monomers in solution (ESI,‡ Fig. S7) and we therefore assign it to the singlet state of DBP, which includes both ground state bleach and stimulated emission. We used the singlet spectra from solution measurements as references in our global extraction of the singlet, triplet and DBP dynamics using MCR-ALS (ESI,‡ Section S6).

Fig. 5 (A) Ultrafast TA of rubrene nanoparticles doped with 0.5 mol% DBP. Data is shown for an excitation density of 18 μJ cm⁻². We extracted spectral components using a global MCR-ALS procedure based on measured reference spectra, giving the rubrene singlet (orange), rubrene triplet (blue) and DBP singlet (red) spectra shown in (B). (C) The corresponding dynamics of the rubrene singlet and triplet populations in the DBP-doped NPs are almost identical to those in the pure NPs (both shown for an excitation density of 18 μJ cm⁻²). We find a small reduction in the singlet and triplet populations beyond 50 ps. (D) The principal rise in the DBP singlet population occurs well after initial singlet fission has taken place and is strongly dependent on excitation density. Some DBP molecules are directly photo-excited by the 532 nm pump pulses, which were the same as those used to excite the pure rubrene NP films.

The kinetics of the singlet and triplet states of rubrene resulting from this procedure are shown in Fig. 5C. Strikingly, we find that there is very little change to the excited state dynamics of pure rubrene NPs (grey squares) upon the addition of DBP, when measured under identical experimental conditions. In particular, initial singlet fission, that is S₁ → ¹(TT), still occurs with the same initial yield and rate. We see the same lack of change for polycrystalline films containing the same mole fraction of DBP (ESI,‡ Fig. S11). On timescales of several tens to hundreds of picoseconds, the singlet and triplet populations do appear to decay slightly faster in the DBP-doped nanoparticles, indicating that energy transfer to DBP occurs instead on these longer timescales.

Indeed, this is borne out by the kinetics of the DBP singlet state, shown by red triangles in Fig. 5D. We find that following photo-excitation (which populates the singlet state of both rubrene and DBP), the DBP singlet mainly grows in on timescales of several tens to hundreds of picoseconds, after the first step of singlet fission has taken place. Thus the addition of DBP does not suppress initial singlet fission. Instead, FRET from the rubrene S₁ to the DBP S₁ is competitive with the subsequent step of triplet-pair separation (see Fig. 4A).

The yield of DBP singlet is heavily dependent on the excitation density, which on picosecond timescales affects the dynamics only through singlet–singlet annihilation (Fig. 5D). If there is a distribution of singlet exciton diffusivity within the NPs, singlets with greater mobility are more likely to transfer their energy to the DBP molecules, but it is these same mobile singlets that are quenched by singlet–singlet annihilation in our experiments. This hypothesis is supported by kinetic modelling (ESI,‡ Fig. S13). We can only obtain a quantitative fit to the excited state dynamics by assuming that not all singlet excitons are able to transfer their energy to DBP. Indeed, this is wholly expected based on our calculations of FRET rates and diffusion lengths in ESI,‡ Section S11.

Plenty of singlet excitons evidently do undergo both singlet fission and triplet separation since a substantial triplet signal persists for several nanoseconds after the DBP population has mostly decayed away. The residual triplet signal, relative to the initial photo-excited singlet, is at least half that of pure rubrene NPs, yet we find that the addition of DBP increases the absolute PLQY by a factor of 20. This can nevertheless be rationalised by taking into account the recycling of excitation energy through triplet fusion,⁴⁰ which we explore in the following section.

Singlet energy collection in rubrene nanoparticles

Fig. 6A compares the PL dynamics of rubrene nanoparticles with and without the addition of DBP. The initial ‘prompt’ decay is more pronounced for DBP-containing nanoparticles and makes a larger contribution to the total PL than for pure rubrene NPs. Beyond 30 ns, a slightly faster roll-off of singlet population generated from bimolecular TTA is observed for rubrene–DBP NPs. A comparison of the triplet dynamics, shown in Fig. 6B, reveals almost identical behaviour regardless of the presence of DBP. The underlying photophysics in both cases is therefore predominantly that of concurrent singlet fission and triplet fusion in rubrene. We suggest the following hypothesis to explain the 20-fold increase in PLQY upon doping with DBP.

Fig. 6 (A) DBP-doped nanoparticles show increased prompt PL and a slightly faster roll-off of singlet population on the microsecond timescales associated with TTA. Very similar triplet fusion dynamics are observed on these timescales, as shown by transient absorption measurements at 510 nm in (B). Note that the overlap between the TCSPC and iCCD data is not perfect owing to the very different pulse energies used, and that the TCSPC data for the DBP-containing nanoparticles was detected at 640 nm. (C) DBP-doped nanoparticles have a much higher PLQY than pure rubrene nanoparticles at room temperature that increases only moderately for low temperatures. (D) Magnetic field effect on time-gated fluorescence with and without the addition of DBP. (E) Schematic diagram summarising the suggested interplay between singlet energy collection, singlet fission and triplet fusion in rubrene-based nanoparticles.

DBP acts to increase the probability of radiative decay when excitation energy returns to the S₁ ↔ ¹(TT) equilibrium. Correspondingly, the probability of non-radiative decay of fission generated independent triplets is reduced. Since energy is continually moving back and forth between singlets and triplets, including when DBP is present, the cumulative effect results in a substantial increase to the PLQY, from 3% to 61%, as shown in Fig. 6C. Our measurements of polycrystalline rubrene films are also consistent with this conclusion (ESI,‡ Fig. S11), which we summarise schematically in Fig. 6E.

Since less energy is lost through nonradiative triplet decay in DBP-doped rubrene, Fig. 6C shows a much more modest increase in PLQY at low temperature than that measured for pure rubrene. Reducing the temperature is a different way to avoid non-radiative triplet decay, but instead through suppression of triplet diffusion which reduces the likelihood that triplets encounter defects.

The change in the MFE shown in Fig. 6D is consistent with this description of the role of the singlet energy collector in rubrene. The reduced probability that triplet-pairs separate and undergo spin evolution causes a decrease in the magnitude of the MFE at 20 ns delay. At 200 ns delay, the negative MFE associated with triplet fusion is stronger because the positive contribution from triplet separation and subsequent spin evolution is reduced.

Conclusions

In this work we have presented a detailed photophysical characterisation of recently developed rubrene nanoparticle films. Our most striking finding is that the addition of 0.5 mol% of the singlet energy collector DBP has very little discernable effect on the singlet and triplet population dynamics in rubrene, despite increasing the photoluminescence quantum yield by a factor of 20 to 61% at room temperature. We suggest that this behaviour can be rationalised by considering the roles of geminate and non-geminate triplet fusion, which have been extensively studied in rubrene crystals over the last decade.

In rubrene NP films, we have shown that similar concurrent singlet fission and triplet fusion dynamics to those in rubrene crystals occur.^{33–36,38,40,43–45,48} This is surprising, given the lack of peaks in the X-ray diffraction patterns of the rubrene NPs^27,53 and the similarity between their excited state absorption spectra and those measured for singlets and triplets in solution.⁶⁹

It is well known that triplet-quenching defects substantially reduce the PLQY of rubrene crystals,⁴⁵ and we find that similar defects are also the likely cause of the modest 3% PLQY of pure rubrene NP films. We suggested that the effect of the DBP dopant (at the optimized 0.5 mol%) is to reduce the probability that triplets encounter such defects by providing a radiative channel for singlets (∼50 ps) that outcompetes not the formation of triplet-pairs (10 ps) as is usually implied, but their subsequent separation (∼140 ps).

These results point to alternative strategies for achieving efficient TTA-UC in solid rubrene. Whilst singlet fission can be completely suppressed in rubrene by making it amorphous,⁴⁸ or adding bulky side groups,³⁰ the disruption this causes to the crystal structure can hinder the long-range triplet diffusion required.⁸⁴ This leads, overall, to lower upconversion efficiencies.³⁰ Smaller side groups such as t-butyl offer an interesting compromise by reportedly only partially suppressing singlet fission, causing an increase in PLQY which more than compensates for reduced triplet energy transfer, yielding an upconversion efficiency of 0.3%.²⁶ Our results here suggest the alternative strategy of focusing on controlling triplet-pair separation and eliminating triplet-quenching defects rather than suppressing singlet fission. Such a strategy could increase the PLQY whilst maintaining the crystallinity required for triplet diffusion. It may even be possible to forego the addition of DBP altogether, thereby avoiding the associated 200 meV reduction in the upconversion anti-Stokes shift.

Experimental section

Materials

Rubrene, purified by sublimation, was purchased from TCI and used as received. Tetraphenyldibenzoperiflanthene (DBP) and polyvinyl alcohol (PVA, 99+% hydrolyzed, average M_w 130 000) were purchased from Merck and used as received.

Preparation of rubrene-based nanoparticles dispersed in PVA films

Films of rubrene-based nanoparticles (NPs) dispersed in poly(vinyl alcohol) (PVA) were prepared following previously reported procedures.^27,53 Briefly, a tetrahydrofuran solution of rubrene and DBP ([rubrene] = 5 mM, [DBP] = 0 or 0.5 mol%, 3 mL) was injected into an aqueous solution of sodium dodecyl sulfate (10 mM, 15 mL). The NPs formed were collected by centrifugation and dispersed into an aqueous solution of PVA (8 wt%). The solution was cast onto quartz-coated glass substrates and dried overnight to form films. Prepared films were transferred to a nitrogen-filled glovebox and encapsulated using a glass coverslip and epoxy resin. Samples for low-temperature measurements were unencapsulated.

Preparation of polycrystalline rubrene films

Rubrene was dissolved in anhydrous toluene at a concentration of 10 mg mL and shaken until no solids remained visible. The solution was passed through a 0.2 μm pore size PTFE filter and spin-coated onto pre-cleaned quartz-coated glass substrates at 1000 rpm for 60 s. Films were encapsulated using a glass coverslip and epoxy resin. All film preparation was carried out in a nitrogen-filled glovebox.

Steady-state absorption and photoluminescence

Ground state absorption spectra were recorded with a UV-vis spectrophotometer (Cary60, Agilent). Temperature-dependent PL spectra were measured using a spectrofluorometer (FP-8300 and CSH-831, JASCO) combined with a liquid nitrogen cryostat (Optistat DN2, Oxford Instruments). The absolute photoluminescence quantum yield was measured in an integrating sphere using a Hamamatsu Photonics absolute quantum yield measurement system.

Time-correlated single photon counting

Time correlated single photon counting (TCSPC) measurements were carried out by using a lifetime spectroscopy system (Quantaurus-Tau C11367-02, Hamamatsu). The excitation wavelength was 470 nm.

Nanosecond time resolved photoluminescence

532 nm pump pulses (temporal width <500 ps, 5 kHz) were provided by the frequency-doubled output of a Q-switched Nd:YVO₄ laser (Picolo-AOT, Innolas). The photoluminescence was detected by a spectrograph (Shamrock 303i, Andor) and a time-gated intensified charge-coupled device (iCCD; iStar DH334T-18U-73, Andor). A 532 nm notch filter was used to eliminate pump scatter. For low-temperature measurements samples were situated in the helium exchange gas of a nitrogen bath cryostat (Optistat DN, Oxford Instruments). Data processing procedures and further details regarding the TRPL setup have been reported previously.⁷⁸ The pump beam spot size was measured at the sample position by translating a razor blade through the focus and monitoring the transmitted power.

Magnetic field dependent time-gated PL

A Ti:sapphire regenerative amplifier (Solstice, Spectra-Physics) providing 800 nm pulses (90 fs FWHM, 1 kHz, 4 mJ) was used to generate the pump beam. A portion of the 800 nm beam was frequency doubled in a BBO crystal to generate 400 nm pump pulses. The sample was positioned between the poles of an electromagnet. PL was collected and sent via optical fibre to the same detection system used for TRPL measurements. The 400 nm excitation source was preferred for magnetic field dependent measurements due to its good power stability over time. The excitation intensity was 25 μJ cm⁻².

Picosecond transient absorption spectroscopy

A Ti:sapphire regenerative amplifier (Spitfire ACE PA-40, Spectra-Physics) providing 800 nm pulses (40 fs full-width at half-maximum (FWHM), 10 kHz, 1.2 mJ) was used to generate both the pump and probe beams. Tunable narrowband pump pulses at 532 nm were generated in an optical parametric amplifier (TOPAS Prime, Light Conversion). The pump was modulated by an optical chopper. Probe pulses spanning the range 350–750 nm were generated by focusing a portion of the 800 nm beam through a continuously translating calcium fluoride crystal. Pump–probe delay was controlled using a motorized linear stage. Detection was carried out using a commercial instrument (Helios, Ultrafast Systems). The pump and probe polarizations were set to the magic angle. The pump beam spot size was measured at the sample position using a CCD beam profiler (Thorlabs). Transient absorption (TA) spectroscopy data were processed by background subtraction and chirp correction. Details of the spectral deconvolution can be found in ESI,‡ Section S6.

Nanosecond transient absorption spectroscopy

A Ti:sapphire regenerative amplifier (Solstice, Spectra-Physics) providing 800 nm pulses (90 fs FWHM, 1 kHz, 4 mJ) was used to generate the probe beam. Probe pulses spanning the range 450–700 nm were generated by focusing a portion of the 800 nm beam through a sapphire crystal. 532 nm pump pulses (temporal width <500 ps, 500 Hz) were provided by the frequency-doubled output of a Q-switched Nd:YVO₄ laser (Picolo-AOT, Innolas). Pump–probe delay was controlled electronically using a digital delay generator (DG645, Stanford). The pump and probe polarizations were set to the magic angle and the beams were overlapped at the sample adjacent to a reference beam obtained by passing the probe through a 50 : 50 beamsplitter. The reference is used to correct for shot-to-shot variation in the probe spectrum. The probe and reference beams were dispersed by a volume phase holographic grating (Wasatch) and detected by a pair of linear image sensors (S7030, Hamamatsu) driven and read out at the full laser repetition rate by a custom-built board from Entwicklungsbüro Stresing. TA data was acquired using home-built software. The pump beam spot size was measured at the sample position using a CCD beam profiler (Thorlabs).

Author contributions

DGB, YS, NY and JC conceived the project, which was supervised by NY, NK and JC. DGB and YS prepared samples. DGB performed the TA and TRPL experiments. DGB and YS performed temperature dependent TRPL experiments. YS performed steady-state PL, PLQY and TCSPC measurements. SW built the magnetic-field setup. DC assisted with the TA setup. DGB analysed the data and performed the simulations. DGB wrote the manuscript with input from YS, NY and JC.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

DGB thanks the EPSRC Centre for Doctoral Training in New and Sustainable Photovoltaics (EP/L01551X/1) for studentship support. YS thanks the JSPS Overseas Challenge Program for Young Researchers. JC and SW thank EPSRC for funding (EP/S002103/1 and EP/M025330/1). We thank EPSRC for a Capital Equipment award (EP/L022613/1 and EP/R042802/1), which provided the Lord Porter Laser Laboratory Facility used in this study. This work was partly supported by JSPS KAKENHI (grant numbers JP20H02713, JP20K21211, JP20H05676 and JP18J21140).

References

1. V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71.
2. J. Zhao, S. Ji and H. Guo, RSC Adv., 2011, 1, 937–950.
3. T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573.
4. L. Nienhaus, M. Wu, N. Geva, J. J. Shepherd, M. W. B. Wilson, V. Bulović, T. Van Voorhis, M. A. Baldo and M. G. Bawendi, ACS Nano, 2017, 11, 7848–7857.
5. N. J. Ekins-Daukes and T. W. Schmidt, Appl. Phys. Lett., 2008, 93, 63507.
6. J. C. Goldschmidt and S. Fischer, Adv. Opt. Mater., 2015, 3, 510–535.
7. B. McKenna and R. C. Evans, Adv. Mater., 2017, 29, 1606491.
8. M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378.
9. T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125.
10. J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465.
11. L. Huang, E. Kakadiaris, T. Vaneckova, K. Huang, M. Vaculovicova and G. Han, Biomaterials, 2019, 201, 77–86.
12. Y. Sasaki, M. Oshikawa, P. Bharmoria, H. Kouno, A. Hayashi-Takagi, M. Sato, I. Ajioka, N. Yanai and N. Kimizuka, Angew. Chem., Int. Ed., 2019, 58, 17827–17833.
13. W. Wang, Q. Liu, C. Zhan, A. Barhoumi, T. Yang, R. G. Wylie, P. A. Armstrong and D. S. Kohane, Nano Lett., 2015, 15, 6332–6338.
14. F. Lewitzka and H.-G. Löhmannsröben, Z. Phys. Chem., 1986, 150, 69–86.
15. T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2008, 112, 3550–3556.
16. Y. Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799.
17. V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352.
18. M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. Van Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Photon., 2016, 10, 31–34.
19. M. Mahboub, Z. Huang and M. L. Tang, Nano Lett., 2016, 16, 7169–7175.
20. Z. Huang, X. Li, M. Mahboub, K. M. Hanson, V. M. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 15, 5552–5557.
21. P. Bharmoria, H. Bildirir and K. Moth-Poulsen, Chem. Soc. Rev., 2020, 49, 6529–6554.
22. Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, Phys. Chem. Chem. Phys., 2010, 12, 66–71.
23. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
24. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386.
25. A. Abulikemu, Y. Sakagami, C. Heck, K. Kamada, H. Sotome, H. Miyasaka, D. Kuzuhara and H. Yamada, ACS Appl. Mater. Interfaces, 2019, 11, 20812–20819.
26. E. Radiunas, M. Dapkevičius, S. Raišys, S. Juršėnas, A. Jozeliūnaitė, T. Javorskis, U. Šinkevičiūtė, E. Orentas and K. Kazlauskas, Phys. Chem. Chem. Phys., 2020, 22, 7392–7403.
27. M. Kinoshita, Y. Sasaki, S. Amemori, N. Harada, Z. Hu, Z. Liu, L. K. Ono, Y. Qi, N. Yanai and N. Kimizuka, ChemPhotoChem, 2020, 4, 5271–5278.
28. S. Wieghold, A. S. Bieber, Z. A. VanOrman, A. Rodriguez and L. Nienhaus, J. Phys. Chem. C, 2020, 124, 18132–18140.
29. R. Nagata, H. Nakanotani, W. J. Potscavage Jr. and C. Adachi, Adv. Mater., 2018, 30, 1801484.
30. E. Radiunas, M. Dapkevičius, L. Naimovičius, P. Baronas, S. Raišys, S. Juršėnas, A. Jozeliūnatė, T. Javorskis, U. Šinkevičiūtė, E. Orentas and K. Kazlauskas, J. Mater. Chem. C, 2021, 9, 4359–4366.
31. O. D. Jurchescu, A. Meetsma and T. T. M. Palstra, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 330–334.
32. P. Irkhin, A. Ryasnyanskiy, M. Koehler and I. Biaggio, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085143.
33. L. Ma, K. Zhang, C. Kloc, H. Sun, M. E. Michel-Beyerle and G. G. Gurzadyan, Phys. Chem. Chem. Phys., 2012, 14, 8307–8312.
34. Y. Ishibashi, Y. Inoue and T. Asahi, Photochem. Photobiol. Sci., 2016, 15, 1304–1309.
35. K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989.
36. I. Breen, R. Tempelaar, L. A. Bizimana, B. Kloss, D. R. Reichman and D. B. Turner, J. Am. Chem. Soc., 2017, 139, 11745–11751.
37. K. Bera, C. J. Douglas and R. R. Frontiera, J. Phys. Chem. Lett., 2017, 8, 5929–5934.
38. A. Ryasnyanskiy and I. Biaggio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 193203.
39. P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 017402.
40. I. Biaggio and P. Irkhin, Appl. Phys. Lett., 2013, 103, 263301.
41. H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Nat. Mater., 2010, 9, 938–943.
42. E. A. Wolf, D. M. Finton, V. Zoutenbier and I. Biaggio, Appl. Phys. Lett., 2018, 112, 83301.
43. E. A. Wolf and I. Biaggio, Phys. Rev. B, 2021, 103, L201201.
44. K. Seki, T. Yoshida, T. Yago, M. Wakasa and R. Katoh, J. Phys. Chem. C, 2021, 125, 3295–3304.
45. P. Irkhin, I. Biaggio, T. Zimmerling, M. Döbeli and B. Batlogg, Appl. Phys. Lett., 2016, 108, 63302.
46. G. B. Piland, J. J. Burdett, D. Kurunthu and C. J. Bardeen, J. Phys. Chem. C, 2013, 117, 1224–1236.
47. C.-H. Chen, P.-H. Sher, C.-P. Chen, W.-K. Choi, C. J. Bardeen, T.-L. Chiu, J.-K. Wang and J.-H. Lee, J. Phys. Chem. C, 2020, 124, 25729–25737.
48. D. M. Finton, E. A. Wolf, V. S. Zoutenbier, K. A. Ward and I. Biaggio, AIP Adv., 2019, 9, 95027.
49. V. Jankus, E. W. Snedden, D. W. Bright, E. Arac, D. Dai and A. P. Monkman, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224202.
50. C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953.
51. S. Takahashi, K. Watanabe and Y. Matsumoto, J. Chem. Phys., 2019, 151, 074703.
52. O. L. Griffith and S. R. Forrest, Nano Lett., 2014, 14, 2353–2358.
53. S. Amemori, Y. Sasaki, N. Yanai and N. Kimizuka, J. Am. Chem. Soc., 2016, 138, 8702–8705.
54. H. Tamura, M. Huix-Rotllant, I. Burghardt, Y. Olivier and D. Beljonne, Phys. Rev. Lett., 2015, 115, 107401.
55. W. Kim and A. J. Musser, Adv. Phys.: X, 2021, 6, 1918022.
56. C. Grieco, G. S. Doucette, J. M. Munro, E. R. Kennehan, Y. Lee, A. Rimshaw, M. M. Payne, N. Wonderling, J. E. Anthony, I. Dabo, E. D. Gomez and J. B. Asbury, Adv. Funct. Mater., 2017, 27, 1703929.
57. T. S. Lee, Y. L. Lin, H. Kim, R. D. Pensack, B. P. Rand and G. D. Scholes, J. Phys. Chem. Lett., 2018, 9, 4087–4095.
58. K. T. Munson, J. Gan, C. Grieco, G. S. Doucette, J. E. Anthony and J. B. Asbury, J. Phys. Chem. C, 2020, 124, 23567–23578.
59. T. S. Lee, Y. L. Lin, H. Kim, B. P. Rand and G. D. Scholes, Can. J. Chem., 2019, 97, 465–473.
60. E. Frankevich, V. Lesin and A. Pristupa, Chem. Phys. Lett., 1978, 58, 127–131.
61. R. D. Pensack, E. E. Ostroumov, A. J. Tilley, S. Mazza, C. Grieco, K. J. Thorley, J. B. Asbury, D. S. Seferos, J. E. Anthony and G. D. Scholes, J. Phys. Chem. Lett., 2016, 7, 2370–2375.
62. G. D. Scholes, J. Phys. Chem. A, 2015, 119, 12699–12705.
63. J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597–8607.
64. R. Wang, C. Zhang, B. Zhang, Y. Liu, X. Wang and M. Xiao, Nat. Commun., 2015, 6, 8602.
65. Z. Wang, C. Zhang, R. Wang, G. Wang, X. Wang and M. Xiao, J. Chem. Phys., 2019, 151, 134309.
66. C. D. Cruz, E. L. Chronister and C. J. Bardeen, J. Chem. Phys., 2020, 153, 234504.
67. V. V. Tarasov, G. E. Zoriniants, A. I. Shushin and M. M. Triebel, Chem. Phys. Lett., 1997, 267, 58–64.
68. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822.
69. W. A. Yee, V. A. Kuzmin, D. S. Kliger, G. S. Hammond and A. J. Twarowski, J. Am. Chem. Soc., 1979, 101, 5104–5106.
70. J. Jaumot, R. Gargallo, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2005, 76, 101–110.
71. J. Jaumot, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2015, 140, 1–12.
72. H. G. Löhmannsröben, Appl. Phys. B: Photophys. Laser Chem., 1988, 47, 195–199.
73. A. D. Poletayev, J. Clark, M. W. B. Wilson, A. Rao, Y. Makino, S. Hotta and R. H. Friend, Adv. Mater., 2014, 26, 919–924.
74. A. I. Shushin, Chem. Phys. Lett., 2017, 678, 283–288.
75. R. C. Johnson and R. E. Merrifield, Phys. Rev. B: Solid State, 1970, 1, 896–902.
76. J. J. Burdett, G. B. Piland and C. J. Bardeen, Chem. Phys. Lett., 2013, 585, 1–10.
77. H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205–1212.
78. D. G. Bossanyi, M. Matthiesen, S. Wang, J. A. Smith, R. C. Kilbride, J. D. Shipp, D. Chekulaev, E. Holland, J. E. Anthony, J. Zaumseil, A. J. Musser and J. Clark, Nat. Chem., 2021, 13, 163–171.
79. R. Zeis, C. Besnard, T. Siegrist, C. Schlockermann, X. Chi and C. Kloc, Chem. Mater., 2006, 18, 244–248.
80. P.-H. Sher, C.-H. Chen, T.-L. Chiu, C.-F. Lin, J.-K. Wang and J.-H. Lee, J. Phys. Chem. C, 2019, 123, 3279–3284.
81. T.-S. Yeh, C.-S. Chu and Y.-L. Lo, Sens. Actuators, B, 2006, 119, 701–707.
82. S. Arnold, W. B. Whitten and A. C. Damask, J. Chem. Phys., 1970, 53, 2878–2884.
83. N. C. Giebink, Y. Sun and S. R. Forrest, Org. Electron., 2006, 7, 375–386.
84. L. Frazer, J. K. Gallaher and T. W. Schmidt, ACS Energy Lett., 2017, 2, 1346–1354.

---

Footnotes

† The data underlying all numerical figures in this Article and the Supporting Information is freely available at 10.15131/shef.data.16815022. The simulation code is freely available at https://github.com/davidbossanyi/rubrene-nanoparticle-dynamics.

‡ Electronic supplementary information (ESI) available: Additional data analysis and modelling details. See DOI: 10.1039/d1tc02955j

§ These authors contributed equally to this work.

¶ Present address: University of Strasbourg, CNRS, ISIS, 8 allée Gaspard Monge, 67000, Strasbourg, France.

---