Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydride ion intercalation and conduction in the electride Sr3CrN3†
Miaoting
Xu
a,
Cuicui
Wang
a,
Benjamin J.
Morgan
 b and
Lee A.
Burton
b and
Lee A.
Burton
 *a
*a
aInternational Centre for Quantum and Molecular Structures, Department of Physics, Shanghai University, Shanghai 200444, China. E-mail: leeburton@shu.edu.cn
bDepartment of Chemistry, University of Bath, Claverton Down, BA2 7AY, UK
First published on 31st March 2022
Abstract
The electride Sr3CrN3 has a one-dimensional channel of electron density, which is a rare feature that offers great potential for fast ion conduction. Using density functional theory, we find that Sr3CrN3 is an excellent hydride conductor within this channel, with a diffusion barrier as low as 0.30 eV and an estimated diffusion coefficient of 5.37 × 10−8 cm2 s−1. This diffusion barrier is lower than those reported for the best hydride conductors to date. We also show the most-stable amount of hydride in the host material under standard conditions and the corresponding change in electronic structure from metal to wide-gap insulator. Our results highlight the potential offered by 1D electride materials for ion-transport applications such as energy storage or gas separation.
Introduction
The global emphasis on restricting carbon emissions continues to increase the demand for clean technologies.1 For example, renewable energies are predicted to phase-out coal and gas power, while electric vehicles are projected to replace those with internal combustion engines.2 Both of these advancements require continuing advances in electrochemical energy storage technologies, such as lithium-ion batteries or fuel cells.3Solid-state ion-conducting materials have been long-studied for their potential use in energy storage systems.4 Recent years have seen particular advances in the development of highly-conducting lithium-ion solid electrolytes with potential application in all-solid-state lithium-ion batteries.5–8 The limited global availability of lithium, however, means that lithium-ion batteries are expected to meet only part of the projected future energy-storage needs.9 This motivates the continuing search for alternate materials, including solid-state electrolytes, that could be used in non-lithium energy-storage devices.
Hydride ions have small ionic radii, large electronic polarizability and a high standard redox potential for H2/H− (−2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V).10 These characteristics make H− ions promising for applications in next-generation electrochemical energy storage with high voltage and high energy density. Furthermore, hydrogen is highly abundant, globally available and low cost. To date, materials with high ion conduction for H− have been reported but these were only achieved at relatively high temperatures.11 Thus, there is still ample scope for improvement in this area.
V).10 These characteristics make H− ions promising for applications in next-generation electrochemical energy storage with high voltage and high energy density. Furthermore, hydrogen is highly abundant, globally available and low cost. To date, materials with high ion conduction for H− have been reported but these were only achieved at relatively high temperatures.11 Thus, there is still ample scope for improvement in this area.
Electrides are class of rare ionic compounds that possess free electrons localized within cavities in the host structure, with these electrons acting as anions. To date, only a few inorganic electrides have been experimentally identified,12 but they are typically classified according to dimensionality of their free electron density. For example, if the excess electron density occupies cavities or pores the electrides are classified as 0D (e.g., Ca12Al14O3213), if the density is in a one-dimensional channel they are 1D (e.g. Y5Si314) or if the density is continuous in a plane they are 2D (e.g. Ca2N15). The anionic electrons of electrides have been shown to effectively interact with external hydrogen, leading to excellent hydride absorption and desorption properties,16,17 even in 1D electrides.14
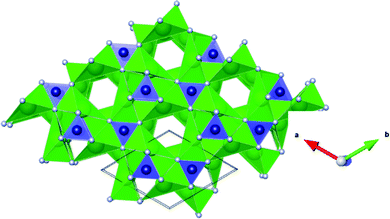
In this work we consider Sr3CrN3, a recently identified 1D electride, as a hydride conductor.18 Sr3CrN3 can be described with the formal oxidation states Sr32+Cr4+N33−:e− and the excess electrons aggregating in one-dimensional channels (see Fig. 1). The assignment of Cr(IV) was demonstrated with previous DFT calculations and subsequently confirmed by experimental analysis.18,19 Here, we explore the optimal diffusion path of hydride ions in the channel using the climbing-image nudged-elastic-band (CI-NEB) method. We also investigate the hydrogen capacity by calculating insertion energies of hydride ions in the structure. Finally, we report the electronic nature of the host material before and after hydride intercalation, showing a shift from metallic to insulating behaviour. Overall, we find that Sr3CrN3 has a low capacity for hydrogen under standard conditions but the diffusion barrier of 0.3 eV within the 1D channels is significantly lower than barriers reported for best-in-class hydride ion conductors previously e.g. 0.52 eV for barium hydride.11
Methods
Density function theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP),21,22 with the Projector Augmented Wave (PAW) method for modelling core electrons.23,24 The Perdew–Burke–Enzerhof (PBE) exchange-correlational functional of the Generalized Gradient Approximation (GGA) was used.25For the Sr3CrN3Hx (0 < x < 3) calculations, an energy cut-off of 520 eV was employed. Any H atoms were added to the system as neutral species so no charge image or charge balancing considerations are required and all computations were spin polarized. Magnetic ions were initialised in a high-spin ferromagnetic configuration and then allowed to relax during each calculation. To sample k-space we used a 6 × 6 × 9 Monkhorst–Pack set of k-points with the tetrahedron method.26 Electronic convergence criterion was set to 1 × 10−6 eV and ionic convergence criterion was set to 1 × 10−5 eV Å−1 in all cases. The H2 gas was calculated in a unit cell of 10 Å3 with a gamma centred single point k-grid.
To investigate potential diffusion pathways for mobile H-we performed a series of Climbing Image Nudged Elastic Band (CI-NEB) calculations with fixed mid-points, as implemented in VASP combined with the VTST-Tools27 by Henkelman et al.28
Finally the screened–exchange hybrid density functional of Heyd–Scuseria–Ernzerhof (HSE06)29 was used for calculations of electronic properties. This method is known to correct the underestimation of band gap and over delocalisation of conventional DFT.30 For plotting the band structures we use Pymatgen's “electronic_structure” module BSPlotter.31
Results and discussion
The crystal structure of Sr3CrN3 has the hexagonal space group P63/m, with lattice constants a = 7.84, b = 7.84, c = 5.24, α = 90.00, β = 90.00, γ = 120.00. The lattice constants obtained from the DFT structure relaxation compare well to the experimentally determined values (see Table 1).20 The structure contains trigonal-planar [CrN3]5− anions and Sr2+ cations arranged to form 1D channels as shown in Fig. 1. This 1D channel contains the excess electron density that allows the material to be defined as an electride.32| Lattice constant | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) |
|---|---|---|---|---|---|---|
| DFT relaxed | 7.84 | 7.84 | 5.24 | 90.0 | 90.0 | 120.0 |
| Experiment | 7.72 | 7.72 | 5.25 | 90.0 | 90.0 | 120.0 |
In Sr3CrN3, Sr and N ions occupy Wyckoff 6h sites and Cr occupies 2c sites. The remaining high-symmetry Wyckoff sites are vacant in the stoichiometric material and are therefore available as potential sites to accommodate anionic hydrogen.
To analyse the ability of Sr3CrN3 to accommodate intercalated hydrogen, we consider all possible H− configurations for x(H) = 1 to 6, where x(H) = 6 corresponds to all available Wyckoff sites being occupied by H. The intercalation energy as a function of x(H) is calculated as
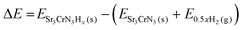 | (1) |
The energy change (ΔE) for all 25 total combinations of hydride position are listed in Table S1 (ESI†) and plotted in Fig. 2, although symmetry equivalence means fewer than 25 data points are visible in the plot. These results show that under standard conditions one intercalated hydride per formula unit has the lowest energy overall compared to the pure electride. There are two formula units of Sr3CrN3 in a unit cell, each one providing an excess electron that makes the material an electride. Thus, the addition of two hydrogen atoms to the unit cell creates the material Sr3CrN3H, which agrees with experimental reports on the related material Ba3CrN3H.33 The positions of the hydride ions corresponding to the lowest energy are on the 2b Wyckoff positions with the fractional unit cell coordinates (0, 0, 0) and (0, 0, 0.5). The continued addition of hydrides is still favourable up to the addition of the 3rd hydride ion per formula unit, at which point the change in energy becomes positive. This indicates that increasing chemical potential of H would be needed for additional uptake of H to proceed.
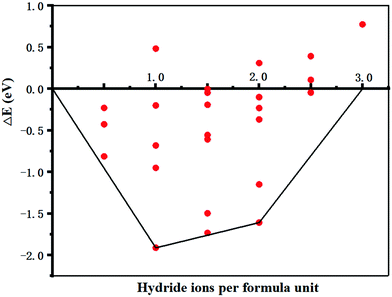 | ||
| Fig. 2 The energy change as a function of hydrogen atoms added to Sr3CrN3 relative to the phase pure material. The lowest energies are connected to form a convex hull. The full data for this figure, corresponding to 25 total calculations, can be found in the ESI.† | ||
McColm et al.34 previously reported promise for electrides in the area of hydrogen storage. However, we find that under standard conditions at most 2.5 hydride ions per formula unit can be placed in the Sr3CrN3. Given that the volume of the unit cell is 282.68 Å3 we calculate the corresponding volumetric H2 density (V(H2)) and relative gravimetric H2 density (ω(H2)) as 29.61 kg m−3 and 0.70% respectively. These are calculated using eqn (2) and (3), below. Compared with other hydrogen storage materials, the hydrogen storage density of Sr3CrN3is low—even lower than pressurised H2 gas—owing to the elemental composition and structure of this material.35 Firstly, there are two rather heavy metal elements present, which makes the relative molecular mass large. Secondly, Sr3CrN3 has a 1D cavity channel, so the available volume is relatively low compared to other open-pore materials.
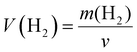 | (2) |
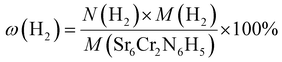 | (3) |
Hydride migration pathways and diffusion coefficients
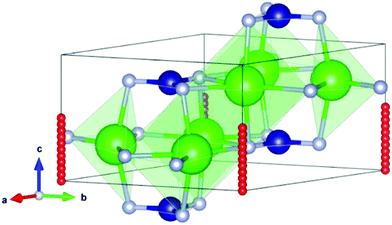
We continue to assess the hydride ion migration properties of Sr3CrN3. Specifically, we calculate the energy barrier to ionic diffusion which directly relates to diffusivity and hence various device properties including necessary operating temperature and power output.36 According to the results above, (0,0,0) and (0,0,0.5) are the optimum positions for hydride ions in the material. Therefore, these two positions are used as the initial and final positions for exploring the migration path of hydride ions using the CI-NEB method, as shown in Fig. 3. These positions are within the one-dimensional cavity channel that is surrounded by strontium cations in the material.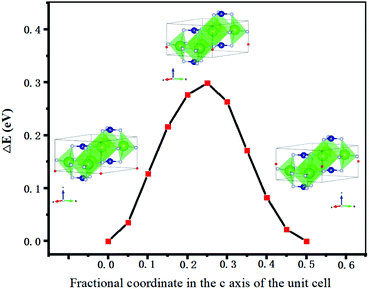 | ||
| Fig. 3 The lowest energy hydride ion pathway in the Sr3CrN3 structure. The green spheres are Sr, the blue spheres are Cr, the light grey spheres are N, and the red spheres are H. | ||
The CI-NEB method generates a direct linear path connecting the start and end points with a very low energy barrier of 0.30 eV as shown in Fig. 4. Even if the atoms of the host material remain fixed at the phase-pure positions, the energy is still found to be remarkably low at 0.35 eV. Our calculated energy barrier is smaller than those reported in the literature for the fastest reported hydride ion conducting materials: 0.52 eV for barium hydride,11 or 1.2 eV for oxygen substituted lanthanum hydride.10 Furthermore, proton migration is usually associated with an activation energy of higher than 0.5 eV in oxide materials,37 despite protons having a smaller ionic radii than hydrides. As a result, these are among the most favourable properties for ionic diffusion reported previously.
 | ||
| Fig. 4 The energy barriers from the CI-NEB method for the in-channel migration corresponding between (0, 0, 0) and (0, 0, 0.5) internal coordinates as shown in Fig. 3. | ||
We sample increasing displacement from the linear path within the channel to confirm the route calculated here is the ground state. We also analysed alternate migration routes outside of the one-dimensional channel. When we select (0.10, 0.25, 0.25) as midpoint, the migration barrier is 2.40 eV; for (0.25, 0, 0.25) the barrier is 2.64 eV and for (0.15, 0.10, 0.23), the barrier is 3.94 eV. Finally, we also sampled the paths along the other 2 unit-cell axes with a direction (0, 0, 0 → 0, 0, 0.5) giving a barrier of 5.04 eV and b direction (0, 0, 0 → 0, 0.5, 0) giving a barrier of 4.92 eV. Thus, we conclude that migration within the electride channel is highly favourable relative to alternate routes through the material. The large difference between energy barriers means that this material will be highly directional in its ionic migration, suggesting that so-called superionic fast conduction may be possible.38
Given that the NEB barrier of 0.3 eV is still much greater than KBT at 298 K the H diffusion process falls into a so-called “independent hopping” regime, meaning that transition-state theory can be applied to calculate diffusivity. This allows us to effectively account for temperature.39 The full equation for calculating diffusivity (D) is shown below in eqn (4):
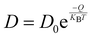 | (4) |
Furthermore, ionic conductivity can be estimated using the Nernst–Einstein approximation from the diffusion coefficient, as shown in eqn (5).
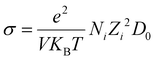 | (5) |
Using the relaxed volume of the unit cell we get a V of 322.1 cubic angstroms. For T we can use 300 K, N as 2 ions per unit cell and Z of 1. Finally, for D0 we use = 6.3 × 10−3 cm2 s−1 as before. This gives an estimated conductivity of 242.4 Siemens per centimetre. Finally, the ionic transference number will be exactly 1, because the only mobile species in this material is the H− ion.42
Electronic structures of the Sr3CrN3 and Sr3CrN3H
We consider the effect of hydride intercalation into Sr3CrN3 on the electronic structure to elucidate the nature of the interaction between the hydride and the anionic electron and to ascribe possible application in devices. We use the hybrid functional HSE06 to calculate the electronic properties of Sr3CrN3 and Sr3CrN3H based on occupation of 2H ions on the 2b Wyckoff site, i.e., the lowest energy configuration under standard conditions (see Fig. 2). The band structure diagrams for Sr3CrN3 and Sr3CrN3H are shown in Fig. 5. We find that Sr3CrN3 is metallic, which agrees with earlier analysis that places the anionic electron density of the electride at the Fermi level.18 On the addition of the hydride ions, however, the compound becomes a wide band-gap semiconductor, presenting a band gap value of 2.99 eV, for the global energy minimum configuration shown in Fig. 2. This is consistent with analogous data reported for the related material Ba3CrN3H,33 as well as for other electrides in the literature.43 The large shift in electronic properties suggests that the anionic electrons reduce the hydrogen to hydride and are then not available in the structure. This is further corroborated by the fact that the bands of the hydride phase are relatively flat across the entire Brillouin zone, meaning that charges are tightly bound.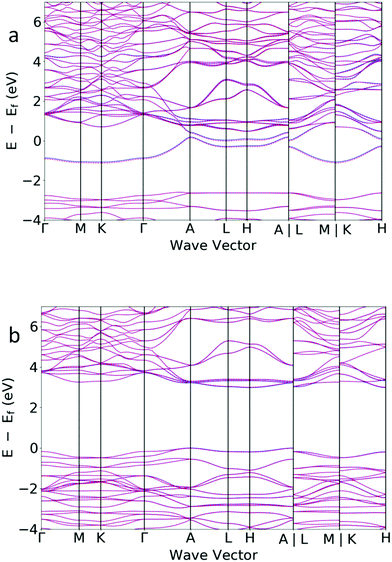 | ||
| Fig. 5 The band structure for (top) Sr3CrN3 showing metallic behaviour and (bottom) Sr3CrN3H showing a relatively wide band gap. The solid lines are spin up and dashed lines are spin down. | ||
We also perform HSE06 calculations on supercell structures with partial H ion occupancy on the 2b Wyckoff sites i.e. the location of the anionic electrons. The data for these calculations is shown in full in Table S2 (ESI†). When not all anionic electrons are used in the reduction of the H atoms there is still an opening of a band gap, although smaller in magnitude than for the full case. We believe that this is because the delocalised anionic electron density in the channel is disrupted by the presence of the hydride, even in relatively dilute amounts, leading to semiconductor rather than metallic behaviour.
Druffel et al.44 have suggested that electrides might find use in high-capacity electrodes that realise electron–anion reversible exchange at room temperature. In the case of Sr3CrN3 we predict no significant structural reorganisation and very small changes in unit cell volume upon hydrogen intercalation. Our analysis of the electronic nature of the material precludes such an application as the intercalated Sr3CrN3H is strongly insulating, whereas an electrode is typically sought to be metallic in nature. What's more the flat bands mean a high charge effective mass and low conductivity, which is again unfavourable for application as an electrode. The hydride capacity is also relative low for such an application. However, the wide-band gap in the presence of hydride ions suggests that the material could be employed as an electrolyte in a fuel cell configuration, wherein a constant flow of hydride ions could maintain electrically insulating behaviour, which is what forces the electrons around the external circuit to produce electricity available for work. Finally, the band structure shows that the spin-up and spin-down states are virtually degenerate, which indicates no intrinsic ferromagnetism for either the hydride or phase pure material.
Conclusions
In summary, we have investigated the electride Sr3CrN3 as a hydrogen storage material and hydride ion conductor. The overall energy minimum under standard conditions is obtained on addition of one hydride per unit formula forming Sr3CrN3H, although up to 2.5 should still be thermodynamically stable, forming Sr6Cr2N6H5. While uptake and desorption of hydrogen is readily observed in experiment for electrides,14,16,17 this material is not likely to be a candidate of a hydrogen storage material due to the heavy constituent elements and relatively unopen structure.On the other hand, we find Sr3CrN3H to be an excellent conductor of hydride ions. Within the 1D channel hydrogen ions show a migration barrier of 0.30 eV, which is significantly lower than for even some of the best performing hydride-ion conductors reported to date, e.g., 0.52 eV for barium hydride,11 or 1.2–1.3 eV for oxygen substituted lanthanum hydride.10 While it is tempting to attribute the low diffusion barrier to the anionic electrons in a one-dimensional channel in the material facilitating conduction, the electronic structure indicates that the excess electrons are used in reducing the H to H−; becoming a wide-band gap ionic material in the process. Thus, we assume that the partially-coordinated Sr2+ cations surrounding the 1D channel provide a uniquely favourable environment to unimpeded anion conduction. We foresee ample scope for further study of ionic conduction in this material and other electrides including a broader range of intercalated ions; molecular dynamics or phonon calculations to more extensively explore temperature effects and surface or kinetic considerations to better understand absorption/desorption processes. Overall, we find that Sr3CrN3H exhibits exceptional ionic transport properties and could be particularly useful for energy storage devices, catalysis or gas separation applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. A. B acknowledges support by the Shanghai Municipal Science and Technology Commission Program, number 19010500500, and the Natural National Science Foundation of China (NSFC) number 51950410585.References
- J. P. Weyant, Costs of Reducing Global Carbon Emissions, J. Econ. Perspect., 1993, 7, 27–46 CrossRef.
- F. Manzano-Agugliaro, A. Alcayde, F. G. Montoya, A. Zapata-Sierra and C. Gil, Scientific production of renewable energies worldwide: An overview, Renewable Sustainable Energy Rev., 2013, 18, 134–143 CrossRef.
- C.-J. Winter, Hydrogen energy—expected engineering breakthroughs, Int. J. Hydrogen Energy, 1987, 12, 521–546 CrossRef CAS.
- J. W. Fergus, Electrolytes for solid oxide fuel cells, J. Power Sources, 2006, 162, 30–40 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, A lithium superionic conductor, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- S. Ohno, A. Banik, G. F. Dewald, M. A. Kraft, T. Krauskopf, N. Minafra, P. Till, M. Weiss and W. G. Zeier, Materials design of ionic conductors for solid state batteries, Prog. Energy, 2020, 2, 022001 CrossRef.
- B. J. Morgan, Understanding fast-ion conduction in solid electrolytes, Philos. Trans. R. Soc., A, 2021, 379, 20190451 CrossRef CAS PubMed.
- C. Helbig, Supply risks associated with lithium-ion battery materials, J. Cleaner Prod., 2018, 13 Search PubMed.
- K. Fukui, S. Iimura, T. Tada, S. Fujitsu, M. Sasase, H. Tamatsukuri, T. Honda, K. Ikeda, T. Otomo and H. Hosono, Characteristic fast H–ion conduction in oxygen-substituted lanthanum hydride, Nat. Commun., 2019, 10, 2578 CrossRef PubMed.
- M. C. Verbraeken, C. Cheung, E. Suard and J. T. S. Irvine, High H− ionic conductivity in barium hydride, Nat. Mater, 2015, 14, 95–100 CrossRef CAS PubMed.
- C. Liu, S. A. Nikolaev, W. Ren and L. A. Burton, Electrides: a review, J. Mater. Chem. C, 2020, 8, 10551–10567 RSC.
- S. Matsuishi, High-Density Electron Anions in a Nanoporous Single Crystal: [Ca24Al28O64]4 + (4e−), Science, 2003, 301, 626 CrossRef CAS PubMed.
- Q. Zheng, T. Feng, J. A. Hachtel, R. Ishikawa, Y. Cheng, L. Daemen, J. Xing, J. C. Idrobo, J. Yan, N. Shibata, Y. Ikuhara, B. C. Sales, S. T. Pantelides and M. Chi, Direct visualization of anionic electrons in an electride reveals inhomogeneities, Sci. Adv., 2021, 7, 6819 CrossRef PubMed.
- K. Lee, S. W. Kim, Y. Toda, S. Matsuishi and H. Hosono, Dicalcium nitride as a two-dimensional electride with an anionic electron layer, Nature, 2013, 494, 336–340 CrossRef CAS PubMed.
- M. Kitano, Y. Inoue, H. Ishikawa, K. Yamagata, T. Nakao, T. Tada, S. Matsuishi, T. Yokoyama, M. Hara and H. Hosono, Essential role of hydride ion in ruthenium-based ammonia synthesis catalysts, Chem. Sci., 2016, 7, 4036–4043 RSC.
- T. Inoshita, S. Jeong, N. Hamada and H. Hosono, Exploration for Two-Dimensional Electrides via Database Screening and Ab Initio Calculation, Phys. Rev. X, 2014, 4, 031023 CAS.
- P. Chanhom, K. E. Fritz, L. A. Burton, J. Kloppenburg, Y. Filinchuk, A. Senyshyn, M. Wang, Z. Feng, N. Insin, J. Suntivich and G. Hautier, Sr3CrN3: A New Electride with a Partially Filled d-Shell Transition Metal, J. Am. Chem. Soc., 2019, 141, 10595–10598 CrossRef CAS PubMed.
- L. A. Burton, F. Ricci, W. Chen, G.-M. Rignanese and G. Hautier, High-Throughput Identification of Electrides from All Known Inorganic Materials, Chem. Mater., 2018, 30, 7521–7526 CrossRef CAS.
- M. G. Barker, M. J. Begley, P. P. Edwards, D. H. Gregory and S. E. Smith, Synthesis and crystal structures of the new ternary nitrides Sr3CrN3 and Ba3CrN3, J. Chem. Soc., Dalton Trans., 1996, 1 RSC.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- Transition State Tools for VASP — Transition State Tools for VASP, http://theory.cm.utexas.edu/vtsttools/, accessed 14 February 2021.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2006, 124, 8207–8215 CrossRef.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- C. Wang, M. Xu, K. T. Butler and L. A. Burton, Ultralow Work Function of the Electride Sr3CrN3, arXiv:2108.12865 [cond-mat].
- N. W. Falb, J. N. Neu, T. Besara, J. B. Whalen, D. J. Singh and T. Siegrist, Ba3CrN3H: A New Nitride-Hydride with Trigonal Planar Cr4+, Inorg. Chem., 2019, 58, 3302–3307 CrossRef CAS PubMed.
- I. J. McColm and J. M. Ward, Hydrogen sorption properties of D88-type systems: IV. Y5Ge3 and Y5Si3·Y5Ge3 solid solutions, J. Alloys Compd., 1992, 178, 91–100 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- M. Okubo, Y. Tanaka, H. Zhou, T. Kudo and I. Honma, Determination of Activation Energy for Li Ion Diffusion in Electrodes, J. Phys. Chem. B, 2009, 113, 2840–2847 CrossRef CAS PubMed.
- Y. Meng, J. Gao, Z. Zhao, J. Amoroso, J. Tong and K. S. Brinkman, Review: recent progress in low-temperature proton-conducting ceramics, J. Mater. Sci., 2019, 54, 9291–9312 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- C. R. A. Catlow, Static lattice simulation of structure and transport in superionic conductors, Solid State Ionics, 1983, 8, 89–107 CrossRef CAS.
- Y. He, Y. Li, C. Chen and H. Yu, Diffusion coefficient of hydrogen interstitial atom in α-Fe, γ-Fe and ε-Fe crystals by first-principle calculations, Int. J. Hydrogen Energy, 2017, 42, 27438–27445 CrossRef CAS.
- S. T. Hartman and R. Mishra, Layered electrides as fluoride intercalation anodes, J. Mater. Chem. A, 2020, 8, 24469–24476 RSC.
- S. Zugmann and H. J. Gores, in Encyclopedia of Applied Electrochemistry, ed. G. Kreysa, K. Ota and R. F. Savinell, Springer New York, New York, NY, 2014, pp. 2086–2091 Search PubMed.
- M. Kitano, S. Kanbara, Y. Inoue, N. Kuganathan, P. V. Sushko, T. Yokoyama, M. Hara and H. Hosono, Electride support boosts nitrogen dissociation over ruthenium catalyst and shifts the bottleneck in ammonia synthesis, Nat. Commun., 2015, 6, 6731 CrossRef CAS PubMed.
- D. L. Druffel, J. T. Pawlik, J. D. Sundberg, L. M. McRae, M. G. Lanetti and S. C. Warren, First-Principles Prediction of Electrochemical Electron–Anion Exchange: Ion Insertion without Redox, J. Phys. Chem. Lett., 2020, 11, 9210–9214 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc05850a |
| This journal is © The Royal Society of Chemistry 2022 |