Additive transport in DNA molecular circuits

Abstract

This work describes additive transport in DNA molecules due to a self-assembly of complementary single-stranded deoxyribonucleic acid chains, i.e. DNA hybridization. Charge transport properties in the DNA junctions at the single molecule level were studied experimentally by the break junction technique in an aqueous environment and theoretically including a non-equilibrium Green's function approach within the density functional based tight-binding method and molecular orbital calculations using density functional method and molecular dynamics simulations. Two types of anchoring groups, namely, amino and thiolate moieties were used to connect the single-stranded DNA (anchor-linker-3′-GGCACTCGG-5′-linker-anchor) to gold electrodes. Double-stranded DNA junctions were prepared by hybridization of single-stranded DNA with a complementary oligonucleotide chain (5′-CCGTGAGCC-3′) not containing linkers and anchoring groups. Three stable junction configurations were observed for both single-stranded and double-stranded DNA irrespective of the anchoring group, whereas junction conductance almost doubled upon DNA hybridization. Thiolate anchoring led to more robust and longer junction configurations compared to NH₂ groups. Reasons for the observed conductance enhancement and the anchoring group effect on the overall conductance are being discussed.

---

Introduction

The deoxyribonucleic acid (DNA) was assumed to transport the electric charge since the resolution of its chemical structure. Early works using carefully dried double-stranded DNA (dsDNA) samples claimed its semiconducting properties due to the electronic orbital overlap of the bases along the DNA helix and postulated that the presence of water would increase its conducting properties.^1,2 Later, an exponential increase of the bulk DNA conductivity with increasing sample humidity has been reported.³

Nowadays, dsDNA as a naturally occurring biomolecule is regarded as a suitable platform for applications in single-molecule electronics due to its easily tunable structural and electronic properties.⁴ The dsDNA can perform not only as a molecular electronic element with insulating,⁵ semiconducting,⁶ metal-like conducting^4a and superconducting⁷ properties, but also as a rectifier⁸ or a molecular switch.⁹ Recent discovery of a metallo-DNA, i.e. dsDNA involving site-specifically intercalated metal atoms or ions, further expanded the usability of DNA scaffolds for the construction of advanced molecular electronic elements.¹⁰

Scanning tunneling microscopy break junction (STM-BJ) technique has been a method of choice for determining single molecule conductance values of dsDNA in different environments.^6,9,11–22 A selection of proper experimental conditions enabled STM-BJ studies of DNA duplexes in one of the three most common dsDNA forms: A, B or Z.⁹ The conductance was studied as a function of the varied molecular length and composition (i.e. number of base pairs, their type and position as well as the guanine content) or the presence of mismatches.

Single stranded oligonucleotides containing guanine bases were found to have the highest single molecule conductance compared to oligonucleotides consisting of equal number of either cytosine, thymine or adenosine bases.²⁰ Double stranded DNA containing guanine–cytosine base pairs displayed higher single molecule conductance compared to that containing only thymine–adenine base pairs. It was also shown that the base pair mismatch lowers the dsDNA conductance due to a disrupted base pair stacking.^10f,21,23 Other indirect methods employed the photochemical,²⁴ biochemical²⁵ and electro-chemical²⁶ processes to study the charge transport (CT) in DNA.

Two principal CT mechanisms (tunnelling and hopping) have been invoked for explanation of dsDNA conductance properties.^13a,27 Indeed, a multistep charge hopping over a long DNA path plays an important role in biochemical processes.^6,28,29 The tunnelling, by contrast, dominates within much shorter distances. Both CT mechanisms have been used to explain theoretically the effect of DNA hybridization on its conductance properties.^{10,23,30–32} According to quantum chemical calculations, CT in dsDNA employs the HOMO/LUMO involving the π-electronic system of stacked base-pairs.^9,10d,24d,33 On the contrary, in single-stranded DNA the conformational stability of the extended π-system of stacked nucleobases is unlikely. Therefore, the effect of stacking on CT upon DNA hybridization may be anticipated. The experimental verification of this hypothesis is rather compelling. The conductance of dsDNA increases as a result of more tightly packed base pairs upon the transition of B-form to the A-form DNA duplex.^9,24d,34 To complete the story one also needs to consider another hypothesis which assumes CT through the outer-sphere of the sugar phosphodiester backbone of the DNA including tightly bound water molecules.^4b,31a,f,35 In such a case the increased DNA conductance upon hybridization may be simply due to increased number of the conductance pathways. Indeed, dsDNA molecular conductance was substantially suppressed when a discontinuity (missing phosphate) was introduced on each DNA strand.^31e One may then ask (i) which of the two hypotheses is correct upon DNA hybridization or (ii) if the base pair stacking as well as the backbone involvement are both needed to correctly describe the CT process. If (ii) is correct then one must consider the entire chemical structure of DNA molecule for a proper design of the DNA-based systems with desired CT properties. One indication that (ii) may be correct comes from a theoretical interpretation of the conductance differences between the A- and B-form of dsDNA.⁹ Indeed, it was necessary to include the backbone in the electronic structure calculations to reproduce the experimental results.

In spite of the fact that CT processes in dsDNA molecules have been studied by theoretical approaches quite extensively, the effect of hybridization on the CT process through individual DNA molecule remains still experimentally unconfirmed. This is related to the fact that the conductance of one single-stranded DNA molecule was too low to be measured by then available experimental techniques.²⁸ Thus, the influence of individual bases on the CT upon hybridization has been addressed only after further development of the STM-BJ technique. In 2006 van Zalinge et al.²⁰ studied the conductance properties of a series of homopolymeric oligonucleotides of different length and compared them to the results obtained for corresponding dsDNA structures both in the air and in the aqueous environment. Although the CT mechanism and the effect of DNA hybridization was not elucidated in this work it showed that single stranded DNA terminated at both ends by thiolate anchoring groups can provide measurable single molecule conductance values by the STM-BJ technique. This modification of single stranded DNA by anchoring groups at both ends inspired us and enabled us to investigate the effect of hybridization on the DNA conductance at the single molecule level.

Hereby we report systematic STM-BJ single molecule charge transport studies of single stranded and double stranded DNA molecules in their fully hydrated state (aqueous environment) with the goal of investigating the effect of DNA hybridization (dsDNA formation from two complementary ssDNA strands). Furthermore, our STM-BJ methodology³⁶ enabled the determination of two important experimental parameters, namely, the single molecule conductance value and the most probable molecular junction (MJ) length. Presented statistical analysis of obtained CT parameters allowed more detailed characterization of the metal–DNA–metal MJs than previously reported.^5,17,20,37 The non-equilibrium Green's function approach within the density functional based tight-binding method (NEGF³⁸/DFTB³⁹) in combination with molecular dynamics (MD)⁴⁰ simulation have been used to illustrate the effects of the anchoring groups and geometry fluctuations on CT for single stranded DNA. DFTB method in connection with MD method was used for calculations of interaction energies between DNA and surface of gold electrodes. Furthermore, MD simulations were used to show possible MJ configurations of fully hydrated ssDNA and dsDNA molecule between two gold electrodes. Finally, molecular orbital calculations using density functional theory (DFT) were used for explanation of conductance difference between single stranded and double stranded DNA. For this task, the fluctuation of structure of single stranded and double stranded DNA in water environment was described by the MD simulation using DNA model without explicit inclusion of gold electrodes.

Results and discussion

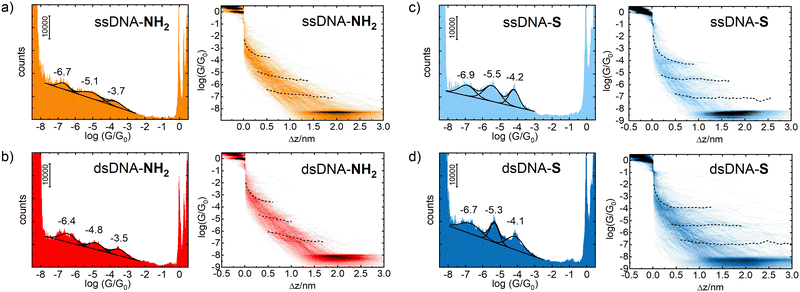
Two single-stranded and two double stranded DNA molecules were used for STM-BJ single molecule conductance measurements. Chemical structures of these systems are given in Fig. S1 and S2 in ESI.† Single stranded DNA included 5′-GGCTCACGG-3′ oligonucleotide with either 5′-(CH₂)₆-NH₂ and 3′-CH₂CH(CH₂OH)(CH₂)₄-NH₂ (ssDNA-NH₂) or 5′-(CH₂)₆-S- and 3′-(CH₂)₃-S- (ssDNA-S) anchoring groups, where 5′- and 3′-refer to the substituent position on deoxyribose. Molecule ssDNA-S was prepared in situ from a precursor containing 5′-(CH₂)₆-S-S-(CH₂)₆-OH and 3′-(CH₂)₃-S-S-(CH₂)₃-OH substituents after dissociation of a disulphide bond upon its contact with the gold surface.^41,42 The complementary 5′-CCGTGAGCC-3′ oligonucleotide (ssDNA) was used for preparation of the double-stranded DNA molecules dsDNA-S and dsDNA-NH₂. The dsDNA-NH₂ duplex formation between ssDNA and ssDNA-NH₂ and its stability at room temperature was confirmed by NMR and CD spectroscopy measurements (see Fig. S3–S6 in ESI†). The duplex formation between thiolate terminated single-stranded DNA and its complementary chain has been reported previously.⁴³ Most of the previous experimental and theoretical works consider localization of HOMO on the bases (namely on the guanine) and regard such HOMO as the charge transporting pathway (hole transport) in DNA. Therefore, we selected amino and thiolate as the anchoring groups since it is well known that they also promote CT through HOMO of the molecular wire.^44,45

The STM-BJ method was used to determine the most probable single molecule conductance values of ssDNA-NH₂, ssDNA-S, dsDNA-NH₂ and dsDNA-S in the aqueous solution. The STM-BJ method is based on the repeated formation and breaking of the nanojunction between the STM tip and gold substrate in the absence and presence of studied molecules. During this process the current is monitored at a constant bias voltage applied between the tip and the substrate and the conductance is obtained using Ohm's law.⁴⁶ The advantage of this technique is that both the gold–gold atomic contact conductance, so-called conductance quantum G₀ = 77.5 μS, as well as the conductance corresponding to a single molecule trapped between the electrodes are being obtained in the same junction breaking process (see Fig. S7 in ESI†). Such junctions were formed and broken several hundreds of times. Recorded current–time traces were collected and treated statistically.^36b Data are cumulatively presented as 1D logarithmic conductance and 2D logarithmic conductance–distance histograms. The characteristic conductance–distance behaviour can be obtained by constructing the master curves.⁴⁴

Further experimental details concerning chemicals and materials, sample preparation, NMR, CD spectroscopic and STM-BJ measurements as well as detailed description of the methods used for theoretical calculations are given in ESI,† Sections S1–S7.

Fig. 1 shows 1D logarithmic conductance and 2D logarithmic conductance–distance histograms of ssDNA-NH₂ (a), dsDNA-NH₂ (b), ssDNA-S (c), and dsDNA-S (d), respectively. All molecules contain the same 5′-GGCTCACGG-3′ sequence wired to the gold electrodes by aliphatic linkers terminated by either the amino (ssDNA-NH₂ and dsDNA-NH₂) or thiolate (ssDNA-S and dsDNA-S) anchoring groups. The complementary ssDNA chain was used solely for the duplex formation (dsDNA-NH₂ and dsDNA-S molecules) and did not contain any anchoring group. For each molecule, three peaks have been observed in 1D logarithmic conductance histogram. They are labelled high (H), medium (M) and low (L) based on the conductance values. The peak maxima based on the best Gaussian fits are summarized in Table 1. 2D logarithmic conductance–distance histograms in Fig. 1 represent the probability distribution of experimental pairs of [log(G/G₀);Δz] values in the ensemble of the retraction curves. A conductance plateau (excluding the gold–gold atomic contacts appearing at log(G/G₀) ≥ 0 as well as the noise level plateau at log(G/G₀) ≈ −8) is observed only when the molecule bridges the electrodes. Up to three conductance plateaus were observed in this work for each studied molecule. For representative examples of individual logarithmic conductance–distance retraction curves see Fig. S7 (ESI†). The plateau length in 2D logarithmic conductance–distance histogram was determined statistically by the construction of the characteristic plateau length Δz histograms.⁴⁷ The most probable characteristic plateau length Δz* value was obtained by the best Gaussian fit of the peak with the highest Δz value in the characteristic plateau length histogram (see Fig. S8–S11 in ESI†). Finally, the experimental MJ length z^exp was obtained after the correction of Δz* for a snap-back distance. Further details on data analysis are provided in Section 5 of ESI.† The experimental MJ lengths are listed in Table 1.

Fig. 1 Experimental 1D logarithmic conductance (counts–log(G/G₀)) and 2D logarithmic conductance–distance (log(G/G₀)–Δz) histograms for (a) ssDNA-NH₂ (b) dsDNA-NH₂ (c) ssDNA-S and (d) dsDNA-S molecules. The master curves are shown as black dashed lines.

Table 1 Experimental conductance log(G/G₀) and MJ length z^exp values for three DNA junction states labelled high (H), medium (M) and low (L) based on the conductance magnitude

DNA	log(GH/G0)	z ^expH [nm]	log(GM/G0)	z ^expM [nm]	log(GL/G0)	z ^expL [nm]
a Experimental MJ length z^exp = Δz* + 0.4 nm was obtained after correction of the most probable plateau length Δz* for a snap-back distance of 0.4 nm. The most probable plateau length Δz* values were obtained from the characteristic plateau length histograms shown in Fig. S8–S11 (ESI).
ssDNA-NH2	−3.7 ± 0.4	0.8 ± 0.2	−5.1 ± 0.5	1.6 ± 0.2	−6.7 ± 0.3	2.0 ± 0.3
dsDNA-NH2	−3.5 ± 0.4	0.8 ± 0.2	−4.8 ± 0.4	1.2 ± 0.2	−6.4 ± 0.4	1.8 ± 0.3
ssDNA-S	−4.2 ± 0.3	1.1 ± 0.2	−5.5 ± 0.5	1.7 ± 0.4	−6.9 ± 0.5	2.7 ± 0.3
dsDNA-S	−4.1 ± 0.4	1.3 ± 0.4	−5.3 ± 0.3	1.8 ± 0.5	−6.7 ± 0.6	2.9 ± 0.6

---

Multiple conductance values have been reported for DNA molecular junction in the past.^12,14,17,21 They represented integer multiples of a certain conductance value and were interpreted as conductances of junctions involving one, two or more molecules. In contrast to these reports, our work gives conductance values of distinct single molecule junction configurations differing by order(s) of magnitude from each other as well as in their length. A common feature for MJs involving a single DNA molecule is that their conductance value (G_H, G_M and G_L) decreases exponentially with increasing MJ length, see Table 1 and Fig. 2. This fact strongly suggests that tunnelling is the dominant CT mechanism in reported systems containing either nine bases or nine base-pairs. Indeed, this CT mechanism was found to be operative within DNA molecules involving less than ca. twelve base pairs.⁴⁸ For example, Hihath et al.^9,34 observed tunnelling CT mechanism in a series of dsDNA molecules having an increasing number of guanine–cytosine base pairs. They obtained log(G/G₀) value of −3.6 ± 0.2 for dsDNA containing nine base pairs comparable to CT characteristics of dsDNA molecules used in this work, see Table 1. Their dsDNA molecule consisted of the NH₂–(CH₂)₃-3′-CCCGCGCCC-5′-(CH₂)₃–NH₂ strand and complementary strand without the linkers and anchoring groups.

Fig. 2 Left: The correlation between log(G/G₀) conductance and z^exp junction length for (a) ssDNA-NH₂ (black ●), dsDNA-NH₂ (red ●); (b) ssDNA-S (black ●), dsDNA-S (blue ●). The error bars indicate the standard deviations of log(G/G₀) and z^exp values. Right: The conductance G ratio of dsDNA and ssDNA for H, M and L junction state for molecules terminated with (a) NH₂– and (b) S– anchoring groups.

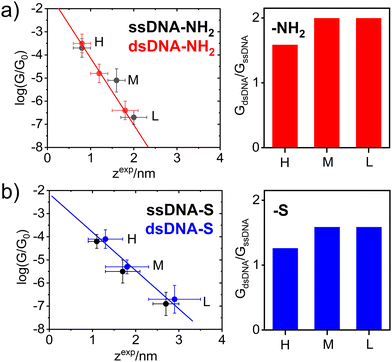
Fig. 2 further demonstrates the effect of anchoring groups on log(G/G₀) and z^exp values. DNA molecules (both single stranded as well as double stranded) form longer MJ configurations when thiolates are employed as anchoring groups, which can be explained by higher mechanical stability of the junction due to a strong covalent bonding between sulphur and gold atoms.⁴⁹ The NH₂ anchoring groups are more directional but their interaction with gold is weaker.^44c Thus, the MJs terminated by NH₂ anchoring groups break on average at much shorter length than thiol-based molecules, compare Fig. 2(a) and (b). The available experimental evidence confirms that breaking of MJs based on thiolate-terminated molecules requires three times higher force compared to amino-anchored ones.⁴⁹ Qualitatively different MJ evolution is seen also from the master curve analysis (black lines) in Fig. 1. All three MJ configurations (H, M, L) of ssDNA-NH₂ and dsDNA-NH₂ molecules display master curves of slightly decreasing logarithmic conductance with increasing junction length (black dashed lines in Fig. 1(a) and (b)), whereas length independent trends are observed for thiol-anchored DNA molecules (Fig. 1(c) and (d)). This observation is consistent with previously reported differences in the MJ breaking process for organic molecular wires terminated by these two types of anchoring groups.⁴⁴ It is generally accepted that the anchoring groups can control not only the strength of the electronic coupling between molecules and metallic leads, but also the energetic alignment of molecular orbitals involved in CT through the molecule and Fermi levels of surrounding electrodes.

In order to get deeper insight into the MJ evolution and breaking process we scrutinized and categorized individual logarithmic conductance–distance retraction curves according to the occurrence of molecular plateaus. Exemplary logarithmic conductance–distance curves are shown in Fig. S7 (ESI†). All possible combinations of plateau types in individual logarithmic conductance–distance retraction curves corresponding to three MJ configurations (H, M and L) have been identified for each studied molecule. Each ensemble contained retraction curves with no plateau, with one plateau only (H, M, L), two plateaus (H + M, H + L, M + L) and three plateaus (H + M + L), respectively. A percentual distribution of curves belonging to such defined categories is given for ssDNA-NH₂, dsDNA-NH₂, ssDNA-S and dsDNA-S molecules in Fig. S12 of ESI.† Taking into consideration only junctions with plateaus (i.e. excluding the category of curves showing no plateau) one arrives at the conclusion that H, M and L states are almost equally probable (see Table S1, ESI,† highlighted part in orange colour) independent of DNA being single or double stranded or having different type of anchoring groups. Retraction curves that end up (MJ finally breaks off) in the L state are observed with the highest probability followed by curves that end up in the M state and the smallest number represent curves showing only the shortest H state of the junction (see Table S1 of ESI,† highlighted part in light blue colour). Similar trend was observed for detection probability of curves showing one, two and three plateaus (MJ configurations), see Table S1 (ESI†), highlighted part in light green colour. The highest number of retraction curves contains one plateau, followed by two and three plateaus. Comparison between single and double stranded DNA molecules indicates that after the DNA hybridization curves with only one plateau increase in number at the expense of curves with three plateaus. This increase is more pronounced for dsDNA-S compared to dsDNA-NH₂. The number of curves where the last state before junction breaking is L increases for dsDNA-NH₂ and decreases for dsDNA-S upon hybridization, which may be a consequence of the decreased flexibility of molecular structure upon hybridization as well as different mechanical stability of the MJ. One may relate this different stability to the anchoring groups. One should remind the reader that ssDNA-S molecules form systematically shorter H, M and L junction configurations than dsDNA-S molecules (Fig. 2(b)). This is not the case for ssDNA-NH₂ and dsDNA-NH₂, where the trend is just opposite (Fig. 2(a)). Molecules dsDNA-NH₂ form MJs with shorter length than their single stranded counterparts. Importantly, the conductance values increase upon hybridization for DNA molecules terminated by both types of the anchoring groups (Fig. 2(a) and (b), right panel).

A theoretical model of single stranded DNA containing two guanine bases connected to the gold electrodes via linkers terminated by thiolate (ssDNA(GG)-S) or amino (ssDNA(GG)-NH₂) anchoring groups identical to those used in STM-BJ measurements performed in this work (Fig. S13 and S14, ESI†) was developed to study the effect of anchoring groups on the DNA conductance. Molecular conductance was calculated with the DFTB³⁹/NEGF³⁸ approach. The effect of molecular dynamics was included. For more computational details see Section 6 of ESI.† The average interaction energy E_int between ssDNA(GG)-S and Au₁₀₈ electrodes was by 44.9 kcal mol⁻¹ more negative compared to E_int of NH₂- anchored molecules (Fig. S15 of ESI†). The junction length differences found experimentally during the MJ evolution process are consistent with computed differences in the interaction energies of these two anchoring groups with the gold surface. This model served also as a benchmark for understanding of the effect of geometrical fluctuations within one MJ configuration on the distribution of the conductance values. The MJ was studied by MD throughout 10 ns time period providing eleven consecutive MJ configuration snapshots. Within this time window the original stacking of 2 guanine bases was partially disrupted (Fig. S16, ESI†), whereas NEGF-calculated conductance values based on DFTB/MD snapshots varied substantially (almost two orders of magnitude) among individual snapshots (see Fig. S17, ESI†). Results of DFTB/NEGF calculations clearly illustrate the essential contribution of geometric fluctuations towards the experimentally-obtained conductance peak widths (see Fig. S17, ESI†). Finally, DFTB/NEGF calculations support the notion that the difference in molecular conductance values between ssDNA-S and ssDNA-NH₂ molecules is governed rather by the length (distance between two gold electrodes) of individual experimentally observed MJs (dependent on the type of the anchoring groups) than by the electronic properties of the anchoring groups themselves.

The experimentally obtained single molecule conductance was enhanced upon hybridization for DNA molecules terminated by both types of anchoring groups, see Fig. 2. Higher conductance increase observed for NH₂- anchored DNA is only apparent due to the systematically smaller MJ length values compared to the S anchoring, compare data in Table 1 and right graphs in Fig. 2. Indeed, dsDNA-NH₂ forms shorter MJ compared to ssDNA-NH₂ molecular junction, whereas the opposite trend is observed for S anchored DNA molecules. Based on purely geometrical considerations, the G_L conductance of dsDNA-S represents most likely the MJ configuration with double-helix chain oriented perpendicularly to the surface plane of the gold substrate. This statement is based on the fact that the estimated length of the B-form of dsDNA⁵⁰ amounts to ca. 2.72 nm (eight steps multiplied by 0.34 nm), considering the molecule without any linkers and anchoring groups. The length of DNA molecules including linkers and thiolate anchors roughly corresponds to z^exp_L value of 2.9 ± 0.6 nm obtained for dsDNA-S and is also very close to z^exp_L value observed for ssDNA-S molecule (2.7 ± 0.3 nm). In analogy with the β conductance decay parameter obtained from G ∼ e^−βL dependence (tunnelling CT mechanism) reported for dsDNA molecules of different base-pair composition,^17,20,34,48 we have determined β values considering H, M and L states of ssDNA-S and dsDNA-S junctions from the slopes in Fig. 2(b). An identical value β = 3.7 ± 0.2 nm⁻¹ was obtained for both thiol-based molecules. This observation may serve as additional evidence that the oligonucleotide chains in ssDNA-S and dsDNA-S MJs share similar spatial arrangement. This value compares well with β parameters^17,34,48 obtained from the variation of single molecule length by changing the number of nucleotides. As discussed above, ssDNA-NH₂ and dsDNA-NH₂ molecules form much shorter MJs compared to ssDNA-S and dsDNA-S molecules (related to reduced bond strength between the anchor and gold). As a result, we did not find meaningful to associate the slope in Fig. 2(a) for MJs of NH₂-terminated DNA molecules with β parameter. Nonetheless, this experimental observation (shorter MJs) may also indicate a qualitatively different characteristic configuration of ssDNA-NH₂ and dsDNA-NH₂ molecules in the junction. To explore the effect of hybridization on the single molecule conductance and MJ evolution, we have further evaluated G_dsDNA/G_ssDNA ratios for all three experimentally observed MJ states (H, M and L). Such ratios determined for molecules terminated by both types of anchoring groups are summarized in Fig. 2 right. For thiol-terminated molecules this ratio is always lower than 2. However, for these molecules one can further account for the effect of different z^exp length on G_dsDNA/G_ssDNA ratio by employing G ∼ e^−βL expression and recalculating G_dsDNA/G_ssDNA ratio for one z^exp = L since the same β parameter was found experimentally for both ssDNA-S and dsDNA-S MJs. Such corrected G_dsDNA/G_ssDNA ratio amounts to 2.7 ± 0.5. In any case one can conclude that the conductance of studied DNA molecules approximately doubles upon the DNA hybridization in the CT tunnelling regime.

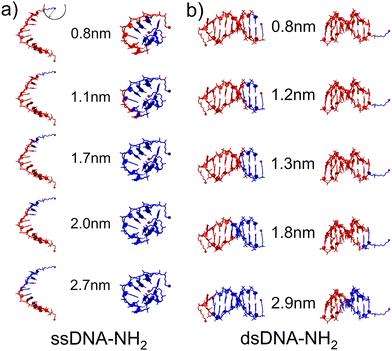
Three distinct conductance states indicate the existence of different DNA configurations and possible transitions between them during the MJ evolution. Thus, as a first step in our theoretical characterization of these systems we have performed MD simulations for ssDNA-NH₂ and dsDNA-NH₂ molecules in the aqueous solution (see Section 6 of ESI† for details). Fig. 3 shows the representative MD snapshots for these molecules. For the sake of simplicity, water molecules are not shown. The hypothetical CT pathway lengths indicated by numbers in between two configuration types in Fig. 3 represent the range of experimentally-observed MJ length values (z^exp) given in Table 1. A blue sphere centred on one of the two NH₂ anchoring groups (see top left snapshot in Fig. 3) relates to each number through its radius. Blue-coloured parts of the DNA molecule are those found within this sphere for each given pathway length. For ssDNA-NH₂, the starting configuration derived from a B-form DNA duplex (Fig. 3(a) left) swiftly transfers to a “cyclic” one (Fig. 3(a) right) that is sustained during the rest of MD simulation and is therefore considered in further discussion. The fluctuations within the anchoring groups and those within terminal 3′ and 5′ phosphates follow the same pattern (see Fig. S22, ESI†). A CT pathway for MJs with z^exp larger than 1.1 nm (i.e. corresponding to experimentally observed M and L states, see Table 1) involves almost the entire ssDNA-NH₂ (blue coloured part of the molecule). Nevertheless, partially buried anchoring groups indicate that the MJ formation through both NH₂ terminal groups may not be straightforward. Fig. S23 (ESI†) clearly indicates the proximity of 5′ and 3′ phosphates in such single-stranded DNA system(s). The existence of the “cyclic” DNA in solution does not exclude the possibility of molecular anchoring only to one electrode either.

Fig. 3 Hypothetical CT pathway domains indicated by blue-colored atoms for characteristic configurations of (a) ssDNA-NH₂ and (b) dsDNA-NH₂ calculated with MD in the aqueous solution. The domains include all atoms within a sphere of the radius corresponding to the experimental MJ length values given by numbers. Sphere is centered on the nitrogen atom of one of the NH₂ anchoring groups (magenta ball) as indicated in the upper-left corner. (a) “Open” duplex-like (left) and “cyclic” (right) configuration for ssDNA-NH₂. (b) “Nucleobase-like” (left) and “backbone-like” (right) orientation of linkers bearing NH₂ anchoring group for dsDNA-NH₂.

The dsDNA-NH₂, by contrast, behaves regularly like a canonical duplex (see Fig. 3(b) and Fig. S22, ESI†), where the hypothetical CT pathway is affected largely by a specific orientation of the linkers bearing anchoring groups (Fig. 3(b)). A closer look on structurally dynamical behaviour of the linkers and anchoring groups in dsDNA-NH₂ unveiled two principal orientations, where the predominant one labelled as “nucleobase-like” refers to the parallel orientation of the linker-NH₂ group (see Fig. 3(b) left and Fig. S24–S26, ESI†). The other orientation denoted as “backbone-like” involves the linker and anchoring group bent out of the duplex, see Fig. 3(b) right. Relatively free variation of the linker orientation thus may be anticipated in the experiment owing to its substantial flexibility. For dsDNA-NH₂ junctions z^exp values vary from 0.8 to 1.8 nm (H to L state, see Table 1). These numbers are represented by four out of five configurations depicted in Fig. 3(b). For the “backbone-like” configuration, the hypothetical CT pathway involves only the NH₂- anchoring group and the alkyl linker, without the involvement of nucleotides. We consider such MJ configuration as highly unlikely. On the contrary, the “nucleobase-like” configuration involves gradually increasing number of nucleotides in the hypothetical CT pathway. We find such MJ configuration as much more realistic. We further presume that for both ssDNA-NH₂ and dsDNA-NH₂ molecules, the existence of three distinct MJ states (H, M and L) and sharp transitions among them (see Fig. S7, ESI†) reflect increasing number of nucleotides involved in the CT pathway in the course of the MJ elongation. Furthermore, to obtain the ratio between conductance of double and single stranded DNA we calculated molecular orbital energies using DFT method and geometries based on MD snapshots taken from previously mentioned MD simulations of ssDNA-NH₂ and dsDNA-NH₂ molecules in aqueous solution (see Fig. S27 and S28, ESI†). Calculated transmission functions are depicted in Fig. S29 (ESI†). These calculations provided the ratio 2.7 between conductances of double and single stranded DNA.

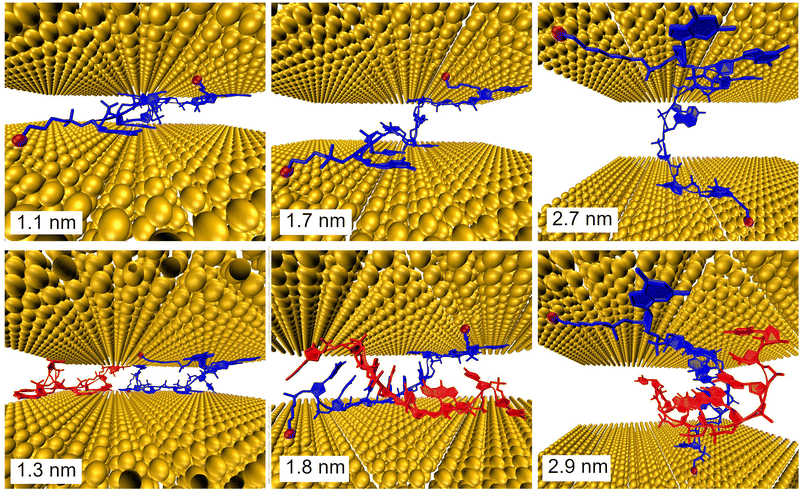
Further, MD simulations of MJ configurations of ssDNA-S and dsDNA-S molecules were conducted in the aqueous solution in the presence of the gold electrodes (see Section 6 of ESI†). The distance between the surface planes of gold clusters representing electrodes was set to the respective experimental MJ length values reported in Table 1 for H, M and L configurations. The MD simulations were performed by stepwise closing of the MJ to achieve the desired z^exp values. Fig. 4 (water molecules are not visualized) shows that simulated MJ configuration corresponding to the experimental L state preserves the original conformation of both ssDNA-S and dsDNA-S systems. Only after a decrease of the z^exp distance to that corresponding to H state the tendency to squeeze out the complementary chain in dsDNA-S is predicted. It cannot be verified that squeezing of DNA strands indeed occurs in the H state of experimentally formed MJs, but such configuration may partially explain the lower G_dsDNA/G_ssDNA ratio observed for the H state (see Fig. 2 right). Based on these computations one may say that thus obtained predictions support the claim regarding the importance of the base pairing interactions in the overall CT process. This theoretical observation together with the fact that the experimentally obtained single molecule conductance approximately doubles upon hybridization (involving two backbone chains) could be in favour of the statement that both base-pair formation as well as an increased number of identical sugar phosphodiester backbone chains contribute to the observed conductance changes. To further corroborate the hypothesis that the sugar phosphodiester backbone plays an important role in the CT through the DNA molecule, we have performed control STM-BJ experiments in which the single stranded DNA of the same oligonucleotide sequence as used in this work had only one anchor at 5′ position. In particular, we studied CT properties of three molecules: single stranded H₂N–(CH₂)₆-5′-GGCTCACGG-3′ and H₂N–(CH₂)₆-5′-CCGAGTGCC-3′ and the double stranded DNA formed by hybridization of these two chains. Such prepared dsDNA contains one NH₂ anchoring group on each of its complementary strands. The anchoring groups are located on the opposite side of the duplex providing spatially favorable arrangement for being contacted by the substrate and by the tip. STM-BJ histograms obtained from these measurements are summarized in Section 7 of ESI.† No single molecule conductance features were observed for these three additionally inspected systems indicating that the presence of the anchoring group on each end of one DNA strand is critical for obtaining functional MJs. The realization of MJs via hybridization of two strands each bearing only one anchoring group failed too. Such finding supports our hypothesis that the sugar phosphodiester backbone must be involved in the CT through the DNA molecule. To confirm this hypothesis, we calculated the difference in charge transport properties between ssDNA(GG)-S and ssDNA(abasic)-S junction using DFTB/NEGF method. The results show that ssDNA(GG)-S junction is indeed more effective in charge transport than ssDNA(abasic)-S junction, however, calculated ssDNA(abasic)-S conductance value is relatively close to that calculated for ssDNA(GG)-S junction. This result implies that sugar phosphodiester backbone chain can contribute to the charge transport pathway in DNA, for more details see Section 6 of the ESI.†

Fig. 4 Configurations of the ssDNA-S (upper part) and dsDNA-S (lower part) molecules within gold electrodes calculated with MD. The indicated distances between electrodes in MD simulations corresponded to the experimentally obtained MJ length z^exp values for the H (left), M (middle) and L (right) junction configuration. The S- anchoring groups are indicated as magenta balls.

It is important to remind the reader that three distinct conductance states with roughly similar occurrence probability were observed during the MJ evolution irrespective of the number of DNA chains (one versus two) and of the type of the anchoring groups (S- versus NH₂-). This observation suggests that such states are related to the MJ configurations involving the interactions between the electrodes and the sugar phosphodiester backbone (rather than directly bases or base-pairs). Presumably, distinct states are due to geometrically and energetically favourable MJ configurations that differ in the number of “electrode free” nucleotides in their entirety (i.e. not having a direct contact with the electrodes) involved in the CT pathway of increasing length in the course of the MJ evolution.

Conclusions

The conductance properties of single stranded DNA molecules containing at both backbone ends either thiolate ssDNA-S or amino ssDNA-NH₂ anchoring groups have been obtained at the single molecule level by STM-BJ measurements in the aqueous environment. The evidence of the conductance enhancement upon hybridization with its complementary oligonucleotide chain ssDNA was clearly demonstrated. The conductance almost doubled after the hybridization process reflecting additive transport in DNA molecular circuits. These findings compare well with recently observed current doubling in the (gold)–semiconductor (DNA) Schottky junctions containing 0.5 mm thick layers of single stranded or double stranded DNA.⁵¹ Three distinct MJ configurations (H, M, L) were observed for both single stranded and double stranded DNA irrespective of the anchoring group used. Thiolate anchoring led to longer MJ configurations upon hybridization in all three states compared to NH₂ groups, where the tendency was just the opposite. Quantum mechanical calculations supported our findings pointing to the differences in the interaction energies as well as in the DNA configuration. The upmost double enhancement of the DNA conductance due to hybridization is thus consistent with doubled number of CT pathways through DNA molecules. A control experiment with only one amino anchoring group on each strand of dsDNA-NH₂ (opposite sides) failed to detect any single molecule junction conductance within the available conductance range of our STM-BJ setup. Based on the combined experimental and theoretical evidence we are able to postulate that sugar phosphodiester backbone chains can contribute to the charge transport pathway and the π-system of stacked nucleobases involving the base-pair formation is important factor in the explanation of CT through double and single stranded DNA molecules.

Author contributions

Táňa Sebechlebská: STM-BJ investigation, data curation and analysis, Viliam Kolivoška: STM-BJ investigation, data curation and analysis, writing – review & editing, funding acquisition, Jakub Šebera: investigation, project administration, funding acquisition, DFTB and DFTB/NEGF calculations, Jiří Fukal: molecular dynamics simulations, NMR calculations, David Řeha: parametrization of molecular dynamics simulations of gold surface and DNA linkers, Miloš Buděšínský: data curation and analysis, NMR measurement, Ivan Rosenberg: data curation and analysis, Lucie Bednárová: data curation and analysis, CD spectroscopy, Jindřich Gasior: formal analysis, validation, Gábor Mészáros: formal analysis and validation, Magdaléna Hromadová: investigation, funding acquisition, writing of original draft, writing – review & editing, Vladimír Sychrovský: investigation, project administration, funding acquisition, writing of original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Czech Science Foundation (project 18-14990S) and the Czech Academy of Sciences (RVO: 61388963 and 61388955). Computational resources were supplied by MetaCentrum computational centre.

Notes and references

1. D. D. Eley and D. I. Spivey, Trans. Faraday Soc., 1962, 58, 411.
2. D. Han, Ha, H. Nham, K.-H. Yoo, H.-M. So, H.-Y. Lee and T. Kawai, Chem. Phys. Lett., 2002, 355, 405.
3. T. Kleine-Ostmann, C. Jordens, K. Baaske, T. Weimann, M. H. de Angelis and M. Koch, Appl. Phys. Lett., 2006, 88, 102102.
4. (a) H. W. Fink and C. Schonenberger, Nature, 1999, 398, 407; (b) J. C. Genereux and J. K. Barton, Chem. Rev., 2010, 110, 1642; (c) I. Bâldea, Molecular Electronics: An Experimental and Theoretical Approach, Pan Stanford, 2016; (d) K. Wang, J. Funct. Biomater., 2018, 9, 8.
5. E. Braun, Y. Eichen, U. Sivan and G. Ben-Yoseph, Nature, 1998, 391, 775.
6. D. Porath, A. Bezryadin, S. de Vries and C. Dekker, Nature, 2000, 403, 635.
7. A. Y. Kasumov, M. Kociak, S. Guéron, B. Reulet, V. T. Volkov, D. V. Klinov and H. Bouchiat, Science, 2001, 291, 280.
8. L. Kekedy-Nagy and E. E. Ferapontova, Angew. Chem., Int. Ed., 2019, 58, 3048.
9. J. M. Artés, Y. H. Li, J. Q. Qi, M. P. Anantram and J. Hihath, Nat. Commun., 2015, 6, 8870.
10. (a) Y. Tanaka, J. Kondo, V. Sychrovsky, J. Sebera, T. Dairaku, H. Saneyoshi, H. Urata, H. Torigoe and A. Ono, Chem. Commun., 2015, 51, 17343; (b) J. Muller, Eur. J. Inorg. Chem., 2008, 3749; (c) P. Auffinger and E. Ennifar, Nat. Chem., 2017, 9, 932; (d) I. Kratochvilova, M. Golan, M. Vala, M. Sperova, M. Weiter, O. Pav, J. Sebera, I. Rosenberg, V. Sychrovsky, Y. Tanaka and F. M. Bickelhaupt, J. Phys. Chem. B, 2014, 118, 5374; (e) I. Kratochvilova, K. Kral, M. Buncek, A. Viskova, S. Nespurek, A. Kochalska, T. Todorciuc, M. Weiter and B. Schneider, Biophys. Chem., 2008, 138, 3; (f) I. Kratochvilova, T. Todorciuc, K. Kral, H. Nemec, M. Buncek, J. Sebera, S. Zalis, Z. Vokacova, V. Sychrovsky, L. Bednarova, P. Mojzes and B. Schneider, J. Phys. Chem. B, 2010, 114, 5196; (g) E. Toomey, J. Xu, S. Vecchioni, L. Rothschild, S. Wind and G. E. Fernandes, J. Phys. Chem. C, 2016, 120, 7804; (h) S. Roy, H. Vedala, A. D. Roy, D. H. Kim, M. Doud, K. Mathee, H. K. Shin, N. Shimamoto, V. Prasad and W. B. Choi, Nano Lett., 2008, 8, 26; (i) C. L. Guo, K. Wang, E. Zerah-Harush, J. Hamill, B. Wang, Y. Dubi and B. Q. Xu, Nat. Chem., 2016, 8, 484; (j) D. Reha, A. A. Voityuk and S. A. Harris, ACS Nano, 2010, 4, 5737; (k) K. Siriwong and A. A. Voityuk, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 780.
11. L. Zhang, J. Zhang and J. Ulstrup, Curr. Opin. Electrochem., 2017, 4, 166.
12. R. Venkatramani, K. L. Davis, E. Wierzbinski, S. Bezer, A. Balaeff, S. Keinan, A. Paul, L. Kocsis, D. N. Beratan, C. Achim and D. H. Waldeck, J. Am. Chem. Soc., 2011, 133, 62.
13. (a) L. Xiang, J. L. Palma, Ch Bruot, V. Mujica, M. A. Ratner and N. J. Tao, Nat. Chem., 2015, 7, 221; (b) L. Xiang, J. L. Palma, Y. Li, V. Mujica, M. A. Ratner and N. J. Tao, Nat. Commun., 2017, 8, 14471.
14. (a) J. Hihath, F. Chen, P. Zhang and N. J. Tao, J. Phys.: Condens. Matter, 2007, 19, 215202; (b) J. Hihath, B. Xu, P. M. Zhang and N. J. Tao, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16979; (c) J. Hihath, S. Guo, P. Zhang and N. J. Tao, J. Phys.: Condens. Matter, 2012, 24, 164204.
15. M. W. Shinwari, M. J. Deen, E. B. Starikov and G. Cuniberti, Adv. Funct. Mater., 2010, 20, 1865.
16. P. T. Bui, T. Nishino, H. Shiigi and T. Nagaoka, Chem. Commun., 2015, 51, 1666.
17. B. Xu, P. Zhang, X. Li and N. Tao, Nano Lett., 2004, 4, 1105.
18. (a) C. Nogues, S. R. Cohen, S. S. Daube and R. Naaman, Phys. Chem. Chem. Phys., 2004, 6, 4459; (b) C. Nogues, S. R. Cohen, S. Daube, N. Apter and R. Naaman, J. Phys. Chem. B, 2006, 110, 8910.
19. S. M. Iqbal, G. Balasundaram, S. Ghosh, D. E. Bergstrom and R. Bashir, Appl. Phys. Lett., 2005, 86, 153901.
20. H. van Zalinge, D. J. Schiffrin, A. D. Bates, W. Haiss, J. Ulstrup and R. J. Nichols, ChemPhysChem, 2006, 7, 94.
21. (a) E. Wierzbinski, R. Venkatramani, K. L. Davis, S. Bezer, J. Kong, Y. Xing, E. Borguet, C. Achim, D. N. Beratan and D. H. Waldeck, ACS Nano, 2013, 7, 5391; (b) R. Venkatramani, E. Wierzbinski, D. H. Waldeck and D. N. Beratan, Faraday Discuss., 2014, 174, 57.
22. X. Guo, A. A. Gorodetsky, J. Hone, J. K. Barton and C. Nuckolls, Nat. Nanotechnol., 2008, 3, 163.
23. M. H. Lee, G. Brancolini, R. Gutiérrez, R. Di Felice and G. Cuniberti, J. Phys. Chem. B, 2012, 116, 10977.
24. (a) C. J. Murphy, M. R. Arkin, Y. Jenkins, N. D. Ghatlia, S. H. Bossmann, N. J. Turro and J. K. Barton, Science, 1993, 262, 1025; (b) C. J. Murphy, M. R. Arkin, N. D. Ghatlia, S. Bossmann, N. J. Turro and J. K. Barton, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 5315; (c) F. D. Lewis, T. F. Wu, Y. F. Zhang, R. L. Letsinger, S. R. Greenfield and M. R. Wasielewski, Science, 1997, 277, 673; (d) I. Kratochvilova, M. Vala, M. Weiter, M. Sperova, B. Schneider, O. Pav, J. Sebera, I. Rosenberg and V. Sychrovsky, Biophys. Chem., 2013, 180, 127; (e) B. Giese, J. Amaudrut, A. K. Kohler, M. Spormann and S. Wessely, Nature, 2001, 412, 318.
25. (a) D. B. Hall, R. E. Holmlin and J. K. Barton, Nature, 1996, 382, 731; (b) E. Meggers, D. Kusch, M. Spichty, U. Wille and B. Giese, Angew. Chem., Int. Ed., 1998, 37, 460; (c) I. Saito, T. Nakamura, K. Nakatani, Y. Yoshioka, K. Yamaguchi and H. Sugiyama, J. Am. Chem. Soc., 1998, 120, 12686.
26. (a) S. O. Kelley, N. M. Jackson, M. G. Hill and J. K. Barton, Angew. Chem., Int. Ed., 1999, 38, 941; (b) T. Liu and J. K. Barton, J. Am. Chem. Soc., 2005, 127, 10160.
27. Y. A. Berlin, A. L. Burin and M. A. Ratner, Chem. Phys., 2002, 275, 61.
28. H. Cohen, C. Nogues, R. Naaman and D. Porath, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11589.
29. (a) M. E. Nunez, D. B. Hall and J. K. Barton, Chem. Biol., 1999, 6, 85; (b) B. Giese and M. Spichty, ChemPhysChem, 2000, 1, 195.
30. (a) R. G. Endres, D. L. Cox and R. R. P. Singh, Rev. Mod. Phys., 2004, 76, 195; (b) K. Senthilkumar, F. C. Grozema, C. F. Guerra, F. M. Bickelhaupt, F. D. Lewis, Y. A. Berlin, M. A. Ratner and L. D. A. Siebbeles, J. Am. Chem. Soc., 2005, 127, 14894; (c) T. Kubar, R. Gutierrez, U. Kleinekathofer, G. Cuniberti and M. Elstner, Phys. Status Solidi B, 2013, 250, 2277; (d) K.-I. Dedachi, T. Natsume, T. Nakatsu, S. Tanaka, Y. Ishikawa and N. Kurita, Chem. Phys. Lett., 2007, 436, 244; (e) D. Řeha, W. Barford and S. Harris, Phys. Chem. Chem. Phys., 2008, 10, 5436.
31. (a) U. Diederichsen, Angew. Chem., Int. Ed. Engl., 1997, 36, 2317; (b) C. Bruot, L. M. Xiang, J. L. Palma, Y. Q. Li and N. J. Tao, J. Am. Chem. Soc., 2015, 137, 13933; (c) S. O. Kelley, R. E. Holmlin, E. D. A. Stemp and J. K. Barton, J. Am. Chem. Soc., 1997, 119, 9861; (d) S. O. Kelley, E. M. Boon, J. K. Barton, N. M. Jackson and M. G. Hill, Nucleic Acids Res., 1999, 27, 4830; (e) R. Zhuravel, H. Huang, G. Polycarpou, S. Polydorides, P. Motamarri, L. Katrivas, D. Rotem, J. Sperling, L. A. Zotti, A. B. Kotlyar, J. C. Cuevas, V. Gavini, S. S. Skourtis and D. Porath, Nat. Nanotechnol., 2020, 15, 836; (f) E. Beall, S. Ulku, C. Liu, E. Wierzbinski, Y. Zhang, Y. Bae, P. Zhang, C. Achim, D. N. Beratan and D. H. Waldeck, J. Am. Chem. Soc., 2017, 139, 6726.
32. M. Wolter, M. Elstner and T. Kubař, J. Chem. Phys., 2013, 139, 125102.
33. T. Uchiyama, T. Miura, H. Takeuchi, T. Dairaku, T. Komuro, T. Kawamura, Y. Kondo, L. Benda, V. Sychrovsky, P. Bour, I. Okamoto, A. Ono and Y. Tanaka, Nucleic Acids Res., 2012, 40, 5766.
34. Y. H. Li, J. M. Artes, J. Qi, I. A. Morelan, P. Feldstein, M. P. Anantram and J. Hihath, J. Phys. Chem. Lett., 2016, 7, 1888.
35. J. M. Warman, M. P. de Haas and A. Rupprecht, Chem. Phys. Lett., 1996, 249, 319.
36. (a) V. Kolivoška, M. Mohos, I. V. Pobelov, S. Rohrbach, K. Yoshida, W. Hong, Y. C. Fu, P. Moreno-García, G. Mészáros, P. Broekmann, M. Hromadová, R. Sokolová, M. Valášek and Th Wandlowski, Chem. Commun., 2014, 50, 11757; (b) J. Šebera, V. Kolivoška, M. Valášek, J. Gasior, R. Sokolová, G. Mészáros, W. Hong, M. Mayor and M. Hromadová, J. Phys. Chem. C, 2017, 121, 12885; (c) Š. Nováková Lachmanová, J. Šebera, V. Kolivoška, J. Gasior, G. Mészáros, G. Dupeyre, P. P. Lainé and M. Hromadová, Electrochim. Acta, 2018, 264, 301; (d) J. Šebera, T. Sebechlebská, Š. Nováková Lachmanová, J. Gasior, P. Moreno Garcia, G. Mészáros, M. Valášek, V. Kolivoška and M. Hromadová, Electrochim. Acta, 2019, 301, 267.
37. (a) M. Ratner, Nat. Nanotechnol., 2013, 8, 378; (b) Y. Okahata, T. Kobayashi, K. Tanaka and M. Shimomura, J. Am. Chem. Soc., 1998, 120, 6165; (c) Y. Zhang, R. H. Austin, J. Kraeft, E. C. Cox and N. P. Ong, Phys. Rev. Lett., 2002, 89, 198102; (d) Y. H. Li, J. M. Artes and J. Hihath, Small, 2016, 12, 432.
38. S. Datta, Superlattices Microstruct., 2000, 28, 253.
39. G. Seifert, J. Phys. Chem. A, 2007, 111, 5609.
40. (a) D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701; (b) H. J. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43; (c) S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. van der Spoel, Bioinformatics, 2013, 29, 845.
41. C. D. Bain, H. A. Biebuyck and G. M. Whitesides, Langmuir, 1989, 5, 723.
42. X. D. Cui, A. Primak, X. Zarate, J. Tomfohr, O. F. Sankey, A. L. Moore, T. A. Moore, D. Gust, G. Harris and S. M. Lindsay, Science, 2001, 294, 571.
43. (a) T. Ohshiro and M. Maeda, Chem. Commun., 2010, 46, 2581; (b) T. Harashima, Y. Hasegawa, S. Kaneko, Y. Jono, S. Fujii, M. Kiguchi and T. Nishino, Chem. Sci., 2021, 12, 2217.
44. (a) W. Hong, D. Z. Manrique, P. Moreno-García, M. Gulcur, A. Mishchenko, C. J. Lambert, M. R. Bryce and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 2292; (b) P. Moreno-García, M. Gulcur, D. Z. Manrique, T. Pope, W. Hong, V. Kaliginedi, C. Huang, A. S. Batsanov, M. R. Bryce, C. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2013, 135, 12228; (c) F. Chen, X. Li, J. Hihath, Z. Huang and N. J. Tao, J. Am. Chem. Soc., 2006, 128, 15874.
45. K. W. Hipps, Science, 2001, 294, 536.
46. M. Hromadová and V. Kolivoška, in Encyclopedia of Interfacial Chemistry: Surface Science and Electrochemistry, ed. K. Wandelt, Elsevier, Amsterdam, 2018, vol. 5, pp. 271–280.
47. I. V. Pobelov, M. Mohos, K. Yoshida, V. Kolivoska, A. Avdic, A. Lugstein, E. Bertagnolli, K. Leonhardt, G. Denuault and B. Gollas, Nanotechnology, 2013, 24, 115501.
48. Y. Q. Li, L. M. Xiang, J. L. Palma, Y. Asai and N. J. Tao, Nat. Commun., 2016, 7, 11294.
49. (a) B. Xu, X. Xiao and N. J. Tao, J. Am. Chem. Soc., 2003, 125, 16164; (b) M. Frei, S. V. Aradhya, M. Koentopp, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2011, 11, 1518; (c) I. V. Pobelov, K. Primdal Lauritzen, K. Yoshida, A. Jensen, G. Mészáros, K. W. Jacobsen, M. Strange, T. Wandlowski and G. C. Solomon, Nat. Commun., 2017, 8, 15931.
50. H. F. Lodish, A. Berk, Ch Kaiser, M. Krieger, M. P. Scott, A. Bretscher, H. L. Ploegh and P. T. Matsudaira, Molecular cell biology, Macmillan, New York, 2008.
51. S. M. A. Daraghma, S. Talebi and V. Periasamy, Eur. Phys. J. E: Soft Matter Biol. Phys., 2020, 43, 40.

---

Footnotes

† Electronic supplementary information (ESI) available: Chemicals and materials; sample preparation; NMR, CD and STM break junction measurements; theoretical calculations; STM break junction results for DNA chains with one anchoring group. See DOI: https://doi.org/10.1039/d2tc01219g

‡ These authors contributed equally.

§ Present address: Department of Physical and Theoretical Chemistry, Faculty of Natural Sciences, Comenius University in Bratislava, Mlynská dolina, Ilkovičova 6, 84215 Bratislava, Slovakia.

¶ Present address: Department of Physical Chemistry, Faculty of Science, Palacký University Olomouc, tr. 17. listopadu 1192/12, 771 46 Olomouc, Czech Republic.

---