Open Access Article
Open Access ArticleHigh-pressure synthesis, spin-glass behaviour, and magnetocaloric effects in FexTi2S4 heideite sulphides†
R. S.
Silva Jr
 ab,
J.
Gainza
ab,
J.
Gainza
 a,
J. E.
Rodrigues
a,
J. E.
Rodrigues
 ac,
L.
Martínez
ac,
L.
Martínez
 a,
E.
Céspedes
a,
E.
Céspedes
 a,
N. M.
Nemes
a,
N. M.
Nemes
 ad,
J. L.
Martínez
ad,
J. L.
Martínez
 a and
J. A.
Alonso
a and
J. A.
Alonso
 *a
*a
aInstituto de Ciencia de Materiales de Madrid (ICMM), CSIC, E-28049 Madrid, Spain. E-mail: ja.alonso@icmm.csic.es
bDepartment of Physics, Federal University of Sergipe, 49100-000, São Cristóvão, SE, Brazil
cEuropean Synchrotron Radiation Facility (ESRF), 71 Avenue des Martyrs, 38000 Grenoble, France
dDepartamento de Física de Materiales, Universidad Complutense de Madrid, E-28040 Madrid, Spain
First published on 27th September 2022
Abstract
Intercalation compounds based on layered TiS2 sulphides are gaining much attention, since the incorporation of transition metals often dramatically change the physical properties and unlocks new intriguing phenomena. Here, we report a rapid high-pressure preparation method under 3.5 GPa at moderate temperatures for the synthesis of FexTi2S4 polycrystalline materials, starting from TiS2 and Fe metals. Three different compositions with x = 0.24, 0.32, and 0.42 have been stabilized at decreasing temperatures in the range of 800–900 °C; at room temperature, the crystallographic features have been probed by a neutron powder diffraction (NPD) experiment for the x = 0.42 sample. All the compounds crystallize in a Heideite-type phase with space group C12/m1; the structure consists of layers of [TiS6] octahedra sharing edges with Fe atoms located in between the layers, also in octahedral coordination. The NPD study unveils a discrete Fe/Ti inversion (<6%) at the TiS2 layers. The surface chemistry from XPS at Fe 2p and Ti 2p core levels revealed the presence of Fe2+ in all samples, whereas the Ti main contribution mainly arises from the Ti3+ state, with a smaller contribution of Ti2+ and Ti4+ states. The magnetic properties stemming from Fe2+ and Ti3+ spins offer a complex scenario with antiferromagnetic interactions, characterized by a strongly negative Weiss constant (e.g. θW = −398 K for x = 0.42), predominant for the Fe-rich phase Fe0.42Ti2S4, combined with ferromagnetic-like interactions as x decreases (e.g. θW = 204 K for x = 0.24), leading to spin–glass or cluster–glass behaviours. The study of the magnetocaloric effect yields relative cooling power (RCP) values at a 7 T of 135.3, 124.5, and 96.0 J kg−1 for the x = 0.24, 0.32 and 0.42 samples, respectively, better than other transition-metal sulphides already reported in the literature, with a temperature stability that is desirable for an ideal Ericson refrigeration cycle.
1. Introduction
Intercalation sulphides with the general formula Mx2+B3+S22− may accommodate different 3d transition metal elements, including M2+ = Ni, Co, Fe, and Cu and B3+ = V, Ti, and Cr, which attract much attention for technological applications due to their enhanced electrical conductivity and richer redox chemistry when compared to the traditional binary metal disulphides (BS2).1 The M2+ atom insertion into BS2 layers results in new bulk MxBS2 materials, driving physical properties such as magnetoelectric coupling, colossal magnetocapacitive effects or magnetocaloric effects.2–4 Such a rich scenario opens opportunities for designing new promising materials with high functionality for different applications, such as electrochemical energy storage conversion,5 electrocatalysis,6 thermoelectric materials,7 and so on.Interestingly, the physical properties of MxTiS2 (x < 1) intercalated disulphides diverges from those of the TiS2 host matrix due to the “host–guest” and “guest–guest” interactions.8 Normally, the intercalated 3d metal atoms partially occupy octahedral interstices among the layers. Depending on their concentration, both vacancy ordering and superstructure formation,8,9 as well as the spin-glass or cluster-glass magnetic states and long-range magnetic ordering,10,11 can arise from the metal intercalation. For instance, different magnetic states were observed in 3d metal intercalates, such as (Cr, Co, Ni, or Fe)xTiS2.10 Generally, the site-occupation disorder of the transition-metal atoms, frustrations, and local competition between exchange interactions are suggested as main factors affecting the observed magnetic properties.11,12 Apparently, the frustrations are responsible for the large dispreads of the magnetic ordering temperatures observed in this class of compounds with different concentrations. An important case encompasses the FexTiS2 family, where the magnetic ordering temperatures in the range of 70–160 K were already reported.11,13 Moreover, the intercalation can lead to the hybridization of their Fe 3d states with the band states of the TiS2 matrix,10 which is accompanied by a distortion of the crystal lattice, thus affecting the electrical conductivity and effective magnetic moment.8
In particular, FeTi2S4 was described to exhibit a monoclinic 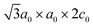 superstructure of the M3X4 type (space group: I12/m1), where a0 and c0 are the hexagonal unit-cell parameters,11,14 and it can be considered as a superstructure of the parent compound TiS2 (space group: P3m1).14 Previous reports showed that this compound may present other superstructures depending on the Fe(x)-content. Selezneva et al.11 reported changes in the unit-cell volume (∼57 Å3 to ∼59 Å3) of the crystal structure, and different space groups (P3m1, C12/m1, and P31c for x < 0.5, and I12/m1 for x > 0.5) were described with increasing Fe-content in FexTiS2. For lower Fe concentrations (x < 0.5), the Fe atoms can occupy octahedral site positions between S–Ti–S tri-layers randomly, while at higher Fe concentrations (x = 0.5) some mixing between Fe and Ti on the neighbouring cationic layers may occur; an Fe atom can either occupy positions within the Ti layers, or the Ti atoms can be sandwiched along with Fe atoms.11 Consequently, such variations have a strong influence on the observed magnetic behaviour.
superstructure of the M3X4 type (space group: I12/m1), where a0 and c0 are the hexagonal unit-cell parameters,11,14 and it can be considered as a superstructure of the parent compound TiS2 (space group: P3m1).14 Previous reports showed that this compound may present other superstructures depending on the Fe(x)-content. Selezneva et al.11 reported changes in the unit-cell volume (∼57 Å3 to ∼59 Å3) of the crystal structure, and different space groups (P3m1, C12/m1, and P31c for x < 0.5, and I12/m1 for x > 0.5) were described with increasing Fe-content in FexTiS2. For lower Fe concentrations (x < 0.5), the Fe atoms can occupy octahedral site positions between S–Ti–S tri-layers randomly, while at higher Fe concentrations (x = 0.5) some mixing between Fe and Ti on the neighbouring cationic layers may occur; an Fe atom can either occupy positions within the Ti layers, or the Ti atoms can be sandwiched along with Fe atoms.11 Consequently, such variations have a strong influence on the observed magnetic behaviour.
According to Baranov et al.,14 FeTi2S4(or Fe0.5TiS2) with the monoclinic crystal structure exhibits an antiferromagnetic (AFM) ground state below TN = 140 K. Besides, additional heat treatments do not substantially affect the AFM state, but they change the order–disorder degree of Fe atoms and vacancies. On the other hand, the application of a magnetic field below TN induces a metamagnetic phase transition to the ferromagnetic (FM) state, as well as a large magnetoresistance effect (i.e. |Δρ/ρ| up to 27%). This metamagnetic transition to the FM state is stable unless the temperature is increased well above TN. For a lower Fe concentration (e.g. Fe0.25TiS2), a greater magnetoresistance effect (|Δρ/ρ| up to 35%) has been reported,15 which is also attributed to the phase transition from the AFM to the FM state. Selezneva et al.15 also reported for Fe0.25TiS2 a magnetic transition at around 50 K, which could be considered a sign of AFM order. However, the field-cooled (FC) regime looks rather unusual for AFM ordered compounds, where the significant increase in magnetization upon cooling in the vicinity of the critical temperature (TC ∼ 80 K), as well as the large difference between the zero-field cooled (ZFC) and FC curves, can most likely be considered characteristics of a strongly anisotropic FM order with large coercivity. Nevertheless, a coercive field very close to zero is frequently associated with ferrimagnetic (FiM) or FM orderings,7 which can be visualized through the positive paramagnetic Curie temperature, as in the case of Fe0.5TiS2 with θ = 127 K.14 However, a detailed neutron diffraction study rules out the possibility of a FM ground state.16 In addition, a clear dependence of the magnetic susceptibility is observed with the variation of the Fe-content.17 Therefore, the magnetic transition at 50 K can be explained considering different magnetic exchange interactions coexisting and/or competing in the system, as well as by the charge transfer between Fe and Ti.18
Sulphides that do not present majority FM long-range ordering can also show the magnetocaloric effect (MCE); however, surprisingly, only a few works explore the MCE of these compounds. For instance, FeCr2S4 presents a reversible MCE around a FiM transition (TN = 167 K) with maximum magnetic entropy change ΔSmaxM = 3.72 J kg−1 K−1 for ΔH = 50 kOe, along with a cusp-like anomaly at around 70 K.4 Recently, Delacotte et al.19 showed a larger MCE for NaGdS2 that presents very weak local AFM interactions because of its negligible exchange interactions. Such a compound exhibits a ΔSmaxM of up to 54 J kg−1 K−1 at 2.5 K for μ0ΔH = 5 T, being then suggested as a promising material for cryogenic magnetic cooling. Some sulphides with FM ordering, however, can present different values of ΔSmaxM, including CdCr2S4 (7.04 J kg−1 K−1), Cd0.7Fe0.3Cr2S4 (5.4 J kg−1 K−1), and Co0.2Cu0.8Cr2S4 (2.05 J kg−1 K−1),2,20,21 which may be related to a variation of the spontaneous magnetization and Curie temperature with doping. Particularly, the EuS single phase powder also presents an FM order with TC = 16.5 K and ΔSmaxM ≈ 6.3 J kg−1 K−1 at 5 T, which corresponds to 36% of the maximum magnetic entropy R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) with S = 7/2.22 On the other hand, D. X. Li et al.23 reports a ΔSmaxM ≈ 37 J kg−1 K−1 for the EuS single crystal with a TC ≈ 18 K. Additionally, the presence of unusual properties such as colossal electroresistance, giant blue-shift of the absorption edge in passing through the FM phase transition, and anomalous expansion coefficient at low temperatures can favour a large magnetic entropy change over a wide temperature range.24 Therefore, this scenario highlights the unflagging search for new systems with better magnetocaloric performances for practical technology and encourages exploration of the underlying physics concerning the MCE. As far as we know, few works have explored the MCE in disulphides; moreover, none of them was devoted to the FexTi2S4 system.
ln(2S + 1) with S = 7/2.22 On the other hand, D. X. Li et al.23 reports a ΔSmaxM ≈ 37 J kg−1 K−1 for the EuS single crystal with a TC ≈ 18 K. Additionally, the presence of unusual properties such as colossal electroresistance, giant blue-shift of the absorption edge in passing through the FM phase transition, and anomalous expansion coefficient at low temperatures can favour a large magnetic entropy change over a wide temperature range.24 Therefore, this scenario highlights the unflagging search for new systems with better magnetocaloric performances for practical technology and encourages exploration of the underlying physics concerning the MCE. As far as we know, few works have explored the MCE in disulphides; moreover, none of them was devoted to the FexTi2S4 system.
Most discrepancies observed in the physical properties of the intercalated disulphides could have originated from the different sample preparation methods and conditions. The magnetization trends are observed to be dependent on the preparation procedures, and annealing, and cooling conditions.11 Therefore, interesting preparation strategies have been developed for improving these materials, which normally involve long annealing treatments in sealed quartz capsules16 and/or modified heat-up methods.25 Different synthesis procedures can lead to different stoichiometries, affecting structural defects, order/disorder and vacancies, which modify the final material properties. Particularly, the high-pressure methods to synthesize new compounds have some advantages over the conventional ambient pressure methods, including stabilization of metastable phases with unusual valence states and enhanced densification.26 In this paper, we report on a straightforward high-pressure synthesis procedure and a profound investigation of the crystallographic structure by both neutron and X-ray diffraction techniques. We have performed an X-ray photoelectron spectroscopy (XPS) analysis, and also the magnetic and magnetocaloric properties of some members of the FexTi2S4 Heideite family are determined, showing some appealing results concerning MCE for some compositions.
The synthesis procedure proposed here can be qualified as “straightforward” with respect to the standard methods for preparing transition-metal sulphides, usually involving long thermal treatments (several days, several times) under SH2 currents, many times yielding mixtures of several phases. The synthesis conditions can be reached in a modest piston-cylinder press. Additionally, simple temperature tuning under the same experimental conditions (pressure, time) was utilized to prepare 3 different sulphides with diverse chemical compositions and properties.
2. Experimental methods
2.1. High-pressure synthesis
We have successfully synthesized polycrystalline samples of FexTi2S4 in a single step by thermal treatment under high-pressure conditions. Stoichiometric amounts of 0.5Fe + 2TiS2 were inserted into a Nb capsule (5 mm in diameter, 15 mm in length), sealed, and placed in a cylindrical graphite heater. The reaction was carried out in a piston-cylinder press (Rockland Research Co) under a hydrostatic pressure of 3.5 GPa at 800, 850 or 900 °C for 1 h. Then, the materials were quenched to room temperature and the pressure was subsequently released. Depending on the temperature, different amounts of Fe were incorporated into the FexTi2S4 structure. The reaction involves the oxidation of the Fe metal to Fe2+ and the reduction of Ti4+ to Ti3+ within the sealed capsule, avoiding the volatilization or oxidation of sulphur.2.2. Structural characterization
Initial phase characterization was carried out using X-ray diffraction (XRD) on a Bruker-AXS D8 diffractometer (40 kV, 30 mA) in Bragg–Brentano reflection geometry with Cu Kα radiation (λ = 1.5418 Å). The NPD pattern for a selected specimen was collected at the HRPT diffractometer of the SINQ spallation source (PSI, Paul Scherrer Institute, Villigen, Switzerland) with a wavelength of 1.494 Å at room temperature. The sample was contained in a vanadium cylinder of 6 mm diameter, rotating during data collection, and enclosed in a vacuum chamber. The data acquisition lasted for 2 h.Both laboratory XRD and NPD data were analysed by Rietveld refinement using the FullProf program.27 The peak shape was described using a pseudo-Voigt function. The background was interpolated between areas devoid of reflections. The full refinement included the following parameters: scale factors, zero-point error, background coefficients, asymmetry correction factors, lattice parameters, atomic positions, occupancy factors of Fe, and isotropic displacement parameters, as well the occupancies of Fe at Ti sites. For the neutron refinements, the coherent scattering lengths for Fe, Ti and S were 9.45, −3.438 and 2.847 fm, respectively, enabling a good scattering contrast to define the Fe and Ti site occupancy.
2.3. Surface chemistry analysis
The powders of different compositions were glued to a double sided carbon tape. The XPS chamber has a base pressure of 10−10 mbar and is equipped with a hemispherical electron energy analyzer (SPECS Phoibos 100 spectrometer) and an Al Kα (1486.29 eV) X-ray source. The angle between the hemispherical analyzer and the plane of the surface was kept at 60°. Wide scan spectra were recorded using an energy step of 0.5 eV and a pass-energy of 40 eV while specific core levels spectra (Fe 2p, Ti 2p and S 2p) were recorded using an energy step of 0.1 eV and a pass-energy of 20 eV. Data processing was performed using CasaXPS software (Casa software Ltd, Cheshire, UK). The absolute binding energies (BE) of the photoelectron spectra were determined by referencing the Ti 2p at 457.1 eV.28 The contributions of the Al Kα satellite lines were subtracted and the spectra were normalized to the maximum intensity for easier comparison.2.4. Magnetic measurements
The magnetic properties were measured with a SQUID magnetometer (MPMS-3), from Quantum Design (San Diego, USA) in the temperature range from 1.8 up to 350 K and a range of magnetic fields up to 7 T. The AC susceptibility was measured in the SQUID magnetometer in the frequency range from 0.1 Hz up to 1 kHz, with an oscillatory field with an amplitude of 1 Oe.3. Results and discussion
3.1. Crystalline structure
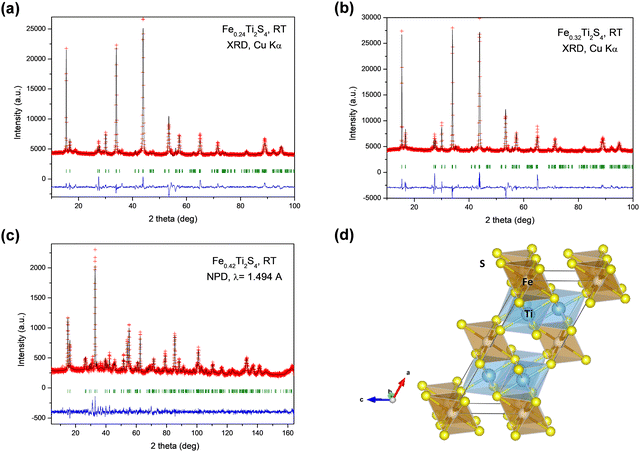
The obtained products were identified as specimens with a Heideite crystal structure, typified for CrNb2S4. Minor amounts of FeS and FeS2 were also identified in the XRD patterns. The three materials prepared under high-pressure conditions at slightly different temperatures yielded distinct crystallographic features and, therefore, physical properties, mainly stemming from the incorporated Fe contents into the TiS2 layers. The crystal structure was refined from NPD data for the product synthesized at T = 800 °C, whereas XRD data were employed for the compounds prepared at 850 °C and 900 °C. The crystal structure of FeTi2S429 was taken as the starting model, defined in the monoclinic C12/m1 space group (No. 12). Fe atoms are located at the 2a (0, 0, 0) sites, while Ti and the two types of sulphur atoms S1 and S2 are located at 4i (x, 0, z) Wyckoff sites. The Fe occupancy at 2a sites was refined, allowing the evaluation of x in FexTi2S4 Heideite-type compounds. On the other hand, neutron diffraction is a suitable tool to assess the possible partial occupancy of Fe at Ti positions, given their contrasting scattering lengths (strongly positive for Fe and negative for Ti). After the refinement from NPD data, it resulted in a slight occupation (less than 6%) of Fe at 4i Ti sites. Fig. 1a–c illustrates the goodness of the fits for the three compounds, either from XRD data or NPD data. Table 1 summarizes the main crystallographic features for the three materials, including unit-cell parameters and refined stoichiometry. Table 2 lists the structural parameters obtained from NPD.| Refined x | Synthesis T (°C) | a (Å) | b (Å) | c (Å) | β (°) | V (Å3) | Ref. |
|---|---|---|---|---|---|---|---|
| 0.24(1) | 900 | 12.905(2) | 3.4275(4) | 5.945(1) | 117.29(2) | 233.71(8) | This work |
| 0.32(1) | 850 | 12.903(2) | 3.4283(4) | 5.958(1) | 117.19(1) | 234.44(6) | This work |
| 0.42(1) | 800 | 12.924(1) | 3.4233(4) | 5.948(1) | 117.18(1) | 234.09(4) | This work |
| 1 | — | 12.9428 | 3.4370 | 5.9530 | 117.355 | 235.20 | 29 |
| Monoclinic C12/m1 | Crystal data | |||||
|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | β (°) | V (Å3) | Z | |
| T = 295 K | 12.9242(12) | 3.4233(4) | 5.9477(6) | 117.176(9) | 234.09(4) | 2 |
| R p (%) | R wp (%) | R exp (%) | R Bragg (%) | χ 2 | ||
|---|---|---|---|---|---|---|
| Reliability factors | 5.35 | 6.91 | 5.52 | 6.51 | 1.59 |
| Atom | Fractional atomic coordinates and isotropic displacement parameters (Å2) | |||||
|---|---|---|---|---|---|---|
| Wyckoff site | x | y | z | U iso (Å2) | Occ. (<1) | |
| Fe1 | 2a | 0.00000 | 0.00000 | 0.00000 | 0.0101(9) | 0.37(1) |
| Fe2 | 4i | 0.7462(6) | 0.00000 | 0.745(3) | 0.0100(16) | 0.056(6) |
| Ti | 4i | 0.7462(6) | 0.00000 | 0.745(3) | 0.0100(16) | 0.944(6) |
| S1 | 4i | 0.6258(7) | 0.00000 | 0.9558(18) | 0.0088(15) | 1.000 |
| S2 | 4i | 0.1207(7) | 0.00000 | 0.4508(19) | 0.017(2) | 1.000 |
Fig. 1d displays a view of the Heideite crystal structure for the x = 0.24 compound. The crystal structure consists of layers of [TiS6] octahedra sharing edges, intercalated with FeS6 octahedra, the layers being parallel to the bc plane. In fact, Takahashi et al.29 defined this Heideite structure as a type of filled TiS2 layered structure containing extra Fe between the layers of [TiS6] octahedra. The a unit-cell parameter and volume are sensitive to the degree of filling of the Fe layer, i.e. the x contents of the FexTi2S4 stoichiometry, spanning from a = 12.9428 Å, V = 235.20 Å3, for bibliographic FeTi2S429 with x = 1.0, to a = 12.905(2) Å, V = 233.71(8) Å3 for x = 0.24 compound (see in Table 1). Hereafter, we will refer to the three materials by its x Fe contents.
3.2. XPS analysis
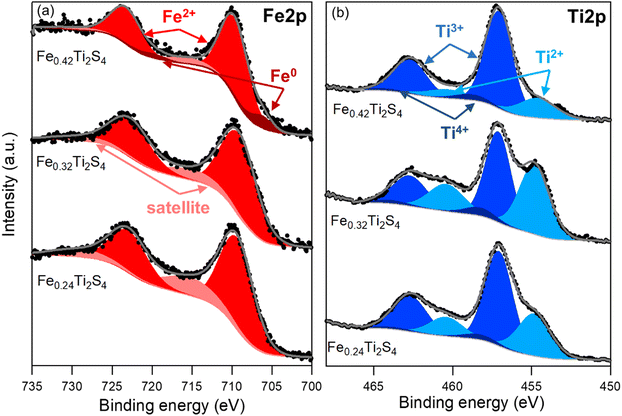
A detailed analysis of the Fe 2p and Ti 2p core level peaks is presented in Fig. 2 for the samples with x = 0.24, 0.32 and 0.42. For simplicity, the BE reported for all peaks corresponds to the 2p3/2 emission. The analysis of the Fe 2p core level peak (Fig. 2a) evidenced that iron is present in the samples in the form of Fe2+, as revealed by the peak at 709.7 ± 0.2 eV for Fe 2p3/2.30 The smaller contribution at higher BE corresponds to the characteristic satellite of this oxidation state. For the sample with x = 0.42, there is a 9% contribution of the metallic component at 706.4 ± 0.2 eV.The analysis of the Ti 2p core level peak (Fig. 2b) revealed that titanium is present within the samples in three different oxidation states. The fitting was carried out according to ref. 28. The main contribution in the three samples arises from the Ti3+ oxidation state at a BE of 457.1 ± 0.1 eV, followed by the Ti2+ state at lower BE and, to a much lower extent, the Ti4+ could also be detected at higher BE. The proportion of each oxidation state is detailed in Table S1 (ESI†).
Table S1 (ESI†) presents the composition of the samples extracted from the analysis of the wide energy range scans. Apart from iron, titanium and sulphur, the samples also presented carbon and oxygen, as expected from ex situ analysis and a small proportion of nitrogen in the samples with x = 0.32 and 0.42. In this table, the percentage of each oxidation state found in the analysis of the Ti 2p core level spectra is also reported.
3.3. Magnetic properties
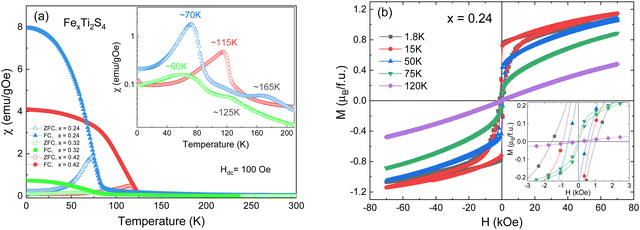
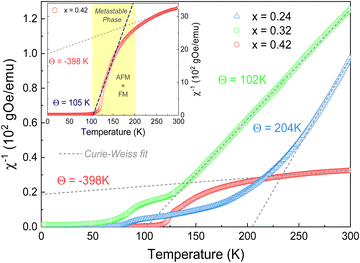
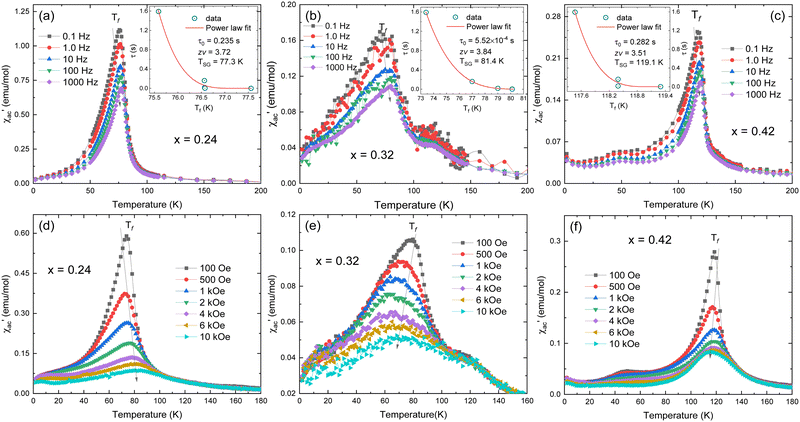
Fig. 3a shows the temperature dependence of the magnetic susceptibility (M/H) measured at Hdc = 100 Oe under zero-field cooling (ZFC) and field-cooling (FC) conditions, for the different FexTi2S4 samples (x = 0.24, 0.32 and 0.42). The temperature of the magnetic transition was determined by taking the minimum in the ZFC mode curve derivative (dM/dT) as a function of temperature (T) (not shown here). The temperatures were found to be around 82, 74, and 114 K for the x = 0.24, 0.32 and 0.42 samples, respectively. The inset in Fig. 3a shows the ZFC curves with pronounced peaks at ∼60, 70 and 115 K (x = 0.24, 0.32 and 0.42 samples, respectively). Similar results were reported by Selezneva et al.15 for Fe0.25TiS2 at ∼50 K, the authors considered that these peaks are a sign of an AFM order. The FC regime looks rather unusual for AFM ordered compounds, such that a significant increase in the magnetization upon cooling at the critical temperature, as well as the large difference between the ZFC and FC curves, can most likely be considered as features of the strongly anisotropic FM. As mentioned, minor impurities of iron sulfide were identified from XRD data, which show temperature-independent susceptibility, too weak to interfere with the properties arising from the main phase.Fig. 3b displays the isothermal magnetization (M–H) measurements collected at different temperatures (1.8 up to 120 K) for the x = 0.24 sample, revealing that, with a decrease in the temperature (<75 K), the coercive field is increased (as can be seen in the inset of Fig. 3b) and tends to exhibit a paramagnetic (PM) behaviour at T > 75 K. Such a trend resembles more FiM or FM ordering.11 This is additionally supported by the fits to the Curie–Weiss (C–W) law χ−1 = T − Θ/C, where C is the Curie constant, Θ is the Weiss temperature, and T is the temperature,11 as represented in Fig. 4. Here, a positive paramagnetic Curie temperature Θ = 204 K was obtained for x = 0.24 through the reciprocal susceptibility above the magnetic ordering temperature. A similar result was found by Baranov et al.14 for Fe0.5TiS2 with Θ = 127 K, being indicative of a dominant FM exchange. Interestingly, the x = 0.24 sample exhibits a much higher Θ value when compared to those previously reported (Θ = 27 and 57 K).15 Such a discrepancy can occur due to exchange FM (Fe–S–Ti) and AFM (Fe–S–Fe, Ti–S–Ti) interactions coexisting and competing within the crystal structure.18 Additionally, a charge transfer between Fe and Ti is not excluded. The x = 0.42 sample has a peak at approximately 115 K (inset of Fig. 3a), which coincides with the magnetic transition temperature at 114 K (by dM/dT). Such a result describes the Néel temperature (TN) of AFM ordering, which is confirmed by the negative value of Θ = −398 K, as shown in Fig. 4. This result diverges from that observed by N. V. Selezneva et al.11 for Fe0.45TiS2 (Θ = 100 K). However, the authors showed that for the range of 0.33 < x < 0.5 of Fe concentration, a heterogeneous magnetic state is possible with coexisting AFM and FM phases.11 Thus, we believe that in our sample Fe0.42Ti2S4 a majority AFM order is observed (which explains the Θ negative value), while a metastable phase (AFM + FM) appears in the temperature range 100 K < T < 200 K, with Θ = 105 K (see inset of Fig. 4), which corroborates previous results.11,14 Also, in order to check the consistency, we analyzed the inverse of the real part of the ac magnetic susceptibility, measured at f = 1 kHz with an amplitude of 1 Oe at temperatures ranging from 150 K to 300 K, 320 K and 355 K, for the x = 0.24, 0.32, and x = 0.42 samples, respectively (see Fig. S1 in the ESI†). In the three cases, the Θ values obtained from the real part of the ac magnetic susceptibility are very close to those originally obtained from dc magnetic susceptibility.
The effective magnetic moments (μeff) were obtained from the fitting from the Curie constant as 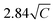 .31 The estimated experimental values were found to be 2.74, 3.39, and 5.23 μB f.u.−1 for the x = 0.24, 0.32, and 0.42 samples, respectively. The theoretical values for FexTi2S4 are 2.67, 3.09 and 3.53 μB f.u.−1, respectively, considering spin-only magnetic moments for Fe2+ and Ti3+ ions when μeff = [xμ(Fe2+)2 + 2xμ(Ti3+)2]1/2. Note that the Ti3+ contents is 2x per formula. The S-values for Fe2+ and Ti3+ cations used in this calculation are S = 2 (Fe2+) and S = 1/2 (Ti3+), yielding 4.9 and 1.73 μB, respectively. The effective magnetic moment for x = 0.24 is close to that expected, but μeff becomes progressively higher than expected for x = 0.32 and 0.42, and this is probably due to the increasing presence of AFM interactions even in the high-temperature region, breaching the conditions for a C–W fit. On the other hand, the ZFC and FC magnetization curves exhibited a large irreversibility, especially at T < 130 K (see in Fig. 3a), being most pronounced for the x = 0.24 sample. Such a trend can be due to the magnetic frustration or canting of the spins that allows the presence of weak FM/AFM components to the magnetic moment in an AFM/FM matrix.
.31 The estimated experimental values were found to be 2.74, 3.39, and 5.23 μB f.u.−1 for the x = 0.24, 0.32, and 0.42 samples, respectively. The theoretical values for FexTi2S4 are 2.67, 3.09 and 3.53 μB f.u.−1, respectively, considering spin-only magnetic moments for Fe2+ and Ti3+ ions when μeff = [xμ(Fe2+)2 + 2xμ(Ti3+)2]1/2. Note that the Ti3+ contents is 2x per formula. The S-values for Fe2+ and Ti3+ cations used in this calculation are S = 2 (Fe2+) and S = 1/2 (Ti3+), yielding 4.9 and 1.73 μB, respectively. The effective magnetic moment for x = 0.24 is close to that expected, but μeff becomes progressively higher than expected for x = 0.32 and 0.42, and this is probably due to the increasing presence of AFM interactions even in the high-temperature region, breaching the conditions for a C–W fit. On the other hand, the ZFC and FC magnetization curves exhibited a large irreversibility, especially at T < 130 K (see in Fig. 3a), being most pronounced for the x = 0.24 sample. Such a trend can be due to the magnetic frustration or canting of the spins that allows the presence of weak FM/AFM components to the magnetic moment in an AFM/FM matrix.
In order to further confirm the multi-magnetic phase state in iron disulphide samples, as well as the Spin–Glass (SG) behaviour and its dynamics, magnetic AC susceptibility measurements have been carried out in the temperature range of 1.8 to 300 K, with an AC field of Hac = 1.0 Oe and different frequencies (0.1 Hz to 1 kHz). The real part of magnetic AC susceptibility 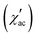 is shown in Fig. 5a–c.
is shown in Fig. 5a–c.
As observed in Fig. 5, the peak of 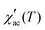 exhibits frequency-dependence: the peak position shifts to higher temperatures when AC frequency increases, while the peak magnitude decreases. This is a typical behaviour reported for the SG systems.32,33 For further clarification, the relative shift (k) in the freezing temperature can be used to describe the magnetic order of the system, which is denoted as
exhibits frequency-dependence: the peak position shifts to higher temperatures when AC frequency increases, while the peak magnitude decreases. This is a typical behaviour reported for the SG systems.32,33 For further clarification, the relative shift (k) in the freezing temperature can be used to describe the magnetic order of the system, which is denoted as 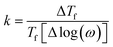 ,34 where ΔTf is maximum in the freezing temperature. We found k = 0.0085, 0.0229, and 0.0077 for the x = 0.24, 0.32 and 0.42 samples, respectively. The calculated value of k for x = 0.24 and 0.42 samples lies typically in the observed range for canonical SG systems.35 In the case of the x = 0.32 sample, the value is approximately one order of magnitude higher than that for canonical SG systems, but one order lower than that observed in typical superparamagnetic systems, corresponding to that generally observed in spin cluster-glass materials.36 Interestingly, the x = 0.42 sample that was previously described to exhibit AFM interactions (with very negative Weiss constant) also displays a SG behaviour near TN. Although unusual, this behaviour has been reported for other materials.33,35,37
,34 where ΔTf is maximum in the freezing temperature. We found k = 0.0085, 0.0229, and 0.0077 for the x = 0.24, 0.32 and 0.42 samples, respectively. The calculated value of k for x = 0.24 and 0.42 samples lies typically in the observed range for canonical SG systems.35 In the case of the x = 0.32 sample, the value is approximately one order of magnitude higher than that for canonical SG systems, but one order lower than that observed in typical superparamagnetic systems, corresponding to that generally observed in spin cluster-glass materials.36 Interestingly, the x = 0.42 sample that was previously described to exhibit AFM interactions (with very negative Weiss constant) also displays a SG behaviour near TN. Although unusual, this behaviour has been reported for other materials.33,35,37
Typically, the relaxation time τ around the transition temperature in a SG system is described by the following power-law:
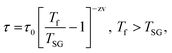 | (1) |
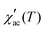 .35 The τ vs. Tf plot along with the fit to the critical power-law is shown in insets of Fig. 4a–c. In a conventional SG system, zv ∼ 4–13 and τ0 ∼ 10−10–10−13 s.38 Here, the best-fitting parameters were estimated to be TSG = 77.3 K, zv = 3.72, and τ0 = 0.235 s; TSG = 81.4 K, zv = 3.84, and τ0 = 5.52 × 10−4 s; and TSG = 119.1 K, zv = 3.51, and τ0 = 0.282, for the x = 0.24, 0.32 and 0.42 samples, respectively. The obtained higher value of τ0 and lower value of zv imply a co-operative slower spin flipping, attributed to the presence of randomly oriented FM clusters (clustered spin-glass),39 which is much more evident for x = 0.24 and 0.32 samples. TSG values obtained are near the transition temperatures of FexTi2S4 samples. The SG/CG behaviour is probably due to the competing magnetic interactions between Fe2+ and Ti3+ ions. Finally, no apparent frequency dispersion at any other temperature range is shown for the x = 0.24 sample. However, we note one complementary feature in
.35 The τ vs. Tf plot along with the fit to the critical power-law is shown in insets of Fig. 4a–c. In a conventional SG system, zv ∼ 4–13 and τ0 ∼ 10−10–10−13 s.38 Here, the best-fitting parameters were estimated to be TSG = 77.3 K, zv = 3.72, and τ0 = 0.235 s; TSG = 81.4 K, zv = 3.84, and τ0 = 5.52 × 10−4 s; and TSG = 119.1 K, zv = 3.51, and τ0 = 0.282, for the x = 0.24, 0.32 and 0.42 samples, respectively. The obtained higher value of τ0 and lower value of zv imply a co-operative slower spin flipping, attributed to the presence of randomly oriented FM clusters (clustered spin-glass),39 which is much more evident for x = 0.24 and 0.32 samples. TSG values obtained are near the transition temperatures of FexTi2S4 samples. The SG/CG behaviour is probably due to the competing magnetic interactions between Fe2+ and Ti3+ ions. Finally, no apparent frequency dispersion at any other temperature range is shown for the x = 0.24 sample. However, we note one complementary feature in 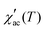 [frequency and field varying] around ∼120 K and ∼50 K for the x = 0.32 and 0.42 samples, respectively, indicating an absence of any re-entrant SG behaviour.40
[frequency and field varying] around ∼120 K and ∼50 K for the x = 0.32 and 0.42 samples, respectively, indicating an absence of any re-entrant SG behaviour.40
Fig. 5d–f display the real part of AC susceptibility 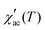 at different DC magnetic fields Hdc (0.01–10 kOe) under Hac = 1.0 Oe and fix frequency f = 1 kHz, in the temperature range from 1.8 to 180 K, for the FexTi2S4 samples.
at different DC magnetic fields Hdc (0.01–10 kOe) under Hac = 1.0 Oe and fix frequency f = 1 kHz, in the temperature range from 1.8 to 180 K, for the FexTi2S4 samples. 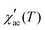 shows a field-dependent behaviour at ∼77, ∼80, and ∼120 K for the x = 0.24, 0.32 and 0.42 samples, respectively. This behaviour is similar to that observed for frequency-dependent
shows a field-dependent behaviour at ∼77, ∼80, and ∼120 K for the x = 0.24, 0.32 and 0.42 samples, respectively. This behaviour is similar to that observed for frequency-dependent 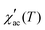 . Clearly, the peaks exhibit a drastic decrease in the magnitude of Tf with increasing Hdc and the shape becomes more rounded for all samples. Moreover, a shift in Tf towards lower temperatures is observed for the x = 0.32 and x = 0.42 samples. Such a behaviour is well known for a number of SG systems, which can be attributed to a random distribution of magnetic clusters of different sizes and anisotropy fields or negative nonlinear susceptibility.10 On the other hand, for the x = 0.24 sample the Tf peak temperature shifts to the higher temperature side with increasing Hdc field, which may indicate a greater FM nature in this sample and, consequently, a more AFM nature for the x = 0.42 sample. This is supported once again by the magnetization curves (see in Fig. 3) as well as by the values of the experimental Weiss temperatures (see in Fig. 4).
. Clearly, the peaks exhibit a drastic decrease in the magnitude of Tf with increasing Hdc and the shape becomes more rounded for all samples. Moreover, a shift in Tf towards lower temperatures is observed for the x = 0.32 and x = 0.42 samples. Such a behaviour is well known for a number of SG systems, which can be attributed to a random distribution of magnetic clusters of different sizes and anisotropy fields or negative nonlinear susceptibility.10 On the other hand, for the x = 0.24 sample the Tf peak temperature shifts to the higher temperature side with increasing Hdc field, which may indicate a greater FM nature in this sample and, consequently, a more AFM nature for the x = 0.42 sample. This is supported once again by the magnetization curves (see in Fig. 3) as well as by the values of the experimental Weiss temperatures (see in Fig. 4).
3.4. Magnetocaloric effect
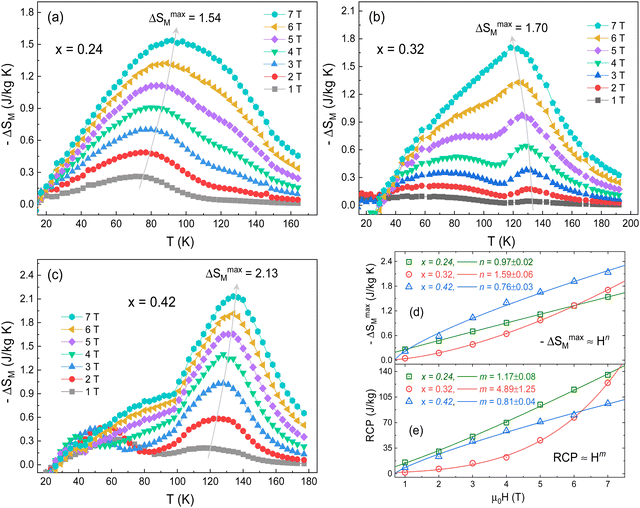
The MCE study provides a powerful tool for investigating the magnetic transitions. To study the MCE in FexTi2S4 samples, a series of isothermal magnetization curves (M–H) were recorded in a large temperature range of 8 < T < 195 K with temperature interval ΔT = 3 K under fields up to 7 T, as shown in Fig. 6. The magnetization rapidly increases at low field values and at low temperatures, followed by a linear increase reaching a saturation tendency, being more evident for the x = 0.24 and x = 0.42 samples, see in Fig. 6a and c. Above TC and/or TN, the magnetization increases almost linearly in the scanning field range, ascribed to the PM ground state. The M–H isotherms have been transformed into Arrott plots (M2vs. H/M),41,42 which are widely referred to determine the phase transition order, as shown in Fig. 5b, d and f. According to the Banerjee criterion, the positive slope of the Arrott plots over the whole measuring temperature range indicates that the transition order is a second-order phase transition (SOPT).43,44 Such a result is consistent with that found for other similar materials.2,4,45 Furthermore, it indicates that samples present reversible magnetic entropy change due to the negligible thermal and magnetic hysteresis, which can increase the usability of these samples as a refrigerant material.46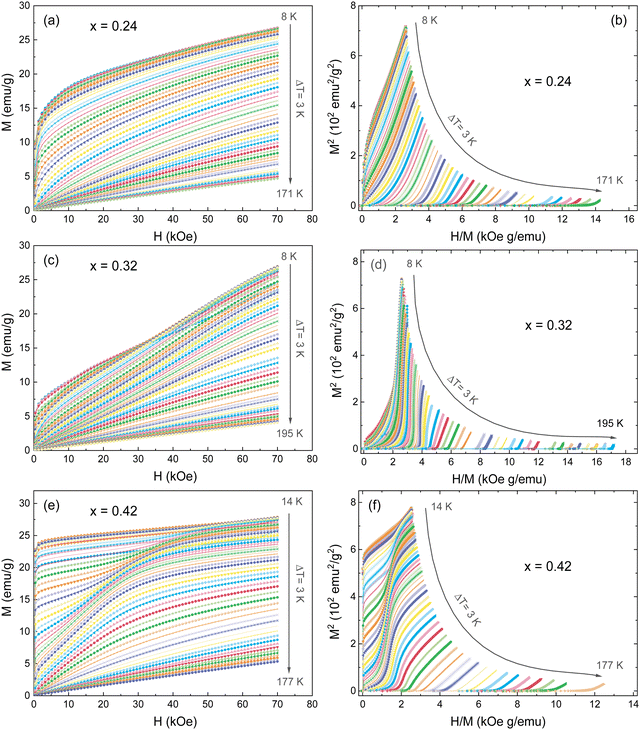 | ||
| Fig. 6 (a, c, e) Isotherms M–H measured at different temperatures from 8 to 195 K (ΔT = 3K), and (b, d, f) the Arrott plots (M2vs. H/M) for the FexTi2S4 samples. | ||
The magnetic entropy change (−ΔSM) for any magnetic material under a variation of the applied magnetic field from 0 to Hmax can be expressed as:47,48
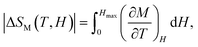 | (2) |
However, for magnetization measurements with a small discrete field and temperature intervals, ΔSM can be approximately calculated as:
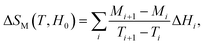 | (3) |
To further estimate the effectiveness of a magnetic material for application in the magnetic refrigeration industry, we have calculated the relative cooling power (RCP), which corresponds to the amount of heat that can be transferred between the cold and hot parts of the refrigerator in an ideal thermodynamic cycle, being an essential parameter for magnetic refrigerators.55 The RCP is expressed as RCP = |ΔSmaxM| × δTFWHM, where δTFWHM is full width at half maximum of −ΔSM(T) curves.56 The variation of RCP with the magnetic field near TC/TN is presented in Fig. 6e. Similar to ΔSmaxM, RCP follows a power law as RCP ≈ bHm, where b is the normalization constant and m is the power exponent. In this case, the obtained m values were 1.17 ± 0.08, 4.89 ± 1.25, and 0.81 ± 0.04, for the x = 0.24, 0.32 and 0.42 samples, respectively. For x = 0.24 and x = 0.42 samples, RCP shows an almost linear increasing trend with increasing ΔH. However, the m value of the x = 0.32 sample is very large, with a positive exponential trend. This is due to the change in the shape of the ΔSmaxM peak about TC/TN as the applied magnetic field increases. The RCP maximum value for a magnetic field change of 7 T was found to be 135.3, 124.5, and 96.0 J kg−1 for the x = 0.24, 0.32 and 0.42 samples, respectively. Particularly, at 5 T these values reach about 23% of that estimated in pure gadolinium (Gd).57 On the other hand, our RCP values are close or greater than those recently observed by Massoudi et al.52 for the Ni0.6Zn0.4Al0.5Fe1.5O4 spinel with RCP ≈ 70 J kg−1 (at 5T). Table 3 presents a comparison between the ΔSmaxM and RCP values of the FexTi2S4 samples and other reported spinels systems. Therefore, fundamental requirements such as the moderate value of the ΔSmaxM and cooling capacity (RCP), and the lack of thermal hysteresis are all satisfied in the studied FexTi2S4 sulphides. Therefore, these Heideite-type materials can be considered as promising candidates for magnetic refrigerants working in a wide temperature range, which is essential for an ideal Ericson refrigeration cycle.58
| Composition | Ref. | T C/TN (K) | ΔH (T) | −ΔSmaxM (J kg−1 K−1) | RCP (J kg−1) |
|---|---|---|---|---|---|
| Fe0.24Ti2S4 | This work | 82 | 0–7 | 1.54 | 135 |
| Fe0.32Ti2S4 | This work | 74 | 0–7 | 1.70 | 124 |
| Fe0.42Ti2S4 | This work | 114 | 0–7 | 2.13 | 96 |
| CdCr2S4 | 2 | 87 | 0–5 | 7.04 | 360 |
| Cd0.7Fe0.3Cr2S4 | 20 | 119 | 0–5 | 5.4 | — |
| FeCr2S4 | 4 | 167 | 0–5 | 3.72 | — |
| Co0.2Cu0.8Cr2S4 | 21 | 339 | 0–5 | 2.05 | — |
| Cd0.7Zn0.3Cr2S4 | 59 | 45 | 0–2 | 1.03 | 52 |
| α-Gd2S3 | 19 | 10 | 0–5 | 0.1 | — |
4. Conclusions
In summary, we have shown that a facile synthesis procedure to prepare intercalation sulphides derived from TiS2 by a straightforward high-pressure method is feasible. We have reported on the synthesis of three members of the FexTi2S4 family (x = 0.24, 0.32, and 0.42) with a Heideite-type crystal structure (space group C12/m1) analysed by XRD and NPD, which is a unique tool to characterize the possible Ti/Fe inversion. The XPS studies at Fe 2p and Ti 2p core levels showed the occurrence of Fe2+ in all samples, whereas the Ti contribution arises from the Ti3+ state, with a smaller contribution of Ti2+ and Ti4+ states. The magnetic susceptibility investigation indicates the presence of AFM interactions, accounting for the large and negative Weiss constant for Fe0.42Ti2S4. For lower intercalation levels, it is combined with the signature of FM coupling, as supported by the magnetization isotherms, characteristic of canted spin states with a significant remnant magnetization of about 1 μB for x = 0.24. AC susceptibility curves displayed typical features of SG or cluster-glass states, with the frequency-dependent peaks in the real part. The x = 0.42 sample that was previously described to exhibit AFM interactions (with a very negative Weiss constant) also displays a SG behaviour near TN. A substantial magnetocaloric effect has been described for the three compounds, especially for Fe0.24Ti2S4 with a relative cooling power of 135.3 J kg−1, depicting a remarkable temperature stability for magnetic refrigerators.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research was partially funded by the Spanish Ministry for Science and Innovation (MCIN/AEI/10.13039/501100011033) for granting project number: PID2021-122477OB-I00, by “ERDF, A way of making Europe”, by the “European Union”, and by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-CAPES (Finance Code-001). J. G. thanks MICINN for granting the contract PRE2018-083398.References
- H. H. Kim, K. H. Kim, J. Lee and S. H. Hong, ACS Sustainable Chem. Eng., 2021, 9, 9680–9688, DOI:10.1021/acssuschemeng.1c01497.
- L. Q. Yan, J. Shen, Y. X. Li, F. W. Wang, Z. W. Jiang, F. X. Hu, J. R. Sun and B. G. Shen, Appl. Phys. Lett., 2007, 90, 262502, DOI:10.1063/1.2751576.
- J. Hemberger, P. Lunkenheimer, R. Fichtl, H. A. Krug Von Nidda, V. Tsurkan and A. Loidl, Nature, 2005, 434, 364–367, DOI:10.1038/nature03348.
- K. Dey, A. Indra, A. Karmakar and S. Giri, J. Magn. Magn. Mater., 2020, 498, 166090, DOI:10.1016/j.jmmm.2019.166090.
- X. Y. Yu and X. W. (David) Lou, Adv. Energy Mater., 2018, 8, 1701592, DOI:10.1002/aenm.201701592.
- C. Simon, J. Zander, T. Kottakkat, M. Weiss, J. Timm, C. Roth and R. Marschall, ACS Appl. Energy Mater., 2021, 4, 8702–8708, DOI:10.1021/acsaem.1c01341.
- C. Bourgès, V. Pavan Kumar, H. Nagai, Y. Miyazaki, B. Raveau and E. Guilmeau, J. Alloys Compd., 2019, 781, 1169–1174, DOI:10.1016/j.jallcom.2018.12.102.
- A. S. Shkvarin, Y. M. Yarmoshenko, A. I. Merentsov, E. G. Shkvarina, E. A. Suslov, M. S. Brezhestovsky, O. V. Bushkova and A. N. Titov, RSC Adv., 2016, 6, 106527–106539, 10.1039/c6ra16857d.
- M. Inoue, H. P. Hughes and A. D. Yoffe, Adv. Phys., 2006, 38, 565–604, DOI:10.1080/00018738900101142.
- H. Negishi, A. Shoube, H. Takahashi, Y. Ueda, M. Sasaki and M. Inoue, J. Magn. Magn. Mater., 1987, 67, 179–186, DOI:10.1016/0304-8853(87)90227-7.
- N. V. Selezneva, N. V. Baranov, E. M. Sherokalova, A. S. Volegov and A. A. Sherstobitov, Phys. Rev. B, 2021, 104, 064411, DOI:10.1103/PhysRevB.104.064411.
- B. L. Morris, V. Johnson, R. H. Plovnick and A. Wold, J. Appl. Phys., 1969, 40, 1299–1300, DOI:10.1063/1.1657639.
- N. M. Toporova, E. M. Sherokalova, N. V. Selezneva, V. V. Ogloblichev and N. V. Baranov, J. Alloys Compd., 2020, 848, 156534, DOI:10.1016/j.jallcom.2020.156534.
- N. V. Baranov, E. M. Sherokalova, N. V. Selezneva, A. V. Proshkin, A. F. Gubkin, L. Keller, A. S. Volegov and E. P. Proskurina, J. Phys.: Condens. Matter, 2013, 25, 066004, DOI:10.1088/0953-8984/25/6/066004.
- N. V. Selezneva, N. V. Baranov, E. M. Sherokalova, A. S. Volegov and A. A. Sherstobitov, J. Magn. Magn. Mater., 2021, 519, 167480, DOI:10.1016/j.jmmm.2020.167480.
- A. F. Gubkin, E. M. Sherokalova, L. Keller, N. V. Selezneva, A. V. Proshkin, E. P. Proskurina and N. V. Baranov, J. Alloys Compd., 2014, 616, 148–154, DOI:10.1016/j.jallcom.2014.06.195.
- M. Inoue, M. Matsumoto, H. Negishi and H. Sakai, J. Magn. Magn. Mater., 1985, 53, 131–138, DOI:10.1016/0304-8853(85)90141-6.
- Y. Tazuke, Y. Ohta and S. Miyamoto, J. Phys. Soc. Jpn., 2005, 74, 2644–2645, DOI:10.1143/JPSJ.74.2644.
- C. Delacotte, T. A. Pomelova, T. Stephant, T. Guizouarn, S. Cordier, N. G. Naumov and P. Lemoine, Chem. Mater., 2022, 34, 1829–1837, DOI:10.1021/acs.chemmater.1c04105.
- J. Shen, L. Q. Yan, J. Zhang, F. W. Wang, J. R. Sun, F. X. Hu, C. B. Rong and Y. X. Li, J. Appl. Phys., 2008, 103, 07B317, DOI:10.1063/1.2830973.
- X. C. Zheng, X. Y. Li, L. H. He, S. Y. Zhang, M. H. Tang and F. W. Wang, Chin. Phys. B, 2017, 26, 037502, DOI:10.1088/1674-1056/26/3/037502.
- K. Matsumoto, L. Li, S. Hirai, E. Nakamura, D. Murayama, Y. Ura and S. Abe, Cryogenics, 2016, 79, 45–48, DOI:10.1016/j.cryogenics.2016.08.001.
- D. X. Li, T. Yamamura, S. Nimori, Y. Homma, F. Honda, Y. Haga and D. Aoki, Solid State Commun., 2014, 193, 6–10, DOI:10.1016/j.ssc.2014.05.024.
- C. Pang, L. Gao, A. Chaturvedi, N. Bao, K. Yanagisawa, L. Shen and A. Gupta, J. Mater. Chem. C, 2015, 3, 12077–12082, 10.1039/c5tc02727f.
- K. Guo, Y. Ding, J. Luo and Z. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 19673–19681, DOI:10.1021/acsami.8b03588.
- J. Gainza, F. Serrano-Sánchez, J. E. F. S. Rodrigues, N. M. Nemes, J. L. Martínez and J. A. Alonso, Materials, 2021, 14, 1946, DOI:10.3390/ma14081946.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69, DOI:10.1016/0921-4526(93)90108-I.
- M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 1980, 5, 361–373, DOI:10.1016/j.apsusc.2010.07.086.
- T. Takahashi and O. Yamada, J. Solid State Chem., 1973, 7, 25–30, DOI:10.1016/0022-4596(73)90116-3.
- A. P. Grosvenor, B. A. Kobe, M. C. Biesinger and N. S. McIntyre, Surf. Interface Anal., 2004, 36, 1564–1574, DOI:10.1002/sia.1984.
- P. Kayser, A. Muñoz, J. L. Martínez, F. Fauth, M. T. Fernández-Díaz and J. A. Alonso, Acta Mater., 2021, 207, 116684, DOI:10.1016/j.actamat.2021.116684.
- H. Lei, M. Abeykoon, E. S. Bozin and C. Petrovic, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 180503(R), DOI:10.1103/PhysRevB.83.180503.
- S. Ghosh, D. C. Joshi, P. Pramanik, S. K. Jena, S. Pittala, T. Sarkar, M. S. Seehra and S. Thota, J. Phys.: Condens. Matter, 2020, 32, 485806, DOI:10.1088/1361-648X/aba6a6.
- R. C. Sahoo, S. K. Giri, D. Paladhi, A. Das and T. K. Nath, J. Appl. Phys., 2018, 123, 013902, DOI:10.1063/1.4958980.
- S. Lin, D. F. Shao, J. C. Lin, L. Zu, X. C. Kan, B. S. Wang, Y. N. Huang, W. H. Song, W. J. Lu, P. Tong and Y. P. Sun, J. Mater. Chem. C, 2015, 3, 5683–5696, 10.1039/c5tc00423c.
- S. Pakhira, C. Mazumdar, R. Ranganathan, S. Giri and M. Avdeev, Phys. Rev. B, 2016, 94, 104414, DOI:10.1103/PhysRevB.94.104414.
- E. Maniv, N. L. Nair, S. C. Haley, S. Doyle, C. John, S. Cabrini, A. Maniv, S. K. Ramakrishna, Y. L. Tang, P. Ercius, R. Ramesh, Y. Tserkovnyak, A. P. Reyes and J. G. Analytis, Sci. Adv., 2021, 7, eabd8452, DOI:10.1126/sciadv.abd8452.
- P. N. Lekshmi, G. R. Raji, M. Vasundhara, M. R. Varma, S. S. Pillai and M. Valant, J. Mater. Chem. C, 2013, 1, 6565–6574, 10.1039/c3tc31203h.
- J. P. Palakkal, C. Raj Sankar and M. R. Varma, J. Appl. Phys., 2017, 122, 073907, DOI:10.1063/1.4999031.
- S. Pal, S. Jana, S. Govinda, B. Pal, S. Mukherjee, S. Keshavarz, D. Thonig, Y. Kvashnin, M. Pereiro, R. Mathieu, P. Nordblad, J. W. Freeland, O. Eriksson, O. Karis and D. D. Sarma, Phys. Rev. B, 2019, 100, 045122, DOI:10.1103/PhysRevB.100.045122.
- A. Arrott and J. E. Noakes, Phys. Rev. Lett., 1967, 19, 786, DOI:10.1103/PhysRevLett.19.786.
- A. Arrott, Phys. Rev., 1957, 108, 1394, DOI:10.1103/PhysRev.108.1394.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16–17, DOI:10.1016/0031-9163(64)91158-8.
- J. Y. Law, V. Franco, L. M. Moreno-Ramírez, A. Conde, D. Y. Karpenkov, I. Radulov, K. P. Skokov and O. Gutfleisch, Nat. Commun., 2018, 9, 2680, DOI:10.1038/s41467-018-05111-w.
- K. Dey, A. Indra and S. Giri, J. Alloys Compd., 2017, 726, 74–80, DOI:10.1016/j.jallcom.2017.07.282.
- A. O. Ayaş, A. Kandemir, S. K. Çetin, G. Akça, M. Akyol and A. Ekicibil, J. Mater. Sci.: Mater. Electron., 2022, 33, 7357–7370, DOI:10.1007/s10854-022-07843-4.
- V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, Prog. Mater. Sci., 2018, 93, 112–232, DOI:10.1016/j.pmatsci.2017.10.005.
- V. Franco, J. S. Blázquez and A. Conde, Appl. Phys. Lett., 2006, 89, 222512, DOI:10.1063/1.2399361.
- S. Mondal, A. Midya, M. M. Patidar, V. Ganesan and P. Mandal, Appl. Phys. Lett., 2020, 117, 092405, DOI:10.1063/5.0019985.
- S. Sun, H. Qin, L. Kong, R. Ning, Y. Zhao, Z. Gao and W. Cai, ACS Appl. Mater. Interfaces, 2021, 13, 57372–57379, DOI:10.1021/acsami.1c18587.
- H. J. Lun, L. Xu, X. J. Kong, L. S. Long and L. S. Zheng, Inorg. Chem., 2021, 60, 10079–10083, DOI:10.1021/acs.inorgchem.1c00993.
- J. Massoudi, O. Messaoudi, S. Gharbi, T. Mnasri, E. Dhahri, K. Khirouni, E. K. Hlil, L. Alfhaid, L. Manai and A. Azhary, J. Phys. Chem. C, 2022, 126, 2857–2867, DOI:10.1021/acs.jpcc.1c09838.
- D. Mazumdar and I. Das, Phys. Chem. Chem. Phys., 2021, 23, 5596–5606, 10.1039/d0cp06447e.
- M. K. Sharma, K. Singh and K. Mukherjee, J. Magn. Magn. Mater., 2016, 414, 116–121, DOI:10.1016/j.jmmm.2016.04.047.
- X. Yang, J. Pan, S. Liu, M. Yang, L. Cao, D. Chu and K. Sun, Phys. Rev. B, 2021, 103, 104405, DOI:10.1103/PhysRevB.103.104405.
- S. Tillaoui, A. El Boubekri, A. Essoumhi, M. Sajieddine, E. K. Hlil, R. Moubah, M. Sahlaoui, A. Razouk and H. Lassri, Mater. Sci. Eng., B, 2021, 266, 115052, DOI:10.1016/j.mseb.2021.115052.
- M. Jeddi, J. Massoudi, H. Gharsallah, S. I. Ahmed, E. Dhahri and E. K. Hlil, RSC Adv., 2021, 11, 7238–7250, 10.1039/d0ra10118d.
- T. Hashimoto, T. Kuzuhara, M. Sahashi, K. Inomata, A. Tomokiyo and H. Yayama, J. Appl. Phys., 1997, 32, 192–202, DOI:10.1063/1.339232.
- M. Bouhbou, R. Moubah, W. Belayachi, A. Belayachi, L. Bessais and H. Lassri, Chem. Phys. Lett., 2017, 688, 84–88, DOI:10.1016/j.cplett.2017.09.059.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc02160a |
| This journal is © The Royal Society of Chemistry 2022 |