Local chemical origin of ferroelectric behavior in wurtzite nitrides

Abstract

Ferroelectricity enables key modern technologies from non-volatile memory to precision ultrasound. The first known wurtzite ferroelectric Al_1−xSc_xN has recently attracted attention because of its robust ferroelectricity and Si process compatibility, but the chemical and structural origins of ferroelectricity in wurtzite materials are not yet fully understood. Here we show that ferroelectric behavior in wurtzite nitrides has local chemical rather than extended structural origin. According to our coupled experimental and computational results, the local bond ionicity and ionic displacement, rather than simply the change in the lattice parameter of the wurtzite structure, is key to controlling the macroscopic ferroelectric response in these materials. Across gradients in composition and thickness of 0 < x < 0.35 and 140–260 nm, respectively, in combinatorial thin films of Al_1−xSc_xN, the pure wurtzite phase exhibits a similar c/a ratio regardless of the Sc content due to elastic interaction with neighboring crystals. The coercive field and spontaneous polarization significantly decrease with increasing Sc content despite this invariant c/a ratio. This property change is due to the more ionic bonding nature of Sc–N relative to the more covalent Al–N bonds, and the local displacement of the neighboring Al atoms caused by Sc substitution, according to DFT calculations. Based on these insights, ionicity engineering is introduced as an approach to reduce coercive field of Al_1−xSc_xN for memory and other applications and to control ferroelectric properties in other wurtzites.

---

1 Introduction

Ferroelectricity, which is a characteristic of materials possessing a spontaneous polarization that is reversible by applying an electric field, was discovered more than a hundred years ago.¹ Since that time ferroelectric materials have enabled and advanced ubiquitous electronic technologies in the forms of capacitors, piezoelectric actuators/sensors, energy harvesters, non-linear optics, pyroelectric sensors, and PTC thermistors.^2–7 Thin film ferroelectrics have further enabled integrated devices such as FeRAM and PiezoMEMS.^8,9 Research continues into use of ferroelectrics for multiferroic¹⁰ and photovoltaic^11,12 applications as well as negative capacitance,¹³ and new concepts keep emerging.^13–18 The race to develop new polar—and potentially ferroelectric—materials has seen significant recent expansion into nitride chemistries, most notably with the wurtzite and perovskite structures.^19–23

Among nitride ferroelectrics, the wurtzite aluminum scandium nitride alloy (Al_1−xSc_xN) ferroelectric has received significant attention because of its enhanced piezoelectric response,²⁴ robust ferroelectricity,²⁰ and compatibility with both Si and III-N semiconductor processes. Chemistry, stress, strain, and film thickness have been rigorously investigated to control ferroelectricity in this material system.^20,25–30 Higher Sc/Al ratio simultaneously reduces the crystallographic c/a ratio, spontaneous polarization, and coercive field,^20,31 and in-plane tensile strain lowers the coercive field.^20,27 Understanding how properties—particularly coercive field (voltage)—scale with film thickness is also important from a future device perspective.^29,30

The prior studies of ferroelectricity in Al_1−xSc_xN^20,25–30 included explicit and implicit variables such as residual strain state, process parameters, target condition, chamber type, substrate type/treatment, etc. These variables convolute experimental effects, and the resulting data scatter can easily mask important but unrepresented factors such as microstructure and defects. Combinatorial techniques reduce uncontrolled process variables because a single film library can include all samples of interest and also offer significant advantages for rapid screening.^32,33 In such high-throughput methods, experimental variables (e.g., composition, thickness, substrate temperature) are smoothly varied across a single sample library,

Previously, combinatorial ferroelectric property screening has been reported for perovskite materials based on BaTiO₃,^34,35 Pb(Zr,Ti)O₃,³⁶ BiFeO₃,^37,38 and Bi₄Ti₃O₁₂.³⁹ Those studies validated the combinatorial method for ferroelectric materials, but they missed the opportunity to directly address the effect of residual elastic strain in the sample library.⁴⁰ Lacking information about the underlying thermodynamic coefficients, it is difficult to separate elastic strain from total strain in order to isolate effects of electromechanical coupling and chemistry on ferroelectric properties in wurtzite ferroelectrics. Thus, systematic crystallographic analysis along with corresponding ferroelectric property evaluation in a combinatorial study is key for understanding the chemical and elastic contributions to ferroelectric response.

In this study, we decouple effects of composition and wurtzite c/a ratio on ferroelectric properties in Al_1−xSc_xN by investigating chemistry–structure–thickness–property relations using combinatorial libraries with simultaneous gradients in both composition and thickness. The pure wurtzite phase in the Al-rich region (Sc < 0.35) of the library exhibits a constant wurtzite c/a ratio regardless of Sc content likely due to elastic clamping across the composition gradient in the combinatorial library. In this composition region without measurable change in the crystal lattice, the remanent polarization and coercive field decrease with Sc content, similar to homogeneous films for which c/a ratio varies directly with composition. The composition-dependent and structure-independent change in ferroelectric properties is attributed to the more ionic nature of the Sc–N bonds and the resulting local distortions of the neighboring Al–N bonds, as indicated by DFT calculations. These results show that the local chemical bonding and atomic distortions are more significant than global crystallographic c/a ratio for determining ferroelectric properties in the wurtzite ferroelectrics, and suggest new ways for future material discovery and development of ferroelectric wurtzite materials.

2 Results and discussion

2.1 Structural analysis

Analysis of the crystalline structure of the deposited Al_1−xSc_xN/Pt/TiO_x/SiO₂/Si library (Fig. 1) shows textured pure wurtzite at relatively low Sc contents (x < 0.35), and mixed-phase wurtzite plus rocksalt at higher Sc content (x > 0.35). Two-dimensional (2θ–chi) diffraction mapping in a specific location (Sc content: 0.4, thickness: 230 nm) is a representative result of phase coexistence of the well-oriented wurtzite 002 and rocksalt 111 diffraction peaks along with Pt 111 (textured bottom electrode) and Au 111/200 peaks (polycrystalline top electrode) as shown in Fig. 1(a). Diffraction profiles, each of which integrates a chi range of 72 degrees, taken from a series of points along the x-axis of the sample library (Sc content ranges from 0.25 to 0.50 while film thickness is similar, 230–260 nm) are stacked in Fig. 1(b). The intensity of the wurtzite 002 peak is highest when Sc content is lowest. A shoulder peak at lower 2θ angle attributed to the rocksalt phase appears when the Sc content is > 0.35. This wurtzite and rocksalt phase co-existence has also been seen in homogeneous films^24,41,42 and is associated with the wurtzite–rocksalt miscibility gap.⁴³Fig. 1(c) shows lattice parameters a and c for the pure wurtzite region in the thickness–composition space. The color scale shows the c lattice parameter, and the marker size represents the a lattice parameter. The a lattice parameter is calculated with the off axis wurtzite 103 diffraction peak shown in Fig. S1 in ESI.† The c lattice parameter gradually increases up to Sc = 0.3 and then decreases, while the a lattice parameter keeps increasing up to Sc = 0.35. This trend is in good agreement with reported homogeneous films and calculations.^24,44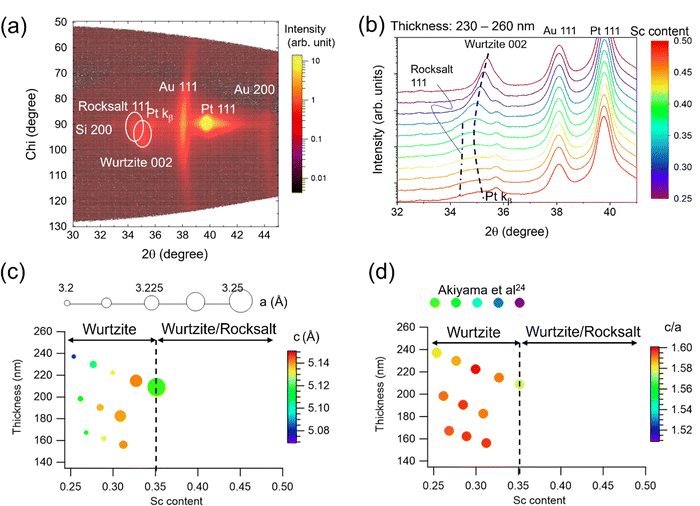

Fig. 1 Crystal structure analysis of Al_1−xSc_xN/Pt/TiO_x/SiO₂/Si using XRD. (a) 2D (2θ–chi) diffraction scan for Sc = 0.4 and thickness = 230 nm showing wurtzite/rocksalt coexistence. Chi 90 degree represents the surface normal direction (see Fig. S2 in ESI† for the definition of the chi direction.) (b) Wurtzite peak shift in integrated 2θ profiles for varying Sc content from 0.25 to 0.5. (c) Lattice parameter map in composition–thickness space. Color scale shows the c lattice parameter, and plot size represents the a lattice parameter. (d) c/a ratio map in composition–thickness space. Comparison to homogeneous film data reported by Akiyama²⁴ indicates significantly invariant c/a ratio with regard to composition in this study.

Fig. 1(d) represents the c/a ratio in the thickness–composition space. The value of c/a increases slightly from 1.58 to 1.59 with increasing Sc content towards Sc = 0.3 then decreases to 1.57 at Sc = 0.35. The change that we see in the c/a ratio across this sample library is notably less than the reported c/a reduction from 1.57 (Sc = 0.25) to 1.51 (Sc = 0.35) in homogeneous films, each grown separately.²⁴ This difference likely comes from the difference in elastic strain state in the gradient library, namely our film undergoes more out-of-plane tensile and/or in-plane compressive strains compared to the homogeneous film set, although the absolute elastic strains in both cases are unknown. This relative elastic strain likely originates from the composition gradient of the combinatorial deposition, i.e., because of the continuous composition gradient, the Sc-rich regions are elastically clamped by their stiffer Al-rich neighboring grains.⁴⁵ As a result, the library has a unique feature that the crystal lattice—and in particular, the c/a ratio—is essentially invariant with composition across the pure wurtzite region. There is also no significant thickness dependence on c/a ratio so that the thickness effect on the crystal lattice is minimal in the 140–260 nm range.

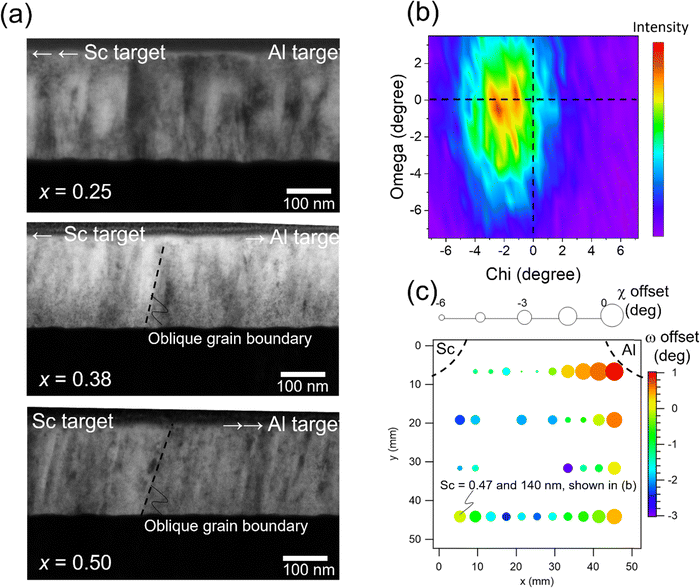
Film microstructure, such as texture and grain orientation, influences ferroelectric properties and is therefore investigated in this work.^46–50 In combinatorial sputtering, the particle flux has a asymmetric directionality with respect to the substrate, which causes oblique grain growth in addition to the desired composition gradient(s). Cross-sectional TEM micrographs are shown in Fig. 2(a) for films for Sc = 0.25, Sc = 0.38 and Sc = 0.50. The right sides of the cross-sectional micrographs correspond to the side nearest the Al target. Grain growth directs to the Al target, clearly seen in the Sc rich (far from the Al target) region, where grain boundary angles are ∼10–15° from the surface normal (Sc = 0.50). The oblique angle is less (6–13°) across the middle portion (Sc = 0.38), and grain boundaries are nearly straight for the portion of the film directly above the Al target (Sc = 0.25). These results suggest that the Al flux is controlling the growth of the columnar grains.

Fig. 2 Grain and crystal growth direction analysis of Al_1−xSc_xN. (a) Cross-sectional TEM micrographs for Sc = 0.25 (under Al target), Sc = 0.38 (middle of library), and Sc = 0.5 (under Sc target) showing oblique grain growth. (b) XRD omega–chi plan view map for (002) wurtzite peak with respect to substrate Pt (111) normal direction. (c) Omega and chi offsets across the sample library mapping out crystal growth direction with respect to Pt (111) normal.

Crystal misorientation is particularly important for ferroelectric properties in wurtzites because the spontaneous polarization is aligned with—and limited to—the c-axis of the wurtzite crystal. Chi–omega scans of the wurtzite 002 peak show the crystal misorientation (Fig. 2(b)) at a sample position where Sc content is 0.47 and thickness is 140 nm. The 0 degree position in both chi and omega offsets aligns to the substrate Pt (111) peak. The wurtzite peak is −2 degrees off-centered in chi and −1 degrees off-centered in omega. Based on the chi and omega directions found in Fig. S2 (ESI†), the (002) plane normal is directed slightly towards the Al target in both chi and omega, which is consistent with the grain growth direction seen in Fig. 2(a). Fig. 2(c) maps the chi and omega offsets with respect to the Pt (111) normal direction across the sample library. The color bar represents the omega offset, and the marker size shows the chi offset. The region close to the Al target (x = 44 and y = 6 mm) aligns well to Pt (111) in both omega and chi, and the offset angles in both chi and omega are larger at positions further away from the Al target, which supports Al flux-dominated growth. However, the angle is not as significant as the oblique grain growth angle shown in Fig. 2(a). At most, the chi offset is −6 degrees, and omega offset is −3 degrees. This means that the effect of the flux directionality on crystal orientation exists but is limited compared to that on the grain growth direction. A 5° crystallographic misalignment corresponds to a 0.5% loss in remanent polarization because of the cosine projection; this is less than the uncertainties in either thickness or area, so the crystallographic misorientation is considered to be insignificant in this work.

2.2 Electrical properties

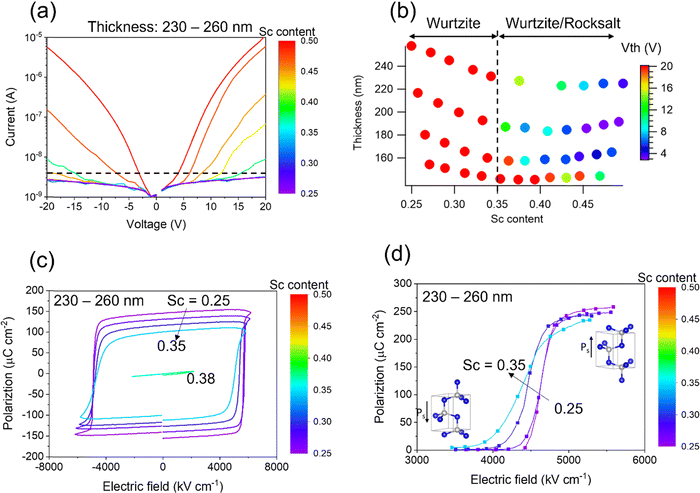
Electrical properties for the library are shown in Fig. 3. Leakage current was measured using a bent probe with gauge of ∼300 μm contacting the bare surface of the film. Compositional dependence (similar thickness ranging from 230–260 nm) of I–V measurements is shown in Fig. 3(a). An exponential current increase is observed for Sc > 0.35, and the threshold voltage for the exponential increase decreases with increased Sc content. The threshold voltage is defined here as the voltage at which the current exceeds 4 × 10⁻⁹ A (the dashed line in Fig. 3(a)). Because the compositions of Sc ≥ 0.35 correspond to the presence of mixed wurtzite and rocksalt phases, the current increase is attributed to the presence of a conductive (bandgap of ∼1 eV) rocksalt phase.^51,52 The threshold voltage is presumably associated with the volume fraction of the rocksalt phase, corresponding to the decrease in the wurtzite XRD peak intensity with higher Sc content (Fig. 1(b)). Fig. 3(b) maps the threshold voltage in thickness–composition space. Pure wurtzite regions where the Sc content < 0.35 do not exhibit an exponential increase in leakage current, so the threshold voltage is > 20 V for these film thicknesses. Interestingly, the thinner region (140–150 nm) shows relatively higher threshold voltages even for high Sc contents, which implies that the rocksalt phase fraction varies depending on the thickness. Indeed, XRD profiles of thinner regions show smaller changes in the wurtzite phase peak intensity as a function of Sc content compared to that of thicker regions (Fig. 1(b)) as shown in Fig. S3 (ESI†).

Fig. 3 Electrical properties of the Al_1−xSc_xN library. (a) Leakage current for films with varying Sc content from 0.25 to 0.5 and film thicknesses from 230–260 nm. (b) Threshold voltage V_th map in thickness–composition space showing significant conduction for Sc contents >0.35. (c) P–E hysteresis loops for the subset of films with Sc contents from 0.25 to 0.38. (d) Switched polarization under various applied electric field pulses using the PUND method for films with Sc contents from 0.25 to 0.35.

The pure wurtzite phase region (Sc < 0.35) exhibits robust ferroelectric behavior. The compositional dependence of polarization–electric field hysteresis loops taken at 10 kHz for the similar thickness points ranging from 230–260 nm (same y position on the sample library) is shown in Fig. 3(c). Coercive field and polarization values decrease with increasing Sc content up to 0.35, in agreement with prior reports.^20,25 A device at Sc = 0.38 (green loop) breaks down at 2500 kV cm⁻¹, which is below the coercive field, so that no hysteresis is observed. This breakdown field relates to the large leakage current when the rocksalt phase is present. Positive-up-negative-down (PUND) measurements are carried out to quantify the switched polarization without the leakage contribution^53,54 (see ESI† Fig. S4 for the polarization values for each pulse sequence). Fig. 3(d) shows the remanent polarization (+P_r − (−P_r)) values as a function of applied electric field for each composition of the 230–260 nm thickness devices. The pulse width is 100 μs, and duty cycle ratio is 10%. The decrease in switchable polarization with increasing Sc content is consistent with the P–E hysteresis measurements.

2.3 Correlation of crystal structure–ferroelectric properties

Fig. 4 summarizes the ferroelectric properties, c/a ratio (marker size) and film thickness (marker color) as a function of Sc content in our combinatorial library compared with homogeneous films reported in systematic composition–property studies (dotted and dashed lines),^20,25 and from our chamber with nominally identical deposition condition and characterization method (black circles).^27,42 The coercive field measured at 10 kHz and remanent polarization from PUND measurements both consistently decrease with Sc content (Fig. 4(a and b)). Note that the coercive fields of homogeneous films are results of our films using the same measurement condition, since the coercive field has a strong frequency dependence.⁵⁵ Despite the agreement in ferroelectric property change with literature, the c/a ratio in the library does not significantly change in the composition range as seen in the plot size in Fig. 4(a and b). As discussed above in Fig. 1(d), the c/a ratio is invariant with composition across the pure wurtzite region due to elastic interaction in the composition gradient library.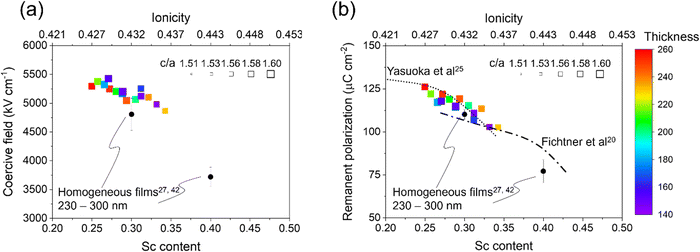

Fig. 4 Composition–structure–property relations in Al_1−xSc_xN: (a) coercive field and (b) remanent polarization as a function of Sc content along with c/a and thickness in library, compared to reported homogeneous films.^20,25,27,42

The key findings of this work come from comparing our combinatorial library to literature values and trends relating composition, crystallography, and ferroelectric properties. Prior studies have observed consistent and simultaneous reductions in c/a ratio, coercive field, and switchable polarization with increases in Sc content.²⁵ Crucially, the fact that Sc content is correlated with a reduction in c/a ratio has been repeatedly identified as the key mechanistic factor enabling ferroelectric polarization reversal in this system, but our results suggest that the underlying nature of the Sc–N chemical bonds is more important to enabling polarization reversal than simply via a change in the crystallographic c/a ratio. Indeed, Landau-Devonshire thermodynamic analysis suggests that the ferroelectric properties of Al_1−xSc_xN are less sensitive to lattice strain effects compared to classic perovskite ferroelectric PbTiO₃.⁵⁶ Therefore, when learning from the Al_1−xSc_xN system to engineer other ferroelectric wurtzites, it is important to look beyond the simple lattice parameters.

2.4 Al_1−xSc_xN alloy calculations

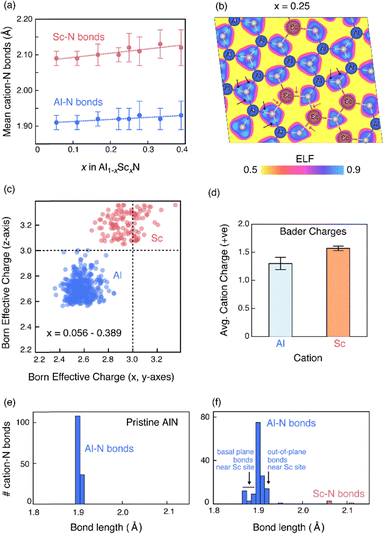
The importance of bond chemistry on ferroelectric properties has long been recognized in the oxide ferroelectrics (e.g., see frequent references to cations such as Ti, Ta, and Nb as “ferroelectrically active” and Mg, Zn, and Sc as “ferroelectrically inactive” when in octahedral coordination⁵⁷), but such concepts require further consideration for the wurtzite nitrides. Considering classic Pauling electronegativity difference, the ionicity of the Al–N bond is 0.4 while the Sc–N bond is > 0.5 ionic.⁵⁸ Al–N bonding is dominated by directional sp³ bonds whereas Sc–N is better described by non-directional ionic bonding, consistent with the endmember crystal structures (tetrahedral coordination in wurtzite AlN vs. octahedral coordination in rocksalt ScN). As shown on the secondary abscissa in Fig. 4(a and b), the average bond ionicity increases with increased Sc content. It stands to reason that the reduced directionality of such bonding would reduce barriers to polarization reversal.

We computationally modeled Al_1−xSc_xN alloys and performed density functional theory (DFT) calculations at 8 different compositions in the x range of 0.056–0.389 to better understand the differences in Al–N and Sc–N bonding character (see computational methods for details). Fig. 5(a) illustrates the average first nearest neighbor Al–N and Sc–N bond lengths as a function of composition x, with error bars representing the standard deviation of the bond lengths in the supercell at a given composition. The significant difference in the Al–N and Sc–N bond lengths could be attributed to the differences in the ionic radii of Al and Sc, and to the unfavorable tetrahedral coordination of Sc³⁺ (prefers octahedral coordination).

Fig. 5 Theoretical calculations of composition-dependent structural properties and local ionic distortions in Al_1−xSc_xN: (a) average first nearest neighbor Al–N and Sc–N bond lengths as a function of composition x in DFT-relaxed SQS supercells. The errors bars are the standard deviations in the bond lengths. (b) Cross-sectional of isosurface of electron localization function (ELF) heat map computed at x = 0.25 composition. The black and red arrows point to representative Al–N and Sc–N bonds, respectively, showing the differences in ELF. (c) Calculated Born effective charges of Al and Sc aggregated across 8 different compositions in the range x = 0.056–0.389. (d) Average Bader charges of Al and Sc (averaged across compositions). Error bars denote the standard deviation. The higher Bader charge of Sc is consistent with more ionic Sc–N bonds. (e) Histograms of bond lengths in pristine AlN and (f) dilute Al_1−xSc_xN alloy (x = 0.028) showing a wider distribution of Al–N bond lengths.

While Fig. 5(a) suggests local structural differences in the neighborhood of Al and Sc cations, it does not provide insights into the nature of the chemical bonds. To investigate the cation-N bonding, we calculated the electron localization function (ELF). The calculated ELF at Sc content x = 0.25 is shown in Fig. 5(b) as a cross-section across the c-axis. Al–N bonds, indicated by black arrows, are characterized by large ELF values along the bonds suggesting directional polar covalent bonds consistent with sp³ hybridization. In contrast, ELF contours are more isotropic and centered around Sc and neighboring N atoms, which is indicative of non-directional ionic bonds. We arrive at similar conclusions about the bonding nature when examining the ELF maps at other compositions.

The calculated Born effective charges (BECs) and Bader charges provide further evidence that Sc–N bonds are more ionic than Al–N bonds. The BECs of Al and N aggregated across the 8 compositions are presented in Fig. 5(c). There is a clear demarcation between Al and Sc BECs, with an average BEC of 2.62 ± 0.07 for Al and 3.03 ± 0.14 for Sc. BEC of Sc is closer to the formal charge of +3 while that of Al is much smaller than 3, again supporting the greater ionicity of Sc–N compared to polar covalent Al–N bonds. Our calculations also show that Sc with an average Bader charge of 1.6 is more ionic than Al (∼1.25). It has been previously argued that this well-known difference in the Bader charge^59,60 and nominal charge is meaningful and reflects the degree of ionicity of the bond.⁵⁹ While both Al and Sc are cations in +3 formal oxidation states, the difference in their Bader charges (Sc 1.6 vs. Al 1.25) clearly indicates a difference in the Sc–N and Al–N bond ionicity.

2.5 Local bonding distortion hypothesis

To understand the effect of Al–N vs. Sc–N bonding differences on the local structure, we simulated dilute Al_1−xSc_xN alloys (x = 0.028) with 72-atom SQS supercells (see Methods) and relaxing the atomic positions with DFT while keeping the volume and cell shape fixed. In a dilute alloy, we ensure that the local structural changes do not arise from changes to the global crystal structure in a way that is consistent with our experimental results discussed above (Fig. 4). Fig. 5(e and f) show the histogram of first nearest neighbor Al–N bond lengths in pristine AlN and in dilute Al_0.972Sc_0.028N alloy, respectively. Pristine AlN features a sharp distribution with the basal plane Al–N bonds slightly shorter than the out-of-plane bonds in the AlN₄ tetrahedra. In contrast, in dilute Al_0.972Sc_0.028N alloy, the histogram of Al–N bond lengths (Fig. 5(f)) shows a significant departure from the distribution in pristine AlN (Fig. 5(e)), suggesting that Sc substitution, even in the dilute limit, locally affects the Al–N bond lengths.

The local structural changes affected by the Sc substitution is elucidated in Fig. S5 in ESI,† where each panel shows the first nearest neighbor Al–N bonds lengths in different ranges from the shortest (1.865–1.875 Å) to longest (1.915–1.925 Å). These ranges correspond to the histogram bars in Fig. 5(e and f). It is evident that the shorter Al–N bond lengths are located in the basal plane in the vicinity of the Sc-substituted site while the longer bonds are observed along the polar axis. The Al–N bonds lengths away from the Sc-substituted site are the same as in pristine AlN. These results indicate that Sc substitution drives local ion displacement such that Al–N basal plane bonds become shorter and out-of-basal plane bonds are stretched.

These local changes in the Al–N bond lengths can be directly correlated to the macroscopic ferroelectric response in substantially Sc substituted AlN (e.g., > 10 at%: 0.2 Sc ion in a unit cell). The Al–N bond shortening and stretching discussed above is consistent with the local structure becoming 6/mmm hBN like, which is regarded as the intermediate non-polar state in the polarization switching of wurtzite ferroelectrics.^20,56,61 We hypothesize that Sc substitution reduces the energy difference between the nominally wurtzite structure (polar) and intermediate hBN structure (non-polar), which consequentially reduces the coercive field for switching. The ion positions determine the spontaneous polarization, P_s;⁶² as Al approaches the N basal plane upon Sc substitution, P_s is reduced.⁶³ Those polarization and coercive field reductions with increasing Sc content are consistent with existing DFT calculations^44,64,65 and experimental results^20,25 including this study.

The effect of local chemical (bonding) and structural changes on the ferroelectric response is convoluted with changes in the elastic properties, which also depend on the bonding and structure. Indeed, reported DFT calculations suggest that the global elastic properties of Al_1−xSc_xN change with composition.^64,66

The importance of chemical bonding and local distortion as a controlling factor of ferroelectric properties proposes a guide for tetrahedral-based ferroelectric material design and discovery.^61,67 For example, the large electronegativities of oxygen and fluorine are expected to decrease coercive field making it easier to realize spontaneous polarization switching, all else being equal. Similarly, elements with low electronegativity such as alkali metal, alkaline earth, or rare-earth cations are expected to increase ionicity. Thus, oxide or halide wurtzite materials based on alkali-earth/rare-earth cations (e.g., AlN, GaN, ZnO, AgI, and CdS) can be a good candidates for ferroelectricity.⁶¹ Indeed, Zn_1−xMg_xO, which has a larger ionicity ranging from 0.55 to 0.68,⁵⁸ exhibits a lower coercive field (∼3000 kV cm⁻¹ for x = 0.34 at 100 Hz) compared to Al_1−xSc_xN with ionicity ranging from 0.40 to 0.51, even with higher c/a ratio (= 1.595) for Zn_1−xMg_xO⁶⁷ compared to Al_1−xSc_xN. As another example, Al_1−xYb_xN is another nitride material system that undergoes mechanical softening,^68,69 but large differences in ionic radii complicate both solubility and polarization reversal. Also, incorporation of more ionic elements into the sp³ bonded covalent tetrahedral framework to ease polarization reversal has a tradeoff between of disrupting the tetrahedral network and leading to phase separation, as seen in the Al_1−xSc_xN system with large Sc content.²⁰

3 Conclusions

In summary, here we show the local atomistic origin of ferroelectric behavior in wurtzite nitrides, by tuning the crystal structure and ferroelectric properties of a combinatorial co-sputtered Al_1−xSc_xN film with simultaneous composition and thickness gradients, analyzed in concert with theoretical calculations. Pure wurtzite phase is achieved for Sc < 0.35, whereas wurtzite and rocksalt phase coexistence is seen for Sc > 0.35 for the thickness range (140–260 nm). The c/a ratio remains constant in the pure wurtzite region presumably due to the elastic interaction among neighboring grains. Leakage current exponentially increases in the wurtzite–rocksalt phase coexistence region, which is likely attributed to the higher conductivity of the smaller band gap rocksalt phase. Well saturated polarization–electric field hysteresis loops are observed in the pure wurtzite phase region, and coercive field and remanent polarization decrease with increasing Sc content, as previously reported.

Comparing ferroelectric properties, composition, and crystallographic c/a ratio, we find that the ferroelectric response of Al_1−xSc_xN is controlled by the difference in chemical bonding between more ionic Sc–N bonding and covalent Al–N sp³ bonding, rather than by the c/a ratio as sometimes stated in prior literature. Indeed, DFT calculations reveal that Sc cations possess a more isotropic electron distribution and a BEC of 3.03 ± 0.14 close to the formal charge, while Al cations have directional electron distribution towards nitrogen and BEC of 2.62 ± 0.07. The impact of Sc substitution on displacements of nearby Al–N bonds driven by the greater ionicity of Sc–N is observed in the DFT results, and provides the direct connection between chemical bonding and ferroelectric response in this system. These results point to studying material candidates for decreasing coercive field of future ferroelectric wurtzite materials for memory and other applications.

4 Methods

4.1 Al_1−xSc_xN thin film growth

A co-sputtered Al_1−xSc_xN thin film with composition and thickness gradients is deposited on a Pt/TiO_x/SiO₂/Si substrate using reactive RF magnetron sputtering (Fig. S6(a) in ESI†). Elemental Al and Sc targets are located in a sputter-up configuration along the direction of the corners of the 2′′ Pt/TiO_x/SiO₂/Si substrate, resulting in orthogonal thickness and composition gradients (Fig. S6(b) in ESI†). Fig. S6(c and d) in ESI† show the thickness and composition map of the deposited film. The color is interpolated based on an array of discrete measurement points shown as white circles. The Sc content ranges from 0.25 to 0.5 across the x direction parallel to the Al and Sc target configuration, and film thickness varies between 140 and 260 nm across y direction, perpendicular to x. Other deposition conditions are as follows: 3 mtorr of Ar/N₂ (13.9/4.6 sccm flow), substrate temperature of 400 °C, 90 W on a 2′′ diameter Al target, and 98 W on a 2′′ diameter Sc target. The base pressure, partial oxygen and partial water vapor pressure at 400 °C are <5 × 10⁻⁸ torr, P_O2 < 2 × 10⁻⁸ torr and P_H2O < 1 × 10⁻⁸ torr, respectively.

4.2 Film characterization

The crystal structure of the film is investigated using X-ray diffraction (XRD) on Bruker D8 Discover and Panalytical Empyrean diffractometers. The lattice parameters are determined by pseudo-Voigt fitting of wurtzite 002 and 103 diffraction peaks (Fig. 1b and Fig. S1, ESI†) assuming a hexagonal lattice and taking into account the overlapped Au 220 diffraction peak. The cation composition is measured using X-ray fluorescence analysis calibrated with calibration standards and homogeneous Al_0.7Sc_0.3N and Al_0.6Sc_0.4N films. Cross-sectional transmission electron microscope (TEM) specimens were prepared by focused ion beam (FIB) in an FEI Nova NanoLab 200 dual beam FIB workstation using standard lift-out methods.⁷⁰ Final thinning of the TEM specimen was done in the FIB with a Ga+ beam energy of 5 kV and current of 41 pA. Cross-sectional TEM micrographs were acquired on a Philips CM30 TEM operated at 300 kV accelerating voltage. For electrical characterizations, top Au/Ti contacts are deposited on the film via electron beam evaporation through a shadow mask. Current–voltage (I–V) curves are measured using a bent probe whose gauge is ∼300 μm contacting the bare surface of the library and a second probe contacting the exposed bottom Pt electrode. The applied voltage is a DC step function with delay time 0.1 s. Ferroelectric properties of the Au/Al_1−xSc_xN/Pt stacks were collected using a Precision Multiferroic system from Radiant Technologies. High throughput data analysis is carried out using COMBigor,⁷¹ the files have been harvested using research data infrastructure (RDI),⁷² and will be made publicly available through High Throughput Experiment Materials Database (HTEM DB).⁷³

4.3 DFT calculation

Special quasirandom structures (SQS)⁷⁴ were used to model the wurtzite Al_1−xSc_xN alloys at 8 different compositions in the range x = 0.056–0.389. SQSs are constructed through a stochastic search over many possible configurations of local environments within the chosen supercell to best reproduce the pairwise correlation of random alloys. The SQS supercells at each composition were constructed with the Alloy Theoretic Automated Toolkit (ATAT) code.⁷⁵ Following the methodology in a previous study,⁴³ we constructed 72-atom SQS supercells and performed structural relaxations (volume, cell shape, and atomic positions) with density functional theory (DFT). The DFT calculations were performed with the Vienna Ab Initio Software (VASP) package.⁷⁶ The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)⁷⁷ was used as the exchange-correlation functional with a plane-wave energy cutoff of 340 eV. The supercells were relaxed with Γ-centered k-point mesh. The electron localization function (ELF) and Bader charges were calculated on a dense k-mesh with a fixed number of k-points. The k-point grid is determined according to the equation n_kpts × n_atoms ≈ 8000, where n_kpts is the number of k-points and n_atoms is the number of atoms in the supercell. The Bader charges were calculated using the code developed by Henkelman and coworkers.⁷⁸ For calculating the Born effective charges, the SQS supercells were relaxed with stricter convergence criteria; a higher plane-wave energy cutoff of 520 eV and k-point grid corresponding to n_kpts × n_atoms ≈ 2000 was used. The structures were relaxed until the energies were converged to below 10⁻⁸ eV and forces below 0.005 eV A⁻¹. Born effective charges were calculated with density functional perturbation theory, as implemented in VASP.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was co-authored by Colorado School of Mines and the National Renewable Energy Laboratory, operated by the Alliance for Sustainable Energy, LLC, for the US Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding was provided by the Office of Science (SC), Office of Basic Energy Sciences (BES) as part of the Early Career Award “Kinetic Synthesis of Metastable Nitrides” (material synthesis); and by the DARPA Tunable Ferroelectric Nitrides (TUFEN) program (DARPA-PA-19-04-03) as a part of Development and Exploration of FerroElectric Nitride Semiconductors (DEFENSE) project (structural and electrical characterization). K. Y., P. G., G. L. B., and A. Z. also acknowledge support for electrical measurements and theoretical calculations from NSF through the DMREF program award DMR-2119281. The data affiliated with this study are available from the corresponding author upon reasonable request. The views expressed in the article do not necessarily represent the views of the DOE or the US Government.

References

1. J. Valasek, Phys. Rev., 1921, 17, 475–481.
2. K. Uchino, Ferroelectric Devices, Marcel Dekker; New York, 2000.
3. I. Burn and D. M. Smyth, J. Mater. Sci., 1972, 7, 339–343.
4. P. Muralt, J. Micromech. Microeng., 2000, 10, 136–146.
5. H. A. Sodano, D. J. Inman and G. Park, Shock Vib. Dig., 2004, 36, 197–205.
6. M. DiDomenico and S. H. Wemple, J. Appl. Phys., 1969, 40, 720–734.
7. M. H. Lee, R. Guo and A. S. Bhalla, J. Electroceram., 1998, 2, 229–242.
8. J. F. Scott and C. A. Paz De Araujo, Science, 1989, 246, 1400–1405.
9. S. Trolier-Mckinstry and P. Muralt, J. Electroceram., 2004, 12, 7–17.
10. R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21–29.
11. S. Y. Yang, J. Seidel, S. J. Byrnes, P. Shafer, C. H. Yang, M. D. Rossell, P. Yu, Y. H. Chu, J. F. Scott, J. W. Ager, L. W. Martin and R. Ramesh, Nat. Nanotechnol., 2010, 5, 143–147.
12. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051.
13. M. Hoffmann, F. P. G. Fengler, M. Herzig, T. Mittmann, B. Max, U. Schroeder, R. Negrea, L. Pintilie, S. Slesazeck and T. Mikolajick, Nature, 2019, 565, 464–467.
14. A. K. Yadav, C. T. Nelson, S. L. Hsu, Z. Hong, J. D. Clarkson, C. M. Schlepuëtz, A. R. Damodaran, P. Shafer, E. Arenholz, L. R. Dedon, D. Chen, A. Vishwanath, A. M. Minor, L. Q. Chen, J. F. Scott, L. W. Martin and R. Ramesh, Nature, 2016, 530, 198–201.
15. C. Dai, V. A. Stoica, S. Das, Z. Hong, L. W. Martin, R. Ramesh, J. W. Freeland, H. Wen, V. Gopalan and L. Chen, Adv. Mater., 2022, 34, 2106401.
16. L. Qi, S. Ruan and Y. Zeng, Adv. Mater., 2021, 33, 2005098.
17. H. Ishiwara, Y. Aoyama, S. Okada, C. Shimamura and E. Tokumitsu, Comput. Electr. Eng., 1997, 23, 431–438.
18. S. Oh, H. Hwang and I. K. Yoo, APL Mater., 2019, 7, 091109.
19. Y. W. Fang, C. A. J. Fisher, A. Kuwabara, X. W. Shen, T. Ogawa, H. Moriwake, R. Huang and C. G. Duan, Phys. Rev. B, 2017, 95, 014111.
20. S. Fichtner, N. Wolff, F. Lofink, L. Kienle and B. Wagner, J. Appl. Phys., 2019, 125, 114103.
21. C. Gui and S. Dong, Phys. Rev. B, 2020, 102, 180103.
22. K. R. Talley, C. L. Perkins, D. R. Diercks, G. L. Brennecka and A. Zakutayev, Science, 2021, 374, 1488–1491.
23. R. Sherbondy, R. W. Smaha, C. J. Bartel, M. E. Holtz, K. R. Talley, B. Levy-Wendt, C. L. Perkins, S. Eley, A. Zakutayev and G. L. Brennecka, Chem. Mater., 2022, 34, 6883–6893.
24. M. Akiyama, T. Kamohara, K. Kano, A. Teshigahara, Y. Takeuchi and N. Kawahara, Adv. Mater., 2009, 21, 593–596.
25. S. Yasuoka, T. Shimizu, A. Tateyama, M. Uehara, H. Yamada, M. Akiyama, Y. Hiranaga, Y. Cho and H. Funakubo, J. Appl. Phys., 2020, 128, 114103.
26. J. Hayden, M. D. Hossain, Y. Xiong, K. Ferri, W. Zhu, M. V. Imperatore, N. Giebink, S. Trolier-Mckinstry, I. Dabo and J. P. Maria, Phys. Rev. Mater., 2021, 5, 044412.
27. K. Yazawa, D. Drury, A. Zakutayev and G. L. Brennecka, Appl. Phys. Lett., 2021, 118, 162903.
28. S. Rassay, F. Hakim, C. Li, C. Forgey, N. Choudhary and R. Tabrizian, Phys. Status Solidi RRL, 2021, 15, 2100087.
29. S. L. Tsai, T. Hoshii, H. Wakabayashi, K. Tsutsui, T. K. Chung, E. Y. Chang and K. Kakushima, Jpn. J. Appl. Phys., 2021, 60, SBBA05.
30. R. Mizutani, S. Yasuoka, T. Shiraishi, T. Shimizu, M. Uehara, H. Yamada, M. Akiyama, O. Sakata and H. Funakubo, Appl. Phys. Express, 2021, 14, 105501.
31. S. Yasuoka, T. Shimizu, A. Tateyama, M. Uehara, H. Yamada, M. Akiyama and H. Funakubo, Phys. Status Solidi A, 2021, 218, pssa.202100302.
32. R. C. Pullar, in Springer Series in Materials Science, Springer Verlag, 2015, vol. 225, pp. 241–270.
33. M. L. Green, I. Takeuchi and J. R. Hattrick-Simpers, J. Appl. Phys., 2013, 113, 231101.
34. I. Takeuchi, H. Chang, C. Gao, P. G. Schultz, X. D. Xiang, R. P. Sharma, M. J. Downes and T. Venkatesan, Appl. Phys. Lett., 1998, 73, 894–896.
35. H. Chang, C. Gao, I. Takeuchi, Y. Yoo, J. Wang, P. G. Schultz, X. D. Xiang, R. P. Sharma, M. Downes and T. Venkatesan, Appl. Phys. Lett., 1998, 72, 2185–2187.
36. M. Murase, T. Yoshimura and N. Fujimura, Jpn. J. Appl. Phys., 2020, 59, SPPC05.
37. S. Fujino, M. Murakami, V. Anbusathaiah, S. H. Lim, V. Nagarajan, C. J. Fennie, M. Wuttig, L. Salamanca-Riba and I. Takeuchi, Appl. Phys. Lett., 2008, 92, 202904.
38. D. Kan, R. Suchoski, S. Fujino and I. Takeuchi, in Integrated Ferroelectrics, Taylor & Francis Group; 2009, vol. 111, pp. 116–124.
39. K. W. Kim, M. K. Jeon, K. S. Oh, T. S. Kim, Y. S. Kim and S. I. Woo, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1134–1139.
40. M. Sasaki, S. Ju, Y. Xu, J. Shiomi and M. Goto, ACS Comb. Sci., 2020, 22, 782–790.
41. D. Solonenko, C. Lan, C. Schmidt, C. Stoeckel, K. Hiller and D. R. T. Zahn, J. Mater. Sci., 2020, 55, 17061–17071.
42. D. Drury, K. Yazawa, A. Mis, K. Talley, A. Zakutayev and G. L. Brennecka, Phys. Status Solidi RRL, 2021, 15, 2100043.
43. K. R. Talley, S. L. Millican, J. Mangum, S. Siol, C. B. Musgrave, B. Gorman, A. M. Holder, A. Zakutayev and G. L. Brennecka, Phys. Rev. Mater., 2018, 2, 063802.
44. K. Furuta, K. Hirata, S. A. Anggraini, M. Akiyama, M. Uehara and H. Yamada, J. Appl. Phys., 2021, 130, 024104.
45. Y. Lu, M. Reusch, N. Kurz, A. Ding, T. Christoph, M. Prescher, L. Kirste, O. Ambacher and A. Žukauskaitė, APL Mater., 2018, 6, 076105.
46. G. Arlt, Ferroelectrics, 1990, 104, 217–227.
47. C. A. Randall, N. Kim, J.-P. Kucera, W. Cao and T. R. Shrout, J. Am. Ceram. Soc., 1998, 81, 677–688.
48. F. Xu, S. Trolier-McKinstry, W. Ren, B. Xu, Z.-L. Xie and K. J. Hemker, J. Appl. Phys., 2001, 89, 1336–1348.
49. K. Yazawa, H. Uchida and J. E. Blendell, Adv. Funct. Mater., 2020, 30, 1909100.
50. S. Yang, J. Li, Y. Liu, M. Wang, L. Qiao, X. Gao, Y. Chang, H. Du, Z. Xu, S. Zhang and F. Li, Nat. Commun., 2021, 12, 1–10.
51. D. Gall, M. Städele, K. Järrendahl, I. Petrov, P. Desjardins, R. T. Haasch, T. Y. Lee and J. E. Greene, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 1251191–1251199.
52. H. A. Al-Brithen, H. Yang and A. R. Smith, J. Appl. Phys., 2004, 96, 3787–3792.
53. S. Y. Yang, F. Zavaliche, L. Mohaddes-Ardabili, V. Vaithyanathan, D. G. Schlom, Y. J. Lee, Y. H. Chu, M. P. Cruz, Q. Zhan, T. Zhao and R. Ramesh, Appl. Phys. Lett., 2005, 87, 102903.
54. H. Naganuma, Y. Inoue and S. Okamura, Appl. Phys. Express, 2008, 1, 0616011–0616013.
55. J. F. Scott, Integr. Ferroelectr., 1996, 12, 71–81.
56. K. Yazawa, A. Zakutayev and G. L. Brennecka, Appl. Phys. Lett., 2022, 121, 042902.
57. I. W. Chen, J. Phys. Chem. Solids, 2000, 61, 197–208.
58. L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582.
59. N. Mammen, L. Spanu, E. C. Tyo, B. Yang, A. Halder, S. Seifert, M. J. Pellin, S. Vajda and S. Narasimhan, J. Phys.: Condens. Matter, 2019, 31, 144002.
60. J. P. Allen, D. O. Scanlon and G. W. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161103.
61. H. Moriwake, R. Yokoi, A. Taguchi, T. Ogawa, C. A. J. Fisher, A. Kuwabara, Y. Sato, T. Shimizu, Y. Hamasaki, H. Takashima and M. Itoh, APL Mater., 2020, 8, 121102.
62. N. A. Spaldin, J. Solid State Chem., 2012, 195, 2–10.
63. C. E. Dreyer, A. Janotti, C. G. Van de Walle and D. Vanderbilt, Phys. Rev. X, 2016, 6, 021038.
64. O. Ambacher, B. Christian, N. Feil, D. F. Urban, C. Elsässer, M. Prescher and L. Kirste, J. Appl. Phys., 2021, 130, 045102.
65. H. Wang, N. Adamski, S. Mu and C. G. Van de Walle, J. Appl. Phys., 2021, 130, 104101.
66. M. A. Caro, S. Zhang, T. Riekkinen, M. Ylilammi, M. A. Moram, O. Lopez-Acevedo, J. Molarius and T. Laurila, J. Phys.: Condens. Matter, 2015, 27, 245901.
67. K. Ferri, S. Bachu, W. Zhu, M. Imperatore, J. Hayden, N. Alem, N. Giebink, S. Trolier-McKinstry and J.-P. Maria, J. Appl. Phys., 2021, 130, 044101.
68. J. Jia and T. Yanagitani, Phys. Rev. Appl., 2021, 16, 044009.
69. K. Hirata, Y. Mori, H. Yamada, M. Uehara, S. A. Anggraini and M. Akiyama, Materials, 2021, 14, 309.
70. L. A. Giannuzzi, J. L. Drown, S. R. Brown, R. B. Irwin and F. A. Stevie, in Materials Research Society Symposium - Proceedings, MRS; 1997, vol. 480, pp. 19–27.
71. K. R. Talley, S. R. Bauers, C. L. Melamed, M. C. Papac, K. N. Heinselman, I. Khan, D. M. Roberts, V. Jacobson, A. Mis, G. L. Brennecka, J. D. Perkins and A. Zakutayev, ACS Comb. Sci., 2019, 21, 537–547.
72. K. R. Talley, R. White, N. Wunder, M. Eash, M. Schwarting, D. Evenson, J. D. Perkins, W. Tumas, K. Munch, C. Phillips and A. Zakutayev, Patterns, 2021, 2, 100373.
73. A. Zakutayev, N. Wunder, M. Schwarting, J. D. Perkins, R. White, K. Munch, W. Tumas and C. Phillips, Sci. Data, 2018, 5, 1–12.
74. A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356.
75. A. van de Walle, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2009, 33, 266–278.
76. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
77. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
78. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 7.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc02682a

---