Open Access Article
Open Access ArticleSingle-entity coccolithophore electrochemistry shows size is no guide to the degree of calcification†
Minjun
Yang
a,
Christopher
Batchelor-McAuley
 a,
Samuel
Barton
b,
Rosalind E. M.
Rickaby
b,
Heather A.
Bouman
b and
Richard G.
Compton
a,
Samuel
Barton
b,
Rosalind E. M.
Rickaby
b,
Heather A.
Bouman
b and
Richard G.
Compton
 *a
*a
aPhysical and Theoretical Chemistry Laboratory, Department of Chemistry, University of Oxford, South Parks Road, Oxford, UK. E-mail: Richard.Compton@chem.ox.ac.uk
bDepartment of Earth Sciences, University of Oxford, South Parks Road, Oxford, UK
First published on 30th March 2022
Abstract
We report single-entity measurements of the degree of calcification of individual phytoplankton cells. Electrogenerated acid is used to dissolve the calcium carbonate (CaCO3) shell (coccosphere) of individual coccolithophores and the changes in size are monitored by simultaneous optical measurements, allowing the CaCO3 content of the single phytoplankton cell to be inferred via analysis of the dissolution kinetics. Three species of coccolithophore, E. huxleyi, G. oceanica and C. braarudii, were studied with CaCO3 masses measured over 3 orders of magnitude ranging from 2.6 pg to 8.3 ng of CaCO3 per cell. Surprisingly, within a species, the CaCO3 content is not correlated to the size of the coccosphere but the volume of its shell. Further, the variation of the CaCO3 content with the cell size and the particulate inorganic carbon (PIC) to particulate organic carbon (POC) ratio at different stages of the growth phase is reported.
Environmental significanceMarine calcifiers, coccolithophores, are responsible for sequestering more than 1015 g of atmospheric CO2 per year to the deep ocean as CaCO3. This is directly comparable to the rate of released by humans. Coccolithophores play a crucial part in the marine carbon cycle and are jeopardised by climate change. There is currently no way of measuring the mass of biogenic calcite of individual coccolithophores. This work presents a proof-of-concept approach combining optics with electro-generated acid to “titrate” the biogenic calcite of each of the coccolithophores. The amount of acid reacted reveals the mass of biogenic calcite (pico- to nano-grams) and we show that, surprisingly, size is no good indication of the calcification degree. |
Introduction
Single-entity measurement is often the ultimate challenge in any scientific discipline. At the most basic level, characterising the behaviour of a single unit in any system, for example, in catalysis, cellular biology, enzyme or reaction kinetics, allows the ensemble response to be better understood and optimised. In the modern era, with advances in electronic components and with a large arsenal of redox systems at the user's disposal, electrochemistry has claimed notable successes in stochastic measurements1 in the detection of, but not limited to, single nanoparticles,2 electrocatalysis,3,4 red blood cells,5 bacteria6,7 and viruses.8In the world's ocean, calcifying marine phytoplankton – coccolithophores – play a crucial role in the global carbon cycle9 owing to their ability to sequester in excess of 1015 g of CaCO3 to the deep ocean per annum.10,11 For the past tens of millions of years, coccolithophores, alongside foraminifera, have been the dominant pelagic calcifiers.10 These microscopic unicellular species bioaccumulate elaborate plates of CaCO3 (coccoliths) in open-surface waters ultimately encrusting themselves with inter-locking coccoliths (coccospheres, Fig. 1).12 The dense CaCO3 shell (particulate inorganic carbon, PIC) act as ‘ballast’ and provides protection towards bio-remineralization of particulate organic carbon (POC) as it traverses down the water column forming a continuous flux of carbon to the deep, where it is stored for millennia.13,14
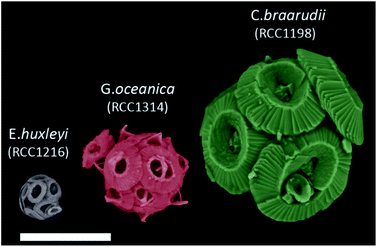 | ||
| Fig. 1 False coloured SEM images of E. huxleyi, G. oceanica and C. braarudii coccosphere at day 9 of incubation. Scale bar = 10 μm. | ||
This ability of the ocean to sequester atmospheric CO2 to the deep is generally referred to as the biological carbon pump.15,16 This occurs at a global scale and the rate of CO2 export to the deep ocean is directly comparable to that released by man-kind.17 However, the ability of coccolithophores to continue to biomineralize CaCO3 (PIC) under conditions of “climate crisis” is unclear due to different species- and strain-specific responses towards changes such as pH, illumination and sea surface temperature conditions.18 The mass of particulate inorganic and organic carbon sequestered by coccolithophores, PIC and POC respectively, and also the ‘rain-ratio’ of PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC, provides crucial information to feed into global models of the carbon cycle for accurate assessment of the impacts of anthropogenic change.19,20
POC, provides crucial information to feed into global models of the carbon cycle for accurate assessment of the impacts of anthropogenic change.19,20
Coccoliths are the predominant form of CaCO3 on the ocean floor with ancient fossils dating as far back as 225 million years.21 Single coccoliths may become detached from coccolithophores either during the lifecycle of the latter or after cellular death. Although existing techniques allow the PIC content of individual coccoliths to be either measured22–24 or estimated,25 this, ultimately, provides calcification information about the past, not the present. To monitor and predict the imminent threat of climate change on our dominant open-ocean calcifiers we must quantify the PIC content bioaccumulated by coccolithophores in the present marine environment. Currently, there are two methods to quantify PIC contents per coccolithophore. First, an ensemble of coccolithophores is filtered and treated, or not, with acid, with the difference in the carbon mass between the two samples measured via, for example, elemental analysis providing the total CaCO3 content of the ensemble prior to acid dissolution.26,27 By dividing the total PIC content of the ensemble by the estimated number of coccolithophore cells present, a PIC cell−1 value can be estimated. Second, alternatively, by obtaining the average coccolith mass from either direct measurements or an estimation of the average coccolith length and shape factor,25 the PIC content of a coccolithophore can be approximated by multiplying by the estimated number of coccoliths.28,29 Note that the size of the coccoliths on any coccolithophore can vary by up to ∼50%30 and the number of coccolith per cell can only be estimated if the number of coccoliths can be seen, which is not possible via traditional scanning electron microscopy (SEM),26 which inevitably precludes the 3-dimensional imaging needed. However, more sophisticated 3D techniques such as X-ray nanotomography30 and focused ion beam combined with SEM31 allows individual coccolithophores to be reconstructed in 3D, thus providing a measure of individual coccolithophore PIC contents, but such approaches are extremely expensive and time consuming.
More recently, proof-of-concept electrochemical methods have shown their ability to identify, in combination with fluorescence spectroscopy, the speciation of marine phytoplankton and,32 separately, single-entity measurement of detached coccolith CaCO3 masses.22 In the present study, electrochemistry is utilised to provide a high-throughput single-entity PIC content measurement of living coccolithophores. Herein, acid is generated electrochemically to dissolve away the CaCO3 shell of the individual coccolithophores to reveal the underlying ‘naked’ cell. In situ optical imaging reveals the dissolution kinetics which is used to accurately infer the PIC content of coccolithophores on a single-entity basis. Then the size of the ‘naked’ cell after complete acid dissolution, as measured by optics, provides an estimation of POC content which, in combination with the former measurement, allows the ratio of PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC to be inferred.
POC to be inferred.
Experimental section
See ESI.†Results and discussion
The following work utilises electrochemistry to induce acid dissolution of three coccolithophores species revealing their biomineralized calcium carbon contents (CaCO3, PIC) on a single-entity basis. The three species under investigation are Emiliania huxleyi, Gephyrocapsa oceanica and Coccolithus pelagicus subsp. braarudii. By dissolving away the CaCO3via electrogenerated acid with optical imaging, a range of cellular properties are extracted on a single-entity basis: plankton size before and after complete acid dissolution revealing the shell thickness and size of the underlying biological cell, PIC content of the calcareous shell and an estimation of the PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio. Moreover, these experiments are conducted at different parts of the growth curve to reveal the variation of the above-mentioned properties due to the change in physiology.
POC ratio. Moreover, these experiments are conducted at different parts of the growth curve to reveal the variation of the above-mentioned properties due to the change in physiology.
Fig. 1 shows representative SEM images of the three species of coccolithophores at day 9 of growth. The largest of the three species, C. braarudii, measures ∼20 μm in diameter whereas E. huxleyi is approximately 4 times smaller with a diameter of around 5 μm. Moreover, from the SEM images, one can see that on an individual coccolith level, not only the size differs from one species to another, but there is also a change in both the morphology and ‘solidity’ of the coccoliths produced. Fig. S1† shows the surface elemental mapping of the three coccolithophores using energy-dispersive X-ray microscopy (EDX). A relatively high ratio atom percentage of carbon (∼35%) and oxygen (∼53%) was measured to that of calcium (∼10%) for pure CaCO3. Note that this ratio is not reflective of the entire coccosphere as EDX rays penetrate only microns below the surfaces. The high ratio of measured carbon and oxygen signal, compared to that expected from CaCO3, likely reflects the polysaccharide present on the surface of coccoliths, which accounts for less than 3% of the coccolith by mass.33
To estimate the total PIC content of the coccospheres, at the crudest level one might initially simply assume the coccosphere is a solid ‘ball’ of calcite and upscale the measured radius (r) obtained via SEM or other imaging techniques, by the density of calcite (ρCaCO3 = 2.71 g cm−3 (ref. 34))
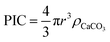 | (1) |
This, however, over-estimates the CaCO3 mass because first, the underlying biological cell is particulate organic carbon (POC) and should be separated from PIC calculation, second, due to the nature of interlocking coccoliths the unfilled voids are not accounted for, and third, coccoliths are not perfect discs and therefore the volume of each disc is smaller than a short-cylinder of the same geometric size. To overcome these challenges, we dissolve away the calcareous shell by generating acid controllably via electrochemistry whilst imaging the changes in the coccolithophore via in situ optical imaging.
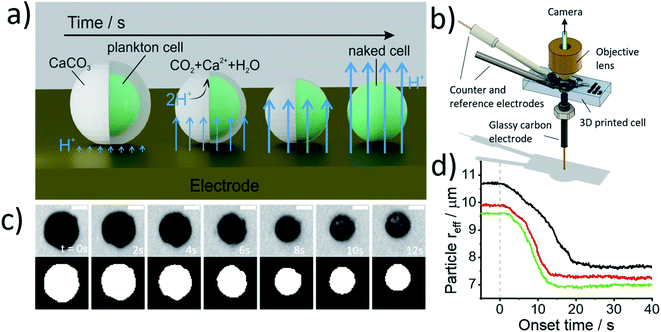
Fig. 2a illustrates the physicochemical processes that occur in such opto-electrochemical experiments. A coccolithophore residing on the electrode is exposed to electrogenerated acid which reacts with the calcareous shell of the coccolithophore leading to the full dissolution of the latter revealing the underlying ‘naked’ cell. Under strong acid conditions, acid dissolution of calcite goes to completion and consumes two stoichiometric equivalents of protons35
| CaCO3(s) + 2H+(aq) → Ca2+(aq) + CO2(g) + H2O(l) | (2) |
Fig. 2b shows the 3D-printed cell in which the opto-electrochemical experiments were conducted. The 3D-printed cell facilitates a three-electrode setup with a reaction chamber approximately 1 cm3 in volume and is fully discussed in the Experimental section in the ESI.† Synchronised optical images of the coccolithophores are taken following the switch-on of the electrochemical proton formation revealing the dissolution of each coccosphere present on the electrode surface to allow single-entity measurements to be made. Kinetic information is inferred by monitoring the shrinkage of the CaCO3 shell and allows the total PIC content of the coccosphere to be calculated, as discussed below, and the size of the ‘naked’ coccolithophore cell provides an estimate for the particulate organic carbon (POC) content, as will also be discussed below.
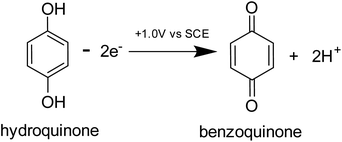
Prior to the electrochemical dissolution, coccolithophore samples were dropcasted onto a glassy carbon electrode (diameter = 3 mm). The surface of the electrode acts as a supporting substrate for the coccolithophores and as a mean for electrochemically generating acid. The solution chamber was then filled with 0.7 M KCl inert electrolyte with 20 mM Ca2+ and millimolar concentrations of hydroquinone (2 mM for G. oceanica and E. huxleyi, and 10 mM for C. braarudii). 20 mM of Ca2+ was used to prevent the dissolution of biogenic calcite prior to the start of the experiment, discussed in detail in ESI Section 3,† and hydroquinone was used as an acid precursor which releases two stoichiometric equivalents of protons when electrochemically oxidised at the electrode interface (Scheme 1).22
Shown in Fig. 2c are optical images of a representative C. braarudii coccosphere undergoing electrochemically induced acid dissolution with 10 mM of hydroquinone. The top row of images shown in Fig. 2c are raw images obtained directly from the camera and the bottom row are those after image thresholding which is used to calculate the effective radius of the coccosphere during the experiment, assuming a perfect circle (area = πreff2, where reff is the radius of a circle of equivalent area to the image of the coccolithophore). An anodic potential of +1.0 V vs. saturated calomel electrode (SCE) was applied to the working electrode to initiate the release of a local concentration of approximately millimolar of H+. As can be seen in Fig. 2c, within tens of seconds of the acid generation, the calcium carbonate shell of the coccolithophore is seen to dissolve completely to reveal the underlying ‘naked’ biological cell. The cell-wall composition of the ‘naked’ cell is typically cellulose or similar polysaccharide based.36 The change in the effective coccolithophore radius, reff(t), is plotted in Fig. 2d for three representative C. braarudii coccospheres studied after 9 days of growth (see ESI Section 1† for cell cultures). The effective coccosphere radius, reff, is seen to decrease quasi-linearly as a function of time after the generation of acid until it reaches a constant value of around 7–8 μm. It is clear that the decrease in coccolithophore size is associated with the acid-dissolution of biogenic calcite (eqn (2)) and the underlying biological cell is ‘inert’ to acid attack over the timescale of this experiment. Before the calcite dissolution kinetics are discussed, first, on the most basic level, the reff(t) transients provide direct physiological properties of the coccolithophore, size with and without the shell.
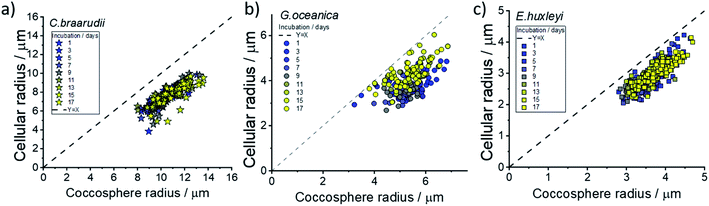
Fig. 3 plots the size of the individual coccolithophores measured optically, before and after, complete acid dissolution. Each data point represents data for an individual coccolithophore and the colour represents the ‘age’ of the culture sample from day 1 (blue) to day 17 (yellow) since the initial inoculation. Note that data below the dashed reference line is an indication of some form of a calcareous shell, which is dissolved under acid attack. The size of the coccolithophores, before and after complete acid dissolution, is in agreement with that seen under SEM and decreases in the order of: C. braarudii > G. oceanica > E. huxleyi. Due to the limitation of the wavelength of light used in optical measurements, the sizing measured herein is found to overestimate by approximately 0.5 μm as compared to those measured in SEM. This is fully discussed as part of the measurement uncertainties in ESI Section 5.† As can be seen in Fig. 3, the distribution of coccosphere and cellular size of C. braarudii and E. huxleyi are relatively invariant over 17 days of growth. On the other hand, towards the later stage of the growth phase, a thinner calcareous shell is seen on G. oceanica coccospheres. Separately, when the experiments were conducted in Ca2+-free electrolytes, the predominant data points for E. huxleyi and G. oceanica in their early growth phase overlay on the y = x reference line (Fig. S3†). This is because the time required to set up the opto-electrochemical experiment after filling the reaction chamber with Ca2+-free electrolyte, which is approximately 1–2 minutes, is sufficient to dissolve away the biomineralized CaCO3 prior to the onset of electro-generation of acid at t = 0. In the later growth phase, however, E. huxleyi and G. oceanica were not completely ‘deshelled’ in Ca2+-free electrolyte at the onset of the electro-generated acid. This is likely because of a higher number density of coccospheres, and detached coccoliths, present on the surface of the electrode resulting in an overlap of the diffusion field37,38 causing a local saturation of Ca2+ and HCO3−. Complete ‘deshelling’ of the C. braarudii coccospheres was not seen by the exposure of 1–2 minutes in Ca2+-free electrolyte. This likely reflects a much larger quantity of calcite is present on C. braarudii as revealed below. Having discussed the physicochemical processes that occur in the opto-electrochemical experiment, we next examine and discuss the different growth phases of the coccolithophores over 17 days following the initial inoculation.
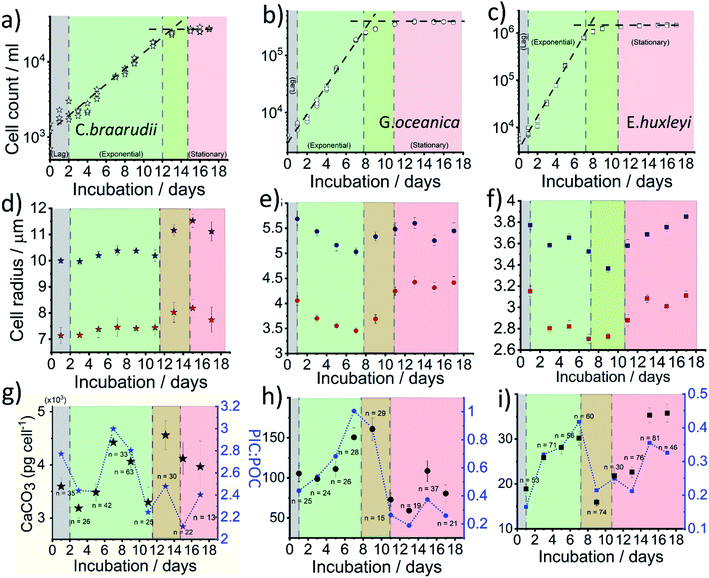
Fig. 4a–c plots the measured cellular density of the coccolithophores in the growth medium over a 17 day period following inoculation. For all three species, a ‘lag’ phase in growth is seen in days 0–1 as time is typically required for them to acclimate to the new culture environment.39 Between approximately days 2–10, cellular division is fast as can be inferred from the exponential increase in the number density until it reaches a plateau at 2 × 104, 3 × 105 and 1 × 106 cell per mL for C. braarudii, G. oceanica and E. huxleyi, respectively. Note that the culturing flask has a filter cap allowing air exchange but the total amount of nutrients is limited to what is initially present as detailed in ESI Section 1.† The plateau regime in the growth curve with no net increase in cell count is commonly known as the stationary phase39 and arises from either depletion of nutrients essential for cellular division, build-up of toxins or bacterial infection.40 Interestingly, it has been suggested that the invariance in the coccolithophore number density as seen across all three species in the stationary phase is not due to a balanced rate of ‘birth and death’, but arises because the cellular division rate slows to a halt.41 Despite the near net-zero cellular division, the coccolithophores continue to grow in size.41 The three above-mentioned growth phases, lag, exponential and stationary, are shown in Fig. 4. The green/red regime represents the transition from late-exponential into the early-stationary phase.
In situ optical measurements of the coccolithophores as the calcareous shell is being dissolved away by electrogenerated acid reveal, first, the size of the coccosphere and, at the end of the dissolution, the underlying biological cell. Fig. 4d and e shows the average coccolithophore radius optically measured before and after complete acid dissolution. A size decrease of both the coccosphere and the ‘naked’ cell are seen for G. oceanica and E. huxleyi during the exponential growth phase whilst a slight upward trend is seen for C. braarudii. As the rate of cellular division increases in the exponential phase, the growth time for the coccolithophores in between divisions are shortened. Consequently, this results in a decrease in cellular and coccosphere size for G. oceanica and E. huxleyi as each cellular division halves the biomass and coccoliths for individual plankton.42 This trend is, however, not seen for C. braarudii possibly due to a much slower cellular division rate as compared to G. oceanica and E. huxleyi. For all three species, in the stationary phase, an increase in both the coccosphere and cellular size are seen as cellular division slows to a halt, with excellent agreement with literature observations.40,43 Having discussed the physiological data directly extractable from the shape transient of the coccolithophore shown in Fig. 2d, next we discuss how the PIC content can be calculated for each individual coccolithophores.
At the start of the opto-electrochemical experiment, the onset of the electrochemical potential is jumped to drive the complete oxidation of hydroquinone to form two stoichiometric equivalents of protons at the electrode interface (eqn (2)). As shown schematically in Fig. 2a, the acid diffuses from the electrode to react with the calcareous shell of the coccolithophore, which in the following is treated as a calcite-organism “core–shell” particle with the shell being CaCO3. The total flux of proton, jtot (mol s−1) reacting with the coccosphere is controlled by (1) how fast the protons can diffuse to the particle, i.e. mass transport of protons, jMT (mol s−1) to a sphere on a plate,44 and (2), the rate of heterogeneous reaction of calcite with protons, jsurf (mol s−1)
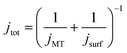 | (3) |
jMT = 8π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2)(DH2BQDH+)0.5cH2BQ,bulk(rsphere(t)) ln(2)(DH2BQDH+)0.5cH2BQ,bulk(rsphere(t)) |
| jsurf = 8πRf(rsphere(t))2k0cH2BQ,bulk(DH2BQ/DH+)0.5 |
The total number of moles of electrogenerated acid reacting with the calcareous shell per unit time during the experiment, jtot(t), can be calculated knowing rsphere(t), which is extracted from the experiment and shown in Fig. 2d. Thus, by knowing each CaCO3 reacts with 2 stoichiometric equivalents of protons, the total mass of calcite, or PIC per coccolithophore cell, can be calculated
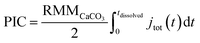 | (4) |
The CaCO3 contents (PIC) calculated for C. braarudii, G. oceanica and E. huxleyi are shown in Fig. 4g–i and 5 using an estimated surface roughness factor (Rf) of 4. See ESI Section 5† for a discussion of Rf and the extent of uncertainty this, among other factors, contribute towards the calculation of the CaCO3 mass. Fig. 4g–i plots the average CaCO3 mass plotted against days of growth for the three coccolithophore species and Fig. 5 shows individual coccolithophore CaCO3 mass versus the volume of the calcareous shell calculated measured before and after complete acid dissolution. Unsurprisingly, C. braarudii, the largest out of the three species, carries the most calcium carbonate (averaging 3.0–4.5 ng cell−1 at different parts of the growth curve), followed by G. oceanica (50–160 pg per cell) and E. huxleyi (15–35 pg per cell). These results are in good agreement with the CaCO3 masses estimated by multiplying the literature reported coccolith mass range25,30 by the expected number of ∼10–20 coccoliths per cell. The estimated CaCO3 per cell from literature reported coccolith values are shown in Fig. 5. For G. oceanica (Fig. 4h) and E. huxleyi (Fig. 4i), an increase in their average PIC content is clearly evidenced throughout their exponential growth followed by a drop in the PIC content as it transits into the stationary phase. In the stationary phase, an increase in PIC is seen for E. huxleyi but not for G. oceanica, no clear trend was seen for C. braarudii.
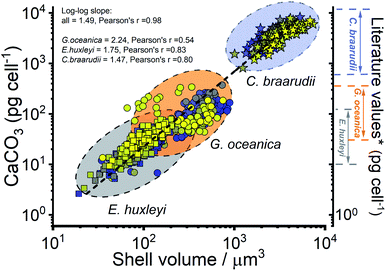 | ||
| Fig. 5 Calculated calcium carbonate content of individual coccospheres plotted against the shell volume of the coccolithophore, calculated using the size before and after complete acid dissolution. Note the log–log scale. Squares – E. huxleyi, circles – G. oceanica and stars – C. braarudii. *The range of literature values for CaCO3 mass per coccolithophore cell (pg per cell) were calculated by using the range of reported coccolith masses25,30 multiplied by an estimate of 10–20 coccoliths per cell. The colours of the symbols represent days of growth, from day 1 (blue) to day 17 (yellow), see the legends shown in Fig. 3. | ||
The organic carbon content of the phytoplankton cell is reported to be correlated positively with the volume of the phytoplankton cell48
| POC = 0.109V0.991 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio for the three species. To compare like for like, the value of PIC used to calculate PIC
POC ratio for the three species. To compare like for like, the value of PIC used to calculate PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio is converted to the inorganic carbon mass (PIC = CaCO3 mass cell−1 × 12.0/100.1). C. braarudii has the highest PIC
POC ratio is converted to the inorganic carbon mass (PIC = CaCO3 mass cell−1 × 12.0/100.1). C. braarudii has the highest PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio (2.0–3.0) followed by G. oceanica (0.2–1.0) and E. huxleyi (0.1–0.4). Interestingly, the PIC
POC ratio (2.0–3.0) followed by G. oceanica (0.2–1.0) and E. huxleyi (0.1–0.4). Interestingly, the PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio shows a similar trend to the calculated PIC as a function of phytoplankton growth.
POC ratio shows a similar trend to the calculated PIC as a function of phytoplankton growth.
Hitherto, physiological data of single-entity coccolithophores such as the coccosphere size, the internal cellular size, the quantity of PIC and POC are reported. It is clear that, between species, an increase in CaCO3 mass is seen for the bigger coccolithophores. But a question arises, as within a species, does the amount of biomineralized CaCO3 intraspecies scale with the size of the coccosphere? If so, knowing the speciation of the coccolithophore, could one then estimate the CaCO3 mass empirically using only the size information of the coccosphere analogues to POC as shown in eqn (5). For G. oceanica and E. huxleyi it is clear from Fig. 4 that the changes in the CaCO3 content along the growth curve (h and i) are not correlated with the coccosphere size (e and f). Specifically, during days 2–7 in the exponential growth an increase of CaCO3 cellular content are seen for G. oceanica and E. huxleyi but their respective coccosphere and naked cell size decreases. Moreover, as G. oceanica transits into the stationary phase (days 8–17) an increase in the average coccosphere size is seen but the CaCO3 content per cell drops. A closer look at Fig. 4d–f reveals that the size variation of the underlying ‘naked’ cell mirrors closely to that of the coccosphere prior to acid dissolution (cell + calcareous shell). In Fig. 5, a clear trend between the CaCO3 mass and the shell volume can be seen. The latter is calculated using the optically measured radius before and after complete acid dissolution assuming a spherical shell. Since the calcareous shell is composed of inter-locking coccoliths encrusting the underlying biological cell, it is perhaps unsurprising that the CaCO3 mass is not correlated to the initial coccosphere size (shell + cell), but to the volume of the calcareous shell.
Conclusion
Single-entity measurements of calcifying coccolithophores were realised via in situ opto-electrochemical acid-induced dissolutions. Simultaneous optical measurement of the coccolithophore before and after complete acid dissolution reveals the calcareous shell thickness and the size of the underlying ‘naked’ cell of the same coccolithophore. This allows the following single-entity measurements to be made: PIC calculated via calcite dissolution kinetics, POC estimated from the volume of the ‘naked’ cell and, hence, an estimation of the PIC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) POC ratio on a single-cell basis. We have noted the masses of biomineralized CaCO3 content of individual coccolithophores varies over 3-orders of magnitudes ranging from a few picograms (E. huxleyi) to tens of nanograms (C. braarudii). These weights are too small to be measured via traditional methods of ‘weighing’. Importantly, our data reveal that the calcification degree of the coccolithophore is not correlated with the size of the coccosphere but to the volume of the calcareous shell because the underlying biological cell scales proportionally with the coccosphere size. Therefore, it is impossible to resolve the calcification degree without this internal measurement.
POC ratio on a single-cell basis. We have noted the masses of biomineralized CaCO3 content of individual coccolithophores varies over 3-orders of magnitudes ranging from a few picograms (E. huxleyi) to tens of nanograms (C. braarudii). These weights are too small to be measured via traditional methods of ‘weighing’. Importantly, our data reveal that the calcification degree of the coccolithophore is not correlated with the size of the coccosphere but to the volume of the calcareous shell because the underlying biological cell scales proportionally with the coccosphere size. Therefore, it is impossible to resolve the calcification degree without this internal measurement.
Author contributions
Conceptualization: MY, CBM, RGC, REMR, HAB.Methodology: MY, CBM.
Experiment: MY (lead), SB (culture).
Formal analysis: MY.
Visualization: MY, CBM.
Supervision: RGC.
Writing—original draft: MY, CBM, RGC.
Writing—review & editing: MY, CBM, SB, RGC, REMR, HAB.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was carried out with the support of the Oxford Martin School Programme on Monitoring Ocean Ecosystems.Notes and references
- S. V. Sokolov, S. Eloul, E. Kätelhön, C. Batchelor-McAuley and R. G. Compton, Phys. Chem. Chem. Phys., 2017, 19, 28–43 RSC.
- Y.-G. Zhou, N. V. Rees, J. Pillay, R. Tshikhudo, S. Vilakazi and R. G. Compton, Chem. Commun., 2011, 48, 224–226 RSC.
- W. Yu, C. Batchelor-McAuley, X. Chang, N. P. Young and R. G. Compton, Phys. Chem. Chem. Phys., 2019, 21, 20415–20421 RSC.
- R.-C. Xie, M. Volokhova, A. Boldin, L. Seinberg, M. Tsujimoto, M. Yang, B. Rasche and R. G. Compton, ChemElectroChem, 2020, 7, 1261–1276 CrossRef CAS.
- L. Sepunaru, S. V. Sokolov, J. Holter, N. P. Young and R. G. Compton, Angew. Chem., Int. Ed., 2016, 55, 9768–9771 CrossRef CAS PubMed.
- S. Kuss, E. Tanner, M. Ordovas-Montanes and R. G. Compton, Chem. Sci., 2017, 8, 7682–7688 RSC.
- L. Sepunaru, K. Tschulik, C. Batchelor-McAuley, R. Gavish and R. G. Compton, Biomater. Sci., 2015, 3, 816–820 RSC.
- L. Sepunaru, B. J. Plowman, S. V. Sokolov, N. P. Young and R. G. Compton, Chem. Sci., 2016, 7, 3892–3899 RSC.
- U. Passow and C. A. Carlson, Mar. Ecol.: Prog. Ser., 2012, 470, 249–271 CrossRef CAS.
- J. D. Milliman, Global Biogeochem. Cycles, 1993, 7, 927–957 CrossRef CAS.
- K. M. Krumhardt, N. S. Lovenduski, M. C. Long, M. Levy, K. Lindsay, J. K. Moore and C. Nissen, J. Adv. Model. Earth Syst., 2019, 11, 1418–1437 CrossRef.
- A. R. Taylor, M. A. Russell, G. M. Harper, T. f. T. Collins and C. Brownlee, Eur. J. Phycol., 2007, 42, 125–136 CrossRef.
- R. A. Armstrong, C. Lee, J. I. Hedges, S. Honjo and S. G. Wakeham, Deep Sea Res., Part II, 2001, 49, 219–236 CrossRef.
- C. Klaas and D. E. Archer, Global Biogeochem. Cycles, 2002, 16, 63 CrossRef.
- T. Volk and M. I. Hoffert, The Carbon Cycle and Atmospheric CO2: Natural Variations Archean to Present, 1985, vol. 32, pp. 99–110 Search PubMed.
- M. Hain, D. Sigman and G. Haug, Treatise Geochem., 2014, 8, 485–517 Search PubMed.
- P. Friedlingstein, M. W. Jones, M. O'Sullivan, R. M. Andrew, D. C. Bakker, J. Hauck, C. Le Quéré, G. P. Peters, W. Peters and J. Pongratz, Earth Syst. Sci. Data Discuss., 2021, 1–191 Search PubMed.
- B. D'Amario, C. Pérez, M. Grelaud, P. Pitta, E. Krasakopoulou and P. Ziveri, Sci. Rep., 2020, 10, 1–14 CrossRef PubMed.
- A. Ridgwell, D. Schmidt, C. Turley, C. Brownlee, M. Maldonado, P. Tortell and J. Young, Biogeosciences, 2009, 6, 2611–2623 CrossRef CAS.
- J. J. Kharbush, H. G. Close, B. A. Van Mooy, C. Arnosti, R. H. Smittenberg, F. A. Le Moigne, G. Mollenhauer, B. Scholz-Böttcher, I. Obreht and B. P. Koch, Front. Mar. Sci., 2020, 7, 518 CrossRef.
- P. R. Bown, J. A. Lees and J. R. Young, in Coccolithophores, Springer, 2004, pp. 481–508 Search PubMed.
- M. Yang, C. Batchelor-McAuley, S. Barton, R. E. M. Rickaby, H. A. Bouman and R. G. Compton, Angew. Chem., 2021, 133, 21167–21174 CrossRef.
- M.-Á. Fuertes, J.-A. Flores and F. J. Sierro, Mar. Micropaleontol., 2014, 113, 44–55 CrossRef.
- L. Beaufort, N. Barbarin and Y. Gally, Nat. Protoc., 2014, 9, 633–642 CrossRef CAS PubMed.
- J. R. Young and P. Ziveri, Deep Sea Res., Part II, 2000, 47, 1679–1700 CrossRef.
- G. Langer, M. Geisen, K.-H. Baumann, J. Kläs, U. Riebesell, S. Thoms and J. R. Young, Geochem., Geophys., Geosyst., 2006, 7, Q09006 CrossRef.
- P. G. Matson, T. M. Ladd, E. R. Halewood, R. P. Sangodkar, B. F. Chmelka and M. D. Iglesias-Rodriguez, PLoS One, 2016, 11, e0162313 CrossRef PubMed.
- X. Jin, C. Liu, A. J. Poulton, M. Dai and X. Guo, Biogeosciences, 2016, 13, 4843–4861 CrossRef CAS.
- S. A. O'Dea, S. J. Gibbs, P. R. Bown, J. R. Young, A. J. Poulton, C. Newsam and P. A. Wilson, Nat. Commun., 2014, 5, 1–7 Search PubMed.
- T. Beuvier, I. Probert, L. Beaufort, B. Suchéras-Marx, Y. Chushkin, F. Zontone and A. Gibaud, Nat. Commun., 2019, 10, 1–8 CrossRef PubMed.
- R. Hoffmann, C. Kirchlechner, G. Langer, A. S. Wochnik, E. Griesshaber, W. W. Schmahl and C. Scheu, Biogeosciences, 2015, 12, 825–834 CrossRef.
- M. Yang, C. Batchelor-McAuley, L. Chen, Y. Guo, Q. Zhang, R. E. M. Rickaby, H. A. Bouman and R. G. Compton, Chem. Sci., 2019, 10, 7988–7993 RSC.
- M. Andersson, C. Hem, L. Schultz, J. Nielsen, C. Pedersen, K. Sand, D. Okhrimenko, A. Johnsson and S. Stipp, J. Phys. Chem. A, 2014, 118, 10720–10729 CrossRef CAS PubMed.
- J. W. Anthony, Handbook of Mineralogy: Borates, Carbonates, Sulfates, Mineral Data Pub, 1990 Search PubMed.
- K. Lund, H. S. Fogler, C. McCune and J. Ault, Chem. Eng. Sci., 1975, 30, 825–835 CrossRef CAS.
- C. E. Walker, S. Heath, D. L. Salmon, N. Smirnoff, G. Langer, A. R. Taylor, C. Brownlee and G. L. Wheeler, Front. Mar. Sci., 2018, 5, 306 CrossRef.
- T. J. Davies, C. E. Banks and R. G. Compton, J. Solid State Electrochem., 2005, 9, 797–808 CrossRef CAS.
- R. G. Compton and C. E. Banks, Understanding Voltammetry, World Scientific, Singapore, 2018 Search PubMed.
- G. E. Fogg and B. Thake, Algal Cultures and Phytoplankton Ecology, Univ of Wisconsin Press, 1987 Search PubMed.
- I. Zondervan, Deep Sea Res., Part II, 2007, 54, 521–537 CrossRef.
- S. J. Gibbs, A. J. Poulton, P. R. Bown, C. J. Daniels, J. Hopkins, J. R. Young, H. L. Jones, G. J. Thiemann, S. A. O'Dea and C. Newsam, Nat. Geosci., 2013, 6, 218–222 CrossRef CAS.
- C. E. Walker, A. R. Taylor, G. Langer, G. M. Durak, S. Heath, I. Probert, T. Tyrrell, C. Brownlee and G. L. Wheeler, New Phytol., 2018, 220, 147–162 CrossRef CAS PubMed.
- E. Paasche, Eur. J. Phycol., 1998, 33, 33–42 CrossRef.
- P. Bobbert, M. Wind and J. Vlieger, Phys. A, 1987, 141, 58–72 CrossRef.
- R. G. Compton and P. R. Unwin, Philos. Trans. R. Soc., A, 1990, 330, 1–45 CAS.
- R. G. Compton, K. L. Pritchard and P. R. Unwin, J. Chem. Soc., Chem. Commun., 1989, 249–251 RSC.
- R. G. Comptom, K. L. Pritchard and P. R. Unwin, Freshwater Biol., 1989, 22, 285–288 CrossRef.
- D. J. Montagnes, J. A. Berges, P. J. Harrison and F. Taylor, Limnol. Oceanogr., 1994, 39, 1044–1060 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d2va00025c |
| This journal is © The Royal Society of Chemistry 2022 |