Open Access Article
Open Access ArticleEvaluating the consistency of the TRMM over the rain gauge for drought monitoring in the semi-arid region of Karnataka, India, using statistical methods†
Sanjay
Kumar
 *,
S. A.
Ahmed
and
Jyothika
Karkala
*,
S. A.
Ahmed
and
Jyothika
Karkala

Department of Applied Geology, Kuvempu University, Shankaraghatta, India-577451. E-mail: mrsanjayror@gmail.com
First published on 9th August 2022
Abstract
Nowadays there is an increase in the utilization of satellite-based precipitation products which makes it crucial to examine the accuracy of such products. The current study aims at achieving the same by validating the quality of TRMM 3B43 data along with the ground-based gauge data in the analysis of drought conditions during the period 1998 to 2019. Even though both the grid datasets represent the same rainfall resolution (0.25° × 0.25°), there is an evident difference in the analysis outcome. Hence, drought indices such as RAI, MCZI, PN, and DI are used to compare the results of the TRMM and rain gauge. The rain gauge data tend to show more drought months under all categories, especially in severe drought in comparison to the TRMM for the RAI. Chikkanayakanahalli showed 115 months of severe drought from the rain gauge while the TRMM only showed 107 months. The maximum correlation of the data was found for the MCZI at 35.2% while the minimum was for the PN with R2 being 19.3%. Statistical methods helped to create a better picture of the reliability of the dataset. Variability in the Pearson correlation is greater from September to December for all indices.
Environmental significanceWith erratic increases in temperature and frequent occurrences of extreme events, it is crucial to combat the ill effects of climate change immediately. Drought being one of the frequent disasters poses a serious threat to all the components of the ecosystem and millions of lives are lost every year for this cause. This paper focuses on finding a suitable dataset for precipitation in order to analyse and monitor the precipitation extremes. Lack of drinking water, fail in agricultural outcome, and farmer suicides are the societal and environmental concerns that this research study aims to combat. The study suggests that a combination of both TRMM and ground based rainfall data provides the best detection of drought, especially in semiarid regions. |
Introduction
Climate change is continually adding pressure on the water system of the world drawing an even bigger focus on the study of extreme events. Dealing with such disasters on a global scale is crucial not only for the sustenance of the planet but also for the socio-economic scenario of the world due to the extreme events that we are witnessing with increasing frequency. Over the past couple of decades, there is an acute shortage of drinking water as a direct result of the prolonged periods of abnormally dry weather. There is an acceleration in the rate of drying up of freshwater resources along with a downward trend in the precipitation amount resulting in drought. Drought is a complex phenomenon impacted by various natural and human factors, and at the same time, it is very poorly understood. This draws our attention to the urgency in the need for evaluating and understanding the drought condition to escape from the trail of the havoc caused by drought. Quantifying the characteristic features of dry events is an important step in the study of drought. For this purpose, various drought indices are developed to analyze the magnitude, intensity, duration, and distribution of drought such as the rainfall anomaly index (RAI),1 standardised precipitation index (SPI),2 modified China Z index (MCZI),3 Palmer drought severity index (PDSI),4 decile index (DI),5 standardised precipitation evapotranspiration index (SPEI),6 percent of normal index (PN)7 and standardised runoff index (SRI).8 Drought indices are a crucial tool that facilitates studying drought and also the decision-making process. The selection of suitable and accurate data is crucial not only for the study of rainfall irregularities but also to arrive at appropriate mitigation methods and prediction models to deal with the anomalies. The importance of meteorological parameters, especially precipitation, in climate, hydrological and agricultural studies is immense. In order to fulfill the requirements of various fields of research, different rainfall data products have been proved successful. Large scale data sets are used to study the precipitation extreme at different temporal and spatial scales.9 To identify early warning signs of drought and develop a system for continuous monitoring in time and space, indices play a crucial role. Satellite data provide valuable information with better temporal resolution facilitating better monitoring but lacks long-term data availability. Many studies have emerged in recent years concerning the comparison of climate datasets. The comparative study of rainfall data from multiple data sources has been gaining popularity and a few are mentioned here. In the semi-arid region of Iran, rain gauge and TRMM rainfall data were used to compare the precipitation extremes by ref. 10. It was concluded that a method to solve the issue could not be arrived at. Ref. 11 worked on how applying bias correction methods to the TRMM data could enhance the dependability of the data and find wide application in the Himalayan region. Ref. 12 aimed at figuring out the possibility of using TRMM-3B42V6 and the point gauge data over the Ganga, Brahmaputra, and Meghna river basins in forecasting flood and predicting the changes in climate. Ref. 13 compared the reliability of the global satellite-based rainfall datasets such as CHIRPS, SM2RAIN-ASCAT, and TRMM in comparison to ground based gauge rainfall (IMD) data in India. The result found that the TRMM product was the closest to the IMD in comparison, while intensity-based indices showed that TRMM and CHIRPS were close to IMD data. During the southwest monsoon over the Indian land mass, the study by ref. 14 compared the IMERG product with the IMD gridded data. The IMERG adequately reflected the gauge data for very light and very heavy rain but proved unsatisfactory for depicting extreme heavy rain events. Ref. 15 assessed the GPM estimates over the Indian subcontinent where the study revealed that the performance of IMERG was better than that of TRMM even though both the products fell short of the ground based measurements. Monthly TRMM data have a better linear correlation with the rain gauge precipitation data over the daily TRMM dataset which shows a poor description of the occurrence and accuracy of precipitation in the Poyang Lake Basin, China.16 Ref. 17 evaluated the gauge data along with the satellite rainfall product in the Congo basin and concluded that gauge data provide greater reliability to estimate rainfall. In comparison to the TRMM 3B42 and CMORPH, the former had greater compatibility with the rain gauge data than the latter in the Amazon region as analyzed by ref. 18. The study carried out by ref. 19 in China brings to light the incapability of the 3B42 product in capturing extreme wet events, all the while as its accuracy falls with increasing intensity of rainfall. The correlation of TRMM-3B42V7 with other products as mentioned by ref. 20 was higher on the monthly scale rather than a weekly or daily time period in regions of Ecuador and Peru. Satellite products when infused with gauge correction show a significant enhancement in the reliability of data by bringing down the bias in the prediction of hydrological parameters especially in mountainous areas as analysed by ref. 21. Ref. 22 deduced that between the rain gauge data and 3B42 and 3B43, the correlation was better in the dry season while the level of statistical error was much better during the wet season over the Bali Island. In Thailand, the difference between the gauge and TRMM-3B42 and TRMM-3B43 were analyzed by ref. 23 resulting in 3B43 having less bias than 3B42 concerning gauge data along with apparent seasonal and regional differences.Tumakuru district in Karnataka, being a semi-arid region, is often prone to drought, which in turn has caused huge agricultural loss. Over the past decade, farmer suicides have persisted in being a reason for major concern. One of the ways to turn the tables on the situation is to build a better prediction model along with devising mitigation methods. To fulfill this objective, (1) this study aims at validating ground and satellite-based rainfall products in the analysis of meteorological drought. (2) The rain gauge data from the IMD along with TRMM-3B43 monthly precipitation data are utilized to derive various drought indices such as the DI, PN, MCZI, and RAI. (3) In addition to this, statistical methods like correlation, t-test, and RMSE are employed to evaluate the variations in the output from both datasets.
Study area and data
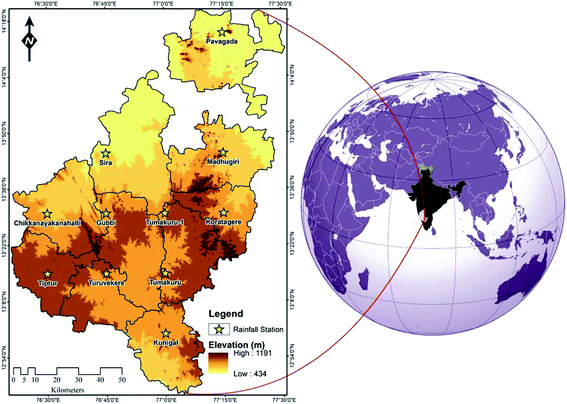
Panning the entire area of the Tumakuru district, the study area lying between 12°44′31′′ to 14°21′2′′ north latitudes and 76°21′2′′ to 77°30′12′′ east longitudes is located in the SE of the Karnataka, India as seen in Fig. 1. The area with an extent of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 km2 is witness to the arid steppe hot and tropical savannah zone of the Köppen–Geiger classification. The temperature ranges between 34 °C and 16 °C while the mean rainfall calculated from 1981 to 2019 is 668.74 mm. The least annual rainfall is received in the north in Pavagada (503 mm) and the highest in the south in Kunigal (883 mm). Rainfall variation is not apparent with the elevation in the study area which varies from 434 m to 1191 m above the mean sea level.
603 km2 is witness to the arid steppe hot and tropical savannah zone of the Köppen–Geiger classification. The temperature ranges between 34 °C and 16 °C while the mean rainfall calculated from 1981 to 2019 is 668.74 mm. The least annual rainfall is received in the north in Pavagada (503 mm) and the highest in the south in Kunigal (883 mm). Rainfall variation is not apparent with the elevation in the study area which varies from 434 m to 1191 m above the mean sea level.
Rain gauge
The ground-based precipitation data were obtained from the India Meteorological Department (IMD)24 with a spatial resolution of 0.25° × 0.25°. Apart from the systemic error due to evaporation, IMD data have been known to be reliable in both spatial and temporal aspects. The daily gridded dataset was collected from 1998 to 2019 and the daily rainfall data is averaged to obtain the monthly data for all the 11 grid stations for meteorological observations in the extent of the study area. The data is available in the .grd file format which is converted to excel readable format by using a C program which is available at https://www.imdpune.gov.in/Clim_Pred_LRF_New/Grided_Data_Download.html#.TRMM 3B43
The Tropical Rainfall Measuring Mission (TRMM) was devised to understand the variability and distribution of rainfall in the tropics and the sub-tropics. With the monthly temporal resolution and a spatial resolution of 0.25° × 0.25°, rainfall data from 1998 to 2019 were obtained from the Goddard Earth Sciences Data and Information Services Center (GES DISC) in NetCDF format (https://doi.org/10.5067/TRMM/TMPA/MONTH/7). The TRMM 3B43 provides monthly precipitation values which are obtained by adjusting the 3B42 daily product. The NetCDF format of TRMM data is imported to ArcMap as a raster layer. Later spatial analysis was performed where based on a grid, and values from the raster were extracted to points. This step is done so that the grid points from the TRMM can be compared to the rain gauge data. The study of meteorological conditions, especially when it comes to prediction models, heavily depends on long term data patterns and fluctuations. Even though TRMM products such as 3B43 are discontinued, they will still hold prominence when it comes to acquiring long term data.Methodology
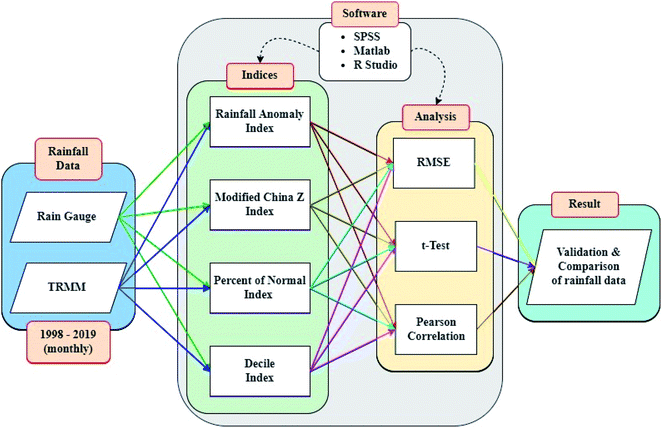
The flow of workings of this study is shown in in Fig. 2 detailing the data, methods used, and the analysis. The range of drought/wet categories for the indices is mentioned in Table 1. Matlab, R Studio, and SPSS software were used to obtain the indices and plot the data.| Category | RAI | MCZI | PN | DI |
|---|---|---|---|---|
| Extreme wet | ≥4 | ≥2.0 | >115 | 9 to 10 |
| Severe wet | 2 to 4 | 1.5 to 1.99 | 110 to 115 | 8 |
| Moderate wet | 0 to 2 | 1.0 to 1.49 | 80 to 110 | 7 |
| Near normal | — | −0.99 to 0.99 | 70 to 80 | 5 to 6 |
| Moderate dry | −2 to 0 | −1.49 to −1.0 | 55 to 70 | 4 |
| Severe dry | −4 to −2 | −1.99 to −1.5 | 40 to 55 | 3 |
| Extreme dry | ≤−4 | ≤−2.0 | <40 | 1 to 2 |
Rainfall anomaly index (RAI)
The RAI defines a system to indicate the deficit or surplus of rainfall in the range of −4 to +4. The index helps recognize the magnitude of deviation in rainfall. It categorizes the positive and negative anomalies of the rainfall extremes.1For a positive anomaly when P > ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ,
,
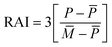 | (1) |
For a negative anomaly when P < ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ,
,
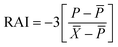 | (2) |
The terms of the equations are defined as P is the present monthly rainfall, ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) shows the average of the historical monthly rainfall data,
shows the average of the historical monthly rainfall data, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) indicates the mean of 10 of the maximum monthly rainfall values and
indicates the mean of 10 of the maximum monthly rainfall values and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) denotes the mean of 10 of the minimum monthly rainfall values.
denotes the mean of 10 of the minimum monthly rainfall values.
Modified China Z index (MCZI)
The Wilson–Hilferty cube root transformation forms the basis for the China Z index.3 The MCZI serves as a good alternative to the SPI when mean precipitation follows the Pearson type III distribution. The China Z index follows the equation: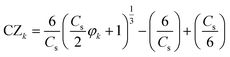 | (3) |
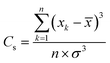 | (4) |
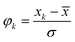 | (5) |
Percent of normal index (PN)
Percent of normal7 is a simple method to indicate drought which shows the percentage of the precipitation that occurred, in comparison to the long-term mean rainfall. The index is obtained by multiplying 100 with the ratio of actual rainfall (Pi) to normal rainfall (![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ).
). ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) is typically calculated using long term rainfall data.
is typically calculated using long term rainfall data.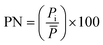 | (6) |
Deciles index (DI)
Deciles index is a method for analyzing meteorological drought. To attain the most accurate result, long-term precipitation data are required for the estimation of the index. For the available historical data set of rainfall, the decile index defines the ranking of precipitation at a particular time. The monthly rainfall data are rearranged from the highest to the lowest rainfall which is divided into 10% parts termed deciles. The lowest and highest deciles represent the precipitation extremes indicating drought and flood respectively.5 Deciles help provide useful knowledge about the deviation of the rainfall value from the normal.Root mean square error (RMSE)
The RMSE helps us arrive at an average magnitude of the error to assess the dependability of the data available.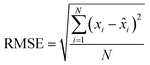 | (7) |
t-Test
This is a statistical method to figure out if the average between the two sets of data results in a zero.25 It is predominantly used to compare two sets of data by paring the observation in one data set to the corresponding one in the other data set.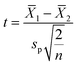 | (8) |
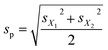 | (9) |
Pearson correlation
The Pearson correlation coefficient is calculated to draw a linear correlation between the rain gauge and the TRMM data. The value is calculated as a ratio of their covariances and the multiplicative result of standard deviations.26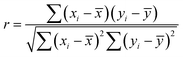 | (10) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) denotes the mean of the rain gauge values. yi is the TRMM values and ȳ is the mean of the TRMM values.
denotes the mean of the rain gauge values. yi is the TRMM values and ȳ is the mean of the TRMM values.
Result and discussion
The TRMM and rain gauge, although representing the same data, tend to show variations in their values. Drought indices are chosen to know the deviations of one data set from the other. The study solely relies on a precipitation data set and hence, only meteorological drought is established from the results. The study region is mostly covered with plains and there are barely any variations in the topography. The fluctuation in data is assumed to be uniform throughout. To study the compatibility of the TRMM and the rain gauge data for drought analysis, statistical methods were employed. The Pearson correlation coefficient draws a detailed correlation between the two datasets whereas the homogeneity is described by the two-sample t-test. The RMSE is also calculated to denote the deviation of the rainfall values.Rainfall anomaly index
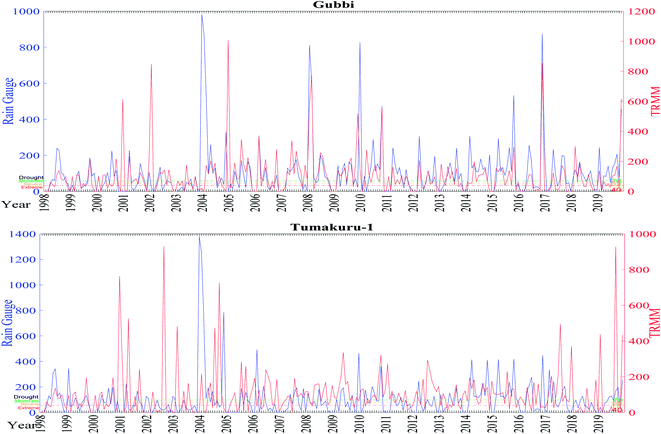
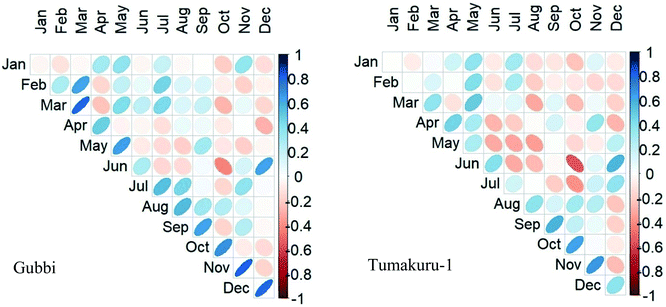
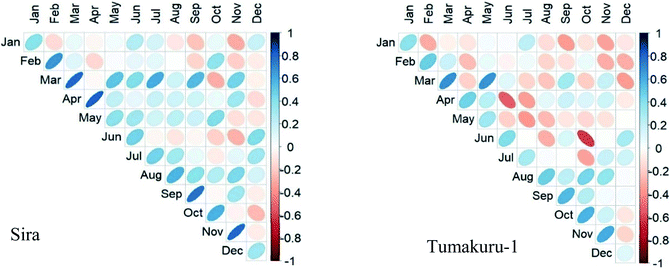
The rainfall anomaly index is prominently used to assess the deviation of rainfall. The index obtained for the rain gauge and TRMM data goes well beyond the range of +4 and −4 for a good portion of data. While comparing the total number of months for the categories of the index, the Tiptur station showed very good matching with a difference of not more than 2 months. At the same time for Kunigal, the same difference was up to 5 months. Fig. 4 shows the month-wise variation in data between the TRMM and rain gauge from 1998 to 2019. The index has an average RMSE of 4 with the error reaching a maximum of more than 10 in January, while the lowest error is seen across June and July as shown in Fig. 3. The t-test result for the majority of the data indicates a negative value showing low correlation which are seen especially in January and February months for all the stations. The positive t-test result is seen predominantly in June and December. A positive correlation coefficient is seen in all the stations in March, September, October, November, and December. The least similarity is seen in January and February where the coefficient value is closer to zero (Fig. 5). Chikkanayakanahalli shows the maximum correlation of 30.68% on the whole, while moderate, severe, and extreme dry events hold 3.41%, 28.41%, and 2.65% correlation, respectively. Gubbi shows a total of 27.65% similarity and 4.55%, 26.89%, and 3.03% similarity for moderate, severe, and extreme droughts. The Koratagere station has a 26.52% match while moderate, severe, and extreme dry events are at 5.30%, 23.48%, and 3.79% match, respectively. 22.73% harmony is defined for the Kunigal station and moderate, severe, and extreme dry events show 4.17%, 22.73%, and 1.14% similarity respectively. Madhugiri has an overall 30.30% of equivalence at the same time, and moderate, severe, and extreme dry spells are at 5.30%, 27.65%, and 3.03% equivalence, respectively. Pavagada has moderate, severe, and extreme dry events with a similarity of 3.41%, 24.62%, and 2.65%, respectively, with 23.11% being the total match. Sira with a total of 28.03% shows moderate, severe, and extreme spells at 4.55%, 27.65%, and 1.89%, respectively. Tiptur has an overall 26.52% harmony while 5.3%, 25%, and 1.14% are the similarities for moderate, severe, and extreme droughts. Tumakuru has 27.27% in the entirety while moderate, severe, and extreme dry are defined with 7.2%, 23.48%, and 2.27%, respectively. Tumakuru-1 holds a total of 28.79% commonality all the while with the moderate, severe, and extreme dry event being 6.82%, 22.73%, and 1.52% similar, respectively. Turuvekere displays 26.89% similarity for all categories with 5.30%, 24.62%, and 1.14% similarity for moderate, severe, and extreme dry extremes respectively. The data concerning the detailed statistical analysis are attached in the ESI.† The correlation of the datasets for wetness indicated by the index can be understood by looking at the stations individually. Kunigal shows a very low match for severe conditions at 0.38% while extreme and moderate wet conditions are at 5.68% and 4.92% match, respectively. The extreme, severe, and moderate events of Tiptur show a similarity of 5.68%, 2.65%, and 1.89%, respectively.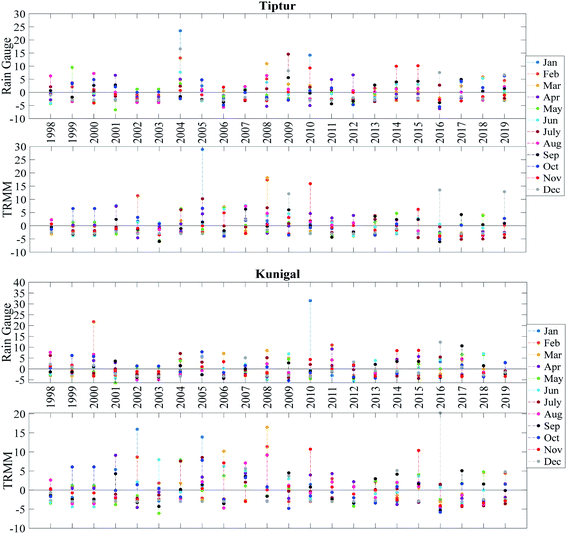 | ||
| Fig. 4 Monthly RAI for Tiptur and Kunigal stations.‡ | ||
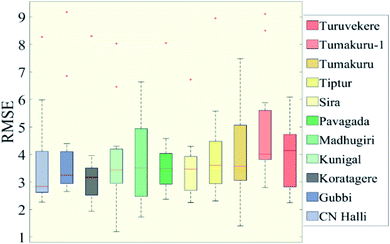
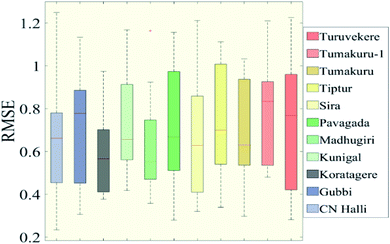
It is necessary to talk about the disparity or the similarity expressed in the data to draw further analysis. For the RAI, with a range of −4 to +4, the result obtained fluctuates from −10 to +10, and a few scattered data beyond this range. The data results carry a fairly similar correlation as we see an average RMSE of 4 throughout the year. In comparison of each month for the severe dry condition, both rain gauge and TRMM data show about 25% similarity in drought months while similarities in all other categories are below 5%.
Modified China Z index
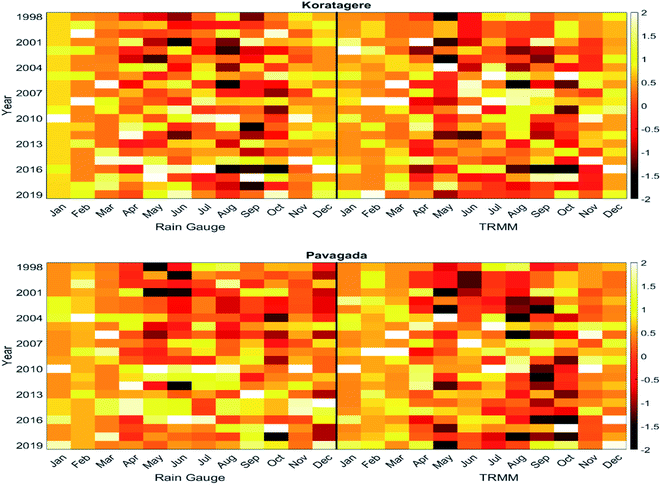
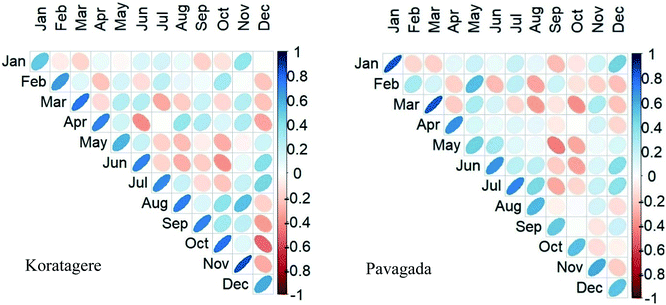
The result of the index varies only slightly beyond the defined limit of −2 and +2. Under normal conditions, the index shows about 61% of a match between the data sets. Koratagere and Pavagada are chosen as the two representative stations to describe the index as shown in Fig. 7. Augustto September of 2016 experienced extreme drought conditions according to both the datasets in Koratagere station, as is apparent from the figure, and the rest of the data also find similarities to a certain extent, while Pavagada shows contradictory conditions between the datasets. For example, May 2003 had the wet condition as seen from rain gauge data while the TRMM shows drought. As shown in Fig. 6, the average RMSE is about 0.68 for the months from April to October carrying higher values compared to other months in all the stations. Tiptur in August (−2.71) and Pavagada in December (−3.16) are the only stand-out values among all the stations while all other t-test values are closer to zero. From Fig. 8, we find that the coefficient values are only positive for March, holding the largest values. Chikkanayakanahalli shows an overall match of only 10.61% while there is a correlation of 0% for extreme drought, and severe and moderately dry conditions account for 0.76% and 0.38% match, respectively. Gubbi holds an overall match of 19.32% while moderate and severe drought is defined by 1.89% and 0% match, respectively. Koratagere exhibits an overall 13.26% match and 1.89% match for moderate and 0.38% for severe drought. Kunigal has 0 for both severe and extreme while moderate drought makes a 0.38% correlation only. Madhugiri with an all-around 11.36% equivalence, has 1.52% equivalence for moderate and 0.38% equivalence for the extreme dry event, being the only station with a slight value for extreme drought conditions. Pavagada has an overall 15.53% harmony while there is absolutely no correlation for any of the drought categories at all. Sira has no match for severe and extreme drought categories while moderate drought shows that 0.38% of the data matches both the datasets. In total, Sira has a 7.95% match for all categories. Tiptur recorded a total of 7.2% similarity on the whole and 0.76% for a moderate and severe dry spell while extreme drought found no match. Both Tumakuru and Tumakuru-1 stations show a total of 6.82% correlation while that for both severe and extreme drought is 0. Moderate drought defined for the stations Tumakuru and Tumakuru-1 shows that 0.38% and 0.76% of the data matches between TRMM and rain gauge. respectively. Turuvekere station had a 14.03% match for all categories and 0.38% match for moderate drought. There is no match for severe and extreme drought for this station. Koratagere had values for extreme, severe, and moderate wet scenarios respectively at 1.14%, 2.65%, and 2.27%. Pavagada holds the value of 1.52% for both extreme and severe wet conditions and 1.89% for moderate wet conditions.The MCZI shows greater similarity to the scatter diagram as the range of values is close to the defined range of −2 to +2. Few of the points reach up to +2.5. The RMSE is fairly lower and again holds consistency for all the months of the year. The months indicating normal conditions match up to 61% of the datasets while all other categories indicate a match of less than 1% when comparing the rain gauge and TRMM data of each month.
Percent of normal
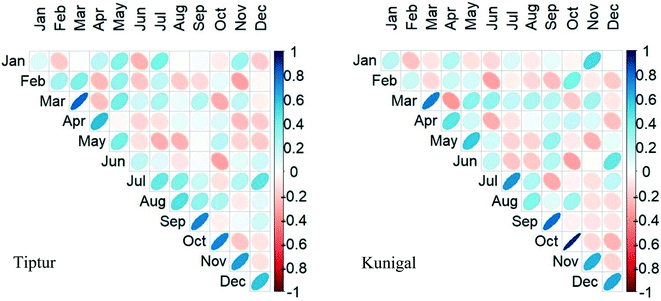
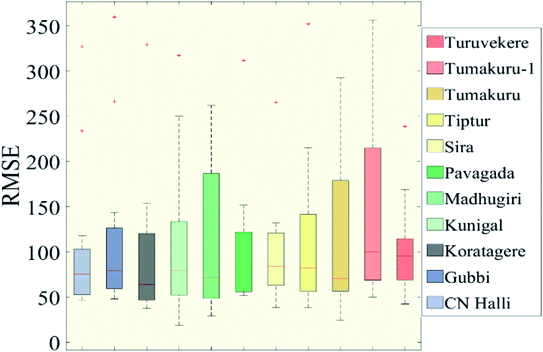
The percent of normal index gives the percentage of rainfall at a particular time with respect to the long-term normal rainfall value. PN values for both rain gauge and TRMM-3B42 data were derived to verify the compatibility of the data to determine the drought conditions. None of the eleven stations shows an exact match of the PN value from two data sources as there are variations found throughout the output. At certain locations and times, the TRMM depicts drought while the rain gauge describes flood-like conditions and vice versa. As shown in Fig. 10, Gubbi shows a good correlation between the two datasets while holding an apparent shift throughout the period at the same time following a similar pattern of the graph, while Tumakuru-1 shows polar opposite values in many instances. The error is maximum in January and February while the minimum error is for September and October (Fig. 9). All the values for the t-test resulted in a nearly zero value indicating a null hypothesis. Fig. 11 indicates that January has the minimum correlation and March has the maximum correlation for various stations. Gubbi shows a negative coefficient for January. The maximum match found for overall value is at the Chikkanayakanahalli station with 27.65% match. The similarity for drought is 0.76%, 1.52%, and 26.89% for moderate, severe, and extreme events, respectively. Gubbi has a total of 26.14% similarity and moderate, severe, and extreme events correlate 0.76%, 1.89%, and 25.76%, respectively. Koratagere holds a total match of 26.14% for all and 0.383%, 1.14%, and 24.62%, respectively, for moderate, severe, and extreme dry spells. Kunigal has a match of 1.52%, 0.76%, and 21.97% for moderate, severe, and extreme dry spells, respectively, and 25.76% on the whole. The Madhugiri station has a total match of 24.24% while moderate, severe, and extreme events recorded 0.38%, 0.76%, and 26.52% match, respectively. Pavagada shows a total of 23.48% similarity while severe and extreme events find a similarity of 0.38% and 23.86% respectively. Moderate dry event finds no match for this station. Sira finds a total of 26.52% harmony while moderate, severe, and extreme events are at 0.76%, 1.52%, and 26.14% harmony respectively. Tiptur though having a total of 21.21% match, has no match for severe dry events. Moderate and extreme dry spells are defined with 1.52% and 23.86% respectively. Tumakuru has a total of 23.86% match for all categories and 0.38% match for both moderate and severe drought and 21.97% match for extreme drought conditions. Tumakuru-1 has the least match for the percent of normal index with a total of 10.23% on the whole. There is only a 0.76% and 13.26% match for moderate and extreme dry periods, while the severe dry event has no match at all. Turuvekere has a 22.7% similarity while moderate, severe, and extreme events have 0.38%, 1.89%, and 22.73% similarity, respectively. To define the correlation for the wet events, most of the stations have 0% similarity when it comes to the severe wet event except for Kunigal, Madhugiri, and Tumakuru, all at 0.38% similarity. Gubbi station recorded 18.18% and 1.89% for extreme and moderate wet events, respectively. Tumakuru-1 recorded the least correlation of 10.98% for the extreme event and no match for the moderate event in the wet category.Percent of normal holds values way beyond the range reaching up to 400 on an average while they scatter beyond 1000. We see a large fluctuation of the index value from the defined value. The RMSE value also varies in the larger sense. About 18% and 23% of the monthly data matches for extremely wet and extremely dry conditions respectively. All the other conditions have a value of less than 1% when comparing the rain gauge and TRMM.
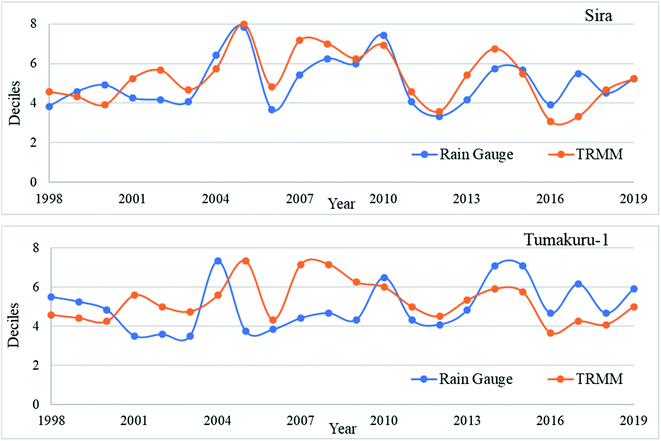
Deciles index
The deciles plotted in Fig. 12 show the example of Sira and Tumakuru-1 stations. While Sira shows a great correlation between TRMM and rain gauge data especially in 2005 and 2010 following a very similar pattern, Tumakuru-1 witnesses a stark difference between the two datasets showing a greater difference. The plot of TRMM and gauge data for the period from 1998 to 2019 shows a very good correlation. This is evident by the similar peaks found in the years 2004 and 2015 especially. While comparing the total number of months for various categories, there is a very good correlation between the datasets. Most of the results agree with each other with a variation of not more than 5 months with an exception of normal and extremely dry conditions. While there is a certain match for the normal condition, extremely dry months do not match for any of the stations and there is a bigger gap between the values obtained.The deciles as per Fig. 13 show an average error of 2.81 while the maximum error is seen in December and January. The t-test resulted in zero for the months April to November while the rest of the months recorded majorly negative values. The Pearson correlation coefficient in Fig. 14 shows a good positive correlation of 0.6 on average. The Chikkanayakanahalli station shows a good correlation of 28.41% on the whole. The extreme wet and extreme dry events show a match of 8.71% and 17.05% respectively. Moderately dry and severe dry categories of the drought showed 1.14% and 1.18% similarity between the two datasets. There is no match at all for moderately wet conditions. Similarities of 0.76%, 1.52%, and 16.67% are found for moderate, severe, and extremely dry conditions respectively. Koratagere has an overall match of 20.08%. The percentage match for the moderate, severe, and extreme dry spells is 1.14%, 1.52%, and 12.88% respectively. Kunigal displayed a total of 23.48% similarity. Also, the match for the moderate, severe, and extreme dry periods is 0.76%, 2.27%, and 14.02% respectively. Madhugiri portrays a total of 23.86% match between the values. The similarities for the moderate, severe, and extreme dry period are 1.14%, 1.52%, and 12.12% respectively. Pavagada shows an overall 20.45% similarity. For moderate, severe, and extreme dry events, there is 0.76%, 2.65%, and 9.85% harmony respectively. Sira in the total exhibits 25.38% common values. The percentage of similarity for the severe and extreme dry periods is 1.52% and 15.15% respectively. There is no match for the moderate dry event at all. 27.97% is the total match for the Tiptur station. For moderate, severe, and extreme dry periods, the match is 0.76%, 1.14%, and 11.36%, respectively. Tumakuru has a similarity of 25.76%. The dry period severity has a match of 1.14%, 1.89%, and 14.02% respectively for moderate, severe, and extreme periods. Tumakuru-1 displayed a total of 24.62% similarity. Also, the match for the moderate, severe, and extreme dry periods is 1.14%, 1.89%, and 13.26%, respectively. Turuvekere on the whole shows 21.59% similarity. 0.76%, 2.27%, and 13.64% of equivalence are found for moderate, severe, and extreme dry spells, respectively. Sira and Tumakuru-1 showed better responses of 9.47% and 8.71%, respectively, for extremely wet conditions, 3.79%, and 3.41%, respectively, for severe wet conditions, and 3.979% and 0.38%, respectively, for moderate dry conditions.
The deciles index carries a comparatively lower value holding good for all seasons. The index exhibits 9% and 14% similarity, respectively, for extremely wet and extremely dry conditions. Under severely wet, and normal conditions, there is about 3.5% of correlation while that of the rest of the values lies below 2% for the rain gauge and TRMM data.
Comparison of rain gauge and TRMM through indices
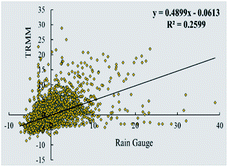
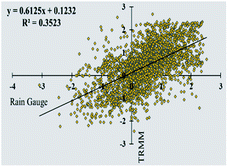
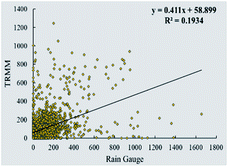
The scatter plot for the RAI, MCZI, and PN are utilized to draw a comparison between the indices. The plots indicate the index value obtained from both the rain gauge and TRMM. Fig. 15 presents the scatter plot of the RAI with an R2 value of 0.2599 indicating the variance in the data. For the MCZI, data fall on the trend line defined by y = 0.6125x + 0.1232 with the variance not going beyond 0.3523 which indicates the similarity portrayed by the data (Fig. 16). The index includes values that go way beyond the limits defined for it with the R2 being a low 0.1934 as seen in Fig. 17 for the percent of normal index. The result of the indices shows 26%, 35%, and 19% similarity, respectively, for the RAI, MCZI, and PN. The values of the RAI obtained for the study area from 1998 to 2019 is mainly concentrated in the range of −5 to +10 while MCZI ranges from −2 to +2.5 and PN ranges from 0 to 400 where the maximum correlation of the data can be seen.Conclusion
Mitigating disasters like drought is a challenge requiring powerful tools. Precise data help us determine the spatio-temporal distribution and help in monitoring the situation. The study aims at providing a suitable data source to determine the condition of meteorological drought.• Although a clear result was not determined from the study regarding the effectiveness of the datasets, a lot is understood in terms of how different indices respond to different datasets. The compatibillity of the long term data tend to be greater when applied to a larger area.
• The result of the PN shows a good match for moderate drought since the frequency of moderate drought is much higher. There are very few severe and extreme drought events and hence, the probability of finding similarities becomes even slimmer.
• Among the four indices, the MCZI bears the most similarity between the TRMM and gauge rainfall data.
• There are extreme variations in the index value, especially of TRMM data going way beyond the given range of the data which again poses a difficulty in validation.
• While comparing the data for each month, all the drought indices show relatively low homogeneity between the two data sets which is represented in the percentage comparison of the datasets. But on the whole, when comparing the individual number of months for each station for each category of drought, there is a much higher similarity between the data sets. From this, we can concur that the rain gauge and TRMM show a nearly equal amount of drought categories when talking about long-term data, since the number of months of individual data for each category shows a good match.
The scope of the research lies in meteorological drought monitoring by using suitable data and also serves as a means to build atmospheric models having high accuracy and resolutions.
Author contributions
(1) Sanjay Kumar worked on conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing – original draft, writing – review & editing. (2) Syed Ashfaq Ahmed focused on the conceptualization, methodology, resources, supervision, validation, writing – review & editing. (3) Jyothika Karkala rendered support in formal analysis, methodology, resources, software, visualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to the India Meteorological Department for providing the precipitation dataset with a high resolution of 0.25° × 0.25° and Goddard Earth Sciences Data and Information Services Center for the TRMM precipitation data.References
- M. P. van Rooy, A Rainfall Anomally Index Independent of Time and Space, Notos, 1965 Search PubMed.
- T. B. McKee, N. J. Doesken and J. R. Kleist, The Relationship of Drought Frequency and Duration to Time Scales, 1993 Search PubMed.
- E. B. Wilson and M. M. Hilferty, The Distribution of Chi-Square, Proc. Natl. Acad. Sci. U. S. A., 1931, 17(12), 684–688 CrossRef CAS PubMed , https://pubmed.ncbi.nlm.nih.gov/16577411.
- W. C. Palmer, Keeping Track of Crop Moisture Conditions, Nationwide: The New Crop Moisture Index, Weatherwise, 1968, 21(4), 156–161, DOI:10.1080/00431672.1968.9932814.
- N. Haied, A. Foufou, S. Chaab, M. Azlaoui, S. Khadri and K. Benzahia, et al., Drought assessment and monitoring using meteorological indices in a semi-arid region, Energy Procedia, 2017, 119, 518–529 CrossRef , https://www.sciencedirect.com/science/article/pii/S1876610217326061.
- S. M. Vicente-Serrano, S. Beguería and J. I. López-Moreno, A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index, J. Clim., 2010, 23(7), 1696–1718 CrossRef , https://journals.ametsoc.org/view/journals/clim/23/7/2009jcli2909.1.xml.
- G. Willeke, J. R. M. Hosking, J. R. Wallis and N. B. Guttman, The National Drought Atlas, Institute for Water Resources Report 94-NDS-4, U.S. Army Corps of Engineers Search PubMed.
- S. Shukla and A. Wood, Use of a standardized runoff index for characterizing hydrologic drought, Geophys. Res. Lett., 2008, 35, L02405, DOI:10.1029/2007GL032487..
- Q. Sun, C. Miao, Q. Duan, H. Ashouri, S. Sorooshian and K.-L. Hsu, A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons, Rev. Geophys., 2018, 56(1), 79–107 CrossRef , https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2017RG000574.
- M. Mahbod, A. Shirvani and F. Veronesi, A comparative analysis of the precipitation extremes obtained from tropical rainfall-measuring mission satellite and rain gauges datasets over a semiarid region, Int. J. Climatol., 2019, 39(1), 495–515 CrossRef , https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/joc.5824.
- A. K. Shukla, C. S. P. Ojha, R. P. Singh, L. Pal and D. Fu, Evaluation of TRMM Precipitation Dataset over Himalayan Catchment: The Upper Ganga Basin, India, Water, 2019, 11(3), 613 CrossRef , https://www.mdpi.com/2073-4441/11/3/613.
- V. Prasanna, J. Subere, D. K. Das, S. Govindarajan and T. Yasunari, Development of daily gridded rainfall dataset over the Ganga, Brahmaputra and Meghna river basins, Meteorol. Appl., 2014, 21(2), 278–293 CrossRef , https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/met.1327.
- V. Gupta, M. K. Jain, P. K. Singh and V. Singh, An assessment of global satellite-based precipitation datasets in capturing precipitation extremes: a comparison with observed precipitation dataset in India, Int. J. Climatol., 2020, 40(8), 3667–3688 CrossRef , https://rmets.onlinelibrary.wiley.com/doi/abs/10.1002/joc.6419.
- M. Thakur, T. Kumar, M. Narayanan and B. H. Koteswara, Analytical study of the performance of the IMERG over the Indian landmass, Meteorol. Appl., 2020, 27, 1–11 CrossRef.
- U. V. Murali Krishna, S. K. Das, S. M. Deshpande, S. L. Doiphode and G. Pandithurai, The assessment of Global Precipitation Measurement estimates over the Indian subcontinent, Earth and Space Science, 2017, 4(8), 540–553 CrossRef , https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1002/2017EA000285.
- X. Li, Q. Zhang and X. Ye, Dry/Wet Conditions Monitoring Based on TRMM Rainfall Data and Its Reliability Validation over Poyang Lake Basin, China, Water, 2013, 5(4), 1848–1864 CrossRef , https://www.mdpi.com/2073-4441/5/4/1848.
- S. E. Nicholson, D. Klotter, L. Zhou and W. Hua, Validation of Satellite Precipitation Estimates over the Congo Basin, Journal of Hydrometeorology, 2019, 20(4), 631–656 CrossRef , https://journals.ametsoc.org/view/journals/hydr/20/4/jhm-d-18-0118_1.xml.
- D. C. Buarque, R. C. D. de Paiva, R. T. Clarke and C. A. B. Mendes, A comparison of Amazon rainfall characteristics derived from TRMM, CMORPH and the Brazilian national rain gauge network, J. Geophys. Res., 2011, 116(D19), D19105 CrossRef.
- Y. Cai, C. Jin, A. Wang, D.-X. Guan, J. Wu and F. Yuan, et al., Comprehensive precipitation evaluation of TRMM 3B42 with dense rain gauge networks in a mid-latitude basin, Northeast, China, Theor. Appl. Climatol., 2015, 126, 659–671, DOI:10.1007/s00704-015-1598-4.
- A. Ochoa-Sánchez, L. Pineda, P. Willems and P. Crespo, Evaluation of TRMM 3B42 (TMPA) Precipitation Estimates and WRF Retrospective Precipitation Simulation over the Pacific-Andean Basin into Ecuador and Peru, Hydrol. Earth Syst. Sci. Discuss., 2014, 18(8), 3179–3193, DOI:10.5194/hess-18-3179-2014.
- M. Pan, H. Li and E. Wood, Assessing the Skill of Satellite-Based Precipitation Estimates in Hydrologic Applications, Water Resour. Res., 2010, 46(9), 535 CrossRef.
- A. R. As-syakur, T. Tanaka, R. Prasetia, S. Ketut and I. Kasa, Comparison of TRMM Multisatellite Precipitation Analysis (TMPA) Products and Daily-Monthly Gauge Data over Bali Island, International Journal of Remote Sensing, 2011, 32, 8969–8982 CrossRef.
- R. Chokngamwong and L. Chiu, Comparisons of Daily Thailand Rain Gauge with GPCC and TRMM Satellite Precipitation Measurements, 2022 Search PubMed.
- D. Pai, L. Sridhar, M. Rajeevan, O. P. Sreejith, N. S. Satbhai and B. Mukhopadhyay, Development of a new high spatial resolution (0.25° × 0.25°) long period (1901-2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region, Mausam, 2014, 65, 1–18 CrossRef.
- Student's t-Test Student's t-Test, in Encyclopedia of Public Health, ed. W. Kirch, Springer Netherlands, Dordrecht, 2008, p. 1358, DOI:10.1007/978-1-4020-5614-7_3378.
- Pearson's Correlation Coefficient, in Encyclopedia of Public Health, ed. W. Kirch, Springer Netherlands, Dordrecht, 2008, pp. 1090–1091, DOI:10.1007/978-1-4020-5614-7_2569.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2va00113f |
| ‡ Only two representative stations are chosen to explain the index with the best and least correlation in order to avoid page filling. |
| This journal is © The Royal Society of Chemistry 2022 |