Open Access Article
Open Access ArticleEnhancing the photocatalytic hydrogen generation performance and strain regulation of the vertical GeI2/C2N van der Waals heterostructure: insights from first-principles study†
Francis
Opoku
 *a,
Samuel Osei-Bonsu
Oppong
b,
Noah Kyame
Asare-Donkor
a,
Osei
Akoto
a and
Anthony Apeke
Adimado
a
*a,
Samuel Osei-Bonsu
Oppong
b,
Noah Kyame
Asare-Donkor
a,
Osei
Akoto
a and
Anthony Apeke
Adimado
a
aDepartment of Chemistry, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana. E-mail: ofrancis2010@gmail.com
bMarine Engineering Department, Regional Maritime University, P.O. Box GP 1115, Accra, Ghana
First published on 21st January 2022
Abstract
A suitable electronic structure and efficient charge separation are significant for the performance of photocatalytic water splitting. Herein, we have designed a two-dimensional GeI2/C2N van der Waals (vdW) heterostructure and systematically examined its stability, electronic, photocatalytic, optoelectronic and optical properties, and the effects of applying biaxial strain using density functional theory calculations. Based on ab initio molecular dynamic simulations and phonon dispersion calculations, the dynamic and thermal stability of the GeI2/C2N vdW heterostructure was confirmed. The GeI2/C2N vdW heterostructure showed an inherent type-II indirect bandgap energy of 2.02 eV and excellent visible light absorption, which were significantly improved compared to those of the monolayers. The projected band structure showed that the valence band minimum and conduction band maximum were contributed by the C2N and GeI2 monolayers, respectively, which was favourable for efficient charge separation, thus increasing the solar energy conversion. Moreover, the GeI2/C2N vdW heterostructure band edges precisely straddled the water redox potential energies for pH values ranging from 0 to 9, allowing it to meet the conditions for spontaneous water splitting. The charge density difference revealed that about 0.263 electrons were transferred from the C2N to GeI2 monolayer, and the potential drop at the interface was estimated to be 7.16 eV. We further hypothesised that strain might be utilised to tune the band edges and bandgap of the GeI2/C2N vdW heterostructure, resulting in a transition from a type-II indirect to a type-I direct bandgap semiconductor under tensile biaxial strain. Our findings provide a theoretical design for strategies to improve the performance of GeI2/C2N in solar conversion, nanoelectronic and optoelectronic devices.
I. Introduction
Given the scarcity of fossil fuels and the deterioration of the environment, developing clean and sustainable alternative energy sources that are renewable, cost-effective, environmentally friendly and can be replenished is urgently required to address the energy demands and ever-growing pollution of the environment.1,2 The strong demand for renewable energy has created a research hotspot to explore high-efficiency photocatalyst and photovoltaic materials. Today, to address the energy scarcity and environmental pollution, hydrogen (H2) produced by photocatalytic water splitting3–5 has emerged as a viable alternative to fossil fuels due to its zero pollutant emission (the only combustion product is water vapour), higher energy density per unit mass, and lightweight, the abundance of solar energy and the fact that it is the highest energy carrier.6https://0-pubs-rsc-org.ujlink.uj.ac.za/en/content/articlehtml/2021/ta/d1ta04256d? page = search - cit3. After overall water splitting was experimentally achieved with TiO2,7 several photocatalysts, such as metal nitrides, sulphides and oxides, and other bulk materials, have been reported to play a vital role in solar energy conversion and storage processes.8 However, the low solar utilisation of bulk materials hinders their practical applications as high-efficiency photocatalysts.After successful fabrication of graphene, other two-dimensional (2D) materials, such as black phosphorene, monochalcogenides, silicene, graphite-like carbon nitride, MXenes, stanene, transition metal dichalcogenides and others,9–12 exfoliated from their bulk materials, have been fabricated experimentally and predicted theoretically,13 showing great potential for photocatalytic water splitting.14 For practical applications, a promising 2D photocatalyst semiconductor must possess a small exciton binding energy, low exciton recombination rate and high separation efficiency of photogenerated charge carriers, a bandgap value greater than 1.23 eV, sufficiently large specific surface area, good visible light response and appropriate band edge positions for overall water splitting.15
Carbon nitride (C2N), a novel 2D layered semiconductor material, was successfully synthesised by thermally depositing a C2N-h2D crystal sample on a Cu(111) substrate via a simple bottom-up wet-chemical reaction technique.16 Based on their bonding analyses, the C–N bonds in C2N exhibit sp2 hybridisation comparable to the C–C bonds in graphene.17 The primary distinction between 2D C2N and graphene is that the C2N layer has periodic holes in the form of a delocalised benzene structure. The two aromatic rings are joined together by pyrazine rings that are made up of a six-membered D2h point group with two N atoms facing one another. Recently, carbon nitride materials, including C2N, C6N6 and C3N4,18,19 have been identified as potential photocatalysts due to their good biocompatibility, non-toxicity, abundance and low cost. C2N has high water permeability, superior chemical activity and better visible light absorption than the other carbon nitride materials.20 C2N has an excellent direct bandgap and optical properties, and has been demonstrated experimentally as an effective H2 generation photocatalyst.21 Because N and C are lighter elements, the hydrogen storage capacity of C2N may be significant as a result of its high surface-to-volume ratio compared to other 2D materials.6 2D germanium iodide (GeI2) has potential in solar cells, and electronic and optoelectronic devices.22 Ozisik et al.23 found that GeI2 is thermodynamically and mechanically stable. Though 2D materials may provide more efficient redox reactions than their bulk equivalents, their photocatalytic efficacy is limited due to the high electron–hole recombination rate because the orbitals in the conduction band (CB) and valence band (VB) are not completely separated in space.24 C2N also suffers from a significantly high electron–hole recombination rate, which prohibits its further applications.25,26 As a result, a technique for the effective separation of photogenerated charge carriers must be investigated as soon as possible.
Recently, van der Waals (vdW) heterostructures have been developed to boost the optical, electronic and photocatalytic properties of 2D materials.27,28 Experimentally, vdW heterostructures can be obtained by direct growth and mechanical assembly,29 while theoretically they can be predicted by stacking two or more 2D materials on top of each other.30 2D heterostructures are energetically stable and undergo easy exfoliation since the two materials are held together by weak vdW interactions. Recently, type-II heterostructures have attracted much attention since they can effectively separate photogenerated charge carriers to different sheets for H2 and O2 generation.31,32 Several type-II C2N-based heterostructures, such as C2N/BlueP,33 GeC/C2N,26 BCN/C2N,34 C2N/MoSe2,35 C2N/InTe,36 C2N/GaTe,37 g-C3N4/C2N,38 C2N/WS2,39 C2N/MoS2,40 GaX/C2N (X = S, Se)41,42 and C2N/GaTe,36 have exhibited high power conversion efficiency with enhanced photocatalytic/photovoltaic performance compared to isolated C2N due to the improved separation of electrons.https://0-pubs-rsc-org.ujlink.uj.ac.za/en/content/articlehtml/2020/cp/c9cp06696a? page = search - cit31.
The search for suitable 2D materials to create type-II heterostructures opens up a wide range of possibilities for photocatalytic water splitting to generate H2. Surprisingly, the lattice constant of the GeI2 monolayer is almost double that of C2N. Given this, the new GeI2/C2N vdW heterostructure might be an effective material with better photocatalytic activity than C2N. Therefore, the small lattice mismatch between the GeI2 monolayer and C2N makes the experimental fabrication of a vdW heterostructure highly achievable. The reason for using C2N is that it has the properties of a direct bandgap and high H2 storage capability. The successful exfoliation of 2D GeI2 and C2N also provides more possibilities for designing GeI2/C2N heterostructures. The newly designed 2D vdW heterostructure can enhance the electronic and optical properties of the isolated monolayers and overcome the limitation of their applicability in many fields. Using density functional theory (DFT) calculations, this study explores the photocatalytic performance, and structural, optical and electronic properties of 2D vertical GeI2/C2N heterostructures (DFT). It is not easy to provide an adequate theoretical explanation of the electrical characteristics of the ground and excited states of 2D materials. Excitation or optical absorption is a more difficult task. The theoretical techniques available include the Bethe–Salpeter equation (BSE)43 and time-dependent DFT (TD-DFT)44,45 The former includes excitonic phenomena that are important for 2D materials. However, local relaxation and electron–phonon coupling effects are difficult to include. After being tested in many systems, the BSE approach46 has been shown to be a dependable tool, but it also has drawbacks: long processing durations, especially for complex systems, and not necessarily well-adjusted approximations for the vertex function in solving the BS equation.44 TDDFT, on the other hand, is free of the aforementioned shortcomings, as it is computationally significantly less costly and does not require any approximation for the exchange–correlation (XC) potential. TDDFT, an effective theory of charge density in which the effects of electron–electron interactions and hence all nontrivial excitations are characterized by the XC potential, is the dominant current ab initio technique for studying excitations in finite systems and solids.45 In this study, we employ a simplified but effective TDDFT approach to simulate the optical properties of semiconducting materials. Through ab initio molecular dynamics (AIMD) and phonon dispersion calculations, the thermal and dynamic stabilities of the optimised structures were analysed. The band edges and the bandgap width, which are a research focus in photocatalysis, can be effectively modulated by strain.47–49 Moreover, the electronic properties of isolated 2D GeI2 monolayers and C2N can be easily modulated by applying strain.21,50 With this in mind, we examine how strain may be used to adjust the bandgap and band alignment of the GeI2/C2N heterostructure. Our theoretical findings suggest that the GeI2/C2N heterostructure can be utilised to develop novel electronics, optoelectronics and photocatalyst devices.
II. Computational details
First-principles calculations were performed using the Quantum ESPRESSO package.51 For structural relaxations, the generalised gradient approximation of Perdew–Burke–Ernzerhof was employed to account for the XC effects.52 The conjugate-gradient technique53 of Broyden–Fletcher–Goldfarb–Shannon (BFGS) was used for all the structural optimisations with the variable-cell relaxation method. We employ optimised norm-conserving Vanderbilt pseudopotentials54 to account for the electron–ion interaction. A large vacuum of 30 Å was added to prevent the interactions of the periodic images. This vacuum distance was wide enough not to affect the band positions with reference to the vacuum energy level. Besides, the vdW interaction between the two monolayers was treated using the Grimme D3 method with Becke–Johnson damping dispersion correction.55,56 The Brillouin zone integration was sampled using a Monkhorst–Pack grid57 of 7 × 7 × 1. The plane wave cutoff energy, the energy convergence criteria and the Hellmann–Feynman force of 55 Ry, 10−6 Ry and 10−3 Ry Bohr−1, respectively, are sufficient to give well-converged results. The harmonic interatomic force constants and phonon dispersions were calculated with density functional perturbation theory.58 Due to the underestimation of the bandgap by the generalised gradient approximation of the Perdew–Burke–Ernzerhof functional,59 the Heyd–Scuseria–Ernzerhof functional (HSE06)60 with the fraction of exact local exchange of 0.25 and screening parameter of 0.2 Å−1 was used to obtain accurate optical and electronic properties, with band structures drawn using the Wannier90 package.61 Optical properties were calculated using the time-dependent density functional theory (TDDFT) method62,63 within the Quantum ESPRESSO code.51 The NVT ensemble with a Nosé–Hoover thermostat64,65 at room temperature (300 K) was used to examine the thermal stability of the GeI2/C2N heterostructures. We utilised the XCrySDen package66 to visualise the optimised structures, charge density and electron localisation function.III. Results and discussion
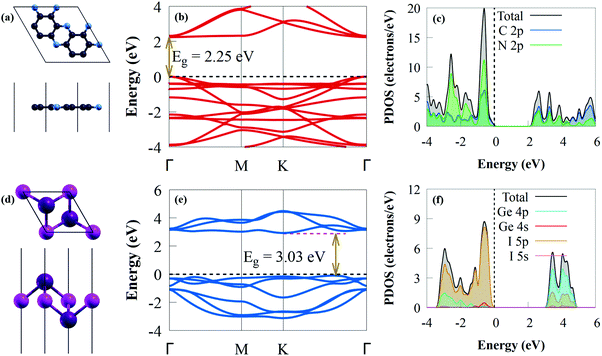
Before exploring the vdW heterostructures, the structural and electronic properties of C2N and GeI2 were initially studied, as shown in Fig. 1.The optimised lattice constants are a = b = 4.213 Å for the GeI2 monolayer and a = b = 8.332 Å for C2N, which agreed with earlier experimental and theoretical data.67,68 The C–C bond lengths in the pyrazine and benzene rings are 1.428 and 1.465 Å, respectively, and the C–N bond length is 1.335 Å for the optimised C2N (Fig. 1a), which agreed with results from earlier studies.67,69 To understand the effect of interlayer interaction, the change in bandgap along the Γ–M–K–Γ high-symmetry direction between the isolated monolayers and the heterostructure was systematically studied. The C2N band structure in Fig. 1b is a direct bandgap semiconductor (2.25 eV), which agrees with an earlier study.70 Because the experimental measurement is done on multilayer materials,70 this value is higher than the experimental value (1.96 eV).71 The valence band maximum (VBM) and conduction band minimum (CBM) of C2N are at the Γ point. Our findings show that the VBM and CBM mostly consist of C 2p and N 2p states, respectively (Fig. 1c), where the contribution of the C 2p orbital to the CB is quite dominant. The Ge–I bond length is about 3.005 Å in the case of the GeI2 monolayer (Fig. 1d). The GeI2 monolayer has indirect semiconductor properties (Fig. 1e) with a bandgap energy of 3.03 eV. This agrees with earlier results (3.05 eV).72 The CBM and VBM are positioned on the K point and K–Γ path, respectively. The calculated projected density of states (PDOS) (see Fig. 1f) shows that the VBM comprises I 5p states, while the Ge 4p states mainly contribute to the CBM.
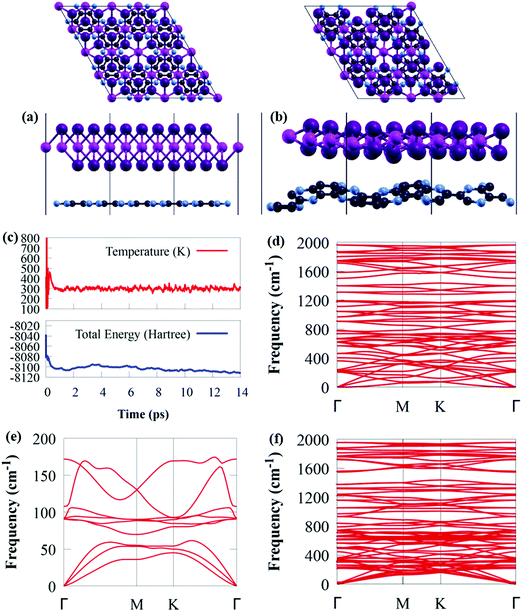
The GeI2/C2N vdW heterostructure in Fig. 2a is constructed by stacking a 4 × 4 supercell of GeI2 monolayer on a 2 × 2 supercell of C2N. In general, a stable heterojunction may favourably form when the lattice mismatch is less than 5%.73,74 For the GeI2/C2N vdW heterostructure, the lattice mismatch is only 1.06% along the a and b axes, which is relatively small compared to the acceptable maximum epitaxial growth value of 5%,75 ensuring the experimental feasibility.37,76–78 Moreover, the optimised interlayer distance between the GeI2 monolayer and C2N is 3.374 Å.
The structural stability of the GeI2/C2N heterostructure is verified under different conditions. Firstly, to confirm the stability of the GeI2/C2N vdW heterostructure, the interfacial binding energy (ΔE) is examined:
| ΔE = (EGel2/C2N − EGel2 − EC2N)/S | (1) |
Thermal stability is extremely important in photocatalysis. Before delving into the electronic properties of the GeI2/C2N vdW heterostructure, AIMD simulations and phonon dispersion calculations were used to ensure its thermodynamic stability. The AIMD simulation shows that the GeI2/C2N heterostructure retained its structure with no bonds broken at 300 K after heating for 14 ps, as shown in Fig. 2b. Furthermore, the difference in total energy and temperature in Fig. 2c before and after 14 ps is quite small. As a result, at room temperature, the GeI2/C2N vdW heterostructure is thermally stable. The phonon spectra of the GeI2 monolayer and C2N were computed, as shown in Fig. 2d and e. The absence of negative frequency in the phonon spectra confirms that the GeI2 monolayer and C2N are dynamically stable. It is worth mentioning that no imaginary phonon mode is observed in the GeI2/C2N vdW heterostructure across the Brillouin zone, indicating its dynamic stability.
Having verified the experimental feasibility and the intrinsic stability of the GeI2/C2N vdW heterostructure, we evaluated the projected band structure, as shown in Fig. 3a, to further analyse the change in electronic properties.
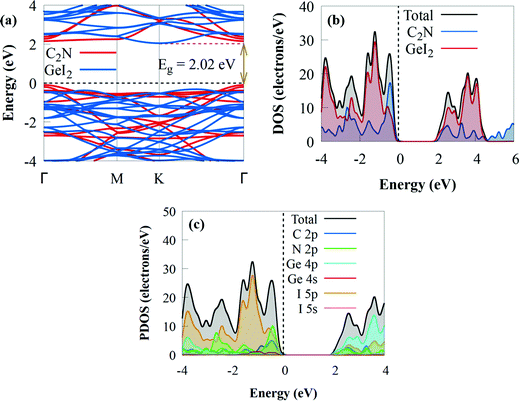 | ||
| Fig. 3 (a) Projected electronic band structure, (b) DOS and (c) PDOS of the GeI2/C2N vdW heterostructure. The Fermi level is set to zero. | ||
The electronic band structures of the GeI2 monolayer and C2N are well retained after creating the GeI2/C2N heterostructure, indicating the weak interaction between the GeI2 monolayer and C2N. The indirect bandgap of the GeI2/C2N vdW heterostructure is 2.02 eV, which is less than those of the GeI2 monolayer and C2N. The bandgap was slightly lower than those of CdSe/C2N (2.12 eV),78 h-BN/C2N (2.30 eV),26 blueP/g-GeC (2.213 eV),81 WSSe/BSe (2.151 eV),82 and WSSe/g-GaN (2.39 eV)83 vdW heterostructures, but slightly higher than that of the C2N/g-ZnO heterostructure (2 eV).84 The smaller bandgap may be more conducive to the transfer of photogenerated charge carriers, effectively enhancing its photocatalytic activity. The CBM is located at the K point, whereas the VBM is positioned at the Γ high-symmetry point, which makes the GeI2/C2N heterostructure an indirect semiconductor. Furthermore, the CBM is particularly dispersive compared to the VBM, meaning that photogenerated electrons have smaller effective masses, which may increase electron–hole pair separation during the water redox reaction and photocatalytic activity. The minimum energy in the CB and the maximum energy in the VB occur at distinct crystal momentum levels in indirect bandgap semiconductors. Because the curves are parabolic, a direct electron transfer from the VB to the CB needs a photon with a larger energy than the band gap. However, it is feasible to perform an electronic transition at lower energy, but a phonon is required. Moreover, the reduced bandgap energy will benefit more visible light absorption with significant solar energy conversion efficiency and make the transfer and separation of photogenerated charge carriers easy with the contribution of phonons, which is similar to other indirect C2N-based heterostructures, such as InSe/C2N85 and SiC/C2N.70 The bandgap value of the GeI2/C2N heterostructure is greater than the minimum bandgap energy (1.23 eV) necessary for photocatalysis processes,86 implying that it might be used as an efficient visible light photocatalyst for H2 generation.87 The density of states in Fig. 3b shows that the VBM and CBM are dominated by the GeI2 monolayer and C2N, respectively, resulting in a type-II band alignment. Because the photogenerated charge distribution is kept in different layers and spontaneously separated at the interface, the type-II band alignment makes the GeI2/C2N vdW heterostructure promising as a solar energy conversion device. Furthermore to get a fundamental understanding of the electronic properties of the GeI2/C2N vdW heterostructure, we investigate the PDOS. The results demonstrate that the VBM is mostly dominated by the C 2p state, whereas the CBM is primarily from the Ge 4p state with contributions from the I 5p state, confirming the type-II band alignment (Fig. 3c). As a result, electron transfer from the C 2p orbitals of C2N into the Ge 4p states of GeI2 monolayer is favoured.
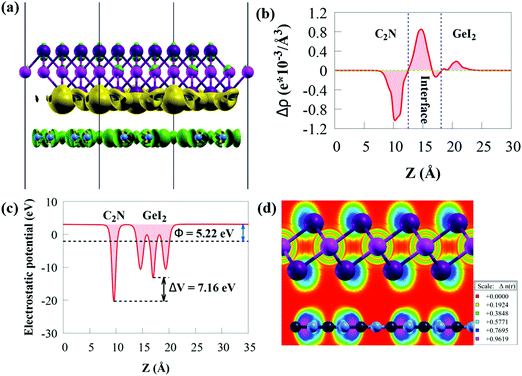
The three-dimensional charge density difference (CDD) and the average planar potential drop (ΔV) in the z-direction are determined to investigate the interface impacts on the charge transfer mechanism of the GeI2/C2N vdW heterostructure, as given in Fig. 4a.
The CDD (Δρ) is computed by subtracting the charge densities of the GeI2 monolayer and C2N from the charge density of the GeI2/C2N vdW heterostructure:
| Δρ = ρGel2/C2N − ρGel2 − ρC2N | (2) |
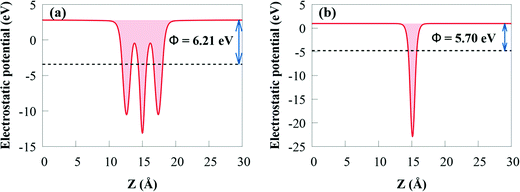
The work function (Φ) is an important parameter to comprehend charge separation and transfer at the GeI2/C2N vdW heterostructure interface. Φ was calculated by aligning the Fermi energy to the vacuum energy:
| Φ = EVacuum − EFermi, | (3) |
When the GeI2/C2N vdW heterostructure is constructed by stacking the GeI2 monolayer and C2N together perpendicular to the 2D plane, electrons will transfer from the C2N to the GeI2 due to the higher Φ of the GeI2 monolayer. Accordingly, the C2N and the GeI2 monolayer are positively and negatively charged, respectively, across the interfacial region. The Φ of the GeI2/C2N vdW heterostructure lies between the C2N and the GeI2 monolayer. With an increase in electron transfer, the Fermi energies of C2N and the GeI2 monolayer shift upwards and reach the same level after interface equilibrium. The lower Φ in the vdW heterostructure corresponds to an efficient interfacial electron transfer, which induces a built-in electric field, reducing the recombination rate of charge carriers. Moreover, the difference in the Φ values between the GeI2 monolayer and C2N induces charge redistribution at the interface.
The band bending (ΔEband bending) is evaluated to further understand the charge transfer:92
| ΔEband bending = ΦHS − ΦML | (4) |
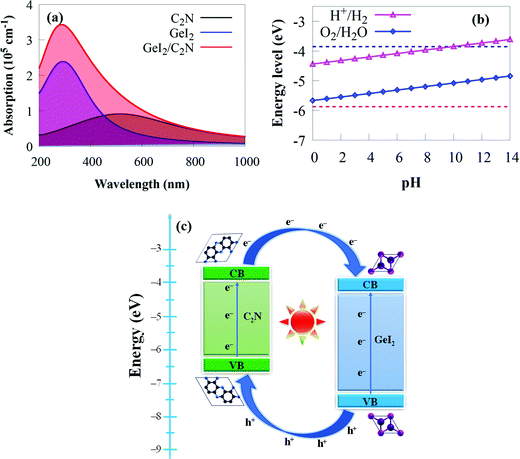
Another critical element in constructing photocatalytic devices is optical absorption. A broad and strong absorption edge is required to achieve efficient solar energy conversion during water splitting processes. The initial stage in water splitting is photon absorption, which produces electron–hole pairs. A strong visible light-harvesting capacity and appropriate electronic and interface properties are required for promising photocatalytic materials. With this in mind, the optical properties of the GeI2/C2N vdW heterostructure are calculated to access its photocatalytic application. It is clear that the GeI2 monolayer slightly absorbs visible light. But the visible light absorption coefficient of C2N is higher than that of the GeI2 monolayer (Fig. 6).
Considering the influence of interface contact on the optical properties, we compared the absorption coefficients of the GeI2/C2N vdW heterostructure to those of the C2N and the GeI2 monolayer. As expected, the vdW heterostructure shows a higher redshift around 720 nm than the individual monolayers, which is particularly useful for capturing solar energy. This enhancement is due to its narrower bandgap energy than the GeI2 monolayer and C2N. The efficient absorption of solar light for the GeI2/C2N vdW heterostructure mainly results from the coupling activity between the GeI2 and C2N, including the electron transfer from C2N to the GeI2 monolayer and the charge redistribution at the interface.79 Therefore, the GeI2/C2N vdW heterostructure is more effective in utilising solar energy, which holds great promise in visible light-harvesting photocatalytic devices.
Furthermore, the proper band position for water redox potentials is a key criterion for photocatalytic water splitting, where the VBM and CBM must be lower and higher than the O2 (−5.67 eV) and H2 (−4.44 eV) potentials at pH = 0, respectively.94 The CBMs for the GeI2 monolayer, C2N and the GeI2/C2N vdW heterostructure are −4.33, −4.07 and −4.02 eV, respectively, while their VBMs are −7.36, −6.31 and −5.98 eV, respectively. This demonstrates that all of these materials meet the overall water splitting criteria. The high bandgap of the GeI2 monolayer, on the other hand, substantially restricts its efficiency in solar energy utilisation. Because C2N lacks an electric field, it has a fast electron–hole pair recombination rate,25,26,37 which is unfavourable for photocatalysis. The CBM and VBM potentials of the GeI2/C2N vdW heterostructure are 0.442 eV and 0.308 eV higher and lower than the H+/H2 reduction and O2/H2O oxidation potentials at pH = 0, respectively, which is sufficient for H2 and O2 generation. As a result, the GeI2/C2N vdW heterostructure straddles the water redox potentials at pH = 0. Furthermore, pH has an effect on the redox potential of water.95 The H+/H2 and O2/H2O potentials are calculated as −4.44 eV + pH × 0.059 eV and −5.67 + pH × 0.059 eV, respectively.95 Furthermore, the band edges of the GeI2/C2N vdW heterostructure in comparison to aqueous solution straddle the water redox potential at pH values ranging from 0 to 9 (Fig. 6b). This suggests that the GeI2/C2N vdW heterostructure may be a better water splitting material, whether under acidic, neutral or alkaline environments without an external bias voltage.
The spatial separation of charge carriers at the GeI2/C2N vdW heterostructure interface is investigated further. The VBM (CBM) of C2N is lower (higher) than that of the GeI2 monolayer, as shown in the schematic diagram in Fig. 6c, allowing us to establish a type-II band alignment of the vdW heterostructure. In solar conversion and optoelectronic devices, the conduction band offset (CBO) and valence band offset (VBO) are critical. The VBO and CBO of the GeI2/C2N vdW heterostructure are calculated as 1.05 and 0.26 eV, respectively. Under light irradiation, the photogenerated particles get energy from photons to excite the photogenerated electrons in the VBs of both monolayers and transfer them to their CBs by creating holes in the VBs. The band offset will allow the transport of photoinduced holes from the VB of the GeI2 monolayer to the VB of C2N and photoinduced electrons from the CB of C2N to the CB of the GeI2 monolayer, thereby reducing photogenerated charge carrier recombination. As a result, both the VBO and CBO can improve photogenerated charge carrier separation.96 Because the CBM is located on the GeI2 monolayer, the OER will mostly take place on it, whereas the HER will take place on the C2N.
Applying external strain has been an efficient technique to tune the electronic, optical and structural properties of 2D vdW heterostructures,97 which is beneficial in photocatalysis, optoelectronic and nanoelectronic devices.98 Herein, we investigate the effect of biaxial strain on the electronic, optical and structural properties of the GeI2/C2N vdW heterostructure by varying the lattice parameters as follows:
| ε = [(a0 − a1)/a1] × 100%, |
| Es = Estrain − Eunstrain | (5) |
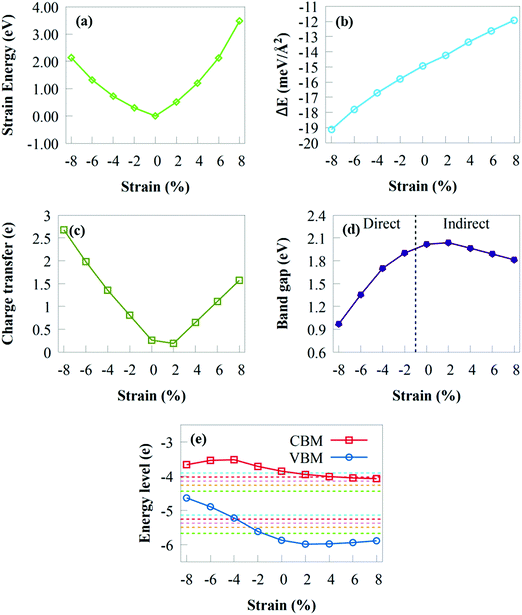
As the compressive or tensile strain increases, Es fluctuates smoothly as a quadratic curve, demonstrating that the GeI2/C2N vdW heterostructure has no phase transition and retains its hexagonal structure under a biaxial strain of ±8%. As a result, the imposed biaxial strain is ensured to be under the elastic limit and totally reversible.98 The interface binding energy under compressive/tensile strain is given in Fig. 7b to provide a fundamental understanding of the effect of biaxial strain on the interfacial interactions. The interface binding energy remains negative under a biaxial strain of ±8%, demonstrating the energy stability of the GeI2/C2N heterostructure. The stability increases when the compressive strain varies from −2% to −8%, whereas it decreases when the tensile strain changes from +2% to +8%. This suggests that the GeI2/C2N vdW heterostructure is more stable with an increasing/decreasing compressive/tensile biaxial strain.
The amount of charge transfer at the GeI2/C2N vdW heterostructure interface under biaxial strain is shown in Fig. 7c. The positive ΔQ values indicate that electrons are transferred from the C2N to the GeI2 monolayer under compressive/tensile biaxial strain. Therefore, a built-in electric field may occur in a biaxial strain of ±8%. Δq of the GeI2/C2N vdW heterostructure decreases with a tensile strain of +2%, while it increases when the tensile strain increases from +4% to +8%. This is in agreement with the bandgap energy obtained shown in Fig. 7d. Moreover, it increases from 0.809e to 2.697e with a compressive strain from −2% to −8%.
Fig. 7d depicts the fluctuation of the bandgap energies in the GeI2/C2N vdW heterostructure under biaxial strains from +8% to −8%. When the tensile biaxial strain is less than +2%, the bandgap energy of the GeI2/C2N vdW heterostructure slightly increases. Obviously, tensile biaxial strains from +4% to +8% monotonically decrease the bandgap energy due to the increasing amount of charge transferring at the heterostructure interface, while the indirect bandgap energy remains unchanged. Electrons in semiconductors with a reduced bandgap are less likely to recombine during charge transfer, which is critical in solar conversion devices. Compared with the unstrained system, tensile biaxial strains from +4% to +8% reduce the GeI2/C2N vdW heterostructure bandgap, which indicates the importance of biaxial strain in tuning the bandgap of the GeI2/C2N vdW heterostructure. The smaller bandgap observed under tensile biaxial strain is more conducive to solar energy conversion because the energy required to excite electrons from the VB to the CB of the heterostructure is smaller. The bandgap energy decreases linearly with a compressive biaxial strain. This shows the different variation patterns of the bandgap energy under compressive strain.
Fig. 7e depicts the fluctuation of the band edges of the GeI2/C2N vdW heterostructure under various biaxial strains and pH. The heterostructure has an appropriate band edge position for overall water splitting at pH 0 to 5 under an applied biaxial strain range from +2% to +8%. Moreover, overall water splitting is achieved under pH 0 up to 6 and 7, respectively, under tensile strain from +2% to +4% and +2%. Clearly, as tensile strain increases, the VBM and CBM increasingly move towards the water oxidation and reduction potentials. This indicates that the reducing potential of the GeI2/C2N vdW heterostructure becomes weak with increasing pH, which is not favourable to generate H2 at a higher pH. Nevertheless, when compressive strain increases, the VBM steadily decreases, indicating that the oxidising power weakens. The GeI2/C2N heterostructure bandgap is 0.97 eV under a compressive strain of −2%, which is less than the minimum bandgap energy (1.23 eV) needed for water splitting. Nevertheless, under compressive strains from −4% to −8%, the GeI2/C2N vdW heterostructure is only suited for H2 generation and not for O2 generation. The VBM is lower than the H2O/O2 potential at pH 3 to 7, indicating that the system may achieve overall water splitting under a compressive strain of −2%. The favourable band edge position suggests that the GeI2/C2N vdW heterostructure has strong tensile strain resistance for overall water splitting.
We computed the phonon spectra under biaxial strain ranging from −8% to +8% to ensure that the GeI2/C2N vdW heterostructure is dynamically stable throughout the tensile strain range. As seen in Fig. S1 (ESI†), phonon dispersion spectra reveal positive frequencies, suggesting the dynamic stability of the GeI2/C2N vdW heterostructure under biaxial strain.
The band structure of the GeI2/C2N vdW heterostructure under biaxial strain from +8% to −8% is shown in Fig. S2 (ESI†). The CBM and VBM are fixed at the Γ high-symmetry point when the tensile biaxial strain changes from +2% to +8%, indicating that the type-II indirect bandgap nature of the unstrained GeI2/C2N vdW heterostructure has altered dramatically. Thus, tensile biaxial strain pushed the sub-bands in the CB of C2N closer to the Fermi energy. As tensile strain increases from +2% to +8%, the position of the CBM progressively shifted from the K to Γ point, resulting in the type-II indirect to type-I direct band structure transition. Because the CBM and VBM of semiconductor 1 lie between the CBM and VBM of semiconductor 2 in the type-I vdW heterostructure, charge carriers are spatially localised in the same component, which efficiently promotes charge carrier recombination and lowers their separation. Thus, the type-I vdW heterostructure is more suitable for light-emitting diodes and lasers.99 The type-II indirect band structure of the GeI2/C2N vdW heterostructure, however, remains intact during compressive strain engineering, as seen in Fig. S2 (ESI†). This increases the charge carrier lifetime, which could be useful in optoelectronic, photoelectric, and solar energy conversion devices.100 Thus, the band alignment transition makes the GeI2/C2N vdW heterostructure promising for application in multi-functional devices. Also, flat bands can occur along the Γ–M–K–Γ Brillouin zone under a larger compressive strain from −4% to −8%. This illustrates that a large compressive biaxial strain of −8% may push the valence band extrema (VBE) along the Γ–K or Γ–M direction near the VBM. The formation of flat bands around the VBM has been reported in other strained 2D materials.101,102
Under tensile strain, the C 2p and N 2p orbitals contribute significantly to the CBM and VBM as illustrated in Fig. S3 (ESI†). This shows that the type-II band alignment changes dramatically under tensile biaxial strain. On the other hand, a compressive biaxial strain of −2% to −8% did not affect the orbital contributions at the VBM and CBM. The N 2p and Ge 4p orbitals contributed to the VBM and CBM, respectively. Considering the electronic transition selection rules, the electrons are primarily excited from the N 2p orbitals to the Ge 4p orbitals, making the system type-II. We observed that the electronic properties of the GeI2/C2N vdW heterostructure respond sensitively to compressive biaxial strain by investigating the PDOS and band structure, causing the GeI2/C2N vdW heterostructure to transition from a type-II indirect to type-I direct electronic band structure.
Fig. S4 (ESI†) depicts the computed DOS of the GeI2/C2N vdW heterostructure with biaxial strain. When tensile biaxial strain changes from +2% to +8%, we see that C2N contributes the most to the VBM and CBM, confirming that the system is a type-I heterostructure. Fig. S4 (ESI†) shows that the type-II heterojunction is retained when the compressive strain varies from −2% to −8%.
IV. Conclusions
To explore the potential applications in photocatalysis, we explored the work function, band structure, optical properties, band alignment, charge transfer and band offset of the proposed 2D vertical GeI2/C2N vdW heterostructure using DFT calculations. By assessing its interface binding energy, AIMD simulation and vibrational phonon spectra at room temperature, the vdW heterostructure was created by weak vdW forces with thermal and dynamic stability. Furthermore, the small lattice mismatch confirms the experimental realisation of the GeI2/C2N vdW heterostructure. The proposed heterostructure is found to have a conventional type-II band alignment with an indirect bandgap of 2.02 eV and electrons tend to move from the C2N to the GeI2 monolayer. Besides, the charge density difference analysis showed that C2N transferred about 0.263|e| to the GeI2 monolayer. Furthermore, the GeI2/C2N vdW heterostructure exhibits high visible light absorption due to its smaller bandgap as compared to those of the isolated GeI2 monolayer and C2N. The band edges of the GeI2/C2N vdW heterostructure met the criteria of overall water splitting at a pH range of 0 to 9. Furthermore, the potential drop of 7.16 eV and the built-in electric field at the interface help in the effective separation of photoinduced electron–hole pairs. Under tensile biaxial strain, the band alignment changes from a type-II indirect to type-I direct band alignment. Our theoretical findings offer fundamental insights into designing solar conversion and other high performance optoelectronic or electronic devices.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research was performed using the computational facilities provided by the Centre for High Performance Computing (CHPC), Cape Town, South Africa.References
- A. S. Arico, P. Bruce, B. Scrosati, J.-M. Tarascon and W. Van Schalkwijk, Mater. Sustainable Energy Appl., 2011, 148–159 Search PubMed
.
- G. Kumar, S.-H. Kim, C.-H. Lay and V. K. Ponnusamy, Bioresour. Technol., 2020, 317, 124010 CrossRef CAS PubMed
.
- I. Shahid, S. Ahmad, N. Shehzad, S. Yao, C. V. Nguyen, L. Zhang and Z. Zhou, Appl. Surf. Sci., 2020, 523, 146483 CrossRef CAS
.
- N. Shehzad, I. Shahid, S. Yao, S. Ahmad, A. Ali, L. Zhang and Z. Zhou, Int. J. Hydrogen Energy, 2020, 45, 27089–27097 CrossRef CAS
.
- I. Shahid, A. Ali, J.-M. Zhang, I. Muhammad, I. Ahmad and F. Kabir, Int. J. Hydrogen Energy, 2021, 46, 14247–14258 CrossRef CAS
.
- R. Varunaa and P. Ravindran, Phys. Chem. Chem. Phys., 2019, 21, 25311–25322 RSC
.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed
.
- A. R. Amani-Ghadim, F. Khodam and M. S. S. Dorraji, J. Mater. Chem. A, 2019, 7, 11408–11422 RSC
.
- Z. Cui, N. Lyu, Y. Ding and K. Bai, Phys. E, 2021, 127, 114503 CrossRef CAS
.
- J. Li, Z. Huang, W. Ke, J. Yu, K. Ren and Z. Dong, J. Alloys Compd., 2021, 866, 158774 CrossRef CAS
.
- Z. Ma, B. Wang, L. Ou, Y. Zhang, X. Zhang and Z. Zhou, Nanotechnology, 2016, 27, 415203 CrossRef PubMed
.
- F. Opoku, K. K. Govender, C. G. C. E. van Sittert and P. P. Govender, New J. Chem., 2017, 41, 8140–8155 RSC
.
- D. K. Pham, S.-T. Nguyen and C. Q. Nguyen, New J. Chem., 2021, 45, 15942–15948 RSC
.
- K. Zheng, H. Cui, H. Luo, J. Yu, S. Wang, C. Tan, L. Wang, X. Li, L.-Q. Tao and X. Chen, J. Mater. Chem. C, 2020, 8, 11980–11987 RSC
.
- H. L. Zhuang, M. D. Johannes, M. N. Blonsky and R. G. Hennig, Appl. Phys. Lett., 2014, 104, 022116 CrossRef
.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae and S.-D. Sohn, Nat. Commun., 2015, 6, 1–7 Search PubMed
.
- P. Netrattana and P. Reunchan, J. Phys.: Conf. Ser., 2017, 901, 012102 CrossRef
.
- L. Wang, W. Si, Y. Tong, F. Hou, D. Pergolesi, J. Hou, T. Lippert, S. X. Dou and J. Liang, Carbon Energy, 2020, 2, 223–250 CrossRef CAS
.
- B. Peng, L. Xu, J. Zeng, X. Qi, Y. Yang, Z. Ma, X. Huang, L.-L. Wang and C. Shuai, Catal. Sci. Technol., 2021, 11, 3059–3069 RSC
.
- W. Wei and T. Jacob, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085202 CrossRef
.
- J. Mahmood, F. Li, S.-M. Jung, M. S. Okyay, I. Ahmad, S.-J. Kim, N. Park, H. Y. Jeong and J.-B. Baek, Nat. Nanotechnol., 2017, 12, 441–446 CrossRef CAS PubMed
.
- R. Wu, K. Zhou, C. Y. Yue, J. Wei and Y. Pan, Prog. Mater. Sci., 2015, 72, 1–60 CrossRef CAS
.
- H. Ozisik, K. Colakoglu, H. B. Ozisik and E. Deligoz, Comput. Mater. Sci., 2010, 50, 349–355 CrossRef CAS
.
- L. Xu, Z. Ma, Q. Li, T. Chen, B. Peng, J. Zeng, Y. Zhang, K.-W. Luo, L.-L. Wang and C. Shuai, New J. Chem., 2020, 44, 15439–15445 RSC
.
- C. Li, Y. Xu, W. Sheng, W.-J. Yin, G.-Z. Nie and Z. Ao, Phys. Chem. Chem. Phys., 2020, 22, 615–623 RSC
.
- G. Wang, Z. Li, W. Wu, H. Guo, C. Chen, H. Yuan and S. A. Yang, Phys. Chem. Chem. Phys., 2020, 22, 24446–24454 RSC
.
- S. J. Liang, B. Cheng, X. Cui and F. Miao, Adv. Mater., 2020, 32, 1903800 CAS
.
- Y. Gan, J. Liang, C.-W. Cho, S. Li, Y. Guo, X. Ma, X. Wu, J. Wen, X. Du and M. He, Front. Phys., 2020, 15, 1–7 Search PubMed
.
- G. X. Zheng, J. M. Terry, P. Belgrader, P. Ryvkin, Z. W. Bent, R. Wilson, S. B. Ziraldo, T. D. Wheeler, G. P. McDermott and J. Zhu, Nat. Commun., 2017, 8, 1–12 CrossRef PubMed
.
- M. U. Farooq, V. Novosad, E. A. Rozhkova, H. Wali, A. Ali, A. A. Fateh, P. B. Neogi, A. Neogi and Z. Wang, Sci. Rep., 2018, 8, 1–12 CAS
.
- Z. Zhang, Y. Zhang, Z. Xie, X. Wei, T. Guo, J. Fan, L. Ni, Y. Tian, J. Liu and L. Duan, Phys. Chem. Chem. Phys., 2019, 21, 5627–5633 RSC
.
- F. Opoku, O. Akoto, S. O.-B. Oppong and A. A. Adimado, New J. Chem., 2021, 45, 20365–20373 RSC
.
- H. Zhou, W. Cai, J. Li, X. Liu, W. Xiong, Y. Zhou, Z. Xu, B. Wang and C. Ye, Phys. Chem. Chem. Phys., 2020, 22, 1485–1492 RSC
.
- R. Zhang, L. Zhang, Q. Zheng, P. Gao, J. Zhao and J. Yang, J. Phys. Chem. Lett., 2018, 9, 5419–5424 CrossRef CAS PubMed
.
- Z. Zheng, X. Wang and W. Mi, Carbon, 2017, 117, 393–398 CrossRef CAS
.
- X. Zhang, A. Chen, Z. Zhang, M. Jiao and Z. Zhou, Nanoscale Adv., 2019, 1, 154–161 RSC
.
- Y. Bai, Q. Zhang, N. Xu, K. Deng and E. Kan, J. Phys. Chem. C, 2018, 122, 15892–15902 CrossRef CAS
.
- H. Wang, X. Li and J. Yang, ChemPhysChem, 2016, 17, 2100–2104 CrossRef CAS PubMed
.
- R. Kumar, D. Das and A. K. Singh, J. Catal., 2018, 359, 143–150 CrossRef CAS
.
- Z. Guan, C.-S. Lian, S. Hu, S. Ni, J. Li and W. Duan, J. Phys. Chem. C, 2017, 121, 3654–3660 CrossRef CAS
.
- S. E. Tsoeu, F. Opoku and P. P. Govender, J. Electron. Mater., 2021, 50, 620–628 CrossRef CAS
.
- S. E. Tsoeu, F. Opoku and P. P. Govender, SN Appl. Sci., 2020, 2, 341 CrossRef CAS
.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS
.
- V. Turkowski, N. U. Din and T. S. Rahman, Computation, 2017, 5, 39 CrossRef
.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS
.
- W. Hanke and L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 4656–4673 CrossRef CAS
.
- Z. Wang, Y. Zhang, X. Wei, T. Guo, J. Fan, L. Ni, Y. Weng, Z. Zha, J. Liu and Y. Tian, Phys. Chem. Chem. Phys., 2020, 22, 9647–9655 RSC
.
- H. M. Tang, A.-A. Sun and S.-P. Gao, Phys. Rev. Mater., 2020, 4, 084004 CrossRef CAS
.
- F. Opoku and P. P. Govender, Mater. Chem. Phys., 2019, 224, 107–116 CrossRef CAS
.
- D. M. Hoat, T. V. Vu, M. M. Obeid and H. R. Jappor, Chem. Phys., 2019, 527, 110499 CrossRef CAS
.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
-
W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling and P. B. Kramer, Numerical recipes, Cambridge University Press, Cambridge, 1989 Search PubMed
.
- D. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef
.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS
.
- S. Kümmel and L. Kronik, Rev. Mod. Phys., 2008, 80, 3–60 CrossRef
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS
.
- X. Ge, S. J. Binnie, D. Rocca, R. Gebauer and S. Baroni, Comput. Phys. Commun., 2014, 185, 2080–2089 CrossRef CAS
.
- O. B. Malcıoğlu, R. Gebauer, D. Rocca and S. Baroni, Comput. Phys. Commun., 2011, 182, 1744–1754 CrossRef
.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- W. G. Hoover, PhRvA, 1985, 31, 1695–1697 Search PubMed
.
- A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179 CrossRef CAS PubMed
.
- G. Wang, Z. Li, W. Wu, H. Guo, C. Chen, H. Yuan and S. A. Yang, Phys. Chem. Chem. Phys., 2020, 22, 24446–24454 RSC
.
- H. M. Powell and F. M. Brewer, J. Chem. Soc., 1938, 197–198 RSC
.
- D. Nafday, H. Fang, P. Jena and T. Saha-Dasgupta, Phys. Chem. Chem. Phys., 2019, 21, 21128–21135 RSC
.
- L. Xu, Z. Ma, Q. Li, T. Chen, B. Peng, J. Zeng, Y. Zhang, K.-W. Luo, L.-L. Wang and C. Shuai, New J. Chem., 2020, 44, 15439–15445 RSC
.
- J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae, S.-D. Sohn, N. Park, J. H. Oh, H.-J. Shin and J.-B. Baek, Nat. Commun., 2015, 6, 6486 CrossRef CAS PubMed
.
- C.-S. Liu, X.-L. Yang, J. Liu and X.-J. Ye, J. Phys. Chem. C, 2018, 122, 22137–22142 CrossRef CAS
.
- J. Hu, W. Duan, H. He, H. Lv, C. Huang and X. Ma, J. Mater. Chem. C, 2019, 7, 7798–7805 RSC
.
- Z. Zhang, Z. Xie, J. Liu, Y. Tian, Y. Zhang, X. Wei, T. Guo, L. Ni, J. Fan and Y. Weng, Phys. Chem. Chem. Phys., 2020, 22, 5873–5881 RSC
.
- Y. Chen and J. Washburn, Phys. Rev. Lett., 1996, 77, 4046–4049 CrossRef CAS PubMed
.
- X. Zhang, A. Chen, Z. Zhang, M. Jiao and Z. Zhou, Nanoscale Adv., 2019, 1, 154–161 RSC
.
- X. Luo, G. Wang, Y. Huang, B. Wang, H. Yuan and H. Chen, Phys. Chem. Chem. Phys., 2017, 19, 28216–28224 RSC
.
- M. Ashwin Kishore, K. Larsson and P. Ravindran, ACS Omega, 2020, 5, 23762–23768 CrossRef CAS PubMed
.
- X.-H. Li, B.-J. Wang, H. Li, X.-F. Yang, R.-Q. Zhao, X.-T. Jia and S.-H. Ke, New J. Chem., 2020, 44, 16092–16100 RSC
.
- T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108, 235502 CrossRef PubMed
.
- X. Gao, Y. Shen, Y. Ma, S. Wu and Z. Zhou, Appl. Phys. Lett., 2019, 114, 093902 CrossRef
.
- Z. Zhu, K. Ren, H. Shu, Z. Cui, Z. Huang, J. Yu and Y. Xu, Catalysts, 2021, 11, 991 CrossRef CAS
.
- M. Idrees, C. V. Nguyen, H. Bui, I. Ahmad and B. Amin, Phys. Chem. Chem. Phys., 2020, 22, 20704–20711 RSC
.
- J. Song, H. Zheng, M. Liu, G. Zhang, D. Ling and D. Wei, Phys. Chem. Chem. Phys., 2021, 23, 3963–3973 RSC
.
- B. Wang, H. Yuan, J. Chang, X. Chen and H. Chen, Appl. Surf. Sci., 2019, 485, 375–380 CrossRef CAS
.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098 CrossRef CAS PubMed
.
- Y. Li, Y.-L. Li, B. Sa and R. Ahuja, Catal. Sci. Technol., 2017, 7, 545–559 RSC
.
- D. Sanchez-Portal, E. Artacho and J. M. Soler, Solid State Commun., 1995, 95, 685–690 CrossRef CAS
.
- C. Lei, Y. Ma, X. Xu, T. Zhang, B. Huang and Y. Dai, J. Phys. Chem. C, 2019, 123, 23089–23095 CrossRef CAS
.
- J. Zeng, L. Xu, Y. Yang, X. Luo, H.-J. Li, S. Xiong and L.-L. Wang, Phys. Chem. Chem. Phys., 2021, 23, 8318–8325 RSC
.
- K. Rahimi and A. Z. Moshfegh, Phys. Chem. Chem. Phys., 2021, 23, 20675–20685 RSC
.
- J. E. Padilha, A. Fazzio and A. J. R. da Silva, Phys. Rev. Lett., 2015, 114, 066803 CrossRef CAS PubMed
.
- A. Singh, M. Jain and S. Bhattacharya, Nanoscale Adv., 2021, 3, 2837–2845 RSC
.
- V. Chakrapani, J. C. Angus, A. B. Anderson, S. D. Wolter, B. R. Stoner and G. U. Sumanasekera, Sci, 2007, 318, 1424–1430 CrossRef CAS PubMed
.
- X. Zhang, Z. Zhang, D. Wu, X. Zhang, X. Zhao and Z. Zhou, Small Methods, 2018, 2, 1700359 CrossRef
.
- N. Goel, R. Kumar and M. Kumar, Nanotechnology, 2021, 32, 375711 CrossRef CAS PubMed
.
- H. Li, H. Liu, L. Zhou, X. Wu, Y. Pan, W. Ji, B. Zheng, Q. Zhang, X. Zhuang, X. Zhu, X. Wang, X. Duan and A. Pan, ACS Nano, 2018, 12, 4853–4860 CrossRef CAS PubMed
.
- X.-H. Li, B.-J. Wang, X.-L. Cai, L.-W. Zhang, G.-D. Wang and S.-H. Ke, RSC Adv., 2017, 7, 28393–28398 RSC
.
- S. Nakamura, M. Senoh, N. Iwasa and S.-I. Nagahama, JaJAP, 1995, 34, L797–L799 CAS
.
- K. Cheng, Y. Guo, N. Han, X. Jiang, J. Zhang, R. Ahuja, Y. Su and J. Zhao, Appl. Phys. Lett., 2018, 112, 143902 CrossRef
.
- H. T. T. Nguyen, V. V. Tuan, C. V. Nguyen, H. V. Phuc, H. D. Tong, S.-T. Nguyen and N. N. Hieu, Phys. Chem. Chem. Phys., 2020, 22, 11637–11643 RSC
.
- S.-D. Guo, X.-S. Guo and Y. Deng, J. Appl. Phys., 2019, 126, 154301 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ya00047k |
| This journal is © The Royal Society of Chemistry 2022 |