Open Access Article
Open Access ArticleConformational analysis of amphetamine and methamphetamine: a comprehensive approach by vibrational and chiroptical spectroscopy†
Kristýna
Dobšíková‡
 a,
Pavel
Michal‡
a,
Pavel
Michal‡
 e,
Dita
Spálovská
e,
Dita
Spálovská
 a,
Martin
Kuchař
a,
Martin
Kuchař
 bcf,
Natalie
Paškanová
bcf,
Natalie
Paškanová
 bc,
Radek
Jurok
bc,
Radek
Jurok
 bcd,
Josef
Kapitán
bcd,
Josef
Kapitán
 e and
Vladimír
Setnička
e and
Vladimír
Setnička
 *a
*a
aDepartment of Analytical Chemistry, University of Chemistry and Technology, Prague 6, 166 28, Czech Republic. E-mail: Vladimir.Setnicka@vscht.cz
bForensic Laboratory of Biologically Active Substances, University of Chemistry and Technology, Prague 6, 166 28, Czech Republic
cDepartment of Chemistry of Natural Compounds, University of Chemistry and Technology, Prague 6, 166 28, Czech Republic
dDepartment of Organic Chemistry, University of Chemistry and Technology, Prague 6, 166 28, Czech Republic
eDepartment of Optics, Palacký University Olomouc, Olomouc, 771 46, Czech Republic. E-mail: michal@optics.upol.cz
fNational Institute of Mental Health, Klecany 250 67, Czech Republic
First published on 16th February 2023
Abstract
After cannabis, the most commonly used illicit substance worldwide is amphetamine and its derivatives, such as methamphetamine, with an ever-increasing number of synthetic modifications. Thus, fast and reliable methods are needed to identify them according to their spectral patterns and structures. Here, we have investigated the use of molecular spectroscopy methods to describe the 3D structures of these substances in a solution that models the physiological environment. The substances were analyzed by Raman and infrared (IR) absorption spectroscopy and by chiroptical methods, vibrational circular dichroism (VCD) and Raman optical activity (ROA). The obtained experimental data were supported by three different computational approaches based on density functional theory (DFT) and molecular dynamics (MD). Successful interpretation relies on good agreement between experimental and predicted spectra. The determination of the conformer populations of the studied molecules was based on maximizing the similarity overlap of weighted conformer spectra by a global minimization algorithm. Very good agreement was obtained between the experimental spectra and optimized-population weighted spectra from MD, providing a detailed insight into the structure of the molecules and their interaction with the solvent. The relative population of three amphetamine and six methamphetamine conformers was determined and is consistent with a previous NMR study. However, this work shows that only a few isolated conformers are not sufficient for the successful interpretation of the spectra, but the entire conformational space needs to be sampled appropriately and explicit interaction with the solvent needs to be included.
1. Introduction
Nowadays, synthetic modifications of stimulant drugs of abuse amphetamine and methamphetamine are exploited worldwide. Their main effect is in increasing the levels of noradrenaline, dopamine and serotonin in the brain.1–3 According to the European Monitoring Centre for Drugs and Drug Addiction (EMCDDA) and Europol (2016–2018),4,5 the highest number of illegal laboratories were dismantled in Central Europe. Hence there is a need for quick and reliable analysis to identify them.Most studies perform the determination of amphetamines in biological samples (hair, blood, saliva or urine) or in seized drug samples by commonly used techniques – gas chromatography (GC) with mass spectrometry (MS),6–8 high-performance liquid chromatography (HPLC),9,10 nuclear magnetic resonance (NMR) spectroscopy11 or vibrational techniques such as infrared (IR)12 and Raman spectroscopy.13,14 IR and Raman spectroscopy are widely employed as qualitative and quantitative methods for drug identification for their fast analysis and reliability. It is of particular importance to analyse and study the drugs of abuse in the same form as they are taken into the organism.15–19 Based on that, this work examines amphetamine and methamphetamine hydrochloride diluted in an aqueous solution.
Amphetamine and its derivative methamphetamine are both chiral molecules. In both cases, the (S)-enantiomer has greater biological activity than the (R)-enantiomer. Standard analytical methods detect amphetamine and methamphetamine in the sample but cannot indicate the absolute configuration. Thus, an additional analysis must be performed in order to determine the presence of an individual enantiomer. Enantiomer identification is necessary because (R)-methamphetamine is actually part of several over-the-counter medicines (e.g. Vicks® Vapor Inhaler in North America).20 The abuse of this enantiomer is rarely reported. Almost all abused methamphetamine contains the (S)-enantiomer or the mixture of both enantiomers. Isomer differences appear due to the availability of different precursors on the drug market.21–23
NMR spectroscopy provides detailed information about the structure of the studied molecules. Despite the fact that NMR is blind to chirality,24 in some cases, it is possible to determine the absolute configuration using complexes with chiral shift reagents and empirical correlations associated with interpreting the chemical shifts.25–27 A conformational preference of amphetamine and methamphetamine hydrochloride salts diluted in D2O was already studied using high-resolution NMR spectroscopy analysing vicinal proton coupling with the help of the Karplus relationship. The study revealed a high preference for trans-phenylamino rotamers.11
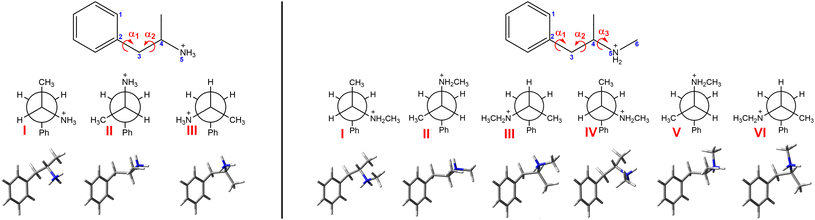
Chiroptical spectroscopy allows direct determination of the absolute configuration of native chiral compounds in a liquid phase. The first attempt to measure ROA of amphetamine salt, namely di-D-amphetamine sulfate in water solution, was already reported and analysed by comparison with ab initio calculations.14 The mode assignment of the (S)-(+)-amphetamine-H+ ion was also given. Unfortunately, the experimental spectrum of only one enantiomer was reported and was hampered by the relatively high level of noise. By comparison with three analysed conformations the measured sample seems to adopt conformation II (Fig. 1), which corresponds to the results of the previous NMR study, but it was not possible to resolve the conformational ratio.
In order to verify and expand the previous preliminary findings, we present the first comprehensive structural study of amphetamine and methamphetamine hydrochlorides in an aqueous solution performed by methods like VCD, ROA, IR and Raman spectroscopy and supplemented by corresponding dimensionless quantities, dissymmetry factor (DF) and normalized circular intensity difference (CID). Furthermore, the interaction of amphetamine derivatives with solvent molecules is taken into account directly in the calculations by a combination of a density functional theory (DFT) and molecular dynamics (MD) approach.28–35
For successful interpretation of the analysed spectra and deriving the molecular structural information, the correlation between experimental and predicted spectra is discussed. As was recently confirmed, the conformer populations derived from Gibbs free energies suffer from large uncertainties originating from the calculation limits.36,37 As an alternative, methods that fit a set of calculated spectra in order to minimize the difference with the experimental spectra were suggested. The first conformational analysis based on the linear fitting of calculated and experimental dipole and rotational strengths of the methylcyclohexanone was introduced in 1999 by F. J. Devlin and P. J. Stephens.38 Another approach used the genetic algorithm to continuously modify the calculated conformational energies according to the predefined mutation rules to find the best overlap between calculated and experimental intensities.36,39 In the manuscript, we present a robust approach to determine the conformer populations of amphetamine and methamphetamine based on maximizing the similarity overlap independently of energies of molecular conformers. This approach uses the minimization algorithm to optimize the conformer populations and wavenumber scaling factor. As the complexity of conformational space increases with the flexibility of the studied molecular system, careful selection of the starting points in the optimization procedure is needed due to the tendency to slide down to the nearest local minimum. Therefore, the effective two-step optimization including the Monte Carlo method is demonstrated in the methamphetamine case. By application of the presented algorithm to three different computational models – the conformers derived from the single molecule (SM) DFT calculations with only implicit solvent model (COSMO), MD geometries with fixed selected torsion angles without explicit solvent molecules and partially optimized solute–solvent cluster-based MD geometries, the importance of appropriate conformational averaging and a need for explicit solvent models are emphasized.
This complex study provides important insight into the 3D structure characterization of the illicit substances in solution, which is crucial for in vivo studies.
2. Materials and methods
2.1. Chemicals and sample preparation
Both enantiomeric standards of amphetamine and methamphetamine were synthesized and enantioseparated (see sections 1 and 2 of the ESI†) at the Forensic Laboratory of Biologically Active Substances (UCT Prague) with a purity exceeding 98% (see Fig. S1, S2 and Tables S1, S2 in the ESI†).The standard of amphetamine was prepared according to the standard oxime route from 1-phenylpropan-2-one. The chiral separation of racemic (R/S)-amphetamine was performed by crystallization with (2R,3R)-tartaric acid to provide (S)-1-phenylpropan-2-amine·(2R,3R) hydrogentartrate (in 51% yield) and (2S,3S)-tartaric acid to provide (R)-1-phenylpropan-2-amine·(2S,3S)-hydrogentartrate (in 62% yield). Both hydrogentartrate salts were converted to the corresponding hydrochlorides by treatment with NaOH and later HCl in diethyl ether to provide (S)-1-phenylpropan-2-amine hydrochloride: mp 153–154 °C [α]20D = +24.2° (c = 5.00, H2O). From (R)-1-phenylpropan-2-amine·(2S,3S) hydrogentartrate (R)-1-phenylpropan-2-amine hydrochloride, it was possible to analogously obtain: mp 154–155 °C, [α]20D = −24.7° (c = 5.00, H2O).
The (R)-methamphetamine hydrochloride standard was synthesized from (R)-1-phenylpropan-2-amine hydrochloride using methyl chloroformate to provide the corresponding carbamate. The carbamate was reduced by lithium aluminum hydride (LAH) in dry tetrahydrofuran (THF). The crude free base was converted to the hydrochloride salt by the addition of HCl in diethyl ether and the precipitate was recrystallized from acetonitrile to afford (R)-N-methyl-1-phenylpropan-2-amine hydrochloride in 85% yield as white needles: mp 172–173 °C, [α]20D = −17.4° (c = 3.00, H2O).
The (S)-methamphetamine hydrochloride standard was prepared from (1R,2S)-ephedrine according to the standard procedure including hydrogen iodide/red phosphorous reduction. The crude free base was converted to the hydrochloride salt by the addition of HCl in diethyl ether and the precipitate was recrystallized from acetonitrile to afford (S)-N-methyl-1-phenylpropan-2-amine hydrochloride in 80% yield as white needles: mp 173–174 °C, [α]20D = +17.9° (c = 3.00, H2O).
Deuterium oxide (D2O; 99.9% D) for the dissolution of amphetamine and methamphetamine was purchased from ISOSAR GmbH, Germany.
2.2. Experimental spectra
The VCD and IR absorption spectra were measured on an FTIR IFS 66/S spectrometer equipped with a VCD/IRRAS PMA 37 module (Bruker, Germany), a ZnSe photoelastic modulator (Hinds Instrument, The United States), a BaF2 polarizer, and an MCT detector (InfraRed Associates, The United States).40 The samples were prepared by dissolution in D2O (400.0 g L−1) and were placed into a BioCell cuvette with CaF2 windows (Biotools, Inc., The United States) and an optical path length of 27.3 μm. The spectra were measured in a spectral range of 1250–1800 cm−1 with a resolution of 8 cm−1 at ambient temperature. Each VCD spectrum was an average of 12 blocks and each of them was measured for 20 min and contained 3680 scans. The IR absorption spectra were presented as an average of 32 scans measured with a resolution of 8 cm−1. The baseline for the IR and VCD spectra was corrected by subtracting the solvent spectrum measured under the same conditions. VCD spectra are plotted as averages of both enantiomers “(S–R)/2”. IR and VCD intensities are given in epsilon units as molar circular dichroism (L mol−1 cm−1). The raw spectra can be found in the ESI (Fig. S3 and S4†).The Raman and ROA spectra were acquired on a ROA instrument developed at Palacký University, Olomouc,41 largely based on the design of W. Hug.42,43 The samples were dissolved in deionized water to concentrations of approximately 100 g L−1. The prepared solutions were filtered by a centrifugal filter (PTFE membrane, 0.45 μm pore size). The samples were measured in a rectangular fused silica cell of 70 μL volume at stabilized temperature (298.0 K), using back-scattering geometry, the scattered circular polarization (SCP) modulation scheme,44 a solid-state continuous wave laser with 532 nm excitation wavelength, ∼600 mW laser power at the sample, and 9–13 hours of accumulation time (for more experimental details, see Table S3†). The water signal was subtracted from the Raman spectra and the ROA spectra are plotted as averages of both enantiomers “(S–R)/2” with an approximate resolution of 8 cm−1. The raw spectra can be found in the ESI (Fig. S5 and S6†). Further corrections were not performed, except for mild third-order five-point Savitzky–Golay smoothing. The frequency scale was calibrated using a neon lamp. The intensity calibration was evaluated against a broadband calibration source (tungsten-halogen lamp) and in correspondence to the detected photoelectrons normalized by the excitation energy in a wavenumber interval and sample concentration (e− cm J−1 g−1 L).
Raman spectra are dominated by strongly polarized phenyl group vibration at 1000 cm−1 and since the phenyl group is not directly linked to the chiral centre, its ROA signal is very weak and prone to artifacts (the ROA to Raman ratio is in a range of only a few ppm). Successful measurement of reliable spectra therefore required a ROA spectrometer with a very high level of artifact control (see Fig. S5 and S6†).
From this point of view and due to their good water solubility, it seems that amphetamine and its analogues could be very good reference materials for ROA spectroscopy. However, this may be largely hampered by the fact that they are strictly controlled substances.
2.3. Computations
After the initial optimization at the B3LYP45/6-31G(d) level of theory, three and six stable conformers of amphetamine and methamphetamine, respectively, were revealed and further optimized using a larger basis set and hybrid DFT functionals (Fig. 1). Due to a longer alkyl chain and an increased number of torsional angles in the molecule, a higher number of stable conformers were obtained for methamphetamine than for amphetamine. Torsional angles, Gibbs free energies and corresponding Boltzmann weights (BWs) for optimized stable conformers at the B3PW91/6-311++G** level are listed in Table S4.† The IR, VCD, Raman and ROA intensities were calculated at several levels of theory using the Gaussian 16 program.46 The solvation effects were considered involving the conductor-like screening model (COSMO) for water.47–49 The electrical charge of the molecules was set to +1 (an explicit chlorine ion was not used).MD simulations were performed using the Amber 18 software,50,51 using the GAFF252 and TIP3P53 force fields for the solute and explicit waters, respectively. The Antechamber54 tool set was used to generate the Amber topology files for amphetamine and methamphetamine using partial charges calculated at the B3LYP/6-311++G** level. The solute molecule was placed in a cubic box (13.1 Å for amphetamine, 13.6 Å for methamphetamine) filled with water molecules (67 for amphetamine, 75 for methamphetamine) and chlorine counterion using Packmol script.55 The series of minimizations and short equilibrations were performed to partially relax the molecular system before it was subjected to a production run of 100 ns, 1 fs integration time, NVT ensemble and temperature of 295 K. The distributions of characteristic angles according to Fig. 1 derived from a 100 ns MD run of amphetamine and methamphetamine are shown in Fig. S7 and S8,† respectively. As was expected, neither side of the phenyl ring is preferred (cf. Fig. S7a and S8a†). Obviously three amphetamine conformers and six methamphetamine conformers are present in the MD run. The preferred conformers were categorized according to the chosen torsional angle intervals and their relative abundance is noted in Table S5.† From snapshots saved each 10 ps, 100 clusters in each conformer category were generated consisting of water molecules closer than 3 Å to the solute in the centre. The first water solvation shell of the amphetamine and methamphetamine comprises on average 18 water molecules, detailed distribution of the number of water molecules is presented in Fig. S9.† The clusters were partially optimized in the normal mode coordinates.56–59 Modes with frequencies below 225 cm−1 (or below 100i cm−1 when imaginary) were fixed during the optimization. Harmonic frequencies, IR and VCD were calculated at the same level B3PW91/6-31G**/COSMO(Water) with Grimme's dispersion correction with Becke–Johnson damping (GD3BJ)60,61 as the normal mode optimization. The rDPS62 basis set was combined with the B3PW91/6-31G**/GD3BJ/COSMO(Water) force field for the Raman and ROA intensity tensors, based on the previous experiences.63 For spectra generation the water molecular property tensors were set to zero.
Alternatively, the simplified MD approach was used. The solute geometries were extracted from saved MD snapshots and then optimized considering the fixed torsion angles (Fig. 1) at the higher B3PW91/6-311++G** level using the implicit model COSMO(Water) instead of explicit water molecules. Following the calculation of the force field, the IR and VCD intensities were determined at the same level, while for Raman and ROA intensities the rDPS basis set was preferred in this model.
For the visualization, all simulated spectra were obtained by convolution with a Lorentzian profile of 8 cm−1 bandwidth (full width at half maximum) that justifies the comparison to the experimental spectra. The effects of the deuteration of all amine hydrogens were included in the calculations of the IR and VCD spectra.
2.4. Spectral comparison
Precise conformational analysis lies on the comparison of experimental and predicted spectra. All spectra in the presented manuscript are compared first qualitatively and then quantitatively. The aim of the qualitative analysis is the assignment of the most characteristic spectral patterns in the experimental spectrum by a subjective comparison of band intensities and a sign pattern to the reference. However, this procedure should be taken with caution as it may lead to unwanted bias or mode assignment errors caused by the observer. The experimental and simulated vibrational spectra were compared using the similarity factor defined as64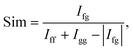 | (1) |
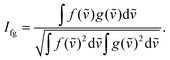 | (2) |
An alternative definition of similarity factor can be used as long as it is consistent in all spectral comparisons.66 Similarity results were supported by a quantitative comparison of the ratio of VCD over IR absorption spectrum labelled as the dimensionless dissymmetry factor (DF) and analogously by the ratio of the ROA and Raman spectrum called circular intensity difference (CID). The similarity values (1) for the IR and Raman spectral comparison are in a range from 0 to 1, while the range of similarity values for VCD, DF, ROA and CID is −1 to 1.
The real chiral sample should be considered as a mixture of all possible conformers with different abundance. The predicted spectrum can then be specified as normalized linear combination of all stable conformers
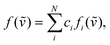 | (3) |
It has been a common practice to use a Boltzmann weighting factor derived from Gibbs free energy of the individual calculated conformation at the specific temperature as the linear combination coefficients to build a more realistic shape of the simulated spectra. However, as Boltzmann weights strongly depend on the computational level and molecular structure, large uncertainties in the conformational energies, varying more than 2 kcal mol−1, significantly affect the final predicted spectrum and subsequent assignment of the absolute configuration as has already been demonstrated in previous studies.36,37 To overcome the described uncertainties in the conformational analysis, two approaches based on genetic algorithms have recently been developed.36,39 Both methods use Gibbs energies as the starting point and optimizing Boltzmann weights against the experimental spectrum using a customized genetic algorithm to maximize the similarity factor (1).
In this paper we present an approach where the conformer population is determined from the global optimization algorithm67 of function (1). For a molecule with N conformations, N − 1 conformer populations ci in relation (3) are independent variables and the scaling factor for the predicted wavenumbers are allowed to change towards maximizing similarity assuming that the population of the remaining conformer is calculated as 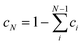 . Amphetamine was used as the first test of the described conformational approach because of well localized global maximum in the relatively restricted conformational space (three main conformations). The evenly distributed conformer populations were taken as the starting point. However, as the complexity and number of local similarity maxima increase with the number of populated conformers (N > 3), one starting point becomes insufficient to explore conformational space and the presented optimization algorithm results in a different local similarity maximum. Therefore, a more general two step global optimization procedure was defined for six stable conformers of methamphetamine. In the first step 10
. Amphetamine was used as the first test of the described conformational approach because of well localized global maximum in the relatively restricted conformational space (three main conformations). The evenly distributed conformer populations were taken as the starting point. However, as the complexity and number of local similarity maxima increase with the number of populated conformers (N > 3), one starting point becomes insufficient to explore conformational space and the presented optimization algorithm results in a different local similarity maximum. Therefore, a more general two step global optimization procedure was defined for six stable conformers of methamphetamine. In the first step 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sets of N − 1 randomly distributed coefficients were taken from space where
000 sets of N − 1 randomly distributed coefficients were taken from space where  as the starting points (Monte-Carlo method) and the wavenumber scaling factor was left fixed in order to localize a global maximum in the N − 1 dimensional conformational space by optimizing function (1). In the second part, the local optimization was repeated with the optimized sets from the first step as the new starting points and the wavenumber scaling factor was allowed to modify to get the best similarity in the region of global maxima. All data were processed and further analysed in the MATLAB environment.
as the starting points (Monte-Carlo method) and the wavenumber scaling factor was left fixed in order to localize a global maximum in the N − 1 dimensional conformational space by optimizing function (1). In the second part, the local optimization was repeated with the optimized sets from the first step as the new starting points and the wavenumber scaling factor was allowed to modify to get the best similarity in the region of global maxima. All data were processed and further analysed in the MATLAB environment.
3. Results and discussion
The IR, Raman, VCD and ROA spectra of (S)-amphetamine hydrochloride and (S)-methamphetamine hydrochloride were compared to simulated spectra in Fig. 2 and 3, respectively. | ||
| Fig. 2 IR (a), Raman (b), VCD (c) and ROA (d) spectra of (S)-amphetamine hydrochloride. Experimental spectra (black, bottom) were compared to the Boltzmann average of three conformers (yellow), single molecule geometry (red), MD cluster-based models including only one (cyan), two (blue) or three (purple) closest water molecules, the cluster of the first water shell (magenta) and without explicit water molecules (green). The similarity factors (SIM) are given for individual spectra. Conformer populations and wavenumber scaling factors for each simulation are listed in Table 1 and Table S14.† Spectra of the three conformers (averages of 100 snapshots per conformer, 1st solvation shell) are shown in Fig. S19.† The experimental IR and VCD were measured in D2O with a concentration of 400.0 g L−1 and path length of 27.3 μm. The experimental Raman and ROA spectrum were measured in water with a concentration of ∼100 g L−1, an excitation wavelength of 532 nm, ∼600 mW laser power at the sample, and 9–13 hours of accumulation time. The IR and VCD intensities are in epsilon units (L mol−1 cm−1), experimental Raman and ROA spectra in (e− cm J−1 g−1 L) and Raman and ROA simulations are in arbitrary units, details can be found in the ESI.† | ||
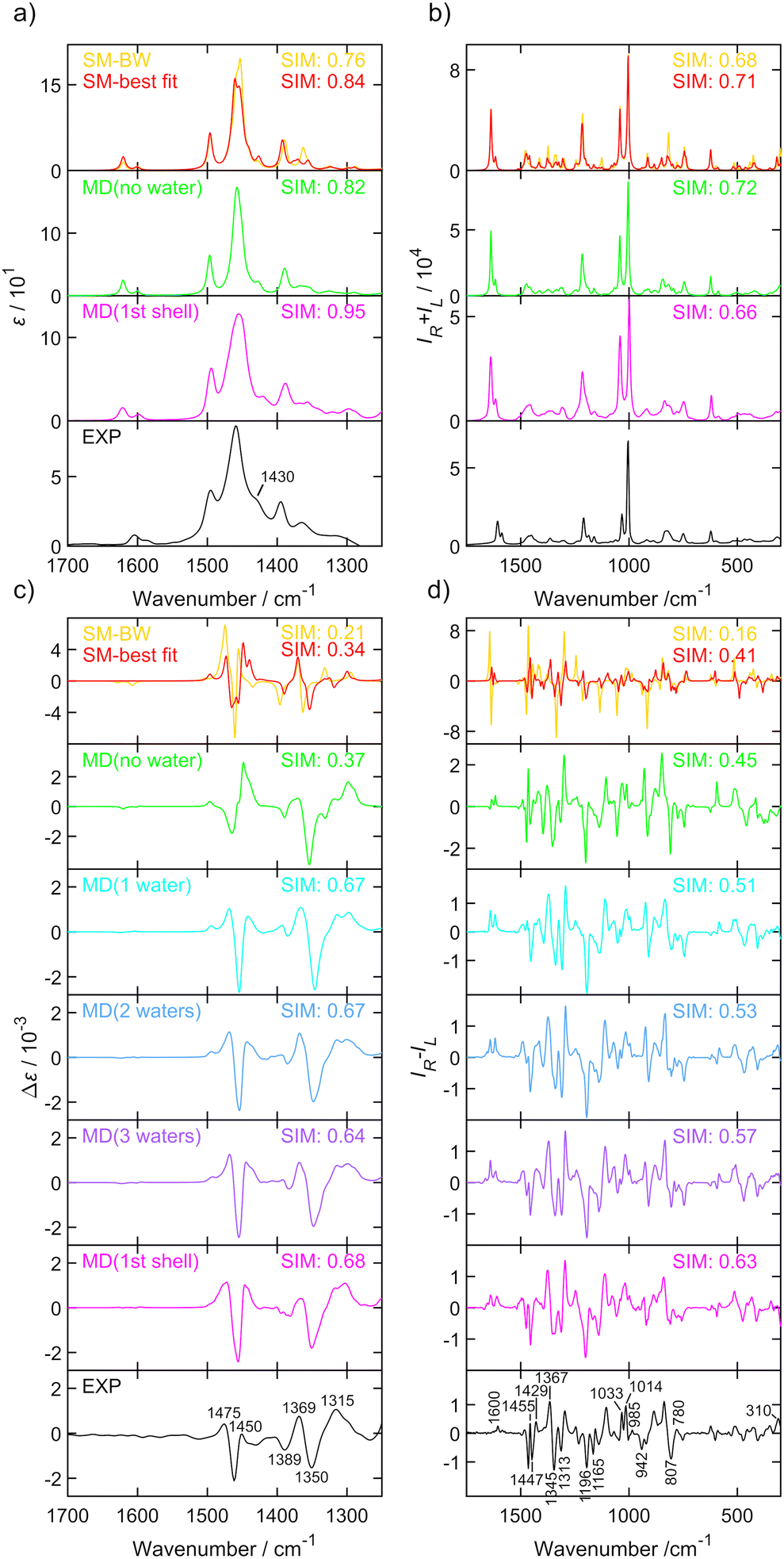 | ||
| Fig. 3 IR (a), Raman (b), VCD (c) and ROA (d) spectra of (S)-methamphetamine hydrochloride. Experimental spectra (black, bottom) were compared to the Boltzmann average of six conformers (yellow), single molecule geometry (red), MD cluster-based models including only one (cyan), two (blue) or three (purple) closest water molecules, the cluster of the first water shell (magenta) and without explicit water molecules (green). The similarity factors (SIM) are given for individual spectra. Conformer populations and wavenumber scaling factors for each simulation are listed in Table 2 and Table S15.† Spectra of the six conformers (averages of 100 snapshots per conformer, 1st solvation shell) are shown in Fig. S20.† The experimental IR and VCD were measured in D2O with a concentration of 400.0 g L−1 and a path length of 27.3 μm. The experimental Raman and ROA spectrum were measured in water with a concentration ∼100 g L−1, an excitation wavelength 532 nm, ∼600 mW laser power at the sample, and ∼9 hours of accumulation time. The IR and VCD intensities are in epsilon units (L mol−1 cm−1), experimental Raman and ROA spectra in (e− cm J−1 g−1 L) and Raman and ROA simulations are in arbitrary units, details can be found in the ESI.† | ||
The spectra of both substances were similar in the overall pattern and the total number of bands and displayed key features that helped to classify these analogues as belonging to the amphetamine family. Although the IR (Fig. 2a and 3a) and VCD (Fig. 2c and 3c) provide less structured vibrational spectra than the Raman (Fig. 2b and 3b) and ROA (Fig. 2d and 3d) techniques, there are characteristic bands that help distinguish the studied compounds. The appearance of an absorption shoulder band 1430 cm−1 in the experimental IR spectrum (Fig. 3a) reflects the bending vibration of the methamphetamine –CH3 group. The presence of VCD bands 1475 and 1389 cm−1 in the methamphetamine spectrum (Fig. 3c) and their absence in the amphetamine spectrum (Fig. 2c) can be used to distinguish between these two compounds as well as the different VCD intensity patterns in the spectral range from 1350 to 1500 cm−1. The maximum of amphetamine bands 1373 and 1356 cm−1 (Fig. 2c) is slightly blue-shifted approximately by 5 cm−1. In the experimental Raman spectra of both analysed compounds (Fig. 2b and 3b), the most significant differences were in the relative intensities of less intense bands, 1374 (C–C linear chain stretching vibration), a couplet ∼1300, 1251, 1106, 942, 821 and 500 cm−1 (corresponding to the chain vibrations of the aliphatic groups). The biggest spectral differences between amphetamine and methamphetamine were observed in the ROA spectra (Fig. 2d and 3d). Therefore, the ROA is the most useful technique for the purposes of the identification of illicit substances. Both analysed compounds significantly differ especially in the spectral range of 900–1500 cm−1. Compared to the (S)-amphetamine, (S)-methamphetamine bands at 1429, 1196, 1033, 1014, 985 and 310 cm−1 turned in the sign. A different position was also observed for ROA (S)-methamphetamine bands at 1367 (blue-shifted by 31 cm−1), 1345 (blue-shifted by 22 cm−1), 1313 (blue-shifted by 22 cm−1), 807 (blue-shifted by 11 cm−1) and 1014 (red-shifted by 13 cm−1) cm−1 compared to (S)-amphetamine bands.
Several different computational approaches were used to interpret the vibrational spectra of both amphetamine and methamphetamine hydrochlorides. The SM calculation with an implicit solvent model (COSMO) is a simple and timesaving model that is significantly better than calculation in a vacuum but does not provide information about detailed conformational changes in the vicinity of local energetic minima or interaction of the studied molecule with the solvent.
The cluster model based on MD overcomes the shortcomings of the previous model to a considerable extent. Since the water molecules predominantly interact with the NH3+ and NH2+ group for amphetamine and methamphetamine, respectively (see Fig. S10 and S12†), the simplified MD cluster models including only one, two or three closest water molecules were analyzed and compared with the first solvation shell model comprising around 18 water molecules. The cluster model is more computationally demanding due to additional solvent molecules and the need for more snapshots with different solvent positions around the molecule in order to achieve sufficient convergence of the results. Therefore, a concession in the form of a smaller basis set selection is usually chosen.
As a potential compromise between the chosen simulation approaches, the third simpler model based on MD snapshots with excluded water molecules was chosen. In addition to simplifying the calculations, this model also aims to simulate to some extent the conformational flexibility without the explicit influence of the solvent and to determine how much influence the explicit inclusion of the solvent has. This simplified MD approach allowed to optimize and calculate vibrational frequencies and spectral intensities on the same DFT level as the SM calculation, but the optimization of the molecular geometry is constrained to selected fixed torsion angles taken from the MD snapshots (for the definition of the characteristic angles, see Fig. 1). Based on the torsion angle distributions (Table S5†) the spectra of 100 snapshots per conformer were calculated and averaged for both MD models, with and without explicit waters. The magnitude of the imaginary frequencies of all partially optimized the structure with fixed torsion angles was mostly below i100 cm−1 and thus affected the calculated spectrum very little.
The conformer population and wavenumber scaling factor were then determined using the described optimization algorithm to achieve the best similarity overlap of the averaged conformer spectra with the experiment.
The optimization approach was firstly tested for three SM amphetamine conformers calculated at several levels of DFT theory. The similarity overlap was determined separately for each conformer (Table S6†) as well as for weighted conformer average (Tables S7 and S8†). The similarity achieved for each conformer separately is in general lower compared to the conformational mixture. Comparison of individual conformations may result in negative similarity as in the case of amphetamine conformer II (Table S6,† ROA) or III (Table S6,† VCD). This may lead to a hasty judgment that such conformers are not present in the sample or even to incorrect assignment to the opposite enantiomer. However, the spectral comparison with the weighted conformer average suggests that the contribution of conformer II and III is significant to the resulting spectra and increases the overall similarity with the experiment. Although the spectral overlap for different DFT levels is similar, the relative conformer populations differ (cf. Fig. S14 and S15†). For further comparison with other computational models only the calculation at the B3PW91/6-311++G** level was selected as the most suitable approach (Tables S6–S8†).
One has to be cautious as the degree of similarity (1) is dependent on the spectral range selection, the number of compared vibrational bands, the band integral intensity and the number of conformations taken into account. The spectral range dependence of ROA similarity overlap was tested for SM geometries of both analysed compounds calculated at the B3PW91/6-311++G** level of theory. Obviously, limiting spectral range and including fewer spectral features in the comparison (Fig. S16†) increase the overlap, but the determination of conformer populations is more prone to errors (Table S9†). Therefore, it is desirable to compare experimental and calculated spectra in the widest possible spectral range. The selected spectral ranges were 1250–1700 cm−1 for VCD and 300–1750 cm−1 for ROA for studied samples. The VCD spectral region was limited by the D2O absorption bands. Although we were able to measure Raman and ROA spectra in the much wider spectral range of 50–4500 cm−1, the low-frequency region of 50–300 cm−1 is strongly affected by intermolecular interactions63 that can bias the conformer population determination. On the other hand, CH stretching vibrations have a relatively low ROA signal, they are highly anharmonic and a different wavenumber scaling factor will be needed. Including these regions in the comparison would likely lead to larger inaccuracies.
We were also interested in the reproducibility of the demonstrated conformational results. For evaluation, the experimental ROA data of amphetamine were exported in 5 blocks of ∼2.6 hours of accumulation time and compared to the weighted average from the cluster-based MD model (Table S10†). In the second test, the calculated ROA spectra were averaged in five blocks of 20 snapshots each (Table S11†) and cumulatively (Table S12†) and compared to the experiment. From standard deviations at the bottom line of the tables, the relative conformer populations vary up to 0.06, with maximum deviation for less populated amphetamine conformer III. The similarity values for ROA spectra (SimROA) deviate less than 0.03. These results confirmed the reliability of the presented approach.
The results of the conformational analysis for amphetamine hydrochloride are summarized in Table 1 and the IR, Raman, VCD and ROA spectra are depicted in Fig. 2 for all computational models and the experiment. The IR and VCD spectra were compared in the spectral range from 1700 to 1250 cm−1, while the Raman, ROA and CID spectra made it possible to compare spectra in a wider spectral range of 300–1750 cm−1. Due to uncertain and large values (“singularities”) caused by dividing the VCD signal by IR numbers close to zero, dimensionless DF spectra were compared only within a narrow wavenumber interval of 1300–1550 cm−1, therefore the determined conformer populations cannot be trusted despite the overlaps begin close to 1 (see Table 1) and utilization of VCD is certainly preferable.
| Type | Spectral range | Scaling factord | c 1 | c 2 | c 3 | SIM |
|---|---|---|---|---|---|---|
| a Boltzmann weights were calculated at the B3PW91/6-311++G** level. Similarity and wavenumber scaling factor were determined only for ROA spectra. b Populations taken from the ref. 11. Similarity and wavenumber scaling factor were determined only for ROA spectra. c Populations taken from the MD distribution in Table S5.† Similarity and wavenumber scaling factor were determined only for ROA spectra. d See Fig. S17† and comments herein. e Similar results for clusters with 1–3 water molecules are shown in Table S14.† | ||||||
| SM geometry | ||||||
| IR | 1250–1700 | 0.98 | 0.70 | 0.09 | 0.20 | 0.75 |
| VCD | 1250–1700 | 0.98 | 0.36 | 0.60 | 0.04 | 0.50 |
| DF | 1300–1550 | 0.98 | 0.24 | 0.55 | 0.22 | 0.77 |
| Raman | 300–1750 | 0.99 | 0.35 | 0.41 | 0.24 | 0.68 |
| ROA | 300–1750 | 0.98 | 0.60 | 0.13 | 0.26 | 0.34 |
| CID | 300–1750 | 0.98 | 0.59 | 0.25 | 0.16 | 0.34 |
| ROA-BWsa | 300–1750 | 0.99 | 0.78 | 0.16 | 0.07 | 0.28 |
| ROA-NMRb | 300–1750 | 0.99 | 0.45 | 0.50 | 0.05 | 0.20 |
| ROA-MDc | 300–1750 | 0.99 | 0.50 | 0.10 | 0.39 | 0.27 |
| Geometries from MD, water molecules excluded, B3PW91/6-311++G**/COSMO level with rDPS for Raman, ROA and CID | ||||||
| IR | 1250–1700 | 0.98 | 0.96 | 0.00 | 0.04 | 0.79 |
| VCD | 1250–1700 | 0.98 | 0.52 | 0.32 | 0.15 | 0.54 |
| DF | 1300–1550 | 0.97 | 0.23 | 0.22 | 0.55 | 0.76 |
| Raman | 300–1750 | 0.99 | 0.25 | 0.61 | 0.14 | 0.67 |
| ROA | 300–1750 | 0.98 | 0.58 | 0.25 | 0.17 | 0.33 |
| CID | 300–1500 | 0.99 | 0.42 | 0.33 | 0.25 | 0.42 |
| Geometries from MD with explicit 1 st solvation shell , B3PW91/6-31G**/GD3BJ/COSMO level with rDPS for Raman, ROA and CID | ||||||
| IR | 1250–1700 | 0.97 | 0.80 | 0.00 | 0.20 | 0.82 |
| VCD | 1250–1700 | 0.97 | 0.40 | 0.47 | 0.13 | 0.82 |
| DF | 1300–1550 | 0.97 | 0.28 | 0.54 | 0.19 | 0.88 |
| Raman | 300–1750 | 0.98 | 0.70 | 0.09 | 0.21 | 0.66 |
| ROA | 300–1750 | 0.97 | 0.43 | 0.41 | 0.16 | 0.64 |
| CID | 300–1750 | 0.97 | 0.42 | 0.46 | 0.12 | 0.52 |
Using the Boltzmann weights derived from Gibbs energies at the B3PW91/6-311++G** level to weigh the spectra gives the worst overlap with the experiment (e.g. SimROA = 0.28). This overlap is also less than the threshold of 0.4 suggested previously for a satisfactory agreement.36,39 It is therefore recommended not to use the Gibbs energies-derived populations to weigh the conformational spectra. Similarly, conformational populations generated from the MD do not provide satisfactory agreement with the observed spectra (see Table 1, “ROA-MD” and Fig. S18†).
From Table 1, it can be observed that the similarity overlaps with the IR spectrum (SimIR) and Raman spectrum (SimRaman) obtained with optimized populations for all different computational approaches are without exception larger than those for the corresponding chiroptical spectra (except for the similarity values for the DF comparison (SimDF)). However, conformer populations are wrongly determined as the optimization algorithm tends to favor one conformer if the conformers’ spectra are nearly identical. As was expected, the model derived from the MD geometries with explicit water molecules leads to a much better overlap with the experiment (SimVCD = 0.82, SimROA = 0.64) than the SM calculation (SimVCD = 0.50, SimROA = 0.34). Additionally, this agreement can be further confirmed from the observation of the spectra in Fig. 2. The band pattern is relatively well reproduced in most of the cases, but the biggest differences are obvious in the comparison of the VCD and ROA spectra, where SM calculations overestimate relative intensities except for the ROA couplet 1465/1455 cm−1 and the chain C–C stretching band at 1367 cm−1. This is probably due to the flexibility of the alkyl chain and the cluster averaging. Despite that, some spectral features of the MD model without water molecules are improved towards the MD cluster-based spectra, the overlap (SimVCD = 0.54, SimROA = 0.33) is similar to the SM calculation. From the ROA comparison of the MD model with and without explicit waters (Fig. 2d), it is apparent that the regions 800–1120 cm−1 and below 380 cm−1 are strongly affected by solvent–solute interactions. Particularly, bands 1101, 1001, 937, 893 and 838 cm−1 with the “+−++” sign pattern were correctly determined only by the MD clusters.
The amphetamine relative conformational populations derived from similarity overlaps for different spectroscopic techniques are compared by the 2D conformational map in Fig. 4 according to similarity values in Table 1. The conformational ratios from SM calculation and MD geometries without water molecules are scattered over the entire conformational space. As mentioned earlier, the DF spectra are more prone to errors as the limited spectral interval of IR and VCD is used and high similarity factors are obtained for various simulation methods when conformer populations differ significantly. This is not the case for ROA and CID spectra, where low-level computations give significantly smaller similarity factors and recording of the data in a wider spectral range is clearly beneficial. The chiroptical spectra with the best similarity overlap (SimVCD = 0.82, SimROA = 0.64, SimCID = 0.52 from MD with explicit waters, Table 1) are consistent with the conformational ratio 0.45/0.50/0.05 determined by NMR11 and confirms the high sensitivity of the vibrational optical activity to the determination of the spatial arrangement and dominant conformation of the studied sample.
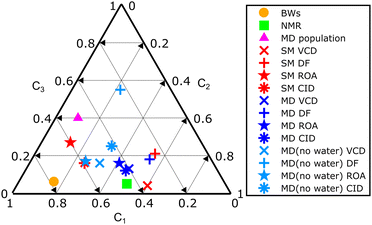 | ||
| Fig. 4 Summary 2D plot of amphetamine relative conformer populations derived from similarity overlaps in Table 1. Labels C1, C2 and C3 (C1 + C2 + C3 = 1) correspond to the amphetamine conformer I, II and III, respectively. | ||
The conformational analysis of methamphetamine hydrochloride is more complex as the number of stable conformers increases due to a longer alkyl chain (Fig. 1). Similarity overlaps with corresponding conformer populations are listed in Table 2 and spectra depicted in Fig. 3. IR, VCD, Raman, ROA and CID spectra are compared in the same spectral ranges as for amphetamine hydrochloride. The DF spectra were compared within the range of 1300–1700 cm−1. Similarity overlaps for different spectroscopic methods confirm the findings discussed for amphetamine hydrochloride in the previous section. Overall, a significantly poorer agreement with the experiment was achieved for conformer populations derived from Gibbs energies leading to SimROA = 0.16 (Table 2). This value of similarity factor is too low for reliable agreement with the experiment. In the NMR study11 only three methamphetamine conformers were resolved without an included orientation of the methamphetamine –CH3 group that is described by characteristic angle α3 and its distribution is shown in Fig. S8.†
| Type | Spectral range | Scaling factor | c 1 | c 2 | c 3 | c 4 | c 5 | c 6 | SIM |
|---|---|---|---|---|---|---|---|---|---|
| a Boltzmann weights were calculated at the B3PW91/6-311++G** level. Similarity and wavenumber scaling factor were determined only for ROA spectra. b Populations taken from the ref. 11. Similarity and wavenumber scaling factor were determined only for (I + IV, II + V, III + VI) ROA spectra. c Populations taken from the MD distribution in Table S5.† Similarity and wavenumber scaling factor were determined only for ROA spectra. d Similar results for clusters with 1–3 water molecules are in Table S15.† | |||||||||
| SM geometry | |||||||||
| IR | 1250–1700 | 0.98 | 0.00 | 0.08 | 0.04 | 0.52 | 0.37 | 0.00 | 0.84 |
| VCD | 1250–1700 | 0.98 | 0.00 | 0.33 | 0.00 | 0.39 | 0.04 | 0.23 | 0.34 |
| DF | 1300–1700 | 0.98 | 0.83 | 0.00 | 0.00 | 0.08 | 0.00 | 0.08 | 0.43 |
| Raman | 300–1750 | 0.99 | 0.17 | 0.44 | 0.20 | 0.00 | 0.00 | 0.18 | 0.71 |
| ROA | 300–1750 | 0.98 | 0.21 | 0.16 | 0.07 | 0.11 | 0.36 | 0.08 | 0.41 |
| CID | 300–1750 | 0.99 | 0.32 | 0.40 | 0.08 | 0.06 | 0.10 | 0.05 | 0.40 |
| ROA-BWsa | 300–1750 | 0.99 | 0.77 | 0.12 | 0.03 | 0.02 | 0.03 | 0.03 | 0.16 |
| ROA-NMRb | 300–1750 | 0.99 | 0.39 | 0.55 | 0.06 | — | — | — | 0.38 |
| ROA-MDc | 300–1750 | 0.99 | 0.22 | 0.37 | 0.32 | 0.03 | 0.03 | 0.03 | 0.25 |
| Geometries from MD, water molecules excluded, B3PW91/6-311++G**/COSMO level with rDPS for Raman, ROA and CID | |||||||||
| IR | 1250–1700 | 0.98 | 0.07 | 0.36 | 0.00 | 0.58 | 0.00 | 0.00 | 0.82 |
| VCD | 1250–1700 | 0.98 | 0.00 | 0.00 | 0.00 | 0.50 | 0.14 | 0.36 | 0.37 |
| DF | 1300–1700 | 0.98 | 0.00 | 0.39 | 0.00 | 0.61 | 0.00 | 0.00 | 0.46 |
| Raman | 300–1750 | 0.99 | 0.00 | 0.76 | 0.18 | 0.00 | 0.00 | 0.07 | 0.72 |
| ROA | 300–1750 | 0.99 | 0.43 | 0.00 | 0.00 | 0.00 | 0.49 | 0.08 | 0.45 |
| CID | 300–1750 | 0.99 | 0.40 | 0.26 | 0.00 | 0.00 | 0.21 | 0.13 | 0.43 |
| Geometries from MD with explicit 1 st solvation shell , B3PW91/6-31G**/GD3BJ/COSMO level with rDPS for Raman, ROA and CID | |||||||||
| IR | 1250–1700 | 0.97 | 0.06 | 0.38 | 0.00 | 0.00 | 0.00 | 0.56 | 0.95 |
| VCD | 1250–1700 | 0.97 | 0.10 | 0.08 | 0.14 | 0.34 | 0.33 | 0.00 | 0.68 |
| DF | 1300–1700 | 0.97 | 0.00 | 0.00 | 0.15 | 0.51 | 0.34 | 0.00 | 0.50 |
| Raman | 300–1750 | 0.98 | 0.11 | 0.49 | 0.00 | 0.00 | 0.00 | 0.40 | 0.66 |
| ROA | 300–1750 | 0.98 | 0.37 | 0.29 | 0.05 | 0.00 | 0.26 | 0.03 | 0.63 |
| CID | 300–1750 | 0.98 | 0.40 | 0.27 | 0.00 | 0.00 | 0.27 | 0.07 | 0.52 |
Explicit inclusion of water molecules into the calculation clearly improves the overlap for all vibrational spectra in general. If we reduce conformer discrimination from six to three conformers (I + IV, II + V, III + VI), ignoring the methyl group orientation, the VCD conformer ratio 0.44/0.41/0.14, the ROA ratio 0.37/0.55/0.08 and the CID ratio 0.40/0.54/0.07 are in good agreement with the conformer population 0.39/0.55/0.06 from the NMR study. The DF conformer ratio 0.51/0.34/0.15 is less precise due to lower similarity overlap. DF also depends on the VCD to IR ratio, which can be a source of errors by dividing numbers close to zero. A better approach to reliable calculations of the dimensionless dissymmetry factor and CID is needed.
In order to investigate the importance of less populated conformers III, IV and VI, these conformers were systematically excluded from the similarity overlap (cf. Table S13†). Interestingly, the similarity factor remains unchanged until conformer III was removed while conformer populations vary by a value of 0.03. These results give us an idea about the similarity robustness and confirm the presence of the most significant methamphetamine conformers I, II, III and V in the aqueous solution.
Fig. 3 compares the experimental IR, VCD, Raman and ROA spectra with three different computational methods. The simulated spectra were generated as weighted averages according to the optimized conformer populations from Table 2. The interpretation of the experimental spectra by SM calculations is not sufficient, clearly some bands are missing or predicted to have a very different intensity or sign, such as the ROA band 602 cm−1. As expected, the MD model without water molecules improves the interpretation only partially, the spectral pattern of the most prominent bands, but the spectral intensities are overestimated, for example the VCD band 1450 cm−1 or ROA band 1455 cm−1, and caused the similarity values to be almost as low as for the SM calculation. The spectral region close to the negative ROA band 1196 cm−1 was already improved by spectral averaging over MD geometries without the necessary use of the explicit waters. In contrast, within 1355–1500 cm−1, the solvent–solute interactions are important. The observations confirm that only by explicitly taking into account MD with water molecules showed very good agreement between experiment and theory.
It should be emphasized that the calculation of a large number (here several hundred) of individual clusters from MD snapshots, followed by averaging of the spectra, is a necessary step in the simulation of the spectra – since the individual clusters (snapshots) have highly variable spectral features strongly dependent on the individual position and orientation of the solvent molecules (please see Fig. S11 and S13† where spectra of several individual conformers with various water positions were generated). Therefore, the manual construction of clusters containing few solvent molecules cannot lead to satisfactory results.
The results show that the greatest improvement in agreement with the experiment is already achieved for the average spectra from the clusters with a single water molecule. While VCD spectra of clusters with an increasing number of water molecules are almost identical, the ROA spectra improve in several details, but still systematically, which can be demonstrated by the monotonously increasing similarity factor with the increasing number of water molecules in the clusters for both studied molecules.
It is legitimate to ask again whether the increasing similarity factor corresponds to a real improved agreement of the calculated spectra with the experiment, especially when we compare such a wide spectral range as in the case of ROA spectra. We believe that this is the case, based on the tests of similarity factor described earlier, and also because noticeable improvements in the spectra can be observed for the bands around 800–940, 1200, and 1600 cm−1 for amphetamine and for the bands around 610, 750, 1160–1200, and 1420–1500 cm−1 for methamphetamine. Larger clusters with explicit water molecules are also needed for the low-wavenumber spectral region below 400 cm−1 where the intermolecular interactions play a very important role.63
The Raman and IR spectra reflect the conformations of chiral molecules only partially as they are not sensitive to chirality, therefore, the determination of the population of states from the similarity index in Tables 1 and 2 is confirmed to be burdened with a large error. More interesting and important is the comparison of VCD and ROA methods. The achieved results showed that both VCD and ROA give a significantly smaller similarity index for simpler models, and with a more advanced model of the molecular system including more realistic solvents and conformational effects, the similarity index increases substantially, and the determination of the population of states thus better converges to reliable values (that are also close to values determined by NMR11). Simulations of clusters with different numbers of water molecules (cf.Fig. 2 and 3) show that ROA is even able to distinguish the influence of different numbers of solvent molecules. We believe that this advantage of ROA originates from the larger usable spectral range and especially access to the low wavenumber spectral range.
4. Conclusions
In this paper, we present the first comprehensive structural study of amphetamine and methamphetamine hydrochlorides in aqueous solutions performed by the methods of VCD, ROA, IR and Raman spectroscopy at the same time. The performance of three different computational models based on DFT and molecular dynamics was quantified by the similarity overlap of the simulated and experimental spectra. We demonstrated a different approach to the analysis of conformer populations of studied molecules based on maximizing the similarity overlap of weighted conformer spectra with the experiment by optimizing the general similarity function. A very good agreement in the comparison of the MD cluster-based model with explicit solvent molecules and the experiment was obtained for all spectroscopic techniques used. The study also confirmed that Boltzmann weights based on Gibbs free energies of the single molecule calculation are not reliable due to large uncertainties in the DFT calculations. Three and six stable conformers of amphetamine and methamphetamine, respectively, were identified. The conformational analysis of this study underlines the relative conformer abundances of amphetamine and methamphetamine hydrochloride in aqueous solutions from the previous NMR study.We conclude that the combined power of chiroptical vibrational spectroscopy and cluster-based calculations proved to be a valuable non-destructive technique allowing precise structural analysis of abused drugs in their native environment. We have shown that chiroptical techniques are not only able to differentiate amphetamine from its analogue methamphetamine very well, but also provide detailed information regarding the conformation of these molecules and their interaction with the solvent. We believe that the presented approach will be helpful for the study of seized amphetamine and methamphetamine samples and new derivatives.
Author contributions
Kristýna Dobšíková – methodology, VCD experiment, DFT calculations, conceptualization, and writing the original draft; Pavel Michal – methodology, ROA experiment, DFT and MD calculations, software for the analysis, analysis, writing the draft, and review and editing; Dita Spálovská – review and editing; Martin Kuchař – review and editing, funding acquisition, and project administration; Natálie Paškanová – methodology and enantioseparation; Radek Jurok – synthesis; Josef Kapitán – methodology, ROA experiment, analysis, review and editing; Vladimír Setnička – review and editing, supervision, and conceptualization. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
J. Kapitán and P. Michal are involved in commercialization of the ROA spectrometer. The other authors have no interest to declare.Acknowledgements
The work was supported by Specific University Research (A2_FCHI_2022_027), the Czech Science Foundation (22-04669S), a student grant of Palacký University Olomouc (IGA_PrF_2023_002) and was a part of the research project supported by the Ministry of Interior of the Czech Republic (grant no. VJ01010065). Computational resources were provided by the e-INFRA CZ project (ID:90140), supported by the Ministry of Education, Youth and Sports of the Czech Republic. The authors thank Prof. Petr Bouř, Institute of Organic Chemistry and Biochemistry, Czech Academy of Sciences, Prague, for providing computational resources.References
- S. J. Kish, Can. Med. Assoc. J., 2008, 178, 1679 CrossRef PubMed.
- M. Ferrucci, F. Limanaqi, L. Ryskalin, F. Biagioni, C. L. Busceti and F. Fornai, Front. Neuroanat., 2019, 13 DOI:10.3389/fnana.2019.00048.
- Y. Sekine, Y. Ouchi, N. Takei, E. Yoshikawa, K. Nakamura, M. Futatsubashi, H. Okada, Y. Minabe, K. Suzuki, Y. Iwata, K. J. Tsuchiya, H. Tsukada, M. Iyo and N. Mori, Arch. Gen. Psychiatry, 2006, 63, 90 CrossRef CAS PubMed.
- European Monitoring Centre for Drugs and Drug Addiction, European drug report 2018: trends and developments, Office of the European Union, Luxembourg, 2019 Search PubMed.
- European Monitoring Centre for Drugs and Drug Addiction, European drug report 2018: trends and developments, Office of the European Union, Luxembourg, 2020 Search PubMed.
- G. Mercieca, S. Odoardi, M. Cassar and S. Strano Rossi, J. Pharm. Biomed. Anal., 2018, 149, 494 CrossRef CAS PubMed.
- N. Raikos, K. Christopoulou, G. Theodoridis, H. Tsoukali and D. Psaroulis, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2003, 789, 59 CrossRef CAS PubMed.
- F. Westphal, T. Schäfer, L. Zechlin and S. Stoll, Toxichem Krimtech, 2011, 78, 306 Search PubMed.
- M. Kumihashi, K. Ameno, T. Shibayama, K. Suga, H. Miyauchi, M. Jamal, W. Wang, I. Uekita and I. Ijiri, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2007, 845, 180 CrossRef CAS PubMed.
- O. Y. Al-Dirbashi, N. Kuroda, M. Wada, M. Takahashi and K. Nakashima, Biomed. Chromatogr., 2000, 14, 293 CrossRef CAS PubMed.
- G. A. Neville, R. Deslauriers, B. J. Blackburn and I. C. Smith, J. Med. Chem., 1971, 14, 717 CrossRef CAS PubMed.
- J. Eliaerts, P. Dardenne, N. Meert, F. Van Durme, N. Samyn, K. Janssens and K. De Wael, Drug Test. Anal., 2017, 9, 1480 CrossRef CAS PubMed.
- F. Taplin, D. O'Donnell, T. Kubic, M. Leona and J. Lombardi, Appl. Spectrosc., 2013, 67, 1150 CrossRef CAS PubMed.
- R. Berg, Am. J. Anal. Chem., 2012, 3, 410 CrossRef CAS.
- D. Spálovská, T. Maříková, M. Kohout, F. Králík, M. Kuchař and V. Setnička, Forensic Toxicol., 2019, 37, 366 CrossRef.
- D. Spálovská, F. Králík, M. Kohout, B. Jurásek, L. Habartová, M. Kuchař and V. Setnička, Chirality, 2018, 30, 548 CrossRef PubMed.
- P. Fagan, L. Kocourková, M. Tatarkovič, F. Králík, M. Kuchař, V. Setnička and P. Bouř, ChemPhysChem, 2017, 18, 2258 CrossRef CAS PubMed.
- F. Králík, P. Fagan, M. Kuchař and V. Setnička, Chirality, 2020, 32, 854 CrossRef PubMed.
- D. Spálovská, M. Paškan, B. Jurásek, M. Kuchař, M. Kohout and V. Setnička, New J. Chem., 2021, 45, 850 RSC.
- J. E. Mendelson, D. McGlothlin, D. S. Harris, E. Foster, T. Everhart, P. Jacob 3rd and R. T. Jones, BMC Clin. Pharmacol., 2008, 8, 4 CrossRef PubMed.
- J. L. Campbell, A. Kafle, Z. Bowman, J. C. Y. L. Blanc, C. Liu and W. S. Hopkins, Anal. Sci. Adv., 2020, 1, 233–244 CrossRef.
- T. J. Gelmi, M. Verrijken and W. Weinmann, Regul. Toxicol. Pharmacol., 2020, 116, 104747 CrossRef CAS PubMed.
- European Monitoring Centre for Drugs and Drug Addiction, Drug precursor developments in the European Union, 2019 Search PubMed.
- R. A. Harris and C. J. Jameson, J. Chem. Phys., 2006, 124, 096101 CrossRef CAS PubMed.
- I. Ohtani, T. Kusumi, Y. Kashman and H. Kakisawa, J. Am. Chem. Soc., 1991, 113, 4092 CrossRef CAS.
- C.-H. Tan, Y. Kobayashi and Y. Kishi, Angew. Chem., Int. Ed., 2000, 39, 4282 CrossRef CAS PubMed.
- J. M. Seco, E. Quiñoá and R. Riguera, Chem. Rev., 2004, 104, 17 CrossRef CAS.
- Y. Yang, X. Sun, M. Reza Poopari, C. Jian, H. Zeng, T. Tang and Y. Xu, ChemPhysChem, 2022, e202200608 Search PubMed.
- Y. Yang, J. Cheramy, M. Brehm and Y. Xu, ChemPhysChem, 2022, 23, e202200161 CAS.
- L. Weirich, J. Magalhães de Oliveira and C. Merten, Phys. Chem. Chem. Phys., 2022, 22, 1525 RSC.
- L. Weirich, K. Blanke and C. Merten, Phys. Chem. Chem. Phys., 2020, 22, 12515 RSC.
- K. Bünnemann, C. H. Pollok and C. Merten, J. Phys. Chem. B, 2018, 122, 8056 CrossRef PubMed.
- S. Ghidinelli, S. Abbate, J. Koshoubu, Y. Araki, T. Wada and G. Longhi, J. Phys. Chem. B, 2020, 124, 4512 CrossRef CAS PubMed.
- V. P. Nicu, E. J. Baerends and P. L. Polavarapu, J. Phys. Chem. A, 2012, 116, 8366 CrossRef CAS PubMed.
- P. L. Polavarapu, E. Santoro, C. L. Covington, J. L. Johnson, A. R. Puente, N. D. Schley, Z. Kallingathodi, P. C. Prakasan, S. Haleema, A. A. Thomas and I. Ibnusaud, Spectrochim. Acta, Part A, 2021, 247, 119094 CrossRef CAS PubMed.
- M. A. J. Koenis, Y. Xia, S. R. Domingos, L. Visscher, W. J. Buma and V. P. Nicu, Chem. Sci., 2019, 10, 7680 RSC.
- A. N. Bootsma and S. Wheeler, ChemRxiv, 2019, preprint, DOI:10.26434/chemrxiv.8864204.v5.
- F. J. Devlin and P. J. Stephens, J. Am. Chem. Soc., 1999, 121, 7413 CrossRef CAS.
- P. L. Polavarapu, E. Santoro, C. L. Covington and V. Raghavan, Chirality, 2020, 32, 564 CrossRef CAS PubMed.
- M. Urbanová, V. Setnička and K. Volka, Chirality, 2000, 12, 199 CrossRef.
- P. Michal, R. Čelechovský, M. Dudka, J. Kapitán, M. Vůjtek, M. Berešová, J. Šebestík, K. Thangavel and P. Bouř, J. Phys. Chem. B, 2019, 123, 2147 CrossRef CAS PubMed.
- W. Hug and G. Hangartner, J. Raman Spectrosc., 1999, 30, 841 CrossRef CAS.
- W. Hug, Appl. Spectrosc., 2003, 57, 1 CrossRef CAS PubMed.
- L. Nafie, Vibrational optical activity: Principles and applications, Wiley, Chichester, 2011 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. A. 03, Wallingford CT, 2016 Search PubMed.
- A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669 CrossRef CAS PubMed.
- D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. Debolt, D. M. Ferguson, G. Seibel and P. A. Kollman, Comput. Phys. Commun., 1995, 91, 1 CrossRef CAS.
- D.A. Case, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, D. Ghoreishi, M. K. Gilson, H. Gohlke, A. W. Goetz, D. Greene, R. Harris, N. Homeyer, S. Izadi, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, D. J. Mermelstein, K. M. Merz, Y. Miao, G. Monard, C. Nguyen, H. Nguyen, I. Omelyan, A. Onufriev, F. Pan, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, J. Smith, R. Salomon-Ferrer, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, L. Xiao, D. M. York and P.A. Kollman, Amber18, University of California, San Francisco, 2018 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157 CrossRef PubMed.
- P. Bouř and T. A. Keiderling, J. Chem. Phys., 2002, 117, 4126 CrossRef.
- P. Bouř, Collect. Czech. Chem. Commun., 2005, 70, 1315 CrossRef.
- P. Bouř, Qgrad, Prague, Academy of Sciences, Prague, 2006 Search PubMed.
- J. Hudecová, K. H. Hopmann and P. Bouř, J. Phys. Chem. B, 2012, 116, 336 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- G. Zuber and W. Hug, J. Phys. Chem. A, 2004, 108, 2108 CrossRef CAS.
- P. Michal, J. Kapitán, J. Kessler and P. Bouř, Phys. Chem. Chem. Phys., 2022, 24, 19722 RSC.
- J. Shen, C. Zhu, S. Reiling and R. Vaz, Spectrochim. Acta, Part A, 2010, 76, 418 CrossRef PubMed.
- T. Kuppens, W. Langenaeker, J. P. Tollenaere and P. Bultinck, J. Phys. Chem. A, 2003, 107, 542 CrossRef CAS.
- P. L. Polavarapu, Chiroptical Spectroscopy: Fundamentals and Applications, CRC Press, Boca Raton, 1 edn, 2016 Search PubMed.
- J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, SIAM J. Optim., 1998, 9, 112 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an02014a |
| ‡ These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |