Hidden symmetry of the flavivirus protein shell and pH-controlled reconstruction of the viral surface
Olga V.
Konevtsova
a,
Ivan Yu.
Golushko
a,
Rudolf
Podgornik
*bcd and
Sergei B.
Rochal
 *a
*a
aPhysics Faculty, Southern Federal University, Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
bSchool of Physical Sciences and Kavli Institute for Theoretical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
cCAS Key Laboratory of Soft Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: podgornikrudolf@ucas.ac.cn
dWenzhou Institute of the University of Chinese Academy of Sciences, Wenzhou, Zhejiang 325000, China
First published on 18th November 2022
Abstract
Using recent Zika virus structural data we reveal a hidden symmetry of protein order in immature and mature flavivirus shells, violating the Caspar–Klug paradigmatic model of capsid structures. We show that proteins of the outer immature shell layer exhibit trihexagonal tiling, while proteins from inner and outer layers conjointly form a double-shelled close-packed structure, based on a common triangular spherical lattice. Within the proposed structural model, we furthermore rationalize the structural organization of misassembled non-infectious subviral particles that have no inner capsid. We consider a pH-controlled structural reconstruction of the outer shell from the trimeric to the dimeric state, and demonstrate that this transition, occurring during the virus maturation, can be induced by changes in protein charges at lower pH, leading to a decrease in the electrostatic interaction free energy. This transition could also be assisted by electrostatic attraction of shell proteins to the interposed lipid membrane substrate separating the shells.
Introduction
Flavivirus is the most common genus of the Flaviviridae family including over 50 species, which are transmitted predominantly through bites of infectious mosquitoes and ticks to both animals and humans.1 The major human pathogens of this genus are dengue, Zika, West Nile, Japanese encephalitis, and yellow fever viruses,2 causing various pathologies ranging from asymptomatic to life-threatening ones, including encephalitis and hemorrhagic fever. Annually over 500 million people are infected with the dengue virus (DENV) alone.3 Currently there are no approved antiviral drugs for the treatment of flavivirus infections,4,5 and known vaccines are effective only against certain serotypes,6–8 sparking strong motivation to study the life cycle and structures of flaviviruses, as understanding their assembly, maturation and infection mechanisms is essential for the development of effective antiviral strategies.All flaviviruses follow the same life cycle and exhibit similar icosahedral proteinaceous capsid structures. The inner protein shell of the capsid, containing a single positive-strand RNA, is formed from capsid protein C.9 The capsid is surrounded by a lipid membrane, which is then covered by an outer protein shell, consisting of 180 complex proteins called heterodimers, consisting of Envelope (E) and precursor Membrane (prM) domains.9,10 The interposed membrane thus mediates the interactions between the two protein layers. The outer shell assembles on the endoplasmic reticulum (ER) membrane at neutral pH from 60 pre-assembled symmetrical trimers consisting of three identical heterodimers. While being transported to the cell surface through the trans-Golgi network, the immature virus is subjected to acidic pH and its spiky trimeric outer shell reconstructs to smooth densely packed structures formed by 90 dimers.11–13 The maturation process is complete with the cleavage of prM domains by furin endoprotease and the subsequent release of pr particles induced by the neutral pH of the extracellular milieu.
In the absence of the C protein, heterodimers in vitro can self-assemble into subviral particles (SVPs)14–16 but most of them are smaller in size than the virions assembled in vivo and consist only of 60 heterodimers. While SVPs consisting of 180 heterodimers are also assembled, they differ in structure from the surface of native flaviviruses. In spite of the importance of C-proteins for the “proper” assembly of the virus, it was established only recently that the immature Zika virus (ZIKV) capsid consists of 120 C proteins organized into 60 dimers forming an icosahedral shell.9,13
Most icosahedral shells are described in terms of the geometrical model proposed by Caspar and Klug (CK) in 1962.17 The applicability of the CK model is almost universal, since many processes typical of the viral life cycle are governed not by genetic control, but by physical and chemical laws, which, in particular, manifest themselves in universal features of protein structural arrangement. Since the original CK model describes only the capsids assembled from pentamer and hexamer protein units (structural units (SUs) with 5-fold and 6-fold symmetry, respectively), it consequently cannot interpret anomalous flavivirus shells consisting of dimers and trimers.13,18,19 A few other anomalous shells are also known, and several approaches were proposed to rationalize them.20–28
Importantly, protein order in many capsids, violating the original CK model, still satisfies the CK quasi-equivalence principle,25,26 according to which identical proteins that cannot occupy symmetrically equivalent positions tend to occupy positions with structurally close environments,17 resulting in local symmetry and local periodicity of protein order. However, unlike in the case of capsids following the CK model phenomenology, the packing features of flaviviruses are not obvious but remain hidden and need to be first of all revealed. In order to reveal and rationalize them, we use spherical lattices (SLs), being smooth mappings of an appropriate periodic hexagonal order onto a sphere,25 which allow us to demonstrate that the arrangement of heterodimers in trimeric and dimeric states is based on trihexagonal and ordinary triangular lattices. In this way we first uncover a commensurability between inner and outer protein shells in immature flaviviruses, and furthermore also explain the structural organization of SVPs.
Besides identifying the hidden symmetries, we also propose some possible physicochemical mechanisms that could drive the trimer-to-dimer reconstruction in flaviviruses. Surprisingly, at early stages of maturation, this drastic structural transition is reversible, which has been shown in vitro by manipulating the pH of the bathing solution.29 This experimental finding, combined with the fact that several canonical amino acids (AAs) are strongly responsive to the acidity of the bathing environment,30 suggests the important role of electrostatic interactions in the viral maturation process. Therefore, using the examples of dengue and Zika viruses, we examine the pH-induced variations in protein charges and analyze how electrostatic protein–protein interactions and interactions of the proteins with the anionic lipid membrane could induce the observed shell transformation.
Results and discussion
Hidden structural features of immature flavivirus shells
Before analyzing the structures of flaviviruses, let us first recall how to map a periodic hexagonal lattice onto an icosahedron. First, the icosahedron surface is unwrapped into a net of 20 identical equilateral triangles. Then, the net is superimposed onto a lattice so that the net edges (which are also icosahedron edges) coincide with the lattice translations connecting the nodes with 6-fold symmetry. This procedure ensures that the surface of the icosahedron is smoothly covered with the nodes of the planar lattice. Note that the squared length of the icosahedron edge, the triangulation number, equals T = h2 + k2 + hk, where (h, k) are integer indexes of lattice translations.17Many viral capsids have almost spherical shapes, and their structures can be described in terms of the appropriate SLs, which are obtained by projecting the icosahedron surface onto a sphere. In the simplest mapping, based on the radial projection, the initially equal distances between the nearest lattice nodes are modified and we use an additional procedure to make these distances more even (see Methods).
In what follows, the SLs based on the primitive hexagonal lattice (PHL), which consists of equilateral triangles, are referred to as primitive icosahedral spherical lattices. These SLs are the basis of the CK theory of virus shells. The CK model decorates the primitive icosahedral SLs with capsomeres so that 12 pentamers occupy positions at 5-fold axes, whereas all other lattice nodes are filled with hexamers. Thus, the total number of nodes equals 10T + 2, meaning that the corresponding protein shell has N = 60T identical proteins (more rigorously speaking 60T asymmetrical structural units, which can consist of several protein domains each).17
Although CK theory successfully describes the majority of known icosahedral viruses, there is a steadily increasing group of anomalous shell structures,31–35 which either have T values forbidden by the CK theory (e.g., T = 2,6, etc.) or, like in the case of flaviviruses, are assembled from SUs other than pentamers and hexamers. Nevertheless, SLs can be used to describe such shells as well26 and asymmetrical proteins can directly occupy the nodes of primitive icosahedral SLs, provided that the filled nodes do not coincide with icosahedron symmetry axes. If a protein shell is formed by SUs with rotational symmetry, e.g., dimers or trimers, they can occupy positions at icosahedron axes with the same or lower trivial symmetry.26–36 Such an approach allows the construction of capsid models forbidden by the classic CK theory and in what follows we will develop a theory based on this approach that allows us to rationalize the protein order in flavivirus shells.
First, let us consider the structural features of protein shells of immature flaviviruses using the example of the Zika virus9,13 because it is the only flavivirus with both inner and outer shells fully resolved. Nevertheless, the structure of the outer shell is well studied in immature trimeric and fully mature dimeric states of different flaviviruses and there are more than 60 corresponding entries in the protein data bank (PDB).37 Note also that in the same state, the surfaces of different flaviviruses are almost indistinguishable upon simple visualization, e.g., using the UCSF Chimera package.38
The main building block of the outer shell (Fig. 1a) is E protein. It has an elongated shape, which is thicker on one side (head) and thinner on the other (tail), and together with prM protein forms the so-called heterodimer. The M parts of the prM proteins are attached to the heads of E proteins, whereas the pr parts reside at their tails. Both E and M proteins have transmembrane regions binding heterodimers to the lipid membrane on which the virus assembles (Fig. 1b).9 Initially, the heterodimers connected by E protein heads form symmetrical trimers. Then these trimers bind to each other by the tails of their E proteins, forming complexes with a 3-fold rotational symmetry.9,39,40 In Fig. 1a, three heterodimers forming such a complex are colored in light-green, purple, and pink. Let us note that the asymmetric triplets of E protein tails, often referred to as spikes, reside just over the trimer centers.
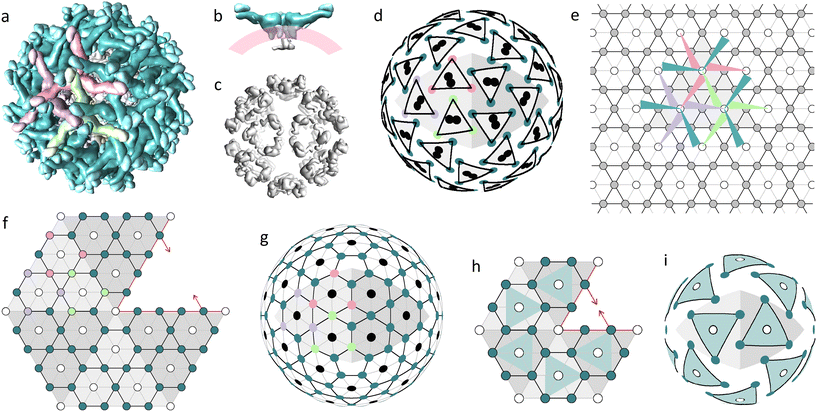 | ||
| Fig. 1 Two proteinaceous shells of the immature Zika virus and their modelling. (a) Outer protein layer (surface) assembled from 180 prM–E heterodimers, with pr peptides crowning the tails of E proteins. (b) Side view showing a dimer of C proteins (gray), the lipid membrane (pink) and three heterodimers forming a trimer (teal). (c) Inner protein layer (capsid) assembled from 60 C protein dimers. (d) Mass centers of C and E proteins (black circles and colored vertices of triangles, respectively) radially projected onto a spherical surface. (e) Trihexagonal lattice superimposed onto the primitive hexagonal one; edges and nodes of the trihexagonal lattice are shown with black lines and filled circles, respectively; edges of the primitive hexagonal lattice (PHL) are shown with both grey and black lines; arrangement of heterodimers belonging to one icosahedron face is shown using colored triangles with sharp angles corresponding to the tails of E proteins. (f) Fragment of the icosahedron net consisting of five translationally inequivalent faces with mutually shifted trihexagonal orders compatible with a common PHL. (g) Decorated SL (5,0) describing the hidden symmetry of the protein arrangement in the inner and outer shells of flaviviruses; the same color code as in (a) is used. (h) Fragment of the icosahedron net presumably describing the arrangement of trimers in the miss-assembled shell of the subviral particle (SVP) formed by 60 prM–E heterodimers. (i) Model of the SVP based on the SL (3,0). Figures (a–c) corresponding to the 6LNT structure from Protein Data Bank (PDB)37 were obtained using the UCSF Chimera package.38 | ||
The inner capsid consists of 60 C protein dimers, which form 20 pseudo hexamers (Fig. 1c), located around 3-fold icosahedron axes. Despite its relative simplicity, the structure of the capsid was obtained only in 2020 by Tan et al. after stabilizing the outer surface of the immature virus particle with antigen-binding fragments (Fab) HMAb DV62.5.9,13
Fig. 1d uncovers the structural relationship between the inner and outer shells. Note that the mass centers (MCs) of the inner shell proteins are paired and each of these pairs is located between the MCs of three nearest E-proteins forming a trimer of the outer shell. E-protein MCs are shown as vertices of equilateral triangles with black edges. The colors of the vertices correspond to protein colors in Fig. 1a. Fig. 1e, using the same color code, shows schematically a complex of three trimers on a plane. Heterodimers are depicted as narrow triangles with sharp angles corresponding to their tails. This complex can be periodically translated, and the resulting packing is based on the trihexagonal lattice (see Fig. 1e). Triple connections of tails and heads of E-proteins ensure the local pseudohexagonal symmetry of the outer immature shell. Fig. 1d shows that due to this symmetry, the vertices of each small triangle, which represents a trimer, are concurrently the vertices of a slightly deformed hexagon with additional vertices related to E-proteins from the other trimers.
Note that the trihexagonal lattice describes the protein arrangement only within one face of the icosahedron. Consequently, it is impossible to superimpose the icosahedron net of the outer flavivirus shell onto this lattice, since the environment of trimers at the icosahedron face differs from their coordination at the icosahedron edge. Construction of the appropriate icosahedral net is greatly simplified if one notices that the trihexagonal lattice can be obtained from the PHL lattice if the unit cell of the latter is four-fold increased. In Fig. 1f, we superimpose translationally nonequivalent regions with trihexagonal order, which correspond to the icosahedron faces, onto the common PHL. The resulting fragment of the icosahedron net is centered around the 5-fold axis; all filled circles correspond to E-proteins.
Fig. 1g shows a SL based on the constructed icosahedron net. Previously vacant positions are highlighted with black circles and correspond to radial projections of MCs of capsid C dimers (compare Fig. 1g and d). Thus, projections of MCs calculated for proteins belonging to both the inner (Fig. 1c) and outer (Fig. 1a) shells result in a common SL (5,0) with vacant positions located only at 5-fold icosahedron axes. Existence of this common lattice demonstrates the commensurability between flavivirus proteinaceous shells that obey the close packing principle characteristic of layered structures: the occupied positions of the outer shell reside between those of the inner one, making the double-layered structure more homogeneous and possibly also more stable.
Note that the positions shown by black circles in Fig. 1d and g also coincide with the trimer centers, near which the transmembrane regions of E and prM proteins are inserted into the outer leaflet of the lipid bilayer. These regions probably interact with the alpha helices of capsid dimers embedded in the inner leaflet of the bilayer,9 establishing commensurability between immature flavivirus shells.
Earlier,36 we discussed another type of commensurability in multi-shelled viruses Reoviridae and Cystoviridae. In these families the outer CK shell (T = 13) is commensurate with the inner anomalous shell (T = 2): the positions of inner proteins are located under the centers of outer hexamers. This arrangement also satisfies the close packing principle of layered structures since the mass density in hexamer centers is minimal. Nevertheless, there is a substantial difference compared to the flavivirus structure. In Reoviridae and Cystoviridae families the outer shell is self-assembled on the previously assembled inner one, whereas in flaviviruses, both proteinaceous shells coherently assemble on different sides of the ER membrane.9 Surprisingly, as we have shown, this fact affects neither the commensurability between layers nor the principle of their close packing.
Importance of the commensurability in flaviviruses is also confirmed by the experimental observations of the outer shell mis-assembly phenomenon.14 Multiple studies report that E and prM proteins self-assemble into icosahedral SVPs in the absence of C proteins but on rare occasions empty SVPs can be also observed during normal in vivo assembly.9 These SVPs are substantially smaller than flaviviruses, do not contain the viral genome and predominantly consist of 60 prM–E heterodimers. Some studies14,15,41 also report the existence of other SVPs that are slightly larger than mature flaviviruses. It seems to us, based on the model14 of SVPs consisting of 180 heterodimers, that these particles have a structure similar to that of an alphavirus shell.42 According to ref. 43, similarly to virions, some small and large genomeless viral particles are also first assembled as spiky trimeric shells.
If we assume that the spiky trimeric shells of 60 heterodimers have the same coordination of SUs as normal immature shells, then the corresponding SL can be constructed by reducing the net shown in Fig. 1f so that each icosahedron face contains only one heterodimer (see the reduced net and corresponding trimeric model shell in Fig. 1h and i, respectively). Note that the trimer centers in this model coincide with the 3-fold icosahedron axes and cannot be occupied by asymmetric proteins or C protein dimers of the capsid. Thus, the T = 1 shell that consists of 60 prM–E heterodimers cannot have inner C proteins, not just because of its relatively small size, but also because this is forbidden by the symmetry. Analogously, instead of decreasing the edges of the icosahedral net, we can increase them, while keeping the spiky coordination of the heterodimers unchanged, so that the shell would have 6 trimers per icosahedron face.
Hidden structural features of mature flavivirus shells
Before a flavivirus particle becomes capable of infecting cells, it must undergo a maturation process, which includes a drastic reconstruction of its outer shell, induced by the change in the pH of the bathing environment. Currently, it is thought that the maturation process is universal in all flaviviruses and involves two intermediate structural states.19,29 Despite the fact that the outer shell structures of DENV and ZIKV are among the most studied structures of flaviviruses,11 data on intermediate states are known only for DENV.29,44 After the self-assembly at neutral pH, the immature virus is transported to the low pH environment of the exosome. In its acidic environment (pH ≈ 5.5), 60 trimers of the outer shell are repacked into 90 dimers, and deposited onto the lipid membrane surface.29 Triplets of dimers aligned parallel to each other form the so-called rafts and the overall structure becomes more densely packed. How exactly this reconstruction occurs remains unclear and several competing scenarios have been proposed.29,45,46 What is nevertheless clear is that this first maturation step is reversible and fully controlled by the bathing solution pH level.29Fig. 2a shows the emerging structure.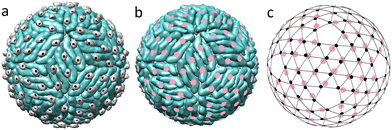 | ||
| Fig. 2 Correspondence between the protein packing in the dimeric flavivirus surface and spherical lattice (3,2). (a) Surface of the first intermediate state (3C6R DENV). Black circles show the mass centers of pr peptides. (b) Completely mature surface. Pink circles show the mass centers of E proteins. In the figure scale, structures of the mature surfaces of 6CO8 ZIKV and 7V3F DENV are indistinguishable. (c) SL (3,2) combined with the mass centers of E proteins (pink circles) in the fully mature state (b) and pr peptides (small black circles) in the first intermediate state (a). | ||
Interestingly, after the reconstruction to the dimeric state, pr peptides, residing at the tails of the E proteins, occupy almost equidistant positions, forming a regular structure (compare Fig. 2a and c). MCs of both pr peptides and E proteins almost coincide with the nodes of the SL (3,2), which reveals the hidden symmetry of the dimeric structure.
The next step of the maturation process is irreversible and involves furin protease, which cleaves the pr and M parts of the prM proteins. Nevertheless, the pr and M parts remain associated with E proteins and the protein packing is practically preserved in the resulting structure (3IYA DENV).44
The maturation process is complete (Fig. 2b) when the virus is extruded into the extracellular milieu with pH = 7.0. At this stage pr peptides are released into the solution, exposing fusion loops at the tails of the E proteins, which are then used by the mature virus to enter host cells.11,40
Unfortunately, there are no detailed structural data on the flavivirus inner shells in the mature state, and the only work that contains the capsid structural data addresses the immature ZIKV (6LNT).9,13 However, since the capsid is protected by the lipid membrane and the state of the flavivirus surface is controlled by the acidity of the solution,11 it seems reasonable to assume that upon transition, the capsid structure remains unchanged. In that case the MCs of capsid C dimers should still correspond to the SL (5,0) with Tin = 25, whereas in the dimeric outer shell, the protein MCs belong to the SL (3,2) with Tout = 19. As the triangulation factors of the above SLs do not have a common divisor, commensurability and matching between the layers decrease after the trimer-to-dimer reconstruction.
The ability of dissociable AAs with ionizable side chains, which can be either deprotonated (Asp, Glu, Tyr) or protonated (His, Lys, Arg),30 to change their charging state depending on the acidity of the bathing solution is crucial for phenomena such as protein folding and denaturation, and protein–membrane and protein–protein binding. It also plays a crucial role in a plethora of physiological processes in various biological systems,47 specifically also in the context of virus structure stability48 and virus substrate interactions.49 In what follows, by developing a semi-quantitative electrostatic model of the virion, we demonstrate how the pH-induced variation of protein charges due to dissociable AA residues and the corresponding change in electrostatic interactions between SUs control the reversible trimer-to-dimer reconstruction in flaviviruses.
pH-Induced structural changes in flavivirus shells during their maturation
In general, the calculation of electrostatic interactions in viruses is a complex problem due to the inhomogeneous dielectric constant of the medium, incompleteness of the available structural data, and the presence of mobile ions in the bathing solution.48 In flaviviruses, an additional layer of complexity stems from their multilayered structure with proteins of the inner and outer shells interacting closely with the interposed negatively charged lipid membrane.13 As our aim here is to highlight the salient trends rather than obtaining a complete numerical solution of the problem, we use a simplified coarse-grained model that considers amino acids as point charges in a bathing solution of known salinity and acidity. The complex non-linear electrostatic problem of charge regulation is thus simplified and mimicked by the screened electrostatic interactions between fixed charges at the MCs of the dissociable AAs, which are determined from the Henderson–Hasselbalch (Langmuir) isotherm.50,51An important fraction of naturally occurring charged lipids is anionic,52 being particularly common in biological membranes and having an important effect also on membrane proteins.53 It is therefore not surprising that the lipid membrane in flaviviruses contains about 10% anionic lipids.46 However, for a variety of reasons the electrostatic interactions between charged lipids and proteins are difficult to evaluate and most if not all theoretical approaches are by necessity approximate and based on different coarse graining simplifications.54 In our case the effective electrostatic energy of the system will be calculated as the sum of pair interaction energies involving AAs belonging to different heterodimers (or their parts) in the framework of the classical Debye–Huckel theory55 (see Methods). In addition, since the structural and even chemical identity data on the membrane components are scarce, the electrostatic interactions between the virus proteins and the lipid membrane can be addressed only on a qualitative level. In addition, we assume that the ionic environment inside the membrane-enclosed region is characterized by a slow exchange dynamics and remains largely unaffected by the external environment, preserving the original neutral pH at which the virus is assembled.12,14,25
The flavivirus maturation process is most extensively studied in the DENV, for which structures of all four states are known: the initial immature trimeric state (3C6D), two intermediate dimeric states with integral (3C6R) and cleaved prM protein (3IYA), and the fully mature virion (1THD).11,29,44,56 However, the corresponding PDB structures have a relatively low resolution, ∼25.0 Å, and do not contain data on the transmembrane regions of the E and prM proteins, lipid membrane, and the overall arrangement of the capsid. In contrast, the full structures of both the capsid and surface (6LNT) of the immature trimeric state were recently obtained for the ZIKV,9,13 but the PDB data on intermediate states of this virus are not available. Thus, when discussing the electrostatic aspects of flavivirus maturation we consider the structural data of both viruses.
As is usually assumed, the dissociation of AAs can proceed only for those that are located within the solvent accessible surface (SAS) of the protein, while those buried inside remain undissociated.51,57 Due to the relatively low resolution of both new (6LNT) and old (3C6D, 3C6R) data (positions of all AAs are defined by a single carbon atom) we were unable to adequately calculate SASs and thus considered all residues as exposed to the solvent. Nonetheless, as we show below, predictions of the proposed simplified model are in good agreement with experimental data and provide a valuable insight into the mechanisms driving the maturation process.
Fig. 3 shows the charges of the pr peptides and M–E proteins as well as the electrostatic energies of the DENV and ZIKV surfaces as functions of pH in the 5.5–7.0 range (which is relevant for flavivirus maturation).11,29 The electrostatic (free) energies (all plots in (b) and red plots in (d)) correspond only to interactions between proteins forming the outer shells. Since the structural data on the DENV capsid and the transmembrane regions of DENV heterodimers are absent, plots in Fig. 3a and b were obtained without the contribution of transmembrane residues. In contrast, plots in Fig. 3c and d were calculated for the complete immature ZIKV structure (6LNT) and they take into account the effect of the lipid membrane on the transmembrane residues. It is easy to see that the impermeability of the lipid bilayer to external pH changes only slightly decreases the total charges of the proteins and thus has no qualitative effect on the electrostatic interactions.
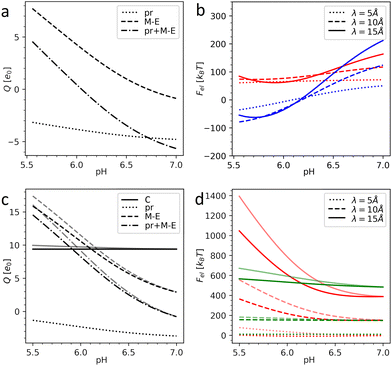 | ||
| Fig. 3 Electrostatics of the flavivirus shell maturation. (a) Charges of the DENV heterodimer and its pr and M–E parts depending on the pH level. (b) Electrostatic energy of the interaction between dengue surface proteins as a function of pH for immature trimeric 3C6D (colored in red) and immature dimeric 3C6R (colored in blue) states. (c) Charges of the ZIKV heterodimer, its pr and M–E parts, and C protein as a function of pH. (d) Electrostatic energy of the interaction between Zika surface proteins as a function of pH (colored in red) and electrostatic energy of the interaction between the surface and inner capsid of the immature trimeric state 6LNT (colored in green). Plots in (b) and (d) are calculated for three different values of the screening length λ. In (c) and (d), the pale and bright lines correspond to the cases of fully permeable (pH is homogeneous) and fully impermeable membranes (pH inside the lipid membrane is constant and equals 7.0), respectively. | ||
By comparing panels (a) and (c) one can see that in both flaviviruses, charges of surface proteins show similar behavior. All plots increase monotonically with the acidity increase: the M–E complex, which has a negative charge in a neutral environment, becomes highly positively charged, while the negative charge of pr peptides decreases. Nevertheless, the values of the charges and isoelectric points of the heterodimers (pH ≈ 6.1 for the DENV and pH ≈ 6.8 for the ZIKV) differ, not only because of the unresolved transmembrane regions of the DENV, which we cannot take into account, but also because of substantial differences in the AA composition of the viruses.
Under physiological conditions, an average value of the electrostatic screening length can be estimated as λ = 10 Å (see Methods). To demonstrate that the local salt concentration does not change the behavior of the system qualitatively, we calculated electrostatic energies for three screening length values, namely: 5, 10 and 15 Å. Fig. 3b demonstrates that in the trimeric state, at pH < 6.6, the electrostatic interactions between heterodimers tend to destabilize the surface of the DENV and the immature dimeric state becomes more energetically favorable. As we have shown in our previous work,58 upon pH-induced 3C6D → 3C6R transition, the electrostatic energy of the outer shell is significantly reduced due to the relocation of negatively charged pr peptides, which are grouped into three peptides in the trimeric state and shift to almost equidistant positions in the dimeric structure (see Fig. 2a and c), and this drastically decreases the repulsive forces between them. In the ZIKV, however, the absolute value of the pr peptide charge is lower than that in the DENV (see Fig. 3a and c), implying that the contribution of the repulsive interactions between the peptides to the total energy is also decreased. This difference between DENV and ZIKV cases thus raises the question whether the electrostatic interactions of the heterodimers with the capsid and/or lipid membrane can stimulate trimeric-to-dimeric reconstruction in the ZIKV surface.
Let us consider the inter-shell interaction. Fig. 3d shows that in the trimeric state at physiological salt concentration the electrostatic interaction energy depends only slightly on pH (see the green solid line), and as the calculation demonstrates, it is primarily related to the repulsion of closely located alpha helices of C and prM–E proteins residing inside the membrane. As the structural commensurability is lowered at the dimeric-to-trimeric reconstruction, the electrostatic interaction between the shells should consequently also decrease, e.g., due to the changes in the separation between transmembrane helices originating from inner and outer shells. It seems likely that similar to the electrostatic inter-shell interaction in the trimeric state (see Fig. 3d), this interaction also weakly depends on the pH in the dimeric state. This conclusion is supported by a calculation based on a virtual structure whose core is in the immature trimeric state of ZIKV, while the surface corresponds to the fully mature, dimeric state. We have thus reasons to believe that the electrostatic interaction between shells cannot strongly affect the surface reconstruction but can be important for self-assembly of the complex flavivirus structure, since, as we have shown, any small relative rotation of the shells increases their interaction energy. Mutual orientation of the shells that preserves the common icosahedral symmetry is thus energetically more favorable.
Considering the size of the lipid membrane9 and its composition46 we estimate that the total membrane charge at the relevant pH level 5.5–7.0 amounts to ∼103 elementary charges. In ZIKV, heterodimers are positively charged at pH < 6.8 (in DENV at pH < 6.1) and this charge increases with the oxidation of the environment (see Fig. 3a and c). Thus, at a low pH level, the negatively charged lipid membrane (Fig. 1b) would promote electrostatic binding of inner and outer protein shells in both trimeric and dimeric states. Let us stress, however, that in the dimeric structure, in contrast to the trimeric one, elongated heterodimers are located directly on the membrane surface, decreasing the average distance between charged AAs and lipids and lowering the energy of the dimeric state. Due to the increase of heterodimer charge, the energetic gap between the dimeric and trimeric states should also increase with oxidation and therefore stimulate the reconstruction. This proposed mechanism can be further developed provided that the structural data for the first ZIKV intermediate state become available.
Overall, although our mainly qualitative electrostatic model is based on several simplifications, the performed analysis rationalizes the available experimental data and allows us to clarify the crucial role of pH-dependent electrostatic interactions between the surface proteins and lipid membrane in the maturation process of flaviviruses.
Conclusions
This study is part of continuing research24–26,36 elucidating the principles of protein packing and symmetry in anomalous (i.e., violating the CK model) single- and multi-shelled viral capsids with icosahedral symmetry. Here, we reveal the hidden features of protein order in a complex flavivirus shell, which self-assembles simultaneously on two opposite sides of an interposed lipid membrane. Like many other anomalous icosahedral capsids, the layered complex protein–lipid–protein assembly displays hidden features of protein order caused by the CK quasi-equivalence principle.17,25 As elucidated in this work, the arrangement of proteins within the icosahedron faces of the immature flavivirus surface is based on the trihexagonal lattice, while the radial projections of the mass centers calculated for the proteins of both inner and outer immature shells form a common icosahedral triangular spherical lattice (5,0). Thus, despite the interposed lipid membrane separating the proteinaceous layers, their structural organization is consistent with the close packing principle of layered structures: the positions of surface proteins (outer side) reside between those of capsid proteins (inner side), which makes the whole system more homogeneous and possibly also more stable. During the maturation, the self-assembled outer shell goes through a transition from a trimer into a dimer protein state, so that the protein locations coincide with the spherical lattice (3,2), thereby significantly reducing the matching between the layers.As is known, at the initial stage of maturation this transformation is reversible and controlled by the acidity of the solution, which by necessity implicates electrostatic interactions between protonated/deprotonated AAs of the shell proteins as the driving mechanism of the reconstruction transformation. Using recent structural data on both shells of the immature Zika virus,9 we calculated the protein charges as a function of pH based on the simple Henderson–Hasselbalch isotherm and the corresponding energy of electrostatic interactions in the virus. By comparing our results with the ones previously obtained for the dengue virus,58 we found that the pH-dependent changes of electrostatic interactions between constituting proteins can contribute to the driving mechanism of the transformation, which is also assisted by an increase in the attraction of positively charged heterodimers to a negatively charged interposed lipid bilayer membrane of flaviviruses.
Besides flaviviruses, there are other enveloped viruses that self-assemble on the surfaces of host lipid membranes, e.g., alphaviruses, coronaviruses, and hepatitis B. All these viruses, however, have different self-assembly mechanisms and shell structures, so general conclusions are difficult to reach. For example, unlike flaviviruses, alphaviruses self-assemble on the cell membrane; shells of hepatitis B viruses, similar to flaviviruses, self-assemble from trimers on the ER membrane, but the outer lattice has a T = 4 structure; coronaviruses, while also assembling on the ER membrane, do not exhibit an icosahedral symmetry and are pleomorphic. Despite the obvious diversity of enveloped viruses, symmetry considerations and electrostatic interactions as detailed in this work are universal and can be applied to other viruses of this group. We hope that both the methods and the results obtained for flaviviruses will help to further improve our understanding of the self-assembly and maturation processes of the enveloped viruses in general.
Results of our work could also be useful for the design and modelling of liquid crystalline porous composite nanobiomaterials based on charged lipid membranes associated with protein complexes.64,65 The ability of such systems to undergo structural transitions when the pH of the environment changes, similarly to flavivirus surfaces, opens new possibilities for targeted drug delivery. For example, tumor environments are usually more acidic because of the accumulation of metabolic waste products under the conditions of high metabolic activity and insufficient perfusion.66 Viral superstructures (e.g., cypovirus polyhedra) and various polymorphs assembled from capsid proteins can as well serve as nano-containers, since their assembly, disassembly and structure can be controlled by the pH and ionic strength of the solution.67–69
Methods
Constructing icosahedral spherical lattices
To construct a primitive icosahedral SL, we first transfer the PHL onto the icosahedron surface and then project radially the nodes onto the circumscribing sphere. If it is needed (see the main text), the nodes located on icosahedron axes can be eliminated. With the radial projection, the distances between neighboring nodes, which were equal in the icosahedron net, are inhomogeneously deformed. The deformation is maximal in the vicinity of the icosahedron vertices. By equalizing these distances, one can improve the local translational symmetry and increase the quasi-equivalence of the SL positions.17,26,59In ref. 26, a harmonic interaction potential was used for that purpose. Here, we follow a more efficient approach and minimize the repulsion energy:
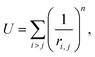 | (1) |
For n → ∞, minimization of energy (1) equalizes all distances between the nearest nodes exactly.61,62 However, since the maximum number of nearest neighboring disks for a disk retained on the sphere is five, the local 6-fold symmetry of SL nodes is always approximate. To obtain SLs with optimally equalized edges, we used n = 200 and minimized energy (1) by applying a conventional gradient descent method. It is also important to note that for some SLs, e.g., (5,0), minimization of energy (1) breaks the initial icosahedral symmetry. In that case, along with retaining nodes on the spherical surface, one should preserve the initial symmetry (I or Ih) of the SL during the minimization of its energy.
Note also that the above method allows one to obtain only the optimized primitive icosahedral SLs. Trihexagonal SLs are obtained from the appropriate primitive ones by eliminating redundant nodes.
Calculating energy of electrostatic interactions between proteins
In our simple model, we consider proteins as sets of point charges interacting with each other through a screened Coulomb potential.36,51 The normalized (free) energy of the electrostatic interaction between proteins reads: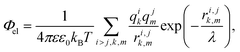 | (2) |
Screening length under physiological conditions λ ≈ 10 Å was estimated following ref. 55 as:
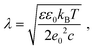 | (3) |
Partial charges of the ionizable residues were calculated using the Henderson–Hasselbalch equation which follows the Langmuir isotherm:55
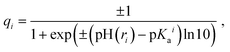 | (4) |
When considering the impermeable membrane and calculating (2) as a function of the solution pH, we used constant pH = 7.0 for ri < Rout and solution pH for ri > Rout, where Rout defines the outer border of the lipid membrane; Rout = 201 Å was chosen according to experimental data.9 This choice presumably describes the slow dynamics of the charge migration through the lipid membrane. At this Rout value the transmembrane domains of the E and prM proteins are fully immersed into the lipid membrane, whereas all other ionizable residues are in the bathing solution.
Author contributions
O. K. and S. R. proposed the main approach to the structural part of this study, while R. P. and. I. G developed the electrostatic model. S. R. with the substantial help of all authors wrote the draft and managed the project. All authors reviewed and edited the text.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. R., I. G., and O. K. acknowledge the financial support from the Russian Science Foundation, Grant No. 22-12-00105. R. P. acknowledges funding from the Key Project No. 12034019 of the National Natural Science Foundation of China.References
- ICTV Report Chapters|ICTV, https://ictv.global/report, (accessed 19 August 2022).
- G. Kuno, G.-J. J. Chang, K. R. Tsuchiya, N. Karabatsos and C. B. Cropp, J. Virol., 1998, 72, 73–83 CrossRef CAS PubMed.
- S. Bhatt, P. W. Gething, O. J. Brady, J. P. Messina, A. W. Farlow, C. L. Moyes, J. M. Drake, J. S. Brownstein, A. G. Hoen, O. Sankoh, M. F. Myers, D. B. George, T. Jaenisch, G. R. William Wint, C. P. Simmons, T. W. Scott, J. J. Farrar and S. I. Hay, Nature, 2013, 496, 504–507 CrossRef CAS PubMed.
- S. N. Dighe, O. Ekwudu, K. Dua, D. K. Chellappan, P. L. Katavic and T. A. Collet, Eur. J. Med. Chem., 2019, 176, 431–455 CrossRef CAS.
- B. Troost and J. M. Smit, Curr. Opin. Virol., 2020, 43, 9–21 CrossRef CAS.
- A. D. T. Barrett, Vaccine, 2017, 35, 5951–5955 CrossRef PubMed.
- X. Li, S. J. Ma, X. Liu, L. N. Jiang, J. H. Zhou, Y. Q. Xiong, H. Ding and Q. Chen, Hum. Vaccines Immunother., 2014, 10, 3579–3593 CrossRef.
- K. L. Carpio and A. D. T. Barrett, Vaccines, 2021, 9, 622 CrossRef CAS.
- T. Y. Tan, G. Fibriansah, V. A. Kostyuchenko, T. S. Ng, X. X. Lim, S. Zhang, X. N. Lim, J. Wang, J. Shi, M. C. Morais, D. Corti and S. M. Lok, Nat. Commun., 2020, 11, 1–13 CrossRef.
- V. A. Kostyuchenko, E. X. Y. Lim, S. Zhang, G. Fibriansah, T. S. Ng, J. S. G. Ooi, J. Shi and S. M. Lok, Nature, 2016, 533, 425–428 CrossRef CAS PubMed.
- D. Sirohi and R. J. Kuhn, J. Infect. Dis., 2017, 216, S935–S944 CrossRef CAS.
- T. C. Pierson and M. S. Diamond, Curr. Opin. Virol., 2012, 2, 168 CrossRef CAS.
- T. Y. Tan, G. Fibriansah and S.-M. Lok, PLoS Pathog., 2020, 16, e1008542 CrossRef CAS.
- I. Ferlenghi, M. Clarke, T. Ruttan, S. L. Allison, J. Schalich, F. X. Heinz, S. C. Harrison, F. A. Rey and S. D. Fuller, Mol. Cell, 2001, 7, 593–602 CrossRef CAS PubMed.
- S. L. Allison, Y. J. Tao, G. O'Riordain, C. W. Mandl, S. C. Harrison and F. X. Heinz, J. Virol., 2003, 77, 11357–11366 CrossRef CAS.
- G. Fibriansah, X. N. Lim and S. M. Lok, Viruses, 2021, 13, 1–18 CrossRef PubMed.
- D. L. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS.
- M. Sevvana, F. Long, A. S. Miller, T. Klose, G. Buda, L. Sun, R. J. Kuhn and M. G. Rossmann, Structure, 2018, 26, 1169 CrossRef CAS.
- V. M. Prasad, A. S. Miller, T. Klose, D. Sirohi, G. Buda, W. Jiang, R. J. Kuhn and M. G. Rossmann, Nat. Struct. Mol. Biol., 2017, 24, 184–186 CrossRef CAS.
- R. Twarock, J. Theor. Biol., 2004, 226, 477–482 CrossRef CAS.
- R. Twarock and R. W. Hendrix, J. Theor. Biol., 2006, 240, 419–424 CrossRef CAS.
- T. Keef, R. Twarock and K. M. Elsawy, J. Theor. Biol., 2008, 253, 808–816 CrossRef CAS PubMed.
- A. Raguram, V. Sasisekharan and R. Sasisekharan, Trends Microbiol., 2017, 25, 438–446 CrossRef CAS.
- V. V. Pimonov, O. V. Konevtsova and S. B. Rochal, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 135–141 CrossRef CAS.
- S. B. Rochal, O. V. Konevtsova and V. L. Lorman, Nanoscale, 2017, 9, 12449–12460 RSC.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC.
- O. V. Konevtsova, S. B. Rochal and V. L. Lorman, Phys. Rev. Lett., 2012, 108, 038102 CrossRef CAS PubMed.
- O. V. Konevtsova, V. V. Pimonov, V. L. Lorman and S. B. Rochal, J. Phys.: Condens. Matter, 2017, 29, 284002 CrossRef CAS PubMed.
- I. M. Yu, W. Zhang, H. A. Holdaway, L. Li, V. A. Kostyuchenko, P. R. Chipman, R. J. Kuhn, M. G. Rossmann and J. Chen, Science, 2008, 319, 1834–1837 CrossRef CAS PubMed.
- R. J. Nap, A. L. Božič, I. Szleifer and R. Podgornik, Biophys. J., 2014, 107, 1970–1979 CrossRef CAS.
- H. Naitow, J. Tang, M. Canady, R. B. Wickner and J. E. Johnson, Nat. Struct. Biol., 2002, 9, 725–728 CrossRef CAS PubMed.
- I. Rayment, T. S. Baker, D. L. D. Caspar and W. T. Murakami, Nature, 1982, 295, 110–115 CrossRef CAS PubMed.
- R. C. Liddington, Y. Yan, J. Moulai, R. Sahli, T. L. Benjamin and S. C. Harrison, Nature, 1991, 354, 278–284 CrossRef CAS PubMed.
- R. J. Kuhn, W. Zhang, M. G. Rossmann, S. V. Pletnev, J. Corver, E. Lenches, C. T. Jones, S. Mukhopadhyay, P. R. Chipman, E. G. Strauss, T. S. Baker and J. H. Strauss, Cell, 2002, 108, 717 CrossRef CAS.
- S. Mukhopadhyay, B. S. Kim, P. R. Chipman, M. G. Rossmann and R. J. Kuhn, Science, 2003, 302, 248 CrossRef CAS PubMed.
- O. V. Konevtsova, D. S. Roshal, A. Lošdorfer Božič, R. Podgornik and S. Rochal, Soft Matter, 2019, 15, 7663–7671 RSC.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- V. A. Kostyuchenko, Q. Zhang, J. L. Tan, T.-S. Ng and S.-M. Lok, J. Virol., 2013, 87, 7700–7707 CrossRef CAS.
- L. Li, S. M. Lok, I. M. Yu, Y. Zhang, R. J. Kuhn, J. Chen and M. G. Rossmann, Science, 2008, 319, 1830–1834 CrossRef CAS PubMed.
- L. H. Chao, D. E. Klein, A. G. Schmidt, J. M. Peña and S. C. Harrison, eLife, 2014, 3, e04389 CrossRef.
- H. Garoff, M. Sjöberg and R. H. Cheng, Virus Res., 2004, 106, 103–116 CrossRef CAS PubMed.
- E. Krol, G. Brzuska and B. Szewczyk, Trends Biotechnol., 2019, 37, 1202–1216 CrossRef CAS PubMed.
- I.-M. Yu, H. A. Holdaway, P. R. Chipman, R. J. Kuhn, M. G. Rossmann and J. Chen, J. Virol., 2009, 83, 12101 CrossRef CAS PubMed.
- N. D. Newton, J. M. Hardy, N. Modhiran, L. E. Hugo, A. A. Amarilla, S. Bibby, H. Venugopal, J. J. Harrison, R. J. Traves, R. A. Hall, J. Hobson-Peters, F. Coulibaly and D. Watterson, Sci. Adv., 2021, 7, 1–12 Search PubMed.
- Q. Zhang, C. Hunke, Y. H. Yau, V. Seow, S. Lee, L. B. Tanner, X. L. Guan, M. R. Wenk, G. Fibriansah, P. L. Chew, P. Kukkaro, G. Biuković, P. Y. Shi, S. G. Shochat, G. Grüber and S. M. Lok, J. Biol. Chem., 2012, 287, 40525–40534 CrossRef CAS PubMed.
- H.-X. Zhou and X. Pang, Chem. Rev., 2018, 118, 1691–1741 CrossRef CAS PubMed.
- A. Šiber, A. L. Božič and R. Podgornik, Phys. Chem. Chem. Phys., 2012, 14, 3746–3765 RSC.
- L. Javidpour, A. Božič, A. Naji and R. Podgornik, Soft Matter, 2021, 17, 4296–4303 RSC.
- L. Javidpour, A. Lošdorfer Božič, A. Naji and R. Podgornik, J. Chem. Phys., 2013, 139, 154709 CrossRef PubMed.
- A. Lošdorfer Božič, C. Micheletti, R. Podgornik and L. Tubiana, J. Phys.: Condens. Matter, 2018, 30, 084006 CrossRef PubMed.
- V. V. Galassi and N. Wilke, Membrane, 2021, 11, 478 CrossRef CAS.
- S. Pöyry and I. Vattulainen, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2322–2333 CrossRef PubMed.
- G. V. Bossa, K. Bohinc and S. May, Handb. Lipid Membr, 2021, pp. 223–240 Search PubMed.
- T. Markovich, D. Andelman and R. Podgornik, Handb. Lipid Membr., 2021, pp. 99–128 Search PubMed.
- Y. Zhang, W. Zhang, S. Ogata, D. Clements, J. H. Strauss, T. S. Baker, R. J. Kuhn and M. G. Rossmann, Structure, 2004, 12, 1607–1618 CrossRef CAS PubMed.
- T. J. Richmond, J. Mol. Biol., 1984, 178, 63–89 CrossRef CAS.
- S. B. Rochal, O. V. Konevtsova, D. S. Roshal, A. Božič, I. Yu. Golushko and R. Podgornik, Nanoscale Adv., 2022, 4, 4677–4688 RSC.
- A. Klug and D. L. D. Caspar, Adv. Virus Res., 1961, 7, 225–325 CrossRef.
- P. M. L. Tammes, Recueil Trav. Bot. Néerl., 1930, 87, 1–84 Search PubMed.
- J. H. Conway and N. J. A. Sloane, Sphere Packings, Lattices and Groups, Springer New York, New York, NY, 1988, vol. 290 Search PubMed.
- M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 2016 Search PubMed.
- A. Angelova, B. Angelov, R. Mutafchieva and S. Lesieur, J. Inorg. Organomet. Polym. Mater., 2014, 25, 214–232 CrossRef.
- O. Mertins, P. D. Mathews and A. Angelova, Nanomaterials, 2020, 10, 963 CrossRef CAS PubMed.
- E. Boedtkjer and S. F. Pedersen, Annu. Rev. Physiol., 2020, 82, 103–126 CrossRef CAS.
- J. B. Bancroft, Adv. Virus Res., 1970, 16, 99–134 CrossRef CAS.
- K. W. Adolph and P. J. G. Butler, J. Mol. Biol., 1974, 88, 327–341 CrossRef CAS.
- X. Ji, D. Axford, R. Owen, G. Evans, H. M. Ginn, G. Sutton and D. I. Stuart, J. Struct. Biol., 2015, 192, 88–99 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |
