Bonding and the role of electrostatics in driving C–C bond formation in high valent organocopper compounds

Abstract

The electronic structures and contrasting reactivity of [Cu(CF₃)₄]⁻ and [Cu(CF₃)₃(CH₃)]⁻ were probed using coupled cluster and ab initio valence bond calculations. The Cu–C bonds in these complexes were found to be charge shift bonds. A key finding is that electrostatics likely prevent [Cu(CF₃)₄]⁻ from accessing a productive transition state for C–C bond formation while promote one for [Cu(CF₃)₃(CH₃)]⁻. These results therefore highlight essential design criteria for Cu-mediated C–C/C–heteroatom bond formation.

---

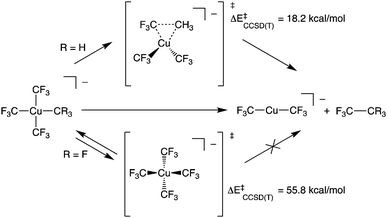
Copper has attracted considerable interest as a mediator of C–C and C–heteroatom bond formation given its earth abundance and relatively low toxicity compared to conventional catalysts based on 4d and 5d metals.^1–3 Copper's utility in many such transformations has been proposed to arise from its complexes’ participation in 2-electron redox couples. This redox behaviour is ascribed to an accessible +3 formal oxidation state for the metal.⁴ To test this hypothesis, there has been considerable synthetic effort expended toward expanding the catalogue of isolable, formally Cu(III) complexes. Recently, such species have been demonstrated to be competent for C–CF₃ bond formation.^5–7 Experimental and computational results support intramolecular C–C bond formation by these systems. Curiously, the reactivity of these species starkly contrasts that of homoleptic [Cu(CF₃)₄]⁻ (1), a stable, formally Cu(III) complex ion that does not undergo elimination of C₂F₆ (Scheme 1).^8,9

Scheme 1

The electronic structure of 1 has been the topic of prolonged debate. We and others^10–14 have argued on the basis of experimentally-ascertained electron population at Cu that 1 is best described as bearing a physically Cu(I) centre due to having an inverted ligand field (ILF), while others have favoured a more classical, Cu(III) description.^15,16 Experimentally-calibrated density functional theory (DFT) calculations of the electronic structure of heteroleptic [Cu(CF₃)₃(alkyl)]⁻ centres also indicate ILFs. Intriguingly, the calculated electron population at Cu changes minimally during alkyl-CF₃ elimination, suggesting that Cu remains effectively redox inert during C–C bond formation. We and others^10,17 have speculated that such reactions are better described not as “reductive eliminations” but rather as simply “eliminations.” We have also speculated that the divergent reactivity of heteroleptic [Cu(CF₃)₃(alkyl/aryl)]⁻ species from 1 could be attributed to electrostatics: between the electron withdrawing nature of F and the high degree of donation to Cu, substantial positive charge accumulates on the CF₃ ligands.¹⁰ The alkyl/aryl donor C bears negative charge, and thus electrostatics lower the activation barrier to C–C bond formation.

To offer a clearer understanding of the conditions required to manifest productive bond formation from formally Cu(III) complexes, we now present high-level molecular orbital (MO) calculations (coupled cluster, CCSD(T)) and ab initio valence bond (VB) calculations that probe the remarkably contrasting reactivity of practically identical complex ions. Owing to the computational expense of the methods employed (vide infra), we compared 1 to the simplest [Cu(CF₃)₃(alkyl)]⁻ case, [Cu(CF₃)₃(CH₃)]⁻ (2). Although 2 has yet to be synthetically realized, it is related to other [Cu(CF₃)₃(alkyl)]⁻ species prepared and examined by Liu and co-workers.⁵ Our results show that the Cu–C bonding in formally Cu(III) tetraalkyl species is predominantly charge-shift (CS) in nature,^18,19 and provides further support for physical Cu(I) oxidation state assignments. By interrogating the nature of the encountered transition states, we can rationalize the disparate reactivity in terms of a redox-neutral elimination process that leverages the highly oxidized nature of the bound ligands as a driving force for bond formation. The emergent details should inform future design of Cu-based platforms for C–C bond formation.

All geometry optimizations, potential energy surface scans and transition state (TS) searches were performed at the PBE0/D3/def2-tzvp level of theory. Subsequent CCSD(T) single point calculations on these structures employed Dunning's correlation consistent basis sets (cc-pVnZ) extrapolated to the basis set limit. To interrogate the bonding in these complexes and TS structures, we leveraged ab initio VB calculations using the XMVB software package²⁰ at the breathing orbital valence bond (BOVB) level and the Sapporo-DVP-2012 basis sets. The many-electron VB wavefunction (Ψ_VB) results from a combination of Heitler–London–Slater–Pauling (HLSP) state functions (Φ_i, termed VB structures herein for simplicity) weighted by structural coefficients: 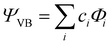. Here, each Φ_i is a normalized, antisymmetrized set of bond-functions comprised of non-orthogonal localized orbitals (ϕ_k). At the lowest level of ab initio VB theory, the VBSCF level, the VB structures are represented by the same set of orbitals. Allowing the orbitals to optimize for each VB structure, or “breathe,” captures a significant amount of the correlation energy missing at the VBSCF level. The ab initio VB calculations presented herein employ this “breathing orbital effect” into the VB calculations (BOVB) with the inactive orbitals treated in a quasi-MO fashion.²¹ Our BOVB calculations exploring the nature of the Cu–C bonds in 1 and 2 considered three VB structures: a covalent structure comprised of overlapping Cu- and C-localized AOs of σ-type symmetry (Φ_cov) and two ionic structures corresponding to (i) a lone pair on the C-centre (Φ_ion1), or (ii) a lone pair on the Cu-centre (Φ_ion2; Fig. 1).‡

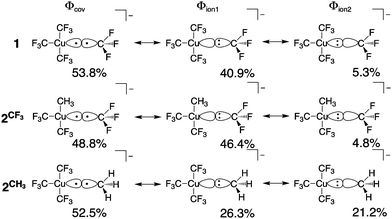Fig. 1 Weights of the individual Heitler–Slater–London–Pauling (HSLP) state functions contributing to Ψ_VB describing the Cu–C bonds of 1 and 2.

The weights§ of the individual HSLP state functions comprising Ψ_VB reveals immediately that the nature of the R-group exerts a large influence on the nature of the Cu–C bond. In the case of the Cu–CF₃ in 1 and 2 as well as the Cu–CH₃ bond in 2, Φ_cov is the leading VB structure, comprising approximately 50% of Ψ_VB. What differs are the two ionic contributions. In the case of the Cu–CF₃ bond, Φ_ion1 (lone-pair on the C-centre) significantly contributes to Ψ_VB with Φ_ion2 (lone-pair on the Cu-centre) only contributing ca. 5%. In contrast, the Cu–CH₃ bond in 2 has approximately equal weighting of the two ionic HSLP state functions. This can be reconciled in terms of the nature of CH₃vs. CF₃. Electron withdrawal by the highly electronegative F-atom builds a large positive charge on the C-atom, reducing electron donation from C to the Cu-centre, while the more electron-rich C-centre of CH₃ can better support the formation of Φ_ion2. This is reflected in the charge on C in 1 and 2. A Mulliken analysis of these results yields an average charge on C of the CF₃ groups of 1 and 2 of +0.7e (ranging between +0.43e to +0.73e) despite the large contribution of Φ_ion1 to Ψ_VB. In contrast, the C atom of the CH₃ group of 2 has a charge of −0.76e.¶ We note that the charge on the copper centre is +0.69e for 1 and +0.55e for 2 consistent with other experimental and theoretical studies describing the Cu-centre in “high-valent” organocopper species as more similar to Cu(I) not Cu(III). In fact, there is a larger difference in charge on the ligating C-atoms than on Cu in 1 and 2vs. the organocopper reductive elimination product [Cu(CF₃)₂]⁻.||

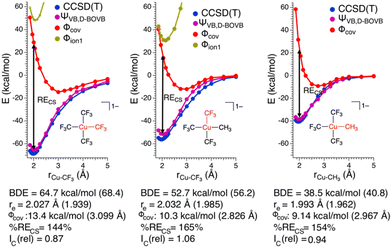
To gain further insight into the nature of these Cu–C bonds, we constructed potential energy surfaces (PESs) for Cu–C bond homolysis (Fig. 2) at the CCSD(T) and BOVB levels of theory. There is overall excellent agreement between the CCSD(T) and BOVB calculations; the calculated Cu–C bond dissociation energies (BDEs) are within 10% (<5 kcal mol⁻¹) agreement between the two methods while the calculated equilibrium Cu–C bond lengths (r_e) differ by no more than 0.05 Å. We find that the Cu–CF₃ bond is ca. 20 kcal mol⁻¹ more stable than the Cu–CH₃ bond with respect to bond homolysis.

Fig. 2 Calculated energies of the singlet state as a function of interatomic Cu–C distance for 1 (left) and 2 (Cu–CF₃: middle; Cu–CH₃: right). The CCSD(T) energies are given in blue, total Ψ_VB energies in purple, Φ_cov energies in red, and Φ_ion1 energies in gold. The CCSD(T) BDE and r_e are provided in parentheses next to the BOVB results. Also provided are the BDE and r_e from Φ_cov, %RE_CS and I_c(rel) for the Cu–C bonds.

A more detailed analysis of the HSLP state functions demonstrates that all the Cu–C bonds in these complexes are CS bonds. Along with covalent and ionic bonds, CS bonds comprise a distinct class of bonds that arise from the resonance interaction energy (RE_CS) between covalent and ionic structures.²² For the Cu–C bonds of 1 and 2 the two ionic HLSP state functions are unstable with respect to Cu–C dissociation at all Cu–C distances while consideration of only the covalent HLSP state function overestimates the Cu–C bond lengths (r_e,covca. 3.0 Å) and underestimate the Cu–C BDEs (BDE ca. 10 kcal mol⁻¹). In fact, at the equilibrium Cu–C bond length, Φ_cov is higher in energy than the energy of the two separated fragments by ca. 20–30 kcal mol⁻¹. Instead, the main driving force for Cu–C bond formation in these complexes is the resonance stabilization energy between the covalent and ionic configurations. The resonance energy provided through the CS mechanism at the equilibrium bond length can be defined by:

RE_CS = E_ΨVB − E_Φcov

and the percent of the total BDE resulting from the CS mechanism as:
In the case of both 1 and 2, RE_CS is larger than the BDE leading to %RE_CS values ranging from 145 to 165%, which is consistent with the assignment of the Cu–C bond as being CS in nature.

Also consistent with the CS nature of the Cu–C bonds in these complexes is the relative lack of contraction of the ϕ_k involved in σ-bonding upon bond formation. In a covalent bond, the orbitals involved in bond formation will shrink to ca. 50% of their size at the dissociated limit. In the case of CS bond formation, the orbitals will display either a modest contraction or an expansion. Hiberty and Shaik have shown that orbital contraction upon bond formation can be readily quantified from electronic structure calculations using a so-called “orbital compactness index” (I_c).²³I_c is the square-root of the ratio of the summed-squares of the inner and outer basis functions describing the active valence bond orbitals. By taking the I_c ratio of the bonded complex vs. the infinitely separated molecular fragments, one obtains a relative orbital compactness index for bond formation (I_c(rel)); the larger the value of I_c(rel), the more diffuse the orbital is upon bond formation. We obtain I_c(rel) values for the Cu–C valence orbitals of 1 = 0.87 and 2 = 1.06 (Cu–CF₃) and 0.94 (Cu–CH₃), consistent with CS-bonds. Thus, on the basis of the large %RE_CS, long r_e for the Φ_cov VB configurations, and I_c(rel) values approaching 1, we conclude the Cu–C bonds are CS in nature for these complexes.

We now turn to the TS structures located for 1 and 2 along shortening C–C trajectories. We can readily locate a TS for the concerted elimination of 1,1,1-trifluoroethane from 2. Consistent with previous findings on related systems, the reaction proceeds with a relatively low calculated activation barrier (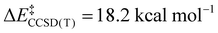; Scheme 1). In contrast, the TS for a concerted C–C elimination pathway could not be located for 1.** Rather, what consistently emerges is a TS leading to ligand isomerization (1^iso) with a high activation barrier (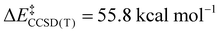; Scheme 1). This accords with the stability characteristic of salts of 1. These two pathways were noted by Hoffmann and Kochi in elimination from Au.²⁴

The structures of these elimination vs. isomerization TS structures are markedly different. Complex 2 reaches a low-energy distorted tetrahedral geometry that leads to F₃C–CH₃ formation, while 1^iso is a high-energy D_2d structure that collapses back to 1. The differences in TS structures and reaction pathways can be largely rationalized in terms of electrostatics. The CCSD(T) calculations show structural distortions do not dramatically alter the atomic charges on the C-atoms. In the TS structure of 2, the CH₃ and a cis CF₃ carbon atom come into close contact (1.982 Å) with one another. At both the ground- and transition-states, the CH₃vs. CF₃ atoms in 2 have opposite charges (F₃C^+0.48vs. H₃C^−0.26).†† It is thus electrostatically favourable to bring these two fragments together. In contrast, the C-atoms in 1 all have large partial positive charges (ca. +0.5e). Thus, the estimated elimination TS structure leading to C–C bond formation in 1 is high in energy owing to electrostatic repulsion.

To probe this further, we examined the influence of fluorination of the CH₃ group of 2 on TS energy and charge on C at the CCSD(T) level. For both 1 and [Cu(CF₃)₃(CHF₂)]⁻ the TS for C–C elimination had to be estimated from the C–C elimination TS of [Cu(CF₃)₃(CH₂F)]⁻ (F₃C⋯CR₂F length of 2.035 Å). We note a systematic increase in TS energy as the methyl group is fluorinated; the ΔE^‡ increases from 18.2 kcal mol⁻¹ for [Cu(CF₃)₃(CH₃)]⁻ to 37.4 kcal mol⁻¹ for [Cu(CF₃)₃(CH₂F)]⁻ to 50.0 kcal mol⁻¹ for [Cu(CF₃)₃(CHF₂)]⁻ and to 57.7 kcal mol⁻¹ for [Cu(CF₃)₃(CF₃)]⁻ (1^re). The increase in TS energy coincided with an increase in positive charge of the C-atom within the fluorinated methyl fragment (H₃C^−0.26vs. H₂FC^−0.02vs. HF₂C^+0.27vs. F₃C^+0.48). Thus, a physical reason why 1 does not undergo C–C elimination reactions is the large electrostatic repulsion between CF₃ fragments prevents the complex from achieving a productive TS. This assertion is supported by VB calculations.

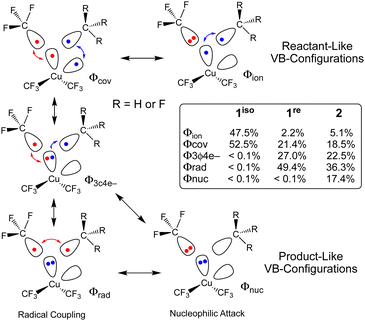
The different TS structures of 1^isovs.2 exhibit major differences in their VB descriptions. To adequately describe these TSs, we increased the number of active orbitals; we considered two Cu-localized VB-orbitals and two VB-orbitals localized to the cis-C-atoms that would form the C–C bond (Fig. 3). Of the 20 possible VB structures, five dominate Ψ_VB (weight ≥ 0.1). Two of these VB structures are directly related to the reactant VB-configurations: one describes two covalent Cu–C bonds (Φ_cov) and one describes a covalent Cu–C bond and a lone pair on the CF₃ ligand (Φ_ion). Two additional VB structures are important for product formation. Both of these “product” VB structures possess a lone-pair on Cu and describe either a covalent (Φ_rad) or ionic (Φ_nuc) C–C bond. A final VB structure describes a 3-centre-4-electron bond between a Cu-centred VB orbital and two C-centred VB orbitals (Φ_3c4e⁻).

Fig. 3 Dominate VB configurations at the transition state of 1 (isomerization 1^iso; elimination 1^re) and 2 (elimination). The red and blue colours indicate which electrons are spin-coupled while the arrows indicate covalent interactions.

Not surprisingly, only reactant-like VB structures contribute to 1^iso. In contrast, the reactant-like VB structures are minor contributors to the C–C elimination TS of 2 (Φ_ion = 5.1%; Φ_cov = 18.5%). Instead, Φ_3c4e⁻ (22.5%) and the product-like VB structures (Φ_rad = 36.3%; Φ_nuc = 17.4%) are the major contributors to Ψ_VB at the TS. Mechanistically, the two product like VB-structures of 2 represent contributions from different processes. The covalent-structure Φ_rad represents a C˙˙C radical coupling mechanism, while the ionic-structure Φ_nuc represents a :C⁻ nucleophilic attack on C⁺. Thus, we can describe the C–C elimination reaction promoted by 2 as an admixture of a radical coupling reaction and a Lewis acid/base reaction.

What is interesting is that the BOVB calculations strongly suggest that 1^re, which resembles a C–C elimination TS structure, will yield C₂F₆. Ψ_VB for 1^re is dominated by the Φ_3c4e⁻ (27.0%) and Φ_rad (49.4%) VB configurations. The key difference between the C–C elimination TS for 1^re and 2 is that the ionic product-like VB structure no longer contributes significantly to Ψ_VB at the C–C elimination TS for 1^re (Φ_nuc < 0.1%) owing to the difficulty of generating a trifluoromethyl carbocation. These VB results reinforce our supposition from above; electrostatic repulsion of the CF₃ fragments prevents 1 from achieving the appropriate geometry of a productive TS for concerted C₂F₆ elimination.

These findings highlight the features that promote productive bond-forming elimination processes from high-valent copper complexes. The key factor that must be overcome for bond formation is electrostatic—the atoms participating in bond-formation must exhibit attractive electrostatics. Consequently, C–C bond formation mediated by high-valent Cu species is expected to be limited to cases where C-donor ligand substitution differentiates charges of the participating atoms. This accords with the preponderance of C–N and C–O forming processes reported to be mediated by Cu.⁴

The authors thank the NIH (No. R15-GM141650-01 to JS) and NSF (CHE-1954515 to KML) for financial support.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. Lindley, Tetrahedron, 1984, 40, 1433–1456.
2. N. Yoshikai and E. Nakamura, Chem. Rev., 2012, 112, 2339–2372.
3. D. S. Surry and S. L. Buchwald, Chem. Sci., 2010, 1, 13–31.
4. A. Casitas and X. Ribas, Chem. Sci., 2013, 4, 2301–2318.
5. M. Paeth, S. B. Tyndall, L.-Y. Chen, J.-C. Hong, W. P. Carson, X. Liu, X. Sun, J. Liu, K. Yang, E. M. Hale, D. L. Tierney, B. Liu, Z. Cao, M.-J. Cheng, W. A. Goddard and W. Liu, J. Am. Chem. Soc., 2019, 141, 3153–3159.
6. S. Liu, H. Liu, S. Liu, Z. Lu, C. Lu, X. Leng, Y. Lan and Q. Shen, J. Am. Chem. Soc., 2020, 142, 9785–9791.
7. Z. Lu, H. Liu, S. Liu, X. Leng, Y. Lan and Q. Shen, Angew. Chem., Int. Ed., 2019, 58, 8510–8514.
8. A. M. Romine, N. Nebra, A. I. Konovalov, E. Martin, J. Benet-Buchholz and V. V. Grushin, Angew. Chem., Int. Ed., 2015, 54, 2745–2749.
9. D. Naumann, T. Roy, K.-F. Tebbe and W. Crump, Angew. Chem., Int. Ed. Engl., 1993, 32, 1482–1483.
10. I. M. DiMucci, J. T. Lukens, S. Chatterjee, K. M. Carsch, C. J. Titus, S. J. Lee, D. Nordlund, T. A. Betley, S. N. MacMillan and K. M. Lancaster, J. Am. Chem. Soc., 2019, 141, 18508–18520.
11. R. C. Walroth, J. T. Lukens, S. N. MacMillan, K. D. Finkelstein and K. M. Lancaster, J. Am. Chem. Soc., 2016, 138, 1922–1931.
12. J. P. Snyder, Angew. Chem., Int. Ed. Engl., 1995, 34, 986–987.
13. J. P. Snyder, Angew. Chem., Int. Ed. Engl., 1995, 34, 80–81.
14. C. Gao, G. Macetti and J. Overgaard, Inorg. Chem., 2019, 58, 2133–2139.
15. B. L. Geoghegan, Y. Liu, S. Peredkov, S. Dechert, F. Meyer, S. DeBeer and G. E. Cutsail, J. Am. Chem. Soc., 2022, 144, 2520–2534.
16. M. Kaupp and H. G. von Schnering, Angew. Chem., Int. Ed. Engl., 1995, 34, 986.
17. J. S. Steen, G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2019, 58, 13133–13139.
18. S. Shaik, D. Danovich, B. Silvi, D. L. Lauvergnat and P. C. Hiberty, Chem. – Eur. J., 2005, 11, 6358–6371.
19. S. Shaik, P. Maitre, G. Sini and P. C. Hiberty, J. Am. Chem. Soc., 1992, 114, 7861–7866.
20. Z. Chen, F. Ying, X. Chen, J. Song, P. Su, L. Song, Y. Mo, Q. Zhang and W. Wu, Int. J. Quantum Chem., 2015, 115, 731–737.
21. P. C. Hiberty and S. Shaik, Theor. Chem. Acc., 2002, 108, 255–272.
22. S. Shaik, D. Danovich, J. M. Galbraith, B. Braïda, W. Wu and P. C. Hiberty, Angew. Chem., Int. Ed., 2020, 59, 984–1001.
23. P. C. Hiberty, R. Ramozzi, L. Song, W. Wu and S. Shaik, Faraday Discuss., 2006, 135, 261–272.
24. S. Komiya, T. A. Albright, R. Hoffmann and J. K. Kochi, J. Am. Chem. Soc., 1976, 98, 7255–7265.

---

Footnotes

† Electronic supplementary information (ESI) available: Computational methods, plots of CCSD(T) and BOVB energies with fitted Morse potentials and parameters, and Cartesian coordinates of reactant and transition state structures. See DOI: https://doi.org/10.1039/d2cc05865k

‡ Additional active Cu/C VB-orbitals led to <5% reduction in the energy of Ψ_VB owing to additional resonance stabilization energy.

§ Expressed as Coulson–Chirgwin weights.

¶ Less charge separation is noted at the CCSD(T) level. See ESI.†

|| At the BOVB level the charges on linear F₃C–Cu–CF₃⁻ are Cu: +0.58e and C: +0.35e.

** Forcing a C–C bond leads to high energy defluorination reactions with subsequent perfluoro-ethene/ethyne formation.

†† Higher charge separation is noted at the BOVB level (F₃C^+0.8vs. H₃C^−0.5). Charge for Cu at the TS are −0.05e (CCSD(T))/+0.21e (BOVB) for 1^iso and +0.06e (CCSD(T))/+0.34e (BOVB) for 2.

---