Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Not antiaromaticity gain, but increased asynchronicity enhances the Diels–Alder reactivity of tropone†
Eveline H.
Tiekink
 ,
Pascal
Vermeeren
,
Pascal
Vermeeren
 * and
Trevor A.
Hamlin
* and
Trevor A.
Hamlin
 *
*
Department of Theoretical Chemistry, Amsterdam Institute of Molecfular and Life Sciences (AIMMS), Amsterdam Center for Multiscale Modeling (ACMM), Vrije Universiteit Amsterdam, De Boelelaan 1083, Amsterdam 1081 HV, The Netherlands. E-mail: p.vermeeren@vu.nl; t.a.hamlin@vu.nl
First published on 27th February 2023
Abstract
Tropone is an unreactive diene in normal electron demand Diels–Alder reactions, but it can be activated via carbonyl umpolung by using hydrazone ion analogs. Recently, the higher reactivity of hydrazone ion analogs was ascribed to a raised HOMO energy induced by antiaromaticity (L. J. Karas, A. T. Campbell, I. V. Alabugin and J. I. Wu, Org. Lett., 2020, 22, 7083). We show that this is incorrect, and that the activation barrier is lowered by increased asynchronicity.
The cycloaddition reactivity of tropone is well documented in literature, although its use as a diene in normal electron demand Diels–Alder reactions is rare.1 The low reactivity of tropone can be circumvented by reversing the polarity of the carbonyl group (umpolung), e.g., by converting tropone into its hydrazone analog. In 1985, Kajigaeshi et al. showed the synthetic power of tropone hydrazones in cycloaddition reactions.2 Recently, Karas et al. studied hydrazone analogs where the carbonyl oxygen of tropone was replaced by
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NNH2 (2-prot),
NNH2 (2-prot), ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NNHSO2CH3 (3-prot) and their anions (2 and 3, respectively, Scheme 1).3 They attributed the accelerated reactivity of the hydrazone analogs to their antiaromaticity, which destabilizes the HOMO and leads to a smaller, more favorable normal electron demand (NED) gap. This antiaromaticity-induced HOMO-raising strategy is frequently evoked in organic synthesis.4
NNHSO2CH3 (3-prot) and their anions (2 and 3, respectively, Scheme 1).3 They attributed the accelerated reactivity of the hydrazone analogs to their antiaromaticity, which destabilizes the HOMO and leads to a smaller, more favorable normal electron demand (NED) gap. This antiaromaticity-induced HOMO-raising strategy is frequently evoked in organic synthesis.4
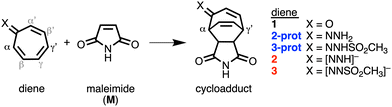 | ||
| Scheme 1 The studied Diels–Alder reaction between maleimide (M) and diene 1, 2-prot, 2, 3-prot, and 3. | ||
Herein, we confirm that HOMO-raising enhances the normal electron demand interaction, but simultaneously the LUMO-raising weakens the inverse electron demand (IED) interaction to the same extent. These two effects effectively cancel each other! Instead, we trace the accelerated reactivity of hydrazone analogs of tropone back to the increased asynchronicity of the Diels–Alder (DA) reaction mode. Similar conclusions were found by us and others when studying catalyzed DA reactions.5 In this work, we challenge the frequently used antiaromaticity-induced HOMO-raising rationale. We computationally studied the DA reaction between maleimide and tropone (1) and hydrazone analogs 2-prot, 2, 3-prot, and 3 (Scheme 1) using the activation strain model (ASM)6 with a matching energy decomposition analysis (EDA)7 and quantitative Kohn-Sham molecular orbital theory.8 All calculations were conducted using the Amsterdam Modeling Suite (AMS2021.104).9 Stationary points were optimized at ZORA-BP86-D3(BJ)/TZ2P.10 Activation strain6 and energy decomposition analyses7 were performed at ZORA-ωB97X-D/TZ2P11 using PyFrag 2019.12 See the ESI† for computational details.
First, we investigate the reaction profiles of the DA reactions between M and 1, 2-prot, 2, 3-prot, and 3, by inspecting the electronic activation energies of these reactions (Table 1). Our computed trend in electronic activation barriers is identical to the findings of Karas et al. (Table S1, ESI†).3,13 The activation barrier of the DA reaction with 1 is 24.3 kcal mol−1 and it increases when reacting to the weakly antiaromatic32-prot and 3-prot to 25.1 kcal mol−1 and 28.7 kcal mol−1, respectively. Interesting to see that dearomatizing tropone does not always lead to enhanced reactivity. Only upon deprotonation, the tropone hydrazones become more reactive and the activation barrier lowers to −4.8 kcal mol−1 and 9.4 kcal mol−1 for 2 and 3, respectively. We, therefore, solely focus on the enhanced reactivity of 2 and 3 compared to 1. Changing the diene also modifies the DA reaction mode as both 1 and 3 follow a concerted asynchronous reaction mode, whereas the DA reaction of 2 goes stepwise. For 1, although in one reaction step, the C–Cα bond at the α-position of 1 is formed ahead of the second C–Cγ′ bond at the γ′-position. However, for both 2 and 3, the C–Cγ′ bond forms ahead of the C–Cα bond. Insight into the differences in asynchronicity and order of bond formation are provided in the ESI.†
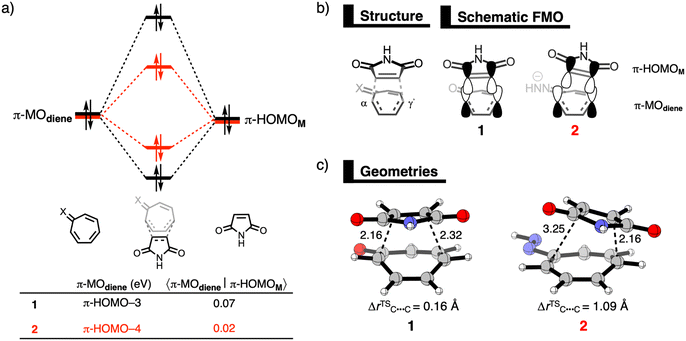
Next, the physical factors behind the enhanced reactivity of the DA reaction are elucidated using the activation strain model (ASM).6 The ASM analyzes the cost to deform the original reactants and their ability to interact by decomposing the electronic energy (ΔE) into the strain energy (ΔEstrain) and the interaction energy (ΔEint). We focus on explaining the origin of the lower activation barrier associated with the DA reaction of 2 compared to the DA reaction of 1. Table 2 shows the results from the activation strain analysis performed at consistent TS-like geometries where the shorter forming bond between M and the diene CM⋯Cdiene is 2.160 Å.14 The same conclusions emerge from the analysis along the entire reaction coordinate and of the DA reaction with 3 in comparison to 1 (Fig. S2–S5, ESI†). The accelerated reactivity of 2 compared to 1 originates from a combination of less destabilizing ΔEstrain, 33.0 kcal mol−1 for 1 to 21.2 kcal mol−1 for 2, and more stabilizing ΔEint, from −8.7 kcal mol−1 for 1 to −24.5 kcal mol−1 for 2 (Table 2). The lower ΔEstrain of the DA reaction of 2 compared to 1 is caused by the higher degree of asynchronicity of this reaction, that is, a larger difference between the newly forming C⋯C bond lengths. At a consistent geometry, the difference between the two newly forming C–C bonds are ΔrC⋯C = 0.16 Å for 1 and ΔrC⋯C = 1.09 Å for 2 (Fig. 1c). The more asynchronous the reaction, the lower the degree of deformation of the reactants in the saddle-point region of the reaction's PES since one C⋯C bond forms behind the other C⋯C bond, resulting in a less destabilizing ΔEstrain.15
| Diene | ΔE | ΔEstrain | ΔEint | ΔVelstat | ΔEPauli | ΔEoi |
|---|---|---|---|---|---|---|
| a Computed at consistent TS-like geometries (CM⋯Cdiene = 2.160 Å) at ZORA-ωB97X-D/TZ2P//ZORA-BP86-D3(BJ)/TZ2P. | ||||||
| 1 | 24.3 | 33.0 | −8.7 | −48.6 | 98.0 | −58.1 |
| 2 | −3.3 | 21.2 | −24.0 | −51.5 | 83.4 | −55.9 |
To understand why the ΔEint becomes more stabilizing on going from 1 to 2, we apply our energy decomposition analysis (EDA),7 which decomposes the ΔEint into four physically meaningful terms: the classical electrostatic interaction (ΔVelstat), the Pauli repulsion (ΔEPauli) arising from the repulsion between occupied closed-shell orbitals of both deformed reactants, the orbital interaction (ΔEoi) that accounts for charge transfer and polarization, and the dispersion energy (ΔEdisp). The EDA results reveal that a less destabilizing Pauli repulsion for 2 is the main cause for the more stabilizing interaction energy (ΔΔEPauli = 14.6 kcal mol−1), see Table 2. The orbital interactions of the DA reactions with 1 and 2 are very similar (ΔΔEoi = 2.2 kcal mol−1) which directly challenges the findings of Karas et al.3
Now, we explain why the DA reaction of 2 is accelerated by a less destabilizing Pauli repulsion and not by stronger orbital interactions because of the higher energy of the HOMO. First, we examine the origin of the less destabilizing Pauli repulsion for the DA reaction of 2 compared to 1 by performing a Kohn-Sham molecular orbital analysis.8 The key occupied π-orbitals of M, 1, and 2 are quantified at consistent TS-like geometries. The key occupied π-orbitals are the π-HOMOM of M, where the 2pz atomic orbitals (AOs) of the reactive carbon atoms are in-phase, and the π-MOdiene of the diene, where all 2pz AOs are in-phase. The destabilizing occupied–occupied orbital interaction, π-MOdiene–π-HOMOM, sets the trend in Pauli repulsion and the corresponding orbital overlap decreases from 0.07 for 1 to only 0.02 for 2 (Fig. 1a). The main origin of this decrease in orbital overlap is the difference in asynchronicity between these two reactions. As already mentioned, the DA reaction of 2 goes via a more asynchronous reaction mode than 1. As a result, M overlaps, due to the longer C⋯C bond, less at the Cα-atom of 2 than of 1, manifesting in less Pauli repulsion for the former (Fig. 1b).
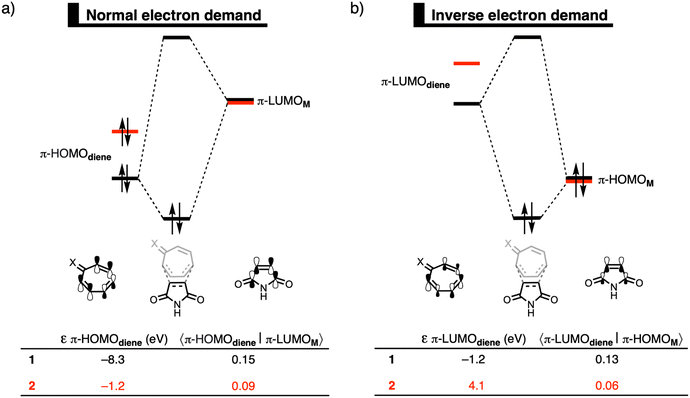
Finally, we explain why the orbital interactions for the DA reaction with 1 and 2 are very similar. This contradicts the rationale of Karas et al., who ascribe the lower activation barrier to a gain in antiaromaticity of the diene, which raises the HOMO energy.3Fig. 2 shows the molecular orbital diagrams of the DA reaction with 1 and 2. In line with the work of Karas et al., the normal electron demand (NED) interaction becomes more stabilizing from −29.3 kcal mol−1 for the DA reaction of 1 to −42.6 kcal mol−1 for the DA reaction of 2 (Table S2, ESI†),16 due to the destabilization of the HOMO from −8.3 eV for 1 to −1.2 eV for 2 (Fig. 2a). However, simultaneously, the inverse electron demand (IED) between the π-LUMO of the diene and π-HOMO of M is suppressed. The IED interaction was weakened from −23.0 kcal mol−1 for the DA reaction of 1 to −8.4 kcal mol−1 for 2.16 Going from 1 to 2 not only destabilizes the π-HOMO of the diene, but also the π-LUMO of the diene from −1.2 eV for 1 to 4.1 eV for 2 (Fig. 2b), causing the weakening of the IED interaction. Additionally, the orbital overlap decreases from 1 to 2 which originates from the increased asynchronicity (vide supra). Thus, the gain in NED interactions is effectively cancelled by the loss in IED interactions and the orbital interactions are similar for the DA reactions of 1 and 2. The HOMO-raising effect is, therefore, not the driving force behind DA reactions of tropone hydrazone ions. A correlation between the HOMO-raising effect and the accelerated reactivity can be observed, but this does not imply a causality. Thus, caution should be required in demonstrating causal relationships and hence detailed insight into the physical mechanism, as demonstrated in this work, is needed.
To conclude, conversion of tropone into a hydrazone ion analog via carbonyl umpolung leads to enhanced Diels–Alder reactivity. Recently, this enhanced reactivity was ascribed to the antiaromatic character of the hydrazone ion analogs, raising the energy of the HOMO.3 We challenge this frequently used antiaromaticity-induced HOMO-raising rationale and propose that the increased reactivity is not caused by enhanced orbital interactions, but instead by an amplified asynchronicity of the reaction mode resulting in (i) less destabilizing strain and (ii) a diminished destabilizing Pauli repulsion between the reactants.
Conflicts of interest
There are no conflicts to declare.Notes and references
- (a) V. Nair and K. G. Abhilash, Synlett, 2008, 301 CrossRef CAS; (b) S. Frankowski, M. Romaniszyn, A. Skryńska and Ł. Albrecht, Chem. – Eur. J., 2020, 26, 2120 CrossRef CAS PubMed.
- S. Kajigaeshi, S. Matsuoka, S. Kanemasa and M. Noguchi, J. Heterocycl. Chem., 1986, 23, 49 CrossRef CAS.
- L. J. Karas, A. T. Campbell, I. V. Alabugin and J. I. Wu, Org. Lett., 2020, 22, 7083 CrossRef CAS.
- (a) S.-L. You, Asymmetric Dearomatization React., Wiley-VCH, 2016 CrossRef; (b) C. Zheng and S.-L. You, ACS Cent. Sci., 2021, 7, 432 CrossRef CAS; (c) X. Song, Z.-C. Chen, W. Du and Y.-C. Chen, in Asymmetric Organocatalysis: New Strategies, Catalysts, and Opportunities, ed. Ł. Albrecht and A. Albrecht, L. Dell’Amico, Wiley-VCH, Weinheim, 2023, 16, pp. 539–575 Search PubMed.
- (a) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201 CrossRef CAS PubMed; (b) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Chem. Sci., 2020, 11, 8105 RSC; (c) P. Vermeeren, F. Brinkhuis, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Asian J., 2020, 15, 1167 CrossRef CAS PubMed; (d) P. Vermeeren, M. D. Tiezza, M. van Dongen, I. Fernández, F. M. Bickelhaupt and T. A. Hamlin, Chem. – Eur. J., 2021, 27(41), 10610 CrossRef CAS; (e) S. Yu, F. M. Bickelhaupt and T. A. Hamlin, ChemistryOpen, 2021, 10, 784 CrossRef CAS; (f) S. Portela, J. J. Cabrera-Trujillo and I. Fernández, J. Org. Chem., 2021, 86, 5317 CrossRef CAS PubMed; (g) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2022, 28, e202200987 CAS; (h) S. Portela and I. Fernández, Chem. – Asian J., 2022, e202201214 Search PubMed; (i) S. Portela and I. Fernández, Tetrahedron Chem., 2022, 1, 100008 CrossRef.
- (a) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187 CrossRef CAS; (b) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef CAS; (c) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649 CrossRef CAS PubMed; (d) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880 RSC.
- (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, 1, pp. 1–86 Search PubMed; (b) T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analysis, ed. S. Grabowsky, De Gruyter, Berlin, 2021, 8, pp. 199–212 Search PubMed.
- R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432 CrossRef CAS PubMed.
- (a) R. Rüger, M. Franchini, T. Trnka, A. Yakovlev, E. van Lenthe, P. Philipsen, T. van Vuren, B. Klumpers and T. Soini, AMS2021.104, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, 2021; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed; (c) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS; (b) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (c) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed; (d) E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed; (e) E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS; (f) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (g) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS; (h) E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943 CrossRef CAS; (i) P. Vermeeren, M. Dalla Tiezza, M. E. Wolf, M. E. Lahm, W. D. Allen, H. F. Schaefer, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2022, 24, 18028 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- (a) X. Sun, T. M. Soini, J. Poater, T. A. Hamlin and F. M. Bickelhaupt, J. Comput. Chem., 2019, 40, 2227 CrossRef CAS PubMed; (b) X. Sun, T. Soini, L. P. Wolters, W.-J. van Zeist, C. Fonseca Guerra, T. A. Hamlin and F. M. Bickelhaupt, PyFrag 2019, Vrije Universiteit, Amsterdam, 2019 Search PubMed.
- The computed trend in electronic activation barriers is identical to the trend in Gibbs free activation barriers, see Table S1 (ESI).
- Performing this analysis at a consistent point along the reaction coordinate (close to the transition state structures), rather than on the individual transition state structures, assures that the analyses are not skewed by the location of the transition state, see the following reference: T. A. Hamlin, D. Svatunek, S. Yu, L. Ridder, I. Infante, L. Visscher and F. M. Bickelhaupt, Eur. J. Org. Chem., 2019, 378 CrossRef CAS.
- P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2021, 23, 20095 RSC.
- The strength of the normal electron demand (NED) interactions is obtained by performing EDA computations while artificially deleting the virtual orbitals of the diene. Whereas the strength of the inverse electron demand (IED) interactions is obtained by performing EDA computations while artificially deleting the virtual orbitals of M.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational results; computational details; Cartesian coordinates, energies, and the number of imaginary frequencies of all stationary points. See DOI: https://doi.org/10.1039/d3cc00512g |
| This journal is © The Royal Society of Chemistry 2023 |